Observer-Based Exponential Stabilization for Time Delay Takagi–Sugeno–Lipschitz Models

Abstract

This paper addresses the problem of observer-based control (OBC) for nonlinear systems with time delay (TD). A novel hybrid modeling framework for nonlinear TD systems is first introduced by synergistically combining TD Takagi–Sugeno (TDTS) fuzzy and Lipschitz approaches. The proposed methodology broadens the range of representable systems by enabling Lipschitz nonlinearities to fulfill dual functions: they may describe essential dynamic behaviors of the system or represent aggregated uncertainties, depending on the specific application. The proposed TDTS–Lipschitz (TDTSL) model class features measurable premise variables while accommodating Lipschitz nonlinearities that may depend on unmeasurable system states. Then, through the construction of an appropriate Lyapunov–Krasovskii (L-K) functional, we derive sufficient conditions to ensure exponential stability of the augmented closed-loop model. Subsequently, through a decoupling methodology, these stability conditions are reformulated as a set of linear matrix inequalities (LMIs). Finally, the proposed OBC design is validated through application to a continuous stirred tank reactor (CSTR) with lumped uncertainties.

1. Introduction

Most real-world systems we encounter daily are fundamentally nonlinear, often displaying unusual characteristics and behaviors that differ from idealized linear models. On one hand, some researchers have increasingly focused on Takagi–Sugeno (TS) fuzzy model [1] as a framework for representing nonlinearities in real-world systems. Notably, the TS fuzzy paradigm provides a computationally efficient and theoretically sound approach to nonlinear function approximation. Consequently, diverse control-theoretic problems for systems represented by TS fuzzy models has been extensively investigated in the literature, e.g., output stabilization [2], robust control [3], reliable control [4], estimation of faults and design of fault-tolerant control [5,6], Observer-Based Control (OBC) [7,8].

On the other hand, certain researchers have focused on modeling the nonlinear features of practical systems using Lipschitz-based approaches, which simplify stability analysis and control design through straightforward bounding conditions. The OBC problem is one of the most widely studied control problems for systems modeled using Lipschitz-based approaches. For instance, reference [9] investigates the OBC problem for Lipschitz nonlinear systems subject to parametric uncertainties and exogenous disturbances bounded in the ${\mathcal{L}}_2$ norm. This problem for one-sided Lipschitz nonlinear systems is examined in [10]. The main drawback of these works is that the design procedure is carried out in two separate steps: first, the observer design, followed by the controller design. This limitation was overcome in [11] for Lipschitz nonlinear models and in [12] for one-sided Lipschitz nonlinear models by designing the observer-based controller in a single step through the adoption of a decoupling technique.

In addition to the nonlinear dynamics present in most real-world systems, time delay (TD) frequently arises in practical applications. Moreover, even in systems that are nominally delay-free, TD can emerge as perturbations, particularly when physical separation exists between sensors and actuators. Similar to its use in general nonlinear systems, the TS fuzzy model was first employed in 2000 [13] to address nonlinear systems with TD, providing an effective framework for stability analysis and control design. Hitherto, diverse analysis and control problems have been investigated for nonlinear systems represented by TD Takagi–Sugeno (TDTS) fuzzy models. For instance, reference [14] develops a robust control. The work in [15] stands out by addressing the filtering problem via an input–output approach. A novel state-feedback control synthesis for TDTS fuzzy models with nonlinear consequents and concurrent state/input delays has been developed in [16].

Not only has the TS fuzzy model been advanced to address nonlinear systems with delayed dynamics, but models characterized by Lipschitz nonlinearities have also been adapted for such systems. To review pertinent research, ref. [17] derives a separation principle for the design of an OBC for nonlinear TD systems satisfying the quasi–one-sided Lipschitz condition. To review pertinent research, the problem of OBC for nonlinear TD systems satisfying the quasi–one-sided Lipschitz condition is investigated in [17] by applying the separation principle, in [18,19] by using reduced-order OBC, and in [20] by using a decoupling approach while taking into account input saturation.

To date, the framework proposed in [21] remains the only systematic approach that unifies TS fuzzy modeling with Lipschitz continuity theory, establishing a new class of hybrid models that significantly expands the representational capacity for complex nonlinear systems. For this class of models, Lipschitz nonlinearities are capable of representing not only part of the nonlinear dynamics, as commonly noted in the literature, but also lumped uncertainties, provided these uncertainties satisfy a Lipschitz condition. Yet, the integration of TS fuzzy and Lipschitz nonlinear modeling for delayed nonlinear systems remains unexplored, posing an open challenge. In this work, this challenge is addressed by using an appropriate L-K functional together with a suitable matrix decoupling technique to derive LMI-based conditions. Furthermore, it is observed that all existing results for Lipschitz nonlinear models focus exclusively on asymptotic stabilization. Building upon these observations, this work investigates the OBC design problem for TDTS–Lipschitz (TDTSL) models, with guaranteed $\mu$–exponentially stability. The key contribution of this work lies in its consideration of a more general model, which, unlike previous studies, simultaneously accounts for both TDTS fuzzy and Lipschitz nonlinear modeling. Furthermore, this work prioritizes exponential stabilization over mere asymptotic stabilization, as it not only ensures system stability but also guarantees a faster convergence rate.

The rest of the paper is structured as follows. Section 2 outlines the problem statement, while Section 3 details the main theoretical contributions. Section 4 provides an application to a Continuous Stirred Tank Reactor (CSTR) with lumped uncertainties, and Section 5 concludes the paper with final remarks.

2. Problem Statement

Notation 1.

In this paper, we adopt the following notations: ${\mathbb{R}}_{\ge 0}$ and ${\mathbb{R}}_{>0}$ represent, in order, the sets of nonnegative real numbers and positive real numbers; We denote as ${ϵ}_t\in \mathcal{C}\left(\left[\begin{array}{cc}-\delta & 0\end{array}\right],{\mathbb{R}}^{\varsigma }\right)$ the history segment of ϵ, defined by ${ϵ}_t:=\{ϵ(t+\varpi ),\varpi \in \left[\begin{array}{cc}-\delta & 0\end{array}\right]\}$, where $\mathcal{C}\left(\left[\begin{array}{cc}-\delta & 0\end{array}\right],{\mathbb{R}}^{\varsigma }\right)$ is the space of continuous functions mapping the interval $\left[\begin{array}{cc}-\delta & 0\end{array}\right]$ into ${\mathbb{R}}^{\varsigma }$; $\parallel .\parallel$ denotes the Euclidean norm, given $i\in \mathbb{N}$, ${\mathcal{I}}_i:=\{1,\dots ,i\}$. The symbol ∗ denotes the term required to complete the symmetry of a symmetric matrix; given $n\in \mathbb{N}$, for an $n\times n$ matrix, Q, ${\lambda }_{min}\left(Q\right)\left({\lambda }_{max}\left(Q\right)\right)$ represents the smallest (largest) eigenvalue, $Q\in {\mathbb{S}}^{n\times n}$ means that Q is a symmetric matrix, and $Q>0$ indicates that Q is positive definite. For a matrix, R, ${\left\{R\right\}}_{†}=R+R^T$.

Throughout the paper, $(m,n)\in {\mathcal{I}}_i$ and $l\in {\mathcal{I}}_r$.

Our study focuses on a nonlinear TD system expressible through the following TDTSL model incorporating i plant rules:

Plant Rule m: If $p_1\left(t\right)$ is $P_{m1}$ and ⋯ and $p_r\left(t\right)$ is $P_{mr}$ then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\xi }\left(t\right)={\varphi }_m\xi \left(t\right)+{\phi }_m\xi (t-\delta )+B_m\iota \left(t\right)+f\left(\xi \left(t\right)\right),\hfill \\ \sigma \left(t\right)={\theta }_m\xi \left(t\right)+{\vartheta }_m\xi (t-\delta ),\hfill \\ \xi \left(t\right)=h\left(t\right),t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(1)

where $p_l$, $P_{ml}$, $\xi \left(t\right)\in {\mathbb{R}}^{{\varsigma }_1}$, $\iota \left(t\right)\in {\mathbb{R}}^{{\varsigma }_2}$, $\sigma \left(t\right)\in {\mathbb{R}}^{{\varsigma }_3}$, $\delta \in {\mathbb{R}}_{>0}$ denote, in order, the r premise variables, their corresponding fuzzy sets, the state vector, control input vector, measured output vector, and TD. $h\left(t\right)\in \mathcal{C}\left(\left[\begin{array}{cc}-\delta & 0\end{array}\right],{\mathbb{R}}^{{\varsigma }_1}\right)$ is a continuous vector-valued function defining the initial conditions on the interval $\left[\begin{array}{cc}-\delta & 0\end{array}\right]$. ${\varphi }_m$, ${\phi }_m$, $B_m$, ${\theta }_m$, and ${\vartheta }_m$ are the state-space matrices. $f\left(\xi \right(t)$ denotes a nonlinear vector-valued function modeling either the nonlinear dynamics or the lumped state-dependent uncertainties.

Consider the following assumptions:

Assumption 1.

The TDTSL (41) is controllable and observable.

Assumption 2.

The vector $\mathrm{p}\left(t\right)=\left[\begin{array}{ccc}{\mathrm{p}}_1\left(t\right)& \cdots & {\mathrm{p}}_r\left(t\right)\end{array}\right]$ is measurable.

Assumption 3.

$f\left(\xi \right(t\left)\right)$ satisfies the following Lipschitz condition

$$\begin{array}{c}\hfill \parallel f\left({\xi }_1\left(t\right)\right)-f\left({\xi }_2\left(t\right)\right)\parallel \le \ell \parallel {\xi }_1\left(t\right)-{\xi }_2\left(t\right)\parallel ,\forall ({\xi }_1\left(t\right),{\xi }_2\left(t\right))\in {\mathbb{R}}^{{\varsigma }_1},\end{array}$$

(2)

where $f\left(0\right)=0$.

Remark 1.

The class of TDTSL considered in this paper is more general than conventional TS fuzzy models. It can represent both nonlinearities approximated by TS fuzzy rules and nonlinearities expressed directly as Lipschitz functions, including Lipschitz-type uncertainties. This generality allows each class of nonlinearities to be analyzed separately and highlights the broader applicability of the proposed framework compared to existing approaches.

The global TDTSL fuzzy model is as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\xi }\left(t\right)={\displaystyle \sum _{m=1}^i}{\rho }_m\left(p\left(t\right)\right)[{\varphi }_m\xi \left(t\right)+{\phi }_m\xi (t-\delta )+B_m\iota \left(t\right)]+f\left(\xi \left(t\right)\right),\hfill \\ \sigma \left(t\right)={\displaystyle \sum _{m=1}^i}{\rho }_m\left(p\left(t\right)\right)[{\theta }_m\xi \left(t\right)+{\vartheta }_m\xi (t-\delta )],\hfill \\ \xi \left(t\right)=h\left(t\right),t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(3)

where

$$\begin{array}{ccc}\hfill {\rho }_m\left(p\left(t\right)\right)& =& \frac{{\prod }_{l=1}^r{P}_{ml}\left(p\left(t\right)\right)}{{\displaystyle \sum _{m=1}^i}{\displaystyle \prod _{l=1}^r}{P}_{ml}\left(p\left(t\right)\right)}.\hfill \end{array}$$

Evidently,

$$\begin{array}{c}\hfill {\rho }_m\left(p\left(t\right)\right)\ge 0,\sum _{m=1}^i{\rho }_m\left(p\left(t\right)\right)=1.\end{array}$$

(4)

In accordance with Assumptions 1 and 2, we consider the following OBC with initial conditions $\widehat{h}\left(t\right)$:

OBC Rule: If $p_1\left(t\right)$ is $P_{m1}$ and ⋯ and $p_r\left(t\right)$ is $P_{mr}$ then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\widehat{\xi }}\left(t\right)={\varphi }_m\widehat{\xi }\left(t\right)+{\phi }_m\widehat{\xi }(t-\delta )+B_m\iota \left(t\right)+f\left(\widehat{\xi }\left(t\right)\right)+Q_m(\sigma \left(t\right)-\widehat{\sigma }\left(t\right)),\hfill \\ \widehat{\sigma }\left(t\right)={\theta }_m\widehat{\xi }\left(t\right)+{\vartheta }_m\widehat{\xi }(t-\delta ),\hfill \\ \iota \left(t\right)=R_m\widehat{\xi }\left(t\right),\hfill \\ \widehat{\xi }\left(t\right)=\widehat{h}\left(t\right),t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(5)

where $\widehat{\xi }\left(t\right)$ and $\widehat{\sigma }\left(t\right)$ are in order, the estimates of the state and output. $Q_m$ and $R_m$ are the observer gain matrices to be computed.

The global OBC is as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\widehat{\xi }}\left(t\right)={\displaystyle \sum _{m=1}^i}{\rho }_m\left(p\left(t\right)\right)[{\varphi }_m\widehat{\xi }\left(t\right)+{\phi }_m\widehat{\xi }(t-\delta )+B_m\iota \left(t\right)+f\left(\widehat{\xi }\left(t\right)\right)+Q_m(\sigma \left(t\right)-\widehat{\sigma }\left(t\right))],\hfill \\ \widehat{\sigma }\left(t\right)={\displaystyle \sum _{m=1}^i}{\rho }_m\left(p\left(t\right)\right)[{\theta }_m\widehat{\xi }\left(t\right)+{\vartheta }_m\widehat{\xi }(t-\delta )],\hfill \\ \iota \left(t\right)={\displaystyle \sum _{m=1}^i}{\rho }_m\left(p\left(t\right)\right)R_m\widehat{\xi }\left(t\right),\hfill \\ \widehat{\xi }\left(t\right)=\widehat{h}\left(t\right),t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(6)

Under Assumption 2, the augmented model is defined as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{ϵ}\left(t\right)={\displaystyle \sum _{m=1}^i}{\displaystyle \sum _{n=1}^i}{\rho }_m\left(p\left(t\right)\right){\rho }_n\left(p\left(t\right)\right)[{\Psi }_{mn}ϵ\left(t\right)+{\Phi }_{mn}ϵ(t-\delta )+L(\xi \left(t\right),\widehat{\xi }\left(t\right))],\hfill \\ ϵ\left(t\right)=H\left(t\right),t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(7)

where

$$\begin{array}{ccc}\hfill ϵ\left(t\right)& =& \left[\begin{array}{c}\xi \left(t\right)\\ \xi \left(t\right)-\widehat{\xi }\left(t\right)\end{array}\right],{\Psi }_{mn}=\left[\begin{array}{cc}{\varphi }_m+B_m{R}_n& -B_m{R}_n\\ 0& {\varphi }_m-Q_m{\theta }_n\end{array}\right],\hfill \\ \hfill {\Phi }_{mn}& =& \left[\begin{array}{cc}{\phi }_m& 0\\ 0& {\phi }_m-Q_m{\vartheta }_n\end{array}\right],L(\xi \left(t\right),\widehat{\xi }\left(t\right))=\left[\begin{array}{c}f\left(\xi \right(t\left)\right)\\ f\left(\xi \left(t\right)\right)-f\left(\widehat{\xi }\left(t\right)\right)\end{array}\right],H\left(t\right)=\left[\begin{array}{c}h\left(t\right)\\ h\left(t\right)-\widehat{h}\left(t\right)\end{array}\right].\hfill \end{array}$$

Definition 1.

For the given $\mu \in {\mathbb{R}}_{>0}$, the equilibrium point at zero for system (7) is called μ-Exponential ($\mu -$E) stable if $\exists \alpha \in {\mathbb{R}}_{>0}$, ensuring that all trajectories $ϵ\left(t\right)$ decay exponentially with rate μ and satisfying

$$\parallel ϵ(t,H)\parallel \le \alpha e^{-\mu t}{\parallel H\parallel }_S,\forall t\in {\mathbb{R}}_{\ge 0}.$$

(8)

where ${\parallel H\parallel }_S=su{p}_{\varpi \in \left[\begin{array}{cc}-\delta & 0\end{array}\right]}\parallel H\left(\varpi \right)\parallel$.

Lemma 1

([22]). For matrices $\Omega$, $\mathcal{Y}$, $\mathcal{Z}$, and $\mathcal{X}$ of compatible dimensions and a scalar $\mathrm{q}$, if the following condition is satisfied:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\Omega & \mathrm{q}\mathcal{Y}+{\mathcal{Z}}^T{\mathcal{X}}^T\\ \ast & -\mathrm{q}\left({\left\{\mathcal{X}\right\}}_{†}\right)\end{array}\right]<0,\end{array}$$

(9)

then,

$$\begin{array}{c}\hfill \Omega +{\left\{\mathcal{Y}\mathcal{Z}\right\}}_{†}<0.\end{array}$$

(10)

We aim to design the OBC in (6) to guarantee the $\mu$-E stability of the system (7).

In the remainder of the paper, for brevity and clarity, ${\rho }_m\left(p\left(t\right)\right)$ is denoted as ${\rho }_m$; t is omitted in delay-free terms such as $\xi \left(t\right)$, and is kept only in delayed terms such as $\xi (t-\delta )$.

3. Main Results

This section derives OBC design conditions to ensure $\mu$-E stability of the augmented system (7).

Theorem 1.

For a given $\mu \in {\mathbb{R}}_{>0}$, system (7) is μ-E stable at the origin if there are $\tau \in \mathbb{R}$, $(\mathcal{V},\mathcal{W})\in {\mathbb{S}}^{2{\varsigma }_1\times 2{\varsigma }_1}$, such that:

$$\begin{array}{ccc}\hfill & & \tau >0,\mathcal{V}>0,\mathcal{W}>0,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & & {\mathrm{Y}}_{mm}<0,\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill & & {\mathrm{Y}}_{mn}+{\mathrm{Y}}_{nm}<0,m<n,\hfill \end{array}$$

(13)

where

$$\begin{array}{c}\hfill {\mathrm{Y}}_{mn}=\left[\begin{array}{ccc}{\{\mathcal{V}{\Psi }_{mn}+\mu \mathcal{V}\}}_{†}+\mathcal{W}+\tau {\ell }^{2}I& \mathcal{V}{\Phi }_{mn}& \mathcal{V}\\ \ast & -e^{-2\mu \delta }\mathcal{W}& 0\\ \ast & \ast & -\tau I\end{array}\right].\end{array}$$

Furthermore, the solution $ϵ(t,H)$ to the system fulfills

$$\begin{array}{c}\hfill \parallel ϵ(t,H)\parallel \le \sqrt{\frac{\overline{\lambda }}{\underline{\lambda }}}{e}^{-\mu t}{\parallel H\parallel }_S,\end{array}$$

(14)

where

$$\begin{array}{ccc}\hfill \underline{\lambda }& =& {\lambda }_{min}\left(\mathcal{V}\right),\overline{\lambda }={\lambda }_{max}\left(\mathcal{V}\right)+\delta {\lambda }_{max}\left(\mathcal{W}\right).\hfill \end{array}$$

Proof. 

The L-K functional can be selected as

$$\begin{array}{c}\hfill \Gamma \left({ϵ}_t\right)={\Gamma }_1+{\Gamma }_2,\end{array}$$

(15)

where

$$\begin{array}{ccc}\hfill {\Gamma }_1& =& {ϵ}^T\mathcal{V}ϵ,{\Gamma }_2={\int }_t^{t+\delta }{e}^{2\mu (z-t-\delta )}{ϵ}^T(z-\delta )\mathcal{W}ϵ(z-\delta )dz.\hfill \end{array}$$

(16)

Clearly,

$$\begin{array}{c}\hfill \underline{\lambda }{\parallel ϵ\left(t\right)\parallel }^2\le \Gamma \left({ϵ}_t\right)\le \overline{\lambda }{\parallel {ϵ}_t\parallel }_S^2.\end{array}$$

(17)

Consequently, we obtain

$$\begin{array}{ccc}\hfill {\dot{\Gamma }}_1& =& 2{ϵ}^T\mathcal{V}\dot{ϵ}=2{ϵ}^T\mathcal{V}\left(\sum _{i=1}^n\sum _{j=1}^n{\rho }_m{\rho }_n\{{\Psi }_{mn}ϵ+{\Phi }_{mn}ϵ(t-\delta )\}+L(\xi ,\widehat{\xi })\right),\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\dot{\Gamma }}_2& =& {ϵ}^T\mathcal{W}ϵ-e^{-2\mu \delta }{ϵ}^T(t-\delta )\mathcal{W}ϵ(t-\delta )-2\mu {\Gamma }_2.\hfill \end{array}$$

(19)

Let

$$\begin{array}{c}\hfill J({ϵ}_t,L(\xi ,\widehat{\xi }))=\dot{\Gamma }\left({ϵ}_t\right)+2\mu \Gamma \left({ϵ}_t\right)-\tau (\parallel L(\xi ,\widehat{\xi }){\parallel }^2-{\ell }^2{\parallel ϵ\parallel }^2).\end{array}$$

(20)

Using (18) and (19), we obtain, for any $\tau \in {\mathbb{R}}_{>0}$:

$$\begin{array}{c}\hfill J({ϵ}_t,L(\xi ,\widehat{\xi }))\le \sum _{m=1}^i\sum _{n=1}^i{\rho }_m{\rho }_n{\widetilde{ϵ}}^T{\mathrm{Y}}_{mn}\widetilde{ϵ}=\sum _{m=1}^i{\rho }_m^2{\widetilde{ϵ}}^T{\mathrm{Y}}_{mm}\widetilde{ϵ}+\sum _{m=1}^i\sum _{m<n}^i{\rho }_m{\rho }_n{\widetilde{ϵ}}^T({\mathrm{Y}}_{mn}+{\mathrm{Y}}_{nm})\widetilde{ϵ},\end{array}$$

(21)

where $\widetilde{ϵ}=\left[\begin{array}{c}ϵ\\ ϵ(t-\delta )\\ L(\xi ,\widehat{\xi })\end{array}\right].$

Considering (4), one can deduce from conditions (12) and (13) that

$$\begin{array}{c}\hfill J({ϵ}_t,L(\xi ,\widehat{\xi }))<0.\end{array}$$

(22)

Following Assumption 3, we establish

$$\begin{array}{c}\hfill \tau (\parallel L(\xi ,\widehat{\xi }){\parallel }^2-{\ell }^2\parallel ϵ{\parallel }^2)\le 0.\end{array}$$

(23)

From (22) and (23), we obtain

$$\begin{array}{ccc}\hfill \dot{\Gamma }\left({ϵ}_t\right)& \le & -2\mu \Gamma \left({ϵ}_t\right),\hfill \end{array}$$

(24)

which yields

$$\begin{array}{c}\hfill \Gamma \left({ϵ}_t\right)\le \Gamma \left(H\right)e^{-2\mu t}.\end{array}$$

(25)

It follows from (17) and (25) that (14) holds. □

Remark 2.

We note that the conditions presented in Theorem 1 are not LMIs and, therefore, cannot be directly solved using standard convex optimization tools. In the next theorem, these conditions are transformed into LMIs by employing an appropriate decoupling technique, which allows them to be efficiently solved using the LMI toolbox.

Theorem 2.

For given $(\mu ,q)\in {\mathbb{R}}_{>0}$, if there exist $\tau \in \mathbb{R}$, $({\mathcal{V}}_j,{\mathcal{W}}_j)\in {\mathbb{S}}^{{\varsigma }_1\times {\varsigma }_1}$ for $j\in {\mathcal{I}}_2$, ${\tilde{R}}_n\in {\mathbb{R}}^{{\varsigma }_2\times {\varsigma }_1}$, ${\tilde{Q}}_m\in {\mathbb{R}}^{{\varsigma }_1\times {\varsigma }_3}$, $\tilde{\mathcal{K}}\in {\mathbb{R}}^{{\varsigma }_2\times {\varsigma }_2}$ under which the following LMIs are satisfied:

$$\begin{array}{ccc}\hfill & & \tau >0,{\mathcal{V}}_j>0,{\mathcal{W}}_j>0,\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill & & {\mathbb{G}}_{mm}<0,\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill & & {\mathbb{G}}_{mn}+{\mathbb{G}}_{nm}<0,m<n,\hfill \end{array}$$

(28)

with

$$\begin{array}{c}\hfill {\mathbb{G}}_{mn}=\left[\begin{array}{cc}{\Omega }_{mn}& {\tilde{\mathcal{Y}}}_{mn}\\ \ast & -{\left\{\tilde{\mathcal{K}}\right\}}_{†}\end{array}\right],\end{array}$$

(29)

where

$$\begin{array}{ccc}\hfill {\Omega }_{mn}& =& \left[\begin{array}{cccccc}{\Omega }_{mn}(1,1)& -B_m{\tilde{\mathrm{R}}}_n& {\mathcal{V}}_1{\phi }_m& 0& {\mathcal{V}}_1& 0\\ \ast & {\Omega }_{mn}(2,2)& 0& {\Omega }_{mn}(2,4)& 0& {\mathcal{V}}_2\\ \ast & \ast & -e^{-2\mu \delta }{\mathcal{W}}_1& 0& 0& 0\\ \ast & \ast & \ast & -e^{-2\mu \delta }{\mathcal{W}}_2& 0& 0\\ \ast & \ast & \ast & \ast & -\tau I& 0\\ \ast & \ast & \ast & \ast & \ast & -\tau I\end{array}\right],{\tilde{\mathcal{Y}}}_{mn}=\left[\begin{array}{c}{\tilde{\mathcal{Y}}}_{mn}\left(1\right)\\ -{\tilde{\mathrm{R}}}_n^T\\ 0\\ 0\\ 0\\ 0\end{array}\right],\hfill \end{array}$$

in which

$$\begin{array}{ccc}\hfill {\Omega }_{mn}(1,1)& =& {\{{\mathcal{V}}_1{\varphi }_m+B_m{\tilde{\mathrm{R}}}_n+\mu {\mathcal{V}}_1\}}_{†}+{\mathcal{W}}_1+\tau {\ell }^{2}I,\hfill \\ \hfill {\Omega }_{mn}(2,2)& =& {\{{\mathcal{V}}_2{\varphi }_m-{\tilde{\mathrm{Q}}}_m{\theta }_n+\mu {\mathcal{V}}_2\}}_{†}+{\mathcal{W}}_2+\tau {\ell }^{2}I,\hfill \\ \hfill {\Omega }_{mn}(2,4)& =& {\mathcal{V}}_2{\varphi }_m-{\tilde{\mathrm{Q}}}_m{\vartheta }_n,\hfill \\ \hfill {\tilde{\mathcal{Y}}}_m\left(1\right)& =& \mathrm{Q}{\mathcal{V}}_1{B}_m-B_m\tilde{\mathcal{K}}+{\tilde{\mathrm{R}}}_n^T,\hfill \end{array}$$

then, conditions (11)–(13) of Theorem 1 hold for

$$\begin{array}{ccc}\hfill \mathcal{V}& =& \left[\begin{array}{cc}{\mathcal{V}}_1& 0\\ 0& {\mathcal{V}}_2\end{array}\right],\mathcal{W}=\left[\begin{array}{cc}{\mathcal{W}}_1& 0\\ 0& {\mathcal{W}}_2\end{array}\right],\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\mathrm{R}}_n& =& {\mathcal{X}}^{-1}{\tilde{\mathrm{R}}}_n,{\mathrm{Q}}_m={\mathcal{V}}_2^{-1}{\tilde{\mathrm{Q}}}_m,\hfill \end{array}$$

(31)

with

$$\begin{array}{c}\hfill \mathcal{X}=\frac{1}{q}\tilde{\mathcal{K}}.\end{array}$$

(32)

Proof. 

Under conditions (27), we have $-{\left\{\tilde{\mathcal{K}}\right\}}_{†}<0$, which implies that $\mathcal{X}$ is nonsingular. ${\tilde{\mathcal{Y}}}_{mn}$ can be expressed as

$$\begin{array}{c}\hfill {\tilde{\mathcal{Y}}}_{mn}=q{\mathcal{Y}}_m+{\mathcal{Z}}_n^T{\mathcal{X}}^T,\end{array}$$

(33)

where

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_m=\left[\begin{array}{c}{\mathcal{Y}}_m\left(1\right)\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right],{\mathcal{Z}}_n& =& {\mathcal{X}}^{-1}\left[\begin{array}{cccccc}{\tilde{\mathrm{R}}}_n& -{\tilde{\mathrm{R}}}_n& 0& 0& 0& 0\end{array}\right],\hfill \end{array}$$

(34)

in which ${\mathcal{Y}}_m\left(1\right)={\mathcal{V}}_1{B}_m-B_m\mathcal{X}$.

Then, ${\mathbb{G}}_{mn}$ can be represented as

$$\begin{array}{c}\hfill {\mathbb{G}}_{mn}=\left[\begin{array}{cc}{\Omega }_{mn}& \mathrm{Q}{\mathcal{Y}}_m+{\mathcal{Z}}_n^T{\mathcal{X}}^T\\ \ast & -\mathrm{Q}\left({\left\{\mathcal{X}\right\}}_{†}\right)\end{array}\right].\end{array}$$

(35)

Using Lemma 1, we deduce from conditions (27) and (28) that

$$\begin{array}{ccc}\hfill & & {\Xi }_{mm}<0,\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill & & {\Xi }_{mn}+{\Xi }_{nm}<0,m<n,\hfill \end{array}$$

(37)

where ${\Xi }_{mn}={\Omega }_{mn}+{\left\{{\mathcal{Y}}_m{\mathcal{Z}}_n\right\}}_{†}$.

It is straightforward that ${\Xi }_{mn}={\mathrm{Y}}_{mn}$ for $\mathcal{V}$, $\mathcal{W}$, ${\mathrm{R}}_n$ and ${\mathrm{Q}}_n$ in the form of (30) and (31). □

Remark 3.

The TDTSL provides greater modeling flexibility. It can handle two types of nonlinearities: those approximated by standard TS fuzzy rules and those expressed as Lipschitz nonlinearities, which can naturally capture Lipschitz-type uncertainties. This forms a general modeling framework, enabling each class of nonlinearities to be analyzed separately, which simplifies the study and can reduce implementation complexity.

Remark 4.

The LMI conditions (27) and (28) include two tuning parameters: the decay rate μ and q. While μ can be selected directly based on the desired decay rate, q is determined via a logarithmically spaced search, as proposed in [12].

Remark 5.

In contrast to the OBC design for TS–Lipschitz systems in [21], the proposed approach explicitly considers the presence of TD.

Remark 6.

The decoupling technique employed in this work, as established in Lemma 1, has previously been applied in the design of LMI-based OBC to guarantee the asymptotic stability of uncertain one-sided Lipschitz nonlinear systems [12] and of Lipschitz nonlinear systems [11]. The main advantages of the present result can be summarized as follows:

• We explicitly account for time delay, addressing a critical gap in practical system modeling.
• While prior works focus on asymptotic stability, we establish the more demanding exponential stability, ensuring faster convergence and enhanced robustness.
• Instead of restricting the analysis to Lipschitz nonlinearities, we address a broader class of nonlinearities that can be approximated using the TS fuzzy modeling approach.

Remark 7.

The asymptotic stability results for OBC of the following class of models:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\xi }=\varphi \xi +B\iota +f\left(\xi \right),\hfill \\ \sigma =\theta \xi ,\hfill \end{array}\right.\end{array}$$

(38)

can be directly derived as a special case of our approach. Specifically,

• By neglecting the time-delay terms in our formulation and using the functional $\Gamma \left(ϵ\right)={\Gamma }_1$.
• Reducing the stability requirement from exponential to asymptotic convergence by setting $\mu =0$.

Remark 8.

The problem of quasi–one-sided Lipschitz nonlinear systems with time delay is addressed in [17] through a two-step procedure: first, the observer design; then, the controller design. In contrast, the present work achieves both designs in a single step. Moreover, we employ the TS fuzzy model to approximate a broader class of nonlinearities, and we focus on exponential stability, which is more demanding than asymptotic stability.

Discussion 1.

Although the present work offers notable advantages, particularly by accounting for the presence of time delay and by addressing exponential, rather than asymptotic stability, the scope for comparative studies could be further expanded by extending the framework to more challenging problems, such as the following:

• Considering quasi–one-sided Lipschitz nonlinearities instead of Lipschitz nonlinearities, such as in [17,18,19,20].
• Incorporating input saturation effects, such as in [20].
• Accounting for system with parameter uncertainties, such as in [9,10,11,12].
• Event-triggered control, such as in [23].
• Large-scale nonlinear systems, such as in [24].

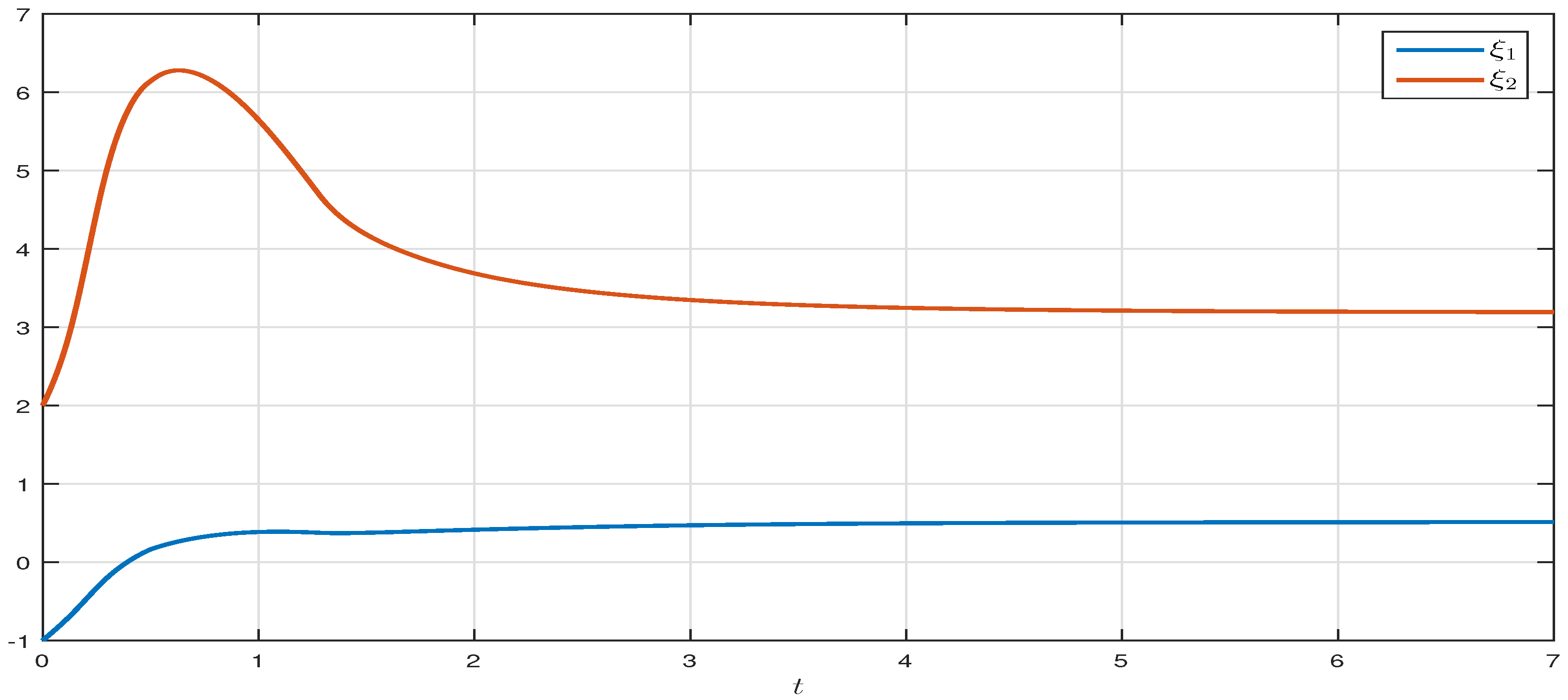
4. Application to a CSTR with Lumped Uncertainties

Consider a nonlinear dynamical model for a CSTR (as discussed in [13,25]):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\xi }}_1=n_1\left(\xi \right)+0.25{\xi }_1(t-\delta ),\hfill \\ {\dot{\xi }}_2=n_2\left(\xi \right)+0.25{\xi }_2(t-\delta )+0.3\iota ,\hfill \\ \xi =h,t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(39)

where

$$\begin{array}{ccc}\hfill n_1\left(\xi \right)& =& -1.25{\xi }_1+0.072(1-{\xi }_1)exp(\frac{{\xi }_2}{1+\frac{{\xi }_2}{20}}),\hfill \\ \hfill n_2\left(\xi \right)& =& -1.55{\xi }_1+0.579(1-{\xi }_1)exp(\frac{{\xi }_2}{1+\frac{{\xi }_2}{20}}).\hfill \end{array}$$

(40)

Next, we incorporate modeling uncertainties into the aforementioned CSTR system. The model, including lumped uncertainty, is expressed as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\xi }}_1=n_1\left(\xi \right)+0.25{\xi }_1(t-\delta ),\hfill \\ {\dot{\xi }}_2=n_2\left(\xi \right)+0.25{\xi }_2(t-\delta )+0.3\iota +f_1\left(\xi \right),\hfill \\ \xi =h,t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(41)

where $f_1\left(\xi \right)=0.1sin\left({\xi }_1\right)$.

Let $h={\left[\begin{array}{cc}-1& 2\end{array}\right]}^T$ and $\delta =0.5$.

Figure 1 illustrates the response of the system for $\iota =0$, revealing its unstable behavior.

As demonstrated in [13], the CSTR can be represented by a three-rule TDTSL model, with the global model given as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\xi }={\displaystyle \sum _{m=1}^3}{\rho }_m[{\varphi }_m\xi +{\phi }_m\xi (t-\delta )+B_m\iota ]+f\left(\xi \right),\hfill \\ \xi =h,t\in [-\delta ,0],\hfill \end{array}\right.\end{array}$$

(42)

where

$$\begin{array}{ccc}\hfill f\left(\xi \right)& =& \left[\begin{array}{c}0\\ f_1\left(\xi \right)\end{array}\right],\mathrm{which}\mathrm{satisfies}\mathrm{Assumption}3,\hfill \\ \hfill {\rho }_1& =& \left\{\begin{array}{c}1,\mathrm{if}{\xi }_2\le 0.8862,\hfill \\ 1-\frac{{\xi }_2-0.8862}{2.752-0.8862},\mathrm{if}0.8862<{\xi }_2<2.7520,\hfill \\ 0,\mathrm{if}{\xi }_2\ge 2.7520,\hfill \end{array}\right.\hfill \\ \hfill {\rho }_2& =& \left\{\begin{array}{c}1-{\rho }_1,\mathrm{if}{\xi }_2\le 2.7520,\hfill \\ 1-{\rho }_3,\mathrm{if}{\xi }_2>2.7520,\hfill \end{array}\right.\hfill \\ \hfill {\rho }_3& =& \left\{\begin{array}{c}0,\mathrm{if}{\xi }_2\le 2.7520,\hfill \\ \frac{{\xi }_2-2.7520}{4.7520-2.7520},\mathrm{if}2.7520<{\xi }_2<4.7052,\hfill \\ 1,\mathrm{if}{\xi }_2\ge 4.7052.\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\varphi }_1& =& \left[\begin{array}{cc}-1.4274& 0.0757\\ -1.4189& -0.9442\end{array}\right],{\varphi }_2=\left[\begin{array}{cc}-2.0508& 0.3958\\ -6.4066& 1.6168\end{array}\right],{\varphi }_3=\left[\begin{array}{cc}-4.5279& 0.3167\\ -26.2228& 0.9837\end{array}\right],\hfill \\ \hfill {\phi }_1& =& {\phi }_2={\phi }_3=\left[\begin{array}{cc}0.25& 0\\ 0& 0.25\end{array}\right],B_1=B_2=B_3=\left[\begin{array}{c}0\\ 0.3\end{array}\right].\hfill \end{array}$$

Assuming that the dimensionless temperature, corresponding to the second state ${\xi }_2$, can be measured by a sensor, we define $\sigma ={\xi }_2$.

First, we set $\mu =0.001$. Upon solving the LMIs (27) and (28), we obtain the following feasible solution when $\mathrm{Q}={10}^3$:

$$\begin{array}{ccc}\hfill {\mathrm{R}}_1& =& \left[\begin{array}{cc}197.49631& -970.9905\end{array}\right],{\mathrm{R}}_2={10}^3\left[\begin{array}{cc}0.1895& -1.0197\end{array}\right],{\mathrm{R}}_3={10}^3\left[\begin{array}{cc}0.2287& -1.1333\end{array}\right],\hfill \\ \hfill {\mathrm{Q}}_1& =& \left[\begin{array}{c}8.8061\\ 120.9504\end{array}\right],{\mathrm{Q}}_2=\left[\begin{array}{c}9.7471\\ 131.4592\end{array}\right],{\mathrm{Q}}_3=\left[\begin{array}{c}11.3341\\ 147.4196\end{array}\right].\hfill \end{array}$$

Second, setting $\mu =1.5$, yields

$$\begin{array}{ccc}\hfill {\mathrm{R}}_1& =& \left[\begin{array}{cc}36.2196& -900.5508\end{array}\right],{\mathrm{R}}_2=\left[\begin{array}{cc}54.0740& -995.8765\end{array}\right],{\mathrm{R}}_3={10}^3\left[\begin{array}{cc}0.0992& -1.1001\end{array}\right],\hfill \\ \hfill {\mathrm{Q}}_1& =& \left[\begin{array}{c}-17.7333\\ 100.9661\end{array}\right],{\mathrm{Q}}_2=\left[\begin{array}{c}-20.2878\\ 116.5835\end{array}\right],{\mathrm{Q}}_3=\left[\begin{array}{c}-21.6693\\ 129.3846\end{array}\right].\hfill \end{array}$$

Let $\widehat{h}={\left[\begin{array}{cc}0& 0\end{array}\right]}^T$. Figure 2 and Figure 3 illustrate the time evolution of the state vector $\xi$ and its estimate for $\mu =0.001$ and $\mu =1.5$. These figures highlight the influence of the decay rate on the response rapidity. In Figure 2, the left and right panels show ${\xi }_1$ and ${\widehat{\xi }}_1$ for $\mu =1.5$ and $\mu =0.001$, respectively. In Figure 3, the left and right panels show ${\xi }_2$ and ${\widehat{\xi }}_2$ for the same values of $\mu$. A larger $\mu$ leads to faster transient responses. Simulation times of 7 for ${\xi }_1$ and 2 for ${\xi }_2$ ensure the full transient and steady-state behaviors are captured.

5. Conclusions

The design of OBC is investigated for a class of TDTSL models in this study. The premise variables are considered measurable, whereas the Lipschitz-continuous nonlinearities can be functions of unmeasurable states. Sufficient conditions for the joint design of observer and controller gains are derived in terms of a set of LMIs using a single-step approach, guaranteeing $\mu -$E stability of the augmented closed-loop model. An application to a CSTR with lumped uncertainties is provided to demonstrate the efficacy of the OBC design method. The proposed results open up several potential avenues for further investigation. For instance, adopting the one-sided Lipschitz property, or its more recent extension, the quasi one-sided Lipschitz property, can lead to less conservative LMI-based synthesis conditions. Another direction is to enhance controller performance by incorporating input saturation effects.