An Adjusted CUSUM-Based Method for Change-Point Detection in Two-Phase Inverse Gaussian Degradation Processes

Abstract

Degradation data plays a crucial role in the reliability assessment and condition monitoring of engineering systems. The stage-wise changes in degradation rates often signal turning points in system performance or potential fault risks. To address the issue of structural changes during the degradation process, this paper constructs a degradation modeling framework based on a two-stage Inverse Gaussian (IG) process and proposes a change-point detection method based on an adjusted CUSUM (cumulative sum) statistic to identify potential stage changes in the degradation path. This method does not rely on complex prior information and constructs statistics by accumulating deviations, utilizing a binary search approach to achieve accurate change-point localization. In simulation experiments, the proposed method demonstrated superior detection performance compared to the classical likelihood ratio method and modified information criterion, verified through a combination of experiments with different change-point positions and degradation rates. Finally, the method was applied to real degradation data of a hydraulic piston pump, successfully identifying two structural change points during the degradation process. Based on these change points, the degradation stages were delineated, thereby enhancing the model’s ability to characterize the true degradation path of the equipment.

1. Introduction

Today, enterprises in industries such as manufacturing, aerospace, and high-speed rail systems are facing the dual pressure of ensuring high product reliability while enhancing market competitiveness. In this context, product reliability has become a key factor in determining system availability and operational safety. To achieve effective product reliability assessment and remaining useful life (RUL) prediction, various degradation analysis methods have been proposed [1,2]. In degradation modeling, certain physical quantities or performance indicators are typically selected as representations of degradation, reflecting the underlying or unobservable failure mechanisms within the product. When these indicators reach a preset threshold, the product is considered to have failed. Typical degradation indicators include bearing vibration signals, battery voltage, gear crack length, and milling cutter wear values, among others.

For degradation data of modern engineering systems, two common scenarios are frequently encountered in practice. One is sparse observations [3], which means that the degradation state of the product is only recorded at discrete time points due to limitations in testing resources or maintenance conditions. The second is continuous observations [4], where degradation information of the product is continuously updated over time through online monitoring devices. Both types of data scenarios impose higher demands on degradation modeling and have driven the development of data-driven degradation analysis methods.

In degradation analysis, degradation path models can be categorized into general path models (GPMs) and stochastic process models. GPMs offer intuitive advantages and ease of interpretation, making them the primary approach in early-stage degradation reliability research. In recent years, these models have been applied in degradation modeling, degradation test design, and system reliability analysis [5,6]. However, subsequent investigations revealed their limitations in characterizing the inherent randomness of product degradation under varying operational conditions and environmental factors. Stochastic process models demonstrate superior capability in capturing time-dependent uncertainty, owing to their clear physical interpretability, operational simplicity, effective incorporation of prior knowledge, and flexible handling of covariates and random effects. Current research mainly focuses on the Gamma process [7,8,9], Wiener process [10,11], and Inverse Gaussian process [12,13,14]. Among these, the Inverse Gaussian process, with its unique monotonicity and independent increment characteristics, is widely used to model degradation systems with irreversible wear characteristics, such as metal corrosion, light source attenuation, and crack growth. In some applications (e.g., the gallium arsenide laser data analyzed in Wang et al. [12]), the Wiener process and the gamma process fail to adequately fit the data, and their direct application may lead to misleading conclusions. In contrast, the Inverse Gaussian (IG) process, owing to its unique monotonicity and independent increment properties, has been widely employed for modeling degradation systems with irreversible wear characteristics, such as metal corrosion, light source attenuation, and crack propagation. Furthermore, Ye et al. [13] incorporated explanatory variables into the IG process by parameterizing its distributional parameters as functions of covariates, thereby enabling flexible integration into both simple IG processes and random effects models. This approach facilitates the construction of various covariate-dependent IG process models and, when applied to the laser dataset, demonstrated superior adaptability and flexibility compared to the conventional gamma model.

Regarding the application of the Inverse Gaussian process in degradation problems, Wang et al. [12] studied the maximum likelihood estimation method for the Inverse Gaussian process in degradation data, using the EM algorithm to estimate unknown parameters and employing the bootstrap method to assess the variability of the estimated parameters. Research by Ye et al. [13] demonstrated that the Inverse Gaussian process is a constrained compound Poisson process, considering it as a first-passage process of the Wiener process, and explored statistical inference and model selection issues for three types of random effect models. Peng [14] and Guan [15] conducted Bayesian analyses on the application of the Inverse Gaussian process model in degradation modeling and inference. Pan [16] developed an Inverse Gaussian process degradation model with random effects and proposed a Bayesian method capable of real-time updating of parameters in the degradation model.

Although the single-stage Inverse Gaussian process performs well in modeling single-stage degradation paths, in many engineering practices, the actual degradation process is often not dominated by a single mechanism but exhibits multi-stage, multi-rate characteristics. For example, in fields such as lithium-ion batteries, optical components, and sensors, devices may show a rapid degradation trend in the early stages, while stabilizing or even changing slowly in the later stages. This behavior is typically attributed to material fatigue, environmental adaptation, or changes in system control strategies. Most current degradation models adopt a single-stage structure. However, this often does not align with reality, as the degradation rates in the initial stage and subsequent stages are typically different. Ignoring the multi-stage nature and modeling the degradation process using a single-stage model may lead to inaccurate estimates of the degradation process. Given the multi-stage nature of the degradation process, there exist one or more turning points in the degradation rate, which is known as the change-point problem in statistics. This refers to a point in time, an unknown time point, where the statistical properties (such as mean, variance, or degradation rate) of the degradation process undergo a sudden change.

Shen [17] conducted a failure analysis of locking mechanisms with multiple interdependent components. In response to the multi-stage degradation characteristics of lubrication rotary joints, a joint change-point model combining the Wiener process and the Inverse Gaussian process was developed. Wang [18] constructed a two-stage capacity degradation model with dynamic change points to predict the remaining useful life of lithium batteries. Duan [19] performed reliability assessment of a two-stage model based on the Inverse Gaussian process, using the SIC criterion to detect change points and discussing the reliability function for each device under the two-stage IG model. Bae [20] proposed a hierarchical Bayesian change-point regression model to fit the two-stage degradation pattern of plasma display panels (PDPs) and developed an associated Gibbs sampling algorithm. Duan and Wang [21] modeled the reliability of the two-phase Gamma degradation process, using the Akaike Information Criterion (AIC) to detect change points, applying maximum likelihood estimation (MLE) for parameter estimation, and deriving the reliability function.

The CUSUM (cumulative sum) method, as a classic detection technique, is highly sensitive to small parameter changes. However, traditional CUSUM statistics exhibit significant bias and failure risks when dealing with non-normal distributed degradation quantities, particularly in the case of the Inverse Gaussian process. Therefore, this paper constructs a statistical testing framework for the two-stage Inverse Gaussian process degradation model that does not rely on prior distributions, and proposes an adjusted CUSUM statistic based on the characteristics of the Inverse Gaussian process, aiming to more effectively identify potential structural change points within the degradation trajectory.

The structure of this paper is arranged as follows: Section 2 introduces the modeling methods and statistical properties of the two-stage Inverse Gaussian process. Section 3 presents the adjusted CUSUM statistic and its implementation in detection. Section 4 validates the effectiveness of the proposed method under different parameters through simulation experiments. Section 5 applies real data from hydraulic piston pump degradation to conduct empirical analysis, demonstrating the applicability of the proposed method to practical problems. Section 6 concludes the paper and discusses future research.

2. The Model of Inverse Gaussian Process

2.1. The Inverse Gaussian Process

The Inverse Gaussian process (IGP) is an important class of continuous-time stochastic processes, widely used in fields such as biostatistics, reliability analysis, and financial modeling. It is a process with the Markov property, meaning that the future state of the process depends only on the current state and is independent of past states. The Inverse Gaussian process is typically used to model degradation phenomena with a monotonic increasing trend, effectively capturing the degradation process in many practical applications, such as equipment failure and lifetime analysis. The IGP $\left\{\mathrm{X}\right(t;\mu ,\eta );t\ge 0\}$ is a stochastic process that satisfies the following conditions [22]:

• $\mathbf{X}(0;\mu ,\eta )=0$;
• $\mathrm{X}(t;\mu ,\eta )$ has independent increments; i.e., for any $s_1<s_2\le t_1<t_2$, the increments $\mathrm{X}(t_2;\mu ,\eta )-\mathrm{X}(t_1;\mu ,\eta )$ and $\mathrm{X}(s_2;\mu ,\eta )-\mathrm{X}(s_1;\mu ,\eta )$ are independent;
• For any $0\le s<t$, the degradation increment $\mathrm{X}(t;\mu ,\eta )-\mathrm{X}(s;\mu ,\eta )$ within the time interval $(s,t)$ follows an Inverse Gaussian distribution, i.e.,

  $$\mathrm{X}(t;\mu ,\eta )-\mathrm{X}(s;\mu ,\eta )\sim IG(\mu \Delta \Lambda (s:t),\eta \Delta {\Lambda }^2(s:t)),$$

  where $\mu$ and $\eta$ are the mean and scale parameters, both greater than 0. $\Delta \Lambda (s:t)=\Lambda \left(t\right)-\Lambda \left(s\right)$ and $\Lambda \left(t\right)$ is a monotonically increasing function of time with $\Lambda \left(0\right)=0$.

The probability density function (PDF) of the Inverse Gaussian distribution is expressed as

$$\begin{array}{c}\hfill f(x;\mu ,\eta )={\left({\displaystyle \frac{\eta {\Lambda }^2\left(t\right)}{2\pi x^3}}\right)}^{{\displaystyle \frac{1}{2}}}exp\left[-{\displaystyle \frac{\eta }{2x}}{\left({\displaystyle \frac{x}{\mu }}-\Lambda \left(t\right)\right)}^2\right].\end{array}$$

(1)

The cumulative distribution function (CDF) is given by

$$\begin{array}{cc}\hfill F(x;\mu ,\eta )=& \Phi \left[\sqrt{{\displaystyle \frac{\eta {\Lambda }^2\left(t\right)}{x}}}\left({\displaystyle \frac{x}{\mu \Lambda \left(t\right)}}-1\right)\right]+exp\left\{{\displaystyle \frac{2\eta \Lambda \left(t\right)}{\mu }}\right\}\Phi \left[-\sqrt{{\displaystyle \frac{\eta {\Lambda }^2\left(t\right)}{x}}}\left({\displaystyle \frac{x}{\mu \Lambda \left(t\right)}}+1\right)\right],\hfill \end{array}$$

(2)

where $\Phi (·)$ is the cumulative distribution function of the standard normal distribution.

The mean and variance of the Inverse Gaussian distribution can be calculated as

$$\begin{array}{c}\hfill \mathbb{E}\left[\mathrm{X}\left(t\right)\right]=\mu \Lambda \left(t\right),\mathrm{Var}\left[\mathrm{X}\left(t\right)\right]={\displaystyle \frac{{\mu }^3\Lambda \left(t\right)}{\eta }}.\end{array}$$

(3)

2.2. The Two-Stage Inverse Gaussian Degradation Model

In many practical applications, the degradation process is typically not a single process but rather consists of multiple stages, each influenced by different factors. The degradation rate and behavior may vary across these stages. This phenomenon is commonly observed in industrial equipment, mechanical life, electronic products, and other fields. For example, some equipment may experience rapid wear during the initial usage phase due to insufficient lubrication or other environmental factors, whereas in later stages, the degradation rate may slow down, or in some cases, accelerate due to specific loss mechanisms. To better capture the degradation process of equipment at different lifecycle stages, it is necessary to adopt degradation models that reflect the characteristics of each stage. Since a multi-stage degradation process can always be transformed into multiple two-stage degradation processes through binary segmentation methods [23], this paper focuses only on the two-stage Inverse Gaussian degradation model and characterizes the degradation characteristics of equipment in different stages by introducing change points.

Suppose the degradation process ${\mathrm{X}}_j\left(t\right)$ of each device is measured at multiple observation time points $t=(t_1,t_2,\dots ,t_n)$, where $j=1,2,\dots ,m$ represents the device number, and m is the sample size. The degradation observations of device j at times $t_1,t_2,\dots ,t_n$ are denoted as ${\mathrm{X}}_j\left(t\right)=(x_{1j},x_{2j},\dots ,x_{nj})$. For each device, $t_0=0$ and $x_{0j}=0$ represent the initial degradation values. Therefore, the degradation increment for each device can be expressed as

$$\Delta x_{ij}=x_{ij}-x_{i-1,j},i=1,2,\dots ,n,j=1,2,\dots ,m,$$

where $x_{ij}$ denotes the degradation value of the j-th device at the i-th time point, and $\Delta x_{ij}$ represents the degradation increment of the device at the i-th time point relative to the previous time point.

Assume that the degradation process of the device can be divided into two stages, and there exists a change point ${\tau }_j$ between these two stages. The two-stage degradation process is assumed to follow an Inverse Gaussian process with different parameters for each stage. The parameters of the two-stage Inverse Gaussian degradation model differ across devices. For the j-th device, the degradation process in the first stage is an Inverse Gaussian process with parameters ${\mu }_{1j}>0$ and ${\eta }_{1j}>0$, while the degradation process in the second stage follows an Inverse Gaussian process with parameters ${\mu }_{2j}>0$ and ${\eta }_{2j}>0$. Based on these model assumptions, the degradation process ${\mathrm{X}}_j\left(t\right)$ can be expressed as

$$\begin{array}{c}\hfill {\mathrm{X}}_j\left(t\right)=\left\{\begin{array}{cc}{\mathrm{X}}_{01j}(0;{\mu }_{1j},{\eta }_{1j})+{\mathrm{X}}_{1j}(t;{\mu }_{1j},{\eta }_{1j}),\hfill & 0\le t\le {\tau }_j,\hfill \\ {\mathrm{X}}_{02j}({\tau }_j;{\mu }_{1j},{\eta }_{1j})+{\mathrm{X}}_{2j}(t-{\tau }_j;{\mu }_{2j},{\eta }_{2j}),\hfill & {\tau }_j<t,\hfill \end{array}\right.\end{array}$$

(4)

where ${\tau }_j$ denotes the change point for the j-th device, marking the transition from one stage to another. ${\mathrm{X}}_{01j}(0;{\mu }_{1j},{\eta }_{1j})$ and ${\mathrm{X}}_{02j}({\tau }_j;{\mu }_{1j},{\eta }_{1j})$ represent the initial degradation values for the j-th device. ${\mathrm{X}}_{1j}(t;{\mu }_{1j},{\eta }_{1j})$ and ${\mathrm{X}}_{2j}(t-{\tau }_j;{\mu }_{2j},{\eta }_{2j})$ denote the degradation increments for the first and second stages, respectively. Specifically, ${\mathrm{X}}_{1j}(t;{\mu }_{1j},{\eta }_{1j})\sim IG({\mu }_{1j}{\Lambda }_{1j}\left(t\right),{\eta }_{1j}{\Lambda }_{1j}^2\left(t\right))$, ${\mathrm{X}}_{2j}(t-{\tau }_j;{\mu }_{2j},{\eta }_{2j})\sim IG({\mu }_{2j}{\Lambda }_{2j}(t-{\tau }_j),{\eta }_{2j}{\Lambda }_{2j}^2(t-{\tau }_j))$, where ${\Lambda }_{1j}\left(t\right)$ and ${\Lambda }_{2j}\left(t\right)$ are the degradation functions for the first and second stages, respectively. The degradation process is assumed to be continuous, i.e., ${\mathrm{X}}_{02j}={\mathrm{X}}_{01j}+{\mu }_{1j}{\Lambda }_{1j}\left({\tau }_j\right)$.

Based on this, to detect whether there exists a change point ${\tau }_j$ in the degradation process of device j, we propose the following hypothesis test

$$\begin{array}{cc}\hfill H_{0j}& :x_j\left(t\right)\sim IG({\mu }_j,{\eta }_j,t),\hfill \\ \hfill H_{1j}& :{\mathrm{X}}_j\left(t\right)\sim \left\{\begin{array}{cc}IG({\mu }_{1j},{\eta }_{1j},t),\hfill & 0\le t\le {\tau }_j,\hfill \\ IG({\mu }_{2j},{\eta }_{2j},t-{\tau }_j)\hfill & ,{\tau }_j<t,\hfill \end{array}\right.\hfill \end{array}$$

(5)

where ${\mu }_{1j}\ne {\mu }_{2j}$ and ${\eta }_{1j}\ne {\eta }_{2j}$.

The degradation process of the device is divided into two stages, and at the change point ${\tau }_j$, the parameters of the degradation process in the two stages may change. Specifically, we are concerned with whether there is a significant difference in the parameters of the degradation process between the two stages. Therefore, an equivalent hypothesis test can be formulated as Equation (6)

$$\begin{array}{cc}\hfill H_{0j}& :{\mu }_{1j}={\mu }_{2j}={\mu }_j,{\eta }_{1j}={\eta }_{2j}={\eta }_j,\hfill \\ \hfill H_{1j}& :{\mu }_{1j}\ne {\mu }_{2j},{\eta }_{1j}\ne {\eta }_{2j}.\hfill \end{array}$$

(6)

3. Change-Point Detection Method

3.1. Maximum Likelihood Estimation

Maximum likelihood estimation (MLE) aims to estimate the model parameters by maximizing the likelihood function. Under the assumption of independent and identically distributed observations, we estimate the parameters for the degradation observation sequence ${\mathrm{X}}_j\left(t\right)=(x_{1j},x_{2j},\dots ,x_{nj})$ of device j at time points $t_1,t_2,\dots ,t_n$. Define the time increment as $\Delta {\Lambda }_j={\Lambda }_j\left(t_i\right)-{\Lambda }_j\left(t_{i-1}\right)$ and the degradation increment as $\Delta x_{ij}=x_{ij}-x_{i-1,j}$ for $i=1,2,\dots ,n$, $j=1,2,\dots ,m$. Without loss of generality, we assume that $\Lambda \left(t\right)=t$ in this paper. When $\Lambda \left(t\right)=t$, $\Delta {\Lambda }_j=t_{ij}-t_{i-1,j}=\Delta t_{ij}$. Based on the properties of the Inverse Gaussian process and its probability density function in Equation (1), for the j-th device, let ${\theta }_j=({\mu }_j,{\eta }_j)$. Under the null hypothesis $H_{0j}$, the likelihood function $L_{H_{0j}}\left({\theta }_j\right)$ can be expressed as

$$\begin{array}{c}\hfill L_{H_{0j}}\left({\theta }_j\right)=\prod _{i=1}^{n}f(x_{ij};{\mu }_j,{\eta }_j)=\prod _{i=1}^n\sqrt{{\displaystyle \frac{{\eta }_j\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}}exp\left[-{\displaystyle \frac{{\eta }_j}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_j}}-\Delta t_{ij}\right)}^2\right].\end{array}$$

(7)

To simplify the calculation, we usually compute the log-likelihood function

$$\begin{array}{c}\hfill ln{L}_{H_{0j}}\left({\theta }_j\right)=\sum _{i=1}^n\left[{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{{\eta }_j\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}\right)-{\displaystyle \frac{{\eta }_j}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_j}}-\Delta t_{ij}\right)}^2\right].\end{array}$$

(8)

Then compute the partial derivatives with respect to ${\mu }_j$ and ${\eta }_j$

$$\begin{array}{cc}\hfill {\displaystyle \frac{𝜕}{𝜕{\mu }_j}}ln{L}_{H_{0j}}\left({\theta }_j\right)& =\sum _{i=1}^n\left[{\displaystyle \frac{{\eta }_j}{{\mu }_j^2}}\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_j}}-\Delta t_{ij}\right)\right],\hfill \\ \hfill {\displaystyle \frac{𝜕}{𝜕{\eta }_j}}ln{L}_{H_{0j}}\left({\theta }_j\right)& =\sum _{i=1}^n\left[{\displaystyle \frac{1}{2{\eta }_j}}-{\displaystyle \frac{1}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_j}}-\Delta t_{ij}\right)}^2\right].\hfill \end{array}$$

(9)

Setting the partial derivatives equal to zero, we obtain

$$\begin{array}{c}\hfill {\widehat{\mu }}_j={\displaystyle \frac{{\sum }_{i=1}^n\Delta x_{ij}}{{\sum }_{i=1}^n\Delta t_{ij}}},{\widehat{\eta }}_j={\displaystyle \frac{n}{{\sum }_{i=1}^n\frac{1}{\Delta x_{ij}}{\left(\frac{\Delta x_{ij}}{{\mu }_j}-\Delta t_{ij}\right)}^2}}.\end{array}$$

(10)

For the j-th device, let ${\theta }_{ij}=({\mu }_{1j},{\eta }_{1j},{\mu }_{2j},{\eta }_{2j})$, and let ${\tau }_j$ denote the time at which the degradation process parameters for the j-th device change. The degradation increments are given by $\Delta x_{ij}\sim \mathrm{IG}({\mu }_{1j}\Delta t_{ij},{\eta }_{1j}\Delta t_{ij}^2),i=1,2,\dots ,{\tau }_j,j=1,2,\dots ,m$, $\Delta x_{ij}\sim \mathrm{IG}({\mu }_{2j}\Delta t_{ij},{\eta }_{2j}\Delta t_{ij}^2),i={\tau }_j+1,\dots ,n,j=1,2,\dots ,m$. Thus, under the alternative hypothesis $H_{1j}$, the likelihood function $L_{H_{1j}}\left({\theta }_{ij}\right)$ can be expressed as

$$\begin{array}{cc}\hfill L_{H_{1j}}\left({\theta }_{ij}\right)& =\prod _{i=1}^{{\tau }_j}f(x_{ij};{\mu }_{1j},{\eta }_{1j})\times \prod _{i={\tau }_j+1}^{n}f(x_{ij};{\mu }_{2j},{\eta }_{2j})\hfill \\ \hfill & =\prod _{i=1}^{{\tau }_j}\left\{\sqrt{{\displaystyle \frac{{\eta }_{1j}\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}}exp\left[-{\displaystyle \frac{{\eta }_{1j}}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_{1j}}}-\Delta t_{ij}\right)}^2\right]\right\}\hfill \\ \hfill & \times \prod _{i={\tau }_j+1}^n\left\{\sqrt{{\displaystyle \frac{{\eta }_{2j}\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}}exp\left[-{\displaystyle \frac{{\eta }_{2j}}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_{2j}}}-\Delta t_{ij}\right)}^2\right]\right\}.\hfill \end{array}$$

(11)

Similarly, as shown in Appendix A, we obtain,

$$\begin{array}{cc}\hfill {\widehat{\mu }}_{1j}& ={\displaystyle \frac{{\sum }_{i=1}^{{\tau }_j}\Delta x_{ij}}{{\sum }_{i=1}^{{\tau }_j}\Delta t_{ij}}},{\widehat{\eta }}_{1j}={\displaystyle \frac{{\tau }_j}{{\sum }_{i=1}^{{\tau }_j}\left[\frac{1}{\Delta x_{ij}}{\left(\frac{\Delta x_{ij}}{{\widehat{\mu }}_{1j}}-\Delta t_{ij}\right)}^2\right]}},\hfill \\ \hfill {\widehat{\mu }}_{2j}& ={\displaystyle \frac{{\sum }_{i={\tau }_j+1}^n\Delta x_{ij}}{{\sum }_{i={\tau }_j+1}^n\Delta t_{ij}}},{\widehat{\eta }}_{2j}={\displaystyle \frac{n-{\tau }_j}{{\sum }_{i={\tau }_j+1}^n\left[\frac{1}{\Delta x_{ij}}{\left(\frac{\Delta x_{ij}}{{\widehat{\mu }}_{2j}}-\Delta t_{ij}\right)}^2\right]}}.\hfill \end{array}$$

(12)

3.2. The Adjusted CUSUM Statistic

The CUSUM (cumulative sum) method was first introduced by E.S. Page [24] as a statistical quality control tool to monitor changes in production processes. Subsequently, numerous studies have conducted in-depth research on the CUSUM statistic in the context of change-point detection. Chen and Gupta [25] introduced the classic form of the CUSUM statistic, while Fryzlewicz [26] proposed a new CUSUM statistic for cases where multiple change points exist in the signal source. In addition to the aforementioned global statistics, there is another class of local statistics. Chen [27] was the first to propose a local test statistic based on CUSUM, applicable to at most one jump in the mean. Niu and Zhang [28] further introduced other forms of local CUSUM statistics for cases involving multiple change points. The main idea is to detect whether the data deviates from the predetermined target or baseline by calculating the cumulative deviation. The CUSUM method is highly suitable for change-point detection in two-stage Inverse Gaussian degradation processes because it accumulates data deviations at each moment, allowing for prompt detection of changes in the system. Hence, this section constructs a new adjusted CUSUM test statistic in model (4). According to (3), the mean and variance of the degradation process ${\mathrm{X}}_j\left(t\right)$ are given by ${\mu }_{j}t$ and ${\mu }_j^{3}t/{\eta }_j$ under $\Lambda \left(t\right)=t$, respectively, where $j=1,2,\dots ,m$. This paper constructs the CUSUM statistic through the forward cumulative sum $S_{ij}^{+}$ and the backward cumulative sum $S_{ij}^{-}$, where $i=1,2,\dots ,n$.

$$\begin{array}{c}\hfill S_{ij}^{+}=max(0,S_{i-1,j}^{+}+w_{ij}),\\ \hfill S_{ij}^{-}=min(0,S_{i-1,j}^{-}+w_{ij}),\end{array}$$

(13)

where

$$w_{ij}={\displaystyle \frac{\Delta x_{ij}-{\mu }_j\Delta t_{ij}}{\sqrt{\frac{{\mu }_j^3\Delta t_{ij}}{{\eta }_j}}}},$$

and the initial values are $S_{0j}^{+}=0$ and $S_{0j}^{-}=0$. Thus, the CUSUM statistic for each device j can be defined as

$$\begin{array}{c}\hfill T_j=\underset{1\le i\le n}{max}(S_{ij}^{+},-S_{ij}^{-}).\end{array}$$

(14)

To effectively distinguish between normal fluctuations and true change points, it is necessary to set a reasonable threshold $C_{Ad-CUSUM}$, which can typically be optimized using historical data or through model training. When the CUSUM statistic exceeds the set threshold, it indicates that a change point may have occurred. At this point, further analysis of the change-point characteristics can be conducted to confirm whether it is a true shift. By calculating the cumulative sum changes of both the forward and backward CUSUM, the possible change point ${\widehat{\tau }}_j$ for device j can be identified as

$$\begin{array}{c}\hfill {\widehat{\tau }}_j=arg\underset{1\le i\le n}{max}\left|T_j\right|.\end{array}$$

(15)

3.3. Likelihood Ratio Statistic

The likelihood ratio test (LRT) in change-point detection is a classic statistical method used to determine whether there is a structural change in a data sequence. The core idea is to test for the presence of a change point by comparing the likelihood functions under two hypotheses. The null hypothesis assumes that the data comes from the same distribution, while the alternative hypothesis assumes that the data changes at some point, with a shift in the distribution parameters. Specifically, LRT constructs a likelihood ratio statistic by computing the maximum likelihood values under the no-change-point and change-point scenarios, which allows us to test for the presence of a change point. As a classic framework in change-point theory, the LRT method has been widely studied and applied.

Compared to the traditional LRT statistic, this paper constructs the LRT statistic based on the two-stage Inverse Gaussian degradation model, with the change-point position as an unknown parameter. Combining Equations (7) and (11), the likelihood ratio test statistic for device j under model (4) is given by

$$\begin{array}{cc}\hfill Z_j& =\underset{k_0\le {\tau }_j\le n-k_0}{max}{\Lambda }_k=\underset{k_0\le {\tau }_j\le n-k_0}{max}-2log\left({\displaystyle \frac{L_{H_{0j}}}{L_{H_{1j}}}}\right),\hfill \\ \hfill & =\underset{k_0\le {\tau }_j\le n-k_0}{max}-2\left[ln{L}_{H_{0j}}({\widehat{\mu }}_j,{\widehat{\eta }}_j)-ln{L}_{H_{1j}}({\widehat{\mu }}_{1j},{\widehat{\eta }}_{1j},{\widehat{\mu }}_{2j},{\widehat{\eta }}_{2j})\right],\hfill \\ \hfill & =\underset{k_0\le {\tau }_j\le n-k_0}{max}-2\left\{\sum _{i=1}^n\left[{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{{\eta }_j\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}\right)-{\displaystyle \frac{{\eta }_j}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_j}}-\Delta t_{ij}\right)}^2\right]\right.\hfill \\ \hfill & -\sum _{i=1}^{{\tau }_j}\left[{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{{\eta }_{1j}\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}\right)-{\displaystyle \frac{{\eta }_{1j}}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_{1j}}}-\Delta t_{ij}\right)}^2\right]\hfill \\ \hfill & \left.-\sum _{i={\tau }_j+1}^n\left[{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{{\eta }_{2j}\Delta t_{ij}^2}{2\pi \Delta x_{ij}^3}}\right)-{\displaystyle \frac{{\eta }_{2j}}{2\Delta x_{ij}}}{\left({\displaystyle \frac{\Delta x_{ij}}{{\mu }_{2j}}}-\Delta t_{ij}\right)}^2\right]\right\}.\hfill \end{array}$$

(16)

In practice, if the change point of the data is located at the beginning or the end of the data sequence, the parameter estimation using the MLE method may become inaccurate. This is because the amount of data at the start or end is too small to provide sufficient information for reliable parameter estimation. To avoid this issue, the location of the change point is typically restricted. It is usually set that ${\tau }_j\in [k_0,n-k_0]$, where $k_0=2[logn]$ [29]. If there is a significant likelihood improvement at some ${\tau }_j$, i.e., if $Z_j$ exceeds the given threshold $C_{LRT}$, the null hypothesis is rejected, and it is concluded that a change point exists at that position. In this case, the estimated location of the change point for device j is

$${\widehat{\tau }}_j=\underset{k_0\le {\tau }_j\le n-k_0}{argmax}{Z}_j.$$

3.4. Modified Information Criterion

The change-point detection problem can be regarded as a model selection problem, that is, making a choice between the null hypothesis and the alternative hypothesis in change-point analysis. If the null hypothesis is accepted, it corresponds to selecting a model without change points. Otherwise, a model with at least one change point is selected. Therefore, model selection criteria such as the Akaike Information Criterion (AIC) [30] and the Schwarz Information Criterion (SIC) [31] can be applied in change-point detection research. Among these, the SIC criterion is often used since it yields asymptotically consistent estimates and is considered a practical model selection method.

When using information criterion-based methods for model selection, model complexity is a crucial factor and is usually measured by the dimensionality of the parameter space. However, in change-point problems, in addition to the parameters from the model, there is a special parameter $\tau$. To avoid non-unique parameter estimation, the range of values for $\tau$ is determined as described above, representing the location of the change point. When the change point is near the ends of the sequence, redundant parameters may arise in the model. If the complexity of the model parameters is not adjusted accordingly, it may result in biased model selection outcomes.

Therefore, Chen et al. [32] proposed a modification to the SIC criterion. Under $H_{0j}$, the MIC statistic is

$$MI{C}_j\left(n\right)=-2log{L}_{H_{0j}}({\widehat{\mu }}_j,{\widehat{\eta }}_j)+2log\left(n\right),$$

(17)

where ${\widehat{\mu }}_j,{\widehat{\eta }}_j$ are the MLEs of the parameters under $H_{0j}$.

For each device j, the MIC statistic under the alternative hypothesis is

$$MI{C}_j\left({\tau }_j\right)=-2log{L}_{H_{1j}}({\widehat{\mu }}_{1j},{\widehat{\eta }}_{1j},{\widehat{\mu }}_{2j},{\widehat{\eta }}_{2j})+\left\{4+{\left({\displaystyle \frac{2{\tau }_j}{n}}-1\right)}^2\right\}log\left(n\right),$$

(18)

where ${\widehat{\mu }}_{1j},{\widehat{\eta }}_{1j},{\widehat{\mu }}_{2j},{\widehat{\eta }}_{2j}$ are the MLEs of the parameters under $H_{1j}$, and ${\tau }_j$ represents the possible location of the for each device j, satisfying $k_0\le {\tau }_j<n-k_0$.

When

$$MI{C}_j\left(n\right)\le \underset{k_0\le {\tau }_j<n-k_0}{min}MIC\left({\tau }_j\right),$$

the null hypothesis is accepted, indicating that there is no change existing in the data. If

$$MI{C}_j\left(n\right)>\underset{k_0\le {\tau }_j<n-k_0}{min}MIC\left({\tau }_j\right),$$

the null hypothesis $H_{0j}$ is rejected, indicating the presence of a change point in the sequence. In this case, the position of the change point can be determined by

$${\widehat{\tau }}_j=arg\underset{k_0\le {\tau }_j<n-k_0}{min}MIC\left({\tau }_j\right).$$

To establish statistically rigorous conclusions from the hypothesis testing, Chen et al. [32] defined the test statistic

$$S_{nj}=MI{C}_j\left(n\right)-\underset{k_0\le {\tau }_j<n-k_0}{min}MI{C}_j\left({\tau }_j\right)+2log\left(n\right).$$

(19)

By substituting Equations (18) and (17) into Equation (19), we obtain

$$\begin{array}{cc}\hfill S_{nj}& =-2log{L}_{H_{0j}}({\widehat{\mu }}_j,{\widehat{\eta }}_j)+2log\left(n\right)\hfill \\ \hfill & -\underset{k_0\le {\tau }_j<n-k_0}{min}\left[-2log{L}_{H_{1j}}({\widehat{\mu }}_{1j},{\widehat{\eta }}_{1j},{\widehat{\mu }}_{2j},{\widehat{\eta }}_{2j})+\left\{4+{\left({\displaystyle \frac{2{\tau }_j}{n}}-1\right)}^2\right\}log\left(n\right)+2log\left(n\right)\right]\hfill \\ \hfill & =-2log{L}_{H_{0j}}({\widehat{\mu }}_j,{\widehat{\eta }}_j)-\underset{k_0\le {\tau }_j<n-k_0}{min}\left[-2log{L}_{H_{1j}}({\widehat{\mu }}_{1j},{\widehat{\eta }}_{1j},{\widehat{\mu }}_{2j},{\widehat{\eta }}_{2j})+{\left({\displaystyle \frac{2{\tau }_j}{n}}-1\right)}^{2}log\left(n\right)\right].\hfill \end{array}$$

4. Numerical Experiments

In this section, simulations are conducted to calculate the threshold for the change-point test, the probability of Type I error, and the power of the test.

There are two methods that can be used to compute the critical value. One method is to conduct a series of simulations under a given null distribution and calculate the value of the test statistic for each simulation. Then the corresponding quantile in the sorted values of all statistics is the critical value. Another method is based on the Bootstrap procedure to calculate the threshold. In this approach, a certain number of sample groups are drawn from the approximate distribution of the null distribution. Then the corresponding quantiles of these sorted test statistics, obtained from each Bootstrap sample, serve as the threshold for the test. The Bootstrap method offers greater flexibility compared to the simulation method when deriving the threshold for the test statistic under the null hypothesis, particularly in cases with small sample sizes or undefined data distributions, as it can effectively handle complex or irregular data structures. Hence, this method is widely applied in real data analysis, providing more reliable threshold estimates, especially when sample sizes are small or the data distribution is uncertain. In these simulations, the null distribution has been predetermined, and it is known to satisfy $H_0$, which can be used to generate new samples. The specific steps of the Bootstrap method are described as follows:

Step 1.

Assume that no change point exists; i.e., under $H_0$, calculate the corresponding parameter estimates.

Step 2.

Generate a new set of samples based on the results from Step 1.

Step 3.

Resample B sets of Bootstrap samples with replacements from the samples obtained in Step 2, and calculate the value of the test statistic for each group Bootstrap sample, which is denoted as $S_n^{\left(i\right)},i=1,2,\dots ,B$.

Step 4.

Obtain the p-value by the following equation,

$$\widehat{p}={\displaystyle \frac{1}{B}}\sum _{i=1}^{B}I(S_n\le S_n^{\left(i\right)}),$$

(20)

where $I(·)$ is the indicator function, $S_n$ is the value of the test statistic under the original data, and typically $B=1000$. For a given significance level $\alpha$, if $\widehat{p}<\alpha$, reject the null hypothesis. Otherwise, accept the null hypothesis.

4.1. The Probability of Type I Error

This section investigates the performance of the proposed test statistic in controlling the Type I error under different sample sizes and parameter settings, and compares it with the LRT and MIC methods. For the selection of parameters, to ensure the validity and fairness of the experiment, the parameter settings we chose are consistent with those used in Qiao et al. [33]. The parameters ${\mathit{\theta }}_1=({\mu }_1,{\eta }_1)$ are given as $\left\{\right(1,1.3),(1.5,1.5),(1.5,2),(1.2,1.7),(1.4,2.7\left)\right\}$. The sample size is $m=10$, time point size n is set as $\{60,70,80,90,100\}$.

All simulations are based on 100 replications, with the significance level set at 0.05. As shown in

Table 1. Empirical Type I error rates at $\alpha =0.05$. Bold formatting has been used to emphasize the method proposed in this paper.

n	Method	${\mathit{\theta }}_1=({\mathit{\mu }}_1,{\mathit{\eta }}_1)$
		(1, 1.3)	(1.5, 1.5)	(1.5, 2)	(1.2, 1.7)	(1.4, 2.7)
60	LRT	0.051	0.049	0.055	0.051	0.059
	MIC	0.051	0.046	0.043	0.058	0.060
	Ad-CUSUM	0.048	0.043	0.039	0.046	0.039
70	LRT	0.051	0.050	0.045	0.047	0.053
	MIC	0.041	0.049	0.057	0.048	0.058
	Ad-CUSUM	0.059	0.046	0.053	0.054	0.064
80	LRT	0.054	0.061	0.063	0.058	0.041
	MIC	0.051	0.049	0.052	0.053	0.048
	Ad-CUSUM	0.063	0.060	0.054	0.041	0.049
90	LRT	0.049	0.040	0.050	0.045	0.049
	MIC	0.043	0.051	0.042	0.058	0.052
	Ad-CUSUM	0.062	0.054	0.065	0.049	0.051
100	LRT	0.063	0.063	0.054	0.052	0.061
	MIC	0.062	0.044	0.071	0.051	0.048
	Ad-CUSUM	0.052	0.061	0.059	0.048	0.055

, the minimum frequency of Type I error for all test methods is 0.039, and the maximum is 0.063, fluctuating within the range of [0.0293, 0.0707], indicating that the tests conducted are valid.

4.2. The Power of Change-Point Detection

In this section, we simulate the power of change-point detection under different scenarios to evaluate the performance of three change-point detection methods. For model (4), we set the parameters ${\mathit{\theta }}_1=({\mu }_1,{\eta }_1)$ as $(0.5,1)$ before the change point, while the parameters ${\mathit{\theta }}_2=({\mu }_2,{\eta }_2)$ are set as $\left\{\right(1,1.3),(1.5,1.5),(1.5,2),(1.2,1.7),(1.4,2.7\left)\right\}$ after the change point. The sample sizes $m=10$, the time point sizes are set as $\{60,80,100\}$, and the change-point positions are ${\tau }_j=\{n/4,n/2,3n/4\}$. The specific test results are shown in

Table 2. The power comparison at $\alpha =0.10$. Bold formatting has been used to emphasize the method proposed in this paper.

n	k	Method	${\mathit{\theta }}_2=({\mathit{\mu }}_2,{\mathit{\eta }}_2)$
			(1, 1.3)	(1.5, 1.5)	(1.5, 2)	(1.2, 1.7)	(1.4, 2.7)
60	15	LRT	0.557	0.916	0.979	0.853	0.992
		MIC	0.608	0.935	0.984	0.888	0.998
		Ad-CUSUM	1.000	0.992	1.000	1.000	1.000
	30	LRT	0.750	0.984	0.998	0.961	1.000
		MIC	0.830	0.992	0.999	0.981	1.000
		Ad-CUSUM	0.996	1.000	1.000	1.000	1.000
	45	LRT	0.591	0.929	0.965	0.855	0.982
		MIC	0.631	0.944	0.976	0.880	0.991
		Ad-CUSUM	0.829	1.000	1.000	0.954	1.000
80	20	LRT	0.727	0.985	0.998	0.954	1.000
		MIC	0.769	0.990	0.998	0.964	1.000
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	40	LRT	0.875	0.997	0.999	0.992	1.000
		MIC	0.923	0.998	1.000	0.995	1.000
		Ad-CUSUM	0.998	1.000	1.000	1.000	1.000
	60	LRT	0.800	0.992	0.997	0.964	1.000
		MIC	0.816	0.993	0.998	0.973	1.000
		Ad-CUSUM	0.915	1.000	1.000	0.991	1.000
100	25	LRT	0.834	0.997	1.000	0.986	1.000
		MIC	0.868	0.999	1.000	0.991	1.000
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	50	LRT	0.949	1.000	1.000	0.999	1.000
		MIC	0.973	1.000	1.000	1.000	1.000
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	75	LRT	0.855	0.996	1.000	0.991	1.000
		MIC	0.887	0.997	1.000	0.990	1.000
		Ad-CUSUM	0.959	0.999	1.000	0.995	1.000

,

Table 3. The power comparison at $\alpha =0.05$. Bold formatting has been used to emphasize the method proposed in this paper.

n	k	Method	${\mathit{\theta }}_2=({\mathit{\mu }}_2,{\mathit{\eta }}_2)$
			(1, 1.3)	(1.5, 1.5)	(1.5, 2)	(1.2, 1.7)	(1.4, 2.7)
60	15	LRT	0.454	0.858	0.942	0.770	0.983
		MIC	0.503	0.890	0.966	0.926	0.989
		Ad-CUSUM	0.999	1.000	1.000	1.000	1.000
	30	LRT	0.653	0.970	0.992	0.925	0.997
		MIC	0.747	0.987	0.999	0.958	1.000
		Ad-CUSUM	0.994	1.000	1.000	1.000	1.000
	45	LRT	0.507	0.904	0.946	0.787	0.967
		MIC	0.541	0.914	0.955	0.816	0.973
		Ad-CUSUM	0.775	0.987	0.996	0.938	0.998
80	20	LRT	0.595	0.960	0.992	0.902	0.998
		MIC	0.629	0.975	0.995	0.921	0.998
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	40	LRT	0.807	0.994	0.998	0.979	1.000
		MIC	0.850	0.996	0.998	0.989	1.000
		Ad-CUSUM	0.998	1.000	1.000	1.000	1.000
	60	LRT	0.706	0.978	0.994	0.930	0.997
		MIC	0.723	0.984	0.995	0.939	0.999
		Ad-CUSUM	0.853	0.997	1.000	0.982	1.000
100	25	LRT	0.705	0.993	1.000	0.960	1.000
		MIC	0.752	0.995	1.000	0.974	1.000
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	50	LRT	0.895	1.000	1.000	0.993	1.000
		MIC	0.937	1.000	1.000	0.999	1.000
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	75	LRT	0.774	0.994	0.998	0.971	1.000
		MIC	0.804	0.994	0.999	0.981	1.000
		Ad-CUSUM	0.917	0.998	1.000	0.988	1.000

and

Table 4. The power comparison at $\alpha =0.01$. Bold formatting has been used to emphasize the method proposed in this paper.

n	k	Method	${\mathit{\theta }}_2=({\mathit{\mu }}_2,{\mathit{\eta }}_2)$
			(1, 1.3)	(1.5, 1.5)	(1.5, 2)	(1.2, 1.7)	(1.4, 2.7)
60	15	LRT	0.235	0.671	0.847	0.562	0.928
		MIC	0.541	0.732	0.884	0.629	0.955
		Ad-CUSUM	0.999	1.000	1.000	1.000	1.000
	30	LRT	0.426	0.892	0.962	0.797	0.988
		MIC	0.531	0.942	0.985	0.877	0.955
		Ad-CUSUM	0.979	1.000	1.000	1.000	1.000
	45	LRT	0.287	0.770	0.858	0.579	0.908
		MIC	0.344	0.797	0.890	0.654	0.920
		Ad-CUSUM	0.586	0.946	0.967	0.846	0.965
80	20	LRT	0.341	0.843	0.960	0.738	0.989
		MIC	0.421	0.898	0.976	0.807	0.995
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	40	LRT	0.581	0.966	0.993	0.910	0.997
		MIC	0.703	0.990	0.997	0.961	1.000
		Ad-CUSUM	0.994	1.000	1.000	1.000	1.000
	60	LRT	0.488	0.921	0.975	0.830	0.988
		MIC	0.566	0.944	0.985	0.867	0.994
		Ad-CUSUM	0.712	0.988	0.996	0.936	0.995
100	25	LRT	0.468	0.946	0.992	0.888	0.998
		MIC	0.497	0.954	0.994	0.899	0.998
		Ad-CUSUM	1.000	1.000	1.000	1.000	1.000
	50	LRT	0.752	0.997	1.000	0.975	1.000
		MIC	0.807	0.999	1.000	0.984	1.000
		Ad-CUSUM	0.995	1.000	1.000	1.000	1.000
	75	LRT	0.594	0.981	0.996	0.912	0.999
		MIC	0.611	0.984	0.996	0.925	0.999
		Ad-CUSUM	0.786	0.991	0.998	0.964	0.999

.

Based on the simulation results from Table 2, Table 3 and Table 4, the following conclusions can be drawn.

(1)

The Ad-CUSUM method outperforms in most scenarios. Overall, the Ad-CUSUM method offers higher test power compared to LRT and MIC methods, particularly when the time point size is small and the significance level is low. Regardless of whether the time point size is small or large, the test power of the Ad-CUSUM method is nearly 1.000, demonstrating its high sensitivity in detecting changes in the two-stage Inverse Gaussian degradation model. In contrast, the LRT method exhibits relatively lower power, and although the MIC method performs well, it is still slightly inferior to the Ad-CUSUM method in most cases. This may be attributed to the Ad-CUSUM method’s direct consideration of data discrepancies and its monitoring of changes by gradually accumulating data variations, thereby enhancing its sensitivity to changes.

(2)

Improvement of test power with increasing time point size. As the time point size n increases, the test powers of the LRT, MIC, and Ad-CUSUM methods all improve. For LRT and MIC, the enhancement in power is relatively significant. However, the Ad-CUSUM method already exhibits high test power (nearly 1.000) with small n.

(3)

The effect of the significance level on test power. With the same parameter settings, as the significance level decreases from 0.10 to 0.01, the test power of both methods generally decreases. However, the decrease in power for the Ad-CUSUM method is relatively small, and it still maintains a high test power. This is because, with increasing n, parameter estimation becomes more accurate, thereby enhancing the power of change-point detection.

(4)

The relationship between change-point location and test power. For the same sample size and parameter settings, the closer the change point occurs to the middle, the higher the test power tends to be.

(5)

The stability of the Ad-CUSUM method. The Ad-CUSUM method demonstrates high stability, particularly under different parameter combinations, where its test power remains stable and close to 1.000, especially at significance levels $\alpha =0.05$ and $\alpha =0.01$, where it performs exceptionally well.

The above conclusions indicate that the Ad-CUSUM method exhibits superior performance in detecting change points in the Inverse Gaussian process models, particularly with small n and low significance levels. Its stability and sensitivity make it highly advantageous for practical applications.

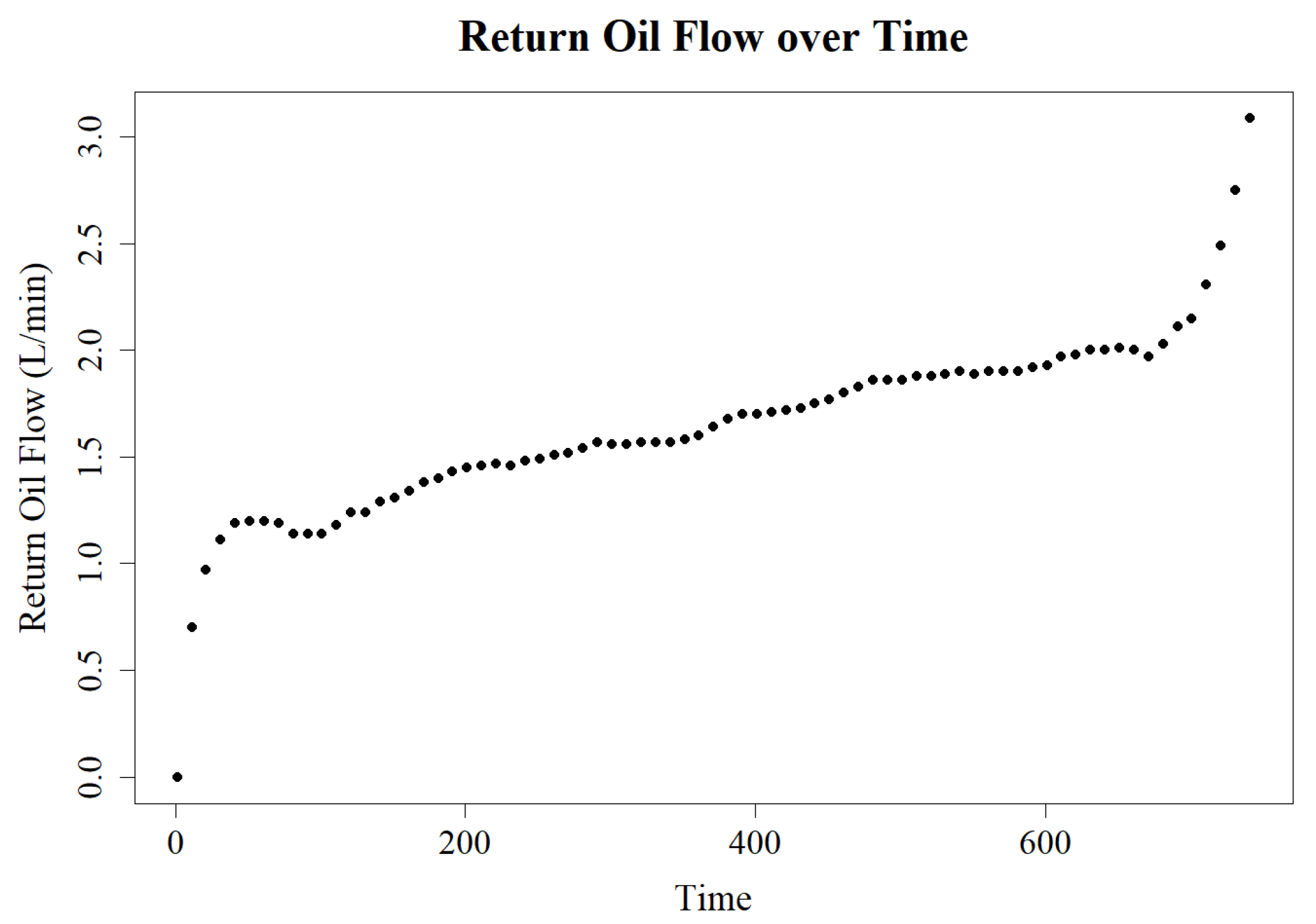
5. Empirical Analysis: Return Oil Flow Data of the Hydraulic Piston Pump

The hydraulic piston pump is a key component in aircraft hydraulic systems, primarily used to provide hydraulic power. It is widely used in various functions such as flight attitude control, braking systems, and others. The degradation of its performance directly affects the reliability and safety of the entire system. Therefore, studying the degradation process of the hydraulic pump is of significant importance. In this study, we use the return oil flow data of the hydraulic piston pump as a key indicator of performance degradation. The dataset is taken from Ma et al. [34], in which the return oil flow is used as the degradation index, and it is verified that the Inverse Gaussian process can be applied to fit this dataset. In this test, the hydraulic pump operates under different working loads, and the return oil flow serves as an indirect reflection of the internal leakage of the pump, thus representing the degradation process of the pump. After smoothing the original data, one smoothed data point is selected every 10 h, resulting in a total of 75 data samples. Building on the previous analysis, we explore different model fits to further elucidate the degradation process of the hydraulic piston pump.

Considering the empirical validity of the model, we now fit the dataset to the Wiener process, as well as the Inverse Gaussian process. We computed and compared the log-likelihood (logLik), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC). In all cases, the Inverse Gaussian process model performed better. However, this superior performance may not always be statistically significant, and we cannot necessarily generalize this finding to other situations. In fact, our dataset was specifically chosen based on the Inverse Gaussian model. For other scenarios, the Wiener process or alternative models may be more suitable and provide a better fit to the data. The comparison results are shown in

Table 5. Model comparison results.

Model	logLik	AIC	BIC
Inverse Gaussian	105.708	−207.415	−203.006
Wiener	57.115	−110.230	−105.821

.

The performance degradation trend shown in Figure 1 aligns with a typical mechanical wear process. As clearly demonstrated in Figure 1, the degradation process of the hydraulic pump can be divided into three phases.

(I)

Initial Wear Stage. During the first 80 h of the test, the return oil flow increases sharply, indicating that the pump experiences rapid initial wear, resulting in a rapid performance decline.

(II)

Stable Wear Stage. Around 200 h, the return oil flow stabilizes at approximately 2.0 L/min, showing that the wear rate of the pump has stabilized, and its performance remains steady.

(III)

Accelerated Degradation Stage. As wear continues to accumulate, the return oil flow begins to gradually rise, indicating that the pump has entered the critical failure period. The wear rate increases sharply, eventually leading to the loss of pump functionality.

To identify the change points of the hydraulic pump at different degradation stages, the proposed improved test method based on the CUSUM statistic is applied, combined with the binary segmentation method to analyze the return oil flow data. The details are listed as follows:

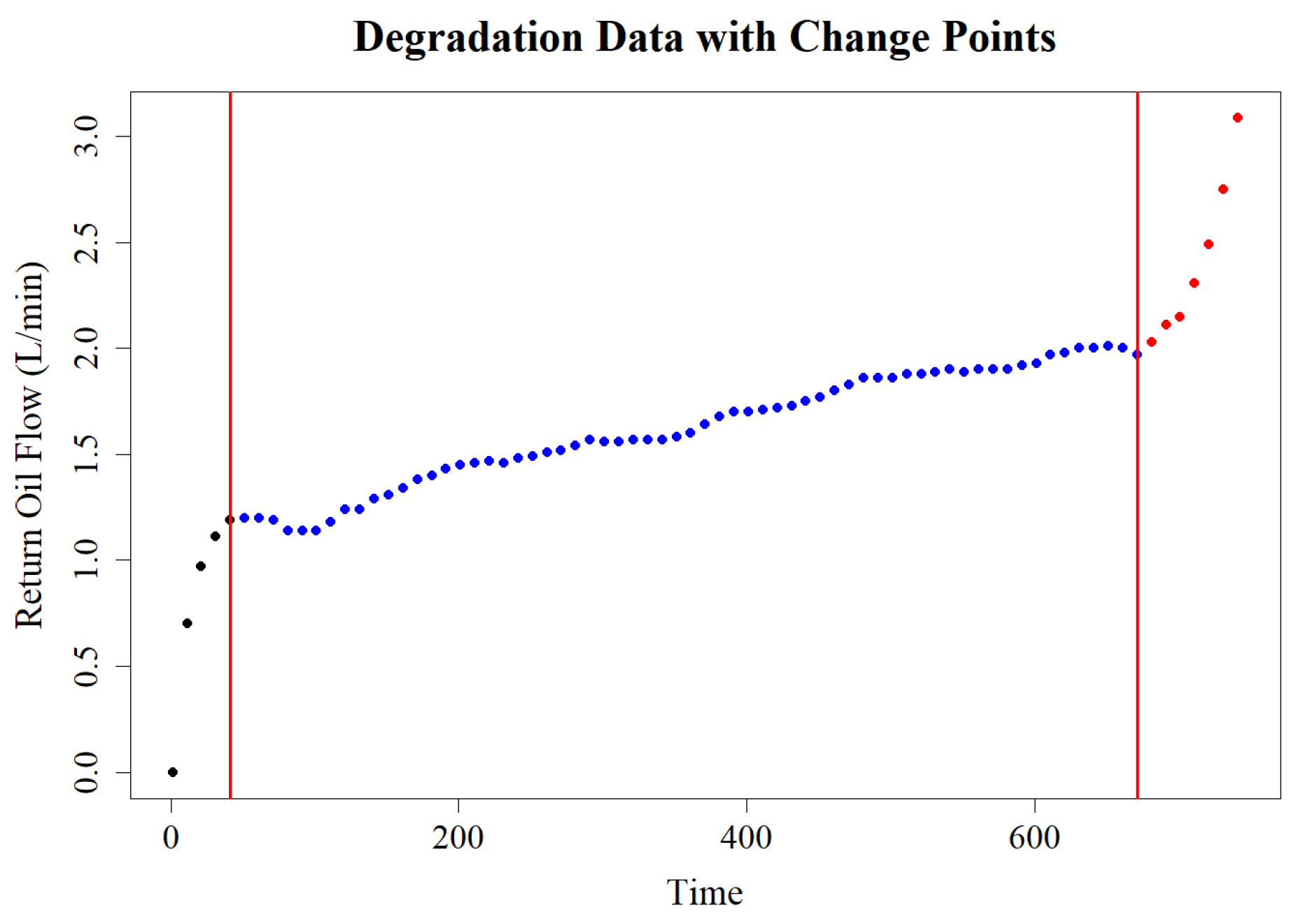
Step 1.

First, perform change-point detection procedure on the entire return oil flow data sequence from 1 to 75, and calculate the test statistic value of the original data using the adjusted CUSUM statistic, as shown in Figure 2. Here, the Bootstrap method is used, with $B=1000$, yielding a p-value far smaller than 0.05. Therefore, we reject the null hypothesis and conclude that a change point exists. During this process, the first change point is detected at position 5, with a CUSUM statistic value of 11.416 and a p-value of 0.02, indicating that this change point is statistically significant. The occurrence of this change point suggests that the return oil flow undergoes a significant change at 41.25 h, possibly indicating the early stages of degradation in the hydraulic piston pump.

Step 2.

After determining the first change-point location, we divide the data into two subsequences and calculate the adjusted CUSUM statistic for each subsequence to further identify potential change points. In the subsequence from 6 to 75, the CUSUM statistic reaches a maximum value of 12.581, and the change point is located at position 68, with a p-value of 0.001, indicating extremely high statistical significance. This change point marks 671.25 h as the second critical moment in the performance degradation of the hydraulic piston pump, likely related to the accumulation of wear or failure in the pump. Repeating the above steps, no further change points are detected.

Step 3.

Continuing from Step 2, subsequences are further divided, and the adjusted CUSUM statistic is calculated for each segment. For the subsequence from 5 to 68, the p-value is 0.4620, which is greater than 0.05. No change point is detected, indicating that after this stage, the performance degradation of the pump entered a relatively stable phase.

In summary, this study successfully identified two significant change points in the return oil flow data of the hydraulic piston pump by combining the adjusted CUSUM statistic with the binary segmentation method. These change points are located at 41.25 h and 671.25 h, respectively. The change points are marked with a red line in Figure 3.

As shown in Figure 3, these change points provide important quantitative analysis for the performance degradation process of the hydraulic pump. The first change point may be related to the early wear and system instability of the hydraulic pump, while the appearance of the second change point is likely associated with the pump’s long-term operation and accumulation of wear, indicating that the degradation rate of the pump significantly accelerated at this point. This aligns with the actual situation. The pump first undergoes a break-in period, during which the return oil flow rapidly increases. Then, as the pump enters the stable wear stage, the increase in return oil flow slows down. Finally, the pump enters the rapid wear stage, and the return oil flow rises sharply again. Through the identification of these change points, we can better understand the performance changes of the hydraulic pump at different stages and promptly replace the pump based on usage conditions.

6. Conclusions

This paper proposes an improved change-point detection method suitable for the Inverse Gaussian process to address the issue of structural changes in engineering degradation data. The method is based on CUSUM, and its detection capability under change-point structured data is validated through multiple simulation experiments. The results demonstrate that the adjusted CUSUM method outperforms the classical likelihood ratio method and modified information criterion in terms of both test power and computational efficiency. Through empirical analysis of the hydraulic piston pump degradation data, the method accurately identifies two structural change points, clearly dividing the degradation phases into break-in, stable, and aging periods. The effectiveness of this method in engineering degradation process modeling is validated, and it provides decision support for preventive maintenance and health condition management by evaluating the performance evolution trends before and after the change points.

However, there are several directions worth further exploration. In this study, it is assumed that change points occur only at discrete observation time points. While this assumption facilitates mathematical derivation and computational implementation, in actual engineering, changes in degradation rates may occur at any position on a continuous-time axis. Therefore, future work could explore the introduction of continuous-time change-point modeling methods, such as those based on sliding window estimation or Bayesian segmentation processes, to achieve more accurate estimation of change points at non-observed points. Additionally, consideration could be given to degradation models involving $\Lambda \left(t\right)$ in nonlinear form. Practically, due to environmental complexities in real-world operation, the cumulative intensity function $\Lambda \left(t\right)$ in degradation processes typically exhibits nonlinear temporal characteristics rather than following a simple linear pattern. Consequently, accurate estimation of $\Lambda \left(t\right)$ becomes a prerequisite for reliable change-point detection analysis. The Inverse Gaussian process is particularly suitable for modeling degradation processes with irreversible wear characteristics. However, for certain mechanical equipment that degrades in the short term due to lack of lubrication but can partially recover performance after maintenance, the Inverse Gaussian process may no longer be applicable. In such cases, a two-stage Gamma-Inverse Gaussian process might need to be considered.