Abstract
The arrival of tracers at boundaries with defined distances from the origin of their motion in stochastically fluctuating advection processes is investigated. The advection model is a stationary one-dimensional integrated stochastic process with an arbitrary a priori known correlation and with possible mean drift. The current (direction-sensitive), the total flux (direction-insensitive) of tracers through a non-absorbing boundary, and the first-passage times of the tracers at an absorbing boundary are derived depending on the correlation function of the carrying flow velocity. While the general derivations are universal with respect to the distribution function of the advection’s increments, the current and the total flux are explicitly derived for a Gaussian distribution. The first-passage time is derived implicitly through an integral that is solved numerically in the present study. No approximations or restrictions to special cases of the advection process are used. One application is one-dimensional Gaussian turbulence, where the one-dimensional random velocity carries tracer particles through space. Finally, subdiffusive or superdiffusive behavior can temporarily be reached by such a stochastic process with an adequately designed correlation function.
MSC:
58J65
1. Introduction
Currents and arrival rates on non-absorbing boundaries, or first-arrival times on absorbing boundaries (also called first-arrival rates or first-passage times), in integrated stochastic processes are relevant to practical applications such as diffusion reactions, turbulence, animal movements, epidemic dynamics, and financial markets. Flow meters often use the time of flight of natural tracers or artificial markers between two detection locations separated by a given distance to determine the flow rate.
Currents, counting tracer arrivals at a boundary moving upwards with a positive sign and those in the opposite direction with a negative sign, and total arrival rates, counting all tracer arrivals at the boundary regardless of their direction of motion, basically depend on the distribution of tracer-particle locations over time and their actual velocities at that time. If both parts of that are known, then these quantities can be obtained by integrating over all possible arrival velocities with their respective probability densities, either from explicit solutions or through one-dimensional numerical integration.
Unfortunately, the prediction of first-arrival statistics is much more complicated. If tracers cross the virtually defined boundary for the first time, then a certain probability remains that the same tracers will return to the boundary later—a second, third, or even more times. A possible solution to match a virtual boundary for prediction with the absorbing character is to take the total arrival rate without absorption, including the first and all higher-order arrivals, and reduce it by the portions that result from tracers returning after having reached the boundary once before. This leads to an integral formulation of the relation between first arrivals and all arrivals together, including returns, see [1], which can be arbitrarily complex, e.g., if the velocity has a temporal correlation.
There exist a few methods for solving such problems, e.g., involving the Laplace transform in cases where the integral formulation can be interpreted as a deconvolution, solved by dividing the respective Laplace transforms [2]. A second method is that of reflected negative images of the tracers, which can be used when tracers that have reached the boundary are introduced and superimposed with a negative amplitude to imitate their removal from the ensemble of tracers [3]. This requires symmetry in the distribution of their motion and independence from history. Therefore, this method is limited to special cases in which the processes comply with these conditions. Otherwise, approximations must be made, and the deviations between the process under investigation and the predictions for the approximated process need quantification; see [4].
In the present paper, stationary one-dimensional integrated stochastic processes are investigated with arbitrary correlations and possible mean drift. The tracers start at a fixed position at a fixed time , and travel with the time-dependent velocity .
First, general formulations of currents, total arrival rates, and first arrivals are derived for the general case of an arbitrary probability density function of velocities u. Then, for the case of Gaussian-distributed velocities with the mean drift velocity and the variance , where denotes the expectation, the current and the total arrival rate of the tracers at non-absorbing boundaries are given as explicit solutions of the respective integrals involving the arbitrary but a priori known correlation function
The process is assumed to be stationary; thus, and do not change with time. While and are fixed, is not given; it is randomly chosen from the distribution .
Unfortunately, the probability density of the first-passage times for such processes with correlation does not comply with the boundary conditions of the effective methods described above. Therefore, the method of numerical integration is used here, including for arbitrary correlation functions.
For random walks, the initial conditions are usually chosen as and , and the tracers typically prefer the positive direction of motion () if a mean drift is encountered. However, for first-passage problems, the initial position at the starting time is commonly chosen as positive, , and the absorbing boundary is placed at . However, the calculations below use only relative quantities like distances traveled in a certain time interval, such that they are independent of the specific arrangements. In the present study, the example scenarios simulated comply with the usual arrangement for first-passage problems. The derivations in the appendix then consistently yield equations for relative displacements within time intervals. The only difference that requires consideration is whether the tracer is bound to the positive or negative side of the boundary. Coming from the positive side, the tracer passes the virtual boundary for the first time in the negative direction, that is, with a negative velocity; the second time with a positive velocity, and so on. Conversely, coming from the negative side, the first and all odd counts of boundary crossings occur with positive velocity, and all even boundary crossings occur with negative velocity. The drift velocity can also be chosen arbitrarily. However, to ensure that all tracers released will hit the boundary sooner or later, the drift velocity must be negative if the tracer is released above the boundary. For positive drift, tracers may move away from the boundary and never reach it. While the calculations below stay valid, the interpretation of the first-passage distribution as a probability density function becomes problematic because some tracers are lost and do not yield any specific first-passage time. The situation can be resolved by interpreting all lost tracers as having an infinite first-passage time. Such cases can be constructed and treated with the framework below, and the equations will still lead to meaningful estimates. However, this is beyond the scope of the present investigation.
2. General Cases for Arbitrary Distribution and Correlation
2.1. The Current of Tracers Through a Boundary
Assuming is the spatial probability density that a tracer has traveled the distance within time t, the current through a boundary at distance x (relative to ) at time t is (method Q1):
The integral is the probability that the tracer is above the boundary (between and ∞) at time t, regardless of whether it was released above or below the boundary (the distance x can be positive or negative). The temporal derivative of the probability given by the integral, then, is the current through the boundary per tracer released. Note that the tracers may cross the boundary multiple times. The upwards flux from below the boundary is counted as positive, whereas the opposite flux is counted as negative, similar to a current of charges through the boundary, where equal positive and negative fluxes cancel each other out. This method of deriving the current through a non-absorbing boundary is very general with respect to the investigated process and the distributions of velocities. The task is to find an appropriate . For stationary integrated processes with increments u having a Gaussian distribution and correlation , explicit expressions are given in Section 3 for all quantities occurring in the derivations, including , which is the same function as with its argument replaced; see 3 in Section 3.
Since the different methods for deriving the various currents, fluxes, and arrival rates will be compared quantitatively in the Results section, the methods will be indicated by a numerical index for the specific quantity, e.g., the method above will be denoted as Q1, and the following alternative method as Q2.
Alternatively (method Q2), the current through the boundary is obtained from the probability density that a tracer is positioned at the boundary at distance x from the origin at time t. However, the current additionally depends on the velocity of the tracer u at its arrival at the boundary. If a certain spatial number density of tracers is in infinitesimal proximity to the boundary, then this spatial number density moves through the boundary with its arrival velocity, and the current is therefore proportional to that velocity. Consequently, the relation between the spatial number density f and the current q depends on the arrival velocity u, namely,
where is the current–velocity probability density and is the space–velocity probability density of having traveled the distance x within time t and having reached the boundary (at position ) with the velocity u. Taking the arrival velocity as the independent variable, can be obtained as
where is the spatial probability density of having traveled the distance x within time t, conditioned on the arrival velocity u at the boundary at time t, and is the probability density of all possible arrival velocities u. Then, the current through the boundary at time t is given by the integral
over all these possible arrival velocities, u. Note that can be any distribution. However, for Gaussian distributed velocities, explicit expressions are given in Section 3 for all probability densities occurring in the derivations, which make use of an arbitrary but a priori known correlation function . For , see 1 in Section 3; for , see 4. The explicit solution of the integral in Equation (5) is given in 7.
2.2. The Arrival Rate (Absolute Flux) of Tracers at a Boundary
Similarly, the arrival rate, or absolute flux, of tracers at a non-absorbing boundary depends on the absolute magnitude of the arrival velocity and on the spatial probability density of having reached the distance x after time t, as
where both directions of tracer arrivals at the boundary are counted as positive. Then, the total arrival rate at the non-absorbing boundary at time t (method J1) is given by the integral
over all possible arrival velocities u from its probability density function .
Limiting the integration to only positive velocities
yields the flux of tracers passing the boundary in the positive x direction, that is, those with positive velocities u. Accordingly,
yields the flux of tracers passing the boundary in the negative x direction, that is, with negative velocities u. For the arrangement where the tracers are released above the boundary, is the sum of all arrivals of tracers passing the boundary away from their origin with negative velocity, which occurs for the first, third, and all further arrivals of odd order. The remaining arrivals with even orders all have positive velocities and are included in . If the third and all other higher odd arrivals can be neglected, may be used as an approximation for first-passage times (method P1). This is the case only for strong mean drift velocities or strong temporal correlations of the varying advection velocity. This approximation is limited in its applicability and is shown in the Results section below for comparison only. Again, the expressions above are valid for various probability densities of velocities u. For the Gaussian distribution, Section 3 gives explicit expressions for in 1, in 4, and for , and in 8.
2.3. First-Passage Probability Density
2.3.1. Rough Approximation
For the arrangement of releasing the tracers above the boundary, counts the first and all higher odd orders of arrivals as negative and all even orders of arrivals as positive; inverts the counting directions; counts the first and all higher orders together; and counts the first and all higher odd orders of arrivals. Therefore, all of these quantities deviate from the distribution of first arrivals because of the included contributions from higher-order arrivals. In Figure 1a, the quantities , , and are shown in comparison with the first-passage distribution obtained from a numerical simulation of a stochastic process with an artificial correlation function (see Section 4.4), chosen such that repeated returns of tracers to the boundary location are possible. In the diagram, intervals can be identified with changing contributions of different orders of arrivals, which can be identified in the drawn example traces in Figure 1b.
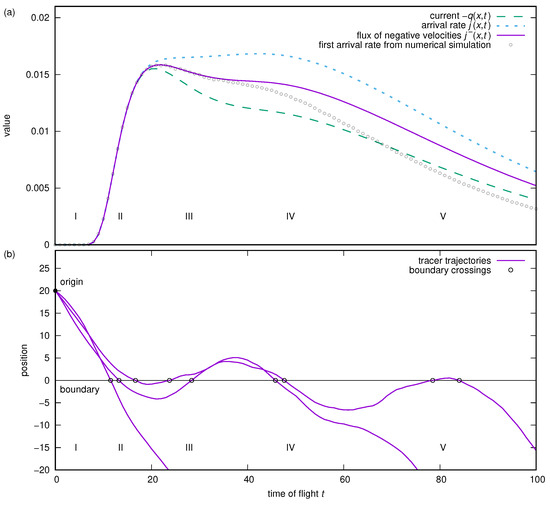
Figure 1.
(a) Current, total arrival rate (absolute flux), and flux from negative velocities only, in comparison with the empirical first-passage distribution from simulated tracers; (b) sketch of the arrangement of tracer release and the boundary, and three example traces.
- Below a certain time (interval I), no arrivals occur because the tracers need a certain time to reach the boundary.
- Then (interval II) tracers arrive at the boundary for the first time. Because of the correlation of the velocity, which corresponds to a certain inertia of the tracers, no immediate return is expected, and higher-order arrivals do not occur. Up to this time of flight, there is no difference between the various quantities shown; they all follow the distribution of first arrivals from the simulated process.
- Then (interval III) tracers return to the boundary with positive velocities. Here, the current and the arrival rate start to deviate because of their opposite sign when counting arrivals with positive velocities. If only negative velocities are considered with , the second arrivals are not counted, and this flux still follows the distribution of first arrivals from the simulated process.
- Then (interval IV), the third arrivals occur. Unfortunately, they contribute to because of their negative velocities, resulting in a deviation of this flux from the first-arrival distribution.
- Later (interval V), the fifth and all higher odd orders of arrivals occur. These also contribute to and cause a further deviation of this flux from the first-arrival distribution.
With long-lasting correlations or a strong mean velocity, the probability of returning tracers may be low enough, or delayed long enough, to allow the prediction of the flux to be used as an approximation of the first-arrival distribution for small times of flight (method P1). However, if third- and higher-order odd arrivals must be considered, this prediction requires further corrections.
The following numerical solution primarily makes use of the arrival rate, allowing only negative velocities, counting first arrivals together with all higher-order odd arrivals. Then, the fraction of this arrival rate is calculated from the returns of tracers that have been at the boundary previously. After removing these fractions of higher-order arrivals, only the first arrivals remain in the predicted rate.
2.3.2. Numerical Solution
To distinguish between first and higher-order odd arrivals within the actual arrival rate, the possibility of tracer returns must be considered, which strongly depends on the velocity over time. For that, the actual arrival rate–velocity density at the boundary at distance x from the origin of the motion is split into first arrivals at time t with arrival velocity u at the boundary, and those in which the tracer has returned to the boundary at time t with velocity u from a previous first arrival at the boundary at time and with first-arrival velocity , according to an appropriate first-arrival rate–velocity density . For clarity in notation, velocity and position at a particular time t are denoted without the prime symbol, as u and x, whereas both are denoted with the prime symbol at a different time , namely and . In the given case, where the tracer returns to the same distance x from the origin, is identical to x. Figure 2 shows the composition of from first arrivals and higher-order arrivals with a previous first arrival at the boundary.
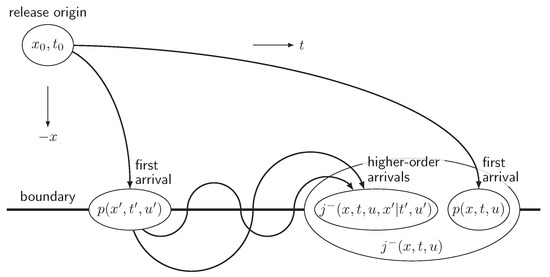
Figure 2.
Distinguishing between first and higher-order arrivals by identifying portions of the total arrival rate–velocity density that had their first arrival at time with velocity , according to the appropriate first-arrival rate–velocity density .
By integrating over all possible times and all possible velocities at the first arrival before t, all portions of originating from tracers that have been at the boundary previously are identified. For that, the correlation of the velocities must be considered, because and u are correlated as a function of the time lapse between and t, and the location of the tracer at the two time instances strongly depends on the velocities and their correlation. With being the arrival rate–velocity density at the boundary at distance x from the origin at time t with arrival velocity u, conditioned on having a previous observation of the tracer at distance from the origin at time with arrival velocity , the actual rate of tracer returns with negative velocities is given by
Together with the first arrivals at time t and velocity u, this yields the actual total arrival rate–velocity density, consisting of the first arrivals together with all odd-order arrivals for a specific arrival velocity u.
For confirmation of the correctness of the units— is a first-arrival rate–velocity density with units of . Integrated over all velocities and over a time t, this becomes unitless, because the first-arrival rate–velocity density p integrated over all possible arrival velocities and over all possible first-arrival times (before and beyond t) must ultimately be unity. The remaining quantities, namely , , and , all are arrival rate–velocity densities with the unit .
The actual first-passage rate–velocity density can just be obtained from by subtracting the returning tracers as
where, obviously, p is implicitly reused in the integral. Note that the distances x and are arguments of the function p; however, p is a joint probability density for time and velocity only. If x and are chosen to be identical, as for the return to the boundary, then and are the same function evaluated at different arguments—t and u at the actual arrival, and and at the previous (first) arrival, respectively. In this way, it is possible to derive the actual first-arrival rate–velocity density numerically by integration or summation over all values of p obtained up to times shortly before t. The integration or summation for numerical integration over must stop before t, because becomes infinite and describes the actual tracers passing the boundary instead of the tracers that are returned.
Note the inherent dependence of the first-arrival rates on both velocities, u and . Therefore, arrival rate–velocity densities have been kept so far without integrating over one or the other velocity. Accordingly, the numerical integration or summation requires the stepwise calculation of the two-dimensional joint probability density along the time axis, resolved for various arrival velocities. The integration over the arrival velocity u is performed last to obtain the final first-passage time density as a function of time in Equation (16).
Including the fact that all arrival rates depend on the appropriate spatial number density f and the actual velocity magnitude , this further leads to
The spatial number density f conditioned on the previous arrival needs to be reformulated, considering the dependence on u and as
where is the joint spatial number–velocity density at distance x from the origin at time t with arrival velocity u, conditioned on the previous arrival at the boundary at time with arrival velocity , as used before, whereas is the spatial density at distance x from the origin at time t, conditioned on the previous arrival at the boundary at time with arrival velocity and on the actual velocity u. The probability density of the actual velocity u at time t is , conditioned on having previously had velocity at time . Since the process is assumed to be stationary and time-invariant, depends not on a specific but on the time span between the two arrival instances at and t only. Therefore, the formal condition of on has been dropped. Since the process is assumed to be linear, is closely related to the correlation function of the velocity. For Gaussian distributed velocities, Section 3 gives an explicit expression for in 2.
On the other hand, the spatial number density conditioned on the previous arrival at with and the actual velocity u, can be obtained from the joint probability density of having reached distance at and x at t, conditioned on velocity at and velocity u at t, together with the spatial number density of having reached at under the condition of velocity at and velocity u at t, independent of x.
Note that in the specifications for the Gaussian distribution in Section 3, for the denominator, the quantities with and without prime symbols are exchanged as in 5, however, with exactly the same function. The numerator is given in 6.
Finally, by integrating over all possible arrival velocities u from its distribution , one obtains the first-arrival rate (method P2):
Because of the negative drift velocity, all tracers will eventually arrive at the boundary. Therefore, the predicted rate of first arrivals per tracer is identical to the probability density of the flight times until the first arrivals.
3. Specifications for Gaussian Distribution of Increments
For the numerical solution of the integrals above, probability densities of the increments (velocities) and of the distances traveled within time t are needed. To derive the portions of trajectories that return to the boundary, in addition to the unconditioned probability densities, the probability densities of observing velocity u at time t conditioned on one observation of a specific velocity at time , and those conditioned on two observations, at and at time , are required. If a Gaussian distribution of increments is assumed (velocity observed by a fluid element along its path), the following ingredients of the above formulas can be specified:
- is the (unconditioned) probability density of a tracer with velocity u. Then, is the probability that a fluid element observes a velocity within the range . Assuming a Gaussian distribution of velocities, this becomeswith a given mean drift velocity and velocity variance .
- is the probability density of a tracer having velocity u at a time after a previous observation, conditioned on having had velocity at that observation. Then, is the probability that a fluid element has a velocity within the range under the condition of having had velocity at the previous observation ago. Since the process is assumed to be stationary, velocity statistics are time-reversible; hence, . Assuming a Gaussian distribution of velocities, this iswithand
- is the (unconditioned) probability density that a tracer has traveled the distance x within time t. Then, is the probability that a fluid element is within the range at a given time t. Assuming a Gaussian distribution of velocities, this iswithand following [5]which is, following [6]withwhere, again, is the given mean drift velocity and is the given variance of the velocity.
- is the probability density that a tracer has traveled the distance x within time t, conditioned on the arrival velocity u at the boundary at distance x to the origin of motion at time t. Then, is the probability that a fluid element is within the range at a given time t under the condition of having the arrival velocity u at the boundary at distance x at time t. Assuming a Gaussian distribution of velocities, this is given by (derivation in Appendix A.2)withandwithand , as above, where, again, is the given mean drift velocity and is the given variance of the velocity.Both integrals and are characteristic of the diffusive behavior of the process. Therefore, these two integrals are shown for the various test processes in the following test section, together with the corresponding correlation functions.
- is the probability density that a tracer has traveled distance x within time t conditioned on having velocity u at the boundary at distance x at time t and velocity at a previous (or later, as in the case of the derivations of the numerical solution of first arrivals above) observation at time . Then, is the probability that a fluid element is within the range at a given time t under the condition of having the arrival velocity u and having velocity at time . Assuming a Gaussian distribution of velocities, this is given by (derivation in Appendix A.4)withandNote that both and also depend on . The functional dependence is dropped in the notations because of the simplification of the notation in the following derivations. Particular specifications are given in each of the following cases.
- is the joint probability density that a tracer has traveled the distance x within time t and distance at time , conditioned on the arrival velocity u at distance x at time t and arrival velocity at distance at time . Then, is the probability that a fluid element is within the range at a given time t and within the range at time under the condition of having the arrival velocity u at time t and arrival velocity at time . Assuming a Gaussian distribution of velocities, this is given by (derivation in Appendix A.5)withand withwithandandwith
- With and being Gaussian, one obtainsUsing the substitutionsone obtains the following (method Q3):
- With and being Gaussian, one obtainsUsing the substitutions , , and as above, one obtains the following (method J2):By limiting the integration range to positive velocities only, one obtainsBy limiting the integration range to negative velocities only, one obtains the following (method P1):
4. Test Cases
The following calculations (numerical integrations for the predictions and simulations) were carried out with a time step of . The numerical integration for the first-passage prediction further requires integration over velocities, including the storage of the time- and velocity-dependent probability densities . For this, the velocity was resolved in steps of within plus/minus six standard deviations. The results shown in the diagrams were obtained using a notebook computer within a few hours. The programs used are provided on request to the corresponding author.
4.1. Telegrapher’s Process
The first test case is a random walk process with discrete time and continuous, random, and independent increments. This process is also known as the Telegrapher’s process. The time step is , the increments are Gaussian distributed with a mean value of and a variance of . This yields a mean value of the position reached by summation of the steps within time t of and a variance of . Figure 3a shows the correlation function of this process, which has a rectangular shape. It is one between and , and zero outside this interval, since the velocity of motion is held constant over each time step and consecutive steps are uncorrelated. The two appropriate integrals and are shown in Figure 3b,c.
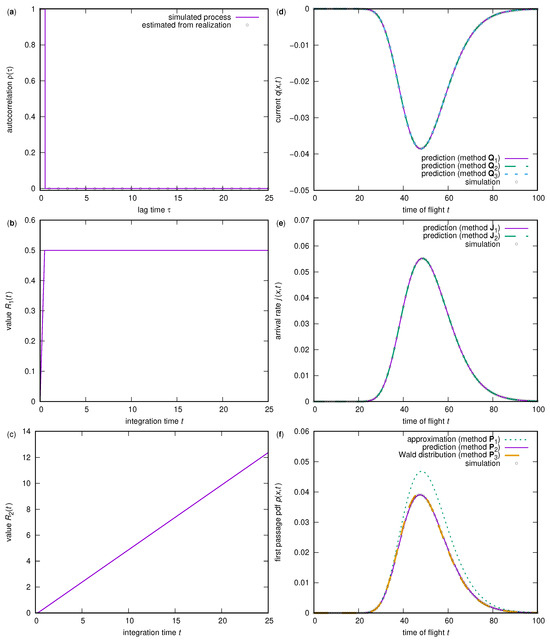
Figure 3.
Telegrapher’s process: (a) correlation function , (b) integral , (c) integral , (d) current , (e) total arrival rate through a non-absorbing boundary, and (f) first-passage time probability density for a given distance from the origin to the boundary.
The simulated tracers are released at and the boundary assumed is located at . Since the random walk, with a standard deviation of compared to a mean velocity of , yields significant backflow, the currents through the boundary and the total arrival rate of tracers at the boundary differ in their absolute amplitudes (Figure 3d,e) due to different sign conventions for counting returning flows through the boundary toward the release origin of the tracers. The methods for predicting the current and the total arrival rate are Q1, as given by Equation (2), Q2, as given by Equation (5), and J1, as given by Equation (7), which are numerically resolved integrals, as well as Q3, as given by Equation (50), and J2, as given by Equation (53), which are explicit solutions for the Gaussian distribution. All methods agree well with the results from a Monte Carlo simulation of the process, with numerical realizations of the process.
Due to the frequent steps in the positive direction, tracers may return to the boundary, and third- and higher-order odd crossings of the boundary become significant. Therefore, the approximation of the first-arrival rates by method P1, as given in Equation (55), which counts fluxes with negative velocities only, is not appropriate. A deviation of this prediction method from the first arrivals obtained from the simulation can be seen in Figure 3f. Method P2, as introduced in Equation (16), yields suitable results.
Assuming , while the diffusion coefficient remains finite leads to Wald’s distribution
for first arrivals (method P3). Due to the finite time step for the simulated process, Wald’s distribution shows a small but noticeable systematic deviation from the values obtained from the simulated process in Figure 3f.
The maximum absolute deviations between the predictions and the simulations in Figure 3 are as follows: Q1: ; Q2: ; Q3: ; J1: ; J2: ; P1: ; P2: ; P3: . The deviations between the various current predictions and those between the total arrival rates are negligible (< and <, respectively). The deviation between P2 and Wald’s distribution (P3) is , whereas the deviations between P2 and the simulation are smaller than those between P3 and the simulation.
4.2. Exponential Decay
The second test case is an integrated Ornstein–Uhlenbeck process with Gaussian distributed increments (velocities) with a mean value of and a variance of . The simulated tracers are released at and the boundary assumed is located at . The correlation function for the Ornstein–Uhlenbeck process has an exponential decay (Figure 4a):
and yields the appropriate integrated functions and (Figure 4b,c), given by
The integral timescale for the chosen process is , which can be read directly from Figure 4b.
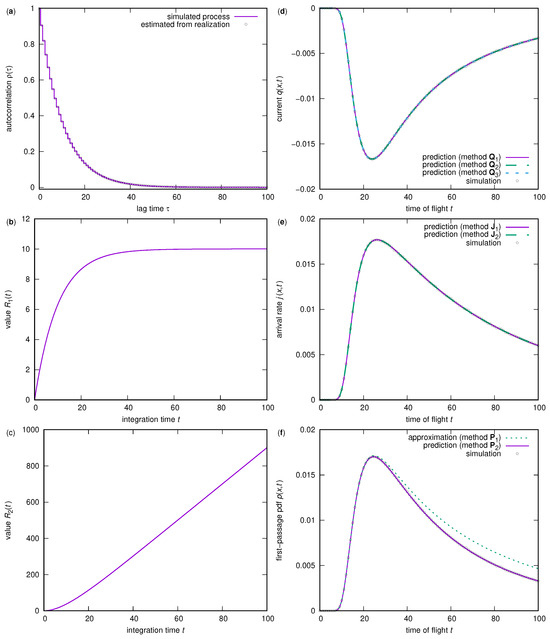
Figure 4.
Ornstein–Uhlenbeck process: (a) correlation function , (b) integral , (c) integral , (d) current , (e) total arrival rate through a non-absorbing boundary, and (f) first-passage time probability density for a given distance from the origin to the boundary.
The methods for predicting the current and the total arrival rate are Q1, as given by Equation (2), Q2, as given by Equation (5), and J1, as given by Equation (7), which are numerically resolved integrals, as well as Q3, as given by Equation (50) and J2, as given by Equation (53), which are explicit solutions for the Gaussian distribution. All methods agree well with the results from a Monte Carlo simulation of the process with numerical realizations of the process.
Due to possible positive velocities and the resulting returns of tracers to the boundary, third- and higher-order odd crossings of the boundary become significant. Therefore, the approximation of the first-arrival rates by method P1, as given by Equation (55), counting fluxes with negative velocities only, is appropriate for small travel times only, where higher-order arrivals are still rare. A deviation of this prediction method from the first arrivals obtained from the simulation can be seen in Figure 3f, at longer passage times on the descending slope of the curve. Method P2 as introduced here in Equation (16), yields suitable results, which agree well with the simulation.
An explicit solution for the first-arrival rate is not provided here. Such solutions exist only for special cases, either without drift or with a cooperative relation between the mean drift, the velocity fluctuation, and the position of the boundary [7,8,9,10,11,12]. However, the general case has no explicit solution so far.
The maximum absolute deviations between the predictions and the simulations in Figure 4 are as follows: Q1: ; Q2: ; Q3: ; J1: ; J2: ; P1: ; P2: . The deviations between the various current predictions and those between the total arrival rates are negligible (<).
4.3. Strong Correlation
The third test case is a process in which a tracer starts at time at position with a random velocity that remains constant during the travel of this particular tracer. Since this ballistic behavior yields infinitely lasting correlations, this test case is called a “strong” correlation.
The individual tracers move with a randomly chosen velocity that remains constant during the traveling time. Therefore, the traveling time to reach the boundary at distance x is inversely proportional to the tracer’s velocity. The velocities are Gaussian distributed with a mean value of and a variance of . This yields a reciprocal Gaussian distributed traveling time of the tracers to reach the boundary at . Since the velocities stay unchanged, only negative velocities will let the tracer reach the boundary without any later backflow. Therefore, the magnitudes of all three given quantities—the current , the total arrival rate , and the first-arrival rate —are all identical,
except for the minus sign of the current, with the probability density of the velocities u. Note that the integral of the reciprocal Gaussian distribution may deviate from one, since positive velocities are possible, but they will not lead the tracer to reach the boundary. A common interpretation of this fact is to relocate all missing arrivals to infinity, thereby yielding a correct integral of one.
The simulation releases again tracers with the given Gaussian distribution of their velocities. Since some of the methods compared in Figure 5 cannot handle a constant correlation function, the process was additionally approximated with a very slowly decaying exponential correlation function (Ornstein–Uhlenbeck process) with an integral timescale of 10,000. The appropriate correlation functions and the integrals and are shown in Figure 5a–c for both the process with constant traveling velocity as well as for the very slowly decaying process, proving that the differences between the two processes are marginal and that the other results are comparable.
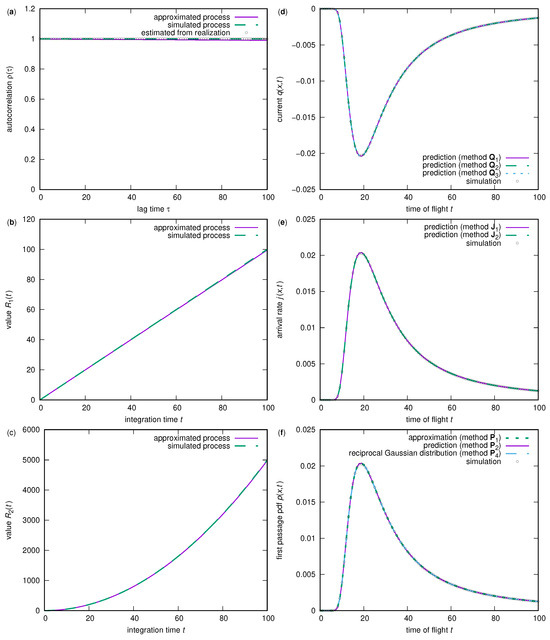
Figure 5.
Strong correlation: (a) correlation function , (b) integral , (c) integral , (d) current , (e) total arrival rate through a non-absorbing boundary, and (f) first-passage time probability density for a given distance from the origin to the boundary.
Since there is no backflow, the currents, total arrival rates, and first arrivals in Figure 5d–f are all identical, except for the minus sign of the current. All previously introduced methods—Q1, as given by Equation (2), Q2, as given by Equation (5), Q3, as given by Equation (50), J1, as given by Equation (7), J2, as given by Equation (53), P1, as given by Equation (55), and P2, as given by Equation (16)—yield identical results when based on the approximated process with slow exponential decay, whereas the empirical results are based on the simulation of the original process with constant velocity and constant correlation. However, no deviations are visible between the simulation and the prediction. Even the arrival rate with only negative velocities, as a rough approximation of the first-arrival rates, is valid for this test case, because no returns of the tracers to the boundary can occur. For comparison, the reciprocal Gaussian distribution as given by Equation (60) is shown in Figure 5f (method P4), which is an exact solution for the process with the constant tracer velocity, with no visible deviations from the other methods based on the approximated process with a slow decay.
The maximum absolute deviations between the predictions and the simulations in Figure 5 are as follows: Q1: ; Q2: ; Q3: ; J1: ; J2: ; P1: ; P2: ; P4: . The deviations between the various current predictions and those between the total arrival rates are negligible (<). The deviation between P2 and the reciprocal Gaussian distribution (P4) as the ground proof for this process is .
4.4. Artificial Correlation
In the last test case, a process is designed with an artificial correlation (see Figure 6a), causing relevant backflows. The integrals and are appropriate (Figure 6b,c). The fluctuating tracer velocity has a mean value of and a variance of . The simulated tracers are released at , and the boundary is located at .
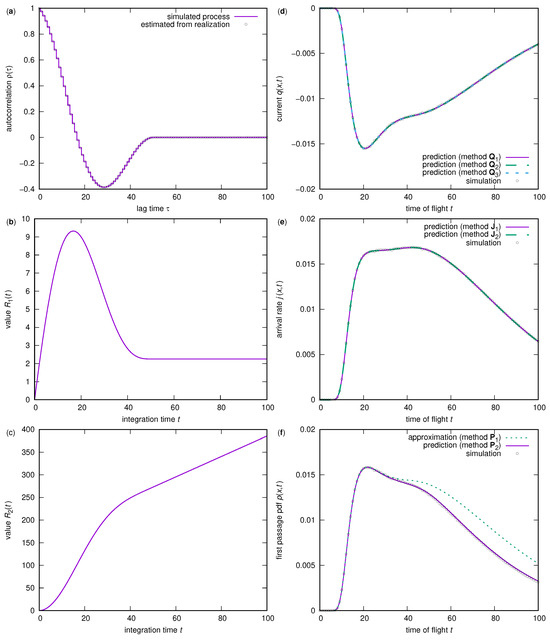
Figure 6.
Artificial correlation, using a cosine function modulated by a triangular envelope with finite duration: (a) correlation function ; (b) integral ; (c) integral ; (d) current ; (e) total arrival rate through a non-absorbing boundary; and (f) first-passage time probability density for a given distance from the origin to the boundary.
The methods for predicting the current and the total arrival rate are Q1, as given by Equation (2), Q2, as given by Equation (5), and J1, as given by Equation (7), which are numerically resolved integrals, as well as Q3, as given by Equation (50) and J2, as given by Equation (53), which are explicit solutions for the Gaussian distribution. Due to the complexity of the chosen correlation function, the shapes of the currents and total arrival rates are rich. However, all tested methods agree well with the results from a Monte Carlo simulation with numerical realizations of the process.
For this process, the approximation of the first-arrival rates by method P1, as given by Equation (55), counting fluxes with negative velocities only, is suitable for small travel times only, where higher-order arrivals are still rare. However, due to the middle part of the correlation function with negative correlation and a certain time delay, substantial backflow occurs, with many tracer returns, and deviations of this approximation method from the first arrivals obtained from the simulation become evident in Figure 6f. Method P2, as introduced here in Equation (16), yields suitable results for this test case as well.
The maximum absolute deviations between the predictions and the simulations in Figure 6 are as follows: Q1: ; Q2: ; Q3: ; J1: ; J2: ; P1: ; P2: . The deviations between the various current predictions and those between the total arrival rates are negligible ( and , respectively).
5. A Note on Anomalous Diffusivity
It has been shown that integrated linear stochastic processes, depending on the correlation function of their increments, can also lead to mean-square displacements that deviate from normal diffusion (see the function ). With a long-lasting correlation function, e.g., a power-law dependence on time, a simple form of superdiffusive behavior can be temporarily obtained (see Figure 7), whereas short correlation functions yield normal diffusion after a brief initialization period. With an appropriately chosen correlation function with negative values after a short initialization phase, even a simple form of a subdiffusive behavior is possible. This holds only over a limited time range. In the long term, however, the correlations of all these processes vanish and, finally, normal diffusive behavior will be reached again. Furthermore, the enhanced or suppressed convection due to the correlation of step increments is one aspect of anomalous diffusivity, and it is not conclusive for other processes exhibiting anomalous diffusivity.
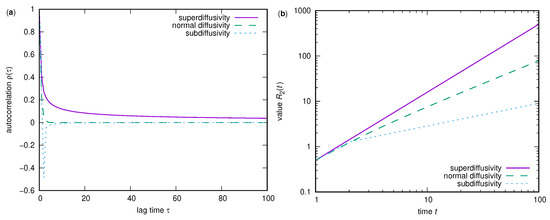
Figure 7.
(a) Correlation functions and (b) corresponding integrals yielding various diffusive behavior.
6. Conclusions
Currents (positive contributions from positive velocities and negative contributions from negative velocities), total arrival rates, and first-passage times of tracers through a boundary have been investigated. The distance traveled by the tracers from their release position follows a one-dimensional integrated stationary linear stochastic process with correlations and a mean drift. Except for stationarity, no restrictions are imposed on the correlation function or the spectral characteristics of the process, nor on the mean drift velocity, its variance, or the distance to the boundary.
General integral expressions are given for arbitrary velocity distributions. Currents and total arrival rates at a non-absorbing boundary are given as explicit solutions for Gaussian distributed velocities. The first-passage time probability density at an absorbing boundary is given as an implicit integral formulation, which is solvable numerically in an iterative procedure. No approximations are needed to derive the currents, total arrival rates, and first-passage probability densities. Therefore, the solutions have no systematic errors, except for (unfortunately, steadily growing) errors from imperfections of the numerical integration.
In four test cases with processes with different correlation functions, the introduced derivations have been tested successfully. Furthermore, with appropriate correlation functions, linear stochastic integrated processes can also mimic simple forms of anomalous diffusive behavior.
Author Contributions
Conceptualization, H.N. and S.E.; methodology, H.N. and S.E.; software, H.N.; validation, H.N. and S.E.; formal analysis, H.N. and S.E.; investigation, H.N. and S.E.; writing—original draft preparation, H.N.; writing—review and editing, S.E.; visualization, H.N. and S.E.; supervision, S.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no specific funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. (Un-)Conditional Probability Densities
In all cases, linearity and stationarity are assumed and used, and it is assumed that velocity u is Gaussian distributed.
Appendix A.1. Unconditioned Case
Here, the unconditioned probability densities of having velocity u (at any time t) and of having traveled the distance x within the time interval t are given. The probability density of the Gaussian distributed velocity u is
with the stationary mean and the stationary variance of the velocity. The velocity itself changes over time, following the correlation function
with velocities and at two arbitrary time instances, and , and with the expectation . For such a process, the distance x reached within time t is
which is also Gaussian distributed with
Following [5,6], the parameters of this distribution for a particular time t are
using the substitution
Note that the distribution of u is invariant with time, while the distribution of x changes with time. This fact impacts the following conditional distributions: the distribution of u can be expressed as a function of time intervals, whereas the distribution of x always depends on times relative to the starting or release time.
Finally, the joint probability density of having traveled after time and after time is given. If u is Gaussian distributed with a stationary mean and a stationary variance , then is also Gaussian
with
and with the mean values and and the respective variances and for the traveled distances and , as defined above as functions of t for a given distance x, together with the correlation coefficient , which is
Appendix A.2. One-Point Prediction Around One Observation
Here, the probability density of having velocity u conditioned on a previous (or later) observation , occurring earlier or later, and , the probability density of having traveled the distance x within time t, conditioned on the arrival velocity u (at time t), are presented.
Let be the probability density of velocity u at a time later than a previous observation under the condition that the velocity at that previous observation was . If u is Gaussian distributed with a stationary mean and a stationary variance , then is also Gaussian
with a mean and a variance .
To derive the mean , first, a globally mean-free process is assumed (). The mean value is reintroduced afterward. Assuming a mean-free process and the relation
with the expectation and the lag-time-dependent coefficient , which is independent of , the correlation function yields the following:
and the time invariance of velocity yields the following:
Combining the three expressions yields the following:
which finally gives
and
Reintroducing the stationary mean then yields
To derive the variance , the stationary variance is subdivided into a fraction , which is the effect of the (varying) velocity and a second fraction, which originates from the varying velocity within , which equals the desired conditioned variance .
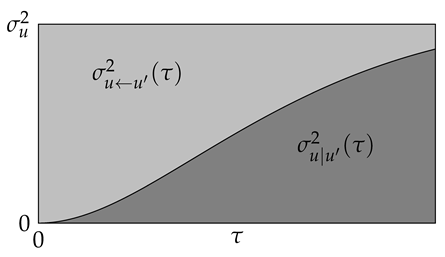
Because neither nor depends on the mean velocity , one can assume a mean-free process here without limiting universality. If a particular is given, it influences velocity u at time later through the value (in the mean-free case). If is chosen randomly from the distribution with the variance , the variance of is
The remainder up to is
Now, global stationarity and reversibility are used to shift and invert times. The distance traveled within time t is
It is assumed that the velocity at time is known, namely, it is . If the velocity for all is Gaussian distributed, then the distance traveled in time t is Gaussian distributed
with a mean and a variance . Note that both and also depend on . The functional dependence is dropped because of too many dependencies in the following derivations. Particular specifications are given in each of the following cases.
The mean distance traveled in time t is the integral of the mean velocity over t (for the known at , and the otherwise unknown for , which is only partially predictable and also holds for ):
making use of the substitution:
To derive the variance , the variance from the unconditioned case is subdivided into a fraction , which is the effect of the (varying) velocity at time and a second fraction, which originates from the varying velocity before t, which equals the desired conditioned variance .
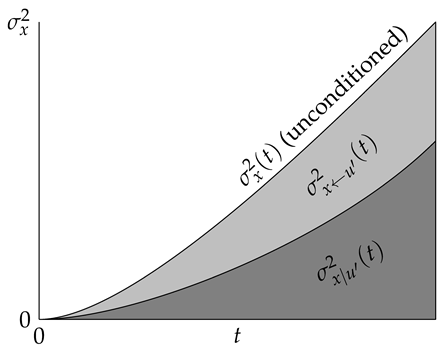
If is unknown, this corresponds to the unconditioned case. In this case, the observed variance of the distance traveled in time t is given by the expression from above. By choosing a specific instead, the observed variance of the distance traveled in time t is reduced by , which is the effect of the (varying) velocity .
If a particular is given, it influences the distance x at time t through the value (assuming the mean-free case). If is chosen randomly from the distribution with the variance , then the variance of is
The remainder up to is
With and , the above equations simplify to
where was previously written as in the more general notation, with
and
Appendix A.3. Two-Point Joint Prediction Around One Observation
The joint probability density of having traveled after time and after time , under the condition of having observed velocity at time , is given. If u is Gaussian distributed with a stationary mean and a stationary variance , then is also Gaussian:
with
and with mean values and and respective variances and for the traveled distances and , as given above as functions of t for a given distance, x, under the condition of having observed velocity at time , and with the correlation coefficient , which is
with
Appendix A.4. One-Point Prediction Around Two Observations
Here, the probability densities of having velocity u at time t conditioned on two additional observations ( at time and at time ), and , the probability density of having traveled the distance x within time t, conditioned on the arrival velocity u (at time t) and another observation of velocity at time , are given.
To derive the probability density of a distance traveled, first, the probability density of velocity u at time t is needed under the condition of two observations, at time and at time . If u is Gaussian distributed with a stationary mean and a stationary variance , then is also Gaussian:
with a mean and a variance . Note that both and also depend on and . The functional dependence is dropped because of too many dependencies in the following derivations. Particular specifications are given in each of the following cases.
To derive the mean , first, a globally mean-free process is assumed (). The mean value is reintroduced afterward. Assuming a mean-free process and the relation
with the time-dependent coefficients and , which are independent of and , the correlation function yields the following:
Combining the four previous expressions yields the following:
and
and
Reintroducing the stationary mean then yields the following:
The following is not necessary for the predictions of the first-passage times. However, it might be useful in other investigations, and it completes the picture of conditioned probability densities.
To derive the variance , the stationary variance is subdivided into a fraction , which reflects the effect of the (varying) velocities and , and a second fraction, originating from the varying velocity between and beyond the observations, which equals the desired conditioned variance .
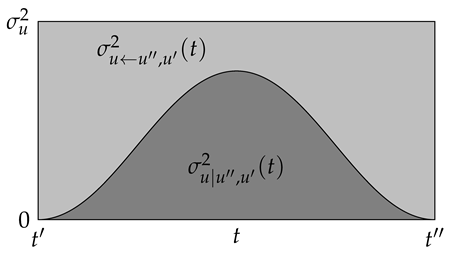
Because neither nor depends on the mean velocity , one can assume a mean-free process here without limiting generality. If particular and values are given, they influence the velocity u at time t through the value (in the mean-free case). If is chosen randomly from the distribution with the variance , then is
where has the variance .
It follows that
and the variance of is
The remainder up to is
Now, global stationarity and reversibility are used to shift and invert times. The distance traveled within time t is
It is assumed that the velocities at time and are known, namely, they are and . If the velocity for all is Gaussian distributed, then the distance traveled in time t is also Gaussian distributed:
with a mean and a variance . Note that both and also depend on and . The functional dependence is dropped because of too many dependencies in the following derivations. Particular specifications are given in each of the following cases.
The mean distance traveled in time t is the integral of the mean velocity over t (for the known and at and , and the otherwise unknown for , which is only partially predictable and also holds for ).
with
To derive the variance , the variance from the unconditioned case is subdivided into a fraction , which is the effect of the (varying) velocities and , and a second fraction, originating from the varying velocity between and beyond the observations, which equals the desired conditioned variance .
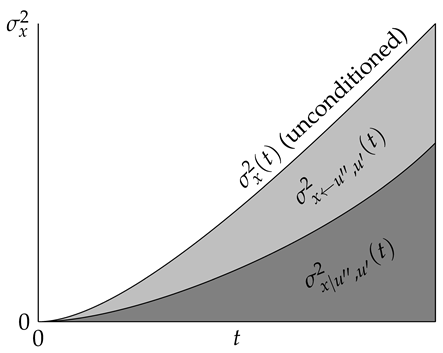
If and values are unknown, this corresponds to the unconditioned case. In this case, the observed variance of the distance traveled in time t is given by the expression from above. By choosing specific and instead, the observed variance of the distance traveled in time t is reduced by , which is the effect of the (varying) velocities and .
If particular and values are given, they influence the distance x at time t by the value (still for the mean-free case). If is chosen randomly from the distribution with the variance , then is
where has the variance .
It follows
and then the variance of is
The remainder up to is
with
With and , the above equations simplify to
where was formally written as in the more general notation before, with
and
Appendix A.5. Two-Point Joint Prediction Around Two Observations
Finally, the joint probability density of having traveled the distance x after time t and the distance after time , conditioned on the arrival velocity u at distance x after time t and the velocity at distance after time , is given.
First, the general case of the joint probability density of having traveled after time and after time , under the condition of having observed velocities at time and at time , is investigated. If u is Gaussian distributed with a stationary mean and a stationary variance , then is also Gaussian:
with
and with the mean values and , and the variances and for the traveled distances and , and with their correlation coefficient .
The two mean values and two variances, without the correlation, are identical to the derivations above:
with , and , as above.
The correlation coefficient is
with
With , , , , and , the above equations simplify to
where was formally written as in the more general notation before, with
and with
with
and
and
with
References
- Hu, Z.; Cheng, L.; Berne, B.J. First passage time distribution in stochastic processes with moving and static absorbing boundaries with application to biological rupture experiments. J. Chem. Phys. 2010, 133, 034105. [Google Scholar] [CrossRef] [PubMed]
- Blake, I.; Lindsey, W. Level-crossing problems for random processes. IEEE Trans. Inf. Theory 1973, 19, 295–315. [Google Scholar] [CrossRef]
- Resnick, S.I. Adventures in Stochastic Processes; Birkhäuser: Boston, MA, USA, 1992. [Google Scholar]
- Reith-Braun, M.; Pfaff, F.; Thummy, J.; Hanebeck, U.D. Approximate First-Passage Time Distributions for Gaussian Motion and Transportation Models. In Proceedings of the 26th International Conference on Information Fusion (FUSION), Charleston, SC, USA, 27–30 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Taylor, G.I. Diffusion by Continuous Movements. Proc. R. Math. Soc. Ser. 2 1921, 20, 196–212. [Google Scholar] [CrossRef]
- Wilson, J.D.; Zhuang, Y. Restriction on the Timestep to be Used in Stochastic Lagrangian Models of Turbulent Dispersion. Bound.-Layer Meteorol. 1989, 49, 309–316. [Google Scholar] [CrossRef]
- Alili, L.; Patie, P.; Pedersen, J.L. Representations of the first hitting time density of an Ornstein-Uhlenbeck process. Stoch. Models 2005, 21, 967–980. [Google Scholar] [CrossRef]
- Benedetto, E.; Sacerdote, L.; Zucca, C. A first passage problem for a bivariate diffusion process: Numerical solution with an application to neuroscience when the process is Gauss–Markov. J. Comput. Appl. Math. 2013, 242, 41–52. [Google Scholar] [CrossRef]
- Hesse, C.H. The One-sided Barrier Problem for an Integrated Ornstein-Uhlenbeck Process. Commun. Stat. Stoch. Models 1991, 7, 447–480. [Google Scholar] [CrossRef]
- Lefebvre, M. Moment generating function of a first hitting place for the integrated Ornstein-Uhlenbeck process. Stoch. Processes Their Appl. 1989, 32, 281–287. [Google Scholar] [CrossRef]
- Lipton, A.; Kaushansky, V. On the First Hitting Time Density of an Ornstein-Uhlenbeck Process. arXiv 2018, arXiv:1810.02390. [Google Scholar] [CrossRef]
- Ricciardi, L.M.; Sato, S. First-Passage-Time Density and Moments of the Ornstein-Uhlenbeck Process. J. Appl. Probab. 1988, 25, 43–57. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).