1. Introduction
Over the past few decades, multi-agent systems (MASs) have garnered significant attention due to their extensive applications in various domains such as industrial processes [
1], sensor networks [
2], the military [
3], etc. A system whose states and outputs are always non-negative is called a positive system [
4]. A controller design approach was proposed in [
5] for continuous-time delay positive systems. Using homogeneous linear matrix inequality (LMI), the consensus of positive MASs (PMASs) was considered in [
6] under a hierarchical control protocol. Generally speaking, the study of nonlinear systems is extremely challenging owing to their inherent high complexity [
7,
8]. T-S fuzzy model is widely recognized as an effective approach to nonlinear problems since it holds rigorous mathematical structure and excellent nonlinear processing capability [
9]. It has gained great popularity in the research on nonlinear MASs [
10]. In [
11], a distributed event-triggering method was presented. There has been some research on T-S fuzzy MASs such as the consensus of MASs [
12], the leader-following consensus under spoofing attacks [
13], etc. However, there is still much room to study T-S fuzzy PMASs (TS-PMASs). To the best of the authors’ knowledge, there is no suitable consensus framework on TS-PMASs.
An important topic is to achieve consensus among a group of agents with one agent acting as the leader. The leader moves independently of others and is unanimously followed by the rest. Consensus between the leader and the followers is called the leader-following consensus. Leader-following control has extensive applications such as robot tracking control [
14], unmanned aerial vehicle (UAV) formation control [
15], missile guidance and control [
16], etc. Compared with the leaderless consensus, leader-following consensus is generally considered to be more practical [
17,
18]. In leader-following control, the designed controller not only ensures consensus among the MASs but also guides the states of the following agents to track the trajectory of the leader system. Leader-following consensus of higher-order MASs was considered in [
19], where a consensus protocol was designed using local information and the leader-following consensus was addressed for both fixed and switching interaction topologies. In [
20], the output consensus of MASs with direct graph was studied based on an event-triggered strategy. The predefined-time consensus tracking problem of second-order MASs was investigated in [
21]. In [
13], an event-triggering scheme was proposed for MASs and faster leader-following consensus was achieved by adjusting fewer errors. A feasible robust leader-following control strategy was proposed in [
22] for positive nonlinear systems with disturbance. For directed dwell time switching networks, the leader-following consensus of a group of positive agents was investigated in [
23]. The positive consensus was considered in [
24] for a class of MASs with average dwell time switching. However, the consensus of leader-following TS-PMASs is still an open issue, which motivates us to carry out this work.
In practical applications, system state is usually not directly measurable. Hence, an observer that relies on the system output should be proposed. A distributed control scheme was proposed in [
25] using adaptive distributed observers to solve the cooperative output regulation problem of MASs. Observer-based asynchronous event-triggered control protocols for multi-agent systems under injection attacks were proposed in [
26] to achieve bipartite consensus. The distributed containment control framework resistant to attacks was established for multi-agent systems under denial-of-service attacks [
27], without utilizing any global information about the network topology. The observer-based leader-following consensus of discrete-time PMASs over time-varying graphs was proposed in [
28]. In [
29], the consensus of fractional PMASs was addressed. However, few efforts are devoted to the observers’ design of TS-PMASs. In particular, linear programming (LP) and co-positive Lyapunov functions (CLFs) are regarded as popular approaches in dealing with the issues of positive systems. Therefore, this paper attempts to construct a new observer-based control protocol for leader-following consensus of TS-PMASs by virtue of CLF and LP. Naturally, some issues need to be discussed: How to construct a fuzzy observer for TS-PMASs? How to guarantee the leader-following consensus and positivity of TS-PMASs? And how to design the control protocol and observer gain matrices? These questions further motivate us to carry out this research.
Existing design approaches of observer and control protocol of general systems are not suitable for positive systems. In addition, it is also challenging to study the combination issues of positivity constraints, TS-MASs, leader-following consensus, as well as fuzzy observer and controller. To make up for the previous work, this paper is devoted to the observer-based controller design and leader-following consensus of TS-PMASs. The main contributions lie in the following three aspects:
(i) A novel fuzzy observer is constructed for TS-PMASs. Compared with the observer designs in [
26,
27], this design not only considers fuzzy models that can handle nonlinearities and uncertainties, but also improves the design flexibility of the observer by using multiple gain matrices. In brief, the designs in [
26,
27] are a special case of the present design in this paper.
(ii) Unlike the conventional consensus controllers in [
23,
24,
28], this paper designs a set of fuzzy observer-based consensus controllers and introduces a target item for the leader’s control. Furthermore, the controller gain design proposed in this paper introduces an improved matrix decomposition technique and it reduces the computational burden.
(iii) The literature [
6,
28,
29] also solves the consensus problem of PMASs, where the conditions that ensure system consensus and positivity are presented in the form of a linear matrix inequality. In this paper, the derived conditions for positivity and consensus are formulated in LP. This approach is not only more suitable for positive systems, but also has lower conservatism and computational burden.
Additionally, we also provide a comparison between this paper and existing works in
Table 1. The comparison highlights the advantages and innovations of this paper.
The rest of this paper is organized as follows:
Section 2 provides some preliminaries.
Section 3 proposes the main results. Then, two illustrative examples are presented in
Section 4. Finally,
Section 5 concludes the paper.
Notations , , , , and represent the sets of n-dimensional vectors, n-dimensional non-negative vectors, dimension real matrices, non-negative integers, and positive integers, respectively. The symbols and ⊗ represent the transpose of A and the Kronecker product, respectively. is the 1-norm. For a matrix , means that holds for .
Graph theory A directed graph is utilized to depict the communication structure of TS-PMASs. A directed graph . An adjacency matrix . If agent i can receive information from agent j, then and , otherwise . It is assumed that the directed graphs in this paper are not self-looping, which implies that . The Laplacian matrix for this directed graph, where and , . Denote as the connection constant between the leader and the follower i, where if the leader can communicate with the follower i, otherwise .
2. Preliminaries
Assumption 1. In the context of leader-following control, all following agents are only able to directly obtain the measured output of their immediate neighbors.
Definition 1 ([
30,
31]).
If the system is deemed positive, for any non-negative initial condition, all states and outputs remain non-negative. Lemma 1 ([
32])
. A matrix is Metzler if and only if there exists a constant λ such that is a non-negative matrix, denoted as . Lemma 2 ([
30,
31])
. Consider a continuous-time systemthe above system is called a positive system, if and only if is Metzler, , and . A leader model is defined as follows:
where
and
are the state and the output;
and
are the system matrix and output matrix. It is assumed that
is Metzler and
.
By Lemma 2 and the assumption on the system matrices in system (1), it is easy to deduce that the leader system (1) is positive.
Considering follower agents with nonlinear dynamics, the follower model can be given based on interval type-2 (IT2) fuzzy set theory [
33] as
Rule
r: IF
is
and
is
, ⋯, and
is
, THEN
where
,
, and
are the system state, the input, and the output, respectively.
,
, and
are the system matrices.
is an IT2 fuzzy set of rule
r corresponding to the function
,
,
,
and
. The firing strength of the
rth rule is the following interval sets:
, where
and
denote the lower and upper grades of membership, respectively.
and
represent the lower and upper membership functions (LUMFs), respectively. Since
, then
for all
r. The IT-2 TS-PMASs is defined as follows:
where
, and
are nonlinear functions and exhibit the property of
for all
r. It is assumed that
is Metzler and
,
.
By Lemma 2, it can be derived that system (3) is positive based on the assumptions on system matrices.
Definition 2. System (2) is said to be consensus if the following statements hold:
- (i)
System (2) is positive;
- (ii)
, .
Definition 3. System (2) is said to be the practical consensus if system (2) is positive and fulfills for , where .
Remark 1. For general MASs [34], only condition (ii) in Definition 2 is required to achieve leader-following consensus. However, due to the positivity, it is necessary to satisfy both (i) and (ii) in Definition 2 when considering the consensus of PMASs. Positive systems are used in some practical applications because these variables represent actual physical quantities that cannot be negative (such as concentration, water level, height, etc.). Therefore, it is necessary to investigate the leader-following consensus of PMASs. Remark 2. A definition of leader-following asymptotic consensus for TS-PMASs is presented in Definition 2. This definition has been widely used in leader-following research. For example, the higher-order leader-following consensus has been studied in [20,21]. Different from Definition 2, the tracking error in Definition 3 converges to a constant greater than 0. This practical consensus can improve the safety of agents. If all agents only achieve asymptotic consensus, the system is vulnerable to attacks when the attacker can identify an individual path through agents. However, in real-world scenarios, each agent follows a distinct trajectory, making it difficult for an attacker to target all agents, even if the paths of some are compromised. Therefore, the leader-following practical consensus is more robust and practical than the traditional asymptotic consensus approach. 4. Numerical Examples
A UAV is a vehicle that is not manned but is capable of completing a mission through remote maneuvering, pre-programmed control, or autonomous control. UAVs are used in a wide variety of applications, including military, civil, scientific, and recreational. In the field of drones, leader tracking control refers to the ability of a drone to follow, track a particular drone, or perform a task related to a specific leader object. The tracking control design of the leader system and collision avoidance schemes for multiple UAV flights were investigated in [
36]. A nonlinear controller capable of guiding a leader–follower formation of UAVs for positioning and trajectory tracking tasks was proposed by [
37]. With the development of MASs theory, MASs-based UAV formation control has become a common method to study UAV control. UAV modeling involves the flight speed of a single UAV, the flight altitude of the UAV, the UAV heading angle, etc., and these variables have non-negative characteristics. Therefore, it is more realistic to use the positive system model to describe the UAV. In fact, in some special cases, the UAV is required to go to a designated area to complete the corresponding task, which is very consistent with the positive system model that limits the state to the non-negative quadrant. When performing tasks in such specific areas, if the general system model is used to represent the UAV, it can cause system redundancy and resource waste. In addition, when the UAV encounters internal faults or interference during the mission, the unpredictability of its state and the changing nonlinearity make the traditional linear modeling method no longer applicable. To solve the above problems, this paper proposes a UAV cooperative control method based on the T-S PMASs model.
Referring to the literature [
38], the motion model of the UAV can be described as
where
,
, and
are the positions of the i-th UAV in the
X,
Y, and
Z directions.
,
, and
are the flight speed, elevation angle, and azimuth angle of the UAV. Reference [
39] gives a motion model of an unmanned ship and models it as a T-S PMASs. Referring to the modeling method of [
39], the motion of the UAV in the two-dimensional plane can be considered and a mathematical model can be established for it. Based on this, it is assumed that the UAV moves only in the X-Y plane, that is, the elevation angle
and
are set to 0. Accordingly, the above model can be rewritten as
Then, by using the Taylor expansion at the reference point and the T-S fuzzy theory, the UAV system (45) can be modeled as T-S PMASs (3).
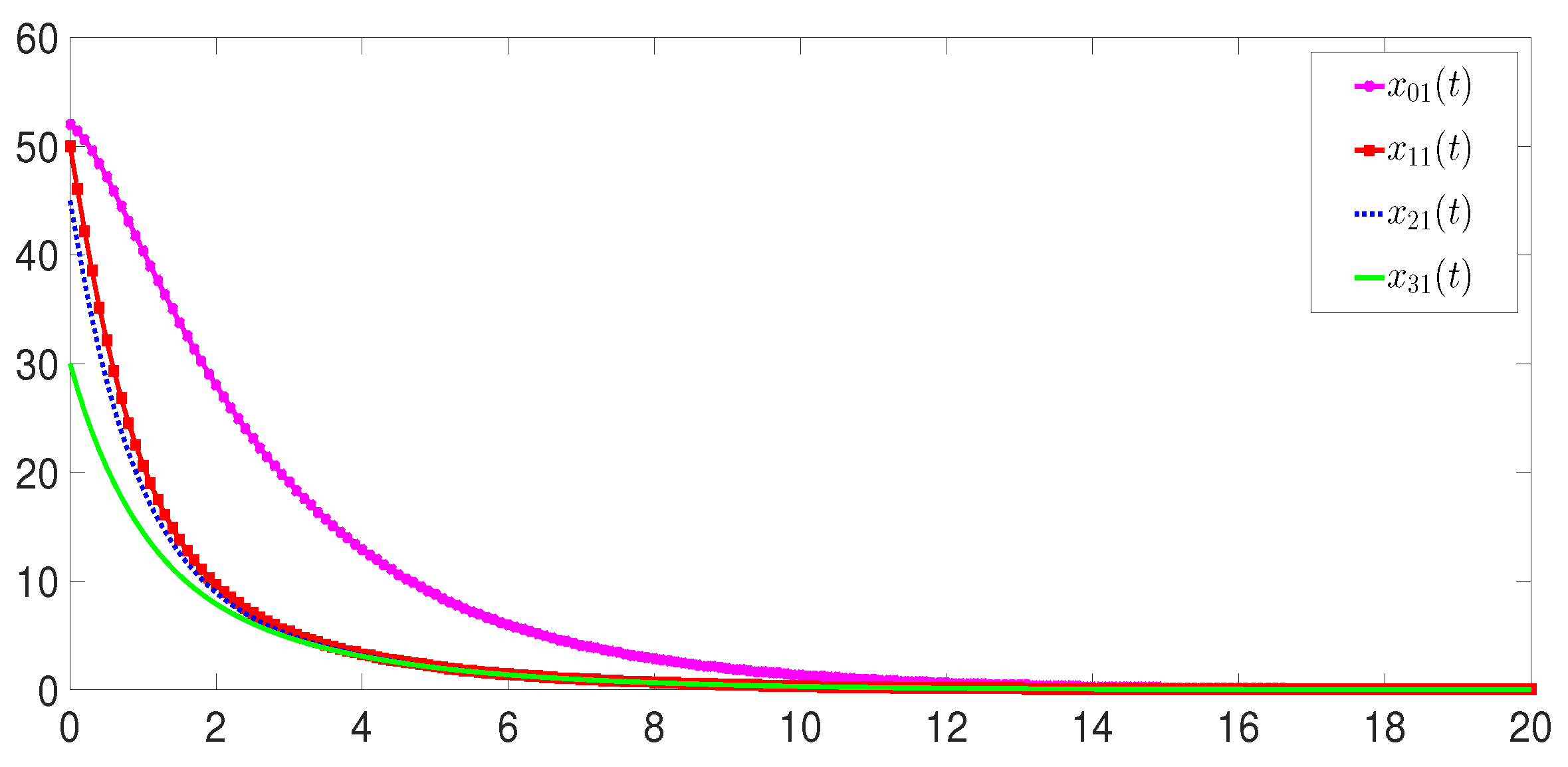
Example 1. Based on the above analysis, the parameters for systems (1) and (2) can be selected asWe choose the parameters , , , , , , , , and . LUMFs and uncertainty-related nonlinear type functions are chosen as , , , , and , . The concept of imperfect premise matching is used to enhance the degree of freedom of controller design. Then, LUMFs and the uncertainty-related nonlinear type functions of the controller are selected as , , , , , and . Moreover, the schematic of UAV and the Laplace matrix of the communication topology are shown in Figure 3. Based on Theorem 1, the controller gain matrices and observer gain matrices are obtained: The state observation error response curves of all follower agents are plotted in Figure 4, Figure 5 and Figure 6. As can be seen from the figures, the state observation errors of the agents converge asymptotically to 0. This means that the observed states of the agents accurately track their true states, further verifying the effectiveness of the designed fuzzy observer. Subsequently, Figure 7, Figure 8 and Figure 9 depict the state response curves for all agents. The simulation results demonstrate that, under the designed IT-2 T-S fuzzy consensus control protocol, asymptotic leader–follower consensus is achieved between the follower agents and the leader. This demonstrates the effectiveness of the proposed control scheme. To demonstrate the reliability and robustness of the proposed scheme, comparative simulations are performed under different disturbances, uncertainties, faults, and switching topologies. The corresponding steady-state errors of and are listed in Table 2. (1) Simulations under different disturbances: Two types of disturbance are considered: sinusoidal and Gaussian white noise with values of and . represents Gaussian noise with mean 0 and variance 1. Using the observer and controller proposed in Theorem 1, the consensus and observation errors are simulated (we set the simulation time to 40 s). The maximum steady-state error of each state component after 25 s is recorded. The corresponding results in Table 2 show that the proposed observation and control scheme can still achieve leader–follower consensus under disturbances of relatively small magnitudes. It is important to note that the consensus under disturbances is a practical consensus, as the consensus error does not converge to 0 compared to normal conditions. (2) Simulations under different uncertainty: The system matrix is considered to contain both random and fixed uncertainties. The values are and , respectively. Similarly, the simulation results in Table 2 demonstrate that the performance of the consensus error and observation error is not affected by small uncertainties. In fact, the uncertainty value should be selected to ensure that the system matrix with uncertainty is still a Metzler matrix. If the uncertainty value is large, it will damage the positivity and performance of the system. (3) Simulations under different faults: To verify the reliability of the proposed work, the system performance is discussed under constant and exponentially decaying faults. Agent 2 is subjected to a constant fault () or agent 1 is subjected to an exponentially decaying fault (). According to Theorem 1, the corresponding consensus error and observation error performance are obtained in Table 2. Thus, it is found that the proposed controller can still achieve practical leader–follower consensus under small-amplitude or decaying faults. Excessively large fault values can undermine system stability. (4) Simulations under switching topology: Assume that the communication topology between agents switches periodically between two topologies due to various external factors. The Laplacian matrix and pinning matrix of topology 1 are shown in Figure 3, and the Laplacian matrix and pinning matrix of topology 2 are selected asThe switching rules between the two topologies are periodic and multiple periods have been tested. The results presented in Table 2 also demonstrate that the proposed observation-based control scheme remains unaffected by topology switching and can still ensure the realization of leader–follower consensus. Based on the above analysis and discussion, it can be concluded that the control scheme developed in this paper is robust to small-amplitude uncertainties and switching topologies. It also demonstrates reliability in the face of small-amplitude faults and disturbances. This further demonstrates the effectiveness and priority of the proposed approach. Finally, it can be found that the designed controller and observer are insensitive to small-magnitude uncertain parameters and disturbances by comparing the steady-state errors under normal, disturbance, and uncertain conditions. However, they are sensitive to large-magnitude uncertain parameters and disturbances, which can undermine the system’s positivity or stability.
Example 2. For the system (2), the system matrices areWe choose the parameters and Example 2 takes the same values for the IT-2 parameters as Example 1. By Theorem 2, the observer and controller gain matrices can be obtained: Figure 10, Figure 11 and Figure 12 show the state response curves of the follower agent’s consensus error under the fuzzy consensus controller (29). The error curves of the leader agent and the virtual target are depicted in Figure 13. As shown in the figure, the consensus error of the agents converges to a finite positive value under non-negative initial conditions. At the same time, Figure 13 shows that the leader is able to track the virtual target under the designed controller . This also shows that the leader–follower practical consensus considered in Section 3.2 is achieved, which further leads to the conclusion that the fuzzy control scheme proposed in Section 3.2 is effective. Additionally, the observation error response curves of each follower agent are shown in Figure 14, Figure 15 and Figure 16. It can be seen from the figures that the observation error of the agent converges quickly to a stable value close to 0. This once again confirms the effectiveness of the fuzzy observer proposed in this paper. To further prove that the proposed scheme enables the practical consensus of the system to be achieved, Table 3 gives the steady-state error bounds of consensus error and target error. From the table, it can be seen that all error states converge to a set of positive values. Combined with the calculation of ℏ in the definition of practical consensus, it can be concluded that the practical consensus of systems (27) and (2) is achieved. 5. Conclusions
This paper has addressed the leader-following consensus problem of TS-PMASs using an observer-based control protocol. The primary contribution is the development of a fuzzy control protocol formulated via LP, which ensures the leader-following consensus and positivity of the considered systems. Fuzzy state observers are introduced to estimate system states and their gain matrices are constructed via a matrix decomposition approach. Moreover, the proposed results are extended to general multi-agent systems. Utilizing the CLF, the positivity and consensus of TS-PMASs are rigorously guaranteed. Compared with existing results, the proposed scheme not only reduces the computational burden and conservatism, but also can handle nonlinearities and uncertainties.
However, there are still issues that need to be resolved, such as turning a single leader into multiple leaders, considering external disturbance, time delay, faults, etc. Therefore, we will focus on leader-following consensus under multiple leaders, disturbances, faults, and delays in the future. On the other hand, the inequality constraints between the leader and follower matrices are also issues that need to be addressed in the future.