Abstract
Consider the problem of approximating an integral of a real-valued integrand on a real interval by a Gauss quadrature rule. The classical approach to estimate the quadrature error of a Gauss rule is to evaluate an associated Gauss–Kronrod rule and compute the difference between the value of the Gauss–Kronrod rule and that of the Gauss rule. However, for a variety of measures and a number of nodes of interest, Gauss–Kronrod rules do not have real nodes or positive weights. This makes these rules impossible to apply when the integrand is defined on a real interval only. This has spurred the development of several averaged Gauss quadrature rules for estimating the quadrature error of Gauss rules. A significant advantage of the averaged Gauss rules is that they have real nodes and positive weights also in situations when Gauss–Kronrod rules do not. The most popular averaged rules include Laurie’s averaged Gauss quadrature rules, optimal averaged Gauss quadrature rules, weighted averaged Gauss quadrature rules, and two-measure-based generalized Gauss quadrature rules. This paper reviews the accuracy, numerical construction, and internality of averaged Gauss rules.
Keywords:
Gauss quadrature rule; averaged Gauss quadrature rule; precision; convergence; numerical construction; error estimate; matrix function; matrix functional MSC:
65D30; 65D32
1. Introduction
Let be a positive measure on the interval such that all moments
exist and are bounded. We are interested in approximating integrals of the form
by an n-node quadrature rule
with real nodes and positive weights that may depend on n. Gauss quadrature rules are particularly useful for this purpose. The nodes and weights of the n-node Gauss rule
associated with the measure are such that the rule is of (algebraic) degree of precision , i.e.,
where denotes the set of all polynomials of degree at most . The requirement (5) determines the nodes and weights uniquely. The nodes of the Gauss rule (4) are known to be distinct and to live in the interval , and the weights are positive; see, e.g., Gautschi [1], Chihara [2], and Szegő [3] for properties of Gauss quadrature formulas.
The Gauss rule (4) can be associated with the symmetric tridiagonal matrix
where the and are recursion coefficients for the sequence of monic orthogonal polynomials (with deg) associated with the inner product
determined by the measure . Thus,
where , , and
The eigenvalues of are the nodes and the squared first component of suitably normalized eigenvectors are the weights of ; see [1,4]. Fairly efficient numerical methods are available for computing the nodes and weights of from for a quite general positive measure ; see [5,6].
It is important to be able to estimate the quadrature error
to assess whether the number of nodes, n, has been chosen large enough to achieve an approximation of the integral (2) of desired accuracy. Moreover, we would like not to choose n much larger than necessary for the Gauss rule to achieve the requested accuracy. Generally, the error (9) is estimated by replacing by a quadrature rule of higher degree of precision than , and several new quadrature rules have recently been developed for this purpose.
This paper reviews classical and new quadrature rules for estimating the error (9), discusses their properties and computational aspects, and illustrates their performance. Section 2 examines known results for the averaged Gauss rules by Laurie [7] and the optimal averaged rules proposed by Ehrich [8] and Spalević [9]. The internality of the quadrature rules is considered. A quadrature rule is said to be internal if all its nodes live in the convex hull of the support of the measure . Gauss rules are known to be internal, but quadrature rules that are used to estimate the quadrature error of Gauss rules might not be. It is desirable that a quadrature rule be internal, because then the rule can be applied to approximate the integral (2) for any integrand that is defined on the convex hull of the support of the measure .
2. Some Methods for Estimating the Quadrature Error of Gauss Rules
A classical approach to estimate the quadrature error (9) is to replace the integral by the -node Gauss–Kronrod quadrature rule associated with the n-node Gauss rule (4). This Gauss–Kronrod rule is a quadrature formula of the form
such that the nodes , are the nodes of the Gauss rule (4), and the Kronrod nodes , and the weights , are determined so that
see Kronrod [10] and Gautschi [1,11]. Generally, the Kronrod nodes , , are required to be real and to be interlaced by the Gauss nodes , . In addition, the Gauss–Kronrod weights , should be positive. Efficient numerical methods for computing the nodes and weights of the Gauss–Kronrod rule , whose nodes , and weights , , satisfy these conditions are described in [12,13]. The quadrature error (9) then can be estimated by
and the integral (2) can be approximated by .
However, for many measures , including various measures determined by a Jacobi weight function
and for certain numbers of nodes, Gauss–Kronrod rules with real nodes and positive weights do not exist; see Notaris [14] for a detailed survey of Gauss–Kronrod rules and their properties, as well as [15,16,17]. This difficulty with Gauss–Kronrod rules has prompted the development of other quadrature rules for estimating the error in Gauss quadrature formulas.
For instance, one may construct an -node quadrature rule for approximating the functional
and use a linear combination of and for some real scalar ,
to estimate the error ; see [18,19] for discussions of this approach. The rule (13) generally has distinct nodes and its evaluation then requires the calculation of the integrand f at nodes, in addition to the n values of f needed to calculate . Thus, the number of required evaluations of the integrand f generally is the same as for the -node Gauss–Kronrod rule (10).
A special case of the quadrature Formula (13) was proposed by Laurie [7], who introduced the so-called -node anti-Gauss rule associated with the n-node Gauss rule . The rule is characterized by
This rule corresponds to choosing in (12) and letting in (13). The quadrature Formula (13) then becomes
We refer to this rule as Laurie’s averaged Gauss rule associated with . It has degree of precision at least .
The nodes of (15) are the nodes of as well as the zeros of the polynomial
for ; see Spalević [9] for a proof. The special cases when is a Hermite or Laguerre measure are discussed by Ehrich [8], and when is a Gegenbauer measure by Hascelik [20]. The attractions of Laurie’s averaged Gauss rule (15), when compared to the Gauss–Kronrod rule , include that the former rule is guaranteed to have real nodes and positive weights and is easier to compute.
When Ehrich [8] considered Gauss–Hermite and Gauss–Laguerre quadrature rules, he varied in (13) or, equivalently, in (16), to increase the degree of precision of the rule (13). He referred to the quadrature rule (13) with chosen to give the highest degree of precision as the optimal averaged Gauss rule associated with .
Using results by Peherstorfer [21,22] on positive quadrature formulas, Spalević [9] derived a simple method for constructing the -node optimal averaged Gauss rule that is associated with the Gauss rule (4). Its nodes that are not nodes of are the zeros of the polynomial in (16) with . We denote this quadrature rule by . They have degree of precision at least .
The difference
furnishes an estimate of the quadrature error (9) and the integral (2) can be approximated by . The optimal averaged quadrature formula shares the following advantages of Laurie’s averaged Gauss rule when compared to the Gauss–Kronrod rule : The rule is guaranteed to have real nodes and positive weights, and it is simpler to compute than .
Neither Laurie’s averaged Gauss rules nor optimal averaged Gauss rules are guaranteed to be internal. A possible technique of constructing internal averaged Gauss quadrature rules is to use modified anti-Gauss rules
whose nodes and weights depend on a parameter . This is described in [23]. The quadrature rule (18) has nodes and is determined by the requirement that
for some scalar , where we note that may depend on n. These kind of quadrature rules have been discussed in [8,20,24]. When the rule (18) simplifies to the anti-Gauss rule (14) due to Laurie [7].
Analogously to Laurie’s averaged Gauss rule (15), one can define the weighted averaged Gauss formula
This quadrature rule was first considered by Ehrich [8]. It is shown in [23] how the parameter can be chosen to make the rule (19) internal for certain measures . Moreover, it is pointed out in [23] that for , the quadrature rule (19) can be represented by
where the modified anti-Gauss quadrature rule is associated with the symmetric tridiagonal matrix
The modified anti-Gauss quadrature rules (18) are not guaranteed to be internal. The same can be said for the weighted averaged Gauss quadrature rules (19). However, when satisfies certain conditions, these rules are internal for some measures; see [23,25].
Thorough investigations about the internality of Laurie’s averaged rules and of optimal averaged rules, as well as of related quadrature rules, can be found in [7,9,23,26,27,28,29,30,31,32]. A few ways to construct internal rules, when the rules or are not internal, are described in [23,25,26].
We conclude this section by describing a new approach for estimating the quadrature error in . This technique has recently been described and analyzed in [33,34,35]. It is based on constructing a -node quadrature rule by using the measure as well as an auxiliary measure , whose support is in the convex hull of the measure . We refer to these quadrature rules as two-measure-based generalized Gauss quadrature rules. They were referred to as new averaged Gauss (NAG) quadrature formulas in [35]. We will use this acronym in the present paper as well.
Let
denote the -node NAG rule associated with the Gauss rule . The application of NAG quadrature formulas to the estimation of the error in is particularly attractive when the rule is internal but the rules , , and are not. The internality of NAG quadrature rules for certain weight functions is discussed in [33,34,35].
The NAG rule is easy to compute; this is discussed in the next section. Its nodes are generally distinct from the nodes of . This is not a major concern when it is inexpensive to evaluate the integrand f at the quadrature nodes. The rule has the same degree of precision as the optimal averaged Gauss quadrature rule , i.e., at least ; see [35].
3. Computation of Averaged Gauss Quadrature Rules
The evaluation of Laurie’s averaged rules can be carried out by evaluating the Gauss rule and the associated anti-Gauss rule . The tridiagonal matrix associated with the Gauss rule is given by (6) and the tridiagonal matrix associated with the corresponding anti-Gauss rule is (21) with . The eigenvalues of are the nodes of the Gauss rule and the eigenvalues of the matrix (21) with are the nodes of the anti-Gauss rule . The weights of the rule are the square of the first components of suitably scaled eigenvectors of these matrices. These nodes and weights can be computed quite efficiently in arithmetic floating point operations by a divide-and-conquer method that exploits that the matrix (6) is the leading principal submatrix of the matrix (21). This is described by Alqahtani et al. [36]. Computed examples reported in [5] show this approach to be faster than application of the Golub–Welsch algorithm [6] and to yields nodes and weights with higher accuracy. Software is provided with [5].
We also are interested in calculating the nodes and weights of optimal averaged quadrature rules. The optimal averaged Gauss rule associated with the Gauss rule is given by (20) with . It follows that the nodes and weights of can be evaluated quite efficiently by a divide-and-conquer method analogously as the nodes and weights of Laurie’s averaged rule . This is discussed in [36]. Further computed examples as well as code can be found in [5].
NAG rules also can be evaluated quite efficiently by the divide-and-conquer approach described in [5,36]. The computations are analogous to those for the rules .
Concerning with the stable computation of the averaged Gaussian quadrature rules we mention and the methods proposed in [37,38].
We conclude this section by noting that algorithms for evaluating the nodes and weights of Gauss–Kronrod and Patterson-type rules (which have almost the same precision as Gauss–Kronrod; cf. [39]) are described in [12,13] and [40], respectively. The computation of these rules is more complicated than the computation of any of the averaged Gauss rules with the same number of nodes considered in this paper.
4. Some Extensions and Applications of Laurie’s Averaged and Optimal Averaged Gauss Quadrature Rules
We already have discussed the application of averaged Gauss rules to the estimation of the quadrature error (9). This section mentions a few additional applications and some extensions of the quadrature rules considered above.
- Let be a large symmetric matrix, let , and let the function f be defined on the convex hull of the spectrum of A. The need to evaluate matrix functionals of the formwhere the superscript T denotes transposition, arises in a variety of applications including in network analysis and the solution of linear discrete ill-posed problems; see, e.g., [41,42,43,44]. When the matrix A is large, it may be prohibitively expensive, or impossible, to first compute the matrix and then evaluate (22). The Lanczos method provides a less expensive approach to compute an approximation of (22). The application of n steps of the Lanczos process to A with initial vector v yields, generically, a symmetric tridiagonal matrix (6) that determines an n-node Gauss quadrature rule that is associated with a nonnegative measure . This measure is defined by the vector v and the spectral factorization of A; see Golub and Meurant [44] for a thorough discussion. In particular, the Lanczos algorithm allows the computation of Gauss quadrature rules without explicit knowledge of the measure that defines these rules. The quadrature error of Gauss rules generated in this manner can be estimated with the aid of averaged Gauss rules.
- The problem of evaluating expressions of the formwhere A and f are as in (22) and for some , also arises in various applications including color image restoration [45] and the determination of the optical absorption spectrum of a material [46]. An application of m steps of the symmetric block Lanczos algorithm to A with initial block V gives a symmetric block tridiagonal matrix that can be associated with a block Gauss quadrature rule for the approximation of (23). Analogues of Laurie’s averaged rule and the optimal averaged rule for the estimation of the quadrature error in the block Gauss rule are described in [47], where applications to network analysis are discussed.
- Let be a large symmetric matrix, let , and let f be a function that is defined on the convex hull of the spectrum of A. The need to evaluate expressions of the formarises, e.g., in network analysis, see [48,49], as well as when solving systems of ordinary differential equations; see [50,51]. The expression (24) can be approximated by carrying out a few steps of the symmetric Lanczos algorithm applied to A with initial vector v. Estimates of the error can be determined with the aid of Laurie’s averaged or optimal averaged Gauss quadrature rules; see [52].
- Averaged quadrature rules associated with Gauss–Radau and Gauss–Lobatto quadrature formulas are described in [53]. They can be applied to estimate the quadrature error in Gauss–Radau and Gauss–Lobatto rules.
- Analogues of Laurie’s averaged rules and of optimal averaged rules have been developed for the estimation of the quadrature error of Gauss–Szegő rules; see [54] and [55], respectively. Gauss–Szegő rules are Gauss-type quadrature rules for the approximation of integrals of a periodic function.
- Padé-type approximants are rational functions that approximate a formal series of polynomials; see Djukić et al. [56] describe the construction and performance of Padé-type approximants that correspond to optimal averaged Gauss quadrature rules.
- The conjugate gradient method is the default iterative method for the solution of linear systems of equations with a large symmetric positive definite matrix. This method is closely related to the symmetric Lanczos method and, therefore, to orthogonal polynomials. Almutairi et al. [57] discuss how Gauss quadrature rules, Laurie’s averaged Gauss rules, and optimal averaged Gauss rules can be applied to estimate the norm of the error in approximate solutions computed by the conjugate gradient method.
- The iterative solution of linear systems with a large symmetric, indefinite, nonsingular matrix by a Lanczos-type method is discussed by Alibrahim et al. [58], who describe how the norm of the error in computed approximate solutions can be estimated by Gauss rules, Laurie’s averaged Gauss rules, and optimal averaged Gauss rules.
- Fredholm integral equations of the second kind that are defined on a finite or infinite interval arise in many applications. Djukić et al. [59], Díaz de Alba et al. [60], and Fermo et al. [61] discuss their numerical solution by Nyström methods that are based on Gauss quadrature rules. It is important to be able to estimate the error in the computed solution because this makes it possible to choose an appropriate number of nodes in the Gauss quadrature rule used. These papers explore the application of anti-Gauss, Laurie’s averaged Gauss, and weighted averaged Gauss quadrature rules for this purpose and analyze the numerical stability of these methods.
- Cubature rules that generalize Laurie’s averaged rule are described in [59,62]. The development of averaged rules for problems in several space-dimensions is still an active area of research. A difficulty is that the domain of integration in higher dimensions may be of a variety of shapes, see, e.g., [63]. Another issue is that when the domain of integration is simple, say, the unit square in the first quadrant, and the integral is approximated by integrating one space-dimension at a time by Gauss quadrature, integration along the first dimension, say, the horizontal axis, yields approximations that are used when integrating along the vertical axis. It remains to be investigated how the errors in the approximations obtained when integrating in the horizontal direction affect the error estimates obtained when integrating in the vertical direction.
5. Internality of Averaged and Optimal Averaged Gauss Rules
Laurie’s averaged Gauss rule and the optimal averaged Gauss rule are not guaranteed to be internal; the smallest and largest nodes may be outside the convex hull of the support of the measure . For notational simplicity, we will, in this section, assume that the convex hull of the support of is the interval . Nodes that are inside the interval are said to be internal, while nodes that are outside this interval are said to be external. A quadrature rule with all nodes internal is said to be internal. The smallest and largest nodes are internal if and only if
respectively, where for Laurie’s averaged Gauss rule and for the optimal averaged Gauss rule .
When external nodes occur, one possibility is to remove up to last rows and columns from the corresponding Jacobi matrix; see [26,64]. It follows from the interlacing property of the eigenvalues of Jacobi matrices that in this way, the outermost nodes will get closer to the middle of the interval, while the degree of precision will not fall below . Hence, the highest chance of obtaining an internal quadrature rule is achieved by removing the last rows and columns. The resulting Jacobi matrix will be of order and the corresponding quadrature rule is denoted by and referred to as the truncated (averaged Gauss) quadrature rule. Its nodes are the zeros of the polynomial
They are interlaced by the Gauss nodes. Therefore, only the two outermost nodes may be external. The rule is internal if and only if
5.1. Results for Classical Weight Functions
We provide a short overview of the internality of Laurie’s averaged Gauss rules and of optimal averaged Gauss rules for several classical weight functions, and we first note that in the case of Hermite and generalized Hermite weight functions on , for , all the discussed formulas are trivially internal. For the generalized Laguerre weight function
Laurie [7] shows that the anti-Gauss formula is internal for . Ehrich [8] proves that the optimal averaged Gauss formula is internal for and, that for , there is precisely one negative node.
In the case of the Jacobi weight function w on the interval for ,
the anti-Gauss formula with is internal if and only if (see [7])
and the optimal averaged Gauss quadrature formula is internal if and only if (see [65])
Hence, when n is large enough,
- if or , then both averaged Gauss formulas are internal;
- if or , then both averaged Gauss formulas are external;
- if , then for , only the optimal averaged Gauss formula is internal, and for , only Laurie’s averaged Gauss formula is internal.
Modifications by Linear Divisors and Factors
Given a weight function on the interval , one often needs to work with its modifications by a linear divisor or factor,
where z is a given real constant with . It follows from [1] (Theorem 2.52 (Uvarov)) that the monic orthogonal polynomials for the weight function given by (28) satisfy
The sequence can be computed inductively by the relations
The recurrence coefficients and for the polynomials can be computed in terms of the sequence by an algorithm described in [1] (Equations (2.4.26–27)):
Similarly, by [1] (Theorem 2.52), the monic orthogonal polynomials with respect to the weight function given by (28) satisfy
The coefficients can be computed inductively by using the relations
and the recurrence coefficients and for the polynomials can be computed by the corresponding algorithm in [1] (Equations (2.4.12–13)):
5.2. Chebyshev Weight Functions
Here, we will discuss the internality of averaged and optimal averaged quadrature rules when the weight function has one of the forms
and is one of the Chebyshev weight functions:
Here, is an arbitrary real constant with and
The relation between z and was first studied by Milovanović et al. [15] and was later extended to averaged Gauss and optimal averaged Gauss quadrature rules in [28,29,31].
5.2.1. Modifications by a Linear Divisor
Throughout this subsection, we will use the notation . When the weight function is for , given by (35) and (36), the recurrence relations (30) imply that for . Using the relations (31), the recurrence coefficients can be shown to satisfy
By (29), the monic orthogonal polynomials are
with and , where the , , and are the monic Chebyshev orthogonal polynomials of the first, second, and third kind, respectively, defined by
In all three cases, it is easily verified that the averaged, optimal averaged, and truncated quadrature rules are internal for .
5.2.2. Modifications by a Linear-Over-Linear Factor
The orthogonal polynomials with respect to any of the weight functions defined by (35) are given by Formula (32). In this case, the recurrence (33) simplifies to
It is known ([28] Theorem 4) that every sequence with that satisfies (37) has the form
for some constant A. The constant A is determined from the initial term , which is easy to evaluate for each of the three weight functions . The following values are obtained:
Knowing the terms and the coefficients and , and using the relations (34), we easily obtain formulas for the recurrence coefficients and for the weight functions , . Now, the internality of the rules , , and can be verified by using (25) and (26). The following results are shown in [28,31], and [29], respectively.
Theorem 1.
Let the weight function be and let . The averaged rule and the optimal averaged rule have one and two external nodes, respectively. However, the truncated rule is internal.
Theorem 2.
Let the weight function be and let . Then, the optimal averaged rule and the truncated rule are internal.
Theorem 3.
Let the weight function be and let . The averaged rule has an external node, while the optimal averaged rule is internal if and only if . The truncated rule is internal.
5.3. Modifications of the Jacobi Weight Functions
We now consider modifications of the Jacobi weight functions (27) of the form
where z is a given real constant with . The condition on z is conveniently secured by setting
In [32] asymptotic expansions for the recurrence coefficients , and are obtained, leading to the following results.
Theorem 4.
Let the weight function be any of the two weight functions defined by (38): or . Then, for n large enough, the averaged Gauss rule has
- the largest node internal if , or and ,
- the smallest node internal if , or and .
For n large enough, the optimal averaged Gauss rule has
- the largest node internal if , or and ,
- the smallest node internal if , or and .
Thus, the averaged and optimal averaged Gauss quadrature rules are simultaneously internal or external, except when .
Theorem 5.
The truncated rule associated with either one of the weight functions given by (38) is internal when n is large enough.
Numerical experiments suggest that, generally, n does not have to be very large in order for the rule to be internal; see Table 1 for an illustration.

Table 1.
Example 1. Extreme nodes of averaged, optimal averaged, and truncated averaged Gauss rules associated with the Gauss rule .
Example 1.
Consider a weight function given by (38) with the pole z clear from the interval of integration: , , and . The conclusions of Theorems 4 and 5 hold already for fairly small values of n. Since , the two averaged rules are external on the left, and only the truncated rules are internal.
As mentioned above, it is desirable for a quadrature rule to be internal. Gauss rules are internal, but averaged rules are not, in some cases. Figure 1 and Figure 2 depict the distribution of the nodes of Gauss, optimal averaged Gauss, averaged Gauss, and NAG quadrature rules with respect to some Jacobi weight functions in (11) and n or nodes for . The auxiliary measure used to define the NAG rules is the Chebyshev measure of the second kind. The internality of these averaged and optimal averaged Gauss quadrature rules is discussed in [7,9], and of NAG rules in [35]. Figure 1 displays the nodes of the quadrature rules when and . All quadrature rules can be seen to be internal.
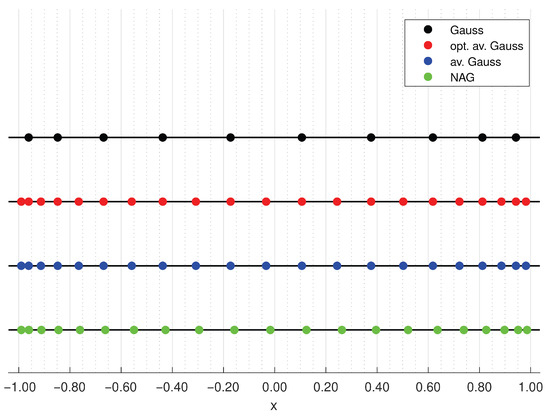
Figure 1.
The distribution of the nodes of the Gauss rule (marked by black dots), of the optimal averaged Gauss rule (marked by red dots), of the averaged Gauss rule (marked by blue dots), and of the NAG quadrature rule (marked by green dots) for with respect to the Jacobi weight function (11) with .
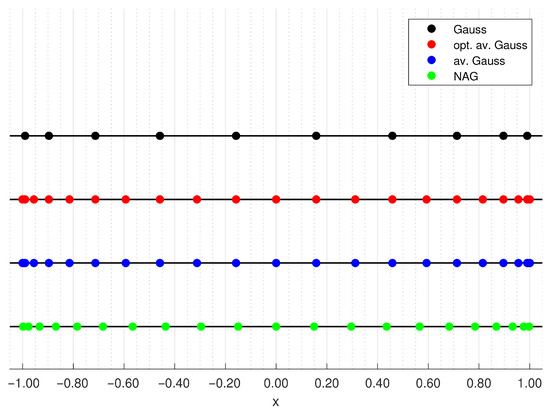
Figure 2.
The distribution of the nodes of the Gauss rule (marked by black dots), of the optimal generalized averaged Gauss rule (marked by red dots), of the averaged Gauss rule (marked by blue dots), and of the NAG quadrature rule (marked by green dots) for with respect to the Jacobi weight function (11) with .
Figure 2 shows the nodes of the quadrature rules when . The averaged and optimal averaged Gauss quadrature rules are not internal. However, the NAG rule is internal for this Jacobi weight function. This is a reason for our interest in NAG quadrature rules.
Table 2 summarizes some properties of the quadrature rules considered. None of the quadrature rules are guaranteed to be internal, but all nodes of the averaged and optimal averaged Gauss rules are real and all weights are positive. Moreover, modifications of averaged and optimal averaged Gauss rules have been proposed that can be internal when the “standard” averaged or optimal averaged rules are not. Gauss–Kronrod rules may have complex-valued nodes. We remark that the nodes and weights of the -node Gauss–Kronrod rule are more difficult to compute than those of the other quadrature rules considered.

Table 2.
Properties of the Gauss–Kronrod, optimal averaged Gauss, averaged Gauss, and NAG rules with nodes. Positivity refers to the weights of the quadrature rules; interlacing refers to that the nodes are interlaced by those of the n-node Gauss rules that they are associated with. Complexity refers to the difficulty of computing the quadrature rules.
Numerous computed results with NAG rules for Jacobi-type measures that use the Chebyshev measure of the second kind as auxiliary measure suggest the conjecture that the nodes of the NAG quadrature rule so obtained interlace (separate) the nodes of the corresponding Gauss quadrature rule ; see Figure 1 and Figure 2 for illustrations. It would be interesting to prove this conjecture.
Let us mention some of our very recent work in this theory. At first let us mention the paper [66] on the error bounds for the averaged Gauss quadrature rules for functions analytic on an ellipse. There are measures for which precision of averaged Gauss quadrature rules increases; see [67]. During our investigation of the averaged and optimal averaged Gauss rules we observed that they typically are much more accurate than their degrees of precision suggest. The paper [68] discusses and illustrates this property. It is based on an analog investigation of the Clenshaw-Curtis quadrature rules (see [69,70]), and their accuracy, derived by Trefethen (see [71,72,73]).
6. Conclusions
Gauss quadrature rules are frequently used to approximate integrals over a real interval. It is important to be able to estimate the quadrature error to choose a Gauss rule with an appropriate number of nodes. Laurie’s averaged Gauss rule and the optimal averaged Gauss rule are useful for this purpose. This paper reviews recent developments in the analysis of these averaged rules and discusses some applications. In particular, the location of the extreme nodes of the averaged rules is discussed and illustrated.
Author Contributions
Conceptualization, D.L.D., R.M.M.D., L.R. and M.M.S.; methodology, D.L.D., R.M.M.D., L.R. and M.M.S.; software, D.L.D., R.M.M.D., L.R. and M.M.S.; validation, D.L.D., R.M.M.D., L.R. and M.M.S.; formal analysis, D.L.D., R.M.M.D., L.R. and M.M.S.; investigation, D.L.D., R.M.M.D., L.R. and M.M.S.; resources, D.L.D., R.M.M.D., L.R. and M.M.S.; data curation, D.L.D., R.M.M.D., L.R. and M.M.S.; writing—original draft preparation, D.L.D., R.M.M.D., L.R. and M.M.S.; writing—review and editing, D.L.D., R.M.M.D., L.R. and M.M.S.; visualization, D.L.D., R.M.M.D., L.R. and M.M.S.; supervision, D.L.D., R.M.M.D., L.R. and M.M.S. The authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
The research by D.L.D., R.M.M.D. and M.M.S. was supported in part by the Serbian Ministry of Science, Technological Development, and Innovations, according to Contract 451-03-137/2025-03/200105 dated on 4 February 2025.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gautschi, W. Orthogonal Polynomials: Computation and Approximation; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Chihara, T.S. An Introduction to Orthogonal Polynomials; Gordon and Breach, Science Publishers: New York, NY, USA; London, UK; Paris, France, 1978. [Google Scholar]
- Szegő, G. Orthogonal Polynomials, 4th ed.; American Mathematical Society: Providence, RI, USA, 1975. [Google Scholar]
- Wilf, H.S. Mathematics for the Physical Sciences; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Borges, C.F.; Reichel, L. Computation of Gauss-type quadrature rules. Electron. Trans. Numer. Anal. 2024, 61, 121–136. [Google Scholar] [CrossRef]
- Golub, G.H.; Welsch, J.H. Calculation of Gauss quadrature rules. Math. Comp. 1969, 23, 221–230. [Google Scholar] [CrossRef]
- Laurie, D.P. Anti-Gaussian quadrature formulas. Math. Comp. 1996, 65, 739–747. [Google Scholar] [CrossRef]
- Ehrich, S. On stratified extensions of Gauss–Laguerre and Gauss–Hermite quadrature formulas. J. Comput. Appl. Math. 2002, 140, 291–299. [Google Scholar] [CrossRef]
- Spalević, M.M. On generalized averaged Gaussian formulas. Math. Comp. 2007, 76, 1483–1492. [Google Scholar] [CrossRef]
- Kronrod, A.S. Integration with control of accuracy. Soviet Phys. Dokl. 1964, 9, 17–19. [Google Scholar]
- Gautschi, W. A historical note on Gauss–Kronrod quadrature. Numer. Math. 2005, 100, 483–484. [Google Scholar] [CrossRef]
- Calvetti, D.; Golub, G.H.; Gragg, W.B.; Reichel, L. Computation of Gauss–Kronrod rules. Math. Comp. 2000, 69, 1035–1052. [Google Scholar] [CrossRef]
- Laurie, D.P. Calculation of Gauss–Kronrod quadrature rules. Math. Comp. 1997, 66, 1133–1145. [Google Scholar] [CrossRef]
- Notaris, S.E. Gauss–Kronrod quadrature formulae—A survey of fifty years of research. Electron. Trans. Numer. Anal. 2016, 45, 371–404. [Google Scholar]
- Kahaner, D.K.; Monegato, G. Nonexistence of extended Gauss–Laguerre and Gauss–Hermite quadrature rules with positive weights. Z. Angew. Math. Phys. 1978, 29, 983–986. [Google Scholar] [CrossRef]
- Peherstorfer, F.; Petras, K. Ultraspherical Gauss–Kronrod quadrature is not possible for λ > 3. SIAM J. Numer. Anal. 2000, 37, 927–948. [Google Scholar] [CrossRef]
- Peherstorfer, F.; Petras, K. Stieltjes polynomials and Gauss–Kronrod quadrature for Jacobi weight functions. Numer. Math. 2003, 95, 689–706. [Google Scholar] [CrossRef]
- Laurie, D.P. Stratified sequence of nested quadrature formulas. Quest. Math. 1992, 15, 365–384. [Google Scholar] [CrossRef]
- Patterson, T.N.L. Stratified nested and related quadrature rules. J. Comput. Appl. Math. 1999, 112, 243–251. [Google Scholar] [CrossRef][Green Version]
- Hascelik, A.I. Modified anti-Gauss and degree optimal average formulas for Gegenbauer measure. Appl. Numer. Math. 2008, 58, 171–179. [Google Scholar] [CrossRef]
- Peherstorfer, F. On positive quadrature formulas. In ISNM International Series of Numerical Mathematics; Brass, H., Hämmerlin, G., Eds.; Numerical Integration IV; Birkhäuser: Basel, Switzerland, 1993; Volume 112, pp. 297–313. [Google Scholar]
- Peherstorfer, F. Positive quadrature formulas III: Asymptotics of weights. Math. Comp. 2008, 77, 2241–2259. [Google Scholar] [CrossRef][Green Version]
- Reichel, L.; Spalević, M.M. Averaged Gauss quadrature formulas: Properties and applications. J. Comput. Appl. Math. 2022, 410, 114232. [Google Scholar] [CrossRef]
- Calvetti, D.; Reichel, L. Symmetric Gauss–Lobatto and modified anti-Gauss rules. BIT Numer. Math. 2003, 43, 541–554. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Weighted averaged Gaussian quadrature rules for modified Chebyshev measures. Appl. Numer. Math. 2024, 200, 195–208. [Google Scholar] [CrossRef]
- Djukić, D.L.; Reichel, L.; Spalević, M.M. Truncated generalized averaged Gauss quadrature rules. J. Comput. Appl. Math. 2016, 308, 408–418. [Google Scholar] [CrossRef]
- Djukić, D.L.; Reichel, L.; Spalević, M.M. Internality of generalized averaged Gaussian quadratures and their truncated variants for measures induced by Chebyshev polynomials. Appl. Numer. Math. 2019, 142, 190–205. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Internality of generalized averaged quadrature rules and truncated variants for modified Chebyshev measures of the first kind. J. Comput. Appl. Math. 2021, 398, 113696. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Internality of generalized averaged quadrature rules and truncated variants for modified Chebyshev measures of the third and fourth kind. Numer. Algorithms 2023, 92, 523–544. [Google Scholar] [CrossRef]
- Djukić, D.L.; Reichel, L.; Spalević, M.M.; Tomanović, J.D. Internality of the averaged Gaussian quadratures and their truncated variants with Bernstein-Szegő weight functions. Electron. Trans. Numer. Anal. 2016, 45, 405–419. [Google Scholar]
- Djukić, D.L.; Reichel, L.; Spalević, M.M.; Tomanović, J.D. Internality of generalized averaged Gaussian quadrature rules and their truncated variants for modified Chebyshev measures of the second kind. J. Comput. Appl. Math. 2019, 345, 70–85. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Internality of averaged Gauss quadrature rules for certain modification of Jacobi measures. Appl. Comput. Math. 2023, 22, 426–442. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Pejčev, A.V.; Reichel, L.; Spalević, M.M.; Spalević, S.M. Internality of two-measure-based generalized Gauss quadrature rules for modified Chebyshev measures. Electron. Trans. Numer. Anal. 2024, 61, 157–172. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Pejčev, A.V.; Reichel, L.; Spalević, M.M.; Spalević, S.M. Internality of two-measure-based generalized Gauss quadrature rules for modified Chebyshev measures II. Mathematics 2025, 13, 513. [Google Scholar] [CrossRef]
- Pejčev, A.V.; Reichel, L.; Spalević, M.M.; Spalević, S.M. A new class of quadrature rules for estimating the error in Gauss quadrature. Appl. Numer. Math. 2024, 204, 206–221. [Google Scholar] [CrossRef]
- Alqahtani, H.; Borges, C.; Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Computation of pairs of related Gauss quadrature rules. Appl. Numer. Math. 2025, 208, 32–42. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M. A new representation of generalized averaged Gauss quadrature rules. Appl. Numer. Math. 2021, 165, 614–619. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Decompositions of optimal averaged Gauss quadrature rules. J. Comput. Appl. Math. 2024, 438, 115586. [Google Scholar] [CrossRef]
- de la Calle Ysern, B.; Spalević, M.M. Modified Stieltjes polynomials and Gauss–Kronrod quadrature rules. Numer. Math. 2018, 138, 1–35. [Google Scholar] [CrossRef]
- de la Calle Ysern, B.; Spalević, M.M. On the computation of Patterson-type quadrature rules. J. Comput. Appl. Math. 2022, 403C, 113850. [Google Scholar] [CrossRef]
- Baglama, J.; Fenu, C.; Reichel, L.; Rodriguez, G. Analysis of directed networks via partial singular value decomposition and Gauss quadrature. Linear Algebra Appl. 2014, 456, 93–121. [Google Scholar] [CrossRef]
- Calvetti, D.; Golub, G.H.; Reichel, L. Estimation of the L-curve via Lanczos bidiagonalization. BIT Numer. Math. 1999, 39, 603–619. [Google Scholar] [CrossRef]
- Fenu, C.; Martin, D.; Reichel, L.; Rodriguez, G. Network analysis via partial spectral factorization and Gauss quadrature. SIAM J. Sci. Comput. 2013, 35, A2046–A2068. [Google Scholar] [CrossRef]
- Golub, G.H.; Meurant, G. Matrices, Moments and Quadrature with Applications; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Bentbib, A.; Ghomari, M.E.; Jbilou, K.; Reichel, L. The extended symmetric block Lanczos method for matrix-valued Gauss-type quadrature rules. J. Comput. Appl. Math. 2022, 407, 113965. [Google Scholar] [CrossRef]
- Shao, M.; da Jornada, F.H.; Lin, L.; Yang, C.; Deslippe, J.; Louie, S.G. A structure preserving Lanczos algorithm for computing the optical absorption spectrum. SIAM J. Matrix. Anal. Appl. 2018, 39, 683–711. [Google Scholar] [CrossRef]
- Reichel, L.; Rodriguez, G.; Tang, T. New block quadrature rules for the approximation of matrix functions. Linear Algebra Appl. 2016, 502, 299–326. [Google Scholar] [CrossRef]
- De la Cruz Cabrera, O.; Matar, M.; Reichel, L. Edge importance in a network via line graphs and the matrix exponential. Numer. Algorithms 2020, 83, 807–832. [Google Scholar] [CrossRef]
- Estrada, E.; Higham, D.J. Network properties revealed through matrix functions. SIAM Rev. 2010, 52, 696–714. [Google Scholar] [CrossRef]
- Beckermann, B.; Reichel, L. Error estimation and evaluation of matrix functions via the Faber transform. SIAM J. Numer. Anal. 2009, 47, 3849–3883. [Google Scholar] [CrossRef]
- Hochbruck, M.; Lubich, C. On Krylov subspace approximations to the matrix exponential operator. SIAM J. Numer. Anal. 1997, 34, 1911–1925. [Google Scholar] [CrossRef]
- Eshghi, N.; Reichel, L. Estimating the error in matrix function approximations. Adv. Comput. Math. 2021, 47, 57. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M. Radau- and Lobatto-type averaged Gauss rules. J. Comput. Appl. Math. 2024, 437, 115477. [Google Scholar] [CrossRef]
- Kim, S.-M.; Reichel, L. Anti-Szegő quadrature rules. Math. Comp. 2007, 76, 795–810. [Google Scholar] [CrossRef]
- Jagels, C.; Reichel, L.; Tang, T. Generalized averaged Szegő quadrature rules. J. Comput. Appl. Math. 2017, 311, 645–654. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Optimal averaged Padé-type approximants. Electron. Trans. Numer. Anal. 2023, 59, 145–156. [Google Scholar] [CrossRef]
- Almutairi, H.; Meurant, G.; Reichel, L.; Spalević, M.M. New error estimates for the conjugate gradient method. J. Comput. Appl. Math. 2025, 459, 116357. [Google Scholar] [CrossRef]
- Alibrahim, M.; Darvishi, M.T.; Reichel, L.; Spalević, M.M. Error estimators for a Krylov subspace method for the solution of linear systems of equations with a symmetric indefinite matrix. Axioms 2025, 14, 179. [Google Scholar] [CrossRef]
- Djukić, D.L.; Fermo, L.; Mutavdžić Djukić, R.M. Averaged Nyström interpolants for bivariate Fredholm integral equations on the real positive semi-axis. Electron. Trans. Numer. Anal. 2024, 61, 51–65. [Google Scholar] [CrossRef]
- Díaz de Alba, P.; Fermo, L.; Rodriguez, G. Solution of second kind Fredholm integral equations by means of Gauss and anti-Gauss quadrature rules. Numer. Math. 2020, 146, 699–728. [Google Scholar] [CrossRef]
- Fermo, L.; Reichel, L.; Rodriguez, G.; Spalević, M.M. Averaged Nyström interpolants for the solution of Fredholm integral equations of the second kind. Appl. Math. Comput. 2024, 467, 128482. [Google Scholar] [CrossRef]
- Djukić, D.L.; Fermo, L.; Mutavdžić Djukić, R.M. Averaged cubature schemes on the real positive semiaxis. Numer. Algorithms 2023, 92, 545–569. [Google Scholar]
- Orive, R.; Santos-León, J.C.; Spalević, M.M. Cubature formulae for the Gaussian weight. Some old and new rules. Electron. Trans. Numer. Anal. 2020, 53, 426–438. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M.; Tang, T. Generalized averaged Gaussian quadrature rules for the approximation of matrix functionals. BIT Numer. Math. 2016, 56, 1045–1067. [Google Scholar] [CrossRef]
- Spalević, M.M. A note on generalized averaged Gaussian formulas. Numer. Algorithms 2007, 76, 253–264. [Google Scholar] [CrossRef]
- Spalević, M.M. Error bounds of positive interpolatory quadrature rules for functions analytic on ellipses. TWMS J. Pure Appl. Math. 2025; in press. [Google Scholar]
- Spalević, M.M. On generalized averaged Gaussian formulas. II. Math. Comp. 2017, 86, 1877–1885. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M. On the Accuracy of Averaged Gauss Quadrature Rules, in preparation.
- Clenshaw, C.W.; Curtis, A.R. A method for numerical integration on an automatic computer. Numer. Math. 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Trefethen, L.N. Is Gauss quadrature better than Clenshaw-Curtis? SIAM Rev. 2008, 50, 67–87. [Google Scholar] [CrossRef]
- Trefethen, L.N. Approximation Theory and Approximation Practice; Extended Edition; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Trefethen, L.N. Exactness of quadrature formulas. SIAM Rev. 2022, 64, 132–150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).