Generalized Averaged Gauss Quadrature Rules: A Survey
Abstract
1. Introduction
2. Some Methods for Estimating the Quadrature Error of Gauss Rules
3. Computation of Averaged Gauss Quadrature Rules
4. Some Extensions and Applications of Laurie’s Averaged and Optimal Averaged Gauss Quadrature Rules
- Let be a large symmetric matrix, let , and let the function f be defined on the convex hull of the spectrum of A. The need to evaluate matrix functionals of the formwhere the superscript T denotes transposition, arises in a variety of applications including in network analysis and the solution of linear discrete ill-posed problems; see, e.g., [41,42,43,44]. When the matrix A is large, it may be prohibitively expensive, or impossible, to first compute the matrix and then evaluate (22). The Lanczos method provides a less expensive approach to compute an approximation of (22). The application of n steps of the Lanczos process to A with initial vector v yields, generically, a symmetric tridiagonal matrix (6) that determines an n-node Gauss quadrature rule that is associated with a nonnegative measure . This measure is defined by the vector v and the spectral factorization of A; see Golub and Meurant [44] for a thorough discussion. In particular, the Lanczos algorithm allows the computation of Gauss quadrature rules without explicit knowledge of the measure that defines these rules. The quadrature error of Gauss rules generated in this manner can be estimated with the aid of averaged Gauss rules.
- The problem of evaluating expressions of the formwhere A and f are as in (22) and for some , also arises in various applications including color image restoration [45] and the determination of the optical absorption spectrum of a material [46]. An application of m steps of the symmetric block Lanczos algorithm to A with initial block V gives a symmetric block tridiagonal matrix that can be associated with a block Gauss quadrature rule for the approximation of (23). Analogues of Laurie’s averaged rule and the optimal averaged rule for the estimation of the quadrature error in the block Gauss rule are described in [47], where applications to network analysis are discussed.
- Let be a large symmetric matrix, let , and let f be a function that is defined on the convex hull of the spectrum of A. The need to evaluate expressions of the formarises, e.g., in network analysis, see [48,49], as well as when solving systems of ordinary differential equations; see [50,51]. The expression (24) can be approximated by carrying out a few steps of the symmetric Lanczos algorithm applied to A with initial vector v. Estimates of the error can be determined with the aid of Laurie’s averaged or optimal averaged Gauss quadrature rules; see [52].
- Averaged quadrature rules associated with Gauss–Radau and Gauss–Lobatto quadrature formulas are described in [53]. They can be applied to estimate the quadrature error in Gauss–Radau and Gauss–Lobatto rules.
- Padé-type approximants are rational functions that approximate a formal series of polynomials; see Djukić et al. [56] describe the construction and performance of Padé-type approximants that correspond to optimal averaged Gauss quadrature rules.
- The conjugate gradient method is the default iterative method for the solution of linear systems of equations with a large symmetric positive definite matrix. This method is closely related to the symmetric Lanczos method and, therefore, to orthogonal polynomials. Almutairi et al. [57] discuss how Gauss quadrature rules, Laurie’s averaged Gauss rules, and optimal averaged Gauss rules can be applied to estimate the norm of the error in approximate solutions computed by the conjugate gradient method.
- The iterative solution of linear systems with a large symmetric, indefinite, nonsingular matrix by a Lanczos-type method is discussed by Alibrahim et al. [58], who describe how the norm of the error in computed approximate solutions can be estimated by Gauss rules, Laurie’s averaged Gauss rules, and optimal averaged Gauss rules.
- Fredholm integral equations of the second kind that are defined on a finite or infinite interval arise in many applications. Djukić et al. [59], Díaz de Alba et al. [60], and Fermo et al. [61] discuss their numerical solution by Nyström methods that are based on Gauss quadrature rules. It is important to be able to estimate the error in the computed solution because this makes it possible to choose an appropriate number of nodes in the Gauss quadrature rule used. These papers explore the application of anti-Gauss, Laurie’s averaged Gauss, and weighted averaged Gauss quadrature rules for this purpose and analyze the numerical stability of these methods.
- Cubature rules that generalize Laurie’s averaged rule are described in [59,62]. The development of averaged rules for problems in several space-dimensions is still an active area of research. A difficulty is that the domain of integration in higher dimensions may be of a variety of shapes, see, e.g., [63]. Another issue is that when the domain of integration is simple, say, the unit square in the first quadrant, and the integral is approximated by integrating one space-dimension at a time by Gauss quadrature, integration along the first dimension, say, the horizontal axis, yields approximations that are used when integrating along the vertical axis. It remains to be investigated how the errors in the approximations obtained when integrating in the horizontal direction affect the error estimates obtained when integrating in the vertical direction.
5. Internality of Averaged and Optimal Averaged Gauss Rules
5.1. Results for Classical Weight Functions
- if or , then both averaged Gauss formulas are internal;
- if or , then both averaged Gauss formulas are external;
- if , then for , only the optimal averaged Gauss formula is internal, and for , only Laurie’s averaged Gauss formula is internal.
Modifications by Linear Divisors and Factors
5.2. Chebyshev Weight Functions
5.2.1. Modifications by a Linear Divisor
5.2.2. Modifications by a Linear-Over-Linear Factor
5.3. Modifications of the Jacobi Weight Functions
- the largest node internal if , or and ,
- the smallest node internal if , or and .
- the largest node internal if , or and ,
- the smallest node internal if , or and .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gautschi, W. Orthogonal Polynomials: Computation and Approximation; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Chihara, T.S. An Introduction to Orthogonal Polynomials; Gordon and Breach, Science Publishers: New York, NY, USA; London, UK; Paris, France, 1978. [Google Scholar]
- Szegő, G. Orthogonal Polynomials, 4th ed.; American Mathematical Society: Providence, RI, USA, 1975. [Google Scholar]
- Wilf, H.S. Mathematics for the Physical Sciences; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Borges, C.F.; Reichel, L. Computation of Gauss-type quadrature rules. Electron. Trans. Numer. Anal. 2024, 61, 121–136. [Google Scholar] [CrossRef]
- Golub, G.H.; Welsch, J.H. Calculation of Gauss quadrature rules. Math. Comp. 1969, 23, 221–230. [Google Scholar] [CrossRef]
- Laurie, D.P. Anti-Gaussian quadrature formulas. Math. Comp. 1996, 65, 739–747. [Google Scholar] [CrossRef]
- Ehrich, S. On stratified extensions of Gauss–Laguerre and Gauss–Hermite quadrature formulas. J. Comput. Appl. Math. 2002, 140, 291–299. [Google Scholar] [CrossRef]
- Spalević, M.M. On generalized averaged Gaussian formulas. Math. Comp. 2007, 76, 1483–1492. [Google Scholar] [CrossRef]
- Kronrod, A.S. Integration with control of accuracy. Soviet Phys. Dokl. 1964, 9, 17–19. [Google Scholar]
- Gautschi, W. A historical note on Gauss–Kronrod quadrature. Numer. Math. 2005, 100, 483–484. [Google Scholar] [CrossRef]
- Calvetti, D.; Golub, G.H.; Gragg, W.B.; Reichel, L. Computation of Gauss–Kronrod rules. Math. Comp. 2000, 69, 1035–1052. [Google Scholar] [CrossRef]
- Laurie, D.P. Calculation of Gauss–Kronrod quadrature rules. Math. Comp. 1997, 66, 1133–1145. [Google Scholar] [CrossRef]
- Notaris, S.E. Gauss–Kronrod quadrature formulae—A survey of fifty years of research. Electron. Trans. Numer. Anal. 2016, 45, 371–404. [Google Scholar]
- Kahaner, D.K.; Monegato, G. Nonexistence of extended Gauss–Laguerre and Gauss–Hermite quadrature rules with positive weights. Z. Angew. Math. Phys. 1978, 29, 983–986. [Google Scholar] [CrossRef]
- Peherstorfer, F.; Petras, K. Ultraspherical Gauss–Kronrod quadrature is not possible for λ > 3. SIAM J. Numer. Anal. 2000, 37, 927–948. [Google Scholar] [CrossRef]
- Peherstorfer, F.; Petras, K. Stieltjes polynomials and Gauss–Kronrod quadrature for Jacobi weight functions. Numer. Math. 2003, 95, 689–706. [Google Scholar] [CrossRef]
- Laurie, D.P. Stratified sequence of nested quadrature formulas. Quest. Math. 1992, 15, 365–384. [Google Scholar] [CrossRef]
- Patterson, T.N.L. Stratified nested and related quadrature rules. J. Comput. Appl. Math. 1999, 112, 243–251. [Google Scholar] [CrossRef][Green Version]
- Hascelik, A.I. Modified anti-Gauss and degree optimal average formulas for Gegenbauer measure. Appl. Numer. Math. 2008, 58, 171–179. [Google Scholar] [CrossRef]
- Peherstorfer, F. On positive quadrature formulas. In ISNM International Series of Numerical Mathematics; Brass, H., Hämmerlin, G., Eds.; Numerical Integration IV; Birkhäuser: Basel, Switzerland, 1993; Volume 112, pp. 297–313. [Google Scholar]
- Peherstorfer, F. Positive quadrature formulas III: Asymptotics of weights. Math. Comp. 2008, 77, 2241–2259. [Google Scholar] [CrossRef][Green Version]
- Reichel, L.; Spalević, M.M. Averaged Gauss quadrature formulas: Properties and applications. J. Comput. Appl. Math. 2022, 410, 114232. [Google Scholar] [CrossRef]
- Calvetti, D.; Reichel, L. Symmetric Gauss–Lobatto and modified anti-Gauss rules. BIT Numer. Math. 2003, 43, 541–554. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Weighted averaged Gaussian quadrature rules for modified Chebyshev measures. Appl. Numer. Math. 2024, 200, 195–208. [Google Scholar] [CrossRef]
- Djukić, D.L.; Reichel, L.; Spalević, M.M. Truncated generalized averaged Gauss quadrature rules. J. Comput. Appl. Math. 2016, 308, 408–418. [Google Scholar] [CrossRef]
- Djukić, D.L.; Reichel, L.; Spalević, M.M. Internality of generalized averaged Gaussian quadratures and their truncated variants for measures induced by Chebyshev polynomials. Appl. Numer. Math. 2019, 142, 190–205. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Internality of generalized averaged quadrature rules and truncated variants for modified Chebyshev measures of the first kind. J. Comput. Appl. Math. 2021, 398, 113696. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Internality of generalized averaged quadrature rules and truncated variants for modified Chebyshev measures of the third and fourth kind. Numer. Algorithms 2023, 92, 523–544. [Google Scholar] [CrossRef]
- Djukić, D.L.; Reichel, L.; Spalević, M.M.; Tomanović, J.D. Internality of the averaged Gaussian quadratures and their truncated variants with Bernstein-Szegő weight functions. Electron. Trans. Numer. Anal. 2016, 45, 405–419. [Google Scholar]
- Djukić, D.L.; Reichel, L.; Spalević, M.M.; Tomanović, J.D. Internality of generalized averaged Gaussian quadrature rules and their truncated variants for modified Chebyshev measures of the second kind. J. Comput. Appl. Math. 2019, 345, 70–85. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Internality of averaged Gauss quadrature rules for certain modification of Jacobi measures. Appl. Comput. Math. 2023, 22, 426–442. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Pejčev, A.V.; Reichel, L.; Spalević, M.M.; Spalević, S.M. Internality of two-measure-based generalized Gauss quadrature rules for modified Chebyshev measures. Electron. Trans. Numer. Anal. 2024, 61, 157–172. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Pejčev, A.V.; Reichel, L.; Spalević, M.M.; Spalević, S.M. Internality of two-measure-based generalized Gauss quadrature rules for modified Chebyshev measures II. Mathematics 2025, 13, 513. [Google Scholar] [CrossRef]
- Pejčev, A.V.; Reichel, L.; Spalević, M.M.; Spalević, S.M. A new class of quadrature rules for estimating the error in Gauss quadrature. Appl. Numer. Math. 2024, 204, 206–221. [Google Scholar] [CrossRef]
- Alqahtani, H.; Borges, C.; Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Computation of pairs of related Gauss quadrature rules. Appl. Numer. Math. 2025, 208, 32–42. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M. A new representation of generalized averaged Gauss quadrature rules. Appl. Numer. Math. 2021, 165, 614–619. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Decompositions of optimal averaged Gauss quadrature rules. J. Comput. Appl. Math. 2024, 438, 115586. [Google Scholar] [CrossRef]
- de la Calle Ysern, B.; Spalević, M.M. Modified Stieltjes polynomials and Gauss–Kronrod quadrature rules. Numer. Math. 2018, 138, 1–35. [Google Scholar] [CrossRef]
- de la Calle Ysern, B.; Spalević, M.M. On the computation of Patterson-type quadrature rules. J. Comput. Appl. Math. 2022, 403C, 113850. [Google Scholar] [CrossRef]
- Baglama, J.; Fenu, C.; Reichel, L.; Rodriguez, G. Analysis of directed networks via partial singular value decomposition and Gauss quadrature. Linear Algebra Appl. 2014, 456, 93–121. [Google Scholar] [CrossRef]
- Calvetti, D.; Golub, G.H.; Reichel, L. Estimation of the L-curve via Lanczos bidiagonalization. BIT Numer. Math. 1999, 39, 603–619. [Google Scholar] [CrossRef]
- Fenu, C.; Martin, D.; Reichel, L.; Rodriguez, G. Network analysis via partial spectral factorization and Gauss quadrature. SIAM J. Sci. Comput. 2013, 35, A2046–A2068. [Google Scholar] [CrossRef]
- Golub, G.H.; Meurant, G. Matrices, Moments and Quadrature with Applications; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Bentbib, A.; Ghomari, M.E.; Jbilou, K.; Reichel, L. The extended symmetric block Lanczos method for matrix-valued Gauss-type quadrature rules. J. Comput. Appl. Math. 2022, 407, 113965. [Google Scholar] [CrossRef]
- Shao, M.; da Jornada, F.H.; Lin, L.; Yang, C.; Deslippe, J.; Louie, S.G. A structure preserving Lanczos algorithm for computing the optical absorption spectrum. SIAM J. Matrix. Anal. Appl. 2018, 39, 683–711. [Google Scholar] [CrossRef]
- Reichel, L.; Rodriguez, G.; Tang, T. New block quadrature rules for the approximation of matrix functions. Linear Algebra Appl. 2016, 502, 299–326. [Google Scholar] [CrossRef]
- De la Cruz Cabrera, O.; Matar, M.; Reichel, L. Edge importance in a network via line graphs and the matrix exponential. Numer. Algorithms 2020, 83, 807–832. [Google Scholar] [CrossRef]
- Estrada, E.; Higham, D.J. Network properties revealed through matrix functions. SIAM Rev. 2010, 52, 696–714. [Google Scholar] [CrossRef]
- Beckermann, B.; Reichel, L. Error estimation and evaluation of matrix functions via the Faber transform. SIAM J. Numer. Anal. 2009, 47, 3849–3883. [Google Scholar] [CrossRef]
- Hochbruck, M.; Lubich, C. On Krylov subspace approximations to the matrix exponential operator. SIAM J. Numer. Anal. 1997, 34, 1911–1925. [Google Scholar] [CrossRef]
- Eshghi, N.; Reichel, L. Estimating the error in matrix function approximations. Adv. Comput. Math. 2021, 47, 57. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M. Radau- and Lobatto-type averaged Gauss rules. J. Comput. Appl. Math. 2024, 437, 115477. [Google Scholar] [CrossRef]
- Kim, S.-M.; Reichel, L. Anti-Szegő quadrature rules. Math. Comp. 2007, 76, 795–810. [Google Scholar] [CrossRef]
- Jagels, C.; Reichel, L.; Tang, T. Generalized averaged Szegő quadrature rules. J. Comput. Appl. Math. 2017, 311, 645–654. [Google Scholar] [CrossRef]
- Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Optimal averaged Padé-type approximants. Electron. Trans. Numer. Anal. 2023, 59, 145–156. [Google Scholar] [CrossRef]
- Almutairi, H.; Meurant, G.; Reichel, L.; Spalević, M.M. New error estimates for the conjugate gradient method. J. Comput. Appl. Math. 2025, 459, 116357. [Google Scholar] [CrossRef]
- Alibrahim, M.; Darvishi, M.T.; Reichel, L.; Spalević, M.M. Error estimators for a Krylov subspace method for the solution of linear systems of equations with a symmetric indefinite matrix. Axioms 2025, 14, 179. [Google Scholar] [CrossRef]
- Djukić, D.L.; Fermo, L.; Mutavdžić Djukić, R.M. Averaged Nyström interpolants for bivariate Fredholm integral equations on the real positive semi-axis. Electron. Trans. Numer. Anal. 2024, 61, 51–65. [Google Scholar] [CrossRef]
- Díaz de Alba, P.; Fermo, L.; Rodriguez, G. Solution of second kind Fredholm integral equations by means of Gauss and anti-Gauss quadrature rules. Numer. Math. 2020, 146, 699–728. [Google Scholar] [CrossRef]
- Fermo, L.; Reichel, L.; Rodriguez, G.; Spalević, M.M. Averaged Nyström interpolants for the solution of Fredholm integral equations of the second kind. Appl. Math. Comput. 2024, 467, 128482. [Google Scholar] [CrossRef]
- Djukić, D.L.; Fermo, L.; Mutavdžić Djukić, R.M. Averaged cubature schemes on the real positive semiaxis. Numer. Algorithms 2023, 92, 545–569. [Google Scholar]
- Orive, R.; Santos-León, J.C.; Spalević, M.M. Cubature formulae for the Gaussian weight. Some old and new rules. Electron. Trans. Numer. Anal. 2020, 53, 426–438. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M.; Tang, T. Generalized averaged Gaussian quadrature rules for the approximation of matrix functionals. BIT Numer. Math. 2016, 56, 1045–1067. [Google Scholar] [CrossRef]
- Spalević, M.M. A note on generalized averaged Gaussian formulas. Numer. Algorithms 2007, 76, 253–264. [Google Scholar] [CrossRef]
- Spalević, M.M. Error bounds of positive interpolatory quadrature rules for functions analytic on ellipses. TWMS J. Pure Appl. Math. 2025; in press. [Google Scholar]
- Spalević, M.M. On generalized averaged Gaussian formulas. II. Math. Comp. 2017, 86, 1877–1885. [Google Scholar] [CrossRef]
- Reichel, L.; Spalević, M.M. On the Accuracy of Averaged Gauss Quadrature Rules, in preparation.
- Clenshaw, C.W.; Curtis, A.R. A method for numerical integration on an automatic computer. Numer. Math. 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Trefethen, L.N. Is Gauss quadrature better than Clenshaw-Curtis? SIAM Rev. 2008, 50, 67–87. [Google Scholar] [CrossRef]
- Trefethen, L.N. Approximation Theory and Approximation Practice; Extended Edition; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Trefethen, L.N. Exactness of quadrature formulas. SIAM Rev. 2022, 64, 132–150. [Google Scholar] [CrossRef]
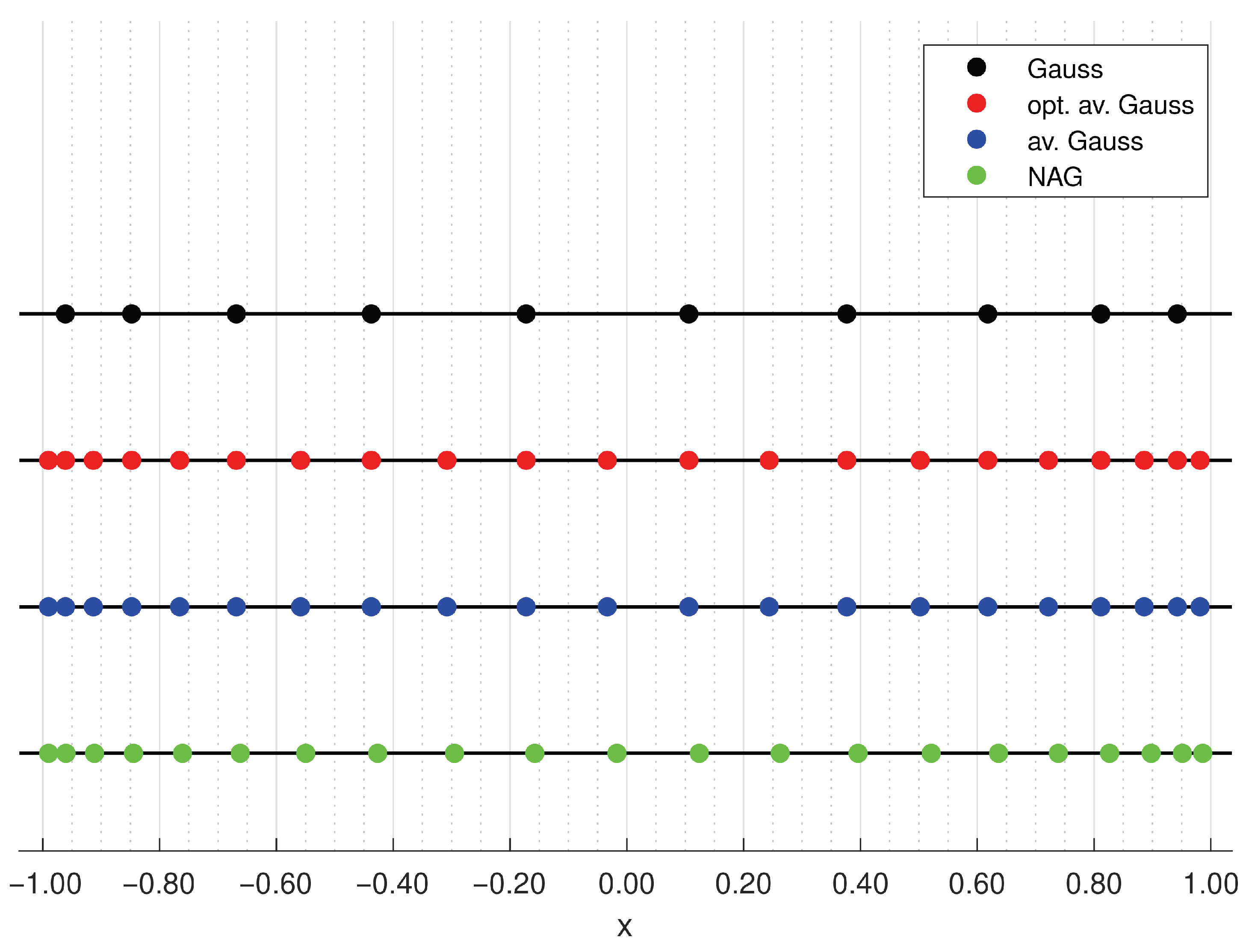
| n | ||||
| 5 | ||||
| 10 | ||||
| 25 | ||||
| 50 | ||||
| , , and . The outermost nodes of and . | ||||
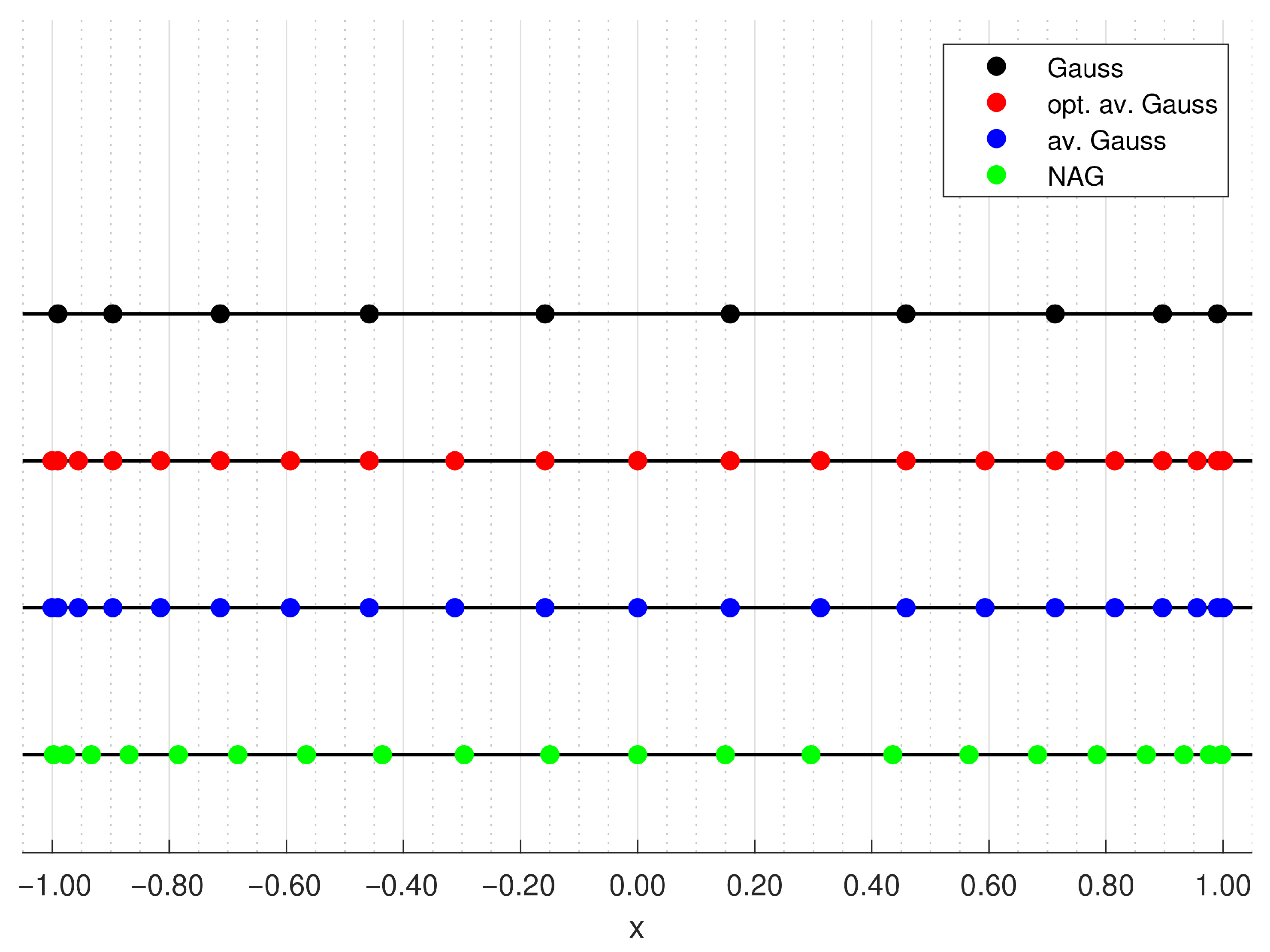
| n | ||||
| 5 | ||||
| 10 | ||||
| 25 | ||||
| 50 | ||||
| , , and . The outermost nodes of . | ||||
| Property | Gauss–Kronrod | Optimal Averaged Gauss | Averaged Gauss | NAG |
|---|---|---|---|---|
| existence | not always | yes | yes | yes |
| positivity | not always | yes | yes | yes |
| internality | not always | not always | not always | not always |
| interlacing | yes | yes | yes | no |
| complexity | high | low | low | low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djukić, D.L.; Mutavdžić Djukić, R.M.; Reichel, L.; Spalević, M.M. Generalized Averaged Gauss Quadrature Rules: A Survey. Mathematics 2025, 13, 3145. https://doi.org/10.3390/math13193145
Djukić DL, Mutavdžić Djukić RM, Reichel L, Spalević MM. Generalized Averaged Gauss Quadrature Rules: A Survey. Mathematics. 2025; 13(19):3145. https://doi.org/10.3390/math13193145
Chicago/Turabian StyleDjukić, Dušan L., Rada M. Mutavdžić Djukić, Lothar Reichel, and Miodrag M. Spalević. 2025. "Generalized Averaged Gauss Quadrature Rules: A Survey" Mathematics 13, no. 19: 3145. https://doi.org/10.3390/math13193145
APA StyleDjukić, D. L., Mutavdžić Djukić, R. M., Reichel, L., & Spalević, M. M. (2025). Generalized Averaged Gauss Quadrature Rules: A Survey. Mathematics, 13(19), 3145. https://doi.org/10.3390/math13193145








