A Cluster-Level Information Fusion Framework for D-S Evidence Theory with Its Applications in Pattern Classification

Abstract

Multi-source information fusion is a key challenge in uncertainty reasoning. Dempster–Shafer evidence theory (D-S evidence theory) offers a flexible framework for representing and fusing uncertain information. However, the classical Dempster’s combination rules may yield counter-intuitive results when faced with highly conflicting evidence. To overcome this limitation, we introduce a cluster-level information fusion framework, which shifts the focus from pairwise evidence comparisons to a more holistic cluster-based perspective. A key contribution is a novel cluster–cluster divergence measure that jointly captures the strength of belief assignments and structural differences between clusters. Guided by this measure, a reward-driven evidence assignment rule dynamically allocates new evidence to enhance inter-cluster separability while preserving intra-cluster coherence. Building upon the resulting structure, we propose a two-stage information fusion algorithm that assigns credibility weights at the cluster level. The effectiveness of the framework is validated through a range of benchmark pattern classification tasks, in which the proposed method not only improves classification accuracy compared with D-S evidence theory methods but also provides a more interpretable, cluster-oriented perspective for handling evidential conflict.

1. Introduction

Uncertainty reasoning is a powerful tool for representing, quantifying, and manipulating incomplete, imprecise, ambiguous, or conflicting information. Several theories have been proposed to model different uncertainty problems, including probability theory [1], fuzzy sets [2], rough sets [3], D-S evidence theory [4,5], and Bayesian inference [6,7], which have been further applied in many scenarios, including time-series analysis [8], decision-making [9,10], deep learning [11,12], game theory [13], and disaster reduction [14].

D-S evidence theory has attracted significant attention for its effectiveness in managing the discordance and non-specificity of evidence [15]. The core principle of Dempster’s Rule of Combination (DRC) is to resolve conflicts by discarding contradictory components. However, this approach may produce counter-intuitive results when the evidence is highly conflicting [16,17,18]. Various methods have been proposed to address this issue, which can generally be divided into two main categories: the first category emphasizes modifying the combination rule, while the second focuses on pre-processing the evidence before fusion.

Several contributions to the first type of methods include the unnormalized combination rule in the transferable belief model [19], the disjunctive rule [20], and alternative normalization schemes [21]. However, uncertainty can arise from a lack of knowledge, particularly when the sources of evidence are unreliable or corrupted. Modifying the combination rule alone cannot fully rectify the situation, as counter-intuitive results often originate from the evidence sources rather than just the fusion mechanism [22]. As a result, many researchers have shifted their focus to the second type of methods, which highlight the pre-processing of evidence to reduce conflict before fusion. Representative methods in this category include simple averaging of basic belief assignments (BBAs) [23] and weighted averaging of BBAs [24] based on the Jousselme divergence [25]. Building on this direction, a key challenge is designing measures that provide a clear mathematical foundation while yielding more reliable credibility assessments for use in weighted-average fusion. From the perspective of the mathematical tools employed, these methods can be broadly classified into three categories: The first is belief-entropy-based weighting [26,27,28], which evaluates the uncertainty associated with a single piece of evidence. The second is divergence-based weighting [24,29], which quantifies the informational difference between evidence pairs. The third is hybrid approaches integrating belief-entropy-based weighting and divergence-based weighting to enhance credibility assessment [30,31,32].

The essence of handling conflicting evidence is to identify one or more unreliable sources of evidence. Research on belief entropy mainly focuses on depicting discordance and non-specificity [33,34,35], modeling the amount of information required to reduce uncertainty to certainty. Therefore, divergence-based methods, which directly quantify the differences between pairs of BBAs, are more suitable for calculating credibility. A representative work of the divergence-based method is the Belief Jensen–Shannon divergence (BJS) [36], the first to extend the Jensen–Shannon divergence [37] into the context of the D-S evidence theory. Following the paradigm established by BJS, subsequent works in this context often focus on mining deeper semantic relationships between pairs of evidence to enhance credibility assessment. Some works model the set-structural correlations among all focal subsets to better characterize their correlation within BBAs [29,38,39,40]. Others introduce fractal-based divergences to separate similar and conflicting evidence across scales [41,42]. A third line quantifies BJS-generalized divergence among BBAs and develops a GEJS-weighted fusion method [43]. A fourth line extends belief divergence contexts based on quantum-theoretic tools [44,45,46]. Methods built on these mathematical foundations have generally performed well in pattern classification tasks. They are seen as generalizations of classical probabilistic methods in the context of D-S evidence theory, which establish strong links to information-theoretic principles.

Most existing methods primarily evaluate either the differences between pairs of BBAs or the divergence among multi-source evidence [43]. However, there is a significant gap in our understanding of the deeper mathematical and informational relationships among the entire set of BBAs from a broader perspective. In practice, some BBAs show high similarity, reflecting a consensus, while others differ significantly, indicating distinct belief groups. Simply determining the credibility of a BBA based on the evaluations of all other BBAs, or relying solely on pairwise comparisons, overlooks the valuable information gathered at the group level through consensus. By grouping BBAs with similar belief structures into clusters and assigning those with dissimilar structures to separate clusters [47,48], we can better interpret conflicts among BBAs. This approach allows us to optimize fusion outcomes by leveraging both intra-cluster and inter-cluster information, leading to more transparent decision-making. This challenge is especially critical in real-world applications such as multi-sensor target recognition, where a single conflicting report can distort consensus among multiple sources [49].

Therefore, we introduce a novel cluster-level information fusion framework to fill the gap in modeling group-level consensus among BBAs, shifting the analytical perspective from traditional BBA-to-BBA comparisons to a more holistic view of BBAs-to-BBAs. A key contribution is the development of a new cluster–cluster divergence measure, $D_{CC}$, which captures both the mass distribution and the structural differences between evidence groups. This measure is integrated into a reward-based greedy evidence assignment rule that dynamically assigns new evidence to optimize inter-cluster separation and intra-cluster consistency. Validation on benchmark pattern classification tasks shows that the proposed method outperforms traditional D-S evidence theory methods, demonstrating the effectiveness of its novel cluster-level perspective.

The rest of this paper is organized as follows: Section 2 introduces foundational theories. Section 3 proposes our cluster-level information fusion framework. Section 4 illustrates the method with numerical examples. Section 5 validates the method on classification tasks. Section 6 concludes the paper.

2. Preliminaries

This section lays the theoretical groundwork for our proposed framework. We begin by reviewing the fundamentals of D-S evidence theory, which forms the basis for representing and combining uncertain information. We then introduce fractal theory, a concept that we will later leverage to construct representative centroids for evidence clusters. Finally, we summarize several key divergence measures from information theory, as these will be essential for quantifying the dissimilarity between evidence clusters.

2.1. D-S Evidence Theory

D-S evidence theory [4,5] is a mathematical framework for representing uncertain and ambiguous information. It allows for allocating trust to a set of hypotheses $\Theta$, rather than to a single hypothesis, and is therefore considered to be an extension of traditional probability theory. Key concepts of D-S evidence theory are outlined below.

Definition 1 (Frame of Discernment).

Let Θ be a set of N mutually exclusive and exhaustive non-empty hypotheses, called a frame of discernment, denoted by

$$\Theta =\{{\theta }_1,{\theta }_2,\dots ,{\theta }_N\}.$$

(1)

The power set of Θ, denoted as $2^{\Theta }$, consists of all of its subsets:

$$2^{\Theta }=\{⌀,\left\{{\theta }_1\right\},\left\{{\theta }_2\right\},\dots ,\left\{{\theta }_N\right\},\{{\theta }_1,{\theta }_2\},\{{\theta }_1,{\theta }_3\},\dots ,\Theta \},$$

(2)

where the empty set is denoted by ⌀. Singleton sets denote sets containing only one element, and a set containing multiple elements is called a multi-element set. All of the above sets are subsets of $2^{\Theta }$.

Definition 2 (Basic Belief Assignment).

A basic belief assignment (also called a mass function) is a function $m:2^{\Theta }\to [0,1]$ satisfying

$$m(⌀)=0,$$

(3)

and

$$\sum _{A\subseteq \Theta }m\left(A\right)=1,$$

(4)

where each set $A\subseteq \Theta$ with $m\left(A\right)>0$ is called a focal element.

Specifically, a set of basic belief assignments is:

$$\mathcal{M}=\{m_1,m_2,\dots ,m_j,\dots ,m_n\}.$$

(5)

Definition 3 (Dempster’s Rule of Combination).

Dempster’s Rule of Combination fuses basic belief assignments from multiple independent information sources into a single consensus BBA. Given two basic belief assignments $m_1$ and $m_2$ defined on the same Θ, the combined mass function m is defined as follows:

$$m\left(A\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{1-K}\sum _{B\cap C=A}{m}_1\left(B\right)m_2\left(C\right),}\hfill & A\ne ⌀,\hfill \\ 0,\hfill & A=⌀,\hfill \end{array}\right.$$

(6)

where the conflict coefficient

$$K=\sum _{B\cap C=⌀}{m}_1\left(B\right)m_2\left(C\right)$$

(7)

is defined to measure the degree of conflicts between two BBAs.

The information fusion problem can be regarded as recursively combining n basic belief assignments into a new basic belief assignment $\overline{m}$ using Dempster’s Rule of Combination, in the following form:

$$\overline{m}=m_1\oplus m_2\oplus \dots \oplus m_j\oplus \dots \oplus m_n=\underset{j=1}{\overset{n}{⨁}}{m}_j.$$

(8)

Dempster’s Rule of Combination is a commonly used mechanism in evidential reasoning. However, it can produce counter-intuitive results when applied to highly conflicting evidence, which poses a challenge to motivating the development of our cluster-based information fusion framework.

2.2. Fractal

Fractal theory offers a mathematical framework for describing objects that embody statistical self-similarity, a property where their structural patterns are replicated on various magnification scales [50].

The generalization of fractal theory in D–S evidence theory formalizes belief refinement as a self-similar process of unit-time splitting. This process uncovers the hierarchical structure in a piece of evidence by iteratively redistributing the mass of a multi-element focal element to its members in the power set.

In uncertainty representation, the Maximum Deng Entropy Separation Rule (MDESR) [51], based on Deng entropy (also called belief entropy) [52,53], can recursively separate a mass function in a way that maximizes the Deng entropy at each step. It guarantees that the information volume [54] strictly increases and converges to a stable value during iterations. Previous work [54] has investigated how to maximize the Deng entropy of the mass function after each step of fractalization and derived its analytical optimal solution: the maximum Deng entropy.

In our work, this fractal-based maximum entropy principle is instrumental in defining the centroid of an evidence cluster, guaranteeing that it evolves in the most unbiased manner as new evidence is incorporated, a concept further detailed in Section 3.2.

Definition 4 (Maximum Deng Entropy).

When BBA is set to

$$m\left(A\right)={\displaystyle \frac{2^{\left|A\right|}-1}{{\displaystyle \sum _{B\subseteq \Theta }(2^{\left|B\right|}-1)}}},$$

(9)

the Deng entropy reaches its maximum value, which is called information volume. Therefore, the maximum Deng entropy can be expressed as follows:

$$\overline{H}\left(m\right)={log}_2\sum _{A\subseteq \Theta }(2^{\left|A\right|}-1).$$

(10)

2.3. Divergence

Definition 5 (Kullback–Leibler Divergence).

In information theory, the Kullback–Leibler divergence [55] measures the discrepancy from one probability distribution to another. For discrete distributions $P=\left(p_i\right)$ and $Q=\left(q_i\right)$ with the same sample space, it is defined as follows:

$$D_{KL}(P\parallel Q)=\sum _i{p}_i{log}_2{\displaystyle \frac{p_i}{q_i}}.$$

(11)

Definition 6 (Jensen–Shannon Divergence).

The Jensen–Shannon divergence [37], which has its roots in earlier concepts like the "increment of entropy" for measuring distances between random graphs [56], overcomes the asymmetric issue of Kullback–Leibler divergence by taking the average distribution $M=\frac{1}{2}(P+Q)$ and defining

$$\begin{array}{c}\hfill D_{JS}(P\parallel Q)=\frac{1}{2}{D}_{KL}(P\parallel M)+\frac{1}{2}{D}_{KL}(Q\parallel M)=\frac{1}{2}\sum _i{p}_i{log}_2{\displaystyle \frac{2p_i}{p_i+q_i}}+\frac{1}{2}\sum _i{q}_i{log}_2{\displaystyle \frac{2q_i}{p_i+q_i}}.\end{array}$$

(12)

where $D_{JS}$ is always finite, symmetric, and its square root is a metric.

Definition 7 (Belief Jensen–Shannon Divergence).

Belief Jensen–Shannon divergence is a generalization of Jensen–Shannon divergence. Consider two BBAs, $m_1$ and $m_2$, defined on Θ. The Belief Jensen–Shannon divergence [36] is defined as follows:

$$\begin{array}{c}\hfill BJS(m_1,m_2)={\displaystyle \frac{1}{2}}\sum _{A\subseteq \Theta }{m}_1\left(A\right){log}_2{\displaystyle \frac{2m_1\left(A\right)}{m_1\left(A\right)+m_2\left(A\right)}}+{\displaystyle \frac{1}{2}}\sum _{A\subseteq \Theta }{m}_2\left(A\right){log}_2{\displaystyle \frac{2m_2\left(A\right)}{m_1\left(A\right)+m_2\left(A\right)}}.\end{array}$$

(13)

Definition 8 (Euclidean Distance).

For two vectors $\mathit{x}=\left(x_i\right)$ and $\mathit{y}=\left(y_i\right)$ in the same real coordinate space, the Euclidean distance is the ${\ell }_2$-norm of their difference:

$${\parallel \mathit{x}-\mathit{y}\parallel }_2=\sqrt{\sum _i{(x_i-y_i)}^2},$$

(14)

which corresponds to the standard geometric distance between points.

Definition 9 (Hellinger Distance).

Given two discrete probability distributions $P=\left(p_i\right)$ and $Q=\left(q_i\right)$ with the same sample space, the Hellinger distance [57] is defined as follows:

$$H(P,Q)={\displaystyle \frac{1}{\sqrt{2}}}{∥\sqrt{P}-\sqrt{Q}∥}_2={\displaystyle \frac{1}{\sqrt{2}}}\sqrt{\sum _i{\left(\sqrt{p_i}-\sqrt{q_i}\right)}^2}.$$

(15)

Hellinger distance is symmetric, bounded in $[0, 1]$, and a proper metric.

These divergences are foundational to our framework, providing the mathematical tools to quantify both the internal consistency of BBAs within a cluster and an important baseline used in D-S evidence theory.

3. The Cluster-Level Information Fusion Framework

In this section, we introduce a comprehensive framework for cluster-level information fusion. The framework first groups multiple pieces of evidence into appropriate clusters. A cluster centroid is then established based on fractal geometry principles, after which inter-cluster divergences are quantified and new evidence is dynamically assigned to the most suitable cluster. Finally, a weighted fusion of evidence is carried out using cluster-level credibility weights.

3.1. Inspirations of the Cluster-Level View and Information Fusion Framework

In information fusion, the reliability of a given piece of evidence is often assessed by measuring its divergence, entropy, and inherent properties within D-S evidence theory, typically through pairwise BBA comparisons. However, this conventional process tends to overlook the structural differences between multiple pieces of evidence. Within a given collection of evidence, many of the corresponding mass functions are often highly similar. In contrast, conflicting evidence is typically characterized by mass functions that deviate significantly from those of the majority.

A classical example in the literature [24] is illustrated to show both the source of the conflict and how the results of the fusion can vary depending on the relationships among pieces of evidence.

Example 1 (Sensor Data for Target Recognition).

In an automatic target recognition system based on multiple sensors, assume that the real target is $\left\{A\right\}$. The system collects the following five pieces of evidence from five different sensors in

Table 1. BBAs from five sensors for the target recognition task.

BBAs	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{C}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{C}\left\}\right)$
$m_1$	0.50	0.20	0.30
$m_2$		0.90	0.10
$m_3$	0.55	0.10		0.35
$m_4$	0.55	0.10		0.35
$m_5$	0.60	0.10		0.30

:

In Example 1, intuitively, the BBAs $m_1$, $m_3$, $m_4$, and $m_5$ all assign their belief to $\left\{A\right\}$, but none of them achieve a relatively high confidence. Meanwhile, the maximum value of $m_2$ is 0.90, pointing to $\left\{B\right\}$ decisively. Therefore, although most of the evidence supports $\left\{A\right\}$, the conflicting evidence $m_2$ precludes the possibility of making a direct and accurate judgment. To demonstrate the source of the conflict, we compare three situations in terms of pairwise average Dempster conflict coefficient:

• Case 1: Only similar BBAs $\{m_1,m_3,m_4,m_5\}$ are considered; $K_{\mathrm{coherent}}$ is the average of $K(m_i,m_j)$ over all pairs $i<j$ with $i,j\in \{1,3,4,5\}$.
• Case 2: The conflicting BBA $m_2$ versus the others. $K_{\mathrm{conflict}}$ is the average of $K(m_2,m_j)$ for $j\in \{1,3,4,5\}$.
• Case 3: All five BBAs $\{m_1,m_2,m_3,m_4,m_5\}$ are considered; $K_{\mathrm{mixed}}$ is the average of $K(m_i,m_j)$ on all pairs.

For each case, we compute the average Dempster conflict coefficient K. The results show the following:

• When only similar BBAs are counted, the average conflict coefficient $K_{\mathrm{coherent}}=$$0.3050$, indicating high consistency.
• When the conflicting BBA $m_2$ is compared to the others, $K_{\mathrm{conflict}}=$$0.8550$, revealing its direct disagreement with the majority.
• When all BBAs are included, the average conflict coefficient $K_{\mathrm{mixed}}=$$0.5250$, indicating increased overall inconsistency.

For Cases 1 and 3, we fuse the BBAs using the Dempster combination rule. The fusion result is listed in

Table 2. Fusion result from Example 1.

BBAs	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{C}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{C}\left\}\right)$
Case 1	0.9701	0.0005	0.0293
Case 3		0.1404	0.8596

.

As illustrated in Example 1 and Table 2, including conflicting evidence amplifies the overall conflict, resulting in an unreliable and counter-intuitive fusion outcome. In contrast, fusing only similar evidence leads to a more robust and accurate result. These results demonstrate that if BBAs are fused too hastily, without considering their similarities and discrepancies at the group level, there is a much greater chance of evidence conflicts, which can damage the reliability of the fusion result.

However, when evidence sources with similar characteristics are grouped into clusters and dissimilar sources are separated, the original conflicts among individual BBAs are not eliminated but reappear as discrepancies between clusters. This cluster-level perspective facilitates a more systematic and interpretable analysis of evidential conflict by distinguishing intra-cluster consensus from inter-cluster divergence. By aggregating similar BBAs, one can more clearly reveal the intrinsic structure of information, enabling the identification of consensus within clusters and the isolation of conflicting perspectives across clusters. This approach helps to reveal the underlying relationships among evidence sources and establishes the foundations for more interpretable information fusion and decision-making.

Motivated by these observations, we propose a novel cluster-level information fusion framework. In this framework, cluster centroids are defined via the maximum Deng entropy fractal operation, which captures the representative feature of each cluster. Incoming BBAs are assigned to the most appropriate cluster using an adaptive evidence allocation rule. Once all BBAs have been allocated, the cluster-level information fusion algorithm performs a weighted average using intra-cluster and inter-cluster information. Ultimately, the fusion results are converted into probabilistic values [58,59] for pattern classification or decision-making processes.

3.2. The Construction of a Cluster

Definition 10 (A Single Cluster ($Clu{s}_i$)).

Given a collection of BBAs $\mathcal{M}=\{m_j:2^{\Theta }\to [0,1]\mid j=1,2,\dots ,n\}$, the i-th cluster, denoted by $Clu{s}_i$, is any subset of BBAs from $\mathcal{M}$:

$$Clu{s}_i=\left\{m_1,m_2,\dots ,m_{n_i}\right\}\subseteq \mathcal{M},n_i=\left|Clu{s}_i\right|,$$

(16)

where $n_i=\left|Clu{s}_i\right|$ denotes the number of BBAs contained in the i-th cluster. If $n_i=0$, we set $Clu{s}_i=⌀$, representing an “empty cluster” currently holding no BBAs. Each cluster is an unordered set with no repeated elements. Each BBA $m\in \mathcal{M}$ is assigned to exactly one cluster, which is denoted as $m\in Clu{s}_i$. In other words, each BBA is exclusively allocated to a single cluster. The allocation algorithm is proposed in Algorithm 1.

The cluster partition, denoted as $\mathcal{C}=\{Clu{s}_1,\dots ,Clu{s}_K\}$, forms a partition of the full BBA set $\mathcal{M}$ such that

$$\forall i\ne j:Clu{s}_i\cap Clu{s}_j=⌀,$$

(17)

and

$$\bigcup _{i=1}^{K}Clu{s}_i=\mathcal{M},$$

(18)

where K is defined as the number of clusters containing at least one BBA.

The primary objective of clustering within our framework is to model two fundamental effects: the aggregation of similar beliefs within a cluster and the separation of conflicting beliefs between clusters, akin to fractals, which exhibit self-similarity and multiscale characteristics [34,60]. In the literature, fractal operators have been used to analyze BBAs by quantifying the maximum information volume that a single BBA can achieve, which reflects its highest level of uncertainty [51,54]. Fractal operations also simulate the dynamic evolution process of pignistic probability transformation (PPT) [34,61]. During the fractal process, the masses associated with non-singleton sets gradually decrease, while the masses on singleton sets increase. As a result, a BBA approximately converges to a pignistic probability distribution [62]. When applying fractal theory to multiple pieces of evidence, the self-similar nature of fractals amplifies the intrinsic information of these pieces of evidence. As fractal iterations proceed, the unity among similar BBAs becomes more apparent, while the differences between dissimilar BBAs are magnified [63]. As a result, modeling a cluster centroid using a fractal-based approach yields a representative summary for each cluster.

There are several ways to define fractal operators on BBAs [51,62,63,64]. However, the most justifiable construction is the maximum Deng entropy fractal. This approach yields the most conservative evolution, maximizing entropy to avoid introducing any unjustified bias in the belief update process [65,66]. In practice, we utilize the MDESR method [51] to ensure that the BBA fractal strictly follows maximum entropy principles.

Definition 11 (Maximum Deng Entropy Fractal Operator F).

We define the maximum Deng entropy fractal operator F, which redistributes the mass of each non-empty focal element $A_i\subseteq \Theta$ in a BBA $m_j$ to all of its non-empty subsets in the splitting result:

$$F\left(m_j\left(A_i\right)\right)=\sum _{\begin{array}{c}{A}_k\supseteq A_i\\ A_k\ne ⌀\end{array}}{m}_j\left(A_k\right)\times {\displaystyle \frac{2^{|A_i|}-1}{{\displaystyle \sum _{\begin{array}{c}B\subseteq A_k\\ B\ne ⌀\end{array}}(2^{\left|B\right|}-1)}}},\forall A_i\subseteq \Theta ,A_i\ne ⌀.$$

(19)

Definition 12 (h-Order Fractal BBA $m_{F_j}^{\left(h\right)}$).

Given the original BBA $m_j$, we define its h-order fractal mass function $m_{F_j}^{\left(h\right)}$ after h fractal iterations as follows:

$$m_{F_j}^{\left(h\right)}=F^h\left(m_j^{\left(0\right)}\right)=\underset{h\mathrm{times}}{\underbrace{F\left(F\left(\dots F\left(m_j^{\left(0\right)}\right)\right)\right)}}.$$

(20)

where h is called the fractal order ($h\in {\mathbb{N}}^{+}$), which indicates how many times the fractal operator is applied to the BBA. Besides the above explicit form, an equivalent recursive form is given by

$$\left\{\begin{array}{c}{m}_{F_j}^{\left(0\right)}=m_j,\hfill \\ m_{F_j}^{\left(h\right)}=F\left(m_{F_j}^{(h-1)}\right),h\in {\mathbb{N}}^{+}.\hfill \end{array}\right.$$

(21)

In particular, when $h=0$, the fractal-order mass function $m_{F_j}^{\left(0\right)}$ degrades to the original BBA $m_j$. Additionally, for every $h\in {\mathbb{N}}_0$, $m_{F_j}^{\left(h\right)}$ defines a valid mass function on $2^{\Theta }$, taking values in $[0, 1]$, satisfying ${\sum }_{A\subseteq \Theta }{m}_{F_j}^{\left(h\right)}\left(A\right)=1$ and $m_{F_j}^{\left(h\right)}\left(A\right)\ge 0$ for all $A\subseteq \Theta$.

While the h-order fractal BBA $m_{F_j}^{\left(h\right)}$ refines individual evidence, our framework requires a representative BBA to summarize the collective belief of a cluster. We then introduce the cluster centroid, which is constructed by aggregating the fractal BBAs of all of its members.

Definition 13 (Cluster Centroid ${\tilde{m}}_{F_i}^{\left(h\right)}$).

The cluster centroid refers to a virtual BBA that summarizes the overall characteristics of all BBAs within a cluster. It is given by the arithmetic mean of these fractal BBAs on the power set of Θ:

$${\tilde{m}}_{F_i}^{\left(h\right)}\left(A\right)={\displaystyle \frac{1}{n_i}}\sum _{j=1}^{n_i}{m}_{F_j}^{\left(h\right)}\left(A\right),\forall A\subseteq \Theta$$

(22)

where $n_i$ is the number of BBAs in cluster $Clu{s}_i$ and $m_{F_j}^{\left(h\right)}\left(A\right)$ denotes the mass assigned to set A after applying the h-th-order fractal operator F to $m_j$ within $Clu{s}_i$. It follows that ${\sum }_{A\subseteq \Theta }{\tilde{m}}_{F_i}^{\left(h\right)}\left(A\right)=1$ and ${\tilde{m}}_{F_i}^{\left(h\right)}\left(A\right)\ge 0$ for all $A\subseteq \Theta$, so ${\tilde{m}}_{F_i}^{\left(h\right)}$ is itself a valid BBA.

Remark 1.

To maintain consistency between the scale of the cluster and the fractal operation, we adopt the convention that the cluster size determines the fractal order:

$$h=n_i-1.$$

(23)

The fractal order h increases linearly with the number of elements in the cluster: for a singleton cluster, $h=0$; for a cluster of two elements, $h=1$; and so on. When $n_i=1$, we have ${\tilde{m}}_{F_i}^{\left(0\right)}=m_{F_j}^{\left(0\right)}=m_j$, so the cluster centroid degrades to the original BBA. If a new BBA $m_{new}$ is later added to $Clu{s}_i$, the following parameters are updated as follows:

$$n_i\leftarrow n_i+1,h\leftarrow h+1,Clu{s}_i\leftarrow Clu{s}_i\cup \left\{m_{new}\right\}.$$

(24)

While the arithmetic mean definition of the cluster centroid ${\tilde{m}}_{F_i}^{\left(h\right)}$ is straightforward, updating it from scratch requires $O(n_i^2·2^{|\Theta |})$ operations. As $n_i$ increases, this cost becomes prohibitive for large-scale or online clustering. To address this, the equivalent recursive update definition that we introduce significantly reduces this burden, lowering the per-update complexity to $O(n_i·2^{|\Theta |})$.

Definition 14 (Recursive Update of the Cluster Centroid ${\tilde{m}}_{F_i}^{\left(h\right)}$).

Given a cluster with $n_i$ existing elements and its previous centroid ${\tilde{m}}_{F_i}^{(h-1)}$, the centroid is updated to order h upon the insertion of a new BBA $m_j$. The new centroid ${\tilde{m}}_{F_i}^{\left(h\right)}$ is computed as the weighted average of the transformed existing centroid and the transformed new BBA:

$${\tilde{m}}_{F_i}^{\left(h\right)}\left(A\right)={\displaystyle \frac{n_i·F\left({\tilde{m}}_{F_i}^{(h-1)}\left(A\right)\right)+m_{F_j}^{\left(h\right)}\left(A\right)}{n_i+1}},\forall A\subseteq \Theta ,$$

(25)

where $m_{F_j}^{\left(h\right)}$ is the h-order fractal BBA corresponding to the newly inserted $m_j$, and F is the fractal operator.

The equivalence between Definitions 13 and 14 is established in Theorem 1. The proof for Theorem 1 is provided in Appendix A for completeness.

Theorem 1 (Equivalence of Definitions 13 and 14).

The cluster centroid, ${\tilde{m}}_{F_i}^{\left(h\right)}\left(A\right)$, has two definitions, the recursive form and the arithmetic average form, which are identical for any shared linear fractal operator F.

3.3. The Divergence Between Clusters

A measure is required to quantify the informational divergence between clusters. However, since cluster centroids constructed via fractal operators can reside on different fractal orders, direct comparison would violate the axioms of a metric. Therefore, unifying all cluster centroids into the same fractal order is necessary before divergence calculation.

Definition 15 (Global Maximal Fractal Order H).

To address the incomparability arising from different fractal orders, we introduce the global maximal fractal order:

$$H=\underset{1\le i\le K}{max}{h}_i,$$

(26)

where $h_i$ denotes the fractal order of cluster i.

The choice of a fractal order unification strategy is an open question. We use the maximum fractal order, as it may more thoroughly reveal the informational difference within the cluster’s fractal structure.

Remark 2.

Given any two clusters $Clu{s}_p$ and $Clu{s}_q$ with fractal orders $h_p$ and $h_q$, respectively, their centroids are aligned to order H as follows:

$${\widehat{m}}_{F_p}^{\left(H\right)}=F^{H-h_p}\left({\tilde{m}}_{F_p}^{\left(h_p\right)}\right),{\widehat{m}}_{F_q}^{\left(H\right)}=F^{H-h_q}\left({\tilde{m}}_{F_q}^{\left(h_q\right)}\right).$$

(27)

Directly comparing cluster centroids is insufficient, as it overlooks their internal structure. Different clusters may concentrate their belief on entirely different focal elements. For instance, one cluster might gain high confidence in a proposition because many of its member BBAs strongly support it. In contrast, another cluster’s support for the same proposition might be weak and sparse, indicating a lack of consensus belief within the group. To capture this structural difference, we need to quantify how a cluster’s support is distributed across focal elements. Accordingly, we propose a scale weight for each subset $A\subseteq \Theta$.

Definition 16 (Scale Weight $w_p$).

The scale weight $w_p\left(A\right)$ quantifies the proportion of BBAs in the cluster that assign a non-negligible mass to a set A. Formally, for every BBA $m_i$ in cluster p, and each set A, a soft weighting function is computed:

$$h_{\epsilon }\left(m_i\left(A\right)\right)=\sigma \left({\displaystyle \frac{m_i\left(A\right)-\delta }{\epsilon }}\right)={\displaystyle \frac{1}{1+exp\left(-\frac{m_i\left(A\right)-\delta }{\epsilon }\right)}},\delta >0,\epsilon >0,$$

(28)

where the parameters δ and ε determine the sensitivity and softness of the counting threshold, respectively, and both are chosen as small positive constants. The aggregated and normalized scale weight is then defined as follows:

$${\tilde{n}}_p\left(A\right)=\sum _{m_i\in {\mathrm{Clus}}_p}{h}_{\epsilon }\left(m_i\left(A\right)\right),w_p\left(A\right)={\displaystyle \frac{{\tilde{n}}_p\left(A\right)}{{\sum }_{B\subseteq \Theta }{\tilde{n}}_p\left(B\right)}},$$

(29)

where $w_p\left(A\right)$ indicates the relative support degree of set A in cluster p, normalized over all focal elements, ranging from $(0,1)$ and summing up to 1.

Thus, we associate each cluster p with a feature vector, whose component ${\varphi }_p\left(A\right)$ for each focal set A is defined as follows:

$${\varphi }_p\left(A\right)=\sqrt{w_p\left(A\right)·{\widehat{m}}_{F_p}^{\left(H\right)}\left(A\right)},$$

(30)

and analogously for q.

Definition 17 (Cluster–Cluster Divergence $D_{CC}$).

The cluster-to-cluster divergence $D_{CC}$ is defined as follows:

$$D_{CC}(Clu{s}_p,Clu{s}_q)=\sqrt{\sum _{A\subseteq \Theta }{\left(\sqrt{w_p\left(A\right){\widehat{m}}_{F_p}^{\left(H\right)}\left(A\right)}-\sqrt{w_q\left(A\right){\widehat{m}}_{F_q}^{\left(H\right)}\left(A\right)}\right)}^2}.$$

(31)

The divergence between clusters is determined by two factors: the scale weight of a focal set A, given by $w\left(A\right)$; and the support strength, measured by ${\widehat{m}}_F^{\left(H\right)}\left(A\right)$. From a mathematical perspective, it is defined as the Euclidean distance between clusters in a high-dimensional space; thus, it naturally satisfies non-negativity, symmetry, and the triangle inequality. This formulation allows the divergence $D_{CC}$ to be viewed as an unnormalized generalization of the Hellinger distance to the D-S evidence theory level. Additionally, the range of $D_{CC}$ is $0\le D_{CC}(Clu{s}_p,Clu{s}_q)<\sqrt{2}$. The full theorem and proof for these properties are given in Appendix B. Based on the proofs, we conclude that $D_{CC}$ satisfies all of the properties of a pseudo-metric.

3.4. Cluster-Driven Evidence Assignment Rule

The core idea of this section is how to optimally assign a newly observed BBA, denoted as $m_{new}$, to either an existing cluster ($Clu{s}_i$) or a new one ($Clu{s}_{K+1}$). This process sequentially allocates each BBA in the set $\mathcal{M}$ to its most suitable cluster, balancing the cohesion of similar beliefs within a cluster and the separation of conflicting beliefs across clusters. The decision criterion is based on the reward of each evidence assignment strategy, selecting the one with the highest reward greedily.

Definition 18 (Evidence Assignment Strategy).

Let the current cluster partition be denoted by $\mathcal{C}=\{Clu{s}_1,\dots ,Clu{s}_K\}$, and consider all possible assignment decisions for $m_{new}$. We formulate the assignment problem as the selection of an optimal strategy among $K+1$ alternatives:

$${\left\{{\mathrm{Strategy}}_k\right\}}_{k=1}^{K+1},\begin{array}{ccc}\hfill {\mathrm{Strategy}}_k& :m_{\mathrm{new}}\to Clu{s}_k,\hfill & \hfill 1\le k\le K,\\ \hfill {\mathrm{Strategy}}_{K+1}& :m_{\mathrm{new}}\to Clu{s}_{K+1}\left(newcluster\right).\hfill \end{array}$$

(32)

For each candidate strategy k, we construct a temporary clustering result $Clu{s}_k^{+}$, in which $m_{new}$ is either added to the k-th existing cluster (for $k\le K$) or forms a singleton cluster (for $k=K+1$). Denote the number of clusters after this assignment as $K_k$, with

$$K_k=\left\{\begin{array}{cc}K,\hfill & k\le K,\hfill \\ K+1,\hfill & k=K+1,\hfill \end{array}\right.$$

(33)

and, thus, the number of inter-cluster pairs is $P_k={\displaystyle \frac{K_k(K_k-1)}{2}}$.

We measure the internal consistency of a cluster using the BJS divergence [36], introduced in Section 2.3. In our framework, we define the intra-cluster divergence as the average of all pairwise divergences between cluster BBA members, calculated using $\sqrt{BJS}$ as a confirmed metric [36]. A lower intra-cluster BJS value therefore indicates a higher degree of consensus within the cluster.

Definition 19 (Intra-Cluster Divergence $D_{intra}$).

The intra-cluster divergence of cluster $Clu{s}_i$ is defined as follows:

$${\displaystyle D_{intra}\left(Clu{s}_i\right)={\displaystyle \frac{2}{n_i(n_i-1)}}\sum _{1\le p<q\le n_i}\sqrt{BJS(m_p,m_q)}.}$$

(34)

Definition 20 (Strategy Reward $R_k$).

For each candidate BBA $m_{new}$ and evidence assignment strategy k, the corresponding reward $R_k$ is

$$R_k={\displaystyle \frac{{\left({\displaystyle \frac{1}{P_k}\sum _{1\le i<j\le K_k}{D}_{CC}(Clu{s}_i,Clu{s}_j)}\right)}^{\mu }}{{\left({\displaystyle \frac{1}{K_k}\sum _{i=1}^{K_k}{D}_{intra}\left(Clu{s}_i^{+}\right)}\right)}^{\lambda }}}.$$

(35)

The primary component of the numerator reflects the average divergence between clusters. In contrast, the main component of the denominator captures the average divergence within clusters, which is temporarily updated based on the new cluster structure $m_{new}$ derived from strategy k.

By default, the hyperparameters $\mu$ and $\lambda$ are set to 1, giving the same weight to cluster separation and internal consistency. However, the relative importance of these two objectives should not be assumed to be the same across all situations. Different application scenarios often have unique structural and statistical properties, making the use of a one-size-fits-all approach for parameterization impractical. Ideally, the values of $\lambda$ and $\mu$ should be determined by data-driven approaches or based on specific requirements. Our work employs a data-driven approach to determine the optimal hyperparameter pair suitable for each classification task. The details are presented in Section 5.

The optimal strategy is then obtained by selecting the strategy $k^{*}$ that maximizes the reward:

Definition 21 (Optimal Strategy $k^{*}$).

$$k^{*}=arg\underset{k\in 1,\dots ,K+1}{max}{R}_k.$$

(36)

Guided by the reward $R_k$, each new BBA is sequentially tested in all $K+1$ possible strategies, and the best option is executed.

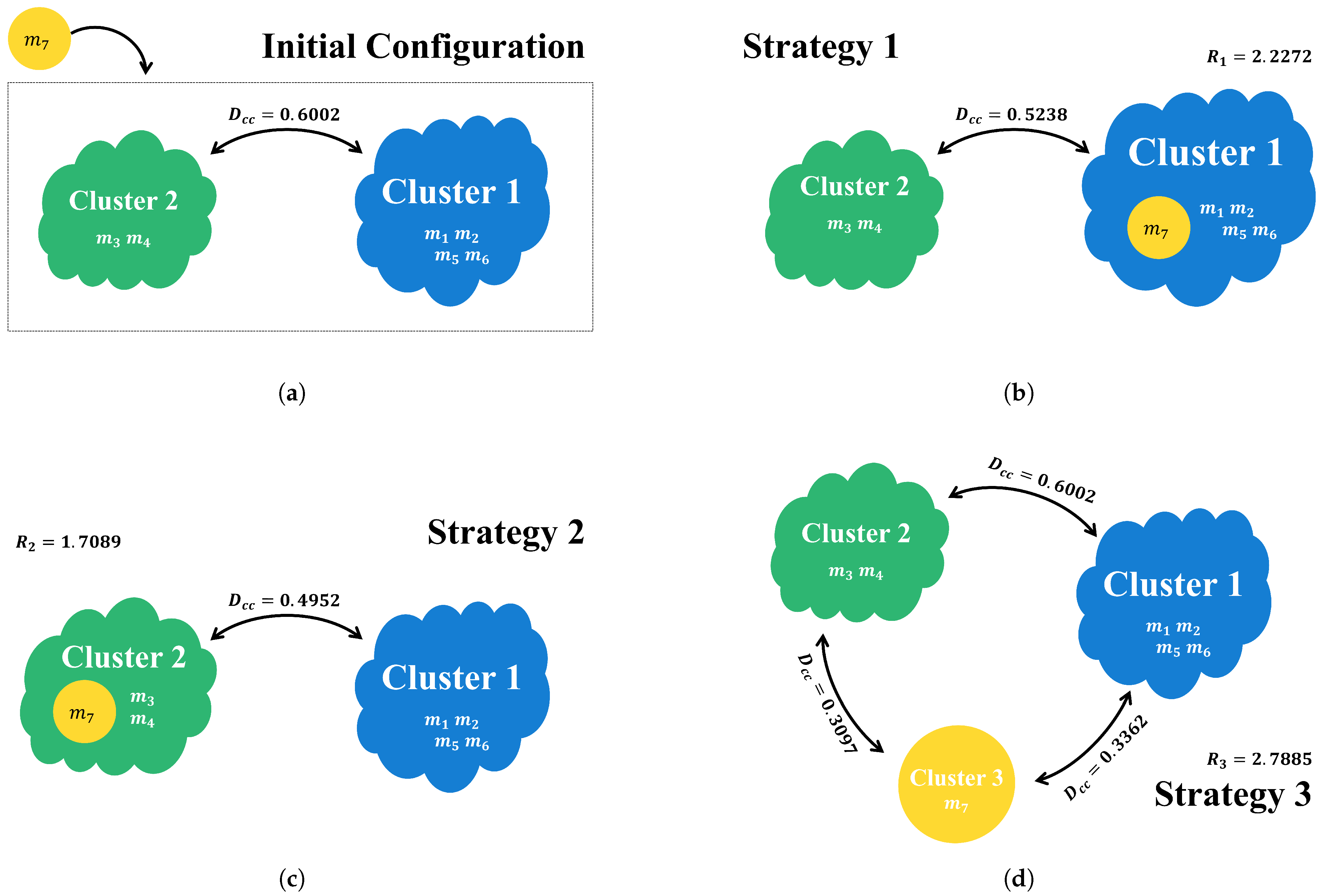
In Example 8, when $m_7$ is incorporated, the initial configuration and the outcome of each candidate strategy are as illustrated in Figure 1. The process demonstrates the reward associated with each strategy and the justification for the optimal assignment.

3.5. The Cluster-Level Information Fusion Algorithm

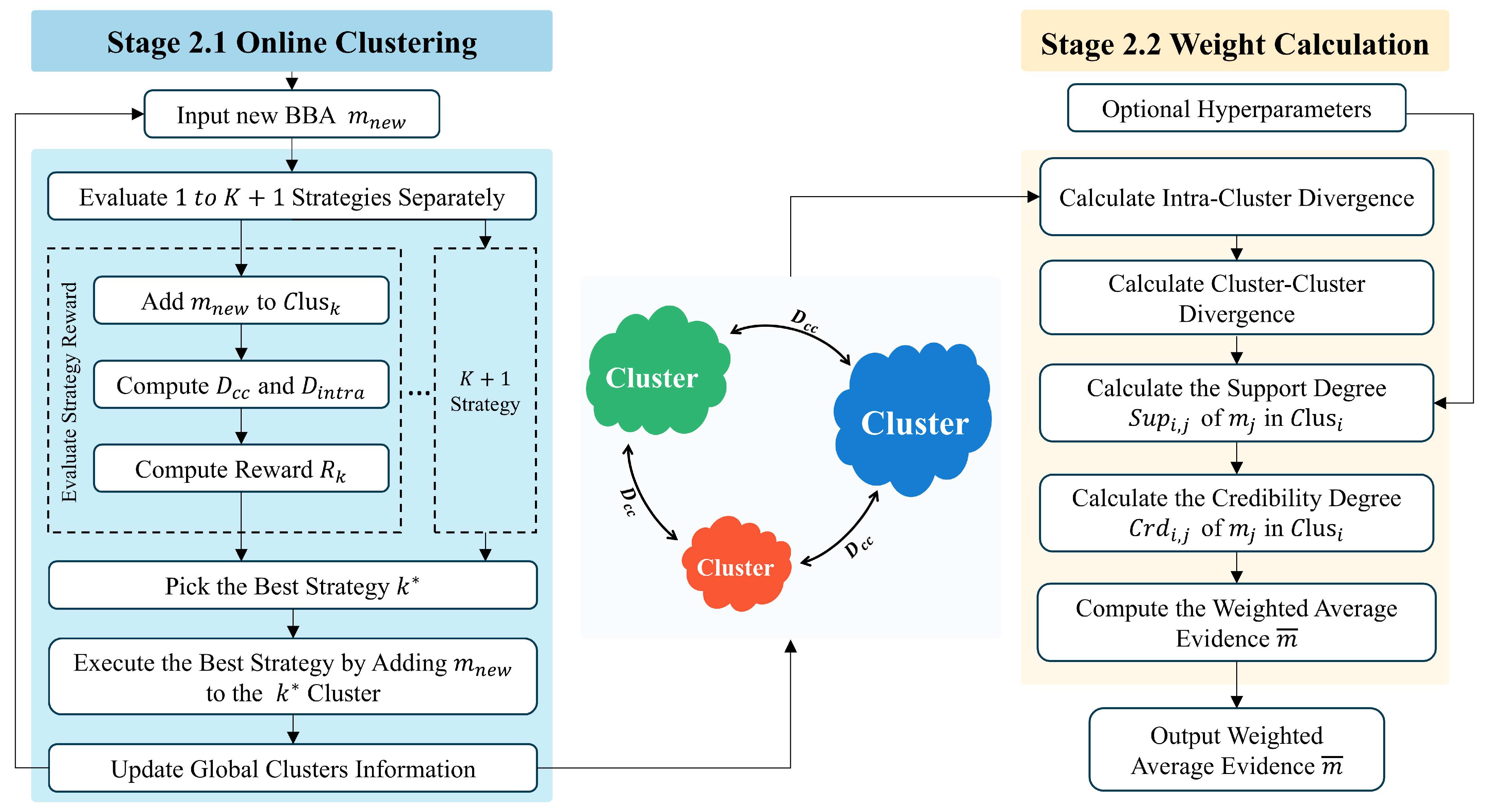
This subsection outlines our proposed framework for cluster-level information fusion, which consists of two stages. In the first stage, we sequentially add the incoming BBAs to the clusters while updating the cluster framework. The second stage involves fusing all of the evidence by taking into account both the divergence within clusters and the divergence between clusters.

3.5.1. The First Stage of the Algorithm

During the first stage, the incoming BBAs are processed sequentially through the following steps:

• Cluster Construction: Construct the centroid of each cluster based on the maximum-entropy fractal operation F.
• Evaluate Strategies: For each newly arriving BBA, compute the reward $R_k$ for all potential assignments, whether to an existing cluster or a new one.
• Evidence Assignment: Assign the BBA to the cluster that yields the highest reward, and update the corresponding cluster centroid.

The detailed steps of the first stage are outlined in Algorithm 1.

Remark 3.

When only a single BBA $m_1$ exists in the system, the arrival of a second BBA $m_2$ must determine whether to create a new cluster or merge into the existing cluster. This "cold-start" decision is made only once. Since there is no prior empirical structure at this stage, we treat each BBA as a random point drawn from a uniform Dirichlet distribution over the entire range of evidence. By setting the threshold at the $\sqrt{BJS}$ distance median, denoted as $\tau \left(\right|\Theta \left|\right)$, this approach is designed so that, on average, half of all equally uninformative evidence pairs are merged while the other half are split. The closed-form expression for this parameter-free boundary is

$$\tau \left(\right|\Theta \left|\right)=\sqrt{1-\left(2^{|\Theta |}-1\right){\left(\frac{\sqrt{\pi }}{2}\frac{\Gamma (2^{|\Theta |}-1)}{\Gamma (2^{|\Theta |}-\frac{1}{2})}\right)}^2},$$

(37)

which evaluates to $0.3830,0.4314,0.4488,0.4563$ for $|\Theta |=2,3,4,5$ and stabilizes at $0.4633$ for larger frames. Consequently, identical BBAs ($d=0$) are always merged, while maximally conflicting BBAs ($d=1$) are always split. The complete derivation process is listed in Appendix C.

Algorithm 1: Sequential Incorporation of BBAs into Clusters

3.5.2. The Second Stage of the Algorithm

In the second stage, we start with the cluster partition $\mathcal{C}=\{Clu{s}_1,\dots ,Clu{s}_K\}$ generated by the online procedure (Algorithm 1), which remains fixed throughout this stage. This stage transforms the cluster-level structure into credibility weights for each piece of evidence, which are then used to compute a weighted average evidence $\overline{m}$ for the final information fusion outcome.

It is worth noting that the first-stage output provides valuable structural information for decision-making. Clustering helps identify which BBAs convey similar beliefs and which diverge. This information is the foundation for an interpretable adjustment mechanism implemented through an expert bias coefficient, $\alpha$, used in Equation (40), where $\alpha >0$. This coefficient controls the relative trust placed in larger versus smaller clusters. When $\alpha >1$, the credibility of larger clusters is reinforced, emphasizing consensus. In contrast, when $0<\alpha <1$, the influence of large clusters is weakened, allowing smaller clusters to have a greater impact. Small $\alpha$ values can potentially highlight rare but valuable perspectives. Conceptually, larger clusters containing multiple similar BBAs are generally considered to be more trustworthy. Therefore, higher values of $\alpha$ may seem preferable. However, as demonstrated in Section 5.5.2, application experiments show that increasing the weight of larger clusters may not always lead to better outcomes.

In the second stage of the algorithm, each BBA $m_{i,j}\in Clu{s}_i$ receives a credibility, which is then used in weighted fusion methods [24] and a probability transformation (PT). The algorithm closes the loop from “forming clusters” to “using clusters”. Let $m_{i,j}$ denote the j-th BBA in $Clu{s}_i$, $n_i$ be the number of BBAs contained in $Clu{s}_i$, and K be the total number of clusters in the partition $\mathcal{C}$. The whole algorithm is described as follows:

Step 1:

Compute Intra-Cluster Divergence: For each cluster $Clu{s}_i$, compute the BJS divergence between all pairs of BBAs and obtain the average intra-cluster divergence for each $m_{i,j}$:

$$d_{i,j}={\displaystyle \frac{1}{n_i-1}}\sum _{\begin{array}{c}{m}_{i,k}\in Clu{s}_i\\ k\ne j\end{array}}BJS\left(m_{i,j},m_{i,k}\right),n_i>1.$$

(38)

Step 2:

Compute Inter-Cluster Divergence: For each cluster $Clu{s}_i$, compute the mean divergence to all other clusters:

$$D_i={\displaystyle \frac{1}{K-1}}\sum _{\begin{array}{c}q=1\\ q\ne i\end{array}}^K{D}_{CC}\left(Clu{s}_i,Clu{s}_q\right).$$

(39)

Step 3:

Calculate Support Degree: Using the expert bias coefficient $\alpha$ and hyperparameter pair $(\mu ,\lambda )$, calculate the support degree for BBA $m_{i,j}$:

$$Su{p}_{i,j}=n_i^{\alpha }·exp\left(-d_{i,j}^{\lambda }\right)·exp\left(-D_i^{\mu }\right).$$

(40)

The support degree reflects the combined effect of cluster size, intra-cluster conformity, and inter-cluster separability.

Step 4:

Calculate Credibility Degree: Normalize all support degrees to obtain the credibility degree of each BBA:

$$Cr{d}_{i,j}={\displaystyle \frac{Su{p}_{i,j}}{{\displaystyle \sum _{p=1}^K\sum _{q=1}^{n_p}Su{p}_{p,q}}}}.$$

(41)

Step 5:

Compute Weighted-Average Evidence: Construct the weighted-average BBA:

$$\overline{m}\left(A\right)=\sum _{i=1}^K\sum _{j=1}^{n_i}Cr{d}_{i,j}{m}_{i,j}\left(A\right),\forall A\subseteq \Theta .$$

(42)

Step 6:

Fuse via Dempster’s Rule: Combine $\overline{m}$ with itself $n-1$ times to obtain the fused mass function $MAE\left(\overline{m}\right)$:

$$MAE\left(\overline{m}\right)=\underset{n-1\mathrm{times}}{\underbrace{\overline{m}\oplus \overline{m}\oplus \dots \oplus \overline{m}}}.$$

(43)

Step 7:

Make Final Decision: Apply PT to the fused mass function $MAE\left(\overline{m}\right)$ to make the final decision. In this framework, we use the PPT [67], denoted as $BetP$, to convert $MAE\left(\overline{m}\right)$ into a probability distribution. The singleton hypothesis with the highest probability is selected as the output:

$$\mathcal{O}=arg\underset{A_i\in \mathbb{H}}{max}{\mathrm{BetP}}_{MAE\left(\overline{m}\right)}\left(A_i\right).$$

(44)

Section 3.5.1 organizes the incoming BBAs into distinct clusters in sequential order, as shown on the left side of Figure 2. Subsequently, Section 3.5.2 uses this structure to calculate credibility weights and perform fusion, as depicted on the right side of Figure 2. This process creates a framework that spans from cluster construction to decision-making.

3.5.3. Algorithm Complexity Analysis

In the previous sections, we have defined n as the total number of BBAs and K as the number of non-empty clusters. The dimension of each BBA on the frame of discernment $\Theta$ is $2^{|\Theta |}$. Throughout the discussion, we assume the use of the recursive centroid update from Definition 14. Consequently, updating a centroid by adding a BBA to a cluster of size $n_i$ costs $O(n_i·2^{|\Theta |})$ in time, while its storage remains $O\left(2^{|\Theta |}\right)$.

The analysis of the framework’s computational complexity begins with the online clustering stage. We evaluate the cost of assigning a single incoming BBA, $m_{new}$:

• Cluster Structure Construction: Creating a temporary cluster by adding $m_{new}$ to a cluster $Clu{s}_i$ of size $n_i$ is dominated by the centroid update. This requires computing the $n_i$-th-order fractal of $m_{new}$, which costs $O(n_i·2^{|\Theta |})$.
• ${\mathit{D}}_{\mathit{CC}}$Complexity: A single pairwise ${\mathit{D}}_{\mathit{CC}}({\mathit{Clus}}_{\mathit{p}},{\mathit{Clus}}_{\mathit{q}})$ calculation is dominated by computing scale weights, ${\mathit{w}}_{\mathit{p}}$, taking $\mathit{O}({\mathit{n}}_{\mathit{p}}·{\mathit{2}}^{|\Theta |})$. Other steps are less costly, so the overall cost is bounded by $\mathit{O}({\mathit{n}}_{\mathit{i}}·{\mathit{2}}^{|\Theta |})$, where ${\mathit{n}}_{\mathit{i}}$ is the larger cluster’s size.
• An Evidence Assignment Strategy: Evaluating a single strategy, e.g., adding ${\mathit{m}}_{\mathit{new}}$ to ${\mathit{Clus}}_{\mathit{k}}$, requires temporary updates to the cluster’s centroid, its intra-cluster divergence ${\mathit{D}}_{\mathit{intra}}$, and inter-cluster ${\mathit{D}}_{\mathit{CC}}$ values. Recomputing up to $\mathit{K}-\mathit{1}$ of these ${\mathit{D}}_{\mathit{CC}}$ divergences is the complexity bottleneck, at a cost of $\mathit{O}(\mathit{K}·{\mathit{n}}_{\mathit{k}}·{\mathit{2}}^{|\Theta |})$.
• Evaluate All of the Strategies: To assign one BBA, all $\mathit{K}+\mathit{1}$ strategies are evaluated. For balanced clusters of average size $\overline{\mathit{n}}=\mathit{n}/\mathit{K}$, the cost per BBA is approximately $\mathit{O}(\mathit{K}·\left(\mathit{K}\overline{\mathit{n}}\right)·{\mathit{2}}^{|\Theta |})=\mathit{O}(\mathit{Kn}·{\mathit{2}}^{|\Theta |})$. Summing over all $\mathit{n}$ BBAs, the total online clustering cost becomes $\mathit{O}({\mathit{n}}^{\mathit{2}}\mathit{K}·{\mathit{2}}^{|\Theta |})$.

Having established the complexity of the online clustering stage, we now evaluate the computational cost of the weight calculation stage, performed once after clustering is complete:

• BBA Credibility Weights: This stage computes weights in three steps. Step 1 calculates all intra-cluster divergences ($d_{i,j}$), costing up to $O(n^2·2^{|\Theta |})$. Step 2, the dominant operation, computes average inter-cluster divergences ($D_i$) from a full pairwise $D_{CC}$ matrix, at a cost of $O(K^2·n·2^{|\Theta |})$. Step 3 is a negligible $O\left(n\right)$ calculation.
• Cluster-Level BBA Fusion: This stage performs the BBA fusion (Steps 4–6). The normalization and weighted averaging steps cost up to $O(n·2^{|\Theta |})$. The main cost is from Step 6, which recursively applies Dempster’s rule $n-1$ times. With each combination costing $O\left(4^{|\Theta |}\right)$, the total cost is $O(n·4^{|\Theta |})$, a significant term that is independent of K. This final step is also common to several other classical methods.

Combining the costs from both stages, the dominant terms are the total online clustering cost and the calculation of BBA credibility weights. The complexity is

$$T_{\mathrm{total}}=O\left(n^{2}K·2^{|\Theta |}+n·4^{|\Theta |}\right).$$

(45)

For a fixed frame of discernment $\Theta$, the algorithm’s runtime is primarily determined by the online clustering stage, scaling polynomially with the number of BBAs n and the number of clusters K.

In parallel with time analysis, the total complexity of the algorithm’s memory is composed of several key components. The main costs are to store the complete set of n BBAs, the K cluster centroids, and the pairwise $D_{CC}$ and BJS matrices. These require $O(n·2^{|\Theta |})$, $O(K·2^{|\Theta |})$, $O\left(K^2\right)$, and $O\left(n^2\right)$ space, respectively. Therefore, the total memory consumption can be expressed as follows:

$$S_{\mathrm{total}}=O\left(n·2^{|\Theta |}+n^2\right).$$

(46)

The $O\left(n^2\right)$ term for storing pairwise BJS divergences for intra-cluster calculations is the dominant factor in terms of space. In typical scenarios where $K\ll n$, the space complexity simplifies to being governed by the storage of the BBAs and their pairwise internal divergences.

4. Numerical Example and Discussion

In this section, we provide illustrative examples of the proposed methods, with a focus on $D_{CC}$, the evidence assignment rule, and the numerical information fusion results. The hyperparameter $(\mu ,\lambda )$ pair and the expert bias coefficient $\alpha$ are set to 1 throughout this section.

4.1. The Properties of Cluster–Cluster Divergence

4.1.1. Metric Properties

Example 2 is illustrated to show the metric properties of $D_{CC}$, including non-negativity, symmetry, and triangle inequality.

Example 2 (A Weakly Clustered Case in a Low-Dimensional Frame of Discernment).

Consider a frame of discernment $\Theta =\{A_1,A_2\}$ with three focal elements $\left\{A_1\right\}$, $\left\{A_2\right\}$, and $\{A_1\cup A_2\}$. Five BBAs are given in

Table 3. BBAs in a weakly clustered case.

BBAs	$\mathit{m}\left(\left\{{\mathit{A}}_1\right\}\right)$	$\mathit{m}\left(\left\{{\mathit{A}}_2\right\}\right)$	$\mathit{m}\left(\{{\mathit{A}}_1\cup {\mathit{A}}_2\}\right)$
$m_1$	0.1	0.7	0.2
$m_2$	0.7	0.1	0.2
$m_3$	0.6	0.2	0.2
$m_4$	0.5	0.3	0.2
$m_5$	0.2	0.2	0.6

.

In the example, the cluster characteristics are not obvious: the BBAs display varying tendencies. From an intuitive perspective, the set is most likely to be divided into three clusters: (i) a cluster biased towards $\left\{A_2\right\}$: $\left\{m_1\right\}$, (ii) a cluster biased towards $\left\{A_1\right\}$: $\{m_2,m_3,m_4\}$, and (iii) a highly uncertain cluster with most mass on $\{A_1\cup A_2\}$: $\left\{m_5\right\}$.

Following the proposed method, we compute the cluster–cluster divergence matrix $D_{CC}$, as shown in

Table 4. $D_{CC}$ divergence matrix among clusters.

	${\mathit{Clus}}_1$	${\mathit{Clus}}_2$	${\mathit{Clus}}_3$
$Clu{s}_1$	0.0000	0.3151	0.2228
$Clu{s}_2$	0.3151	0.0000	0.1701
$Clu{s}_3$	0.2228	0.1701	0.0000

.

From the matrix above, several metric properties are immediately evident:

• Non-Negativity: All entries are greater than or equal to zero.
• Symmetry: $D_{CC}(i,j)=D_{CC}(j,i)$ holds for all $i,j$.
• Identity of Indiscernibles: $D_{CC}(i,i)=0$ for all clusters i.

We further verify that $D_{CC}$ satisfies the triangle inequality. For any three distinct clusters i, j, and k, it must hold that

$$D_{CC}(i,j)\le D_{CC}(i,k)+D_{CC}(k,j).$$

(47)

We enumerate all three possible cases:

$$\begin{array}{cc}\hfill D_{CC}(Clu{s}_1,Clu{s}_2)& =0.3151<0.2228+0.1701=0.3929,\hfill \\ \hfill D_{CC}(Clu{s}_1,Clu{s}_3)& =0.2228<0.3151+0.1701=0.4852,\hfill \\ \hfill D_{CC}(Clu{s}_2,Clu{s}_3)& =0.1701<0.3151+0.2228=0.5379.\hfill \end{array}$$

(48)

Each inequality holds, illustrating that $D_{CC}$ satisfies the triangle inequality. Additionally, the divergence matrix satisfies both non-negativity and symmetry. This example demonstrates that $D_{CC}$ is a valid pseudo-metric over clusters of BBAs, even in weakly separable scenarios.

4.1.2. Numeric Examples Demonstrating Cluster–Cluster Divergence

To validate the effectiveness of the proposed cluster–cluster divergence $D_{CC}$, we present a sequence of designed examples, where each cluster is composed of four BBAs. We start by directly extracting four similar BBAs $m_1,m_3,m_4,m_5$ from Example 1 and renumbering them as $m_1$ to $m_4$.

Example 3 (Cluster $Clu{s}_1$).

This cluster is composed of the BBAs in

Table 5. BBAs in $Clu{s}_1$ constructed by extracting and renumbering similar BBAs from Example 1.

BBAs	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{C}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{C}\left\}\right)$
$m_1$	0.50	0.20	0.30
$m_2$	0.55	0.10		0.35
$m_3$	0.55	0.10		0.35
$m_4$	0.60	0.10		0.30

, sharing supports for the singleton focal set $\left\{A\right\}$ and supports for the multi-element set $\{A,C\}$:

$$Clu{s}_1=\{m_1,m_2,m_3,m_4\}.$$

(49)

Example 4 is derived from Example 3, maintaining singleton sets’ distribution while changing the distribution among multi-element sets.

Example 4 (Cluster $Clu{s}_2$).

This cluster closely resembles $Clu{s}_1$ but focuses its multi-element set on $\{A,B\}$ rather than $\{A,C\}$. It consists of the BBAs listed in

Table 6. BBAs in $Clu{s}_2$ with a multi-element set on $\{A,B\}$.

BBAs	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{C}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{B}\left\}\right)$
$m_5$	0.50	0.20	0.30
$m_6$	0.55	0.10		0.35
$m_7$	0.55	0.10		0.35
$m_8$	0.60	0.10		0.30

:

$$Clu{s}_2=\{m_5,m_6,m_7,m_8\}.$$

(50)

Example 5 has an identical multi-element set structure to Example 3, but it expresses an opposing belief on the singleton set:

Example 5 (Cluster $Clu{s}_3$).

This cluster mirrors the focal structure of Example 3 but places most of the beliefs on $\left\{C\right\}$ instead of $\left\{A\right\}$, forming an opposing belief pattern. It consists of the BBAs listed in

Table 7. BBAs in $Clu{s}_3$ with a shared multi-element set $\{A,C\}$.

BBAs	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{C}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{C}\left\}\right)$
$m_9$	0.30	0.20	0.50
$m_{10}$		0.10	0.55	0.35
$m_{11}$		0.10	0.55	0.35
$m_{12}$		0.10	0.60	0.30

:

$$Clu{s}_3=\{m_9,m_{10},m_{11},m_{12}\}.$$

(51)

The preceding analysis in Section 3 has mentioned that the cluster–cluster divergence $D_{CC}$ can capture both structural and belief-based differences across clusters. Specifically, the structural disparity is captured by the scale weights $w\left(X\right)$, which reflect the relative importance of each focal element. To better understand the impact of these weights, we now examine how variations in cluster structure affect the divergence values.

The scale weight $w\left(X\right)$ in examples reflects how strongly a cluster supports multi-element sets. In Example 3 and Example 4, the support for multi-element sets varies significantly. Some clusters assign substantial belief to certain multi-element sets through multiple BBAs, while others provide little or no support to the same set, resulting in different structural weights.

For example, in cluster $Clu{s}_1$, we compute the support ${\tilde{n}}_1\left(X\right)$ and the corresponding scale weight $w_1\left(X\right)$:

$$\begin{array}{c}\hfill {\tilde{n}}_1\left(\{A,C\}\right)=3.1192,w_1\left(\{A,C\}\right)=0.2243,\\ \hfill {\tilde{n}}_1\left(\{A,B\}\right)=0.4768,w_1\left(\{A,B\}\right)=0.0343,\\ \hfill {\tilde{n}}_1\left(\{B,C\}\right)=0.4768,w_1\left(\{B,C\}\right)=0.0343.\end{array}$$

(52)

Accordingly, the weights of all multi-element sets $\{A,C\}$, $\{A,B\}$, $\{B,C\}$ of all clusters are summarized in

Table 8. Structural scale weights $w\left(X\right)$ for three multi-element sets in each cluster.

Focal Set	${\mathit{w}}_{{\mathit{Clus}}_1}$	${\mathit{w}}_{{\mathit{Clus}}_2}$	${\mathit{w}}_{{\mathit{Clus}}_3}$
$\{A,C\}$	0.2243	0.0343	0.2243
$\{A,B\}$	0.0343	0.2243	0.0343
$\{B,C\}$	0.0343	0.0343	0.0343

.

Clusters $Clu{s}_1$ and $Clu{s}_3$ share identical values of $w\left(X\right)$ because they have exactly the same ratio of BBAs supporting the focal element $\{A,C\}$. In contrast, $Clu{s}_2$ shows an obviously different weighting pattern, with a dominant focus on $\{A,B\}$.

To better understand the full origin of the divergence values, we further analyze the contributions of both singleton sets and multi-element sets to each pairwise divergence. Specifically, for each pair of clusters $(p,q)$, we compute the partial squared difference originating from multi-element sets via

$$\sum _{X\in \left\{\right\{A,B\},\{A,C\},\{B,C\left\}\right\}}{\left[{\varphi }_p\left(X\right)-{\varphi }_q\left(X\right)\right]}^2,$$

(53)

and then separate this from the contribution of singleton focal sets. The results are summarized in

Table 9. Decomposition of $D_{CC}$ into singleton and multi-element sets’ contributions.

Cluster Pair	Multi-Element Part	Singleton Part	${\left({\mathit{D}}_{\mathbf{CC}}\right)}^2$	${\mathit{D}}_{\mathbf{CC}}$
$Clu{s}_1$ vs. $Clu{s}_2$	0.0242	0.0061	0.0303	0.1739
$Clu{s}_1$ vs. $Clu{s}_3$	0.0000	0.1821	0.1821	0.4268
$Clu{s}_2$ vs. $Clu{s}_3$	0.0242	0.2149	0.2392	0.4890

.

The results reveal distinct patterns of divergence among the clusters. The difference between $Clu{s}_1$ and $Clu{s}_2$ primarily arises from conflicting support on multi-element sets ($\{A,C\}$ vs. $\{A,B\}$), while their singleton beliefs remain largely aligned, resulting in a low divergence of $D_{CC}\approx 0.174$. In contrast, the divergence between $Clu{s}_1$ and $Clu{s}_3$ is entirely based on singleton sets. Despite both clusters showing identical support for $\{A,C\}$, they express opposing beliefs regarding singletons ($\left\{A\right\}$ vs. $\left\{C\right\}$), leading to a higher divergence of approximately $D_{CC}\approx 0.427$. Similarly, $Clu{s}_2$ and $Clu{s}_3$ diverge in both multi-element sets and singleton sets, but the dominant contribution still originates from singleton sets, pushing the overall divergence to $D_{CC}\approx 0.489$.

The results in Table 8 and Table 9 demonstrate that the proposed divergence measure can capture structural differences among clusters. It also captures the opposing belief distributions across clusters, whether these disparities originate from differing multi-element sets or direct conflicts in singleton sets.

4.1.3. Comparison of the Existing Conflict Measurements

The following examples show a direct comparison of $D_{CC}$ against several classical belief divergences: BJS divergence [36], B divergence and RB divergence [29], and the classical Dempster conflict coefficient K [4]. Since $D_{CC}$ is designed to measure cluster–cluster divergence, whereas most other divergences operate at the BBA-BBA level, it is natural to regard the case $Clu{s}_1=\left\{m_1\right\}$ and $Clu{s}_2=\left\{m_2\right\}$ as a degenerate form of BBA-level divergence.

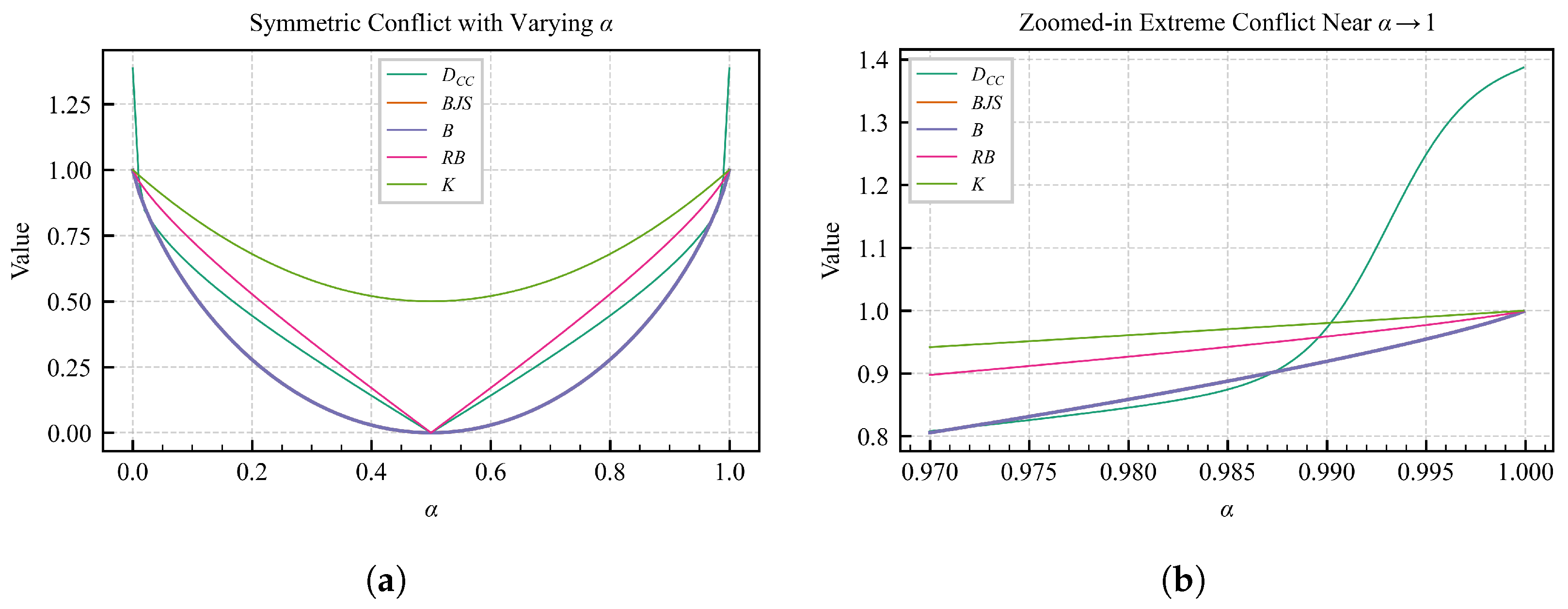
Example 6 (Symmetric Conflict).

We construct a symmetric pair of conflicting BBAs on the singleton frame of discernment $\Theta =\{A,B\}$:

$$\begin{array}{c}\hfill m_1\left(A\right)=\alpha ,m_1\left(B\right)=1-\alpha ,\\ \hfill m_2\left(A\right)=1-\alpha ,m_2\left(B\right)=\alpha .\end{array}$$

(54)

where α varies continuously over the interval $[0.0001,0.9999]$. This formulation guarantees that $m_1$ and $m_2$ show symmetric belief structures with opposing preferences.

Figure 3 compares the divergence $D_{CC}$ with classical belief divergences and the Dempster conflict coefficient K under symmetric belief settings. In Figure 3a, it is evident that $D_{CC}$ responds sharply to minor changes in belief, exceeding $0.2$ when $\alpha =0.02$, whereas the BJS, B, and RB divergences remain close to zero. Figure 3b focuses on the high-conflict region ($\alpha >0.97$), where $D_{CC}$ approaches its upper limit of $\sqrt{2}$.

Example 7 (Asymmetric Conflict).

We construct an asymmetric conflict scenario between two BBAs defined over the frame of discernment $\Theta =\{A,B\}$. The belief structures are given by

$$\begin{array}{c}\hfill m_1\left(A\right)=\alpha ,m_1\left(B\right)=1-\alpha ,\\ \hfill m_2\left(A\right)=0.0001,m_2\left(B\right)=0.9999,\end{array}$$

(55)

where α varies within $[0.0001,0.9999]$. In this formulation, $m_2$ holds a constant belief in hypothesis $\left\{B\right\}$, while $m_1$ gradually transitions from agreement to complete opposition.

Figure 4 illustrates the divergence behavior in the asymmetric setting described in Example 7, where $m_2$ is fixed with near-certain confidence in $\left\{B\right\}$. The proposed $D_{CC}$ demonstrates sharp sensitivity across the entire range of $\alpha$, rising above $0.3$ even when $\alpha =0.02$. In contrast, the BJS, B, and RB divergences remain below $0.1$. As $\alpha$ approaches 1, $D_{CC}$ continues to increase smoothly, nearing its theoretical upper bound of $\sqrt{2}$.

4.2. The Cluster Construction

To demonstrate the online clustering stage proposed in this framework, we provide a detailed numerical simulation based on Example 8.

Example 8 (Fractal BBA Example).

This example consists of seven BBAs listed in

Table 10. Seven BBAs used in Example 8.

BBAs	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$
$m_1$	0.8	0.15	0.05
$m_2$	0.9	0.1
$m_3$	0.03	0.12	0.85
$m_4$	0.05	0.03	0.92
$m_5$	0.87	0.11	0.02
$m_6$	0.95	0.03	0.02
$m_7$	0.25	0.50	0.25

. The BBAs $m_1$, $m_2$, and $m_5$ show a strong preference for hypothesis $\left\{A\right\}$. In contrast, $m_3$ and $m_4$ strongly support hypothesis $\left\{B\right\}$. The BBA $m_6$ shows an even more decisive preference for hypothesis $\left\{A\right\}$, while $m_7$ represents the complete uncertainty for all of the hypotheses.

$$\mathcal{M}=\{m_1,m_2,m_3,m_4,m_5,m_6,m_7\}$$

(56)

Following the evidence assignment rule in Section 3.4, the cluster centroids are recursively updated. At each iteration, we evaluate the reward $R_k$ for each strategy, determine the optimal cluster assignment, and compute the updated centroid ${\tilde{m}}_{F_i}^{\left(h\right)}$. The complete clustering process is demonstrated as follows:

Round 1:

Arrival of $m_1$: No clusters exist, so $m_1$ initiates a new cluster:

$$Clu{s}_1=\left\{m_1\right\},{\tilde{m}}_{F_1}^{\left(0\right)}=m_1=(0.8000,0.1500,0.0500).$$

(57)

Round 2:

Arrival of $m_2$: There is a single cluster. Decide whether to merge $m_2$ into $Clu{s}_1$ by comparing the threshold $\tau$:

$$\begin{array}{cc}\hfill \sqrt{BJS}(m_1,m_2)& =0.1754\le \tau \left(2\right)=0.3830\Rightarrow \mathrm{Assign}\mathrm{to}Clu{s}_1,\hfill \\ \hfill {\tilde{m}}_{F_1}^{\left(1\right)}& ={\displaystyle \frac{1}{2}}\left[F\left({\tilde{m}}_{F_1}^{\left(0\right)}\right)+m_{F_2}^{\left(1\right)}\right]=(0.8750,0.0750,0.0500).\hfill \end{array}$$

(58)

Round 3:

Arrival of $m_3$: Evaluate gain from merging versus new cluster creation:

$$\begin{array}{cc}\hfill R_{Clu{s}_1}& =0.6092,R_{\mathrm{new}}=3.5747\Rightarrow \mathrm{Create}Clu{s}_2,\hfill \\ \hfill {\tilde{m}}_{F_2}^{\left(0\right)}& =m_3=(0.0300,0.1200,0.8500).\hfill \end{array}$$

(59)

Round 4:

Arrival of $m_4$: Three strategies considered, with rewards:

$$\begin{array}{cc}\hfill R_{Clu{s}_1}& =0.6433,R_{Clu{s}_2}=3.8457,R_{\mathrm{new}}=2.5639\Rightarrow \mathrm{Assign}\mathrm{to}Clu{s}_2,\hfill \\ \hfill {\tilde{m}}_{F_2}^{\left(1\right)}& ={\displaystyle \frac{1}{2}}\left[F\left({\tilde{m}}_{F_2}^{\left(0\right)}\right)+m_{F_4}^{\left(1\right)}\right]=(0.0550,0.0450,0.9000).\hfill \end{array}$$

(60)

Round 5:

Arrival of $m_5$: Rewards across all clusters:

$$\begin{array}{cc}\hfill R_{Clu{s}_1}& =4.3863,R_{Clu{s}_2}=1.0526,R_{\mathrm{new}}=2.5812\Rightarrow \mathrm{Assign}\mathrm{to}Clu{s}_1,\hfill \\ \hfill {\tilde{m}}_{F_1}^{\left(2\right)}& ={\displaystyle \frac{2·F\left({\tilde{m}}_{F_1}^{\left(1\right)}\right)+m_{F_5}^{\left(2\right)}}{2+1}}=(0.8951,0.0432,0.0617).\hfill \end{array}$$

(61)

Round 6:

Arrival of $m_6$: BBA aligns with $Clu{s}_1$:

$$\begin{array}{cc}\hfill R_{Clu{s}_1}& =4.0293,R_{Clu{s}_2}=1.0536,R_{\mathrm{new}}=3.1371\Rightarrow \mathrm{Assign}\mathrm{to}Clu{s}_1,\hfill \\ \hfill {\tilde{m}}_{F_1}^{\left(3\right)}& ={\displaystyle \frac{3·F\left({\tilde{m}}_{F_1}^{\left(2\right)}\right)+m_{F_6}^{\left(3\right)}}{4}}=(0.9182,0.0607,0.0211).\hfill \end{array}$$

(62)

Round 7:

Arrival of $m_7$: Completely uncertain BBA results in highest reward for new cluster:

$$\begin{array}{cc}\hfill R_{Clu{s}_1}& =2.2272,R_{Clu{s}_2}=1.7089,R_{\mathrm{new}}=2.7885\Rightarrow \mathrm{Create}Clu{s}_3,\hfill \\ \hfill {\tilde{m}}_{F_3}^{\left(0\right)}& =m_7=(0.2500,0.5000,0.2500).\hfill \end{array}$$

(63)

After all BBAs are assigned, the final cluster structure is as visualized in Figure 5. Cluster 1 strongly supports hypothesis $\left\{A\right\}$, Cluster 2 supports hypothesis $\left\{B\right\}$, and Cluster 3 represents an uncertain or neutral belief. This validates the effectiveness of the proposed rule in separating conflicting evidence while maintaining internal consistency.

4.3. Comparison with Classical Information Fusion Methods

To assess the effectiveness of the proposed framework, we conduct a comparative analysis against several classical information fusion methods, including the Dempster method [4,5], the Murphy method [23], the Deng method [24], the BJS-based method [36], and the RB-based method [29]. The evaluation uses the classical example presented in Example 1. The objective is to evaluate whether each method yields the correct target recognition outcome.

The results of the information fusion from different methods are presented in

Table 11. Fusion result from Example 1 under different classical methods and the proposed method.

Method	$\mathit{m}\left(\right\{\mathit{A}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{B}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{C}\left\}\right)$	$\mathit{m}\left(\right\{\mathit{A},\mathit{C}\left\}\right)$
Dempster		0.1404	0.8596
Murphy	0.9688	0.0156	0.0127	0.0029
Deng	0.9869	0.0010	0.0088	0.0032
BJS	0.9856	0.0012	0.0081	0.0036
RB	0.9869	0.0007	0.0096	0.0027
Proposed	0.9880	0.0006	0.0079	0.0035

. Each row shows the fused mass function $MAE\left(\overline{m}\right)$ on focal elements after applying the corresponding information fusion method to the five BBAs. A direct comparison reveals that the classical Dempster’s rule yields highly counter-intuitive results, assigning the vast majority of belief to an incorrect hypothesis ($m\left(C\right)=0.8596$) due to the high degree of conflict. In contrast, all weighted-average methods successfully identify the true target $\left\{A\right\}$. Among this group, our proposed method concludes a satisfying final decision. It assigns a mass of $m\left(A\right)=0.9880$ to the correct hypothesis, the highest value across all compared methods, narrowly surpassing other classical baselines like Deng’s method and the RB-based method (both at $0.9869$). This result demonstrates that our method effectively concentrates belief mass on the correct hypothesis.

In addition to comparing the fused mass functions $MAE\left(\overline{m}\right)$, we also examine the final weights assigned to each BBA, as shown in

Table 12. Final weights assigned to each BBA under different information fusion methods.

BBA	Murphy’s Method	Deng et al. Method	Xiao’s BJS Method	Xiao’s RB Method	Proposed Method
$m_1$	0.2000	0.2101	0.1820	0.2469	0.1967
$m_2$	0.2000	0.0824	0.0959	0.0645	0.0684
$m_3$	0.2000	0.2370	0.2392	0.2199	0.2444
$m_4$	0.2000	0.2370	0.2392	0.2199	0.2444
$m_5$	0.2000	0.2335	0.2437	0.2489	0.2461

. The weight distribution reveals each method’s reliability assessment of the input evidence.

Compared with classical methods, the proposed method achieves more decisive belief concentration on the correct target while effectively suppressing the impact of conflicting evidence $m_2$. The proposed method also demonstrates a smooth and balanced allocation: it assigns relatively high weights to reliable BBAs ($m_1$, $m_3$, $m_4$, $m_5$). This demonstrates greater detectiveness to outlier BBAs and a more substantial ability to extract consensus from the input BBAs. Notably, unlike Murphy’s method, which uniformly distributes weights and fails to distinguish between reliable and conflicting evidence, our approach adaptively discounts outliers. It accentuates trustworthy sources, resulting in more robust and interpretable information fusion outcomes.

5. Applications of Cluster-Level Information Fusion Framework in Pattern Classification Tasks

This section applies the proposed cluster-level information fusion framework to pattern classification tasks and compares its performance with that of several representative baselines. We begin by introducing the overall problem statement for pattern classification within the D-S evidence theory. Next, we detail the practical methodology used to identify and determine the optimal hyperparameter pairs. The experimental results are then presented, followed by an in-depth analysis of the framework’s hyperparameters and a comprehensive ablation experiment to assess the contribution of each component.

5.1. Problem Statement

Pattern classification is a fundamental application area for uncertainty reasoning. In D-S evidence theory, the overall methodology of uncertainty reasoning is as detailed in the following section:

• BBA Generation: Transforming classical datasets into BBAs is crucial in applying D-S evidence theory to pattern classification. Various representative methods have been proposed to achieve this transformation, including statistical, geometric, and heuristic approaches [68,69,70]. Among these methods, the statistical-based methods for generating BBAs are as follows: Each attribute of the training samples is used to estimate Gaussian parameters for each class. A likelihood-based intersection degree between each class’s observed attribute value and the Gaussian models is calculated when a new test sample arrives. The intersection degrees are then normalized and converted into BBAs over a frame of discernment.

• Information Fusion: Multiple BBAs generated from the same sample are fused using various methods. In traditional methods, DRC [4,5] is employed in most of the cases. However, DRC can lead to counter-intuitive outcomes when conflicting evidence exists. Alternative methods have been proposed to address such issues, including Murphy’s simple averaging method [23] and Deng’s weighted-average method [24]. Additionally, Xiao proposed a BJS-based information fusion method [36] to evaluate credibility better. To enhance the BJS method in capturing the non-specificity of evidence, Xiao further introduced the RB divergence [29], which can be seen as a generalization form from BJS divergence.

• Probability Transformation: After the fused mass function is obtained, the probability transformation is applied to transform the function into a probability distribution. This allows a final decision to be made in a probabilistic classification manner. Classic PT methods include the PPT [67] (which distributes the mass proportionally among singleton sets), entropy-based PT methods [71], and network-based PT methods [72].

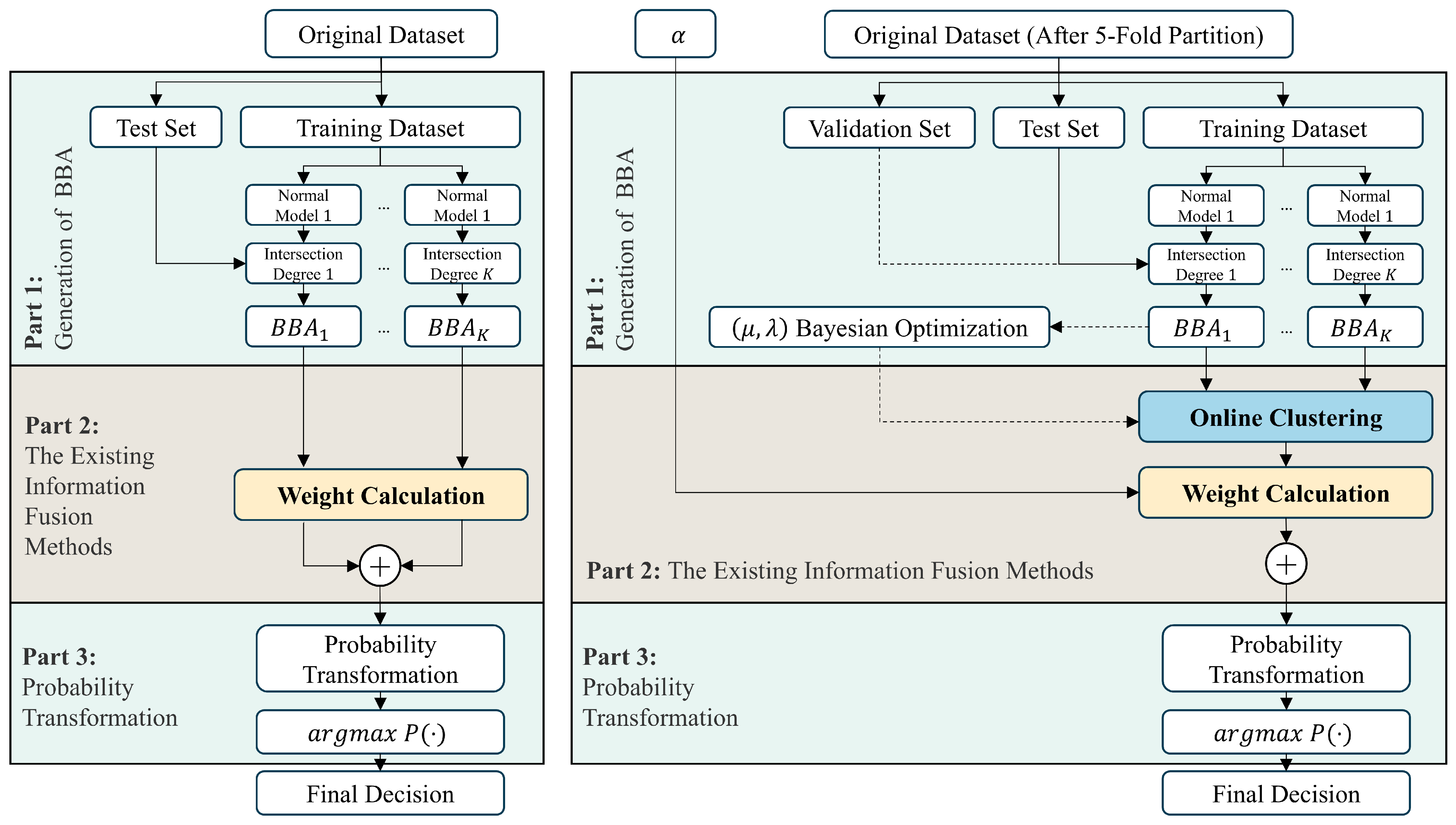
The pipeline of the classification experiment is depicted in Figure 6, which contrasts the conventional approach—where all BBAs are fused in a single step—with our proposed cluster-level framework. In contrast to the traditional method, our framework incorporates online clustering, data-driven selection of hyperparameter pairs, and expert bias coefficient adjustment prior to the final decision-making stage.

5.2. Experiment Description

We conducted pattern classification experiments on four widely used benchmark datasets from the UCI Machine Learning Repository: Iris [73], Wine [74], Seeds [75], and Glass [76].

• The Iris dataset consists of 150 samples, each characterized by four continuous attributes. The dataset is evenly divided among three classes: Setosa, Versicolor, and Virginica. Due to its low dimensionality and clear class separability, it serves as a standard benchmark for pattern classification tasks.
• The Wine dataset consists of 178 instances, each characterized by 13 chemical features, including alcohol, malic acid, and proanthocyanins. The samples are categorized into three different types of wine. Compared to the Iris dataset, the Wine dataset has more features (more BBAs in a sample) and shows a slight imbalance in class distribution.
• The Seeds dataset consists of 210 samples representing three varieties of wheat seeds. Each sample has seven morphological features. Unlike the Iris dataset, the class boundaries in this dataset are much less distinct, making it a moderately challenging classification task.
• The Glass dataset contains 214 samples, each characterized by 9 chemical components and organized into 6 different glass types. These types include three types of window glass—building windows float-processed (BF), building windows non-float-processed (BN), and vehicle windows float-processed (VF)—as well as containers, tableware, and headlamps. This dataset raises significant challenges due to its high class cardinality, imbalanced sample distribution, and many conflicting or indistinguishable features.

For each dataset, we follow the same experimental pipeline. BBAs are generated using the Gaussian distribution-based method described by Xu et al. [69], where each class is modeled by a Gaussian estimated from training data, and sample likelihoods are normalized across classes to generate valid BBAs. All experiments utilize a nested 5-fold cross-validation method. The raw datasets are first stratified into five equally sized folds. In the i-th outer iteration, one fold is held out as an independent test set, while the remaining four folds constitute a large training set for that test set. Within each iteration of the outer loop, a complete inner 4-fold cross-validation is performed on the four available folds to generate the validation set that belongs to that test fold. In this inner loop, an inner Gaussian distribution model is trained on three folds to generate a validation fold. This process is repeated for all four inner folds, and all of the folds are then concatenated to assemble a single, comprehensive validation set that belongs to that test fold.

For each test fold, we used Bayesian optimization (BO) to select the optimal hyperparameter pair $(\mu ,\lambda )$ that maximizes classification accuracy, with the expert bias coefficient $\alpha$ fixed at 1. This process produces a unique $(\mu ,\lambda )$ pair for each fold. Our method, applied with these optimal hyperparameter pairs, is assessed on the corresponding test fold. We discuss the detailed methods for BO in Section 5.3. The final performance is reported as the average across all five folds. Because the entire selection procedure is data-driven, the resulting set of optimal hyperparameters may reflect structural properties of the dataset, which are further discussed in Section 5.5.

After the BBA generation, the information fusion method is applied, and the fusion results are converted into probabilities using the PPT method. We compare the proposed method against seven representative baselines, which are grouped into two categories. The first includes modern machine learning-based hybrid methods: evidential deep learning [12] and DS-SVM [77,78]. The second category consists of five representative baselines in D-S evidence theory: Dempster’s combination rule [4,5], Murphy’s simple averaging method [23], Deng’s distance-weighted fusion [24], Xiao’s BJS-based approach [36], and Xiao’s RB-based approach [29].

5.3. Determination of Hyperparameter Pairs

Selecting appropriate hyperparameter pairs $(\mu ,\lambda )$ is a key challenge in this work. A well-chosen pair can significantly boost the performance of the proposed framework, as demonstrated in Section 5.6. However, the relationship between these hyperparameters and the framework performance is highly complex and non-linear. Brute-force methods, such as grid search, become computationally expensive in this scenario, as they require evaluating a vast combination of values and may still miss the true optimum. We therefore employ a Bayesian optimization strategy to approximate the optimal hyperparameter pair with a tractable number of computational evaluations.

5.3.1. Bayesian Optimization Principle and Procedure

In our approach, we treat the selection of $(\mu ,\lambda )$ as a black-box optimization problem. The objective function takes a candidate pair $(\mu ,\lambda )$ as the input and returns the classification accuracy on the validation fold as the output. Notably, each objective function evaluation can be computationally expensive, as its complexity can grow exponentially with the frame of discernment of BBA, in line with the statement in Section 3.5.3. This high cost motivates the use of BO.

BO constructs a surrogate model of the objective function. In this work, we use a Tree-structured Parzen Estimator (TPE), a type of sequential model-based optimization, which predicts performance for untried hyperparameters and provides uncertainty estimates. This surrogate model captures the non-linear, possibly multi-modal relationship between $(\mu ,\lambda )$ pairs and accuracy. It allows the optimizer to infer promising regions of the search space from limited data. We utilize an acquisition function based on the expected improvement criterion to guide the search. At each iteration, the expected improvement criterion selects the next $(\mu ,\lambda )$ to evaluate by quantifying the expected gain in accuracy over the current best, given the surrogate’s predictions. This balances exploration of uncertain regions against exploitation of known high-performance regions, thereby accelerating convergence to an optimum.

In practice, we implemented the above procedure using the Optuna optimization framework with its TPE sampler. A TPE is a form of BO that models the probability densities of good and bad solutions to suggest promising hyperparameters directly. This approach is well suited for our problem, as it efficiently handles the expansive search space. We define log-uniform search ranges for both $\mu$ and $\lambda$, each from $0.001$ to 1000. A log scale was chosen because the optimal values could span several orders of magnitude, and sampling in log-space allows both small and large candidate values to be explored. The $\alpha$ is held fixed at 1 during this search (i.e., we optimize only $\mu$ and $\lambda$). For each outer test fold of the nested cross-validation, we perform 50 BO iterations on the corresponding validation set. In each trial, the optimizer proposes a new pair based on past evaluations. The full pipeline is executed with those values, and the resulting accuracy is returned to the optimizer to guide the next trial. Over all 50 trials, the search refines its focus on better regions of the $(\mu ,\lambda )$ space. Finally, the pair yielding the highest accuracy is selected as the optimal setting for that test fold. This entire process is repeated independently for each test fold in the nested cross-validation process.

5.3.2. Representative Hyperparameter Pairs and Sensitivity Analysis

The representative optimal $(\mu ,\lambda )$ pairs identified for each dataset are summarized in

Table 13. Representative optimal $(\mu ,\lambda )$ pairs for each classification task.

Hyperparameter	Iris	Wine	Seeds	Glass
$\mu$	0.0733	0.0012	0.0017	1000.0
$\lambda$	0.0052	0.0053	0.0103	0.3333

. These pairs vary widely across the four classification tasks, indicating that each dataset demands a different balance of the two hyperparameters. It should be noted that these “representative” pairs are used as reference points rather than as unique true optima. For each dataset, the representative hyperparameters and the underlying information revealed by them are analyzed in detail in Section 5.5.

To understand the stability of the BO and the sensitivity of each dataset to $(\mu ,\lambda )$, we examine the distribution of the selected hyperparameters over 100 independent optimization trials. Figure 7 depicts this variability by illustrating the log-scale values of the optimal hyperparameters, ${log}_{10}\mu$ and ${log}_{10}\lambda$, obtained across these trials for the Iris, Wine, and Seeds datasets.

For the Iris dataset, the optimal hyperparameter pairs are relatively dispersed. The Bayesian optimization returned a variety of $(\mu ,\lambda )$ combinations yielding near-maximal accuracy, rather than a single sharply defined optimum. In the log-scale trace of Figure 7a, both ${log}_{10}\mu$ (orange) and ${log}_{10}\lambda$ (blue) fluctuate over roughly two orders of magnitude across the 100 folds. Notably, one particular pair $(\mu ,\lambda )\approx (0.0733,0.0052)$ recurred as the top choice in many folds, yet other runs found good results at much larger $\mu$ or $\lambda$ values. This broad plateau feature in the accuracy landscape indicates that the Iris classification task is relatively robust to hyperparameter selection. In other words, as long as $(\mu ,\lambda )$ falls within a certain tolerant range, the classification performance remains near-optimal. Occasional outlier runs did pick extreme values, appearing as isolated spikes in Figure 7a, but these likely reflect fold-specific abnormalities or local maxima in the validation objective. Overall, the Iris results suggest that our method’s performance does not sharply deteriorate with small-to-moderate changes in $(\mu ,\lambda )$, a fortunate property that simplifies tuning for this dataset.

In contrast, the Wine dataset demonstrates a much sharper and more sensitive hyperparameter profile. The distribution of selected $(\mu ,\lambda )$ across folds is very similar: in many of the 100 trials, the optimizer converged to nearly the same values. This suggests that the validation accuracy has a pronounced peak in that region, and that the Bayesian optimizer consistently finds it. The globally optimal pair for Wine was identified to be approximately $(\mu ,\lambda )=(0.0012,0.0053)$, which lies in a very small corner of the search space. Indeed, even slight deviations from this pair can cause a noticeable drop in accuracy. Such a narrow optimum means that the Wine task is highly sensitive to the exact hyperparameter setting, requiring fine-grained tuning for the best results. The log-scale trace in Figure 7b highlights this behavior: the majority of folds show ${log}_{10}\mu$ and ${log}_{10}\lambda$ hovering in a tight band, with very few variations. We do observe a handful of outlier runs where the optimizer sampled radically different values. For example, one fold chose $\mu \sim 4.3$ and $\lambda \sim 7.44$, orders of magnitude off the usual optimum. These rare spikes likely indicate that the optimizer is temporarily attracted to a local optimum or experiencing noisy evaluation in that particular fold. Nevertheless, such cases were isolated. The consistency of the chosen hyperparameters in most folds underscores that, for Wine, the most accurate candidate hyperparameter pairs are range-limited. Leaving the optimal region by even a small amount in $(\mu ,\lambda )$ space significantly degrades performance.

The Seeds dataset exhibits an intermediate pattern of behavior. Like Wine, Seeds favors very small hyperparameter values: the representative optimum is $(\mu ,\lambda )\approx (0.0017,0.0103)$, in the order of ${10}^{-3}$ for both parameters. However, the accuracy surface for Seeds is somewhat flatter around its peak, implying a moderate robustness to parameter variation. This can be seen in Figure 7c as a wider scatter in the ${log}_{10}\mu$ and ${log}_{10}\lambda$ traces: while many folds do concentrate near the tiny values, there are several folds where one of the parameters is noticeably larger. For instance, in a few trials, $\mu$ spiked one to two orders higher while $\lambda$ remained very small; conversely, in one case, $\lambda$ took a moderately higher value while $\mu$ stayed minimal. The fact that such divergent pairs could still emerge as optima in different folds suggests that the Seeds dataset’s performance landscape has a broader “near-optimal” basin. There may be a range of $(\mu ,\lambda )$ combinations that yield almost equally good results. We do note a few outliers, which likely correspond to either local minima or idiosyncrasies in that fold’s data split. Overall, the Seeds results indicate a balance between sensitivity and tolerance. The optimal region is small, but it is not so razor-sharp that minor departures are immediately punishing.

5.3.3. Complexity Analysis

From a computational standpoint, the hyperparameter tuning process exhibits a favorable complexity profile by adopting BO. A traditional grid search over two hyperparameters, each with candidate values of G, would necessitate $G^2$ model evaluations. In our case, BO may converge after a fixed number of trials T (e.g., $T=50$ in our experiments), reducing the complexity to $O\left(T\right)$. In other words, instead of testing thousands of combinations, the optimizer approximately locates a high-performing pair in just 50 intelligent iterations. This efficiency is critical to keeping the overall training procedure tractable. Importantly, the $O\left(n·2^{|\Theta |}+n^2\right)$ memory requirements of the hyperparameter search remain unchanged compared to brute-force search. Thus, we achieve a more efficient determination of the $(\mu ,\lambda )$ pair without compromising the integrity of the search.

5.4. Experimental Results

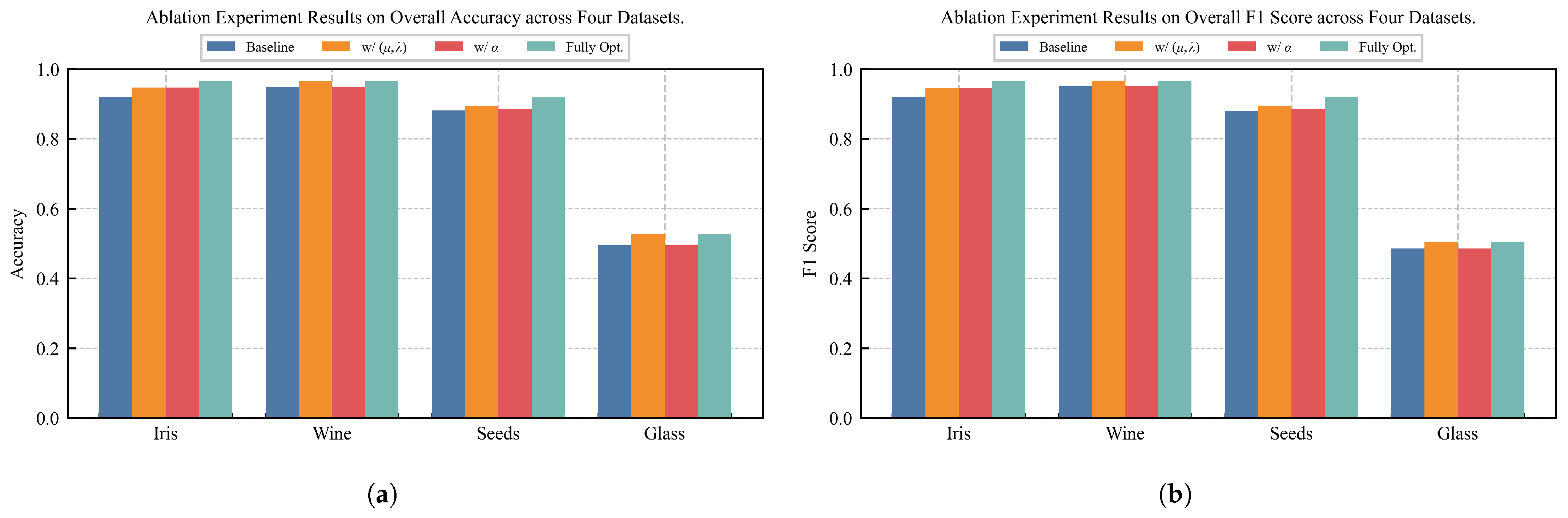
The classification accuracy for each class, along with the overall accuracy and macro F1 score for the proposed method and seven baseline methods, is presented in

Table 14. Per-class accuracy, overall classification accuracy, and F1 score of the eight information fusion methods under the nested five-fold cross-validation on the (a) Iris dataset, (b) Wine dataset, (c) Seeds dataset, and (d) Glass dataset. Bold indicates the best value per category.

	ML Methods		D-S Evidence Theory Methods
Dataset/Class	Evidential Deep Learning	DS-SVM	Dempster’s Rule	Murphy’s Method	Deng et al. Method	Xiao’s BJS Method	Xiao’s RB Method	Proposed Method
(a) Iris Dataset
Setosa	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9796	1.0000
Versicolor	0.9000	0.9200	0.9109	0.9109	0.9231	0.9126	0.8952	0.9495
Virginica	0.9000	0.9200	0.9091	0.9091	0.9167	0.9072	0.8660	0.9505
Accuracy	0.9333	0.9467	0.9400	0.9100	0.9467	0.9400	0.9133	0.9667
F1 Score	0.9333	0.9467	0.9400	0.9100	0.9466	0.9399	0.9136	0.9667
(b) Wine Dataset
Class 1	1.0000	0.9833	0.9655	0.9593	0.9593	0.9593	0.9291	0.9752
Class 2	0.9655	0.9429	0.9504	0.9323	0.9323	0.9323	0.8906	0.9559
Class 3	0.9474	0.9375	0.9697	0.9600	0.9600	0.9600	0.9307	0.9697
Accuracy	0.9722	0.9551	0.9607	0.9494	0.9494	0.9494	0.9157	0.9663
F1 Score	0.9710	0.9546	0.9619	0.9506	0.9506	0.9506	0.9168	0.9669
(c) Seeds Dataset
Kama	0.8750	0.8777	0.8551	0.8201	0.8143	0.8143	0.8227	0.8811
Rosa	0.8333	0.9412	0.9353	0.9275	0.9197	0.9197	0.9265	0.9420
Canadian	1.0000	0.9379	0.9241	0.8951	0.8951	0.8951	0.8951	0.9353
Accuracy	0.9048	0.9190	0.9048	0.8810	0.8762	0.8762	0.8810	0.9190
F1 Score	0.9028	0.9189	0.9045	0.8809	0.8764	0.8764	0.8814	0.9195
(d) Glass Dataset
BF	0.7000	0.7051	0.1699	0.4667	0.4654	0.4730	0.4706	0.4966
BN	0.4762	0.5882	0.3537	0.4478	0.4000	0.4853	0.3243	0.4965
VF	0.0000	0.1053	0.0000	0.3030	0.2941	0.3030	0.3529	0.3448
Containers	0.5714	0.6400	0.3529	0.3158	0.3000	0.3158	0.3158	0.3158
Tableware	0.4444	0.6667	0.7826	0.4865	0.5806	0.4737	0.2857	0.4615
Headlamps	0.0000	0.8421	0.8627	0.9091	0.8889	0.8889	0.9091	0.9091
Accuracy	0.5349	0.6495	0.3551	0.5000	0.4860	0.5093	0.4486	0.5280
F1 Score	0.3653	0.5912	0.4203	0.4881	0.4882	0.4899	0.4431	0.5040

. Notably, the results for our method were obtained using optimal hyperparameter pairs $(\mu ,\lambda )$ established independently for each outer fold of the cross-validation. Our method’s results are also based on an optimized hyperparameter $\alpha$, which is 1/8, 1, 1/5, and 1 on the Iris, Wine, Seeds, and Glass datasets, respectively.

In the context of classical D-S evidence theory methods, the results suggest that the proposed framework offers a competitive performance advantage over the other D-S evidence theory baselines across the four classification tasks. For instance, on the Iris dataset, our method achieves an overall accuracy of 96.67%, compared to 94.67% from the next best-performing D-S evidence theory method. This advantage is also notable on the highly complex Glass dataset. In this task, where the accuracy of some classical methods is limited—such as Dempster’s rule, which has an accuracy of only 35.51%—our method achieves the highest accuracy among the D-S evidence theory methods, at 52.80%. This result indicates a greater robustness in managing severe class imbalance and feature conflict.

When compared with modern machine learning-based hybrid methods, it is evident that these methods set a high performance benchmark. As shown in Table 14, the DS-SVM model in particular demonstrates excellent performance, achieving the highest overall accuracy on the Wine dataset and a significantly superior result on the complex Glass dataset.

Beyond overall accuracy, it is worthwhile to assess performance, especially for tasks involving significant class imbalance, such as the Glass dataset [79].

Table 15. Additional performance metrics for all methods on the Glass dataset. Bold indicates the best value per category.

	ML Methods		D-S Evidence Theory Methods
Glass Dataset	Evidential Deep Learning	DS-SVM	Dempster’s Rule	Murphy’s Method	Deng et al. Method	Xiao’s BJS Method	Xiao’s RB Method	Proposed Method
Precision	0.3596	0.6524	0.4795	0.5084	0.4982	0.5136	0.4888	0.5328
Recall	0.5000	0.5910	0.4261	0.5469	0.5372	0.5478	0.5143	0.5603
MCC	0.4200	0.5154	0.0903	0.3391	0.3158	0.3516	0.3088	0.3735
AUC	0.7404	0.8882	0.6288	0.8298	0.8241	0.8233	0.8245	0.8266

thus provides an analysis using additional metrics, including precision, recall, the Matthews Correlation Coefficient (MCC), and the Area Under the Curve (AUC). Within this context, our proposed framework’s performance is noteworthy. It achieves the highest scores among the D-S evidence theory methods in precision, recall, and the MCC. The MCC is an informative metric for imbalanced data, as it provides a single, balanced measure of classification quality. Achieving a higher MCC score suggests that our framework provides a more balanced classification outcome than the other D-S baselines. This may suggest that structuring evidence into clusters before information fusion is a promising strategy for mitigating the distortion of class imbalance and contributing to a more robust decision-making process.

Regarding the adaptability of the proposed framework, an analysis of the experimental results provides several insights into its performance under different conditions. The framework appears to be adaptable to the dimensionality of the feature space tested in this work. It achieved the highest overall accuracy on the low-dimensional Iris dataset and maintained competitive accuracy on the higher-dimensional Wine dataset. As all of the experiments were conducted on datasets with small sample sizes, the results demonstrate the method’s applicability in such conditions. Furthermore, the framework was tested on datasets with varying degrees of class separability, from the relatively clear boundaries in Iris to the highly overlapping classes in Seeds and Glass. The model’s effectiveness in these more complex scenarios suggests that the non-linear process inherent in evidence clustering may be a factor in its ability to handle data that is not easily separable.

5.5. Analysis of Hyperparameters

The proposed methods introduce three hyperparameters: a $(\mu ,\lambda )$ pair and the expert bias coefficient $\alpha$. The $(\mu ,\lambda )$ pair is applied in Equations (35) and (40), where it helps to balance the importance of intra-cluster similarity against inter-cluster differences when making decisions. The expert bias coefficient $\alpha$ is used in Equation (40). Experts in the field can calibrate a value to $\alpha$ based on their knowledge and experience after analyzing the results from online clustering, thus balancing consensus with minority opinion. Further analysis and discussion on the $(\mu ,\lambda )$ pair can be found in Section 5.5.1, while Section 5.5.2 discusses the expert bias coefficient $\alpha$.

5.5.1. Analysis of Hyperparameter Pair

In the algorithm’s reward $R_k$ and the support degree calculation process, the average inter-cluster divergence is raised to the power of $\mu$; $\mu$ acts as a sensitivity coefficient, modulating the non-linear importance in weight calculation:

• When $\mu >1$, since the numerator of $R_k$ excluding the $\mu$ value is generally less than 1, larger $\mu$ values attenuate inter-cluster differences: inter-cluster divergences raised to powers greater than 1 become relatively smaller, resulting in a reduced penalty for the corresponding weights.
• When $\mu <1$, similarly, smaller values of $\mu$ amplify differences between clusters, leading the algorithm to focus on the information differences between clusters in the cluster selection.

Meanwhile, $\lambda$ serves as a sensitivity coefficient for intra-cluster divergence, controlling how strongly intra-cluster divergence impacts $R_k$ and the support weight:

• When $\lambda >1$, intra-cluster differences are further suppressed, similar to the effect of increasing $\mu$.
• When $\lambda <1$, a smaller value of $\lambda$ amplifies the effects of intra-cluster conflict: even minor differences within the cluster, when raised to a power less than 1, become relatively larger.

Our experimental pipeline, illustrated in the right part of Figure 6, utilizes a nested five-fold cross-validation process. This procedure yields a distinct optimal $(\mu ,\lambda )$ pair for each of the five outer folds. For analytical clarity, we reuse the representative pair for each classification task, as summarized in Table 13. An analysis of these pairs reveals that the optimal hyperparameter strategy is highly dataset-dependent, with each task favoring a unique balance, as detailed below:

• For the Iris dataset, the strategy favors strict internal consistency. In the Iris dataset, each sample comprises four BBAs, namely, $m_{SL}$, $m_{SW}$, $m_{PL}$, and $m_{PW}$. Under an optimal $(\mu ,\lambda )$ pair, clustering reveals that two-cluster patterns dominate (74.67%), while single- or multi-cluster patterns are rare. The most frequent clusterings show $m_{PL}$, $m_{PW}$, and $m_{SL}$ often grouped together, with $m_{SW}$ separate. The mean credibility weights are highest for $m_{SW}$, followed by $m_{PL}$ and $m_{PW}$, with $m_{SL}$ the lowest. This structure matches the dataset’s properties, with the Setosa class well separated and the other two partially overlapping. The selected $\mu$ moderately amplifies between-cluster separation, while the extremely small $\lambda$ enforces strict within-cluster consistency.
• For the Wine and Seeds datasets, an aggressive differentiation strategy yields optimal results. A common characteristic of these datasets within our framework is their tendency to form highly fragmented clusters, with many BBAs being isolated into singleton clusters. Despite the Wine dataset having higher feature dimensionality and the Seeds dataset having a more balanced class distribution, they benefit from an identical parameterization strategy, as shown in Table 13. The optimal pair serves to maximally amplify differences. An extremely small $\mu$ value improves the separation signal between clusters, while a minimal $\lambda$ imposes a high penalty on internal inconsistency. This strategy is designed to distill the most representative “core” evidence from fragmented or overlapping data.
• The Glass dataset presents a unique challenge due to its structural complexity and class imbalance. Its six classes are highly overlapping in feature space, and the class sizes are extremely imbalanced. Clustering results from the proposed method indicate that 97% of samples are divided into two clusters of sizes 1 and 8. The optimal parameter combination is uncommon, with a very large $\mu$ value that effectively suppresses the influence of inter-cluster differences. This avoids over-penalizing unavoidable cluster conflicts and prevents mistaking true classes, which is essential due to the fuzzy boundaries of classes. Meanwhile, a moderate $\lambda$ value amplifies intra-cluster variation, allowing more internal diversity without harsh penalties. This pair of hyperparameters reduces differences between clusters while encouraging consistency within clusters, which is crucial for data with considerable variation within classes and structural uncertainty.

5.5.2. Analysis of Expert Bias Coefficient

In the proposed method, the expert bias coefficient $\alpha$ is introduced in Equation (40). This coefficient functions as a mechanism to balance the influence of consensus (large clusters) against minority opinions (small clusters):

• $\alpha >1$ amplifies the effect of cluster size, causing credibility to grow exponentially. This strategy reinforces the consensus of the majority.
• $\alpha =1$ establishes a linear relationship where credibility is directly proportional to cluster size. This is regarded as the default, neutral option.
• $\alpha <1$ diminishes the influence of cluster size, thereby giving greater weight to smaller clusters. This approach can highlight rare but valuable patterns.

A common assumption is that larger clusters are generally more reliable. Thus, increasing $\alpha$ is expected to consistently improve performance. However, our experiments revealed a surprising finding: a larger $\alpha$ does not consistently enhance accuracy. To explore this further, we fixed the optimal $(\mu ,\lambda )$ pair and conducted classification experiments using various $\alpha$ values, as shown in

Table 16. Results of different hyperparameter $\alpha$ for the proposed method on the (a) Iris dataset, (b) Wine dataset, (c) Seeds dataset, and (d) Glass dataset. Bold indicates the best value in each column.

Value $\mathit{\alpha }$	(a) Iris Dataset		(b) Wine Dataset		(c) Seeds Dataset		(d) Glass Dataset
	Accuracy	F1 Score	Accuracy	F1 Score	Accuracy	F1 Score	Accuracy	F1 Score
$1/8$	0.9667	0.9667	0.9438	0.9447	0.9190	0.9195	0.4860	0.4919
$1/7$	0.9600	0.9600	0.9494	0.9506	0.9190	0.9195	0.4860	0.4901
$1/6$	0.9533	0.9533	0.9494	0.9500	0.9190	0.9195	0.4860	0.4901
$1/5$	0.9533	0.9533	0.9494	0.9500	0.9190	0.9195	0.4907	0.4926
$1/4$	0.9533	0.9533	0.9494	0.9500	0.9143	0.9149	0.4953	0.4893
$1/3$	0.9467	0.9467	0.9551	0.9558	0.9000	0.9006	0.4953	0.4857
$1/2$	0.9467	0.9466	0.9663	0.9669	0.9000	0.9003	0.5234	0.4996
1	0.9467	0.9466	0.9663	0.9669	0.8952	0.8950	0.5280	0.5040
2	0.9467	0.9466	0.9607	0.9611	0.8810	0.8804	0.5140	0.4966
3	0.9467	0.9466	0.9551	0.9550	0.8762	0.8758	0.5187	0.5005
4	0.9467	0.9466	0.9551	0.9550	0.8762	0.8758	0.5187	0.5005
5	0.9467	0.9466	0.9438	0.9434	0.8762	0.8758	0.5187	0.5005
6	0.9467	0.9466	0.9326	0.9318	0.8714	0.8709	0.5187	0.5005
7	0.9467	0.9466	0.9326	0.9318	0.8714	0.8709	0.5187	0.5005
8	0.9467	0.9466	0.9326	0.9318	0.8714	0.8709	0.5187	0.5005

. The results indicate that the optimal $\alpha$ is also highly dependent on the intrinsic characteristics of each dataset.

For datasets with well-defined and balanced class structures, such as Iris and Seeds, a smaller $\alpha$ value that trusts minority clusters proves optimal. Optimal performance is achieved with $\alpha =1/8$ for the Iris dataset and $\alpha =1/5$ for the Seeds dataset. Both datasets feature a balanced class composition, limited classes and relatively clear feature separability. In such cases, small clusters often represent high-purity class information rather than noise. A low $\alpha$ value prevents this valuable information from being diluted by the consensus of larger clusters by assigning more equitable weights across clusters of all sizes.

In contrast, for datasets characterized by high complexity, massive BBA amounts, obvious class overlap, or severe imbalance, such as Wine and Glass, a neutral $\alpha \approx 1$ is the most effective strategy. Optimal performance for both datasets is achieved when $\alpha =1$. These datasets feature significant class overlap or severe imbalance, leading to clustering results with a mix of large, dominant clusters and small clusters representing minority classes. A neutral $\alpha$ value strikes a critical balance: it avoids over-amplifying the influence of potential outliers (which would occur with a low $\alpha$) while also preventing the dismissal of information from rare classes (which would occur with a high $\alpha$). The linear weighting of this neutral strategy is thus optimal for handling their complex data structures.

Based on the empirical results presented in Section 5.5.2, the selection of an optimal $\alpha$ should be guided by the structural characteristics of the cluster revealed during the final clustering phase, rather than by a fixed rule. The following principles can serve as a guide for practical applications:

• A lower $\alpha$ ($0<\alpha <1$) is preferable for well-structured data or a small number of BBAs. When clustering reveals groups with high internal consistency and clear separation between them (as seen in the Iris and Seeds cases), it is advisable to reduce the influence of cluster size. This approach values the quality of information in each cluster over its size, ensuring that distinct, high-purity minority groups contribute effectively to the final decision.
• A neutral $\alpha$ ($\alpha \approx 1$) provides a robust baseline for complex or imbalanced data or many BBAs. A neutral standpoint is often the safest and most effective in scenarios with significant class overlap, noisy features, or highly imbalanced class distributions (especially in the Glass cases). This balances the risk of being misled by small, noisy clusters against the risk of ignoring valid, rare-class evidence, providing a stable trade-off.
• A higher value of $\alpha$ (where $\alpha >1$) should be used with caution. This option strongly favors the consensus of the majority. It is advisable to consider this approach only when there is high confidence that the most influential cluster likely represents the truth in the experts’ judgment, and that smaller clusters are mainly composed of noise or irrelevant information.

5.6. Ablation Experiment for the Proposed Method

To evaluate the individual contributions of the hyperparameters in our framework, we conducted ablation experiments on four benchmark datasets. This experiment aimed to disentangle the effects of the $(\mu ,\lambda )$ pair and the expert bias coefficient $\alpha$.

The ablation experiment was organized into four configurations, each applied to the four datasets. The configurations are outlined as follows:

• Baseline: Default parameters for both components ($\alpha =1$, $\mu =1$, $\lambda =1$).
• Optimized Clustering Strategy: Default $\alpha$ with the optimal ($\mu ,\lambda$) pairs.
• Optimized Credibility Adjustment: Optimal $\alpha$ with default ($\mu ,\lambda$) pair $(1,1)$.
• Fully Optimized: Optimal values for all 3 hyperparameters.

The overall ablation experiment results are visualized in Figure 8, while the full numerical experiment results are presented in Appendix D.

To statistically validate our findings, we performed a one-sided paired t-test comparing the classification accuracy of the “Fully Optimized” configuration against the “Baseline" configuration. The test pairs were formed by the accuracy scores from each of the five cross-validation folds for every dataset. Our alternative hypothesis was that the fully optimized model yields a higher accuracy than the baseline, justifying the directional nature of the one-sided test. With a significance level set at $\alpha =0.05$, the results presented in

Table 17. Ablation experiment significance.

Dataset	Metric	t-Statistic	p-Value	Significant ($\mathit{p}<0.05$)
Iris	Accuracy	2.3333	0.0400	Yes
Wine	Accuracy	2.4489	0.0353	Yes
Seeds	Accuracy	2.6667	0.0280	Yes
Glass	Accuracy	2.7599	0.0254	Yes

indicate that the performance improvement is statistically significant across all four datasets.

As shown in Figure 8, the findings indicate that integrated optimization is critical to achieving optimal performance. Across all datasets, the fully optimized configuration consistently outperforms the baseline configuration with default parameters. These performance gains are not coincidental but are statistically confirmed to be significant, as validated by a one-sided paired t-test for each dataset, as detailed in Table 17. This underscores why a data-driven strategy for hyperparameter tuning is crucial for realizing the framework’s full potential.

In addition, the results reveal a coordination effect between the two optimization components. While optimizing either the hyperparameter pairs or $\alpha$ individually often improves performance, their relative importance varies depending on the dataset’s characteristics. Notably, the fully optimized configuration either surpassed or matched the results of the best-performing partially optimized configurations. For datasets like Iris and Seeds, a clear integrated gain was observed, where combining both components unlocked further performance that was not achievable by either one alone.

6. Conclusions

The core contribution of this work lies in introducing a novel analytical perspective to the field of uncertainty reasoning. The proposed framework is designed to offer a more intuitive and interpretable approach to addressing evidential conflicts. The main objectives and contributions of this work can be summarized as follows:

• Proposal of an Innovative Evidence Clustering Framework: By elevating the analytical level from BBA-to-BBA comparisons to a holistic BBAs-to-BBAs perspective, the proposed framework organizes similar pieces of evidence into “clusters”, thereby offering a structured approach to managing and locating conflict. In the benchmark classification tasks, this perspective demonstrated competitive performance, achieving higher classification accuracy compared to classical methods based on D-S evidence theory, while also enhancing the reliability and interpretability of decision-making under uncertainty.
• Introduction of a Novel Cluster–Cluster Divergence Measure: This work presents a divergence measure, named $D_{CC}$, between evidence clusters. The proposed measure not only satisfies key mathematical properties such as non-negativity, symmetry, and the triangle inequality, but also captures both the intensity of belief assignment and the structural support differences between clusters. Inspired by the call for new E-E divergences in [80], our $D_{CC}$ pioneers a novel geometric path. The new divergence provides a non-entropic alternative to the specific E-E paradigm proposed therein and a departure from traditional I-P-E methods.
• Development of a Greedy Evidence Assignment Rule: A reward-based greedy evidence assignment rule is proposed to assign new evidence to the most suitable cluster dynamically. This rule computes the “reward” for joining an existing cluster or creating a new one, selecting the strategy that maximizes inter-cluster differences while minimizing intra-cluster conflict. The approach enables rational and adaptive clustering decisions after taking into account suitable hyperparameters.
• Innovative Fusion Approach and Hyperparameter Analysis: Our work presents a dynamic and adaptive information fusion method, supported by an efficient, data-driven hyperparameter tuning approach and sensitivity analysis. Through experimental analyses, it reveals the mathematical roles and optimal selection strategies for the core hyperparameters, specifically, the $(\mu ,\lambda )$ pair and the expert bias coefficient $\alpha$.

Despite its effectiveness in pattern classification tasks, the framework has several limitations:

• Due to the use of a greedy evidence assignment rule, the clustering result is not always stable. Different insertion orders of BBAs may lead to different clustering outcomes.
• Although $D_{CC}$ compares all $2^{\Theta }$ subsets between two BBAs, it cannot characterize the non-specificity of focal elements. This limitation prevents it from capturing how the belief assigned to more general subsets contributes to the overall uncertainty.
• The framework’s performance depends on hyperparameter pairs $(\mu ,\lambda )$, which require a validation set for tuning. While Bayesian optimization makes this process tractable, finding optimal parameters remains challenging in scenarios without prior data, which is a practical limitation for deployment.

To address these limitations, future work will explore several promising directions. Future work will focus on developing deeper mathematical characterizations of information fusion from a clustering perspective, such as developing measures like cluster entropy or cluster information volume. Another pathway involves refining the representation of focal element specificity at the cluster-to-cluster level. Moreover, we plan to extend and adapt the proposed framework to cutting-edge domains, including deep learning, foundation model reasoning, and interpretable uncertainty reasoning, thereby expanding both its practical applicability and scientific significance.