Renewable-Integrated Agent-Based Microgrid Model with Grid-Forming Support for Improved Frequency Regulation

Abstract

The increasing penetration of renewable energy presents substantial challenges to frequency stability, particularly in low-inertia microgrids. This study introduces an agent-based microgrid model that integrates generators, loads, an energy storage system (ESS), and renewable sources, mathematically formalized through the discrete-event system specification (DEVS) to ensure both structural clarity and extensibility. To dynamically simulate power system behavior, the model incorporates multiple control strategies—including ESS scheduling, automatic generation control (AGC), predictive AGC, and grid-forming (GFM) inverter control—each posed as an mathematically defined control problem. Simulations on the IEEE 13-bus system demonstrates that the coordinated operation of ESS, GFM, and the proposed strategies markedly enhances frequency stability, reducing frequency peaks by 1.14, 1.14, and 0.72 Hz, and shortening the average recovery time by 9.05, 0.15, and 2.58 min, respectively. Collectively, the model provides a systematic representation of grid behavior and frequency regulation mechanisms under high renewable penetration, and establishes a rigorous mathematical framework for advancing microgrid research.

1. Introduction

1.1. Challenges in the Microgrid System

A microgrid refers to a small-scale power system. As shown in Figure 1, it typically comprises distributed generation units, energy storage systems (ESS), loads, and control devices, and can achieve local energy self-sufficiency. Among these components, renewable energy sources such as solar and wind power are increasingly integrated into microgrids because of their low cost and minimal environmental impact [1,2]. However, this increasing integration also presents new challenges. Renewable energy generation is inherently uncertain. For instance, solar output is highly sensitive to weather conditions and cloud coverage [3], while wind power depends on fluctuating wind speeds [4]. These variations can cause unpredictable power outputs, leading to demand–supply imbalances that trigger frequency fluctuations within the system. Furthermore, renewable energy is typically integrated through power-electronic interfaces [5], which lack the mechanical inertia of conventional synchronous generators. Consequently, they cannot inherently provide or absorb kinetic energy to buffer power deviations, resulting in weak frequency support capability [6]. These issues are particularly severe in microgrids, which, owing to their small scale and extremely low inertia [7,8,9], face considerable difficulties in maintaining frequency stability. Additionally, the allowable frequency deviations vary across networks, voltage levels, and standards. For example, large interconnected transmission systems usually impose strict limits [10], whereas distribution systems or microgrids with high renewable penetration often tolerate larger short-term deviations, sometimes exceeding 1–2 Hz [11]. This distinction underscores the unique challenges of maintaining frequency stability in microgrids.

In recent years, the grid-forming (GFM) inverter, an advanced inverter control strategy, has been proposed to mitigate demand–supply imbalances caused by the high penetration of renewable energy sources. It acts as a controlled voltage source within the circuit, and through the GFM inverter, nonsynchronous generators are enabled to emulate the behavior of synchronous generators, thereby providing frequency regulation and virtual inertia support through power electronic interfaces [12]. Accordingly, analyzing its influence on power systems, particularly in microgrids, has become essential. Research on GFM inverters has expanded rapidly; however, compared to conventional inverters, their deployment and application remain associated with relatively higher costs.

To support effective adoption and cost efficiency, modeling and simulation provide valuable alternatives. Computational models are capable of capturing and reproducing complex, nonlinear, and stochastic behaviors that are often difficult to represent with traditional approaches. Moreover, because they do not require physical construction, computational models allow the exploration of diverse structures, scenarios, and even extreme conditions solely through computer-based experimentation, thereby ensuring both modeling accuracy and operational flexibility. In particular, as illustrated in Figure 2, agent-based models are highly modular, intelligent, and easily extensible, rendering them especially well-suited for representing complex power systems.

1.2. Discrete-Event System Specification

In this study, all agent models are designed using the discrete-event system specification (DEVS) formalism [13]. Originally proposed by B. P. Zeigler in 1976, DEVS is an event-based modeling approach for discrete-event systems. Within this framework, each model receives inputs, updates its state, and sends outputs to interact with other models.

DEVS provides a general and modular modeling framework for representing dynamic systems whose behavior evolves over time in a discrete-event manner, rather than continuous time. By alternating between state trajectories and discrete events, it can uniformly represent purely discrete-event systems as well as hybrid systems that combine both continuous and discrete dynamics. An additional advantage lies in its ability to clearly distinguish external inputs, internal state transitions, and output processes, thereby enabling each component to be defined independently and hierarchically composed to construct complex systems.

A simulation model (SM) is the fundamental unit and specifies the dynamics of the model [14]. As described in [14], an SM is formally defined as a 7-tuple, as expressed in Equation (1):

$$SM= <X, Y, S, {\delta }_{ext}, {\delta }_{int},\lambda ,ta>,$$

(1)

where

$X$: a set of input events;

$Y$: a set of output events;

$S :$a set of states;

${\delta }_{ext}$: $S\times X\to S$, an external transition function;

${\delta }_{int}$: $S\to S$, an internal transition function;

$\lambda : S\to S\left(X\right)\to X:S\to Y,$ an output function;

$ta : S\to R_{0,\infty }^{+}$ (non-negative real number), a time advance function.

More specifically, the input event set $X$ is defined as the collection of all possible external inputs, the output event set $Y$ represents the collection of all possible outputs, and the state set $S$ represents the collection of all possible internal states. The external transition function ${\delta }_{ext}$ describes how the system responds to inputs based on its current state and received input, while the internal transition function ${\delta }_{int}$ represents how the system’s state evolves after a certain period in the absence of external inputs. The output function $\lambda$ determines how the system generates outputs based on its current state before an internal transition, and the time advance function $ta$ defines how long the system remains in its current state without external inputs, which is key to simulation time stepping and event scheduling.

When applying this modeling approach to the power system in this study, the input event set typically includes commands such as generator on/off switching and power set value instructions. The output event set includes information such as power output, system frequency status, and ESS capacity. The state set represents the operational status of components such as generators and ESS. The external transition function may include logic such as updating the power output of a generator upon receiving a new power set value while in an active state. The internal transition function could cover behaviors such as updating the state of charge and output power of the ESS at each simulation time step. The output function includes, for instance, the ESS transmitting its current power and capacity information prior to the internal state update.

In summary, this systematic modeling approach establishes a mathematically rigorous framework that accurately characterizes input–output mappings, internal state transitions, and overall system behavior. Each component is formally defined by sets (X, Y, S) and functions (${\delta }_{ext}$, ${\delta }_{int}$, $\lambda$, ta), ensuring that the dynamic processes of event inputs, state evolution, and output responses are strictly and unambiguously represented. Given the inherent complexity of power systems, the absence of such formal specification often results in vague descriptions, limiting the ability to capture internal interactions and thereby constraining in-depth investigations into system dynamics and the effectiveness of control strategies. By adhering to the unified formalism of the DEVS, the proposed model overcomes these limitations, enabling precise interpretation, validation, and reproducibility of the modeling process. Furthermore, the inherent modularity and composability of DEVS allow model to be flexibly replaced or extended without altering the global structure, making the framework particularly suitable for power system studies, where accurate representation and analysis of complex dynamic interactions among heterogeneous components under diverse operating conditions are essential.

1.3. Literature Survey

Several models have been proposed in recent years to address the challenges associated with high renewable energy penetration in microgrids. Tamrakar et al. [15] designed and implemented an islanded microgrid model to mitigate frequency instability caused by the extensive integration of renewable energy sources such as solar power. By introducing a solar-based output regulation method, their model enabled dynamic management of both voltage and frequency within the microgrid. Watson and Kimball [16] proposed a framework based on model predictive control (MPC), which constructs a predictive model of the microgrid and solves optimization problems to alleviate large frequency deviations and slow control responses resulting from low system inertia. Du et al. [17] developed an electromechanical model of three-phase GFM and GFL inverters that supports dynamic simulation of unbalanced three-phase distribution systems with high levels of inverter-based distributed energy resources. Their study confirmed that GFM inverters provide significant advantages in maintaining voltage and frequency stability in power systems. Similarly, Vignesh Babu et al. [18] developed a photovoltaic (PV)–battery integrated microgrid model to address voltage and frequency instability under high renewable penetration. By simulating and comparing GFL and GFM inverter control models across multiple operating scenarios, the study demonstrated the superior performance of GFM inverters in maintaining both voltage and frequency stability. Yameen et al. [19] proposed an adaptive MPC framework to improve the performance of GFM inverters in addressing frequency stability challenges under high renewable energy penetration. By combining offline reinforcement learning with online MPC and employing a hybrid optimization algorithm for parameter tuning, their results demonstrated that the approach enhanced frequency stability to some extent under grid disturbances. Vanashi et al. [20] introduced a multiagent architecture-based control method to mitigate frequency stability issues in microgrids caused by the integration of active devices such as inverters. Their approach combines adaptive dynamic programming with particle swarm optimization and applies it to frequency control in inverter-dominated islanded microgrids, significantly improving the dynamic performance of the system. The study also validated its effectiveness under centralized, distributed, and hierarchical structures, with the hierarchical configuration offering notable advantages in enhancing dynamic performance and reducing communication overhead. Bitew et al. [21] proposed a model-based hierarchical control framework to strengthen the frequency regulation capability of microgrids integrating PV and battery energy storage systems. The model includes switches, loads, PV units, and storage devices, and is formulated primarily with differential equations. In this approach, the controllers are tightly coupled, and overall system behavior depends on centralized coordinated control.

Despite these advances, the above studies present several limitations. Studies [15,16] focused mainly on traditional inverter-based control strategies or algorithmic approaches, without considering GFM inverters—an innovative and effective solution for frequency instability under high renewable energy penetration. Studies [17,18,19,20], although verifying the advantages of GFM inverters for frequency regulation, primarily emphasized the effectiveness of GFM itself while overlooking the potential contributions of additional control strategies that may coexist within the system. As for [21], although the model is capable of dynamic voltage and frequency control, its predefined structure, fixed module interfaces, and high complexity limit its flexibility. It does not readily support microgrid topology expansion or component replacement, thereby constraining the integration of diverse control strategies and reducing adaptability to different operating scenarios and configurations. A summary of the related work and its limitations is presented in

Table 1. Contributions and limitations of the related work.

Model	Contributions and Limitations	GFM Inverter	Control Strategies	Structure
[15,16]	Proposed islanded microgrid frameworks that improve voltage and frequency stability, but did not consider GFM inverters.	Without	Single	Fixed
[17,18,19,20]	Verified the advantages of GFM inverters in maintaining voltage and frequency stability but focused mainly on GFM itself while neglecting the role of multiple controls.	With	Single	Fixed
[21]	Developed a differential equation-based hierarchical control framework capable of dynamic voltage and frequency control, but with a fixed structure and high complexity, limiting flexibility.	Without	Single	Fixed

.

Therefore, a review of the related studies indicates that most existing models exhibit notable limitations, which can be summarized as follows:

• Many studies overlook the critical role of the GFM inverter in frequency regulation under high renewable energy penetration.
• Excessive emphasis is often placed on a single control strategy, without fully considering the coexistence of multiple control strategies within the system, resulting in limited validation of the effectiveness of individual or coordinated strategies.
• Model structures are often complex, rigid, and lack formalized representation at the mathematical level. This limits their flexible adaptation to different system configurations and operating scenarios. Additionally, it impairs the models’ readability and interpretability (e.g., the internal logic of the system is difficult to capture and understand, and tracing the causal relationships between inputs and outputs is challenging). Moreover, it also restricts extensibility, hindering the integration of new modules or adjustment of existing ones.

1.4. Motivation and Main Contributions

To address the aforementioned limitations, this study integrates GFM inverters and multiple control strategies into an agent-based modeling approach for constructing a microgrid model. In this framework, system components—such as generators, ESS, and loads—are represented as agent-based models. This representation decouples the complex structure of the power system and captures the interactions among system components. Simultaneously, it enables flexible configuration, making the model adaptable to diverse scenarios across different scales and operating conditions. Furthermore, GFM inverters and control strategies are embedded within specific agent models, thereby supporting effective performance evaluation. Through these design choices, the model provides a simplified yet reliable digital twin framework for frequency management in microgrids with high renewable energy penetration.

The main contributions of this study can be summarized as follows:

• By recognizing the critical role of the GFM inverter in frequency stability under high renewable penetration, this study designs and embeds the GFM inverter into specific agent-based models, thereby enabling efficient verification of its effectiveness in frequency regulation within microgrids.
• Multiple frequency regulation strategies—including ESS scheduling, Automatic Generation Control (AGC), and Predictive Automatic Generation Control (PAGC)—are integrated into the model, enabling systematic verification of diverse control strategies within the microgrid framework. Importantly, the framework offers high extensibility, allowing additional control strategies to be incorporated and tested in future applications by simply modifying the corresponding Python files (Python 3.7).
• All system components are modeled based on agents and rely on DEVS to achieve rigorous mathematical formalized representation. DEVS endows the modeling process of each component with mathematical logic and derivation basis, while the modular characteristics of agents ensure the flexibility of the overall model. Specifically, the addition, removal, or reconstruction of components can be realized only by adjusting the mathematical parameters and interaction rules of the corresponding agents, without changing the overall mathematical architecture and logical topology of the model. This further ensures that the model can accurately adapt to power systems of different scales and operating scenarios under strict mathematical constraints.

Validation on the IEEE 13-bus test system demonstrates that the coordinated operation of the ESS, GFM inverters, and the proposed control strategies significantly enhances frequency stability. Specifically, frequency peaks are reduced by 1.14, 1.14, and 0.72 Hz, while the average frequency recovery time is shortened by 9.05, 0.15, and 2.58 min, respectively. These results confirm the reliability of the proposed model. Moreover, experiments conducted under diverse system configurations and scenarios demonstrate the exceptional flexibility and scalability of the model. In summary, this research not only achieves rigorous modeling of power systems through mathematical formalization but also provides deeper insights into the optimization of complex power systems and supports the development of high-fidelity, future-oriented microgrid models.

1.5. Organization of the Paper

The remainder of this paper is organized as follows. Section 2 presents the modeling process and details of the proposed microgrid model. Section 3 describes the experimental setup, scenarios, and analysis of the results. Section 4 concludes with a summary of the key findings.

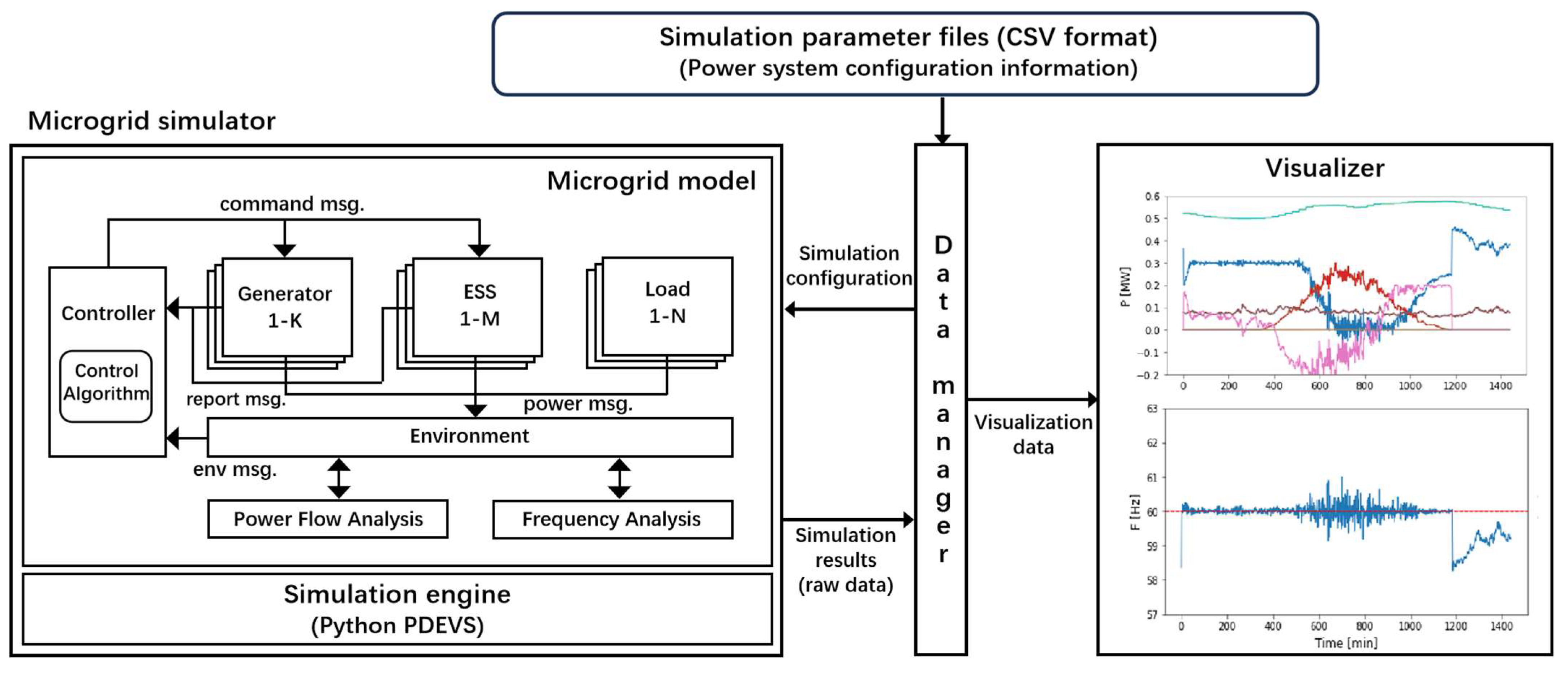
2. Model Design

2.1. System Component Introduction

In microgrid systems, components such as buses, transmission lines, and transformers lack active control capabilities, with their operational states determined primarily by external variables such as voltage and current. Consequently, these elements are classified as passive components and are uniformly represented in the environmental model, which characterizes the fundamental physical configuration and background of the microgrid. By contrast, components such as generators, ESS, and loads can adjust their behaviors—for example, modifying power generation, charging or discharging, or varying load demand—in response to system conditions or external control commands, thereby demonstrating active control capabilities. Because their dynamic characteristics directly influence system operation, these elements are modeled as agent-based models to capture decision-making mechanisms and interactive dynamics during microgrid operation. Notably, in this design, the GFM inverter is treated as an inherent attribute of generators and is incorporated into the generator model. The names, functions, and classifications of the system components are summarized in

Table 2. System components information.

Component	Function	Classification
Bus	A conductive node connecting lines, generators, and transformers.	Environment model
Line	A transmission line connecting two buses.
Transformer	A device that changes voltage levels between buses.
Control system	A system that controls the operation of generators and ESSs to maintain a stable power supply according to load demand.	Control model
Load	Devices consuming both active and reactive power.	Load model
ESS	Energy storage system.	ESS model
Synchronous generator	A generator that induces a three-phase voltage by rotating the rotor.	Generator model
Non-synchronous generator (without GFM)	A generator that does not have a rotor and generates alternating current based on an inverter, which includes renewable energy such as solar and wind power.
Non-synchronous generator (with GFM)	A nonsynchronous generator equipped with GFM inverter capability, applicable to renewable energy such as solar and wind power.

.

2.2. Agent-Based Model Design

The proposed microgrid model comprises five core model types and two computational modules: (1) controller model, (2) environment model, (3) generator model, (4) ESS model, and (5) load model, together with (a) a frequency analysis module and (b) a power flow analysis module. The overall model structure is shown in Figure 3.

Passive components such as buses, lines, and transformers are incorporated into the environment model, whereas active components, including generators, ESS, and loads, are modeled individually as agents. A dynamic instantiation mechanism is applied to active components, allowing their numbers to be flexibly adjusted according to specific application scenarios, while the controller and environment models remain as single instances throughout the simulation. The frequency and power flow analysis modules compute the key operational parameters of system components and provide essential information for the real-time adjustment of generator and ESS power setpoints, thereby supporting comprehensive system assessment and control.

Interactions among the models are conducted through a structured messaging system comprising four message types: command, power, report, and environment. Each type carries specialized information relevant to its function, as summarized in

Table 3. Message details.

Message	Contents
command msg.	Control command ON/OFF/P_SET, active and reactive power set value
power msg.	Active and reactive power
report msg.	Active and reactive power (ESS reports both power and capacity)
environment msg.	Active and reactive power, frequency, and voltage

.

This architecture supports coordinated system operation through continuous message exchange between modules and component models, as well as among the component models themselves. It ensures stable model performance while enabling decentralized control and facilitating adaptive control without compromising distributed operation. The detailed simulation process is illustrated in Figure 4.

In this framework, the simulation time step T denotes the fixed interval governing interactions among agent models. At each time step of length T, every model exchanges information and updates its state, which corresponds to the time required for generators, ESS, loads, and the environment model to produce outputs. In this study, the simulation timeline is divided into fixed-duration slices of 1 min. Within each step, agents sequentially complete information exchange and state updates to maintain synchronous progression of the overall system. At the beginning of each simulation time step, the environment model sends an environment message (env msg.) to the controller, containing system operating parameters such as active power (P), reactive power (Q), system frequency (F), and voltage magnitude (V). These parameters represent the current grid conditions and form the basis for control decisions. Upon receiving the environment message, the controller executes the corresponding control algorithms—for instance, determining the ESS output based on power imbalance, deciding whether AGC is necessary depending on the frequency deviation, and enabling PAGC according to the current time. It then issues command messages (command msg.) to generators and ESS, specifying target active power values. At the end of each simulation time step, generators, ESS, and loads execute the control commands and provide feedback through power messages and report messages, which are used to update the system state and support subsequent adaptive adjustments. The environment model then collects the power messages from all components, recalculates the system state, and generates the next round of environment messages. This process establishes a continuous iterative closed-loop interaction that persists until the simulation time reaches the predefined termination point. Through this mechanism, information exchange among agents is conducted in an event-driven manner, ensuring synchronous coordination throughout the simulation.

2.2.1. Environment Model

The environment model simulates the operation of passive components in the grid, including buses, lines, and transformers. Although this part essentially belongs to a continuous-time system, in this study, its behavior is segmented by time steps and modeled as a discrete-event system. This choice reflects the fact that, while the physical behavior of power systems is inherently continuous, state changes are triggered by events. By correctly defining the simulation time step, event-driven abstract modeling simplifies the system structure while accurately capturing dynamic behavior, thereby closely approximating the characteristics of a continuous-time system.

The environment model is defined as shown in Equation (2):

$$Environment model= <X, Y, S, {\delta }_{ext}, {\delta }_{int},\lambda ,ta>,$$

(2)

where:

$$X=\left\{\begin{array}{c}\left(Generator\_1\right)power msg,\dots ,\left(Generator\_N\right)power msg,\\ \left(ESS\_1\right)power msg,\dots ,\left(ES{S}_M\right)power msg,\\ \left(Load\_1\right)power msg,\dots ,\left(Load\_K\right)power msg\end{array}\right\};$$

$$Y=\{env msg\};$$

S = {START, CONTINUE, END};

$${\delta }_{ext} :\left(CONTINUE,e,power msg\right)\to \left(CONTINUE,T-e\right)\left[continue\right]$$

$$\left(END,e,power msg\right)\to \left(END,\infty \right)\left[continue\right];$$

$${\delta }_{\mathrm{i}\mathrm{n}\mathrm{t}} : \left(START,0\right)\to \left(CONTINUE,T\right)$$

$$\begin{array}{c} if \left(current time<End time\right) then \left(CONTINUE,T\right)\to \left(CONTINUE,0\right)\\ else then(CONTINUE,T)\to (END,\infty );\end{array}$$

$$\lambda : \left(START,0\right)\to env msg$$

$$\left(CONTINUE,T\right)\to env msg$$

$$\mathit{ta} \left(\mathit{START}\right)=0, \mathit{ta} \left(\mathit{CONTINUE}\right)=\mathrm{T}, \mathit{ta} \left(\mathit{END}\right)=\mathrm{\infty }.$$

The initial state of the model is START. In this state, the model sends an environment message and then transitions to the CONTINUE state. The DEVS structure of the environment model is illustrated in Figure 5, and the model parameters are summarized in

Table 4. Environment model parameter.

Parameter	Description	Configuration
T	time required to deliver the environment message to the controller	fixed value
End time	microgrid termination time	fixed value

.

At each fixed simulation time step T, the environment model invokes the frequency analysis and power flow analysis modules to compute active and reactive power data from various components, along with the current system frequency and bus voltage. The computed results are then packaged into an environment message and transmitted to the controller model. While in the CONTINUE state, if the simulation end time has not been reached, the model sends an environment message at every interval of T and remains in the CONTINUE state. Once the simulation end time is reached, the model transitions to the END state. For the two states excluding START, if a power message input is received, the external transition function ${\delta }_{ext}$ is invoked. When the model is in the CONTINUE state and receives the power message, it remains in the current state but updates the remaining time to $T-e$, thereby resetting the state residence time to ensure the model can respond to the new input. By contrast, when the model is in the END state, it ignores all messages and enters a passive state with an infinite time advance value, indicating that no further events will occur.

The frequency analysis module calculates the power imbalance to estimate frequency deviation, which is then added to the nominal frequency to determine the current frequency of the system.

The frequency analysis module is primarily designed to calculate microgrid frequency dynamics under varying operating conditions. The total system active power imbalance $∆P$ is calculated by Equation (3):

$$∆P=P_{load}{-P}_{ESS}{-P}_{async}{-P}_{sync}$$

(3)

Here, $P_{load}$ represents the total power of all loads, $P_{ESS}$ denotes the total power of all ESSs, and $P_{sync}$, $P_{async}$ represents the total power of the two types of generators. Subsequently, the system frequency deviation $∆f$ is computed using Equation (4):

$$∆f={\displaystyle \frac{∆P}{R_{system}}}$$

(4)

Here, the $R_{system}$ shown in Equations (4) and (5) refer to the droop coefficient of the system,

$$R_{system}={\sum }_{i=1}^N{\displaystyle \frac{1}{R_i}}$$

(5)

which reflects the comprehensive response capacity of all synchronous generators in the system to the frequency deviation. Finally, the current system frequency $f$, as shown in Equation (6), is determined by combining the nominal frequency valued $f_{nominal}$with the frequency deviation $∆f$.

$$f=f_{nominal}+∆f.$$

(6)

For the power flow analysis module, the environment model primarily relies on the PyPSA library [22], which enhances both computational efficiency and accuracy. The analysis process is based on the Newton–Raphson method [23]. Using the system parameters provided by the environment model—including active power, reactive power, bus voltage magnitudes, and line parameters—the corresponding nonlinear equations are formulated and solved iteratively to determine the power flow distribution. These results then support subsequent frequency regulation and the implementation of control strategies.

2.2.2. Controller Model

The controller model simulates the operational mechanisms of the control strategies and algorithms within the microgrid. The control system regulates the power output of various energy sources by comprehensively considering the current system state, load demand, and generation status.

The controller model is defined as shown in Equation (7):

$$Controller model= <X, Y, S, {\delta }_{ext}, {\delta }_{int},\lambda ,ta>,$$

(7)

where

$$X=\left\{report msg,env msg\right\};$$

$$Y=\left\{\begin{array}{c}\left(Generator\_1\right)command msg,\dots ,\left(Generator\_N\right)command msg,\\ \left(ESS\_1\right)command msg,\dots ,\left(ESS\_M\right)command msg\end{array}\right\};$$

S = {WAIT, CONTROL};

$${\delta }_{ext} :\left(WAIT,e,report msg\right)\to \left(WAIT,\infty \right)\left[continue\right];$$

$$\left(WAIT,e,env msg\right)\to \left(CONTROL,0\right);$$

$${\delta }_{int} :\left(CONTROL,0\right)\to \left(WAIT,\infty \right);$$

$$\lambda : \left(CONTROL,0\right)\to command msg;$$

$$ta\left(CONTROL\right)=0, ta \left(WAIT\right)=\infty .$$

The initial state of the model is WAIT. When an environment message containing the current active and reactive power, voltage, and system frequency values is received in this state, an external transition occurs and the model moves to the CONTROL state. In the CONTROL state, the model processes the received environment and report messages through the control algorithm and generates a command message. It then transitions back to the WAIT state via the internal transition function ${\delta }_{int}$ and outputs the command message via the output function $\lambda .$

The DEVS structure representing this process is shown in Figure 6, and the parameters of the controller model are summarized in

Table 5. Controller model parameters.

Parameter	Description	Configuration
Control algorithm	An algorithm that distributes active power load among synchronous generators, considering refined dispatch based on the usage of ESS, AGC, and PAGC.	For AGC: distributes based on current active power required by synchronous generators. For PAGC: distributes based on projected active power required after PAGC interval time.
AGC	Controls the no-load frequency of synchronous generators to restore system frequency when deviations exceed threshold values.	Applied when system frequency deviation exceeds 0.05 Hz.
PAGC	Proactively controls the no-load frequency of synchronous generators by predicting future demand to minimize frequency fluctuations.	Applied every 5 min.
Economic Dispatch Solution Algorithm (Solved ED)	Optimization algorithm for efficient active power allocation among synchronous generators.	Incorporates generator cost functions into equations, solves the equations, and allocates active power based on solutions.

.

• Control algorithms

Based on the operational status of synchronous generators and the configuration of ESS, AGC, and PAGC, the controller dynamically allocates active power to ensure both frequency stability and economic performance.

The controller model incorporates two types of control algorithms: AGC and PAGC. When AGC is activated, it gradually adjusts the power allocation of synchronous generators according to the deviation between the current system frequency and the nominal frequency, while simultaneously considering the economic dispatch and the regulation capability of each generator. In addition, the no-load frequency of each synchronous generator—defined as the natural frequency under zero load and used in this study as an indicator of frequency regulation sensitivity—is updated (to monitor whether AGC is activated and the extent of its adjustment). This process achieves fast response and high control accuracy, making it suitable for real-time frequency regulation. The details of power allocation based on economic dispatch are discussed in the following section. By contrast, PAGC is a feedforward control strategy that operates periodically at predefined time intervals. The controller predicts load demand over upcoming steps using current system data, historical load trends, and a predefined prediction accuracy. It then proactively adjusts the power set values of synchronous generators in advance, thereby enhancing system stability under fluctuating and uncertain demand conditions.

• Economic dispatch solution

In this model, the optimal active power allocation of synchronous generators is solved by using the economic dispatch based on the Lagrange multiplier approach. This method incorporates the system constraints into the objective function, enabling the derivation of an optimal solution that satisfies these constraints. Specifically, the model aims to coordinate n synchronous generators to minimize the total generation cost of the system while meeting both the total power demand P and the individual output constraints of each generator. The generation cost of each synchronous generator is represented as a quadratic function, following the modeling approach in [24], as expressed in Equation (8):

$$\underset{p_1{...p}_n}{\min }{y}_1+y_2+...+y_n,$$

(8)

$$y_i=C{1}_i{p}_i^2+C{2}_i{p}_i+z_{i,}$$

$$P=p_1+p_2+\dots +p_n,$$

$$p_{i,min}\le p_i\le p_{i,max},$$

where y represents the generation cost of generator i, $C{1}_{i }and C{2}_i$ represent the cost coefficients of the generator i, and $p_i$ denotes its output power. The output power of each generator is subject to its respective physical upper limit $p_{i,max}$ and lower limit $p_{i,min}$, which serve as the constraints of this optimization problem. The theoretical optimal solution of the economic dispatch problem is achieved when the incremental costs of all generators are equal. The incremental cost $\lambda$ of each generator is obtained by differentiating its generation cost function with respect to its output power as shown in Equation (9):

$$\lambda =2C{1}_i{p}_i+C{2}_i.$$

(9)

By identifying the Lagrange multiplier $\lambda$ that equalizes the incremental costs across all generators, while ensuring that the sum of their output powers matches the total generation demand, the optimal power allocation can be determined. Notably, if the calculated output power $p_i$ for any generator violates its physical output limits, the output of that generator will be fixed at its corresponding maximum or minimum value. Subsequently, the generator is excluded from the optimization process, and the economic dispatch calculation is repeated for the remaining generators. This iterative process continues until all generators satisfy their operating constraints. The final result represents the optimal active power allocation among synchronous generators. The parameters used for economic dispatch in this model are listed in

Table 6. Economic dispatch-related parameters.

Parameter	Description	Example Setting
p_nom	Rated active power, used as an upper bound in case of sudden change.	0.3 MW
p_set_min	Minimum active power, used as the lower limit under steady-state frequency during generation reduction.	0.01 MW
p_set	Active power target, which represents the generation target under nominal frequency; for synchronous generators, the actual output may differ due to frequency changes.	0.2 MW
q_set	Reactive power target, which represents the generation target under nominal frequency; for synchronous generators, the actual output may vary depending on frequency deviations.	0 var
zero_load_cost	No-load generation cost, which represents the generation cost when output is zero.	191.48949 KRW/T
C1	Quadratic coefficient, which is the coefficient of p2 in the cost function (y = C1 × p2 + C2 × p + zero_load_cost).	1418.44067
C2	Linear coefficient, which is the coefficient of p in the cost function (y = C1×p2 + C2 × p + zero_load_cost).	1063.8305

.

• Algorithms execution

Figure 7 illustrates the detailed flow of the control algorithm used in the proposed model, where the boxed areas in the diagram represent the specific control processes.

The execution of control algorithms follows a predefined hierarchy of priorities. First, ESS control is activated with the highest priority to buffer power imbalances in the system. The controller determines the charging or discharging power of the ESS based on the current imbalance and the status of the ESS, as expressed in Equation (10):

$$∆P_{ESS}=P_{load}(t)-{\sum }_{i\in Gsync}{P}_i$$

(10)

The difference $∆P_{ESS}$ between the current time load power $P_{load}\left(t\right)$ and the sum of all synchronous generator output power $\sum _{i\in Gsync}{P}_i$ is used to determine whether the ESS should charge or discharge. Subsequently, if AGC is activated, the frequency deviation at the current time $∆f\left(t\right)$ is calculated as the difference between the measured frequency value $f\left(t\right)$ and the nominal frequency value $f_{nominal}$, as shown in Equation (11):

$$∆f\left(t\right)=f\left(t\right)-f_{nominal}$$

(11)

If the absolute value of the current frequency deviation $\left|\Delta f\left(t\right)\right|$ exceeds the preset threshold ${\delta }_f$, the AGC is triggered, as shown in Equation (12):

$$AGC trigger:\left|\Delta f\left(t\right)\right|\ge {\delta }_f.$$

(12)

Once activated, AGC allocates active power among synchronous generators based on economic dispatch. At the same time, the no-load frequency of each synchronous generator is adjusted., as shown in Equation (13). The no-load frequency $f_{no load }$ is obtained by adding the nominal frequency $f_{nominal}$ and the no-load frequency deviation $\Delta f_{no load}.$

$$f_{no load}=f_{nominal}+\Delta f_{no load}$$

(13)

Here, the no-load frequency deviation $\Delta f_{noload}$ is calculated using Equation (14), where slope represents the regulation coefficient and $P\left(t\right)$ represents the output power of the synchronous generator at the current time.

$$\Delta f_{no load}=-slope \ast P\left(t\right)$$

(14)

In this study, the parameter $slope$ refers to the extent of no-load frequency adjustment caused by a unit change in the active power output of a synchronous generator. It integrates the nominal frequency $f_{nominal}$, the control coefficient $R$ of the synchronous generator, and its nominal power $P_{nominal}$. The specific calculation is shown in the following Equation (15):

$$slope=-f_{nominal} \ast R/P_{nominal}.$$

(15)

Unlike conventional power systems, where AGC operates at fixed intervals, the proposed model adopts an event-triggered mechanism. Once the frequency deviation exceeds the threshold, AGC is activated and executed in the subsequent simulation time step. This design reduces coupling with interval-based control logic and mitigates performance degradation during simulation.

As AGC has a higher priority than PAGC, PAGC is not invoked when AGC is active. If AGC is disabled while PAGC is enabled, the algorithm predicts future active power demand $P_{pre}(t+T)$ within a predefined time interval, as shown in Equation (16):

$$P_{pre}(t+T)={\widehat{P}}_{load}(t+T)-{\widehat{P}}_{ren}(t+T),$$

(16)

where both the future load demand ${\widehat{P}}_{load}(t+T)$ and renewable energy output ${\widehat{P}}_{ren}(t+T)$ are determined by Equation (17):

$$\widehat{P}=P·U\left(1-ϵ,1+ϵ\right).$$

(17)

The predicted power value $\widehat{P}$ equals the actual power value $P$ multiplied by a random factor within the range [$1-ϵ$, $1+ϵ$]. Then PAGC performs power allocation accordingly, following economic dispatch principles. Once the active power allocation is completed, relevant parameters are transmitted through command messages, thereby completing the whole control process.

In summary, the controller model provides fine-grained dynamic adjustment, rapid response capabilities, and the flexibility to switch between different control strategies, making it highly adaptable to diverse and complex operating scenarios.

2.2.3. Generator Model

The generator model functions as a key active control agent in a microgrid system. It simulates generator operations, including turning on, turning off, and adjusting generation output. The model receives turn-on, turn-off, and power-setting command messages from the controller model and dynamically adjusts its output according to the generator type, thereby achieving fine-grained control of power supply.

The generator model is defined in Equation (18):

$$Generator model= <X,Y,S{,\delta }_{ext}{,\delta }_{int},\lambda ,ta>,$$

(18)

where

$$X=\left\{command msg\right\}$$

$$Y=\left\{power msg,report msg\right\}$$

$$S=\left\{STOP,GEN\right\}$$

$$\begin{array}{c}{\delta }_{ext} :if \left(control command==ON\right) then \left(STOP,\infty \right)\to \left(GEN,T\right)\\ else then\left(GEN,T\right)\to \left(GEN,0\right);\end{array}$$

$$\begin{array}{c}{\delta }_{int} :if \left(control command==OFF\right) then \left(GEN,T\right)\to \left(STOP,\infty \right);\\ else then\left(GEN,T\right)\to \left(GEN,0\right).\end{array}$$

$$\lambda : \left(GEN,T\right)\to power msg$$

$$\left(GEN,T\right)\to report msg;$$

$$\mathrm{ta}\left(\mathrm{GEN}\right)=\mathrm{T}, \mathrm{ta} \left(\mathrm{STOP}\right)=\mathrm{\infty }.$$

The DEVS structure representing this process is illustrated in Figure 8. The parameters of the generator model are listed in

Table 7. Generator model parameters.

Parameter	Description	Example Setting
Name	Generator name, which cannot be set as a number only.	MT
Bus	Bus name, which must match a name listed in the bus parameter file.	bus_632
bSync	Synchronous flag, which indicates whether the generator is a synchronous machine involved in frequency regulation (T or F).	T
bOn	Initial status, which indicates whether the generator is turned on at the start of the simulation (T or F).	T
Control	Control mode, which specifies the generator control type: PV or PQ for synchronous generators, PQ for nonsynchronous generators, and slack for the slack bus generator.	PV
data_file	Input file, which contains time-series generation data for the generator.	./param/solar.csv
p_set_change_rate	Ramp rate, which defines how rapidly the target active power is adjusted in response to AGC or PAGC commands,	0.02 MW/min
R	Control coefficient, which defines the sensitivity of a synchronous generator’s active power output to changes in system frequency.	0.05
bGFM	GFM flag, which indicates whether the generator is of GFM inverter type (T or F).	T
price_file	Price file, which contains time-varying generation cost data; if this file is provided, the values of zero_load_cost, C1, and C2 will be ignored.	./param/SMP.csv

.

The initial state of the model is determined by input data. If the generator is on at the beginning, the initial state is GEN; otherwise, it is STOP. In the STOP state, when the model receives a command with the instruction on, it transitions to GEN. Conversely, in the GEN state, if a command message is received, the model sets the power values of the synchronous generator according to the instruction content and remains in GEN, as specified by the external transition function ${\delta }_{ext}$. If no command message is received within time T in the GEN state, the model outputs a power message and a report message. At that point, if the control command is off, the model transitions to STOP; otherwise, it remains in GEN, as defined by the internal transition function ${\delta }_{int}$ and output function $\lambda$. The operation is performed in the GEN state with a fixed simulation time step T. The generator model supports the operating logic of synchronous generators, nonsynchronous generators, and nonsynchronous generators with GFM inverters.

For synchronous generators, upon receiving a command message, the model gradually adjusts the current output power toward the target setpoint within the allowed ramp rate. Based on the updated power output, it recalculates the no-load frequency and derives the corresponding frequency deviation, which is then used in the frequency correction mechanism. By contrast, nonsynchronous generators without GFM inverters cannot independently regulate active or reactive power. Their operation is not directly linked to frequency control; instead, their output is retrieved from a database according to predefined generation data. Figure 9 shows the variation in daily output for the renewable energy source (nonsynchronous generator without GFM inverter) used in this model.

For the nonsynchronous generator equipped with GFM inverter, its DEVS structure representing this process is illustrated in Figure 10.

The core functionality lies in their frequency response based on a droop control mechanism, as illustrated by the droop characteristic curve in Figure 11.

Through this mechanism, nonsynchronous generators emulate the behavior of synchronous generators, thereby enabling autonomous regulation and rapid response to frequency fluctuations. Importantly, this response is governed by a local control strategy rather than external commands from the controller model. The nonsynchronous generator actively participates in establishing and stabilizing system frequency. Specifically, as shown in Equation (19):

$$\omega ={\omega }_{ref}+D_f\left(P^{\mathrm{*}}-P\right).$$

(19)

When a system frequency deviation occurs, the model calculates the corresponding active power adjustment based on the difference between the current frequency $\omega$ and the reference frequency ${\omega }_{ref}$, using a predefined droop coefficient $D_f$. This adjustment is applied to the original power $P^{\mathrm{*}}$, resulting in a new active power output set value $P$, enabling the generator to respond to supply–demand imbalances and mitigate frequency fluctuations. For reactive power, the model simplifies the behavior by maintaining constant apparent power, redistributing active and reactive power accordingly. This approach approximates a constant power factor and reduces computational complexity. At each simulation time step T, all generator models output their current power values and states, which are sent separately to the environment model and the controller model. Through these mechanisms, the generator model achieves high-fidelity simulation of physical behavior and functions as a key component in realizing the dynamic, autonomous, and coordinated control required for microgrid simulation and operation.

2.2.4. ESS Model

The ESS model simulates the operational mechanisms of a real-world battery. In practical power systems, ESS units perform charging and discharging operations in response to supply–demand imbalances, thereby enhancing stability and continuity of power supply. When load demand exceeds supply, the ESS discharges to release stored energy; conversely, it charges during periods of generation surplus.

The ESS model is defined as Equation (20):

$$ESS model= <X,Y,S{,\delta }_{ext}{,\delta }_{int},\lambda ,ta>,$$

(20)

where

X$= \left\{command msg\right\};$

$Y$=$\left\{power msg,report msg\right\}$;

S =$\left\{GEN\right\}$;

${\delta }_{ext}:\left(GEN,e,command msg\right)\to \left(GEN,T-e\right)\left[continue\right]$;

${\delta }_{int}:\left(GEN,T\right)\to \left(GEN,0\right)$;

$\lambda :\left(GEN,T\right)\to powermsg$

$\left(GEN,T\right)\to report msg;$

$\mathrm{ta}\left(\mathrm{GEN}\right) = \mathrm{T}.$

The initial state of the ESS model is GEN. In this state, if the model receives the command message containing the power instruction p_set, it calculates the future power set values and corresponding ESS capacity based on the provided active and reactive power values; subsequently, the model updates the residence time in the current state. At every interval T, the model outputs the power message and the report message and then transitions back to the GEN state, as defined by the internal transition function ${\delta }_{int}$ and the output function $\lambda .$

The DEVS structure is illustrated in Figure 12, and the model parameters are summarized in

Table 8. ESS power parameters.

Parameter	Description	Example Setting
Name	ESS name, which cannot be set as a number only.	ESS
Bus	Bus name, which must match a name listed in the bus parameter file.	bus_671
Capacity	Energy capacity, which defines the total energy storage capacity of ESS.	2 MWh
maxPower	Maximum power, which indicates the maximum charging or discharging power of ESS.	0.2 MW
minSOC	Minimum state of charge, which sets the lower SOC limit during operation (based on capacity).	20%
maxSOC	Maximum state of charge, which sets the upper SOC limit during operation (based on capacity).	90%
initSOC	Initial state of charge, which sets the initial SOC at the beginning of simulation (based on capacity).	70%
Charging	Charging efficiency, which determines the efficiency of energy stored during charging.	95%
Discharging	Discharging efficiency, which determines the efficiency of energy released during discharging.	90%

.

The ESS model executes charge and discharge operations and updates its state based on control commands from the controller model. At each simulation time step T, the model interprets the received power message and calculates the actual power output and capacity change for the next step, considering the specified power, current available capacity, and charge/discharge efficiency. If the instructed power exceeds physical limits, the model applies boundary constraints and updates the SOC accordingly. All updated results are recorded for the current step and transmitted as power and report messages to the environment and controller models, enabling interaction with other system components.

In the ESS model, the above process can be described by Equation (21):

$$P_j=\left\{\begin{array}{c}min\left(∆P_{ESS},P_j^{dis,max},E_j\left(t\right)\right) if ∆P_{ESS}>0\\ -min\left(\left|∆P_{ESS}\right.\left|,P_j^{char,max},E_j^{max}-E_j\left(t\right)\right.\right) if ∆P_{ESS}<0\\ 0 otherwise \end{array}\right.$$

(21)

When $∆P_{ESS}>0,$indicating a discharge period, the actual discharging power is determined by the minimum of the current time power difference $∆P_{ESS}$, the maximum discharging power $P_j^{dis,max}$, and the current time remaining in storage $E_j\left(t\right)$. Conversely when $∆P_{ESS}<0$, indicating charging mode, the actual charging power is determined by the minimum of the absolute value of the power difference $\left|∆P_{ESS}|\right.$, the maximum charging power $P_j^{char,max}$, and the current time remaining in storage $E_j^{max}-E_j\left(t\right)$, where $E_j^{max}$ represents the upper limit of ESS capacity.

This process ensures that ESS operations comply with physical constraints such as capacity and power limits during dynamic processes, while providing accurate and responsive support for energy management and optimal system control.

2.2.5. Load Model

The load model simulates the operational characteristics of actual loads. In practical power systems, loads consume electrical energy from the grid.

The load model is defined as Equation (22):

$$Load model=<X,Y,S,{\delta }_{ext},{\delta }_{int},\lambda ,ta>,$$

(22)

where

X$=\left\{\right\}=\varphi ;$

$Y$=$\left\{power msg\right\}$;

S =$\left\{GEN\right\}$;

${\delta }_{ext }:\varphi$;

${\delta }_{int}:\left(GEN,T\right)\to \left(GEN,T\right)$;

$\lambda : \left(GEN,T\right)\to power msg$;

$\mathit{ta} \left(\mathit{GEN}\right) = \mathit{T}$.

The DEVS structure is shown in Figure 13. The parameters of the load model are shown in

Table 9. Load model parameters.

Parameter	Description	Example Setting
Name	Load name, which cannot consist only of numbers.	Load1
Bus	Bus name, which must match a name listed in the bus parameter file.	bus_646
p_set	Active power, which represents the target active power consumption of the load.	0.065 MW
q_set	Reactive power, which represent the target reactive power consumption of the load.	0.037 MVAr
data_file	Input file, which contains time-series generation data for the load.	./param/demand.csv

. The parameters of the load power factor are shown in

Table 10. Load power factor parameters.

Name	Value
Load 1	0.869
Load 2	0.853
Load 3	0.864
Load 4	0.867
Load 5	0.905
Load 6	0.878
Load 7	0.884
Load 8	0.917
Load 9	0.830

.

The output of the load model is not influenced by command messages from the controller. Instead, it retrieves corresponding values from the database. Figure 14 illustrates the daily variation in the nine loads used in this model.

2.3. Model Implementation

All the agent models based on DEVS were implemented using PythonDEVS [25], a simulation engine capable of executing discrete-event models in Python.

Figure 15 illustrates the overall workflow of the model implementation.

Within the microgrid simulator, the controller, equipped with embedded algorithms, receives environment messages (env msg.) from the environment model and generates command messages (command msg.) based on system conditions. These commands are delivered to generators, ESS, and loads, which in turn provide feedback through power messages (power msg.) and report messages (report msg.) to the environment model and controller. The environment model is coupled with power flow analysis and frequency analysis modules to compute key operational parameters and update the system state. All simulation processes are executed on the simulation engine (Python PDEVS). Simulation parameter files in CSV format supply system configuration and time-series data inputs, which are managed by the data manager. The data manager provides simulation configuration to the microgrid simulator, collects simulation results (raw data), and converts them into visualization data. Finally, the visualizer generates graphical outputs such as active and reactive power, frequency, voltage magnitude, and SOC over time, thereby providing an intuitive representation of system dynamics.

3. Experiments

3.1. Experimental Setup

The proposed model was validated using the IEEE 13-bus system, a standardized test model widely applied in distribution network simulation and power system analysis [26]. The system consists of 13 buses interconnected through various lines and transformers. The configuration employed in this study is illustrated in Figure 16. It includes a total of 9 loads, 2 photovoltaic generators, 2 wind turbines, 1 microturbine (MT) generator, and 1 ESS. Bus 650 is designated as the slack bus and equipped with the slack generator G0, which compensates for system losses. The system investigated in this study is a medium-voltage network operating at 4.16 kV.

The specific simulation parameter settings are listed in

Table 11. Experimental parameters design.

Parameter	Contents	Type
Sim_end	Total simulation time.	1440 min
T	Simulation interval time step.	1 min
Set_frequency	System reference frequency.	60 Hz
AGCFrequency	applied when system frequency deviated from the value beyond the limit.	0.05 Hz
PAGCInterval	future power demand is forecasted to pre-adjust synchronous generator output for frequency stability.	5 min

and

Table 12. Parameters of MT and G0 generators.

Name	Nominal Power [MW]	Min Set Value [MW]	Max Set Value [MW]	Control Type	Set Value Change Rage [MW/min]
MT	0.3	0.01	0.2	PV	0.02
G0	1	0	0	Slack	-

.

3.2. Experimental Scenarios

To validate the effectiveness of the proposed model, three experimental scenarios were designed, as specified in

Table 13. Experimental scenarios and viewpoint.

Number	Scenario	Viewpoint
1	with/without ESS	To verify the flexibility in system configuration
2	with/without sudden load change	To test the effectiveness of control strategies
3	with/without GFM	To verify the effectiveness of GFM inverter

. These scenarios aim to verify the key contributions of the model.

Experiment 1 is designed to analyze the role of the ESS in mitigating generator output fluctuations and reducing frequency variations. This experiment also demonstrates the capability of the model for modular agent-based component design and its flexibility in adapting to diverse system configurations and experimental scenarios.

Experiment 2 evaluates the system’s ability to integrate and coordinate multiple control strategies, such as ESS scheduling, AGC, and PAGC. This scenario demonstrates how the proposed model captures the combined effects of these strategies on frequency regulation and power balance, thereby validating its effectiveness in simulating coordinated control mechanisms.

Experiment 3 is designed to verify the effectiveness of the GFM inverter in enhancing system frequency stability under high renewable energy penetration. This scenario further demonstrates the model’s ability to evaluate the performance of GFM inverters.

3.3. Experimental Results and Analysis

Figure 17, Figure 18 and Figure 19 and

Table 14. Experimental 1 evaluation indicators.

Evaluation Metric	1-1	1-2
Maximum frequency [Hz]	61.00	62.14
Minimum frequency [Hz]	58.26	58.35
Peak-to-peak value [Hz]	2.74	3.79
Maximum frequency deviation rate [%]	2.90	3.57
Frequency recovery time [min]	1.58	10.63

,

Table 15. Experimental 2 evaluation indicators.

Evaluation Metric	2-1	2-2
Maximum frequency [Hz]	62.14	61.00
Minimum frequency [Hz]	57.74	58.26
Peak-to-peak value [Hz]	4.40	2.74
Maximum frequency deviation rate [%]	3.77	2.90
Frequency recovery time [min]	1.73	1.58

and

Table 16. Experimental 3 evaluation indicators.

Evaluation Metric	3-1	3-2
Maximum frequency [Hz]	61.42	62.14
Minimum frequency [Hz]	58.35	58.35
Peak-to-peak value [Hz]	3.07	3.79
Maximum frequency deviation rate [%]	2.75	3.57
Frequency recovery time [min]	8.05	10.63

present the experimental results. The conclusions were derived by analyzing variations in parameters including active power, frequency, reactive power, voltage magnitude, ESS capacity, and no-load frequency. In all figures depicting active and reactive power, the legends from top to bottom correspond to the following: generator MT (blue), G0 (orange), PV_634 (green), PV_611 (red), WT_646 (purple), WT_675 (brown), ESS (pink), Loss (gray), Total power output (light green), and Load demand (light blue). The no-load frequency is used to indicate the extent to which synchronous generators optimize their adjustments within the limits of their regulating capabilities after the application of AGC and PAGC. The analysis of results focuses primarily on indicators such as maximum frequency, minimum frequency, peak-to-peak value, maximum frequency deviation rate, and frequency recovery time, defined as the period during which the frequency deviation exceeds 0.2 Hz. A brief introduction to each evaluation metric is provided below.

• Maximum frequency

The maximum frequency $f_{max}$ represents the highest frequency observed during the operation of the power system. A high frequency suggests an oversupply of power in the system. Thus, this metric helps evaluate the effectiveness of control strategies or the GFM inverter in mitigating power oversupply.

• Minimum frequency

The minimum frequency $f_{min}$ represents the lowest frequency recorded during the operation of the power system. A low frequency typically indicates an insufficient power supply or a sudden surge in load. This indicator is mainly used to assess the effectiveness of control strategies in supporting the system during load surges or sudden power shortages.

• Peak to peak value

Peak-to-peak value $f_P$ represents the difference between the maximum frequency $f_{max}$ and minimum frequency $f_{min}$ during power system operation, as defined in Equation (23). This value reflects the amplitude of frequency fluctuations; smaller values indicate lower overall variations in system frequency. Hence, it serves as an indicator of the system’s oscillatory behavior and is useful for evaluating the damping effectiveness of various control strategies or the GFM inverter.

$$f_P=f_{max}-f_{m_{i}n}$$

(23)

• Maximum frequency deviation rate

Maximum frequency deviation rate $D_{max}$ refers to the maximum relative deviation percentage of the system frequency $f\left(t\right)$ from the nominal frequency $f_{nominal}$, as defined in Equation (24). It indicates the extent of frequency deviation from the nominal frequency, with this study primarily focusing on the maximum deviation observed during operation.

$$D_{max}={\displaystyle \frac{\left|f\right(t)-f_{nominal}|}{f_{nominal}}}\times 100\mathrm{\%}$$

(24)

• Frequency recovery time

Frequency recovery time refers to the time taken for the system frequency to return within a specified threshold after exceeding it during power system operation. As shown in Equation (25), ${\overline{T}}_{rec}$ represents the average frequency recovery time, $N$ denotes the number of times the system frequency exceeds the threshold, and $t_i^{end}$ and $t_i^{\mathrm{s}tart}$ represent, respectively, the end time and start time of each frequency threshold deviation. This metric primarily reflects the dynamic response speed and regulation capability of the system.

$${\overline{T}}_{rec}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(t_i^{end}-t_i^{start}\right)$$

(25)

Specifically, during the simulation process of this study, the start time of each deviation is recorded whenever the frequency deviation exceeds the threshold. When the frequency returns to within the threshold range, the corresponding time is marked as the endpoint. The duration of each deviation is then calculated, and the average across all events is determined. This average frequency recovery time is subsequently used to evaluate the ability of the system to restore frequency stability.

Figure 17 demonstrates that in the absence of ESS, the substantial output fluctuations of synchronous generators result in pronounced frequency variations, with the frequency peak reaching approximately 62.14 Hz, thereby making frequency stability difficult to maintain. By contrast, the buffering effect of the ESS significantly reduces the frequency peak from over 62 Hz to approximately 61 Hz, thereby stabilizing the system frequency and underscoring the pivotal role of ESS in load sharing. Notably, in practical applications, ESS capacity is inherently limited.

Table 14 presents the frequency performance indicators before and after the integration of ESS. With ESS operation, the maximum frequency peak decreased by 1.14 Hz, the peak-to-peak value was reduced by 1.05 Hz, the maximum frequency deviation rate dropped by 0.67%, and the average frequency recovery time was shortened by approximately 9.05 min.

The experimental results further reveal that depletion of the ESS at 1200 min forces synchronous generators to abruptly increase output to compensate for the resulting power deficit, thereby producing observable frequency fluctuations.

This experiment verifies the critical role of ESS in maintaining frequency stability. Moreover, by enabling comparison between the two scenarios—with and without ESS—the experiment also demonstrates the capability of the model to support modular component modeling and flexible system configuration.

Figure 18 demonstrates that, at approximately 200, 400, and 800 min, sudden load increases and decreases caused abrupt changes in system power demand, resulting in significant frequency fluctuations. Nevertheless, the experimental results show that, despite multiple deviations exceeding 2 Hz, the system frequency remained stable at around 60 Hz. This finding indicates that, provided the duration of load fluctuations is relatively short and remains within the ESS capacity range, the coordinated action of ESS, AGC, and PAGC can effectively restore system frequency stability.

Table 15 presents the frequency performance indicators under conditions with and without sudden load changes. In the presence of significant load disturbances, the maximum frequency peak increased by 1.14 Hz, the peak-to-peak amplitude rose by 1.66 Hz, the maximum frequency deviation rate increased by 0.87%, and the average frequency recovery time was extended by approximately 0.15 min.

These experimental results demonstrate that the proposed model can effectively integrate generation data, load variations, and related information, and, through the coordinated operation of multiple control strategies, rapidly respond to load changes while maintaining frequency stability under fluctuating conditions. This not only verifies the value of the designed control strategies themselves but also highlights the model’s capability for comprehensive validation. In other words, the proposed model can serve as a reliable platform for evaluating the effectiveness of frequency regulation strategies.

Figure 19 demonstrates that, compared with the scenario without GFM technology, the amplitude of frequency fluctuations is reduced and the self-stabilization capability of the system is enhanced. During peak fluctuation periods, such as 600–800 min, nonsynchronous generators equipped with GFM functionality can respond rapidly to system changes and adjust their output, reducing frequency fluctuations by approximately 1 Hz compared with the non-GFM case. Therefore, when the system frequency experiences significant deviations, GFM technology strengthens inertial support by adjusting the output of non-synchronous generators, thereby mitigating short-term frequency anomalies caused by supply–demand imbalances. This reduces the frequency regulation burden on synchronous generators and improves overall system frequency stability.

Table 16 presents the frequency performance indicators before and after the application of the GFM inverter. With GFM implementation, the maximum frequency peak decreased by 0.72 Hz, the peak-to-peak amplitude was reduced by 0.72 Hz, the maximum frequency deviation rate declined by 0.82%, and the average frequency recovery time was shortened by approximately 2.58 min.

This experiment results verifies the model’s capability to assess the effectiveness of the GFM inverter in enhancing frequency regulation.

4. Conclusions

This paper proposed an agent-based microgrid model designed to address the frequency stability challenges posed by the high penetration of renewable energy sources such as solar and wind power. The model adopted a modular architecture and incorporated the DEVS, a set-theoretic mathematical formalism, to represent each agent. This framework ensured a clear and rigorous definition of model components. Within it, control strategies including ESS scheduling, AGC, PAGC, and GFM inverters were embedded into specific agent models. Simulation results demonstrated that the model accurately simulated and evaluated the effectiveness of multiple control strategies as well as GFM inverters. Furthermore, the model was adaptable to power systems of varying scales and configurations and supported simulation under diverse and complex scenarios, thereby exhibiting high flexibility and robustness. Overall, the proposed model could be regarded as a highly interpretable and reliable framework for microgrid research, well-suited to advancing power system modeling and simulation.

Despite these contributions, certain limitations remained. In the modeling process, the physical characteristics of some system components, the complexity of load fluctuations, variations in electricity market prices, and generation cost factors were simplified. These simplifications may constrain the applicability of the model to more complex and dynamic real-world scenarios. Future research will therefore proceed in two main directions. Firstly, the model will be expanded to the smart grid level, incorporating power and information exchange mechanisms among multiple microgrids to examine the impact of inter-regional coupling on system stability. Secondly, advanced methods such as reinforcement learning will be integrated to enhance the adaptability of the model in complex, uncertain, and highly dynamic environments. Through these extensions, the model is expected to demonstrate greater feasibility for practical applications and provide stronger support for the development of smart grids.