1. Introduction
The study of finding solutions to simultaneous Diophantine equations is old. Diophantus himself (∼300 AD) formulated the following problem: Find a right-angled triangle where the area added to the hypotenuse is a cube and the circumference is a square (see, e.g., [
1]). This leads to the following three simultaneous equations:
Without the modern use of coefficients and negative numbers, Diophantus arrived at a numerical solution:
Leonhard Euler (18th century) formulated two sets of three simultaneous quartic Diophantine equations (see, e.g., [
2]):
and
He ventured to determine an infinite number of integer solutions in the form of a parametric representation in two parameters. For the first set, the solution is of degree 6 in the parameters, and of degree 10 in the second set. His solution to the last set is
With the study of cubic curves in the 19th and 20th century (see, e.g., [
3,
4,
5]), new methods have been developed to solve more complex sets of simultaneous Diophantine equations (see, e.g., [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22]).
Our main source of inspiration is that John Leech in 1981 wrote the article [
23] with the remarkable title “Two Diophantine Birds With One Stone”. Indeed, he discovered a surprising method to determine an infinite number of integer solutions to the set of equations
and
where
Inspired by the papers by Leech, the main objectives of our paper are as follows:
- (a)
To determine a larger set of integer solutions to the set of equations
for
and secondly to develop a new direct method for obtaining solutions for
- (b)
To determine the requirements for integer-sided Double Crossed Ladders (see
Figure 1), and use the results from (a) to deduce the infinite number of integer-sided Double Crossed Ladders. Finally, we will use this on even more complex geometric structures.
In
Section 2 of this paper, we further develop the ideas of Leech and even point out a “hidden Diophantine bird”, which can be of independent interest. Specifically, in this paper, we shortly reiterate Leech’s solutions of (
2) in order to use his method to derive pseudo-parametric integer solutions of the following set of simultaneous Diophantine equations:
The main result of
Section 2 is formulated in Theorem 1.
In
Section 3, we describe a new method to derive the pseudo-parametric integer solutions of (
2). The main result is presented in Theorem 2.
In
Section 4, we present some new geometric applications of our results. We first introduce what we call Double Crossed Ladders (see
Figure 1), then investigate the requirement for integer solutions of all sides of it, and finally present a set of solutions in Theorem 3. Moreover, we present some more geometric structures (see
Figure 2,
Figure 3 and
Figure 4) for which our methods can be used to derive requirements for an infinite number of solutions with integer values of each side.
The last section includes some final comments and concluding remarks, and we have also included some open questions for further research.
2. New Integer Solutions of (3), the Hidden Diophantine Bird
By developing Leech’s basic idea further, we will deduce infinitely many integer solutions to (
3). In order to perform this, we first need to show Leech’s solutions to his set of equations in (
1).
Leech starts from a parametric solution to a reduced set,
namely
where
In order to complete the solution to (
1), Leech also needed to find a solution to
, which requires that
i.e.,
Solutions to (
6) can be solved by substituting
where
This leads to the requirement
where
and
Equation (
8) can be transformed into a cubic curve, which will give an infinite number of rational solutions for
f of increasing order. Each solution for
f will lead to corresponding numerical values for
a ans
b and further to
m and
n and then ultimately to
The first-order solution is
giving
Substituting these values for
in (
7) lead to
and then by substituting
in (
6) to calculate
. This will lead to an integer solution to (
1):
after eliminating common factors.
To determine solutions to (
2), Leech rewrote the basic requirement for a solution to (
1), (
5), i.e.,
to read
or factorized:
He then defined
where
, i.e.,
and
From these calculations and the fact that the integer solution to (
1) and to (
2), found by computer search, exhibits the same numeric values to the variables
and
, Leech deduced a pseudo-parametric solution to (
2):
For
, we arrive at
after eliminating common factors.
Leech’s mathematical “stone” hit “Two Diophantine Birds”, (
1) and (
2). What he missed is that his “stone”, i.e., his method, can be used to bring down even a third “Diophantine Bird”, (
3).
Computer search shows that integer solutions to (
3) also exhibits the same numerical values to the variables
and
as in both (
1) and (
2). This allows us to also deduce a new pseudo-parametric solution to (
3).
From (
9) and (
10), we can formulate the following two identities:
and
Comparing with the numerical values found by computer search and the numerical values determined for
, we see that
and
where
denotes the absolute value. From (
13), we can deduce that
This assumption proves right for the calculated numerical values of
. For generality we need to show that the symbolic expressions found for
in (
13) and (
14) lead to corresponding symbolic values for
and
Since the assumption is that
, we must require that
where
has been derived from (
4). By using the symbolic values for
from (
13), (
14), and also the relations (
10)–(
12), the requirements (
15) are confirmed. We then have proven the following:
Theorem 1.
The following pseudo-parametric representation gives integer solutions to (3):where satisfy (6) and satisfy (10). Example 1.
Below we have tabulated corresponding values for and of increasing order:and Note: In the calculated numerical solutions to (
2) and (
1) shown above, we used absolute values for
3. A New Method for Solutions to Equation (2)
A new more direct method than the one described in
Section 1 is demonstrated in the following:
The four equations in (
2) are
and
From Equation (
16), we have that
i.e.,
The complete parametric integer solution to solve this equation is given by
where
(see [
24]), leading to
For
to be a complete quadratic expression, we must have that
where
, leading to
The alternative expression
implies that
will be a common factor for
, which then can be eliminated without loss of generality. From (
17) and (
18), it follows that
From this equation we can arrive at representations for and . To separate these representations from the still undefined and , we have in the following chosen to give them separate indices, and . For generality and must be of the same degree in the variables . The alternatives and lead to a trivial solution. The other permutations of the variables all lead to the same end result.
In the following we use the fact that
leading to
We must require that
from (
19) and (
20). These two equations turn out to be identical:
For
, we arrive at
The two second-degree polynomes both lead to the same end result when they are set equal to
Note that
will lead to the same end result.
Remark 1.
The only value for that we have found that leads to integer solutions for , and d are and
For further calculation, we use the following requirement from (
21):
Solving for
a and
b, we find that
The root in Equation (
23) requires that
where
has an infinite number of integer solutions for
c and
d that can be found by using the tools for determining rational solutions to cubic curves (see [
22]). We can then calculate the corresponding values for
by inserting
in (
23). We have then proven the following.
Theorem 2.
The following pseudo-parametric representation gives integer solutions to (2):where the corresponding values for , and d can be calculated from (22). Example 2.
Below we have tabulated corresponding values of and of increasing order: Remark 2.
From (22) and (24), we can deduce the following linear requirement between the solutions to (2):We observe the striking observation that there exists such a linear connection between the solutions to (2). From the solutions to (
1) and (
3) shown in
Section 2 and to (
2), we can deduce solutions to (
1) and to (
3) expressed with the parameters
and
d. We arrive at
Then we find for (
1),
and for (
3),
4. Applications to Double Crossed Ladders and Some
Related Constructions
Some sets of Diophantine equations relate to defined geometrical structures where solutions to the equations also lead to integer-sided geometries. Cases in point are the Single Ladder Problem, the Open and Closed Ladder Problem, and the Common Hypotenuse Problem; see, e.g., [
14]. In the following, we have taken this a step further and defined more complex integer-sided geometrical structures.
In this paper we use a variation of what is called the Crossed Ladders Problem (CLP), a geometrical/mathematical problem of unknown origin; see, e.g., [
15,
16]. The original description is as follows: Two ladders of length
u and
v are leaning against opposite walls of an alley of width
x. The distance from the alley floor to where the ladders cross is
c. Determine the alley width,
x, and the heights,
y and
z, where the ladders meet the walls when
u,
v, and
c are known.
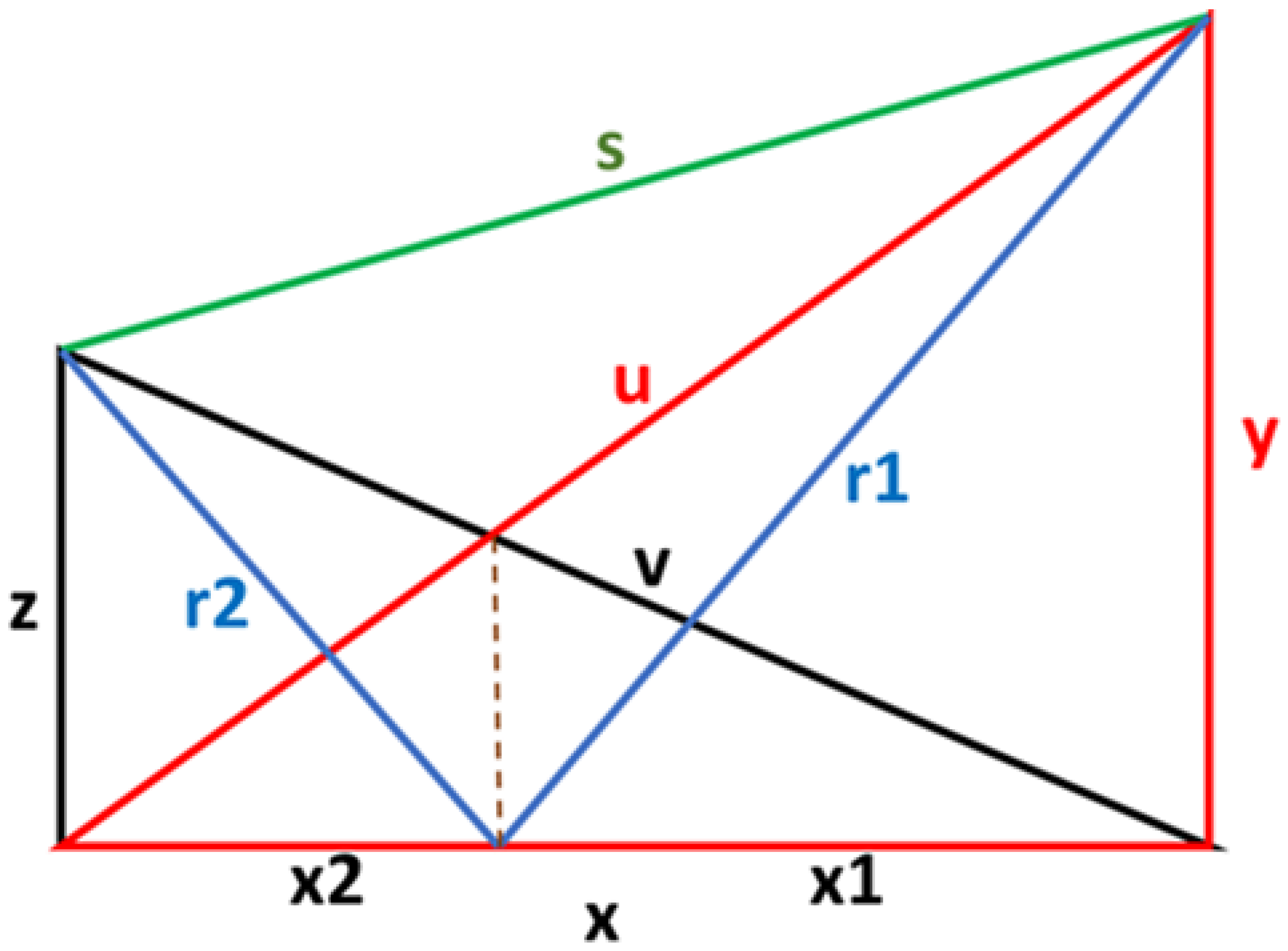
In this paper we consider a new geometric structure, namely what we have chosen to call the Double Crossed Ladder (see
Figure 1). Our objective is to determine the requirements for the sides
to be integer-valued.
Two of the requirements for integer-valued sides are integer solutions to the equations
From the geometry in
Figure 1, we can deduce that
Figure 1.
Double Crossed Ladders.
Figure 1.
Double Crossed Ladders.
When we substitute these values into Formula (
26), they transform to a single requirement:
Hence, we prove the following:
Theorem 3. The complete set of requirements for integer-sided Double Crossed Ladder is then comprised of integer solutions to the following set of equations: We recognize the set of equations for (
2). Using the demonstrated solution in (2), in particular, we can derive an infinite number of integer-sided Double Crossed Ladder. In (
25), we have calculated the integer solution to (
2). We arrive at the first-order integer-sided solution to the Double Crossed Ladders:
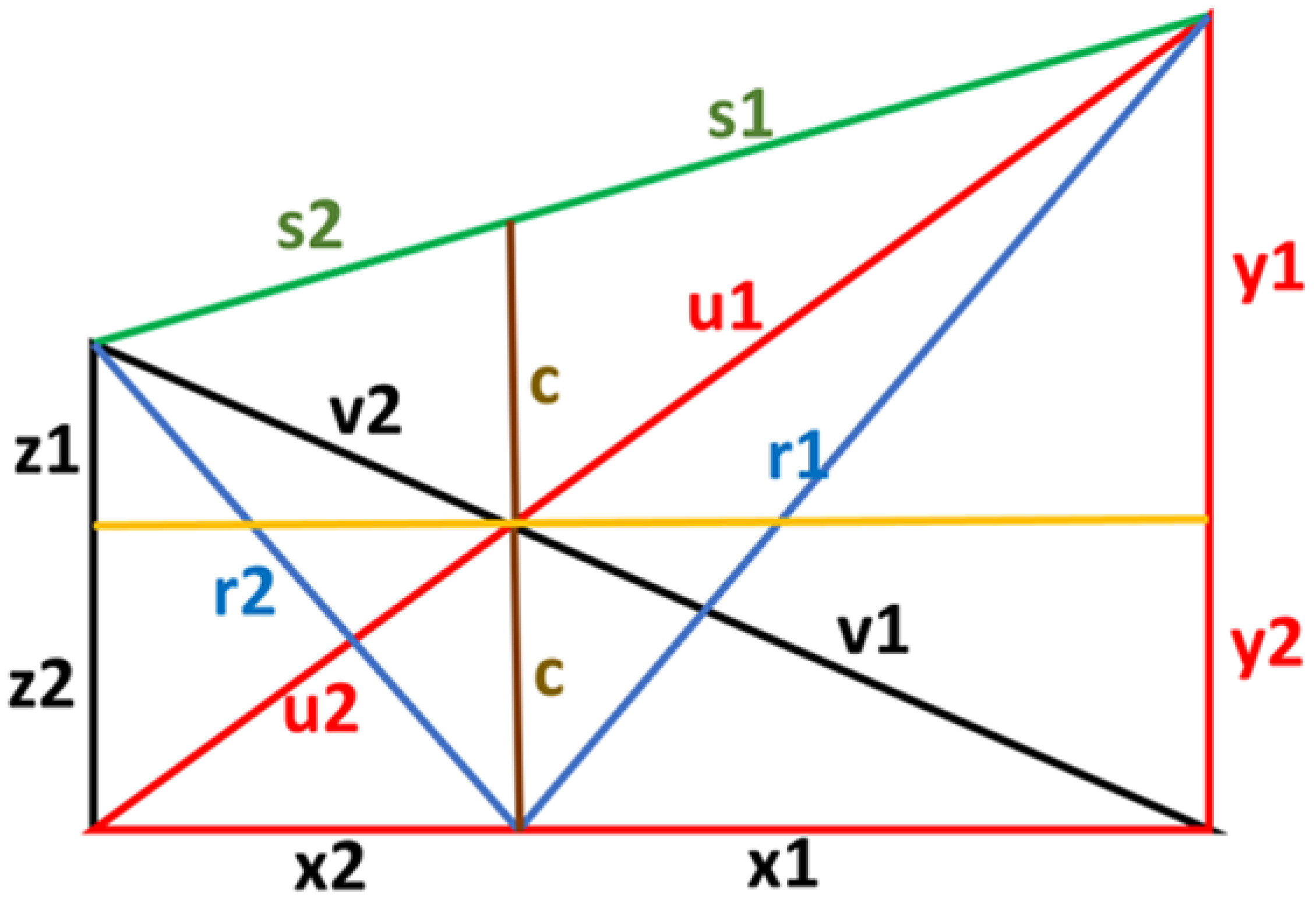
We may refine our geometric structure in several ways; see, e.g.,
Figure 2.
From this geometry, we can deduce
Figure 2.
The refined geometric structure; the detailed Double Crossed Ladder.
Figure 2.
The refined geometric structure; the detailed Double Crossed Ladder.
By using the determined values for
and scaling the calculated values in
Figure 2 with a common factor
we can determine integer solutions to all sides in
Figure 2.
Example 3.
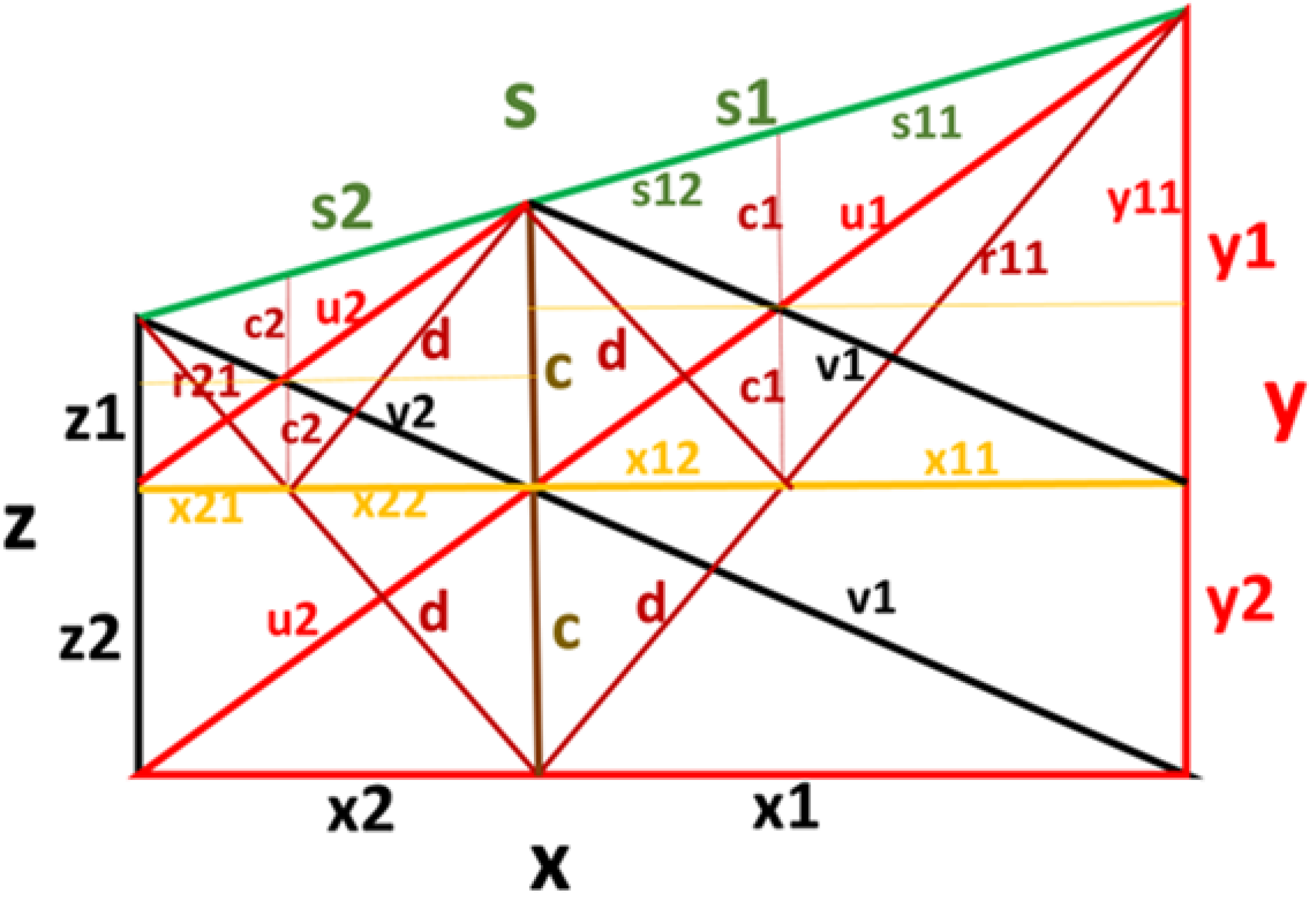
The first-order integer solution to the detailed Double Crossed Ladders is We may refine our geometrical structure even further to what we call Iterative Double Crossed Ladders; see
Figure 3.
Figure 3.
The Iterative Double Crossed Ladders.
Figure 3.
The Iterative Double Crossed Ladders.
We observe that the figures of the two smaller Crossed Ladders in the upper right and upper left corners of the structures are miniaturized versions of the original Crossed Ladders. The individual sections of the Crossed Ladders in the right upper and left corners of
Figure 3, as indicated by
, and
, can all be determined to be of the type
where the nominator is of order
We deduce that
For the sake of clarity, we have avoided marking all the sections with symbols in
Figure 3.
This implies that all the individual sections in
Figure 3 can be made an integer by scaling with a factor
From this, we can conclude that the iterative process of sectioning of the sides can be continued ad infinitum, and that by scaling with appropriate factors, all structures will obtain integer sides.
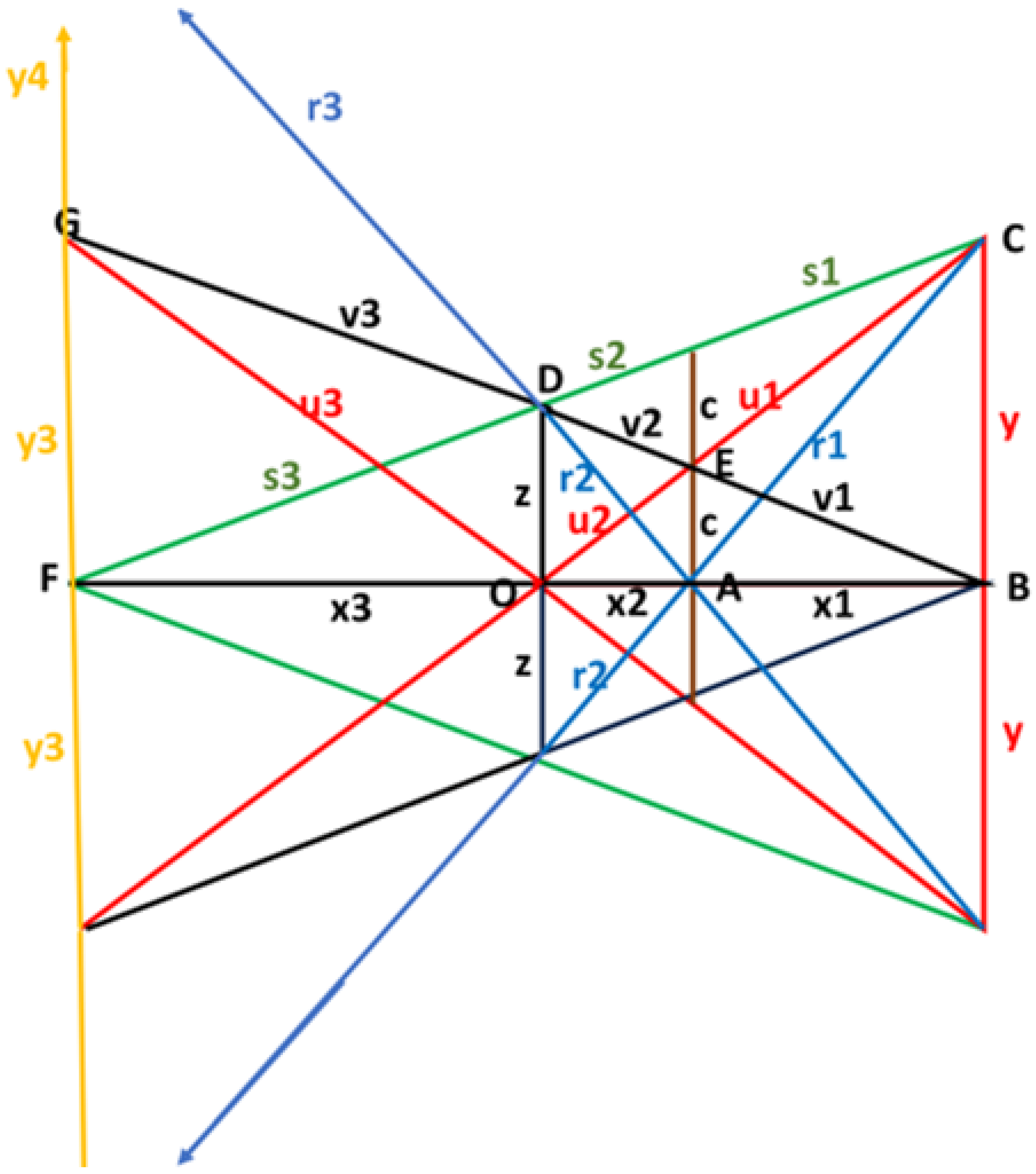
We may even expand our geometry to the following larger structure, which we call the Symmetric Double Crossed Ladders (
Figure 4).
Figure 4.
The Symmetric Double Crossed Ladders.
Figure 4.
The Symmetric Double Crossed Ladders.
We have omitted the horizontal line through point
E and other lines that would obscure visual clarity in
Figure 4.
From this structure, we can deduce that
By scaling with
we can obtain integer solutions to all sides and sections in
Figure 3 and
Figure 4.
Remark 3.
It is possible to derive an infinite number of integer solutions on the pseudo-parametric form of all sides in all of these figures, but we leave this for the reader to formulate the corresponding theorems in each case.
Remark 4.
For some basic ideas in this paper, we refer to the Ph.D. thesis of R. Høibakk [13].