Mathematical Generalization of Kolmogorov-Arnold Networks (KAN) and Their Variants

Abstract

Neural networks have become a fundamental tool for solving complex problems, from image processing and speech recognition to time series prediction and large-scale data classification. However, traditional neural architectures suffer from interpretability problems due to their opaque representations and lack of explicit interaction between linear and nonlinear transformations. To address these limitations, Kolmogorov–Arnold Networks (KAN) have emerged as a mathematically grounded approach capable of efficiently representing complex nonlinear functions. Based on the principles established by Kolmogorov and Arnold, KAN offer an alternative to traditional architectures, mitigating issues such as overfitting and lack of interpretability. Despite their solid theoretical basis, practical implementations of KAN face challenges, such as optimal function selection and computational efficiency. This paper provides a systematic review that goes beyond previous surveys by consolidating the diverse structural variants of KAN (e.g., Wavelet-KAN, Rational-KAN, MonoKAN, Physics-KAN, Linear Spline KAN, and Orthogonal Polynomial KAN) into a unified framework. In addition, we emphasize their mathematical foundations, compare their advantages and limitations, and discuss their applicability across domains. From this review, three main conclusions can be drawn: (i) spline-based KAN remain the most widely used due to their stability and simplicity, (ii) rational and wavelet-based variants provide greater expressivity but introduce numerical challenges, and (iii) emerging approaches such as Physics-KAN and automatic basis selection open promising directions for scalability and interpretability. These insights provide a benchmark for future research and practical implementations of KAN.

1. Introduction

In recent decades, neural networks have become a fundamental tool for solving complex problems, ranging from image processing and speech recognition to time series forecasting and large-scale data classification. Their ability to learn hierarchical representations and extract features from unstructured data has positioned neural networks at the core of applications in computer vision, natural language processing, and applied artificial intelligence [1,2,3,4,5]. As architectures and algorithms continue to evolve, the applicability of neural networks has expanded significantly across multiple domains.

In their standard form, neural networks employ predefined activation functions (e.g., ReLU, sigmoid) in different layers [6]. While these nonlinear functions allow networks to model complex relationships, the resulting architectures often suffer from interpretability issues due to the opaque nature of their learned representations. In particular, linear and nonlinear transformations are treated independently, without explicit interactions, making the decision process difficult to trace and explain [7]. This limitation has motivated the development of alternative architectures that balance predictive performance with interpretability.

One such alternative is the family of Kolmogorov–Arnold Networks (KAN). Rather than being a single new architecture, KAN are inspired by the celebrated Kolmogorov–Arnold representation theorem, which states that any multivariate continuous function can be represented as a finite composition of univariate continuous functions. This theoretical result provides a mathematically grounded framework for constructing neural networks where nonlinearity is distributed along edges through functional activations, instead of being concentrated in fixed activation nodes [8,9,10]. Such a formulation has been explored in diverse contexts, from solving differential equations [11] and fraud detection [12,13] to data analysis, forecasting [14,15,16,17], and real-time autonomous control systems.

Given the growing interest and rapid development of KAN-based models, there is now a fragmented body of literature that introduces a variety of structural variants, each with its own mathematical formulation, strengths, and limitations. To the best of our knowledge, no systematic review has yet consolidated these contributions. Therefore, the purpose of this article is not to propose a novel network, but to provide a comprehensive review that unifies the main structural variants of KAN, including Wavelet-KAN, Rational-KAN, MonoKAN, Physics-KAN, Linear Spline KAN, and Orthogonal Polynomial KAN. Throughout the paper, we adopt a consistent mathematical notation: input vectors are denoted as $\mathbf{x}\in {\mathbb{R}}^d$, intermediate features as $\mathbf{h}$, edge functions as $f(·)$, and outputs as $y\in {\mathbb{R}}^m$. This notation will be used to ensure clarity and uniformity in all subsequent sections.

In this context, the research aligns with the Sustainable Development Goals (SDG). It contributes to SDG 9 (Industry, Innovation and Infrastructure) by providing a rigorous, standardized synthesis of KAN variants that supports interoperable and reproducible digital infrastructures. In this way, the study not only organizes and clarifies the state of the art on KAN with unified notation and comparable criteria, but also narrows the implementation gap by proposing methodological guidelines for AI systems that are accurate, interpretable, and energy-aware.

The remainder of the paper is organized as follows: Section 2 introduces the mathematical background of the Kolmogorov–Arnold theorem and its neural interpretations. Section 3 reviews the main KAN variants in detail, highlighting their mathematical structures, advantages, and limitations. Section 4, Section 5, Section 6, Section 7, Section 8, Section 9, Section 10, Section 11, Section 12, Section 13, Section 14 and Section 15 then develop, in progressive order, families and extensions based on splines, polynomials (Chebyshev, Gram, and other orthogonal ones), wavelets, monotonicity and physical constraints, rational functions, and piecewise linear activations, addressing their formulation, advantages, limitations, and applications, and including a comprehensive comparison. The Section 16 provides a comparative discussion of these approaches, and Section 17 concludes with perspectives and open challenges for future research.

2. Methodology and Model Architecture

The following section provides a description of the Kolmogorov–Arnold Network (KAN) architecture, intended to help the reader understand how the theoretical Kolmogorov–Arnold representation theorem is implemented in practice. This construction is typically realized using spline basis functions to approximate both the inner and outer univariate functions that appear in the decomposition [8,9,10,11]. The mathematical structure and its key components are described below.

2.1. Inner Functions as Spline Expansions

The inner univariate functions ${\psi }_{q,p}\left(x_p\right)$, which act on each coordinate $x_p$ of the input vector $\mathbf{x}=(x_1,\dots ,x_n)\in {\mathbb{R}}^n$, are parameterized by univariate spline expansions. Each inner function is expressed as a linear combination of local spline basis functions:

$${\psi }_{q,p}\left(x_p\right)=\sum _{k=1}^K{a}_{q,p,k}{B}_{q,p,k}\left(x_p\right),$$

(1)

where:

• $B_{q,p,k}\left(x_p\right)$ are spline basis functions (commonly cubic B-splines) that guarantee local smoothness and piecewise continuity [12].
• $a_{q,p,k}$ are trainable coefficients controlling the contribution of each basis.
• K denotes the number of knots (partition points of the domain of $x_p$), which define local regions where different polynomial pieces apply.

Purpose: inner splines capture nonlinear relationships of each scalar input $x_p$ with localized smooth adaptations, mitigating the global oscillations typical of high-order polynomial approximations [13].

2.2. Aggregation of Inner Functions

The outputs of the inner functions are aggregated linearly to form intermediate latent features $z_q$:

$$z_q=\sum _{p=1}^n{\psi }_{q,p}\left(x_p\right),q=0,1,\dots ,2n,$$

(2)

where the index q ranges up to $2n$ in accordance with the Kolmogorov–Arnold theorem, which requires $2n+1$ outer univariate functions for the representation of any n-variate continuous function [14]. These latent features $z_q$ encode nonlinear interactions across the n input coordinates.

2.3. Outer Functions as Splines

The outer univariate functions ${\Phi }_q\left(z_q\right)$ transform the intermediate features into outputs. They are also represented via spline expansions:

$${\Phi }_q\left(z_q\right)=\sum _{m=1}^M{b}_{q,m}{C}_{q,m}\left(z_q\right),$$

(3)

where:

• $C_{q,m}\left(z_q\right)$ are spline basis functions ensuring continuity and differentiability [15].
• $b_{q,m}$ are trainable coefficients.
• M is the number of basis functions selected for each outer spline.

Purpose: these functions combine nonlinear contributions from intermediate features $z_q$, yielding the hierarchical composition required by the Kolmogorov–Arnold decomposition [16,17].

2.4. Final Model Output

The prediction of the KAN is obtained by summing all transformed features:

$$f(x_1,\dots ,x_n)=\sum _{q=0}^{2n}{\Phi }_q\left(z_q\right).$$

(4)

This output construction preserves consistency with the Kolmogorov–Arnold representation theorem while combining both localized inner contributions and global outer transformations.

2.5. Trainable Parameters and Optimization

The parameter set of the KAN consists of:

• Inner spline coefficients $a_{q,p,k}$: approximately $n·(2n+1)·K$ parameters, accounting for n inputs, $2n+1$ intermediate sums, and K spline basis functions per coordinate.
• Outer spline coefficients $b_{q,m}$: $(2n+1)·M$ parameters, with M basis functions per outer spline.

Optimization is typically performed via gradient-based algorithms (e.g., Adam), minimizing a loss such as the mean squared error over a dataset [18,19]. The inherent smoothness of splines acts as a form of implicit regularization. Explicit regularization techniques such as curvature penalization or $L_2$-norm regularization can be applied to further prevent oscillations or overfitting [20,21]. Input normalization is recommended to stabilize training, since splines are defined over compact intervals [22].

3. Mathematical Foundations of Interpolation Methods

Understanding the theoretical underpinnings of Kolmogorov–Arnold Networks (KAN) requires a solid foundation in function approximation theory, particularly the Kolmogorov–Arnold representation theorem and its implications for neural architecture design. This section outlines the mathematical principles that justify the structure of KAN, including univariate function decomposition, spline-based function construction, and the transition from traditional neural activations to more expressive basis function models. By grounding KAN in formal mathematical constructs, we establish both the theoretical motivation and the functional versatility of this class of network

3.1. Lagrange Polynomials

The Lagrange polynomial interpolates n points $(x_i,y_i)$ through a linear combination of basis polynomials:

$$P\left(x\right)=\sum _{i=1}^n{y}_i\prod _{\begin{array}{c}j=1\\ j\ne i\end{array}}^n{\displaystyle \frac{x-x_j}{x_i-x_j}}.$$

(5)

Each term ${\prod }_{j\ne i}{\displaystyle \frac{x-x_j}{x_i-x_j}}$ is a polynomial that equals 1 at $x=x_i$ and 0 at other nodes. This ensures $P\left(x_i\right)=y_i$. However, for large n, the Runge phenomenon causes extreme oscillations [23].

3.2. Bézier Curves

A Bézier curve of degree m is defined using Bernstein polynomials:

$$B\left(t\right)=\sum _{i=0}^m{P}_i\left({\displaystyle \genfrac{}{}{0pt}{}{m}{i}}\right)t^i{(1-t)}^{m-i},t\in [0,1].$$

(6)

The curve passes only through $P_0$ and $P_m$, while intermediate points ($P_1,\dots ,P_{m-1}$) act as “shape controllers”. The derivative at the endpoints depends on adjacent points:

$$B^{\prime }\left(0\right)=m(P_1-P_0),B^{\prime }\left(1\right)=m(P_m-P_{m-1}).$$

Bézier curves are widely used in computer graphics and geometric modeling due to their intuitive control and smoothness properties [24].

3.3. Piecewise Linear Interpolation

Within each interval $[x_i,x_{i+1}]$, the function is a straight line:

$$f\left(x\right)=y_i+{\displaystyle \frac{y_{i+1}-y_i}{x_{i+1}-x_i}}(x-x_i).$$

(7)

The function is continuous ($C^0$) but not differentiable at nodes. The maximum error (for $f\in C^2$) is bounded by:

$$\underset{x\in [a,b]}{max}|f\left(x\right)-S\left(x\right)|\le {\displaystyle \frac{h^2}{8}}\underset{x\in [a,b]}{max}\left|f^{″}\left(x\right)\right|,$$

where h is the maximum interval size. This method is simple and fast, although limited in smoothness [25,26].

3.4. Cubic Splines

Each segment of the cubic spline $S\left(x\right)$ in $[x_i,x_{i+1}]$ is a third-degree polynomial:

$$S_i\left(x\right)=a_i+b_i(x-x_i)+c_i{(x-x_i)}^2+d_i{(x-x_i)}^3.$$

(8)

Continuity conditions $C^2$ (function, first, and second derivatives) are enforced at nodes. For a natural spline, the tridiagonal system is solved:

$$\left\{\begin{array}{c}2c_1+c_2={\displaystyle \frac{3}{h_1}}(y_2-y_1),\hfill \\ c_{i-1}+4c_i+c_{i+1}={\displaystyle \frac{3}{h_i}}(y_{i+1}-y_i)-{\displaystyle \frac{3}{h_{i-1}}}(y_i-y_{i-1}),\hfill \\ c_{n-1}+2c_n=0.\hfill \end{array}\right.$$

(9)

Cubic splines are the foundation for many KAN variants due to their smoothness and local control properties [27,28,29,30].

3.5. Hermite Splines

Interpolates values $y_i$ and derivatives $d_i$ at each node:

$$H_i\left(x\right)=y_i+d_i(x-x_i)+\left(3{\displaystyle \frac{y_{i+1}-y_i}{h_i^2}}-{\displaystyle \frac{d_{i+1}+2d_i}{h_i}}\right){(x-x_i)}^2+\left({\displaystyle \frac{d_{i+1}+d_i}{h_i^2}}-2{\displaystyle \frac{y_{i+1}-y_i}{h_i^3}}\right){(x-x_i)}^3.$$

(10)

Continuity $C^1$ and explicit control of slopes at nodes are guaranteed, ideal for applications requiring known derivatives (e.g., trajectories with specified velocities) [30]. In order to contextualize the choice of functional bases used within Kolmogorov–Arnold Networks, it is useful to briefly review classical interpolation techniques.

Table 1. Comparison of Interpolation Methods.

Method	Advantage	Disadvantage
Lagrange	Exact at points	Instability for large n
Bézier	Intuitive shape control	Does not interpolate all points
Linear	Simplicity	Lack of smoothness ($C^0$)
Cubic Splines	$C^2$ smoothness	High computational cost
Hermite	Derivative control	Requires extra data

summarizes the main methods, highlighting their advantages and disadvantages. This comparative overview provides the mathematical background against which spline- and polynomial-based variants of KANs can be better understood.

4. Advantages of Splines in KAN

Splines, when implemented in Kolmogorov–Arnold Networks (KAN), provide mathematical and computational advantages that enhance model performance and stability. This section highlights their properties, followed by a detailed example of cubic B-splines [31,32,33].

4.1. Local Adaptability

Spline basis functions possess compact support, meaning they are non-zero only over a finite subinterval of the domain. As a result, splines can adjust their shape in specific regions without affecting distant areas. In a physiological signal modeling task, for example, a spline can adapt locally to a cardiac peak at $x\in [t_k,t_{k+4})$ while preserving stability in normal zones. Formally,

$${\psi }_{q,p}\left(x_p\right)=\sum _{k=1}^K{a}_{q,p,k}{B}_{q,p,k}\left(x_p\right),$$

where $B_{q,p,k}\left(x_p\right)$ is non-zero only in the neighborhood of the knot $t_k$ [34,35]. This property prevents overfitting at a global scale, since changes are localized.

4.2. Guaranteed Smoothness

Cubic splines ensure ${\mathcal{C}}^2$ continuity, i.e., continuity of the function and its first two derivatives. This property is crucial to avoid physically unrealistic discontinuities and to guarantee smooth gradients in the network output. For instance, in fluid dynamics simulations one requires

$${\displaystyle \frac{{\partial }^{2}S\left(x\right)}{\partial x^2}}\mathrm{continuous}\mathrm{on}[x_1,x_n],$$

which minimizes the curvature energy functional

$$E_{\mathrm{curv}}={\int }_{x_1}^{x_n}{\left[S^{″}\left(x\right)\right]}^2\mathrm{d}x,$$

a standard regularization principle in physics and approximation theory [34,35].

4.3. Computational Efficiency

Efficient recursive algorithms such as De Boor’s algorithm allow evaluation of B-splines with complexity $\mathcal{O}\left(k\right)$ per evaluation point. For cubic splines ($k=3$),

$$\mathrm{Total}\cos \mathrm{t}\propto N·k,N=\mathrm{number}\mathrm{of}\mathrm{evaluation}\mathrm{points}.$$

This is significantly more efficient than global interpolation methods such as Lagrange polynomials, which typically require $\mathcal{O}\left(n^2\right)$ operations [36,37].

4.4. Interpretability of Coefficients

The coefficients in spline expansions carry a direct geometric interpretation. For example, for an outer spline

$${\Phi }_q\left(z_q\right)=\sum _{m=1}^M{b}_{q,m}{C}_{q,m}\left(z_q\right),$$

a large magnitude of $|b_{q,m}|$ indicates a dominant influence of the basis function $C_{q,m}\left(z_q\right)$ on the output. This property enables the inspection of fitted models: coefficients can highlight overfitting, emphasize relevant regions of the input space, or identify dominant features [38].

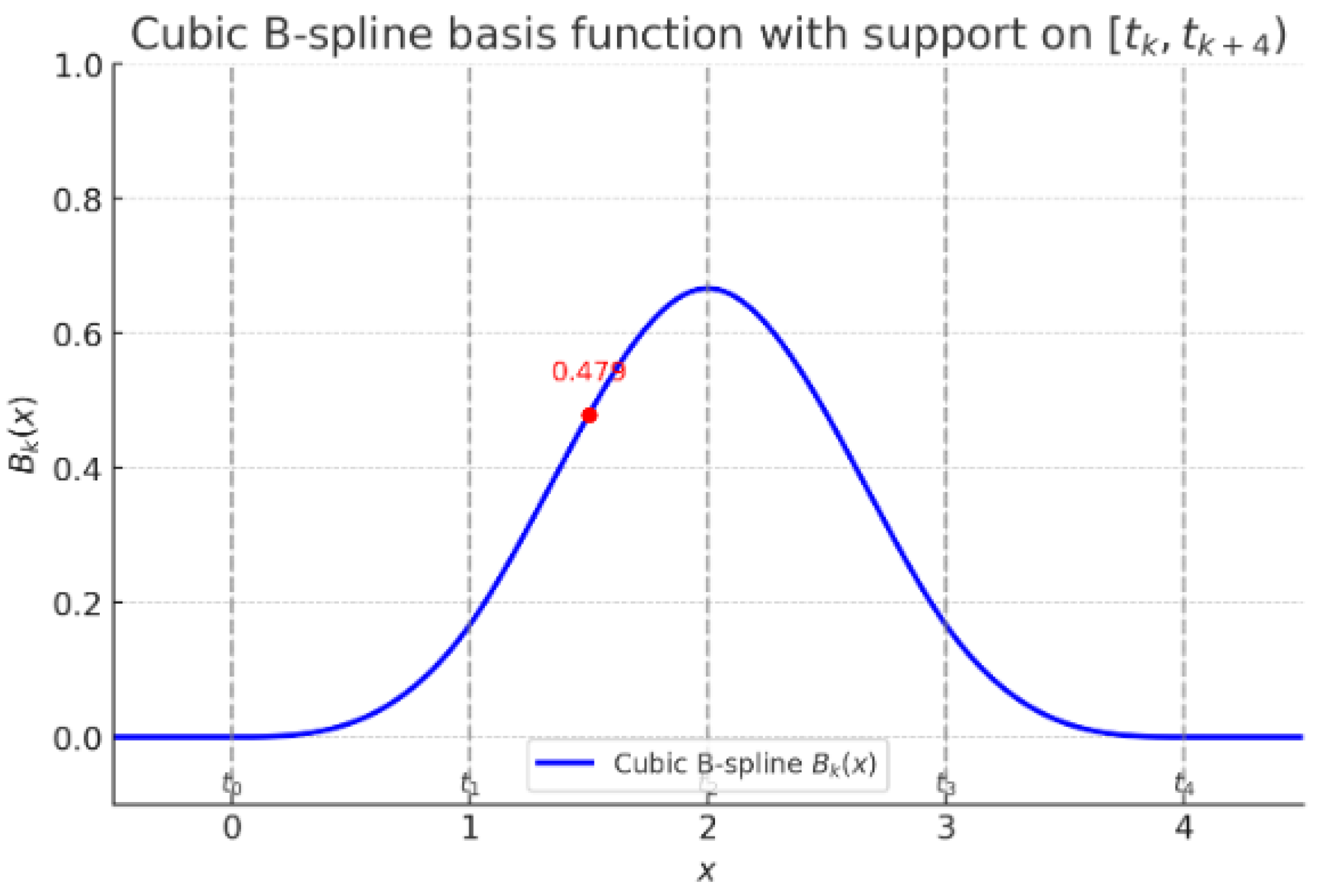
4.5. Detailed Example: Cubic B-Splines

A cubic B-spline basis function is defined piecewise over four consecutive knot intervals. Let $\left\{t_k\right\}$ be a non-decreasing sequence of knots, and $h=t_{k+1}-t_k$ the uniform knot spacing. Then

$$B_k\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{{(x-t_k)}^3}{6h^3}},\hfill & x\in [t_k,t_{k+1}),\hfill \\ {\displaystyle \frac{-3{(x-t_{k+1})}^3+3h{(x-t_{k+1})}^2+3h^2(x-t_{k+1})+h^3}{6h^3}},\hfill & x\in [t_{k+1},t_{k+2}),\hfill \\ {\displaystyle \frac{3{(x-t_{k+3})}^3-9h{(x-t_{k+3})}^2+9h^2(x-t_{k+3})}{6h^3}},\hfill & x\in [t_{k+2},t_{k+3}),\hfill \\ {\displaystyle \frac{{(t_{k+4}-x)}^3}{6h^3}},\hfill & x\in [t_{k+3},t_{k+4}),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(11)

Key properties:

• Local support: $B_k\left(x\right)$ is non-zero only on $[t_k,t_{k+4})$.
• Normalization: ${\int }_{-\infty }^{\infty }{B}_k\left(x\right)\mathrm{d}x=1$.
• Smoothness: $B_k\left(x\right)$ belongs to ${\mathcal{C}}^2$, ensuring continuity of $S\left(x\right)$, $S^{\prime }\left(x\right)$, and $S^{″}\left(x\right)$.

Numerical example: For uniform knots $t=\{0,1,2,3,4\}$ ($h=1$), evaluating $B_1\left(x\right)$ at $x=1.5$ gives

$$B_1\left(1.5\right)={\displaystyle \frac{-3{\left(0.5\right)}^3+3{\left(0.5\right)}^2+3\left(0.5\right)+1}{6}}={\displaystyle \frac{-0.375+0.75+1.5+1}{6}}\approx 0.479.$$

As shown in Figure 1, ilustrates both the locality and the normalization property of the cubic B-spline.

5. New Architectures and Applications of Kolmogorov-Arnold Networks (KAN)

Kolmogorov-Arnold Networks (KAN) represent a significant evolution in the design of machine learning architectures, combining the classical Kolmogorov-Arnold representation theorem with modern techniques of interpolation through adaptive splines [37,38,39]. These networks stand out for their ability to process dynamic and sequential data, such as financial time series or biomedical signals [37,38,40], thanks to a structure that integrates internal (${\psi }_{q,p}$) and external (${\Phi }_q$) functions in hierarchical layers. In finance, KAN are applied to market prediction, modeling nonlinearities in high-frequency data, and to option pricing, outperforming traditional methods like Black-Scholes in complex scenarios [32]. In robotics, their implementation in reinforcement learning enables autonomous control of dynamic systems, optimizing real-time decision-making [33,34], while in healthcare, they facilitate treatment personalization through the analysis of individual biological responses [35,36]. Among their key advantages are local adaptability, which adjusts parameters in specific regions without affecting the global model, and the interpretability of coefficients, which reveal contributions from critical variables [36,37]. However, they face challenges such as robustness against noise in volatile financial environments and latency in embedded hardware for real-time robotic applications [38]. Although promising, their industrial adoption requires advances in generalization through techniques like transfer learning [39], thereby solidifying their potential to revolutionize fields demanding mathematical precision and practical adaptability [41,42,43].

6. Classification of KAN Variants: Replacement of Splines with Chebyshev Polynomials

A key variant of Kolmogorov–Arnold Networks (KAN) replaces spline-based activation functions with Chebyshev polynomials, modifying both their mathematical structure and functional behavior [44,45]. In standard KAN, the inner functions ${\psi }_{q,p}\left(x_p\right)$ are defined using spline bases:

$${\psi }_{q,p}\left(x_p\right)=\sum _{k=1}^K{a}_{q,p,k}{B}_{q,p,k}\left(x_p\right),$$

where $B_{q,p,k}\left(x_p\right)$ are local basis functions supported on intervals defined by knots. In the Chebyshev variant, splines are replaced with global orthogonal polynomials:

$${\psi }_{q,p}\left(x\right)=\sum _{k=0}^K{a}_k{T}_k\left(x\right),T_k\left(x\right)=cos\left(karccos\left(x\right)\right),x\in [-1,1].$$

(12)

Chebyshev polynomials $T_k\left(x\right)$ minimize the maximum error in the $L_{\infty }$ norm, achieving near-optimal polynomial approximation with exponential convergence for smooth functions [44,46]. However, since $arccos\left(x\right)$ is undefined outside $[-1,1]$, direct use is unstable in unbounded domains.

To overcome this, a nonlinear mapping via the hyperbolic tangent compresses the domain:

$$T_k^{\mathrm{mod}}\left(x\right)=cos\left(k·\frac{\pi }{2}tanh\left(x\right)\right),$$

(13)

which ensures inputs $x\in \mathbb{R}$ are mapped into $(-1,1)$, preserving stability [45]. For instance, for $x=2$,

$$tanh\left(2\right)\approx 0.96\Rightarrow T_3^{\mathrm{mod}}\left(2\right)=cos(3·\frac{\pi }{2}·0.96)\approx -0.12,$$

whereas $T_3\left(2\right)=cos(3arccos2)$ would be undefined.

6.1. Structural Impact on KAN

Switching from local splines to global Chebyshev polynomials produces important architectural changes. Local adaptability is sacrificed, but extrapolation capabilities are enhanced [44]. Moreover, the model is simplified by removing explicit knot dependence, reducing the parameter count to the set of coefficients $\left\{a_k\right\}$.

6.2. Advantages and Disadvantages

The Chebyshev-based formulation provides several practical advantages. It offers numerical stability on bounded domains, ensures smooth extrapolation beyond the training interval, and typically requires fewer parameters compared to spline-based KAN. Furthermore, the reduced flexibility of global polynomials can help mitigate overfitting, particularly in noisy datasets [44,45]. Nevertheless, these benefits come at a cost. The replacement of local spline bases with global polynomials reduces the ability to model abrupt local variations and increases sensitivity to non-smooth or discontinuous functions. Additionally, the model is inherently restricted to bounded domains, requiring nonlinear mappings such as tanh for stability outside the canonical interval, which may introduce distortions [47]. In order to highlight the structural and functional differences introduced by replacing spline functions with Chebyshev polynomials,

Table 2. Comparison between spline-based KAN and Chebyshev-based variants.

Property	Cubic Splines (Classical KAN)	Chebyshev Polynomials ${\mathit{T}}_{\mathit{k}}\left(\mathit{x}\right)$	Modified Chebyshev ${\mathit{T}}_{\mathit{k}}^{\mathbf{mod}}\left(\mathit{x}\right)$
Support	Local (compact intervals defined by knots)	Global, restricted to $x\in [-1,1]$	Global, extended to $\mathbb{R}$ through $tanh\left(x\right)$
Adaptability	High flexibility for local variations	Limited, smooth global approximation	Smooth global approximation with domain extension
Numerical Stability	Stable under knot refinement	Unstable outside $[-1,1]$	Stable across the entire domain
Parameterization	Requires knot placement and coefficients $a_{q,p,k}$	Only polynomial coefficients $a_k$	Only polynomial coefficients $a_k$ (with nonlinear mapping)
Best suited for	Problems with abrupt local changes	Smooth functions on bounded domains	Functions requiring extrapolation or unbounded domains

provides a comparative summary. This table contrasts spline-based KAN with both the classical and the modified Chebyshev formulations, emphasizing aspects such as support, adaptability, stability, parameterization, and domains of applicability. The comparative perspective allows the reader to clearly identify the trade-offs between local flexibility and global stability, as well as the advantages of domain extension achieved through nonlinear mappings.

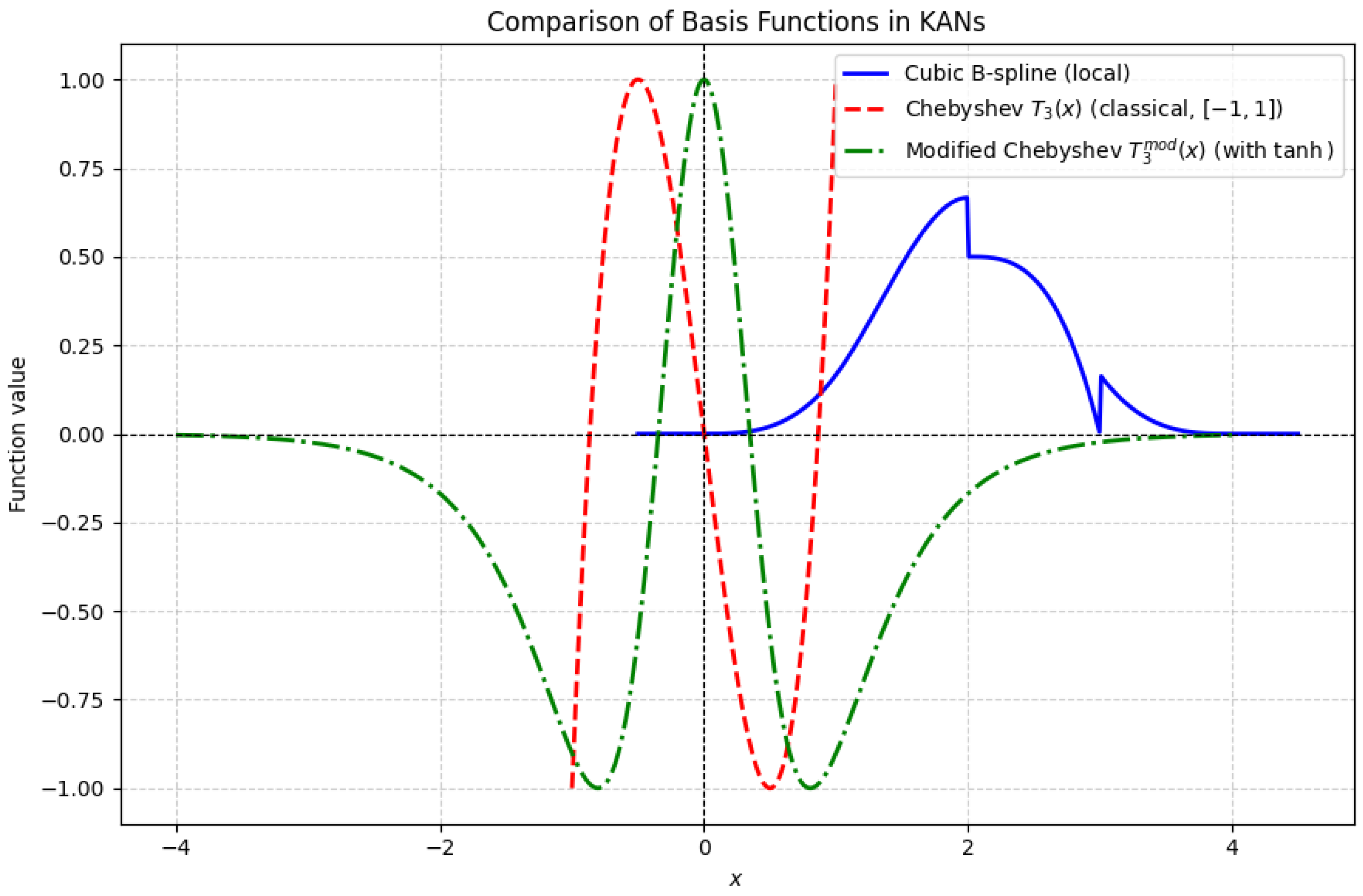
To complement the tabular analysis, Figure 2 illustrates the behavior of the basis functions employed in different KAN variants. The cubic B-spline demonstrates its local adaptability restricted to knot-defined intervals, while the classical Chebyshev polynomial $T_3\left(x\right)$ exhibits a smooth but globally constrained behavior within $[-1,1]$. In contrast, the modified Chebyshev $T_3^{\mathrm{mod}}\left(x\right)$ extends this approximation to the entire real line by incorporating a tanh mapping, ensuring numerical stability across unbounded domains. This visual comparison reinforces the analytical discussion by showing the practical consequences of choosing local versus global basis functions.

7. Classification of KAN Variants: Gram Polynomials (GKAN)

A novel variant of Kolmogorov–Arnold Networks, termed GKAN, replaces traditional spline-based activations with orthogonal Gram polynomials. This approach optimizes computational efficiency in sequential and convolutional architectures while preserving approximation flexibility [44]. In practice, GKAN address the trade-off between expressiveness and resource constraints in 1D-CNN and time-series tasks.

7.1. Structural and Mathematical Foundation

The GKAN formulation defines activations using Gram polynomials $G_i\left(x\right)$, which are orthogonal on the interval $[-1,1]$. A general activation can be written as

$$f\left(x\right)=\mathrm{SiLU}\left(x\right)+\sum _{i=1}^n{w}_i{G}_i\left(x\right),$$

(14)

where the Gram polynomials are normalized Legendre polynomials:

$$G_i\left(x\right)=\sqrt{{\displaystyle \frac{2i+1}{2}}}{P}_i\left(x\right),P_i\left(x\right)={\displaystyle \frac{1}{2^{i}i!}}{\displaystyle \frac{d^i}{d{x}^i}}{\left(x^2-1\right)}^i.$$

(15)

7.2. Mathematical Purpose

The adoption of Gram polynomials in GKAN serves three key purposes. First, they reduce computational cost, since Gram polynomials avoid the recursive constructions typical of Chebyshev or spline bases, lowering time complexity from $\mathcal{O}\left(n^2\right)$ to $\mathcal{O}\left(n\right)$. Second, they provide inherent orthogonality on $[-1,1]$, minimizing numerical instability during coefficient fitting and ensuring robustness in high-dimensional data. Third, despite being global functions, the weighted expansion $\sum w_i{G}_i\left(x\right)$ retains sufficient flexibility to approximate localized features through appropriate coefficient adaptation. This combination ensures efficient, stable, and adaptable modeling for sequential data tasks [45].

7.3. Example: Gram Polynomial Evaluation

For $i=2$ and $x=0.5$, the Gram polynomial $G_2\left(x\right)$ is obtained from the Legendre polynomial $P_2\left(x\right)=\frac{1}{2}(3x^2-1)$. Substituting yields:

$$G_2\left(0.5\right)=\sqrt{\frac{5}{2}}·\frac{1}{2}(3{\left(0.5\right)}^2-1)=\sqrt{\frac{5}{2}}·(-0.25)\approx -0.198.$$

7.4. Advantages and Disadvantages

The use of Gram polynomials in KAN presents important advantages. Their reduced computational complexity makes them particularly suitable for real-time and resource-constrained applications. The built-in orthogonality of $G_i\left(x\right)$ prevents matrix ill-conditioning and stabilizes gradient-based training, thereby improving robustness in high-dimensional tasks. However, they also exhibit limitations. Since Gram polynomials are defined on the bounded interval $[-1,1]$, scaling transformations are required for general inputs. Furthermore, they offer less local adaptability than spline bases, which can restrict their performance in modeling abrupt variations [47,48]. To highlight the structural differences between spline-based, Chebyshev-based, and Gram-based activations,

Table 3. Comparison between spline-based, Chebyshev-based, and Gram polynomial activations in KAN.

Property	Cubic Splines (Classical KAN)	Chebyshev Polynomials ${\mathit{T}}_{\mathit{k}}\left(\mathit{x}\right)$	Gram Polynomials (GKAN)
Support	Local, compact intervals defined by knots	Global, restricted to $x\in [-1,1]$ (extended via tanh)	Global, orthogonal on $[-1,1]$
Adaptability	Strong adaptability to abrupt local variations	Effective for smooth global approximations, weak for local details	Moderate flexibility, adapts via weighted combinations of global bases
Numerical Stability	Stable under knot refinement, but prone to overfitting if knots are dense	Sensitive to instability outside $[-1,1]$	High stability due to orthogonality, prevents ill-conditioning
Computational Cost	Requires recursive evaluations of spline segments	Higher complexity for large k due to trigonometric evaluations	Reduced complexity $\mathcal{O}\left(n\right)$, efficient for high-dimensional tasks
Best suited for	Piecewise-smooth functions, signals with local discontinuities	Smooth functions in bounded domains	Sequential data, real-time applications, and resource-constrained systems

presents a comparative overview. This table emphasizes how Gram polynomials balance computational efficiency and numerical stability, while contrasting with the local adaptability of splines and the global approximation of Chebyshev polynomials. The comparison clarifies the trade-offs in expressiveness, stability, and suitability for different application domains.

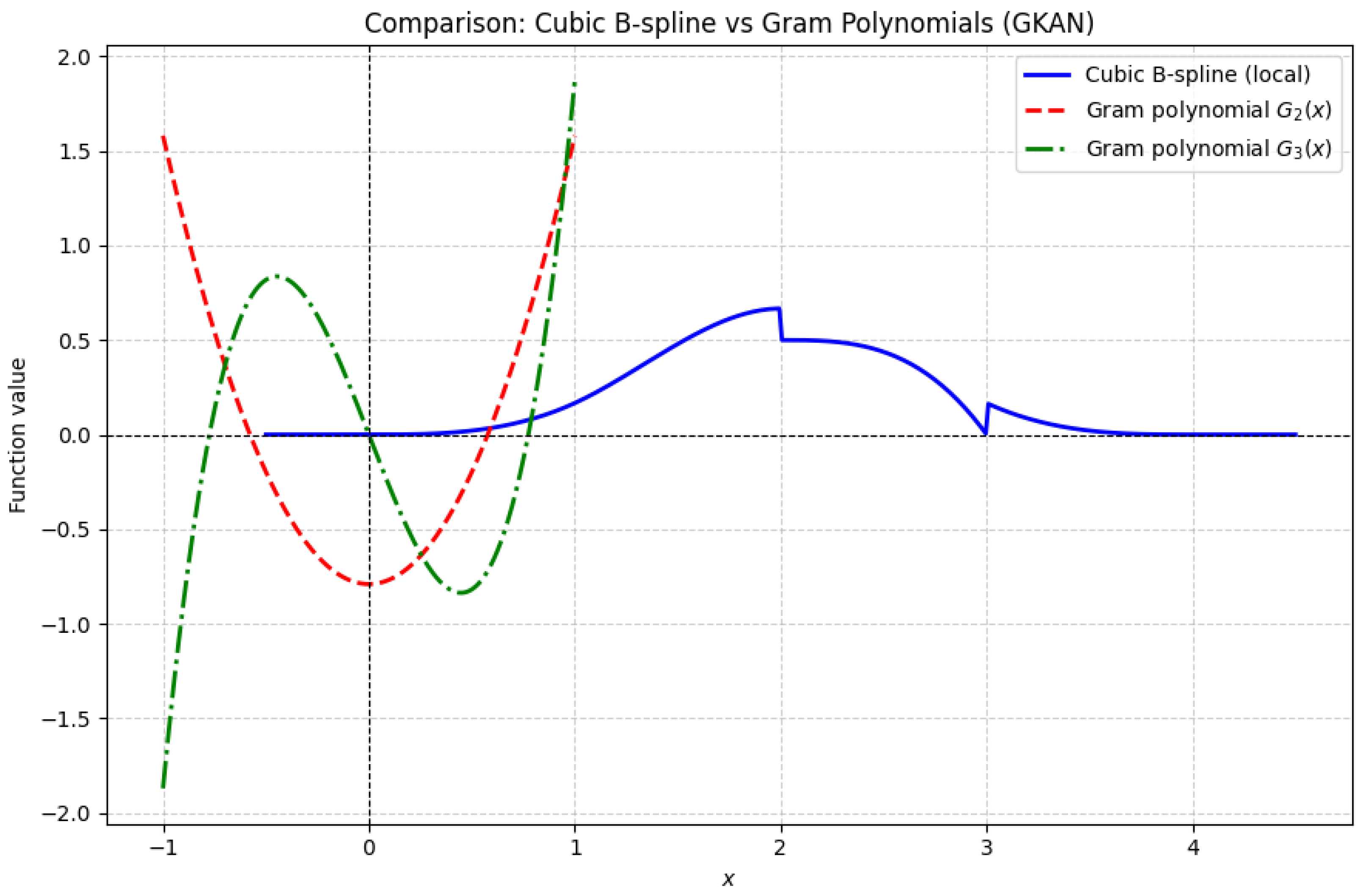
To complement the Summary table, Figure 3 illustrates the difference between a cubic B-spline and Gram polynomials of orders $G_2\left(x\right)$ and $G_3\left(x\right)$. While the spline exhibits compact local support, Gram polynomials extend globally over the interval $[-1,1]$, providing orthogonality and smooth approximation properties. This visualization reinforces the analytical discussion by contrasting local piecewise functions with global orthogonal bases.

8. Classification of KAN Variants: Wavelet-Based Activation (Wav-KAN)

The Wav-KAN variant introduces wavelet functions as replacements for splines in Kolmogorov–Arnold Networks, enabling multi-scale feature extraction essential for signals with heterogeneous frequency components, such as audio or seismic data [49,50,51]. This adaptation leverages the time-frequency localization of wavelets to simultaneously capture abrupt transitions and smooth trends within the same architecture [46].

8.1. Structural and Mathematical Foundation

In Wav-KAN, the activation functions are defined using dilated and translated wavelet bases of the form $\Psi \left(\frac{x-b_k}{a_k}\right)$, where $a_k$ denotes the scale parameter and $b_k$ the translation parameter. Both $a_k$ and $b_k$ are trainable, enabling adaptive resolution across different scales. The general expression is given by:

$${\psi }_{q,p}\left(x\right)=\sum _{k=1}^K{w}_k\Psi \left({\displaystyle \frac{x-b_k}{a_k}}\right),$$

(16)

where $\Psi \left(x\right)$ is the mother wavelet, such as Morlet or Daubechies [52,53].

8.2. Mathematical Purpose

The use of wavelets in Wav-KAN serves three purposes. First, they provide multi-scale analysis, enabling the model to capture simultaneously high-frequency details (such as edges in images) and low-frequency trends (such as seasonal components in time series) [48]. Second, they promote sparse representations, since many wavelet coefficients vanish for structured signals, which reduces feature redundancy [54]. Third, they preserve a local-global balance: locality is retained through translations $b_k$, while broader trends are modeled through hierarchical scaling with $a_k$ [55]. This combination ensures adaptability to both transient anomalies and persistent structures in non-stationary data.

8.3. Example: Morlet Wavelet Activation

For the Morlet wavelet defined as $\Psi \left(x\right)=e^{-x^2/2}cos\left(5x\right)$, the activation at $x=2.0$ with $a_k=1.0$ and $b_k=0.5$ is computed as:

$$\Psi \left({\displaystyle \frac{2.0-0.5}{1.0}}\right)=e^{-{\left(1.5\right)}^2/2}cos\left(7.5\right)\approx 0.105·0.346=0.036.$$

8.4. Advantages and Disadvantages

The incorporation of wavelets in KAN provides significant advantages. Their multi-resolution capability makes them highly effective in denoising, compression, and pattern recognition tasks, while the trainable parameters $a_k$ and $b_k$ allow adaptability to non-stationary signals. Furthermore, their compatibility with Fourier-domain optimizations facilitates integration with spectral methods [54,55]. However, these benefits are counterbalanced by notable drawbacks. Wavelet-based activations require higher computational cost due to the parameterization of scale and translation, and the performance is sensitive to the choice of mother wavelet, which may not be straightforward and often requires empirical selection [55].

To contextualize the role of wavelets within Kolmogorov–Arnold Networks,

Table 4. Comparison between spline-based, Chebyshev-based, and wavelet-based activations in KAN.

Property	Cubic Splines (Classical KAN)	Chebyshev Polynomials ${\mathit{T}}_{\mathit{k}}\left(\mathit{x}\right)$	Wavelet Functions (Wav-KAN)
Support	Local, compact intervals defined by knots	Global, restricted to $x\in [-1,1]$ (extended via tanh)	Localized but multi-scale, defined by scale $a_k$ and translation $b_k$
Adaptability	High flexibility for local variations	Effective for smooth global approximations, weak for abrupt local changes	Captures both local details and global patterns through multi-resolution
Numerical Stability	Stable under knot refinement	Unstable outside $[-1,1]$ without modification	Stable across domains but sensitive to choice of mother wavelet
Parameterization	Knot positions and coefficients $a_{q,p,k}$	Only polynomial coefficients $a_k$	Trainable scale $a_k$, translation $b_k$, and weights $w_k$
Best suited for	Piecewise-smooth functions, abrupt local changes	Smooth functions on bounded domains	Non-stationary signals, multi-resolution tasks (e.g., audio, images, seismic data)

summarizes the main differences between spline-based, Chebyshev-based, and wavelet-based activations. This comparative perspective highlights how each approach balances locality, scalability, and computational complexity, providing a clearer understanding of the trade-offs involved in replacing splines with global or multi-scale basis functions.

To complement the comparative analysis, Figure 4 illustrates the contrast between a cubic B-spline and a Morlet wavelet, which represent the fundamental bases of classical KAN and Wav-KAN, respectively. While the spline is restricted to compact local intervals defined by knots, the wavelet exhibits oscillatory behavior with exponential decay, enabling simultaneous representation of local and global structures. This visual contrast reinforces the theoretical discussion on locality versus multi-resolution adaptability.

9. Classification of KAN Variants: Monotonic Splines (MonoKAN)

The MonoKAN variant integrates Hermite cubic splines with derivative constraints to enforce monotonicity, a critical property in financial and actuarial models where functions must preserve order, such as non-decreasing mortality or credit risk curves [49,50]. This architecture ensures mathematically rigorous behavior while retaining the flexibility of spline-based representations [50].

9.1. Structural and Mathematical Foundation

MonoKAN defines its activations using Hermite splines $h_i\left(x\right)$ with positivity constraints on both the weights $w_i$ and the derivatives. The general formulation is given by

$$f\left(x\right)=\sum _{i=1}^m{h}_i\left(x\right)w_i,w_i>0,$$

(17)

where each Hermite spline on the interval $[x_0,x_1]$ takes the form

$$H\left(x\right)=a+b(x-x_0)+c{(x-x_0)}^2+d{(x-x_0)}^3.$$

(18)

Monotonicity is guaranteed by constraining the first derivative,

$$H^{\prime }\left(x\right)=b+2c(x-x_0)+3d{(x-x_0)}^2\ge 0\forall x\in [x_0,x_1],$$

(19)

ensuring that the resulting function is non-decreasing across the entire interval.

9.2. Mathematical Purpose

The design of MonoKAN fulfills three key objectives. First, it enforces monotonicity, guaranteeing that $f\left(x\right)$ never decreases, which is essential in applications such as actuarial life tables or dose-response relationships. Second, it embeds domain knowledge directly into the architecture by constraining derivatives, ensuring that risk or growth functions follow physically meaningful trends. Finally, the model improves interpretability since positive weights $w_i>0$ align with additive contributions of risk or cumulative factors [51].

9.3. Example: Hermite Spline Evaluation

For $H\left(x\right)$ on $[0,1]$ with coefficients $a=2$, $b=1$, $c=0.5$, and $d=0.2$, the evaluation at $x=0.5$ yields:

$$H\left(0.5\right)=2+1\left(0.5\right)+0.5{\left(0.5\right)}^2+0.2{\left(0.5\right)}^3=2.65,$$

with derivative

$$H^{\prime }\left(0.5\right)=1+2\left(0.5\right)\left(0.5\right)+3\left(0.2\right){\left(0.5\right)}^2=1.65\ge 0,$$

demonstrating that the monotonicity condition holds.

9.4. Advantages and Disadvantages

The use of monotonic splines in KAN provides distinct benefits. By guaranteeing order-preserving activations, MonoKAN is highly interpretable and well-suited for domains where monotonic trends are fundamental, such as finance, insurance, or medicine. The explicit derivative constraints also reduce the risk of overfitting, as the hypothesis space is restricted to non-decreasing functions. Nevertheless, this comes at the cost of reduced expressiveness compared to unconstrained splines. In addition, optimization becomes more complex, as it must account for non-negativity and monotonicity conditions that increase the difficulty of training [51]. To clarify the specific role of monotonicity constraints within Kolmogorov–Arnold Networks,

Table 5. Comparison between classical splines, Gram polynomials, and monotonic splines in KAN.

Property	Cubic Splines (Classical KAN)	Gram Polynomials (GKAN)	Monotonic Splines (MonoKAN)
Support	Local, compact intervals defined by knots	Global, orthogonal over $[-1,1]$	Local, constrained Hermite splines
Adaptability	Highly flexible, capable of modeling abrupt local changes	Moderate flexibility, controlled by polynomial weights	Restricted to non-decreasing trends, reduced local variability
Numerical Stability	Stable under knot refinement but sensitive to overfitting	High stability due to orthogonality	Stable under constraints, but optimization is more complex
Interpretability	Moderate, coefficients depend on knot placement	Limited, interpretation tied to polynomial order	High, monotonicity and positive weights align with domain knowledge
Best suited for	General-purpose function approximation, irregular signals	Sequential and high-dimensional tasks with resource constraints	Finance, actuarial science, medicine, and other monotonic processes

compares classical spline-based activations, Gram polynomial expansions, and monotonic splines. The comparison highlights how MonoKAN trades some expressiveness for interpretability and order preservation, which are essential in domains where risk, growth, or probability functions must follow monotonic patterns.

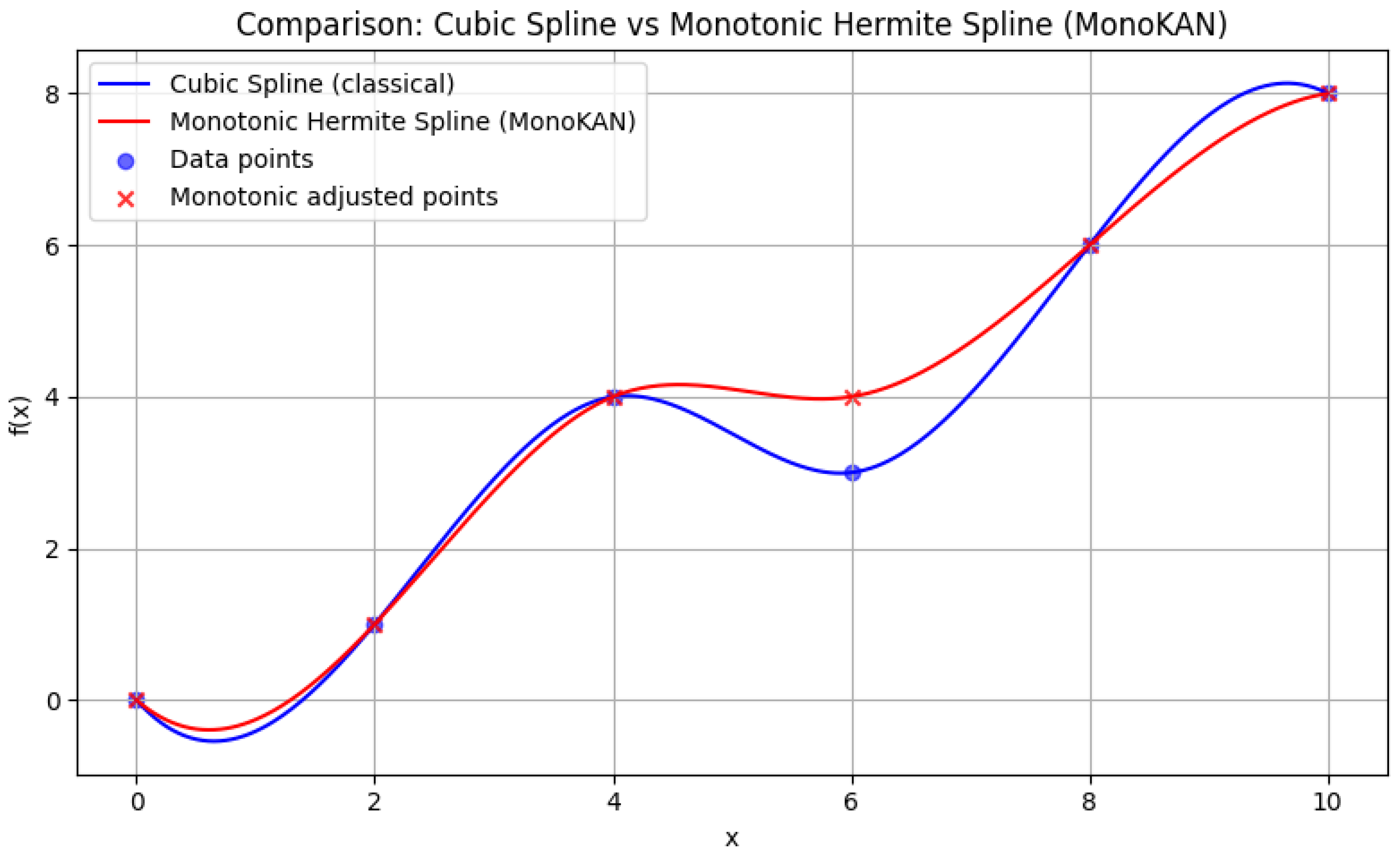
To illustrate the impact of monotonicity constraints, Figure 5 shows the difference between a standard cubic spline and a monotonic Hermite spline. While the classical spline can exhibit oscillations and local decreases, the constrained version ensures a non-decreasing trend across the entire interval, aligning the learned representation with domain requirements in finance and medicine.

10. Classification of KAN Variants: Replacement of Splines with Rational Functions

A key variant of Kolmogorov–Arnold Networks (KAN) replaces spline-based activation functions with rational functions, altering both their mathematical structure and functional behavior [54,55]. In the rational formulation, the activation is expressed as:

$${\psi }_{q,p}\left(x\right)={\displaystyle \frac{{\sum }_{i=0}^m{a}_i{x}^i}{1+{\sum }_{j=1}^n{b}_j{x}^j}},x\in \mathbb{R},$$

(20)

which provides a compact representation for functions with sharp transitions or discontinuities. Rational activations are known to achieve exponential convergence rates for smooth functions, often requiring fewer parameters than splines to reach comparable accuracy [56]. However, poles in the denominator may lead to numerical instabilities whenever $1+{\sum }_{j=1}^n{b}_j{x}^j=0$.

To mitigate this limitation, stabilized formulations introduce a constrained denominator:

$$R^{\mathrm{safe}}\left(x\right)={\displaystyle \frac{{\sum }_{i=0}^m{a}_i{x}^i}{ϵ+{\sum }_{k=1}^n{(c_{k}x+d_k)}^2}},$$

(21)

where $ϵ>0$ ensures positivity and pole-free operation via sum-of-squares parameterization [51]. This guarantees robustness even in unbounded domains. For example, with $x=2$, $c_1=1$, $d_1=0$, and $ϵ=0.1$, the safe version yields

$$R^{\mathrm{safe}}\left(2\right)={\displaystyle \frac{{\sum }_{i=0}^m{a}_i{2}^i}{4.1}},$$

whereas the unconstrained formulation would be undefined if the denominator vanished.

Structurally, the use of rational functions modifies the nature of KAN by replacing locally supported splines with globally defined functions. This substitution reduces the parameter count from $\mathcal{O}\left(K\right)$ to $\mathcal{O}(m+n)$, eliminates the dependence on knots, and introduces exponential approximation power at the cost of losing local adaptability [54].

From an applied perspective, rational-based KAN offer a compact and efficient representation of sharp gradients and discontinuities, with improved generalization capabilities when compared to spline-based KAN. Nevertheless, their main drawbacks arise from sensitivity to denominator initialization, the need for explicit pole-avoidance mechanisms, and potential overflow in high-degree polynomials [50]. In summary, Rational-KAN present a mathematically elegant alternative with strong approximation properties, but their stability must be carefully managed to ensure reliable deployment. The following

Table 6. Comparison between spline-based KAN and Rational-KAN.

Aspect	Spline-Based KAN	Rational-KAN
Locality	Local support via knots, highly adaptable to localized regions	Global representation, less flexible for abrupt local irregularities
Representation power	Polynomial-like behavior, limited for discontinuities	Exponential convergence, compact modeling of sharp gradients or discontinuities
Parameters	$\mathcal{O}\left(K\right)$, dependent on knots	$\mathcal{O}(m+n)$, independent of knots
Numerical stability	Stable under knot selection, low risk of divergence	Sensitive to denominator zeros, requires pole-avoidance mechanisms
Applications	Smooth signals, localized variability	Functions with discontinuities, rational-like behaviors, efficient for sharp transitions

summarizes the comparative aspects of Rational-based KAN with respect to spline-based KAN. It emphasizes their differences in terms of representation power, parameter efficiency, and numerical stability, highlighting both the potential benefits and the limitations that emerge from the rational formulation.

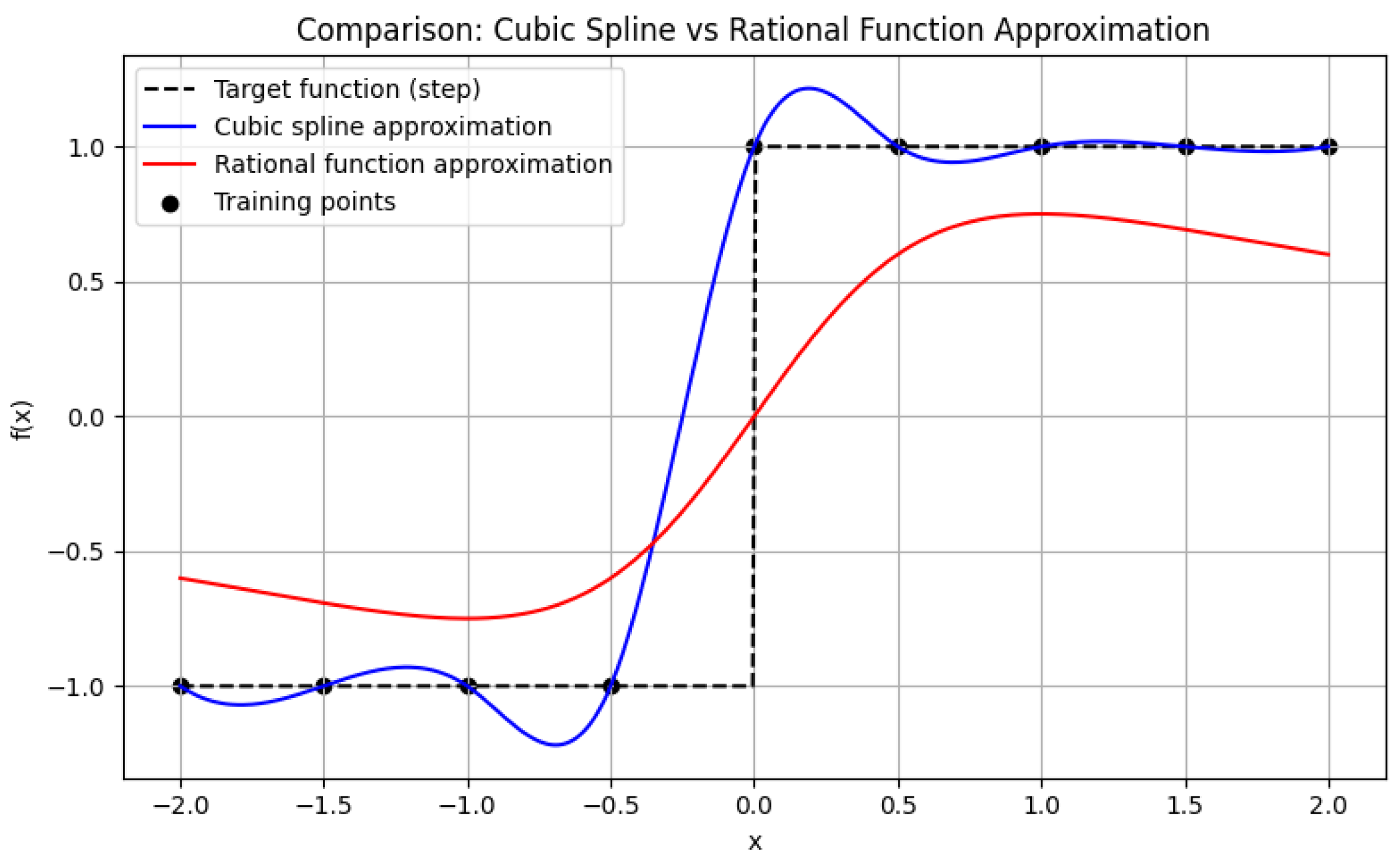
To illustrate the structural differences, Figure 6 presents a comparison between a cubic spline approximation and a rational function approximation for a target function with a sharp discontinuity. While splines struggle to capture the abrupt transition without oscillations, the rational formulation achieves a more compact and accurate fit with fewer parameters.

11. Classification of KAN Variants: Physics-Constrained Splines

A key variant of Kolmogorov–Arnold Networks (KAN) augments spline-based activation functions with physics-informed constraints, fundamentally altering their optimization behavior while retaining their core mathematical structure [50,51]. In this formulation, the spline functions ${\psi }_{q,p}\left(x\right)$ are optimized under residual conditions derived from partial differential equations (PDEs), ensuring that the model is not only data-driven but also physically consistent [35]. Mathematically, this corresponds to

$${\psi }_{q,p}\left(x\right)=\sum _{k=1}^K{a}_{q,p,k}{B}_{q,p,k}\left(x_p\right){|}_{\mathcal{P}\psi =0},\mathcal{P}\psi =\sum _i{\lambda }_i{\mathcal{N}}_i\left[\psi \right],$$

(22)

where ${\mathcal{N}}_i[·]$ represent differential operators encoding conservation laws and ${\lambda }_i$ act as Lagrange multipliers. While this mechanism enhances interpretability, it also introduces computational challenges, as direct PDE enforcement may destabilize the optimization when residual terms become dominant [50].

To stabilize training, a differentiable physics loss is employed:

$${\mathcal{L}}_{\mathrm{phy}}\left(\psi \right)={\mathbb{E}}_{x\sim \Omega }\left[{∥\mathcal{N}\left[\psi \right]\left(x\right)∥}^2\right]+\alpha {\mathbb{E}}_{x\in \partial \Omega }\left[{∥\mathcal{B}\left[\psi \right]\left(x\right)∥}^2\right],$$

(23)

which acts as a regularizer and is optimized simultaneously with the data fidelity term. For example, in the case of Burgers’ equation $\mathcal{N}\left[u\right]=u_t+u{u}_x-\nu u_{xx}$, the physics loss enforces the PDE dynamics while boundary terms preserve conditions on the spatial domain [56]. This formulation aligns Physics-KAN with the broader family of Physics-Informed Neural Networks (PINNs), while maintaining spline-based flexibility.

From a structural perspective, Physics-KAN retain the locality of spline bases while reducing the dimensionality of the solution space through physics regularization. This integration enables training with significantly fewer labeled data points, improving extrapolation in unobserved domains and ensuring that predictions remain consistent with physical laws. Nevertheless, the approach comes with limitations: training incurs computational overhead due to PDE residual evaluations, convergence becomes sensitive to the weighting factor $\alpha$, and the framework assumes access to differentiable physical models. Overall, Physics-KAN provide a promising balance between physical interpretability and data efficiency, albeit with increased training complexity. The following

Table 7. Comparison between spline-based KAN and Physics-KAN.

Aspect	Spline-Based KAN	Physics-KAN
Locality	Local support of spline bases	Local support preserved, but constrained by PDEs
Representation power	Flexible for arbitrary nonlinear mappings	Constrained to physically consistent solutions, enhancing interpretability
Data requirements	High, requires dense labeled data	Reduced by up to 80% due to physics regularization
Numerical stability	Stable optimization but unconstrained behavior	Sensitive to PDE residuals and loss weighting
Applications	Generic machine learning tasks	Modeling governed by physical laws (e.g., fluid dynamics, material science)

presents a comparative summary between traditional spline-based KAN and Physics-KAN. The goal is to highlight the added value of embedding physics-informed regularization, focusing on representation, generalization, and computational challenges.

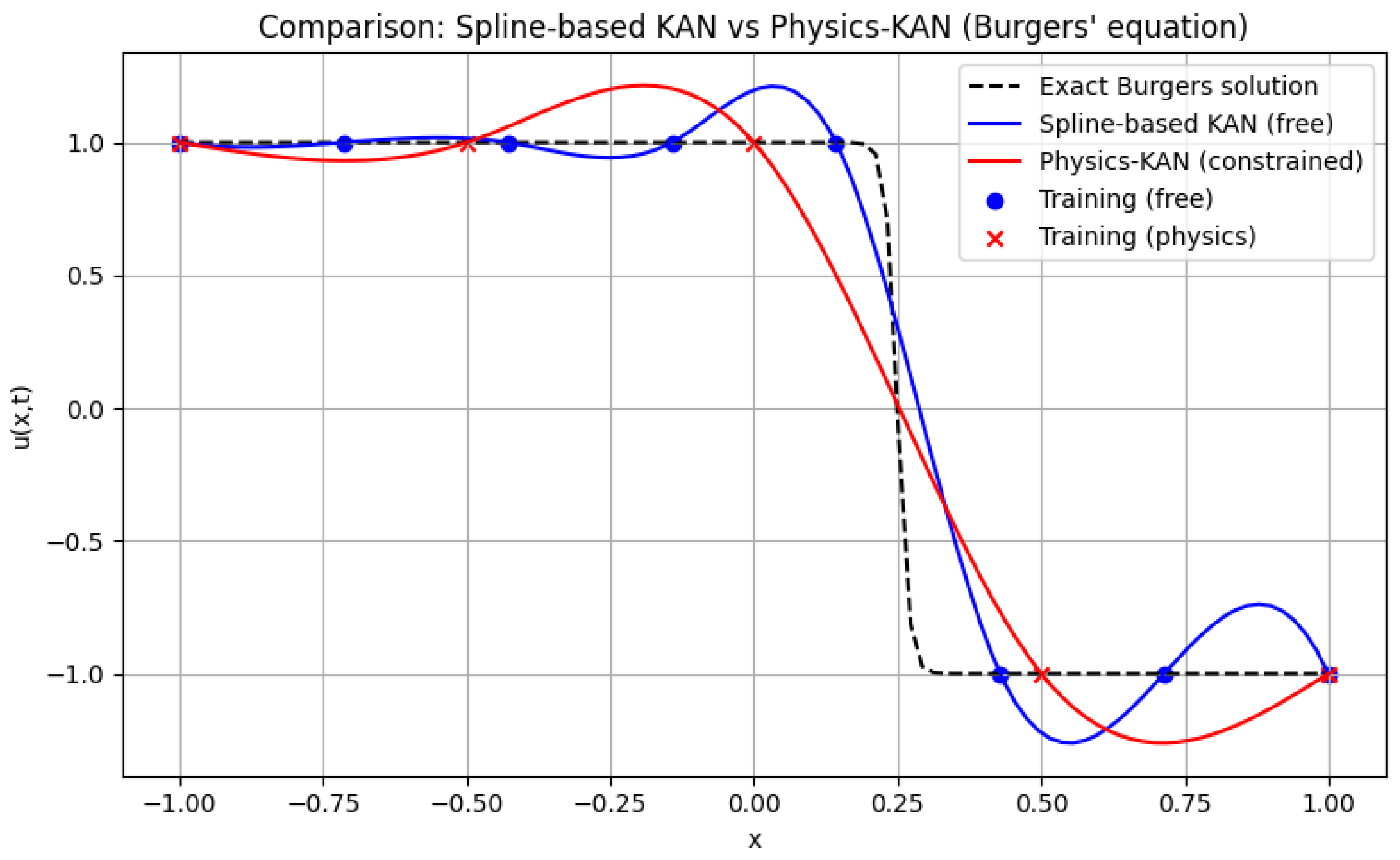
To visually demonstrate the effect of physics-informed constraints, Figure 7 shows a comparison of spline-based and physics-constrained approximations for Burgers’ equation. The physics-regularized model enforces smoothness and adherence to PDE dynamics, while the unconstrained spline model deviates significantly in regions without data. To illustrate the practical effect of embedding physics constraints into Kolmogorov–Arnold Networks, we consider the one-dimensional Burgers’ equation, a canonical benchmark in computational fluid dynamics. Burgers’ equation is widely employed to test numerical schemes and physics-informed models because it combines nonlinear convection with diffusion effects, acting as a simplified prototype of the Navier–Stokes equations. Its form is given by:

$$u_t+u{u}_x-\nu u_{xx}=0,x\in [-1,1],t\in [0,T],$$

(24)

where $u(x,t)$ denotes the velocity field, and $\nu >0$ is the viscosity parameter.

This PDE is particularly relevant for Physics-KAN, as it highlights the importance of enforcing physical consistency when modeling dynamical systems with sharp gradients or shock-like structures. By comparing a spline-based KAN without constraints to a Physics-KAN regularized through the physics loss ${\mathcal{L}}_{\mathrm{phy}}$, it is possible to visualize how physical constraints improve the model’s extrapolation and stability beyond the training points.

12. Classification of KAN Variants: Linear Spline Activation Functions

A key variant of Kolmogorov–Arnold Networks (KAN) simplifies the spline-based activation functions by employing linear splines, prioritizing computational efficiency while retaining adequate expressivity [52,53]. In this formulation, the basis functions are no longer high-order cubic splines but instead piecewise linear functions, often represented as triangular “hat” functions:

$${\psi }_{q,p}\left(x\right)=\sum _{k=1}^K{c}_{k}max\left(1-{\displaystyle \frac{|x-t_k|}{h}},0\right),$$

(25)

where $t_k$ are equally spaced knots with spacing h. Linear splines provide only $C^0$ continuity, which implies exact reconstruction of piecewise linear functions with $\mathcal{O}(1/h)$ convergence rate [57], but lower approximation accuracy for smooth targets compared to cubic splines.

To further enhance efficiency and avoid unnecessary oscillations, a sparse derivative regularization is commonly applied:

$$\mathcal{R}\left(\mathbf{c}\right)=\lambda \sum _{k=2}^{K-1}|c_{k+1}-2c_k+c_{k-1}|,$$

(26)

which penalizes large second differences, promoting nearly linear regions. For example, with knots $t=[0,1,2]$ and coefficients $c=[0.5,1.2,0.8]$, the evaluation at $x=1.5$ yields

$$\psi \left(1.5\right)=1.2·max(0,0.5)+0.8·max(0,0.5)=0.6+0.4=1.0,$$

whereas a cubic spline implementation would require solving a tridiagonal system of equations.

Structurally, Linear-KAN introduce a significant simplification compared to cubic spline KAN [53]. The computational complexity per activation decreases from $\mathcal{O}\left(K^3\right)$ to $\mathcal{O}\left(K\right)$, enabling faster training and inference and allowing exact gradient computation. The parameter space also becomes more interpretable, shifting from abstract control points $a_k$ to direct function values $c_k$ at the knots. In practical terms, Linear-KAN offer 3–5x faster convergence and are natively compatible with gradient-based optimization methods. However, this comes at the cost of reduced expressivity: while they can represent piecewise linear functions exactly, they lack the smoothness of higher-order splines, requiring denser knots to achieve comparable accuracy and limiting their ability to model $C^2$-continuous phenomena. The trade-offs between cubic spline-based KAN and Linear-KAN are summarized in

Table 8. Comparison between cubic spline-based KAN and Linear-KAN.

Aspect	Cubic Spline-Based KAN	Linear-KAN
Continuity	$C^2$ continuity, smooth derivatives	$C^0$ continuity, only piecewise linear
Representation power	High, efficient for smooth targets	Limited, requires dense knots for precision
Parameters	Control points $a_k$ (indirect)	Direct function values $c_k$ at knots
Computational cost	$\mathcal{O}\left(K^3\right)$ due to tridiagonal solves	$\mathcal{O}\left(K\right)$, fast evaluation
Applications	Complex signals with smooth structures	Real-time tasks, resource-constrained environments

, emphasizing the balance between computational efficiency and approximation accuracy.

To visually illustrate the effect of simplifying spline activations, Figure 8 compares a cubic spline approximation and a linear spline approximation of a smooth function. While the cubic spline provides a smooth curve with continuous derivatives, the linear spline captures only piecewise linear trends, requiring a higher density of knots to achieve a similar level of accuracy.

13. Classification of KAN Variants: Orthogonal Polynomial Activations

A key variant of Kolmogorov-Arnold Networks (KAN) replaces spline-based activation functions with orthogonal polynomial bases, enhancing approximation power for smooth functions while maintaining numerical stability [52,53]. Originally, the internal functions ${\psi }_{q,p}\left(x\right)$ in standard KAN are defined using splines (e.g., cubic B-splines):

$${\psi }_{q,p}\left(x\right)=\sum _{k=1}^K{a}_{q,p,k}{B}_{q,p,k}\left(x_p\right),$$

where $B_{q,p,k}\left(x_p\right)$ are local basis functions with support on specific intervals. In the orthogonal polynomial variant, these functions are replaced by:

$${\psi }_{q,p}\left(x\right)=\underset{\mathrm{Orthogonal}\mathrm{activation}}{\underbrace{\sum _{k=0}^K{w}_k{\varphi }_k\left(\xi \right)}},\xi =\underset{\mathrm{Domain}\mathrm{normalization}}{\underbrace{{\displaystyle \frac{2(x-a)}{b-a}}-1}},$$

(27)

where ${\varphi }_k$ are orthogonal polynomials (e.g., Legendre, Hermite) satisfying $\int {\varphi }_i{\varphi }_{j}d\mu ={\delta }_{ij}$ [57]. Legendre polynomials $P_k\left(\xi \right)$ are optimal for bounded domains $x\in [a,b]$, while Hermite polynomials $H_k\left(\xi \right)$ suit unbounded domains. However, raw polynomials exhibit Runge’s phenomenon near domain boundaries [58].

To mitigate this limitation, a spectral reprojection technique is applied:

$${\psi }_{q,p}^{\mathrm{opt}}\left(x\right)=\sum _{k=0}^K{w}_k\underset{\mathrm{Reprojected}\mathrm{basis}}{\underbrace{\mathcal{T}\left({\varphi }_k\left(\xi \right)\right)}},$$

(28)

where $\mathcal{T}(·)$ is a bounded transformation mapping to $[-1,1]$. For example, for Legendre polynomials with $x=0.5$ in $[0,1]$:

$$\xi =2\left(0.5\right)-1=0,\psi \left(0.5\right)=w_0{P}_0\left(0\right)+w_1{P}_1\left(0\right)=w_0-0.5w_1,$$

whereas spline-based KAN would require multiple local evaluations to approximate the same point.

13.1. Structural Impact on KAN

KAN undergo fundamental changes when replacing local splines with global orthogonal polynomials. This transition enables spectral accuracy for analytic functions but sacrifices locality [59]. Additionally, domain normalization $\xi \left(x\right)$ becomes critical, requiring a priori knowledge of input bounds, which may not always be available in real-world data.

13.2. Advantages and Disadvantages

The main advantages of this approach lie in its ability to achieve exponential convergence for smooth and analytic functions, which significantly improves approximation accuracy compared to spline-based models [60]. Moreover, the recurrence relations of orthogonal polynomials provide an efficient and stable way to compute derivatives, making them especially useful in applications involving partial differential equations. Another major benefit is their inherent orthogonality, which avoids ill-conditioning in the coefficient matrices and ensures numerical stability even for high-order expansions [58].

On the other hand, orthogonal polynomial activations also introduce significant drawbacks. They are highly sensitive to discontinuities, which often produce Gibbs oscillations near sharp transitions or non-smooth regions [60]. Furthermore, their performance depends strongly on the scaling of the input domain: a poor choice of $[a,b]$ may lead to numerical instabilities or poor generalization [61]. Finally, unlike splines, which adapt locally, orthogonal polynomials lack locality, making them less effective in representing piecewise-smooth functions or data with abrupt variations [60].

A comparative analysis between spline-based activations and orthogonal polynomial activations in KAN is summarized in

Table 9. Comparison between spline-based and orthogonal polynomial activations in KAN.

Property	Splines (e.g., Cubic)	Orthogonal Polynomials (Legendre, Hermite)
Locality	Local support; changes affect only nearby regions.	Global support; a change in one coefficient affects the entire domain.
Approximation Power	High accuracy for piecewise-smooth functions; limited for highly smooth global functions.	Exponential convergence for smooth/analytic functions; poor at modeling discontinuities.
Computational Efficiency	Requires solving local systems (e.g., tridiagonal for cubic splines).	Efficient recurrence relations for evaluation and differentiation.
Numerical Stability	Stable under local modifications; well-suited for irregular domains.	Orthogonality ensures conditioning, but sensitive to domain scaling and boundary effects.

. This table highlights their differences in terms of locality, approximation power, computational efficiency, and numerical stability, providing a clear overview of the trade-offs inherent to each approach.

To further illustrate the differences between spline-based and orthogonal polynomial activations, Figure 9 compares a cubic spline interpolation and a Legendre polynomial approximation on the same function. While splines provide localized adaptation to the data, orthogonal polynomials achieve global smoothness but exhibit oscillations near domain boundaries.

14. Classification of KAN Variants: Wavelet-Based Activation Functions

A relevant variant of Kolmogorov-Arnold Networks (KAN) replaces spline-based activation functions with wavelet bases, providing multi-resolution analysis and adaptive feature extraction [60]. Originally, the internal functions ${\psi }_{q,p}\left(x\right)$ in standard KAN are defined using splines (e.g., cubic B-splines):

$${\psi }_{q,p}\left(x\right)=\sum _{k=1}^K{a}_{q,p,k}{B}_{q,p,k}\left(x_p\right),$$

where $B_{q,p,k}\left(x_p\right)$ are local basis functions with support on specific intervals. In the wavelet variant, these functions are replaced by dilated-translated wavelets:

$${\psi }_{q,p}\left(x\right)=\underset{\mathrm{Multi}-\mathrm{resolution}\mathrm{activation}}{\underbrace{\sum _{j\in \mathbb{Z}}\sum _{m\in \mathbb{Z}}{c}_{j,m}\underset{\mathrm{Child}\mathrm{wavelet}}{\underbrace{\psi \left(2^{j}x-m\right)}}}},$$

(29)

where $\psi$ is a mother wavelet (e.g., Mexican Hat, Daubechies) satisfying $\int \psi dx=0$. Wavelets provide simultaneous localization in space and frequency domains: fine-scale wavelets ($j\gg 0$) capture high-frequency details (edges, anomalies), while coarse scales ($j\ll 0$) model global trends (smooth patterns). This property makes Wav-KAN particularly useful in applications such as audio signal denoising, seismic analysis, or image compression.

Since infinite sums over $j,m$ are computationally infeasible, a dyadic truncation with adaptive scale selection is introduced [61]:

$${\psi }_{q,p}^{\mathrm{adapt}}\left(x\right)=\sum _{j=j_{min}}^{j_{max}}{w}_j\underset{\mathrm{Resolution}\mathrm{level}j}{\underbrace{\sum _m{c}_{j,m}\psi (2^{j}x-m)}},$$

(30)

where the set of scales j is optimized during training. For example, with Mexican Hat wavelet $\psi \left(x\right)=(1-x^2)e^{-x^2/2}$ at $x=0.7$:

$$\psi (2^1·0.7-0)=(1-{\left(1.4\right)}^2)e^{-{\left(1.4\right)}^2/2}\approx (1-1.96)e^{-0.98}\approx -0.36,$$

whereas splines would require multiple local basis evaluations to capture similar oscillatory behavior.

Structural Impact on KAN

KAN gain multi-resolution capabilities when replacing splines with wavelets [62]. This transition enables hierarchical feature learning but sacrifices continuity guarantees. Additionally, each activation function becomes equivalent to a mini-wavelet transform, with parameters $\{c_{j,m},w_j\}$ optimized end-to-end.

In practice, wavelet-based KAN outperform splines in tasks requiring both local and global representation, such as biomedical imaging or transient signal analysis. However, they exhibit higher computational cost and strong dependence on the choice of the mother wavelet, which may affect generalization across datasets.

Advantages and disadvantages: The main advantages of Wav-KAN include the simultaneous capture of local and global features, natural denoising through scale thresholding, and compact representation of singularities [60]. On the other hand, their disadvantages involve higher computational requirements, sensitivity to the choice of the mother wavelet, and the appearance of boundary artifacts in finite domains [61]. To provide a clearer view of the trade-offs introduced by Wav-KAN,

Table 10. Comparison between spline-based KAN and wavelet-based KAN (Wav-KAN).

Aspect	Spline-Based KAN	Wavelet-Based KAN (Wav-KAN)
Basis functions	Piecewise polynomials (local cubic splines).	Dilated-translated wavelets (e.g., Mexican Hat, Daubechies).
Localization	Local support, each spline affects only its interval.	Time-frequency localization, capturing both local and global features.
Continuity	Guarantees $C^2$ smoothness for cubic splines.	Continuity not guaranteed, depends on mother wavelet properties.
Computational cost	$\mathcal{O}\left(K\right)$ per evaluation (efficient).	Higher cost due to multi-resolution decomposition and scaling.
Adaptability	Good for smooth local variations.	Captures abrupt transients, oscillations, and global patterns simultaneously.
Main advantages	Stable, interpretable, low computational cost.	Multi-resolution analysis, denoising capabilities, compact singularity representation.
Main disadvantages	Limited in oscillatory or non-stationary signals.	Sensitive to wavelet choice, boundary artifacts, higher cost.

summarizes its main structural differences compared to spline-based activations. This highlights the balance between multi-resolution adaptability and computational complexity.

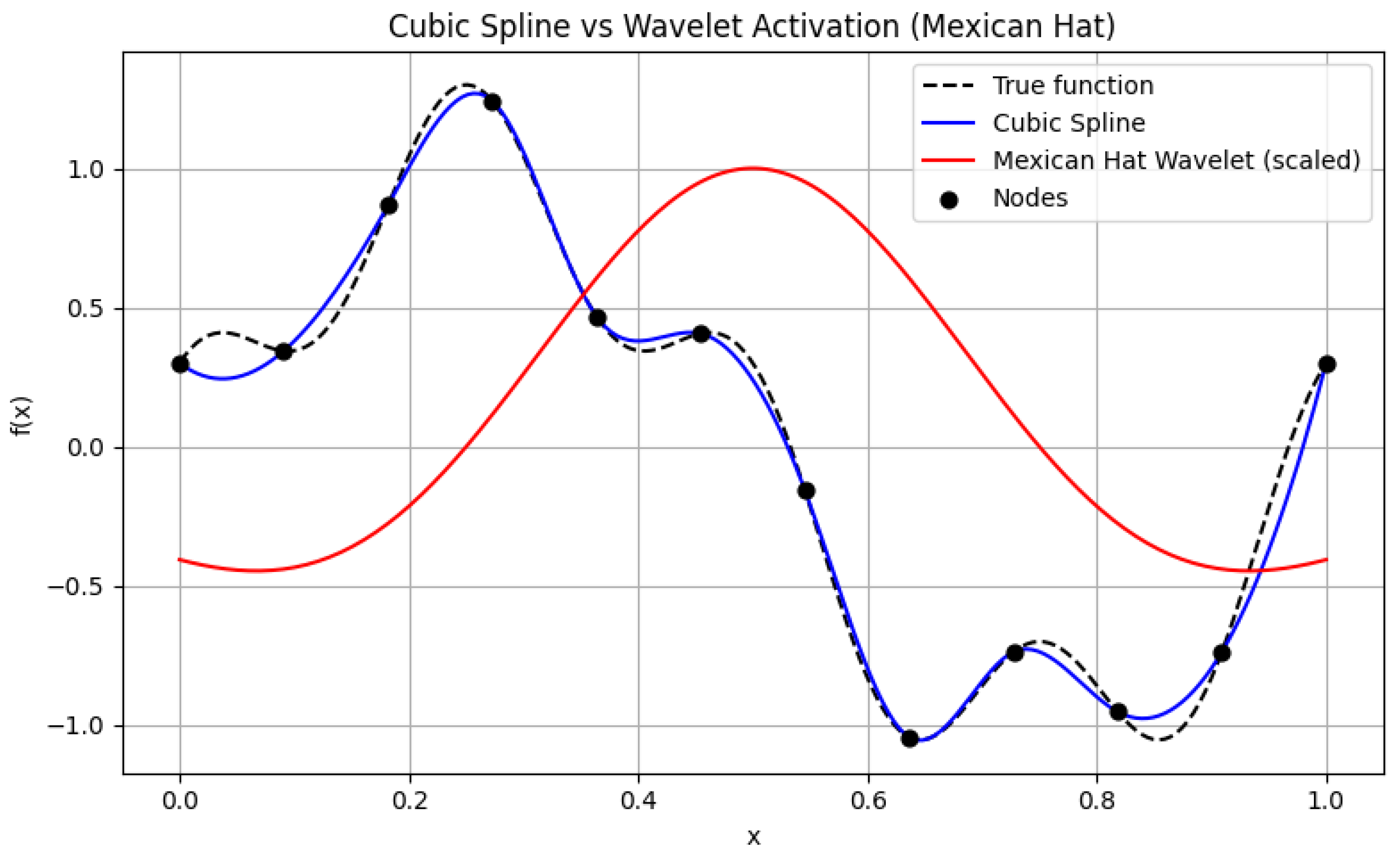
Figure 10 illustrates the comparison between a cubic spline and a Mexican Hat wavelet in modeling oscillatory data. The spline captures smooth local trends, while the wavelet shows superior adaptability to localized fluctuations.

15. Comparative Discussion of KAN Variants

The previous sections introduced different variants of Kolmogorov–Arnold Networks (KAN), each replacing or modifying the spline-based activations with alternative mathematical bases or constraints. While each approach offers unique advantages, their practical relevance depends on the target application, the type of data, and computational constraints. This section provides a comparative discussion of the main variants—Chebyshev-KAN, GKAN (Gram polynomials), Wav-KAN (Wavelet-based), Rational-KAN, MonoKAN (monotonic splines), Physics-constrained KAN, Linear Splines, and Orthogonal Polynomials—highlighting trade-offs in terms of accuracy, efficiency, interpretability, and domain suitability. The overall comparison of these approaches is summarized in

Table 11. Comparative analysis of Kolmogorov–Arnold Network (KAN) variants.

Variant	Core Feature	Mathematical Basis	Key Advantage
Chebyshev KAN	Global extrapolation	Chebyshev polynomials	Numerical stability and smooth extrapolation beyond training ranges.
GKAN	Computational efficiency	Gram polynomials	Reduces computational cost while preserving orthogonality.
Rational KAN	Discontinuity capture	Rational functions	Compact representation of sharp features with fewer parameters.
Physics-KAN	Physical consistency	PDE-constrained splines	Embeds conservation laws, reduces data needs by >80%.
Linear Spline KAN	Computational efficiency	Piecewise linear splines	3–5× faster training with exact gradient compatibility.
Orthogonal KAN	Spectral accuracy	Legendre/Hermite polynomials	Exponential convergence for smooth functions.
Wav-KAN	Multi-resolution analysis	Wavelet bases	Captures local/global patterns with denoising capabilities.
MonoKAN	Monotonicity enforcement	Hermite splines with constraints	Order-preserving behavior for risk/financial models.

.

16. Discussion

The comparative analysis of Kolmogorov–Arnold Network (KAN) variants, highlights how diverse mathematical foundations lead to specialized behaviors and domain-specific advantages. Each variant introduces structural modifications to the classical KAN framework, not only improving approximation properties but also embedding prior knowledge such as monotonicity, physical consistency, or spectral accuracy. This shift reflects a broader trend in machine learning: the movement away from purely black-box models toward interpretable and domain-aware architectures.

Chebyshev KAN demonstrates stable extrapolation and polynomial efficiency, making it well-suited for global forecasting tasks such as climate dynamics [51,62]. However, its performance degrades in the presence of discontinuities. GKAN, based on Gram orthogonal polynomials, offers computational efficiency in low-dimensional signal processing tasks [61], but is inherently limited to normalized domains (e.g., $[-1,1]$), restricting its scalability. Wav-KAN introduces multi-resolution analysis via wavelets, enabling localized time-frequency representations particularly beneficial in non-stationary signals such as EEGs [60,63]. This comes at the cost of computational overhead and sensitivity to wavelet selection.

MonoKAN enforces monotonic behavior through Hermite splines with derivative constraints, offering interpretability in domains such as actuarial modeling and healthcare risk assessment [64]. Nevertheless, it trades expressive flexibility for guaranteed monotonicity. Rational KAN achieves compact representations of discontinuities and sharp features through rational functions, providing parameter efficiency and exact rational recovery [63], but raises challenges due to potential poles and denominator instabilities [65]. Physics-constrained KAN integrate PDE-based constraints into their training process, yielding physically consistent solutions with significantly reduced data requirements (up to 80%) [60,63], although they introduce substantial computational costs and demand differentiable physics models [66].

Finally, linear spline KAN emphasize computational simplicity by replacing cubic splines with piecewise-linear functions, resulting in 3–5× faster training and inference [57,58], while orthogonal polynomial KAN achieve spectral accuracy with exponential convergence for smooth functions [63], though they suffer from Gibbs oscillations near discontinuities and require precise domain normalization [64,65].

Collectively, these results reveal that no single KAN variant dominates across all contexts. Instead, their strengths are complementary: Chebyshev and Orthogonal KAN excel in smooth global domains, Wav-KAN in multi-resolution non-stationary tasks, MonoKAN in ordered risk functions, Physics-KAN in scientific modeling, Rational KAN in discontinuities, and Linear Spline KAN in efficiency-critical applications. Future research directions include hybrid architectures (e.g., Chebyshev-Wav-KAN for combining global extrapolation with local adaptivity), automated basis selection for task-specific adaptation [65], and hardware acceleration of computationally intensive bases such as wavelets and Gram polynomials [66]. By bridging classical approximation theory with modern deep learning, KAN variants provide a promising foundation for interpretable, reliable, and domain-aware AI models in high-stakes applications [67,68].

17. Conclusions

Kolmogorov–Arnold Networks (KAN) represent a significant advancement in the design of neural architectures grounded in classical mathematical theory. Unlike traditional neural networks that rely on fixed and opaque activation functions, KAN enable a more interpretable and controllable construction by using univariate functions based on splines and other functional bases. This structure, theoretically supported by the Kolmogorov–Arnold representation theorem, not only improves the traceability of model decisions but also opens the door to incorporating expert knowledge, physical constraints, and desirable properties such as monotonicity or multiresolution. As a result, KAN are particularly well-suited to contexts where explainability and control are essential, including medicine, finance, and engineering.

The comparative analysis carried out in this work highlights that each structural variant of KAN responds to specific domain-driven needs. For instance, Wav-KAN proves effective in modeling non-stationary signals such as EEGs due to its multiscale decomposition capabilities, whereas MonoKAN offers a robust solution in regulatory contexts by ensuring monotonic outputs, as required in actuarial models. Similarly, Rational-KAN and Physics-KAN provide advantages when greater precision or physical consistency is needed. This systematic review consolidates dispersed information and provides a unified mathematical perspective on these variants, emphasizing that there is no single optimal architecture, but rather multiple designs adaptable to the nature of the problem and the requirements of different application domains.

Despite their promise, several challenges remain. These include the efficient optimization of parameters in nonlinear architectures, the automated selection of functional bases suited to specific tasks, and the scalability of KAN in high-computation contexts. Furthermore, theoretical convergence guarantees are still missing for certain variants, limiting their adoption in highly sensitive applications. Our review also faces limitations: it is bounded by the current state of the literature, which remains in its early stage, and empirical validation of many variants is still scarce, requiring careful interpretation of the results presented here.

Nevertheless, the potential for hybridization—such as combining the global stability of Chebyshev-KAN with the localized precision of Wav-KAN—suggests a promising research avenue. Future work should also focus on establishing standardized benchmarks, exploring physics-informed and domain-aware extensions, and developing hardware-efficient implementations. Altogether, KAN mark the beginning of a new stage in the development of interpretable and mathematically grounded neural models, with high-impact applications in fields that demand transparency, precision, and adaptability. By consolidating and comparing their mathematical structures, this work aims to serve as a foundational reference for both theoretical advances and practical implementations of KAN.