Radio Frequency Fingerprint-Identification Learning Method Based-On LMMSE Channel Estimation for Internet of Vehicles
Abstract
1. Introduction
- (1)
- A novel RFF extraction method based on LMMSE channel estimation is proposed. This method optimizes the channel response estimation by combining the channel covariance matrix and noise statistical information and removes the channel response to generate initial fingerprint features, improving the robustness of fingerprint extraction in complex environments.
- (2)
- The ShuffleNet V2 network architecture is optimized for low SNR and dynamic channel conditions through the integration of an attention mechanism module. This approach can preserve high feature-extraction capabilities while maintaining a lightweight network, enhancing the model’s adaptability and generalization performance to ensure stable identification results.
- (3)
- During the training process, data collected from diverse scenarios is integrated to enhance the model’s generalization ability. By increasing the informational richness of the features, both computational load and the number of parameters are effectively reduced. This strategy improves computational efficiency while ensuring detection accuracy, thereby achieving a lightweight network. Experimental validation demonstrates the effectiveness of the proposed method, achieving classification accuracies of 96.76% and 91.05% in low-SNR stationery and mobile scenarios, respectively.
2. Related Work
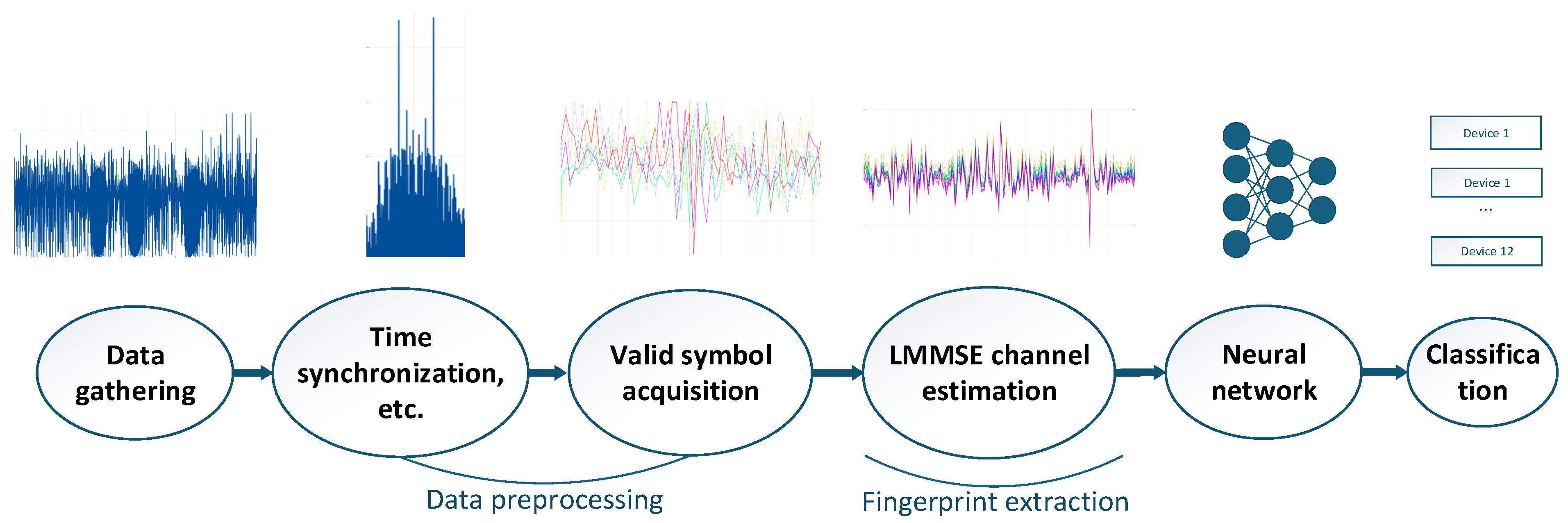
3. System Overview
3.1. PSBCH
3.2. System Framework
4. Data Preprocessing
4.1. Signal Detection
4.2. Frame Synchronization
4.3. CFO Compensation
4.4. Resource Grid Demodulation
5. Fingerprint Extraction and Classification
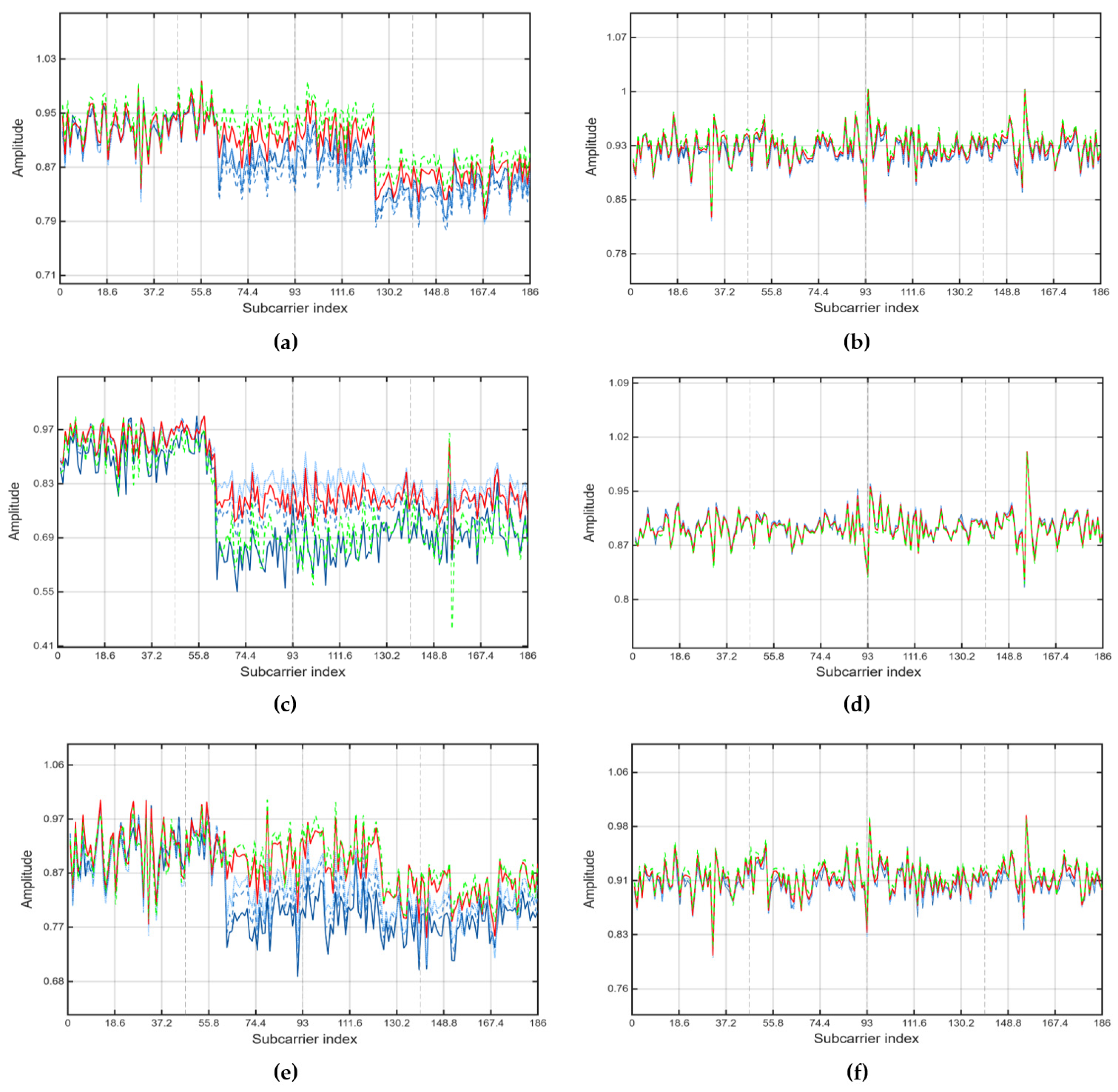
5.1. Channel Estimation and Equalization
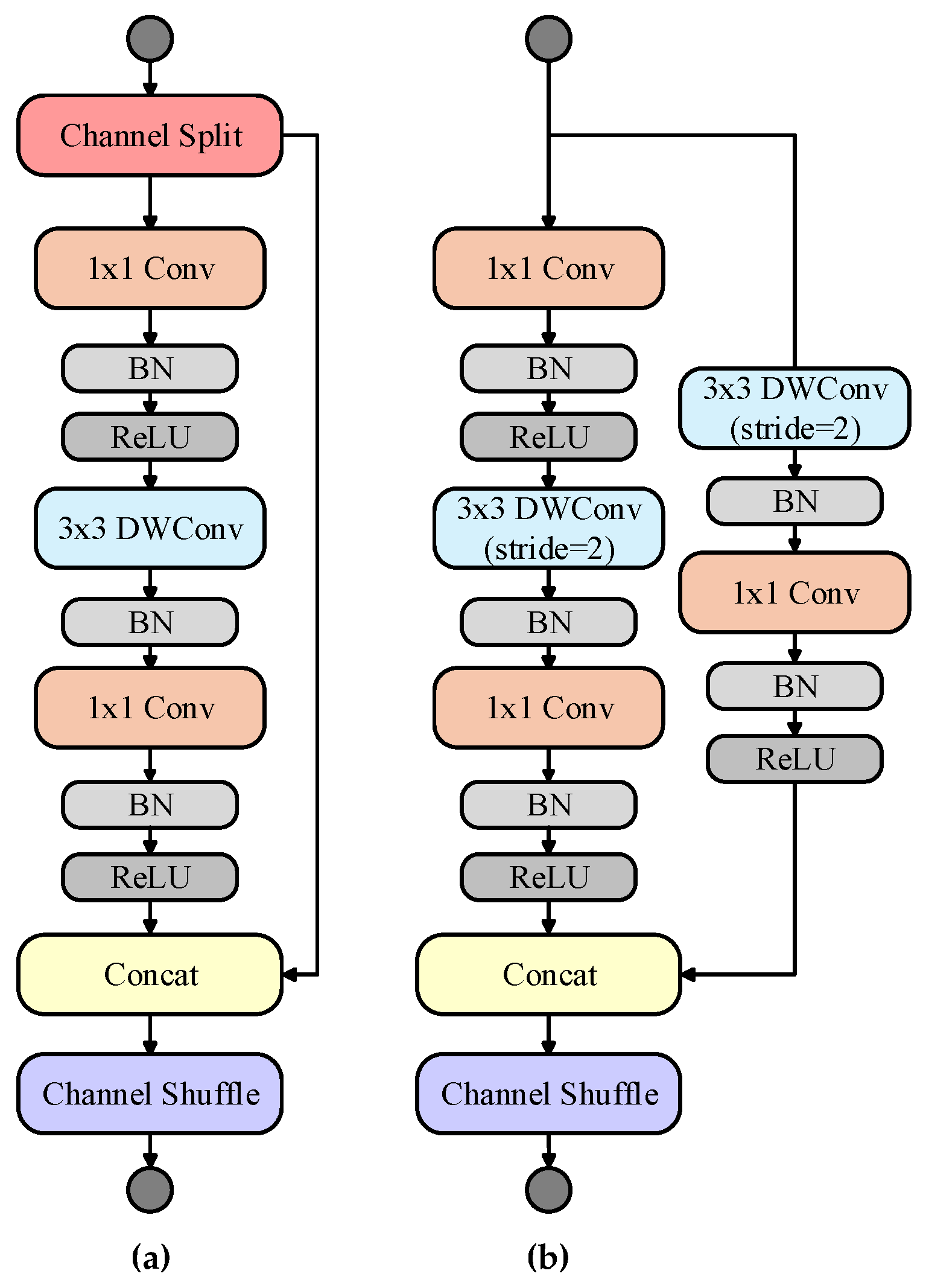
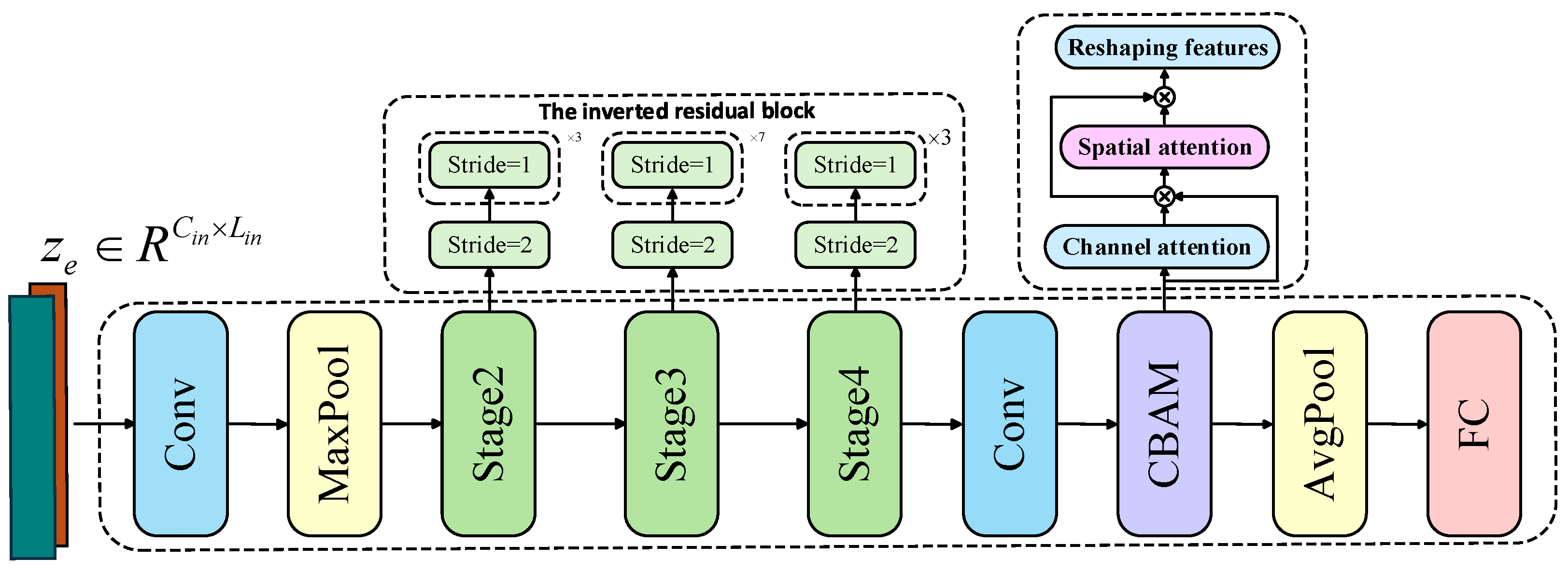
5.2. Improved ShuffleNet V2 Network
5.2.1. Network Architecture Design
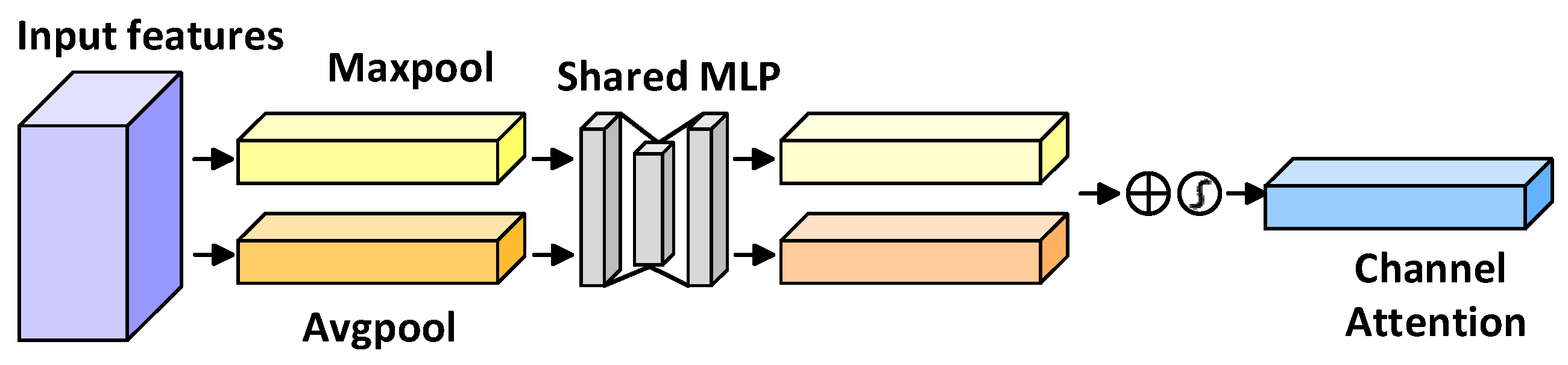
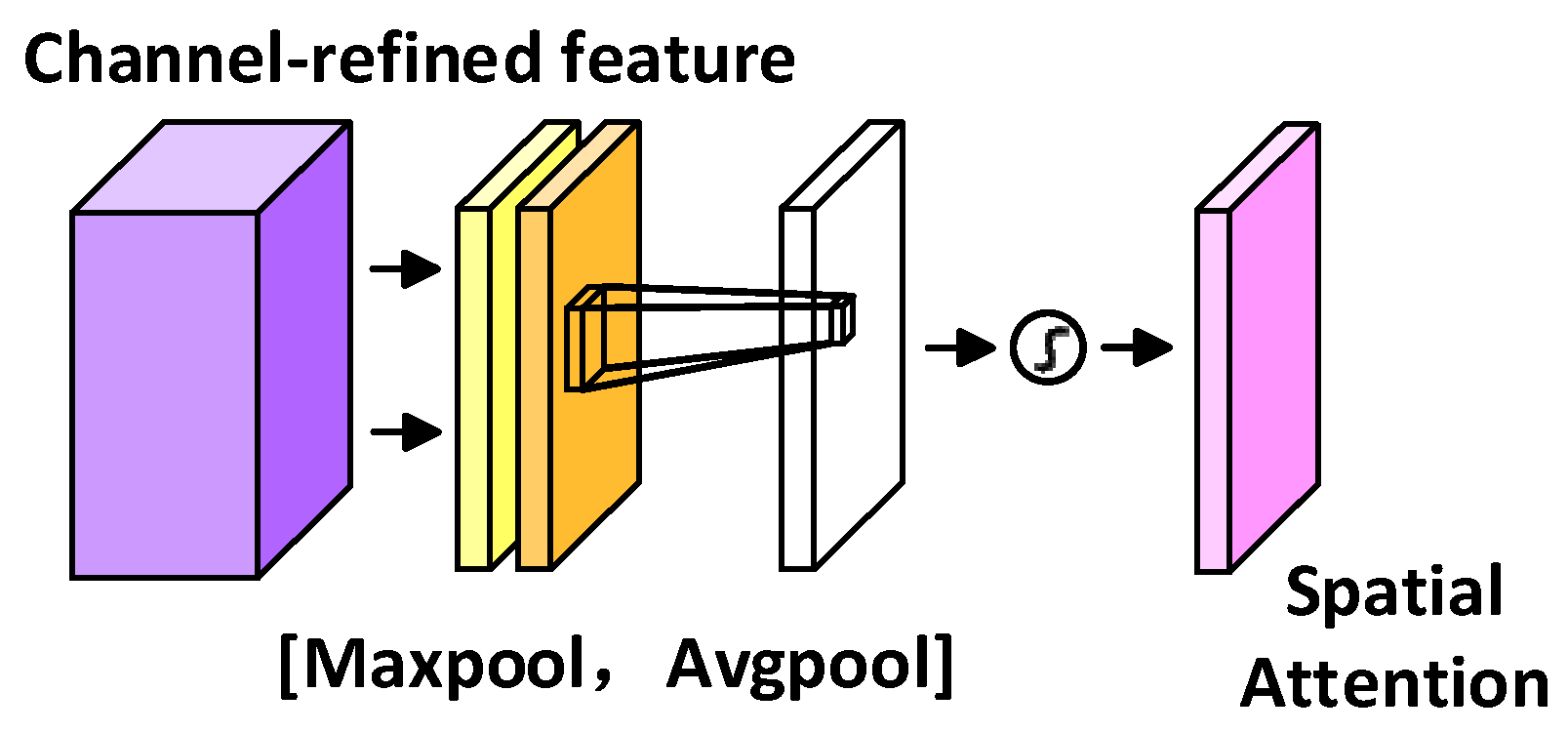
5.2.2. Attention Mechanism
6. Results and Discussion
6.1. Experimental Environment
6.2. Evaluation Criteria
6.3. Experimental Results and Discussion
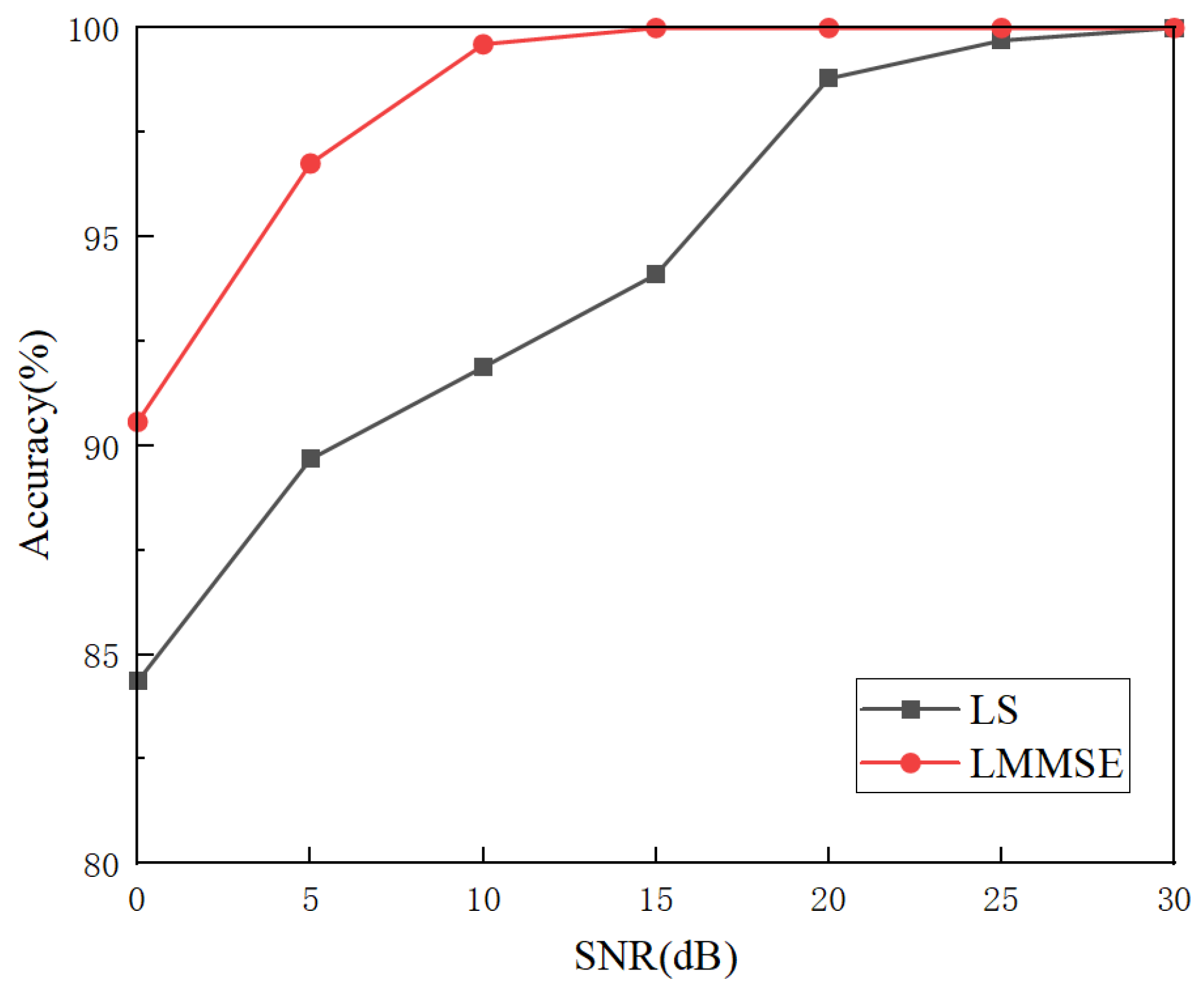
6.3.1. Classification Under Different SNR
6.3.2. Classification in Different Scenarios
6.3.3. Comparison of Different Models
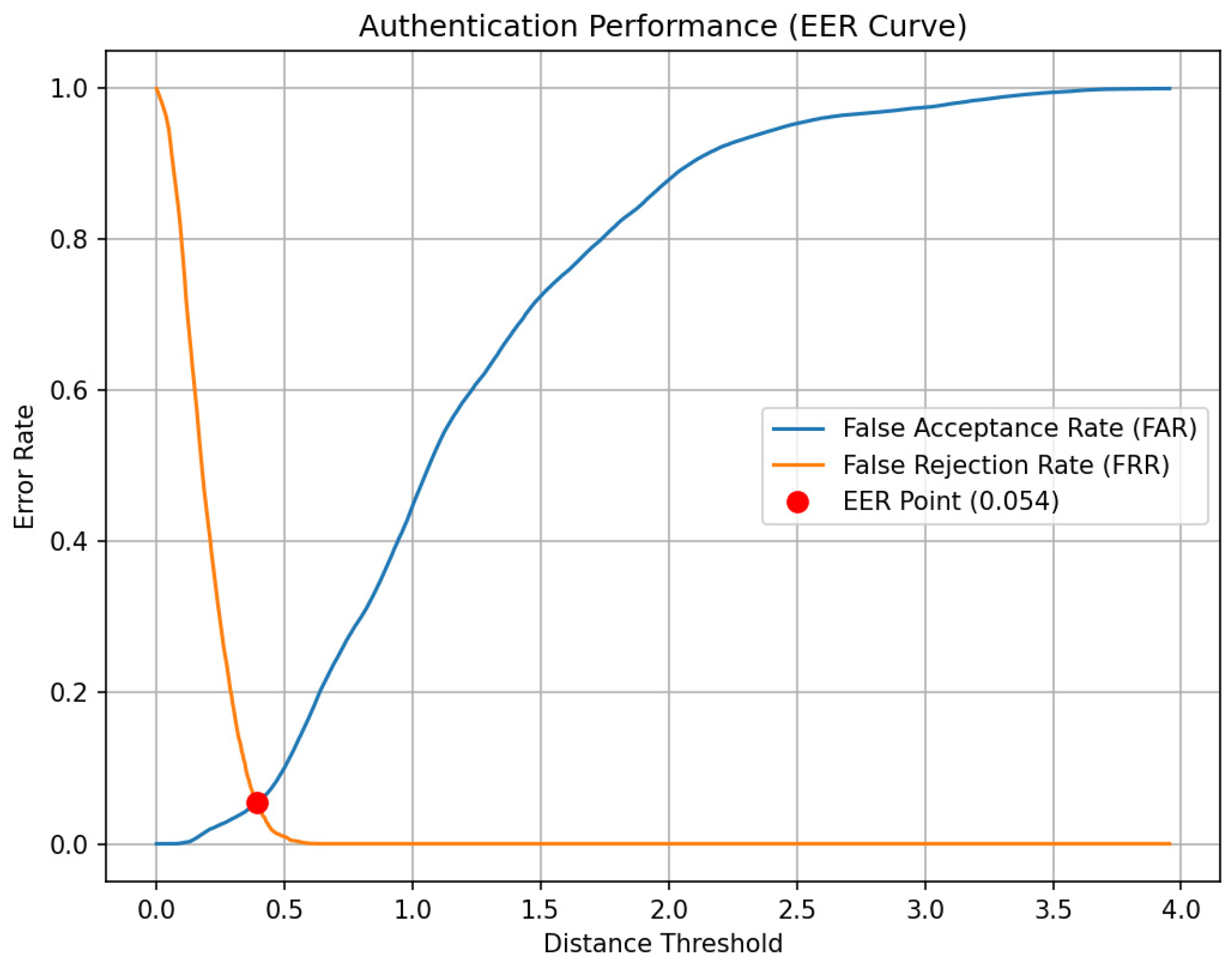
6.3.4. Model-Authentication Performance Evaluation
- (1)
- Experimental Setup
- (2)
- Authentication Method
- (3)
- Performance Metrics
- (4)
- Evaluation Criteria
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, C.; Kwon, D.K.; Son, S.; Yu, S.; Park, Y. An Anonymous and Efficient Authentication Scheme with Conditional Privacy Preservation in Internet of Vehicles Networks. Mathematics 2024, 12, 3756. [Google Scholar] [CrossRef]
- Aziz, S.; Faiz, M.T.; Adeniyi, A.M.; Loo, K.H.; Hasan, K.N.; Xu, L.; Irshad, M. Anomaly detection in the internet of vehicular networks using explainable neural networks (xnn). Mathematics 2022, 10, 1267. [Google Scholar] [CrossRef]
- Anwar, W.; Franchi, N.; Fettweis, G. Physical layer evaluation of V2X communications technologies: 5G NR-V2X, LTE-V2X, IEEE 802. 11 bd, and IEEE 802.11 p. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019. [Google Scholar]
- Zhou, H.; Xu, W.; Chen, J.; Wang, W. Evolutionary V2X technologies toward the Internet of Vehicles: Challenges and opportunities. Proc. IEEE 2020, 108, 308–323. [Google Scholar] [CrossRef]
- Tan, Z.; Ding, B.; Zhao, J.; Guo, Y.; Lu, S. Breaking cellular IoT with forged data-plane signaling: Attacks and countermeasure. ACM Trans. Sens. Netw. 2022, 18, 59. [Google Scholar] [CrossRef]
- Ludant, N.; Robyns, P.; Noubir, G. From 5g sniffing to harvesting leakages of privacy-preserving messengers. In Proceedings of the 2023 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–25 May 2023. [Google Scholar]
- Mosca, M. Cybersecurity in an era with quantum computers Will we be ready? IEEE Secur. Priv. 2018, 16, 38–41. [Google Scholar] [CrossRef]
- Zeng, K.; Govindan, K.; Mohapatra, P. Non-cryptographic authentication and identification in wireless networks [security and privacy in emerging wireless networks]. IEEE Wirel. Commun. 2010, 17, 56–62. [Google Scholar] [CrossRef]
- Yang, X.; Li, D. LED-RFF: LTE DMRS-based channel robust radio frequency fingerprint identification scheme. IEEE Trans. Inf. Forensics Secur. 2023, 19, 1855–1869. [Google Scholar] [CrossRef]
- Al-Shawabka, A.; Restuccia, F.; D’Oro, S.; Jian, T.; Rendon, B.C.; Soltani, N.; Dy, J.; Ioannidis, S.; Chowdhury, K.; Melodia, T. Exposing the fingerprint: Dissecting the impact of the wireless channel on radio fingerprinting. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020. [Google Scholar]
- Köse, M.; Taşcioğlu, S.; Telatar, Z. RF fingerprinting of IoT devices based on transient energy spectrum. IEEE Access 2019, 7, 18715–18726. [Google Scholar] [CrossRef]
- Vo-Huu, T.D.; Vo-Huu, T.D.; Noubir, G. Fingerprinting Wi-Fi devices using software defined radios. In Proceedings of the 9th ACM Conference on Security & Privacy in Wireless and Mobile Networks, Darmstadt, Germany, 18–20 July 2016. [Google Scholar]
- Hua, J.; Sun, H.; Shen, Z.; Qian, Z.; Zhong, S. Accurate and efficient wireless device fingerprinting using channel state information. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018. [Google Scholar]
- Xing, Y.; Hu, A.; Zhang, J.; Peng, L.; Wang, X. Design of a channel robust radio frequency fingerprint identification scheme. IEEE Internet Things J. 2022, 10, 6946–6959. [Google Scholar] [CrossRef]
- Tsipras, D.; Santurkar, S.; Engstrom, L.; Turner, A.; Madry, A. Robustness may be at odds with accuracy. arXiv 2018. [Google Scholar] [CrossRef]
- Xie, R.; Xu, W.; Yu, J.; Hu, A.; Ng, D.W.K.; Swindlehurst, A.L. Disentangled representation learning for RF fingerprint extraction under unknown channel statistics. IEEE Trans. Commun. 2023, 71, 3946–3962. [Google Scholar] [CrossRef]
- Al-Shawabka, A.; Pietraski, P.; Pattar, S.B.; Restuccia, F.; Tommaso, M. DeepLoRa: Fingerprinting LoRa devices at scale through deep learning and data augmentation. In Proceedings of the 22nd International Symposium on Theory, Algorithmic Foundations, and Protocol Design for Mobile Networks and Mobile Computing, Shanghai, China, 26–29 July 2021. [Google Scholar]
- Soltani, N.; Sankhe, K.; Dy, J.; Ioannidis, S.; Chowdhury, K. More is better: Data augmentation for channel-resilient RF fingerprinting. IEEE Commun. Mag. 2020, 58, 66–72. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, A.; Li, G.; Peng, L.; Xing, Y.; Yu, J. A robust radio-frequency fingerprint extraction scheme for practical device recognition. IEEE Internet Things J. 2021, 8, 11276–11289. [Google Scholar] [CrossRef]
- Li, G.; Yu, J.; Xing, Y.; Hu, A. Location-invariant physical layer identification approach for WiFi devices. IEEE Access 2019, 7, 106974–106986. [Google Scholar] [CrossRef]
- Shen, G.; Zhang, J.; Marshall, A.; R. Cavallaro, J. Towards scalable and channel-robust radio frequency fingerprint identification for LoRa. IEEE Trans. Inf. Forensics Secur. 2022, 17, 774–787. [Google Scholar] [CrossRef]
- Dong, B.; Hu, A.; Yu, J.; Chen, H.; Shi, Z. A robust radio frequency fingerprint extraction method based on channel reciprocity. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024. [Google Scholar]
- Yin, P.; Peng, L.; Zhang, J.; Liu, M.; Fu, H.; Hu, A. LTE device identification based on RF fingerprint with multi-channel convolutional neural network. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021. [Google Scholar]
- Chen, T.; Shen, H.; Hu, A.; He, W.; Xu, J.; Hu, H. Radio frequency fingerprints extraction for LTE-V2X: A channel estimation based methodology. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022. [Google Scholar]
- van de Beek, J.-J.; Edfors, O.; Sandell, M.; Wilson, S.K.; Borjesson, P.O. On channel estimation in OFDM systems. In Proceedings of the 1995 IEEE 45th Vehicular Technology Conference, Chicago, IL, USA, 25–28 July 1995. [Google Scholar]
- ETSI 3rd Generation Partnership Project. LTE; Evolved Universal Terrestrial Radio Access (E-UTRA); Physical Channels and Modulation (Release 14), 3GPP TS 36.211 version 14.2.0; Sophia Antipolis Cedex: Biarritz, France, 2016. [Google Scholar]
- Qi, X.; Hu, A.; Chen, T. Lightweight Radio Frequency Fingerprint Identification Scheme for V2X Based on Temporal Correlation. IEEE Trans. Inf. Forensics Secur. 2023, 19, 1056–1070. [Google Scholar] [CrossRef]
- Van de Beek, J.J.; Sandell, M. ML Estimation of Time and Frequency Offset in OFDM Systems. IEEE Trans. Signal Process. 1997, 45, 1800–1805. [Google Scholar] [CrossRef]
- Moose, P.H. A Technique for Orthogonal Frequency Division Multiplexing Frequency Offset Correction. IEEE Trans. Commun. 1994, 42, 2908–2914. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Cham, Switzerland, 2018. [Google Scholar]

| (Method/Approach) | Advantages | Limitations |
|---|---|---|
| Transient Features [11,23] | No data demodulation required. | Significant performance degradation on persistent symbols. |
| CFO Features [12,13] | Simple concept, channel estimation-free. | Insufficient stability and inter-class separability. |
| Adversarial Training [15]/Disentanglement [16] | Data-driven, automatic decoupling. | Risk of “over-purifying” and losing RFF details. |
| Data Augmentation [17,18] | Enhances model’s tolerance to variations. | Increases model training overhead. |
| Noise Injection [19] | Leverages physical principles, no preamble needed. | Mismatches with the physical model of the actual channel. |
| Protocol-Specific Compensation [20,21] | Performs well within its native system. | Relies on specific frame structures. |
| Channel Reciprocity [22] | Enhances model’s tolerance to variations. | Requires stacking of multiple consecutive frames from the same transmitter. |
| LS Channel Estimation [24] | Simple to implement, direct channel removal. | Performance degrades under low SNR. |
| Training Set | ACC/F1 (%) | ||||
|---|---|---|---|---|---|
| LOS | NLOS | MOV1 | MOV2 | MOV3 | |
| DC | 99.75/99.73 | 98.82/98.56 | 99.01/98.05 | 98.09/98.51 | 99.59/99.59 |
| DC + LOS | 100/100 | 99.96/99.94 | 99.28/98.23 | 99.41/99.51 | 100/100 |
| DC + NLOS | 95.64/95.06 | 100/100 | 99.89/99.92 | 96.51/97.35 | 99.67/99.67 |
| DC + MOV1 | 100/100 | 99.32/99.33 | 100/100 | 97.72/98.6 | 99.87/99.87 |
| DC + MOV2 | 99.96/99.97 | 99.82/99.8 | 98.73/97.19 | 100/100 | 99.96/99.96 |
| DC + MOV3 | 100/100 | 99.58/99.67 | 99.6/99.57 | 99.54/99.63 | 100/100 |
| LOS | 100/100 | 99.28/98.74 | 98.07/98.19 | 95.68/95.71 | 99.87/99.85 |
| LOS + NLOS | 99.99/99.99 | 99.99/99.97 | 99.98/99.98 | 98.27/98.12 | 100/100 |
| LOS + MOV1 | 100/100 | 98.99/99.16 | 100/100 | 98.89/98.92 | 99.93/99.91 |
| LOS + MOV2 | 100/100 | 99.28/99.4 | 99.92/99.92 | 100/100 | 100/100 |
| LOS + MOV3 | 100/100 | 98.27/98.68 | 99.24/99.48 | 95.74/95.22 | 100/100 |
| Model | Overall Accuracy (%) | Macro Precision (%) | Macro F1 (%) |
|---|---|---|---|
| DenseNet | 95.19 | 93.15 | 93.92 |
| MobileNet | 92.7 | 88.93 | 88.12 |
| EfficientNet | 96.63 | 97.02 | 96.24 |
| MobileVit | 86.47 | 85.08 | 84.22 |
| ConvNeXt | 96.72 | 94 | 95.43 |
| ShuffleNet V2 | 96.74 | 95.02 | 95.19 |
| Ours | 99.01 | 97.44 | 98.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, L.; Xu, Y.; Li, Y.; Yang, Y.; Fu, N. Radio Frequency Fingerprint-Identification Learning Method Based-On LMMSE Channel Estimation for Internet of Vehicles. Mathematics 2025, 13, 3124. https://doi.org/10.3390/math13193124
Sheng L, Xu Y, Li Y, Yang Y, Fu N. Radio Frequency Fingerprint-Identification Learning Method Based-On LMMSE Channel Estimation for Internet of Vehicles. Mathematics. 2025; 13(19):3124. https://doi.org/10.3390/math13193124
Chicago/Turabian StyleSheng, Lina, Yao Xu, Yan Li, Yang Yang, and Nan Fu. 2025. "Radio Frequency Fingerprint-Identification Learning Method Based-On LMMSE Channel Estimation for Internet of Vehicles" Mathematics 13, no. 19: 3124. https://doi.org/10.3390/math13193124
APA StyleSheng, L., Xu, Y., Li, Y., Yang, Y., & Fu, N. (2025). Radio Frequency Fingerprint-Identification Learning Method Based-On LMMSE Channel Estimation for Internet of Vehicles. Mathematics, 13(19), 3124. https://doi.org/10.3390/math13193124






