On Bi-Univalent Function Classes Defined via Gregory Polynomials

Abstract

In this paper, we introduce and study a new subclass of bi-univalent functions related to Mittag–Leffler functions associated with Gregory polynomials and satisfy certain subordination conditions defined in the open unit disk. We derive coefficient bounds for the Taylor–Maclaurin coefficients $|{\gamma }_2|$ and $|{\gamma }_3|$, and also explore the Fekete–Szegö functional.

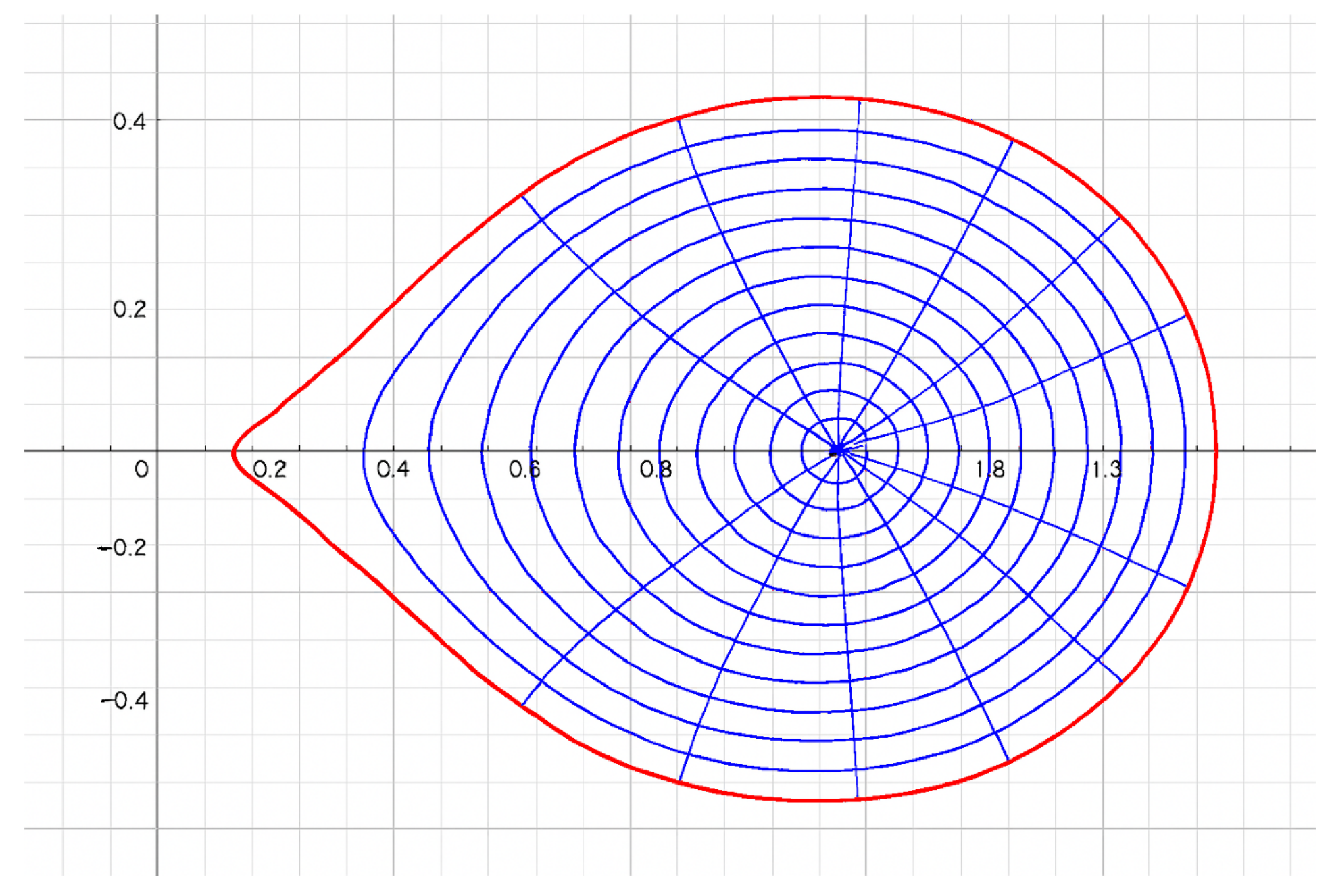
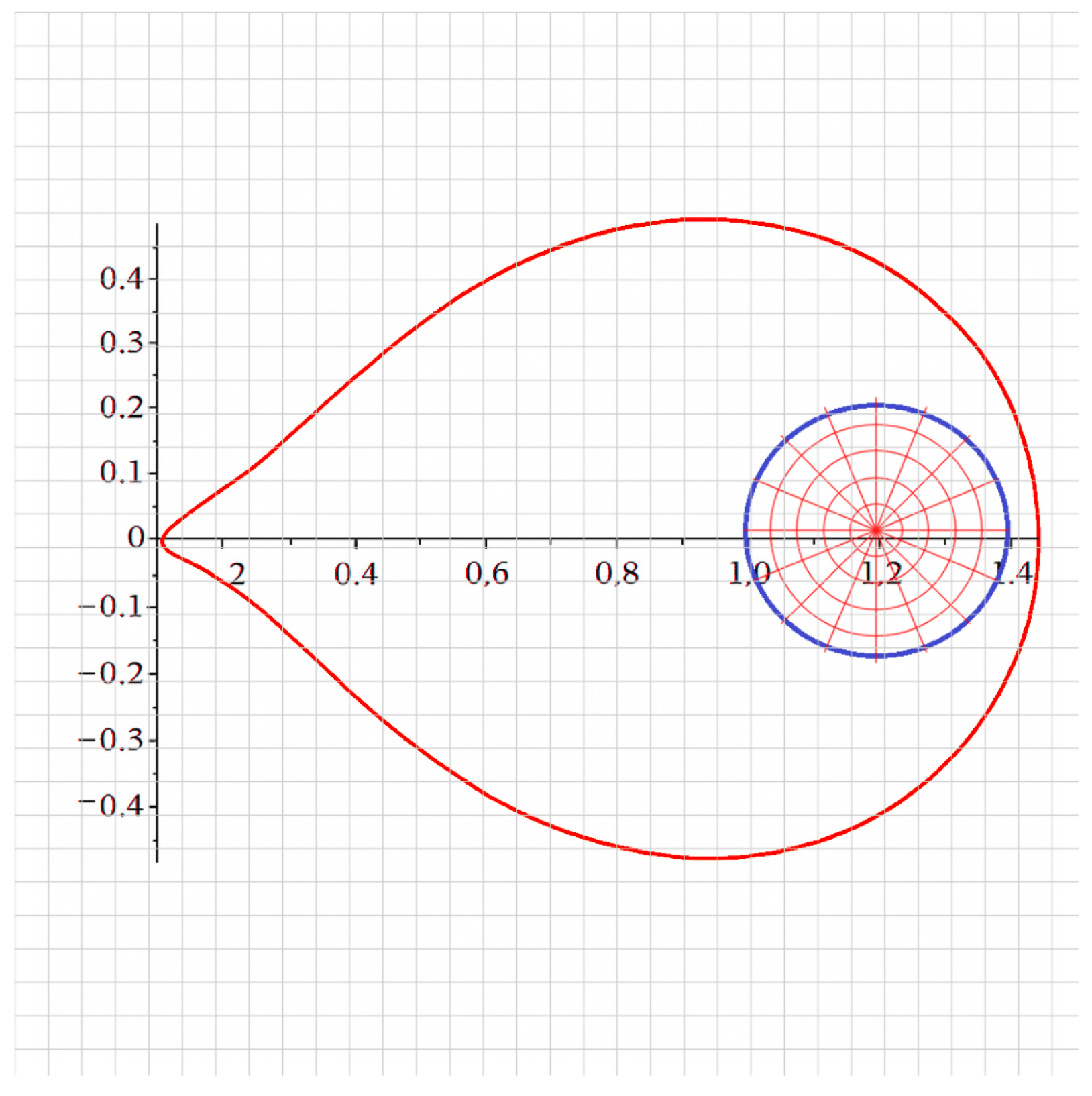
1. Introduction

Let $\mathcal{H}$(Ω) denote the class of functions which are analytic in the open unit disk $\Omega =\{\varsigma \in \mathbb{C}:|\varsigma |<1\}$ where $\mathbb{C}$ is the set of complex numbers and let $\mathcal{A}$ be the class of analytic functions having the form

$$\begin{array}{c}\hfill l\left(\varsigma \right)=\varsigma +\sum _{b=2}^{\infty }{\gamma }_b{\varsigma }^b(\forall \varsigma \in \Omega ),\end{array}$$

(1)

in the open unit disk Ω, centered at origin and normalized by the conditions

$$l\left(0\right)=0\mathrm{and}{l}^{\prime }\left(0\right)=1.$$

Furthermore, let $\mathcal{S}$ denote the set of functions in $\mathcal{A}$ that are univalent within Ω. For a function $\begin{array}{c}\hfill m\left(\varsigma \right)=\varsigma +{\sum }_{b=2}^{\infty }{j}_b{\varsigma }^b\in \mathcal{A}\end{array}$, the Hadamard product (the convolution) of l and m is characterized as

$$\begin{array}{c}\hfill (l\ast m)\left(\varsigma \right)=\varsigma +\sum _{b=2}^{\infty }{\gamma }_b{j}_b{\varsigma }^b=(m\ast l)\left(\varsigma \right).\end{array}$$

(2)

A function $l\in \mathcal{A}$ belongs to ${\mathcal{S}}^{*}\left(\rho \right)$, where $\rho \in [0,1)$, as demonstrated in [1] and further examined in ([2], Vol. I, p. 138) if and only if

$$\mathrm{Re}\left({\displaystyle \frac{\varsigma l^{\prime }\left(\varsigma \right)}{l\left(\varsigma \right)}}\right)>\rho ,\varsigma \in \Omega .$$

According to the well-known result obtained in [3] (see also [4], p. 42), a function $l\in \mathcal{A}\mathrm{belongs}\mathrm{to}\mathcal{C}\left(\rho \right),\mathrm{where}\rho \in [0,1),\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}$

$$\mathrm{Re}\left(1+{\displaystyle \frac{\varsigma l^{″}\left(\varsigma \right)}{l^{\prime }\left(\varsigma \right)}}\right)>\rho ,\varsigma \in \Omega .$$

The value ${\displaystyle \frac{\varsigma l^{\prime }\left(\varsigma \right)}{l\left(\varsigma \right)}}$ or $1+{\displaystyle \frac{\varsigma {ł}^{″}\left(\varsigma \right)}{l^{\prime }\left(\varsigma \right)}}$ generally defines these functions, which are restricted to a certain region in the right half-plane that is starlike concerning 1. It is well known that we have the inclusions

$${\mathcal{S}}^{*}\left(\rho \right)\subset {\mathcal{S}}^{*}\left(0\right)={\mathcal{S}}^{*},\mathcal{C}\left(\rho \right)\subset \mathcal{C}\left(0\right)=\mathcal{C},\mathrm{and}\mathcal{C}\subset {\mathcal{S}}^{*}\subset \mathcal{S}.$$

It is a well-established fact that

$$l\left(\varsigma \right)\in \mathcal{C}\left(\rho \right)\iff \varsigma {ł}^{\prime }\left(\varsigma \right)\in {\mathcal{S}}^{*}\left(\rho \right).$$

We define two functions, l and m, to be subordinate, denoted as $l\prec m$, if there exists an analytic function $h\left(\phi \right)$ (known as a Schwarz function) defined in $\mathbb{U}$ such that $l\left(\phi \right)=m\left(h\right(\phi \left)\right),$ with the condition $h\left(0\right)=0$, and $\left|h\right(\phi \left)\right|\le 1$. Specifically, if the function m is univalent within $\mathbb{U}$, then

$$l\left(\phi \right)\prec m\left(\phi \right)\iff l\left(0\right)=m\left(0\right)\mathrm{and}l\left(\mathbb{U}\right)\subset m\left(\mathbb{U}\right)$$

(see [5]).

It is well known that every function $l\in \mathcal{S}$ has an inverse $l^{-1}$, defined by

$$\begin{array}{c}\hfill l^{-1}\left(l\left(\varsigma \right)\right)=\varsigma ,(\varsigma \in \Omega )\end{array}$$

and

$$\begin{array}{c}\hfill l^{-1}\left(l\left(x\right)\right)=x,\left(\left|x\right|<r_0\left(l\right);r_0\left(l\right)\ge {\displaystyle \frac{1}{4}}\right),\end{array}$$

where

$$\begin{array}{c}\hfill g\left(x\right)=l^{-1}\left(x\right)=x-a_2{x}^2+(2a_2^2-a_3)x^3-(5a_2^3-5a_2{a}_3+a_4)x^4+\cdots .\end{array}$$

(3)

A function $l\left(\varsigma \right)\in \mathcal{A}$ is said to be bi-univalent in $\Omega$ if both $l\left(\varsigma \right)$ and $l^{-1}\left(\varsigma \right)$ are univalent in $\Omega$. We denote as $\Sigma$ the class of all functions $l\left(\varsigma \right)$ which are bi-univalent in $\Omega .$ The functions

$${\displaystyle \frac{\varsigma }{1-\varsigma }},log{\displaystyle \frac{1}{1-\varsigma }},log\sqrt{{\displaystyle \frac{1+\varsigma }{1-\varsigma }}},$$

belong to the class $\Sigma$. However, the well-known Koebe function is not part of $\Sigma$, while other common examples of analytic functions in $\Omega$, such as

$${\displaystyle \frac{2\varsigma -{\varsigma }^2}{2}}\mathrm{and}{\displaystyle \frac{\varsigma }{1-{\varsigma }^2}},$$

are also not members of $\Sigma$. Lewin [6] examined the class $\Sigma$ and determined that ${\gamma }_2<1.51$. Subsequently, Brannan and Clunie [7] put forth a conjecture indicating that ${\gamma }_2<\sqrt{2}$. In comparison, Netanyahu [8] showed that the highest value of ${\gamma }_2$ for functions within $\Sigma$ is $4/3$. The problem of estimating the coefficient for each Taylor–Maclaurin coefficient ${\gamma }_n$ of $n\in \mathbb{N},n\ge 3$ is still considered an open problem. Kamble and Shrigan [9] (see also [10]) introduced certain new subclasses of the family $\Sigma$ of bi-univalent functions by employing the framework of q-calculus, and derived bounds for the initial coefficients $|{\gamma }_2|$ and $|{\gamma }_3|$. Subsequently, Yousef et al. [11] investigated the Fekete–Szegö functional for specific subclasses of bi-univalent functions. Recently, Srivastava et al. [12] studied the second Hankel determinant associated with various subclasses of bi-univalent functions within a nephroid domain. It is widely known that the Fekete–Szegö problem relates to the coefficients of functions in $\Omega$. The first study of the Fekete–Szegő problem was given by Fekete–Szegö [13]. In particular, if

$$|a_3-\mu a_2^2 |\le 1+2e^{2\mu /(1-\sigma )},\mu \in \mathbb{R}.$$

The Mittag–Leffler function has significant applications in fractional calculus, operator theory, mathematical analysis, and various areas of science and engineering. It frequently arises in the study of integral and differential equations of fractional order and has remained a central topic of interest, motivating many researchers (see [14,15,16,17]). In 1903, Mittag–Leffler [18] (see also [19]), introduced the function ${\mathbb{E}}_{\rho }\left(\varsigma \right)$, defined by the following power series:

$${\mathbb{E}}_{\rho }\left(\varsigma \right)=\sum _{b=0}^{\infty }{\displaystyle \frac{{\varsigma }^b}{\Gamma (\rho b+1)}},\forall \Re \left(\rho \right)>0$$

(4)

which is the Mittag–Leffler function that converges across the entire complex plane for all $\Re \left(\rho \right)>0$, whereas it diverges at all points in $\mathbb{C}\setminus \left\{0\right\}$ when $\Re \left(\rho \right)<0$. Furthermore, as $\Re \left(\rho \right)=0$, the radius of convergence is determined by

$$R=e^{\pi /2\left|Im\left(\varsigma \right)\right|}.$$

Additionally, the integral form of the Mittag–Leffler function can be expressed as

$${\mathbb{E}}_{\rho }\left(\varsigma \right)={\oint }_C{\displaystyle \frac{t^{\rho -1}{e}^t}{t^{\mu }-\varsigma }}dt,\varsigma \in \mathbb{C},\Re \left(\rho \right)>0,$$

where contour C starts and concludes at infinity, encircling the branch points and singularities of the integrand. In the year 1905, Wiman [20,21] introduced and studied the Mittag–Leffler function of two parameters, where ${\mathbb{E}}_{\rho ,\eta }\left(\varsigma \right)$ is the generalized Mittag–Leffler function, defined by the following power series:

$${\mathbb{E}}_{\rho ,\eta }\left(\varsigma \right)=\sum _{b=0}^{\infty }{\displaystyle \frac{{\varsigma }^b}{\Gamma (\rho b+\eta )}},\varsigma \in \mathbb{C},\Re \left(\rho \right)>0,\Re \left(\eta \right)>0.$$

(5)

It is important to highlight that the two-parameter Mittag–Leffler function ${\mathbb{E}}_{\rho ,\eta }\left(\varsigma \right)$ is not included in the set $\Omega$. In 2016, Bansal and Prajapat [14] introduced the normalized Mittag–Leffler function, which is defined as follows (see also [22]):

$${\mathcal{E}}_{\rho ,\eta }\left(\varsigma \right)=\Gamma \left(\eta \right)\varsigma {\mathbb{E}}_{\rho ,\eta }\left(\varsigma \right)=\varsigma +\sum _{b=2}^{\infty }{\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma \left(\rho \right(b-1)+\eta )}}{\varsigma }^b,$$

(6)

where $\varsigma ,\rho ,\eta \in \mathbb{C},\Re \left(\rho \right)>0,\Re \left(\eta \right)>0$. It is important to mention that the function ${\mathcal{E}}_{\rho ,\eta }$ encompasses various well-known functions as specific instances. For example, we have ${\mathcal{E}}_{2,1}\left(\varsigma \right)=\varsigma cosh\left(\sqrt{\varsigma }\right)$, ${\mathcal{E}}_{2,2}\left(\varsigma \right)=\sqrt{\varsigma }sinh\left(\sqrt{\varsigma }\right)$, ${\mathcal{E}}_{2,3}\left(\varsigma \right)=2[cosh\left(\sqrt{\varsigma }\right)-1]$, ${\mathcal{E}}_{2,4}\left(\varsigma \right)=6\left[{\displaystyle \frac{sinh\left(\sqrt{\varsigma }\right)-\sqrt{\varsigma }}{\sqrt{\varsigma }}}\right]$. For the positive real parameters $\rho ,\eta$ and ${\mathbb{E}}_{\rho ,\eta }$, defined by (6), we define the linear operator ${\mathfrak{M}}_{\rho ,\eta }:\mathcal{A}\to \mathcal{A}$ by employing the convolution, also known as the Hadamard product, ${\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)={\mathcal{E}}_{\rho ,\eta }\left(\varsigma \right)\ast l\left(\varsigma \right)$, as follows:

$${\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)=\varsigma +\sum _{b=2}^{\infty }{\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma \left(\rho \right(b-1)+\eta )}}{\gamma }_b{\varsigma }^b,\varsigma \in \mathbb{C},\rho >0,\eta >0,$$

where ∗ represents the convolution or Hadamard product defined by (2).

The Gregory coefficients, also referred to as reciprocal logarithmic numbers, second-type Bernoulli numbers, or first-type Cauchy numbers, constitute a sequence of rational numbers that decrease in magnitude ${\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{12}},{\displaystyle \frac{1}{24}},-{\displaystyle \frac{19}{720}},\cdots$. These coefficients are present in the Maclaurin series expansion for the function ${\displaystyle \frac{\varsigma }{log(1+\varsigma )}}$, represented as

$$\mathcal{G}\left(\varsigma \right)={\displaystyle \frac{\varsigma }{log(1+\varsigma )}}=1+{\displaystyle \frac{1}{2}}\varsigma -{\displaystyle \frac{1}{12}}{\varsigma }^2+{\displaystyle \frac{1}{24}}{\varsigma }^3-{\displaystyle \frac{19}{720}}{\varsigma }^4+\cdots ,\varsigma \in \Omega .$$

An image $\mathcal{G}\left(\mathbb{U}\right)$ of the open unit disk $\mathbb{U}$ under the function $\mathcal{G}\left(\varsigma \right)$ is shown in the Figure 1. These coefficients are called James Gregory coefficients, as he first introduced them in 1670 in connection with numerical integration. Ultimately, numerous mathematicians have revisited and investigated them, enhancing their significance in the works of prominent figures. Their significance continues to be recognized in modern mathematical literature.

In this paper, we explore the generating function of the Gregory coefficients, represented as $\mathcal{G}\left(\varsigma \right)$, which is defined as follows (see [23,24,25,26]):

$${\mathcal{G}}_g^{*}\left(\varsigma \right)=1+{\displaystyle \frac{1}{2}}\varsigma -{\displaystyle \frac{1}{12}}{\varsigma }^2+{\displaystyle \frac{1}{24}}{\varsigma }^3-{\displaystyle \frac{19}{720}}{\varsigma }^4+{\displaystyle \frac{3}{160}}{\varsigma }^5-{\displaystyle \frac{863}{60,480}}{\varsigma }^6+\cdots .$$

Inspired by the aforementioned studies, we establish the subclass of bi-univalent functions ${\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$ as described below.

Definition 1.

A function $l\in \Sigma$ defined by (1) is said to be in the class ${\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$ if it meets the following criteria:

$$R\left(\varsigma \right):(1-\alpha ){\displaystyle \frac{{\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)}{\varsigma }}+\alpha {\left({\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)\right)}^{\prime }+\beta \varsigma {\left({\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)\right)}^{″}\prec \mathcal{G}\left(\varsigma \right)$$

and

$$K\left(x\right):(1-\alpha ){\displaystyle \frac{{\mathfrak{M}}_{\rho ,\eta }g\left(x\right)}{x}}+\alpha {\left({\mathfrak{M}}_{\rho ,\eta }g\left(x\right)\right)}^{\prime }+\beta x{\left({\mathfrak{M}}_{\rho ,\eta }g\left(x\right)\right)}^{″}\prec \mathcal{G}\left(x\right),$$

where $\varsigma ,x\in \Omega$, $\alpha ,\beta \ge 0$, $\rho ,\eta >-1$, with the function $g\left(x\right)=l^{-1}\left(x\right)$ defined by (3).

Remark 1.

We would like to highlight that the class ${\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$ is not empty. we note that $l_{*}\left(\varsigma \right)=\varsigma +{\displaystyle \frac{(d_1-2)\Gamma (\rho +\eta )}{2(1+\alpha +2\beta )\Gamma \left(\eta \right)}}{\varsigma }^2\in {\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$, it become simple to verify $l_{*}\left(\varsigma \right)\in \mathcal{S}, and, therefore, l_{*}\left(\varsigma \right)\in \Sigma withg\left(x\right)=l^{-1}\left(x\right)=x-{\displaystyle \frac{(d_1-2)\Gamma (\rho +\eta )}{2(1+\alpha +2\beta )\Gamma \left(\eta \right)}}{x}^2.$

Remark 2.

Using the fact that $R(-a\varsigma )=K\left(a\varsigma \right)$ for all $\varsigma \in \Omega$ confirms that the images of the mappings coincide, that is, $R(\Omega )=K(\Omega )$, for particular choices of $l_{*}\left(\varsigma \right)$ and $g_{*}\left(x\right)$. The 2D plot of R, K, and $\mathcal{G}$ is as shown in Figure 2. Since $\mathcal{G}$ is univalent in Ω, we obtain the subordinations $l_{*}\left(\varsigma \right)\prec \mathcal{G}\left(\varsigma \right)$ and $g_{*}\left(x\right)\prec \mathcal{G}\left(x\right)$, which hold whenever $l_{*}\left(0\right)=g_{*}\left(0\right)=\mathcal{G}\left(0\right)$ and $l_{*}(\Omega )=g_{*}(\Omega )\subset \mathcal{G}(\Omega )$.

The following lemma will ultimately be employed for the proof of our result.

Lemma 1

([27], Lemma 7, p.2)). Let $k,s\in \mathbb{R}$ and ${\varsigma }_1,{\varsigma }_2\in \mathbb{C}$. If $|{\varsigma }_1|<R,|{\varsigma }_2|<R$, then

$$\begin{array}{c}\hfill \left|(k+s){\varsigma }_1+(k-s){\varsigma }_2\right|\le \left\{\begin{array}{cc}2\left|s\right|R,\hfill & \mathrm{for}\left|k\right|\le \left|s\right|,\hfill \\ \\ 2\left|k\right|R,\hfill & \mathrm{for}\left|k\right|\ge \left|s\right|.\hfill \end{array}\right.\end{array}$$

The objective of this paper is to introduce two new subclasses of bi-univalent functions and to provide coefficient estimates, $|a_2|$ and $|a_3|$, for the functions belonging to these subclasses.

2. Main Results

This section of the paper is dedicated to analyzing the bounds for the modulus of the initial coefficients of functions within the class ${\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$.

Theorem 1.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$; then

$$\left|a_2\right|\le {\displaystyle \frac{1}{\sqrt{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}},$$

$$\left|a_3\right|\le {\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}+{\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}.$$

Proof. 

Let $l\in {\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$. We can write

$$(1-\alpha ){\displaystyle \frac{{\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)}{\varsigma }}+\alpha {\left({\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)\right)}^{\prime }+\beta \varsigma {\left({\mathfrak{M}}_{\rho ,\eta }l\left(\varsigma \right)\right)}^{″}=\mathcal{G}\left(p\left(\varsigma \right)\right)$$

(7)

and

$$(1-\alpha ){\displaystyle \frac{{\mathfrak{M}}_{\rho ,\eta }g\left(x\right)}{x}}+\alpha {\left({\mathfrak{M}}_{\rho ,\eta }g\left(x\right)\right)}^{\prime }+\beta x{\left({\mathfrak{M}}_{\rho ,\eta }g\left(x\right)\right)}^{″}=\mathcal{G}\left(q\left(x\right)\right),$$

(8)

where $p\left(\varsigma \right)=d_1\varsigma +d_2{\varsigma }^2+d_3{\varsigma }^3+...$ and $q\left(x\right)=e_{1}x+e_2{x}^2+e_3{x}^3...$ such that $p\left(0\right)=q\left(0\right)=0$ and $\left|p\left(\varsigma \right)\right|<1$, $\left|q\left(\varsigma \right)\right|<1$, for all $\varsigma ,x\in \Omega$.

• Equating coefficients of like powers of $\varsigma$ and x in (7) and (8), and using (3), we get

$${\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}(1+\alpha +2\beta ){\gamma }_2={\displaystyle \frac{d_1}{2}}$$

(9)

$${\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta ){\gamma }_3={\displaystyle \frac{1}{2}}\left(d_2-{\displaystyle \frac{d_1^2}{6}}\right)$$

(10)

$$-{\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}(1+\alpha +2\beta ){\gamma }_2={\displaystyle \frac{e_1}{2}}$$

(11)

$${\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )(2{\gamma }_2^2-{\gamma }_3)={\displaystyle \frac{1}{2}}\left(e_2-{\displaystyle \frac{e_1^2}{6}}\right)$$

(12)

From (9) and (11),

$$d_1=-e_1$$

(13)

Squaring and adding (9) and (11), we obtain

$$8{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{(1+\alpha +2\beta )}^2{\gamma }_2^2=d_1^2+e_1^2$$

(14)

Adding (10) and (12), using (14), we obtain

$${\gamma }_2^2={\displaystyle \frac{d_2+e_2}{{\displaystyle \frac{4\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}$$

(15)

$$\left|{\gamma }_2\right|\le {\displaystyle \frac{1}{\sqrt{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}}.$$

Further, subtracting (12) from (10) and using (13), we have

$${\gamma }_3={\displaystyle \frac{\Gamma (2\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}(d_2-e_2)+{\displaystyle \frac{d_2+e_2}{{\displaystyle \frac{4\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}$$

(16)

$$\left|{\gamma }_3\right|\le {\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}+{\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}.$$

□

3. Fekete–Szegö Functional for the Function Class ${\mathcal{M}}_{\Sigma }^{\mathit{\rho },\mathit{\eta }}(\mathit{\alpha },\mathit{\beta })$

Theorem 2.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }^{\rho ,\eta }(\alpha ,\beta )$; then

$$\begin{array}{c}\hfill \left|{\gamma }_3-\varphi {\gamma }_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)(1+2\alpha +6\beta )}},\hfill & \mathit{for}|1-\varphi |\le H_1,\hfill \\ \\ {\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}},\hfill & \mathit{for}|1-\varphi |\ge H_1.\hfill \end{array}\right.\end{array}$$

where

$$H_1=1+{\displaystyle \frac{\Gamma \left(\eta \right)\Gamma (2\rho +\eta ){(1+\alpha +2\beta )}^2}{{\left(\Gamma (\rho +\eta )\right)}^2(1+2\alpha +6\beta )}}.$$

Proof. 

From (15) and (16), we have

$$\begin{array}{cc}\hfill {\gamma }_3-\varphi {\gamma }_2^2& ={\displaystyle \frac{\Gamma (2\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}(d_2-e_2)\hfill \\ \hfill & +{\displaystyle \frac{d_2+e_2}{{\displaystyle \frac{4\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}\hfill \\ \hfill & -\varphi {\displaystyle \frac{d_2+e_2}{{\displaystyle \frac{4\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}\hfill \end{array}$$

$${\gamma }_3-\varphi {\gamma }_2^2=\left[F\left(\varphi \right)+{\displaystyle \frac{\Gamma (2\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}\right]d_2+\left[F\left(\varphi \right)-{\displaystyle \frac{\Gamma (2\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}\right]e_2$$

(17)

where

$$F\left(\varphi \right)={\displaystyle \frac{\left|1-\varphi \right|}{{\displaystyle \frac{4\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}}$$

According to Lemma 1 and (17), we get

$$\begin{array}{c}\hfill \left|{\gamma }_3-\varphi {\gamma }_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{2\Gamma (2\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}},\hfill & \mathrm{for}\left|F\left(\varphi \right)\right|\le {\displaystyle \frac{2\Gamma (\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}},\hfill \\ \\ 2\left|F\right(\varphi \left)\right|,\hfill & \mathrm{for}\left|F\left(\varphi \right)\right|\ge {\displaystyle \frac{2\Gamma (\rho +\eta )}{4\Gamma \left(\eta \right)(1+2\alpha +6\beta )}}.\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left|{\gamma }_3-\varphi {\gamma }_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)(1+2\alpha +6\beta )}},\hfill & \mathrm{for}|1-\varphi |\le H_1,\hfill \\ \\ {\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha +6\beta )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha +2\beta \right)}^2}},\hfill & \mathrm{for}|1-\varphi |\ge H_1.\hfill \end{array}\right.\end{array}$$

where

$$H_1=1+{\displaystyle \frac{\Gamma \left(\eta \right)\Gamma (2\rho +\eta ){(1+\alpha +2\beta )}^2}{{\left(\Gamma (\rho +\eta )\right)}^2(1+2\alpha +6\beta )}}.$$

□

4. Particular Cases

The following results are obtained by considering particular values of the parameters $\beta$ and $\alpha$ in the above theorems.

Example 1.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }(\alpha ,0)$; then

$$\left|{\gamma }_2\right|\le {\displaystyle \frac{1}{\sqrt{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha \right)}^2}}},$$

$$\left|{\gamma }_3\right|\le {\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)(1+2\alpha )}}+{\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha \right)}^2}}.$$

Example 2.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }(\alpha ,0)$; then

$$\begin{array}{c}\hfill \left|{\gamma }_3-\varphi {\gamma }_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)(1+2\alpha )}},\hfill & \mathit{for}|1-\varphi |\le H_2,\hfill \\ \\ {\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}(1+2\alpha )+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2{\left(1+\alpha \right)}^2}},\hfill & \mathit{for}|1-\varphi |\ge H_2.\hfill \end{array}\right.\end{array}$$

where

$$H_2=1+{\displaystyle \frac{\Gamma \left(\eta \right)\Gamma (2\rho +\eta ){(1+\alpha )}^2}{{\left(\Gamma (\rho +\eta )\right)}^2(1+2\alpha )}}.$$

Example 3.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }(1,0)$; then

$$\left|{\gamma }_2\right|\le {\displaystyle \frac{1}{\sqrt{{\displaystyle \frac{6\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}+{\displaystyle \frac{8}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2}}},$$

$$\left|{\gamma }_3\right|\le {\displaystyle \frac{\Gamma (2\rho +\eta )}{6\Gamma \left(\eta \right)}}+{\displaystyle \frac{1}{{\displaystyle \frac{6\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}+{\displaystyle \frac{8}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2}}.$$

Example 4.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }(1,0)$; then

$$\begin{array}{c}\hfill \left|{\gamma }_3-\varphi {\gamma }_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{\Gamma (2\rho +\eta )}{6\Gamma \left(\eta \right)}},\hfill & \mathit{for}|1-\varphi |\le H_3,\hfill \\ \\ {\displaystyle \frac{1}{{\displaystyle \frac{6\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}+{\displaystyle \frac{8}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2}},\hfill & \mathit{for}|1-\varphi |\ge H_3.\hfill \end{array}\right.\end{array}$$

where

$$H_3=1+{\displaystyle \frac{4\Gamma \left(\eta \right)\Gamma (2\rho +\eta )}{3{\left(\Gamma (\rho +\eta )\right)}^2}}.$$

Example 5.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }(0,0)$; then

$$\left|{\gamma }_2\right|\le {\displaystyle \frac{1}{\sqrt{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2}}},$$

$$\left|{\gamma }_3\right|\le {\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)}}+{\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2}}.$$

Example 6.

Let $l\in \Sigma$, as given by (1), belong to the class ${\mathcal{M}}_{\Sigma }(0,0)$; then

$$\begin{array}{c}\hfill \left|{\gamma }_3-\varphi {\gamma }_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{\Gamma (2\rho +\eta )}{2\Gamma \left(\eta \right)}},\hfill & \mathit{for}|1-\varphi |\le H_4,\hfill \\ \\ {\displaystyle \frac{1}{{\displaystyle \frac{2\Gamma \left(\eta \right)}{\Gamma (2\rho +\eta )}}+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{\Gamma \left(\eta \right)}{\Gamma (\rho +\eta )}}\right)}^2}},\hfill & \mathit{for}|1-\varphi |\ge H_4.\hfill \end{array}\right.\end{array}$$

where

$$H_4=1+{\displaystyle \frac{\Gamma \left(\eta \right)\Gamma (2\rho +\eta )}{{\left(\Gamma (\rho +\eta )\right)}^2}}.$$

5. Conclusions

In this work, we have presented a novel subclass of bi-univalent functions associated with Mittag–Leffler functions within the open unit disk, which are linked to Gregory polynomials and fulfill specific subordination criteria. By establishing limits for the Taylor–Maclaurin coefficients $|{\gamma }_2|$ and $|{\gamma }_3|$, we have enhanced the comprehension of these functions’ dynamics. Moreover, our research on the Fekete–Szegö functional has resulted in an improved understanding of the subclass’s attributes. By specializing parameters, we have revealed various new discoveries that enhance the wider theory of bi-univalent functions.