A Novel Dynamic Edge-Adjusted Graph Attention Network for Fire Alarm Data Mining and Prediction

Abstract

Modern fire alarm systems are essential for public safety, yet they often fail to exploit the wealth of historical alarm data and the complex spatiotemporal dependencies inherent in urban environments. Graph Neural Networks (GNNs) are currently among the most popular methods for handling complex spatiotemporal dependencies. While a range of dynamic GNN approaches have been proposed, many existing GNN-based predictors still rely on a static topology, which limits their ability to fully capture the evolving nature of risk propagation. Furthermore, even among dynamic graph methods, most focus on temporal link prediction or social interaction modeling, with limited exploration in safety-critical applications such as fire alarm prediction. DeaGAT dynamically updates inter-building edge weights through an attention mechanism, enabling the graph structure to evolve in response to shifting risk patterns. A margin-based contrastive learning objective further enhances the quality of node embeddings by distinguishing subtle differences in risk states. In addition, DeaGAT jointly models static building attributes and dynamic alarm sequences, effectively integrating long-term semantic context with short-term temporal dynamics. Extensive experiments on real-world datasets, including comparisons with state-of-the-art baselines and comprehensive ablation studies, demonstrate that DeaGAT achieves superior accuracy and F1-score, validating the effectiveness of dynamic graph updating and contrastive learning in enhancing proactive fire early-warning capabilities.

1. Introduction

Fire alarm systems are a critical component of public safety infrastructure, designed to detect signs of fire and promptly alert occupants and emergency responders [1]. Timely and accurate warnings are vital for safeguarding lives and protecting property, as delayed or missed alarms can lead to devastating consequences. However, most current systems remain reactive in nature; they trigger alerts only after sensor thresholds are breached without the ability to anticipate risks before incidents occur. Crucially, these systems often overlook the rich historical alarm records and the complex spatiotemporal dependencies inherent in urban environments, rendering fire prediction a largely unsolved spatiotemporal sequence forecasting problem. To enable proactive fire preparedness, there is a pressing need for predictive frameworks that can leverage historical patterns and evolving urban risk dynamics to forecast where and when fire alarms are likely to occur. GNNs have emerged as one of the most effective methods for spatio-temporal prediction tasks, owing to their ability to naturally model complex spatial interactions and temporal dependencies via message passing on graph-structured data [2]. By modeling entities (e.g., buildings or sensors) as nodes and their relationships as edges, GNNs can learn contextualized representations that incorporate both local and global information. Attention-based GNN variants, such as Graph Attention Networks (GATs), further enhance data-dependent weights to edges, improving interpretability and robustness under varying conditions. These capabilities have led to successful applications of GNNs in domains. However, most existing GNN models either assume a static topology (e.g., STSGCN [3], MTGNN [4]) or modify model parameters over time without explicitly updating the underlying graph structure (e.g., TGAT [5], TGN [6]). This limits their capacity to model dynamic changes in risk propagation across urban environments. Moreover, their black-box weight nature may obscure subtle signals tied to specific locations, reducing interpretability and responsiveness. These challenges call for a new method that can dynamically adapt the graph structure in response to evolving risk conditions while maintaining strong predictive and interpretive capabilities.

2. Related Work

Our proposed method is closely related to advancements in fire alarm data mining and spatio-temporal data analysis using the GNN method. This section provides a comprehensive overview of related work in both areas, with an emphasis on their limitations in modeling dynamic graph evolution. These limitations serve to motivate our proposed method.

2.1. Fire Alarm Data Mining and Prediction

Recent years have witnessed the increasing use of big data analytics to enhance the intelligence and responsiveness of fire warning systems. By analyzing historical fire incidents, climatic conditions, and environmental factors, traditional methods attempt to identify fire risk patterns. Traditional big data analytics [7] leverages historical alarm records and environmental variables to identify risk patterns but often fails to jointly model spatial adjacency and temporal evolution, resulting in coarse-grained forecasts that cannot capture real-time propagation dynamics. Conventional approaches, such as historical data mining [7], satellite remote sensing [8], and multi-sensor fusion [9], each have notable limitations. Specifically, big data methods often fail to jointly model spatial adjacency and temporal dynamics, resulting in coarse-grained forecasts that cannot capture real-time propagation. Remote sensing provides wide coverage but suffers from low spatial resolution and latency, compromising timeliness [8]. Multi-sensor fusion improves detection accuracy via techniques like weighted averaging, Kalman filtering, and Bayesian inference [9]. However, these methods incur significant system complexity, maintenance burden, and error accumulation.

Machine learning models, such as deep neural networks, random forests (RFs) [10], and support vector machines (SVMs) [11], show strong predictive power but lack interpretability and overlook the inherent graph structure in sensor deployments. Meanwhile, IoT- and AI-integrated systems [12] enhance response coordination and evacuation planning yet struggle with cross-agency resource allocation and real-time optimization.

Most existing emergency systems focus on post-event resource management, rather than proactive risk forecasting. This highlights the need for methods capable of simultaneously modeling spatial dependencies and temporal dynamics. GNNs offer a promising solution by modeling sensor networks as graphs, where spatial relationships are encoded via message passing and temporal changes are captured using recurrent or attention-based architectures. Unlike grid-based or sequence-based methods, GNNs preserve the irregular distribution of sensor nodes and support both local and global pattern learning. Attention-based variants further improve interpretability and robustness by dynamically adjusting edge weights.

Although GNNs are still underutilized in fire warning systems, they have demonstrated strong performance in spatio-temporal prediction tasks across various domains, offering valuable insights into fire propagation patterns and potential impacts.

2.2. Spatio-Temporal Data Analysis with GNN

Graph neural networks have shown considerable success in modeling spatio-temporal data, but existing models often fall short when dealing with the dynamic evolution of graph structures. Early models operate on static graphs, where message passing and feature aggregation are performed on a fixed topology to derive node or graph-level representations. Xu et al. proposed TGAT, which incorporates functional time encoding into an attention mechanism [5]. While effective for short sequences, it requires deep stacking for long-range dependencies, suffers from time aliasing, and incurs high latency. Rossi et al. introduced TGN, which maintains memory states for each node and updates them in an event-driven manner [6]. Although this enables streaming inference, it suffers from high memory usage, limited parallelism, and vulnerability to concept drift.

Subsequent methods have attempted to extend static GNNs to dynamic graph scenarios, where nodes and edges may emerge, disappear, or change over time. Zhang et al. introduced STSGCN with spatio-temporal graph convolutions and Huber loss, but its sparse representations and limited temporal depth reduce performance [3]. Pareja et al. developed EvolveGCN, which evolves GCN parameters using recurrent neural networks (RNNs). While adaptive, the method struggles with scalability due to recurrent computation overhead [13]. Gao et al. combined temporal convolutions with graph structure learning in MTGNN, but the model performs poorly with long-range dependencies and rapidly evolving graphs [4]. Zhou et al. developed STGormer, a transformer-based model [14]. Despite its flexibility and ability to capture long-range spatio-temporal dependencies, it suffers from quadratic complexity in sequence length and fixed spatial encodings, which limit scalability and adaptability to large dynamic graphs.

Recent advances have introduced more sophisticated spatio-temporal GNN variants, including Transformer-based methods, diffusion-based models, and event-driven architectures. Spatio-temporal Transformers, such as LVSTformer, leverage self-attention to capture long-range temporal and spatial dependencies, thereby enhancing the representation of complex spatio-temporal patterns [15]. However, they suffer from high computational and memory costs, especially for long sequences or large graphs. Diffusion-based models, such as DiffSTG, integrate denoising diffusion probabilistic models with spatio-temporal GNNs to capture uncertainty and intricate dynamics [16]; yet, the iterative denoising process imposes substantial computational overhead, limiting real-time applicability. Similarly, Wang et al. incorporated Hawkes processes into GNNs (HP-DGNN) to model event cascades, but this approach also entails high computational costs ($O\left(\right|E\left|\right)$ per step) and relies on restrictive assumptions regarding event excitation [17].

Although these methods attempt to extend GNNs for spatio-temporal prediction, they still inadequately capture the evolving nature of graph structures. Key limitations include inefficient dynamic graph updates, challenges with long-term temporal dependencies, poor scalability on large-scale data, and high computational costs for Transformer or diffusion-based approaches. These gaps motivate the development of our Dynamic Edge-Adjusted Graph Attention Network DeaGAT, which explicitly addresses dynamic edge evolution while maintaining robust performance in fire alarm prediction.

3. Dynamic Edge-Adjusted Graph Attention Network

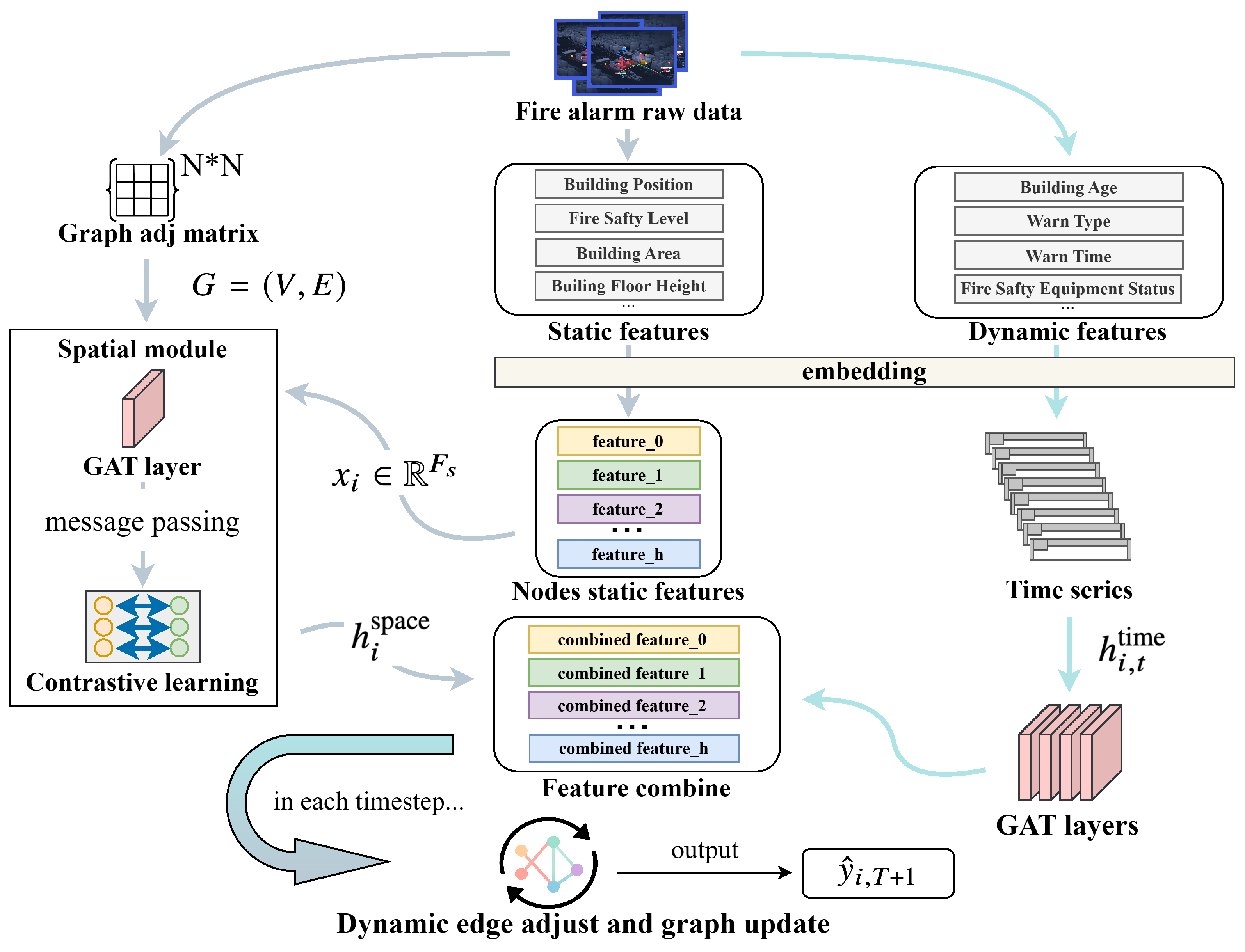
In this section, we propose DeaGAT, a novel dynamic edge adjusted graph attention network. Figure 1 illustrates the overall architecture of the proposed model. The figure highlights the flow of information through the network, showing how static building features and dynamic temporal signals are jointly processed. It also depicts the iterative update of edge weights and node embeddings over time, emphasizing the adaptive nature of the graph structure and the interaction between spatial and temporal information throughout the prediction horizon.

Compared with existing spatio-temporal prediction approaches [3,14], DeaGAT significantly enhances both prediction accuracy and interpretability by effectively integrating spatial and temporal dependencies through adaptive graph learning. This design effectively addresses a key limitation of these methods, namely their of the dynamic evolution of underlying graph structures in spatio-temporal forecasting tasks.

3.1. Task Formulation

We let $G_t=(V,E_t)$ denote the building–sensor graph at time step t, where $V=\{1,\dots ,N\}$ is the set of N building nodes and $E_t\subseteq V\times V$ represents the undirected edge set at time t, which may vary over time to reflect dynamic changes in spatial relationships or risk propagation.

Each node $i\in V$ is associated with static spatial features $x_i$, and at each time step t, $X_t$ collects the dynamic temporal features for all nodes. The multi-class alarm prediction task aims to predict, at the next time step $T+1$, the probability distribution over C possible alarm types for each node i:

$${\widehat{\mathbf{p}}}_{i,T+1}=\mathcal{F}\left({\left\{G_t\right\}}_{t=1}^T,{\left\{x_i\right\}}_{i=1}^N,{\left\{X_t\right\}}_{t=1}^T\right),$$

(1)

where ${\widehat{\mathbf{p}}}_{i,T+1}=({\widehat{p}}_{i,T+1}^{\left(1\right)},\dots ,{\widehat{p}}_{i,T+1}^{\left(C\right)})\in [0,1]$ with ${\sum }_{c=1}^C{\widehat{p}}_{i,T+1}^{\left(c\right)}=1$. The predicted class label is ${\widehat{y}}_{i,T+1}=arg{max}_c{\widehat{p}}_{i,T+1}^{\left(c\right)},$ and $y_{i,T+1}\in \{1,\dots ,C\}$ denotes the ground-truth alarm type for node i at time $T+1$.

3.2. Spatial Feature Extraction Module

This component extracts static node embeddings that summarize the most informative neighbors and regularizes those embeddings so that they respect the topological structure of the graph.

We adopt the Graph Attention Network introduced in [18], as its attention mechanism assigns data-dependent weights to arbitrary-sized neighborhoods, offering improved adaptability over fixed-weight message passing in GCN [19], particularly for irregular sensor layouts. First, each building node is embedding into a latent space that captures static spatial correlations.

A shared linear layer produces the initial hidden vector followed by multi-head attention to aggregate neighbor information. Given a static attribute vector $x_i\in {\mathbb{R}}^{F_s}$, where $F_s$ denotes the dimensionality of the original static node features, a shared linear layer parameterized by weight matrix $W\in {\mathbb{R}}^{F_h\times F_s}$ projects the original features into a lower-dimensional embedding space of size $F_h$:

$$h_i^{\mathrm{space}}=W{x}_i$$

(2)

To further encourage topology-aware representations, we adopt a margin-based contrastive loss inspired by [20]. This loss enlarges the distance between unconnected nodes while contracts the distance between connected ones.

This geometric constraint prevents embedding collapse, enhances class separability under limited supervision, and improves downstream alarm prediction:

$${\mathcal{L}}_{\mathrm{contrast}}={\displaystyle \frac{1}{\left|\mathcal{P}\right|}}\sum _{(i,j)\in \mathcal{P}}{y}_{ij}\parallel h_i^{\mathrm{space}}-h_j^{\mathrm{space}}{\parallel }^2+(1-y_{ij})max\{0,m-\parallel h_i^{\mathrm{space}}-h_j^{\mathrm{space}}{\parallel \}}^2$$

(3)

where $y_{ij}=1$ if $(i,j)\in E$ and 0 otherwise, $\mathcal{P}$ denotes the sampled set of node pairs, and m is a margin hyper-parameter. This spatial regularization term is later integrated with the supervised prediction loss (Equation (8)) to form the final training objective.

3.3. Temporal-Aware Graph Evolution Module

Beyond static spatial relationships, fire alarm events exhibit significant temporal dynamics. This module integrates time-series information and enables the graph structure to evolve over time in response to changing node features. We partition the historical timeline into T discrete intervals (e.g., monthly aggregations). For each node i at time t, we derive a temporal feature vector $h_{i,t}^{\mathrm{time}}$ from the alarm records, such as the number of alarms in interval t, the most recent alarm type, or other time-dependent indicators. This temporal feature is concatenated with the node’s spatial embedding $h_i^{\mathrm{space}}$ to form a joint representation.

Specifically, for each node i at time step t, we concatenate its spatial feature (obtained from the spatial module, which is generally time-invariant or computed from historical data up to t) with its current temporal feature $h_{i,t}^{\mathrm{time}}$:

$$h_{i,t}^{\mathrm{combined}}=h_i^{\mathrm{space}}\oplus h_{i,t}^{\mathrm{time}}$$

(4)

where ⊕ denotes vector concatenation.

We then use a graph attention mechanism (similar to that in the spatial module) [18] to re-evaluate the relationships between nodes based on these combined features. In particular, we compute new attention scores ${\tilde{e}}_{ij,t}$ for node pairs $(i,j)$ by applying the attention formula [18] on $h_{i,t}^{\mathrm{combined}}$ and $h_{j,t}^{\mathrm{combined}}$, and obtain updated attention coefficients ${\tilde{\alpha }}_{ij,t}$ via a softmax [21]. These attention values ${\tilde{\alpha }}_{ij,t}$ now reflect the similarity or influence between nodes i and j at time t, taking into account the latest temporal information.

To allow the graph structure to adapt dynamically, we introduce a threshold-based mechanism: an edge between nodes i and j at time t is retained if and only if the attention coefficient ${\tilde{\alpha }}_{ij,t}$ exceeds a pre-defined threshold k.

Formally, we let $E_t$ be the set of edges active at time t; then after computing ${\tilde{\alpha }}_{ij,t}$, we update the edge set as

$$E_t^{\prime }=\{(i,j)\mid {\tilde{\alpha }}_{ij,t}>k\}$$

(5)

The threshold k serves as a hyperparameter controlling the sparsity of the dynamic graph. A higher k results in a graph sparser, preserving only the most connections, while a lower k retains more edges. In practice, k can be tuned based on validation performance or set heuristically.

Subsequently, we construct an updated graph $G_t^{\prime }$ for the next time step:

$$G_t^{\prime }=\mathrm{UPDATE}(G_t,E_t^{\prime })$$

(6)

where $\mathrm{UPDATE}(G_t,E_t^{\prime })$ produces a new graph $G_t^{\prime }=(V,E_t^{\prime })$ with the same node set V but a modified edge set.

By iteratively updating the graph structure at each time step according to Equation (5), the model can introduce or remove connections between nodes as their feature similarity changes over time. The temporal module processes data sequentially from $t=1$ to T; it combines features (Equation (4)), updates node representations using attention, and adjusts the graph structure (Equations (5) and (6)). After the final time step T, each node possesses an updated feature $h_{i,T}^{\prime }$ that encodes both spatial and recent temporal information, and the graph evolves to $G_T^{\prime }$. These final node features can then be utilized to predict the occurrence of a fire alarm at the next time step $T+1$ (e.g., by feeding $h_{i,T}^{\prime }$ into a classifier or regression layer to output ${\widehat{y}}_{i,T+1}$).

3.4. Training Procedure and Loss Functions

As a result of the joint optimisation detailed below, the trained DeaGAT is able to issue precise and robust early-warning forecasts of future fire-alarm events.

During each training step, the input mini-batch is propagated through the spatial encoder, the contrastive branch, and the temporal module (Algorithm 1).

We let ${\widehat{\mathbf{p}}}_i=({\widehat{p}}_i^{\left(1\right)},{\widehat{p}}_i^{\left(2\right)},\dots ,{\widehat{p}}_i^{\left(C\right)})$ denote the predicted probability distribution over C alarm classes for node i and let ${\mathbf{y}}_i$ represent the corresponding one-hot encoded ground-truth label. The supervised prediction loss is computed using categorical cross-entropy [22], which effectively penalises predictions that diverge from the correct distribution, thus improving model calibration and discriminative power:

$${\mathcal{L}}_{\mathrm{pred}}=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{c=1}^C{y}_i^{\left(c\right)}log\left({\widehat{p}}_i^{\left(c\right)}\right)$$

(7)

where $y_i^{\left(c\right)}=1$ if node i belongs to class c and 0 otherwise.

To regularize the node representations and encourage topology-aware embeddings, we incorporate a contrastive loss term $L_{\mathrm{contrast}}$ (Equation (3)). The final loss function is as follows:

$$L_{\mathrm{total}}=L_{\mathrm{pred}}+\lambda L_{\mathrm{contrast}}$$

(8)

Here, $\lambda$ is a hyperparameter that balances predictive accuracy and representation structure.

Gradients of $\lambda$ are backpropagated to update all trainable parameters of the proposed model via the Adam optimizer.

Only these two loss components are required; no additional auxiliary terms or scheduling tricks are introduced, keeping the optimization pipeline straightforward and reproducible.

Algorithm 1 DeaGAT Model for Fire Alarm Prediction

Require: Static graph $G=(V,E)$ with initial static node features $\{x_i:i\in V\}$; temporal input data $\{X_t:t=1,\dots ,T\}$, where each $X_t=\{h_{i,t}^{\mathrm{time}}:i\in V\}$; attention threshold k.

Ensure: Updated graph $G^{\prime }$ and node feature set $H^{\prime }=\{h_i^{\prime }:i\in V\}$ after processing the current time step t.   1: Spatial Feature Extraction: For each node $i\in V$, apply GAT on G using static features $x_i$ to compute spatial embeddings $h_i^{\mathrm{space}}$.   2: Temporal Feature Extraction: For each node $i\in V$, obtain the current temporal embedding $h_{i,t}^{\mathrm{time}}$.   3: Feature Combination: For each node i, concatenate its temporal embedding $h_{i,t}^{\mathrm{time}}$ with spatial embedding $h_i^{\mathrm{space}}$ to form the combined feature vector (Equation (4)).   4: for each node $i\in V$ do   5:    Update node i’s feature to the combined vector: $X_i\leftarrow h_{i,t}^{\mathrm{combined}}$.   6: end for   7: Attention-based Feature Aggregation: For each node $i\in V$, compute an updated feature $h_i^{\prime }$ by aggregating features of i’s neighbors through the attention mechanism.   8: Graph Update: Determine important connections by thresholding attention coefficients with threshold k, updating edge set $E^{\prime }$(Equation (5)), where ${\alpha }_{ij}$ denotes the attention coefficient between node i and node j. This yields the updated graph $G^{\prime }=(V,E^{\prime })$ for the next time step.   9: Return the updated graph $G^{\prime }$ and node features $H^{\prime }=\{h_i^{\prime }:i\in V\}$.

Algorithm 1 outlines the prediction process of the proposed DeaGAT model. At each time step, the model first applies spatial feature extraction using a GAT to encode the static spatial context into node embeddings $h_i^{\mathrm{space}}$. These spatial embeddings are then concatenated with the corresponding temporal input features $h_{i,t}^{\mathrm{time}}$ to form the combined representations $h_{i,t}^{\mathrm{combined}}$ (Equation (4)). Subsequently, another attention-based aggregation is performed to produce the new node embeddings $h_i^{\prime }$. The attention coefficients obtained during this aggregation are further used to prune and update the graph structure by pruning less significant edges (Equation (5)), thereby generating an updated graph $G^{\prime }$ for the next time step (Equation (6)). Through this recurrent mechanism of feature updating and graph refinement, the DeaGAT effectively captures both spatial and temporal features of the fire alarm data.

4. Experiments

To comprehensively evaluate the practical effectiveness and robustness of the proposed framework, we conduct a series of experiments designed to validate its capability for spatio-temporal fire alarm prediction. We first compare our proposed DeaGAT model with state-of-the-art spatio-temporal baseline methods to verify its advantage in accurately modeling complex spatial interactions and temporal dependencies identified in related work. Then, we perform detailed ablation studies to quantitatively assess the individual contributions of each major component—the static spatial encoder, temporal graph updater, and the joint training objective—demonstrating how these components collaboratively enhance prediction performance. The details of the experimental dataset, selected baselines, evaluation metrics, and implementation settings are presented in the following subsections.

4.1. Dataset and Experimental Setup

Dataset: We evaluate our method on a private, large-scale fire alarm dataset collected from an IoT-based fire alarm platform in a major city. The dataset comprises 371,632 fire alarm records spanning from November 2019 to May 2023.

Each record includes the alarm occurrence time and alarm type as dynamic features, along with static attributes of the associated buildings, such as building area, height, and the number of floors.

An initial building-sensor graph is constructed, where each node represents a building. Edges between buildings are established based on geographic proximity; specifically, an edge is created if the differences in latitude and longitude between two buildings are less than 0.001 degrees, reflecting potential spatial correlations in fire incidents. Each node’s initial features consist of static attributes like fire safety rating and hazard levels, while dynamic alarm events constitute the temporal, time-varying features.

Experimental Setup: All models are trained and evaluated on the same split of the fire alarm dataset to ensure strict comparability. Specifically, we allocate 80% of the 371,632 labeled records to the training set (297,305 samples) and the remaining 20% (74,327 samples) to the test set. We use six metrics: accuracy, precision, recall, F1-score, area under the ROC curve (AUC) and average precision (AP) [23], and run every model 10 independent times with different random seeds, presenting the mean ± standard deviation.

In our DeaGAT model, the spatial module utilizes a GAT with 8 hidden units and 8 attention heads [18]. A dropout rate of 0.6 is applied to the attention coefficients to mitigate overfitting, and the attention weights are normalized using a softmax function. The temporal module begins by linearly projecting the dynamic event features of each time step into a 64-dimensional embedding. This projected vector is then element-wise summed with both the static node embeddings and the embeddings from the previous time step to generate a fused representation. The resulting fused vectors are passed through a graph attention convolution layer configured to map 64 input dimensions to 64 output dimensions using four attention heads. This layer includes automatic self-loop addition and averages the outputs of all heads, followed by a ReLU activation. The process is repeated at each time step to capture the evolving temporal dynamics of the nodes. The initial attention threshold for dynamic graph updates is set to $k=0.3$ [24]. Training is conducted for 200 epochs with a learning rate of 0.005 (with stepwise decay) and a weight decay of $5\times {10}^{-4}$ [25]. Each baseline model is either run with the hyper-parameters recommended in its original publication or tuned on a held-out validation subset drawn from the training data.

4.2. Baseline Methods

To ensure a comprehensive evaluation, we select baselines models that are widely recognized in the spatio-temporal prediction literature.

(1) Traditional non-graph models. Random forest (RF) [10] and support vector machine (SVM) [11] have been extensively employed as reference points in recent spatio-temporal studies [26]. Both models operate directly on tabular features without leveraging explicit graph structures.

(2) Static-graph GNNs. GAT [18] applies attention weighting on a fixed adjacency matrix. TGAT [5] extends attention mechanism to continuous-time edges through functional time encoding. TGN [6] enhances message passing with node memories, facilitating learning from streaming event graphs.

(3) Dynamic-graph GNNs. STSGCN [3] performs localized spatial–temporal convolutions on synchronous graph snapshots. EvolveGCN [13] treats GCN parameters as a recurrent state that evolves over discrete time steps. MTGNN [4] learns a data-driven adjacency matrix coupled with temporal convolutions for multivariate forecasting. STGormer [14] integrates graph structures with temporal position encodings in a Transformer-style architecture. HP-DGNN [17] embeds a Hawkes point process into a dynamic GNN to model mutually exciting event sequences.

(4) Proposed Model. The DeaGAT model dynamically prunes and grows edges via attention threshold k and further sharpens node embeddings with a contrastive objective, jointly leveraging static building attributes and streaming alarm signals.

4.3. Performance Analysis of Fire Alarm Data Prediction

Table 1. Comparison of prediction performance (mean ± standard deviation) with baseline methods. Boldface indicates the best result in each column. We added divider lines in the table to separate traditional machine learning methods, static graph network methods, dynamic graph network methods, and our proposed method.

Method	Accuracy	Precision	Recall	F1-Score	AUC	AP
Random Forest [10]	0.7415 ± 0.004	0.7202 ± 0.005	0.6850 ± 0.006	0.7020 ± 0.005	0.7814 ± 0.007	0.7453 ± 0.008
SVM [11]	0.7568 ± 0.006	0.7437 ± 0.007	0.7026 ± 0.009	0.7226 ± 0.008	0.8012 ± 0.010	0.7645 ± 0.011
GAT [18]	0.8460 ± 0.005	0.8250 ± 0.006	0.8000 ± 0.008	0.8120 ± 0.007	0.8655 ± 0.007	0.8321 ± 0.008
TGAT [5]	0.8580 ± 0.006	0.8400 ± 0.005	0.8205 ± 0.007	0.8300 ± 0.006	0.8850 ± 0.008	0.8173 ± 0.007
TGN [6]	0.8620 ± 0.005	0.8450 ± 0.005	0.8302 ± 0.006	0.8370 ± 0.006	0.8891 ± 0.006	0.8265 ± 0.007
STSGCN [3]	0.8553 ± 0.003	0.8307 ± 0.005	0.7928 ± 0.006	0.8113 ± 0.005	0.8840 ± 0.005	0.8025 ± 0.006
EvolveGCN [13]	0.8603 ± 0.005	0.8381 ± 0.006	0.8051 ± 0.007	0.8213 ± 0.006	0.8875 ± 0.007	0.8204 ± 0.008
MTGNN [4]	0.8682 ± 0.004	0.8528 ± 0.004	0.8374 ± 0.005	0.8450 ± 0.005	0.8922 ± 0.006	0.8541 ± 0.005
STGormer [14]	0.8770 ± 0.004	0.8680 ± 0.003	0.8600 ± 0.005	0.8640 ± 0.004	0.9025 ± 0.005	0.8742 ± 0.004
HP-DGNN [17]	0.8700 ± 0.005	0.8600 ± 0.005	0.8505 ± 0.006	0.8550 ± 0.005	0.8984 ± 0.006	0.8690 ± 0.006
DeaGAT	0.8864 ± 0.002	0.8783 ± 0.003	0.8680 ± 0.004	0.8731 ± 0.003	0.9147 ± 0.004	0.9025 ± 0.003

reports the classification performance of our DeaGAT and baseline models. As shown, DeaGAT consistently achieves the best results across all evaluation metrics, with an accuracy of $88.64\%$ and an F1-score of $87.31\%$. In contrast, STGormer [14] achieves $87.7\%$ accuracy and $86.4\%$ F1-score, while HP-DGNN [17] reaches $87\%$ accuracy and $85.5\%$ F1-score. DeaGAT also outperforms all other models in terms of AUC (91.47%) and AP (90.25%), surpassing the closest competitors by a clear margin.

Traditional machine learning models perform significantly worse. RF [10] achieves $74.15\%$ accuracy and $70.2\%$ F1-score, while SVM [11] yields $75.68\%$ accuracy and $72.26\%$ F1-score. These results highlight the limitations of flat classifiers in modeling the complex spatiotemporal dependencies inherent in fire-alarm data.

Graph-based methods show notable improvements over traditional models. For instance, a vanilla GAT [18], which captures static neighborhood relationships, attains 84.6% accuracy and 81.2% F1, yet still falls short of approaches that incorporate temporal dynamics. STSGCN [3], a spatiotemporal convolutional model, reaches 85.53% accuracy and 81.13% F1 but is limited by its fixed adjacency structure. Temporal GNNs such as TGAT [5] and TGN [6] further improve performance through time-aware attention yet still lag behind the top-performing models.

More advanced approaches demonstrate the benefits of adaptive graph structures and dynamic learning. MTGNN [4] achieves 86.82% accuracy and 84.5% F1, while EvolveGCN [13] achieves 86.03% accuracy and 82.13% F1, leveraging evolutionary weight updates. The transformer-based STGormer further boosts performance by modeling long-range dependencies, but its metrics still fall short of DeaGAT. Likewise, HP-DGNN, which incorporates Hawkes process modeling, improves AUC and AP but does not surpass DeaGAT’s performance.

Overall, these results demonstrate that DeaGAT’s integration of dynamic edge attention and contrastive learning effectively captures evolving spatial-temporal patterns, enabling the most accurate and robust predictions on the fire-alarm dataset.

4.4. Ablation Studies

We conduct ablation studies to evaluate the individual contributions of key components in the DeaGAT model. Specifically, we investigate the following elements: (i) the dynamic graph structure updating mechanism in the spatial module, (ii) the contrastive learning component for node representation enhancement, and (iii) the integration of static input features. To this end, we construct variant models in which each of these components is removed or disabled, and we assess the resulting impact on model performance.

First, we evaluate two simplified versions of the spatial module: one that retains only the GAT message-passing mechanism without contrastive learning and another that applies contrastive learning on node features without incorporating neighbor message passing.

Table 2. Ablation study results with mean ± standard deviation.

Model Variant	Accuracy	Precision	Recall	F1-Score
Without GAT Message Passing	0.6874 ± 0.006	0.6640 ± 0.007	0.6178 ± 0.008	0.6401 ± 0.007
Without Contrastive Learning	0.7523 ± 0.005	0.7475 ± 0.006	0.7190 ± 0.006	0.7329 ± 0.005
Without Static Features	0.8421 ± 0.004	0.8350 ± 0.005	0.8250 ± 0.005	0.8300 ± 0.004
DeaGAT	0.8864 ± 0.002	0.8783 ± 0.003	0.8680 ± 0.004	0.8731 ± 0.003

presents the classification metrics for each ablated variant and DeaGAT. As shown, removing either component leads to a noticeable drop in performance.

Specifically, the model without message passing achieves an accuracy of 68.74%, a recall of 61.78%, and an F1-score of 64.01%, indicating that without neighborhood aggregation, the model fails to capture crucial relational information. On the other hand, the variant without contrastive learning yields an accuracy of $75.23\%$ and an F1-score of $73.29\%$, suggesting that while structural aggregation enables local pattern learning, it lacks the discriminative strength provided by contrastive guidance. By comparison, the full DeaGAT model achieves an accuracy of $88.64\%$, an F1-score of $87.31\%$, and a recall of $86.80\%$, confirming that the synergy between message passing and contrastive learning is essential for achieving better performance in fire alarm prediction. Notably, the larger performance drop resulting from the removal of contrastive learning underscores its critical role in producing robust and discriminative node embeddings.

This table also analyzes the individual contributions of static features to predictive performance, thereby assessing whether the model can still predict alarms solely based on temporal feature variations in the absence of building-specific attributes.

To this end, we construct a “dynamic-only” model that omits static building attributes (using only time-series inputs). The dynamic graph updater and contrastive learning remain active, but the input feature set is restricted. The dynamic-only variant achieves an accuracy of $84.21\%$, a recall of $82.50\%$, and an F1-score of $83.00\%$, indicating that omitting static contextual information such as building size or hazard level significantly hampers overall performance. These findings confirm that static attributes provide essential risk priors while dynamic features convey real-time hazard evolution, and that DeaGAT’s strength derives from their joint exploitation within an adaptive graph structure and contrastive learning framework.

4.5. Hyperparameter Sensitivity

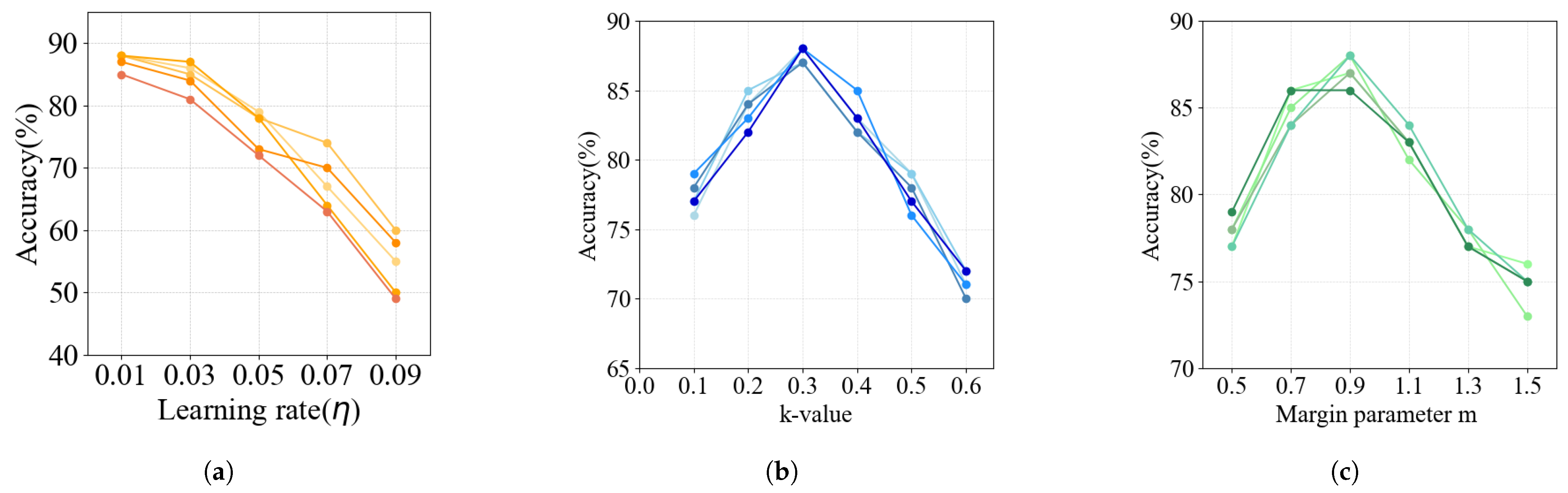
We further investigate the sensitivity of the DeaGAT model to key hyperparameters (Figure 2), including the learning rate $\eta$, the attention threshold k for graph updating, and the contrastive loss margin m. For each hyperparameter, we tune its value based on performance on a held-out validation set while keeping all other settings fixed and report the resulting model performance on the validation data. This procedure allows us to systematically assess how each hyperparameter influences the predictive accuracy of DeaGAT.

Learning rate ($\mathit{\eta }$): We train the model using different learning rates to examine their impact on convergence and accuracy. As shown in Figure 2a, very small learning rates (below 0.01) yield only marginal accuracy improvements but significantly prolong the training time, indicating slow convergence. In contrast, excessively large values (above 0.05) cause the model to diverge or converge to suboptimal solutions due to overshooting.

An intermediate learning rate around $\eta =0.05$ provides the best trade-off, achieving the highest accuracy while ensuring stable convergence. Thus, we set $\eta \approx 0.05$ as the optimal value for our proposed DeaGAT.

Attention threshold ($\mathit{k}$): This threshold in the spatial module determines how dynamically updated edges are selected based on attention weights. A higher k results in a sparser graph (fewer retained edges), while a lower k retains more connections. We test k in the range of 0.1 to 0.6. As shown in Figure 2b, the model achieves peak performance around $k=0.3$, where the attention mechanism effectively filters out weak or noisy connections while preserving the most informative relationships. Higher values (e.g., $k>0.3$) lead to excessive sparsity and the loss of crucial inter-node interactions, while lower values (e.g., $k=0.1$) risk overfitting to irrelevant or weak relationships. Thus, a moderate threshold ($k=0.3$) offers the best balance between informative structure and noise suppression.

Contrastive margin ($\mathit{m}$): The margin m in the contrastive loss determines how far apart representations of unconnected nodes are pushed in the embedding space. We experiment with various values of m. As illustrated in Figure 2c, performance improves as m increases, peaking at $m=0.9$. This value provides a clear separation between unrelated node pairs without destabilizing training. Smaller margins weaken the contrastive effect, resulting in embeddings of dissimilar nodes being insufficiently separated. Larger margins overemphasize negative pairs, potentially degrading the learning of subtle similarities among nodes. We can find that $m=0.9$ achieves the highest F1-score, demonstrating a well-balanced separation that supports both generalization and discrimination. Overall, the DeaGAT model is not overly sensitive to small deviations in hyperparameters around their optimal values. Appropriate tuning of the learning rate, attention threshold, and contrastive margin can enhance performance, but the model remains robust within a reasonable range. Our empirical results confirm that the chosen settings ($\eta =0.05$, $k=0.3$, $m=0.9$) represent a near-optimal configuration for the task, offering strong and stable performance.

4.6. Case Study on Interpretability

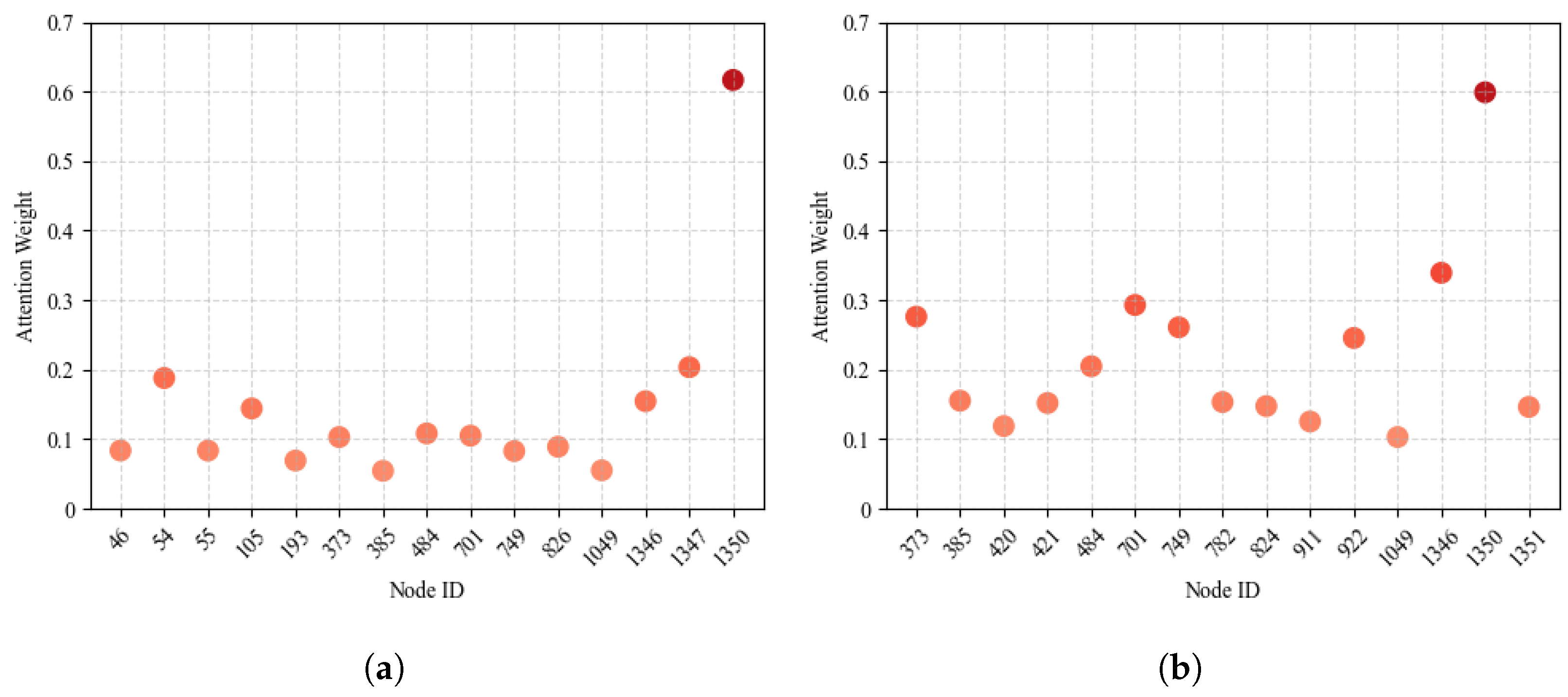
To investigate the interpretability of DeaGAT, we conducted a case study focusing on Node 1350. Specifically, we analyzed a fire alarm event that occurred on 29 July 2022 and tracked the 15 nodes with the highest attention weights in the graph both before and after the alarm. Statistical analysis of these key attention values was performed to examine how the model dynamically shifts focus across nodes in response to evolving conditions. The results, which illustrate the temporal redistribution of attention and highlight nodes that became critical leading up to the alarm, are presented in Figure 3.

From the above figure, several insights can be drawn:

Early detection of critical nodes: Node 1350 exhibits a prominently high attention weight of 0.62 prior to the alarm event, which is substantially higher than that of other nodes. This observation demonstrates that DeaGAT can successfully identify pivotal risk nodes in advance, underscoring the model’s effective early-warning capability in spatio-temporal prediction tasks.

Dynamic adaptation of attention: Following the alarm, the attention weight of Node 1350 decreases slightly to 0.60 afterward, while nodes closely associated with it, such as 1346 and 1351, experience an increase. Concurrently, Nodes 922, 701, and 373 show substantial attention growth, indicating the model’s ability to dynamically redistribute focus to emergent risk nodes as the event unfolds.

Context-sensitive modulation of node importance: Nodes that initially had elevated attention, such as 1347, demonstrate a reduction post-alarm, suggesting that their relative influence diminishes once primary risk nodes are activated. Conversely, nodes with previously low attention, including 54 and 105, maintain minimal weights, reflecting the model’s selective focus on nodes most relevant to the evolving risk scenario.

Collectively, this case study demonstrates the strong interpretability of DeaGAT, as the evolution of attention weights provides clear evidence of how the model prioritizes nodes under different risk conditions. By highlighting critical nodes before the alarm and adaptively redistributing attention to correlated nodes after the event, DeaGAT offers transparent insights into the mechanisms driving its predictions, thereby enhancing trust and practical applicability in safety-critical scenarios such as fire hazard forecasting.

5. Conclusions

In this study, we proposed a novel predictive model, DeaGAT, designed to enhance the early warning capabilities of fire alarm systems. Built upon the GAT architecture, the method effectively captures complex inter-node relationships and dynamically adjusts edge weights to reflect evolving spatial dependencies. By integrating contrastive learning, DeaGAT improves the discrimination of fire risk states and highlights key environmental factors contributing to alarm events. Extensive experimental results demonstrated that our method outperforms existing spatio-temporal data mining and machine learning approaches, particularly in dynamic edge adaptation, risk factor analysis, and generalization across diverse scenarios.

Looking forward, DeaGAT has the potential to be extended to a broader range of domains, including traffic flow management, public health monitoring, and environmental protection. To apply the model in these domains, certain adaptations may be required: for example, incorporating domain-specific node and edge features, handling heterogeneous or missing data, and ensuring scalability to larger and more complex networks. Moreover, practical deployment may face challenges such as real-time data streaming, system integration, and robustness to noisy or incomplete information. In particular, the reliability of DeaGAT under perturbations—such as noise in node features or temporal signals—requires careful consideration, as such uncertainties could affect attention-based edge refinement or contrastive loss components. Future work could explore strategies like adversarial training, robust attention mechanisms, or uncertainty-aware contrastive losses to enhance robustness. By addressing these challenges, DeaGAT can provide interpretable and reliable predictions, offering valuable insights for decision-making and policy support in diverse urban and societal contexts.