Abstract
Information geometry provides a data-informed geometric lens for understanding data or physical systems, treating data or physical states as points on statistical manifolds endowed with information metrics, such as the Fisher information. Building on this foundation, we develop a robust mathematical framework for analyzing data residing on Riemannian manifolds, integrating geometric insights into information-theoretic principles to reveal how information is structured by curvature and nonlinear manifold geometry. Central to our approach are tools that respect intrinsic geometry: gradient flow lines, exponential and logarithmic maps, and kernel-based principal component analysis. These ingredients enable faithful, low-dimensional representations and insightful visualization of complex data, capturing both local and global relationships that are critical for interpreting physical phenomena, ranging from microscopic to cosmological scales. This framework may elucidate how information manifests in physical systems and how informational principles may constrain or shape dynamical laws. Ultimately, this could lead to groundbreaking discoveries and significant advancements that reshape our understanding of reality itself.
MSC:
46; 49; 53; 60; 62
1. Introduction
Information geometry provides insights into understanding data or physical systems by treating data or physical states as points on statistical manifolds, which are equipped with information metrics such as the Fisher information. This viewpoint has become a vibrant interdisciplinary frontier at the crossroads of information and physics, enabling principled analysis of complex data and new information-derived formulations of physical laws [1]. The resulting program promises both conceptual advances—clarifying the link between information and state spaces—and practical benefits for data analysis and the exploration of physical phenomena, ranging from the quantum to the cosmological scale.
Building upon this conceptual foundation, we introduce a robust mathematical framework that leverages advanced geometric and statistical techniques to analyze data residing on Riemannian manifolds [2]. Central to our approach are methods that respect the intrinsic curvature and nonlinear structure of manifold data, such as flow lines of gradient vector fields, exponential and logarithmic maps, and kernel-based principal component analysis (PCA). Throughout the document, we provide a detailed explanation of these tools. They enable accurate, low-dimensional representations and insightful visualization of complex data structures, capturing both the local and global geometric relationships that are critical for understanding the underlying phenomena [3].
By integrating geometric insights with an information-theoretic perspective, our novel framework aims to elucidate the mechanisms by which information emerges in physical systems. This approach reinforces the compelling idea that informational principles are fundamental to the universe’s fabric [4]. It paves the way for exciting possibilities in both pioneering theoretical exploration and significant practical applications across various fields, including data analysis, physics, and more.
The concept that information functions as a fundamental building block of the universe is gaining remarkable momentum among scientists and philosophers [5]. This enlightening perspective suggests that, beyond the realms of matter and energy, information intricately weaves the very fabric of reality, shaping the structure and dynamics of everything from subatomic particles to vast cosmic phenomena. Recognizing information as a core component unlocks deep insights into the nature of physical laws, the origins of the universe, and the intricate interconnectedness of all existence. This paradigm shift not only enhances our understanding but also paves the way for groundbreaking explorations into the universe’s most profound mysteries.
In this initial article, we aim to present a solid mathematical framework and innovative conceptual tools for investigating the deep relationship between information and the physical universe, which has been explored in previous studies [4]. We begin by describing the information sources, the Riemannian structure of the parameter space, and Kernel methods. A significant portion of the article is dedicated to illustrating a data analysis application of the framework, with a particular focus on Kernel PCA. Additionally, we briefly introduce a physical application by expanding upon the variational principle previously published [4]. This information principle will be studied in greater detail in a subsequent manuscript.
By formalizing the principles that govern information processing and its manifestation within physical systems, we aim to uncover the intricate mechanisms through which information may emerge from or be embedded in the fundamental laws of physics. This approach not only establishes strong connections between abstract informational concepts and concrete physical models, but it also provides a solid foundation for investigating how information-theoretic principles could transform our understanding and inspire the development of new theories about the nature of reality.
2. Materials and Methods
In this section, we will meticulously establish a comprehensive mathematical framework by thoroughly defining the information sources and the intricate structure of the parameter space in Section 2.1. We will then examine the rich Riemannian geometry that characterizes this parameter space in Section 2.2, leading to an insightful discussion on the powerful applications of kernel methods in Section 2.3. Section 2.4 examines data analysis in low-dimensional spaces, and Section 2.5 presents a framework for understanding reality.
2.1. The Information Sources and the Parameter Space
Data analysis and physics are inherently connected through their dependence on information sources that supply the data or physical states for examination. However, physical models typically provide a more nuanced and detailed representation of reality, often rooted in causal relationships. With this in mind, we intend to introduce practical tools that can be applied in both fields. Our exploration will begin with an in-depth examination of the vital role of observation, a fundamental aspect that significantly shapes our understanding.
Although the entirety of this phenomenon is located in the observer’s consciousness, it is convenient to simplify the discussion by distinguishing three fundamental elements. The first element is the object studied. The second element is the knowing subject, who is really experimenting: They are aware of what happens. The third element is the environment. These three elements are part of reality in any observation process, and they appear as different elements in the consciousness of the knowing subject, although the reality that underlies and makes observation possible remains hidden. In a simplified sense, we will consider that the said reality is formed by entities that can be viewed as information sources, providing sequences of data for analysis. Some of these entities are used to maintain the underlying structure that makes the internal experience of the knowing subject possible. Let us introduce some notation to establish a convenient and simplified mathematical framework for our work.
To describe the observation process, we will introduce a set, , which we will call the parameter space. As a first approximation, we can consider it to be an m-dimensional real manifold, although infinite-dimensional Hilbert or Banach manifolds could also be considered; see [6] for instance. Furthermore, for many purposes, it will suffice to consider the case where is a connected open set of , and in this case, it is customary to use the same symbol, , to denote points and coordinates. Bearing this observation in mind, we will adopt this case and notation from now on to present the results more familiarly, although they could be written in more general terms.
The manifold is really a manifold generated by the observer, regardless of whether this is an immediate abstraction from reality is apprehended directly by the observer’s brain–sensory complex or whether it is constructed from it, following well-defined logical procedures. Observe also that the manifold has a natural topology induced by its atlas structure, and thus, this topology allows the construction of the Borel -algebra, , the -algebra induced by the topology, that is, the -algebra generated by the open sets in . Moreover, in the measurable space , we may consider a -finite positive measure absolutely continuous with respect to any local Lebesgue measure induced through the atlas structure that we shall take as a reference measure of this manifold.
We shall consider that all relevant aspects of the observation process, determined by the object, the subject, the environment, or a mixture of all of them, can be adequately described by the elements of through a family of complex-valued maps that we describe below.
Therefore, to further investigate the behavior and properties of information sources, we will introduce a new tool: a regular parametric family of functions, , as a family of measurable maps . These can be expressed in their complex exponential form, that is, for convenient real-valued functions and , the modulus and the argument of , when necessary, and we shall assume that the function is independent of the reference measure ; however, if we set , the square of the function r, i.e., is a probability density with respect to , that is, is a probability measure in , . The function is therefore dependent on the reference measure , although the probability measure itself, , is independent. Specifically, if is another reference measure, by the Radon–Nikodym Theorem we shall have that for a convenient measurable positive function , then , obtaining , which explicitly indicates the dependence of r with respect to the reference measure . In addition, we will implicitly assume all the regularity conditions that we will require for the development of subsequent calculations, such as the necessary smoothness with respect to and that the closure of the set where the function is strictly positive is independent of the parameter . We refer to as a reference measure of the model, h as the model function, and as the density of the model below.
2.2. The Riemannian Structure in the Parameter Space
The exploration of Riemannian structures in parameter spaces provides a profound geometric perspective on models and their underlying function spaces. By endowing these spaces with a Riemannian metric, we can investigate the intrinsic geometric properties that influence model behavior, estimation, and inference. Such a perspective enables a more nuanced understanding of the complexity and curvature of the parameter space, offering insights that extend beyond traditional Euclidean approaches.
Letting be the Hilbert space of these complex-valued measurable functions q in such that the Lebesgue integral , where , if we denote by the square of the Hilbert distance
once given the model function of a parametric family, , since these functions are naturally identifiable with elements of , we are able to build the function
where is a positive constant which determines the units of the dissimilarity measure on ; and when , we have taken into account . Notice that since , if we change the reference measure to accordingly, r changes to , and when we integrate (2) now with respect to , we find that remains invariant.
We are going to consider the Riemannian metric induced in by following the same basic ideas of [7]. If we define , we will have , and, taking into account that the Jacobian of in is also null, since the function has an absolute minimum at , the second-order expansion of at will be given by its Hessian at , , which will be positive definite or semidefinite. Using matrix notation, we will have
Notice also that if we consider an appropriate smooth coordinate change given by , the function expressed under the new coordinate system as is an invariant, that is, , and we will have, in classical notation, without using the repeated index summation convention criteria unless we explicitly state otherwise, by the chain rule,
Moreover, since the second-order partial derivatives are
when evaluating them at , we will have . Therefore,
where we have denoted by the coordinates of the point expressed under the transformed coordinate system, obtaining that the components of the Hessian at are the components of a second-order covariant symmetric tensor in the tangent space ; see [8,9] and Appendix A for further details. This tensor is at least semidefinite positive, but hereafter, we will assume the case that is positive definite, as in most of the interesting examples that we will consider. Then, it may be used to define a scalar product at each tangent space, and thus a Riemannian metric in the whole manifold . The metric tensor components, under the coordinates , will be given by
i.e., the components of the metric tensor will be equal to one half times the second partial derivatives of the function , and the line element corresponding to the above-mentioned induced Riemannian metric, under , is given through its square by
This formulation is typical in classical information geometry, where the metric is derived from second derivatives of divergence functions or similar measures.
If we express the complex-valued function in its exponential form, that is, for a convenient real-valued function of , from (2), taking into account that if then , we obtain
and then, if we denote by the square of the normalized Hellinger distance between the densities and
since , we have
Taking into account that and , we shall have
Observe, additionally, that for , the quantity is the square of the distance between and , functions that are on a radius 2 sphere of . Additionally, the aforementioned amount is, locally, the information metric on ; for instance, see [7].
At the point , we have
since , and any partial derivative with respect to is equal to zero.
Additionally, since the second-order partial derivatives of divided by 2 are
at the point , we have
However, if we take into account that is the real square root of a probability density with respect to the reference measure , we shall have
and since
we have
Moreover, let be the Fisher information matrix corresponding to the density of the model, that is, , and additionally define
We obtain that the fundamental tensor of , (7), converting it as a Riemannian manifold, is equal to
The Riemannian metric, using repeated index summation convention, can also be expressed as
where is the information metric, and is a metric specifically related to the imaginary part of the function that defines the model. Observe that locally the Riemannian metric induced in is the distance induced by the Hilbert metric structure in on a radius 2 sphere and that it coincides, when , with the information metric when is constant. More results on the information metric can be found in [7,10,11], among others. Additional aspects of the information metric are briefly recalled in Appendix A.
This structure suggests a Kähler-like or complex Riemannian geometry, often encountered in quantum information geometry, where complex structures naturally appear, and the metric encodes both probabilistic and phase information. Quantum information geometry explores the geometric aspects of quantum states and their transformations. Unlike classical probability spaces, quantum state spaces are inherently complex and require a framework that can incorporate both the probabilistic nature of quantum mechanics and the phase information, which is crucial for phenomena like interference and entanglement. The complex structure naturally appears because quantum states are represented by vectors in complex Hilbert spaces, and their evolution and measurement outcomes depend on both amplitude and phase.
The metric in this geometric setting is not just a measure of “distance” between states; it encodes multiple layers of information. On one hand, it captures probabilistic information—how distinguishable two quantum states are based on measurement outcomes—mirroring classical statistical distances but adapted to quantum mechanics. On the other hand, it also encodes phase information, reflecting the relative quantum phases that influence interference effects and the dynamics of quantum systems.
By combining these elements, the described structure offers a comprehensive geometric language that unifies the probabilistic and phase aspects of quantum states. This unified approach facilitates an understanding of quantum state transformations, optimal measurements, and quantum information processing tasks. The resemblance to Kähler geometry provides powerful mathematical tools, such as complex differential calculus and symplectic geometry, which facilitate the analysis of the complex landscape of quantum states and their evolutions. Overall, this geometric perspective enhances our conceptual and computational grasp of quantum phenomena, revealing deep connections between geometry, probability, and phase in the quantum realm.
Please note that while we assume that all properties of an information source are determined by or , the exact value of has to be estimated from the data generated by the source. Although we assume that these data can remain partially hidden, it should still allow a reasonably good estimate of both and .
2.3. Kernel Methods
Kernel methods have become a cornerstone of modern machine learning, enabling flexible and powerful approaches to non-linear data analysis. By implicitly mapping data into high-dimensional (often infinite-dimensional) feature spaces, kernel methods enable linear algorithms to capture intricate patterns that would be difficult to model directly in the original input space. This approach not only enhances the expressive power of models, but it also provides computational advantages through the so-called “kernel trick,” which allows inner products in feature space to be computed efficiently without explicit transformation. At the heart of kernel methods lies the concept of defining kernels based on underlying parametric families.
Given a regular parametric family , we can define a natural kernel in , using as a feature space, the Hilbert space of measurable functions with complex value and square integrability in , and as a feature map, which maps to , defined as . Then, we can define a kernel in as
for a convenient positive proportionality constant .
A kernel can be interpreted as a measure of similarity between points in the parameter space, and it allows us to identify, though a kernel K, each with a complex-valued function, , which we assume to contain all relevant features of the point , or, more formally, through a function , which we refer to as the canonical feature map, defined as
Observe that is properly a function, much simpler than the previously mentioned , which is an element of and, therefore, an equivalent class of functions, although it can be identified with one of the equivalence classes to which it belongs. We will consider hereafter that the parametric family is such that the corresponding map , with the natural kernel (25), is 1–1, i.e., then , as happens in most cases. Then, we can identify with for almost all pursuit purposes. Notice that , which we will call the feature manifold, inherits a natural m-dimensional differentiable manifold structure induced by the manifold structures of . The parameter , identifiable with , characterizes what we shall call the state of the observation process and can be expressed using the complex exponential form when necessary.
At this point, it is convenient to outline the following well-known mathematical construction that will lead us to a simpler feature space. See [12,13] for details. We start by recalling the concept of a positive definite kernel. A map is a positive definite kernel if and only if, for any mutually distinct points and for any scalars , where n is an arbitrary positive integer, we have that where is the complex conjugate of . Notice that the Hermitian property, , is a consequence of the positive-definiteness. Moreover, if for mutually distinct , the equality only holds for , it is often said that K is a strictly positive definite Hermitian kernel, although there are small variations in that name to designate this property according different authors. It is also possible to consider real-valued kernels satisfying such that and for any positive integer , , . Observe that (25) satisfies all of the above-mentioned properties, and is thus, in addition, a positive definite kernel because , since clearly and for any scalars , where n is an arbitrary positive integer, . Therefore, it is a complex-valued Hermitian kernel.
Therefore, taking into account that and that has a natural vector space structure over , corresponding to each kernel K, we can build a vector space , i.e., the set of all finite linear combinations of elements of . Observe also that the elements of are complex-valued functions f with domains the parameter space, , which can be expressed as for a convenient and , .
Moreover, the kernel K allows one to define a Hermitian inner product in as follows: If , then and , with the Hermitian inner product defined as
which turns into a pre-Hilbert space. After a standard completion, we can turn our pre-Hilbert vector space into a true Hilbert space , which is also a norm and a metric space with the standard norm and the distance defined as from (27). Moreover, this Hilbert space is the reproducing kernel Hilbert space (RKHS) induced by the kernel function K, see [13,14], which satisfies the so-called reproducing property, i.e., . Therefore, . Additionally, it is a functional Hilbert space, i.e., a Hilbert space in which elements are functions (on ) such that the point evaluation functional is a continuous linear functional on , with norm , because for the natural kernel (25) we have since . Let us recall now that with additional assumptions about the parameter space from measure and topological theory, many other properties of kernels can be established, like Mercer’s theorem and relationships of square-integrable function spaces to RKHS, via linear operators; see, for instance, ref. [13]. Notice also that the distance in the feature space, , induces a distance in the parameter space, , through the map such that
which is equal to (9). Observe that this distance reflects the differences between the parameter space points——or, equivalently, between their images——and locally defines in any of these manifolds or , the Riemannian metric (24), when .
We finally remark that the obtained RKHS, , which can be identified as a closed subspace of , will also be considered as a feature space of the kernel K, defined in (25), and can be considered as the smallest feature space corresponding to this kernel. Indeed, if is another Hilbert space that allows us to obtain the same kernel K, as in , then there exists a canonical metric surjection from onto . As an aside, in later physical applications, we will think of this RKHS as the most convenient abstract model for identifying objects in the physical world, viewing them as vectors in this infinite-dimensional Hilbert space.
Therefore, at this moment, a point in the parameter space can be viewed as an element of the manifold , a function of , , a function of , , or any other equivalent mathematical object, such as composing the function h with a suitable 1-1 smooth function, i.e., , for example.
For the sake of simplicity, we continue considering that as an open subset of and, with some customary abuse of notation, given the local chart where I is the identity map, we will identify its points with their coordinates. Under this simplified approach, can also be viewed as the coordinates of , a point in the feature manifold. Figure 1 illustrates this framework.
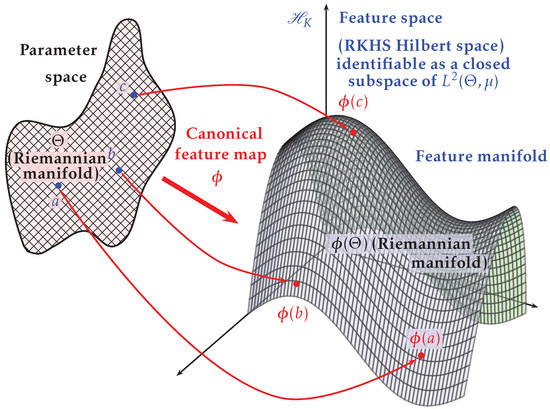
Figure 1.
In the parameter space , a manifold, for example an open set of , is mapped into , which also acts as a feature space of the natural kernel (25) defined at initio through , via the canonical feature map . is a Hilbert space of functions that is identifiable with a closed subspace of and satisfies the reproducing property, with the point evaluation functional being continuous.
It is also interesting to examine the different representations of the tangent space of in . Under adequate regularity conditions, an obvious representation consists of considering the span of the functions . The Hilbert inner product between them will be given by
Furthermore, with adequate smooth and continuity assumptions, the tangent space will also be identifiable with the space spanned by a linear combination of the partial derivatives of the functions obtained through the canonical feature map, , with the Hilbert inner product between them given by
Notice that, given a smooth map , if we fix a point on the manifold , then we obtain a function , which, under regularity conditions, may be approximated through an intrinsic Taylor expansion of rth at , the coefficients of which are the components of convenient tensors—that is, an expansion independent of the coordinate system in constructed via the inverse of the Riemannian exponential map corresponding to (24), specifically
Here, is their corresponding residual, indicates the covariant derivative of k-th order corresponding to the Levi–Civita connection of the Riemannian metric (24), and we have assumed that belongs to a regular normal neighborhood of to ensure the existence of the inverse of the exponential map of the connection mentioned above, which is always the case if is close enough to .
This development shows that the function has different associated covariant tensor fields that can be used in future developments, as well as the contravariant or mixed tensors required by the well-known operation of raising or lowering tensor indices in a Riemannian manifold. Several of the concepts introduced in the present section will be briefly described in Appendix A.
Observe also that, given a second-order mixed tensor field , it corresponds to a linear map operator field, , defined through . In any case, we hope to relate these fields of linear operators on the tangent bundle of , , with the classical spectral analysis of these operators in a Hilbert space. In other words, we can consider the appropriate spectral decompositions carried out in each tangent space and eventually interpret them in physical terms, at least as an approximation. Furthermore, through this framework, we can view the statistical estimates of , say , as convenient tensor fields in .
Additionally, it may be useful to apply the same development to the expected value of these estimations. Given a regular parametric family of functions , defined as before, let be defined as
As before, under regularity conditions, this map may be approximated through an intrinsic Taylor expansion of the rth at , that is,
where is their corresponding residual.
2.3.1. The Case of the Gradient Operator
It might sometimes be convenient to consider and represent, in the above framework, real-valued smooth functions defined on and their variations throughout the manifold. However, the problem can be stated equivalently in through the canonical feature map, since we assume that the canonical feature map is 1–1, and therefore, there is a natural identification not only between smooth functions on both manifolds but also between vectors and tensors via the map , defined as , with and its differential. In other words, we may identify our parameter space with its image through the feature map. Figure 1 can help visualize all these considerations.
In this context, it will be convenient to represent a certain function q, for example, or , in terms of its gradient vector field (see Appendix A for details) since, from a geometric point of view, the gradient of a function indicates the direction of maximum growth of this function per unit of length. Observe that, under the coordinate system , the components of the gradient of q are
where are the components of the contravariant metric tensor, i.e., the components of the scalar product in the dual of the tangent space at , , equal to the components of the inverse of the matrix at . To simplify the notation, we have identified the points of with their coordinates and with the ordinary partial derivative in , . Notice that in the graphic outputs, in order to describe the behavior of the function q along the entire manifold, it will be enough to represent the field at some specific points of of : those where it seems most relevant to the applied researcher to determine the direction of growth of q. Observe also that the represented gradient vector at one point will be distorted due to the multidimensional character of the problem, which would have implied some reduction of the dimension, as we will see later. So, it is recommended to calculate the final percentage of the norm of the represented vector. We also note that the growth directions may vary significantly along the manifold.
In a complementary way, it may be interesting to find the curves corresponding to the integral flow of the gradient, that is, the curves whose tangent vectors at t are , which indicate, locally, the maximum variation directions of q per unit of length; see Figure 2. Observe that the trace of these curves orthogonally cuts the level hypersurfaces, a multidimensional extension of the typical contour lines of geographic maps, which we could hypothetically examine. In any case, the posterior representation of these curves in 2D or 3D will be affected by ordinary problems of dimension reduction.
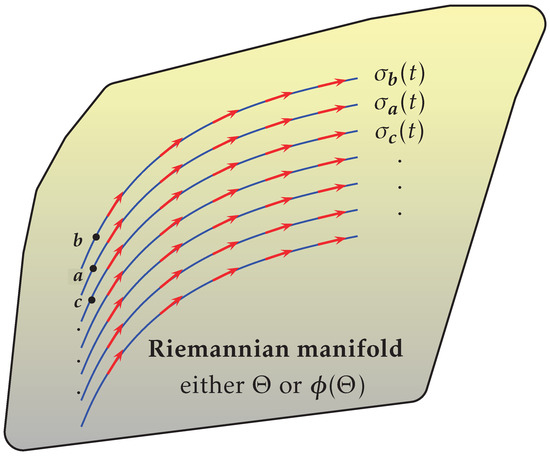
Figure 2.
A bundle of smooth, blue integral curves winds through the space, each representing a trajectory moving according to the underlying vector field. These curves emanate from various points, illustrating the flow lines that define the field’s behavior. Overlaid on the scene are red vector fields, with arrows indicating the direction and magnitude of the vectors at each point. The interplay between the flowing blue curves and the red vectors visualizes the dynamic structure and flow patterns of the vector field.
Precisely, under the coordinates , and denoting the curve by its coordinates , the integral flow of the gradient of q is the general solution of the first-order differential equation system
which always has a local solution given initial conditions , granted by the Picard–Lindelöf theorem; see, for instance [15]. In any case, the curves obtained corresponding to different initial conditions will have to be represented in a low-dimensional Euclidean space, which could potentially generate many interpretation problems, at least if we move away from their corresponding initial points. Therefore, we conclude the following observation:
Although the system (35) could be explicitly solved, at least numerically, the most useful way to represent the function q is by evaluating the gradient vector field of q at some particular points of the manifold. This representation will also facilitate the interpretation of the bi- or three-dimensional Euclidean space of representation.
2.3.2. Projecting onto an Affine Manifold
Consider now the manifold immersed in . The tangent space at can be identified with the affine manifold , which is determined by an m-dimensional subspace spanning with adequate smoothness and continuity assumptions, by the vectors , with the Hilbert inner product between them given by (30), and a vector , which, in a certain sense, we can take as the origin of . Any vector can be written as . If we introduce matrix notation, defining the column vectors and and and the matrix , the components of will be given by the following equation:
Additionally, if is the projection operator onto , each point in induces a tensor or vector field in via the projection operator field that should be deeply connected, at least as an approximation, with the Hermitian linear operators corresponding to convenient observables in quantum mechanics formulation.
2.4. Data Analysis Applications: Mapping Objects in a Low-Dimensional Space
If we are interested in representing data points in the parameter space and real functions of in a low-dimensional Euclidean space, usually a plane, we will have two different strategies. In the first, we will require that the final Euclidean distance between points in the plot be, as far as possible, similar to the distance between their images in , which shall lead us to a type of kernel PCA method (Principal Component Analysis). In contrast, in the second, we shall require that the final Euclidean distance in the plot be similar to the Riemannian manifold distance in of induced by the metric in , as in (24). In this case, we shall first map the points in the manifold into a tangent space through the inverse of the exponential map corresponding to the Levi–Civita connection. In this Euclidean space, we shall then use the standard PCA method. Below, we will provide a schematic description of both procedures.
2.4.1. Working in the Feature Space
Among all points we are studying, we may select a specific set of points, which we shall refer to hereafter as principal points, to represent with some optimal property. Specifically, given any set of these principal points and given a positive definite Hermitian kernel K in , we can map them into via the map , and then we can perform a kernel PCA in the reproducing kernel Hilbert space induced by the kernel, . One primary purpose of this analysis is to obtain a low-dimensional Euclidean data representation, such that the distances between the plotted points accurately reflect the differences between the observations. To achieve this, we shall project the points onto a convenient r-dimensional linear manifold (usually with or 3) immersed in . A linear manifold is determined by an r-dimensional subspace spanned by an orthonormal basis and a vector which defines the origin of the data representation. Any vector can be written as and if is the projection operator onto , each observation will be represented as a single point in a r-dimensional Cartesian coordinates system, with coordinates , satisfying . The next step is to find the linear r-dimensional manifold following a convenient optimization criterion. Two approaches lead to the same result:
- (a)
- To obtain a linear r-dimensional manifold immersed in , minimizeObserve that is a goodness-of-fit measure. If we minimize this quantity, we shall obtain the linear manifold of closest fit to the system of points in the space .
- (b)
- To obtain a linear r-dimensional manifold immersed in , maximize
Notice that is a measure of the resolving power of the final output. By maximizing this quantity we shall obtain points separated as much as possible in the low-dimensional Euclidean data representation.
Observe also that both and are non-negative real-valued functions with the variables , i.e., the vectors which determine . Taking into account that
where is the norm in and is the projection operator onto , and defining
as the average feature, we have
In order to minimize (a), it is straightforward to prove that we have to choose
Let be the linear span of , with . If , then the problem has as trivial solutions any satisfying , and therefore, . In this case we can choose in such a way that so as to be a basis of . When , in order to minimize , it is clear that we must have , and thus, is spanned by ; therefore, we can define the matrix with elements given by
Next, we shall define the Gram or kernel matrix corresponding to the kernel k and the sample as the matrix , the elements of which are given by , and the centering data matrix defined as , where is the identity matrix, is an m-dimensional column vector with all components equal to one, and the symbol ⊺ stands for the transpose matrix operator. Then, if we define
where the elements are , we shall have
with the orthonormal basis condition, in matrix form, given by
However, since is a symmetric and positive semidefinite matrix, we can define its symmetric square root , and then, if we let , we shall have
with the condition
It is straightforward to prove that is minimized if the r columns of , , are the normalized eigenvectors
corresponding to the largest eigenvalues of . Observe also that
Therefore, in the final output, the Cartesian coordinates of , , will be given, in matrix notation, by
or
Observe that if the , , the rows of the matrix are
and after some straightforward computations, we shall obtain
which shows that the criteria (a) and (b) are equivalents.
Notice that we can represent any additional point in the output plot. Specifically, to find the Cartesian coordinates of the representation of this point in the final output, we compute the projection of the centered -image of into . For this calculation, notice that
Introducing the vector
from the last expression, we shall have
Notice that Kernel PCA (KPCA) uses only the values of the kernel evaluated at , since the algorithm formulates the reduction of the dimension in the feature space only through the kernel evaluation at these points.
To facilitate the intelligibility of the KPCA output plot, we can represent in it the curve’s solution of (35), which indicates, locally, the maximum variation directions of , or alternatively, the corresponding gradient vector field, given in (34).The curve , with , is the solution of (35). Then, we can compute the projections of this curve onto the subspace spanned by (43). If we define
taking into account Equation (56), the induced curve, , in expressed in matrix form is given by the row vector
where is of the form (57).
We can also represent the gradient vector field of , equal to the tangent vector field corresponding to , through its projection onto the subspace . The tangent vector at , if , is given by , and its projection, in matrix form, is
with
Taking into account (30), we obtain
as a result, which basically coincides with [16]. Figure 3 graphically shows the method outlined in the present subsection.
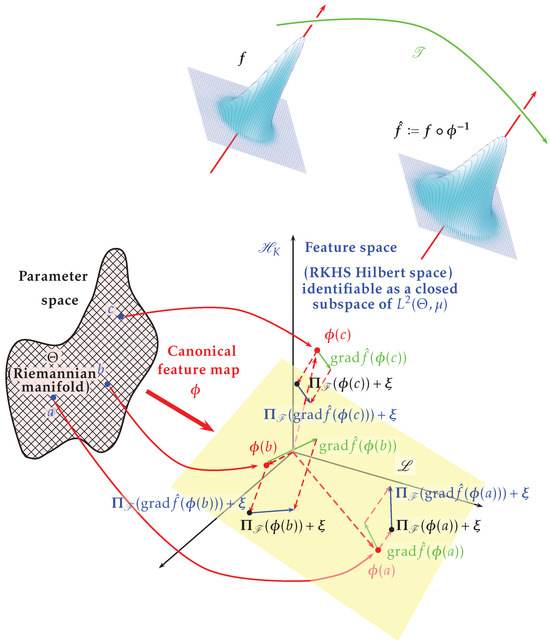
Figure 3.
This illustration visualizes how the points a, b, and c are mapped onto the feature space, facilitating analysis within the RKHS framework. It also depicts the gradient fields in the feature space.
2.4.2. PCA in a Tangent Space
Now, we shall require that the final Euclidean distance in the plot be similar to the Riemannian manifold distance on ; in this case we shall first map the principal points onto a convenient tangent space through the inverse of the exponential map corresponding to Levi–Civita connection; see Appendix A for additional details. In this Euclidean space, we shall use the standard PCA method. First, we will fix a point , which we shall refer to as a reference point on which to base the graphical representation. For reasons that will become apparent later, it seems convenient to choose as the Riemannian center of mass of the points , that is, a point such that it is a minimum of the map , where
Here, is the square of the Riemannian distance between the points and . This point is uniquely defined in many interesting applications; among others, see [8,17].
Then, the principal points , and the remaining points that we are interested in plotting are mapped onto the tangent space through the inverse of the Levi–Civita connection exponential map, , which is well defined (almost everywhere) in most applications. Figure 4 helps us to clarify the role of the inverse of the exponential map. The manifold is the (radius R) basket ball, with the Riemannian metric induced by the Euclidean geometry. See Appendix A for further details.
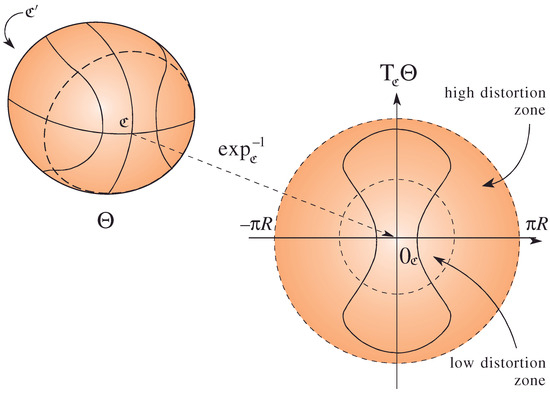
Figure 4.
The inverse of the exponential map illustrated here operates on the set , where represents the antipodal point of on the manifold. This inverse mapping effectively retrieves the tangent vector at that, when exponentiated, reaches a given point in the domain, excluding the antipode to ensure the map’s well-definedness and invertibility.
Principal points play an important role since the computation of the above-mentioned center of mass (if, as we have recommended, it is taken as the reference point ) and the projector is only concerned with them, independently of the other studied points in . The selection of the principal points will depend, of course, on the particular problem, and the possibilities are unlimited. We select as principal points, for example, pairs of points which define the gradient of a particular real-valued function on , computed at certain fixed points. It would be convenient to select these points interactively with suitable computer software. Therefore, we obtain
and, thus, our original points are now represented as points in a m-dimensional Euclidean space , with scalar product corresponding to the basis , given by the information matrix at , where
We shall use the same symbol, , to denote the points at and their coordinates with respect to the basis vector field mentioned above, in matrix notation, as a vector . It is important to note that , considered a map between two metric spaces, preserves the distance between any point and , although it does not preserve, in general, distances between arbitrary points, in such a way that the distortion between both distances is small for points close to .
More precisely, let be a Riemannian convex ball of radius , and let , . We shall have
where on , the closure of the Riemannian ball , with being the Riemannian sectional curvature. Observe that the relative error to approximate , the square of the Riemannian distance between the points and , by is of the order of . See Appendix A for details. To facilitate the reading of the article for the common reader, we have obtained (65), a formula more or less familiar to readers with a background in Riemannian geometry.
This fact suggests the convenience of choosing as the center of a small Riemannian ball that includes the majority of the principal points, with the Riemannian center of mass of the principal points being a good candidate since, in that case, we shall have, lower error bounds for the metric distortions on average. At any rate, it is possible to measure the global distortion introduced through an analogue of the correlation cophenetic coefficient.
Then a usual PCA is performed over the representation of the principal points at , , taking into account the scalar product in the tangent space to obtain a q-dimensional affine manifold, , with or , which allows for an optimal representation of the principal points. Since the scalar product matrix at , with respect to the vector basis mentioned above, is , given by (7), the following diagonalization must be solved:
Here, is the covariance matrix (or any multiple) of the coordinates of the principal points of representation, , in the tangent space, is the inverse of the metric tensor matrix at , is an eigenvalue, and is a corresponding eigenvector. If is an matrix whose columns are the normalized eigenvectors corresponding to the q highest eigenvalues, then the q principal coordinates, in , of a point , in matrix notation, as a column vector , are given by . In other words, if is the projection operator corresponding to the matrix , supplied by PCA, then all statistical objects (not only the principal points) can be represented in as
In summary, the whole procedure can be summarized by
We shall refer hereafter to this procedure as Intrinsic Data Analysis, IDA for short. It is possible to carry out the steps mentioned above, replacing the barycenter by another point , which may be easier to compute or more suitable in a specific application, although in this case, the metric distortion caused by will probably increase.
Once the projector has been computed, each single point on the tangent space can be mapped in , and the curves and their tangent vector field can also be mapped on in a straightforward way.
2.5. Physical Applications
In the mathematical framework succinctly presented above, we can define the notion of extended information, codified by the estimation , obtained from an information source of the true parameter , relative to this true value of the parameter, and referred to as an arbitrary point , as
where log denotes a version of the complex logarithm defined to satisfy , with ln being the standard natural logarithm, and being a constant that determines the units of information with which we will work. The implicit dependence of (69) on is omitted from the notation since its choice will not play any further role when we calculate its gradient in the parametric space. Additionally, (69) will remain invariant under appropriate data changes, and fixed is also invariant under coordinate changes in the parametric manifold, since it is a scalar field on .
The information provided by a source external to the observer is represented within him, allowing him to increase his understanding of the objects. Although we can consider different levels and types of the said representation, we will focus on two critical aspects: the parameter space with its natural extended information geometry and the observer’s ability to construct plausibility regarding the true value of the parameter, , in the parameter space . This estimation is fundamentally a complex square root of a specific kind of subjective conditional probability density with respect the Riemannian volume, induced by the information metric over the parameter space, , up to a normalization constant. Specifically, we shall write at the beginning
although we shall be particularly interested in the case . Observe that in (70), we are integrating with respect to the Riemannian measure defined in (7); therefore, this expression is invariant under coordinate changes. Furthermore, if we intend to define a probability on the parametric manifold, interpretable as a plausibility about the true value of the parameter, we can take the function as the Radon–Nikodym derivative of said probability with respect to the Riemannian volume, also a measure in the same parameter space. Both measures are independent of the coordinate system used and, therefore, will be an invariant scalar field on the parametric manifold . Then, we can simply define the information encoded by the subjective plausibility on the parameter space relative to the true parameter as
This quantity (71) also remains invariant under coordinate changes in the parametric manifold, being another scalar field in ; see also [4].
The Variational Principle
In this context, trusting that many of the abilities of the observer have been efficiently shaped by natural selection in the process of biological evolution, we can propose that the subjective information mentioned above adjusts in some way to the information provided by the source and, in particular, satisfies the following variational principle (see also [4]):
Here, is a minimum, or at least stationary, and subject to the constraint (70), and assuming that and its gradient, , vanish at the boundary or at infinity, which is the case for the model, we have strong reason to believe that the true parameter should belong far from the boundary, clearly inside of .
Observe that the functional is equal to the expected value corresponding to the probability in given by the density with respect to the Riemannian volume induced by the metric (24), , of the square of the norm, corresponding to a complexified vector field in a Riemannian manifold, as indicated in Appendix A. Since the difference between the gradients and is a complexified vector field, i.e., if , then . Observe that (72) is invariant under coordinate changes in since the square of the norm inside the integral is invariant and is as well.
Notice also that the source is considered to be objective or at least, strictly speaking, intersubjective, while the parameter space, with its geometric properties, is in some sense built by the observer and is therefore subjective, although strongly conditioned by the source. In future work, some additional restrictions will be added to the variational principle (72) with the aim of more accurately modeling the observation process as a whole.
Any change in the information encoded by caused by considering a change at the source in the parameter space should correspond to a change in the subjective information proposed by the observer. For this reason, we propose that the squared difference of both gradients and would, on average, result in being as small as possible, at least locally.
This variational principle is an extension of a previous one presented by the authors in [4], where only regular parametric statistical models with the standard information metric were considered. Based on the former variational principle applied to these models and playing only with basic statistical tools, in particular the information carried by the data in a given statistical model, for instance, see [18,19,20], we obtain a probability density in the parameter space by solving a system of partial differential equations. This probability can be viewed as a Bayesian posterior probability over all possible probabilistic mechanisms that have generated the data, probabilistic mechanisms identifiable with the parameters. Furthermore, if we apply this procedure of analyzing data to the simple statistical model corresponding to a multivariate normal distribution with a constant covariance matrix, a model that can be considered at least as an approximation of many regular statistical models for large samples via extensions of the Central Limit Theorem, we obtain, from those above-mentioned partial differential equations in the parameter space, a specific differential equation already studied in Physics and known as the stationary (time-independent) Schrödinger equation applied to a quantum harmonic oscillator.
3. Discussion
Understanding the complex relationship between data analysis and physics necessitates a comprehensive examination of the foundational elements that underpin observation and modeling. This paper emphasizes the intrinsic connection between information sources—conceptualized as entities providing sequences of data—and the physical models that aim to represent reality with causal nuance. Central to this discourse is the role of observation, which is depicted as a triadic interaction involving the studied object, the knowing subject, and the environment.
By dissecting these elements within a mathematical framework, this work bridges the cognitive process of observation with the geometric and probabilistic structures that characterize physical models. The observation process, as articulated, hinges on the recognition that all relevant phenomena are ultimately situated within the observer’s consciousness. However, simplifying assumptions facilitates the development of a formal model, where entities involved in observation—objects, subjects, and environments—are represented through elements of a parameter space . This space, modeled as a smooth manifold, encapsulates the parameters that characterize the underlying data-generating processes.
Such a manifold structure allows for the application of differential geometry, enabling the exploration of the intrinsic properties of models through tools like the Riemannian metric induced by divergence functions or distance measures. The introduction of complex-valued functions and their exponential representations illustrates how models of data sources can be embedded within a Hilbert space framework. By defining a family of functions , we leverage the geometric interpretation of statistical models, where distances between models—quantified via functions such as the Hilbert metric or the Hellinger distance —are instrumental in understanding model complexity and distinguishability.
The construction of a Riemannian metric from these divergence measures aligns with the principles of information geometry, providing a natural geometric framework for analyzing the parameter space. Specifically, the metric tensor components are derived from the second derivatives of divergence functions, which encapsulate the local curvature of the parameter space. This curvature, reflecting the model’s complexity and sensitivity to parameter variations, influences estimation procedures and inference accuracy.
The Fisher information matrix emerges as a pivotal component, quantifying the amount of information that an observable data source contains about the parameters. When combined with phase-related terms arising from complex exponentials (e.g., the functions ), the metric captures both probabilistic and phase information—concepts reminiscent of quantum information geometry. The extension to quantum contexts underscores the universality of such geometric structures. Quantum states, represented by vectors in complex Hilbert spaces, inherently embody both amplitude and phase.
The metric structures derived from complex functions thus encode not only classical probabilistic information—determinable via the Fisher information—but also quantum phases that influence phenomena such as interference and entanglement. This dual encoding exemplifies how geometric tools can unify seemingly disparate layers of information, providing a comprehensive framework for understanding complex systems. This underscores the profound role of geometric and probabilistic structures in modeling physical phenomena and data sources.
Formalizing observation through parameter spaces endowed with Riemannian metrics derived from divergence measures provides a versatile toolkit applicable to both classical and quantum domains. The approach highlights that models are not merely static representations but dynamic entities with curvature and structure that influence estimation, inference, and ultimately, our understanding of reality. Integrating these geometric insights into physical modeling enhances both the conceptual framework and the practical methodologies employed in analyzing complex systems, thereby facilitating more nuanced and precise scientific investigations.
We present a method for effectively connecting two distinct ways of representing data through a specialized mathematical transformation, referred to as a “feature map.” When this feature map is one-to-one—ensuring that each point in the original space corresponds uniquely to a single point in the transformed space—we can establish a reliable method for transferring various functions and objects from the original domain to the new one.
This approach is further enriched by the kernel method, which allows us to implicitly work within a high-dimensional feature space without explicitly computing the feature map. Specifically, kernel functions enable us to compute inner products in the transformed space directly from the original data, facilitating efficient computations even in infinite-dimensional feature spaces. This capability ensures that mathematical entities, such as functions, vectors, and matrices, which characterize the data, can be consistently interpreted within this new context, preserving all information and structural properties.
Moreover, when considering data residing on Riemannian manifolds—smooth, curved spaces that generalize Euclidean geometry—these ideas become even more powerful. Riemannian manifolds provide a natural setting for modeling complex data that intrinsically possesses geometric structure, such as shapes, surfaces, or biological structures. In such contexts, the notion of a feature map can be extended to respect the manifold’s geometric properties, allowing for transformations that preserve curvature and intrinsic distances.
By leveraging kernels adapted to Riemannian manifolds—so-called Riemannian kernels—we can perform implicit high-dimensional embedding that accounts for the manifold’s geometry, enabling meaningful comparisons and analyses of data points lying on curved spaces. This synergy between kernel methods and Riemannian geometry facilitates a more profound understanding of complex data structures, supporting tasks such as classification, regression, and visualization within intrinsically curved spaces. Overall, the integration of Riemannian manifolds into kernel-based feature mappings broadens the scope of data representation, ensuring that the geometric essence of the data is maintained throughout the transformation process.
Then, we present a sophisticated approach to analyzing data on Riemannian manifolds, combining differential geometry, kernel methods, and principal component analysis (PCA). At its core, the methodology emphasizes understanding the intrinsic geometric structure of the data, which is crucial when the data naturally resides in nonlinear, curved spaces rather than Euclidean ones. This approach is particularly relevant in fields where the data’s inherent geometry cannot be ignored.
One of the central themes revolves around the flow lines of the gradient vector field, denoted as curves , which are solutions to a first-order differential system. These curves represent the integral flow of the gradient of a function q, effectively indicating the directions of maximum variation of q on the manifold. Geometrically, these curves intersect the level hypersurfaces orthogonally, much like contour lines on a geographic map, thereby providing a visual and intuitive understanding of the function’s local behavior. The analysis of these flow lines is essential in understanding the local structure of the data and in identifying directions that capture the most significant variations, which can guide dimension reduction strategies.
The representation of these flow lines, especially in low-dimensional projections, is complicated by the manifold’s nonlinear nature. We discuss the challenges associated with dimension reduction, highlighting the potential distortion when projecting high-dimensional manifold data into Euclidean spaces. This issue is addressed through the use of the exponential and logarithmic maps, which transfer points between the manifold and its tangent spaces, preserving local geometric properties. The inverse exponential map, , maps points from the manifold to the tangent space at a reference point, facilitating the application of Euclidean PCA in the tangent space. The choice of the Riemannian center of mass as the reference point is significant, as it ensures that the PCA captures the dominant variation directions in a manner faithful to the manifold’s geometry.
Kernel methods, particularly Kernel PCA (KPCA), are integrated into this framework to perform nonlinear dimension reduction in the feature space induced by a kernel function. The kernel encapsulates the manifold’s intrinsic geometry implicitly, allowing for the analysis of data that may be difficult to embed linearly. We describe how the kernel matrix K, constructed from evaluations of the kernel function at data points, encodes geometric relationships, such as distances and angles, in a high-dimensional feature space. This means that the kernel matrix captures the relationships between data points in a way that respects the manifold’s geometry.
Eigendecomposition of the kernel matrix reveals principal directions of variation, which are then projected back into the original data space. This process enables the visualization of complex structures, such as flow lines and gradient vector fields, in low-dimensional representations that respect the manifold’s intrinsic distances. Furthermore, the methodology incorporates a nuanced treatment of the curvature effects inherent in Riemannian manifolds. The approximation of the squared distances using the inverse exponential map, with bounds related to sectional curvature, ensures that local linearizations remain valid within convex neighborhoods. This means that within these neighborhoods, the manifold can be approximated as a Euclidean space, allowing for the application of linear methods such as PCA.
By selecting a central point, such as the Riemannian barycenter, the analysis minimizes distortion, resulting in more faithful low-dimensional visualizations. The tangent space PCA—referred to as intrinsic PCA—operates on the mapped principal points, allowing for an eigendecomposition that respects the metric tensor, thus accounting for the manifold’s local curvature. This combined geometric and statistical framework underscores the importance of respecting the data’s underlying structure. By integrating differential geometric concepts with kernel methods and PCA, the approach achieves a balance between local fidelity and global interpretability. It enables the extraction of meaningful features, flow patterns, and principal directions that are invariant under the manifold’s curvature, resulting in more robust and insightful analyses.
This methodology exemplifies a comprehensive approach to manifold data analysis, emphasizing the importance of intrinsic geometry. The use of flow lines of the gradient, the application of exponential and logarithmic maps, the implementation of kernel-based reduction, and the intrinsic PCA all serve to capture the complex structure of data residing in nonlinear spaces. Such techniques are increasingly vital in modern data science, where high-dimensional, curved data structures are prevalent, and a faithful representation of their geometry is essential for meaningful interpretation.
Building on this synthesis, the geometric framework we propose opens new avenues for understanding the dynamics of information in physical systems. By conceptualizing inference processes as variational principles operating on Riemannian manifolds, we suggest that the evolution of knowledge—both in scientific models and in fundamental physics—may be described by wave-like phenomena governed by invariant geometric structures. This perspective aligns with the notion that physical laws themselves can be viewed as extremal principles on curved manifolds, where the flow of information and the evolution of states are intrinsically linked. Such a viewpoint encourages us to explore whether the principles underlying quantum mechanics, general relativity, and thermodynamics can be unified within a common geometric language rooted in information theory.
Consequently, this approach not only enriches our theoretical understanding of inference but also suggests a deeper, possibly holographic, nature of reality, where the fabric of spacetime and the behavior of matter emerge from the geometry of information. Future research may reveal whether these geometric and variational insights can lead to new formulations of physical laws, bridging the gap between abstract information geometry and the tangible fabric of the universe.
Of course, this paper is only the first step towards the above-mentioned deep relationship between physical and data analysis. We would certainly like to have a clear path already outlined for developing the variational principle and connecting it with the major existing physical theories. For the time being, in our immediate work, we will limit ourselves to attempting to derive some existing basic equations—the Schrödinger, Klein-Gordon, and Dirac equations—and to the extent possible, we will explore their compatibility with general relativity and thermodynamics. Other relationships, such as decoherence, entanglement, and von Neumann’s entropy, for example, will be addressed in future work.
Author Contributions
Conceptualization, D.B.-C. and J.M.O.; writing—original draft preparation, D.B.-C. and J.M.O.; writing—review and editing, D.B.-C. and J.M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study did not require ethical approval.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We sincerely appreciate the insightful feedback from the reviewers, which has significantly sharpened the clarity of the ideas presented in our article. Their constructive critique has not only highlighted our current limitations but has also sparked an inspiring challenge that will drive our future research forward.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Differential Geometry Remarks
In this appendix subsection, we will briefly review some well-known concepts that can be further explored in classical references on differential geometry, data analysis, and statistics, such as [8,9,13], among many others.
Consider an m-dimensional smooth real manifold , and let r and s be non-negative integers. A is a -tensor field, r times contravariant and s times covariant, in an open set U of a manifold , and, roughly speaking, is a multilinear map defined at
depending smoothly on . Taking into account that a coordinate system induces a basis vector field in each tangent space, , denoted as , and also a basis vector field in each dual, , denoted as , the components of the tensor field A, corresponding to these basis fields, will be denoted by , and when we change to another coordinate system , these components are going to change accordingly to
In (A2), we have used the summation convention of repeated indices; all these quantities are evaluated at , and we have used classical notation. If , then A is a smooth function on , which is just an invariant with respect to coordinate changes. If , we just say that A is an s-covariant tensor field, while if , we just say that A is an r-contravariant tensor field. We shall call intrinsic any object or property independent of the coordinate system in .
Let us recall that if and are smooth real manifolds, and q is a smooth mapping on an open subset to values in , then this map induces, for each , a linear map between and , which we will call the differential of q at and denote by , such that if , then we define , for all smooth function h on a neighborhood of .
Also, we recall that a curve σ in is a smooth map of an open interval in . When we talk about a curve of a closed interval in , we will assume that the domain of the curve is an open containing .
Given a m-dimensional real manifold , let denote the tangent bundle (the set of all the pairs such that with and having the structure of a -dimensional manifold), and let be the projection function, where if . Let I be an open interval in and be a smooth curve in . A vector field over is a map such that , i.e.: for all .
For each point in the domain, , we define the tangent vector to σ at t as the vector defined from , where is the basis vector field corresponding to the identity chart in . The tangent field can also be denoted by . For simplicity, we often overuse notation and identify the tangent fields on curves with their images, that is, we will write as .
A Riemannian manifold will be a manifold equipped with a Riemannian metric, that is, a second-order covariant smooth tensor field, which is additionally positive definite at each tangent space. In simple words, we have a scalar product defined in each tangent space that varies smoothly when we move to different points in the parametric space, which will be denoted by . The local version of the Riemannian metric in will commonly be expressed, using the summation convention of repeated indices, as , as in (8), where .
Corresponding to this fundamental tensor, whose components are given by , there are the well-known operations of raising or lowering indices, which in fact allow us to identify covariant with contravariant tensor fields, or the opposite. For a particular index and for every , these operations are isomorphisms between the tangent bundle and its dual, the cotangent bundle, , the flat map (lowering indexes), symbolized by ♭ and defined through , or the opposite, between the dual of the tangent bundle and its dual, the bidual bundle of canonically identifiable with the tangent bundle itself, , the sharp map (raising indexes), symbolized by ♯ and defined through . In component notation, this is achieved simply by multiplying the components of a specific tensor by the fundamental covariant tensor field at or its inverse , the fundamental contravariant tensor field at the dual of the tangent bundle, the cotangent bundle .
The gradient of a smooth function q in an open neighborhood of a point of a Riemannian manifold is a vector field such that for all vector field , where is the directional derivative of q in the direction given by at . Observe that in the previous notation , it is well known that for , taking into account the definition of the gradient and the Cauchy–Schwarz inequality, we have , and the maximum is reached by the unitary vector . On the other hand, it will be possible to extend these mathematical objects to the complex case. If is a complex-valued function, and if and are the standard real and imaginary parts of a complex number, if we let and , we may define , and we can extend the scalar product in each tangent space to complexified vector fields and , defining the scalar product as , at each point . The corresponding square of the form will be .
The differentiation of vector fields involves the choice of a connection, i.e., a rule which associates to each point a tangent vector and a smooth tensor field defined at least in a neighborhood of a vector , such that and , being smooth vector fields and q being a smooth function in the neighborhood of . It is also required that be linear in and that be a smooth vector field. The vector is commonly called the covariant derivative of with respect to . At this point, let us recall that we can define the divergence of a smooth vector field as the smooth real-valued function defined, at , as , and the Laplacian of a real smooth function q as ; for details and properties see [21]. If we add the requirements that where is the Lie bracket of both vector fields, and , which is another vector field such that their action, over a smooth function q, is given by and, additionally, , we obtain the Levi–Civita connection, which is uniquely determined through the Christoffel symbols of the second kind. These are defined, again using repeated index summation convention, in terms of the metric tensor as
symbols which encode how the basis vectors change from point to point due to curvature, which is properly quantified through several objects, such as the curvature operator
for vector fields , , and in and, also, the Riemann–Christoffel tensor defined as
with being another vector field in , the Riemannian sectional curvatures corresponding to the linearly independent vector fields and being defined as
and the Ricci tensor being defined as . Observe that, if and , if we define , we find that the components of the vector field are given by
where is the ordinary partial derivative. This formula illustrates how the covariant derivative modifies the ordinary derivative by incorporating terms that account for the twisting and turning of the coordinate system in curved space. The covariant derivative concept is a powerful generalization of ordinary derivatives, extending the concept from flat, Euclidean spaces to the more complex realm of curved manifolds. This extension is crucial for understanding how geometric properties evolve in curved spaces. The covariant derivative incorporates additional terms that account for the curvature of the manifold, effectively correcting for the way basis vectors change as one moves from point to point. This enables us to analyze and describe the behavior of vector fields and other geometric objects in a way that respects the underlying curvature.
It is convenient to generalize the covariant derivative to any tensor field. For this purpose, given and q, a real smooth function on an open subset of we denote by , and if and , then define . Moreover, given an -tensor field , the covariant derivative may be extended to obtain an -tensor field. If and , then
and, finally,
Given a connection, the corresponding geodesics, the generalization of straight lines, are the curves whose tangent vector field, T, does not change, i.e., . In components, under a coordinate system , if we denote, with certain overuse of notation, by the coordinates of a geodesic, we shall have, using the summation convention of repeated indices,
In the Riemannian case, with the Levi–Civita connection, the geodesics are also, locally, the minimum-length curves.
Next, we review the definition of the exponential map corresponding to a connection that is defined through geodesics as follows. Let be a point of the manifold , , be the tangent space in , and let be a geodesic such that
Then, the exponential map is given by , and it is well defined for all in an open star-shaped neighborhood of .
Hereafter, we will consider the Riemannian case with the Levi–Civita connection. We now define as , and for each , we let , where is the Riemannian distance, and is a geodesic defined in an open interval containing zero, such that with a tangent vector equal to at the origin. Then, if we set
it is well known that maps diffeomorphically onto . If the manifold is also complete, then the boundary of , is mapped by the exponential map onto , called the cut locus of θ in Θ, which in this case has a zero Riemannian measure. Moreover, if the manifold is simply connected, and the Riemannian curvature is non-positive or positive but with a sufficiently small diameter, the cut locus is empty. Additionally, in this case, the inverse of the exponential map is considered a map between two metric spaces: , a Riemannian manifold, and , the tangent space with Euclidean structure, which preserves the distance between any point to , although it does not preserve distances between arbitrary points in general. For additional details, see [9,21,22].
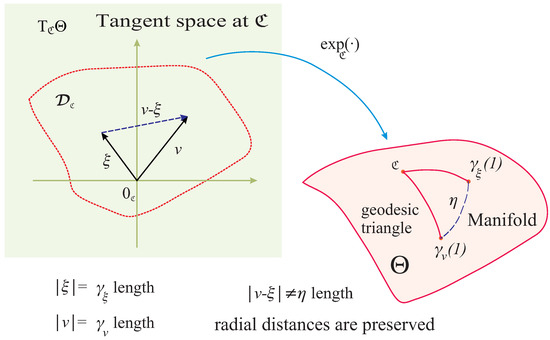
Figure A1.
The figure illustrates the exponential map corresponding to the Levi–Civita connection in a Riemannian manifold. The lengths of the vectors in in the tangent space are equal to the Riemannian distance . This map preserves the radial distances but not the distances in general; the norm is not equal to the Riemannian distance ).
We now briefly review the concept of Jacobi field along a geodesic. Consider a geodesic in and , the tangent vector field over . A Jacobi field along is a field which satisfies the Jacobi equation
where is the covariant derivative in the direction given by along c.
Appendix A.2. Proof of Formula (65)
Let be a geodesically convex open ball of radius around , where is a complete Riemannian manifold. Let be a curve. Let us define and
where is the differential of , and and are the ordinary partial derivative operators on ; observe that is a Jacobi field along the geodesic , with . On the other hand, it is well known, see [9], that for fixed t,
where denotes the natural identification of with (the tangent of the tangent space), and Y is a Jacobi field along , with and .
Let us define , then,
Therefore,
and simultaneously,
with . Thus we obtain
and, identifying the scalar product in with its corresponding in ,
Therefore the length of from to will be given by
Additionally, from the geometric Rauch theorem, see [9], we have
as long as and do not vanish, where
, is the normal component of the Jacobi field, with respect to and
with K being the sectional Riemannian curvature, and being the tangent Riemannian ball bundle. Moreover, taking into account the properties of the tangential Jacobi fields, we have
where is the tangential component of and
and
we obtain
and
Then, taking into account that
we have
with being a strictly positive increasing function if (as long as does not vanish) and a decreasing function such that if . Therefore,
and
since . On the other hand, the Riemannian length of is given by
Therefore,
Let us consider now . In this case, the shortest geodesic that joins and lies in . Let be this geodesic with , , and let us define , i.e., the Riemannian distance between and . Then, we have
On the other hand, if , and if is the straight line in such that and , then with , . Thus, we have
since .
Appendix A.3. Additional Remarks
As a reminder, it has been proven that well-known indices, such as the Kullback–Leibler divergence, locally induce, up to a proportionality constant, the information metric on the parameter space of the statistical model. Further characterizations of the information metric, in terms of invariance under Markov kernels’ transformations, are given in [23]. With the Riemannian distance, say , such that , the manifold or becomes a length space, unlike these manifolds considering the Hilbert metric structure. The information metric has been studied for several parametric regular statistical models; for instance, see [11,24]. Moreover, though the information metric is possible to develop, in a natural way, an intrinsic approach to statistical estimation, invariant under reparametrizations, see [25].
Concerning the Hermitian kernel notion, observe that the Hermitian property is a consequence of the positive-definiteness, and it is not necessary to make it explicit in the definition. If, for mutually distinct , the equality only holds for , it is often said that K is a strictly positive definite Hermitian kernel. It is also possible to consider real-valued kernels satisfying such that and for any positive integer , , .
Moreover, observe that the natural kernel suggested, corresponding to a regular parametric family, satisfies , since clearly , and for any scalars , where n is an arbitrary positive integer, ; therefore, is a complex-valued Hermitian kernel.
With additional assumptions about the parameter space from measure and topological theory, many other properties of kernels can be established, such as Mercer’s theorem and relationships between square-integrable function spaces and RKHS via linear operators. Additionally, to clarify the relationship between the fundamental tensor and the kernel, we can utilize several results made explicit in Chapter 4 of [13].
References
- Frieden, B. Science from Fisher Information: A Unification, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, USA, 2007. [Google Scholar]
- Amari, S.i. Information Geometry and Its Applications, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Bernal-Casas, D.; Oller, J.M. Variational Information Principles to Unveil Physical Laws. Mathematics 2024, 12, 3941. [Google Scholar] [CrossRef]
- Chalmers, D. Constructing the World; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Lang, S. Fundamentals of Differential Geometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 191. [Google Scholar]
- Burbea, J.; Rao, C.R. Entropy differential metric, distance and divergence measures in probability spaces: A unified approach. J. Multivar. Anal. 1982, 12, 575–596. [Google Scholar] [CrossRef]
- Kobayashi, S.; Nomizu, K. Foundations of Differential Geometry; John Wiley & Sons: Hoboken, NJ, USA, 1963; Volumes 1 and 2. [Google Scholar]
- Chavel, I. Riemannian Geometry: A Modern Introduction; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Rao, C. Information and Accuracy Attainable in Estimation of Statistical Parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Atkinson, C.; Mitchell, A.F.S. Rao’s Distance Measure. Sankhyā Indian J. Stat. Ser. A 1981, 43, 345–365. [Google Scholar]
- Aronszajn, N. Theory of Reproducing Kernels. Trans. Am. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Coddington, E.E.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955; Reprinted in December 1984. [Google Scholar]
- Reverter, F.; Vegas, E.; Oller, J. Kernel-PCA data integration with enhanced interpretability. BMC Syst. Biol. 2014, 8, S6. [Google Scholar] [CrossRef] [PubMed]
- Karcher, H. Riemannian center of mass and mollifier smoothing. Commun. Pure Appl. Math. 1977, 30, 509–541. [Google Scholar] [CrossRef]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis; Springer: New York, NY, USA, 1985. [Google Scholar]
- Heyer, H. Theory of Statistical Experiments; Springer: New York, NY, USA, 1983. [Google Scholar]
- Strasser, H. Mathematical Theory of Statistics: Statistical Experiments and Asymptotic Decision Theory; Walter de Gruyter: Berlin, Germany, 1985. [Google Scholar]
- Chavel, I. Eigenvalues in Riemannian Geometry; Elsevier: Philadelphia, PA, USA, 1984. [Google Scholar] [CrossRef]
- Spivak, M. A Comprehensive Introduction to Differential Geometry; Publish or Perish: Berkeley, CA, USA, 1970; Volumes 1–5. [Google Scholar]
- Chentsov, N.N. Statistical Decision Rules and Optimal Inference; Translations of Mathematical Monographs; Translated from the Russian by the Israel Program for Scientific Translations; American Mathematical Society: Providence, RI, USA, 1982; Volume 53. [Google Scholar] [CrossRef]
- Calvo, M.; Oller, J. An explicit solution of information geodesic equations for the multivariate normal model. Stat. Decis. 1991, 9, 119–138. [Google Scholar] [CrossRef]
- Oller, J.M.; Corcuera, J.M. Intrinsic Analysis of Statistical Estimation. Ann. Stat. 1995, 23, 1562–1581. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).