Debiased Maximum Likelihood Estimators of Hazard Ratios Under Kernel-Based Machine Learning Adjustment
Abstract
1. Introduction
2. Theories and Methods
2.1. Exponential Parametric Hazard Model Combined with Machine Learning
2.2. Causal Inference and ML Estimation
2.3. Debiasing ML Estimators
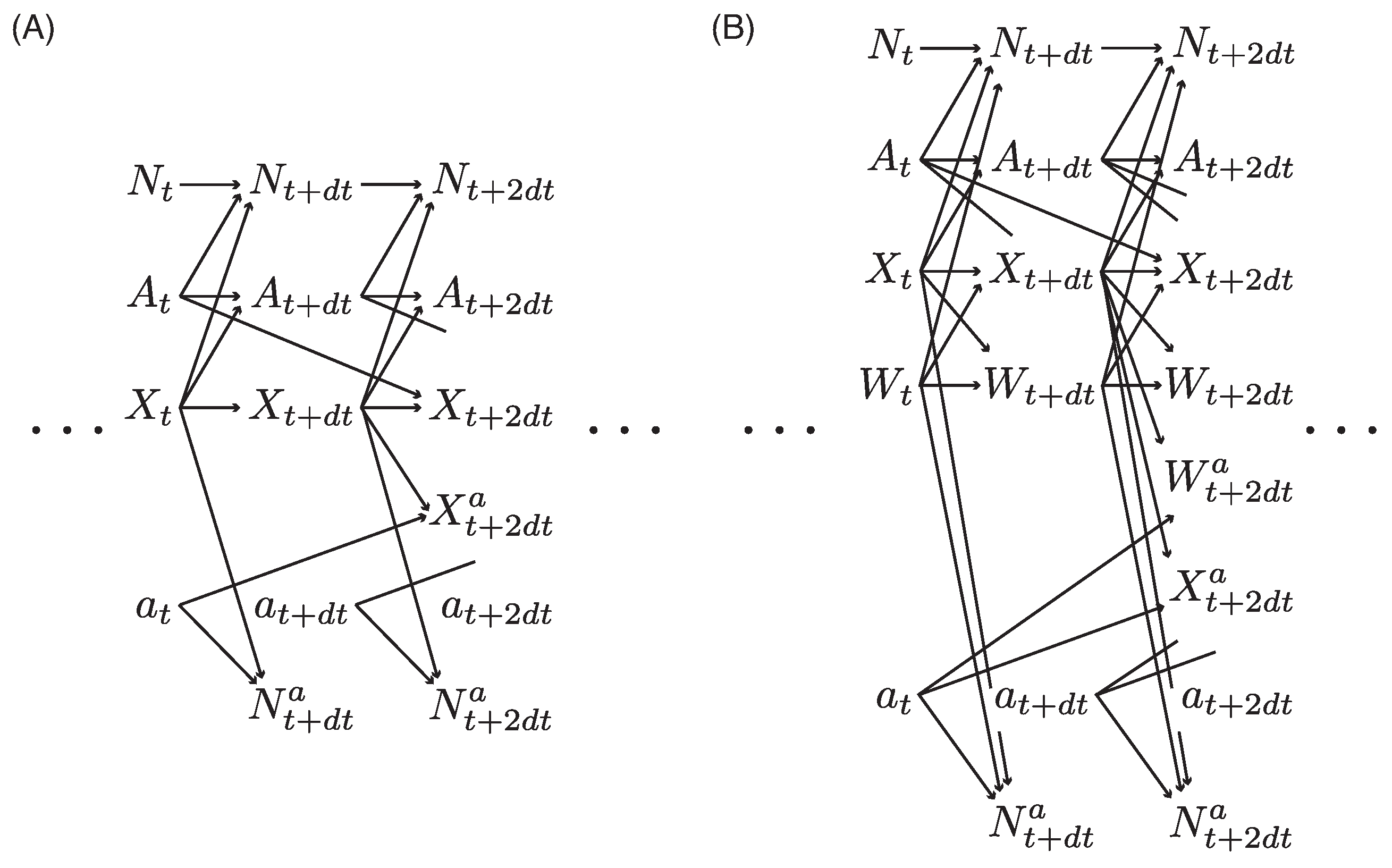
2.4. Extension to Models with Latent Variables
2.5. Design of Models with Multiple RKHSs
2.6. Estimation Algorithm
| Algorithm 1 DML of hazard ratios with cross fitting |
|
- Step 1: Model selection and determination of hyperparameter values
- Step 2: Estimation of nuisance parameters
- Step 3: Debiased estimation of and its standard error.
3. Results of Numerical Simulations
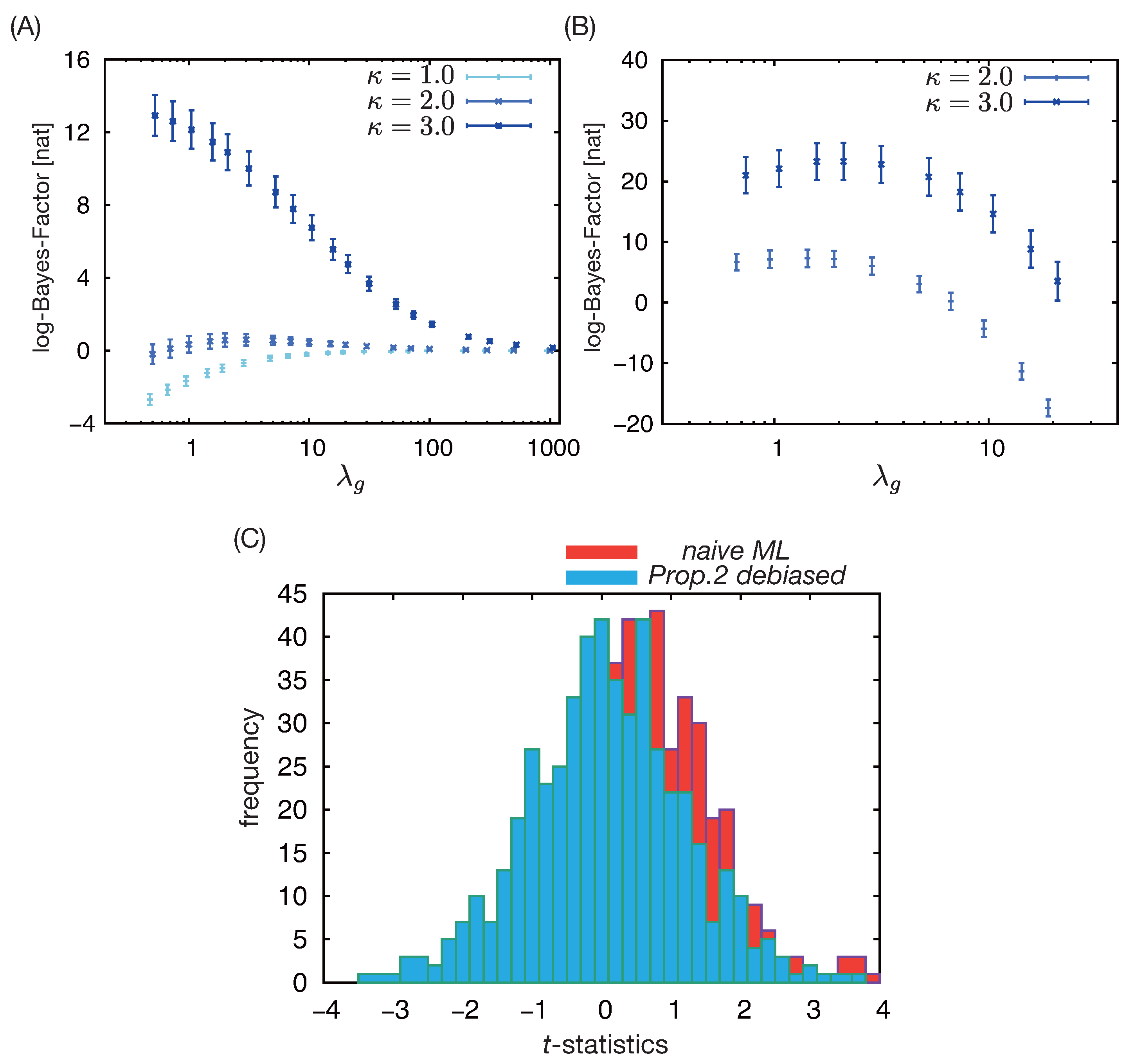
3.1. Simulation Result 1: Adjustment for Observed Confounders
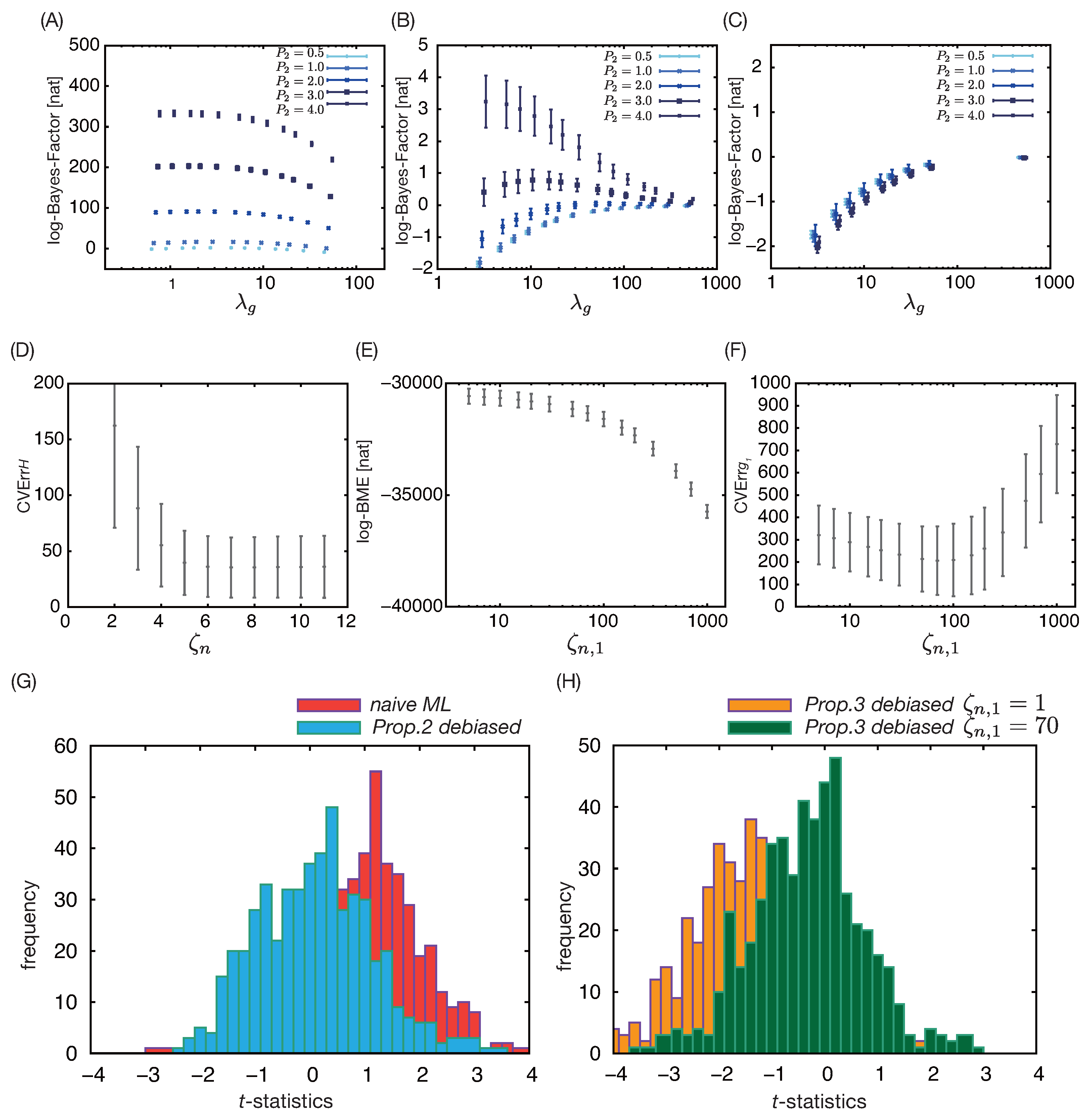
3.2. Simulation Result 2: Estimation of Treatment Effect in Population with Heterogeneous Risk
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Implementation of Inference with Multiple-Kernel Models
| Symbols | Description |
|---|---|
| , | The sets of natural and real numbers and d-dimensional Euclidean space () |
| Product set (or product space) | |
| Measure space with product space and product algebra | |
| Tensor product | |
| , | Transposition of vector v and matrix A |
| The smaller of a and | |
| Element a of a set | |
| Set inclusion (with possible equality) | |
| , | Union and intersection of sets |
| The number of elements in a set | |
| B, | Convergence in probability and in distribution |
| , | Asymptotic notations for (see Ref. [56]) |
| , | Probabilistic asymptotic notations for (see Ref. [56]) |
| (arg) | (Element yielding) minimum of over |
| (arg) | (Element yielding) maximum of over |
| Supremum of over | |
| () | Expectation of the argument random variable (for the specified distribution) |
| Equation defining the object on the left-hand side | |
| , | The norm of the metric vector space and the normed vector space |
| The operator norm of a linear operator A | |
| Independence between A and B (conditioned on ) | |
| , () | Independently and identically distributed (objects drawn from the right-hand side) |
| Integration of over set E with respect to measure on the space for X | |
| Natural mapping of vectors into their product space | |
| Abbreviation of partial derivative | |
| Gateaux derivative | |
| Uniform probability distribution over the interval | |
| Gaussian probability distribution with mean and (co)variance |
Appendix B. Proof of Proposition 1
Appendix C. Proof of Proposition 2
Appendix D. Gradient Functional and Hessian Operator
Appendix E. The Validity of Assumption 9
Appendix F. Proof of Proposition 3
Appendix G. Consideration of the Score Regularity and the Quality of Estimation of Nuisance Parameters Required for DML
Appendix H. Additional Consideration of Causal Interpretation of Hazard Ratios
References
- Lin, R.S.; Lin, J.; Roychoudhury, S.; Anderson, K.M.; Hu, T.; Huang, B.; Leon, L.F.; Liao, J.J.; Liu, R.; Luo, X.; et al. Alternative Analysis Methods for Time to Event Endpoints Under Nonproportional Hazards: A Comparative Analysis. Stat. Biopharm. Res. 2020, 12, 187–198. [Google Scholar] [CrossRef]
- Bartlett, J.W.; Morris, T.P.; Stensrud, M.J.; Daniel, R.M.; Vansteelandt, S.K.; Burman, C.F. The Hazards of Period Specific and Weighted Hazard Ratios. Stat. Biopharm. Res. 2020, 12, 518–519. [Google Scholar] [CrossRef]
- Hernán, M.A. The Hazards of Hazard Ratios. Epidemiology 2010, 21, 13–15. [Google Scholar] [CrossRef]
- Aalen, O.O.; Cook, R.J.; Røysland, K. Does Cox analysis of a randomized survival study yield a causal treatment effect? Lifetime Data Anal. 2015, 21, 579–593. [Google Scholar] [CrossRef] [PubMed]
- Martinussen, T.; Vansteelandt, S.; Andersen, P.K. Subtleties in the interpretation of hazard contrasts. Lifetime Data Anal. 2020, 26, 833–855. [Google Scholar] [CrossRef] [PubMed]
- Martinussen, T. Causality and the Cox Regression Model. Annu. Rev. Stat. Its Appl. 2022, 9, 249–259. [Google Scholar] [CrossRef]
- Prentice, R.L.; Aragaki, A.K. Intention-to-treat comparisons in randomized trials. Stat. Sci. 2022, 37, 380–393. [Google Scholar] [CrossRef]
- Ying, A.; Xu, R. On Defense of the Hazard Ratio. arXiv 2023, arXiv:2307.11971. Available online: http://arxiv.org/abs/2307.11971 (accessed on 22 July 2025). [CrossRef]
- Fay, M.P.; Li, F. Causal interpretation of the hazard ratio in randomized clinical trials. Clin. Trials 2024, 21, 623–635. [Google Scholar] [CrossRef] [PubMed]
- Rufibach, K. Treatment effect quantification for time-to-event endpoints—Estimands, analysis strategies, and beyond. Pharm. Stat. 2019, 18, 145–165. [Google Scholar] [CrossRef]
- Kloecker, D.E.; Davies, M.J.; Khunti, K.; Zaccardi, F. Uses and Limitations of the Restricted Mean Survival Time: Illustrative Examples From Cardiovascular Outcomes and Mortality Trials in Type 2 Diabetes. Ann. Intern. Med. 2020, 172, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Snapinn, S.; Jiang, Q.; Ke, C. Treatment effect measures under nonproportional hazards. Pharm. Stat. 2023, 22, 181–193. [Google Scholar] [CrossRef]
- Cui, Y.; Kosorok, M.R.; Sverdrup, E.; Wager, S.; Zhu, R. Estimating heterogeneous treatment effects with right-censored data via causal survival forests. J. R. Stat. Soc. Ser. Stat. Methodol. 2023, 85, 179–211. [Google Scholar] [CrossRef]
- Xu, S.; Cobzaru, R.; Finkelstein, S.N.; Welsch, R.E.; Ng, K.; Shahn, Z. Estimating Heterogeneous Treatment Effects on Survival Outcomes Using Counterfactual Censoring Unbiased Transformations. arXiv 2024, arXiv:2401.11263. Available online: http://arxiv.org/abs/2401.11263 (accessed on 22 July 2025).
- Frauen, D.; Schröder, M.; Hess, K.; Feuerriegel, S. Orthogonal Survival Learners for Estimating Heterogeneous Treatment Effects from Time-to-Event Data. arXiv 2025, arXiv:2505.13072. Available online: http://arxiv.org/abs/2505.13072 (accessed on 22 July 2025).
- Leviton, A.; Loddenkemper, T. Design, implementation, and inferential issues associated with clinical trials that rely on data in electronic medical records: A narrative review. BMC Med. Res. Methodol. 2023, 23, 271. [Google Scholar] [CrossRef]
- Hernán, M.A.; Brumback, B.; Robins, J.M. Marginal Structural Models to Estimate the Joint Causal Effect of Nonrandomized Treatments. J. Am. Stat. Assoc. 2001, 96, 440–448. [Google Scholar] [CrossRef]
- Van der Laan, M.J.; Rose, S. Targeted Learning in Data Science; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Chernozhukov, V.; Chetverikov, D.; Demirer, M.; Duflo, E.; Hansen, C.; Newey, W.; Robins, J. Double/debiased machine learning for treatment and structural parameters. Econom. J. 2018, 21, C1–C68. [Google Scholar] [CrossRef]
- Ahrens, A.; Chernozhukov, V.; Hansen, C.; Kozbur, D.; Schaffer, M.; Wiemann, T. An Introduction to Double/Debiased Machine Learning. arXiv 2025, arXiv:2504.08324. Available online: http://arxiv.org/abs/2504.08324 (accessed on 22 July 2025). [CrossRef]
- Ren, J.J.; Zhou, M. Full likelihood inferences in the Cox model: An empirical likelihood approach. Ann. Inst. Stat. Math. 2011, 63, 1005–1018. [Google Scholar] [CrossRef]
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Fukumizu, K.; Song, L.; Gretton, A. Kernel Bayes’ Rule: Bayesian Inference with Positive Definite Kernels. J. Mach. Learn. Res. 2013, 14, 3753–3783. [Google Scholar]
- Yang, S.; Eaton, C.B.; Lu, J.; Lapane, K.L. Application of marginal structural models in pharmacoepidemiologic studies: A systematic review. Pharmacoepidemiol. Drug Saf. 2014, 23, 560–571. [Google Scholar] [CrossRef] [PubMed]
- Robins, J.M.; Hernán, M.Á.; Brumback, B. Marginal Structural Models and Causal Inference in Epidemiology. Epidemiology 2000, 11, 550–560. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- van der Laan, M.J.; Petersen, M.L.; Joffe, M.M. History-adjusted marginal structural models and statically-optimal dynamic treatment regimens. Int. J. Biostat. 2005, 1. [Google Scholar] [CrossRef]
- Hille, E.; Phillips, R.S. Functional Analysis and Semi-Groups; 3rd Printing of Rev. Ed. of 1957; Colloquium Publications: Kyiv, Ukraine, 1974; Volume 31. [Google Scholar]
- Lanckriet, G.R.; Cristianini, N.; Bartlett, P.; Ghaoui, L.E.; Jordan, M.I. Learning the kernel matrix with semidefinite programming. J. Mach. Learn. Res. 2004, 5, 27–72. [Google Scholar]
- Suzuki, T.; Sugiyama, M. Fast learning rate of multiple kernel learning: Trade-off between sparsity and smoothness. Ann. Stat. 2013, 41, 1381–1405. [Google Scholar] [CrossRef]
- Aronszajn, N. Theory of reproducing kernels. Trans. Am. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Bach, F.R. Consistency of the group lasso and multiple kernel learning. J. Mach. Learn. Res. 2008, 9, 1179–1225. [Google Scholar]
- Meier, L.; Van de Geer, S.; Bühlmann, P. High-dimensional additive modeling. Ann. Stat. 2009, 37, 3779–3821. [Google Scholar] [CrossRef]
- Koltchinskii, V.; Yuan, M. Sparsity in multiple kernel learning. Ann. Stat. 2010, 38, 3660–3695. [Google Scholar] [CrossRef]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Efron, B. The Efficiency of Cox’s Likelihood Function for Censored Data. J. Am. Stat. Assoc. 1977, 72, 557–565. [Google Scholar] [CrossRef]
- Oakes, D. The Asymptotic Information in Censored Survival Data. Biometrika 1977, 64, 441–448. [Google Scholar] [CrossRef]
- Thackham, M.; Ma, J. On maximum likelihood estimation of the semi-parametric Cox model with time-varying covariates. J. Appl. Stat. 2020, 47, 1511–1528. [Google Scholar] [CrossRef]
- Luo, J.; Rava, D.; Bradic, J.; Xu, R. Doubly robust estimation under a possibly misspecified marginal structural Cox model. Biometrika 2024, 112, asae065. [Google Scholar] [CrossRef]
- Zhang, Z.; Stringer, A.; Brown, P.; Stafford, J. Bayesian inference for Cox proportional hazard models with partial likelihoods, nonlinear covariate effects and correlated observations. Stat. Methods Med. Res. 2023, 32, 165–180. [Google Scholar] [CrossRef] [PubMed]
- Inoue, K.; Adomi, M.; Efthimiou, O.; Komura, T.; Omae, K.; Onishi, A.; Tsutsumi, Y.; Fujii, T.; Kondo, N.; Furukawa, T.A. Machine learning approaches to evaluate heterogeneous treatment effects in randomized controlled trials: A scoping review. J. Clin. Epidemiol. 2024, 176, 111538. [Google Scholar] [CrossRef]
- Ma, J.; Heritier, S.; Lô, S.N. On the maximum penalized likelihood approach for proportional hazard models with right censored survival data. Comput. Stat. Data Anal. 2014, 74, 142–156. [Google Scholar] [CrossRef]
- Allman, E.S.; Matias, C.; Rhodes, J.A. Identifiability of parameters in latent structure models with many observed variables 2009.
- Allman, E.S.; Rhodes, J.A.; Stanghellini, E.; Valtorta, M. Parameter identifiability of discrete Bayesian networks with hidden variables. J. Causal Inference 2015, 3, 189–205. [Google Scholar] [CrossRef]
- Gassiat, E.; Cleynen, A.; Robin, S. Inference in finite state space non parametric Hidden Markov Models and applications. Stat. Comput. 2016, 26, 61–71. [Google Scholar] [CrossRef]
- Gassiat, E.; Rousseau, J. Nonparametric finite translation hidden Markov models and extensions. Bernoulli 2016, 22, 193–212. [Google Scholar] [CrossRef]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tönsing, C.; Timmer, J. On structural and practical identifiability. Curr. Opin. Syst. Biol. 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Watanabe, S. Algebraic Geometry and Statistical Learning Theory; Cambridge University Press: Cambridge, UK, 2009; Volume 25. [Google Scholar]
- Calderhead, B.; Girolami, M. Estimating Bayes factors via thermodynamic integration and population MCMC. Comput. Stat. Data Anal. 2009, 53, 4028–4045. [Google Scholar] [CrossRef]
- Watanabe, S. A widely applicable Bayesian information criterion. J. Mach. Learn. Res. 2013, 14, 867–897. [Google Scholar]
- Drton, M.; Plummer, M. A Bayesian Information Criterion for Singular Models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2017, 79, 323–380. [Google Scholar] [CrossRef]
- Moral, P. Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Chopin, N.; Papaspiliopoulos, O. An Introduction to Sequential Monte Carlo; Springer: Berlin/Heidelberg, Germany, 2020; Volume 4. [Google Scholar]
- Bach, F.; Jordan, M. Kernel independent component analysis. J. Mach. Learn. Res. 2003. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Janson, S. Probability asymptotics: Notes on notation. arXiv 2011, arXiv:1108.3924. Available online: http://arxiv.org/abs/1108.3924 (accessed on 22 July 2025). [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Fukumizu, K.; Bach, F.R.; Gretton, A. Statistical Consistency of Kernel Canonical Correlation Analysis. J. Mach. Learn. Res. 2007, 8, 361–383. [Google Scholar]
- Kanamori, T.; Suzuki, T.; Sugiyama, M. Theoretical analysis of density ratio estimation. Ieice Trans. Fundam. Electron. Commun. Comput. Sci. 2010, 93, 787–798. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayakawa, T.; Asai, S. Debiased Maximum Likelihood Estimators of Hazard Ratios Under Kernel-Based Machine Learning Adjustment. Mathematics 2025, 13, 3092. https://doi.org/10.3390/math13193092
Hayakawa T, Asai S. Debiased Maximum Likelihood Estimators of Hazard Ratios Under Kernel-Based Machine Learning Adjustment. Mathematics. 2025; 13(19):3092. https://doi.org/10.3390/math13193092
Chicago/Turabian StyleHayakawa, Takashi, and Satoshi Asai. 2025. "Debiased Maximum Likelihood Estimators of Hazard Ratios Under Kernel-Based Machine Learning Adjustment" Mathematics 13, no. 19: 3092. https://doi.org/10.3390/math13193092
APA StyleHayakawa, T., & Asai, S. (2025). Debiased Maximum Likelihood Estimators of Hazard Ratios Under Kernel-Based Machine Learning Adjustment. Mathematics, 13(19), 3092. https://doi.org/10.3390/math13193092






