Appendix A
Proof of Lemma 1. 1. This is easy. Notice, for example, that
2.
3.
4.
□
Proof of Lemma 4. This is easy to prove as follows:
But, , and
It follows that .
The last two assertions have similar proofs. □
Proof of Lemma 5. Let
and
Then, according to (
21),
But, , with The random variables are again i.i.d. and uniformly distributed. Moreover, the complement of is , and
It follows that
□
Proof of Proposition 2. We know that
Then, we shall prove that
Let be fixed. Then,
It is convenient to renote the ratio In what follows, we shall use both r and R with the purpose to simplify the writing.
Let the function
be defined as
or, equivalently,
Obviously,
We are interested in the convergence of the series
Let us add and subtract from the general term and write it as
Now, we define and , and we prove that there exist some positive constants such as and Thus, the sequence of inequalities implies that the series is convergent and, finally, Furthermore, taking into account that one can find that , and
Let Then,
In order to simplify the calculus, we put , and we write , and further, equivalently,
Consider the functions and
In other words,
It is easy to verify that ,
and is bounded. It results that there exists a constant such that
Notice that is continuous (indeed, according to L’Hopital,
while ). It follows that it is also bounded, or there exists a constant such as We found ; hence, , with the property
Let us return to the term
Let , with It has the derivative , and the extreme point of is ; therefore, , with In our particular case, namely, , one obtains
This implies further that
In conclusion, we have proved that , with and thus,
It follows that the series is convergent, and finally,
and □
Proof of Lemma 6. By Lagrange ’s mean value theorem, there exists such that , and there exists such that
Thus,
There are two cases:
A. .
Then, .
Again, by the Lagrange theorem, there exists such that
But, , and It follows that
The sequence , with , is increasing as long as
In our case, ; hence,
Thus,
B. .
Now,
.
The sequence , with , increases as long as
In our case, ; hence, It follows that
Therefore,
□
Proof of Proposition 3 Let be arbitrarily fixed. We have
Let Notice that
Apply Proposition 1: check that
Indeed, , with
Let .
By Lemma 6, we know that
This means that the series is convergent; hence, .
Therefore, □
Proof of Lemma 7. We will use the following well-known result (see, for instance, [
11] Theorem 7.17 (p. 152)):
“If converges uniformly on some interval are continuous on , and converges uniformly on the same interval; then, ”.In order to do that, we must check the uniform convergence of the series (
22) and (
23), where
If we use the function
(which increases on the interval
and decreases afterwards), we obtain a more intelligible sum for
h as
Let Let and be fixed. Write
with
We show that all four series are uniformly convergent. The residuals are the following:
For
For
For
< (since )
For (since and v is decreasing on ) < (since if great enough) .
So, we have proved that
□
Proof of Proposition 4. Let and It is convenient to also denote
We consider the function , with
Let us notice that But, this implies that if the function would have a limit at infinity, it should be constant. We shall compute its derivative at , and we shall find conditions for this to be a negative function.
Let , with Therefore,
It is convenient to define the function
Then, from Equation (
A2), we know that
In terms of
and
, the sum
becomes
Considering the monotony of the function
one can notice that
,
and
This implies the following:
Therefore,
is smaller than
A sufficient condition such that
is
Let the function
, with
Then relation (
A5) is
As
and
, it is obvious that
Thus, , and
Thus,
With this estimation, the inequality
is implied by
(because
). Or, in terms of
it follows that
, which is
But, this is exactly the hypothesis (
24). Therefore, relation (
A5) is verified, so
and
are not constant. More exactly, it is decreasing in a neighborhood of
□
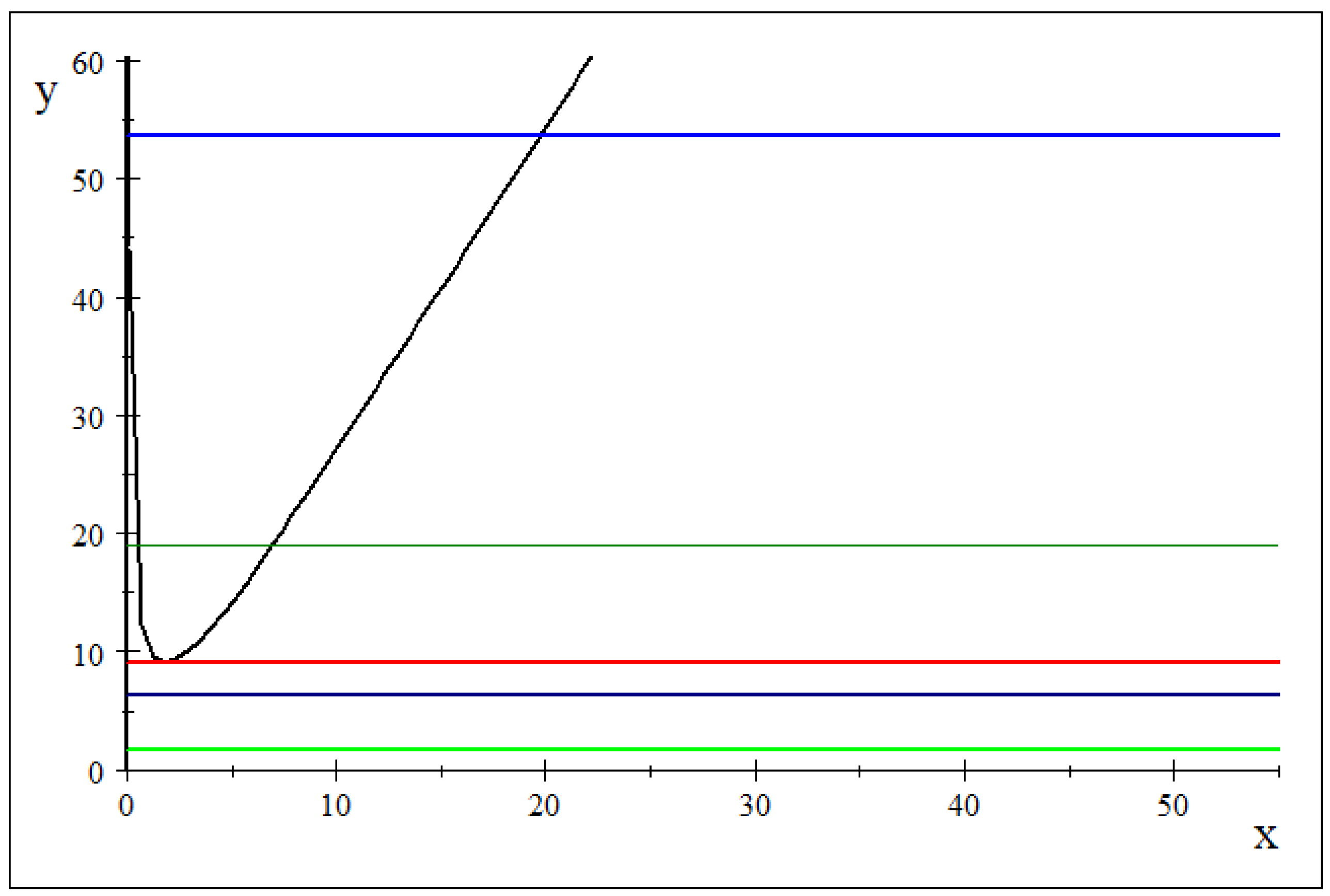
Remark A1. In the graph below, one can see values of which verify condition (24) when As we can observe, the inequality in (24) is actually very restrictive. Here, the graph of is represented with black, the graph of is represented with light green for with blue for green for and light blue for . As we can see, if , the inequality in (24) has no solution. In the figure, the line is represented with red.
Figure A1.
Ranges of
which verify hypothesis (
24) and
in light green,
in blue,
in red,
in green,
in light blue.
Figure A1.
Ranges of
which verify hypothesis (
24) and
in light green,
in blue,
in red,
in green,
in light blue.
Hypothesis (
24) is not verified either if
or if
and
has the property that
In what follows, we represent both the graph of the series (
22) and of the function (
A4) for pairs
which do not verify (
24), and we can see that even for such pairs, the series (
22) is not constant. Therefore, except for the studied case, this assertion remains a conjecture.
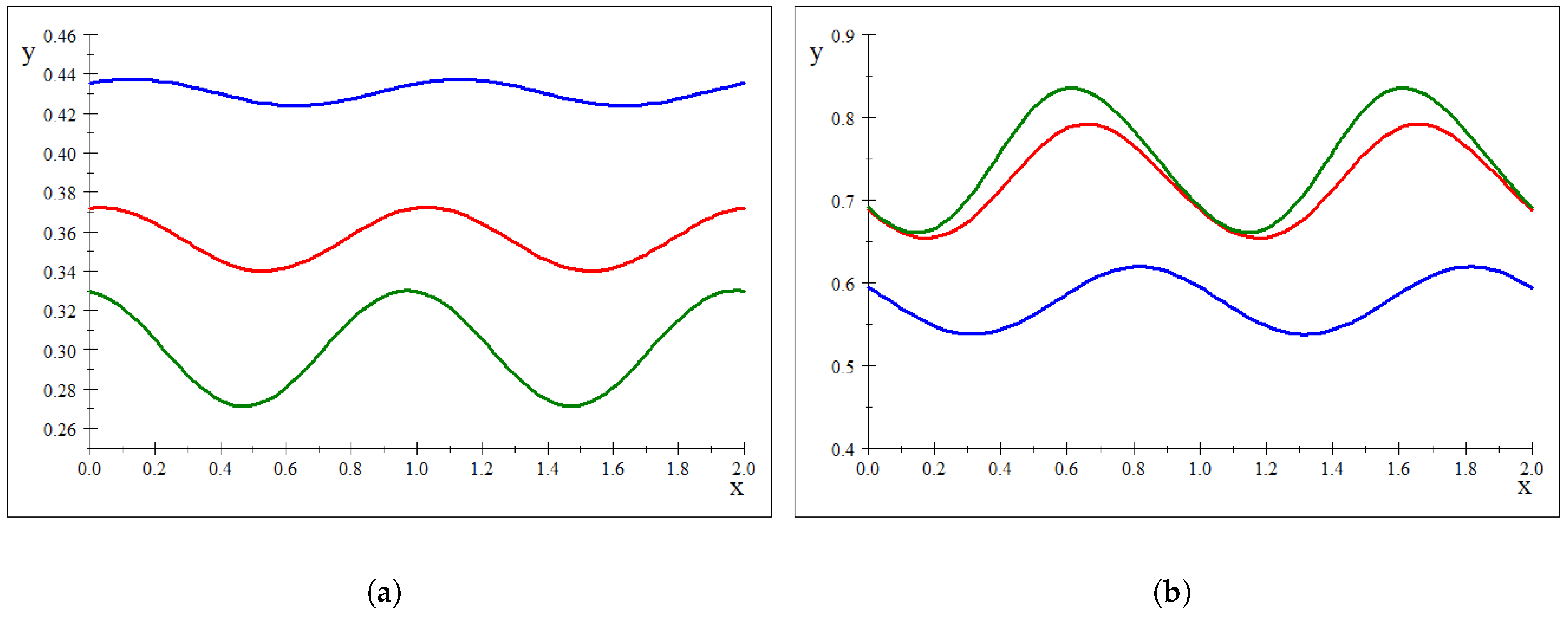
Remark A2. Let the functionmore exactly define partial sums of the series According to the previous remark, if , then there is no ρ with the property (24). However, in Figure A2, we can see that is not constant. In Figure A2a, we have and for the blue curve, for the red one, and for the green one. Figure A2b represents the graph of (A10) for or more exactly, with and ρ such as (or ). Here, as well. So, in Figure A2, we can see the graph of the function as a partial sum of the series (22), which is represented for the particular values and for three different pairs of values .
Figure A2.
The graph of the function . (a) in blue, in red, and in green. (b) in blue, in red, and in green.
Figure A2.
The graph of the function . (a) in blue, in red, and in green. (b) in blue, in red, and in green.
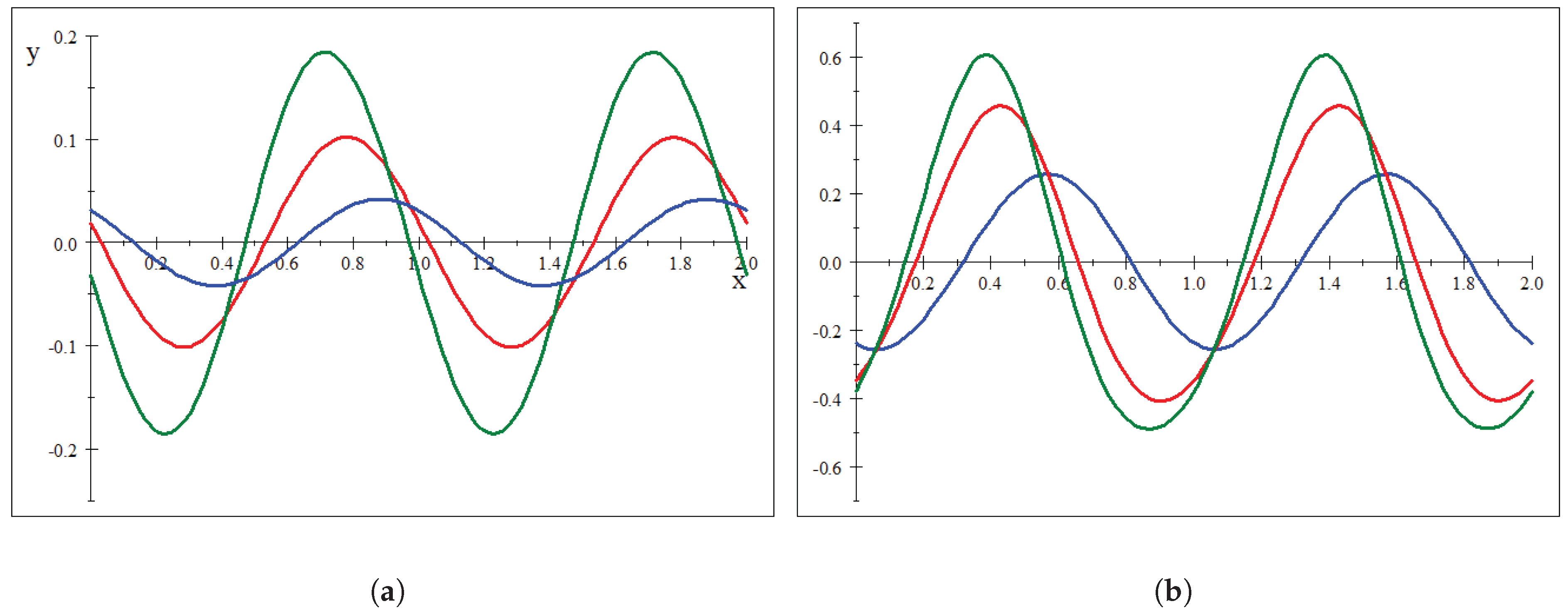
Remark A3. On the other hand, in Figure A3, one can see the graph of the function , withwhich is a partial sum of the function (23). We chose and the same values for the pairs as before.
Figure A3.
The graph of the function . (a) in blue, in red, and in green. (b) in blue, in red, and in green.
Figure A3.
The graph of the function . (a) in blue, in red, and in green. (b) in blue, in red, and in green.
The graph represented in
Figure A3a shows that the derivative is actually positive in a neighborhood of zero if
or
Remark A4. One can refine this approximation by keeping unchanged a finite number of terms in the series We have not used that because it is impossible to formulate a condition of type (24). For instance, we have the following:
E1) Keep unchanged, and we have the following:
, and from (
A7), we can write
; thus, another approximation for our inequality is
If
, then the derivative of the series (
22) calculated in
is negative too.
E2) For the second case, keep and unchanged, and we have the following:
Then, the condition
is sufficient for the function (
A4) to be negative.
Remark A5. In order to see the improvements provided by the relations (A11) and (A12), we present the following table. Here represents the approximation from (A12), is the approximation from (A11) and is the approximation from (A9).
Table A1.
Intervals for Q given .
Table A1.
Intervals for Q given .
| | | | |
|---|
| | | |
| | | |
| | | |
| | | |
If, for instance,
, and we apply (
A9) , then the values of
Q with the property that (
A6) does hold must be greater than
In comparison, if we apply (
A12), we obtain a larger interval for
Q and, in consequence, for
as well.
Even if the approximations (
A11) and (
A12) are less elegant than (
A9), they provide more generous sets for the parameters
and
Proof of Proposition 5. Let us have the sets and , with
Then, , and
According to Example 3, we know that does not exist. We will prove that A and B have the same nature, and, in consequence, does not exist either.
In order to prove that
A and
B have the same nature, let us check that
But,
Let us have and
Then, and
For
, it is known that
For , we have ; hence,
Therefore, , so
For , we have ; hence, , and
To conclude, we obtain that the sets
A and
B have the same nature according to (
25)
□
But this trick does not always hold: see, for instance, the sets already studied, such as
and . We know that they have the same nature. However, writing the difference of
and , we find that
With the same notation as before, we now have
and
We apply (
A14): In the case of
for
and the series is divergent.