Applications of Optimization Methods in Automotive and Agricultural Engineering: A Review
Abstract
1. Introduction
2. Methodology
- What optimization methods are available for automotive optimization problems?
- What optimization methods are available for agricultural optimization problems?
- What obstacles exist in applying different optimization methods to the automotive and agricultural sectors?
- What are the differences in the application of various optimization methods in the automotive and agricultural sectors?
- Articles that do not explicitly apply any of the five categories of optimization algorithms to specific problems in the automotive or agricultural sectors.
- Articles that are severely disconnected from automotive structural optimization, material optimization, collision safety, lightweight design, agricultural product testing, mechanical parameter optimization, and ecosystem optimization.
- Articles authored in languages other than English, conference papers, book chapters, reviews, surveys, Master’s theses, or PhD dissertations.
- Publications published before the year 2000.
3. Literature Review
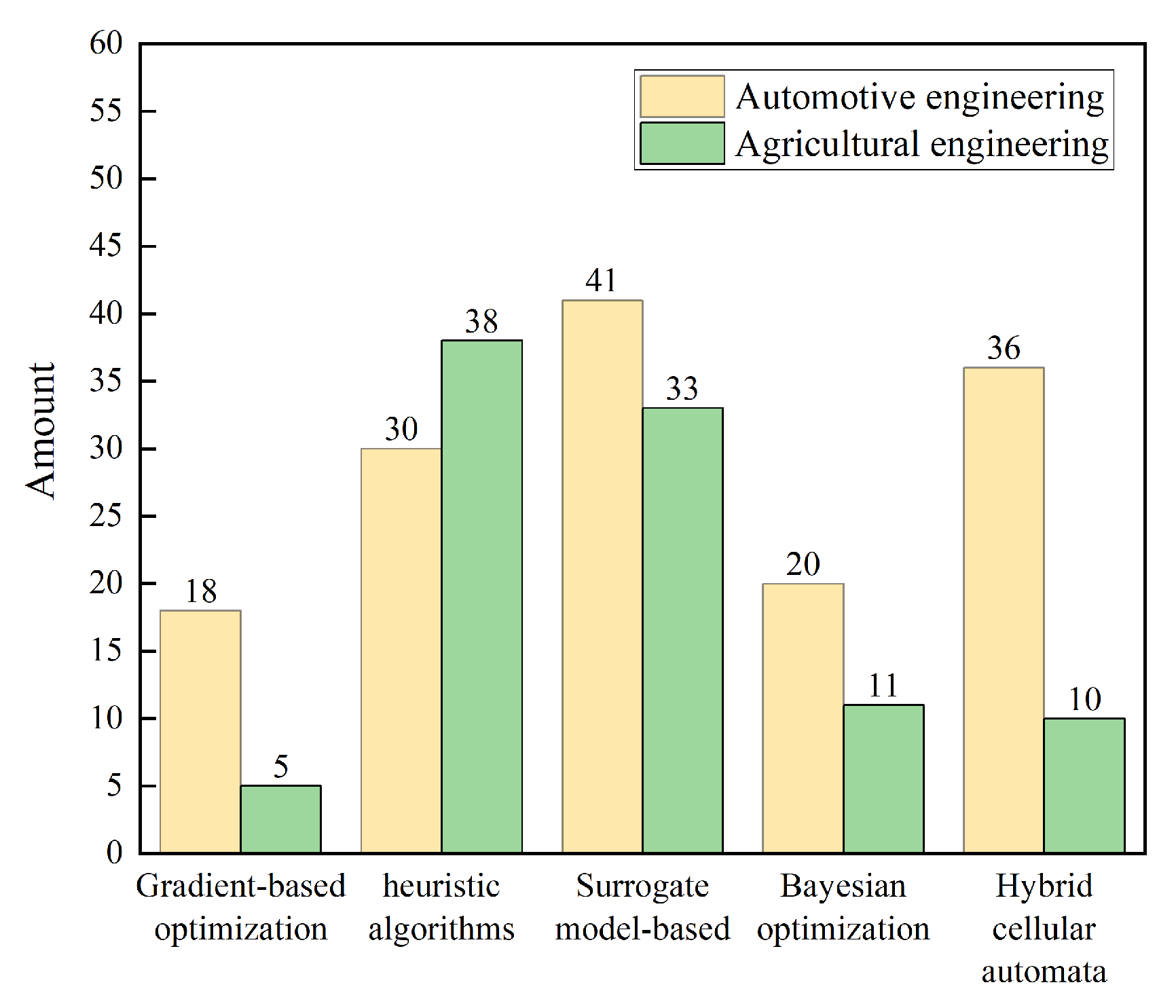
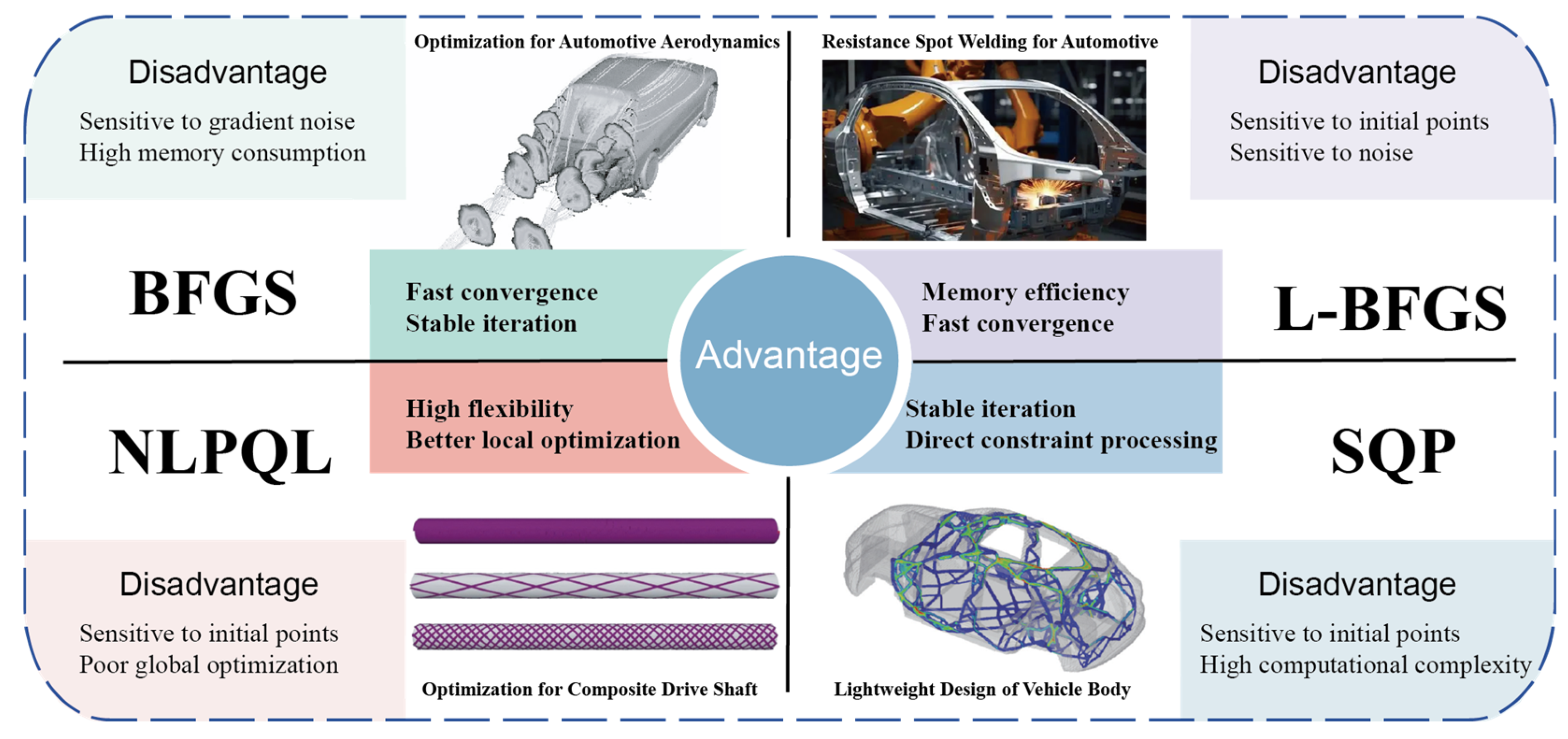
3.1. Gradient-Based Optimization Algorithms
3.1.1. Application of Gradient-Based Optimization in Automotive Engineering
3.1.2. Application of Gradient-Based Optimization in Agricultural Engineering
3.1.3. Future Development of Gradient-Based Optimization Algorithms
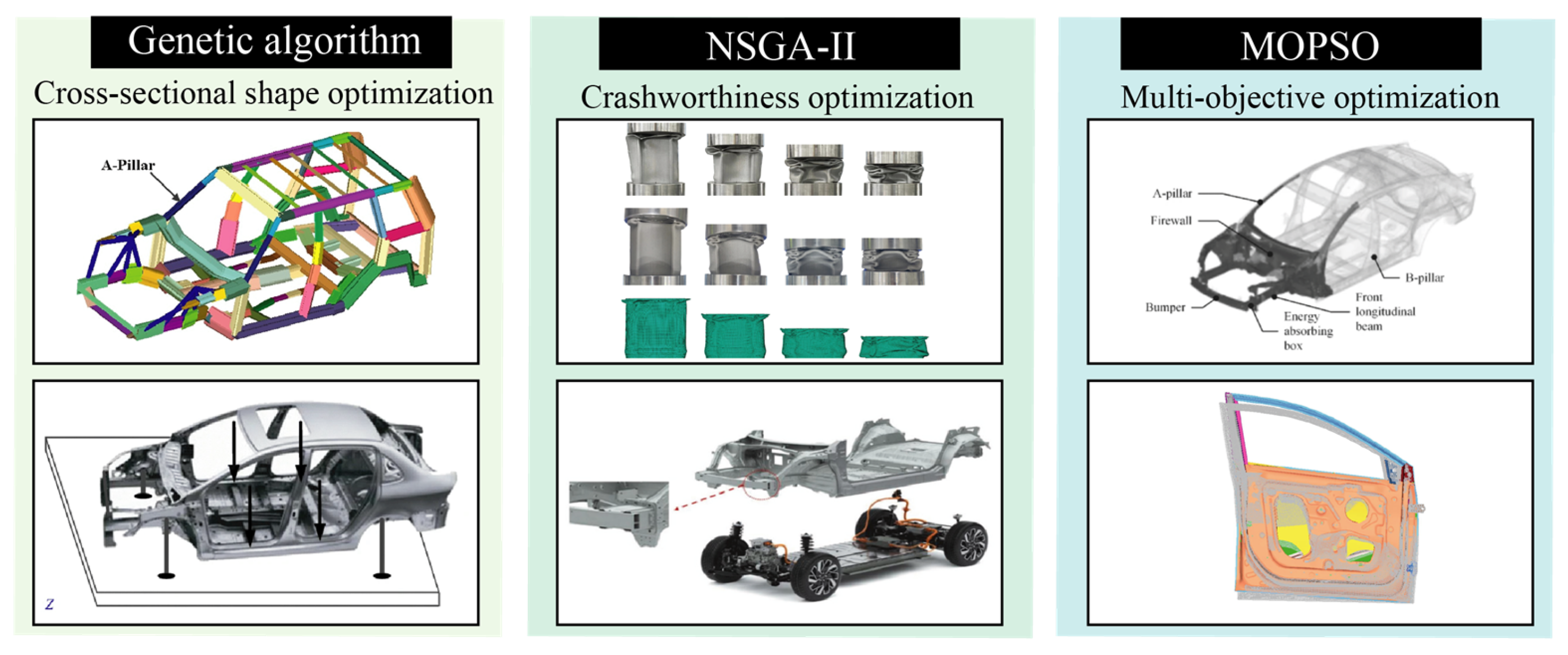
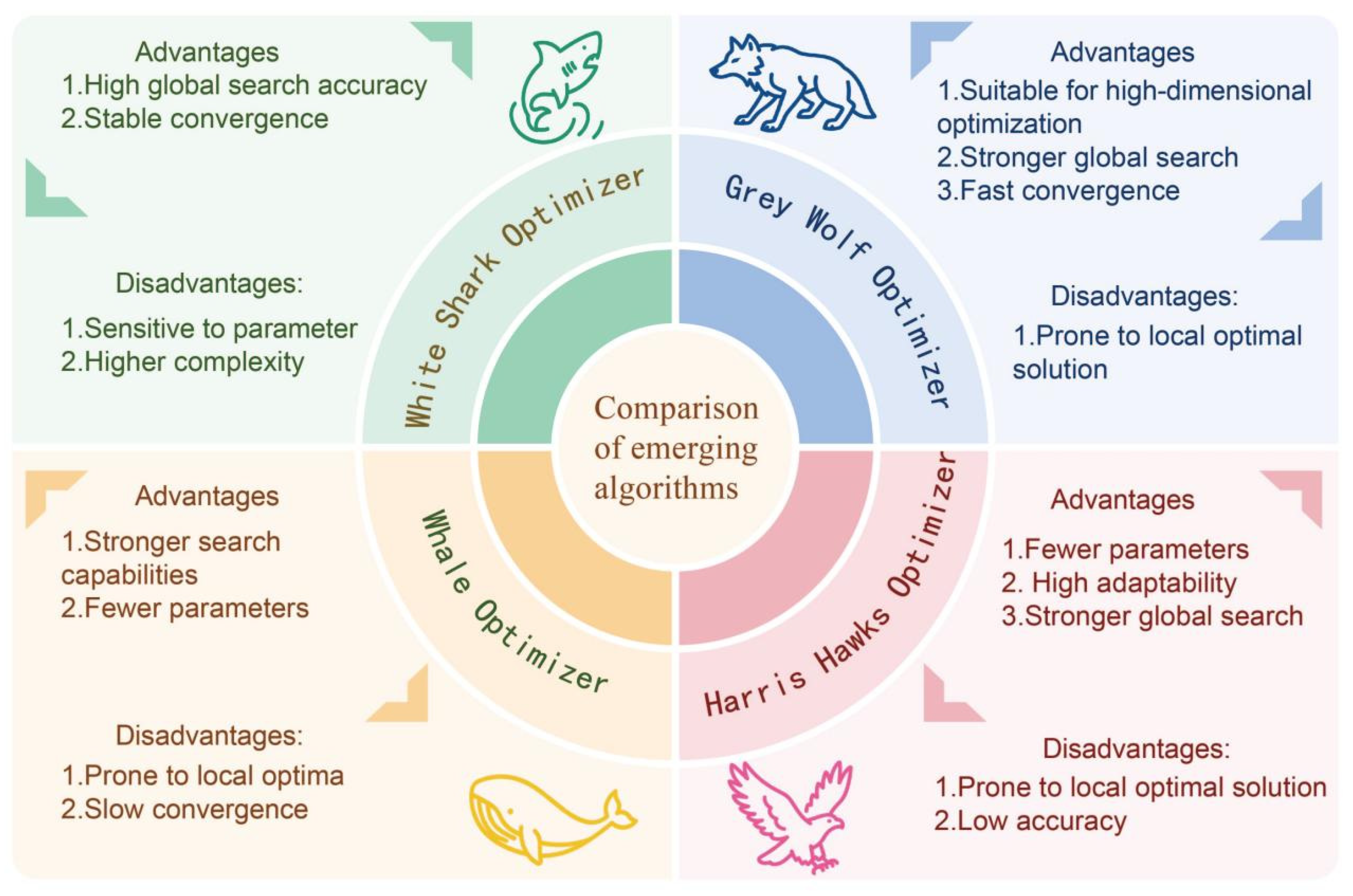
3.2. Heuristic Algorithms Optimization
3.2.1. Applications of Heuristic Algorithms in Automotive Engineering
3.2.2. Applications of Heuristic Algorithms in Agricultural Engineering
3.2.3. Research Progress and Future Development
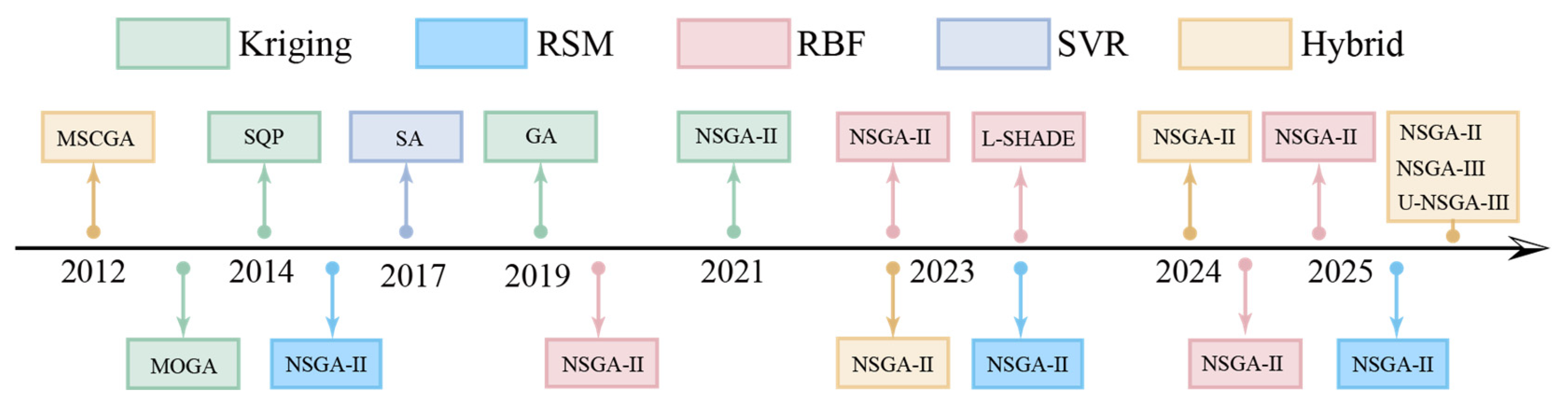
3.3. Surrogate Model-Based Optimization Algorithms
3.3.1. Surrogate Model Applications in Automotive and Agricultural Engineering
3.3.2. Advances in Surrogate Model-Based Optimization Algorithms
- Kriging surrogate model-based optimization algorithms;
- 2.
- Response surface surrogate model-based optimization algorithms;
- 3.
- Radial basis function (RBF) surrogate model-based optimization algorithms;
- 4.
- Support vector regression (SVR) surrogate model-based optimization algorithms;
- 5.
- Hybrid surrogate model-based optimization algorithms;
3.3.3. Future Development of Surrogate Model-Based Optimization Algorithms
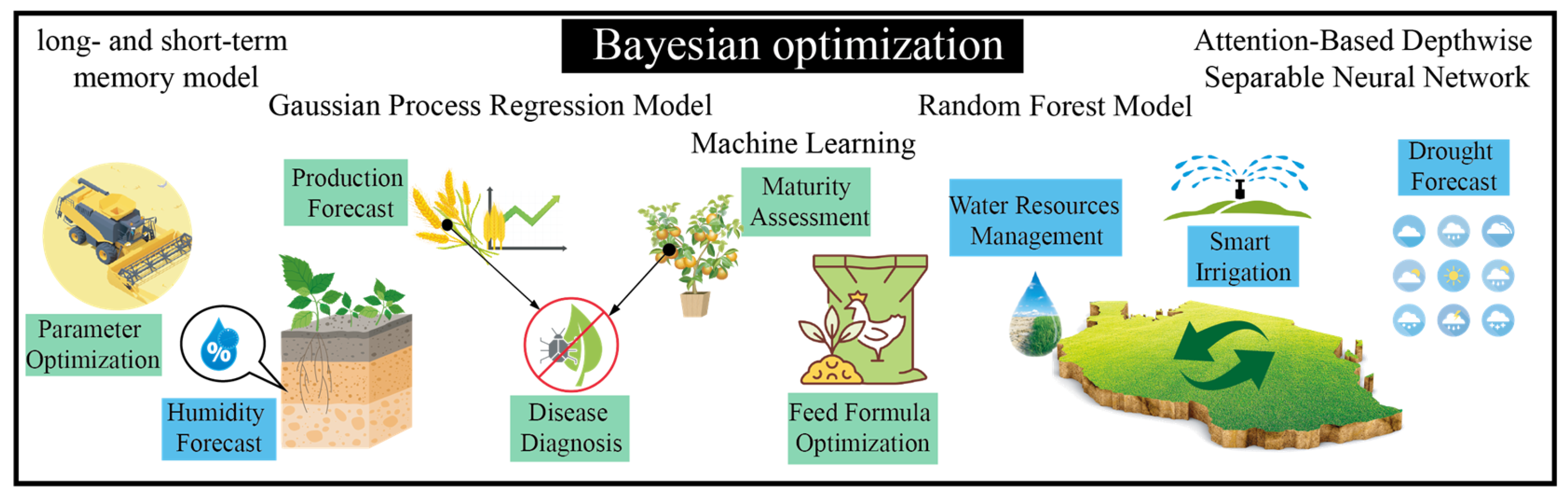
3.4. Bayesian Optimization
3.4.1. Application of Bayesian Optimization in Agricultural Engineering
3.4.2. Application of Bayesian Optimization in Automotive Engineering
3.4.3. Future Development of Bayesian Optimization Algorithms
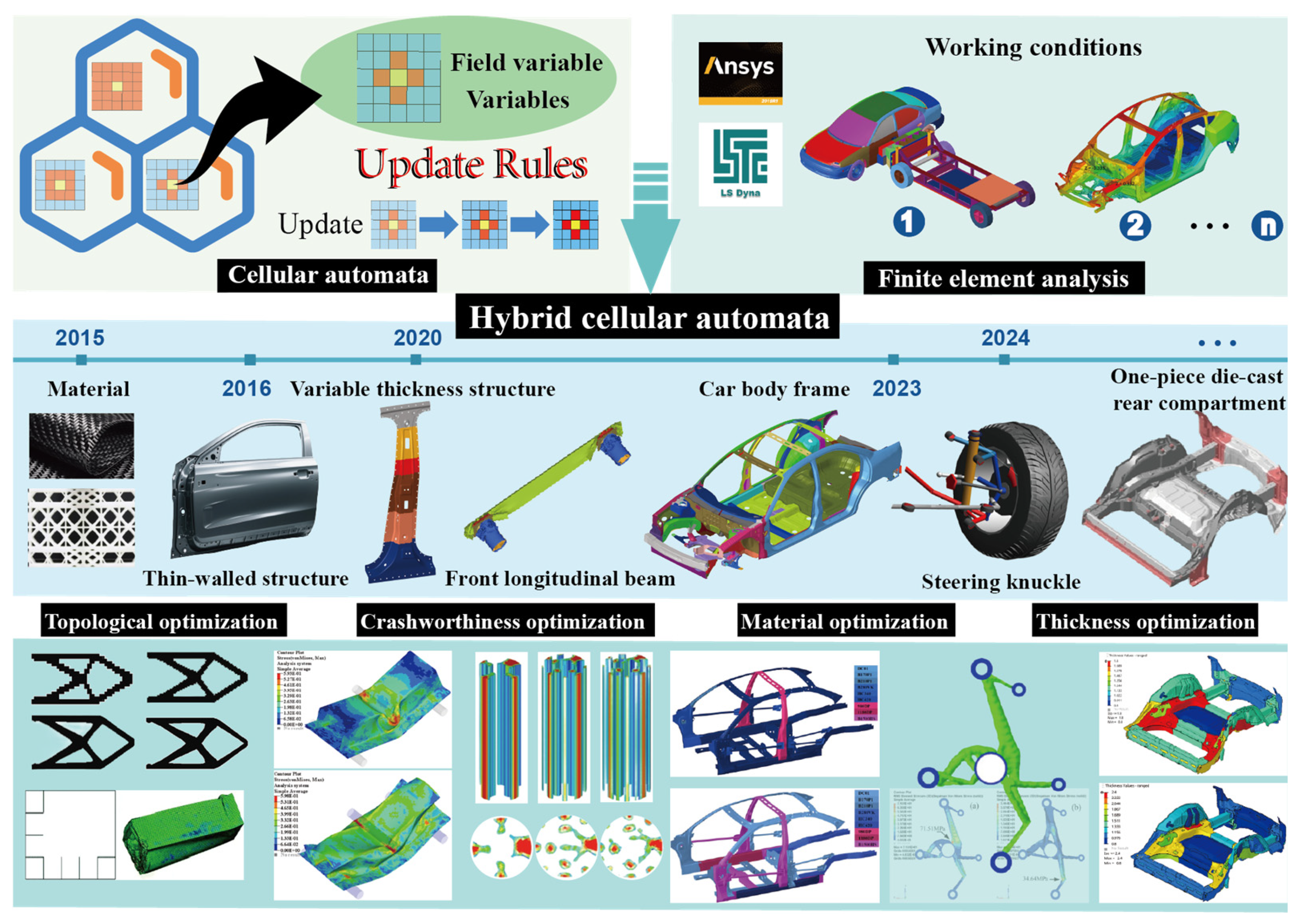
3.5. Hybrid Cellular Automata Optimization
3.5.1. Application of Cellular Automata in Engineering Optimization
3.5.2. Research Progress of Hybrid Cellular Automata Methods
3.5.3. Future Development of Hybrid Cellular Automata
4. Comparative Analysis of Optimization Methods
5. Conclusions and Future Development
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, L.; Xu, H. Lightweight composite materials in automotive engineering: State-of-the-art and future trends. Alex. Eng. J. 2025, 118, 1–10. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, Q.; Tian, S. Impact of the vehicle lightweighting and electrification on the trend of carbon emissions from automotive materials. J. Clean. Prod. 2025, 513, 145677. [Google Scholar] [CrossRef]
- Lian, F.; Wang, D.; Zhang, Z.; Chen, H.; Xu, W. Multi-objective optimization of lightweight and crashworthiness of automotive front-end structures based on stacked regression surrogate. Eng. Appl. Artif. Intell. 2025, 155, 111138. [Google Scholar] [CrossRef]
- Kumar, S.; Yildiz, B.S.; Mehta, P.; Sait, S.M.; Hussien, A.G.; Yildiz, A.R. Optimization of vehicle crashworthiness problems using recent twelve metaheuristic algorithms. Mater. Test. 2024, 66, 1890–1901. [Google Scholar] [CrossRef]
- Apazhev, A.; Fiapshev, A.; Shekikhachev, I.A.; Khazhmetov, L.; Khazhmetova, A.; Ashabokov, K.K. Energy efficiency of improvement of agriculture optimization technology and machine complex optimization. In Proceedings of the E3S Web of Conferences, EDP Sciences, Kazan, Russia, 18–20 September 2019; p. 05054. [Google Scholar] [CrossRef]
- Memmah, M.-M.; Lescourret, F.; Yao, X.; Lavigne, C. Metaheuristics for agricultural land use optimization. A review. Agron. Sustain. Dev. 2015, 35, 975–998. [Google Scholar] [CrossRef]
- Xu, S.; Wang, H.; Liang, X.; Lu, H. Research Progress on Methods for Improving the Stability of Non-Destructive Testing of Agricultural Product Quality. Foods 2024, 13, 3917. [Google Scholar] [CrossRef]
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. Eng. Proc. 2023, 59, 238. [Google Scholar] [CrossRef]
- Han, Z.-H.; Zhang, K.-S. Surrogate-based optimization. Real-World Appl. Genet. Algorithms 2012, 343, 343–362. [Google Scholar]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Recent Advances in Bayesian Optimization. ACM Comput. Surv. 2023, 55, 287. [Google Scholar] [CrossRef]
- Tovar, A.; Patel, N.; Kaushik, A.; Letona, G.; Renaud, J.; Sanders, B. Hybrid Cellular Automata: A biologically-inspired structural optimization technique. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- Shen, Y.; Branscomb, D. Orientation optimization in anisotropic materials using gradient descent method. Compos. Struct. 2020, 234, 111680. [Google Scholar] [CrossRef]
- Zhang, N.; Lei, D.; Zhao, J.F. An Improved Adagrad Gradient Descent Optimization Algorithm. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2359–2362. [Google Scholar] [CrossRef]
- Le, F.; Dong, S. Performance Improvements in Natural Gradient Descent Method. In Proceedings of the 2024 7th International Conference on Advanced Algorithms and Control Engineering (ICAACE), Shanghai, China, 1–3 March 2024; pp. 1089–1092. [Google Scholar] [CrossRef]
- Jentzen, A.; Kuckuck, B.; Neufeld, A.; von Wurstemberger, P. Strong error analysis for stochastic gradient descent optimization algorithms. IMA J. Numer. Anal. 2021, 41, 455–492. [Google Scholar] [CrossRef]
- Dogo, E.M.; Afolabi, O.J.; Nwulu, N.I.; Twala, B.; Aigbavboa, C.O. A Comparative Analysis of Gradient Descent-Based Optimization Algorithms on Convolutional Neural Networks. In Proceedings of the 2018 International Conference on Computational Techniques, Electronics and Mechanical Systems (CTEMS), Belgaum, India, 21–22 December 2018; pp. 92–99. [Google Scholar] [CrossRef]
- Hikmat, S.; Abdulazeez, A.; Saad, H.; Haji, A.; Mohsin, A. Comparison of Optimization Techniques Based on Gradient Descent Algorithm: A Review. Palarch’s J. Archaeol. Egypt/Egyptol. 2021, 18, 2715–2743. [Google Scholar]
- Rezk, H.; Ghani Olabi, A.; Wilberforce, T.; Taha Sayed, E. Metaheuristic optimization algorithms for real-world electrical and civil engineering application: A review. Results Eng. 2024, 23, 102437. [Google Scholar] [CrossRef]
- Oliva, D.; Soleimanian Gharehchopogh, F.; Hacimahmud Abdullayev, V.; Aribowo, W.; Asmunin, A.; Iwan Nurhidayat, A. A Novel Modified Tornado optimizer with Coriolis force Based On Levy Flight to Optimize Proportional Integral Derivative Parameters of DC Motor. Vokasi Unesa Bull. Eng. Technol. Appl. Sci. 2025, 2, 387–400. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization, Technical Report—TR06; Technical Report; Erciyes University: Kayseri, Türkiye, 2005. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl.-Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
- Aye, C.M.; Pholdee, N.; Yildiz, A.R.; Bureerat, S.; Sait, S.M. Multi-surrogate-assisted metaheuristics for crashworthiness optimisation. Int. J. Veh. Des. 2019, 80, 223–240. [Google Scholar] [CrossRef]
- Yildiz, A.R.; Solanki, K.N. Multi-objective optimization of vehicle crashworthiness using a new particle swarm based approach. Int. J. Adv. Manuf. Technol. 2012, 59, 367–376. [Google Scholar] [CrossRef]
- Mendes, J.M.; Oliveira, P.M.; dos Santos, F.N.; Morais dos Santos, R. Nature inspired metaheuristics and their applications in agriculture: A short review. In EPIA Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; pp. 167–179. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Hu, X.; Yang, B.; Lei, Y.; Wang, J.; Li, X.; Liao, L.; Xu, T. Automotive shape optimization using the radial basis function model based on a parametric surface grid. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1808–1821. [Google Scholar] [CrossRef]
- Moustapha, M.; Sudret, B.; Bourinet, J.-M.; Guillaume, B. Adaptive Kriging reliability-based design optimization of an automotve body structure under crashworthiness constraints. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar] [CrossRef]
- Yavari, S.; Malakahmad, A.; Sapari, N.B.; Yavari, S. Sorption properties optimization of agricultural wastes-derived biochars using response surface methodology. Process Saf. Environ. Prot. 2017, 109, 509–519. [Google Scholar] [CrossRef]
- Akpabli-Tsigbe, N.D.K.; Ma, Y.; Ekumah, J.-N.; Osabutey, J.; Hu, J.; Xu, M.; Johnson, N.A.N. Single-frequency ultrasonic extraction of bioactive chlorogenic acid from heilong48 soybean variety: Parametric optimization and comprehensive evaluation of physicochemical and bioactive properties. Food Sci. Nutr. 2022, 10, 374–387. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Hussain, Z. Multi-Objective Optimization of the Fixed Spray-Plate Sprinkler Structure Parameters of Fertigation Sprinkler Based on Response Surface Method. Appl. Eng. Agric. 2025, 41, 1–9. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Phenisee, S.E.; Chen, Z.; Salviato, M.; Yang, J. Ply-drop design of non-conventional laminated composites using Bayesian optimization. Compos. Part A Appl. Sci. Manuf. 2020, 139, 106136. [Google Scholar] [CrossRef]
- Yang, S.-T.; Liang, Y.-J. Stacking sequence optimization of composite laminates for maximum fundamental frequency using Bayesian optimization computational framework. Results Eng. 2024, 23, 102586. [Google Scholar] [CrossRef]
- Binois, M. Uncertainty Quantification on Pareto Fronts and High-Dimensional Strategies in Bayesian Optimization, with Applications in Multi-Objective Automotive Design. Ph.D. Thesis, Ecole Nationale Supérieure des Mines de Saint-Etienne, Saint-Étienne, France, 2015. Available online: https://api.semanticscholar.org/CorpusID:124194335 (accessed on 12 September 2025).
- Nikitin, A.; Fastovets, I.; Shadrin, D.; Pukalchik, M.; Oseledets, I. Bayesian optimization for seed germination. Plant Methods 2019, 15, 43. [Google Scholar] [CrossRef]
- Guo, L.S.; Huang, J.; Tavor, A.; Renaud, J.E. Multidomain topology optimization for crashworthiness based on hybrid cellular automata. Key Eng. Mater. 2011, 486, 250–253. [Google Scholar] [CrossRef]
- Sun, H. Topology optimization of multi-objective crashworthiness structure based on Improved Bi-directional Evolutionary Structural Optimization. Alex. Eng. J. 2022, 61, 10603–10612. [Google Scholar] [CrossRef]
- Chia, C.; Rongong, J.A.; Worden, K. Structural optimisation using a hybrid cellular automata (HCA) algorithm. Appl. Mech. Mater. 2006, 5, 93–100. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Beheshti, Z.; Shamsuddin, S.M.H. A review of population-based meta-heuristic algorithms. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–35. Available online: https://www.academia.edu/75791153/A_review_of_population_based_meta_heuristic_algorithms (accessed on 12 September 2025).
- Cauchy, A. Méthode générale pour la résolution des systemes d’équations simultanées. Comp. Rend. Sci. Paris 1847, 25, 536–538. [Google Scholar]
- Avalle, M.; Chiandussi, G.; Belingardi, G. Design optimization by response surface methodology: Application to crashworthiness design of vehicle structures. Struct. Multidiscip. Optim. 2002, 24, 325–332. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Zhang, Z. A new optimization method for drawbead in sheet forming process based on plastic forming principles. Int. J. Adv. Manuf. Technol. 2017, 92, 3143–3153. [Google Scholar] [CrossRef]
- Kasac, J.; Deur, J.; Novakovic, B.; Kolmanovsky, I.V.; Assadian, F. A Conjugate Gradient-Based BPTT-Like Optimal Control Algorithm with Vehicle Dynamics Control Application. IEEE Trans. Control Syst. Technol. 2011, 19, 1587–1595. [Google Scholar] [CrossRef]
- Ding, J.B. Intelligent Optimization on Test Bench of Electric Power Steering Device in Automobile. In Proceedings of the 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; Volume 4, pp. 367–370. [Google Scholar] [CrossRef]
- Dumas, L. CFD-based Optimization for Automotive Aerodynamics. In Optimization and Computational Fluid Dynamics; Thévenin, D., Janiga, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 191–215. [Google Scholar] [CrossRef]
- Su, Y.; Song, K.; Du, Z.; Yu, K.; Hu, Z.; Jin, H. Quantitative Study of Predicting the Effect of the Initial Gap on Mechanical Behavior in Resistance Spot Welding Based on L-BFGS-B. Materials 2024, 17, 4746. [Google Scholar] [CrossRef]
- Han, S.P. A globally convergent method for nonlinear programming. J. Optim. Theory Appl. 1977, 22, 297–309. [Google Scholar] [CrossRef]
- Powell, M.J. A fast algorithm for nonlinearly constrained optimization calculations. In Proceedings of the Numerical Analysis: Proceedings of the Biennial Conference, Dundee, UK, 28 June–1 July 1977; pp. 144–157. [Google Scholar] [CrossRef]
- Zhu, T.; Wu, Y.; Ouyang, Z.; Wu, T.; Liang, J.; Li, W.; Li, B.; Han, S. Feasibility of Approximate Model Optimization for Lightweight Design of Vehicle Body Structure Based on Sequential Quadratic Programming Algorithm. Sens. Mater. 2022, 34, 3581–3591. [Google Scholar] [CrossRef]
- Sun, G.; Song, X.; Baek, S.; Li, Q. Robust optimization of foam-filled thin-walled structure based on sequential Kriging metamodel. Struct. Multidiscip. Optim. 2014, 49, 897–913. [Google Scholar] [CrossRef]
- Karmarkar, N. A new polynomial-time algorithm for linear programming. In Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 30 April–2 May 1984; pp. 302–311. [Google Scholar] [CrossRef]
- Liu, W.; Gao, Y.; You, Y.; Jiang, C.; Hua, T.; Xia, B. Optimization control strategy for diesel urea-selective catalytic reduction (SCR) urea injection based on the interior point method (IP) + higher order SCR model. J. Environ. Chem. Eng. 2024, 12, 114423. [Google Scholar] [CrossRef]
- Cherniaev, A.; Komarov, V. Multistep Optimization of Composite Drive Shaft Subject to Strength, Buckling, Vibration and Manufacturing Constraints. Appl. Compos. Mater. 2015, 22, 475–487. [Google Scholar] [CrossRef]
- Mantovani, S.; Campo, G.A.; Ferrari, A. Additive manufacturing and topology optimization: A design strategy for a steering column mounting bracket considering overhang constraints. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1703–1723. [Google Scholar] [CrossRef]
- Sebastjan, P.; Kus, W. Hybrid Shape Optimization of Automotive Spring Seat. Int. J. Automot. Technol. 2022, 23, 957–965. [Google Scholar] [CrossRef]
- Zhou, X.; Ju, J.; Long, J. A novel lightweight combinatorial optimization strategy based on ASA-NLPQL optimization algorithm for front seat skeleton of a passenger car. Adv. Eng. Softw. 2025, 205, 103908. [Google Scholar] [CrossRef]
- Barbosa, A.; Hovakimyan, N.; Martin, N.F. Risk-averse optimization of crop inputs using a deep ensemble of convolutional neural networks. Comput. Electron. Agric. 2020, 178, 105785. [Google Scholar] [CrossRef]
- Schoups, G.; Addams, C.L.; Minjares, J.L.; Gorelick, S.M. Sustainable conjunctive water management in irrigated agriculture: Model formulation and application to the Yaqui Valley, Mexico. Water Resour. Res. 2006, 42, 19. [Google Scholar] [CrossRef]
- Kesavan, D.; Periyathambi, E.; Chokkalingam, A. A proportional fair scheduling strategy using multiobjective gradient-based African buffalo optimization algorithm for effective resource allocation and interference minimization. Int. J. Commun. Syst. 2022, 35, e5003. [Google Scholar] [CrossRef]
- Saranya, T.; Deisy, C.; Sridevi, S.; Muthu, K.S.; Khan, M. Performance Analysis of First Order Optimizers for Plant Pest Detection Using Deep Learning. In Proceedings of the Machine Learning, Image Processing, Network Security and Data Sciences, MIND 2022, PT II, Virtual Event, 19–20 January 2022; pp. 37–52. [Google Scholar] [CrossRef]
- Godara, S.; Parihar, A.K.; Hazra, K.K.; Marwaha, S. DL-RSMv2: A deep learning framework for transparent crop yield modeling using simulated virtual experimental runs. Comput. Electron. Agric. 2025, 237, 110628. [Google Scholar] [CrossRef]
- Qin, H.; Liu, Z.; Zhong, H.; Liu, Y.; Lv, C. Two-level multiple cross-sectional shape optimization of automotive body frame with exact static and dynamic stiffness constraints. Struct. Multidiscip. Optim. 2018, 58, 2309–2323. [Google Scholar] [CrossRef]
- Zuo, W.; Lu, Y.; Zhao, X.; Bai, J. Cross-sectional shape design of automobile structure considering rigidity and driver’s field of view. Adv. Eng. Softw. 2018, 115, 161–167. [Google Scholar] [CrossRef]
- Sun, L. Application of improved multi-population genetic algorithm in structural optimization of automotive electrical equipment. Int. J. Adv. Manuf. Technol. 2024, 128, 1–9. [Google Scholar] [CrossRef]
- Qin, H.; Guo, Y.; Liu, Z.J.; Liu, Y.; Zhong, H.L. Shape optimization of automotive body frame using an improved genetic algorithm optimizer. Adv. Eng. Softw. 2018, 121, 235–249. [Google Scholar] [CrossRef]
- Ortmann, C.; Schumacher, A. Graph and heuristic based topology optimization of crash loaded structures. Struct. Multidiscip. Optim. 2013, 47, 839–854. [Google Scholar] [CrossRef]
- Djamaluddin, F. Optimization of foam-filled crash-box under axial loading for pure electric vehicle. Results Mater. 2024, 21, 100505. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, C.; Zhao, L.; Hu, N.; Hou, S.; Han, X. Crashworthiness analysis and optimization design of special-shaped thin-walled tubes by experiments and numerical simulation. Thin-Walled Struct. 2024, 205, 112240. [Google Scholar] [CrossRef]
- Xiong, F.; Wang, D.; Ma, Z.; Chen, S.; Lv, T.; Lu, F. Structure-material integrated multi-objective lightweight design of the front end structure of automobile body. Struct. Multidiscip. Optim. 2018, 57, 829–847. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y.; Yang, J.; Xu, X.; Fang, J.; Xie, F. Multi-objective optimization framework of a vehicle door design in the slamming event for optimal dynamic performances. Appl. Acoust. 2022, 187, 108526. [Google Scholar] [CrossRef]
- Tanlak, N. Cross-sectional shape optimization of thin-walled columns enduring oblique impact loads. Thin-Walled Struct. 2016, 109, 65–72. [Google Scholar] [CrossRef]
- Ying, L.; Dai, M.; Zhang, S.; Ma, H.; Hu, P. Multiobjective crashworthiness optimization of thin-walled structures with functionally graded strength under oblique impact loading. Thin-Walled Struct. 2017, 117, 165–177. [Google Scholar] [CrossRef]
- Qiu, N.; Gao, Y.; Fang, J.; Sun, G.; Kim, N.H. Topological design of multi-cell hexagonal tubes under axial and lateral loading cases using a modified particle swarm algorithm. Appl. Math. Model. 2018, 53, 567–583. [Google Scholar] [CrossRef]
- Cui, X.; Wang, S.; Hu, S.J. A method for optimal design of automotive body assembly using multi-material construction. Mater. Des. 2008, 29, 381–387. [Google Scholar] [CrossRef]
- Wang, X.G.; Sun, P.F.; Zuo, W.J.; Bai, J.T. Multi-objective optimization of automobile body frame considering weight, rigidity, and frequency for conceptual design. Adv. Mech. Eng. 2022, 14, W10417. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, H.; Fu, S.; Xie, H.; Tang, Z.; Zhu, Z. A process-performance coupled design method for hot-stamped tailor rolled blank structure. Thin-Walled Struct. 2019, 140, 132–143. [Google Scholar] [CrossRef]
- Duan, L.; Jiang, H.; Cheng, A.; Xue, H.; Geng, G. Multi-objective reliability-based design optimization for the VRB-VCS FLB under front-impact collision. Struct. Multidiscip. Optim. 2019, 59, 1835–1851. [Google Scholar] [CrossRef]
- Duan, L.; Jiang, H.; Geng, G.; Zhang, X.; Li, Z. Parametric modeling and multiobjective crashworthiness design optimization of a new front longitudinal beam. Struct. Multidiscip. Optim. 2019, 59, 1789–1812. [Google Scholar] [CrossRef]
- Liang, R.; Tang, X.; Huang, J.; Bastien, C.; Zhang, C.; Tuo, W. A machine learning-based crashworthiness optimization for a novel pine cone-inspired multi-cell tubes under bending. Heliyon 2024, 10, e37828. [Google Scholar] [CrossRef]
- Yu, L.; Gu, X.; Qian, L.; Jiang, P.; Wang, W.; Yu, M. Application of tailor rolled blanks in optimum design of pure electric vehicle crashworthiness and lightweight. Thin-Walled Struct. 2021, 161, 107410. [Google Scholar] [CrossRef]
- Gao, F.; Ren, S.; Lin, C.; Bai, Y.; Wang, W. Metamodel-Based Multi-Objective Reliable Optimization for Front Structure of Electric Vehicle. Automot. Innov. 2018, 1, 131–139. [Google Scholar] [CrossRef]
- Lophisarn, S.; Bunsri, P.; Jongpradist, P.; Kongwat, S. Optimization of novel functionally graded FRD-filled crash box for enhanced crashworthiness. Eur. J. Mech. A/Solids 2025, 112, 105616. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, G.; Li, G.; Li, Q. Multi-objective Reliability-Based Design Optimization for Energy Absorption Components Considering Manufacturing Effects. In Advances in Structural and Multidisciplinary Optimization; Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.-U., Maute, K., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 310–319. [Google Scholar] [CrossRef]
- Chen, H.; Yu, P.; Long, J. Multi-objective optimization of automotive seat frames using machine learning. Adv. Eng. Softw. 2025, 199, 103797. [Google Scholar] [CrossRef]
- Abderazek, H.; Sait, S.M.; Yildiz, A.R. Optimal design of planetary gear train for automotive transmissions using advanced meta-heuristics. Int. J. Veh. Des. 2019, 80, 121–136. [Google Scholar] [CrossRef]
- Khulal, U.; Zhao, J.; Hu, W.; Chen, Q. Nondestructive quantifying total volatile basic nitrogen (TVB-N) content in chicken using hyperspectral imaging (HSI) technique combined with different data dimension reduction algorithms. Food Chem. 2016, 197, 1191–1199. [Google Scholar] [CrossRef]
- Cong, S.L.; Sun, J.; Mao, H.P.; Wu, X.H.; Wang, P.; Zhang, X.D. Non-destructive detection for mold colonies in rice based on hyperspectra and GWO-SVR. J. Sci. Food Agric. 2018, 98, 1453–1459. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.T.; Wu, X.H.; Dai, C.X.; Chen, Y. SSC prediction of cherry tomatoes based on IRIV-CS-SVR model and near infrared reflectance spectroscopy. J. Food Process Eng. 2018, 41, e12884. [Google Scholar] [CrossRef]
- Bonah, E.; Huang, X.; Yi, R.; Aheto, J.H.; Osae, R.; Golly, M. Electronic nose classification and differentiation of bacterial foodborne pathogens based on support vector machine optimized with particle swarm optimization algorithm. J. Food Process Eng. 2019, 42, e13236. [Google Scholar] [CrossRef]
- Zhu, X.L.; Zhu, Z.Y. The generalized predictive control of bacteria concentration in marine lysozyme fermentation process. Food Sci. Nutr. 2018, 6, 2459–2465. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, W.D.; Chen, Q.S. Evaluating aroma quality of black tea by an olfactory visualization system: Selection of feature sensor using particle swarm optimization. Food Res. Int. 2019, 126, 108605. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.Z.; Lv, L.Y.; Shi, Y.; Yu, X. Study on Modeling Method of a Multi-Parameter Control System for Threshing and Cleaning Devices in the Grain Combine Harvester. Agriculture 2022, 12, 1483. [Google Scholar] [CrossRef]
- Sun, L.M.; Liu, M.N.; Wang, Z.P.; Wang, C.Q.; Luo, F.Q. Research on Load Spectrum Reconstruction Method of Exhaust System Mounting Bracket of a Hybrid Tractor Based on MOPSO-Wavelet Decomposition Technique. Agriculture 2023, 13, 1919. [Google Scholar] [CrossRef]
- Chen, Y.X.; Chen, L.; Huang, C.; Lu, Y.; Wang, C. A dynamic tire model based on HPSO-SVM. Int. J. Agric. Biol. Eng. 2019, 12, 36–41. [Google Scholar] [CrossRef]
- Ding, Y.H.; Zeng, R.H.; Jiang, H.; Guan, X.P.; Jiang, Q.H.; Song, Z.Y. Classification of tea quality grades based on hyperspectral imaging spatial information and optimization models. J. Food Meas. Charact. 2024, 18, 9098–9112. [Google Scholar] [CrossRef]
- Sun, J.; Wu, M.M.; Hang, Y.Y.; Lu, B.; Wu, X.H.; Chen, Q.S. Estimating cadmium content in lettuce leaves based on deep brief network and hyperspectral imaging technology. J. Food Process Eng. 2019, 42, e13293. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Wu, X.H.; Dai, C.X.; Li, B. Spectral classification of lettuce cadmium stress based on information fusion and VISSA-GOA-SVM algorithm. J. Food Process Eng. 2019, 42, e13085. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, J.; Zhou, X.; Nirere, A.; Wu, X.H.; Dai, R.M. Classification detection of saccharin jujube based on hyperspectral imaging technology. J. Food Process. Preserv. 2020, 44, e14591. [Google Scholar] [CrossRef]
- Sun, J.; Tian, Y.; Wu, X.H.; Dai, C.X.; Lu, B. Nondestructive detection for moisture content in green tea based on dielectric properties and VISSA-GWO-SVR algorithm. J. Food Process. Preserv. 2020, 44, e14421. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Zhou, X.; Yao, K.S.; Tian, Y.; Nirere, A. A method of information fusion for identification of rice seed varieties based on hyperspectral imaging technology. J. Food Process Eng. 2021, 44, e13797. [Google Scholar] [CrossRef]
- He, P.H.; Wu, Y.; Wang, J.J.; Ren, Y.; Ahmad, W.; Liu, R.; Ouyang, Q.; Jiang, H.; Chen, Q.S. Detection of mites Tyrophagus putrescentiae and Cheyletus eruditus in flour using hyperspectral imaging system coupled with chemometrics. J. Food Process Eng. 2020, 43, e13386. [Google Scholar] [CrossRef]
- Guo, Z.M.; Chen, X.; Zhang, Y.Y.; Sun, C.J.; Jayan, H.; Majeed, U.; Watson, N.J.; Zou, X.B. Dynamic Nondestructive Detection Models of Apple Quality in Critical Harvest Period Based on Near-Infrared Spectroscopy and Intelligent Algorithms. Foods 2024, 13, 1698. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zou, X.; Shen, T.; Shi, J.; Zhao, J.; Holmes, M.; Li, G. Determination of total acid content and moisture content during solid-state fermentation processes using hyperspectral imaging. J. Food Eng. 2016, 174, 75–84. [Google Scholar] [CrossRef]
- Guo, Z.M.; Barimah, A.O.; Yin, L.M.; Chen, Q.S.; Shi, J.Y.; El-Seedi, H.R.; Zou, X.B. Intelligent evaluation of taste constituents and polyphenols-to-amino acids ratio in matcha tea powder using near infrared spectroscopy. Food Chem. 2021, 353, 129372. [Google Scholar] [CrossRef] [PubMed]
- Bonah, E.; Huang, X.; Hongying, Y.; Aheto, J.H.; Yi, R.; Yu, S.; Tu, H. Detection of Salmonella typhimurium contamination levels in fresh pork samples using electronic nose smellprints in tandem with support vector machine regression and metaheuristic optimization algorithms. J. Food Sci. Technol. 2021, 58, 3861–3870. [Google Scholar] [CrossRef]
- Kutsanedzie, F.Y.H.; Chen, Q.S.; Hassan, M.M.; Yang, M.X.; Sun, H.; Rahman, M.H. Near infrared system coupled chemometric algorithms for enumeration of total fungi count in cocoa beans neat solution. Food Chem. 2018, 240, 231–238. [Google Scholar] [CrossRef]
- Sun, J.; Nirere, A.; Dusabe, K.D.; Zhong, Y.H.; Adrien, G. Rapid and nondestructive watermelon (Citrullus lanatus) seed viability detection based on visible near-infrared hyperspectral imaging technology and machine learning algorithms. J. Food Sci. 2024, 89, 4403–4418. [Google Scholar] [CrossRef]
- Yao, K.S.; Sun, J.; Zhang, L.; Zhou, X.; Tian, Y.; Tang, N.Q.; Wu, X.H. Nondestructive detection for egg freshness based on hyperspectral imaging technology combined with harris hawks optimization support vector regression. J. Food Saf. 2021, 41, e12888. [Google Scholar] [CrossRef]
- Cao, Y.; Li, H.R.; Sun, J.; Zhou, X.; Yao, K.S.; Nirere, A. Nondestructive determination of the total mold colony count in green tea by hyperspectral imaging technology. J. Food Process Eng. 2020, 43, e13570. [Google Scholar] [CrossRef]
- Guo, Z.M.; Wang, M.M.; Wu, J.Z.; Tao, F.F.; Chen, Q.S.; Wang, Q.Y.; Ouyang, Q.; Shi, J.Y.; Zou, X.B. Quantitative assessment of zearalenone in maize using multivariate algorithms coupled to Raman spectroscopy. Food Chem. 2019, 286, 282–288. [Google Scholar] [CrossRef]
- Guo, Z.M.; Barimah, A.O.; Shujat, A.; Zhang, Z.Z.; Qin, O.Y.; Shi, J.Y.; El-Seedi, H.R.; Zou, X.B.; Chen, Q.S. Simultaneous quantification of active constituents and antioxidant capability of green tea using NIR spectroscopy coupled with swarm intelligence algorithm. Lwt-Food Sci. Technol. 2020, 129, 109510. [Google Scholar] [CrossRef]
- Yin, J.J.; Wang, Z.L.; Zhou, M.L.; Wu, L.N.; Zhang, Y. Optimized design and experiment of the three-arm transplanting mechanism for rice potted seedlings. Int. J. Agric. Biol. Eng. 2021, 14, 56–62. [Google Scholar] [CrossRef]
- Cui, L.F.; Mao, H.P.; Xue, X.Y.; Ding, S.M.; Qiao, B.Y. Optimized design and test for a pendulum suspension of the crop spray boom in dynamic conditions based on a six DOF motion simulator. Int. J. Agric. Biol. Eng. 2018, 11, 76–85. [Google Scholar] [CrossRef]
- Pang, Y.Y.; Li, H.; Tang, P.; Chen, C. Synchronization Optimization of Pipe Diameter and Operation Frequency in a Pressurized Irrigation Network Based on the Genetic Algorithm. Agriculture 2022, 12, 673. [Google Scholar] [CrossRef]
- Amor, N.; Tayyab Noman, M.; Petru, M.; Sebastian, N.; Balram, D. Design and optimization of machinability of ZnO embedded-glass fiber reinforced polymer composites with a modified white shark optimizer. Expert Syst. Appl. 2024, 237, 121474. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, R.; Bai, J.; Zuo, W. Shape Optimization of Thin-Walled Cross Section for Automobile Body Considering Stamping Cost, Manufacturability and Structural Stiffness. Int. J. Automot. Technol. 2020, 21, 503–512. [Google Scholar] [CrossRef]
- Jiang, H.; He, Y.C.; Chen, Q.S. Determination of acid value during edible oil storage using a portable NIR spectroscopy system combined with variable selection algorithms based on an MPA-based strategy. J. Sci. Food Agric. 2021, 101, 3328–3335. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Li, H.; Sun, X.; Zhang, G. Many-objective optimization for overall performance of an electric sport utility vehicle under multiple temperature conditions based on natural gradient boosting model. Energy 2024, 304, 132078. [Google Scholar] [CrossRef]
- Sun, X.; Wang, D.; Li, R.; Zhang, B. Multi-Objective Optimization for Structure Crashworthiness Based on Kriging Surrogate Model and Simulated Annealing Algorithm. J. Shanghai Jiaotong Univ. (Sci.) 2020, 25, 727–738. [Google Scholar] [CrossRef]
- Cimolai, G.; Dayyani, I.; Qin, Q. Multi-objective shape optimization of large strain 3D helical structures for mechanical metamaterials. Mater. Des. 2022, 215, 110444. [Google Scholar] [CrossRef]
- Peng, X.; Guo, Y.; Li, J.; Wu, H.; Jiang, S. Multiple objective optimization design of hybrid composite structures considering multiple-scale uncertainties. Compos. Struct. 2022, 292, 115658. [Google Scholar] [CrossRef]
- Xu, X.; Xu, G.; Chen, J.; Liu, Z.; Chen, X.; Zhang, Y.; Fang, J.; Gao, Y. Multi-objective design optimization using hybrid search algorithms with interval uncertainty for thin-walled structures. Thin-Walled Struct. 2022, 175, 109218. [Google Scholar] [CrossRef]
- Zadeh, P.M.; Mohagheghi, M. An efficient Bi-level hybrid multi-objective reliability-based design optimization of composite structures. Compos. Struct. 2022, 296, 115862. [Google Scholar] [CrossRef]
- Tang, N.Q.; Sun, J.; Yao, K.S.; Zhou, X.; Tian, Y.; Cao, Y.; Nirere, A. Identification of Lycium barbarum varieties based on hyperspectral imaging technique and competitive adaptive reweighted sampling-whale optimization algorithm-support vector machine. J. Food Process Eng. 2021, 44, e13603. [Google Scholar] [CrossRef]
- Hou, W.; He, P.; Yang, Y.; Sang, L. Crashworthiness optimization of crash box with 3D-printed lattice structures. Int. J. Mech. Sci. 2023, 247, 108198. [Google Scholar] [CrossRef]
- Liu, X.; Qin, J.; Zhao, K.; Featherston, C.A.; Kennedy, D.; Jing, Y.; Yang, G. Design optimization of laminated composite structures using artificial neural network and genetic algorithm. Compos. Struct. 2023, 305, 116500. [Google Scholar] [CrossRef]
- Bao, L.; Zheng, M.; Zhou, Q.; Gao, P.; Xu, Y.; Jiang, H. Multi-objective optimization of partition temperature of steel sheet by NSGA-II using response surface methodology. Case Stud. Therm. Eng. 2022, 31, 101818. [Google Scholar] [CrossRef]
- Deng, J.H.; Jiang, H.; Chen, Q.S. Characteristic wavelengths optimization improved the predictive performance of near-infrared spectroscopy models for determination of aflatoxin B1 in maize. J. Cereal Sci. 2022, 105, 103474. [Google Scholar] [CrossRef]
- Lv, T.; Wang, D.; Du, X. Dual-scale parametric modeling and optimal design method of CFRP automotive roof beam. Compos. Struct. 2023, 308, 116695. [Google Scholar] [CrossRef]
- Ding, Y.H.; Yan, Y.L.; Li, J.; Chen, X.; Jiang, H. Classification of Tea Quality Levels Using Near-Infrared Spectroscopy Based on CLPSO-SVM. Foods 2022, 11, 1658. [Google Scholar] [CrossRef]
- Fonseca, J.H.; Jang, W.; Han, D.; Kim, N.; Lee, H. Strength and manufacturability enhancement of a composite automotive component via an integrated finite element/artificial neural network multi-objective optimization approach. Compos. Struct. 2024, 327, 117694. [Google Scholar] [CrossRef]
- Mohammed Sahib, M.; Kovács, G. Multi-objective optimization of composite sandwich structures using Artificial Neural Networks and Genetic Algorithm. Results Eng. 2024, 21, 101937. [Google Scholar] [CrossRef]
- Li, M.; Sang, L.; Liu, Z.; Duan, S.; Hou, W. Crashworthiness optimization of variable stiffness B-pillar with thermoplastic composites. Int. J. Mech. Sci. 2024, 278, 109457. [Google Scholar] [CrossRef]
- Gu, H.Y.; Lv, R.Q.; Huang, X.Y.; Chen, Q.S.; Dong, Y.N. Rapid quantitative assessment of lipid oxidation in a rapeseed oil-in-water (o/w) emulsion by three-dimensional fluorescence spectroscopy. J. Food Compos. Anal. 2022, 114, 104762. [Google Scholar] [CrossRef]
- Pang, Y.Y.; Li, H.; Tang, P.; Chen, C. Irrigation scheduling of pressurized irrigation networks for minimizing energy consumption. Irrig. Drain. 2023, 72, 268–283. [Google Scholar] [CrossRef]
- Liu, T.; He, J.; Yao, W.; Jiang, H.; Chen, Q. Determination of aflatoxin B1 value in corn based on Fourier transform near-infrared spectroscopy: Comparison of optimization effect of characteristic wavelengths. LWT-Food Sci. Technol. 2022, 164, 113657. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, J.; Zhou, X.; Yao, K.S.; Tang, N.Q. Detection of soluble solid content in apples based on hyperspectral technology combined with deep learning algorithm. J. Food Process. Preserv. 2022, 46, e16414. [Google Scholar] [CrossRef]
- Gu, J. An efficient multiple meta-model-based global optimization method for computationally intensive problems. Adv. Eng. Softw. 2021, 152, 102958. [Google Scholar] [CrossRef]
- Jia, W.D.; Tai, K.L.; Wang, X.W.; Dong, X.; Ou, M.X. Design and Simulation of Intra-Row Obstacle Avoidance Shovel-Type Weeding Machine in Orchard. Agriculture 2024, 14, 1124. [Google Scholar] [CrossRef]
- Sun, G.; Wang, X.; Fang, J.; Pang, T.; Li, Q. Parallelized optimization design of bumper systems under multiple low-speed impact loads. Thin-Walled Struct. 2021, 167, 108197. [Google Scholar] [CrossRef]
- Duan, L.; Xiao, N.-C.; Hu, Z.; Li, G.; Cheng, A. An efficient lightweight design strategy for body-in-white based on implicit parameterization technique. Struct. Multidiscip. Optim. 2017, 55, 1927–1943. [Google Scholar] [CrossRef]
- Li, S.; Wang, D.; Wang, S.; Zhou, C. Structure-connection-performance integration lightweight optimisation design of multi-material automotive body skeleton. Struct. Multidiscip. Optim. 2023, 66, 198. [Google Scholar] [CrossRef]
- Li, S.; Wang, D.; Zhou, C. Multi-level structural optimization of thin-walled sections in steel/aluminum vehicle body skeletons. Appl. Math. Model. 2024, 132, 187–210. [Google Scholar] [CrossRef]
- Hunkeler, S.; Duddeck, F.; Rayamajhi, M.; Zimmer, H. Shape optimisation for crashworthiness followed by a robustness analysis with respect to shape variables. Struct. Multidiscip. Optim. 2013, 48, 367–378. [Google Scholar] [CrossRef]
- Song, X.; Sun, G.; Li, Q. Sensitivity analysis and reliability based design optimization for high-strength steel tailor welded thin-walled structures under crashworthiness. Thin-Walled Struct. 2016, 109, 132–142. [Google Scholar] [CrossRef]
- Deng, X.; Liu, W.; Jin, L. On the crashworthiness analysis and design of a lateral corrugated tube with a sinusoidal cross-section. Int. J. Mech. Sci. 2018, 141, 330–340. [Google Scholar] [CrossRef]
- Tran, T.N.; Baroutaji, A.; Estrada, Q.; Arjunan, A.; Le, H.; Thien, N.P. Crashworthiness analysis and optimization of standard and windowed multi-cell hexagonal tubes. Struct. Multidiscip. Optim. 2021, 63, 2191–2209. [Google Scholar] [CrossRef]
- Chen, M.T.; Xiao, X.T.; Tong, J.H.; Guo, H.; Zhou, F.Q.; Zhou, F. Dimensional optimization of variable thickness tube in T-shaped tube hydroforming using response surface methodology. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1270, 012073. [Google Scholar] [CrossRef]
- Dai, C.; Wang, X.; Long, J. A new optimization strategy for multi-objective design of automotive seat frame. Struct. Multidiscip. Optim. 2023, 66, 236. [Google Scholar] [CrossRef]
- Hou, W.; Li, M.; Yang, Y.; Liu, Z.; Sang, L. Layup optimization of composite B-pillar under side impact. Int. J. Mech. Sci. 2025, 287, 109927. [Google Scholar] [CrossRef]
- Ayim, I.; Ma, H.; Alenyorege, E.A. Optimizing and predicting degree of hydrolysis of ultrasound assisted sodium hydroxide extraction of protein from tea (Camellia sinensis L.) residue using response surface methodology. J. Food Sci. Technol. 2018, 55, 5166–5174. [Google Scholar] [CrossRef]
- Dabbour, M.; He, R.H.; Ma, H.L.; Musa, A. Optimization of ultrasound assisted extraction of protein from sunflower meal and its physicochemical and functional properties. J. Food Process Eng. 2018, 41, e12799. [Google Scholar] [CrossRef]
- Luo, X.P.; Cui, J.M.; Zhang, H.H.; Duan, Y.Q. Subcritical water extraction of polyphenolic compounds from sorghum (Sorghum bicolor L.) bran and their biological activities. Food Chem. 2018, 262, 14–20. [Google Scholar] [CrossRef]
- Luo, X.P.; Cui, J.M.; Zhang, H.H.; Duan, Y.Q.; Zhang, D.; Cai, M.H.; Chen, G.Y. Ultrasound assisted extraction of polyphenolic compounds from red sorghum (Sorghum bicolor L.) bran and their biological activities and polyphenolic compositions. Ind. Crops Prod. 2018, 112, 296–304. [Google Scholar] [CrossRef]
- Chen, X.M.; Ding, J.; Ji, D.Y.; He, S.Q.; Ma, H.L. Optimization of ultrasonic-assisted extraction conditions for bioactive components from coffee leaves using the Taguchi design and response surface methodology. J. Food Sci. 2020, 85, 1742–1751. [Google Scholar] [CrossRef]
- Xu, B.G.; Feng, M.; Tiliwa, E.S.; Yan, W.Q.; Wei, B.X.; Zhou, C.S.; Ma, H.L.; Wang, B.; Chang, L. Multi-frequency power ultrasound green extraction of polyphenols from Pingyin rose: Optimization using the response surface methodology and exploration of the underlying mechanism. LWT-Food Sci. Technol. 2022, 156, 113037. [Google Scholar] [CrossRef]
- Zheng, J.W.; Zhang, X.X.; Herrera-Balandrano, D.D.; Wang, J.; Chai, Z.; Beta, T.; Huang, W.Y.; Li, Y. Extraction Optimization of Arctium lappa L. Polysaccharides by Box-Behnken Response Surface Design and Their Antioxidant Capacity. Starch-Starke 2022, 74, 2100305. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Y.; Tang, Z.; Ding, H.; Su, Z.; Ding, Z. Structural Model of Straw Briquetting Machine with Vertical Ring Die and Optimization of Briquetting Performance. Agriculture 2022, 12, 736. [Google Scholar] [CrossRef]
- Fakayode, O.A.; Akpan, D.E.; Ojoawo, O.O. Size characterization of moringa (Moringa oleifera) seeds and optimization of the dehulling process. J. Food Process Eng. 2019, 42, e13182. [Google Scholar] [CrossRef]
- Mustapha, A.T.; Zhou, C.S.; Wahia, H.; Sarpong, F.; Nasiru, M.M.; Adegbemiga, Y.B.; Ma, H.L. Combination of thermal and dual-frequency sonication processes for optimum microbiological and antioxidant properties in cherry tomato. J. Food Process. Preserv. 2020, 44, 12. [Google Scholar] [CrossRef]
- Boateng, I.D.; Yang, X.-M. Process optimization of intermediate-wave infrared drying: Screening by Plackett–Burman; comparison of Box-Behnken and central composite design and evaluation: A case study. Ind. Crops Prod. 2021, 162, 113287. [Google Scholar] [CrossRef]
- Boateng, I.D.; Yang, X.-M.; Li, Y.-Y. Optimization of infrared-drying parameters for Ginkgo biloba L. seed and evaluation of product quality and bioactivity. Ind. Crops Prod. 2021, 160, 113108. [Google Scholar] [CrossRef]
- Gao, R.C.; Li, X.; Liu, H.J.; Cui, Y.X.; Wu, X.Y.; Jin, W.G.; Yuan, L. Optimization of removal of off-odor in mullet (Channa argus) head soup by yeast using response surface methodology and variations of volatile components during fermentation. J. Food Process. Preserv. 2021, 45, e15920. [Google Scholar] [CrossRef]
- Wahia, H.; Zhou, C.S.; Sarpong, F.; Mustapha, A.T.; Liu, S.L.; Yu, X.J.; Li, C. Simultaneous optimization of Alicyclobacillus acidoterrestris reduction, pectin methylesterase inactivation, and bioactive compounds enhancement affected by thermosonication in orange juice. J. Food Process. Preserv. 2019, 43, e14180. [Google Scholar] [CrossRef]
- Xu, F.F.; Wang, B.; Hong, C.; Telebielaigen, S.; Nsor-Atindana, J.; Duan, Y.Q.; Zhong, F. Optimization of spiral continuous flow-through pulse light sterilization for Escherichia coli in red grape juice by response surface methodology. Food Control 2019, 105, 8–12. [Google Scholar] [CrossRef]
- Alenyorege, E.A.; Ma, H.L.; Aheto, J.H.; Ayim, I.; Chikari, F.; Osae, R.; Zhou, C.S. Response surface methodology centred optimization of mono-frequency ultrasound reduction of bacteria in fresh-cut Chinese cabbage and its effect on quality. LWT-Food Sci. Technol. 2020, 122, 108991. [Google Scholar] [CrossRef]
- Huang, J.N.; Guo, Q.; Manzoor, M.F.; Chen, Z.W.; Xu, B. Evaluating the sterilization effect of wheat flour treated with continuous high-speed-stirring superheated steam. J. Cereal Sci. 2021, 99, 103199. [Google Scholar] [CrossRef]
- Wahia, H.; Zhou, C.S.; Fakayode, O.A.; Amanor-Atiemoh, R.; Zhang, L.; Mustapha, A.T.; Zhang, J.; Xu, B.G.; Zhang, R.; Ma, H.L. Quality attributes optimization of orange juice subjected to multi-frequency thermosonication: Alicyclobacillus acidoterrestris spore inactivation and applied spectroscopy ROS characterization. Food Chem. 2021, 361, 130108. [Google Scholar] [CrossRef]
- Qin, W.C.; Xue, X.Y.; Cui, L.F.; Zhou, Q.Q.; Xu, Z.F.; Chang, F.L. Optimization and test for spraying parameters of cotton defoliant sprayer. Int. J. Agric. Biol. Eng. 2016, 9, 63–72. [Google Scholar] [CrossRef]
- Hu, Y.G.; Chen, Y.K.; Wei, W.Z.; Hu, Z.Y.; Li, P.P. Optimization Design of Spray Cooling Fan Based on CFD Simulation and Field Experiment for Horticultural Crops. Agriculture 2021, 11, 566. [Google Scholar] [CrossRef]
- Wang, W.; Lv, X.L.; Yi, Z.Y. Parameter Optimization of Reciprocating Cutter for Chinese Little Greens Based on Finite Element Simulation and Experiment. Agriculture 2022, 12, 2131. [Google Scholar] [CrossRef]
- Yue, R.C.; Hu, J.P.; Liu, Y.J.; Yao, M.J.; Zhang, T.F.; Shi, J.W. Design and Working Parameter Optimization of Pneumatic Reciprocating Seedling-Picking Device of Automatic Transplanter. Agriculture 2022, 12, 1989. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Hu, Y.Y.; Yang, Y.F.; Feng, K.Y.; Han, X.; Li, P.Y.; Zhu, Y.Y.; Song, Q. Optimization of Operating Parameters for Straw Returning Machine Based on Vibration Characteristic Analysis. Agronomy 2024, 14, 2388. [Google Scholar] [CrossRef]
- Han, D.L.; Zhang, H.; Li, G.Y.; Wang, G.L.; Wang, X.Z.; Chen, Y.C.; Chen, X.G.; Wen, X.Y.; Yang, Q.Z.; Zhao, R.Q. Development of a Bionic Picking Device for High Harvest and Low Loss Rate Pod Pepper Harvesting and Related Working Parameter Optimization Details. Agriculture 2024, 14, 859. [Google Scholar] [CrossRef]
- Xing, S.F.; Yu, Y.; Cao, G.Q.; Hu, J.P.; Zhu, L.J.; Liu, J.Y.; Wu, Q.H.; Li, Q.B.; Xu, L.Z. Design and Parametric Optimization Study of an Eccentric Parallelogram-Type Uprighting Device for Ratoon Rice Stubbles. Agriculture 2024, 14, 534. [Google Scholar] [CrossRef]
- Du, Z.; Hu, Y.; Buttar, N.A. Analysis of mechanical properties for tea stem using grey relational analysis coupled with multiple linear regression. Sci. Hortic. 2020, 260, 108886. [Google Scholar] [CrossRef]
- Li, Y.S.J.W.X.C.Q.L.B.D.C. Detection of viability of soybean seed based on fluorescence hyperspectra and CARS-SVM-AdaBoost model. J. Food Process. Preserv. 2019, 43, e14238. [Google Scholar] [CrossRef]
- Paz, J.; Diaz, J.; Romera, L.; Costas, M. Crushing analysis and multi-objective crashworthiness optimization of GFRP honeycomb-filled energy absorption devices. Finite Elem. Anal. Des. 2014, 91, 30–39. [Google Scholar] [CrossRef]
- Gao, D.; Liang, H.; Shi, G.; Cao, L. Multiobjective Optimization of Carbon Fiber-Reinforced Plastic Composite Bumper Based on Adaptive Genetic Algorithm. Math. Probl. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Xing, W.; Cui, Y.K.; Wang, X.H.; Shen, J. Optimization of Operational Parameters of Plant Protection UAV. Sensors 2024, 24, 5132. [Google Scholar] [CrossRef]
- Gu, L.; Yang, R.J.; Tho, C.H.; Makowski, M.; Faruque, O.; Li, Y. Optimization and robustness for crashworthiness of side impact. Int. J. Veh. Des. 2001, 26, 348–360. [Google Scholar] [CrossRef]
- Jansson, T.; Andersson, A.; Nilsson, L. Optimization of draw-in for an automotive sheet metal part An evaluation using surrogate models and response surfaces. J. Mater. Process. Technol. 2005, 159, 426–434. [Google Scholar] [CrossRef]
- Liao, X.; Li, Q.; Yang, X.; Zhang, W.; Li, W. Multiobjective optimization for crash safety design of vehicles using stepwise regression model. Struct. Multidiscip. Optim. 2008, 35, 561–569. [Google Scholar] [CrossRef]
- Shi, L.; Yang, R.-J.; Zhu, P. An adaptive response surface method for crashworthiness optimization. Eng. Optim. 2013, 45, 1365–1377. [Google Scholar] [CrossRef]
- Sun, G.; Xu, F.; Li, G.; Li, Q. Crashing analysis and multiobjective optimization for thin-walled structures with functionally graded thickness. Int. J. Impact Eng. 2014, 64, 62–74. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, T.; Long, J. Lightweight optimization design for automotive front seat frame based on comprehensive Sobol global sensitivity analysis. Proc. Inst. Mech. Eng. Part C—J. Mech. Eng. Sci. 2025, 239, 7321–7340. [Google Scholar] [CrossRef]
- Johnson, N.A.N.; Ekumah, J.-N.; Ma, Y.; Akpabli-Tsigbe, N.D.K.; Adade, S.Y.-S.S.; Manching, X.; Quaisie, J.; Kwaw, E.; Wang, C. Optimization of fermentation parameters for the production of a novel selenium enriched mulberry (Morus nigra) wine. LWT 2023, 178, 114608. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Wu, B.; Tian, Y.; Han, F.; Zheng, C.M. Optimizing conjunctive use of surface water and groundwater for irrigation to address human-nature water conflicts: A surrogate modeling approach. Agric. Water Manag. 2016, 163, 380–392. [Google Scholar] [CrossRef]
- Guang, L.; Yuan, Y.; Longjiang, S.; Xiaoxing, D.; Wensheng, Z. Influence of yaw damper layouts on locomotive lateral dynamics performance: Pareto optimization and parameter analysis. J. Zhejiang Univ.-Sci. A 2023, 24, 450–464. [Google Scholar] [CrossRef]
- Ji, X.; Lu, X.; Li, H.; Ma, P.; Xu, S. Blade optimization design of Savonius hydraulic turbine based on radial basis function surrogate model and L-SHADE algorithm. Ocean Eng. 2023, 286, 115620. [Google Scholar] [CrossRef]
- Fang, H.; Rais-Rohani, M.; Liu, Z.; Horstemeyer, M.F. A comparative study of metamodeling methods for multiobjective crashworthiness optimization. Comput. Struct. 2005, 83, 2121–2136. [Google Scholar] [CrossRef]
- Kiani, M.; Gandikota, I.; Parrish, A.; Motoyama, K.; Rais-Rohani, M. Surrogate-based optimisation of automotive structures under multiple crash and vibration design criteria. Int. J. Crashworthiness 2013, 18, 473–482. [Google Scholar] [CrossRef]
- Li, S.; Zhou, D.; Pan, A. Integrated lightweight optimization design of wall thickness, material, and performance of automobile body side structure. Struct. Multidiscip. Optim. 2024, 67, 95. [Google Scholar] [CrossRef]
- Qin, R.; Zhou, J.; Chen, B. Crashworthiness Design and Multiobjective Optimization for Hexagon Honeycomb Structure with Functionally Graded Thickness. Adv. Mater. Sci. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Cheng, D.; Yao, Y.F.; Liu, R.Y.; Li, X.N.; Guan, B.X.; Yu, F.H. Precision agriculture management based on a surrogate model assisted multiobjective algorithmic framework. Sci. Rep. 2023, 13, 1142. [Google Scholar] [CrossRef] [PubMed]
- Huri, D.; Mankovits, T. Surrogate Model-Based Parameter Tuning of Simulated Annealing Algorithm for the Shape Optimization of Automotive Rubber Bumpers. Appl. Sci. 2022, 12, 5451. [Google Scholar] [CrossRef]
- Pan, F.; Zhu, P. Lightweight design of vehicle front-end structure: Contributions of multiple surrogates. Int. J. Veh. Des. 2011, 57, 124–147. [Google Scholar] [CrossRef]
- Hamza, K.; Saitou, K. A Co-Evolutionary Approach for Design Optimization via Ensembles of Surrogates with Application to Vehicle Crashworthiness. J. Mech. Des. 2012, 134, 011001. [Google Scholar] [CrossRef]
- Shi, L.; Yang, R.J.; Zhu, P. A method for selecting surrogate models in crashworthiness optimization. Struct. Multidiscip. Optim. 2012, 46, 159–170. [Google Scholar] [CrossRef]
- Acar, E. Increasing automobile crash response metamodel accuracy through adjusted cross validation error based on outlier analysis. Int. J. Crashworthiness 2015, 20, 107–122. [Google Scholar] [CrossRef]
- Liao, Y.; Zhou, X.; Xu, H.; Gao, T. Multi-objective optimization design for an automobile rear seat based on multi-objective global optimization. Mech. Based Des. Struct. Mach. 2025, 1–26. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, Q.; Liu, R.; Guo, S.; Zhao, L.; Shen, C.; Zheng, X.; Peng, Y.; Wang, X.; Gao, Q. A pointwise weighted hybrid surrogate model based on hybrid measures for engineering optimization. Struct. Multidiscip. Optim. 2025, 68, 96. [Google Scholar] [CrossRef]
- Zhou, X.; Long, J. A systematic and optimal design method for replacing steel backrest in automotive seat with carbon fiber-reinforced polymer composites. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 15. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, Y.; Wu, Q.W.; Wang, Y.J.; Long, H.; Hu, H.L. Structure optimization design for pre-folded external double-layer biomimetic multi-cell thin-walled tubes. J. Mech. Sci. Technol. 2024, 38, 3465–3475. [Google Scholar] [CrossRef]
- Ma, N.; Han, S.; Xu, W.; Han, Q.; Li, C. Compressive response and optimization design of a novel hierarchical re-entrant origami honeycomb metastructure. Eng. Struct. 2024, 306, 117819. [Google Scholar] [CrossRef]
- Simpson, T.W.; Booker, A.J.; Ghosh, D.; Giunta, A.A.; Koch, P.N.; Yang, R.-J. Approximation methods in multidisciplinary analysis and optimization: A panel discussion. Struct. Multidiscip. Optim. 2004, 27, 302–313. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006; pp. 415–426. [Google Scholar] [CrossRef]
- Felipe, A.; Simpson, T.; Balabanov, V.; Toropov, V. Metamodeling in multidisciplinary design optimization: How far have we really come. AIAA (Am. Inst. Aeronaut. Astronaut.) J. 2014, 52, 670–690. [Google Scholar]
- Seeger, M. Gaussian processes for machine learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar] [CrossRef]
- Hajieghrary, H.; Deisenroth, M.P.; Bekiroglu, Y. Bayesian optimization-based nonlinear adaptive PID controller design for robust mobile manipulation. In Proceedings of the 2022 IEEE 18th International Conference on Automation Science and Engineering (CASE), Mexico City, Mexico, 20–24 August 2022; pp. 1009–1016. [Google Scholar] [CrossRef]
- Calandra, R.; Seyfarth, A.; Peters, J.; Deisenroth, M.P. Bayesian optimization for learning gaits under uncertainty: An experimental comparison on a dynamic bipedal walker. Ann. Math. Artif. Intell. 2016, 76, 5–23. [Google Scholar] [CrossRef]
- Haddad, K. A Comprehensive Review and Application of Bayesian Methods in Hydrological Modelling: Past, Present, and Future Directions. Water 2025, 17, 1095. [Google Scholar] [CrossRef]
- Mabunga, Z.P.; Dela Cruz, J.C. An Optimized Soil Moisture Prediction Model for Smart Agriculture Using Gaussian Process Regression. In Proceedings of the 2022 IEEE 18th International Colloquium on Signal Processing & Applications (CSPA), Selangor, Malaysia, 12 May 2022; pp. 243–247. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Peng, Z. Rice diseases detection and classification using attention based neural network and bayesian optimization. Expert Syst. Appl. 2021, 178, 114770. [Google Scholar] [CrossRef]
- Di, Y.; Gao, M.; Feng, F.; Li, Q.; Zhang, H. A New Framework for Winter Wheat Yield Prediction Integrating Deep Learning and Bayesian Optimization. Agronomy 2022, 12, 3194. [Google Scholar] [CrossRef]
- Fei, S.; Chen, Z.; Li, L.; Ma, Y.; Xiao, Y. Bayesian model averaging to improve the yield prediction in wheat breeding trials. Agric. For. Meteorol. 2023, 328, 109237. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, D.; Ni, X.; Wang, S.; Wang, X. Optimization of a Low Loss Strategy for Combine Harvesters Based on Bayesian Network. IFAC-Pap. 2022, 55, 259–264. [Google Scholar] [CrossRef]
- Momeny, M.; Jahanbakhshi, A.; Neshat, A.A.; Hadipour-Rokni, R.; Zhang, Y.-D.; Ampatzidis, Y. Detection of citrus black spot disease and ripeness level in orange fruit using learning-to-augment incorporated deep networks. Ecol. Inform. 2022, 71, 101829. [Google Scholar] [CrossRef]
- Calderwood, A.; Siles, L.; Eastmond, P.J.; Kurup, S.; Morris, R.J. A causal inference and Bayesian optimisation framework for modelling multi-trait relationships-Proof-of-concept using Brassica napus seed yield under controlled conditions. PLoS ONE 2023, 18, e0290429. [Google Scholar] [CrossRef]
- Wen, T.; He, W.; Nie, Q.; Gong, Z.; Li, D.; Wen, L.; Peng, H. Discrimination of citrus infested with Bactrocera dorsalis (Hendel) using an olfactory detection system based on MIPs-QCM sensor array and Bayesian optimized classification algorithms. Sens. Actuators B-Chem. 2023, 385, 133687. [Google Scholar] [CrossRef]
- Alhashmi, A.A.; Alohali, M.A.; Ijaz, N.A.; Khadidos, A.O.; Alghushairy, O.; Sayed, A. Bayesian optimization with deep learning based pepper leaf disease detection for decision-making in the agricultural sector. Aims Math. 2024, 9, 16826–16847. [Google Scholar] [CrossRef]
- Ma, Y.; Xue, J.; Feng, X.; Zhao, J.; Tang, J.; Sun, H.; Chang, J.; Yan, L. Crop water productivity assessment and planting structure optimization in typical arid irrigation district using dynamic Bayesian network. Sci. Rep. 2024, 14, 17695. [Google Scholar] [CrossRef]
- Tifanto, B.A.; Hadi, M.Z.S.; Sa’adah, N. A Crop Recommendation System for Smart Agriculture Using Random Forest Method. In Proceedings of the 2024 International Electronics Symposium (IES), Denpasar, Indonesia, 6–8 August 2024; pp. 222–227. [Google Scholar] [CrossRef]
- Uribe-Guerra, G.D.; Munera-Ramirez, D.A.; Arias-Londono, J.D. Feed formulation using multi-objective Bayesian optimization. Comput. Electron. Agric. 2024, 224, 109173. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, J.; Liu, C.; Wu, Q.; Xiong, S.; Yang, H.; Chang, S.; Fu, Y.; Yang, M.; Zhang, S.; et al. Enhanced Crop Leaf Area Index Estimation via Random Forest Regression: Bayesian Optimization and Feature Selection Approach. Remote Sens. 2024, 16, 3917. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, F.; Yu, W. Agricultural Pest Image Recognition Algorithm Based on Convolutional Neural Network and Bayesian Method. IEEE Access 2024, 12, 188072–188083. [Google Scholar] [CrossRef]
- Padilla-Esquivel, C.A.; Lopez-Flores, F.J.; Hernandez-Perez, L.G.; Rubio-Castro, E.; Ponce-Ortega, J.M. Optimizing green urea production: Integration of process simulation, artificial intelligence, and sustainable technologies. J. Clean. Prod. 2025, 501, 145371. [Google Scholar] [CrossRef]
- Wu, M.; Li, R.; Lv, C.; Dong, A.; Mu, F.; Niu, W. Hourly photosynthetically active radiation prediction in solar greenhouses using Bayesian optimized machine learning and deep learning based on limited local weather data. Comput. Electron. Agric. 2025, 237, 110680. [Google Scholar] [CrossRef]
- Bhat, S.A.; Hussain, I.; Huang, N.F. Soil suitability classification for crop selection in precision agriculture using GBRT-based hybrid DNN surrogate models. Ecol. Inform. 2023, 75, 102109. [Google Scholar] [CrossRef]
- Perlini, A.; Abergo, L.; Gori, G. A Hybrid Bayesian-Adjoint Framework for Aerodynamic Shape Optimization. In Proceedings of the AIAA Aviation Forum and Ascend 2024, Las Vegas, NV, USA, 29 July–2 August 2024; p. 3753. [Google Scholar] [CrossRef]
- Choi, K.; Singh, S.; Kodali, A.; Pattipati, K.R.; Sheppard, J.W.; Namburu, S.M.; Chigusa, S.; Prokhorov, D.V.; Qiao, L. Novel Classifier Fusion Approaches for Fault Diagnosis in Automotive Systems. IEEE Trans. Instrum. Meas. 2009, 58, 602–611. [Google Scholar] [CrossRef]
- Mathew, S.K.; Zhang, Y. Acoustic-Based Engine Fault Diagnosis Using WPT, PCA and Bayesian Optimization. Appl. Sci. 2020, 10, 6890. [Google Scholar] [CrossRef]
- Stenger, D.; Abel, D. Benchmark of Bayesian Optimization and Metaheuristics for Control Engineering Tuning Problems with Crash Constraints. arXiv 2022, arXiv:2211.02571. [Google Scholar] [CrossRef]
- Winter, J.; Fiebig, S.; Franke, T.; Bartz, R.; Vietor, T. Spline-based shape optimization of large-scale composite leaf spring models using Bayesian strategies with multiple constraints. Struct. Multidiscip. Optim. 2022, 65, 257. [Google Scholar] [CrossRef]
- Borsboom, O.; Lokker, M.; Salazar, M.; Hofman, T. Effective Scaling of High-Fidelity Electric Motor Models for Electric Powertrain Design Optimization. arXiv 2023, arXiv:2307.12741. [Google Scholar] [CrossRef]
- Huang, C. Data-driven lightweight design of bumper based on multi-methods. Int. J. Crashworthiness 2025, 30, 411–423. [Google Scholar] [CrossRef]
- Lee, H.; Yeo, J.; Kong, K.; Myeong, D.; Jang, D.; Lee, J.; Choi, H.; Kim, N.; Ryu, S. Bayesian optimization of tailgate rib structures enhancing structural stiffness under manufacturing constraints of injection molding. J. Manuf. Process. 2025, 134, 739–748. [Google Scholar] [CrossRef]
- Long, F.X.; van Stein, N.; Frenzel, M.; Krause, P.; Gitterle, M.; Back, T. Surrogate-based automated hyperparameter optimization for expensive automotive crashworthiness optimization. Struct. Multidiscip. Optim. 2025, 68, 68. [Google Scholar] [CrossRef]
- Naveen, M.R.; Kamaraj, L.; Ponnarengan, H. Bayesian optimization and neural network prediction of graphene-titanium fiber metal laminates. Mater. Today Commun. 2025, 45, 112355. [Google Scholar] [CrossRef]
- Kita, E.; Toyoda, T. Structural design using cellular automata. Struct. Multidiscip. Optim. 2000, 19, 64–73. [Google Scholar] [CrossRef]
- Tatting, B.; Gurdal, Z. Cellular automata for design of two-dimensional continuum structures. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000; Multidisciplinary Analysis Optimization Conferences. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar]
- Abdalla, M.M.; Gürdal, Z. Structural design using Cellular Automata for eigenvalue problems. Struct. Multidiscip. Optim. 2004, 26, 200–208. [Google Scholar] [CrossRef]
- Bochenek, B.; Tajs-Zielinska, K. Topology optimization with efficient rules of cellular automata. Eng. Comput. 2013, 30, 1086–1106. [Google Scholar] [CrossRef]
- Missoum, S.; Gürdal, Z.; Setoodeh, S. Study of a new local update scheme for cellular automata in structural design. Struct. Multidiscip. Optim. 2005, 29, 103–112. [Google Scholar] [CrossRef]
- Bochenek, B.; Tajs-Zielińska, K. Novel local rules of cellular automata applied to topology and size optimization. Eng. Optim. 2012, 44, 23–35. [Google Scholar] [CrossRef]
- Faramarzi, A.; Afshar, M.H. Application of cellular automata to size and topology optimization of truss structures. Sci. Iran. 2012, 19, 373–380. [Google Scholar] [CrossRef]
- Gholizadeh, S. Layout optimization of truss structures by hybridizing cellular automata and particle swarm optimization. Comput. Struct. 2013, 125, 86–99. [Google Scholar] [CrossRef]
- El Bouzouiki, M.; Sedaghati, R.; Stiharu, I. A non-uniform cellular automata framework for topology and sizing optimization of truss structures subjected to stress and displacement constraints. Comput. Struct. 2021, 242, 106394. [Google Scholar] [CrossRef]
- Gan, N.; Yao, S.; Xiong, Y.; Hong, X. A hybrid cellular automaton–bi-directional evolutionary optimization algorithm for topological optimization of crashworthiness. Eng. Optim. 2018, 50, 2054–2070. [Google Scholar] [CrossRef]
- Tovar, A.; Patel, N.M.; Niebur, G.L.; Sen, M.; Renaud, J.E. Topology optimization using a hybrid cellular automaton method with local control rules. J. Mech. Des. 2006, 128, 1205–1216. [Google Scholar] [CrossRef]
- Mozumder, C.; Renaud, J. Cost and Mass Optimization for Crashworthiness Design of Shell-Based Structure Using Hybrid Cellular Automata. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009; Structures, Structural Dynamics, and Materials and Co-Located Conferences. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar] [CrossRef]
- Guo, L.; Tovar, A.; Penninger, C.L.; Renaud, J.E. Strain-based topology optimisation for crashworthiness using hybrid cellular automata. Int. J. Crashworthiness 2011, 16, 239–252. [Google Scholar] [CrossRef]
- Bandi, P.; Tovar, A.; Renaud, J. Design of 2D and 3D Non-Linear Compliant Mechanisms Using Hybrid Cellular Automata; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar] [CrossRef]
- Bandi, P. Design of Crashworthy Structures with Controlled Behavior in HCA Framework. In Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; Available online: https://api.semanticscholar.org/CorpusID:28539850 (accessed on 12 September 2025).
- Bandi, P.; Schmiedeler, J.P.; Tovar, A. Design of Crashworthy Structures with Controlled Energy Absorption in the Hybrid Cellular Automaton Framework. J. Mech. Des. 2013, 135, 091002. [Google Scholar] [CrossRef]
- Guo, L.; Huang, J.; Zhou, X.; Tovar, A. The Convergence and Algorithm Factors Analysis of Topology Optimization for Crashworthiness Based on Hybrid Cellular Automata. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; Volume 3. [Google Scholar] [CrossRef]
- Wehrle, E.; Han, Y.H.; Duddeck, F. Topology optimization of transient nonlinear structures—A comparative assessment of methods. In Proceedings of the 10th European LS-DYNA Conference, Würzburg, Germany, 15–17 June 2015; Available online: https://www.researchgate.net/publication/285593647_Topology_optimization_of_transient_nonlinear_structures-A_comparative_assessment_of_methods (accessed on 12 September 2025).
- Hesse, S.H.; Lukaszewicz, D.H.J.A.; Duddeck, F. A method to reduce design complexity of automotive composite structures with respect to crashworthiness. Compos. Struct. 2015, 129, 236–249. [Google Scholar] [CrossRef]
- Da, D.C.; Chen, J.H.; Cui, X.Y.; Li, G.Y. Design of materials using hybrid cellular automata. Struct. Multidiscip. Optim. 2017, 56, 131–137. [Google Scholar] [CrossRef]
- Jia, J.; Da, D.; Loh, C.-L.; Zhao, H.; Yin, S.; Xu, J. Multiscale topology optimization for non-uniform microstructures with hybrid cellular automata. Struct. Multidiscip. Optim. 2020, 62, 757–770. [Google Scholar] [CrossRef]
- Raeisi, S.; Tapkir, P.; Tovar, A.; Mozumder, C.; Xu, S. Multi-Material Topology Optimization for Crashworthiness Using Hybrid Cellular Automata; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Afrousheh, M.; Marzbanrad, J.; Göhlich, D. Topology optimization of energy absorbers under crashworthiness using modified hybrid cellular automata (MHCA) algorithm. Struct. Multidiscip. Optim. 2019, 60, 1021–1034. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Huang, L.; Xu, W.; Liang, H.; Liu, B.; Xue, G.; Chen, H.; Huang, B.; Meng, Z. Multi-objective topology optimization method for multi-axis random vibration based on hybrid cellular automata. Appl. Math. Model. 2024, 133, 327–343. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Huang, B.; Wang, S.; Zhang, Z.; Li, S.; Xie, C.; Kong, D. A dynamic-static coupling topology optimization method based on hybrid cellular automata. Structures 2023, 50, 1573–1583. [Google Scholar] [CrossRef]
- Wang, Z.; Song, X.; Kan, Z. A Harmonic Response Topology Optimization Method Based on Hybrid Cellular Automata. J. Mech. Des. 2024, 147, 051702. [Google Scholar] [CrossRef]
- Mozumder, C.; Renaud, J.E.; Tovar, A. Topometry optimisation for crashworthiness design using hybrid cellular automata. Int. J. Veh. Des. 2012, 60, 100–120. [Google Scholar] [CrossRef]
- Mozumder, C. Topometry Optimization of Sheet Metal Structures for Crashworthiness Design Using Hybrid Cellular Automata. Int. J. Veh. Des. 2010, 60, 100–120. [Google Scholar] [CrossRef]
- Bandi, P.; Detwiler, D.; Schmiedeler, J.P.; Tovar, A. Design of progressively folding thin-walled tubular components using compliant mechanism synthesis. Thin-Walled Struct. 2015, 95, 208–220. [Google Scholar] [CrossRef][Green Version]
- Duddeck, F.; Hunkeler, S.; Lozano, P.; Wehrle, E.; Zeng, D. Topology optimization for crashworthiness of thin-walled structures under axial impact using hybrid cellular automata. Struct. Multidiscip. Optim. 2016, 54, 415–428. [Google Scholar] [CrossRef]
- Zeng, D.; Duddeck, F. Improved hybrid cellular automata for crashworthiness optimization of thin-walled structures. Struct. Multidiscip. Optim. 2017, 56, 101–115. [Google Scholar] [CrossRef]
- Zeng, D.; Duddeck, F. Topology Optimization of Thin-Walled Structures Under Static/Crash Loading Case in the Hybrid Cellular Automaton Frame-work. In Advances in Structural and Multidisciplinary Optimization; Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.-U., Maute, K., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1585–1600. [Google Scholar] [CrossRef]
- Wang, H.; Xie, H. Multi-objective optimization of crashworthiness of vehicle front longitudinal beam. Struct. Multidiscip. Optim. 2020, 61, 2111–2123. [Google Scholar] [CrossRef]
- Duan, L.; Jiang, H.; Li, H.; Xiao, N. Crashworthiness optimization of VRB thin-walled structures under manufacturing constraints by the eHCA-VRB algorithm. Appl. Math. Model. 2020, 80, 126–150. [Google Scholar] [CrossRef]
- Duan, L.; Liu, X.; Xu, W.; Xu, D.; Shi, L.; Jiang, H. Thickness-based subdomian hybrid cellular automata algorithm for lightweight design of BIW under side collision. Appl. Math. Model. 2022, 102, 170–193. [Google Scholar] [CrossRef]
- Duan, L.; Xu, Z.; Xu, W.; Zhang, X.; Du, Z.; Liu, X.; Jiang, H. Subdomain hybrid cellular automata method for material optimization of thin-walled frame structure under transverse impact. Int. J. Impact Eng. 2023, 174, 104524. [Google Scholar] [CrossRef]
- Ghajarnia, N.; Bozorg-Haddad, O.; Mariño, M.A. Performance of a novel hybrid algorithm in the design of water networks. Proc. Inst. Civ. Eng.-Water Manag. 2011, 164, 173–191. [Google Scholar] [CrossRef]
- Song, X.D.; Zhang, G.L.; Liu, F.; Li, D.C.; Zhao, Y.G.; Yang, J.L. Modeling spatio-temporal distribution of soil moisture by deep learning-based cellular automata model. J. Arid Land 2016, 8, 734–748. [Google Scholar] [CrossRef]
- Wang, S.F.; Salahou, M.K.; Wang, L.P.; Sang, H.H.; Li, S.W.; Lv, Y.P. A distributed hybrid model for agricultural water-land resource matching. Agric. Water Manag. 2025, 318, 109693. [Google Scholar] [CrossRef]
- Pereira, M.L.; Sadras, V.O.; Batista, W.; Casal, J.J.; Hall, A.J. Light-mediated self-organization of sunflower stands increases oil yield in the field. Proc. Natl. Acad. Sci. USA 2017, 114, 7975–7980. [Google Scholar] [CrossRef]
- Wang, S.F.; Jiao, X.Y.; Wang, L.P.; Gong, A.M.; Sang, H.H.; Salahou, M.K.; Zhang, L.D. Integration of Boosted Regression Trees and Cellular Automata-Markov Model to Predict the Land Use Spatial Pattern in Hotan Oasis. Sustainability 2020, 12, 1396. [Google Scholar] [CrossRef]
- Jana, A.; Jat, M.K.; Saxena, A.; Choudhary, M. Prediction of land use land cover changes of a river basin using the CA-Markov model. Geocarto Int. 2022, 37, 14127–14147. [Google Scholar] [CrossRef]
- Li, Y.T.; Cai, Y.P.; Fu, Q.; Zhang, X.D.; Wan, H.; Yang, Z.F. Dynamics of Land Use/Land Cover Considering Ecosystem Services for a Dense-Population Watershed Based on a Hybrid Dual-Subject Agent and Cellular Automaton Modeling Approach. Engineering 2024, 37, 182–195. [Google Scholar] [CrossRef]
- Meshesha, T.M.; Tsunekawa, A.; Haregeweyn, N.; Tsubo, M.; Fenta, A.A.; Berihun, M.L.; Mulu, A.; Setargie, T.A.; Kassa, S.B. Agroecology-based land use/land cover change detection, prediction and its implications for land degradation: A case study in the Upper Blue Nile Basin. Int. Soil Water Conserv. Res. 2024, 12, 786–797. [Google Scholar] [CrossRef]
- Panda, K.C.; Singh, R.M.; Singh, S.K. Advanced CMD predictor screening approach coupled with cellular automata-artificial neural network algorithm for efficient land use-land cover change prediction. J. Clean. Prod. 2024, 449, 141822. [Google Scholar] [CrossRef]
- Huayna, G.; Pocco, V.; Pino-Vargas, E.; Franco-León, P.; Espinoza-Molina, J.; Cabrera-Olivera, F.; Vera-Barrios, B.; Acosta-Caipa, K.; Ramos-Fernández, L.; Ingol-Blanco, E. Historical Land Cover Dynamics and Projected Changes in the High Andean Zone of the Locumba Basin: A Predictive Approach Using Remote Sensing and Artificial Neural Network-Cellular Automata Model. Land 2025, 14, 1442. [Google Scholar] [CrossRef]

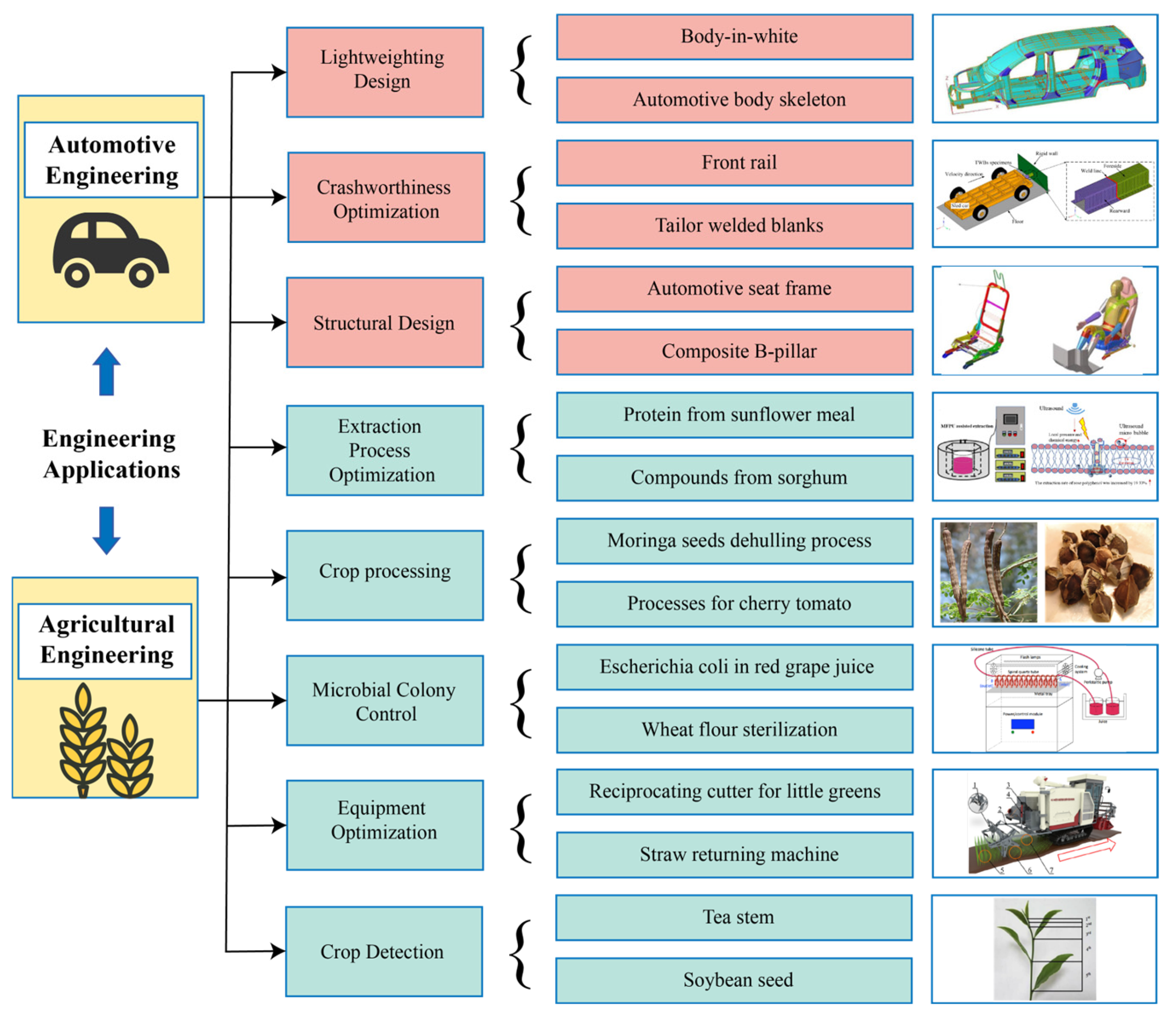
| Database | Number of Articles That Were First Retrieved | Number of Papers Remaining After Exclusion Criteria | Number of Articles After Removing the Repeated Articles |
|---|---|---|---|
| Science Direct | 764 | 94 | 87 |
| Web of Science | 923 | 119 | 112 |
| Google Scholar | 237 | 58 | 43 |
| Total | 1924 | 271 | 242 |
| Method | Kinds | Convergence Speed | Accuracy | Costs |
|---|---|---|---|---|
| Gradient-based | Nonlinear |      |      |    |
| Multi-objective |     |      |    | |
| High-dimensional |   |    |     | |
| Heuristic | Nonlinear |    |    |   |
| Multi-objective |    |     |   | |
| High-dimensional |   |   |   | |
| Surrogate model-based | Nonlinear |     |     |    |
| Multi-objective |     |     |    | |
| High-dimensional |   |   |    | |
| Bayesian | Nonlinear |     |      |     |
| Multi-objective |     |      |     | |
| High-dimensional |  |    |  | |
| Hybrid cellular automata | Nonlinear |      |     |    |
| Multi-objective |      |    |    | |
| High-dimensional |     |    |     |


 is faster/higher accuracy/more costly than
is faster/higher accuracy/more costly than 
 ). These ratings are intended for qualitative comparison only and do not represent absolute quantitative values.
). These ratings are intended for qualitative comparison only and do not represent absolute quantitative values.Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Duan, L.; Ma, B.; Meng, X.; Ren, L.; Ye, D.; Rui, S. Applications of Optimization Methods in Automotive and Agricultural Engineering: A Review. Mathematics 2025, 13, 3018. https://doi.org/10.3390/math13183018
Zhao W, Duan L, Ma B, Meng X, Ren L, Ye D, Rui S. Applications of Optimization Methods in Automotive and Agricultural Engineering: A Review. Mathematics. 2025; 13(18):3018. https://doi.org/10.3390/math13183018
Chicago/Turabian StyleZhao, Wenjing, Libin Duan, Baolin Ma, Xiangxin Meng, Lifang Ren, Deying Ye, and Shili Rui. 2025. "Applications of Optimization Methods in Automotive and Agricultural Engineering: A Review" Mathematics 13, no. 18: 3018. https://doi.org/10.3390/math13183018
APA StyleZhao, W., Duan, L., Ma, B., Meng, X., Ren, L., Ye, D., & Rui, S. (2025). Applications of Optimization Methods in Automotive and Agricultural Engineering: A Review. Mathematics, 13(18), 3018. https://doi.org/10.3390/math13183018