LDS3Pool: Pooling with Quasi-Random Spatial Sampling via Low-Discrepancy Sequences and Hilbert Ordering
Abstract
1. Introduction
- Introducing LDS3Pool, a novel quasi-random spatial pooling method that strategically positions itself between deterministic and purely stochastic approaches, offering controlled randomness with theoretical uniformity guarantees.
- Developing an innovative combination of Hilbert curves with LDS sampling that preserves image spatial relationships while introducing controlled randomness.
- Eliminating the sensitivity to manually tuned hyperparameters found in previous stochastic pooling methods, making LDS3Pool more robust and adaptive across different feature map sizes and network architectures.
- Demonstrating through extensive experiments that LDS3Pool consistently outperforms MaxPool, AvgPool, and S3Pool in image classification accuracy (by 1–5 percentage points) with reasonable computational overhead.
- Providing ablation studies that verify the contributions of Hilbert curve for image pixel ordering.
2. Related Work
2.1. Evolution of Pooling Strategies in CNNs
2.2. Low-Discrepancy Sequences for Quasi-Random Sampling
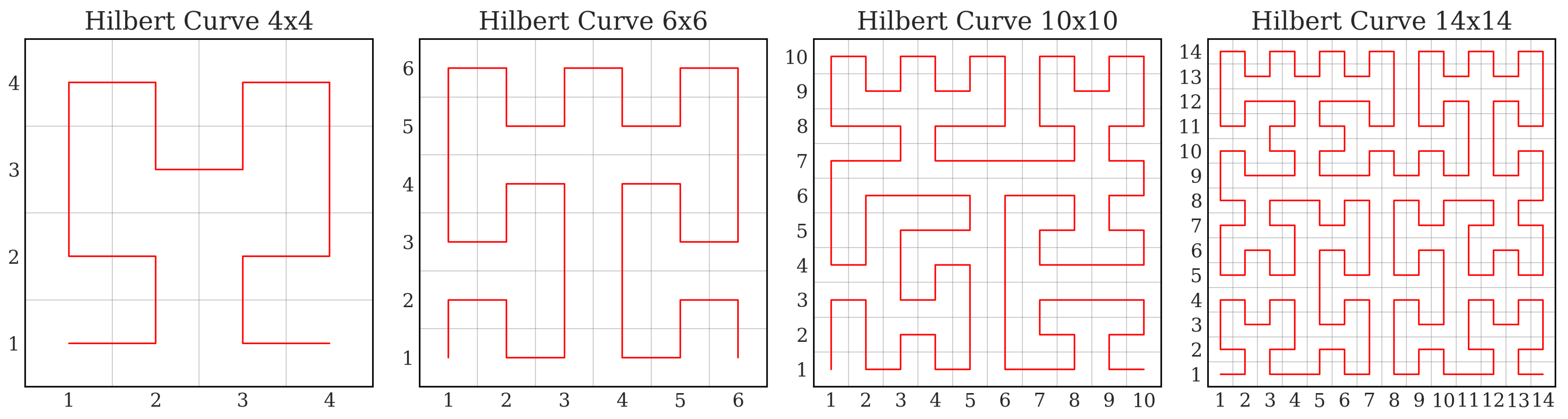
2.3. Hilbert Space-Filling Curves and Spatial Locality Preservation
3. Methods
3.1. The Two-Step Framework of Pooling
- Step1: Local Feature Aggregation
- Apply a local aggregation function with a receptive field of and stride 1 over the input feature map (with appropriate padding if necessary).
- This step generates an intermediate feature map with dimensions matching or nearly matching the input. Specifically:
- Each pixel represents an aggregated summary of information from the neighborhood centered at (or starting from) position in the original input . Common aggregation functions include maximum (Max), average (Average), or even learnable functions in some methods.
- Step 2: Spatial downsampling
- Apply a spatial downsampling function to the intermediate feature map .
- This step reduces the spatial dimensions from to , where and (assuming H and W are divisible by s). That isproducing the final pooling output .
- The critical distinction lies in how is implemented: This function determines which pixel values from are selected and how they are combined to constitute the final output . This is where different pooling strategies fundamentally diverge in their spatial processing approach.
3.2. Quasi-Random Spatial Sampling with Low-Discrepancy Sequences
3.3. The LDS3Pool Algorithm
- Step 1: Local Feature Aggregation
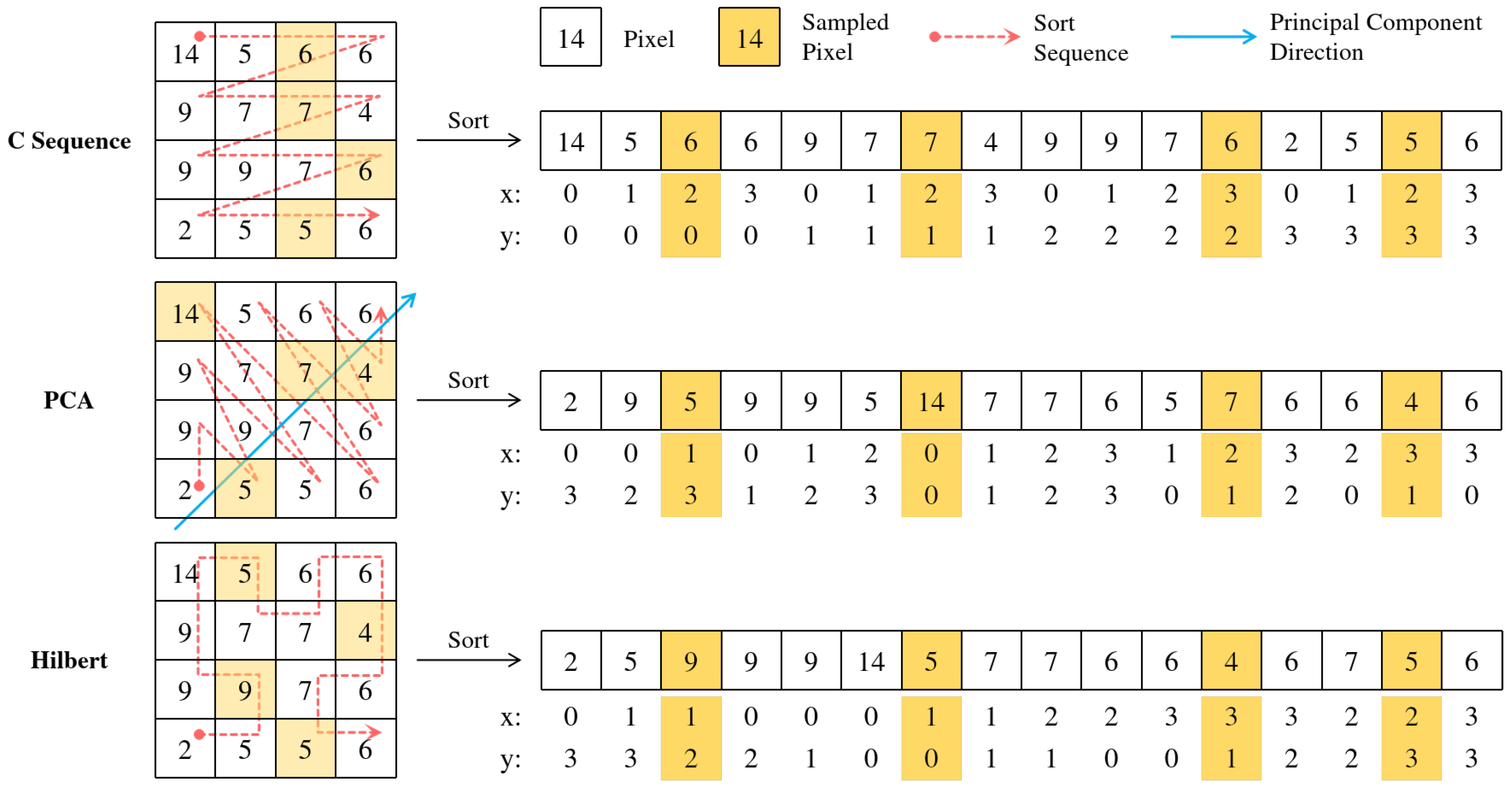
- Step 2: Hilbert Curve-based Pixel Ordering
- Denote each pixel in as ; then, all the pixels in constitute an disordered point set: .
- Generate a generalized Hilbert curve of the same size as . has vertices, which are denoted as , and .
- Since there is a one-to-one correspondence between the vertices on and the point coordinates in , the pixels in can be sorted according to the order of on , resulting in
- Step 3: LDS-based Quasi-Random Sampling
- Generate an LDS of length using the additive recurrence relation based on Euler’s number e:where represents the i-th value in the LDS.
- Create a sorted version of this sequence and compute the inverse sorting vector , so thatThis vector maps each original index i to its position in the sorted LDS.
- Reorder the Hilbert-ordered pixel sequence using the inverse sorting vector:
- Randomly pick a start index t and select coordinates from the reordered sequence:
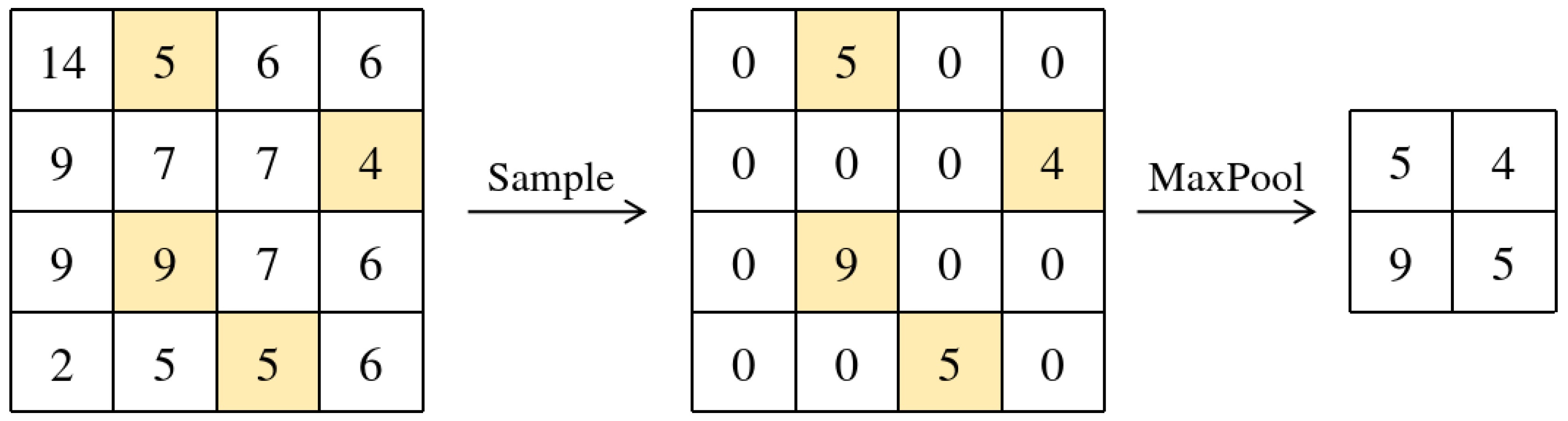
- Step 4: Feature Map Reconstruction
- Copy with the same dimensions as , initialized with zeros.
- For each selected coordinate , set: .
- Apply a standard max pooling operation with window size and stride s to this sparse feature map: . This produces the final downsampled feature map .
| Algorithm 1 LDS3Pool: Pooling with Quasi-Random Spatial Sampling |
| Require: Input feature map , pooling window size s, stride s |
| Ensure: Pooled feature map |
|
3.4. Illustration of LDS3Pool
- Simple C-ordering (row-major traversal) is used to linearize the 2D feature map.
- Principal component analysis is used to project pixel coordinates onto the first principal component direction for ordering.
3.5. Theoretical Analysis
3.5.1. Locality Preservation Analysis of Ordering Schemes
3.5.2. Uniform Coverage Guarantees of Low-Discrepancy Sequences
3.5.3. Synergistic Combination and Empirical Validation of Uniformity
3.5.4. Computational Complexity Analysis
- Initialization Phase Complexity
- Hilbert Curve Generation: The recursive Hilbert curve generation for an input feature map has a time complexity of . The logarithmic factor arises from the recursion depth of approximately needed to traverse all N points through recursive subdivision. This operation is computed only once during model initialization and stored for future use, thus not impacting training or inference time.
- Low-Discrepancy Sequence Generation: Computing the LDS based on the additive recurrence relation has a time complexity of for sequence generation followed by for sorting operations. This is also a one-time cost during initialization.
- Forward Pass Complexity During the forward pass of LDS3Pool, the computational operations can be broken down as follows:
- Local Feature Aggregation: The max pooling operation with stride 1 and window size on an input feature map has a time complexity of , which is asymptotically equivalent to standard max pooling.
- Sampling and Feature Map Reconstruction:
- The random selection of a start index for the LDS sampling is .
- Creating a sparse feature map using the selected coordinates is , where k is the oversampling factor (2 in our implementation).
- The final max pooling operation with stride s is .
4. Experiments
4.1. Experiment Setup
4.1.1. Datasets
- CIFAR10 and CIFAR100: Three-channel RGB images of size pixels, containing 50,000 training and 10,000 validation images. CIFAR10 includes 10 common object classes, while CIFAR100 extends this to 100 more fine-grained categories [30].
- STL10: Higher-resolution RGB images of size pixels, comprising 10 classes with 5000 training and 8000 validation images, focused on animals and transportation vehicles [31].
- OxfordIIITPet: Large RGB images uniformly resized to pixels, containing 37 pet breeds consolidated into a binary cat/dog classification task. The dataset includes 3680 training and 3669 validation images [32].
4.1.2. Network Architectures
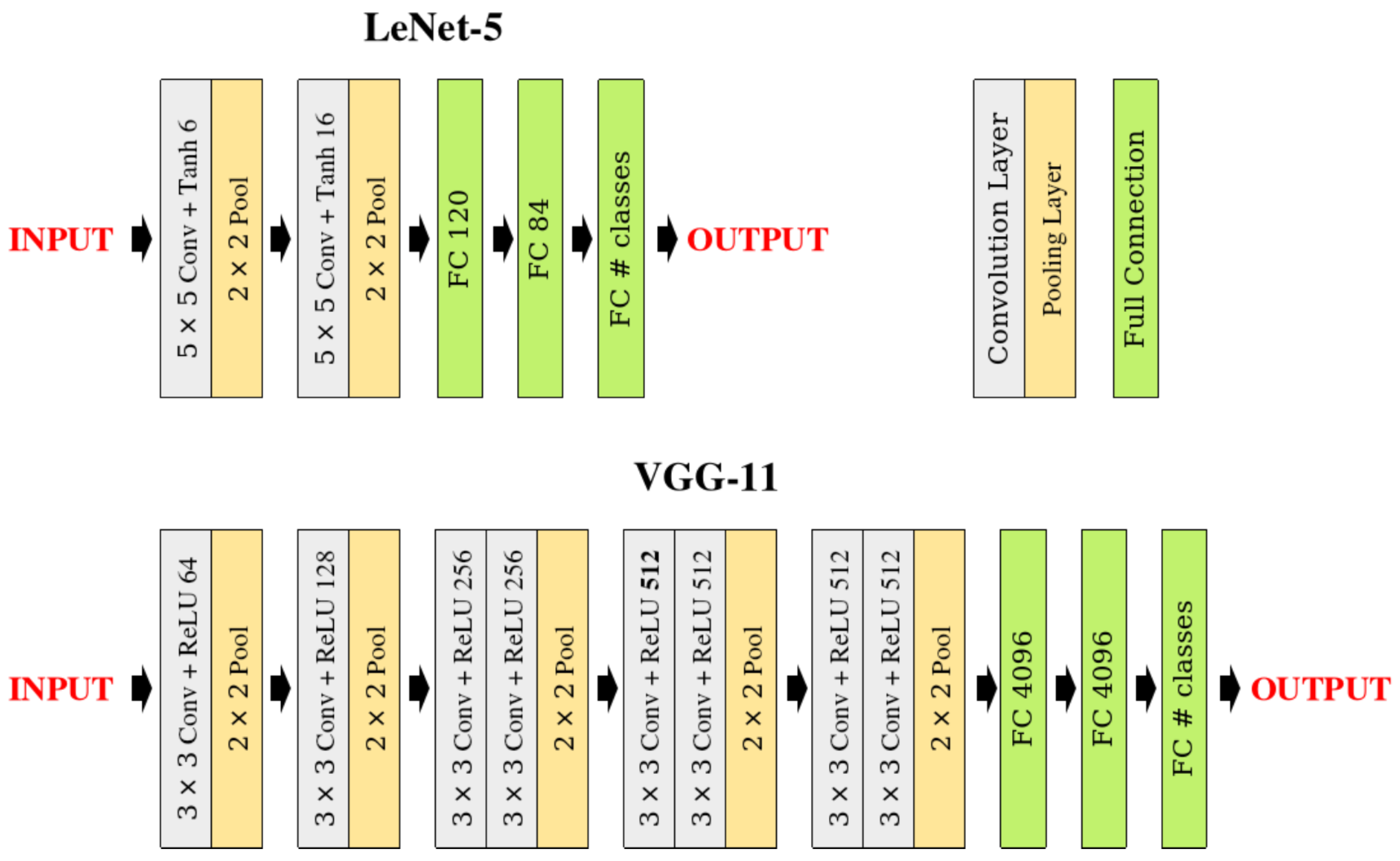
- LeNet5: A relatively shallow architecture originally designed for digit recognition, consisting of two convolutional layers followed by three fully connected layers, with two pooling operations [9]. This network serves as our lightweight model for experiments with smaller datasets.
- VGG11: A deeper architecture featuring eight convolutional layers organized in blocks, with five pooling operations and three fully connected layers [33]. This network provides a more complex testbed for evaluating pooling performance in deeper architectures.
- LeNet5 was applied to MNIST, FashionMNIST, CIFAR10, and CIFAR100.
- VGG11 was applied to CIFAR10, CIFAR100, STL10, and OxfordIIITPet.
4.1.3. Control Experiments and Ablation Study
- Baseline Methods
- MaxPool: Standard max pooling, representing the most common deterministic approach.
- AvgPool: Standard average pooling, providing an alternative deterministic baseline.
- S3Pool: The stochastic spatial sampling pooling method that serves as our primary comparison point.
- CIFAR10/100: ---- = 16-8-4-2-2.
- STL10: ---- = 32-16-8-4-2.
- OxfordIIITPet: ---- = 56-28-14-7-7.
- Ablation Study on Ordering
- LDS3Pool-C uses simple C-ordering (row-major traversal) to linearize the 2D feature map.
- LDS3Pool-PCA uses principal component analysis to project pixel coordinates onto the first principal component direction for ordering.
- LDS3Pool-Hilbert, our proposed method, uses Hilbert curve ordering for linearization.
- Ablation Study on Oversampling
4.1.4. Training Setup
- Loss Function: Cross-entropy loss.
- Optimizer: Adam with initial learning rate of 0.001 [36].
- Learning Rate Schedule: StepLR scheduler with step size 10 and decay factor () of 0.5.
- Batch Size: 32 for all experiments.
- Training Duration: 150 epochs for OxfordIIITPet, 100 epochs for all other datasets.
- Evaluation Metric: Maximum validation accuracy achieved during training and generalization gap between the training accuracy and the validation accuracy.
4.2. Main Results on Classic Architectures
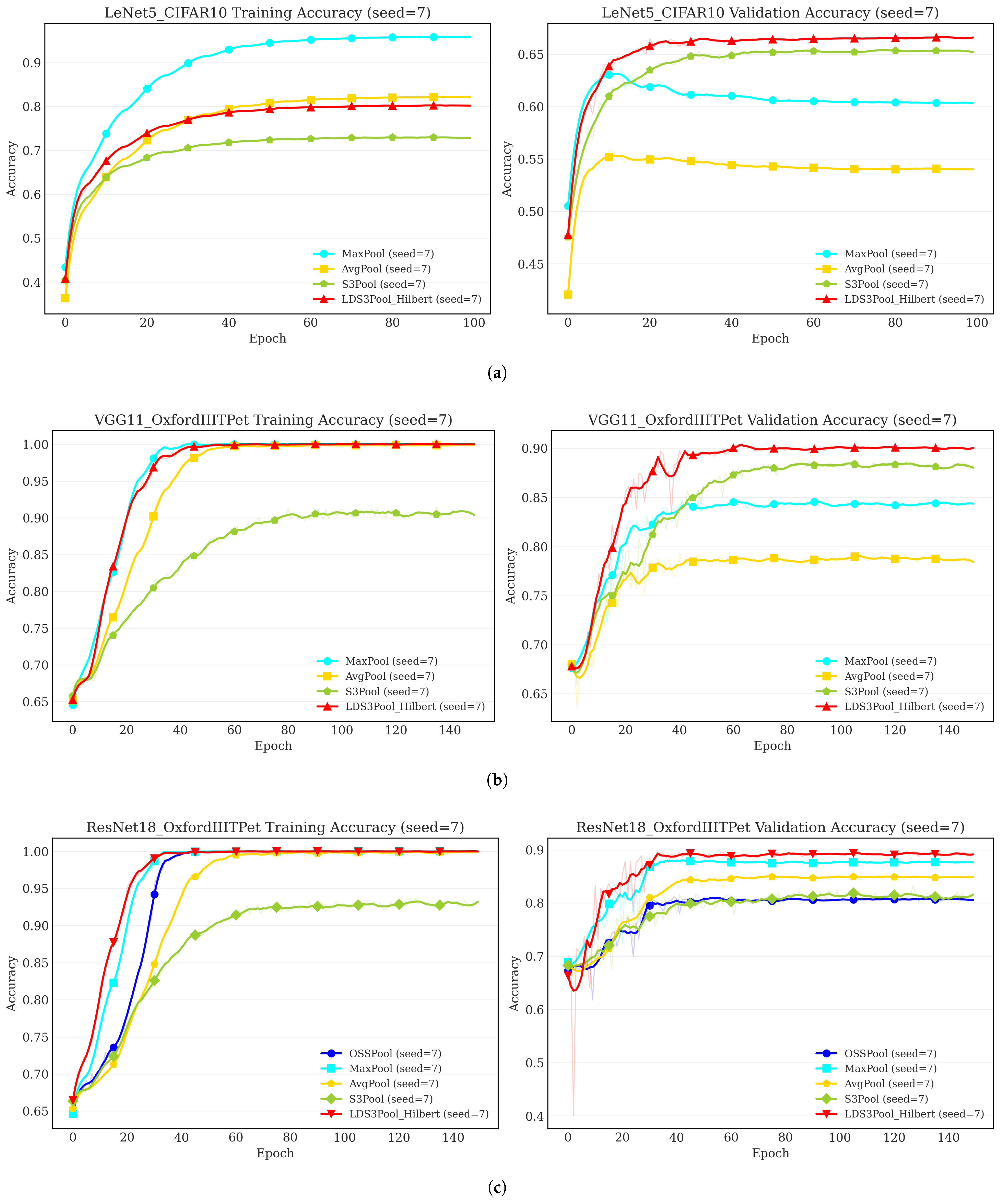
- Across all models and datasets, LDS3Pool-Hilbert consistently achieved the highest or near-highest validation accuracy, outperforming S3Pool, MaxPool, and AvgPool in overall ranking. This confirms the effectiveness of introducing principled randomness for performance enhancement.
- LDS3Pool-Hilbert demonstrated significant accuracy improvements over all baselines. Notably, it improved upon the classic MaxPool by up to 5 percentage points (on VGG11/OxfordIIITPet) and upon the stochastic S3Pool by 1–3 percentage points in many cases. Given that only the pooling layer was modified, these gains are considerable.
- The average coefficient of variation (CV) for LDS3Pool-Hilbert and S3Pool falls between that of MaxPool and AvgPool. This indicates that introducing randomness via these methods does not negatively impact the stability of the training results.
- LDS3Pool-Hilbert generally exhibits a slightly lower average CV than S3Pool, with significantly lower variability on several key configurations (e.g., VGG11/STL10). This suggests that its quasi-random approach offers more controllable randomness, leading to a more stable and representative downsampling of the feature map.
- Per-Configuration Analysis: LDS3Pool-Hilbert demonstrates a statistically significant advantage over the baseline methods in most cases, often with . It is noted that in two specific cases (LeNet5/CIFAR100 and VGG11/CIFAR10), the performance difference compared to S3Pool was not significant, which indicates that the two methods are statistically indistinguishable in these specific settings. This suggests that for certain less complex dataset–architecture combinations, the simpler randomization of S3Pool may already provide a sufficient regularization effect.
- Overall Analysis: When aggregating the results across all eight network–dataset combinations, paired t-tests confirm the overall superiority of LDS3Pool-Hilbert. It achieves a highly significant improvement over traditional MaxPool () and a significant improvement over both AvgPool and S3Pool ().
4.3. Ablation Studies
4.3.1. Ablation Study on Ordering
- Superior Performance on Small Networks: On the small model LeNet5 (and the corresponding small-sized image datasets), Hilbert consistently achieved the highest average validation set accuracy (except on LeNet5/MNIST, where the three variants barely differ). This is particularly evident for CIFAR10, where Hilbert achieved 67.545% accuracy compared to 66.519% for PCA and 66.575% for C-ordering variants, representing a difference of approximately 1 percentage point. Similarly, on CIFAR100, Hilbert showed notable improvements. The paired t-test results confirm that the accuracy improvements of Hilbert relative to C-order are statistically significant on FashionMNIST (p < 0.01) and CIFAR10 (p < 0.01), while improvements over PCA are significant on FashionMNIST (p < 0.05) and CIFAR100 (p < 0.05).
- Consistent Advantages on Larger Networks: On the larger VGG11 model, the Hilbert variant still outperforms the other two across all datasets. Especially on OxfordIIITPet with the largest image size, Hilbert achieves accuracy of 91.012%, outperforming PCA (90.131%) by about 1 percentage point. While the paired t-test results indicate that these differences on the VGG11 model are not statistically significant, they highlight that the Hilbert ordering provides the most substantial benefits when working with smaller feature maps where spatial structure preservation is particularly critical.
- Overall Advantages: Paired tests on the results of eight network–dataset combinations also verify that Hilbert ordering has extraordinary improvement over C-sequence (); it also has a significant improvement over PCA ordering ().
- Enhanced Stability Across Configurations: On multiple network–dataset pairs (LeNet5/CIFAR10, VGG11/CIFAR10, VGG11/STL10, and VGG/OxfordIIITPet), the Hilbert variant achieved the lowest CV. In addition, the Hilbert variant achieved the lowest average coefficient of variation, while the average coefficient of variation of the PCA variant and the C-Sequence variant were almost the same.
4.3.2. Ablation Study on Oversampling
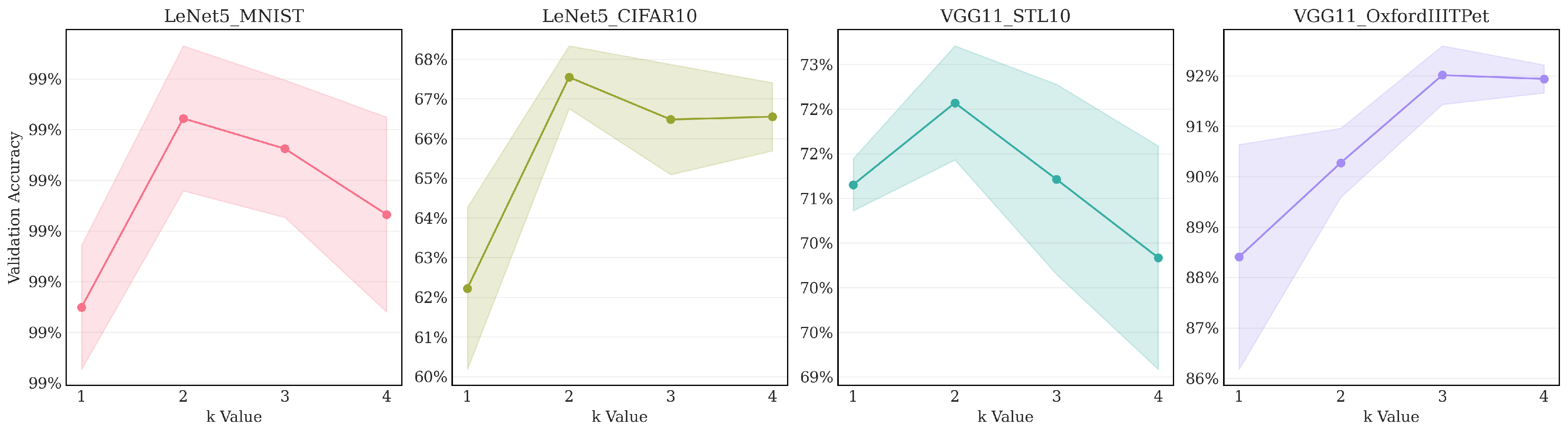
- Benefit of moderate oversampling: Across all four tested configurations, increasing the sampling factor from (minimal sampling) to resulted in a significant improvement in validation accuracy. This demonstrates that providing the reconstruction step with more candidate pixels is clearly beneficial, likely allowing the final MaxPool operation to select more representative high activations from each region.
- Parabolic trend: The optimal performance was achieved at for three out of the four pairs: LeNet5/MNIST, LeNet5/CIFAR10, and VGG11/STL10, while for VGG11/OxfordIIITPet, the peak accuracy occurred at . Performance generally decreases or plateaus after reaching the optimal k. This indicates diminishing returns from further increasing the sampling density. At (representing full sampling when ), the process potentially loses the regularization benefits gained from the quasi-random selection process at lower k values.
- Core method effectiveness: Even with minimal sampling (), the validation accuracy achieved by LDS3Pool is higher than or close to the best results obtained by the baseline methods reported in Table 3 for the corresponding network/dataset pairs. This underscores the inherent effectiveness of the Hilbert-ordered and LDS-guided spatial sampling strategy, independent of the oversampling factor.
4.4. Generalization Study on Modern Architectures
- Potential for Enhancement over the ResNet Baseline. LDS3Pool-Hilbert shows a statistically significant performance gain over the OSSPool baseline across all datasets. The OSSPool baseline, which mirrors the highly efficient, integrated downsampling of the original ResNet, serves as a strong reference. The performance uplift achieved by replacing it suggests that when the downsampling step is explicitly decoupled from the convolution, there is an opportunity to enhance performance by employing more sophisticated sampling strategies. This is further supported by the observation that even standard MaxPool and AvgPool, which aggregate information from a full local window, outperform the simple pixel selection of OSSPool.
- Robustness and Consistency. While some baseline methods show strong performance on specific datasets (e.g., S3Pool on CIFAR10, MaxPool on OxfordIIITPet), none demonstrate universal effectiveness. In contrast, LDS3Pool-Hilbert emerges as the most consistent top-performing strategy across all four diverse datasets. This highlights its robustness and adaptability as a general-purpose downsampling module.
- A More Balanced Approach to Regularization. The comparison with S3Pool reveals a key advantage in how randomness is applied. S3Pool’s performance, while strong in some cases, shows notable instability, with a significant performance drop on CIFAR100 and OxfordIIITPet. LDS3Pool-Hilbert, however, maintains consistent and significant gains. This indicates that its structured, quasi-random approach strikes a more effective balance, achieving the benefits of stochastic regularization without sacrificing the performance stability that is crucial for reliable model training.
4.5. Analysis of Overfitting Mitigation
4.6. Computational Efficiency
- Training Overhead: During the training phase, the stochastic methods, S3Pool and LDS3Pool, introduce additional computational time compared to the deterministic baselines. This is expected, as they require extra operations for random index generation and sparse feature map construction. Across all architectures, including ResNet18, S3Pool consistently brings the largest overhead (approximately 50–60% compared to MaxPool), while LDS3Pool’s overhead is more moderate (approximately 20–35%).
- Inference Overhead: During the inference phase, S3Pool reverts to using MaxPool, thus showing no additional latency. LDS3Pool, however, maintains its sampling mechanism, resulting in a noticeable overhead. This overhead is more pronounced for deeper networks with larger feature maps, such as VGG11 and ResNet18.
5. Conclusions and Limitations
5.1. Conclusions
5.2. Limitations and Future Works
- Performance Optimization: The current implementation introduces a moderate computational overhead. Future work could explore optimized GPU kernels to accelerate the sampling operations for efficiency-critical applications.
- Broader Applications: The method’s effectiveness in other vision tasks, such as object detection and semantic segmentation where fine-grained spatial information is crucial, remains a promising area for exploration.
- Robustness Evaluation: A comprehensive evaluation of LDS3Pool’s robustness under challenging conditions, such as domain shifts or adversarial attacks, is an important direction for future investigation.
- Adaptive Sampling: The oversampling factor is currently fixed. An adaptive approach that adjusts this factor based on feature complexity or network depth could further enhance performance.
- Synergistic Effects: A systematic investigation of combining LDS3Pool with other regularization techniques, like Dropout, could reveal beneficial synergistic effects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saeedan, F.; Weber, N.; Goesele, M.; Roth, S. Detail-Preserving Pooling in Deep Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Graham, B. Fractional Max-Pooling. arXiv 2015, arXiv:1412.6071. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. In Proceedings of the ICLR 2013, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Zhai, S.; Cheng, Y.; Luong, M.T.; Le, Q.V. S3Pool: Pooling with stochastic spatial sampling. In Proceedings of the Computer Vision—ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10 and 15–16 October 2016; Proceedings, Part III 14. Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 415–424. [Google Scholar]
- Niederreiter, H. Low-discrepancy and low-dispersion sequences. J. Number Theory 1988, 30, 51–70. [Google Scholar] [CrossRef]
- Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods; SIAM: Bangkok, Thailand, 1992. [Google Scholar]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Rashmi, P.; Pratap Singh, M. Performance Analysis of Convolutional Neural Networks with Different Optimizers and Hybrid Pooling Methods for Sound Classification. Int. J. Adv. Soft Comput. Its Appl. 2025, 17, 147–173. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, S.; Li, S.; Cheng, B.; Chen, J. Research on Person Re-Identification through Local and Global Attention Mechanisms and Combination Poolings. Sensors 2024, 24, 5638. [Google Scholar] [CrossRef]
- Li, T.; Chan, K.L.; Tjahjadi, T. A learnable motion preserving pooling for action recognition. Image Vis. Comput. 2024, 151, 105278. [Google Scholar] [CrossRef]
- Gaud, N.; Jha, K.K.; Adhikari, J.; S, A.N.P.; Das, J.; Deshpande, S.S.; Barara, N.; Ramya, V.V.; Saha, S.; Baran, M.T.; et al. NIRMAL Pooling: An Adaptive Max Pooling Approach with Non-linear Activation for Enhanced Image Classification. arXiv 2025, arXiv:2508.10940. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Li, P.; Tao, H.; Zhou, H.; Zhou, P.; Deng, Y. Enhanced Multiview attention network with random interpolation resize for few-shot surface defect detection. Multimed. Syst. 2025, 31, 36. [Google Scholar] [CrossRef]
- Hua, L.K.; Wang, Y. Applications of Number Theory to Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar] [CrossRef]
- Lemieux, C. Monte Carlo and Quasi-Monte Carlo Sampling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Guo, L.; Liu, J.; Lu, R. Subsampling bias and the best-discrepancy systematic cross validation. Sci. China Math. 2021, 64, 197–210. [Google Scholar] [CrossRef]
- Zhang, M.; Li, M.; Guo, L.; Liu, J. A low-cost AI-empowered stethoscope and a lightweight model for detecting cardiac and respiratory diseases from lung and heart auscultation sounds. Sensors 2023, 23, 2591. [Google Scholar] [CrossRef] [PubMed]
- Xu, M. BDSR: A Best Discrepancy Sequence-Based Point Cloud Resampling Framework for Geometric Digital Twinning. Master’s Thesis, Shandong University, Jinan, China, 2021. [Google Scholar]
- Hilbert, D. Ueber die stetige Abbildung einer Linie auf ein Flächenstück. Math. Ann. 1891, 38, 459–460. [Google Scholar] [CrossRef]
- Platzman, L.K.; Bartholdi, J.J., III. Spacefilling curves and the planar travelling salesman problem. J. ACM (JACM) 1989, 36, 719–737. [Google Scholar] [CrossRef]
- Moon, B.; Jagadish, H.; Faloutsos, C.; Saltz, J.H. Analysis of the clustering properties of the Hilbert space-filling curve. Trans. Knowl. Data Eng. 2001, 13, 124–141. [Google Scholar] [CrossRef]
- Kamata, S.i.; Niimi, M.; Kawaguchi, E. A gray image compression using a Hilbert scan. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; IEEE: Piscataway, NJ, USA, 1996; Volume 3, pp. 905–909. [Google Scholar]
- Gotsman, C.; Lindenbaum, M. On the metric properties of discrete space-filling curves. IEEE Trans. Image Process. 1996, 5, 794–797. [Google Scholar] [CrossRef]
- Alber, J.; Niedermeier, R. On Multidimensional Curves with Hilbert Property. Theory Comput. Syst. 2000, 33, 295–312. [Google Scholar] [CrossRef]
- Zhang, J.; Kamata, S.i.; Ueshige, Y. A pseudo-hilbert scan algorithm for arbitrarily-sized rectangle region. In Proceedings of the International Workshop on Intelligent Computing in Pattern Analysis and Synthesis, Xi’an, China, 26–27 August 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 290–299. [Google Scholar]
- Červený, J. Generalized Hilbert Space-Filling Curve for Rectangular Domains of Arbitrary Sizes. 2019. Available online: https://github.com/jakubcerveny/gilbert (accessed on 27 April 2025).
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features From Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Coates, A.; Ng, A.Y.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; JMLR Workshop and Conference Proceedings. pp. 215–223. [Google Scholar]
- Parkhi, O.M.; Vedaldi, A.; Zisserman, A.; Jawahar, C. Cats and dogs. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3498–3505. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. Article 721. pp. 8024–8035. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]


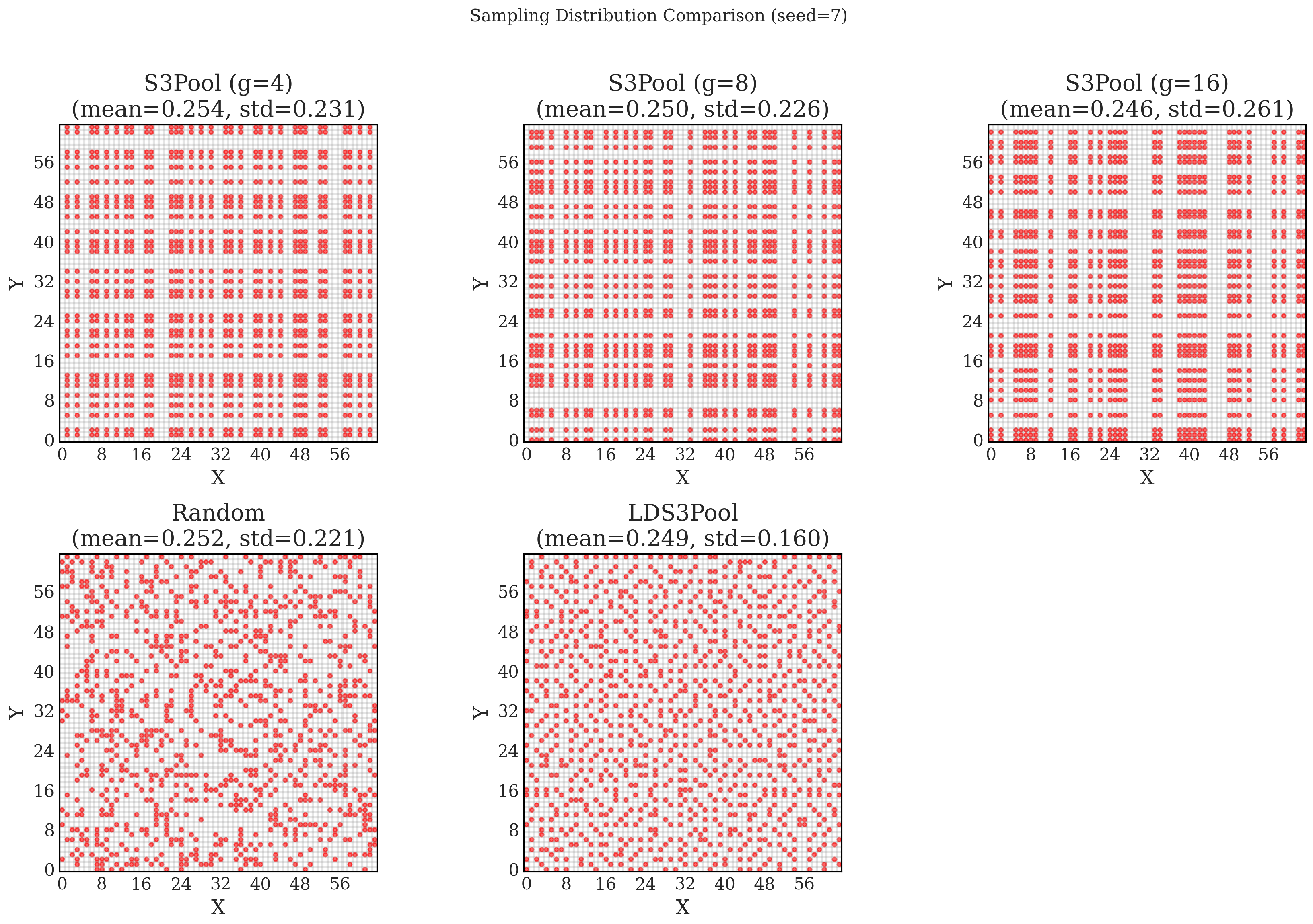



| Method | Seed = 7 | Seed = 42 | Seed = 1309 | Average | |||
|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Std | |
| S3Pool (g = 4) | 0.254 | 0.231 | 0.258 | 0.246 | 0.254 | 0.242 | 0.240 |
| S3Pool (g = 8) | 0.250 | 0.226 | 0.246 | 0.245 | 0.254 | 0.258 | 0.243 |
| S3Pool (g = 16) | 0.246 | 0.261 | 0.254 | 0.254 | 0.246 | 0.256 | 0.257 |
| Random | 0.252 | 0.221 | 0.250 | 0.216 | 0.251 | 0.216 | 0.218 |
| LDS3Pool | 0.249 | 0.160 | 0.249 | 0.161 | 0.250 | 0.174 | 0.165 |
| Dataset | Image Size | Channels | Classes | Training Images | Validation Images |
|---|---|---|---|---|---|
| MNIST | 28 × 28 | 1 | 10 | 60,000 | 10,000 |
| FashionMNIST | 28 × 28 | 1 | 10 | 60,000 | 10,000 |
| CIFAR10 | 32 × 32 | 3 | 10 | 50,000 | 10,000 |
| CIFAR100 | 32 × 32 | 3 | 100 | 50,000 | 10,000 |
| STL10 | 96 × 96 | 3 | 10 | 5000 | 8000 |
| OxfordIIITPet | 224 × 224 | 3 | 2 | 3680 | 3669 |
| Exp ID | Network | Dataset | Pool 1 Input Size | Pool 2 Input Size | Pool 3 Input Size | Pool 4 Input Size | Pool 5 Input Size |
|---|---|---|---|---|---|---|---|
| 1 | LeNet5 | MNIST | 28 × 28 | 10 × 10 | - | - | - |
| 2 | LeNet5 | FashionMNIST | 28 × 28 | 10 × 10 | - | - | - |
| 3 | LeNet5 | CIFAR10 | 28 × 28 | 10 × 10 | - | - | - |
| 4 | LeNet5 | CIFAR100 | 28 × 28 | 10 × 10 | - | - | - |
| 5 | VGG11 | CIFAR10 | 32 × 32 | 16 × 16 | 8 × 8 | 4 × 4 | 2 × 2 |
| 6 | VGG11 | CIFAR100 | 32 × 32 | 16 × 16 | 8 × 8 | 4 × 4 | 2 × 2 |
| 7 | VGG11 | STL10 | 96 × 96 | 48 × 48 | 24 × 24 | 12 × 12 | 6 × 6 |
| 8 | VGG11 | OxfordIIITPet | 224 × 224 | 112 × 112 | 56 × 56 | 28 × 28 | 14 × 14 |
| Exp ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Network | LeNet5 | LeNet5 | LeNet5 | LeNet5 | VGG11 | VGG11 | VGG11 | VGG11 |
| Dataset | MNIST | F-MNIST | CIFAR10 | CIFAR100 | CIFAR10 | CIFAR100 | STL10 | Oxford |
| MaxPool | 99.153% | 90.766% | 63.627% | 31.153% | 85.086% | 48.847% | 68.483% | 86.344% |
| AvgPool | 99.032% | 89.913% | 56.029% | 25.770% | 85.373% | 48.885% | 67.202% | 78.792% |
| S3Pool | 98.527% | 89.672% | 65.964% | 32.947% | 86.908% | 49.279% | 70.360% | 88.538% |
| LDS3Pool-Hilbert | 99.359% | 91.552% | 67.545% | 32.817% | 86.721% | 51.902% | 71.600% | 91.012% |
| Exp ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Average |
|---|---|---|---|---|---|---|---|---|---|
| Network | LeNet5 | LeNet5 | LeNet5 | LeNet5 | VGG11 | VGG11 | VGG11 | VGG11 | |
| Dataset | MNIST | F-MNIST | CIFAR10 | CIFAR100 | CIFAR10 | CIFAR100 | STL10 | Oxford | |
| MaxPool | 0.000730 | 0.002160 | 0.005908 | 0.014380 | 0.003140 | 0.013147 | 0.017075 | 0.026641 | 0.010398 |
| AvgPool | 0.000574 | 0.001226 | 0.006941 | 0.008147 | 0.003883 | 0.009100 | 0.015685 | 0.013862 | 0.007427 |
| S3Pool | 0.001572 | 0.002362 | 0.009743 | 0.014964 | 0.005009 | 0.020434 | 0.012701 | 0.011813 | 0.009825 |
| LDS3Pool-Hilbert | 0.000477 | 0.002776 | 0.012811 | 0.018941 | 0.002183 | 0.011534 | 0.004819 | 0.012841 | 0.008298 |
| Exp ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Network | LeNet5 | LeNet5 | LeNet5 | LeNet5 | VGG11 | VGG11 | VGG11 | VGG11 |
| Dataset | MNIST | F-MNIST | CIFAR10 | CIFAR100 | CIFAR10 | CIFAR100 | STL10 | Oxford |
| MaxPool | 10.362 ** | 7.298 ** | 13.883 ** | 4.282 ** | 9.856 ** | 8.986 ** | 7.504 ** | 5.905 ** |
| AvgPool | 8.359 ** | 14.494 ** | 29.670 ** | 31.883 ** | 8.441 ** | 10.935 ** | 8.587 ** | 38.448 ** |
| S3Pool | 15.965 ** | 21.926 ** | 6.318 ** | 0.359 | 1.017 | 4.875 ** | 3.990 * | 3.085 * |
| Method | t_Value | p_Value | Significance |
|---|---|---|---|
| MaxPool | 4.33 | 0.003 | ** |
| AvgPool | 3.179 | 0.016 | * |
| S3Pool | 3.407 | 0.011 | * |
| Exp ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Network | LeNet5 | LeNet5 | LeNet5 | LeNet5 | VGG11 | VGG11 | VGG11 | VGG11 |
| Dataset | MNIST | F-MNIST | CIFAR10 | CIFAR100 | CIFAR10 | CIFAR100 | STL10 | Oxford |
| LDS3Pool-PCA | 99.319% | 91.189% | 66.519% | 32.050% | 86.620% | 51.795% | 71.233% | 90.131% |
| LDS3Pool-C | 99.374% | 91.296% | 66.575% | 32.495% | 86.530% | 51.446% | 70.975% | 90.495% |
| LDS3Pool-Hilbert | 99.359% | 91.552% | 67.545% | 32.817% | 86.721% | 51.902% | 71.600% | 91.012% |
| Exp ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Network | LeNet5 | LeNet5 | LeNet5 | LeNet5 | VGG11 | VGG11 | VGG11 | VGG11 |
| Dataset | MNIST | F-MNIST | CIFAR10 | CIFAR100 | CIFAR10 | CIFAR100 | STL10 | Oxford |
| LDS3Pool-PCA | 1.244 | 3.397 * | 2.467 | 3.014 * | 0.893 | 0.222 | 1.191 | 0.761 |
| LDS3Pool-C | 0.639 | 4.180 ** | 6.996 ** | 0.819 | 0.985 | 1.893 | 1.204 | 0.52 |
| Method | t_Value | p_Value | Significance |
|---|---|---|---|
| LDS3Pool-PCA | 3.349 | 0.012 | * |
| LDS3Pool-C | 3.907 | 0.006 | ** |
| Exp ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Average |
|---|---|---|---|---|---|---|---|---|---|
| Network | LeNet5 | LeNet5 | LeNet5 | LeNet5 | VGG11 | VGG11 | VGG11 | VGG11 | |
| Dataset | MNIST | F-MNIST | CIFAR10 | CIFAR100 | CIFAR10 | CIFAR100 | STL10 | Oxford | |
| LDS3Pool-PCA | 0.000712 | 0.002385 | 0.017338 | 0.026546 | 0.002904 | 0.015526 | 0.011588 | 0.034465 | 0.013933 |
| LDS3Pool-C | 0.000470 | 0.003177 | 0.009534 | 0.031431 | 0.003712 | 0.006063 | 0.020003 | 0.018308 | 0.011587 |
| LDS3Pool-Hilbert | 0.000477 | 0.002776 | 0.012811 | 0.018941 | 0.002183 | 0.011534 | 0.004819 | 0.012841 | 0.008298 |
| k-Value | LeNet5_MNIST | LeNet5_CIFAR10 | VGG11_STL10 | VGG11_OxfordIIITPet |
|---|---|---|---|---|
| 1 | 99.175% | 62.222% | 71.152% | 88.407% |
| 2 | 99.361% | 67.545% | 72.069% | 90.274% |
| 3 | 99.331% | 66.479% | 71.213% | 92.013% |
| 4 | 99.266% | 66.549% | 70.335% | 91.938% |
| Method | CIFAR10 | CIFAR100 | STL10 | OxfordIIITPet |
|---|---|---|---|---|
| OSSPool | 81.887% | 50.626% | 67.133% | 82.797% |
| MaxPool | 85.338% | 58.789% | 73.204% | 88.329% |
| AvgPool | 84.932% | 57.325% | 72.488% | 84.875% |
| S3Pool | 87.502% | 57.550% | 73.950% | 86.252% |
| LDS3Pool-Hilbert | 87.908% | 61.931% | 74.173% | 88.989% |
| Method | CIFAR10 | CIFAR100 | STL10 | OxfordIIITPet |
|---|---|---|---|---|
| OSSPool | 83.437 ** | 53.266 ** | 71.391 ** | 8.585 ** |
| MaxPool | 20.971 ** | 20.493 ** | 4.960 ** | 1.837 |
| AvgPool | 19.252 ** | 28.880 ** | 6.569 ** | 7.895 ** |
| S3Pool | 2.102 | 12.350 ** | 1.113 | 3.332 * |
| Model | Dataset | OSSPool | MaxPool | AvgPool | S3Pool | LDS3Pool-Hilbert |
|---|---|---|---|---|---|---|
| LeNet5 | MNIST | - | 0.910% | 1.035% | 1.128% | 0.674% |
| LeNet5 | FashionMNIST | - | 10.027% | 9.988% | 2.937% | 4.713% |
| LeNet5 | CIFAR10 | - | 35.859% | 28.712% | 7.201% | 12.805% |
| LeNet5 | CIFAR100 | - | 26.641% | 19.053% | 8.010% | 12.682% |
| VGG11 | CIFAR10 | - | 15.093% | 14.785% | −1.716% | 13.466% |
| VGG11 | CIFAR100 | - | 51.334% | 51.308% | −1.179% | 47.452% |
| VGG11 | STL10 | - | 31.725% | 33.224% | 5.877% | 28.571% |
| VGG11 | OxfordIIITPet | - | 14.032% | 21.842% | 2.752% | 9.332% |
| ResNet18 | CIFAR10 | 18.267% | 14.853% | 15.212% | 6.355% | 12.324% |
| ResNet18 | CIFAR100 | 49.635% | 41.434% | 42.827% | 36.958% | 38.274% |
| ResNet18 | STL10 | 33.204% | 27.096% | 27.760% | 18.516% | 26.459% |
| ResNet18 | OxfordIIITPet | 17.650% | 12.156% | 15.501% | 9.001% | 11.530% |
| Model | Dataset | OSSPool | MaxPool | AvgPool | S3Pool | LDS3Pool | Extra |
|---|---|---|---|---|---|---|---|
| LeNet5 | MNIST | - | 2.762 | 2.629 | 4.438 | 3.316 | 20.058% |
| LeNet5 | FashionMNIST | - | 2.695 | 2.632 | 4.414 | 3.273 | 21.447% |
| LeNet5 | CIFAR10 | - | 2.423 | 2.435 | 3.951 | 2.987 | 23.277% |
| LeNet5 | CIFAR100 | - | 2.421 | 2.400 | 3.933 | 2.944 | 21.603% |
| VGG11 | CIFAR10 | - | 9.172 | 9.087 | 13.517 | 11.197 | 22.078% |
| VGG11 | CIFAR100 | - | 9.276 | 9.150 | 13.586 | 11.326 | 22.100% |
| VGG11 | STL10 | - | 5.132 | 5.171 | 7.625 | 6.567 | 27.962% |
| VGG11 | OxfordIIITPet | - | 16.879 | 17.177 | 26.571 | 22.600 | 33.894% |
| ResNet18 | CIFAR10 | 12.378 | 13.623 | 13.488 | 19.253 | 16.534 | 21.368% |
| ResNet18 | CIFAR100 | 12.338 | 13.645 | 13.515 | 19.272 | 16.547 | 21.268% |
| ResNet18 | STL10 | 4.978 | 6.301 | 6.353 | 10.152 | 8.590 | 36.328% |
| ResNet18 | OxfordIIITPet | 17.315 | 22.172 | 22.431 | 35.895 | 30.069 | 35.617% |
| Average | 11.752 | 8.875 | 8.872 | 13.551 | 11.329 | 25.583% |
| Model | Dataset | OSSPool | MaxPool | AvgPool | S3Pool | LDS3Pool | Extra |
|---|---|---|---|---|---|---|---|
| LeNet5 | MNIST | - | 1.003 | 0.957 | 1.058 | 1.201 | 19.741% |
| LeNet5 | FashionMNIST | - | 1.003 | 1.038 | 1.049 | 1.224 | 22.034% |
| LeNet5 | CIFAR10 | - | 1.161 | 1.121 | 1.170 | 1.334 | 14.901% |
| LeNet5 | CIFAR100 | - | 1.114 | 1.103 | 1.164 | 1.367 | 22.711% |
| VGG11 | CIFAR10 | - | 1.738 | 1.743 | 1.800 | 2.301 | 32.394% |
| VGG11 | CIFAR100 | - | 1.764 | 1.765 | 1.727 | 2.345 | 32.937% |
| VGG11 | STL10 | - | 8.449 | 8.367 | 8.452 | 12.859 | 52.196% |
| VGG11 | OxfordIIITPet | - | 42.276 | 42.098 | 42.623 | 65.776 | 55.587% |
| ResNet18 | CIFAR10 | 2.247 | 2.456 | 2.466 | 2.471 | 3.238 | 31.840% |
| ResNet18 | CIFAR100 | 2.282 | 2.517 | 2.514 | 2.484 | 3.242 | 28.804% |
| ResNet18 | STL10 | 10.031 | 12.396 | 12.268 | 12.351 | 19.635 | 58.398% |
| ResNet18 | OxfordIIITPet | 47.688 | 59.365 | 58.647 | 59.592 | 93.504 | 57.507% |
| Average | 15.562 | 11.270 | 11.174 | 11.328 | 17.336 | 35.754% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Guo, L.; Li, M. LDS3Pool: Pooling with Quasi-Random Spatial Sampling via Low-Discrepancy Sequences and Hilbert Ordering. Mathematics 2025, 13, 3016. https://doi.org/10.3390/math13183016
Ma Y, Guo L, Li M. LDS3Pool: Pooling with Quasi-Random Spatial Sampling via Low-Discrepancy Sequences and Hilbert Ordering. Mathematics. 2025; 13(18):3016. https://doi.org/10.3390/math13183016
Chicago/Turabian StyleMa, Yuening, Liang Guo, and Min Li. 2025. "LDS3Pool: Pooling with Quasi-Random Spatial Sampling via Low-Discrepancy Sequences and Hilbert Ordering" Mathematics 13, no. 18: 3016. https://doi.org/10.3390/math13183016
APA StyleMa, Y., Guo, L., & Li, M. (2025). LDS3Pool: Pooling with Quasi-Random Spatial Sampling via Low-Discrepancy Sequences and Hilbert Ordering. Mathematics, 13(18), 3016. https://doi.org/10.3390/math13183016






