1. Introduction
In classical financial theory, the market is assumed to be arbitrage free and complete, and so standard Brownian motion is often used as noise to characterize the prices of financial derivatives. However, in real-world financial markets, prices often exhibit long-range dependence and non-stationarity, which are inconsistent with the characteristics of standard Brownian motion. Consequently, many authors have proposed using fractional Brownian motion (fBm) to construct market models (see, for examples, Mandelbrot and Van Ness [
1]), with its simple structure and properties in memory noise. Unfortunately, starting with Rogers [
2], there has been an ongoing dispute on the proper usage of fractional Brownian motion in option pricing theory. A troublesome problem arises because fBm is not a semimartingale and therefore, “no arbitrage pricing” cannot be used. Although this is a consensus, the consequences are not clear. The orthodox explanation is simple: fBm is not a suitable candidate for the price process. But, as shown by Cheridito [
3], assuming that market participants cannot react immediately, any theoretical arbitrage opportunities will disappear. On the other hand, in 2003, Hu and ksendal [
4] used the Wick–Itô-type integral to define a fractional market and showed the market was arbitrage free and complete. In that case, the prices of financial derivatives satisfied the following fractional Black–Scholes model:
with
, where
is a fractional Brownian motion with Hurst index
,
and
are two parameters, and the integral
denotes the fractional Itô integral (Skorohod integral). For further studies on fractional Brownian motion in Black–Scholes models, refer to works by Bender and Elliott [
5], Biagini [
6], Bjork-Hult [
7], Cheridito [
3], Elliott and Chan [
8], Greene-Fielitz [
9], Necula [
10], Lo [
11], Mishura [
12], Rogers [
2], Izaddine [
13], and additional references cited therein.
In this paper, we consider the application of the quasi-likelihood method in continuous stochastic systems. Our goal is to establish the quasi-likelihood estimations for parameters
and
in Equation (
1) and to establish their asymptotic behaviors. As is well known, there are many papers on parameter estimation of stochastic differential equations, but the use of the quasi-likelihood method to deal with parameter estimation problems of stochastic differential equations without independent increments has not been seen so far. Clearly, the solution of (
1) does not have independent increments unless
. We briefly describe the quasi-likelihood method as follows.
Let
be a stochastic process such that its distribution contains unknown parameters
with
. Assume that
are samples extracted from
X, and that
is the probability function (e.g., density function) of the increment
for
. Since the process
X generally does not have independent increments, the function
is generally not a likelihood function. However, we can still use the usual method to obtain an estimator, which is called a quasi-likelihood estimator.
Let
be fractional Brownian motion with Hurst index
defined on the probability space
. Consider the fractional Black–Scholes model as follows:
with
, where
, and the stochastic integral is the fractional Itô integral [
14]. By using the Itô formula, we get
with
, which is called the geometric fractional Brownian motion (gmfBm).
In this paper, for simplicity, throughout, we let
H be known. Denote
and
Now, let be known, and let the gmfBm be observed at some discrete time instants satisfying the following conditions:
- (C1)
and as .
- (C2)
There exists such that as .
We get a quasi-likelihood function of parameter
and
as follows
where
is the density of the random variable
. Then, the logarithmic quasi-likelihood function is given by
with
, where
. By using the quasi-likelihood function, we get that the estimators
and
of
and
satisfy the equations
When
, by solving the above equation system, we get the estimators of
and
as follows:
where
and
for every
. When
, we have
and the random variables
are independent identical distributions, the above logarithm quasi-likelihood function is a classical logarithm likelihood function, and we have
and the asymptotic behavior of the two estimators can be easily established, so in the discussion later in this paper, unless otherwise stated, it is assumed that
.
Our study focuses on the asymptotic properties of two estimators. Given the Gaussian properties of the sample, we expect these estimators to exhibit quadratic variation, facilitating the derivation and simplification of their asymptotic behavior using fractional Brownian motion. To fully characterize this behavior, we rely on key properties of fractional Brownian motion, which not only underpin the theoretical understanding of complex stochastic processes but also provide a foundation for applying quasi-likelihood methods in parameter estimation.
The structure of this paper is as follows. In
Section 2, we briefly describe the basic properties of fractional Brownian motion. In
Section 3 and
Section 4 we discuss the strong consistency and asymptotic normality of the estimator
and analyze the asymptotic behavior under the cases where the parameter
is known and unknown. To prove these two asymptotic behaviors, we rely on two key results related to fractional Brownian motion. Although these results have been proven for a finite observation interval, they also hold when the observation length
tends to infinity. In
Section 5, we consider the asymptotic behavior of the estimator
. In
Section 6, we provide numerical verification and empirical analysis of the estimators
and
. In
Section 7, we conclude that the proposed fractional Brownian motion quasi-likelihood method performs well theoretically and empirically, offering a practical framework for financial parameter estimation.
2. Preliminaries
In this section, we briefly recall some basic results on fractional Brownian motion. For more aspects on the material, we refer to Bender [
15], Biagini et al. [
6], Cheridito-Nualart [
16], Gradinaru et al. [
17], Hu [
4], Mishura [
12], Nourdin [
18], Nualart [
19], Tudor [
20], and references therein.
A zero mean Gaussian process
defined on a complete probability space
is called the fBm with Hurst index
provided that
and
for
. Let
be the completion of the linear space
generated by the indicator functions
with respect to the inner product
When
, we know that
, and when
, we have
for all
. The application
is an isometry from
to the Gaussian space generated by
, and it can be extended to
. Denote by
the set of smooth functionals of the form
where
(
f and all its derivatives are bounded) and
. The
derivative operator (the Malliavin derivative) of a functional
F of the above form is defined as
The derivative operator
is then a closable operator from
into
. We denote by
the closure of
with respect to the norm
The
divergence integral is the adjoint of derivative operator
. That is, we say that a random variable
u in
belongs to the domain of the divergence operator
, denoted by
, if
for every
. In this case,
is defined by the duality relationship
for any
. Generally, the divergence
is also called the Skorohod integral of a process
u and denoted as
and the indefinite Skorohod integral is defined as
. If the process
is adapted, the Skorohod integral is called the fractional Itô integral, and the Itô formula
holds for all
and
.
4. Asymptotic Normality of Estimator
In this section, we examine the asymptotic distribution of
. We keep the notations from
Section 3, and denote by
and
the convergence in distribution and probability, as
n tends to infinity, respectively. From the structure of estimator
, one can find its asymptotic distribution depends on the asymptotic distribution of
. By the definition of
, we can check that
for
, where
is given in Lemma 8 and
with
. From the proof later given, we find that the two terms
and
admit same asymptotic velocity under some suitable assumptions of
. However, when
and conditions (C1) and (C2) hold, we know that (see proof of Lemma 9 in the following)
almost surely, as
. But
converges in
for
, and
converges in distribution for
. This indicates that
and
do not have the same asymptotic velocity for all
, which means that such models have inflection points when
. The reason for this situation is that
tends to infinity. If we assume that
tends to infinity logarithmically, the scenario is different. The following lemma provides the asymptotic normality of
, and its proof is given at the end of this section.
Lemma 9. Let be defined in Lemma 2, and let conditions and hold.
- (1)
When , we havewhere denotes the normal random variable with mean a and variance , and - (2)
When , we obtain - (3)
When , we have where .
4.1. The Asymptotic Distribution of When Is Known
In this subsection, we obtain the asymptotic distribution of
, provided
is known. By (
8), Lemma 3, and the fact that
, for all
, we get
with
.
Lemma 10. Let the condition hold, , and denote - (1)
For , we have as .
- (2)
For , we have , as , provided that condition holds with .
- (3)
For , we have as n tends to infinity, provided that condition holds with .
Proof. Let
. By Lemma 7 we have
for all
. Clearly,
for
and
for
if
. It follows from (
15) that
as
n tends to infinity under the conditions of statements (1) and (2).
We now verify statement (3). Let
. It follows from Lemma 2 that
as
n tends to infinity, provided that
since
as
n tends to infinity. □
Theorem 3. Let μ be known and let conditions (C1) and (C2) hold
- (1)
Let and , then, as , we have - (2)
Let , then, as , we have
Proof. Let
. Then, we have
Moreover, we have
for
, and
for all
and
.
For statement (1), we have
for all
, and by (
23) and (
24), we also have
since
for
. Combining these with (
21), (
23), Lemma 9, Lemma 10, and Slutsky’s theorem, we obtain statement (1).
For statement (2), we have
for all
if
. It follows from (
23) and (
24) that
for all
since
. Combining these with (
21), (
23), Lemma 9, Lemma 10, and Slutsky’s theorem, we obtain statement (2) because
. □
Theorem 4. Let μ be known and . If conditions (C1) and (C2) hold with . We then haveas n tends to infinity, where is given in Lemma 9. Proof. By (
8), Lemma 3, and the fact
, for all
, we get
On the other hand, we have
when
. Therefore, the asymptotic normality follows from (
26), (
27), Lemma 9, and Slutsky’s theorem, and we get
when
and as
n tends to infinity. □
4.2. The Asymptotic Distribution of When Is Unknown
In this subsection, we consider the asymptotic distribution of estimator
when
is unknown. Based on (
10), Lemma 4, and the fact that
, we obtain the following result
with
, where
. As a corollary of Lemma 4, the following lemma provides an estimate for the remainder term
Lemma 11. Let conditions and hold.
- (1)
For , we have
- (2)
For , we have , provided .
Proof. By Lemma 7 and the proof of Lemma 4, we get
for all
. Clearly,
and
for all
. Moreover, when
, we have
Similarly,
for all
and
for all
. Noting that
and
for all
, we obtain that
converges almost surely to 0 for
and that it converges almost surely to 0 for
provided
. Thus, the lemma follows from Lemma 4 and (
30). □
Theorem 5. Let μ be unknown and let conditions (C1) and (C2) hold.
- (1)
For , if , we have - (2)
For , we have
Proof. Clearly, we have
for all
and
for
, and moreover
for all
. It follows that
for all
, and
for all
, and
for all
, since
for
and
for all
. Combining this with (
29), Lemma 9, Lemma 11, and Slutsky’s theorem, we obtain the theorem. □
Lemma 12. Let conditions and hold with . For , we have Proof. Similar to the proof of Lemma 11, we get
for all
. It follows from Lemma 7 and Lemma 2 that
as
n tends to infinity. □
Theorem 6. Let and μ be unknown. If conditions and hold with , we then haveas n tends to infinity, where is given in Lemma 9. Proof. Let
. By (
10), Lemma 4, and the fact that
, we get
Therefore, using Equations (
33) and (
34) and Lemma 9, we have
when
and as
n tends to infinity. □
4.3. Proofs of Lemmas in Section 4
In this subsection, we complete the proof of Lemma 9.
Proposition 1. Let the conditions in Lemma 1 hold.
- (1)
For , we havein distribution, where - (2)
For , we havein distribution. - (3)
For , we havein , where denotes a Rosenblatt random distribution with .
The lemma is an insignificant extension for some known results, and its proof is omitted (see, for examples, Theorem 5.4, Proposition 5.4, Theorem 5.5 in Tudor [
20]). In fact, for
, such convergence have been studied and can be found in Breuer and Major [
23], Dobrushin and Major [
24], Giraitis and Surgailis [
25], Nourdin [
26], Nourdin and Reveillac [
27] and Tudor [
20]. On the other hand, for more material on the Rosenblatt distribution and related process, refer to Tudor [
20].
Proof of Lemma 9. Let
be given. We have
We also have
for
and
for
. On the other hand, by Taylor’s expansion, we may prove
for
if
. It follows from Lemma 7 that
for
and
for
. Combining the above three convergences and the proof of Lemma 8, we obtain that
for
and
for
. Thus, by (
16) and Proposition 1, to end the proof, we check that
for all
under some suitable conditions for
. By the fact
with
and
, we get that
for all
, where
for
.
Now, in order to end the proof, we estimate the last three items in (
42) in the two cases
and
.
Cases I:
. Clearly, the sequence
converges. It follows that
and
as
n tends to infinity. Combining these with Lemma 8 and (
42), we obtain convergence (
41) for all
. Thus, by Proposition 1, (
16), (
39), and Slutsky’s theorem, we obtain the desired asymptotic behavior
for all
, and statement (1) follows.
Cases II:
. From
and Taylor’s expansion, we get that
as
n tends to infinity, which implies that
as
n tends to infinity. Similarly, we also have
and
as
n tends to infinity. On the other hand, we have
as
n tends to infinity, where
denotes the classical Beta function. It follows from Taylor’s expansion that
for all
, as
n tends to infinity. Combining these with Lemma 8 and (
42), we obtain convergence (
41) for all
if
. Thus, we obtain the desired asymptotic behavior
for all
by Proposition 1, (
16), and (
40), and statement (2) follows.
Now, we verify statement (3). Let
. By Lemma 7, we have
and moreover, from the proof of statement (2) in Lemma 9, we also have
where
. Noting that
admits a normal distribution for all
, we see that
from (
52). It follows from (
16), statement (3) in Proposition 1, and (
51) that
as
n tends to infinity. Moreover, by (
51) we obtain
Combining this with (
54), (
53), and Proposition 1, we get
as
n tends to infinity. Finally, by Proposition 1, (
53), (
55), and Slutsky’s theorem, we obtain
Thus, the three convergences in statements (2) and (3) follow. □
6. Numerical Simulation and Empirical Analysis
In this section, the effectiveness of the proposed estimator is validated through numerical simulations. The results demonstrate that the estimator exhibits strong applicability and reliable performance in practical scenarios. To further assess the precision of the two estimation methods, Monte Carlo simulations were conducted in MATLAB 2017b, where the simulated estimates were compared against the true values, and their mean values and standard deviations were calculated to provide a comprehensive evaluation of the estimator’s performance. In addition, real trading data from the Chinese financial market were retrieved via the Tushare Pro platform using Python 3.10. With the known value of H, the parameters and were estimated, and track plots were generated in MATLAB and compared with the logarithmic closing prices of the stock, thereby further validating the effectiveness of the pseudo-likelihood estimation.
6.1. Numerical Simulation
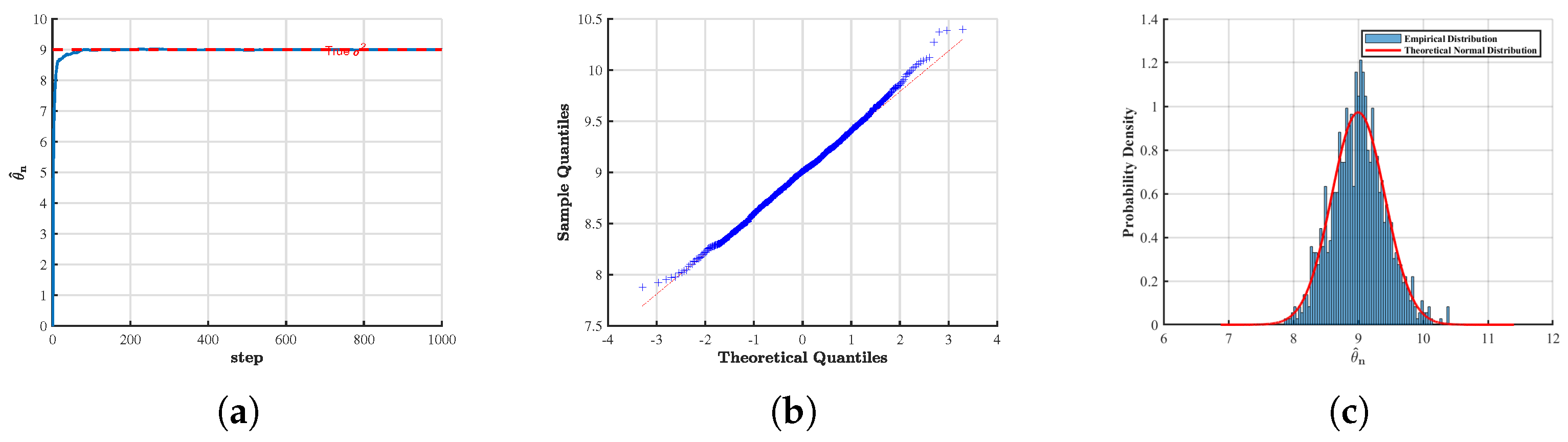
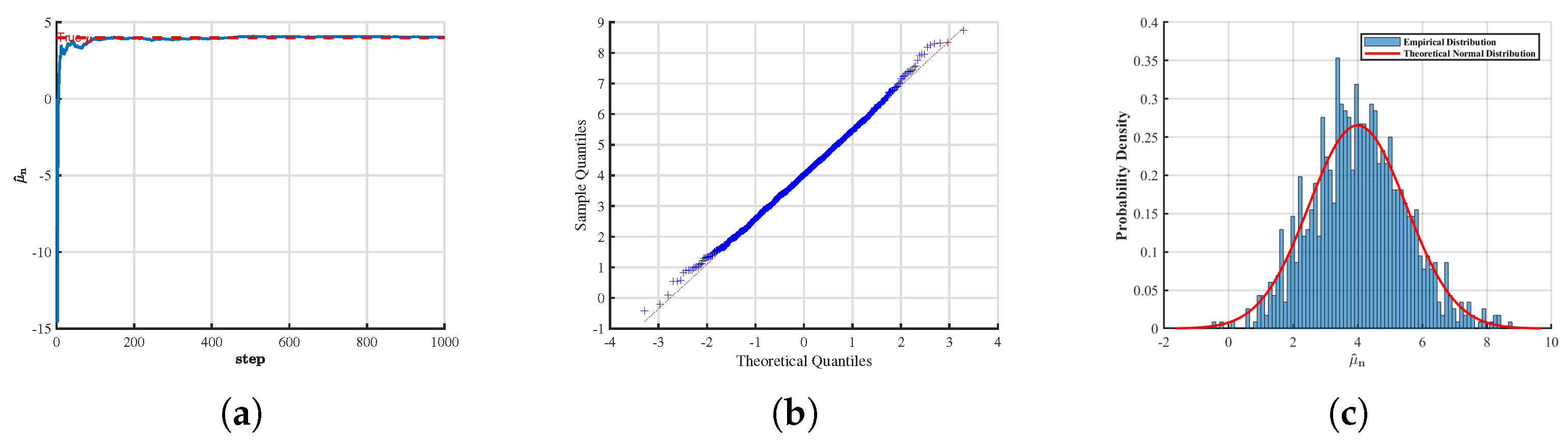
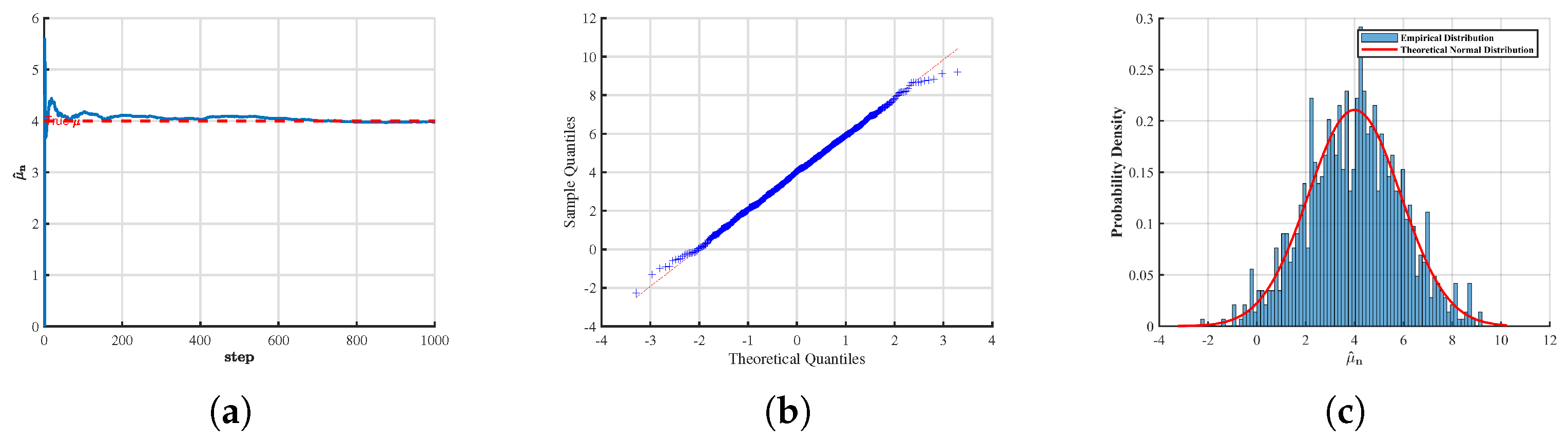
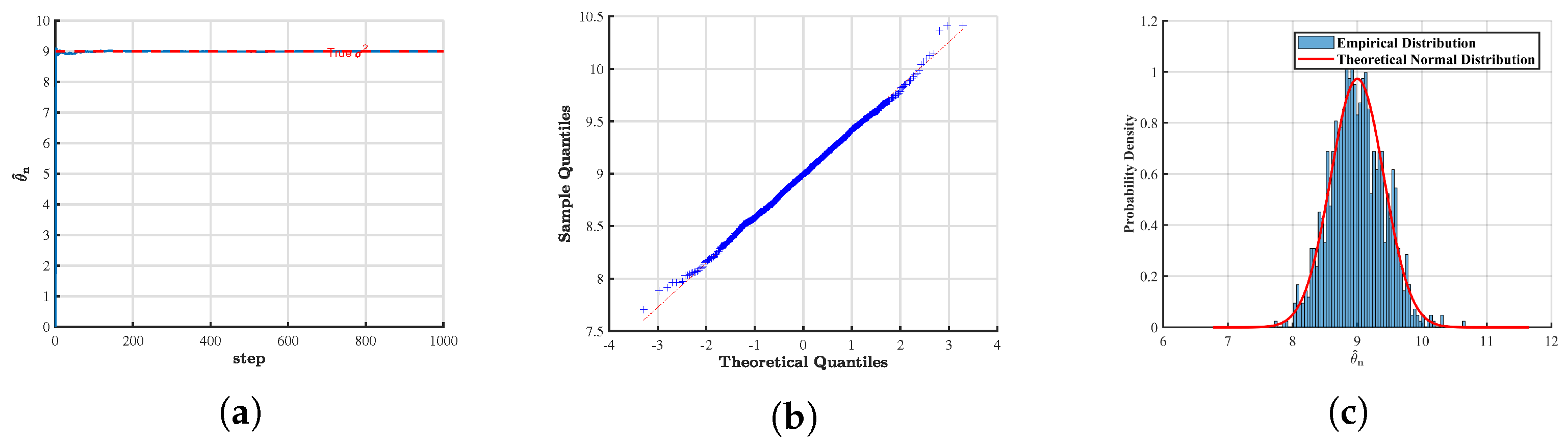
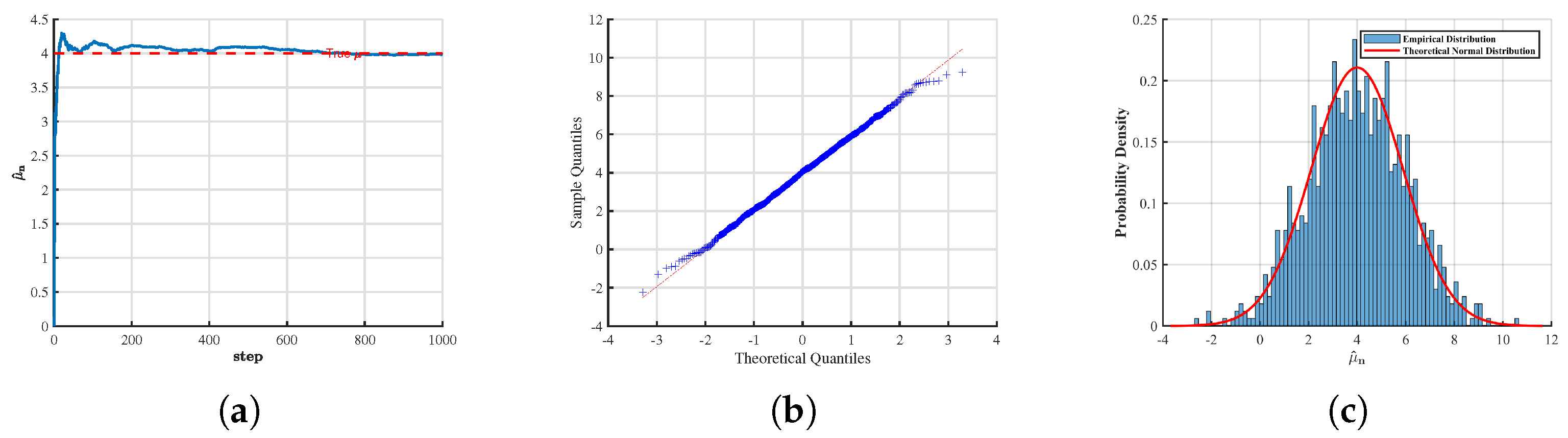
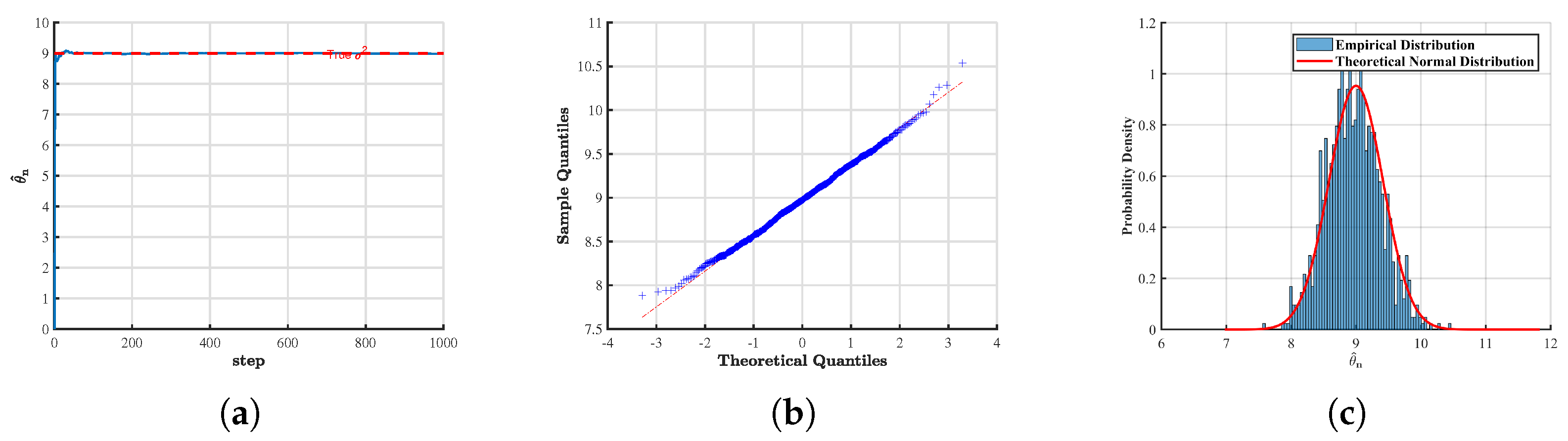
First, we emphasize that in all the figures presented below, the sample size was fixed at , and the time step was chosen as . The parameters were set to and . In the analysis of the asymptotic distribution, the number of replications, i.e., the simulated sample paths, was specified as . For the sake of notational consistency, we denote throughout the subsequent discussion. To assess the effectiveness and robustness of the proposed estimation method, we designed two primary experimental scenarios:
- 1.
Case with Partially Known Parameters
In the case where the parameter
is known, we estimated the parameter
and further examined its estimation path, quantile–quantile plot, and asymptotic distribution. The corresponding results for the estimator
are presented for
(
Figure 1) and
(
Figure 2).
In the case where the parameter
is known, we estimated the parameter
and examined its estimation path and asymptotic distribution. Similarly, figures present the estimation paths and asymptotic distribution of
when
(
Figure 3) and
(
Figure 4).
- 2.
Case with Completely Unknown Parameters
In this scenario, where both
and
are unknown, we estimated both parameters simultaneously and analyzed their estimation paths and asymptotic distributions. Figures present the estimation paths and asymptotic distribution of
and
when
(
Figure 5 and
Figure 6) and
(
Figure 7 and
Figure 8).
Case 1: The asymptotic behavior of the estimators of and when is known.
Case 2: The asymptotic behavior of the estimators of and when both parameters are unknown.
From the above figures, it can be observed that for different values of H, the numerical simulation results of the convergence and asymptotic properties of the estimators and are largely consistent with the theoretical predictions. The discrepancies are minor, indicating that the obtained estimates exhibit a high degree of accuracy.
In addition, to investigate the asymptotic behavior of the proposed estimators for different sample sizes, we considered three sample sizes: , 2000, and 3000. The comparison of theoretical variance with empirical variance, as well as the corresponding errors, was carried out. The specific experimental design is outlined as follows:
Table 1: Theoretical variance, empirical variance, and their errors for parameter
when
is known.
Table 2: Theoretical variance, empirical variance, and their errors for parameter
when
is known.
Table 3: Joint analysis of the variance estimates and errors for both parameters when
and
are unknown.
The discrepancies are minor, indicating that the obtained estimates exhibit a high degree of accuracy.
6.2. Empirical Analysis
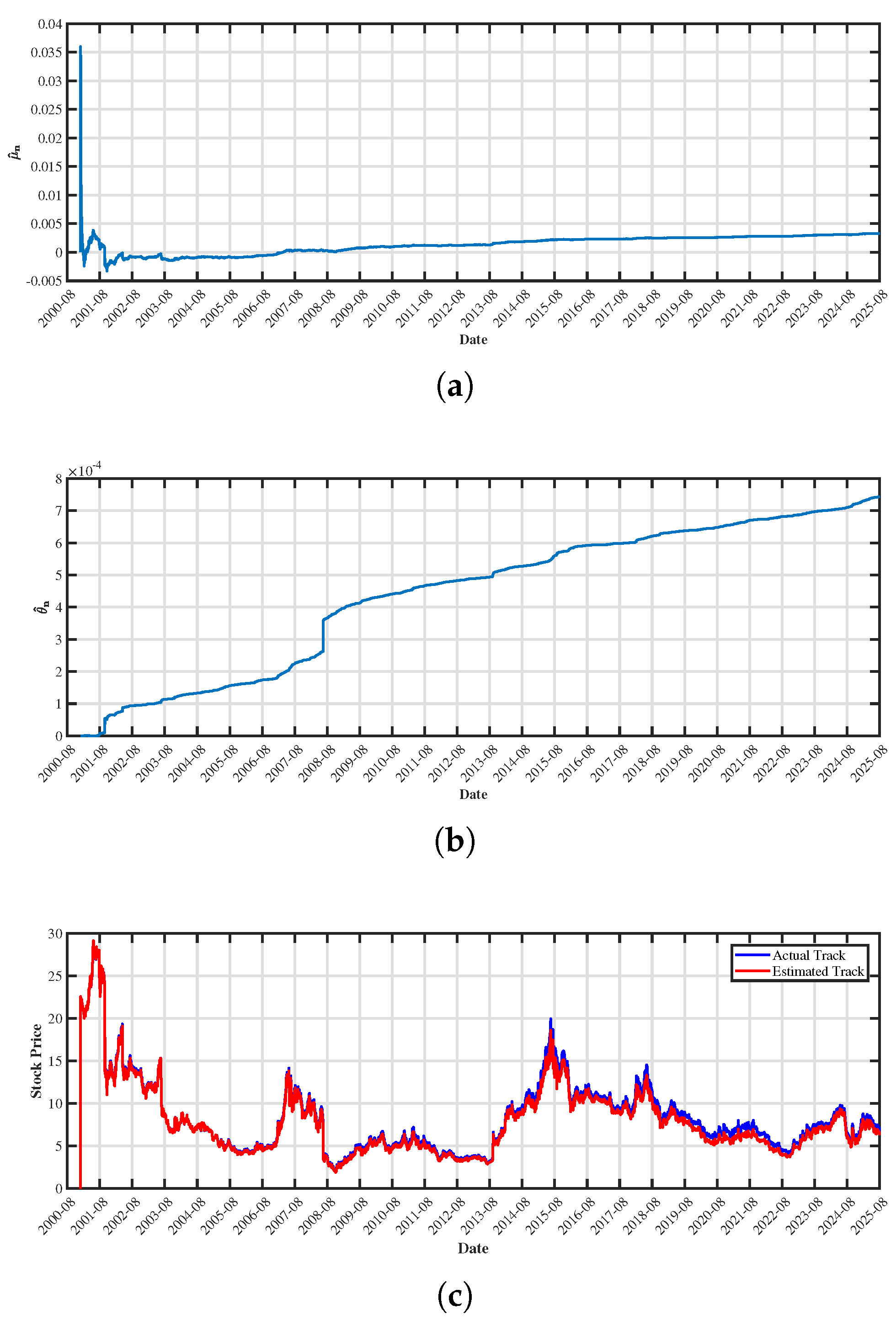
To further evaluate the performance of the proposed model and estimation method in a real-world market setting, we conducted an empirical analysis using Heilan Home Co., Ltd. Jiangyin, Jiangsu Province, China (stock code: 600398), a representative stock from the Chinese A-share market. Daily closing price data were retrieved via the Tushare Pro platform using Python, covering the period from 28 December 2000, to 26 August 2025. Data cleaning and preprocessing were carried out to ensure consistency. As supported by the theoretical results in
Section 3, the estimators were consistent as the sample size
; therefore, the full sample period was employed to guarantee robustness. The Hurst exponent of the stock return series was first estimated using the R/S method, yielding
, which suggested the presence of long-memory effects.
Based on this, the key model parameters
and
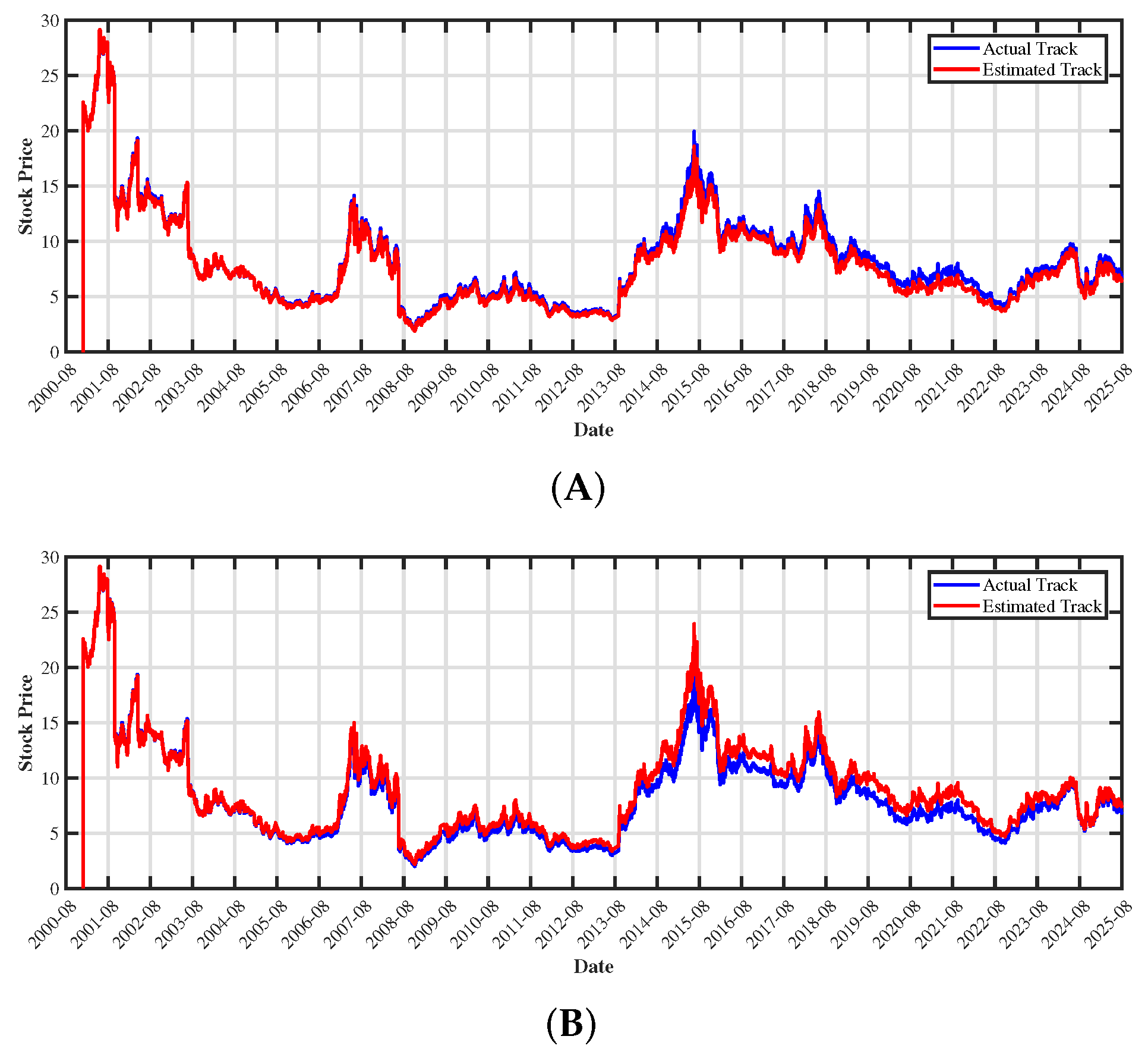
were estimated within the quasi-likelihood framework proposed in this paper. To provide an intuitive evaluation of model fit, simulated price track were generated in MATLAB using the estimated parameters and compared with the actual closing prices observed. The comparison demonstrated that the model captured the overall price dynamics effectively, thereby confirming both the applicability of the mixed fractional Brownian motion Black–Scholes framework and the reliability of the proposed quasi-likelihood estimation method on real financial data. Furthermore, we simulated stock price tracking using both the fractional Brownian motion model proposed in this study and the classical Black–Scholes model. The comparative results are presented in
Figure 9 and
Figure 10. As illustrated, our proposed model provides a notably better fit to the observed price dynamics, particularly in capturing volatility clustering and the long-memory behavior inherent in the price process. These results further highlight the advantages and practical applicability of our model in financial data modeling and empirical analysis.