Abstract
We propose a dynamic extension of the Petford–Welsh coloring algorithm that estimates the chromatic number of a graph without requiring k as an input. The basic algorithm is based on the model that is closely related to the Boltzmann machines that minimize the Ising model Hamiltonian. The method begins with a minimal coloring and adaptively adjusts the number of colors based on solution quality. We evaluate our approach on a variety of graphs from the DIMACS benchmark suite using different initialization strategies. On random k-colorable graphs, proper colorings were found for all combinations of initial strategies and parameter values, while for DIMACS graphs, optimal or near optimal solutions were found frequently, without tuning the parameters. The results show that the algorithm designed is not only capable of providing near optimal solutions but is also very robust. We demonstrate that our approach can be surprisingly effective on real-world instances, although more adaptive or problem-specific strategies may be needed for harder cases. The main advantage of the proposed randomized algorithm is its inherent parallelism that may be explored in future studies.
MSC:
05C15; 68R10; 68W20
1. Introduction
The graph coloring problem is among the most popular NP-hard problems [1] in combinatorial optimization both due to its aesthetic appeal as a simple yet very hard combinatorial challenge and because of its many applications in science and real life. The first is demonstrated, for example, by more than a century-long story of the famous four-color map theorem [2]. As an example of applicability, let us just mention that the graph coloring problem is implicitly present in any nontrivial scheduling problem, cf. timetabling [3]. Due to recent popularity of the quantum computing model that may hopefully answer questions of practical importance that may remain out of reach for classical computation [4,5], we also wish to note that graph coloring is closely related to the quantum computing. On one hand, it can be used for the optimization of the design of computing machines; for example, the depth optimization of a quantum circuit is shown to be reducible to the vertex coloring problem [6]. On the other hand, graph coloring is among the challenging problems on which the potential strengths of the quantum computation is studied [7,8,9,10,11]. Although there are high expectations that the model of quantum computing may provide means to solve problems that are beyond reach of the classical model, years or even decades of research and development are likely to be needed to achieve this [11,12]. One interesting avenue of research is the use of quantum-inspired algorithms that were shown to have an exponential asymptotic speedup compared to previously known classical methods [13]. Roughly speaking, it may be possible to use the quantum model, and with a clever dequantization obtain a competitive algorithm for the classical model of computation [14], or make use of a combination of both [15].
Graph coloring is computationally hard. It is well known [16] that for it is NP-complete to decide if a given graph has a proper k-coloring, and that it is NP-hard to compute the chromatic number. It is also hard to find approximate solutions for the graph coloring problems. In particular, recently NP-hardness of coloring k-colorable graphs with colors was shown [17], improving previously strongest results of Bulín et al. [18], who show that is it NP-hard to color k-colorable graphs with colors, and of Huang et al. [19] who gave NP-hardness of coloring k-colorable graphs with colors for sufficiently large k. Due to the intractability of graph coloring, many algorithms including various heuristics and metaheuristics approaches have been designed and applied; for example, ref. [20]. In 1989, likely inspired by the Ising model in statistical mechanics, Petford and Welsh [21] proposed a simple randomized heuristic algorithm for coloring a graph with three colors that “does seem to work well in a wide variety of graph cases”.
The Ising model (or Lenz–Ising model) is a mathematical model of ferromagnetism in statistical mechanics. In the model, spins are placed on the vertices of a graph and interact with their neighbors and a possible external magnetic field. For ferromagnetism, the lowest-energy states correspond to uniform alignment of all spins (all up or all down). At the opposite extreme, the highest-energy states occur when every neighboring pair of spins is anti-aligned. This configuration is only possible if the underlying graph is bipartite, in which case the maximal-energy arrangement corresponds to a proper two-coloring of the graph. If the graph is not bipartite, the high energy states correspond to colorings with few monochromatic edges. This observation may have led to the idea that a generalization allowing the spins to have more than two states might provide a model that would be useful as a mechanism that naturally converges to proper colorings of the underlying graph. The Ising model and some more complicated version of it can then be used to describe the behavior of spin glasses. It is well-known that the Ising model is in general NP-hard [22]. This model is closely related to graph theory, and in particular to the graph coloring problem.
Graph coloring with colors has been considered in several papers, see [23,24] and the references therein. In a study on random graphs, it was found that the phase transition is strongly related to the mean degree of the graphs. In the same paper [24], the analysis implies that the hardest instances are among random graphs with an average degree between 4.42 and . For , the hard instances for the k-coloring application are conjectured [25] to be instances among random graphs from the model used here, where .
Based on previous studies of the voter and antivoter models by Donnely and Welsh [26], Petford and Welsh proposed a three-coloring algorithm [21]. Later experiments with slightly adopted versions of the algorithm have shown very competitive results on k-coloring problems [27], on channel allocation problems [28], and recently on clustering problems [29]. The basic algorithm [21] aims to solve the decision problem “is the given graph G k-colorable ?”, given G and k by hopefully providing a witness, i.e., a proper k-coloring of G. Another version of the coloring problem is to answer the question “what is the minimal k such that G is k-colorable ?”, or equivalently “what is the chromatic number of G ?”. In [30], the Petford–Welsh algorithm was generalized to solve this optimization problem, showing good performance on several samples of randomly generated graphs. The algorithm in ref. [31] is known to be in close relation to the Boltzmann machine [32]. More precisely, the Petford–Welsh algorithm is equivalent to the operation of the generalized Boltzmann machine, and the energy that is aimed to be minimized is a generalization of the Ising Hamiltonian used in the classical model.
In this paper, we build upon the ideas of [30] to design and implement a randomized algorithm that gives an estimate (upper bound) for the chromatic number. In contrast to the original Petford–Welsh algorithm, our algorithm does not need the number of colors as input, which makes it much more useful in various applications where the target number of colors is not known. In particular, we
- design and implement a randomized algorithm that is based on analogy to the Ising model in statistical mechanics;
- we test the performance on random graphs and on a subset of DIMACS that is a standard library of benchmark instances for graph coloring;
- we show that the algorithm designed is not only able to provide near optimal (or, even optimal) solutions, but it is also very robust in the sense that it is not very sensitive to the choice of parameter(s);
In summary, the main contribution of the work reported is a “proof of concept”; in other words, our aim was to show that the simple heuristics based on a generalization of the Ising model works. In the conclusions section we discuss some natural avenues of future research.
The rest of paper is organized as follows. In Section 2, we recall some preliminary information, including the definitions of graph coloring problems, the original Petford–Welsh algorithm, and its relation to the Boltzmann machines and the Ising model. In Section 3, we define the new algorithm for estimating the chromatic number. Section 4 provides a report on the experiments. In the last section, we write some concluding remarks. In the Appendix A and Appendix B, we provide the tables and convergence figures of our experiments.
2. The Graph Coloring Problem and the Basic Algorithm
We say a mapping is a proper coloring of G if it assigns different colors to adjacent vertices. Any mapping will be called a coloring, and will be considered as one of the feasible solutions of the problem.
2.1. Graph Coloring Problems
Coloring of the vertices of a graph is usually asked either in the form of optimization or in the form of decision problem. The first asks for the chromatic number, i.e., the minimal number of colors that allows a proper coloring.
PROBLEM: Graph coloring optimization problem
Input: graph G,
Task: find the chromatic problem of G.
The k-coloring decision problem is a well known NP-complete problem for . It reads as follows:
PROBLEM: Graph coloring decision problem
Input: graph G, integer k
Question: is there a proper k-coloring of G?
2.2. The Petford–Welsh Algorithm for k-Coloring Decision Problem
We start by defining the cost function as the number of bad edges, i.e., edges whose endpoints receive the same color under a coloring c. A coloring is valid when . Thus, finding a coloring with solves the decision problem, with the resulting coloring serving as a witness that verifies the solution.
The Petford–Welsh algorithm [21] begins with a random three-coloring of the input graph and then iteratively improves it. In each iteration, a vertex involved in a conflict (a bad vertex) is chosen uniformly at random. This vertex is then recolored according to a probability distribution that favors colors less common in its neighborhood, as given in Equation (1).
This procedure naturally extends to the general k-coloring problem [27], with the special case recovering the original algorithm.
The pseudocode is expressed in Algorithm 1.
| Algorithm 1 Petford–Welsh algorithm for k-coloring |
|
The probability distribution for recoloring is defined as follows. Let denote the number of edges incident to v whose other endpoint has color i. Then the probability of recoloring v with color i is approximately
where T is a parameter called temperature, for reasons explained later. Note that the newly chosen color may coincide with the current color of v; in fact, if other colors are heavily represented in the neighborhood, retaining the current color may be the most probable outcome.
2.3. The Petford–Welsh Algorithm and Generalized Boltzmann Machine
It was shown in [31] that the Petford–Welsh algorithm is in close correspondence to the operation of the generalized Boltzmann machine when applied to graph coloring. The generalized Boltzmann machine [31] is a neural network that is defined as follows. Let A be a finite alphabet of k symbols and be any graph with vertex set V and edge set E. A generalized Boltzmann machine is specified by a mapping w from the set of edges E into the set of matrices with real entries indexed by and a mapping z from the set of vertices V to vectors indexed by A. The matrices are called weights and the vectors are thresholds. A state of the machine is an assignment which specifies for each vertex a symbol from A. The energy of a state is given by
The update rule, as with the standard Boltzmann machine, depends on a real parameter T, referred as the temperature of the system. For a randomly selected vertex, the state of the vertex is changed from to b with probability
where denotes the state obtained from by setting the value to b. In [31], it has been shown that
- the generalized Boltzmann machine indeed generalizes the standard model and that probability of state converges toas the number of steps tends to infinity ( is a normalizing constant).
- the update rule of the model corresponds to the Petford–Welsh algorithm when the problem considered is graph coloring.
It may be informative to recall that the generalization to a finite alphabet A from the usual case (or, ) in classical Boltzmann machine [32] was motivated in [31,33] by the idea to handle the graph coloring problem more naturally. Furthermore, note that the energy of the generalized Boltzmann machine generalizes the Ising model Hamiltonian used in the classical Boltzmann machine.
The generalized Boltzmann machine for coloring a graph G with k colors is a special case that is defined as follows. A neuron is attached to every vertex of G. When two vertices are adjacent in G then the weight matrix assigned to the edge is , where is the identity matrix of size . The thresholds are set to 0 for all vertices u. Any coloring of G corresponds to a state of the Boltzmann machine. The energy of the coloring c is then given by
Clearly, an edge contributes −1 to the sum in the energy function exactly when . For proper coloring, we thus have , and otherwise is the number of bad (i.e., monochromatic) edges.
The Petford–Welsh algorithm operates at a fixed value of parameter T. They used which is equivalent to using in (1) (because implies ). This corresponds to the operation of the generalized Boltzmann machine at fixed temperature. As there is no annealing schedule, the stopping criterion is either reaching a time limit (in terms of the number of calls to the function which computes a new color) or the event when a proper coloring is found. If no proper coloring is found, the solution with minimal cost is reported and can be regarded as an approximate solution to the problem.
As already explained, the original Petford–Welsh algorithm uses probabilities proportional to , which corresponds to . Larger values of T result in higher probability of accepting a move which increases the number of bad edges. Clearly, a very high T results in chaotic behavior similar to a pure random walk among the colorings ignoring their energy. On the other hand, with low values of T, the algorithm behaves very much like iterative improvement, quickly converging to a local minimum. We do not intend to discuss the annealing schedules here. Just note that it is known that in order to assure convergence, the annealing schedule must be sufficiently slow [34]. In the experiments below, we rather restrict attention to a selection of fixed temperatures that seemingly behave well.
3. The New Dynamic Algorithm for Estimating
Here, we generalize the Petford–Welsh algorithm to dynamically adjust the number of colors, following and extending the ideas of [30]. The Dynamic k-Coloring Algorithm (Algorithm 2) incrementally tries to find a proper coloring of the graph. It begins with an initial coloring, possibly using a small number of colors (e.g., two), and iteratively improves the coloring by randomly selecting a bad vertex and assigning it a new color based on neighborhood color frequencies. A temporary color expansion is allowed via a switch mechanism, enabling the algorithm to escape local conflicts as in Algorithm 3. Enabling the switch parameter, i.e., setting switch = 1, allows the increment of colors as the available colors are max_color+1. The increments in the available colors will continue until a valid coloring is found.
Once a valid coloring is found, the algorithm proceeds to the next phase, where the switch mechanism is disabled by setting switch=0. The algorithm stores the solution and attempts to reduce the number of colors by decrementing max_color and recoloring weakly bad vertices (i.e., vertices colored with max_color). This process continues until the iteration limit is reached. This dynamic approach adapts the number of colors during execution and can be used to approximate the chromatic number of the graph.
| Algorithm 2 Dynamic k-Coloring Algorithm |
Phase I: Find a valid coloring
Phase II: Reduce number of colors
|
| Algorithm 3 Procedure: ChooseColor |
|
4. Experiments
In this section, we first give information on the instances used in the experiments. Then we outline the results on random graphs, emphasizing some phenomena that were observed. Lastly, we provide the results on all small- and medium-size DIMACS graphs.
4.1. Datasets
4.1.1. Random k-Colorable Graphs
Petford and Welsh originally tested their algorithm on random graphs that are generated as follows. The vertices are divided in k sets of size ( and when N is not a multiple of k), and for each pair of vertices from different sets, an edge is added with probability . The resulting graphs are clearly k-colorable, and k is an upper bound for the chromatic number .
We generate k-partite random graphs, where each partition consists of 20 vertices, following the method described earlier. Each graph is labeled in the format balanced_N_k_P_i, where:
- N is the total number of vertices,
- k is the number of partitions,
- P is the edge probability between vertices in different partitions, expressed as a percentage (e.g., means probability ),
- i is the instance number.
For example, balanced_60_3_10_4 refers to the fourth instance of a graph with 60 vertices, three partitions, and an inter-partition edge probability of .
We generate five instances each for , with edge probabilities . The corresponding graph family is denoted mathematically as , used in figures and discussions for clarity. While table entries use the compact balanced_… naming scheme for space efficiency, the same graphs are referred to as in plots and analysis.
4.1.2. DIMACS Graphs
In addition to the randomly generated k-partite graphs, we test our method on several graphs from the DIMACS dataset. The DIMACS dataset of benchmark instances for graph coloring was used in the Second DIMACS Challenge: Cliques, Coloring, and Satisfiability [35]. Since then, graphs have been used frequently for studies of graph coloring heuristics [36,37]. There are several sites with DIMACS graphs; the instances for this study were downloaded from [38,39,40].
4.1.3. Some More Information on Experiments
To experiment with Algorithm 2, we consider four different values of bases, i.e., .
Based on the original idea of the heuristics, it may seem obvious that a random initial coloring is the most natural to start with. Petford and Welsh [21] previously observed that a small number of bad vertices at the beginning do not contribute to the speed of convergence. They offer the explanation that such a nearly good coloring can be regarded as being a solution close to a local optimum that can be a long way from the true optimum in the metrics of exchanges. Nevertheless, we have decided to test two other initialization strategies besides the random initial coloring. We used three initialization strategies:
- Random2: Coloring the vertices randomly with two colors.
- Greedy: Coloring the graph with the Greedy algorithm colors according to the “largest first” strategy, i.e., nodes are colored in descending order of degree. Note that this method always yields a proper coloring.
- GreedyProp2: A local propagation-based coloring method that starts from a random node and greedily colors neighbors using the least frequent color in their neighborhood. Uses two colors and aims to minimize conflicts.
We set the maximum number of iterations to , where N is the number of vertices in the graph.
For random k-colorable graphs, with each combination of bases and initial coloring methods, we run 100 repetitions of Algorithm 2 for each graph and note the best coloring found. Similarly, for DIMACS graphs, we run the algorithm 10 times and report the best result.
We test Algorithm 2 with its Python (version 3.12) implementation [41] on an HPC node at the Faculty of Mechanical Engineering, University of Ljubljana, equipped with 96 processors. Since both runtime and memory usage depend strongly on the size and structure of the graphs, we chose to compare algorithms in terms of the number of iterations required to reach the . In the tables, we therefore report the average iterations for achieving the best coloring. All experiments were carried out in parallel (100 trials for random k-colorable graphs and 10 trials for DIMACS graphs) using ProcessPoolExecutor on an HPC node.
4.2. Experiment on k-Colorable Random Graphs
We first illustrate the behavior of Algorithm 2 on a representative graph instance using base and initialization method Random2. As shown in Figure 1, the number of colors initially increases as the number of bad vertices decreases—this corresponds to Phase I of the algorithm. Once the coloring becomes proper (i.e., zero bad vertices), the algorithm enters Phase II, attempting to reduce the number of colors while trying to find another proper coloring with less colors.
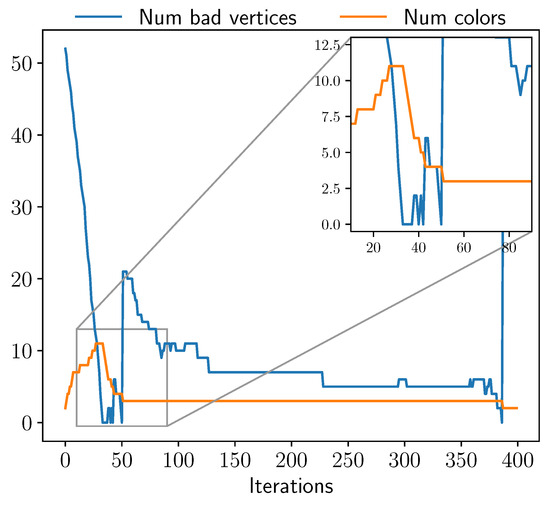
Figure 1.
Convergence to the chromatic number for the graph “balanced_60_3_10_3” using Random2 at base = 4.
Table A1 in Appendix B reports results with base across three initialization strategies. For each case, we show the upper bound on the chromatic number (), the best value found (), how often this value was reached over 100 runs (), and the average number of iterations to achieve it.
Overall, we observe that on the instances tested, the algorithm performs reliably, with in all cases. Recall that the graphs are generated in a way that the upper bound for the number of colors is known, and for sparse graphs (small p) it is possible that fewer colors are needed, which the algorithm indeed proves in some cases. So we conclude that the performance of the algorithm on the random k-colorable graphs is very good and we now provide some evidence that the algorithm is also very robust, both to the change in parameter base and to the variation of the initialization method.
In the experiments performed, Greedy initialization typically leads to faster convergence compared to GreedyProp2 and Random2. In several graphs, Greedy even yields immediately, which means that there is no improvement in the refinement phase. That said, Random2 occasionally outperforms Greedy in terms of convergence speed, e.g., in , , and .
We also compare performance across base values under different initialization methods. The results for Random2 initialization method are shown in Table A2 in Appendix B.
To study the effect of base value b in relation to graph density, we compute Kendall’s correlation between b and the average number of convergence iterations. Kendall’s is a measure of rank correlation:
- A positive indicates that as b increases, the number of iterations tends to increase (i.e., slower convergence).
- A negative implies that higher base values are associated with fewer iterations (i.e., faster convergence).
Figure 2 shows these values, annotated with statistical significance: (***), (**), (*); unmarked values are not statistically significant.
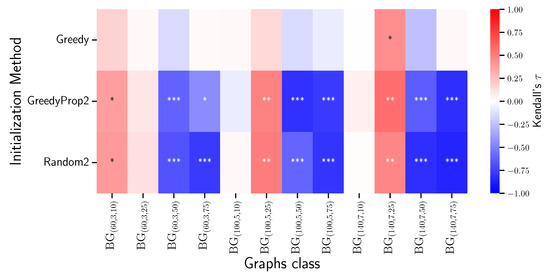
Figure 2.
Kendall’s correlation between base b and average convergence iterations across varying densities. Asterisks indicate statistical significance: * for , ** for , and *** for .
A clear trend emerges for Random2 and GreedyProp2 initialization methods: the case of denser graphs (). Larger bases are more effective (negative ), often with high significance. For graphs with and , smaller bases tend to converge faster (positive ). This supports the idea that the optimal base should be tuned based on density.
In contrast, the Greedy initialization exhibits no consistent pattern, indicating its performance is relatively insensitive to the base.
Figure A1 and Figure A2 in Appendix A visualize convergence behavior. The first shows how convergence varies with base values, while the second compares initialization strategies at fixed base . In each case, the curves represent averages over 100 runs.
Figure 3 shows the best k found among all the bases considered with respect to the initialization methods. The is also plotted. We can see that in two cases, the value of is less than that of . This is because a randomly generated partite sparse graph can be colored with fewer than k colors. Due to overlap, the markers for Greedy (blue circle) and GreedyProp2 (orange triangle) coincide with the marker for Random2 (green diamond), so only the green diamond is visible. The hollow circle represents . When markers overlap, the visible symbol is simply the result of this overlap.
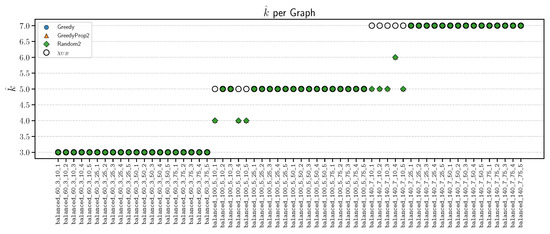
Figure 3.
Best value of k among all the bases, , using different initialization methods. Symbols denote Greedy (blue circle), GreedyProp2 (orange triangle), Random2 (green diamond), and (hollow circle).
4.3. Experiments on DIMACS Graphs
We evaluate our approach on a variety of graphs from the DIMACS benchmark suite using different initialization strategies. Table A3 and Table A4 in Appendix B report the best chromatic number () found and the corresponding mean number of iterations across different base values. For certain DIMACS instances, we found that the number of nodes in the graphs is less than the reported nodes. This is due to the existence of isolated vertices in the graph. We report these values with an asterisk in Table A3 and Table A4. As an example for visualizing the convergence, we plot the convergence of queen14_14 graph w.r.t. the different values of bases and different initial coloring strategies in Figure A3 and Figure A4, respectively, in Appendix A.
Unlike in the synthetic balanced graphs, the DIMACS instances exhibit greater structural diversity, and our method does not consistently recover the true chromatic number (). However, we observe that in many cases, even a simple Greedy coloring initialization suffices to reach the optimal chromatic number. This indicates that for a subset of these graphs, the chromatic number is accessible with relatively straightforward heuristics.
At the same time, for several instances, the inferred chromatic number remains above the known optimum, suggesting that such graphs pose a greater challenge because of their density or structure or both. The variation in performance across instances and base values highlights the sensitivity of the method to initialization and the graph’s internal structure.
While we do not identify a consistent trend as in the random k-partite balanced graphs, these results suggest that simple heuristic methods can be surprisingly effective on real-world instances, although more adaptive or problem-specific strategies may be needed for harder cases. This is in fact well known, as for some instances in the DIMACS dataset, advanced heuristics fail to find near optimal solutions (see, for example, a very recent study [37]).
As a summary of our experiments on DIMACS graphs, Figure 4 shows the percent deviation in the best value of k achieved among all the considered bases from the true chromatic number, .
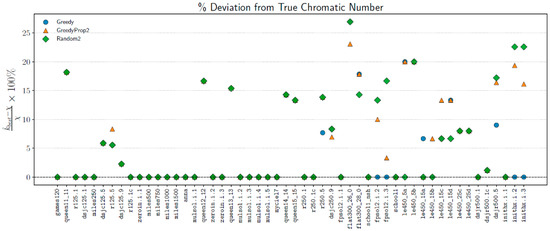
Figure 4.
Percentage deviation of with respect to among all the bases using different initialization methods.
5. Summary and Conclusions
We proposed a dynamic extension of the Petford–Welsh coloring algorithm that estimates the chromatic number of a graph without requiring k as an input. The method begins with a minimal coloring and adaptively adjusts the number of colors based on solution quality. By allowing a temporary increase in the color budget, the algorithm facilitates broader exploration, followed by controlled reduction to encourage convergence toward minimal valid colorings.
The main contribution of the present work is a “proof of concept”. Our aim was to demonstrate that simple heuristics based on a generalization of the Ising model can be effective. This connection is of particular interest due to the relation of the approach to Boltzmann machines and to the Ising model.
Our experiments highlight the importance of both initialization and the choice of base (serving a role analogous to temperature in simulated annealing). In particular, Greedy initialization consistently leads to better convergence and more accurate estimates of the chromatic number than random strategies. Similarly, lower base values tend to encourage global refinement, whereas higher values promote local exploration.
We now discuss some limitations of the proposed approach and add some ideas for future research.
- Hard instances. Our experiments were limited to two datasets: random k-colorable graphs and a subset of benchmark instances from the DIMACS library. It is natural to ask whether the observations on these examples generalize to other domains, including instances in practical applications and graphs that are expected to be hard instances because they are very large or have a special structure, etc. Without an experimental study for each relevant domain, we cannot predict the performance of the approach. However, our moderate optimism can be based on the past experience with the basic Petford–Welsh algorithm for k-coloring that proved to be readily adapted to some other problems, including channel assignment [28] and clustering problems [29]. On the other hand, well-known threshold phenomena [42,43] imply that among random graphs (in any model), there are instances that are hard to color.We expect that the difficult instances discussed in the introduction, i.e., for the random three-colorable graphs with average degree between 4.42 and 4.7 [24] and the random k-colorable graphs, with , where would also be challenging for our approach. However, the algorithm proposed here would always provide a proper coloring with too many colors that might still be of some use in practical applications.
- Selection of value for parameter base. We did not tune the parameters—we just chose four base values that (luckily) proved to all be useful, although there were some differences in the performance observed. Given a domain of instances with some specific properties or instances obtained as practical examples of an industrial problem, a tuning process may be needed as is the case when applying any (meta)heuristics. The robustness observed in our experiments indicates that the tuning may be fast and successful in many situations. On the other hand, instead of looking for “the best” base value, one may try to find a good schedule of bases, in analogy to temperature schedules, a well known idea in combinatorial optimization [33,34,44,45] and recently in the very essence of quantum annealers [8,37,46].
- Initial strategies. In Phase I of our heuristics, we have used three methods to obtain an initial coloring, besides the trivial random coloring in two versions of Greedy heuristics. The choice of the initial strategy obviously has some influence on the convergence behavior, but on the other hand, because of repeating the runs several times on each instance, the importance of this choice seem to be of minor importance. It is an interesting question though whether some other initial strategies would be beneficial. Here, we mean some well-known coloring heuristics, such as DSatur [47], the Welsh–Powell algorithm [48], connected minimum-degree first or connected maximum-degree first [49], etc.
- Lack of more mechanisms to improve convergence and to avoid poor solutions. The proposed heuristic is very simple, its second phase can be understood as a basic local search procedure, more precisely as a random walk, that is, iterative improvement that favors accepting better neighbors but also allows the acceptance of worse quality solutions with some (small) probability. The basic local search can be upgraded with several well-known mechanisms to hopefully improve the convergence. However, we have decided to limit ourselves to the basic ideas and avoided to elaborate more complicated mechanisms as we intended to keep the presentation of the basic idea as clear as possible. Among many possible ideas (some of them may be applied simultaneously), we mention perhaps the most obvious, namely tabu search [50,51,52], that would almost certainly improve the convergence.
As directions for future work, we intend to:
- Investigate more principled strategies for base selection and initialization to improve reliability and convergence speed.
- Explore parallel or distributed implementations to enhance scalability on large graph instances, leveraging the inherent parallelism of the approach [25].
- Benchmark the approach against recent heuristic solvers, including those based on deep learning and quantum optimization.
Author Contributions
Conceptualization, J.Ž.; Methodology, J.Ž.; Software, O.B.; Formal analysis, J.Ž.; Investigation, O.B. and J.Ž.; Resources, O.B.; Data curation, O.B.; Writing—original draft, O.B. and J.Ž.; Writing—review & editing, O.B. and J.Ž.; Visualization, O.B.; Supervision, J.Ž. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partially supported by ARIS through the annual work program of Rudolfovo and by the research grants P2-0248, L1-60136, N1-0278, and J1-4031.
Data Availability Statement
The instances are graphs from DIMACS dataset (sources are given in reference list, [38,39,40].) and random graphs generated for the experiment. The latter are available at [41].
Acknowledgments
The authors would like to sincerely thank the anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
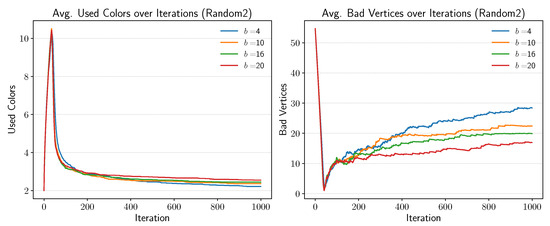
Figure A1.
Effect of base b on convergence for under Random2 initialization.
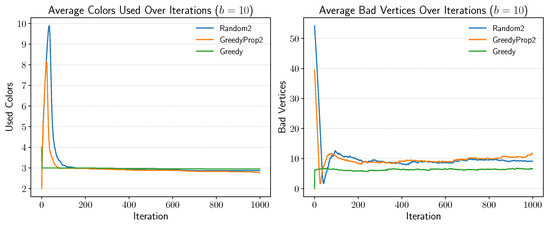
Figure A2.
Comparison of initialization strategies for at base .
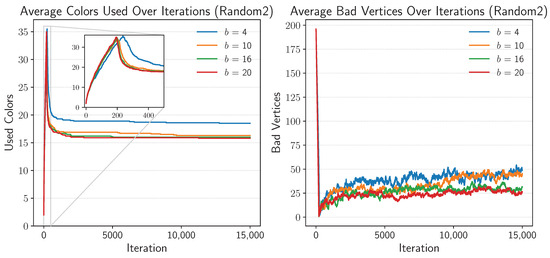
Figure A3.
Effect of base b on convergence for queen14_14 under Random2 initialization.
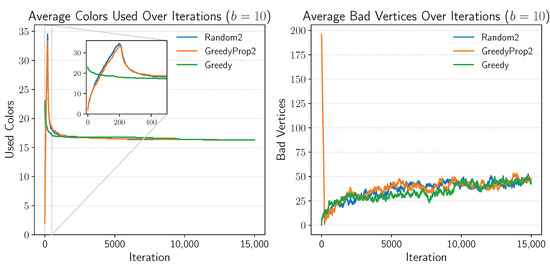
Figure A4.
Comparison of initialization strategies for queen14_14 at base .
Appendix B

Table A1.
Table showing the found, , and mean iterations. from different initial coloring methods at base = 10 for balanced k-partite graphs. The total number of tries was 100.
Table A1.
Table showing the found, , and mean iterations. from different initial coloring methods at base = 10 for balanced k-partite graphs. The total number of tries was 100.
| Graph | N | (, Mean Iters.) | ||||
|---|---|---|---|---|---|---|
| Greedy | GreedyProp2 | RandomProp2 | ||||
| balanced_60_3_10_1 | 60 | 141 | 3 | (3, 100, 642.68) | (3, 100, 1302.94) | (3, 99, 1821.76) |
| balanced_60_3_10_2 | 60 | 113 | 3 | (3, 100, 106.49) | (3, 100, 465.34) | (3, 100, 569.14) |
| balanced_60_3_10_3 | 60 | 133 | 3 | (3, 74, 10,190.38) | (3, 93, 7186.72) | (3, 94, 6029.05) |
| balanced_60_3_10_4 | 60 | 130 | 3 | (3, 100, 1530.08) | (3, 100, 1029.23) | (3, 100, 1176.21) |
| balanced_60_3_10_5 | 60 | 118 | 3 | (3, 100, 459.19) | (3, 100, 541.94) | (3, 100, 977.8) |
| balanced_60_3_25_1 | 60 | 286 | 3 | (3, 100, 138.41) | (3, 100, 244.05) | (3, 100, 310.88) |
| balanced_60_3_25_2 | 60 | 294 | 3 | (3, 100, 75.15) | (3, 100, 313.53) | (3, 100, 375.84) |
| balanced_60_3_25_3 | 60 | 307 | 3 | (3, 100, 780.74) | (3, 100, 253.35) | (3, 100, 347.57) |
| balanced_60_3_25_4 | 60 | 290 | 3 | (3, 100, 42.57) | (3, 100, 312.86) | (3, 100, 343.8) |
| balanced_60_3_25_5 | 60 | 305 | 3 | (3, 100, 416.05) | (3, 100, 380.13) | (3, 100, 366.63) |
| balanced_60_3_50_1 | 60 | 617 | 3 | (3, 100, 0.0) | (3, 100, 134.96) | (3, 100, 167.42) |
| balanced_60_3_50_2 | 60 | 620 | 3 | (3, 100, 12.45) | (3, 100, 139.09) | (3, 100, 161.89) |
| balanced_60_3_50_3 | 60 | 615 | 3 | (3, 100, 0.0) | (3, 100, 139.67) | (3, 100, 167.31) |
| balanced_60_3_50_4 | 60 | 607 | 3 | (3, 100, 101.06) | (3, 100, 140.56) | (3, 100, 155.89) |
| balanced_60_3_50_5 | 60 | 585 | 3 | (3, 100, 13.14) | (3, 100, 151.34) | (3, 100, 162.3) |
| balanced_60_3_75_1 | 60 | 922 | 3 | (3, 100, 18.46) | (3, 100, 123.56) | (3, 100, 144.42) |
| balanced_60_3_75_2 | 60 | 887 | 3 | (3, 100, 0.0) | (3, 100, 132.12) | (3, 100, 141.11) |
| balanced_60_3_75_3 | 60 | 873 | 3 | (3, 100, 0.0) | (3, 100, 127.72) | (3, 100, 148.82) |
| balanced_60_3_75_4 | 60 | 895 | 3 | (3, 100, 0.0) | (3, 100, 122.42) | (3, 100, 145.22) |
| balanced_60_3_75_5 | 60 | 886 | 3 | (3, 100, 0.0) | (3, 100, 125.22) | (3, 100, 145.73) |
| balanced_100_5_10_1 | 100 | 401 | 5 | (4, 87, 13,128.01) | (4, 86, 16,060.19) | (4, 81, 16,753.02) |
| balanced_100_5_10_2 | 100 | 415 | 5 | (5, 100, 20.55) | (5, 100, 240.4) | (5, 100, 264.25) |
| balanced_100_5_10_3 | 100 | 437 | 5 | (5, 100, 55.58) | (5, 100, 306.05) | (5, 100, 321.21) |
| balanced_100_5_10_4 | 100 | 394 | 5 | (4, 78, 11,475.01) | (4, 51, 20,058.78) | (4, 55, 21,395.64) |
| balanced_100_5_10_5 | 100 | 365 | 5 | (4, 100, 2782.52) | (4, 100, 4984.56) | (4, 100, 5133.19) |
| balanced_100_5_25_1 | 100 | 997 | 5 | (5, 100, 983.59) | (5, 100, 1649.32) | (5, 100, 1906.21) |
| balanced_100_5_25_2 | 100 | 955 | 5 | (5, 100, 5284.42) | (5, 100, 2634.18) | (5, 100, 2838.9) |
| balanced_100_5_25_3 | 100 | 1007 | 5 | (5, 100, 564.73) | (5, 100, 2511.9) | (5, 100, 2338.59) |
| balanced_100_5_25_4 | 100 | 1026 | 5 | (5, 100, 1221.94) | (5, 100, 1570.72) | (5, 100, 1549.94) |
| balanced_100_5_25_5 | 100 | 1047 | 5 | (5, 100, 2068.82) | (5, 100, 1785.53) | (5, 100, 1672.43) |
| balanced_100_5_50_1 | 100 | 2032 | 5 | (5, 100, 286.49) | (5, 100, 358.45) | (5, 100, 360.32) |
| balanced_100_5_50_2 | 100 | 2021 | 5 | (5, 100, 103.01) | (5, 100, 357.99) | (5, 100, 364.16) |
| balanced_100_5_50_3 | 100 | 2005 | 5 | (5, 100, 196.63) | (5, 100, 368.24) | (5, 100, 367.94) |
| balanced_100_5_50_4 | 100 | 2014 | 5 | (5, 100, 154.58) | (5, 100, 351.25) | (5, 100, 380.66) |
| balanced_100_5_50_5 | 100 | 2086 | 5 | (5, 100, 139.04) | (5, 100, 356.6) | (5, 100, 357.76) |
| balanced_100_5_75_1 | 100 | 2993 | 5 | (5, 100, 179.48) | (5, 100, 284.43) | (5, 100, 277.5) |
| balanced_100_5_75_2 | 100 | 2990 | 5 | (5, 100, 88.3) | (5, 100, 278.52) | (5, 100, 286.92) |
| balanced_100_5_75_3 | 100 | 3004 | 5 | (5, 100, 44.88) | (5, 100, 270.54) | (5, 100, 288.61) |
| balanced_100_5_75_4 | 100 | 2994 | 5 | (5, 100, 0.0) | (5, 100, 273.09) | (5, 100, 270.02) |
| balanced_100_5_75_5 | 100 | 3042 | 5 | (5, 100, 0.0) | (5, 100, 269.09) | (5, 100, 273.38) |
| balanced_140_7_10_1 | 140 | 826 | 7 | (5, 95, 18,607.58) | (5, 94, 25,152.38) | (5, 93, 24,742.58) |
| balanced_140_7_10_2 | 140 | 837 | 7 | (5, 66, 34,506.83) | (5, 67, 33,209.18) | (5, 53, 27,958.49) |
| balanced_140_7_10_3 | 140 | 836 | 7 | (5, 89, 25,239.54) | (5, 83, 24,031.25) | (5, 89, 29,304.94) |
| balanced_140_7_10_4 | 140 | 880 | 7 | (6, 100, 411.99) | (6, 100, 706.27) | (6, 100, 732.43) |
| balanced_140_7_10_5 | 140 | 866 | 7 | (5, 21, 41,444.86) | (5, 20, 34,369.45) | (5, 27, 34,863.89) |
| balanced_140_7_25_1 | 140 | 2079 | 7 | (7, 100, 8915.54) | (7, 100, 11,801.03) | (7, 100, 10,159.86) |
| balanced_140_7_25_2 | 140 | 2101 | 7 | (7, 100, 6355.96) | (7, 100, 10,853.21) | (7, 100, 10,400.25) |
| balanced_140_7_25_3 | 140 | 2099 | 7 | (7, 100, 8596.3) | (7, 100, 8723.64) | (7, 100, 8021.37) |
| balanced_140_7_25_4 | 140 | 2073 | 7 | (7, 100, 16,328.22) | (7, 100, 11,899.88) | (7, 100, 11,190.06) |
| balanced_140_7_25_5 | 140 | 2081 | 7 | (7, 100, 11,418.61) | (7, 99, 15,249.36) | (7, 98, 15,336.41) |
| balanced_140_7_50_1 | 140 | 4151 | 7 | (7, 100, 262.65) | (7, 100, 690.69) | (7, 100, 690.55) |
| balanced_140_7_50_2 | 140 | 4210 | 7 | (7, 100, 370.72) | (7, 100, 661.65) | (7, 100, 679.32) |
| balanced_140_7_50_3 | 140 | 4263 | 7 | (7, 100, 492.75) | (7, 100, 637.24) | (7, 100, 675.79) |
| balanced_140_7_50_4 | 140 | 4125 | 7 | (7, 100, 467.31) | (7, 100, 694.28) | (7, 100, 691.0) |
| balanced_140_7_50_5 | 140 | 4157 | 7 | (7, 100, 495.34) | (7, 100, 677.32) | (7, 100, 680.06) |
| balanced_140_7_75_1 | 140 | 6320 | 7 | (7, 100, 60.02) | (7, 100, 433.22) | (7, 100, 437.48) |
| balanced_140_7_75_2 | 140 | 6193 | 7 | (7, 100, 73.96) | (7, 100, 445.82) | (7, 100, 446.87) |
| balanced_140_7_75_3 | 140 | 6315 | 7 | (7, 100, 0.0) | (7, 100, 436.23) | (7, 100, 437.4) |
| balanced_140_7_75_4 | 140 | 6288 | 7 | (7, 100, 0.0) | (7, 100, 440.22) | (7, 100, 434.73) |
| balanced_140_7_75_5 | 140 | 6327 | 7 | (7, 100, 51.28) | (7, 100, 427.07) | (7, 100, 437.93) |

Table A2.
Table showing the found, , and mean iterations. at different bases for Random2 initial coloring method for balanced k-partite graphs. The total number of tries was 100.
Table A2.
Table showing the found, , and mean iterations. at different bases for Random2 initial coloring method for balanced k-partite graphs. The total number of tries was 100.
| Graph | N | (, Mean Iters.) | |||||
|---|---|---|---|---|---|---|---|
| 4 | 10 | 16 | 20 | ||||
| balanced_60_3_10_1 | 60 | 141 | 3 | (3, 100, 695.42) | (3, 99, 1821.76) | (3, 84, 2764.3) | (3, 89, 3865.74) |
| balanced_60_3_10_2 | 60 | 113 | 3 | (3, 100, 515.2) | (3, 100, 569.14) | (3, 100, 893.56) | (3, 100, 1006.98) |
| balanced_60_3_10_3 | 60 | 133 | 3 | (3, 99, 4693.02) | (3, 94, 6029.05) | (3, 71, 8626.0) | (3, 83, 8887.23) |
| balanced_60_3_10_4 | 60 | 130 | 3 | (3, 100, 943.75) | (3, 100, 1176.21) | (3, 99, 1645.39) | (3, 96, 2417.18) |
| balanced_60_3_10_5 | 60 | 118 | 3 | (3, 100, 642.64) | (3, 100, 977.8) | (3, 100, 1192.56) | (3, 100, 1638.29) |
| balanced_60_3_25_1 | 60 | 286 | 3 | (3, 100, 381.43) | (3, 100, 310.88) | (3, 100, 369.22) | (3, 100, 370.98) |
| balanced_60_3_25_2 | 60 | 294 | 3 | (3, 100, 395.92) | (3, 100, 375.84) | (3, 100, 465.47) | (3, 100, 377.13) |
| balanced_60_3_25_3 | 60 | 307 | 3 | (3, 100, 360.63) | (3, 100, 347.57) | (3, 100, 350.03) | (3, 100, 398.08) |
| balanced_60_3_25_4 | 60 | 290 | 3 | (3, 100, 422.08) | (3, 100, 343.8) | (3, 100, 403.84) | (3, 100, 520.77) |
| balanced_60_3_25_5 | 60 | 305 | 3 | (3, 100, 397.65) | (3, 100, 366.63) | (3, 100, 525.41) | (3, 100, 367.76) |
| balanced_60_3_50_1 | 60 | 617 | 3 | (3, 100, 195.69) | (3, 100, 167.42) | (3, 100, 159.6) | (3, 100, 153.43) |
| balanced_60_3_50_2 | 60 | 620 | 3 | (3, 100, 188.98) | (3, 100, 161.89) | (3, 100, 156.33) | (3, 100, 155.23) |
| balanced_60_3_50_3 | 60 | 615 | 3 | (3, 100, 203.25) | (3, 100, 167.31) | (3, 100, 161.82) | (3, 100, 160.19) |
| balanced_60_3_50_4 | 60 | 607 | 3 | (3, 100, 191.83) | (3, 100, 155.89) | (3, 100, 156.58) | (3, 100, 155.55) |
| balanced_60_3_50_5 | 60 | 585 | 3 | (3, 100, 205.22) | (3, 100, 162.3) | (3, 100, 165.02) | (3, 100, 162.7) |
| balanced_60_3_75_1 | 60 | 922 | 3 | (3, 100, 168.98) | (3, 100, 144.42) | (3, 100, 134.4) | (3, 100, 128.55) |
| balanced_60_3_75_2 | 60 | 887 | 3 | (3, 100, 170.32) | (3, 100, 141.11) | (3, 100, 134.14) | (3, 100, 139.94) |
| balanced_60_3_75_3 | 60 | 873 | 3 | (3, 100, 169.04) | (3, 100, 148.82) | (3, 100, 139.94) | (3, 100, 134.79) |
| balanced_60_3_75_4 | 60 | 895 | 3 | (3, 100, 172.41) | (3, 100, 145.22) | (3, 100, 139.99) | (3, 100, 133.7) |
| balanced_60_3_75_5 | 60 | 886 | 3 | (3, 100, 167.05) | (3, 100, 145.73) | (3, 100, 140.89) | (3, 100, 143.09) |
| balanced_100_5_10_1 | 100 | 401 | 5 | (4, 97, 13,190.37) | (4, 81, 16,753.02) | (4, 53, 16,991.64) | (4, 46, 22,098.61) |
| balanced_100_5_10_2 | 100 | 415 | 5 | (5, 100, 398.44) | (5, 100, 264.25) | (5, 100, 254.16) | (5, 100, 302.62) |
| balanced_100_5_10_3 | 100 | 437 | 5 | (5, 100, 511.94) | (5, 100, 321.21) | (5, 100, 344.07) | (5, 100, 341.93) |
| balanced_100_5_10_4 | 100 | 394 | 5 | (4, 74, 17,104.27) | (4, 55, 21,395.64) | (4, 36, 15,245.31) | (4, 36, 18,423.08) |
| balanced_100_5_10_5 | 100 | 365 | 5 | (4, 100, 6756.25) | (4, 100, 5133.19) | (4, 92, 7948.3) | (4, 90, 9283.31) |
| balanced_100_5_25_1 | 100 | 997 | 5 | (5, 100, 1912.59) | (5, 100, 1906.21) | (5, 100, 3172.81) | (5, 100, 2970.73) |
| balanced_100_5_25_2 | 100 | 955 | 5 | (5, 100, 2399.05) | (5, 100, 2838.9) | (5, 100, 4031.06) | (5, 98, 4129.43) |
| balanced_100_5_25_3 | 100 | 1007 | 5 | (5, 100, 2155.09) | (5, 100, 2338.59) | (5, 100, 3491.09) | (5, 100, 4366.11) |
| balanced_100_5_25_4 | 100 | 1026 | 5 | (5, 100, 1738.32) | (5, 100, 1549.94) | (5, 100, 2120.71) | (5, 99, 2405.43) |
| balanced_100_5_25_5 | 100 | 1047 | 5 | (5, 100, 1879.04) | (5, 100, 1672.43) | (5, 100, 2205.61) | (5, 99, 2809.86) |
| balanced_100_5_50_1 | 100 | 2032 | 5 | (5, 100, 494.76) | (5, 100, 360.32) | (5, 100, 353.94) | (5, 100, 363.79) |
| balanced_100_5_50_2 | 100 | 2021 | 5 | (5, 100, 486.64) | (5, 100, 364.16) | (5, 100, 356.96) | (5, 100, 362.47) |
| balanced_100_5_50_3 | 100 | 2005 | 5 | (5, 100, 500.43) | (5, 100, 367.94) | (5, 100, 355.03) | (5, 100, 342.84) |
| balanced_100_5_50_4 | 100 | 2014 | 5 | (5, 100, 496.93) | (5, 100, 380.66) | (5, 100, 363.29) | (5, 100, 368.81) |
| balanced_100_5_50_5 | 100 | 2086 | 5 | (5, 100, 468.94) | (5, 100, 357.76) | (5, 100, 352.61) | (5, 100, 343.38) |
| balanced_100_5_75_1 | 100 | 2993 | 5 | (5, 100, 364.13) | (5, 100, 277.5) | (5, 100, 265.89) | (5, 100, 258.95) |
| balanced_100_5_75_2 | 100 | 2990 | 5 | (5, 100, 360.49) | (5, 100, 286.92) | (5, 100, 265.55) | (5, 100, 268.35) |
| balanced_100_5_75_3 | 100 | 3004 | 5 | (5, 100, 366.07) | (5, 100, 288.61) | (5, 100, 268.0) | (5, 100, 266.7) |
| balanced_100_5_75_4 | 100 | 2994 | 5 | (5, 100, 355.45) | (5, 100, 270.02) | (5, 100, 270.02) | (5, 100, 251.35) |
| balanced_100_5_75_5 | 100 | 3042 | 5 | (5, 100, 371.88) | (5, 100, 273.38) | (5, 100, 258.92) | (5, 100, 257.87) |
| balanced_140_7_10_1 | 140 | 826 | 7 | (5, 18, 35,862.94) | (5, 93, 24,742.58) | (5, 64, 28,914.0) | (5, 49, 35,911.02) |
| balanced_140_7_10_2 | 140 | 837 | 7 | (5, 1, 57,864.0) | (5, 53, 27,958.49) | (5, 29, 35,530.97) | (5, 14, 33,685.79) |
| balanced_140_7_10_3 | 140 | 836 | 7 | (5, 13, 36,733.54) | (5, 89, 29,304.94) | (5, 55, 35,117.38) | (5, 41, 27,400.78) |
| balanced_140_7_10_4 | 140 | 880 | 7 | (6, 100, 1512.85) | (6, 100, 732.43) | (6, 100, 784.11) | (6, 100, 773.35) |
| balanced_140_7_10_5 | 140 | 866 | 7 | (5, 1, 16,516.0) | (5, 27, 34,863.89) | (5, 12, 46,650.42) | (5, 3, 41,211.67) |
| balanced_140_7_25_1 | 140 | 2079 | 7 | (7, 100, 11,995.24) | (7, 100, 10,159.86) | (7, 100, 18,648.95) | (7, 93, 20,292.3) |
| balanced_140_7_25_2 | 140 | 2101 | 7 | (7, 100, 10,610.82) | (7, 100, 10,400.25) | (7, 95, 17,490.02) | (7, 89, 19,993.64) |
| balanced_140_7_25_3 | 140 | 2099 | 7 | (7, 100, 12,229.11) | (7, 100, 8021.37) | (7, 96, 15,969.44) | (7, 91, 18,847.48) |
| balanced_140_7_25_4 | 140 | 2073 | 7 | (7, 100, 18,558.72) | (7, 100, 11,190.06) | (7, 92, 19,471.47) | (7, 81, 23,240.46) |
| balanced_140_7_25_5 | 140 | 2081 | 7 | (7, 97, 21,587.37) | (7, 98, 15,336.41) | (7, 87, 24,726.77) | (7, 75, 25,699.41) |
| balanced_140_7_50_1 | 140 | 4151 | 7 | (7, 100, 1008.77) | (7, 100, 690.55) | (7, 100, 668.54) | (7, 100, 621.5) |
| balanced_140_7_50_2 | 140 | 4210 | 7 | (7, 100, 982.48) | (7, 100, 679.32) | (7, 100, 633.29) | (7, 100, 621.91) |
| balanced_140_7_50_3 | 140 | 4263 | 7 | (7, 100, 949.27) | (7, 100, 675.79) | (7, 100, 637.21) | (7, 100, 586.59) |
| balanced_140_7_50_4 | 140 | 4125 | 7 | (7, 100, 989.17) | (7, 100, 691.0) | (7, 100, 672.0) | (7, 100, 652.75) |
| balanced_140_7_50_5 | 140 | 4157 | 7 | (7, 100, 1004.81) | (7, 100, 680.06) | (7, 100, 641.17) | (7, 100, 648.6) |
| balanced_140_7_75_1 | 140 | 6320 | 7 | (7, 100, 615.39) | (7, 100, 437.48) | (7, 100, 414.44) | (7, 100, 401.85) |
| balanced_140_7_75_2 | 140 | 6193 | 7 | (7, 100, 632.38) | (7, 100, 446.87) | (7, 100, 412.05) | (7, 100, 402.7) |
| balanced_140_7_75_3 | 140 | 6315 | 7 | (7, 100, 610.55) | (7, 100, 437.4) | (7, 100, 414.22) | (7, 100, 393.11) |
| balanced_140_7_75_4 | 140 | 6288 | 7 | (7, 100, 619.77) | (7, 100, 434.73) | (7, 100, 411.04) | (7, 100, 395.9) |
| balanced_140_7_75_5 | 140 | 6327 | 7 | (7, 100, 631.73) | (7, 100, 437.93) | (7, 100, 396.85) | (7, 100, 397.37) |

Table A3.
Table showing the found, , and mean iterations. from different initial coloring methods at base = 10 for DIMACS graphs. The total number of tries was 10. An asterisk denotes reported nodes including isolated vertices.
Table A3.
Table showing the found, , and mean iterations. from different initial coloring methods at base = 10 for DIMACS graphs. The total number of tries was 10. An asterisk denotes reported nodes including isolated vertices.
| Graph | N | (, Mean Iters.) | ||||
|---|---|---|---|---|---|---|
| Greedy | GreedyProp2 | RandomProp2 | ||||
| queen10_10 | 100 | 1470 | 11 | (12, 10, 2424.0) | (12, 10, 4409.7) | (12, 10, 6195.8) |
| games120 | 120 | 638 | 9 | (9 , 10, 0.0) | (9, 10, 130.4) | (9, 10, 134.4) |
| queen11_11 | 121 | 1980 | 11 | (13, 9, 20,870.7) | (13, 9, 27,059.1) | (13, 10, 32,604.3) |
| r125.1 | (122, 125 *) | 209 | 5 | (5, 10, 0.0) | (5, 10, 90.7) | (5, 10, 104.4) |
| dsjc125.1 | 125 | 736 | 5 | (5, 8, 34,609.1) | (5, 8, 29,797.5) | (5, 7, 20,002.1) |
| dsjc125.5 | 125 | 3891 | 17 | (18, 1, 20,353.0) | (19, 10, 7272.5) | (18, 1, 17,936.0) |
| dsjc125.9 | 125 | 6961 | 44 | (48, 9, 17,507.1) | (48, 8, 19,232.4) | (47, 1, 42,144.0) |
| miles250 | (125, 128 *) | 387 | 8 | (8, 10, 0.0) | (8, 10, 182.7) | (8, 10, 248.2) |
| r125.1c | 125 | 7501 | 46 | (46, 10, 1130.9) | (46, 10, 7622.2) | (46, 10, 8777.6) |
| r125.5 | 125 | 3838 | 36 | (38, 2, 72.0) | (40, 10, 20,087.7) | (40, 10, 21,611.7) |
| zeroin.i.1 | (126, 211 *) | 4100 | 49 | (49, 10, 0.0) | (49, 4, 35,532.0) | (49, 7, 24,083.0) |
| miles1000 | 128 | 3216 | 42 | (42, 5, 11,994.6) | (42, 3, 38,704.3) | (42, 6, 20,584.8) |
| miles1500 | 128 | 5198 | 73 | (73, 10, 0.0) | (73, 10, 2960.7) | (73, 10, 2937.4) |
| miles500 | 128 | 1170 | 20 | (20, 10, 0.0) | (20, 10, 739.0) | (20, 10, 708.7) |
| miles750 | 128 | 2113 | 31 | (31, 8, 6198.0) | (31, 9, 20,833.4) | (31, 8, 24,205.4) |
| anna | 138 | 493 | 11 | (11, 10, 0.0) | (11, 10, 393.7) | (11, 10, 386.9) |
| mulsol.i.1 | (138, 197 *) | 3925 | 49 | (49, 10, 0.0) | (49, 10, 10,602.4) | (49, 10, 8138.3) |
| queen12_12 | 144 | 2596 | 12 | (14, 2, 61,455.0) | (14, 2, 37,436.5) | (14, 2, 31,584.0) |
| zeroin.i.2 | (157, 211 *) | 3541 | 30 | (30, 10, 0.0) | (31, 1, 76,718.0) | (32, 3, 37,033.3) |
| zeroin.i.3 | (157, 206 *) | 3540 | 30 | (30, 10, 0.0) | (32, 3, 28,664.7) | (31, 1, 28,682.0) |
| queen13_13 | 169 | 3328 | 13 | (16, 10, 3766.9) | (16, 10, 3931.6) | (16, 10, 2236.1) |
| mulsol.i.2 | (173, 188 *) | 3885 | 31 | (31, 10, 0.0) | (32, 2, 21,774.5) | (33, 6, 20,340.2) |
| mulsol.i.3 | (174, 184 *) | 3916 | 31 | (31, 10, 0.0) | (31, 1, 66,168.0) | (32, 2, 53,135.5) |
| mulsol.i.4 | (175, 185 *) | 3946 | 31 | (31, 10, 0.0) | (33, 7, 36,817.3) | (32, 2, 71,797.5) |
| mulsol.i.5 | (176, 186 *) | 3973 | 31 | (31, 10, 0.0) | (32, 2, 46,180.0) | (31, 1, 80,600.0) |
| myciel7 | 191 | 2360 | 8 | (8, 10, 0.0) | (8, 10, 444.9) | (8, 10, 838.4) |
| queen14_14 | 196 | 4186 | 14 | (17, 10, 16,586.2) | (17, 10, 6326.1) | (17, 10, 12,055.2) |
| queen15_15 | 225 | 5180 | 15 | (18, 6, 31,860.2) | (18, 8, 42,906.9) | (18, 5, 46,113.6) |
| dsjc250.9 | 250 | 27897 | 72 | (81, 1, 85,070.0) | (82, 1, 10,028.0) | (81, 1, 69,051.0) |
| r250.1 | 250 | 867 | 8 | (8, 10, 0.0) | (8, 10, 261.9) | (8, 10, 269.6) |
| r250.1c | 250 | 30,227 | 64 | (64, 9, 36,834.7) | (64, 9, 30,456.6) | (64, 7, 34,651.6) |
| r250.5 | 250 | 14849 | 65 | (70, 10, 0.0) | (76, 1, 121,885.0) | (77, 5, 68,487.4) |
| fpsol2.i.1 | (269, 496 *) | 11654 | 65 | (65, 10, 0.0) | (65, 7, 77,886.9) | (65, 9, 88,497.9) |
| flat300_28_0 | 300 | 21695 | 28 | (36, 1, 135,010.0) | (36, 2, 93,484.0) | (36, 6, 102,437.5) |
| school1_nsh | 352 | 14,612 | 14 | (14, 9, 21,266.3) | (14, 9, 8520.3) | (14, 8, 14,151.0) |
| fpsol2.i.2 | (363, 451 *) | 8691 | 30 | (30, 10, 0.0) | (38, 2, 83,531.0) | (38, 1, 90,906.0) |
| fpsol2.i.3 | (363, 425 *) | 8688 | 30 | (30, 10, 0.0) | (38, 2, 102,963.5) | (36, 1, 141,087.0) |
| school1 | 385 | 19,095 | 14 | (14, 9, 23,410.7) | (14, 9, 6986.8) | (14, 10, 11,152.2) |
| le450_15a | 450 | 8168 | 15 | (16, 1, 173,285.0) | (17, 10, 6486.9) | (17, 10, 6299.5) |
| le450_15b | 450 | 8169 | 15 | (17, 10, 9.7) | (17, 10, 7481.9) | (16, 2, 136,735.0) |
| le450_15c | 450 | 16,680 | 15 | (16, 1, 187,434.0) | (17, 9, 154,051.8) | (16, 1, 123,032.0) |
| le450_15d | 450 | 16,750 | 15 | (17, 7, 139,141.7) | (17, 10, 134,227.2) | (16, 1, 175,603.0) |
| le450_25c | 450 | 17,343 | 25 | (29, 6, 101.0) | (29, 1, 185,791.0) | (30, 10, 87,136.5) |
| le450_25d | 450 | 17,425 | 25 | (29, 6, 178.5) | (30, 10, 78,094.9) | (30, 9, 41,700.2) |
| le450_5a | 450 | 5714 | 5 | (6, 3, 96,363.3) | (6, 5, 28,477.6) | (6, 6, 79,516.3) |
| le450_5b | 450 | 5734 | 5 | (6, 4, 144,962.2) | (6, 4, 72,683.5) | (6, 5, 89,260.0) |
| dsjr500.1 | 500 | 3555 | 12 | (12, 10, 127.6) | (12, 10, 1596.9) | (12, 10, 1672.4) |
| dsjr500.1c | 500 | 121275 | 85 | (86, 5, 123,670.8) | (86, 2, 192,601.5) | (87, 6, 145,665.0) |
| dsjr500.5 | 500 | 58862 | 122 | (133, 3, 11.3) | (149, 1, 7558.0) | (150, 3, 127,779.3) |
| inithx.i.1 | (519, 864 *) | 18,707 | 54 | (54, 10, 0.0) | (56, 1, 216,367.0) | (55, 1, 201,835.0) |
| inithx.i.2 | (558, 645 *) | 13,979 | 31 | (31, 10, 0.0) | (40, 1, 217,881.0) | (43, 1, 218,428.0) |
| inithx.i.3 | (559, 621 *) | 13,969 | 31 | (31, 10, 0.0) | (42, 1, 154,076.0) | (43, 1, 25,165.0) |

Table A4.
Table showing the found, , and mean iterations. at different bases for Random2 initial coloring method for DIMACS graphs. The total number of tries was 10. An asterisk denotes reported nodes including isolated vertices.
Table A4.
Table showing the found, , and mean iterations. at different bases for Random2 initial coloring method for DIMACS graphs. The total number of tries was 10. An asterisk denotes reported nodes including isolated vertices.
| Graph | N | (, Mean Iters.) | |||||
|---|---|---|---|---|---|---|---|
| 4 | 10 | 16 | 20 | ||||
| games120 | 120 | 638 | 9 | (9 , 10, 177.3) | (9, 10, 134.4) | (9, 10, 126.9) | (9, 10, 128.1) |
| queen11_11 | 121 | 1980 | 11 | (15, 10, 2769.0) | (13, 10, 32,604.3) | (13, 10, 4902.1) | (13, 10, 2155.5) |
| r125.1 | (122, 125 * ) | 209 | 5 | (5, 10, 121.9) | (5, 10, 104.4) | (5, 10, 104.2) | (5, 10, 97.0) |
| dsjc125.1 | 125 | 736 | 5 | (5, 1, 33,786.0) | (5, 7, 20,002.1) | (5, 6, 18,344.8) | (5, 1, 10,833.0) |
| miles250 | (125, 128 *) | 387 | 8 | (8, 10, 317.3) | (8, 10, 248.2) | (8, 10, 243.8) | (8, 10, 148.8) |
| r125.1c | 125 | 7501 | 46 | (50, 1, 59,577.0) | (46, 10, 8777.6) | (46, 10, 9069.3) | (46, 9, 15,232.7) |
| dsjc125.9 | 125 | 6961 | 44 | (55, 1, 6142.0) | (47, 1, 42,144.0) | (45, 1, 4447.0) | (45, 2, 28,926.0) |
| dsjc125.5 | 125 | 3891 | 17 | (22, 10, 24,273.1) | (18, 1, 17,936.0) | (18, 10, 16,079.5) | (18, 10, 15,916.4) |
| r125.5 | 125 | 3838 | 36 | (43, 6, 19,662.5) | (40, 10, 21,611.7) | (39, 10, 18,904.4) | (38, 2, 31,847.5) |
| zeroin.i.1 | (126, 211 *) | 4100 | 49 | (49, 10, 18,571.4) | (49, 7, 24,083.0) | (49, 2, 38,714.5) | (49, 1, 14,981.0) |
| miles500 | 128 | 1170 | 20 | (20, 10, 4683.0) | (20, 10, 708.7) | (20, 10, 582.5) | (20, 10, 648.7) |
| miles1500 | 128 | 5198 | 73 | (73, 3, 27,536.7) | (73, 10, 2937.4) | (73, 10, 2347.4) | (73, 10, 2365.5) |
| miles750 | 128 | 2113 | 31 | (31, 1, 58,027.0) | (31, 8, 24,205.4) | (31, 10, 9100.0) | (31, 10, 6223.3) |
| miles1000 | 128 | 3216 | 42 | (43, 1, 16,999.0) | (42, 6, 20,584.8) | (42, 8, 11,433.0) | (42, 10, 18,577.8) |
| mulsol.i.1 | (138, 197 *) | 3925 | 49 | (49, 10, 3733.0) | (49, 10, 8138.3) | (49, 10, 11,425.8) | (49, 10, 5581.1) |
| anna | 138 | 493 | 11 | (11, 10, 372.8) | (11, 10, 386.9) | (11, 10, 433.7) | (11, 10, 4241.2) |
| queen12_12 | 144 | 2596 | 12 | (16, 10, 23,088.2) | (14, 2, 31,584.0) | (14, 10, 10,706.6) | (14, 10, 4711.0) |
| zeroin.i.2 | (157, 211 *) | 3541 | 30 | (30, 3, 47,465.0) | (32, 3, 37,033.3) | (32, 1, 27,708.0) | (32, 1, 40,091.0) |
| zeroin.i.3 | (157, 206 *) | 3540 | 30 | (30, 4, 45,605.8) | (31, 1, 28,682.0) | (32, 1, 41,272.0) | (32, 2, 55,011.0) |
| queen13_13 | 169 | 3328 | 13 | (18, 10, 2047.7) | (16, 10, 2236.1) | (15, 8, 21,428.2) | (15, 10, 7008.4) |
| mulsol.i.2 | (173, 188 *) | 3885 | 31 | (31, 4, 27,328.5) | (33, 6, 20,340.2) | (33, 3, 37,431.0) | (33, 6, 34,503.5) |
| mulsol.i.3 | (174, 184 *) | 3916 | 31 | (31, 4, 60,165.0) | (32, 2, 53,135.5) | (33, 4, 31,618.5) | (33, 4, 60,413.5) |
| mulsol.i.4 | (175, 185 *) | 3946 | 31 | (31, 5, 40,779.6) | (32, 2, 71,797.5) | (32, 1, 20,705.0) | (33, 4, 47,436.8) |
| mulsol.i.5 | (176, 186 *) | 3973 | 31 | (31, 2, 21,881.0) | (31, 1, 80,600.0) | (32, 2, 41,175.0) | (33, 4, 61,435.2) |
| myciel7 | 191 | 2360 | 8 | (8, 10, 490.2) | (8, 10, 838.4) | (8, 9, 768.7) | (8, 10, 4736.4) |
| queen14_14 | 196 | 4186 | 14 | (19, 10, 17,020.5) | (17, 10, 12,055.2) | (16, 1, 13,392.0) | (16, 6, 35,802.7) |
| queen15_15 | 225 | 5180 | 15 | (20, 1, 112,258.0) | (18, 5, 46,113.6) | (18, 10, 3611.6) | (17, 2, 59,238.0) |
| r250.1c | 250 | 30,227 | 64 | (68, 1, 39,166.0) | (64, 7, 34,651.6) | (64, 7, 47,749.0) | (64, 6, 48,614.7) |
| r250.1 | 250 | 867 | 8 | (8, 10, 382.2) | (8, 10, 269.6) | (8, 10, 261.3) | (8, 10, 337.1) |
| dsjc250.9 | 250 | 27,897 | 72 | (107, 1, 47,221.0) | (81, 1, 69,051.0) | (79, 3, 43,635.7) | (78, 6, 79,146.7) |
| r250.5 | 250 | 14,849 | 65 | (83, 2, 88,465.5) | (77, 5, 68,487.4) | (74, 2, 65,300.5) | (74, 5, 48,315.4) |
| fpsol2.i.1 | (269, 496 *) | 11654 | 65 | (65, 10, 31,441.9) | (65, 9, 88,497.9) | (65, 5, 105,803.4) | (65, 2, 102,137.0) |
| flat300_28_0 | 300 | 21,695 | 28 | (45, 4, 50,999.5) | (36, 6, 102,437.5) | (33, 1, 143,072.0) | (32, 1, 88,643.0) |
| school1_nsh | 352 | 14,612 | 14 | (14, 10, 10,003.8) | (14, 8, 14,151.0) | (14, 5, 63,549.0) | (14, 6, 27,482.8) |
| fpsol2.i.3 | (363, 425 *) | 8688 | 30 | (35, 2, 119,802.0) | (36, 1, 141,087.0) | (39, 1, 98,128.0) | (40, 1, 162,869.0) |
| fpsol2.i.2 | (363, 451 *) | 8691 | 30 | (34, 2, 109,884.0) | (38, 1, 90,906.0) | (37, 1, 145,146.0) | (40, 1, 66,835.0) |
| school1 | 385 | 19,095 | 14 | (14, 10, 7080.2) | (14, 10, 11,152.2) | (14, 9, 17,417.0) | (14, 10, 11,591.4) |
| le450_5b | 450 | 5734 | 5 | (6, 10, 17,455.8) | (6, 5, 89,260.0) | (7, 10, 19,146.4) | (7, 10, 52,126.6) |
| le450_5a | 450 | 5714 | 5 | (5, 1, 169,416.0) | (6, 6, 79,516.3) | (6, 1, 137,162.0) | (6, 4, 100,053.0) |
| le450_15d | 450 | 16,750 | 15 | (28, 1, 23,854.0) | (16, 1, 175,603.0) | (19, 1, 220,765.0) | (20, 1, 194,484.0) |
| le450_25c | 450 | 17,343 | 25 | (36, 2, 151,978.0) | (30, 10, 87,136.5) | (28, 10, 77,927.4) | (27, 4, 100,118.0) |
| le450_25d | 450 | 17,425 | 25 | (36, 3, 37,371.0) | (30, 9, 41,700.2) | (28, 10, 63,732.8) | (27, 8, 139,768.8) |
| le450_15c | 450 | 16,680 | 15 | (29, 10, 24,378.9) | (16, 1, 123,032.0) | (20, 3, 180,997.3) | (20, 1, 187,445.0) |
| le450_15b | 450 | 8169 | 15 | (19, 1, 150,060.0) | (16, 2, 136,735.0) | (16, 10, 16,153.4) | (15, 2, 112,835.5) |
| le450_15a | 450 | 8168 | 15 | (19, 2, 95,430.5) | (17, 10, 6299.5) | (16, 10, 18,193.5) | (15, 1, 121,410.0) |
| dsjr500.1c | 500 | 121,275 | 85 | (93, 1, 84,314.0) | (87, 6, 145,665.0) | (86, 2, 185,044.5) | (86, 1, 202,039.0) |
| dsjr500.1 | 500 | 3555 | 12 | (12, 10, 5808.9) | (12, 10, 1672.4) | (12, 10, 1355.3) | (12, 10, 1343.8) |
| dsjr500.5 | 500 | 58,862 | 122 | (165, 1, 244,534.0) | (150, 3, 127,779.3) | (145, 4, 121,450.5) | (143, 1, 216,451.0) |
| inithx.i.1 | (519, 864 *) | 18,707 | 54 | (54, 8, 184,365.0) | (55, 1, 201,835.0) | (58, 2, 188,375.0) | (56, 1, 174,260.0) |
| inithx.i.2 | (558, 645 *) | 13,979 | 31 | (38, 1, 181,649.0) | (43, 1, 218,428.0) | (44, 1, 208,224.0) | (44, 1, 113,023.0) |
| inithx.i.3 | (559, 621 *) | 13,969 | 31 | (38, 1, 153,621.0) | (43, 1, 25,165.0) | (43, 2, 138,566.5) | (46, 2, 114,019.0) |
References
- Karp, R. Reducibility among combinatorial problems. In Complexity of Computer Computations; Miller, R., Thatcher, J., Eds.; Plenum Press: New York, NY, USA, 1972; pp. 85–103. [Google Scholar]
- Appel, K.; Haken, W. Solution of the Four Color Map Problem. Sci. Am. 1977, 237, 108–121. [Google Scholar] [CrossRef]
- de Werra, D. Restricted coloring models for timetabling. Discret. Math. 1997, 165–166, 161–170. [Google Scholar] [CrossRef]
- King, A.D.; Nocera, A.; Rams, M.M.; Dziarmaga, J.; Wiersema, R.; Bernoudy, W.; Raymond, J.; Kaushal, N.; Heinsdorf, N.; Harris, R.; et al. Beyond-classical computation in quantum simulation. Science 2025, 388, 199–204. [Google Scholar] [CrossRef]
- Mohseni, N.; McMahon, P.L.; Byrnes, T. Ising machines as hardware solvers of combinatorial optimization problems. To appear in Nature Reviews Physics. arXiv 2022, arXiv:2204.00276. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, K.C.; Kim, P. Quantum Circuit Optimization by Graph Coloring. arXiv 2025, arXiv:2501.14447. [Google Scholar] [CrossRef]
- D’Hondt, E. Quantum approaches to graph colouring. Theor. Comput. Sci. 2009, 410, 302–309. [Google Scholar] [CrossRef]
- Tabi, Z.; El-Safty, K.H.; Kallus, Z.; Haga, P.; Kozsik, T.; Glos, A.; Zimboras, Z. Quantum Optimization for the Graph Coloring Problem with Space-Efficient Embedding. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Los Alamitos, CA, USA, 12–16 October 2020; pp. 56–62. [Google Scholar] [CrossRef]
- Ardelean, S.; Udrescu, M. Graph coloring using the reduced quantum genetic algorithm. Peerj Comput. Sci. 2022, 8, e836. [Google Scholar] [CrossRef]
- Shimizu, K.; Mori, R. Exponential-Time Quantum Algorithms for Graph Coloring Problems. Algorithmica 2022, 84, 3603–3621. [Google Scholar] [CrossRef]
- Krpan, A.; Povh, J.; Pucher, D. Quantum computing and the stable set problem. Optim. Methods Softw. 2025, 40, 837–870. [Google Scholar] [CrossRef]
- Asavanant, W.; Charoensombutamon, B.; Yokoyama, S.; Ebihara, T.; Nakamura, T.; Alexander, R.N.; Endo, M.; Yoshikawa, J.i.; Menicucci, N.C.; Yonezawa, H.; et al. Time-Domain-Multiplexed Measurement-Based Quantum Operations with 25-MHz Clock Frequency. Phys. Rev. Appl. 2021, 16, 034005. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Delgado, A.; Bardhan, B.R.; Lloyd, S. Quantum-inspired algorithms in practice. Quantum 2020, 4, 307. [Google Scholar] [CrossRef]
- Chakhmakhchyan, L.; Cerf, N.J.; Garcia-Patron, R. Quantum-inspired algorithm for estimating the permanent of positive semidefinite matrices. Phys. Rev. A 2017, 96, 022329. [Google Scholar] [CrossRef]
- da Silva Coelho, W.; Henriet, L.; Henry, L.P. Quantum pricing-based column-generation framework for hard combinatorial problems. Phys. Rev. A 2023, 107, 032426. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Wrochna, M.; Živný, S. Improved hardness for H-colourings of G-colourable graphs. In Proceedings of the Thirty-First Annual ACM-SIAM Symposium on Discrete Algorithms, Salt Lake City, UT, USA, 5–8 January 2020; SODA’20. pp. 1426–1435. [Google Scholar]
- Bulín, J.; Krokhin, A.; Opršal, J. Algebraic approach to promise constraint satisfaction. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, New York, NY, USA, 23–26 June 2019; STOC 2019. pp. 602–613. [Google Scholar] [CrossRef]
- Huang, S. Improved Hardness of Approximating Chromatic Number. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, Proceedings of the 16th International Workshop, APPROX 2013, and 17th International Workshop, RANDOM 2013, Berkeley, CA, USA, 21–23 August 2013; Raghavendra, P., Raskhodnikova, S., Jansen, K., Rolim, J.D.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 233–243. [Google Scholar]
- Lewis, R.M.R. A Guide to Graph Colouring; Springer Nature: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Petford, A.; Welsh, D. A Randomised 3-coloring Algorithm. Discret. Math. 1989, 74, 253–261. [Google Scholar] [CrossRef]
- Cipra, B.A. The Ising model is NP-complete. Siam News 2000, 33, 1–3. [Google Scholar]
- Culberson, J.; Gent, I. Frozen development in graph coloring. Theor. Comput. Sci. 2001, 265, 227–264. [Google Scholar] [CrossRef]
- Boettcher, S.; Percus, A. Extremal optimization at the phase transition of the three-coloring problem. Phys. Rev. E 2004, 69, 066703. [Google Scholar] [CrossRef]
- Gabrovšek, B.; Žerovnik, J. A fresh look to a randomized massively parallel graph coloring algorithm. Croat. Oper. Res. Rev. 2024, 15, 105–117. [Google Scholar] [CrossRef]
- Donnelly, P.; Welsh, D. The antivoter problem: Random 2-colourings of graphs. In Graph Theory and Combinatorics (Cambridge, 1983); Academic Press: London, UK, 1984; pp. 133–144. [Google Scholar]
- Žerovnik, J. A Randomized Algorithm for k–colorability. Discret. Math. 1994, 131, 379–393. [Google Scholar] [CrossRef]
- Ubeda, S.; Žerovnik, J. A randomized algorithm for a channel assignment problem. Speedup 1997, 11, 14–19. [Google Scholar]
- Ikica, B.; Gabrovšek, B.; Povh, J.; Žerovnik, J. Clustering as a dual problem to colouring. Comput. Appl. Math. 2022, 41, 147. [Google Scholar] [CrossRef]
- Žerovnik, J. A randomised heuristical algorithm for estimating the chromatic number of a graph. Inf. Process. Lett. 1989, 33, 213–219. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Žerovnik, J. Boltzmann machine with finite alphabet. In RHBNC Departmental Technical Report CSD-TR-92-29, extended abstract appears in Artificial Neural Networks 2; Elsevier Science: Amsterdam, The Netherlands, 1992; Volume 1, pp. 391–394. [Google Scholar]
- Ackley, D.H.; Hinton, G.E.; Sejnowski, T.J. A learning algorithm for boltzmann machines. Cogn. Sci. 1985, 9, 147–169. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Žerovnik, J. Analysis of the Mean Field Annealing Algorithm for Graph Colouring. J. Artif. Neural Netw. 1995, 2, 329–340. [Google Scholar]
- Lundy, M.; Mees, A. Convergence of an annealing algorithm. Math. Program. 1986, 34, 111–124. [Google Scholar] [CrossRef]
- Johnson, D.S.; Trick, M.A. (Eds.) Cliques, Coloring, and Satisfiability: Second DIMACS Implementation Challenge, Proceedings of the Second DIMACS Implementation Challenge, 11–13 October 1993; DIMACS Series in Discrete Mathematics and Theoretical Computer Science; American Mathematical Society: Boston, MA, USA, 1996; Volume 26. [Google Scholar]
- Marappan, R.; Bhaskaran, S. New evolutionary operators in coloring DIMACS challenge benchmark graphs. Int. J. Inf. Technol. 2022, 14, 3039–3046. [Google Scholar] [CrossRef]
- Kole, A.; Pal, A. Efficient Hybridization of Quantum Annealing and Ant Colony Optimization for Coloring DIMACS Graph Instances. J. Heuristics 2025, 31, 29. [Google Scholar] [CrossRef]
- DIMACS Graph Coloring Instances. Available online: https://mat.tepper.cmu.edu/COLOR/instances.html (accessed on 14 August 2025).
- DIMACS Graph Instances (Daniel Porumbel). Available online: https://cedric.cnam.fr/~porumbed/graphs/ (accessed on 14 August 2025).
- Graph Coloring Benchmarks. Available online: https://sites.google.com/site/graphcoloring/links (accessed on 14 August 2025).
- Bihani, O.; Žerovnik, J. A Dynamic Extension of the Petford–Welsh Coloring Algorithm for Estimating the Chromatic Number. Available online: https://zenodo.org/records/16924766 (accessed on 10 September 2025).
- Dubois, O.; Monasson, R.; Selman, B.; Zecchina, R. Editorial. Theor. Comput. Sci. 2001, 265, 1. [Google Scholar] [CrossRef]
- Philathong, H.; Akshay, V.; Samburskaya, K.; Biamonte, J. Computational phase transitions: Benchmarking Ising machines and quantum optimisers. J. Phys. Complex. 2021, 2, 011002. [Google Scholar] [CrossRef]
- Kirckpatrick, S.; Gellat, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Cohn, H.; Fielding, M. Simulated annealing: Searching for an optimal temperature schedule. SIAM J. Optim. 1999, 9, 779–802. [Google Scholar] [CrossRef]
- Matsuura, S.; Nishimori, H.; Albash, T.; Lidar, D.A. Mean Field Analysis of Quantum Annealing Correction. Phys. Rev. Lett. 2016, 116, 220501. [Google Scholar] [CrossRef] [PubMed]
- Brélaz, D. New methods to color the vertices of a graph. Commun. ACM 1979, 22, 251–256. [Google Scholar] [CrossRef]
- Welsh, D.J.A.; Powell, M.B. An upper bound for the chromatic number of a graph and its application to timetabling problems. Comput. J. 1967, 10, 85–86. [Google Scholar] [CrossRef]
- Silva, M.C.; Melo, R.A.; Resende, M.G.; Santos, M.C.; Toso, R.F. The connected Grundy coloring problem: Formulations and a local-search enhanced biased random-key genetic algorithm. Comput. Oper. Res. 2025, 183, 107136. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).