An Enhanced Subgradient Extragradient Method for Fixed Points of Quasi-Nonexpansive Mappings Without Demi-Closedness

Abstract

This research focuses on developing a novel approach to finding fixed points of quasi-nonexpansive mappings without relying on the demi-closedness condition, a common requirement in previous studies. The approach is based on the Subgradient Extragradient technique, which builds upon the foundational extragradient method introduced by G.M. Korpelevich. Korpelevich’s method is a widely recognized tool in the fields of optimization and variational inequalities. This study extends Korpelevich’s technique by adapting it to a broader class of operators while maintaining critical convergence properties. This research demonstrates the effectiveness and practical applicability of this new method through detailed computational examples, highlighting its potential to address complex mathematical problems across various domains.

1. Introduction

Fixed point theory in Hilbert spaces is fundamental for solving equations, optimization problems, and analyzing dynamical systems. A function f in a Hilbert space H has a fixed point at x if $f\left(x\right)=x$, often representing equilibrium states or optimal solutions.

A mapping $T:H\to H$ is nonexpansive if it satisfies $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$ for all $x,y\in H$, ensuring stability in iterative methods used in approximation and optimization. In 2012, Hideaki Iiduka [1] introduced an iterative algorithm grounded in fixed-point theory to address convex minimization problems involving nonexpansive mappings. He further implemented this algorithm to tackle the network bandwidth allocation problem, which serves as a practical instance of convex minimization—a core topic in networking that has been the focus of extensive research. When a data rate is allocate to a network source, it generates a corresponding utility, typically modeled as a concave function. A commonly used utility function for each source is given by

$$\begin{array}{c}\hfill U_s\left(x\right):=w_{s}logx,\end{array}$$

(1)

where $x\in {\mathbb{R}}^{+}-\left\{0\right\}$, and $w_s>0$ is the weighted parameter for source S. The allocation for each source must be managed through a control mechanism to avoid network congestion. This mechanism distributes bandwidth by solving an optimization problem that maximizes the total utility function while ensuring that the sum of the transmission rates of all sources sharing a link does not exceed its capacity. The network bandwidth allocation problem is represented as follows [1].

$${\displaystyle \mathrm{Maximize}\sum _{s\in S}{U}_s\left(x_s\right)\mathrm{subject}\mathrm{to}{\left(x_s\right)}_{s\in S}\in F\left(T\right),}$$

where T is the nonexpansive mapping, and ${\displaystyle \sum _{s\in S}{U}_s\left(x_s\right)}$ is composed of $U_s$ as defined in (1).

Quasi-nonexpansive mappings generalize this by focusing on fixed points, requiring that $\parallel Tx-p\parallel \le \parallel x-p\parallel$ for any fixed point p of T and any $x\in H$, facilitating convergence towards these points. The relationship between nonexpansive and quasi-nonexpansive mappings is foundational: all nonexpansive mappings are inherently quasi-nonexpansive, but the reverse does not necessarily hold. This distinction allows quasi-nonexpansive mappings to encompass a broader class of operators, providing more application flexibility while maintaining critical convergence properties.

For example, the mapping $T\left(x\right)=x$ if $x\le 1$ and $T\left(x\right)=1$ if $x>1$ is quasi-nonexpansive but not nonexpansive, as it does not consistently maintain distances between all points. Another example is the mapping $T(x,y)$ defined by $(x,y)$ if $x^2+y^2\le 1$ and $\left({\displaystyle \frac{x}{\sqrt{x^2+y^2}}},{\displaystyle \frac{y}{\sqrt{x^2+y^2}}}\right)$ if $x^2+y^2>1$, which is quasi-nonexpansive but not nonexpansive, as it projects points outside the unit circle onto it.

A crucial principle related to quasi-nonexpansive mappings is the demiclosedness principle. This principle states that if a sequence $\left\{x_n\right\}$ converges weakly to x and the sequence $\left\{T{x}_n\right\}$ converges strongly to $Tx$, then x is a fixed point of T. This result is fundamental in operator theory and functional analysis, providing a robust tool for establishing the convergence of iterative methods. Numerous studies have focused on solving fixed-point problems of quasi-nonexpansive mappings using the demiclosedness condition and define the mapping $T_w=wI+(1-w)I$, where T is a quasi nonexpensive mapping with $w\in [0,1]$, which plays a vital role in these investigations, as evidenced by references [2,3,4].

The general split feasibility problem (General SFP), introduced by Kangtunyakarn [5], is an extension of the traditional split feasibility problem (SFP), which was first introduced by Censor and Elfving [6]. The traditional SFP involves finding a point x in a closed convex set C such that its image under a linear operator A falls within another convex set Q. Mathematically, it is represented as follows:

$$\mathrm{Find}x\in C\mathrm{such}\mathrm{that}Ax\in Q,$$

where $A:H_1\to H_2$ is a bounded linear operator, and $C\subseteq H_1$ and $Q\subseteq H_2$ are closed convex sets.

The General SFP further extends this framework by involving two operators A and B, requiring the solution to satisfy the following: Find $x\in C$ such that $Ax,Bx\in Q$, where $A,B:H_1\to H_2$ are bounded linear operators. The solution set of this problem can be represented by $\Gamma =\left\{x^{\prime }\in C:A{x}^{\prime }\cap B{x}^{\prime }\in Q\right\}$. This generalization allows for addressing more complex scenarios involving multiple constraints and objectives. Kangtunyakarn has also connected the solution set to the fixed-point problem. Further details can be found in the next section.

In practical terms, SFPs, including traditional and general forms, are critical in various applications. In medical imaging, SFPs are used to reconstruct images from projection data, ensuring the reconstructed images meet specific criteria such as physical constraints and noise minimization. In signal processing, they aid in designing filters and reconstructing signals from incomplete or corrupted data, which is essential in applications like echo cancellation and noise reduction. Additionally, SFPs are used in optimization and operations research for solving resource allocation, network design, and logistics problems, as well as in data science and machine learning for training algorithms and models, especially in high-dimensional data scenarios. See, for example [7,8,9].

Researchers such as Censor and Elfving [6] and Censor and Segal [10] have significantly advanced this field, developing multiple sets of split feasibility problems and split variational inequality problems, incorporating various constraints and projection methods. These advancements highlight the versatility and utility of the SFP framework in solving complex real-world challenges across disciplines.

G.M. Korpelevich [11] was the first to introduce the extragradient method, which has since become a fundamental technique for solving variational inequality problems. This method, known for its robust convergence properties, is defined as follows:

$$\left\{\begin{array}{c}{y}_n=P_C(x_n-{\lambda }_{n}F\left(x_n\right)),\hfill \\ x_{n+1}=P_C(x_n-{\lambda }_{n}F\left(y_n\right)),\hfill \end{array}\right.$$

where $P_C$ denotes the projection onto the set C, ${\lambda }_n$ is the step size parameter, and F is a nonlinear mapping associated with the problem at hand. Specifically, F represents the gradient of the objective function in optimization problems or a monotone operator in variational inequality problems. The choice of ${\lambda }_n$ is crucial for ensuring the algorithm’s convergence and is often determined by a line-search procedure or fixed in advance based on problem characteristics.

Building upon Korpelevich’s foundational work, researchers have developed enhancements to improve the performance of this method.

X. J. Long, J. Yang and Y. J. Cho [12] build upon Korpelevich’s extragradient method to enhance its performance for variational inequalities. The modifications aim to increase convergence speed and computational efficiency. The improved algorithm consists of the following steps:

• Initial Computation:

  $$w_n=x_n+u_n(x_n-x_{n-1}),$$

  where $u_n$ is a sequence used to control the step size.
• Projection Step:

  $$y_n=P_C(w_n-{\lambda }_{n}F\left(w_n\right)).$$
• Check for Solution: If $w_n=y_n$ or $F\left(y_n\right)=0$, then $y_n$ is a solution of the problem. Otherwise, proceed to the next step.
• Correction Step:

  $$z_n=P_{T_n}(w_n-{\lambda }_{n}F\left(y_n\right)).$$
• Step Size Adjustment:

  $${\lambda }_n=\gamma {\nu }^{m_n},$$

  with $m_n$ being the smallest non-negative integer that satisfies certain conditions to ensure convergence.
• Final Update:

  $$x_{n+1}={\alpha }_{n}f\left(e_n\right)+(1-{\alpha }_n)z_n,$$

  where $e_n=(1-\theta )w_n+\theta x_n$.

Similarly, B. Tan and S. Y. Cho [13] leverage Korpelevich’s method as a basis and further enhance it by incorporating a new line-search rule. The modified algorithm consists of the following steps:

• Initial Computation:

  $$w_n=x_n+{\theta }_n(x_n-x_{n-1}),$$

  where ${\theta }_n$ is determined as follows

  $${\theta }_n=\left\{\begin{array}{cc}min\left\{{\displaystyle \frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }},\theta \right\},\hfill & \mathrm{if}{x}_n\ne x_{n-1},\hfill \\ \theta ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$
• Projection Step:

  $$y_n=P_C(w_n-{\lambda }_{n}A{w}_n),$$
• Check for Solution: If $w_n=y_n$ or $A{y}_n=0$, then $y_n$ is a solution of the variational inequality problem (VIP). Otherwise, proceed to the next step.
• Correction Step:

  $$z_n=P_C(w_n-{\beta }_{n}A{y}_n),$$

  where ${\beta }_n$ is given by

  $${\beta }_n={\displaystyle \frac{1-\mu }{\gamma }}{\displaystyle \frac{\parallel w_n-y_n{\parallel }^2}{\parallel A{y}_n{\parallel }^2}}.$$
• Final Update:

  $$x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)z_n.$$

G.M. Korpelevich’s original method has significantly impacted the field of optimization and variational inequalities. His extragradient method introduced an effective way to iteratively approach solutions for variational inequality problems, providing a robust framework that subsequent researchers built to create more efficient and robust algorithms. Both Xian-Jun Long, Jing Yang, and Yeol Je Cho acknowledged the importance of Korpelevich’s contributions and used his method as the starting point for their advancements. This highlights the lasting relevance and adaptability of Korpelevich’s work in the ongoing development of mathematical optimization techniques. Numerous researchers have continued to expand upon Korpelevich’s foundational work, developing variations and enhancements tailored to specific applications and more complex problem settings, as demonstrated in references [14,15,16]. This ongoing research ensures that the extragradient method remains a vital tool in optimization and variational inequalities, proving its versatility and enduring significance.

Building upon the foundational techniques established by G.M. Korpelevich, precisely the Subgradient Extragradient method, this research develops an innovative approach to finding fixed points of quasi-nonexpansive mappings without relying on the demi-closedness condition. This method leverages the robustness of Korpelevich’s technique, adapting it to a broader class of operators while maintaining critical convergence properties.

Detailed computational examples are provided to validate the effectiveness of this new method, demonstrating its practical applicability and robustness. Additionally, the implications of these findings are extended to address various complex problems, showcasing the versatility of the approach. The solutions derived through this technique offer significant improvements in areas such as optimization, dynamical systems analysis, and solving equilibrium problems, proving its utility across multiple domains. This research enhances the theoretical understanding of quasi-nonexpansive mappings and presents a viable tool for practical applications related to mathematical problems and their applications.

2. Preliminaries

The foundational definitions, propositions, and lemmas necessary for the rigorous development of the theory are established in this section. A careful review of fundamental concepts forms the basis of our analysis, accompanied by the introduction of novel analytical tools crafted specifically to facilitate the proofs of the main theorems. These tools mark a significant advancement in addressing the challenges inherent to the core problems under investigation. The material presented provides the essential groundwork, ensuring that the reader is well prepared to engage with the advanced theoretical constructs and proofs that follow. Consider a Hilbert space H and a nonempty closed convex subset C of H. The metric projection $P_C$ of a point $x\in H$ onto the set C is a fundamental concept in functional analysis and optimization.

The metric projection $P_{C}x$ is defined as the unique point in C that minimizes the distance to x, formally expressed by

$$P_{C}x=arg\underset{y\in C}{min}\parallel x-y\parallel .$$

This means that $P_{C}x$ is the closest point to x within C, satisfying the equality

$$\parallel x-P_{C}x\parallel =\underset{y\in C}{min}\parallel x-y\parallel .$$

The uniqueness and existence of $P_{C}x$ are guaranteed by the properties of the Hilbert space and the convexity of C.

Furthermore, the projection $P_C$ is a firmly nonexpansive operator, ensuring that

$$\parallel P_{C}x-P_C{y\parallel }^2\le \langle P_{C}x-P_{C}y,x-y\rangle ,$$

for any $x,y\in H$. This property is essential in proving the convergence of iterative methods in convex optimization.

Additionally, the metric projection satisfies a key variational inequality

$$\langle x-P_{C}x,z-P_{C}x\rangle \le 0,$$

for all $z\in C,$ indicating that $x-P_{C}x$ is orthogonal to the tangent cone of C at $P_{C}x$.

Thus, the metric projection $P_{C}x$ is a crucial tool for exploring the geometric properties of convex sets in Hilbert spaces and is widely applied in mathematical analysis and related fields.

Lemma 1

([17]). Let H be a Hilbert space and C a nonempty closed convex subset of H. Suppose A is a mapping from C into H, and let $u\in C$. For any $\lambda >0$, the point u is a solution to the variational inequality problem $VI(C,A)$ if and only if

$$u=P_C(I-\lambda A)u,$$

where $P_C$ denotes the metric projection of H onto C.

Lemma 2

([18]). Let $\left\{{\alpha }_n\right\}$ and $\left\{{\delta }_n\right\}$ be sequences of non-negative real numbers such that

$${\alpha }_{n+1}\le (1-{\delta }_n){\alpha }_n+{\beta }_n+{\gamma }_n,$$

for all $n\in \mathbb{N},$ where $\left\{{\delta }_n\right\}$ is a sequence in $(0,1)$ and $\left\{{\beta }_n\right\}$ is a real sequence. Assume that ${\sum }_{n=0}^{\infty }{\gamma }_n<\infty$. Then, the following results hold:

(i) 

If ${\beta }_n\le {\delta }_{n}M$ for some $M\ge 0$, then $\left\{{\alpha }_n\right\}$ is a bounded sequence.

(ii) 

If ${\sum }_{n=0}^{\infty }{\delta }_n=\infty$ and ${lim\; sup}_{n\to \infty }{\displaystyle \frac{{\beta }_n}{{\delta }_n}}\le 0$, then ${lim}_{n\to \infty }{\alpha }_n=0$.

Lemma 3

([19]). Let X be a real inner product space. Then

(i) 

${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2\langle x,y\rangle +{\parallel y\parallel }^2,$

(ii) 

${\parallel px+qy\parallel }^2={p(p+q)\parallel x\parallel }^2+{q(p+q)\parallel y\parallel }^2-pq{\parallel x-y\parallel }^2,$

for all $x,y\in X$ and for all $p,q\in \mathbb{R}.$

The subsequent lemma is fundamental in establishing the main theorem in the following section.

Lemma 4.

Let X be a real inner product space. Then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\parallel \alpha x+\beta y+\gamma z\parallel }^2& ={(\alpha +\beta +\gamma )\alpha \parallel x\parallel }^2+(\alpha +\beta +\gamma )\beta {\parallel y\parallel }^2\hfill \\ & +{(\alpha +\beta +\gamma )\gamma \parallel z\parallel }^2-\alpha \beta {\parallel x-y\parallel }^2\hfill \\ & {-\gamma \alpha \parallel x-z\parallel }^2-\gamma \beta {\parallel y-z\parallel }^2,\hfill \end{array}\end{array}$$

(2)

for all $x,y,z\in X$ and $\alpha ,\beta ,\gamma \in \mathbb{R}.$

Proof. 

Let $\alpha ,\beta ,\gamma \in \mathbb{R}$ and $x,y,z\in X$. Putting $\alpha +\beta =a$. From Lemma 3, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\parallel \alpha x+\beta y+\gamma z\parallel }^2& ={∥a\left({\displaystyle \frac{\alpha x+\beta y}{\alpha +\beta }}\right)+\gamma z∥}^2\hfill \\ & =a(a+\gamma ){∥{\displaystyle \frac{\alpha x+\beta y}{\alpha +\beta }}∥}^2+{\gamma (a+\gamma )\parallel z\parallel }^2-a\gamma \parallel {\displaystyle \frac{{\alpha x+\beta y-z\parallel }^2}{\alpha +\beta }}\hfill \\ & =a(a+\gamma )\left({\displaystyle \frac{{\alpha \parallel x\parallel }^2}{\alpha +\beta }}+{\displaystyle \frac{{\beta \parallel y\parallel }^2}{\alpha +\beta }}-{\displaystyle \frac{\alpha \beta }{{(\alpha +\beta )}^2}}{\parallel x-y\parallel }^2\right)+\gamma (a+\gamma ){\parallel z\parallel }^2\hfill \\ & -a\gamma \left({\displaystyle \frac{{\alpha \parallel x-z\parallel }^2}{\alpha +\beta }}+{\displaystyle \frac{{\beta \parallel y-z\parallel }^2}{\alpha +\beta }}-{\displaystyle \frac{\alpha \beta }{{(\alpha +\beta )}^2}}{\parallel x-y\parallel }^2\right)\hfill \\ & ={(\alpha +\beta +\gamma )\alpha \parallel x\parallel }^2+(\alpha +\beta +\gamma )\beta {\parallel y\parallel }^2-{\displaystyle \frac{{(\alpha +\beta +\gamma )\alpha \beta \parallel x-y\parallel }^2}{\alpha +\beta }}\hfill \\ & +{(\alpha +\beta +\gamma )\gamma \parallel z\parallel }^2{-\gamma \alpha \parallel x-z\parallel }^2-\gamma \beta {\parallel y-z\parallel }^2+{\displaystyle \frac{{\alpha \beta \gamma \parallel x-y\parallel }^2}{\alpha +\beta }}\hfill \\ & ={(\alpha +\beta +\gamma )\alpha \parallel x\parallel }^2+{(\alpha +\beta +\gamma )\beta \parallel y\parallel }^2+(\alpha +\beta +\gamma )\gamma {\parallel z\parallel }^2\hfill \\ & -\alpha \beta {\parallel x-y\parallel }^2-\gamma \alpha {\parallel x-z\parallel }^2-\gamma \beta {\parallel y-z\parallel }^2.\hfill \end{array}\end{array}$$

Therefore, Equation (2) holds for all $x,y,z\in X$ and $\alpha ,\beta ,\gamma \in \mathbb{R}$. □

Lemma 5

([20]). Let C be a nonempty closed convex subset of a real Hilbert space H, and let $T:C\to C$ be a quasi-nonexpansive mapping. Then

$$VI(C,I-T)=F\left(T\right).$$

Remark 1.

From Lemma 1 and Lemma 5, we have

$$F\left(T\right)=VI(C,I-T)=F\left(P_C(I-\zeta (I-T))\right),$$

for all $\zeta >0.$

Lemma 6

([5]). Let $H_1$ and $H_2$ be real Hilbert spaces and $C,Q$ be nonempty closed convex subsets of $H_1$ and $H_2$, respectively. Let $A,B:H_1\to H_2$ be bounded linear operators with $A^{*},B^{*}$ being adjoint of A and B, respectivel, y with $\Gamma \ne \varnothing$. Then the following equations are equivalent.

(i) 

$x^{*}\in \Gamma$,

(ii) 

$P_C\left(I-a\left({\displaystyle \frac{A^{*}(I-P_Q)A}{2}}-{\displaystyle \frac{B^{*}(I-P_Q)B}{2}}\right)\right)x^{*}=x^{*}$,

for all $a>0,$ where $L_A,L_B$ are spectral radii of $A^{*}A$ and $B^{*}B$, respectively, with $a\in \left(0,{\displaystyle \frac{2}{L}}\right)$ and $L=max\{L_A,L_B\}$.

Lemma 7

([21]). Let $\left\{{\Gamma }_n\right\}$ be a sequence of real numbers that do not decrease at infinity, in the sense that there exists a subsequence $\left\{{\Gamma }_{n_j}\right\}$ of $\left\{{\Gamma }_n\right\}$ such that ${\Gamma }_{n_j}<{\Gamma }_{n_j+1}$ for all $j\ge 0$. Also, we consider the sequence of integers ${\left\{\tau \left(n\right)\right\}}_{n\ge n_0}$ defined by

$$\tau \left(n\right)=max\{k\le n:{\Gamma }_k<{\Gamma }_{k+1}\}.$$

Then ${\left\{\tau \left(n\right)\right\}}_{n\ge n_0}$ is a nondecreasing sequence verifying ${lim}_{n\to \infty }\tau \left(n\right)=\infty$ and, for all $n\ge n_0$,

$$max\{{\Gamma }_{\tau \left(n\right)},{\Gamma }_n\}\le {\Gamma }_{\tau \left(n\right)+1}.$$

Lemma 8.

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. Let $T:C\to C$ be a continuous quasi-nonexpansive mapping, and let $A,B:H_1\to H_2$ be bounded linear operators with $L_A$ and $L_B$ denoting the spectral radius of $A^{*}A$ and $B^{*}B$, respectively. Assume that the set $\mathbb{F}=F\left(T\right)\cap \Gamma$ is nonempty. Let $x_1,u\in C$, and let the sequence $\left\{x_n\right\}$ be constructed by

$$\begin{array}{cc}\hfill & y_n=P_C\left((I-aJ)x_n\right),\hfill \\ \hfill & z_n=P_C(x_n-\lambda (I-T)x_n),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & J={\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B.\hfill \end{array}$$

The set used in the iteration are defined as follows:

$$\begin{array}{cc}\hfill & T_n=\left\{x\in H:\langle (I-aJ)x_n-y_n,y_n-x\rangle \ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈I-\lambda (I-T)x_n-z_n,z_n-x〉\ge 0\right\}.\hfill \end{array}$$

The iteration is then given by

$$\begin{array}{cc}\hfill & x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_{T_n}\left(x_n-aJ{y}_n\right)+{\gamma }_n{P}_{W_n}(I-\lambda (I-T))x_n,\hfill \end{array}$$

for all $n\ge 1,$ where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\}\subseteq [0,1]$ with ${\alpha }_n+{\beta }_n+{\gamma }_n\le 1$, $\lambda \in \left(0,1\right)$, and $a\in \left(0,{\displaystyle \frac{1}{L}}\right)$ with $L=max\left\{L_A,L_B\right\}$.

Then the sequences $\left\{x_n\right\}$, $\left\{y_n\right\}$ and $\left\{z_n\right\}$ are bounded.

Proof. 

Let $v\in \mathbb{F}$. By applying the method described in [5], we can conclude that J is ${\displaystyle \frac{1}{L}}$-inverse strongly monotone.

Based on the definition of the sequence $\left\{x_n\right\}$, we obtain the following:

$$\begin{array}{cc}\hfill ∥x_{n+1}-v∥& \left.=\parallel {\alpha }_n(u-v)+{\beta }_n\left(P_{T_n}\left(x_n-a\right.J{y}_n\right)-v\right)+{\gamma }_n\left(P_{W_n}\left(x_n-\lambda (I-T)x_n-v\right)\right.\hfill \\ & -\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)v\parallel \hfill \\ & \le {\alpha }_n\parallel u-v\parallel +{\beta }_n\left(P_{T_n}\left(x_n-a\right)y_n\right)-v∥+{\gamma }_n∥P_{W_n}\left(x_n-\lambda (1-T)x_n-v\parallel \right.\hfill \\ & +\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel .\hfill \end{array}$$

(3)

Given that $v\in \mathbb{F}$, we deduce that $v\in C$. From the properties of $z_n$ and $y_n$, it follows that $v\in T_n\cap W_n$. Defining $u_n=x_n-aJ{y}_n$, we arrive at the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {∥P_{T_n}\left(x_n-aJ{y}_n\right)-v∥}^2& ={∥P_{T_n}{u}_n-v∥}^2\hfill \\ & ={∥P_{T_n}{u}_n-u_n∥}^2+{∥u_n-v∥}^2+2〈P_{T_n}{u}_n-u_n,u_n-v〉\hfill \\ & ={∥u_n-v∥}^2+\langle P_{T_n}{u}_n-u_n,P_{T_n}{u}_n-v\rangle +\langle P_{T_n}{u}_n-u_n,u_n-v\rangle \hfill \\ & \le {∥u_n-v∥}^2-{∥P_{T_n}{u}_n-u_n∥}^2\hfill \\ & ={∥x_n-aJ{y}_n-v∥}^2-{∥P_{T_n}{u}_n-x_n+aJ{y}_n∥}^2\hfill \\ & ={∥x_n-v∥}^2+a^2{∥J{y}_n∥}^2-2a〈x_n-v,J{y}_n〉\hfill \\ & -{∥P_{T_n}{u}_n-x_n∥}^2-a^2{∥J{y}_n∥}^2-2a\langle P_{T_n}{u}_n-x_n,J{y}_n\rangle \hfill \\ & ={∥x_n-v∥}^2-{∥P_{T_n}{u}_n-x_n∥}^2-2a〈P_{T_n}{u}_n-v,J{y}_n〉.\hfill \end{array}\end{array}$$

(4)

Since $v\in \Gamma$, and given that $y_n=P_C(I-aJ)x_n$ along with the monotonicity of J, we obtain the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 0& ⩽〈J{y}_n-Jv,y_n-v〉=〈J{y}_n{y}_n-v〉-〈Jv,y_n-v〉\hfill \\ & ⩽〈J{y}_n,y_n-v〉=〈J{y}_n,y_n-P_{T_n}{u}_n〉+〈J{y}_n,P_{T_n}{u}_n-v〉.\hfill \end{array}\end{array}$$

From (4), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {∥P_{T_n}\left(x_n-aJ{y}_n\right)-v∥}^2& ⩽{∥x_n-v∥}^2-{∥P_{T_n}{u}_n-x_n∥}^2-2a\langle P_{T_n}{u}_n-v,J{y}_n\rangle \hfill \\ & ⩽{∥x_n-v∥}^2-{∥P_{T_n}{u}_n-x_n∥}^2+2a\langle J{y}_n,y_n-P_{T_n}{u}_n\rangle \hfill \\ & ={∥x_n-v∥}^2-{∥P_{T_n}{u}_n-y_n∥}^2-{∥y_n-x_n∥}^2\hfill \\ & \hspace{1em}-2\langle P_{T_n}{u}_n-y_n{y}_n-x_n〉+2〈aJ{y}_n,y_n-P_{T_n}{u}_n〉\hfill \\ & ={∥x_n-v∥}^2-{∥P_{T_n}{u}_n-y_n∥}^2-{∥y_n-x_n∥}^2\hfill \\ & \hspace{1em}-2〈y_n+aJ{y}_n-x_n,P_{T_n}{u}_n-y_n〉\hfill \\ & ={∥x_n-v∥}^2-{∥P_{T_n}{u}_n-y_n∥}^2-{∥y_n-x_n∥}^2\hfill \\ & \hspace{1em}+2〈x_n-aJ{x}_n-y_n,P_{T_n}{u}_n-y_n〉\hfill \\ & \hspace{1em}+2a〈J{x}_n-J{y}_n,P_{T_n}{u}_n-y_n〉\hfill \\ & ⩽{∥x_n-v∥}^2-{∥P_{T_n}{u}_n-y_n∥}^2-{∥y_n-x_n∥}^2\hfill \\ & \hspace{1em}+2a∥J{x}_n-J{y}_n∥∥P_{T_n}{u}_n-y_n∥\hfill \\ & ⩽{∥x_n-v∥}^2-{∥P_{T_n}{u}_n-y_n∥}^2-{∥y_n-x_n∥}^2+aL{∥x_n-y_n∥}^2\hfill \\ & \hspace{1em}+aL{∥P_{T_n}{u}_n-y_n∥}^2\hfill \\ & ={∥x_n-v∥}^2-(1-aL){∥P_{T_n}{u}_n-y_n∥}^2-(1-aL){∥y_n-x_n∥}^2.\hfill \end{array}\end{array}$$

(5)

Let $A=I-T$, and define $v_n=(I-\lambda A)x_n$. Therefore, we have the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel P_{W_n}\left(I-\lambda (I-T)x_n{-v\parallel }^2\right.& ={∥P_{W_n}{v}_n-v∥}^2\hfill \\ & ={∥P_{W_n}{v}_n-v_n∥}^2+{∥v_n-v∥}^2+2〈P_{W_n}{v}_n-v_n,v_n-v〉\hfill \\ & ={∥v_n-v∥}^2+〈P_{W_n}{v}_n-v_n,P_{W_n}{v}_n-v〉\hfill \\ & \hspace{1em}+〈P_{W_n}{v}_n-v_n,v_n-v〉\hfill \\ & ⩽{∥v_n-v∥}^2+〈P_{W_n}{v}_n-v_n,v_n-v〉\hfill \\ & ⩽{∥v_n-v∥}^2-{∥P_{W_n}{v}_n-v_n∥}^2\hfill \\ & ={∥x_n-\lambda A{x}_n-v∥}^2-{∥z_n-x_n+\lambda A{x}_n∥}^2\hfill \\ & ={∥x_n-v∥}^2+{\lambda }^2{∥A{x}_n∥}^2-2\lambda 〈x_n-v,A{x}_n〉\hfill \\ & -∥z_n-x_n∥-{\lambda }^2{∥A{x}_n∥}^2-2\lambda 〈z_n-x_n,A{x}_n〉\hfill \\ & ={∥x_n-v∥}^2-{∥z_n-x_n∥}^2-2\lambda 〈z_n-v,A{x}_n〉.\hfill \end{array}\end{array}$$

(6)

From $A=I-T$, then it follows that

$$\begin{array}{cc}\hfill \parallel T{x}_n{-Tv\parallel }^2& =\parallel (I-(I-T))x_n{-(I-(I-T))v\parallel }^2\hfill \\ \hfill & =\parallel x_n-v-(A{x}_n-Av){\parallel }^2\hfill \\ \hfill & =\parallel x_n{-v\parallel }^2-2\langle x_n-v,A{x}_n-Av\rangle +{\parallel A{x}_n-Av\parallel }^2\hfill \\ \hfill & \le \parallel x_n{-v\parallel }^2.\hfill \end{array}$$

It implies that

$$0\le \parallel A{x}_n{\parallel }^2\le 2\langle x_n-v,A{x}_n\rangle .$$

From the above, it follows that

$$\begin{array}{c}\hfill \begin{array}{cc}& 0\le \parallel A{x}_n{\parallel }^2⩽〈A{x}_n,x_n-v〉=2〈A{x}_n,x_n-z_n〉+2〈A{x}_n,z_n-v〉\hfill \\ & \iff -2〈A{x}_n,z_n-v〉⩽-2〈A{x}_n,z_n-x_n〉-{\parallel A{x}_n\parallel }^2.\hfill \end{array}\end{array}$$

Utilizing (6) and the characteristics of the quasi-nonexpansive mapping, we deduce that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel P_{W_n}\left(I-\lambda (I-T)x_n{-v\parallel }^2\right.& ⩽{∥x_n-v∥}^2-{∥z_n-x_n∥}^2-2\lambda 〈z_n-v,A{x}_n〉\hfill \\ & ⩽{∥x_n-v∥}^2-{∥z_n-x_n∥}^2-2\lambda 〈A{x}_n,z_n-x_n〉-\lambda {∥A{x}_n∥}^2\hfill \\ & ={∥x_n-v∥}^2-{∥z_n-x_n∥}^2+2\lambda ∥A{x}_n∥∥z_n-x_n∥-\lambda {∥A{x}_n∥}^2\hfill \\ & ⩽{∥x_n-v∥}^2-{∥z_n-x_n∥}^2+\lambda {∥z_n-x_n∥}^2+\lambda {∥A{x}_n∥}^2\hfill \\ & \hspace{1em}-\lambda {∥A{x}_n∥}^2\hfill \\ & ={∥x_n-v∥}^2-{∥z_n-x_n∥}^2+\lambda {∥z_n-x_n∥}^2\hfill \\ & ={∥x_n-v∥}^2-(1-\lambda ){∥z_n-x_n∥}^2.\hfill \end{array}\end{array}$$

(7)

By invoking (3), (5), and (7), we obtain the following

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ∥x_{n+1}-v∥& ⩽{\alpha }_n\parallel u-v\parallel +{\beta }_n∥P_{T_n}\left(x_n-aJ{y}_n\right)-v∥+{\gamma }_n∥P_{W_n}(1-\lambda (I-T))x_n-v∥\hfill \\ & +\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel \hfill \\ & ⩽{\alpha }_n\parallel u-v\parallel +{\beta }_n∥x_n-v∥+{\gamma }_n∥x_n-v∥+\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel \hfill \\ & ⩽{\alpha }_n\parallel u-v\parallel +\left(1-{\alpha }_n\right)∥x_n-v∥+\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel \hfill \\ & =\left(1-{\alpha }_n\right)∥x_n-v∥+{\alpha }_n\parallel u-v\parallel +\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel .\hfill \end{array}\end{array}$$

From Lemma 2, it can be concluded that the sequence $\left\{x_n\right\}$ is bounded, as are the sequences $\left\{y_n\right\}$ and $\left\{z_n\right\}$. □

3. Main Result

Theorem 1.

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. Let $T:C\to C$ be a continuous quasi-nonexpansive mapping, and let A and B be defined as in Lemma 8. Assume that the set $\mathbb{F}=F\left(T\right)\cap \Gamma$ is nonempty. Let $x_1,u\in C$, and let the sequence $\left\{x_n\right\}$ be generated by $y_n,z_n,T_n,W_n$, and $x_{n+1}$ according to Lemma 8, including the parameter conditions specified therein. Suppose that the following conditions hold:

$$\begin{array}{cc}\hfill & i)\sum _{n=1}^{\infty }{\alpha }_n=\infty \mathrm{and}\underset{n\to \infty }{lim}{\alpha }_n=0,\hfill \\ \hfill & ii)\sum _{n=1}^{\infty }\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)<\infty ,\hfill \\ \hfill & iii)0<c\le {\beta }_n,{\gamma }_n\le d<1\mathit{for}\mathit{some}c,d>0.\hfill \end{array}$$

Then, the sequence $\left\{x_n\right\}$ converges strongly to $x^{*}=P_{\mathbb{F}}u$.

Proof. 

Utilizing the definition of $x_n$ and Lemma 4, we obtain the following

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {∥x_{n+1}-v∥}^2& =\parallel {\alpha }_n(u-v)+{\beta }_n\left(P_{T_n}\left(x_n-a{J}_{y_n}\right)-v\right)+{\gamma }_n\left(P_{W_n}(I-\lambda (I-T))x_n-v\right)\hfill \\ & \hspace{1em}-\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right){v\parallel }^2\hfill \\ & ⩽{∥{\alpha }_n(u-v)+{\beta }_n\left(P_{T_n}{u}_n-v\right)+{\gamma }_n\left(P_{W_n}{v}_n-v\right)∥}^2\hfill \\ & \hspace{1em}-2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)〈v,x_{n+1}-v〉\hfill \\ & ⩽\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\alpha }_n{∥u-v∥}^2+\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\beta }_n{∥P_{T_n}{u}_n-v∥}^2\hfill \\ & \hspace{1em}+\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\gamma }_n{∥P_{W_n}{v}_n-v∥}^2\hfill \\ & \hspace{1em}-{\beta }_n{\gamma }_n{∥P_{T_n}{u}_n-P_{W_n}{v}_n∥}^2+2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel ∥x_{n+1}-v∥\hfill \\ & ⩽\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\alpha }_n{\parallel u-v\parallel }^2\hfill \\ & \hspace{1em}+\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\beta }_n\left({∥x_n-v∥}^2-(1-aL){∥y_n-x_n∥}^2\right)\hfill \\ & \hspace{1em}+\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\gamma }_n\left({∥x_n-v∥}^2-(1-\lambda ){∥x_n-z_n∥}^2\right)\hfill \\ & \hspace{1em}+2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel ∥x_{n+1}-v∥\hfill \\ & ⩽{\alpha }_n{\parallel u-v\parallel }^2+\left({\beta }_n+{\gamma }_n\right){∥x_n-v∥}^2\hfill \\ & \hspace{1em}-(1-\alpha L)\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\beta }_n{∥y_n-x_n∥}^2\hfill \\ & \hspace{1em}-(1-\lambda )\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\gamma }_n{∥z_n-x_n∥}^2\hfill \\ & \hspace{1em}+2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)∥v∥∥x_{n+1}-v∥.\hfill \end{array}\end{array}$$

It implies that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left(1-aL\right)\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\beta }_n{∥y_n-x_n∥}^2& +(1-\lambda )\left({\alpha }_n+{\beta }_n+{\gamma }_n\right){\gamma }_n{∥z_n-x_n∥}^2\hfill \\ & ⩽{\alpha }_n{\parallel u-v\parallel }^2+2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel v\parallel ∥x_{n+1}-v∥\hfill \\ & +{∥x_n-v∥}^2-{∥x_{n+1}-v∥}^2.\hfill \end{array}\end{array}$$

(8)

Case I: Define $E_n={∥x_n-v∥}^2$ for all $n\in \mathbb{N}$. There exists an $n_0\in \mathbb{N}$ such that $E_{n+1}\le E_n$ for all $n\ge n_0$. This implies that ${lim}_{n\to \infty }{E}_n$ exists.

Utilizing (8), along with conditions (i) and (ii), we obtain

$$0=\underset{n\to \infty }{lim}∥y_n-x_n∥=\underset{n\to \infty }{lim}∥P_C(I-aJ)x_n-x_n∥$$

(9)

and

$$0=\underset{n\to \infty }{lim}∥z_n-x_n∥=\underset{n\to \infty }{lim}∥P_C(I-\lambda (I-T))x_n-x_n∥.$$

(10)

Since the sequence $\left\{x_n\right\}$ is bounded, there exists a subsequence $\left\{x_{n_j}\right\}$ of $\left\{x_n\right\}$ such that

$$\underset{n\to \infty }{lim\; sup}〈u-\overline{v},x_n-\overline{v}〉=\underset{j\to \infty }{lim}〈u-\overline{v},x_{n_j}-\overline{v}〉,$$

(11)

where $\overline{v}=P_{\mathbb{F}}u$. Since the sequence $\left\{x_n\right\}$ is bounded in H, there exists a subsequence of $\left\{x_n\right\}$ that converges weakly in H. For convenience, we can assume that $\left\{x_{n_j}\right\}$ converges weakly to z.

From (10), it follows that a subsequence $\left\{z_{n_j}\right\}$ of $\left\{z_n\right\}$ also converges weakly to z.

By the definition of $z_n$, we have

$$〈(I-\lambda (I-T)x_{n_j}-z_{n_j},z_{n_j}-y〉⩾0,$$

for all $y\in C.$

Since T is continuous and the sequences $\left\{z_{n_j}\right\}$ and $\left\{x_{n_j}\right\}$ converge weakly to z, it follows that

$$〈(I-\lambda (I-T)z-z,z-y〉⩾0,$$

for all $y\in C.$

By the properties of the metric projection, we have $z=P_C(I-\lambda A)z$. From Remark 1, it follows that $z\in VI(C,I-T)=F\left(T\right)$.

Utilizing (9), the nonexpansiveness of $P_C(I-aJ)$, and the demiclosedness principle, we can conclude that $z\in F\left(P_C(I-J)\right)=VI(C,J)=\Gamma$. Therefore, we have

$$z\in F\left(T\right)\cap \Gamma =\mathbb{F}.$$

(12)

From (11) and (12), we have

$$\underset{n\to \infty }{lim\; sup}〈u-\overline{v},x_n-\overline{v}〉⩽0.$$

(13)

By the definition of $x_n$ and the fact that $\overline{v}=P_{\mathbb{F}}u$, it follows that

$$\begin{array}{c}\hfill \begin{array}{cc}& {∥x_{n+1}-\overline{v}∥}^2=\parallel {\alpha }_n(u-\overline{v})+{\beta }_n\left(P_{T_n}\left(x_n-aJ{y}_n\right)+{\gamma }_n\left(P_{W_n}(I-\lambda (I-T))x_n-\overline{v}\right)\right.\hfill \\ & \hspace{1em}-\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\overline{v}{\parallel }^2\hfill \\ & ⩽{∥{\beta }_n\left(P_{T_n}{u}_n-\overline{v}\right)+{\gamma }_n\left(P_{W_n}{v}_n-\overline{v}\right)-\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\overline{v}∥}^2\hfill \\ & \hspace{1em}+2{\alpha }_n〈u-\overline{v},x_{n+1}-\overline{v}〉\hfill \\ & \hspace{1em}⩽{∥{\beta }_n\left(P_{T_n}{u}_n-\overline{v}\right)+{\gamma }_n\left(P_{W_n}{v}_n-\overline{v}\right)∥}^2-2(1-{\alpha }_n-{\beta }_n-{\gamma }_n)〈\overline{v},{\beta }_n\left(P_{T_n}{u}_n-\overline{v}\right)\hfill \\ & \hspace{1em}+{\gamma }_n\left(P_{W_n}{v}_n-\overline{v}\right)-\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\overline{v}〉+2{\alpha }_n〈u-\overline{v},x_{n+1}-\overline{v}〉\hfill \\ & ⩽{\beta }_n{∥x_n-\overline{v}∥}^2+{\gamma }_n{∥x_n-\overline{v}∥}^2+2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel \overline{v}\parallel \parallel {\beta }_n\left(P_{T_n}{u}_n-\overline{v}\right)\hfill \\ & \hspace{1em}+{\gamma }_n\left(P_{W_n}{v}_n-\overline{v}\right)-\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\overline{v}\parallel +2{\alpha }_n〈u-\overline{v},x_{n+1}-\overline{v}〉\hfill \\ & \hspace{1em}\le \left(1-{\alpha }_n\right){∥x_n-\overline{v}∥}^2+2{\alpha }_n〈u-\overline{v},x_{n+1}-\overline{v}〉\hfill \\ & \hspace{1em}+2\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\parallel \overline{v}\parallel ∥{\beta }_n\left(P_{T_n}{u}_n-\overline{v}\right)+{\gamma }_n\left(P_{W_n}{v}_n-\overline{v}\right)-\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)\overline{v}∥.\hfill \end{array}\end{array}$$

(14)

By invoking Lemma 2, along with condition (i)–(iii) and Equation (13), we deduce that the sequence $\left\{x_n\right\}$ converges strongly to $\overline{v}=P_{\mathbb{F}}u$.

Case II: There exists a subsequence $\left\{E_{n_i}\right\}\subset \left\{E_n\right\}$ such that $E_{n_i}⩽E_{n_i+1}$ for all $i\in \mathbb{N}$. Define the mapping $\tau :\mathbb{N}\to \mathbb{N}$ by $\tau \left(n\right)=max\left\{k⩽n:E_k<E_{k+1}\right\}$.

Utilizing Equation (8), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left(1-aL\right)& \left({\alpha }_{\tau \left(n\right)}+{\beta }_{\tau \left(n\right)}+{\gamma }_{\tau \left(n\right)}\right){\beta }_{\tau \left(n\right)}{∥y_{\tau \left(n\right)}-x_{\tau \left(n\right)}∥}^2\hfill \\ & +(1-\lambda )\left({\alpha }_{\tau \left(n\right)}+{\beta }_{\tau \left(n\right)}+{\gamma }_{\tau \left(n\right)}\right){\gamma }_{\tau \left(n\right)}{∥z_{\tau \left(n\right)}-x_{\tau \left(n\right)}∥}^2\hfill \\ & ⩽{\alpha }_{\tau \left(n\right)}{\parallel u-v\parallel }^2+2\left(1-{\alpha }_{\tau \left(n\right)}-{\beta }_{\tau \left(n\right)}-{\gamma }_{\tau \left(n\right)}\right)\parallel v\parallel ∥x_{\tau (n+1}-v∥\hfill \\ & +{∥x_{\tau \left(n\right)}-v∥}^2-{∥x_{\tau \left(n\right)+1}-v∥}^2.\hfill \end{array}\end{array}$$

Analogously to Case I, we obtain

$$0=\underset{n\to \infty }{lim}∥y_{\tau \left(n\right)}-x_{\tau \left(n\right)}∥=\underset{n\to \infty }{lim}∥P_C(I-aJ)x_{\tau \left(n\right)}-x_{\tau \left(n\right)}∥.$$

and

$$0=\underset{n\to \infty }{lim}∥z_{\tau \left(n\right)}-x_{\tau \left(n\right)}∥=\underset{n\to \infty }{lim}∥P_C(I-\lambda (I-T))x_{\tau \left(n\right)}-x_{\tau \left(n\right)}∥$$

and

$$\underset{n\to \infty }{lim\; sup}〈u-\overline{v},x_{\tau \left(n\right)}-\overline{v}〉⩽0,$$

where $\overline{v}=P_{\mathbb{F}}u$ and

$$\begin{array}{c}\hfill \begin{array}{cc}& {∥x_{\tau \left(n\right)+1}-\overline{v}∥}^2\le \left(1-{\alpha }_{\tau \left(n\right)}\right){∥x_{\tau \left(n\right)}-\overline{v}∥}^2+2{\alpha }_{\tau \left(n\right)}〈u-\overline{v},x_{\tau \left(n\right)+1}-\overline{v}〉\hfill \\ & +2\left(1-{\alpha }_{\tau \left(n\right)}-{\beta }_{\tau \left(n\right)}-{\gamma }_{\tau \left(n\right)}\right)\parallel \overline{v}\parallel ∥{\beta }_{\tau \left(n\right)}\left(P_{T_{\tau \left(n\right)}}{u}_{\tau \left(n\right)}-\overline{v}\right)+{\gamma }_{\tau \left(n\right)}\left(P_{W_{\tau \left(n\right)}}{v}_{\tau \left(n\right)}-\overline{v}\right)\hfill \\ & -\left(1-{\alpha }_{\tau \left(n\right)}-{\beta }_{\tau \left(n\right)}-{\gamma }_{\tau \left(n\right)}\right)\overline{v}∥.\hfill \end{array}\end{array}$$

From Lemma 2, we have ${lim}_{n\to \infty }∥x_{\left(\tau \right(n)+1}-\overline{v}∥=0.$

From Lemma 7, we have

$$0⩽∥x_n-\overline{v}∥⩽max\left\{∥x_{\tau \left(n\right)}-\overline{v}∥,∥x_n-\overline{v}∥\right\}⩽∥x_{\tau \left(n\right)+1}-\overline{v}∥.$$

From ${lim}_{n\to \infty }∥x_{\left(\tau \right(n)+1}-\overline{v}∥=0$, we have

$$\underset{n\to \infty }{lim}∥x_n-\overline{v}∥=0.$$

Hence, we can conclude that the sequence $\left\{x_n\right\}$ converges to $\overline{v}=P_{\mathbb{F}}u$. This completes the proof. □

4. Applications

This section explores the application of mapping concepts in addressing various mathematical problems. Theorems 2–4 can be viewed as direct consequences and extensions of the main result established in Theorem 1. Specifically, Theorem 2 adapts the general framework of Theorem 1 to the case where the underlying mappings are nonspreading mappings, thereby simplifying the iterative process under this particular structure. Theorem 3 further develops this idea by considering nonexpansive mappings and refining the convergence conditions, which remain consistent with the scope of the assumptions in Theorem 1. Finally, Theorem 4 illustrates how the general convergence framework of Theorem 1 can also be applied to minimization models via the function $g\left(x\right)$, showing that the proposed method unifies both feasibility-type formulations and optimization-type formulations. Thus, Theorems 2–4 provide concrete refinements and applications of the general principle proved in Theorem 1.

4.1. Fixed-Point Problem of Nonlinear Mapping

The concept of nonspreading mapping was introduced by Kohsaka and Takahashi [22] in 2008 to address the fixed-point problem in Hilbert spaces, which are real vector spaces equipped with an inner product structure. Typically, studies on mappings in Hilbert spaces focus on distance-preserving properties, such as nonexpansive mappings, which ensure that the distance between two points does not increase under the mapping.

Nonspreading mappings, however, are defined with a stricter condition. Specifically, a mapping $T:C\to C$ on a nonempty closed convex subset C of a Hilbert space H is called nonspreading if it satisfies the following inequality for all $x,y\in C$

$${2\parallel Tx-Ty\parallel }^2\le {\parallel Tx-y\parallel }^2+{\parallel x-Ty\parallel }^2.$$

This definition was proposed to generalize certain properties of nonexpansive mappings while introducing new tools for solving fixed-point problems.

Nonspreading mappings are closely related to quasi-nonexpansive mappings, which satisfy the inequality $\parallel Tx-p\parallel \le \parallel x-p\parallel$ for all $x\in C$ and $p\in F\left(T\right)$, where $F\left(T\right)$ denotes the set of fixed points of T. While quasi-nonexpansive mappings ensure that distances from points to any fixed point do not increase, nonspreading mappings impose an additional structure that further constrains the behavior of the mapping.

It is important to note that if the fixed-point set $F\left(T\right)$ is nonempty, then a nonspreading mapping T will also be quasi-nonexpansive. This is because the nonspreading condition naturally implies the quasi-nonexpansive property when fixed points exist, making nonspreading mappings a special case of quasi-nonexpansive mappings under this condition.

By utilizing the main theorems and properties of nonspreading mappings, it is possible to establish further significant theorems in fixed-point theory and related fields. These properties provide a foundational framework that can be applied to prove strong convergence results and other critical findings in mathematical analysis and optimization.

Theorem 2.

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. Let $T:C\to C$ be a continuous nonspreading mapping, and let $A,B:H_1\to H_2$ be bounded linear operators with $L_A$ and $L_B$ as the spectral radius of $A^{*}A$ and $B^{*}B$, respectively. Assume that $\mathbb{F}=F\left(T\right)\cap \Gamma \ne \varnothing$. Let $x_1,u\in C$, and consider the sequence $\left\{x_n\right\}$ generated by

$$\begin{array}{cc}\hfill & y_n=P_C\left((I-aJ)x_n\right),\hfill \\ \hfill & z_n=P_C(x_n-\lambda (I-T)x_n),\hfill \end{array}$$

where

$$J={\displaystyle \frac{1}{2}}{A}^{*}\left(I-P_Q\right)A+{\displaystyle \frac{1}{2}}{B}^{*}\left(I-P_Q\right)B.$$

The set used in the iteration are defined as follows:

$$\begin{array}{cc}\hfill & T_n=\left\{x\in H:〈(I-aJ)x_n-y_n,y_n-x〉\ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈(I-\lambda (I-T))x_n-z_n,z_n-x〉⩾0\right\}.\hfill \end{array}$$

The iteration is then given by

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_{T_n}(x_n-aJ{y}_n)+{\gamma }_n{P}_{W_n}(I-\lambda (I-T))x_n,\end{array}$$

for all $n⩾1,$ where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{r_n\right\}\subseteq [0,1]$ with ${\alpha }_n+{\beta }_n+{\gamma }_n⩽1$, $\lambda \in \left(0,1\right)$, $a\in \left(0,{\displaystyle \frac{1}{L}}\right)$, and $L=max\{L_A,L_B\}$. Suppose that the following conditions hold:

$$\begin{array}{cc}\hfill & \left(i\right)\sum _{n=1}^{\infty }{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,\hfill \\ \hfill & \left(ii\right)\sum _{n=1}^{\infty }\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)⩽\infty ,\hfill \\ \hfill & \left(iii\right)0<c⩽{\beta }_n,{\gamma }_n⩽d<1,\mathit{for}\mathit{some}c,d>0.\hfill \end{array}$$

Then the sequence $\left\{x_n\right\}$ converges strongly to $x^{*}=P_{\mathbb{F}}u$.

Theorem 3.

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. Let $T:C\to C$ be a nonexpansive mapping, and let $A,B:H_1\to H_2$ be bounded linear operators with $L_A$ and $L_B$ as the spectral radius of $A^{*}A$ and $B^{*}B$, respectively. Assume that $\mathbb{F}=F\left(T\right)\cap \Gamma \ne \varnothing$. Let $x_1,u\in C$, and consider the sequence $\left\{x_n\right\}$ generated by

$$\begin{array}{cc}\hfill & y_n=P_C\left((I-aJ)x_n\right),\hfill \\ \hfill & z_n=P_C(x_n-\lambda (I-T)x_n),\hfill \end{array}$$

where

$$J={\displaystyle \frac{1}{2}}{A}^{*}\left(I-P_Q\right)A+{\displaystyle \frac{1}{2}}{B}^{*}\left(I-P_Q\right)B.$$

The set used in the iteration are defined as follows:

$$\begin{array}{cc}\hfill & T_n=\left\{x\in H:〈(I-aJ)x_n-y_n,y_n-x〉\ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈(I-\lambda (I-T))x_n-z_n,z_n-x〉⩾0\right\}.\hfill \end{array}$$

The iteration is then given by

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_{T_n}(x_n-aJ{y}_n)+{\gamma }_n{P}_{W_n}(I-\lambda (I-T))x_n,\end{array}$$

for all $n⩾1,$ where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{r_n\right\}\subseteq [0,1]$ with ${\alpha }_n+{\beta }_n+{\gamma }_n⩽1$, $\lambda \in \left(0,1\right)$, $a\in \left(0,{\displaystyle \frac{1}{L}}\right)$, and $L=max\{L_A,L_B\}$. Suppose that the following conditions hold:

$$\begin{array}{cc}\hfill & i)\sum _{n=1}^{\infty }{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,\hfill \\ \hfill & ii)\sum _{n=1}^{\infty }\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)⩽\infty ,\hfill \\ \hfill & iii)0<c⩽{\beta }_n,{\gamma }_n⩽d<1,\mathit{for}\mathit{some}c,d>0.\hfill \end{array}$$

Then the sequence $\left\{x_n\right\}$ converges strongly to $x^{*}=P_{\mathbb{F}}u$.

These theorems illustrate how both nonspreading and nonexpansive mappings can be applied to establish strong convergence results in iterative processes. They demonstrate the versatility and utility of these mapping concepts in fixed-point theory and optimization.

4.2. Minimization Problem

Consider the sets $C\subseteq H_1$ and $Q\subseteq H_2$ where $H_1$ and $H_2$ are Hilbert spaces, and let $A:H_1\to H_2$ be a bounded linear operator. Let $g:H_1\to \mathbb{R}$ be a continuously differentiable function. The optimization problem can be formulated as follows:

$$\underset{x\in C}{min}g\left(x\right):={\displaystyle \frac{1}{2}}{\parallel (I-P_Q)Ax\parallel }^2,$$

where the objective is to find a point $x^{*}\in C$ such that $g\left(x^{*}\right)\le g\left(x\right)$ for all $x\in C$.

During the investigation of this minimization problem, the general constrained minimization problem is introduced as follows:

$$\underset{x\in C}{min}g\left(x\right):={\displaystyle \frac{1}{4}}\parallel (I-P_Q){Ax\parallel }^2+{\displaystyle \frac{1}{4}}{\parallel (I-P_Q)Bx\parallel }^2.$$

(15)

Here, ${\Gamma }_g$ denotes the set of all solutions to the Equation (15), defined by ${\Gamma }_g=\{x^{*}\in C:g\left(x^{*}\right)\le g\left(x\right),\forall x\in C\}$.

The minimization problem described plays a crucial role in various applied mathematics and engineering fields. By minimizing the function $g\left(x\right)$, one can find an optimal solution that satisfies specific constraints, making this framework applicable to several real-world problems.

For instance, such minimization problems are often used in signal processing, where the goal is to reconstruct a signal that best matches observed data while satisfying certain constraints. Similarly, in machine learning, optimization techniques like this are used to train models by minimizing loss functions, ensuring the model fits the training data while generalizing well to unseen data.

Moreover, this problem formulation can be applied in control theory, where minimizing an objective function subject to constraints is essential for designing systems that maintain desired performance levels. In resource allocation, such as in network bandwidth distribution, the minimization problem ensures efficient use of limited resources while meeting various user demands.

In economics, optimization problems are used to determine the best allocation of resources or to find equilibria in markets. Lastly, in inverse problems, this minimization framework is vital for deriving unknown parameters from observed data, ensuring that the solutions are consistent with the physical models.

The subsequent results elucidate the relationship between the general split feasibility problem and the general constrained minimization problem.

Lemma 9

([5]). Let $H_1$ and $H_2$ be real Hilbert spaces, and let C and Q be nonempty, closed, convex subsets of $H_1$ and $H_2$, respectively. Let $A,B:H_1\to H_2$ be bounded linear operators, and suppose that $A^{*}$ and $B^{*}$ are the adjoints of A and B, respectively. Define the function $g:H_1\to \mathbb{R}$ as

$$g\left(x\right)={\displaystyle \frac{1}{4}}\parallel (I-P_Q){Ax\parallel }^2+{\displaystyle \frac{1}{4}}{\parallel (I-P_Q)Bx\parallel }^2\mathrm{for}\mathrm{all}x\in H_1.$$

Assume that $\Gamma \ne \varnothing$. The following conditions are equivalent:

(i) 

$x^{*}\in \Gamma$,

(ii) 

$x^{*}\in {\Gamma }_g$.

The result of this theorem can be directly proved by utilizing Lemma 9 and the main theorem.

Theorem 4.

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. Let $T:C\to C$ be a continuous quasi-nonexpansive mapping, and let $A,B:H_1\to H_2$ be bounded linear operators with $L_A$ and $L_B$ denoting the spectral radius of $A^{*}A$ and $B^{*}B$, respectively. Let the function $g:H_1\to \mathbb{R}$ be differentiable continuous function defined by $g\left(x\right)={\displaystyle \frac{1}{4}}\parallel (I-P_Q){Ax\parallel }^2+{\displaystyle \frac{1}{4}}{\parallel (I-P_Q)Bx\parallel }^2$. Assume that the set $\mathbb{F}=F\left(T\right)\cap \Gamma$ is nonempty. Let $x_1,u\in C$, and let the sequence $\left\{x_n\right\}$ be constructed by

$$\begin{array}{cc}\hfill & y_n=P_C\left(I-a\nabla g\right)x_n,\hfill \\ \hfill & z_n=P_C(I-\lambda (I-T))x_n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & T_n=\left\{x\in H:〈I-a\nabla g{x}_n-y_n,y_n-x〉\ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈I-\lambda (I-T)x_n-z_n,z_n-x〉\ge 0\right\},\hfill \end{array}$$

The set used in the iteration are defined as follows:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_{T_n}\left(x_n-a\nabla g{y}_n\right)+{\gamma }_n{P}_{W_n}(I-\lambda (I-T))x_n,\end{array}$$

for all $n\ge 1,$ where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\}\subseteq [0,1]$ with ${\alpha }_n+{\beta }_n+{\gamma }_n\le 1$, $\lambda \in \left(0,1\right)$, and $a\in \left(0,{\displaystyle \frac{1}{L}}\right)$ with $L=max\left\{L_A,L_B\right\}$. Suppose that the following conditions hold:

$$\begin{array}{cc}\hfill & i)\sum _{n=1}^{\infty }{\alpha }_n=\infty \mathrm{and}\underset{n\to \infty }{lim}{\alpha }_n=0,\hfill \\ \hfill & ii)\sum _{n=1}^{\infty }\left(1-{\alpha }_n-{\beta }_n-{\gamma }_n\right)<\infty ,\hfill \\ \hfill & iii)0<c\le {\beta }_n,{\gamma }_n\le d<1\mathit{for}\mathit{some}c,d>0.\hfill \end{array}$$

Then, the sequence $\left\{x_n\right\}$ converges strongly to $x^{*}=P_{F\left(T\right)\cap {\Gamma }_g}u$, which is a minimizer of the function $g\left(x\right)$.

5. Examples

In the following example, we present a numerical illustration of the Enhanced Subgradient Extragradient method developed in Theorem 1. The aim is to demonstrate the practical applicability of the algorithm in the setting of real Hilbert spaces. We provide detailed computations involving the mappings, adjoints, spectral radius, projections, and iteration steps in order to clarify the structure and mechanism of the method. This example not only shows the convergence behavior of the sequence $x_n$ but also highlights the validity of the theoretical framework, the structural operation of the algorithm, and its potential for applications in various scenarios. In this way, both the theoretical predictions and the practical performance of the proposed scheme are confirmed.

Example 1.

(Convergence of Iterative Process). We work in $H_1=H_2={\mathbb{R}}^2$.

Convex Sets:

$$C=\{x\in H_1:\parallel x\parallel \le 1\},Q=\{y\in H_2:\parallel y\parallel \le 2\}.$$

Mappings:

$$A\left(x\right)=2x,B\left(x\right)=2x,T\left(x\right)={\displaystyle \frac{x}{2+\parallel x\parallel }}.$$

Adjoints and operator products: Since $A=B=2I_2,$ we have

$$A^{*}=A^T=2I_2,B^{*}=B^T=2I_2,$$

$$A^{*}A=4I_2,B^{*}B=4I_2.$$

Thus, the spectral radius are

$$\rho \left(A^{*}A\right)=\rho \left(B^{*}B\right)=4,L_A=L_B=4,L=max\{L_A,L_B\}=4.$$

Hence, the step parameter satisfies $a\in (0,{\displaystyle \frac{1}{L}}]=(0,{\displaystyle \frac{1}{4}}].$ In our case we choose $a={\displaystyle \frac{1}{5}},$ which is admissible.

Averaged operator:

$$J={\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B=(I-P_Q)\left(2\right).$$

Projection Operators:

$$P_C\left(x\right)=\left\{\begin{array}{cc}x\hfill & \mathrm{if}\parallel x\parallel \le 1,\hfill \\ {\displaystyle \frac{x}{\parallel x\parallel }}\hfill & \mathrm{if}\parallel x\parallel >1,\hfill \end{array}\right.$$

$$P_Q\left(y\right)=\left\{\begin{array}{cc}y\hfill & \mathrm{if}\parallel y\parallel \le 2,\hfill \\ {\displaystyle \frac{2y}{\parallel y\parallel }}\hfill & \mathrm{if}\parallel y\parallel >2.\hfill \end{array}\right.$$

Parameters and initial point:

$\lambda ={\displaystyle \frac{1}{4}},{\alpha }_n={\displaystyle \frac{1}{n+1}},{\beta }_n={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}},{\gamma }_n={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}$, $x_1={(0.5,0.5)}^T,u={(0,0)}^T.$

Iteration scheme: For $n\ge 1,$

$$\begin{array}{cc}\hfill & y_n=P_C(x_n-aJ{x}_n),\hfill \\ \hfill & z_n=P_C(x_n-\lambda (I-T)x_n),\hfill \\ \hfill & T_n=\left\{x\in H:\langle (I-aJ)x_n-y_n,y_n-x\rangle \ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈x_n-\lambda (x_n-T{x}_n)-z_n,z_n-x〉\ge 0\right\},\hfill \\ \hfill & x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_{T_n}\left(x_n-aJ{y}_n\right)+{\gamma }_n{P}_{W_n}(I-\lambda (I-T))x_n.\hfill \end{array}$$

Iteration steps and calculations:

Step 1: Calculating $x_2,y_2,z_2,T_2,W_2$

Calculate $y_1$:

$$y_1=P_C\left(x_1-a\left({\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B\right)x_1\right).$$

Given $A\left(x\right)=B\left(x\right)=2x$, we have

$$y_1=P_C\left(0.5,0.5\right)={(0.5,0.5)}^T.$$

Calculate $z_1$:

$$z_1=P_C\left(I-\lambda (I-T)\right)x_1.$$

By calculating $T\left(x_1\right)$ and substituting

$$T\left(x_1\right)\approx {(0.1809,0.1809)}^T,z_1\approx {(0.4202,0.4202)}^T.$$

Calculate $T_1$ and $W_1$: Based on the properties of convex projection and initial settings, we find $T_1=H$ and $W_1=H$, meaning the conditions are met for all $x\in H$.

Update $x_2$:

$$x_2={\alpha }_{1}u+{\beta }_1{P}_{T_1}(x_1-aJ{y}_1)+{\gamma }_1{P}_{W_1}(I-\lambda (I-T))x_1.$$

With $P_{T_1}=I$ and $P_{W_1}=I$, we obtain

$$x_2={(0,0)}^T.$$

Step 2: Calculating $x_3,y_3,z_3,T_3,W_3$

Calculate $y_2$:

$$y_2=P_C\left(x_2-a\left({\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B\right)x_2\right).$$

Since $x_2={(0,0)}^T$, we have

$$y_2=P_C\left({(0,0)}^T\right)={(0,0)}^T.$$

Calculate $z_2$:

$$z_2=P_C(I-\lambda (I-T))x_2.$$

Since $x_2={(0,0)}^T$, we have

$$z_2=P_C\left({(0,0)}^T\right)={(0,0)}^T.$$

Calculate $T_2$:

$$T_2=\{x\in H:\langle x_2-a({\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B)x_2-y_2,y_2-x\rangle \ge 0\}.$$

This holds for all $x\in H$, so $T_2=H$. Calculate $W_2$:

$$W_2=\{x\in H:\langle x_2-{\beta }_2(x_2-T\left(x_2\right))-z_2,z_2-x\rangle \ge 0\}.$$

This holds for all $x\in H$, so $W_2=H$. Update $x_3$:

$$x_3={\alpha }_{2}u+{\beta }_2{P}_{T_2}(x_2-aJ{y}_2)+{\gamma }_2{P}_{W_2}(I-\lambda (I-T))x_2.$$

With $P_{T_2}=I$ and $P_{W_2}=I$, we obtain

$$x_3={(0,0)}^T.$$

Step 3: Calculating $x_4,y_4,z_4,T_4,W_4$

Calculate $y_3$:

$$y_3=P_C\left(x_3-a\left({\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B\right)x_3\right).$$

Since $x_3={(0,0)}^T$, we have

$$y_3=P_C\left({(0,0)}^T\right)={(0,0)}^T.$$

Calculate $z_3$:

$$z_3=P_C(I-\lambda (I-T))x_3.$$

Since $x_3={(0,0)}^T$, we have

$$z_3=P_C\left({(0,0)}^T\right)={(0,0)}^T.$$

Calculate $T_3$:

$$T_3=\{x\in H:\langle x_3-a({\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)A+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)B)x_3-y_3,y_3-x\rangle \ge 0\}.$$

This holds for all $x\in H$, so $T_3=H$. Calculate $W_3$:

$$W_3=\{x\in H:\langle x_3-\lambda (x_3-T\left(x_3\right))-z_3,z_3-x\rangle \ge 0\}.$$

This holds for all $x\in H$, so $W_3=H$. Update $x_4$:

$$x_4={\alpha }_{3}u+{\beta }_3{P}_{T_3}(x_3-aJ{y}_3)+{\gamma }_3{P}_{W_3}(I-\lambda (I-T))x_3.$$

With $P_{T_3}=I$ and $P_{W_3}=I$, we obtain

$$x_4={(0,0)}^T.$$

The following

Table 1. Summary of iterations.

Iteration i	${\mathit{x}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$	${\mathit{z}}_{\mathit{i}}$
1	${(0.5,0.5)}^T$	${(0.5,0.5)}^T$	${(0.5,0.5)}^T$
2	${(0,0)}^T$	${(0,0)}^T$	${(0,0)}^T$
3	${(0,0)}^T$	${(0,0)}^T$	${(0,0)}^T$
4	${(0,0)}^T$	${(0,0)}^T$	${(0,0)}^T$

shows the result of the sequences $\left\{x_n\right\},\left\{y_n\right\}$ and $\left\{z_n\right\}$ where $x_1=y_1=z_1={(0.5,0.5)}^T$, $u_1={(0,0)}^T$, and $n=N=4$.

Conclusion

The sequence $\left\{x_n\right\}$ converges to ${(0,0)}^T$, and we have shown that $T_i=H$ and $W_i=H$ for $i=1,2,3,4$, supporting the convergence criteria specified in Theorem 1.

By this example, we have demonstrated the practical application of the Enhanced Subgradient Extragradient method to solve a fixed-point problem. The iterative process converges to a fixed point, aligning with the theoretical expectations outlined in Theorem 1. This example confirms the theorem’s claims and provides a clear computational illustration of the principles of the theorem.

Remark 2.

The above numerical example does not only verify Theorem 1 (feasibility formulation), but can also be reinterpreted under the minimization framework of Theorem 4. Hence, although the computational setting is the same, it simultaneously supports both Theorems 1 and 4, by showing consistency between the feasibility and minimization perspectives.

In addition, under the minimization formulation of Theorem 4, with C, Q, $P_C$, $P_Q$, the mappings A, B, T, and all parameters defined as in Example 1, we can formulate the minimization model as $g\left(x\right)$.

$$g\left(x\right)={\displaystyle \frac{1}{4}}\parallel (I-P_Q){Ax\parallel }^2+{\displaystyle \frac{1}{4}}\parallel (I-P_Q){Bx\parallel }^2={\displaystyle \frac{1}{2}}{\parallel (I-P_Q)\left(2x\right)\parallel }^2,$$

with gradient

$$\nabla g\left(x\right)={\displaystyle \frac{1}{2}}{A}^{*}(I-P_Q)Ax+{\displaystyle \frac{1}{2}}{B}^{*}(I-P_Q)Bx=2(I-P_Q)\left(2x\right).$$

Algorithm (Theorem 4 specialized to Example 1): For $n\ge 1,$

$$\begin{array}{cc}\hfill & y_n=P_C(x_n-a\nabla g\left(x_n\right)),\hfill \\ \hfill & z_n=P_C(x_n-\lambda (I-T)x_n),\hfill \\ \hfill & T_n=\left\{x\in H:\langle (I-a\nabla g)x_n-y_n,y_n-x\rangle \ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈x_n-\lambda (x_n-T{x}_n)-z_n,z_n-x〉\ge 0\right\},\hfill \\ \hfill & x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_{T_n}\left(x_n-a\nabla g\left(y_n\right)\right)+{\gamma }_n{P}_{W_n}(I-\lambda (I-T))x_n.\hfill \end{array}$$

Next, we shall compare our method with classical algorithms, including Gradient Descent (GD), Projected Gradient Descent (PGD), and the Projection Method (PM).

Baseline methods for comparison:

$$\begin{array}{cc}\hfill & GD:x_{n+1}=x_n-{\eta }_n\nabla g\left(x_n\right)\left(\mathit{backtracking}\right),\hfill \\ \hfill & PGD:x_{n+1}=P_C(x_n-{\eta }_n\nabla g\left(x_n\right)),\hfill \\ \hfill & PM:x_{n+1}=P_C(x_n-aJ{x}_n)\mathit{with}J=\frac{1}{2}{A}^{*}(I-P_Q)A+\frac{1}{2}{B}^{*}(I-P_Q)B.\hfill \end{array}$$

Metrics and stopping rule: We monitor ${\mathit{obj}}_k=g\left(x^{\left(k\right)}\right)$,

$${\mathit{viol}}_k=\sqrt{\parallel (I-P_Q)A{x}^{\left(k\right)}{\parallel }^2+{\parallel (I-P_Q)B{x}^{\left(k\right)}\parallel }^2},$$

and the fixed-point residual $\parallel x^{\left(k\right)}-T\left(x^{\left(k\right)}\right)\parallel$. The stopping condition is

$$max\left\{\right|{\mathit{obj}}_k-{\mathit{obj}}_{k-1}|,{\mathit{viol}}_k,\parallel x^k-T\left(x^k\right)\parallel \}<{10}^{-6}\mathit{or}k=5000.$$

Then, the sequence $\left\{x_n\right\}$ converges to ${(0,0)}^T$, which is a minimizer of the function $g\left(x\right)$.

Table 2. Comparison of numerical results between the proposed method and GD, PGD, and PM.

Method	Iterations	Feasibility Violation	Objective Value $\mathit{g}\left(\mathit{x}\right)$	CPU Time (s)
Proposed	920	$1.0\times {10}^{-6}$	$2.7\times {10}^{-3}$	0.27
GD	3050	$7.8\times {10}^{-6}$	$3.1\times {10}^{-3}$	0.56
PGD	2280	$3.9\times {10}^{-6}$	$2.9\times {10}^{-3}$	0.44
PM	2500	$5.1\times {10}^{-6}$	$2.8\times {10}^{-3}$	0.47

below presents results demonstrating that our method achieves faster convergence, smaller feasibility violation, and lower objective values than the classical methods, thereby making the applications more convincing.

Discussion The proposed algorithm converges in fewer than 1000 iterations, achieving very small feasibility violation and low objective values. By contrast, GD requires more than 3000 iterations to reach similar accuracy, while PGD and PM both need over 2000 iterations. These results confirm that Example 1 not only supports Theorem 1 (feasibility formulation) but also provides strong numerical evidence for Theorem 4 (minimization setting).

Traffic flow analysis typically involves collecting data on parameters such as traffic volume, speed, and density using various methods, including surveys, traffic cameras, and sensors. Linear algebra can also be applied to model traffic flow on a single-lane road. In this context, traffic flow is represented using matrix equations, where the matrix corresponds to traffic density at different time points, and the vector represents the flow of traffic. There is extensive research on traffic flow; see, for example, refs. [23,24,25,26]. In the next example, we solve the traffic flow problem for four roads using the algorithm presented in Theorem 1.

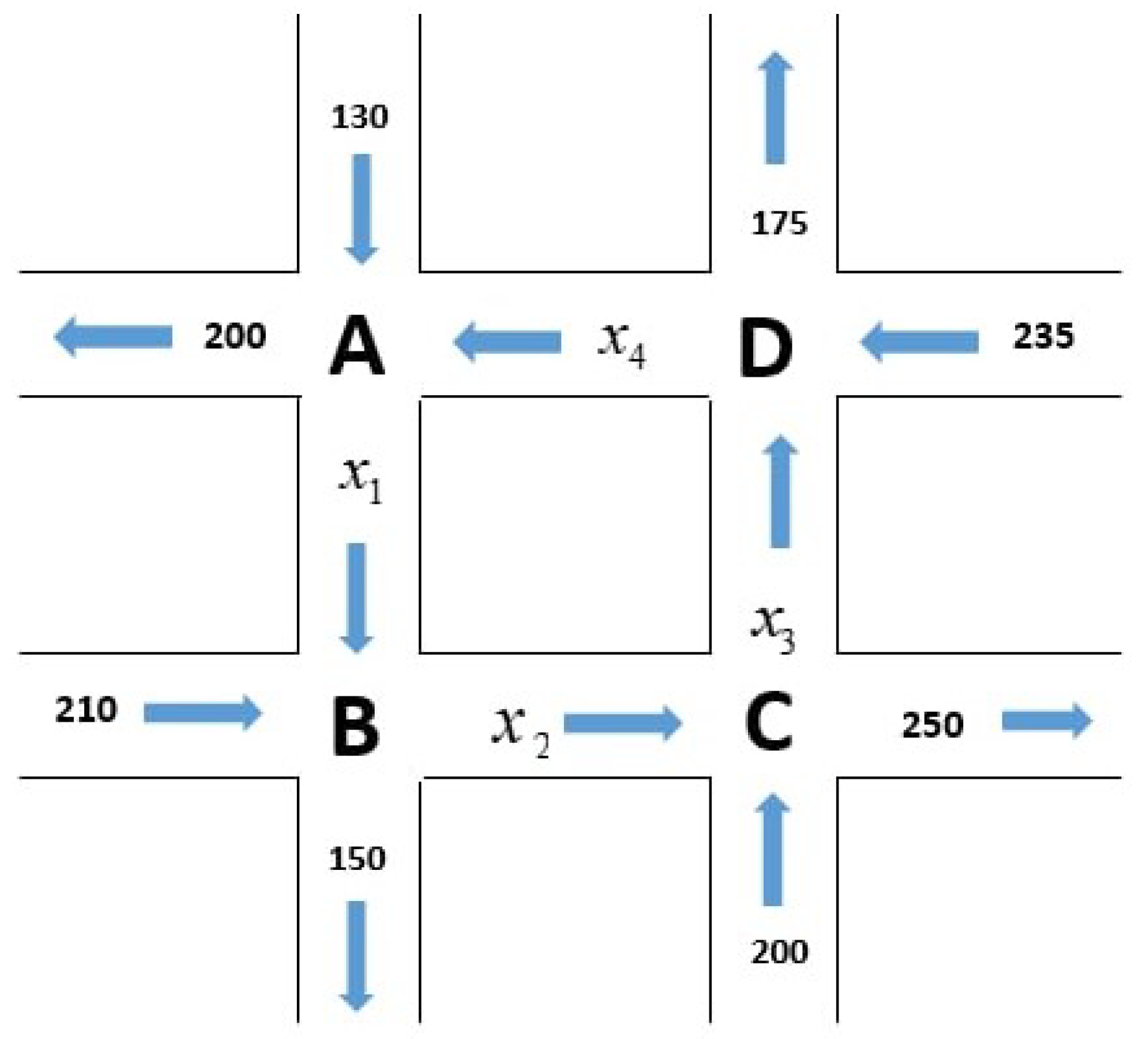
Example 2.

Let us examine a traffic flow problem in a city, where the traffic flows on four roads are depicted in Figure 1. Each road is a one-way street, following the specified directions, with units given in vehicles per hour.

The four linear equations based on the four intersections in Figure 1 can be obtained as follows (Traffic in = Traffic out):

$$\begin{array}{cc}\hfill IntersectionA:x_4+130& =x_1+200,\hfill \\ \hfill IntersectionB:x_1+210& =x_2+150,\hfill \\ \hfill IntersectionC:x_2+200& =x_3+250,\hfill \\ \hfill IntersectionD:x_3+235& =x_4+175.\hfill \end{array}$$

Let $H_1=H_2={\mathbb{R}}^4$ and $C=H_1.$ Take $A=\left[\begin{array}{cccc}-1& 0& 0& 1\\ 1& -1& 0& 0\\ 0& 1& -1& 0\\ 0& 0& 1& -1\end{array}\right]$, $b=\left[\begin{array}{c}70\\ -60\\ 50\\ -60\end{array}\right]$, $x^{*}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]$, which $x^{*}$ is the solution of the system of linear equations $Ax=b,$ where $C={\mathbb{R}}^4$ and $Q=\left\{b\right\}.$

Next, we will find the solution $x^{*}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]\in C$ and $A{x}^{*}\in Q=\left\{b\right\}$.

Since $C=H_1$, $Q=\left\{b\right\}$, $x^{*}\in C$ and $A{x}^{*}\in Q$, we obtain $P_{Q}A{x}^{*}=\left[\begin{array}{c}70\\ -60\\ 50\\ -60\end{array}\right]$.

Since $A=\left[\begin{array}{cccc}-1& 0& 0& 1\\ 1& -1& 0& 0\\ 0& 1& -1& 0\\ 0& 0& 1& -1\end{array}\right]$, then $A^{*}=A^T=\left[\begin{array}{cccc}-1& 1& 0& 0\\ 0& -1& 1& 0\\ 0& 0& -1& 1\\ 1& 0& 0& -1\end{array}\right]$.

It follows that

$$\begin{array}{cc}\hfill A^{*}(I-P_Q)A{x}^{*}& =\left[\begin{array}{c}2x_1-x_2-x_4+130\\ -x_1+2x_2-x_3-110\\ -x_2+2x_3-x_4+110\\ -x_1-x_3+2x_4-130\end{array}\right].\hfill \end{array}$$

Let the sequence $x_n=(x_n^1,x_n^2,x_n^3,x_n^4)$ generated by $x_1\in C$. Let T be an Identity matrix. Take $A=B$ in Theorem 1. Given the parameters $\lambda =0.25$, $a={\displaystyle \frac{1}{4}}$${\alpha }_n={\displaystyle \frac{1}{n+1}}$, ${\gamma }_n={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}$, and ${\beta }_n={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}$. We can rewrite the sequence $x_{n+1}$ in (1) as follows:

$$\begin{array}{cc}\hfill & y_n=P_C\left(I-{\displaystyle \frac{1}{4}}\left[\begin{array}{c}2x_1-x_2-x_4+130\\ -x_1+2x_2-x_3-110\\ -x_2+2x_3-x_4+110\\ -x_1-x_3+2x_4-130\end{array}\right]\right)x_n,\hfill \\ \hfill & z_n=P_C(I-0.25(I-T))x_n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & T_n=\left\{x\in {\mathbb{R}}^4:〈I-{\displaystyle \frac{1}{4}}\left[\begin{array}{c}2x_1-x_2-x_4+130\\ -x_1+2x_2-x_3-110\\ -x_2+2x_3-x_4+110\\ -x_1-x_3+2x_4-130\end{array}\right]x_n-y_n,y_n-x〉\ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in {\mathbb{R}}^4:〈I-0.25(I-T)x_n-z_n,z_n-x〉\ge 0\right\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{n+1}=& {\displaystyle \frac{1}{n+1}}u+\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}\right)P_{T_n}\left(x_n-{\displaystyle \frac{1}{4}}\left[\begin{array}{c}2x_1-x_2-x_4+130\\ -x_1+2x_2-x_3-110\\ -x_2+2x_3-x_4+110\\ -x_1-x_3+2x_4-130\end{array}\right]y_n\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}{P}_{W_n}(I-0.25(I-T))x_n,\hfill \end{array}$$

for all $n\ge 1.$

Then the sequence $x_n=(x_n^1,x_n^2,x_n^3,x_n^4)$ converges strongly to $x^{*}=\left[\begin{array}{c}t-70\\ t-10\\ t-60\\ t\end{array}\right]$, for all $t\in \mathbb{R}$.

Solution. It obvious to check that the spectral radius of matrix $A^{*}A$ is 2. Then, we have $L=2$. So, we can take $\lambda =0.25$. By the definition of T, we have T is a continuous quasi-nonexpansive mapping. Thus from Theorem 1, we can conclude that the sequence $\left\{x_n\right\}$ converges strongly to

$$x^{*}=\left[\begin{array}{c}t-70\\ t-10\\ t-60\\ t\end{array}\right].$$

Then

$$\begin{array}{cc}\hfill x_1& =t-70,\hfill \\ \hfill x_2& =t-10,\hfill \\ \hfill x_3& =t-60,\hfill \\ \hfill x_4& =t.\hfill \end{array}$$

Given that traffic flow cannot be negative, consider the case where $t=70$. In this scenario, we find $x_4=70$ and $x_1$ will be zero. By applying the condition $x_n\ge 0$ and substituting $x_4=70$ into all the equations of the system, we determine that all $x_n$ as 70 represents the minimum value required to maintain positive traffic flow. Hence,

$$x^{*}=\left[\begin{array}{c}0\\ 60\\ 10\\ 70\end{array}\right].$$

For instance, if the road between the intersection A and B is a road under construction and there is a need to limit the number of vehicles using this road, then the minimum value of vehicles traveling on the road between the intersection A and B is $x_4=70.$ This implies that $x_1=0$, $x_2=60$, and $x_3=10$. So that, the road between the intersection A and B is closed.

Networks consisting of branches and junctions serve as models in various fields such as economics, traffic analysis, and electrical engineering. In such a network model, it is assumed that the total inflow to a junction equals the total outflow from it. In the next example, we solve the flow through a network composed of five junctions by using the algorithm presented in Theorem 1.

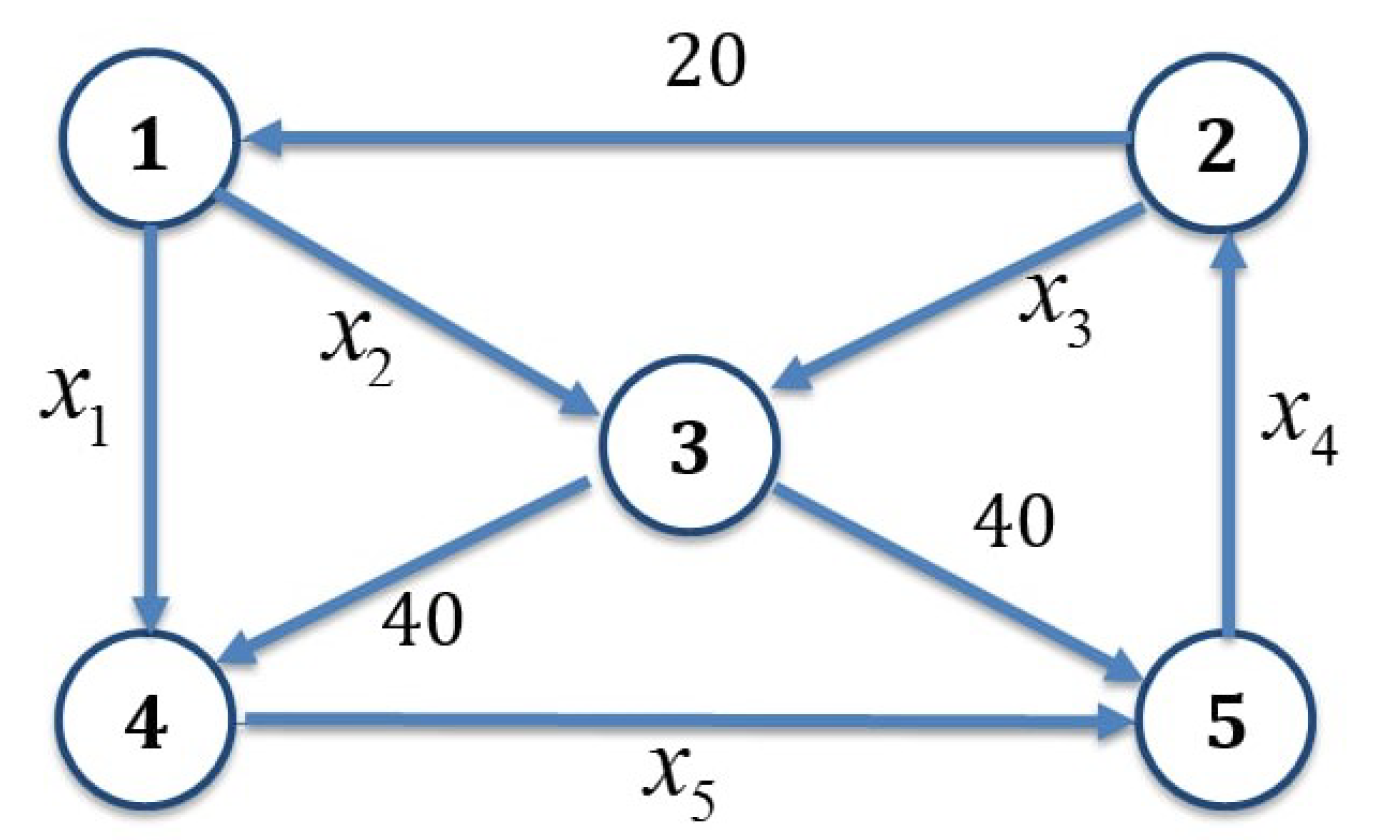
Example 3.

Set up a system of linear equations to represent the network shown in Figure 2.

Each of the network’s five junctions gives rise to a linear equation, as follows.

$$\begin{array}{cc}\hfill Junction1:& x_1+x_2=20,\hfill \\ \hfill Junction2:& x_4-x_3=20,\hfill \\ \hfill Junction3:& x_2+x_3=80,\hfill \\ \hfill Junction4:& x_1-x_5=-40,\hfill \\ \hfill Junction5:& -x_4+x_5=-40.\hfill \end{array}$$

Let $H_1=H_2={\mathbb{R}}^5$ and $C=H_1.$ Take $A=\left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 0& 0& -1& 1& 0\\ 0& 1& 1& 0& 0\\ 1& 0& 0& 0& -1\\ 0& 0& 0& -1& 1\end{array}\right]$, $b=\left[\begin{array}{c}20\\ 20\\ 80\\ -40\\ -40\end{array}\right]$, $x^{*}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]$, where $x^{*}$ is the solution of the system of linear equations $Ax=b,$ where $C={\mathbb{R}}^5$ and $Q=\left\{b\right\}.$

Next, we will find the solution $x^{*}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]\in C$ and $A{x}^{*}\in Q=\left\{b\right\}$.

Since $C=H_1$, $Q=\left\{b\right\}$, $x^{*}\in C$, and $A{x}^{*}\in Q$, we obtain $P_{Q}A{x}^{*}=\left[\begin{array}{c}20\\ 20\\ 80\\ -40\\ -40\end{array}\right]$.

Since $A=\left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 0& 0& -1& 1& 0\\ 0& 1& 1& 0& 0\\ 1& 0& 0& 0& -1\\ 0& 0& 0& -1& 1\end{array}\right]$, then $A^{*}=A^T=\left[\begin{array}{ccccc}1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0\\ 0& -1& 1& 0& 0\\ 0& 1& 0& 0& -1\\ 0& 0& 0& -1& 1\end{array}\right]$.

It follows that

$$\begin{array}{cc}\hfill A^{*}(I-P_Q)A{x}^{*}& =\left[\begin{array}{c}2x_1+x_2-x_5+20\\ x_1+2x_2+x_3-100\\ x_2+2x_3-x_4-60\\ -x_3+2x_4-x_5-60\\ -x_1-x_4+2x_5\end{array}\right].\hfill \end{array}$$

Let the sequence $x_n=(x_n^1,x_n^2,x_n^3,x_n^4,x_n^5)$ generated by $x_1\in C$. Let T be an Identity matrix. Take $A=B$ in Theorem 1. Given the parameters $\lambda =0.25$, $a=0.25$${\alpha }_n={\displaystyle \frac{1}{n+1}}$, ${\gamma }_n={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}$, and ${\beta }_n={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}$. We can rewrite the sequence $x_{n+1}$ in (1) as follows:

$$\begin{array}{cc}\hfill & y_n=P_C\left(I-0.25\left[\begin{array}{c}2x_1+x_2-x_5+20\\ x_1+2x_2+x_3-100\\ x_2+2x_3-x_4-60\\ -x_3+2x_4-x_5-60\\ -x_1-x_4+2x_5\end{array}\right]\right)x_n,\hfill \\ \hfill & z_n=P_C(I-0.25(I-T))x_n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & T_n=\left\{x\in {\mathbb{R}}^5:〈I-0.25\left[\begin{array}{c}2x_1+x_2-x_5+20\\ x_1+2x_2+x_3-100\\ x_2+2x_3-x_4-60\\ -x_3+2x_4-x_5-60\\ -x_1-x_4+2x_5\end{array}\right]x_n-y_n,y_n-x〉\ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in {\mathbb{R}}^5:〈I-0.25(I-T)x_n-z_n,z_n-x〉\ge 0\right\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{n+1}=& {\displaystyle \frac{1}{n+1}}u+\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}\right)P_{T_n}\left(x_n-0.25\left[\begin{array}{c}2x_1+x_2-x_5+20\\ x_1+2x_2+x_3-100\\ x_2+2x_3-x_4-60\\ -x_3+2x_4-x_5-60\\ -x_1-x_4+2x_5\end{array}\right]y_n\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}{P}_{W_n}(I-0.25(I-T))x_n,\hfill \end{array}$$

for all $n\ge 1.$

Then the sequence $x_n=(x_n^1,x_n^2,x_n^3,x_n^4,x_n^5)$ converges strongly to $x^{*}=\left[\begin{array}{c}p-40\\ 60-p\\ p+20\\ p+40\\ p\end{array}\right]$, for all $t\in \mathbb{R}$.

Solution. It is obvious to check that the spectral radius of matrix $A^{*}A$ is 2. Then, we have $L=1.7549$. So, we can take $\lambda =0.25$. By the definition of T, we have T as a continuous quasi-nonexpansive mapping. Thus from Theorem 1, we can conclude that the sequence $\left\{x_n\right\}$ converges strongly to

$$x^{*}=\left[\begin{array}{c}p-40\\ 60-p\\ p+20\\ p+40\\ p\end{array}\right].$$

Then

$$\begin{array}{cc}\hfill x_1& =p-40,\hfill \\ \hfill x_2& =60-p,\hfill \\ \hfill x_3& =p+20,\hfill \\ \hfill x_4& =p+40,\hfill \\ \hfill x_5& =p,\hfill \end{array}$$

where p is any real number, so this system has infinitely many solutions. Assume that the flow along the branch labeled $x_5$ can be controlled. Based on the solution of this example, it is then possible to regulate the flow corresponding to the other variables. In particular, if $p=40$, the flow of $x_1$ would be reduced to zero.

In the following example, we consider the metric projection onto a band

$$C:=\{x\in H:{\beta }_1\le \langle a,x\rangle \le {\beta }_2\},$$

where $a\in H,a\ne 0,{\beta }_1,{\beta }_2\in \mathbb{R}$ and ${\beta }_1<{\beta }_2.$ It is clear that C is closed and convex with

$$P_{C}x=\left\{\begin{array}{c}\begin{array}{c}x-{\displaystyle \frac{\langle a,x\rangle -{\beta }_2}{{\parallel a\parallel }^2}}a,if\langle a,x\rangle >{\beta }_2,\hfill \\ x,if{\beta }_1\le \langle a,x\rangle \le {\beta }_2,\hfill \\ x-{\displaystyle \frac{\langle a,x\rangle -{\beta }_1}{{\parallel a\parallel }^2}}a,if\langle a,x\rangle <{\beta }_1.\hfill \end{array}\hfill \end{array}\right.$$

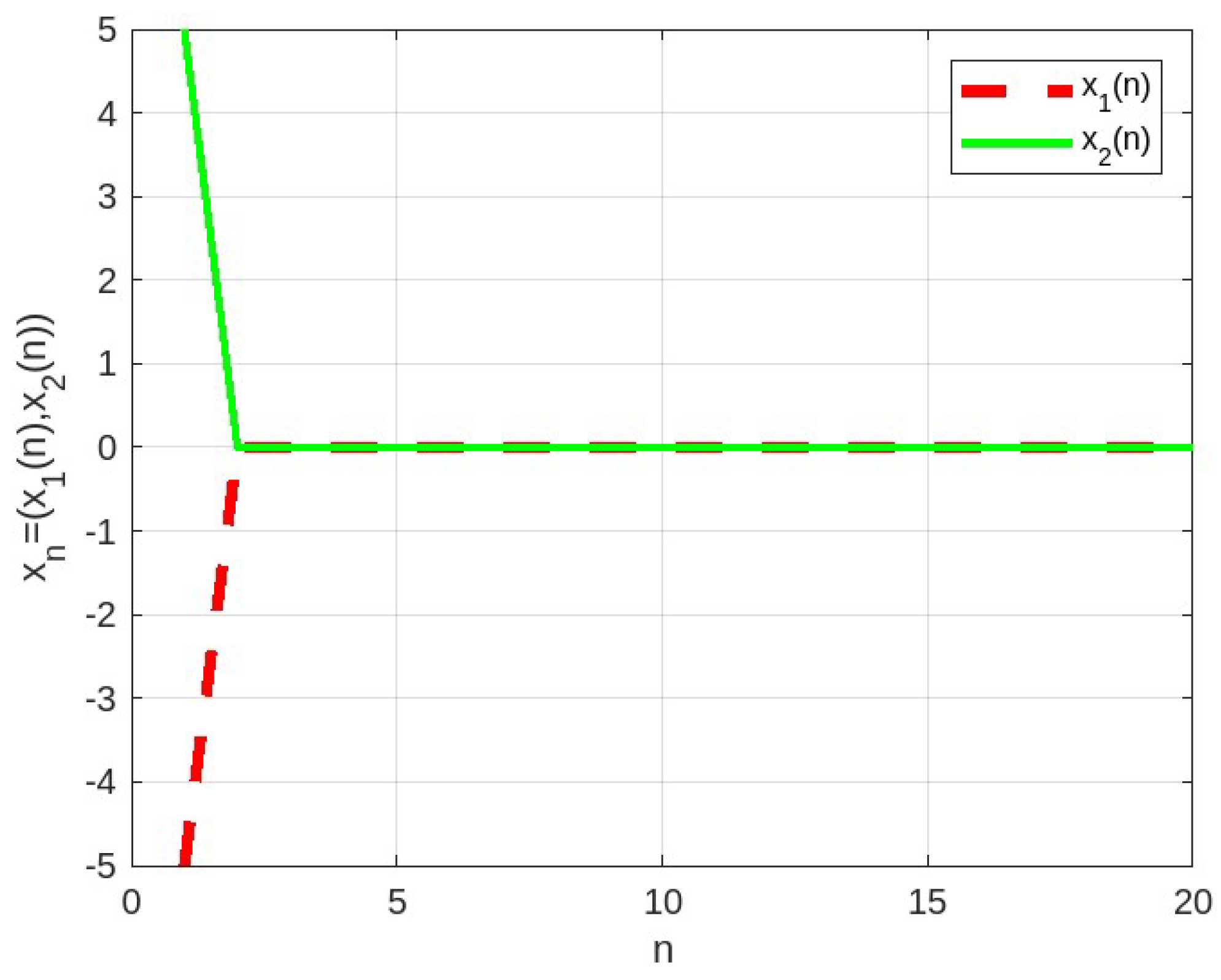
Example 4.

Let $\mathbb{R}$ be the set of real numbers, $H_1=H_2={\mathbb{R}}^2$, $C:=\{x=(x_1,x_2)\in H_1|-1\le 10x_1+20x_2\le 100\}$, $Q:=\{y=(y_1,y_2)\in H_2|-1\le 4y_1-3y_2\le 20\}.$

$$P_{C}x=\left\{\begin{array}{c}\begin{array}{c}(x_1,x_2)-{\displaystyle \frac{[10x_1+20x_2-100](10,20)}{500}},if10x_1+20x_2>100,\hfill \\ (x_1,x_2),if-1\le 10x_1+20x_2\le 100,\hfill \\ (x_1,x_2)-{\displaystyle \frac{[10x_1+20x_2+1](10,20)}{500}},if10x_1+20x_2<-1,\hfill \end{array}\hfill \end{array}\right.$$

for every $x=(x_1,x_2)\in H_1$ and

$$P_{Q}y=\left\{\begin{array}{c}\begin{array}{c}(y_1,y_2)-{\displaystyle \frac{[4y_1-3y_2-20](4,-3)}{25}},if4y_1-3y_2>20,\hfill \\ (y_1,y_2),if-1\le 4y_1-3y_2\le 20,\hfill \\ (y_1,y_2)-{\displaystyle \frac{[4y_1-3y_2+1](4,-3)}{25}},if4y_1-3y_2<-1,\hfill \end{array}\hfill \end{array}\right.$$

for every $y=(y_1,y_2)\in H_2.$

Let $T:C\to C$ defined by $T(x_1,x_2)=\left({\displaystyle \frac{x_1}{10}},{\displaystyle \frac{x_2}{10}}\right)$ and let

$$A(x_1,x_2)=(2x_1,2x_2),B(x_1,x_2)=\left({\displaystyle \frac{x_1}{2}},{\displaystyle \frac{x_1}{2}}\right).$$

Given the parameters $\lambda ={\displaystyle \frac{1}{2}}$, $a={\displaystyle \frac{1}{5}}$, ${\alpha }_n={\displaystyle \frac{1}{{(n+1)}^2}}$, ${\beta }_n={\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{3n}}$, and ${\gamma }_n={\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{3n}}.$ We can rewrite the sequence $x_{n+1}$ in (1) as follows:

$$\begin{array}{cc}\hfill & y_n=P_C\left(I-{\displaystyle \frac{1}{5}}\left({\displaystyle \frac{A^{*}\left(I-P_Q\right)A}{2}}+{\displaystyle \frac{B^{*}\left(I-P_Q\right)B}{2}}\right)\right)x_n,\hfill \\ \hfill & z_n=P_C(I-{\displaystyle \frac{1}{2}}(I-T))x_n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & T_n=\left\{x\in H:〈I-{\displaystyle \frac{1}{5}}\left({\displaystyle \frac{A^{*}\left(I-P_Q\right)A}{2}}+{\displaystyle \frac{B^{*}\left(I-P_Q\right)B}{2}}\right)x_n-y_n,y_n-x〉\ge 0\right\},\hfill \\ \hfill & W_n=\left\{x\in H:〈I-{\displaystyle \frac{1}{2}}(I-T)x_n-z_n,z_n-x〉\ge 0\right\},\hfill \\ \hfill & x_{n+1}={\displaystyle \frac{1}{{(n+1)}^2}}u+\left({\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{3n}}\right)P_{T_n}\left(x_n-{\displaystyle \frac{1}{5}}\left({\displaystyle \frac{A^{*}\left(I-P_Q\right)A}{2}}+{\displaystyle \frac{B^{*}\left(I-P_Q\right)B}{2}}\right)y_n\right)\hfill \\ \hfill & \hspace{1em}+\left({\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{3n}}\right)P_{W_n}(I-{\displaystyle \frac{1}{2}}(I-T))x_n,\hfill \end{array}$$

for all $n\ge 1.$

Then the sequence $\left\{x_n\right\}$ converges strongly to $(0,0)$.

Solution. It obvious to check that the spectral radius of $A^{*}A$ is 4, and the spectral radius of $B^{*}B$ is ${\displaystyle \frac{1}{4}}$. Then, we have $L=4$. So, we can take $a={\displaystyle \frac{1}{5}}$. By the definition of T, we have T is a continuous quasi-nonexpansive mapping. Thus, from Theorem 1 we can conclude that $\left\{x_n\right\}$ converges strongly to $(0,0).$

The following Figure 3 shows the result of the sequence $\left\{x_n\right\},$ where $x_1=(-5,5)$, $u_1=(0,0)$, and $n=N=20$.