Abstract
Cell motility is a process central to life and is undoubtedly influenced by mechanical and chemical signals. Even so, other stimuli are also involved in controlling cell migration in vivo and in vitro. Among these, electric fields have been shown to provide a powerful and programmable cue to manipulate cell migration. There is now a clear consensus that the electromigration of membrane components represents the first response to an external electric field, which subsequently activates downstream signals responsible for controlling cell migration. Here, we focus on a specific mode of electrotaxis: frictionless, amoeboid-like migration. We used the Finite Element Method to solve an active gel model coupled with a mathematical model of the electromigration of aquaporins and investigate the effect of electric fields on ameboid migration. We demonstrate that an electric field can polarize aquaporins in a cell and, consequently, that the electromigration of aquaporins can be exploited to regulate water flux across the cell membrane. Our findings indicate that controlling these fluxes allows modulation of cell migration velocity, thereby reducing the cell’s migratory capacity. Our work provides a mechanistic framework to further study the impact of electrotaxis and to add new insights into specific modes by which electric fields modify cell motility.
MSC:
92C17
1. Introduction
Single [1,2] and collective [3,4,5] cell migrations are foundational processes of life, including morphogenesis and cancer. During migration, cells follow exogenous stimuli to navigate. Chemotaxis [6] and durotaxis [7,8]—the motion of cells along chemical or mechanical gradients—have received most of the attention in fundamental cell science as well as in cell biophysics. Electrotaxis [9,10], the migration of cells along the direction of an electric potential, is much less well studied, but it represents a powerful and programmable mechanism for guiding cell migration. Electrotaxis has been observed in many different cell types, e.g., cancer cells [11], leukocytes [12], and neurons [13], as well as in different physiological contexts such as embryonic development [14] and wound healing [15]. When an exogenous electric field (EF) is applied in vitro, it can alter normal development [9], modify cell behavior [16], or induce directed migration [16,17].
To understand electrotaxis, we must follow all steps in the sensing and transduction of EFs from outside to inside the cell. The cell membrane is crowded with a large set of charged membrane components (CMCs) and lipids. Because of the high resistance of the cell membrane, an external electric field has only a limited intracellular effect, acting mainly on membrane components [18]. Within this context, the electromigration of CMCs has been proposed as the primary mechanism by which cells sense and react to EFs [19,20]. Electromigration of CMCs asymmetrically transduces intracellular pathways that enable cell migration, particularly the actomyosin network [21,22,23] and cell adhesion [24]. Although experimental observations and mathematical models now support this hypothesis of electrotaxis, other electrotactic mechanisms may coexist.
Mathematical and computational models have been widely employed to study cell motility (see, e.g., [25,26,27] for reviews). Continuum approaches to cell migration typically focus on the mechanics and transport of the actomyosin network, most often described using active gel models [28,29,30]. Many of these models can be solved analytically, which imposes clear limitations. Others rely on numerical methods—such as the Finite Element Method (FEM), phase-field models, and the immersed boundary method—to capture complex shape dynamics in two and three dimensions (see, e.g., [31,32,33]). In recent years, we have applied the FEM to reproduce interactions between cellular structures [34], specific stages of migration [31], and diverse forms of directed cell movement, including durotaxis [35] and electrotaxis [36].
Here, we explore electrotaxis in an adhesion-independent confined cell migration model [1,37]. In this context, integrin-based adhesion mechanisms are absent. Moreover, the protruding actin network [38], which propels the cell forward at the front in adhesion-dependent migration, is weak, and the main motility forces are the contractile actomyosin network of the cell cortex and water fluxes driven by pressure gradients across the cell body [1,30,37], as summarized in Figure 1. We investigate how EFs can regulate cell migration within this specific migration mode.
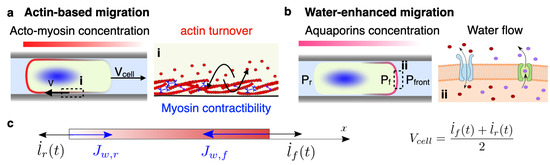
Figure 1.
(a) Actin-based mechanisms in confined cell migration. The velocity of migration, , is controlled by the actin turnover and myosin contractility (i). (b) Water-enhanced cell migration is powered by water flows (ii) through the cell. Aquaporin concentration and pressure gradients at the front and rear of the cell drive water flow through the cell membrane. (c) Sketch of the 1D model, representing the velocity of the moving boundaries, and , which determines the migration velocity of the cell, , and the water fluxes through the front and rear of the cell, and .
2. Mathematical Model
2.1. Actin-Based and Water-Enhanced Cell Migration
We consider a minimal one-dimensional model to capture the essential features of confined cell migration. The modeling framework is adapted from our previous studies (see [31,36] for details). In short, the domain of the cell, , is a continuum segment with moving coordinates , where and represent the rear and front boundary of the cell, and therefore, the length of the cell is determined as . The boundary’s velocity will be given by and , and we define the cell velocity as .
The velocity of the cell ends will depend on a balance of forces. We consider that the motility forces arise from the active contraction of the actomyosin network. We consider the mechanics of the actomyosin network to follow the balance of linear momentum [39] as
where we have assumed negligible inertial terms and a constitutive relation for the internal stresses, that accounts for the viscosity of the actin cortex and the actomyosin contractility, respectively. v is the velocity of the actin cortex in the lab frame, is its shear viscosity, is the density of the actomyosin network (defined below), and is the active contraction exerted by the contractile myosin motors. The term on the r.h.s. represents the friction between the moving cell and the external space, which we assume to be proportional to the cortex velocity with a friction constant . Neumann boundary conditions are imposed at both ends of the cell, , which control the cell length due to the membrane tension [40]. We assume the cell length to be determined by a linear relation , where k is the stiffness of the cell and . is its initial length.
To model the effective transport of the actin–myosin network, we use a transient advection–diffusion equation as
where is the density of the active actomyosin network and is the diffusion constant. Here, we follow the cell frame description where the vector field w represents the advection velocity of the actomyosin network. The lab and cell frame velocities are related such that . We impose zero flux boundary conditions at both cell ends to describe that no actomyosin flow can enter or leave the cell membrane. We also assume that the concentration of actin monomers balances instantaneously in the cell [41]. Therefore, the concentration of actin monomers is constant along the cell length and in time [29,30,31].
2.2. Water Fluxes Through and Across the Cell
Cells are equipped with aquaporins, cell membrane pores, that allow water to cross [42,43]. Aquaporins have been observed at the front of cells migrating in confined environments [1], as well as in migrating keratocytes [44], presumably, to release increasing intracellular pressure through water exchange. The pressure differences between the cell interior and the external space, along with the presence of aquaporins at the cell membrane, induce a flux of water across the cell. The flux of water through the front and rear of the cell is defined as and , respectively, where are the differential pressure between the intracellular and extracellular sides of the cell membrane for the front and rear of the cell, respectively, and [1] is the water permeability of the cell at both ends. During the transient state, the net flow of water across the cell induces a length change as = and, eventually, modifies the Neumann boundary condition in Equation (1) as .
At the exterior of a confined migrating cell, the pressure due to drag forces is , where represents an effective drag coefficient [37]. The water flux at the front may also release the pressure generated in the front of the cell as (). The pressure at the rear is kept constant at atmospheric pressure.
The flux conditions at both ends of the cell membrane allow us to calculate the water velocity through the cytosol. In the limit of the low Reynolds number and using lubrication theory, the flow of water inside the cell due to the pressure gradient is given by Darcy’s law at steady state as , where b is the width of the cell, and P the intracellular pressure [44,45].
2.3. Electromigration of Aquaporins
Next, we study the electromigration of aquaporins due to the application of an external EF. Most cell surfaces bear a negative charge; thus, positive ions accumulate nearby and develop the region of the Electric Double Layer (EDL). When an EF is imposed on the cell, the electrostatic forces act on the mobile ions in the EDL, and when they move, they drag the fluid around them. This creates an electrically generated fluid flow called the electro-osmotic flow (EOF). Moreover, aquaporins have a hydrophobic domain embedded within the membrane and a positively charged extracellular part. When exposed to an EF, aquaporins electromigrate and redistribute along the cell membrane due to electrostatic forces and drag created by the electroosmotic flow [46]. The electromotility velocity of the aquaporin due to these two forces is given by (see, e.g., [36] for details)
Here, is the dielectric constant of the medium, is the permittivity of free space, E is the applied Electric field, and is the viscosity of the cell membrane. and are Zeta potentials of the aquaporin and the cell surface, respectively.
We model the competing drift electrophoretic velocity and the diffusive transport of the charged membrane components, , as a convection–diffusion equation,
where is the diffusivity. We assume natural Neumann boundary conditions at both ends and an initial condition as described above. We assume that the permeabilities at the front and rear of the cell, , vary linearly with , reflecting that membrane regions with higher aquaporin concentrations permit greater water flux, whereas regions lacking aquaporins exhibit no flux.
2.4. Numerical Solution of the Problem and MODEL Parameters
We solve computationally the coupled system of equations in a staggered way. We use the FEM to discretize the system of equations in space. The parabolic equations are discretized in time using an implicit second-order Crank–Nicholson method [47]. The non-linear system of equations is solved iteratively using the Newton–Raphson method. For the derivation and implementation details, we refer to [31]. We have summarized all model variables and parameters in Table 1, unless specified otherwise.

Table 1.
Table of model variables and occurrence.
3. Results
3.1. Cell Migration in a Confined Space
First, we perform a sensitivity analysis of the model parameters (Figure 2a–c) to analyze two scenarios: (a) a confined actin-based migration where no water flow crosses the cell membrane (Figure 2a) and (b) a water-enhanced migration model for a specific value of these parameters (point (i), Figure 2a) where the concentration of aquaporins in the front of the cell is equal (point (ii), Figure 2b) and 20% higher than in the rear (point (iii), Figure 2b), in agreement with experimental observation [1,44]. We plot the kymographs of the density and actomyosin velocity w (Figure 2c). In both cases, cells initiate a process of self-polarization due to an initial disruption of the actomyosin concentration, which lasts less than ∼2 min. During this stage, cells experience an initial quick contraction due to the almost uniform distribution of the contractile cues. After the initial contraction, the polarization of the actomyosin network evolves over ∼10 min. The polarization of the contractile actomyosin network, shown in Figure 2c, is driven by the convection velocity w.
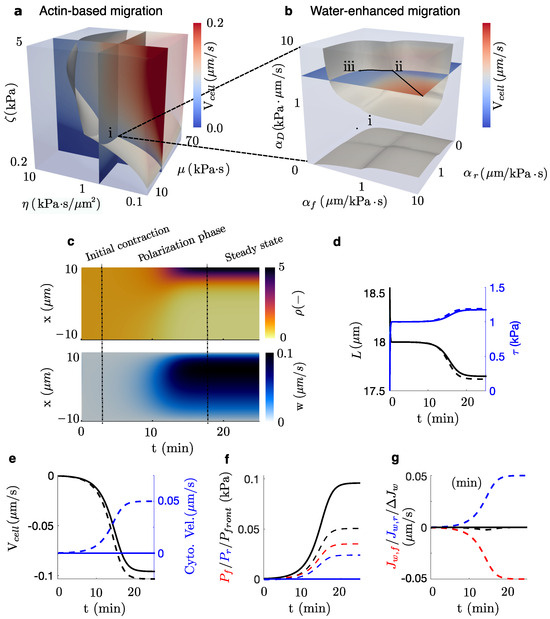
Figure 2.
(a) Cell velocity for a combination of , , and values in an actin-based migration setup. Point (i) represents the combination of parameters chosen for the following water-enhanced and electrotaxis simulations. Point (i) is contained in the grey surface, which shows all combinations of parameters that produce the realistic migration velocity of the isosurface of [1]. (b) Cell velocity for a combination of drag () and permeability of the front and rear of the cell (). Point (ii) represents a cell that migrates with the same concentration of aquaporins in the front and the rear of the cell (). Point (iii) represents a combination of parameters with a 20% higher concentration of aquaporins in the front than in the rear and, still, contained in an isosurface of . The combination of parameters in point (iii) is chosen for the following analysis of electrotaxis. (c) Kymograph of the actomyosin density, , and the velocity of the actomyosin network, w, at steady state. Steady state is reached at t ∼25 min. (d,e) Evolution of the main outputs of the models as a function of time for the actin-based migration (point (i), solid lines) and the water-enhanced migration (point (iii), dashed line). Length of the cell, membrane tension (d), cell and intracellular water velocities (e), pressure at the front of the cell, and intracellular pressure (f), the flow of water across the front and rear, and , and its difference (g) is shown for the combination of parameters in (i) and (iii).
Then, we quantify and compare the time evolution of different cell quantities between cases (a) and (b) (Figure 2d–g). In both cases, the velocity of the cell increases, creating a resisting (Figure 2f) that induces a permeation of water through the cell membrane (Figure 2g) and, consequently, a water flow across the cytosol (Figure 2e). Cells reach a steady-state migration velocity at ∼25 min when the pressure at the front of the cell balances the internal active forces of the crawling cell and the frictional forces. When water is allowed to flow through the cell, we observe a decrease in the front pressure due to an increase in water permeability from the front to the rear of the cell (Figure 2f). We also report a slight decrease in the cell length that, consequently, increases membrane tension (Figure 2d). This change in cell length is due to the water flux difference between the front and rear (Figure 2g). The variation in the cell velocity (Figure 2e) is mainly due to two mechanisms: the decrease in pressure and the change in membrane tension that modifies the B.C. in Equation (1). In summary, our model describes that the permeation of water through the cell enhances cell migration velocity, as has been shown before [1,49].
3.2. Electromigration of Aquaporins Controls Water-Driven Electrotaxis
To analyze the effects of the EF in the polarization of aquaporins and, eventually, in cell migration, we induce an electric field of 1 V/cm, which has been shown to activate electrotaxis. Aquaporins may move individually or in aggregates within lipid rafts. We consider two scenarios (see points (i)–(ii) in Figure 3a): one with two elementary charges and another with eight elementary charges corresponding to a small raft of four aquaporins. For the small raft case (point (ii), Figure 3a), we switch the electric field at steady state ( min, see Figure 2c) under two electrode configurations (Figure 3c). In Configuration A (ConfA), the cathode is placed on the left, causing aquaporins to polarize toward the left side of the cell, whereas in Configuration B (ConfB), the cathode is placed on the right, leading to polarization toward the right side of the cell.
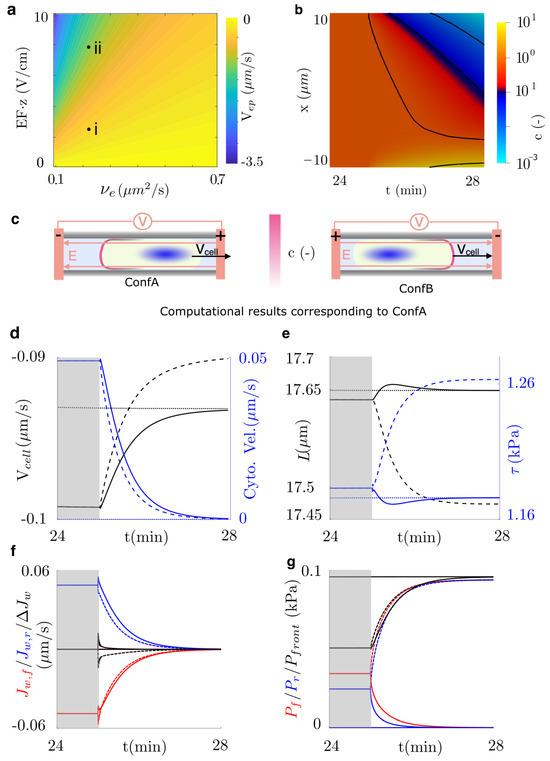
Figure 3.
Electrophoretic control of cell migration. (a) Electrophoretic velocity as a function of the EF, the electric charges, z, and the diffusion constant . The electrophoretic velocity in points (i) and (ii) is 0.024 and 0.1 m/s, respectively. (b) Polarization of the concentration of aquaporins, c, for the electrophoretic velocity indicated in point (ii). (c) The sketch shows the configuration analyzed, which polarizes aquaporins toward the anode or the cathode. (d–g) Electrophoresis is induced by applying an EF at time 25 min. The figure shows results when water flow is not allowed (dotted lines) and when the anode is placed in the direction of migration (dashed lines, ConfA) or in the opposite direction (solid lines, ConfB). Simulation is stopped once the steady-state is achieved, ≈3 min after the EF activation. (d) Cell and intracellular water velocities, (e) length of the cell, membrane tension, (f) flow of water across the front and rear, and its difference, and (g) pressure at the front of the cell, and intracellular pressure are shown.
Our results show that in both electrode configurations, the EF cancels the water flux through the cell membrane, , and consequently, through the cytosol over time (Figure 3d,f). ConfB takes all the variables of the problem, , L, , and , back to an actin-based mechanism (Figure 3d–g). Therefore, the polarization of aquaporins to the rear of the cell diminishes the enhancement induced by the water flow through the cell shown before (see Figure 2). In ConfA, however, and equilibrate up to because of the increased permeability at the front, which allows for balancing the intracellular and the front pressure. In this configuration, the cell length decreases because of a net outflow of water (Figure 3). We also show that the migration velocity in ConfA decreases further than the steady state of the actin-based model to . In both configurations, we observe no significant changes in the density or velocity of the actomyosin network, indicating that regulation of water flux alone can induce electrotactic responses. The electric stimulus shown in point (i), Figure 3, exhibits the same overall tendency as point (ii), but with a slower transition (steady state is reached at 55 min, i.e., 20 min after EF activation) and a less pronounced electrotactic response, as water flow is not fully suppressed at both cell ends.
4. Conclusions
In summary, we have integrated an actin-based model of confined migration [37], such as in the migration through the ECM or in small tubes, with water-enhancement features [1] of cell migration. Here, we have focused our attention on the effect of the water flow through the cell that is induced exclusively by the resisting external pressure that opposes the cell movement. The results confirmed the well-known fact that water flows enhance cell migration [1]. Our results reproduce not only the migration velocity of confined cells observed experimentally but also the values of density and retrograde flow of the actomyosin cortex along the cell length [37]. We showed that water-enhanced migration may arise from both the release of the external pressure opposing the cell movement and the relaxation of the cell membrane tension.
More importantly, our theoretical model suggests that the electrophoresis of aquaporins could dramatically cancel water-enhanced cell migration and switch back to an actin-based migration. We show that moderate EF could dramatically polarize the aquaporins, canceling water flows across the cell, and consequently, the release of pressure at the cell front and cell membrane length.
Our minimal model for confined cell migration during electrotaxis could also be extended to capture additional aspects of the process, including changes in integrin-based adhesion mechanisms [24] and variations in water flux arising from ion exchange across the cell membrane [1,49]. Such variations occur because an electric stimulus generates ion gradients that drive osmotic pressure differences, thereby inducing water flux across the membrane [1]. Furthermore, polarization of ion channels, analogous to the mechanism reported here for aquaporins, could also lead to significant alterations in transmembrane water flux, ultimately affecting cell migration.
Moreover, aquaporins, along with other CMPs such as EGFR, may assemble into rafts whose total negative charge exceeds the -potential of the cell membrane, thereby generating a negative -potential difference and enhancing electrophoretic attraction toward the anode [20]. Conversely, rafts containing oppositely charged molecules could also form, modifying their polarization. A detailed analysis of raft assembly mechanisms and the relative protein composition lies beyond the scope of this study. Finally, cell migration can also involve the formation of membrane protrusions in the lamellipodia and membrane ruffles at the leading edge of the cell, which could be mediated by water exchange through the cell membrane and, consequently, could be potentially modified by electrical stimuli.
Our model provides a simple and efficient framework for guiding future experimental work. It is, however, specifically tailored to confined migration and may not readily generalize to other migration modes. Experiments informed by this model should, therefore, focus on confined migration. The model further predicts that both anodal and cathodal stimulation can reduce electrotaxis, a hypothesis that warrants experimental validation. Finally, the present formulation assumes hypothetical aquaporins. Future studies should identify the specific aquaporins expressed in the cell line under investigation and characterize their size and electric charge, which determine the electromigration capacity of each protein.
Author Contributions
Conceptualization, P.S. and S.K.; methodology, P.S. and S.K.; software, P.S. and S.K.; validation, P.S. and S.K.; formal analysis, P.S. and S.K.; investigation, P.S. and S.K.; writing—original draft preparation, P.S.; writing—review and editing, P.S. and S.K.; supervision, P.S.; project administration, P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank A. Mogilner for valuable discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Stroka, K.M.; Jiang, H.; Chen, S.h.; Tong, Z.; Wirtz, D.; Sun, S.X. Water permeation drives tumor cell migration in confined microenvironments. Cell 2014, 157, 611–623. [Google Scholar] [CrossRef]
- Van Helvert, S.; Storm, C.; Friedl, P. Mechanoreciprocity in cell migration. Nat. Cell Biol. 2018, 20, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Trepat, X.; Wasserman, M.R.; Angelini, T.E.; Millet, E.; Weitz, D.A.; Butler, J.P.; Fredberg, J.J. Physical forces during collective cell migration. Nat. Phys. 2009, 5, 426–430. [Google Scholar] [CrossRef]
- Friedl, P.; Gilmour, D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009, 10, 445–457. [Google Scholar] [CrossRef] [PubMed]
- Mayor, R.; Etienne-Manneville, S. The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 2016, 17, 97–109. [Google Scholar] [CrossRef]
- Van Haastert, P.J.M.; Devreotes, P.N. Chemotaxis: Signalling the way forward. Nat. Rev. Mol. Cell Biol. 2004, 5, 626–634. [Google Scholar] [CrossRef]
- Sunyer, R.; Conte, V.; Escribano, J.; Elosegui-Artola, A.; Labernadie, A.; Valon, L.; Navajas, D.; García-Aznar, J.M.; Muñoz, J.J.; Roca-Cusachs, P.; et al. Collective cell durotaxis emerges from long-range intercellular force transmission. Science 2016, 353, 1157–1161. [Google Scholar] [CrossRef]
- Koser, D.E.; Thompson, A.J.; Foster, S.K.; Dwivedy, A.; Pillai, E.K.; Sheridan, G.K.; Svoboda, H.; Viana, M.; Costa, L.d.F.; Guck, J.; et al. Mechanosensing is critical for axon growth in the developing brain. Nat. Neurosci. 2016, 19, 1592–1598. [Google Scholar] [CrossRef]
- McCaig, C.D.; Rajnicek, A.M.; Song, B.; Zhao, M. Controlling Cell Behavior Electrically: Current Views and Future Potential. Physiol. Rev. 2005, 85, 943–978. [Google Scholar] [CrossRef]
- Cortese, B.; Palamà, I.E.; D’Amone, S.; Gigli, G. Influence of electrotaxis on cell behaviour. Integr. Biol. 2014, 6, 817–830. [Google Scholar] [CrossRef]
- Yan, X.; Han, J.; Zhang, Z.; Wang, J.; Cheng, Q.; Gao, K.; Ni, Y.; Wang, Y. Lung cancer A549 cells migrate directionally in DC electric fields with polarized and activated EGFRs. Bioelectromagnetics 2009, 30, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Song, B.; Pu, J.; Wada, T.; Reid, B.; Tai, G.; Wang, F.; Guo, A.; Walczysko, P.; Gu, Y.; et al. Electrical signals control wound healing through phosphatidylinositol-3-OH kinase-γ and PTEN. Nature 2006, 442, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Patel, N.; Poo, M.M. Orientation of neurite growth by extracellular electric fields. J. Neurosci. 1982, 2, 483–496. [Google Scholar] [CrossRef] [PubMed]
- Hotary, K.B.; Robinson, K.R. Endogenous Electrical Currents and Voltage Gradients in Xenopus Embryos and the Consequences of Their Disruption. Dev. Biol. 1994, 166, 789–800. [Google Scholar] [CrossRef]
- McCaig, C.D.; Song, B.; Rajnicek, A.M. Electrical dimensions in cell science. J. Cell Sci. 2009, 122, 4267–4276. [Google Scholar] [CrossRef]
- Devreotes, P.N.; Bhattacharya, S.; Edwards, M.; Iglesias, P.A.; Lampert, T.; Miao, Y. Excitable signal transduction networks in directed cell migration. Annu. Rev. Cell Dev. Biol. 2017, 33, 103–125. [Google Scholar] [CrossRef]
- Cohen, D.J.; Nelson, W.J.; Maharbiz, M.M. Galvanotactic control of collective cell migration in epithelial monolayers. Nat. Mater. 2014, 13, 409–417. [Google Scholar] [CrossRef]
- Mossop, B.; Barr, R.; Zaharoff, D.; Yuan, F. Electric fields within cells as a function of membrane resistivity-a model study. IEEE Trans. NanoBioscience 2004, 3, 225–231. [Google Scholar] [CrossRef]
- Zhao, M.; Pu, J.; Forrester, J.V.; McCaig, C.D. Membrane lipids, EGF receptors, and intracellular signals colocalize and are polarized in epithelial cells moving directionally in a physiological electric field. FASEB J. 2002, 16, 857–859. [Google Scholar] [CrossRef]
- Lin, B.J.; Tsao, S.H.; Chen, A.; Hu, S.K.; Chao, L.; Chao, P.H.G. Lipid rafts sense and direct electric field-induced migration. Proc. Natl. Acad. Sci. USA 2017, 114, 8568–8573. [Google Scholar] [CrossRef]
- Sun, Y.; Do, H.; Gao, J.; Zhao, R.; Zhao, M.; Mogilner, A. Keratocyte fragments and cells utilize competing pathways to move in opposite directions in an electric field. Curr. Biol. 2013, 23, 569–574. [Google Scholar] [CrossRef]
- Sun, Y.H.Y.; Sun, Y.H.Y.; Zhu, K.; Reid, B.; Gao, X.; Draper, B.W.; Zhao, M.; Mogilner, A. Electric fields accelerate cell polarization and bypass myosin action in motility initiation. J. Cell. Physiol. 2018, 233, 2378–2385. [Google Scholar] [CrossRef] [PubMed]
- Jeon, T.J.; Gao, R.; Kim, H.; Lee, A.; Jeon, P.; Devreotes, P.N.; Zhao, M. Cell migration directionality and speed are independently regulated by RasG and Gβ in Dictyostelium cells in electrotaxis. Biol. Open 2019, 8, bio042457. [Google Scholar]
- Zhu, K.; Takada, Y.Y.; Nakajima, K.; Sun, Y.; Jiang, J.; Zhang, Y.; Zeng, Q.; Takada, Y.Y.; Zhao, M. Expression of integrins to control migration direction of electrotaxis. FASEB J. 2019, 33, 9131–9141. [Google Scholar] [CrossRef] [PubMed]
- Jilkine, A.; Edelstein-Keshet, L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput. Biol. 2011, 7, e1001121. [Google Scholar] [CrossRef]
- Danuser, G.; Allard, J.; Mogilner, A. Mathematical modeling of eukaryotic cell migration: Insights beyond experiments. Annu. Rev. Cell Dev. Biol. 2013, 29, 501–528. [Google Scholar] [CrossRef]
- Physical models of collective cell migration. Annu. Rev. Condens. Matter Phys. 2020, 11, 77–101. [CrossRef]
- Jülicher, F.; Kruse, K.; Prost, J.; Joanny, J.F. Active behavior of the cytoskeleton. Phys. Rep. 2007, 449, 3–28. [Google Scholar] [CrossRef]
- Rubinstein, B.; Fournier, M.F.; Jacobson, K.; Verkhovsky, A.B.; Mogilner, A. Actin-Myosin Viscoelastic Flow in the Keratocyte Lamellipod. Biophys. J. 2009, 97, 1853–1863. [Google Scholar] [CrossRef]
- Mogilner, A.; Manhart, A. Intracellular Fluid Mechanics: Coupling Cytoplasmic Flow with Active Cytoskeletal Gel. Annu. Rev. Fluid Mech. 2018, 50, 347–370. [Google Scholar] [CrossRef]
- Betorz, J.; Bokil, G.R.; Deshpande, S.M.; Kulkarni, S.; Araya, D.R.; Venturini, C.; Sáez, P. A computational model for early cell spreading, migration, and competing taxis. J. Mech. Phys. Solids 2023, 179, 105390. [Google Scholar] [CrossRef]
- Moure, A.; Gomez, H. Phase-field modeling of individual and collective cell migration. Arch. Comput. Methods Eng. 2021, 28, 311–344. [Google Scholar] [CrossRef]
- Liu, W.K.; Liu, Y.; Farrell, D.; Zhang, L.; Wang, X.S.; Fukui, Y.; Patankar, N.; Zhang, Y.; Bajaj, C.; Lee, J.; et al. Immersed finite element method and its applications to biological systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 1722–1749. [Google Scholar] [CrossRef] [PubMed]
- Kechagia, Z.; Sáez, P.; Gómez-González, M.; Canales, B.; Viswanadha, S.; Zamarbide, M.; Andreu, I.; Koorman, T.; Beedle, A.E.M.; Elosegui-Artola, A.; et al. The laminin–keratin link shields the nucleus from mechanical deformation and signalling. Nat. Mater. 2023, 22, 1409–1420. [Google Scholar] [CrossRef]
- Sáez, P.; Venturini, C. Positive, negative and controlled durotaxis. Soft Matter 2023, 19, 2993–3001. [Google Scholar] [CrossRef]
- Kulkarni, S.; Tebar, F.; Rentero, C.; Zhao, M.; Saez, P. Competing signaling pathways controls electrotaxis. iScience 2025, 28, 112329. [Google Scholar] [CrossRef]
- Bergert, M.; Erzberger, A.; Desai, R.A.; Aspalter, I.M.; Oates, A.C.; Charras, G.; Salbreux, G.; Paluch, E.K. Force transmission during adhesion-independent migration. Nat. Cell Biol. 2015, 17, 524–529. [Google Scholar] [CrossRef]
- Ponti, A.; Machacek, M.; Gupton, S.L.; Waterman-Storer, C.M.; Danuser, G. Two distinct actin networks drive the protrusion of migrating cells. Science 2004, 305, 1782–1786. [Google Scholar] [CrossRef]
- Prost, J.; Jülicher, F.; Joanny, J.F. Active gel physics. Nat. Phys. 2015, 11, 111–117. [Google Scholar] [CrossRef]
- Regulation of actin dynamics in rapidly moving cells: A quantitative analysis. Biophys. J. 2002, 83, 1237–1258. [CrossRef]
- Aroush, D.R.B.; Ofer, N.; Abu-Shah, E.; Allard, J.; Krichevsky, O.; Mogilner, A.; Keren, K. Actin Turnover in Lamellipodial Fragments. Curr. Biol. 2017, 27, 2963–2973.e14. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Berendsen, H.J.C. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994, 98, 4155–4168. [Google Scholar] [CrossRef]
- Kozono, D.; Yasui, M.; King, L.S.; Agre, P. Aquaporin water channels: Atomic structure and molecular dynamics meet clinical medicine. J. Clin. Investig. 2002, 109, 1395–1399. [Google Scholar] [CrossRef] [PubMed]
- Keren, K.; Yam, P.T.; Kinkhabwala, A.; Mogilner, A.; Theriot, J.A. Intracellular fluid flow in rapidly moving cells. Nat. Cell Biol. 2009, 11. [Google Scholar] [CrossRef]
- Hawkins, R.J.; Piel, M.; Faure-Andre, G.; Lennon-Dumenil, A.M.; Joanny, J.F.; Prost, J.; Voituriez, R. Pushing off the walls: A mechanism of cell motility in confinement. Phys. Rev. Lett. 2009, 102, 058103. [Google Scholar] [CrossRef]
- Poo, M. In situ electrophoresis of membrane components. Annu. Rev. Biophys. Bioeng. 1981, 10, 245–276. [Google Scholar] [CrossRef]
- Donea, J.; Huerta, A. Finite Element Methods for Flow Problems; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 1–358. [Google Scholar] [CrossRef]
- Houk, A.R.; Jilkine, A.; Mejean, C.O.; Boltyanskiy, R.; Dufresne, E.R.; Angenent, S.B.; Altschuler, S.J.; Wu, L.F.; Weiner, O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell 2012, 148, 175–188. [Google Scholar] [CrossRef]
- Li, Y.; Sun, S.X. Transition from actin-driven to water-driven cell migration depends on external hydraulic resistance. Biophys. J. 2018, 114, 2965–2973. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).