A Review of Fractional Order Calculus Applications in Electric Vehicle Energy Storage and Management Systems

Abstract

Fractional-order calculus (FOC) has gained significant attention in electric vehicle (EV) energy storage and management systems, as it provides enhanced modeling and analysis capabilities compared to traditional integer-order approaches. This review presents a comprehensive survey of recent advancements in the application of FOC to EV energy storage systems, including lithium-ion batteries (LIBs), supercapacitors (SCs), and fuel cells (FCs), as well as their integration within energy management systems (EMS). The review focuses on developments in electrochemical, equivalent circuit, and data-driven models formulated in the fractional-order domain, which improve the representation of nonlinear, memory-dependent, and multi-scale dynamics of energy storage devices. It also discusses the benefits and limitations of current FOC-based models, identifies open challenges such as computational feasibility and parameter identification, and outlines future research directions. Overall, the findings indicate that FOC offers a robust framework with significant potential to advance next-generation EV energy storage and management systems.

1. Introduction

Over the past few decades, growing global concerns about environmental degradation, air pollution, and the finite nature of fossil fuel resources have prompted a search for alternatives to conventional internal combustion engine vehicles (ICEVs) [1]. Research indicates that industries and ICEVs are major sources of carbon dioxide (CO₂), sulfur dioxide (SO₂), carbon monoxide (CO), and nitrogen oxides, all of which contribute significantly to air pollution and the greenhouse effect [2]. One potential solution to mitigate this issue is the global adoption of electric vehicles (EVs) coupled with decarbonized electricity. This shift has led to a substantial increase in the worldwide use of EVs, which are now widely recognized as a viable alternative to ICEVs [3]. Although many countries and companies have implemented policies to encourage the adoption of EVs [4], there is still a long way to transition from ICEVs to full EVs. As the automotive sector intensifies efforts to reduce greenhouse gas emissions and fossil fuel dependency, attention has increasingly focused on the development of more efficient and reliable energy storage and management systems [3].

Regarding EVs, the energy storage system (ESS) is a critical component that is responsible for storing the electrical energy that powers the vehicle’s motor [5]. Due to its essential role, improving the performance, reliability, and lifespan of the ESS is crucial for enhancing the overall efficiency and sustainability of EVs. ESSs typically incorporate various energy storage devices (ESDs), such as lithium-ion batteries (LIBs), supercapacitors (SCs), and fuel cells (FCs), each of which presents unique challenges due to their complex electrochemical behaviors and dynamic characteristics [6,7].

Modeling ESDs is critical for a comprehensive understanding and accurate prediction of their performance across a range of operating conditions. Advanced modeling techniques facilitate the simulation and analysis of ESD behavior, providing valuable insights into parameters such as energy capacity, efficiency, degradation rates, and potential limitations. These models are instrumental in developing optimized control strategies for the ESS, ensuring effective response to the dynamic energy demands of an EV while maintaining long-term durability [7].

Additionally, accurate models of ESDs support the seamless integration of these devices within the broader energy management system (EMS) of the EV [8]. The EMS plays a vital role in regulating energy distribution, ensuring the efficient operation of various components, and maintaining the longevity of the ESD. Therefore, accurate modeling of both ESDs and the EMS is essential for achieving reliable, high-performance energy storage solutions in EVs [9].

Nevertheless, traditional modeling approaches based on integer-order dynamics often fall short in accurately describing the intricate, time-varying behavior of ESDs. These systems are influenced by multiple interacting factors, including electrochemical processes, thermal effects, variations in load conditions, and repeated charge–discharge cycles [2]. The modeling challenge is further compounded by memory-related effects and progressive degradation over time. Phenomena such as capacity loss in LIBs, voltage relaxation in SCs, and performance decline in FCs underscore the need for more advanced modeling tools capable of capturing these long-term and nonlinear behaviors with higher fidelity [10]. It is here that fractional-order calculus provides a better understanding of the dynamics of such systems, as it can model memory effects, long-term adaptation, and complex nonlinear behavior [11].

In recent years, fractional-order calculus (FOC) techniques have gained significant attention as an advanced mathematical framework that addresses the limitations of using traditional integer-order calculus [2]. Unlike integer-order calculus, which uses integer-order derivatives and integer-order integrals, fractional-order calculus incorporates derivatives and integrals of arbitrary order, enabling the modeling of systems with memory effects and long-range dependencies [12]. The memory and hereditary property, inherent in the behavior of ESDs, are often overlooked in conventional models, leading to a less accurate representation of their dynamics. FOC offers a more comprehensive approach by capturing these behaviors, resulting in a more precise prediction of ESD performance, including energy capacity, efficiency, and degradation rates over time [13].

Fractional-order models have been shown to provide better descriptions of systems exhibiting fractional dynamics or long-term memory effects, such as those observed in the electrochemical processes of LIBs, SCs, and FCs [2]. These models not only enhance the understanding of the individual behaviors of ESDs but also improve the overall modeling of interactions between various components in an electric vehicle’s energy management system [14]. Fractional-order models facilitate the development of optimized control strategies for the ESS and an accurate representation of system dynamics, which allows for meeting the dynamic energy demands of an EV more efficiently while maintaining long-term durability [15].

Moreover, the application of FOC in the EMS offers the potential for more robust and adaptive control strategies that can better account for the non-linear and time-dependent behaviors of ESDs [16]. By improving system predictions, fractional-order models enable more efficient energy distribution, enhancing the performance and extending the lifespan of the ESS. In turn, these advancements lead to improved overall efficiency and sustainability of EVs, ensuring that they perform reliably over time while reducing environmental impact and operational costs [17].

This review makes three main contributions. First, it provides a comprehensive survey that systematically categorizes the applications of FOC in EV energy storage systems, encompassing LIBs, SCs, and FCs, and examines their integration within EMS. Second, it highlights methodological advances in electrochemical modeling, fractional-order equivalent circuits, and data-driven approaches, demonstrating their ability to capture the nonlinear, memory-dependent, and multi-scale dynamics of storage devices. Third, it critically evaluates the benefits and limitations of existing FOC-based models, identifies open challenges, and outlines future research directions together with potential pathways for practical deployment in EV platforms.

The remainder of this paper is organized as follows. Section 2 introduces the mathematical foundations and key definitions of FOC. Section 3 discusses the modeling principles of ESSs and reviews FOC-based applications in LIBs, SCs, and FCs. Section 4 examines the integration of fractional-order models into EMS, with emphasis on state estimation strategies. Finally, Section 5 presents the main conclusions and outlines future research directions.

2. Fractional Calculus Definitions

Fractional calculus generalizes classical differential and integral operators by allowing non-integer orders in the derivative and integral operators, thereby enabling the modeling of systems with complex memory characteristics and long-range temporal dependencies [18,19]. These properties are particularly relevant in the context of energy storage devices (ESDs), where diffusion, hysteresis, and degradation phenomena are inherently non-local and history-dependent [20]. As a result, fractional-order calculus (FOC) has become a powerful tool for the analysis and modeling of lithium-ion batteries (LIBs), supercapacitors (SCs), and fuel cells (FCs) in electric vehicle (EV) applications [21,22,23].

This section presents a concise overview of the mathematical principles of FOC, including the most widely used definitions of fractional derivatives and integrals. The objective is to establish a solid foundation for the models and applications discussed in subsequent sections.

2.1. Constant Phase Element

One of the most illustrative examples of FOC in energy systems is the constant phase element (CPE), originally proposed by Cole and Cole [24], which captures non-ideal capacitive behavior observed in electrochemical systems. Its impedance is expressed as:

$$Z_{CPE}={\displaystyle \frac{1}{C_{\alpha }{\left(j\omega \right)}^{\alpha }}}, \forall \alpha ϵ\left(0, 1\right),$$

(1)

where $C_{\alpha }$ is referred to as the pseudo-capacitance and has units of $Fse{c}^{\alpha -1}$. This element produces a constant phase shift of $\alpha \pi /2$ in contrast to the $\pi /2$ shift in an ideal capacitor, and serves as a prototypical fractional-order operator.

The fractional-order derivative operator associated with such systems is commonly denoted as

$${}_0{}^{ }D_t^{\alpha }(·)={\displaystyle \frac{d^{\alpha }(·)}{d{t}^{\alpha }}}, 0<\alpha \le 1,$$

(2)

where $D^{\alpha }(·)$ represents the derivative of order $\alpha$ with respect to time. Unlike integer-order derivatives, this operator encapsulates the full past trajectory of a function, giving rise to infinite-dimensional dynamics and memory effects.

2.2. Classical Definitions of Fractional Derivatives

Several definitions of fractional derivatives exist; each is suited to different analytical and numerical contexts. The three most used are the Riemann–Liouville ($RL)$, Caputo, and Grünwald–Letnikov ($GL$) definitions [25]. Among these, the Caputo derivative is generally preferred in physical modeling due to its compatibility with standard initial conditions. To begin, the $RL$ definition of a fractional-order integral is introduced [26].

Let $f:[0,\infty )\to \mathbb{R}$ be a continuous function. The $RL$ fractional integral of order $\beta >0$ is defined as

$${}_0{}^{RL}I_t^{\beta }f(t)={\displaystyle \frac{1}{\mathit{\Gamma }(\beta )}}{\int }_0^{t}f(\eta ){(t-\eta )}^{\beta -1}d\eta , t>0,$$

(3)

where $\mathit{\Gamma }\left(·\right)$ denotes the Euler Gamma function defined as

$$\mathit{\Gamma }\left(z\right)={\int }_0^{\infty }{t}^{z-1}\mathit{exp}\left(-t\right)dt.$$

(4)

In this context, $\beta \in {\mathbb{R}}^{+}$ represents the order in the integral. Note that, when $\beta =1$, Equation (3) reduces to the classical integral. Under the same assumptions on the function $f(t)$, the $RL$ derivative of order $\alpha$ is defined as

$${}_0{}^{RL}D_t^{\alpha }f(t)={\displaystyle \frac{1}{\mathit{\Gamma }(m-\alpha )}}{\displaystyle \frac{d^m}{{dt}^m}}{\int }_0^{t}f(\eta ){(t-\eta )}^{m-\alpha -1}d\eta , t>0,$$

(5)

where $\alpha > 0$ and $m=\left[\alpha \right]+1$, with $\left[\alpha \right]$ representing the integer part of $\alpha$. Notably, when $\alpha =1$, the $RL$ derivative reduces to the standard first-order derivative known from classical calculus. For completeness, the Caputo fractional derivative of order $\alpha$ is given by

$${}_0{}^{C}D_t^{\alpha }f(t)={\displaystyle \frac{1}{\mathit{\Gamma }(m-\alpha )}}{\int }_0^t{f}^{(m)}(\eta ){(t-\eta )}^{m-\alpha -1}d\eta , t>0.$$

(6)

It is also worth noting that the Caputo derivative becomes equivalent to the classical first-order derivative when $\alpha =1$.

Unlike traditional integer-order derivatives, fractional-order operators are nonlocal in nature [27]. This means they depend not only on the current value of the function but also on their entire history over the interval $\left[0, t\right]$. Such behavior, often referred to as the long memory property, is particularly advantageous for modeling systems with hereditary or path-dependent dynamics. However, this same property significantly increases the computational complexity associated with fractional-order models, especially in real-time applications such as model-based control and optimization [28].

The numerical solution of fractional differential equations is inherently more demanding than their integer-order counterparts due to their integral formulation. Among the numerical methods developed to address these challenges, the $GL$ method has proven to be one of the most widely used and robust approaches. It is compatible with both the RL and Caputo derivatives and offers a straightforward discretization framework for approximating non-integer order derivatives [29].

The $GL$ fractional derivative of order $\theta \in \mathbb{R}$ for a function $f(t)$, defined on $t\in \left[0, T\right]$, is given by

$${}_0{}^{GL}D_t^{\theta }f\left(t\right)=\underset{h\to 0}{\lim }{\displaystyle \frac{1}{h^{\theta }}}\sum _{j=0}^{⌈t/h⌉}{\left(-1\right)}^j\left(\begin{array}{c}\theta \\ j\end{array}\right)f\left(t-jh\right),$$

(7)

where $h>0$ is the time discretization step, $j$ represents the time increment, and $\left(\begin{array}{c}\theta \\ j\end{array}\right)$ is the generalized binomial coefficient defined using the Gamma function expressed as

$$\left(\begin{array}{c}\theta \\ j\end{array}\right)={\displaystyle \frac{\mathit{\Gamma }(\theta +1)}{\mathit{\Gamma }(j+1)\mathit{\Gamma }(\theta -j+1)}},$$

(8)

this formulation allows for both fractional-order derivatives $\left(\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n} \theta \in (0,1] \right)$ and integrals $\left(\theta \in [-1,0)\right)$, providing a unified approach to modeling dynamic systems with memory.

To illustrate its application in the numerical solution of fractional differential equations, consider a general system expressed as

$${}_0{}^{GL}D_t^{\theta }f\left(t\right)=g\left(f\left(t\right)\right).$$

(9)

The $GL$ method enables the discretization of the solution at $t_k=jh$ through the following recursive relation:

$$f\left(t_k\right)=g(f\left(t_{k-1}\right))h^{\theta }-\sum _{j=1}^k{c}_j^{\theta }f\left(t_{k-j}\right),$$

(10)

with memory coefficients defined by

$$c_j^{\theta }=\left(1-{\displaystyle \frac{1+\theta }{j}}\right)c_{j-1}^{\theta }, c_0^{\theta }=\theta ,$$

(11)

hence, the term $c_j^{\theta }$ account for the contribution of the past trajectory of the system and is known as the intrinsic memory trace. The $GL$ method’s simplicity, generality, and ability to preserve the hereditary nature of fractional-order systems make it a preferred choice for simulating fractional dynamics in control, signal processing, and energy system applications [30].

We have presented three of the most used definitions of fractional order derivatives and integrals. However, in recent decades, advances in the FOC have allowed to propose new fractional order operators. These new operators are known for having a non-local kernel or a non-singular kernel Michele Caputo and Mauro Fabrizio proposed a new derivative of an integrable function $f$, on an interval $[0,t]$, and its definition is given as [31]

$${}_0{}^{CF}D_T^{\alpha }f(t)={\displaystyle \frac{M(\alpha )}{1-\alpha }}{\int }_0^t\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\alpha (t-\eta )}{1-\alpha }}\right)f^{\prime }(\eta )d\eta , t>0,$$

(12)

where ${}_0{}^{CF}D_T^{\alpha }$ represents the fractional order operator in the sense of Caputo-Fabrizio, $M(\alpha )$ is a normalization function such as $M\left(0\right)=M\left(1\right)=1$. Caputo-Fabrizio derivative has an exponential kernel which reduces the risk of singularity, this implies that a fractional derivative of a constant result as zero and the kernel does not have a singularity when $t=\eta .$

Another fractional order derivative that avoids singularity on the kernel is the Atangana-Baleanu derivative, which, in addition to its kernel, is non-local; this definition is as follows [32]:

$${}_0{}^{AB}D_T^{\alpha }f(t)= {\displaystyle \frac{M(\alpha )}{1-\alpha }}{\int }_0^t{\mathrm{E}}_{\alpha }\left[-{\displaystyle \frac{\alpha {(t-\eta )}^{\alpha }}{1-\alpha }}\right]f^{\prime }(\eta )d\eta , t>0,$$

(13)

where ${}_0{}^{AB}D_T^{\alpha }$ represents the fractional order operator in the sense of Atangana-Baleanu, $M(\alpha )$ is a normalization function such as $M\left(0\right)=M\left(1\right)=1$, and ${\mathrm{E}}_{\alpha }(.)$ is the Mittag–Leffler function.

3. Energy Storage System in Electrical Vehicles

Electric vehicles (EVs) are powered either fully or partially by electricity, which is replenished by connecting the vehicle to an external power source. Based on the power source, EVs are classified into different categories, such as battery electric vehicles (BEVs), hybrid electric vehicles (HEVs), plug-in hybrid electric vehicles (PHEVs), and fuel cell electric vehicles (FCEVs) [33].

Central to the functionality of EVs are their energy storage systems (ESSs), as they directly influence key factors such as driving range, energy efficiency, and market acceptance of EVs [34]. These systems must achieve high energy and power densities while ensuring safety, cost-effectiveness, and reliability under extreme operating conditions [35]. Among the various ESS technologies, lithium-ion batteries (LIBs) are widely used in BEVs and PHEVs due to their high energy density and long driving range. Supercapacitors (SCs) complement LIBs by offering rapid charge and discharge capabilities, making them suitable for handling peak power demands and regenerative braking. Fuel cells (FCs), although less common, offer extended driving ranges and quick refueling times by converting hydrogen into electricity [36].

To be effective, ESSs must satisfy requirements for safety, resilience to extreme temperatures, cost-efficiency, and the ability to deliver high energy and power densities over long operational lifespans. Recent advancements have focused on model-based methods for state estimation, monitoring, and energy management, emphasizing the development of accurate mathematical models that capture ESS dynamic behavior [37,38].

3.1. Modeling Principles

The performance and reliability of ESS, including LIBs, SCs, and FCs, are significantly influenced by their underlying dynamic processes. A comprehensive understanding of these processes is crucial for optimizing energy storage, improving efficiency, and extending the operational lifespan of these ESDs [39]. In LIBs, for instance, energy storage is governed by the movement of lithium ions between the anode and cathode during charge and discharge cycles, while SCs rely on electrostatic energy storage within the electric double layer. In contrast, FCs generate electrical energy through electrochemical reactions, with performance affected by factors such as fuel and oxidant concentrations, temperature, and pressure. The dynamics of each system are determined by the interplay of electrochemical reactions, ion transport, charge transfer, and material properties [40,41,42].

To accurately capture and predict these behaviors under varying operating conditions, robust modeling frameworks are essential. Dynamic models provide critical insights into electrochemical reactions and transport phenomena, enabling more precise performance predictions and facilitating the design of optimized control strategies. Additionally, real-time monitoring techniques are indispensable for ensuring efficient operation and proactive management of ESS technologies [43].

Electrochemical impedance spectroscopy (EIS) has proven to be a powerful diagnostic tool, offering a non-invasive approach to characterizing the internal resistances, capacitances, and inductances of electrochemical systems over a broad frequency spectrum. By analyzing impedance spectra, EIS enables the assessment of key parameters such as charge transfer resistance, ion diffusion kinetics, and degradation mechanisms in LIBs, SCs, and FCs. This real-time monitoring capability is crucial for evaluating system health, diagnosing performance deterioration, and refining control strategies to enhance both efficiency and longevity [44,45].

Building on the insights provided by EIS, equivalent circuit modeling (ECM) has been widely adopted to approximate the electrochemical behavior of ESSs. ECMs represent experimentally measured impedance data through a network of lumped circuit elements—such as resistors, capacitors, and voltage sources, allowing for computationally efficient simulations that capture essential system dynamics. However, despite their practical advantages, traditional integer-order models often struggle to accurately describe the inherent complexities of ESSs, particularly their nonlinear and history-dependent behaviors [46,47].

To address these limitations, fractional-order calculus (FOC) has emerged as a powerful mathematical framework for enhancing the modeling accuracy of ESSs. By extending conventional modeling approaches, FOC enables more precise representations of system interdependencies, nonlinear dynamics, and long-term aging effects, thus improving predictive capabilities and system optimization [48].

This section provides a comprehensive review of FOC applications in the modeling of ESSs, with a focus on LIBs, SCs, and FCs. It covers electrochemical, equivalent circuit, and data-driven models, emphasizing how FOC enhances model fidelity, captures memory-dependent dynamics, and improves predictive performance.

3.2. Lithium-Ion Batteries

Lithium-ion batteries (LIBs) are the preferred choice for energy storage in electric vehicles (EVs) due to their high energy density, favorable specific energy and power characteristics, and lightweight design [49]. They offer a cleaner alternative to traditional batteries, avoiding memory effects and hazardous materials such as mercury or lead [50]. However, LIBs also come with certain limitations, including higher costs and the need for sophisticated protection systems to ensure safety and maintain performance balance. Additionally, their performance can degrade under extreme conditions, such as high temperatures and deep discharge cycles [51].

The operational efficiency and lifespan of LIBs are influenced by electrochemical processes during charge and discharge cycles, thermal management, and degradation mechanisms impacting capacity and performance. Accurate modeling is essential for optimizing design, managing energy flow, and predicting battery behavior under varying temperatures, load profiles, and charge/discharge rates, while providing insights into the underlying physical and chemical processes [51].

The widespread integration of EVs into modern transportation systems has underscored the need for advanced modeling techniques for LIBs that can reliably predict performance, ensure operational safety, and support long-term durability. Recent research efforts have categorized LIB modeling into three main paradigms: physics-based (electrochemical) models, data-driven approaches, and equivalent circuit models (ECMs) [52]. A growing body of literature has demonstrated that the incorporation of fractional-order calculus (FOC) significantly enhances LIB modeling by capturing history-dependent and nonlinear dynamics more accurately than integer-order counterparts. For instance, Zhang et al. [53] developed a fractional-order model for SoC prediction that showed superior accuracy and robustness compared to traditional methods. Building on the ECM framework, Wang et al. (2023) introduced a fractional-order equivalent-circuit model that improved SoC estimation performance by optimizing both fractional orders and model parameters via a hybrid optimization-identification algorithm [54]. Earlier work by Wu et al. (2013) also highlighted the advantages of fractional-order state-space models over classical integer-order designs in terms of modeling fidelity under different operating conditions [55]. Together, these studies confirm that FOC provides a more flexible and physically consistent framework for representing the complex behavior of LIBs.

3.2.1. Application of Fractional Order Calculus in Electrochemical Models for LIBs

Electrochemical models constitute a fundamental framework for understanding and predicting the internal behavior of LIBs, as they aim to describe the intricate physical and chemical mechanisms governing charge and discharge processes. These mechanisms include lithium-ion diffusion in active materials, electrochemical reactions at the electrode-electrolyte interfaces, and the evolution of the solid-electrolyte interphase (SEI) layer, all of which interact nonlinearly and across multiple time and spatial scales. Traditionally, such phenomena have been modeled through systems of coupled partial differential equations (PDEs) grounded in concentrated solution theory, as exemplified by the seminal Doyle–Fuller–Newman (DFN) model [56].

The DFN model, introduced by Doyle et al. [56], formulates the internal dynamics of LIBs by considering ionic diffusion in the electrolyte, lithium intercalation kinetics in the active material, and the effects of electrical potential gradients within the electrodes. Extensions of this model incorporate thermal effects, aging mechanisms, and stress-induced degradation, leading to highly nonlinear and stiff systems that reflect electrochemical–thermal–mechanical couplings under realistic operating conditions [57,58]. Further theoretical developments have reformulated the DFN model into abstract frameworks to expose its singular perturbation structure, facilitating the application of asymptotic techniques for timescale separation and model-order reduction [59].

Despite the robustness and interpretability of physics-based models such as the DFN framework, their direct application within real-time battery management systems (BMS) remains hindered by significant computational challenges. These stem from the inherently high-dimensional state space, the stiffness of coupled partial differential equations, and the need for dense temporal and spatial discretization [60].

Further complicating their usability, integer-order PDE models typically fail to capture critical phenomena such as anomalous diffusion and long-term memory effects observed in porous electrode structures and the growth of the SEI layer [61]. Studies have demonstrated that incorporating fractional-order dynamics, through mechanisms representing subdiffusive ion transport and history-dependent degradation, substantially improves model fidelity by addressing these limitations [62].

One of the earliest applications of FOC to battery modeling was conducted by Sabatier et al. [63], who proposed a fractional-order reformulation of classical diffusion equations derived from the DFN framework. Their simplified single-electrode model retained electrochemical interpretability while achieving high accuracy using only a few parameters.

Similarly, Li et al. [64] developed a reduced-order physics-based model employing fractional-order transfer functions to describe lithium diffusion in the solid phase. This model demonstrated significant improvements in both computational efficiency and voltage prediction accuracy across varying C-rates.

Subsequent studies have further validated the approach. For example, Zhu et al. [65] proposed a fractional-order electrochemical model of lithium-ion batteries that incorporates electrolyte polarization and aging mechanisms, significantly enhancing state-of-health (SoH) estimation accuracy. Their model captures key degradation indicators, including impedance growth and capacity fade, offering robust performance under dynamic loading and thermal variation.

The inclusion of fractional-order elements, such as a constant phase element (CPE) and a Warburg impedance with fractional exponent, has been shown to significantly enhance the accuracy of EIS fitting, particularly under low-temperature conditions where traditional integer-order models are insufficient to capture the complex diffusion phenomena [66]. As reported in [67], the adoption of a fractional-order Warburg element in the impedance model allowed for an accurate representation of the typical 45° slope observed in the low-frequency region of the EIS spectrum, a feature commonly associated with subdiffusive ion transport in porous electrodes. This improvement was essential for robust state-of-charge (SoC) estimation, as it provided better agreement with experimental data across a wider range of frequencies and thermal environments.

In further developments, Ma et al. [68] developed a fractional-order equivalent circuit model to capture key electrochemical processes in LIBs, including charge-transfer reactions at the SEI, double-layer capacitance behavior, and Warburg diffusion, using fractional dynamics to better represent frequency-dependent behaviors. This approach allowed for improved physical interpretability and enhanced parameter identification for battery diagnostics and online state estimation tasks.

Moreover, models employing Caputo and Grünwald–Letnikov derivatives have shown improved predictive capabilities for SEI layer dynamics, lithium plating, and electrochemical aging phenomena, which are central to accurate SoH estimation and lifetime prediction [69]. Despite these advances, several challenges persist. Chief among them is the problem of parameter identification, as fractional models typically introduce additional non-integer parameters whose estimation requires specialized numerical algorithms and robust optimization routines [70]. Moreover, solving fractional-order PDEs is inherently more computationally intensive due to the global-in-time memory characteristics of fractional operators, which complicate their direct integration into embedded systems for real-time control [71].

Nevertheless, ongoing research into model-order reduction, fractional-adjoint sensitivity analysis, and hybrid fractional-integer formulations offers promising avenues for mitigating these computational burdens [71]. Furthermore, the integration of FOC with data assimilation techniques and uncertainty quantification frameworks could enhance the robustness and reliability of battery models under practical operating conditions [53].

In summary, the incorporation of FOC into electrochemical models of LIBs represents a significant leap forward in accurately capturing the intrinsic, non-local, and history-dependent behaviors that govern battery performance and aging. These models hold immense promises for the development of next-generation BMS that can operate adaptively, safely, and efficiently over extended lifespans and a wide range of environmental and loading conditions.

3.2.2. Application of Fractional Order Calculus in Data-Driven Models for LIBs

In recent years, the integration of data-driven modeling strategies in LIB research has grown substantially, particularly in applications demanding real-time state estimation, fault detection, and long-term performance prediction. Unlike physics-based approaches that rely on first-principles equations, data-driven models rely on input–output measurements rather than detailed electrochemical descriptions, making them particularly attractive in scenarios with limited physical information or strong sensor availability [72]. Notably, models based on neural networks, system identification techniques, and support vector regression have demonstrated robust and accurate performance across a range of dynamic operating conditions [73]. These techniques rely solely on measured input-output data, avoiding the complexity of physical battery models and enabling adaptability under variable conditions. For example, recurrent neural networks (RNNs) and long short-term memory (LSTM) architectures have been widely used to predict SoC with high precision across diverse load profiles [74,75]. However, such flexibility is frequently accompanied by reduced physical interpretability and heightened sensitivity to measurement noise, which may limit its practical applicability.

To address these limitations and embed physical insights within data-driven models, physics-informed neural networks (PINNs) have been introduced. These networks incorporate known physical laws into the training process, improving model robustness and interpretability [76]. Nevertheless, integer-order data-driven models often fall short in capturing essential LIB behaviors such as long-term memory effects, hysteresis, and subdiffusive transport mechanisms. FOC has been proposed as an effective means to represent these hereditary dynamics within data-driven frameworks. For example, Wang et al. [77] developed a physics-informed recurrent neural network augmented with fractional-order constraints, enabling enhanced SoC and SoH tracking under dynamic loading conditions with mean errors below 2%.

Salucci et al. [78] introduced a fractional polynomial model that leverages latent memory effects for long-term prediction of capacity fade, while balancing predictive accuracy with computational efficiency. Similarly, Jiang et al. [79] applied a data-driven fractional differential equation approach to model nonlinear LIB dynamics, effectively capturing hysteresis, variable impedance, and thermal influences over a wider operational range than integer-order models.

Among these methodologies, fractional-order system identification has gained prominence as a powerful technique for capturing the memory-dependent and hereditary behavior of battery dynamics, which are not adequately described by conventional integer-order models [80]. Fractional-order representations are particularly well-suited for modeling the voltage response, impedance spectra, and thermal transients due to their capacity to model nonlocal temporal effects and subdiffusive phenomena [81]. For example, Guo et al. [81] combined transfer learning with backpropagation neural networks to identify parameters in fractional-order models grounded on solid-phase diffusion and capacity dynamics, achieving faithful replication of battery physics while reducing model order. D. Wang et al. [82] proposed a variable fractional-order ECM, where the fractional exponent varies polynomially with SoC, and parameters are identified via chaotic-adaptive fractional particle swarm optimization, effectively capturing SoC-dependent dynamics.

Another advancement lies in fractional-order state-space models, where system dynamics are expressed as

$$D^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right), y\left(t\right)=Cx\left(t\right)+Du\left(t\right),$$

(14)

with $D^{\alpha }$ denoting a vector of Caputo derivatives of order $\alpha \in {\left(0,1\right)}^n$. These models preserve the structure and interpretability of classical linear time-invariant (LTI) systems while incorporating memory effects in a principled manner. Identification procedures often involve reformulation into discrete-time representations using fractional difference operators, followed by optimization via subspace methods or iterative least-squares schemes adapted to fractional dynamics.

Frequency-domain identification methods have also been advanced, where battery impedance measured via electrochemical impedance spectroscopy (EIS) is fitted to fractional-order transfer functions of the form

$$Z\left(s\right)={\sum }_{k=1}^n {\displaystyle \frac{a_k}{\left(s^{{\alpha }_k}+b_k\right)}}+R_s,$$

(15)

where ${\alpha }_k\in (0,1)$ denote fractional orders, and the coefficients $a_k$, $b_k$ and $R_s$ are parameters reflecting charge-transfer resistance double-layer capacitance, and electrolyte resistance, respectively. These models, linear in the Laplace domain but nonlinear in parameters, necessitate sophisticated optimization algorithms such as Levenberg–Marquardt, differential evolution, or Bayesian inference with physics-informed priors [72].

Hybrid modeling strategies combining first-principles physics with fractional-order data-driven frameworks have shown notable promise. Hussein et al. [80] extensively compared data-driven SoC estimation frameworks, white-box, grey-box, and black-box models, highlighting the rising prominence of fractional-order hybrid models that balance accuracy and computational efficiency.

Recently, the integration of machine learning (ML) techniques with fractional-order modeling has opened new avenues for improving LIB state estimation. The intrinsic memory and hereditary properties of fractional calculus complement data-driven algorithms by capturing dynamic electrochemical behavior more faithfully. Zhang et al. [83] proposed a fractional-order multidimensional Taylor network (FMTN) for SoC estimation, demonstrating superior adaptability and generalization across variable load conditions due to long-memory incorporation. Song et al. [84] developed an adaptive fractional-order extended Kalman filter (AFEKF), combining system identification with fractional dynamics to significantly reduce estimation errors under dynamic operations. Furthermore, Xing et al. [85] implemented a hybrid fractional-order square-root cubature Kalman filter (FSRCKF), achieving enhanced SoC estimation during realistic driving cycles relative to traditional filters. These advances highlight the critical role of ML-FOC hybrid frameworks in modeling nonlinear, history-dependent, and uncertain behaviors in real-time applications.

Nonetheless, challenges remain in terms of generalizability, robustness to noise, and computational scalability. Estimating fractional orders is frequently ill-posed and sensitive to measurement noise, prompting research into regularization techniques, fractional Kalman filtering, and uncertainty quantification to improve model reliability. Moreover, the inherent requirement of fractional derivatives for historical input-output data raises storage and latency issues for embedded implementations.

In conclusion, the integration of FOC into data-driven models for LIBs offers a powerful and flexible framework to capture complex, non-local, and memory-dependent phenomena that classical integer-order models cannot adequately represent. By leveraging the synergy between physical insight and data adaptivity, these models pave the way for high-fidelity, real-time estimators and predictors suitable for next-generation energy storage systems.

3.2.3. Application of Fractional Order Calculus in Equivalent Circuit Models for LIBs

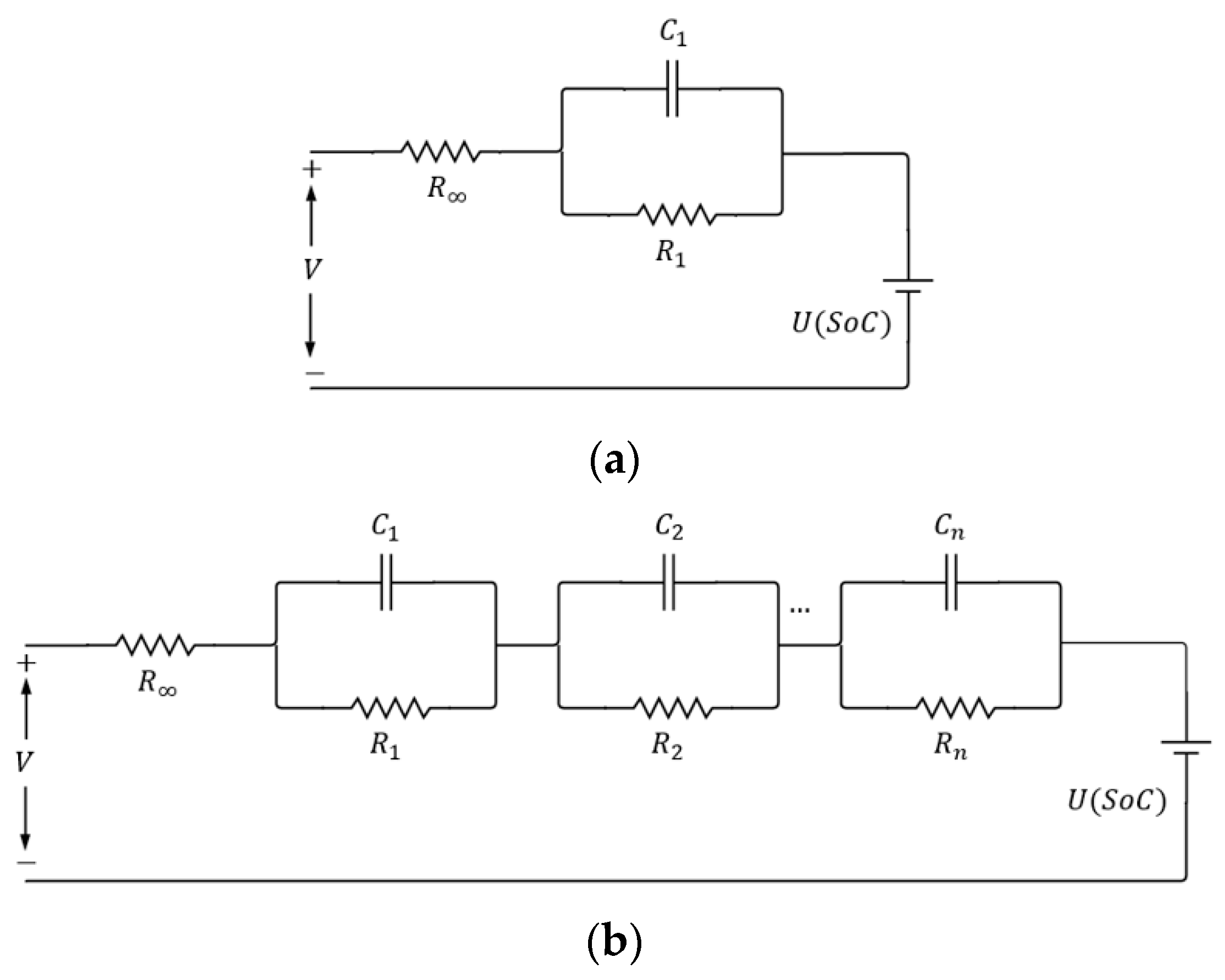
Equivalent Circuit Models (ECMs) are widely employed for the modeling of LIBs owing to their computational efficiency, ease of implementation, and relatively straightforward parameter identification procedures. These models typically represent the dynamics of LIBs through networks of resistors, capacitors, and, in some instances, inductors, capturing key electrochemical phenomena such as ohmic resistance, charge-transfer kinetics, and ionic diffusion processes [62].

Figure 1 illustrates two integer-order ECMs with different numbers of RC elements. Simpler models, such as the single RC network in Figure 1a, are easier to parameterize and implement, but adequately reproduce battery behavior only within a restricted operating range. Models with additional RC elements, as shown in Figure 1b, can represent a broader range of dynamic processes—including ohmic resistance, charge-transfer reactions, and diffusion phenomena—but introduce a larger number of parameters, increasing the dimensionality of the parameter space and computational burden.

Electrochemical Impedance Spectroscopy (EIS) constitutes a critical tool for characterizing the internal dynamic behavior of LIBs in a non-invasive manner. By probing the impedance response of the cell over a wide frequency spectrum, EIS enables the decoupling of various time-scale-dependent processes. The impedance spectrum can generally be decomposed into three distinct regions: the high-frequency region, dominated by the electrolyte and contact resistances (ohmic contribution); the mid-frequency region, characterized by a depressed semicircular feature associated with charge-transfer resistance and double-layer capacitance; and the low-frequency region, often governed by solid-state diffusion processes and typically represented by the Warburg impedance [44].

While integer-order ECMs can capture the high- and mid-frequency responses using a combination of resistors and capacitors, they fail to adequately reproduce the non-ideal, distributed diffusion behavior apparent in the low-frequency region. This discrepancy is rooted in the fact that classical capacitors imply an ideal 90° phase shift between voltage and current, which does not hold for real LIBs. In contrast, experimental observations indicate that the phase response of the impedance deviates significantly from integer-order predictions, especially in the low-frequency regime. This behavior is more accurately described using the concept of phasance, which quantifies the fractional deviation from the ideal capacitive phase response and underscores the need for models grounded in fractional-order dynamics [44,62].

FOC provides a mathematical formalism to describe systems characterized by memory effects and anomalous transport phenomena, hallmarks of electrochemical systems such as LIBs. In the context of ECMs, FOC enables the use of constant phase elements (CPEs), which are defined by their impedance function

$$Z_{CPE}\left(s\right)={\displaystyle \frac{1}{C_{\alpha }{s}^{\alpha }}},$$

(16)

where $C_{\alpha }$ is a pseudo-capacitance with units dependent on the fractional order $\alpha$, and $0<\alpha <1$. The CPE naturally generalizes the ideal capacitor (recovered when $\alpha =1$) and resistor ($\alpha =0$) thereby capturing the distributed nature of interfacial and diffusive processes.

The incorporation of CPEs into ECMs yields fractional-order ECMs (FO-ECMs), which exhibit superior fidelity in replicating EIS spectra across the entire frequency spectrum. Notably, FO-ECMs can model the depressed semicircle in the mid-frequency region and the linear low-frequency Warburg tail without resorting to high-order RC ladder networks. This results in a more parsimonious model structure with fewer parameters, reducing both computational burden and overfitting risk during parameter identification. Furthermore, FO-ECMs offer enhanced robustness to parameter variation under changing temperature and aging conditions, making them particularly suitable for practical deployment in battery monitoring applications [62].

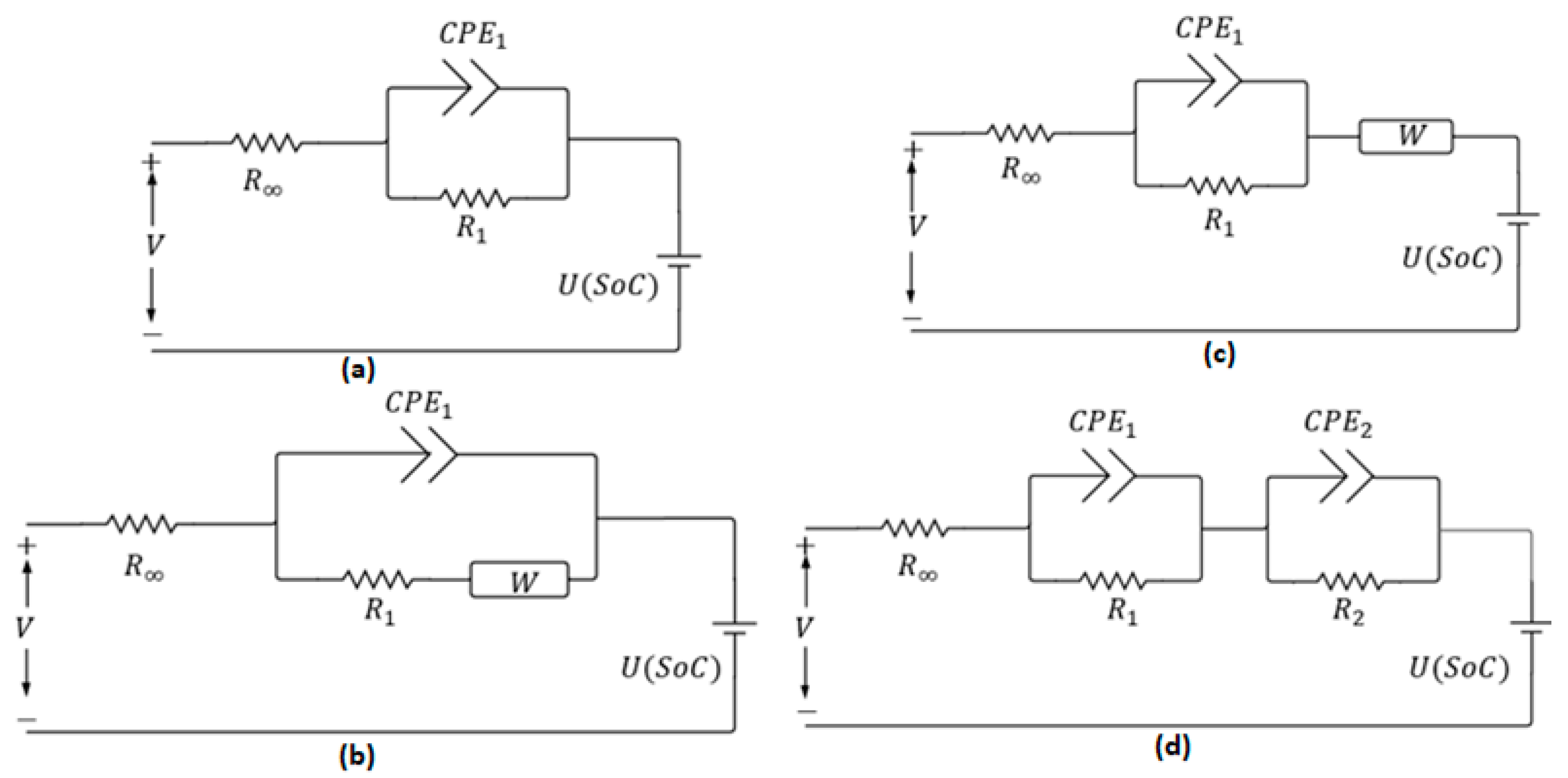
Figure 2 presents typical FO-ECM topologies reported in the literature. Figure 2a illustrates a model with a single CPE, whereas Figure 2b incorporates a Warburg element in series with the charge-transfer resistor to enhance accuracy under dynamic operating conditions. Figure 2c depicts an alternative CPE–Warburg configuration, where the Warburg element is connected in parallel with the charge-transfer resistor. Finally, Figure 2d illustrates a dual-CPE model, which provides increased robustness against parameter variations and modeling uncertainties. These schematics illustrate how various fractional-order components and circuit arrangements can be combined to strike a balance between model fidelity and complexity, providing practical options for battery monitoring and diagnostics [62].

In practice, CPE-based fractional-order models can become computationally prohibitive when multiple fractional elements are required to capture wide, frequency-dependent impedance characteristics or when real-time parameter identification is needed under highly dynamic load conditions, such as acceleration and regenerative braking in EVs. In these scenarios, the recursive nature of fractional derivatives results in high memory demands and increased computational burden, often exceeding the capabilities of typical embedded processors [62].

Several empirical studies have corroborated the advantages of FO-ECMs. For instance, Hidalgo-eyes et al. [17] demonstrated that FO-ECMs significantly enhance state of charge (SoC) estimation accuracy under dynamic driving conditions, especially during high C-rate discharge events where nonlinear and non-ideal behaviors dominate. Wang et al. [82] further established that the fractional-order modeling framework improves state of health (SoH) prognostics, particularly under extreme ambient temperatures where ionic conductivity and reaction kinetics exhibit pronounced nonlinearity and hysteresis. These improvements are attributed to the intrinsic capability of fractional-order operators to encapsulate the history-dependent dynamics of LIBs, which are otherwise difficult to characterize using purely integer-order models.

From a control and estimation perspective, the application of fractional-order models in the design of observers and Kalman filters has also been explored. Recent work by Rodríguez-Iturriaga et al. [86] introduced a fractional-order unscented Kalman filter (FO-UKF) for real-time SoC estimation, showing notable improvements in convergence speed and estimation accuracy. The FO-UKF exploits the non-local nature of fractional derivatives to enhance state observability in partially measured systems.

Nevertheless, several challenges must be addressed to fully leverage FO-ECMs in practical BMS implementations. One key issue is the identification of fractional-order parameters from time-domain or frequency-domain data, which often involves non-convex optimization landscapes and high sensitivity to measurement noise. Various numerical techniques have been proposed, including the use of evolutionary algorithms and convex relaxation strategies, yet a universally accepted standard for fractional parameter estimation remains elusive. Another challenge is the computational overhead associated with the real-time numerical approximation of fractional derivatives, typically implemented using Grünwald-Letnikov or Caputo formulations, which can be demanding for embedded systems with limited processing capabilities [15,63].

3.2.4. Challenges and Future Trends

FOC offers several benefits, including enhanced accuracy in capturing the complex dynamics of LIBs, improved predictions under varying conditions, and better modeling of degradation processes. However, these advantages are accompanied by certain challenges. Notably, the application of FOC entails increased computational demands and requires extensive experimental data for precise parameter identification.

Key challenges in applying FOC to LIB modeling include the development of efficient algorithms for solving fractional differential equations and the absence of standardized methods for parameter identification. Addressing these challenges involves creating robust computational tools and establishing consistent protocols for parameter estimation.

Future research is anticipated to focus on integrating FOC with machine learning techniques to overcome these limitations and enhance the real-time applicability of battery models. Hybrid models that combine FOC with advanced data-driven approaches could potentially offer more accurate and adaptable solutions. Additionally, the integration of FOC into existing Battery Management Systems (BMS) presents technical hurdles that need to be addressed to fully harness the benefits of FOC in practical applications [17,87].

3.2.5. Conclusions

The application of FOC in modeling LIBs represents a significant advancement in the field of EV technology. By providing a more accurate and flexible framework for describing the complex behaviors of LIBs, FOC enhances the performance, safety, and longevity of these batteries in EV applications. As research in this area continues to evolve, the integration of FOC into battery models is expected to play a crucial role in the future development of EVs, supporting their growth and acceptance in the global market.

FOC has proven its value across electrochemical, data-driven, and equivalent-circuit models for LIBs by faithfully capturing sub-diffusive transport, memory effects, and frequency-dependent impedance with greater accuracy and parsimony than integer-order formulations. Nonetheless, realizing these benefits in practical BMS hinges on overcoming six key challenges: robust parameter identification, real-time computational efficiency, multiscale consistency, physical interpretability, hybrid architecture design, and standardization of protocols and tools. Addressing these issues through integrated efforts in materials characterization, numerical methods, embedded-system implementation, and machine-learning integration will be essential. As standardized workflows and open-source toolchains emerge, fractional-order modeling is poised to transition from a research focus to an indispensable component of next-generation battery management.

3.3. Full Cell

The growing integration of fuel cells (FCs) into electric vehicle (EV) architectures, either as range extenders or as primary propulsion source, demands robust, accurate, and computationally efficient models capable of capturing the complex, multi-physical dynamics of these systems. Proton exchange membrane fuel cells (PEMFCs), hereafter referred to as fuel cells (FCs), have become a preferred choice for vehicular applications due to their high-power density, fast dynamic response, and relatively low operating temperatures [88]. However, their nonlinear behavior, multi-scale processes, and pronounced sensitivity to operating conditions pose significant challenges to classical modeling and control strategies [89].

Fractional-order calculus (FOC), which generalizes integer-order derivatives and integrals to non-integer orders, has emerged as a powerful paradigm for modeling the anomalous diffusion, memory, and hereditary properties inherent in FC dynamics [90]. This section reviews the state of the art in the application of FOC to the modeling of FCs for EV applications, structured into three main subsections: fractional-order electrochemical modeling, equivalent circuit representation, and data-driven formulations.

3.3.1. Application of Fractional Order Calculus in Electrochemical Models for FCs

Electrochemical models of fuel cells (FCs) are designed to represent the fundamental physicochemical mechanisms governing their operation, including proton conduction, reactant diffusion, charge transfer kinetics, and water management. Systems of integer-order partial differential equations are typically used to formulate these models, representing the spatial and temporal dynamics of mass and charge transport across the membrane electrode assembly [91].

However, conventional models based on integer-order differential operators often face limitations when attempting to describe anomalous transport behaviors and relaxation phenomena observed under dynamic conditions. These include subdiffusive proton transport, non-uniform charge distribution, and complex time-dependent responses, particularly under highly variable load profiles as encountered in EV applications. FOC has emerged as a promising modeling framework that addresses these challenges by incorporating non-locality and memory effects through the use of non-integer order derivatives. This results in a more accurate and compact representation of electrochemical dynamics across different timescales and spatial regimes [92].

A representative numerical application of FOC in this context is provided by Hosseini et al. [93], who introduced a generalized finite difference method (GFDM) for solving fractional reaction convection diffusion equations (FRCDEs) arising in FC modeling. Their approach employs Caputo fractional derivatives and the moving least squares (MLS) technique within a meshless framework, enabling simulation of transport phenomena in complex geometries and irregular domains.

From a systems-level perspective, Iftikhar et al. [94] developed a fractional-order dynamic model of a PEMFC, using non-integer derivatives to represent diffusion effects with fewer parameters. The model was validated experimentally via electrochemical impedance spectroscopy (EIS) on a commercial air-breathing FC, showing accurate dynamic response across a wide frequency range.

Although not purely fractional in formulation, the work by Kirubadurai et al. [95] integrates CFD modeling with EIS-informed electrochemical analysis to investigate the effects of design and operational parameters—such as membrane conductivity, gas diffusion layer porosity, and humidity—on PEMFC performance. Their use of impedance-based diagnostics aligns with the insights provided by FOC approaches, underscoring the value of frequency-domain methods in informing model development and system optimization.

Lastly, Kato et al. [92] conducted an operando synchrotron X-ray radiography study to visualize liquid water behavior in FCs under varying thermal and humidity conditions. The identification of four distinct water transport regimes and the observed discrepancies between measured and predicted water accumulation profiles point to the limitations of traditional integer-order models. These findings further motivate the exploration of FOC-based techniques, which are better equipped to capture the slow transients and distributed dynamics associated with water management in fuel cells.

In summary, the application of FOC in electrochemical modeling of FCs offers significant advantages in terms of accuracy. By incorporating memory effects and anomalous diffusion into the modeling framework, FOC-based approaches are well-suited to describe the intricate electrochemical and transport behaviors that arise in practical FC systems.

3.3.2. Application of Fractional Order Calculus in Equivalent Circuit Models for FCs

Equivalent circuit models (ECMs) are extensively employed for the modeling of FCs in real-time applications, owing to their low computational complexity and straightforward integration into control-oriented frameworks [96]. In FC systems, ECMs are commonly used to reproduce the dynamic behavior of terminal voltage in response to current excitation, incorporating phenomena such as ohmic losses, activation overpotentials, and mass-transport limitations. This offers a compact yet informative representation of internal electrochemical dynamics, ideal for embedded implementations in energy management and control strategies in EVs [97].

Classical integer-order ECMs often incorporate multiple RC branches to emulate semicircular arcs and Warburg-like tails observed in FC impedance spectra, although these models typically demand extensive parameter tuning and may lack interpretability [97]. To address such limitations, constant phase elements (CPEs) have been introduced, giving rise to fractional-order ECMs (FO-ECMs) that better capture the distributed nature of charge transport and electrode kinetics [91].

Recent contributions have advanced both the theory and application of fractional-order modeling in FCs. Li et al. [98] proposed a general methodology for reducing fractional-order impedance models, providing theoretical insights into the transformation from distributed elements to integer-order approximations. Complementing this theoretical framework, Giner-Sanz et al. [99] experimentally investigated the EIS response of a commercial FC and developed a mechanistically grounded ECM by systematically selecting from twelve candidate topologies. Their emphasis on physical interpretability of circuit parameters underscores the potential of EIS-informed models for diagnostic applications.

In a similar direction, Dhirde et al. [100] analyzed the dynamic behavior of a 1.2 kW FC stack under different current loads. Their ECMs, fitted using nonlinear least-squares optimization, incorporated both CPEs and Warburg diffusion elements. Notably, they captured asymmetries in anode and cathode kinetics and observed inductive features at high load levels, demonstrating the need for flexible modeling approaches that reflect real operating conditions.

Overall, the integration of fractional-order elements into ECMs represents a significant advancement in the modeling of FC dynamics, enabling more compact representations with improved accuracy and physical consistency. These developments not only enhance the understanding of internal electrochemical processes but also support the implementation of reliable and computationally efficient diagnostic and control systems.

3.3.3. Application of Fractional Order Calculus in Data-Driven Models for FCs

The application of FOC to data-driven modeling of FCs has enabled more accurate and robust identification, control, and diagnostics by capturing inherent memory effects and nonlinear dynamic behaviors. Recent studies have employed FOC in diverse contexts, ranging from system identification to optimization and online monitoring, thus opening new avenues for enhancing fuel cell efficiency and reliability. For instance, Qi et al. [101] proposed a nonlinear subspace identification framework for FCs based on a fractional Hammerstein model. Their method integrates canonical correlation analysis to select the most influential input variables and employs a Poisson moment function to construct a fractional-order structure. The resulting model demonstrated accurate dynamic characterization while maintaining low computational complexity.

AbouOmar and El Ferik [102] presented a multi-objective optimization approach for the tuning of fractional-order controllers in the air-feeding system of FCs. Their strategy, based on a Newton-Raphson multi-objective optimizer, seeks to balance compressor energy consumption with accurate tracking of the oxygen excess ratio, two objectives critical for efficient FC operation.

Additional contributions to the identification of FCs using FOC are found in the work of Taleb et al. [103], who compared conventional impedance models with fractional-order equivalents. By adapting the least squares method to fractional dynamics, they demonstrated that fractional models more precisely capture the impedance behavior associated with the internal electrochemical processes of FCs. This capability is particularly valuable for the development of diagnostic methods aimed at detecting phenomena such as flooding.

Yousri et al. [104] proposed a novel fractional-order variant of the Harris Hawks optimizer for parameter estimation in FC models. Their method leveraged FOC to enhance memory and convergence behavior, achieving accurate model fitting across multiple experimental datasets.

To address energy efficiency from a thermodynamic standpoint, Sun et al. [105] employed a fractional-order coyote optimization algorithm for exergy-based performance optimization of high-temperature FC systems. Their optimization strategy, which considered irreversibility and power output, resulted in configurations that closely matched experimental results, underscoring the potential of FOC in multi-variable energy system design.

Finally, Lopes et al. [106] introduced a novel modeling approach for hydrogen-based polymer electrolyte membrane fuel cells (PEMFCs) by employing fractional-order transfer functions to represent their frequency response behavior. This method enables a more flexible and precise characterization of the system dynamics compared to traditional integer-order models. To address the challenges of noisy experimental data and the non-convex nature of the parameter identification process, the authors proposed a robust optimization strategy combining a modified random sample consensus (RANSAC) algorithm with the Levenberg–Marquardt method for solving the internal optimization task.

3.3.4. Challenges and Future Trends

Despite the growing interest in applying FOC to the modeling of FCs in EVs, several pressing challenges and emerging trends must be addressed to ensure the practical deployment and scalability of such approaches in EV platforms.

Computational feasibility in real-time environments remains a primary barrier. Fractional-order models, while more accurate, require more computational resources than their integer-order counterparts, limiting their deployment in embedded control units used in commercial EVs.

Robust parameter identification under dynamic conditions is another open challenge. The performance of FCs is highly sensitive to environmental and operational variations, such as humidity, temperature, and load cycles. Integration within hybrid energy systems is also critical. As FCs are commonly combined with batteries or supercapacitors in hybrid EV architectures, coherent modeling across subsystems is necessary. FOC models for FCs must be harmonized with those of other storage components to enable optimal energy management strategies [17,91].

3.3.5. Conclusions

The application of FOC to the modeling of FCs in EVs represents a growing and technically promising research direction. Unlike conventional integer-order models, fractional-order frameworks allow for a more accurate representation of complex electrochemical and transport phenomena inherent in proton exchange membrane FCs, particularly under dynamic operating conditions typical of vehicular applications. Recent studies have demonstrated that fractional-order models not only enhance impedance fitting and capture low-frequency diffusion and double-layer effects more effectively, but also improve system-level observability and robustness in control design. Despite these advances, challenges remain regarding real-time implementability, parameter identifiability, and integration with advanced hybrid powertrains. Addressing these issues will be essential to fully leverage the potential of fractional modeling in future electric mobility platforms.

3.4. Supercapacitor

Supercapacitors (SCs), also known as ultracapacitors or electrochemical capacitors, have emerged as key energy storage components in electric vehicles (EVs) due to their high-power density, rapid charge/discharge capabilities, wide operating temperature range, and extended cycle life. However, their relatively low energy density compared to lithium-ion batteries (LIBs) limits their stand-alone use in high-energy applications. In EV systems, SCs are often integrated into hybrid energy storage systems to support peak power demands, such as acceleration or regenerative braking [62].

Fractional-order modeling has proven to be a powerful tool in capturing the unique electrochemical and dynamic behaviors of SCs, particularly those associated with memory effects and distributed parameter phenomena [12]. This section presents a detailed review of fractional-order modeling techniques applied to SCs, categorized into three modeling strategies: electrochemical-based models, equivalent circuit models, and data-driven approaches.

3.4.1. Application of Fractional Order Calculus in Electrochemical Models for SCs

The electrochemical dynamics of SCs are inherently governed by complex physical processes, including ion diffusion in porous electrodes and non-ideal double-layer behavior [107]. Traditional integer-order models often fall short in capturing these anomalous transport phenomena, particularly under conditions of wide frequency excitation or during transient operation [108]. In this context, FOC has emerged as a powerful mathematical tool to model SCs more accurately by accounting for the distributed and memory-dependent nature of charge transport and storage mechanisms [109].

One of the pioneering contributions in this domain was proposed by Riu et al. [110], who introduced a half-order model to represent the electrochemical behavior of SCs, explicitly accounting for electrode porosity and the dynamic response during charge–discharge cycles. Model parameters were identified using electrochemical impedance spectroscopy (EIS), and simulation results showed that the proposed model offered predictive accuracy comparable to higher-order ladder network models, while significantly reducing the number of parameters and computational burden.

Further advancement was provided by Quintana et al. [111], by introducing a fractional-order approach that captures the characteristic behavior of electric double-layer capacitors. Their methods demonstrated improved accuracy across frequency ranges and provided empirical validation for the use of fractional-order models in this context.

Expanding upon these early efforts, Fouda et al. [12] showed that fractional-order models incorporating constant phase elements (CPEs) effectively capture ion diffusion and porous electrode effects. Their findings underscored the improved accuracy of fractional-order models in representing energy and power dissipation compared to traditional integer-order approaches. Extending this perspective, Zou et al. [62] presented a comprehensive review of fractional-order models for energy storage devices, including LIBs, lead-acid batteries, and SCs. They emphasized that fractional-order electrochemical models offer superior accuracy while maintaining manageable complexity, an essential characteristic for real-time state estimation in EV systems.

A recent comparative study by Zhang et al. [109] offers valuable insights into the effectiveness of various fractional-order electrochemical models for commercial SCs. Their work systematically evaluated Warburg-type, Caputo-based, and hybrid diffusion models, revealing that FOC-based formulations not only provide better impedance fitting across a wide frequency range but also reduce model complexity, which is crucial for real-time applications in EVs.

In evaluating the fitting accuracy of fractional-order models against experimental EIS data, common performance metrics include the root mean square error (RMSE), mean absolute error (MAE), mean squared error (MSE), and chi-square goodness-of-fit test. These indices are computed by comparing the real and imaginary parts of the measured and modeled impedance spectra across the frequency range. Such quantitative benchmarks are frequently employed in the literature to demonstrate the superior accuracy of FO-based models relative to classical integer-order formulations [12,109].

Overall, fractional-order electrochemical models of SCs capture the distributed and memory-dependent dynamics of diffusion and double-layer phenomena more accurately than integer-order formulations. By achieving this improved physical consistency while maintaining computational tractability, they represent a promising foundation for state estimation and energy management strategies in EV applications.

3.4.2. Application of Fractional Order Calculus in Equivalent Circuit Models for SCs

Fractional-order equivalent circuit models (FO-ECMs) have gained prominence for modeling SCs, providing higher accuracy than classical integer-order models while maintaining simplicity [108]. These models are particularly effective in capturing both time-domain and frequency-domain behaviors, making them attractive for real-world EV applications where high-fidelity and computational efficiency are simultaneously required [109].

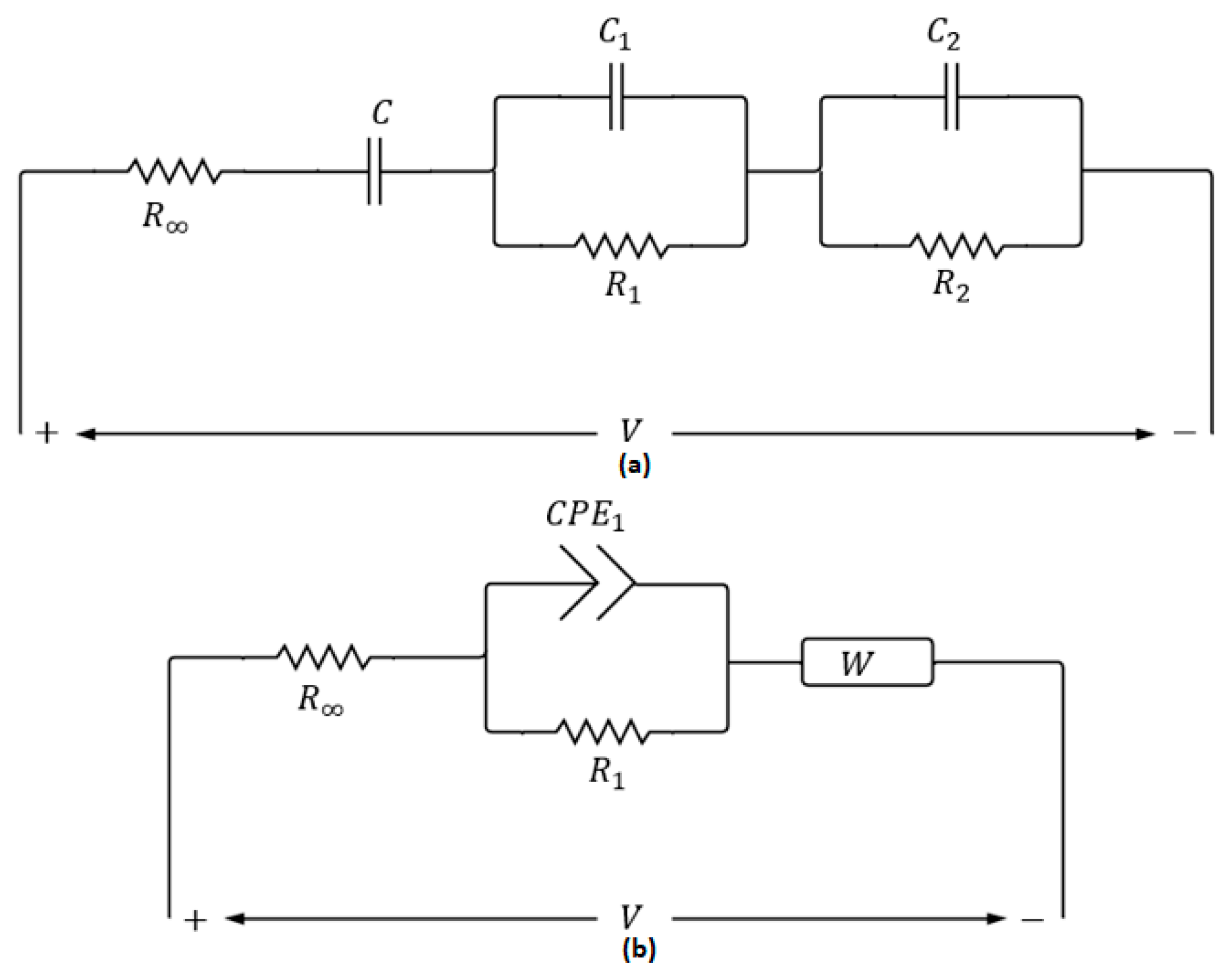
Figure 3 provides representative ECM topologies for SCs. Figure 3a depicts a conventional integer-order model employing basic resistors and capacitors, which offers a simplified description of supercapacitor dynamics but is limited in reproducing frequency-dependent behaviors. Figure 3b illustrates a fractional-order ECM incorporating a constant phase element (CPE) and a Warburg-type component. This formulation captures the distributed and non-ideal electrochemical response more accurately, fitting experimental impedance spectra across a wide frequency range while requiring fewer parameters, thereby facilitating computationally efficient implementations for real-time monitoring and control [62].

One of the early contributions in fractional-order modeling of SCs was proposed by Mitkowski et al. [112], who proposed a fractional-order RC transmission line model to characterize the transient voltage response of SCs under vehicle start–stop conditions. Extending this approach, Martynyuk et al. [113] introduced an ECM incorporating three fractional-order elements. Their model demonstrated improved fitting performance across both frequency and time domains.

Several models have also investigated nonlinear effects in SCs. For instance, Rahman et al. [114] proposed a fractional-order model accounting for hysteresis and residual voltage, with parameters tuned via genetic algorithms. Similarly, Krishnan et al. [115] developed an online identification method using a two-stage least-squares algorithm, enabling real-time estimation of the fractional exponent and equivalent parameters for adaptive control applications.

Martin et al. [116] introduced a Havriliak–Negami-based fractional impedance model to describe SC behavior across wide temperature and frequency ranges, relevant for EV operating conditions. Additional improvements have emerged through hybrid modeling strategies. Kothari et al. [117] incorporated both R-C and constant phase element (CPE) structures into a fractional-order model, which better captured porous electrode effects and enhanced physical interpretability.

A comprehensive review by Zou et al. [62] concluded that FO-ECMs, particularly those including CPEs, typically outperform integer-order models in predictive fidelity, offering 15–30% gains in accuracy without significant increases in model complexity. In a related benchmarking effort, Zhang et al. [109] evaluated various RC–CPE topologies using genetic algorithms for parameter tuning. Their findings indicated that models comprising two or three fractional-order elements achieved the best balance between accuracy and computational efficiency under representative EV load conditions.

In summary, FO-ECMs, particularly those using CPEs or hybrid configurations, present a robust and scalable modeling framework for SCs. Notably, the capability of fractional-order models to capture memory effects provides a direct physical explanation for their effectiveness in reproducing relaxation voltage phenomena observed in SCs. This behavior arises from charge redistribution and ion diffusion processes with long-term memory, which are naturally described by fractional derivatives. However, the lack of systematic comparative evaluations across topologies under EV-relevant profiles remains a research gap, warranting further investigation [109].

3.4.3. Application of Fractional Order Calculus in Data-Driven Models for SCs

The integration of FOC into data-driven modeling frameworks has opened new avenues for accurately capturing the dynamic behavior of SCs, particularly under nonstationary and nonlinear operating conditions typical in EV applications [108]. Unlike purely physics-based or equivalent circuit models, data-driven approaches leverage empirical datasets, such as voltage, current, or impedance measurements, to identify system dynamics. The non-local and memory-preserving properties of FOC make it particularly suitable for representing the distributed processes in SCs, such as charge redistribution and porous electrode diffusion, which are not easily modeled using conventional integer-order techniques [62,107].

Recent developments have increasingly validated the superiority of fractional-order representations in data-driven modeling of SCs. For instance, Allagui et al. [118] demonstrated that both impedance spectroscopy and transient voltage data from commercial SCs are more accurately captured by constant phase elements (CPEs) embedded in fractional-order models. These models consistently outperformed their integer-order counterparts across both time and frequency domains. Similarly, Zou et al. [62] highlighted in their comprehensive review of fractional-order techniques applied to energy storage systems, including SCs, that FOC-based models show particular promise in real-time control and monitoring scenarios due to their superior accuracy and compactness.

Complementing these theoretical developments, Freeborn et al. [119] derived an analytical voltage model for SCs discharged under time-varying polynomial currents. Using Caputo derivatives, they demonstrated that fractional-order models could compactly and accurately replicate the experimentally observed voltage response with fewer parameters than integer-order counterparts.

A significant contribution was made by Zhang et al. [109], who conducted a comparative study evaluating various RC–CPE network structures within EV-relevant operating contexts. Their findings showed that models comprising two to three fractional elements, optimized using genetic algorithms, achieved superior prediction performance under dynamic load profiles typical of EV usage. In a related effort, Lewandowski et al. [120] developed a time-domain identification method based on a Cole–Cole-type fractional impedance model. Their approach enabled parameter estimation during regular operation and accurately reproduced impedance spectra, capturing subtle loss mechanisms beyond those represented by equivalent series resistance alone.

Further advances in fractional-order SC modeling include the optimized resonant fractional-order impedance structure, which integrates a parallel RLC branch to improve matching across frequency bands while maintaining a low-complexity format suitable for system identification [121]. Additionally, Deng et al. [122] introduced a frequency-band division method for parameter identification: by fitting impedance across defined sub-bands, they achieved a mean error of less than 1.6% during dynamic stress testing, demonstrating the precise extraction of fractional parameters across operating regimes.

Despite these advances, challenges remain, particularly in ensuring numerical stability during online optimization, managing computational resource constraints in embedded platforms, and developing universally applicable training datasets. Furthermore, there is a lack of systematic comparison across diverse data-driven fractional structures under standardized EV scenarios. Addressing this gap is vital for guiding practitioners in selecting models that strike an optimal balance between complexity, robustness, and real-world utility [123].

3.4.4. Challenges and Future Trends

Although fractional-order models have demonstrated strong potential in capturing the dynamic behavior of SCs in EV applications, several critical challenges continue to hinder their practical implementation. Real-time deployment remains constrained by the computational complexity introduced by memory-dependent dynamics inherent in fractional-order systems. The identification of model parameters and fractional orders from experimental data is often ill-posed and highly susceptible to measurement noise, limiting the reliability of fractional-order models under varying operational conditions. Furthermore, integrating these models into energy management systems poses compatibility issues with conventional estimation and control algorithms. Another underexplored area involves the thermal–electrochemical coupling in SCs, which plays a central role in degradation and safety but has yet to be fully addressed through fractional-order frameworks [124]. To overcome these limitations, future research should prioritize the development of reduced-order FOMs optimized for embedded platforms, robust and noise-resilient identification techniques, and hybrid modeling strategies that integrate physical principles with data-driven refinement.

3.4.5. Conclusions

Integrating FOC into SC modeling and analysis has significantly enhanced the accuracy and flexibility of predictive tools for EV energy systems. Electrochemical models have benefited from fractional-order formulations that effectively capture anomalous diffusion and porous electrode dynamics, while fractional equivalent circuit models (ECMs) have enhanced impedance representation with minimal complexity. Data-driven approaches constrained by fractional dynamics further extend these capabilities, particularly under uncertain or partially known operating conditions. Despite these advancements, the practical implementation of FOC-based models remains challenged by issues such as computational cost, parameter identifiability, and integration with energy management architectures. Nevertheless, the demonstrated potential of these models underscores their value for future SC design and control in EVs. Continued efforts are required to bridge the gap between theoretical performance and real-time application, particularly through the development of computationally efficient, robust, and hybrid modeling strategies.

4. Energy Management System

The energy management system (EMS) is a critical component in electric vehicles (EVs), responsible for optimizing power flow, safeguarding battery health, and ensuring the overall reliability of energy storage systems. Accurate and real-time monitoring of battery parameters is fundamental to these objectives [8]. Conventional integer-order models, however, often fall short in capturing the complex electrochemical behavior of battery cells, particularly under dynamic and aging conditions. To address these limitations, researchers have increasingly turned to FOC as a powerful modeling and estimation tool [48].

FOC enables the description of hereditary and memory-dependent properties intrinsic to battery systems, offering improved dynamic characterization compared to traditional methods. This modeling framework has demonstrated significant advantages in key EMS tasks, such as state estimation and control [15]. The following section provides a comprehensive overview of FOC-based approaches for battery cell monitoring, with a particular emphasis on state of charge (SoC) and state of health (SoH) estimation techniques, highlighting their modeling strategies, estimation performance, and practical implications for next-generation EMS in EVs [125].

4.1. Applications of Fractional Order Calculus to Energy Management Systems

The integration of FOC into EMS for EVs marks a significant advancement in optimizing their operational efficiency and performance [17]. FOC extends the traditional calculus framework by incorporating non-integer orders, enabling a more detailed and accurate representation of the memory effects and nonlinear behaviors that characterize energy management processes [53].

Accurate battery monitoring is essential for improving safety, maximizing battery life, and enabling efficient power management in EVs. Recent research has increasingly adopted fractional-order models to enhance the estimation of key states such as SoC and SoH, due to their superior ability to model memory-dependent and anomalous diffusion dynamics [53].

Zhou et al. [126] proposed a set of fractional-order sliding-mode observers (FOSMOs) capable of simultaneously estimating SoC and SoH by observing terminal voltage, polarization voltage, and open-circuit voltage (OCV). Their method achieved higher accuracy and faster convergence compared to traditional integer-order observers. Analogously, Chen et al. [127] developed a fractional-order square-root unscented Kalman filter (UKF), which demonstrated improved estimation performance under varying operating conditions.

A variable-order model was introduced by Lu et al. [128], where the fractional derivative order varied with SoC. When combined with fast iterative parameter identification, the model enabled accurate and computationally efficient SoC estimation, highlighting its suitability for embedded battery BMS applications.

Several comparative studies have confirmed the superiority of fractional-order models over integer-order counterparts. Guoqing et al. [129] showed that fractional-order equivalent circuit models reduced SoC estimation errors under dynamic test cycles, while integer-order models experienced significant fluctuations. Wang et al. [130] conducted a broad review of fractional-order estimation techniques, including fractional-order Kalman filters, and concluded that FOC-based strategies consistently outperform classical approaches under varying conditions. Tian et al. [131] also demonstrated that simple fractional models achieved robust estimation performance, even under sensor drift and temperature variations.

Building on these insights, a dual fractional-order extended Kalman filter (DFOEKF) was developed in [86] for concurrent estimation of SoC and fractional parameters derived from multiple RC circuit approximations. Similarly, the adaptive fractional-order UKF proposed in [132] demonstrated improved accuracy and robustness under real-time dynamic conditions.

Another modeling approach was proposed in [133], using a fractional-order kinetic battery model (FO-KiBaM) that effectively captures the nonlinear behaviors of lithium-ion batteries (LIBs) under varying C-rates. The model achieved a mean absolute error of just 1.91%, demonstrating its accuracy across variable current profiles. Zhang et al. [83] introduced a fractional-order multidimensional Taylor network (FMTN) integrated with an adaptive Kalman filter (AKF) for SoC estimation. The use of fractional power activation functions improved accuracy, while the AKF enhanced noise resilience in real-world conditions. Their model reduced the root-mean-square error (RMSE) by up to 51% without compromising computational efficiency.

Implementing fractional-order Kalman filters under dynamic EV load conditions introduces numerical challenges, such as increased memory usage due to non-local derivatives, iterative optimization of fractional parameters, computationally intensive derivative approximations, and sensitivity to measurement noise. Efficient solvers and reduced-order approaches are needed to ensure real-time performance and stability [83,86,132].

For SoH estimation, Zhao et al. [69] developed a hybrid method combining fractional-order differential voltage-capacity analysis with a fusion model integrating support vector machines, elastic net, and Gaussian process regression. This approach considerably improved the extraction of characteristic parameters and the accuracy of SoH prediction.

Finally, an integrated energy estimation strategy was presented in [134], using fractional-order modified moving horizon estimation (FO-mMHE) along with a fractional-order model predictive control (FO-MPC) scheme. The model, developed through pulse testing and evolutionary optimization, achieved SoC estimation errors of less than 1.2% and SoP (state of power) errors of less than 0.35 W under dynamically varying load conditions.

4.2. Challenges and Future Trends

Despite notable progress, several technical and implementation challenges must be addressed before widespread adoption of FOC-based EMS in EVs becomes feasible. One major barrier is the computational complexity associated with solving fractional differential equations in real time. This is particularly critical for embedded applications requiring rapid estimation of SoC and SoH under dynamic conditions [125]. To address this challenge, predictive EMS frameworks can achieve an effective trade-off between model accuracy and computational efficiency by employing reduced-order fractional models alongside optimized numerical algorithms. Such approaches preserve the key memory-dependent and nonlinear dynamics of ESDs while ensuring their practical applicability in real-time implementations.

Another challenge in hybrid energy systems, such as those combining LIBs, SCs, and FCs, lies in temporal inconsistencies arising from the differing memory effects and response times of individual storage elements. These inconsistencies can manifest as delays in voltage or current response, misaligned energy sharing, or suboptimal utilization of certain components, potentially affecting overall system stability and efficiency. To address these issues, strategies such as multi-time-scale control, hierarchical energy management, adaptive fractional-order models, and reduced-order subsystem representations can be employed. Together, they help synchronize the dynamics of heterogeneous sources, improving stability, performance, and efficiency in hybrid EMSs. While still under investigation, these approaches offer a promising framework for integrating fractional-order modeling into hybrid energy systems [48].

Additionally, current research lacks standard protocols for evaluating the performance and robustness of FOC-based EMS under practical conditions, such as fluctuating temperatures, load uncertainties, and component aging. Future directions include the hybridization of FOC with machine learning algorithms to enable predictive energy scheduling, the development of fractional-order digital twins for fault diagnostics, and the use of adaptive EMS frameworks capable of updating model parameters online [131].

4.3. Conclusions

The incorporation of FOC into EMS for EVs has demonstrated significant potential for improving estimation accuracy, control precision, and adaptability under dynamic operating conditions. By effectively capturing memory effects and nonlinear behaviors, FOC-based methods contribute to more efficient battery utilization, extended component lifespan, and enhanced system reliability.

Nonetheless, real-time implementation and integration with heterogeneous energy sources remain open challenges. Future research should focus on algorithmic optimization, hardware-efficient implementations, and hybrid modeling strategies. Combining FOC with AI, embedded systems, and advanced power electronics will be key to enabling the next generation of EMS for sustainable and fully electrified transportation.

5. Conclusions

This review has explored the application of fractional-order calculus (FOC) across various domains of energy storage and management systems in electric vehicles (EVs), with an emphasis on lithium-ion batteries (LIBs), fuel cells (FCs), and supercapacitors (SCs). Through rigorous analysis, it has been shown that FOC offers a powerful and flexible mathematical framework. This framework is capable of accurately capturing the memory-dependent, nonlinear, and multi-scale behaviors inherent in these systems, which are often inadequately represented by classical integer-order models.

Fractional-order models have shown remarkable advantages in a wide range of battery management tasks, including electrochemical modeling, impedance characterization, and state estimation. In particular, the incorporation of FOC into equivalent circuit models (ECMs), electrochemical frameworks, and data-driven approaches has enhanced model fidelity and robustness by more accurately capturing memory effects and complex dynamic behaviors inherent to battery systems, especially under varying operational conditions.

Despite its advantages, the real-time implementation of FOC remains challenging, particularly due to higher model complexity and computational cost. These limitations call for further research into model order reduction techniques, efficient numerical solvers, and hardware-oriented implementations that can enable practical deployment in embedded automotive systems.

Future developments in this area are expected to focus on hybrid modeling strategies that combine the physical interpretability of fractional-order models with the adaptability of machine learning techniques. Such integration could lead to the next generation of digital twins for EV energy systems, enabling more reliable, predictive, and efficient operation under real-world conditions.