Development of Viscosity Iterative Techniques for Split Variational-like Inequalities and Fixed Points Related to Pseudo-Contractions
Abstract
1. Introduction
2. Preliminaries
- When , S becomes a nonexpansive mapping.
- When , S becomes pseudo-contractive.
- For , if is pseudo-contractive, then S is called strongly pseudo-contractive.
- (i)
- For all , the condition (10) is equivalent to
- (ii)
- The mapping S is pseudo-contractive if and only if
- (iii)
- The mapping S is strongly pseudo-contractive if and only if there exists such that
- (1)
- (2)
- is generalized relaxed α-monotone, i.e., for any and , we getwhere such that
- (3)
- is hemicontinuos, for any fixed ;
- (4)
- is convex and lower semicontinuous, for any fixed ;
- (5)
- , for any ;
- (6)
- is skew-symmetric, i.e.,
- (7)
- is weakly continuous and convex for any fixed .
- (i)
- ;
- (ii)
- .
3. Main Outcome
- (i)
- and ;
- (ii)
- , ;
- (iii)
- ;
- (iv)
- , ;
- (v)
- , where L is the spectral radius of and is the adjoint of A;
- (vi)
- .
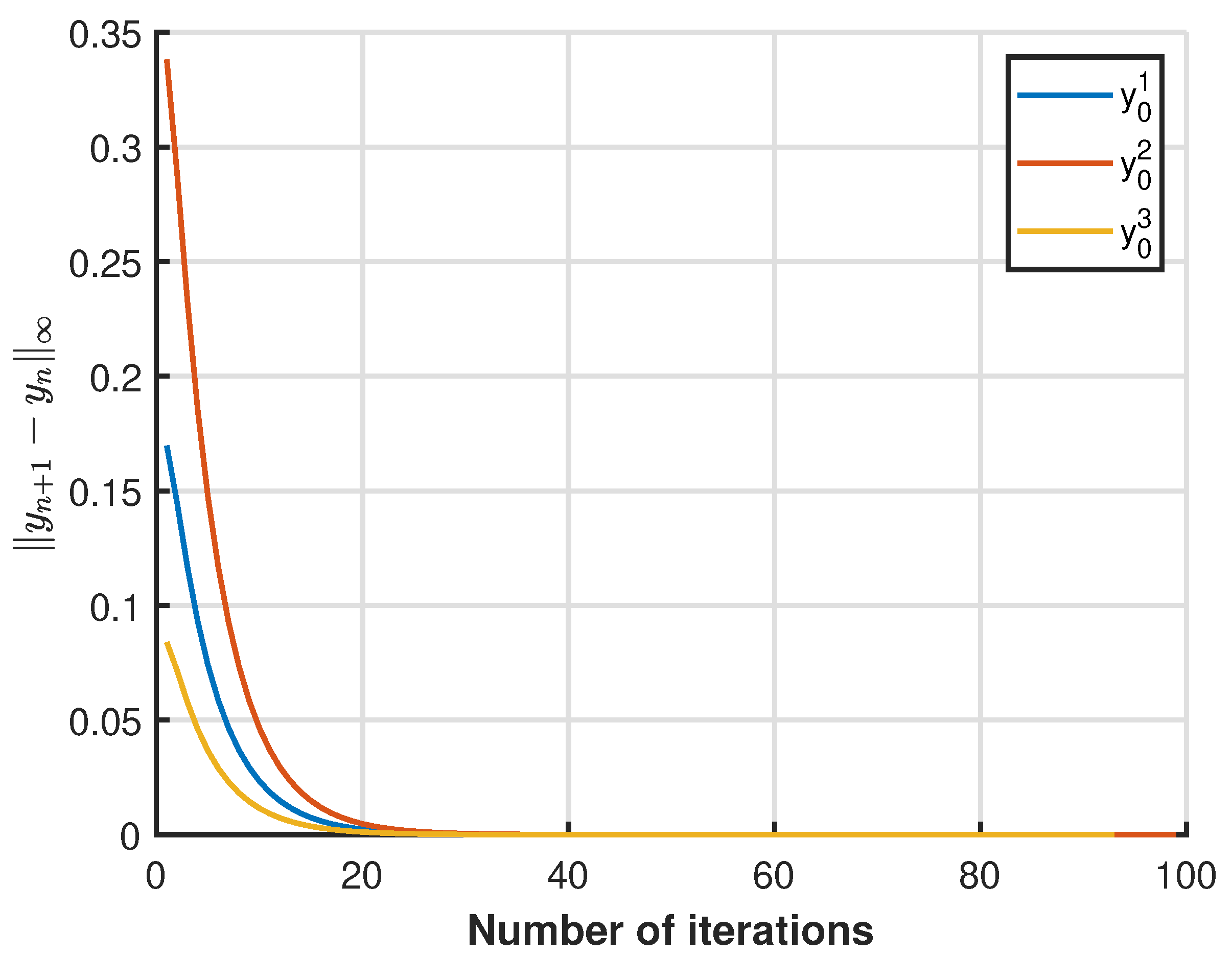
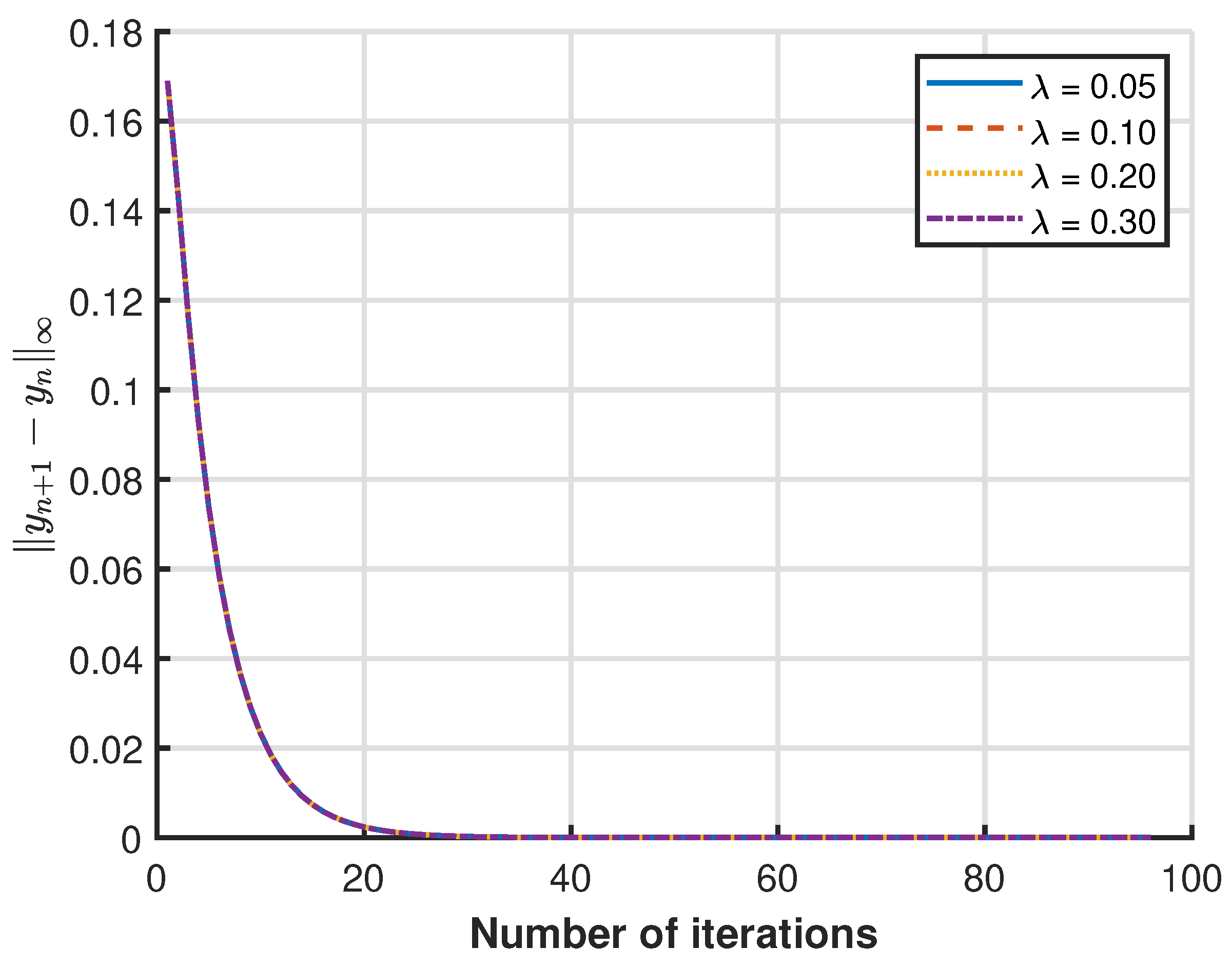
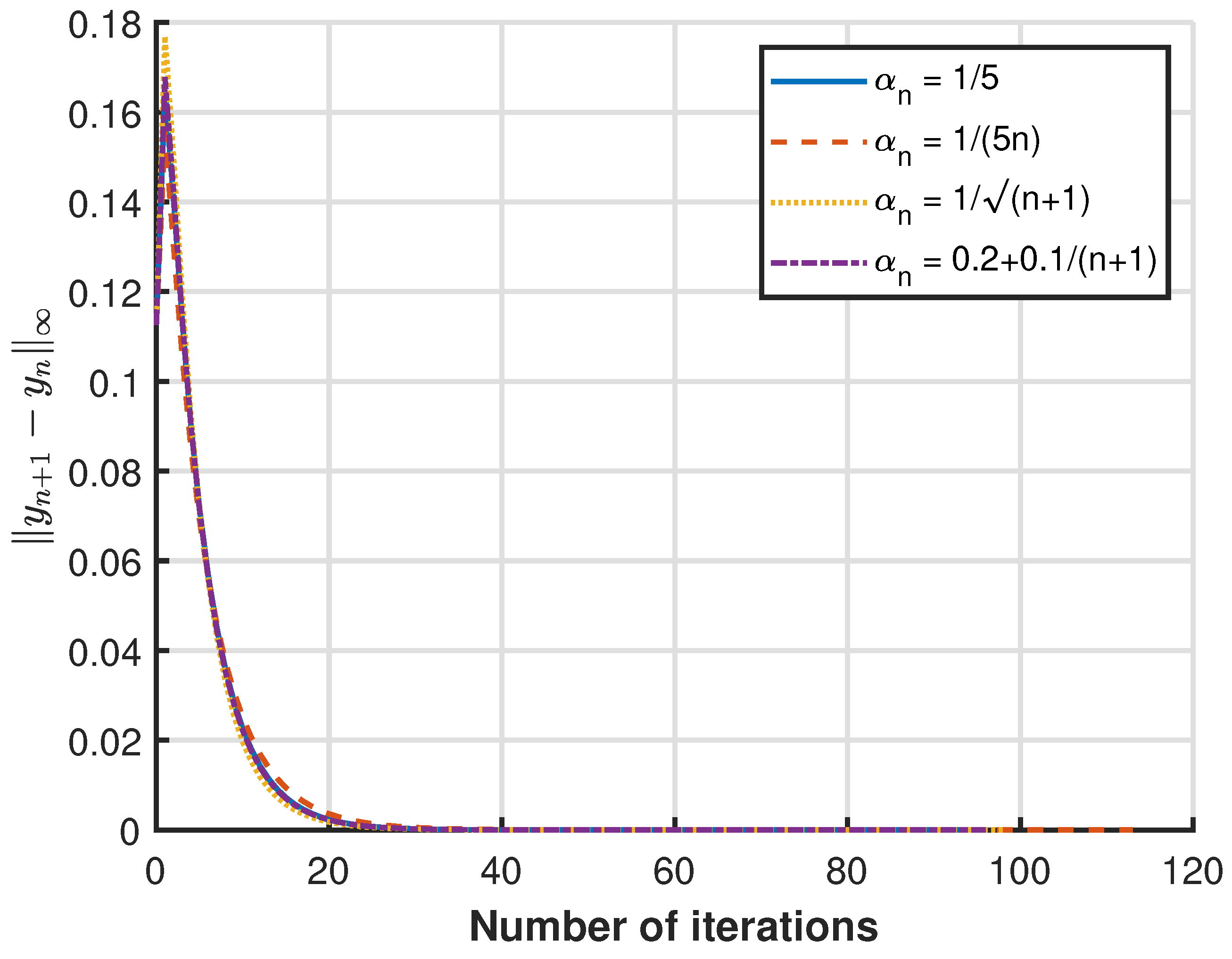
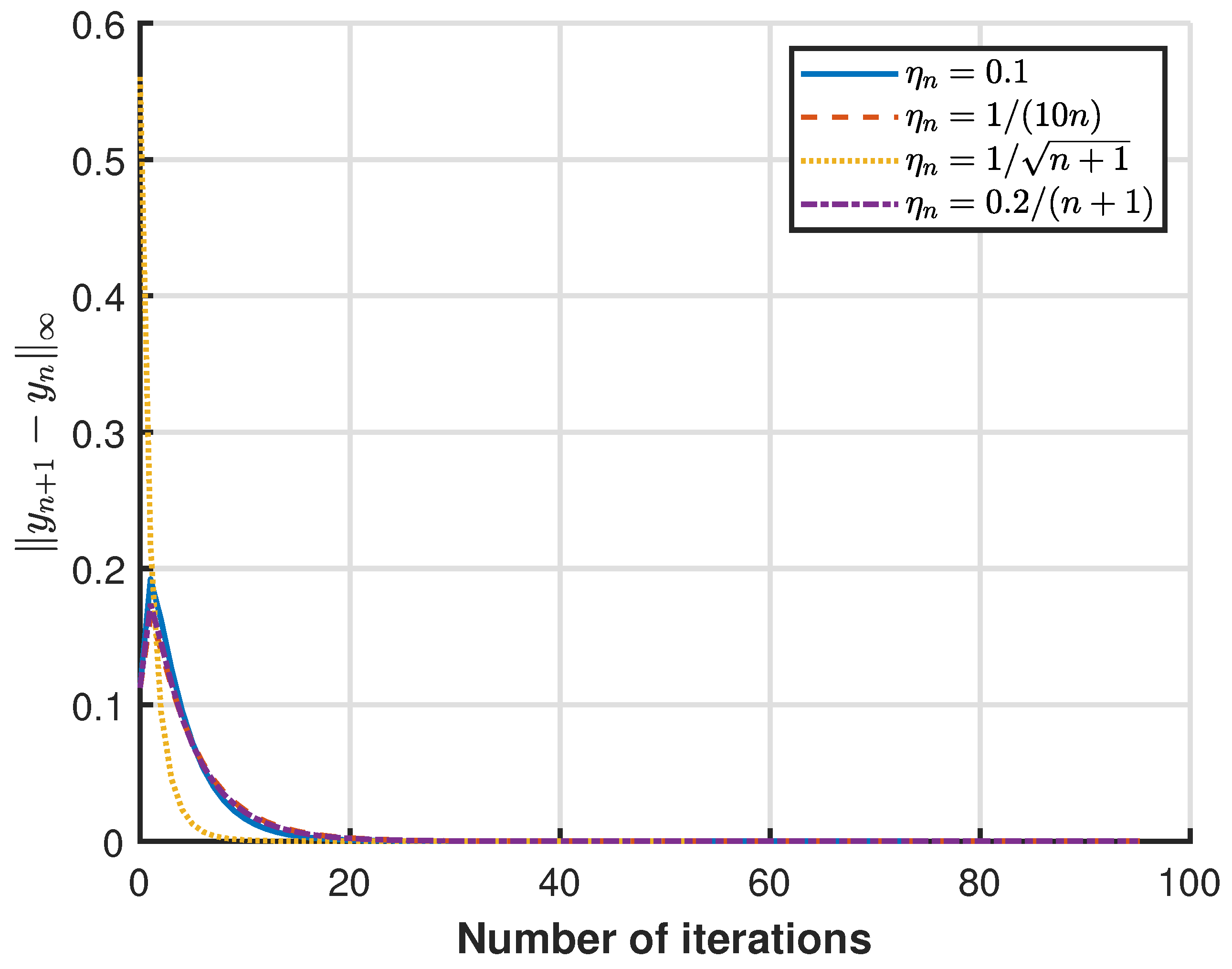
3.1. Numerical Example
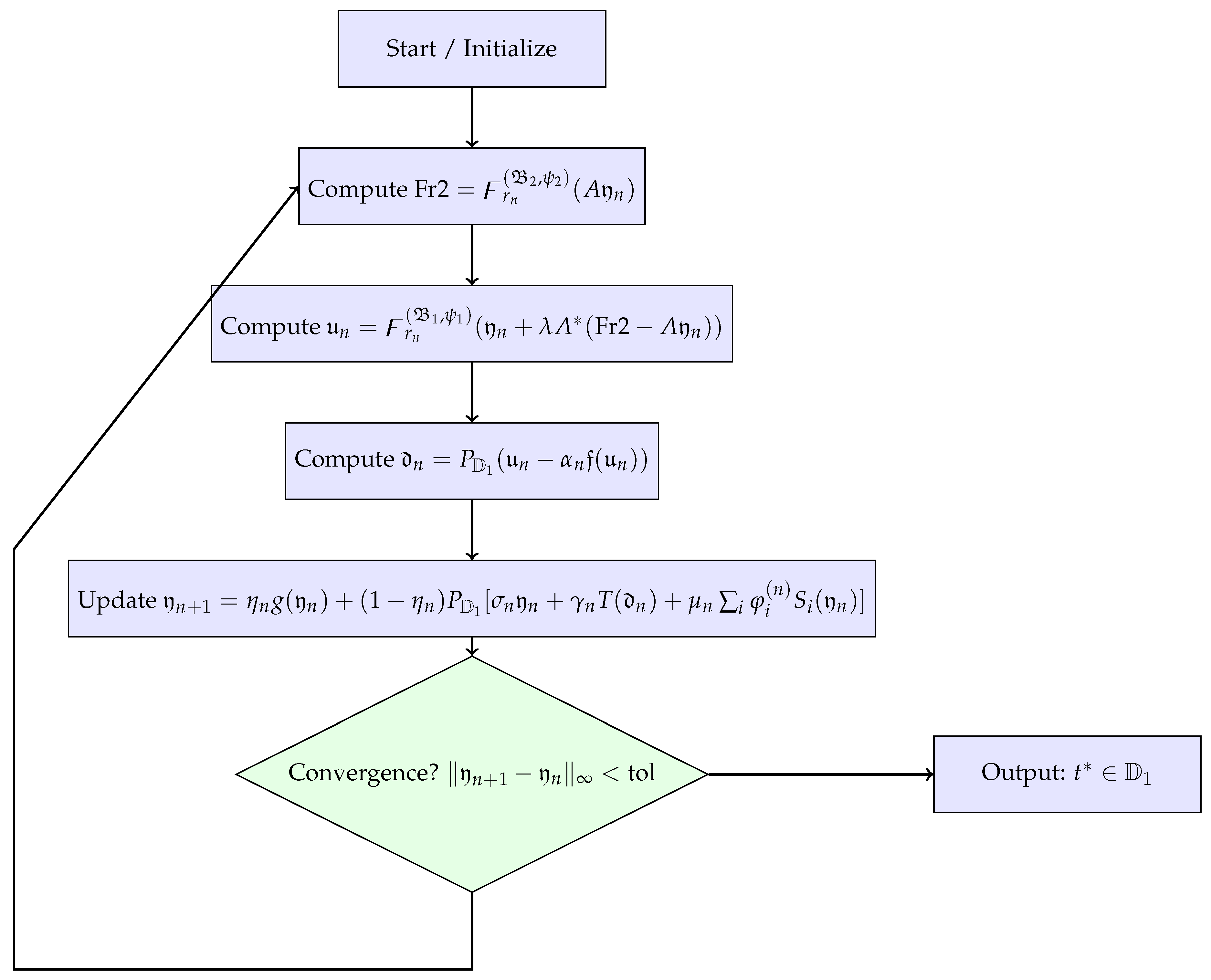
3.2. Application: Image Denoising Problem of Iteration (13)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Acronyms
| Acronym | Meaning |
| FPP | Fixed Point Problem |
| FPPs | Fixed Point Problems |
| VIP | Variational Inequality Problem |
| VLIP | Variational-Like Inequality Problem |
| GVLIP | General Variational-Like Inequality Problem |
| GGVLIP | Generalized General Variational-Like Inequality Problem |
| SFP | Split Feasibility Problem |
| GGVLIP | Split Generalized General Variational-Like Inequality Problem |
Appendix B. Algebraic Details
| Acronym | Meaning |
| := -inverse strongly monotone | |
| := -contraction mapping | |
| := nonexpansive mapping | |
| := -strict pseudo-contractions, () | |
| := bounded linear operator | |
| := be trifunctions, | |
| := be bifunctions, | |
| := are control sequences | |
| := | |
| := | |
| := | |
| := |
References
- Censor, Y.; Elfving, T. A multiprojection algorithms using Bragman prtojection in a product space. Numer. Algorithms 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Censor, Y.; Bortfeld, T.; Martin, B.; Trofimov, A. A unified approach for inversion problems in intensity modulated radiation therapy. Phys. Med. Biol. 2006, 51, 2353–2365. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. Algorithms for the split variational inequality problem. Numer. Algorithms 2012, 59, 301–323. [Google Scholar] [CrossRef]
- Combettes, P.L.; Hirstoaga, S.A. Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 2005, 6, 117–136. [Google Scholar] [CrossRef]
- Kazmi, K.R.; Rizvi, S.H.; Farid, M. A viscosity Cesàro mean approximation method for split generalized vector equilibrium problem and fixed point problem. J. Egypt. Math. Soc. 2015, 23, 362–370. [Google Scholar] [CrossRef]
- Moudafi, A. Split monotone variational inclusions. J. Optim. Theory Appl. 2011, 150, 275–283. [Google Scholar] [CrossRef]
- Byrne, C.; Censor, Y.; Gibali, A.; Reich, S. Weak and strong convergence of algorithms for the split common null point problem. J. Nonlinear Convex Anal. 2012, 13, 759–775. [Google Scholar]
- Moudafi, A. The split common fixed point problem for demicontractive mappings. Inverse Probl. 2010, 26, 055007. [Google Scholar] [CrossRef]
- Takahashi, S.; Takahashi, W. Viscosity approximation method for equilibrium problems and fixed point problems in Hilbert space. J. Math. Anal. Appl. 2007, 331, 506–515. [Google Scholar] [CrossRef]
- Kazmi, K.R.; Ali, R. Hybrid projection methgod for a system of unrelated generalized mixed variational-like inequality problems. Georgian Math. J. 2019, 26, 63–78. [Google Scholar] [CrossRef]
- Farid, M.; Cholamjiak, W.; Ali, R.; Kazmi, K.R. A new shrinking projection algorithm for a generalized mixed variational-like inequality problem and asymptotically quasi-ϕ-nonexpansive mapping in a Banach space. RACSAM 2021, 115, 114. [Google Scholar] [CrossRef]
- Farid, M.; Aldosary, S.F. An Iterative approach with the inertial method for solving variational-like inequality problems with multivalued mappings in a Banach space. Symmetry 2024, 16, 139. [Google Scholar] [CrossRef]
- Preda, V.; Beldiman, M.; Batatoresou, A. On variational-like inequalities with generalized monotone mappings. In Generalized Convexity and Related Topics; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 2006; Volume 583, pp. 415–431. [Google Scholar] [CrossRef]
- Ceng, L.C.; Huan, X.Z.; Liang, Y.; Yao, J.C. On stochastic fractional differential variational inequalities general system with Lévy jumps. Commun. Nonlinear Sci. Numer. Simul. 2025, 140, 108373. [Google Scholar] [CrossRef]
- Ceng, L.C.; Zhu, L.J.; Yin, T.C. Modified subgradient extragradient algorithms for systems of generalized equilibria with constraints. AIMS Math. 2023, 8, 2961–2994. [Google Scholar] [CrossRef]
- Rehman, H.U.; Sitthithakerngkiet, K.; Seangwattana, T. Dual-Inertial Viscosity-Based Subgradient Extragradient Methods for Equilibrium Problems Over Fixed Point Sets. Math. Methods Appl. Sci. Anal. Appl. 2025, 48, 6866–6888. [Google Scholar] [CrossRef]
- Kankam, K.; Cholamjiak, W.; Cholamjiak, P.; Yao, J.C. Enhanced proximal gradient methods with multi inertial terms for minimization problem. J. Appl. Math. Comput. 2025. [Google Scholar] [CrossRef]
- Yao, J.C. The generalized quasi-variational inequality problem with applications. J. Math. Anal. 1991, 158, 139–160. [Google Scholar] [CrossRef]
- Parida, J.; Sahoo, M.; Kumar, A. A variational-like inequalitiy problem. Bull. Austral. Math. Soc. 1989, 39, 225–231. [Google Scholar] [CrossRef]
- Hartman, P.; Stampacchia, G. On some non-linear elliptic differential-functional equation. Acta Mathenatica 1966, 115, 271–310. [Google Scholar] [CrossRef]
- Blum, E.; Oettli, W. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Treanţă, S.; Pîrje, C.F.; Yao, J.C.; Upadhyay, B.B. Efficiency conditions in new interval-valued control models via modified T-objective functional approach and saddle-point criteria. Math. Model. Control 2025, 5, 180–192. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K. Exponential synchronization of fractional order fuzzy memristor neural networks with time-varying delays and impulses. Math. Model. Control 2025, 5, 164–179. [Google Scholar] [CrossRef]
- Korpelevich, G.M. The extragradient method for finding saddle points and other problems. Matecon 1976, 12, 747–756. [Google Scholar] [CrossRef]
- Nadezhkina, N.; Takahashi, W. Strong convergence theorem by a hybrid method for nonexpansive mapping and Lipschitz continuous monotone mappings. SIAM J. Optim. 2006, 16, 1230–1241. [Google Scholar] [CrossRef]
- Nadezhkina, N.; Takahashi, W. Weak convergence theorem by a extragradient method for nonexpansive mappings and monotone mappings. J. Optim. Theory Appl. 2006, 128, 191–201. [Google Scholar] [CrossRef]
- Nakajo, K.; Takahashi, W. Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J. Math. Anal. Appl. 2003, 279, 372–379. [Google Scholar] [CrossRef]
- Ceng, L.C.; Hadjisavvas, N.; Wong, N.C. Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems. J. Global Optim. 2010, 46, 635–646. [Google Scholar] [CrossRef]
- Browder, F.E.; Petryshyn, W.V. Construction of fixed points of nonlinear mappings in Hilbert spaces. J. Math. Anal. Appl. 1967, 20, 197–228. [Google Scholar] [CrossRef]
- Scherzer, O. Convergence criteria of iterative methods based on Landweber iteration for solving nonlinear problems. J. Math. Anal. Appl. 1991, 194, 911–933. [Google Scholar] [CrossRef]
- Marino, G.; Xu, H.K. Weak and strong convergence theorems for k-strict pseudo-contractions in Hilbert spaces. J. Math. Anal. Appl. 2007, 329, 336–349. [Google Scholar] [CrossRef]
- Xu, W. Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Anal. 2007, 67, 2258–2271. [Google Scholar] [CrossRef]
- Maingé, P.E. Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 2008, 16, 899–912. [Google Scholar] [CrossRef]
- Zhou, H.Y. Convergence theorems of fixed points for k-strict pseudo-contractions in Hilbert space. Nonlinear Anal. 2008, 69, 456–462. [Google Scholar] [CrossRef]
- Osilike, M.O.; Igbokewe, D.I. Weak and strong convergence theorems for fixed points of pseudo-contractions and solutions of monotone type operator equations. Comput. Math. Appl. 2000, 40, 559–567. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66, 240–256. [Google Scholar] [CrossRef]

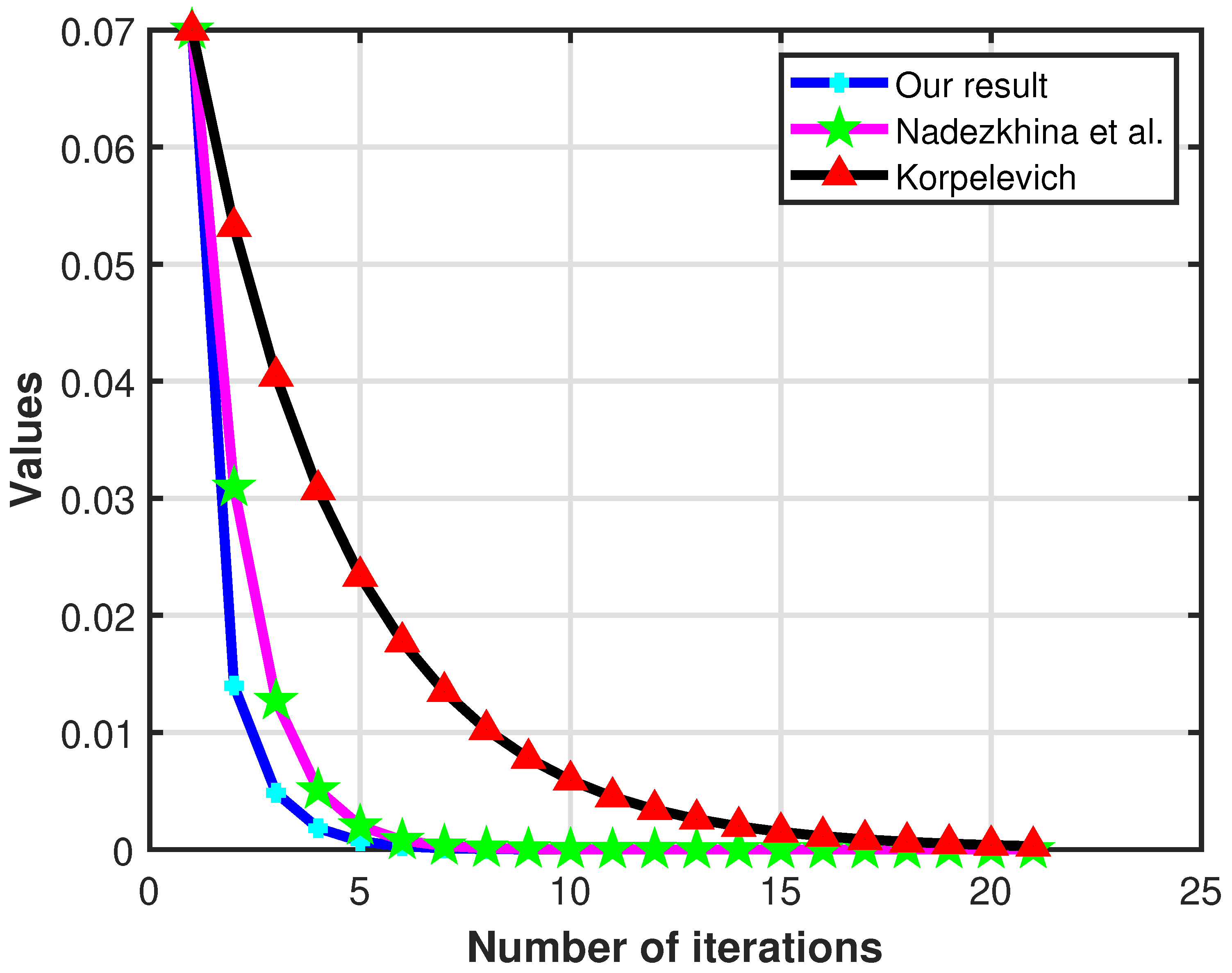
| No. of Iter. | Our Result | Nadezkhina et al. [25] | Korpelevich [24] |
|---|---|---|---|
| cpu Time (in s) | cpu Time (in s) | cpu Time (in s) | |
| 1 | 0.014000 | 0.030940 | 0.053200 |
| 2 | 0.004848 | 0.012716 | 0.040432 |
| 3 | 0.001825 | 0.005095 | 0.030728 |
| 4 | 0.000707 | 0.002015 | 0.023354 |
| 5 | 0.000278 | 0.000791 | 0.017749 |
| 6 | 0.000110 | 0.000309 | 0.013489 |
| 7 | 0.000044 | 0.000120 | 0.010252 |
| 8 | 0.000018 | 0.000047 | 0.007791 |
| 9 | 0.000007 | 0.000018 | 0.005921 |
| 10 | 0.000003 | 0.000007 | 0.004500 |
| 11 | 0.000001 | 0.000003 | 0.003420 |
| 12 | 0.000000 | 0.000001 | 0.002599 |
| No. of Iter. | Our Result | Nadezkhina et al. [25] | Korpelevich [24] |
|---|---|---|---|
| cpu Time (in s) | cpu Time (in s) | cpu Time (in s) | |
| 1 | 0.640000 | 1.490000 | 2.600000 |
| 2 | 0.221612 | 0.497250 | 2.000000 |
| 3 | 0.083414 | 0.199232 | 1.400000 |
| 4 | 0.032335 | 0.078796 | 0.800000 |
| 5 | 0.012712 | 0.030920 | 0.608000 |
| 6 | 0.005037 | 0.012069 | 0.462080 |
| 7 | 0.002006 | 0.004693 | 0.351181 |
| 8 | 0.000802 | 0.001820 | 0.266897 |
| 9 | 0.000321 | 0.000704 | 0.202842 |
| 10 | 0.000129 | 0.000272 | 0.154160 |
| 11 | 0.000052 | 0.000105 | 0.117162 |
| 12 | 0.000021 | 0.000040 | 0.089043 |
| 13 | 0.000008 | 0.000016 | 0.067673 |
| … | … | … | … |
| … | … | … | … |
| 17 | 0.000000 | 0.000001 | 0.022577 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlNemer, G.; Farid, M.; Ali, R. Development of Viscosity Iterative Techniques for Split Variational-like Inequalities and Fixed Points Related to Pseudo-Contractions. Mathematics 2025, 13, 2896. https://doi.org/10.3390/math13172896
AlNemer G, Farid M, Ali R. Development of Viscosity Iterative Techniques for Split Variational-like Inequalities and Fixed Points Related to Pseudo-Contractions. Mathematics. 2025; 13(17):2896. https://doi.org/10.3390/math13172896
Chicago/Turabian StyleAlNemer, Ghada, Mohammad Farid, and Rehan Ali. 2025. "Development of Viscosity Iterative Techniques for Split Variational-like Inequalities and Fixed Points Related to Pseudo-Contractions" Mathematics 13, no. 17: 2896. https://doi.org/10.3390/math13172896
APA StyleAlNemer, G., Farid, M., & Ali, R. (2025). Development of Viscosity Iterative Techniques for Split Variational-like Inequalities and Fixed Points Related to Pseudo-Contractions. Mathematics, 13(17), 2896. https://doi.org/10.3390/math13172896