A Fast and Privacy-Preserving Outsourced Approach for K-Means Clustering Based on Symmetric Homomorphic Encryption

Abstract

Training a machine learning (ML) model always needs many computing resources, and cloud-based outsourced training is a good solution to address the issue of a computing resources shortage. However, the cloud may be untrustworthy, and it may pose a privacy threat to the training process. Currently, most work makes use of multi-party computation protocols and lattice-based homomorphic encryption algorithms to solve the privacy problem, but these tools are inefficient in communication or computation. Therefore, in this paper, we focus on the k-means and propose a fast and privacy-preserving method for outsourced clustering of k-means models based on symmetric homomorphic encryption (SHE), which is used to encrypt the clustering dataset and model parameters in our scheme. We design an interactive protocol and use various tools to optimize the protocol time overheads. We perform security analysis and detailed evaluation on the performance of our scheme, and the experimental results show that our scheme has better prediction accuracy, as well as lower computation and total overheads.

1. Introduction

In modern life, we encounter vast amounts of big data in various fields. Data mining serves as a powerful tool to uncover hidden patterns and extract valuable insights from these massive datasets. However, running data mining algorithms requires significant computational and storage resources. When leveraging cloud-based computing and storage solutions to meet these demands, there is an inherent risk of privacy breaches, as sensitive data may be exposed to unauthorized access or leakage during processing and transmission.

Several privacy-preserving cryptography techniques, such as differential privacy (DP), homomorphic encryption (HE), and secure multi-party computation (SMPC), have been employed to protect sensitive data and algorithm parameters in data mining. The differential privacy technique safeguards individual data privacy by injecting noise into datasets, with high efficiency. However, the model parameters and noise-added data remain in plaintext, leading to weak privacy protection of the whole outsourced process. The technique allows for encrypted data mining but requires multiple nodes to perform ciphertext operations, resulting in high computational and communication overheads. The homomorphic encryption technique allows for single-node computation to be carried out directly on ciphertext without inter-node communication, yet its adoption is constrained due to its computational inefficiency and restricted operational support in some HE schemes.

In this paper, we focus on the privacy-preserving outsourced clustering of k-means, which is a popular unsupervised machine learning (ML) algorithm used for clustering data into groups (clusters) based on similarity. It partitions a dataset into k distinct, non-overlapping clusters by minimizing the within-cluster variance (e.g., the sum of the squared distances between data points and their cluster centroids).

Similarly to other ML algorithms, various HE-based [1,2,3,4,5] and SMPC-based [6] schemes have already been proposed to implement privacy-preserving outsourced k-means clustering. However, constrained by the inherent characteristics of the adopted cryptographic techniques (i.e., HE and SMPC), the existing solutions suffer from either excessive communication overhead, high computational complexity, or suboptimal prediction accuracy. We will provide a detailed discussion of the related work in the subsequent section.

1.1. Related Work

Secret sharing (SS), which is a classic realization of SMPC, has been widely adopted to ensure secure outsourced computation and [7,8,9] makes use of different kinds of secret sharing protocols to implement privacy-preserving k-means outsourced clustering. Although SS-based methods offer strong security under standard assumptions, these protocols usually incur relatively heavy computational and communication overheads, due to the secret splitting and frequent interaction between multiple servers.

In addition to SMPC and SS, numerous studies leverage homomorphic encryption (HE) to preserve the privacy of k-means models and associated datasets. For instance, Ref. [3] employs TFHE [10], which replaces non-linear functions with programmable bootstrapping but suffers from extremely slow homomorphic addition and multiplication operations, severely hindering the efficiency of outsourced training. In contrast, works like [4,5] adopt alternative FHE schemes (i.e., BGV [11] and CKKS [12]), offering faster homomorphic operations than TFHE. However, BGV and CKKS also rely on the Ring-LWE problem, resulting in larger ciphertext sizes and slower encryption/decryption speeds. To obtain faster encryption/decryption speeds, researchers [2,7] have made use of Paillier [13], which is a kind of partially homomorphic encryption that only supports addition operations between ciphertexts. However, multiplication/division operations are carried out when distances are calculated; therefore, the researchers [2,7] needed to develop a secure multiparty ciphertext multiplication/division protocol, which increased the communication overhead between multiple servers.

In summary, we provide a hierarchical comparison between our SHE-based (symmetric homomorphic encryption [14]) work and related works including the deployed cryptographic tools, approximated computation, and the communication overhead of each training, based on the experimental results presented in

Table 1. Comparison of related works (NOTE: SS and SHE separately denote secret sharing and symmetric homomorphic encryption).

Schemes	[7,8,9]	[2,7]	[3]	[5]	[4]	Our Work
Num of servers	>1	>1	1	1	1	1
Techniques	SS	Paillier [13]	TFHE [10]	BGV [11]	CKKS [12]	SHE [14]
Comp. overhead	medium	low	high	medium	medium	low
Comm. overhead	medium	medium	high	medium	medium	low

.

1.2. Example Applications of SHE

SHE was first proposed in [14] and used in the privacy-preserving range query in fog-based IoT. After [14], since SHE provided somewhat efficient (leveled) fully homomorphic encryption, a large amount of research work has used SHE to implement privacy-preserving and efficient federated learning [15,16,17], community/range/similarity queries in cloud computing, eHealthcare, and IoT [18,19,20,21]. Based on these successful applications of SHE, it should be feasible to integrate SHE with privacy-preserving outsourced k-means clustering in order to improve the efficiency of the outsourced scheme.

1.3. Our Contributions

To improve the computation and communication efficiency, we leverage SHE, a (leveled) fully homomorphic encryption scheme supporting efficient additive and multiplicative ciphertext operations, to safeguard the outsourced k-means training process. Our key contributions are as follows:

• During the protocol, we develop the Modified Euclidean Distance (MED) to avoid non-linear operations (e.g., division and square root) and reduce both the computational and communication costs.
• Comprehensive experiments and comparisons were conducted to demonstrate our solution’s superiority in prediction accuracy, computational efficiency, and total runtime (including computation and communication).

2. Preliminaries

2.1. K-Means

K-means is an unsupervised learning algorithm that partitions n data points in a dataset into k clusters, where each data point is assigned to the cluster with the nearest centroid. The algorithm proceeds in the following steps:

Firstly, given a dataset $\mathbf{X}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n\}$, where ${\mathbf{x}}_i\in {\mathbb{R}}^d$ ($i\in [1,n]$ and of the n d-dimensional data points into a predefined integer range), k cluster centroids ${\mathit{\mu }}_1,{\mathit{\mu }}_2,\dots ,{\mathit{\mu }}_k$ are randomly initialized. Each data point ${\mathbf{x}}_i$ is then assigned to the nearest cluster by calculating the cluster index $c^{\left(i\right)}=arg{min}_j{\parallel {\mathbf{x}}_i-{\mathit{\mu }}_j\parallel }^2$, where $j\in \{1,2,\dots ,k\}$, and $c^{\left(i\right)}$ denotes the cluster assignment for ${\mathbf{x}}_i$.

Secondly, each centroid ${\mathit{\mu }}_j$ is recalculated as the mean of all data points assigned to its cluster $C_j$: ${\mathit{\mu }}_j={\displaystyle \frac{1}{|C_j|}}{\sum }_{{\mathbf{x}}_i\in C_j}{\mathbf{x}}_i$, where $C_j$ is the set of points assigned to cluster j. After the new cluster centroids are updated, each data point ${\mathbf{x}}_i$ is then reassigned to the nearest new centroid using the same distance calculation as in the first step.

Thirdly, the algorithm iterates between the centroid update and data point assignment until the cluster assignments stabilize or the movement of the centroids falls below a specified threshold.

Upon convergence, the resulting model, defined by the final k centroids, can assign a new data point ${\mathbf{x}}_{\mathrm{new}}$ by calculating $c_{\mathrm{new}}=arg{min}_j{\parallel {\mathbf{x}}_{\mathrm{new}}-{\mathit{\mu }}_j\parallel }^2$, where $c_{\mathrm{new}}$ is the predicted cluster index.

2.2. Symmetric Homomorphic Encryption (SHE)

The SHE scheme consists of the following three algorithms:

• $(sk,pp)\leftarrow \mathsf{SHE}.\mathsf{KeyGen}(k_0,k_1,k_2)$ is the key generation algorithm, which uses input security parameters $k_0,k_1,$ and $k_2$ (satisfying $k_1\ll k_2<(k_0/2)$) to randomly generate a secret key $sk$ and public parameters $pp$. The secret key is $sk=(p,q,\mathcal{R})$, where p and q are two large prime numbers satisfying $\left|p\right|=\left|q\right|=k_0$, $\mathcal{R}$ is a random number satisfying $\left|\mathcal{R}\right|=k_2$, and the message space $\mathcal{M}=\left\{m\right|m\in [-2^{k_1-1},2^{k_1-1})\}$. Then, $\mathcal{N}=pq$ is computed, and the public parameters $pp$ are set to $(k_0,k_1,k_2,\mathcal{N})$.
• ${\left[\left[m\right]\right]}_{sk}\leftarrow \mathsf{SHE}.\mathsf{Enc}(m,sk)$ is the encryption algorithm, which encrypts a message $m\in \mathcal{M}$ using the secret key $sk=(p,q,\mathcal{R})$. The ciphertext is computed as ${\left[\left[m\right]\right]}_{sk}=\mathsf{SHE}.\mathsf{Enc}(m,(p,q,\mathcal{R}))=(r\mathcal{R}+m)(1+r^{\prime }p)mod\mathcal{N}$, where ${r\in \{0,1\}}^{k_2}$ and ${r^{\prime }\in \{0,1\}}^{k_0}$ are randomly sampled. $m\leftarrow \mathsf{SHE}.\mathsf{Dec}({\left[\right[m\left]\right]}_{sk},sk)$ is the decryption algorithm, which recovers the message m from a ciphertext ${\left[\right[m\left]\right]}_{sk}$ using the secret key sk via the computation ${m=\left(\right[\left[m\right]]}_{sk}\left(\mathrm{mod}p\right)\left)\right(\mathrm{mod}\mathcal{R})$.

Given a plaintext $m_0$ and two ciphertexts, ${\left[\left[m_1\right]\right]}_{sk}$ and ${\left[\left[m_2\right]\right]}_{sk}$ (encrypted under the same key), the scheme supports the following homomorphic operations: $m_0\oplus {\left[\left[m_1\right]\right]}_{sk}={\left[[m_0+m_1]\right]}_{sk}$, $m_0\otimes {\left[\left[m_1\right]\right]}_{sk}={\left[\left[m_0{m}_1\right]\right]}_{sk}$, ${\left[\left[m_1\right]\right]}_{sk}\oplus {\left[\left[m_2\right]\right]}_{sk}={\left[[m_1+m_2]\right]}_{sk}$, and ${\left[\left[m_1\right]\right]}_{sk}\otimes {\left[\left[m_2\right]\right]}_{sk}={\left[\left[m_1{m}_2\right]\right]}_{sk}$, where ⊕ and ⊗, respectively, represent the homomorphic addition and multiplication. Furthermore, the scheme supports an arbitrary number of homomorphic additions but is limited to $\lfloor (k_0/2k_2)-1\rfloor$ sequential homomorphic multiplications.

Although SHE is a symmetric scheme, it can be transformed into an asymmetric one [15] by generating a public key $pk=r_0\otimes {\left[\left[0\right]\right]}_{sk}$, where $r_0$ is a $k_2$-bit random number, and $sk$ serves as the private key. Using this key pair, a message m is encrypted with the public key $pk$ via the operation ${\left[\left[m\right]\right]}_{pk}=m\oplus pk={\left[\left[m\right]\right]}_{sk}$, and the resulting ciphertext is decrypted with the private key $sk$ using the original decryption algorithm: $m=\mathsf{SHE}.\mathsf{Dec}({\left[\left[m\right]\right]}_{pk},sk)$.

3. System Design

3.1. System Architecture

Similar to previous works, our system architecture involves two entities: a data owner ($\mathtt{DO}$) and a cloud service provider ($\mathtt{CSP}$), where the $\mathtt{DO}$ owns the dataset but lacks sufficient computational resources, while the $\mathtt{CSP}$ provides on-demand cloud computing services. Figure 1 illustrates our outsourced k-means clustering protocol, an interactive process between the $\mathtt{DO}$ and the $\mathtt{CSP}$. Before the protocol begins, the $\mathtt{DO}$ generates a key pair, normalizes the dataset, and encrypts the dataset and initial centroids, providing only the public keys to the $\mathtt{CSP}$. During the protocol, the $\mathtt{CSP}$ is responsible for the bulk of the computational tasks, operating on the encrypted dataset and model parameters. However, because SHE does not support the direct comparison of ciphertexts, the $\mathtt{CSP}$ must return intermediate results to the $\mathtt{DO}$ for any necessary comparisons. The $\mathtt{DO}$ then decrypts, compares, re-encrypts, and returns the updated data to the $\mathtt{CSP}$. Finally, upon convergence, the $\mathtt{DO}$ receives the encrypted final k-means model parameters from the $\mathtt{CSP}$ and decrypts them.

3.2. Security Models and Desired Properties

In our protocol’s threat model, the $\mathtt{DO}$ is assumed to be trusted, while the $\mathtt{CSP}$ is considered honest-but-curious with respect to the $\mathtt{DO}$’s dataset and model parameters. Accordingly, our protocol is designed to uphold the following security properties:

• Dataset Privacy: The protocol must ensure the $\mathtt{CSP}$ cannot learn the contents of the original clustering dataset provided by the $\mathtt{DO}$.
• Model Privacy: The protocol must protect the confidentiality of the k-means model parameters throughout the entire outsourced clustering process. Specifically, $\mathtt{CSP}$ should not learn (i) the feature values of the cluster centroids or (ii) the distances between individual data points and these centroids.

To provide these security guarantees, we employ the (leveled) fully homomorphic encryption scheme SHE, which has been proven to be IND-CPA secure [19].

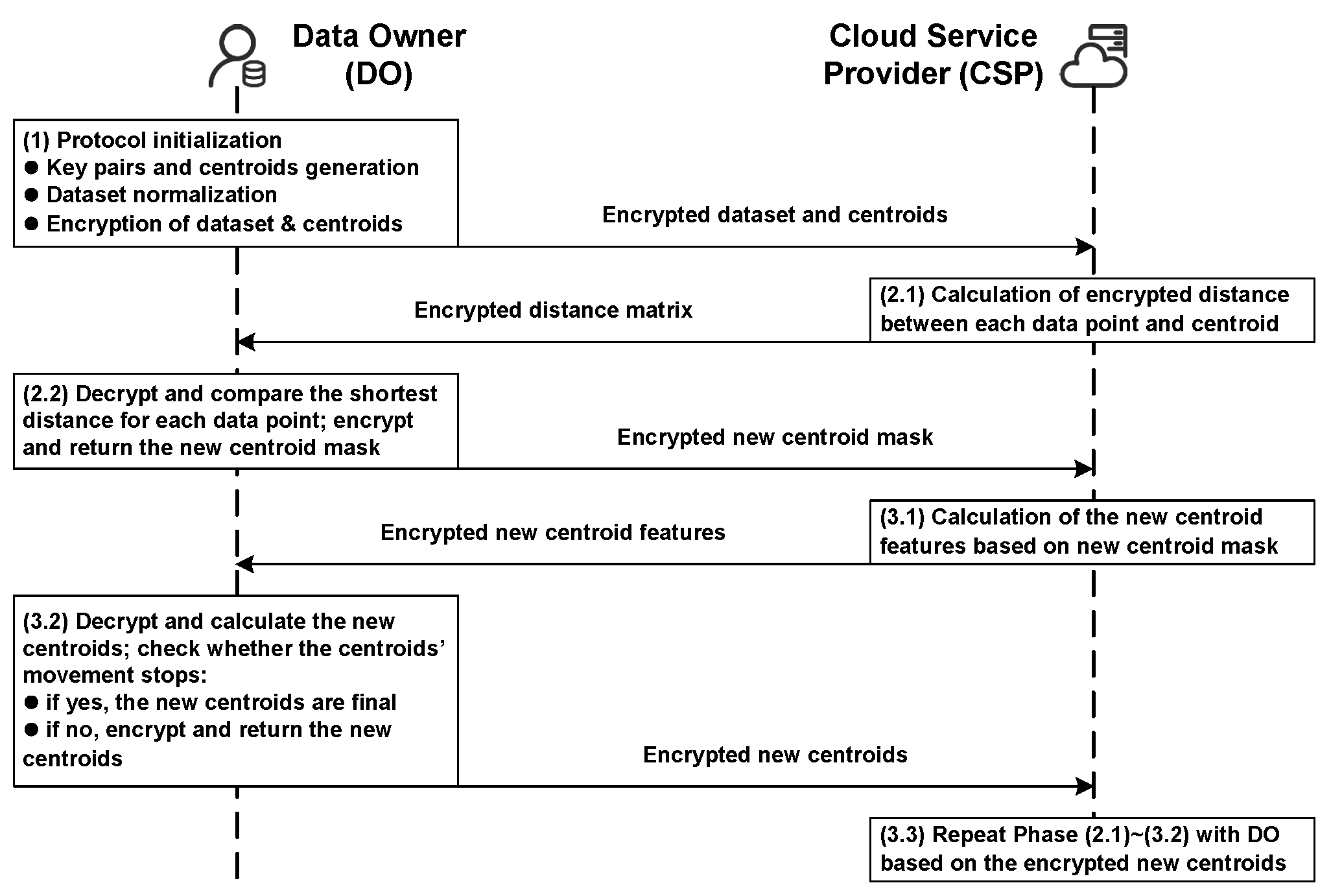
4. Protocol Implementation

In this section, we detail our k-means clustering protocol, aligning with the process illustrated in Figure 1.

4.1. Protocol Initialization

Before the protocol begins, the $\mathtt{DO}$ executes the initialization step, which corresponds to Phase (1) in Figure 1.

Phase (1). The $\mathtt{DO}$’s clustering dataset consists of n data points. To begin, the $\mathtt{DO}$ generates a SHE key pair, denoted as $(p{k}_1,s{k}_1)$. Because SHE only supports operations on integers, the $\mathtt{DO}$ must normalize each feature, $x_{ij}$ (for $i\in [1,n],j\in [1,d]$), of the n d-dimensional data points into a predefined integer range $[-2^{b-1},2^{b-1})$, where $b\in {\mathbb{Z}}^{+}$.

Next, the $\mathtt{DO}$ randomly generates k d-dimensional cluster centroids (${\mathit{\mu }}_1,{\mathit{\mu }}_2,\dots ,{\mathit{\mu }}_k$) and similarly normalizes their features, ${\mu }_{lj}$ (for $l\in [1,k],j\in [1,d]$), into the same integer range. To facilitate subtraction between the data point and centroid features, the $\mathtt{DO}$ negates the centroid features (${\mu }_{lj}$), encodes both data features ($x_{ij}$) and the negated features ($-{\mu }_{lj}$) as complements, and finally encrypts them with $s{k}_1$ to obtain ${\left[\left[x_{ij}\right]\right]}_{s{k}_1}$ and ${\left[[-{\mu }_{lj}]\right]}_{s{k}_1}$.

Finally, the $\mathtt{DO}$ sends all encrypted features of the data points and cluster centroids (${\left[\left[x_{ij}\right]\right]}_{s{k}_1}$ and ${\left[[-{\mu }_{lj}]\right]}_{s{k}_1}$) to the $\mathtt{CSP}$ to begin the protocol’s first round.

4.2. The First Protocol Round (Distance Calculation and Comparison)

The first protocol round corresponds to Phase (2.1)–(2.2) in Figure 1, where the primary tasks for the $\mathtt{CSP}$ and the $\mathtt{DO}$ are distance calculation and comparison, respectively.

Phase (2.1). In this phase, using the encrypted features previously received from the $\mathtt{DO}$, the $\mathtt{CSP}$ calculates the distance between each data point and every cluster centroid. Because SHE does not support the square root operation on ciphertexts, we use a Modified Euclidean Distance (MED) metric, which consists solely of addition, subtraction, and multiplication operations. For instance, the MED between the i-th data point $x_i$ and the l-th cluster centroid ${\mu }_l$ is defined as

$$ME{D}_{(x_i,{\mu }_l)}=\sum _{j\in [1,d]}{(x_{ij}-{\mu }_{lj})}^2.$$

To compute this MED, the $\mathtt{CSP}$ first homomorphically adds the corresponding encrypted features (${\left[\left[x_{ij}\right]\right]}_{s{k}_1}$ and ${\left[[-{\mu }_{lj}]\right]}_{s{k}_1}$), then squares each resulting sum, and finally sums these squared results to obtain the encrypted MED value. As direct ciphertext comparison is not supported by SHE, the $\mathtt{CSP}$ then sends all the encrypted MED values back to the $\mathtt{DO}$ for decryption and comparison.

Phase (2.2). Upon receiving the encrypted MEDs from the $\mathtt{CSP}$, the $\mathtt{DO}$ decrypts and compares them to determine the closest cluster centroid for each data point. On one hand, after the comparisons, the $\mathtt{DO}$ counts the number of data points assigned to each centroid and generates a count vector $[cn{t}_1,cn{t}_2,\dots ,cn{t}_k]$, where $cn{t}_l$ is the number of points closest to centroid l, and ${\sum }_{l=1}^{k}cn{t}_l=n$. For example, the vector $[3,5,7,4,2]$ indicates that 3, 5, 7, 4, and 2 data points are closest to the first, second, third, fourth, and fifth centroids, respectively. This count vector is subsequently used for the centroid update step.

On the other hand, the $\mathtt{DO}$ also generates a centroid mask for each data point i, denoted as a boolean vector $[ms{k}_{i1},ms{k}_{i2},\dots ,ms{k}_{ik}]$ (e.g., $[0,0,1,0,0]$ indicates the point is closest to the third centroid). The $\mathtt{DO}$ then encrypts these n mask vectors and sends the resulting ciphertexts (${\left[\left[{\mathrm{msk}}_{i1}\right]\right]}_{s{k}_1},\dots ,{\left[\left[{\mathrm{msk}}_{ik}\right]\right]}_{s{k}_1}$ for $i\in [1,n]$) to the $\mathtt{CSP}$.

4.3. The Second Protocol Round (Centroid Calculation and Update)

The second protocol round corresponds to Phase (3.1)–(3.3) in Figure 1. During this round, the $\mathtt{CSP}$ and the $\mathtt{DO}$ collaboratively calculate and update the cluster centroids. If the centroids have not yet converged, the $\mathtt{CSP}$ and the $\mathtt{DO}$ repeat Phase (2.1)–(3.2) using the newly updated centroids.

Phase (3.1). After receiving the n encrypted centroid mask vectors from the $\mathtt{DO}$, the $\mathtt{CSP}$ calculates the accumulated features for each new centroid according to the following equation:

$${\left[[\mathrm{acc}\_{\mu }_{lj}]\right]}_{s{k}_1}=\sum _{i\in [1,n]}{\left[\left[ms{k}_{il}\right]\right]}_{s{k}_1}\times {\left[\left[x_{ij}\right]\right]}_{s{k}_1},$$

where ${\left[\left[x_{ij}\right]\right]}_{s{k}_1}$ is the encrypted feature of the data point, and ${\left[\left[ms{k}_{il}\right]\right]}_{s{k}_1}$ is the corresponding encrypted mask value, $i\in [1,n],j\in [1,d]$ and $l\in [1,k]$. Although the new centroid feature is defined as the accumulated feature divided by the number of associated data points, the $\mathtt{CSP}$ cannot perform this division directly on ciphertexts, as this operation is not supported by SHE. Therefore, the $\mathtt{CSP}$ must send the encrypted accumulated features, ${\left[[acc\_{\mu }_{lj}]\right]}_{s{k}_1}$, back to the $\mathtt{DO}$ to perform the final calculation and update of the new centroids.

Phase (3.2). Upon receiving the encrypted accumulated features ${\left[[acc\_{\mu }_{lj}]\right]}_{s{k}_1}$, the $\mathtt{DO}$ first decrypts them using $s{k}_1$ to obtain the plaintext accumulated features, $acc\_{\mu }_{lj}$. After decryption, the $\mathtt{DO}$ calculates the new centroid feature, $new\_{\mu }_{lj}$, by dividing each accumulated feature $acc\_{\mu }_{lj}$ by the corresponding data point count, $cn{t}_l$: $new\_{\mu }_{lj}={\displaystyle \frac{acc\_{\mu }_{lj}}{cn{t}_l}}$ (for $j\in [1,d],l\in [1,k]$).

Next, the $\mathtt{DO}$ checks for convergence by comparing the previous centroid features, ${\mu }_{lj}$, with the new ones, $new\_{\mu }_{lj}$. If $new\_{\mu }_{lj}={\mu }_{lj}$ for all features, the centroids have converged, the clustering process is complete, and these are the final model parameters. Otherwise, the $\mathtt{DO}$ encrypts the updated centroid features ($new\_{\mu }_{lj}$) with $s{k}_1$ and sends the resulting ciphertexts, ${\left[[new\_{\mu }_{lj}]\right]}_{s{k}_1}$, to the $\mathtt{CSP}$ for the next iteration.

Phase (3.3). Using the newly encrypted centroid features ${\left[[new\_{\mu }_{lj}]\right]}_{s{k}_1}$, the $\mathtt{CSP}$ and the $\mathtt{DO}$ repeat Phase (2.1)–(3.2) until the clustering process converges.

5. Experimental Results and Analysis

The performance of our scheme was evaluated with the $\mathtt{DO}$ deployed on a machine equipped with a 2-core 11th Gen Intel Core i7-1195G7 CPU (operating at 2.92 GHz), 4GB of RAM, and Windows 10. The $\mathtt{CSP}$ was hosted on a machine with a 4-core CPU of the same model (2.92 GHz), 16GB of RAM, and Windows 11. Notably, the hardware used in our experiments is less powerful than that of the related works we compare our work against; nevertheless, our scheme demonstrates superior time performance, as will be detailed later.

The datasets used in our experiments, listed in

Table 2. Specifications of the benchmark datasets used in our experiments.

Datasets	Centroid Num. (k)	Dim. (d)	Data Point Num. (n)
iris [23]	3	4	150
wine [24]	3	13	178
breast cancer [25]	2	30	569
banknote [26]	2	5	1372
musk [27]	2	166	6598
sepsis [28]	2	3	110,204
gas [29]	6	128	13,910

, were selected from the standard UCI repository [22] to facilitate a direct comparison with the key related works [2,3,4,5] and demonstrate our scheme’s feasibility and efficiency. For our experiments, we used seven datasets [23,24,25,26,27,28,29], which were partitioned into a 70% training set and a 30% validation set.

To ensure a sufficient security level, we set the SHE parameters for $s{k}_1$ to $(k_0,k_1,k_2)$ = (1048, 30, 90), which offers a security guarantee comparable or superior to that of the related works; a detailed security analysis of these parameters is presented later. For a balance of efficiency and precision, we normalized all dataset features to the integer range $[0,200]$. This range can be extended up to $[0,2^{30}-1]$ with negligible impact on accuracy or performance, as our chosen SHE parameters support the encryption of 30-bit ($k_1$-bit) integers.

5.1. Prediction Accuracy and Comparison

Table 3. Accuracy comparisons between our scheme and related works.

Related Works	Datasets	Evaluation Metrics	Accuracy Comparison
(i) [4]	Iris	Mean error	2.95∼7.21% (>Our 0%)
(ii) [2]	Self-synthetic	Adjusted Rand Index	49∼72.4% (≈Our 40∼80%)
(iii) [3]	FCPS [30]	Misclassification rate	0∼3% (≥Our 0%)
(iv) [5]	Self-synthetic	Relative error	0.65∼26.91% (>Our 0%)

(i) The work in [4] uses the mean error between the centroids from ciphertext-based clustering and those from plaintext-based clustering as its accuracy metric. (ii) The authors of [2] employ the Adjusted Rand Index (ARI) [31], which measures the similarity between the clustering result and the ground-truth labels. (iii) Reference [3] utilizes the misclassification rate, which quantifies the fraction of incorrectly clustered data points, as its accuracy metric. (iv) The scheme in [5] is evaluated using the relative error between centroids computed on ciphertexts versus those computed on plaintexts.

compares the accuracy of our scheme with the key related works [2,3,4,5], each of which utilizes different clustering datasets and evaluation metrics.

Regarding the datasets, some of the compared works utilize self-generated synthetic data [2,5] or the non-UCI FCPS benchmark [3]. In contrast, our experiments use standard UCI datasets with parameters ($k,n,d$) chosen to be comparable to those in the related works.

As detailed in the notes of Table 3 and summarized in its final column, our scheme’s accuracy is benchmarked against these varied metrics. As the results show, our scheme outperforms the methods in [3,4,5] and achieves a clustering accuracy comparable to the work in [2].

The superior accuracy of our scheme can be attributed to our choice of cryptographic primitive. The compared works [3,4,5] rely on lattice-based schemes (e.g., CKKS, TFHE, BGV) that require approximations like polynomial functions to handle non-linear operations. In contrast, our approach utilizes an integer-based SHE scheme combined with data normalization. This method introduces only minimal precision loss by truncating the least significant bits, thereby preserving the accuracy. Furthermore, our interactive protocol is designed such that all homomorphic computations consist of exact integer operations (additions and multiplications), eliminating the need for approximations and thus minimizing the accuracy degradation.

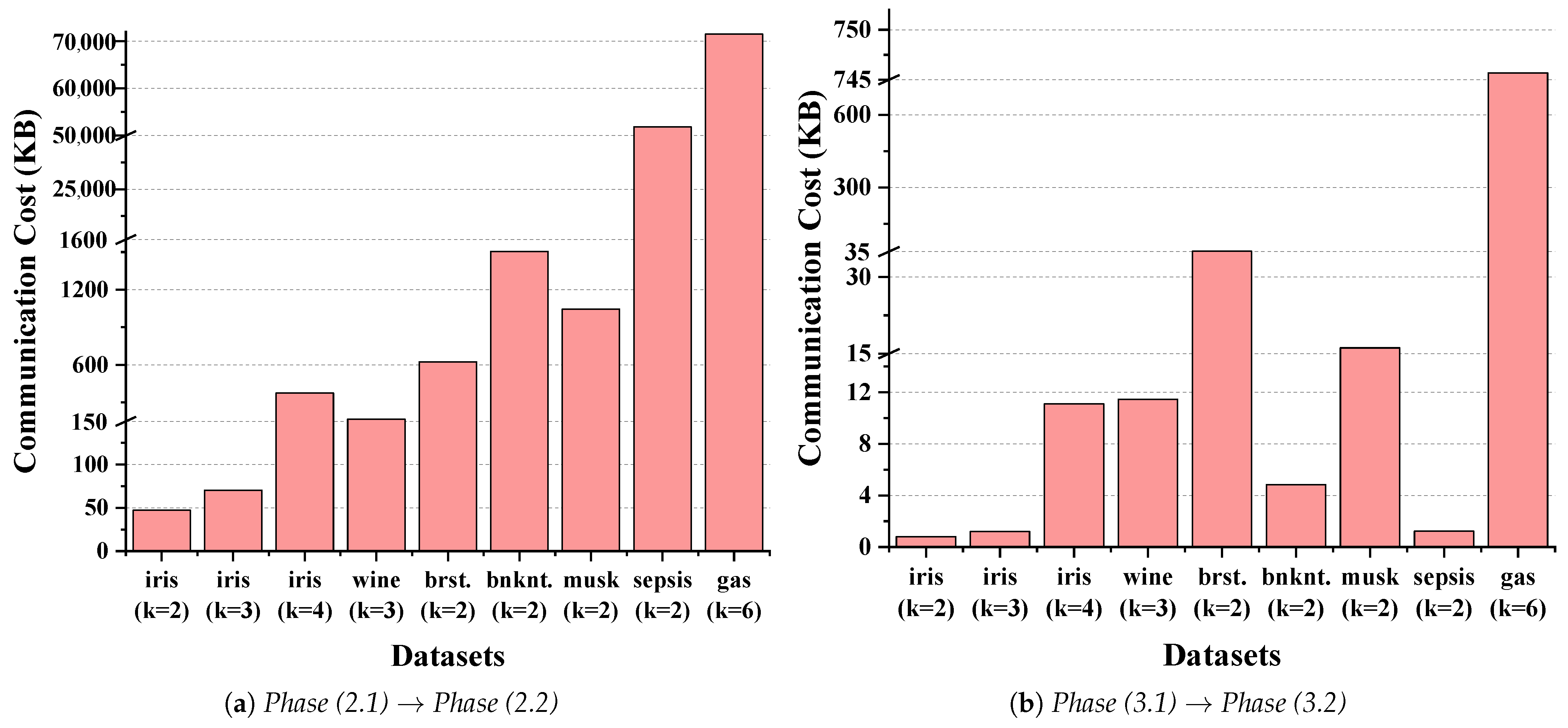
5.2. Communication Overhead of Our Scheme

Figure 2 and Figure 3 illustrate the communication overhead of our scheme for various datasets, corresponding to the interactive data flows between the $\mathtt{DO}$ and $\mathtt{CSP}$ depicted in Figure 1.

In the direction from the $\mathtt{DO}$ to $\mathtt{CSP}$, the communication overhead (illustrated in Figure 2) primarily consists of two components, corresponding to the two transmission steps shown in Figure 1.

• The first component is generated at the end of Phase (1), when the $\mathtt{DO}$ transmits the initial encrypted data package to the $\mathtt{CSP}$, which includes the dataset, initial centroids, and public parameters.
• The second component occurs at the end of Phase (2.2) and consists of the encrypted new centroid mask vectors.

Conversely, in the direction from the $\mathtt{CSP}$ to $\mathtt{DO}$, the communication overhead (Figure 3) is also composed of two main parts, reflecting the two return transmissions in the protocol.

• The first part is the encrypted distance matrix transmitted at the end of Phase (2.1), which the $\mathtt{DO}$ uses for comparison.
• The second part, sent at the end of Phase (3.1), consists of the encrypted accumulated centroid features, which are required for the new centroid calculation.

In summary, all data exchanged between the parties are encrypted, and the resulting communication overhead is of a manageable size. Under typical network conditions, this communication overhead has a negligible impact on the total protocol execution time, a point we will elaborate on in the following subsection.

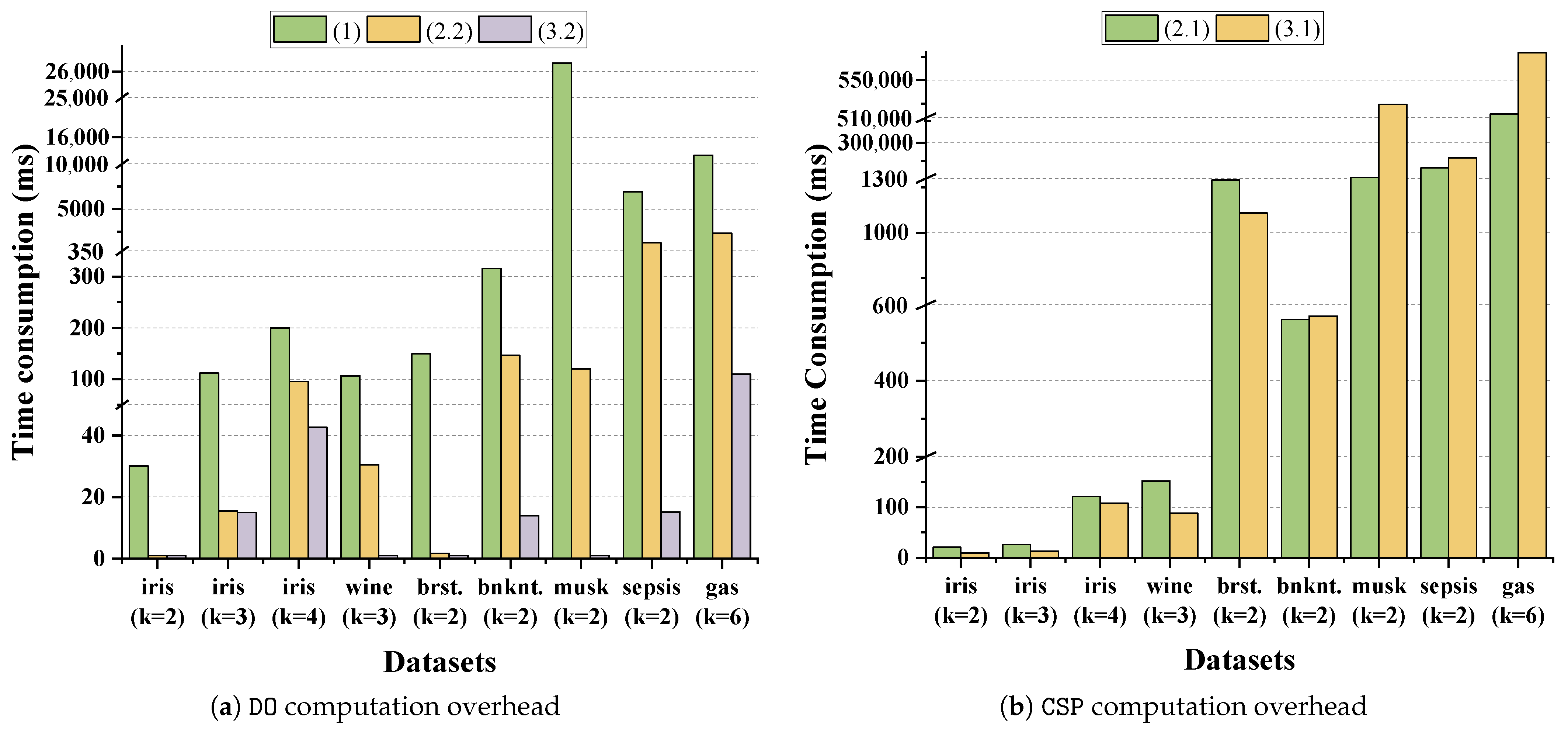
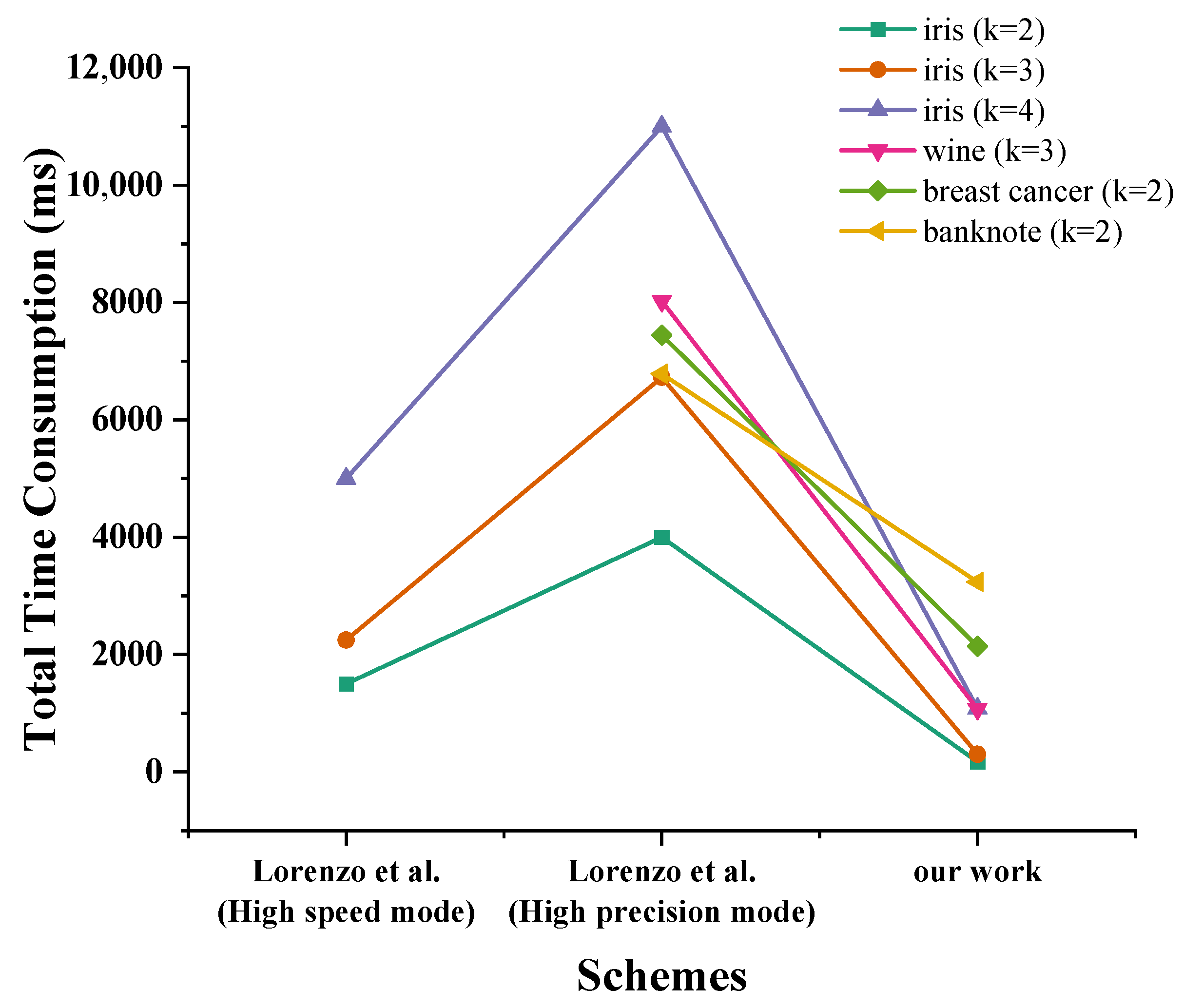
5.3. Time Performance and Comparison

In this subsection, we evaluate the time performance of our protocol by analyzing three key aspects: the computation time for the $\mathtt{DO}$ and $\mathtt{CSP}$, the theoretical computational complexity, and a comparison of the total execution time against the related works. To ensure reliability, all the reported time overheads are the average of 10 independent runs. Our analysis of the computational complexity is presented alongside the empirical computation times for each protocol phase. As plaintext operations are negligible in comparison, this complexity analysis focuses primarily on operations involving ciphertexts.

The empirical computation times for our scheme are presented in Figure 4, which breaks down the performance of both the $\mathtt{DO}$ and the $\mathtt{CSP}$. The $\mathtt{DO}$’s computation time, detailed in Figure 4a, is divided into three parts corresponding to its three phases of activity in the protocol.

• Phase (1). In this phase, the computation time is the time overhead of protocol initialization, mainly including the key pair generation, dataset normalization, and encryption of the dataset and initial centroids. The initial setup requires the $\mathtt{DO}$ to encrypt $n·d$ data point features and $k·d$ centroid features. As typically $n\gg k$, the complexity is dominated by dataset encryption, resulting in the initial computational complexity $O(n·d)$.
• Phase (2.2). This phase involves two main operations: comparing distances to find the nearest centroid for each data point and generating the new centroid masks. During this process, the $\mathtt{DO}$ mainly performs $O(n·k)$ plaintext comparisons to find the nearest centroid for each point and encrypts and returns $n\times k$ mask values. The complexity of this phase is dominated by the $O(n·k)$ cryptographic operations.
• Phase (3.2). In this phase, the $\mathtt{DO}$ mainly needs to perform division operation of the new (accumulated) centroid feature by the number of data points that are closest to the corresponding centroid and check for convergence. Therefore, $k\times d$ decryption of encrypted accumulated features and $k\times d$ encryption of the new centroid features are needed, and the complexity of this phase is thus $O(k·d)$.

As shown in Figure 4a, most of the computation time overheads of the $\mathtt{DO}$ operations in different phases are less than two dozen seconds, and the total $\mathtt{DO}$ computation time overheads are all low (i.e., at most dozens of seconds) based on our different clustering datasets (even for the huge dataset). Based on the theoretical analysis, the total computational complexity of the $\mathtt{DO}$ is $O(n·d)$ when $n\gg k$ is common.

The $\mathtt{CSP}$’s computation time, presented in Figure 4b, comprises two parts corresponding to its two active phases in the protocol.

• Phase (2.1). $\mathtt{CSP}$ performs ciphertext addition and multiplication to calculate the distances between each data point and each centroid. To compute the Modified Euclidean Distance (MED) between one data point and one centroid, the $\mathtt{CSP}$ performs operations for each of the d dimensions. This involves d homomorphic multiplications and $2d-1$ homomorphic additions. Since this must be performed for all n data points and k centroids, the total complexity for this phase is $O(n·k·d)$ homomorphic operations.
• Phase (3.1). In this phase, the $\mathtt{CSP}$ performs homomorphic multiplications and additions to compute the new accumulated centroid features. The $\mathtt{CSP}$ calculates the accumulated features for each new centroid based on the equation in Phase (3.1). For each of the $k\times d$ features, this requires a summation over all n data points, which involves n homomorphic multiplications and $n-1$ homomorphic additions. Therefore, the total complexity of this phase is also $O(n·k·d)$ homomorphic operations.

Similar to the computation execution time of the $\mathtt{DO}$, the total computation time overheads of the $\mathtt{CSP}$ are also low (i.e., less than dozens of seconds for the largest dataset) based on different clustering datasets. The overall computational complexity for the $\mathtt{CSP}$ is $O(n·k·d)$, which constitutes the dominant portion of the protocol’s entire computation time.

While the computation times for both parties are low, the interactive nature of our protocol means that the communication overhead could also impact the total execution time. Therefore, to comprehensively evaluate the impact of different network environments on the communication overheads, we simulated a standard Internet environment (100 Mbps bandwidth, 10 ms round-trip delay) to test the total execution time overheads of our protocol (including the computation time overheads and communication time overheads). The experimental results, as shown in Figure 5, demonstrate that our scheme maintains lower total execution time overheads than the related work [4] based on various UCI datasets.

While a poor network environment (e.g., 10 Mbps bandwidth, 30 ms delay) could become a bottleneck with larger datasets, this effect is mitigated by modern high-speed internet. However, Gigabit-bandwidth Internet, which is quite common nowadays, can significantly reduce the transmission time and further reduce the total execution time overhead of our protocol.

However, since three other related works [2,3,5] used as comparison deployed non-UCI datasets, we selected corresponding UCI datasets having larger dataset parameters, and the total time overhead comparison results are shown in

Table 4. Total time overhead comparison with non-UCI-based related works.

Comparison Results Between [2] Based on Paillier and Our Work
Dataset Size	Research [2]		Our work
2000	99,402.12 s ≈ 27.61 h		1.14 s
3000	255,790.18 s ≈ 71.05 h		1.29 s
4000	377,794.82 s ≈ 104.94 h		1.86 s
5000	680,925.54 s ≈ 189.15 h		4.76 s
Comparison results between [3] (exact/approximate mode) based on TFHE and our work
	[3] (Exact mode)	[3] (Approximate mode)	Our work
Runtime per Iteration	873.46 h	15.56 h	0.166 s
Iteration Number	15	40	5
Total Time	545.91 days ≈ 17.95 months	25.93 days ≈ 0.85 months	0.83 s
Comparison results between [5] (fastest/slowest mode) based on BGV and our work
$d,n$	[5] (Fastest Mode)	[5] (Slowest Mode)	Our work
$d=2$, $n=100$	1479 s	3164 s	$d=4$, $n=100$	0.16 s
$d=10$, $n=100$	150 s	702 s	$d=13$, $n=100$	0.97 s

. As one may see, our work has an overwhelming advantage in the total time overhead over the compared non-UCI-based works, while our work has equal or better accuracy as introduced before.

There are some details that need to be explained in Table 4. When compared to [3], our scheme has converged and stops when the protocol iteration number reaches 5; so, the total time overhead is the multiplication result of our one-iteration runtime and 5. When compared to [5], we chose datasets with larger dimensions (and same for the other parameters) and we still obtained a smaller total time overhead.

5.4. Security Analysis

As proven in [19], the SHE scheme employed in our work satisfies IND-CPA (Indistinguishability under Chosen-Plaintext Attack) security, based on the $(\mathcal{R},p)$-decision assumption. Specifically, the ability of the SHE scheme to resist chosen-plaintext attacks and thus achieve IND-CPA security is conditional upon the lengths of the security parameters $\mathcal{R}$ (length $k_2$) and p (length $k_0$). On one hand, the security of $\mathcal{R}$, a random number of length $k_2$, relies on the infeasibility of a brute-force attack. To render such an attack computationally infeasible (requiring $2^{k_2}$ operations), a length of $k_2\ge 90$ is required. On the other hand, the security of the large prime p is tied to the difficulty of the integer factorization problem. Given the public modulus $N=pq$, an attacker must factor N to recover p. With the currently recommended minimum secure length for N at 1024 bits, the length of p, $k_0$, must be at least 512 bits.

The security parameters selected for our implementation, $k_2=90$ and $k_0=1048$, meet or exceed the required minimums of 90 and 512 bits, respectively. Therefore, our configuration of the SHE scheme satisfies the requirements for IND-CPA security.

Given this IND-CPA secure foundation, we now analyze how our protocol achieves the specific privacy properties defined in Section 3.2 under the honest-but-curious model.

• Dataset Privacy. The clustering dataset $\mathbf{X}$ is encrypted using the secret key $s{k}_1$. Without access to $s{k}_1$, the $\mathtt{CSP}$ has no means to decrypt the data features. This directly guarantees the privacy of the dataset.
• Model Privacy. Throughout the protocol, all sensitive model parameters are encrypted with $s{k}_1$. This includes initial/updated centroid features, intermediate MED values, centroid masks, and accumulated features. The $\mathtt{CSP}$ operates exclusively on these ciphertexts. Given the IND-CPA security of SHE, the $\mathtt{CSP}$ cannot infer any information about these parameters, thus ensuring the privacy of the k-means model.

6. Conclusions

In this paper, we proposed a fast and privacy-preserving outsourced k-means clustering scheme based on symmetric homomorphic encryption (SHE). Our scheme enables a data owner ($\mathtt{DO}$) to securely outsource encrypted data to a cloud service provider ($\mathtt{CSP}$) for k-means model training, while guaranteeing the privacy of both the dataset and the model parameters. We developed a Modified Euclidean Distance (MED) metric to avoid costly non-linear operations, thereby reducing both the computational and communication overheads. The experimental results demonstrate that our scheme achieves superior performance compared to the related works in terms of the prediction accuracy, computation time, and total execution overhead. Building on the success of the SHE for efficient privacy-preserving k-means, our future work will focus on integrating this approach with outsourced incremental clustering and classification schemes to support a broader range of application scenarios.