Third-Order Hankel Determinant for a Class of Bi-Univalent Functions Associated with Sine Function

Abstract

This paper investigates a new subclass of bi-univalent analytic functions defined on the open unit disk in the complex plane, associated with the subordination to $1+\mathrm{s}\mathrm{i}\mathrm{n}z$. Coefficient bounds are obtained for the initial Taylor–Maclaurin coefficients, with a particular focus on the second- and third-order Hankel determinants. To illustrate the non-emptiness of the proposed class, we consider the function $\sqrt{1+tanhz}$, which maps the unit disk onto a bean-shaped domain. This function satisfies the required subordination condition and hence serves as an explicit member of the class. A graphical depiction of the image domain is provided to highlight its geometric characteristics. The results obtained in this work confirm that the class under study is non-trivial and possesses rich geometric structure, making it suitable for further development in the theory of geometric function classes and coefficient estimation problems.

1. Introduction

Hankel determinants, formed from sequences in Hankel matrices, are essential in complex analysis and geometric function theory. They aid in studying analytic function coefficients, especially for bi-univalent functions, and estimating their second and third Hankel determinants reveals structural behavior and subclass properties [1,2,3,4].

Let $\mathrm{\Lambda }$ represent the set of all analytic functions defined in the open unit disk $\mathcal{Q}:=\{z\in \mathbb{C}:|z|<1\}$, which can be written as

$$f\left(z\right)=z+\sum _{k=2}^{\infty }{c}_k{z}^k,$$

(1)

and satisfy the normalization conditions $f\left(0\right)=0$ and $f^{\prime }\left(0\right)=1$.

Further, by S we shall denote the class of all functions in $\mathrm{\Lambda }$ which are univalent in $\mathcal{Q}$; for definitions and further details on analytic and univalent functions, we refer the reader to the standard reference in the field [5]. A classical result known as the Koebe one-quarter theorem [6,7,8] guarantees that the image of $\mathcal{Q}$ under any univalent function $f\in \mathrm{\Lambda }$ always contains a disk of radius at least $\frac{1}{4}$. Because of this, each such univalent function f has an inverse $f^{-1}$ such that

$$f^{-1}\left(f\left(z\right)\right)=z \mathrm{for} z\in \mathcal{Q}, \mathrm{and} f\left(f^{-1}\left(w\right)\right)=w \mathrm{for} \left|w\right|<r_0\left(f\right), \mathrm{where} r_0\left(f\right)\ge \frac{1}{4},$$

with the inverse given by the expansion

$$f^{-1}\left(w\right)=w-c_2{w}^2+(2c_2^2-c_3)w^3-\cdots .$$

(2)

A function $f\in \mathrm{\Lambda }$ is called bi-univalent if both f and its inverse $f^{-1}$ are univalent in the open unit disk $\mathcal{Q}$. The class of all such functions is denoted by $\mathsf{\Sigma }$. Various aspects and properties of bi-univalent functions have been extensively discussed in [9,10].

Research on bi-univalent functions saw a big rise after the contributions of Srivastava and his co-authors [10]. Some well-known examples in the class $\mathsf{\Sigma }$ are as follows:

$${\displaystyle \frac{z}{1-z}}, -log(1-z), {\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1+z}{1-z}}\right).$$

On the other hand, functions like the Koebe function, $z-{\displaystyle \frac{z^2}{2}}$, and ${\displaystyle \frac{z}{1-z^2}}$ are univalent but not bi-univalent [11,12,13].

A lot of work has been done on finding coefficient bounds for bi-univalent functions. For example, Lewin [14] showed that $|c_2|\le 1.51$, while Brannan and Clunie [15] suggested $|c_2|\le \sqrt{2}$. Netanyahu [16] later gave the sharp bound $|c_2|\le {\displaystyle \frac{4}{3}}$. To get better estimates, many subclasses of $\mathsf{\Sigma }$, such as starlike and convex functions, were studied [17,18,19]. A key functional used in this area is the Fekete–Szegö expression $|c_3-\eta c_2^2|$, which has been explored for various subclasses [20,21,22].

Let $f,g\in \mathrm{\Lambda }$. The function $f\left(z\right)$ is said to be subordinate to $g\left(z\right)$, denoted by $f\left(z\right)\prec g\left(z\right)$, if there exists a Schwarz function $u\left(z\right)$, analytic in $\mathcal{Q}$, such that $u\left(0\right)=0$ and $\left|u\right(z\left)\right|<1$ for all $z\in \mathcal{Q}$, satisfying

$$f\left(z\right)=g\left(u\right(z\left)\right).$$

This concept of subordination was discussed in detail in [23,24,25]. Furthermore, if $g\left(z\right)$ is univalent in $\mathcal{Q}$, then the subordination relation $f\left(z\right)\prec g\left(z\right)$ is equivalent to the conditions

$$f\left(0\right)=g\left(0\right) \mathrm{and} f\left(\mathcal{Q}\right)\subseteq g\left(\mathcal{Q}\right).$$

The class of starlike functions is defined by

$${\mathcal{S}}^{\ast }=\left\{f\in \mathcal{S}:{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec {\displaystyle \frac{1+z}{1-z}}, z\in \mathcal{Q}\right\},$$

which is the same as

$${\mathcal{S}}^{\ast }=\left\{f\in \mathcal{S}:\Re \left({\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>0, z\in \mathcal{Q}\right\}.$$

This means that ${\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}$ lies in the right half-plane. For more details, see [10,26,27,28].

In 1976, Noonan and Thomas [29] introduced the idea of the q-th Hankel determinant for the function f defined in (1). It involves forming a square matrix from the Taylor coefficients of f and calculating its determinant. The general form is given by

$${\mathcal{H}}_q\left(\tau \right)=\left|\begin{array}{cccc}{c}_{\tau }& c_{\tau +1}& \cdots & c_{\tau +q-1}\\ c_{\tau +1}& c_{\tau +2}& \cdots & c_{\tau +q}\\ ⋮& ⋮& \ddots & ⋮\\ c_{\tau +q-1}& c_{\tau +q}& \cdots & c_{\tau +2q-2}\end{array}\right| (\tau ,q\in \mathbb{N}; c_1=1).$$

(3)

Over time, many researchers have studied these determinants. For example, the growth of ${\mathcal{H}}_q\left(\tau \right)$ as $\tau \to \infty$ has been explored for functions f with bounded boundaries [26,29,30]. More recently, sharp estimates have been found for special cases like ${\mathcal{H}}_2\left(2\right)$, especially for certain subclasses of analytic or bi-univalent functions [31,32,33].

To get a clearer idea of how Hankel determinants work for small values of q, consider the following examples for $c_1=1$:

$${\mathcal{H}}_2\left(1\right)=\left|\begin{array}{cc}{c}_1& c_2\\ c_2& c_3\end{array}\right|=c_3-c_2^2,$$

$${\mathcal{H}}_2\left(2\right)=\left|\begin{array}{cc}{c}_2& c_3\\ c_3& c_4\end{array}\right|=c_2{c}_4-c_3^2.$$

These compact expressions capture relationships between coefficients and are widely used in geometric function theory. In particular, the quantity ${\mathcal{H}}_2\left(1\right)=c_3-c_2^2$, known as the Fekete–Szegö functional, has been central in many coefficient bound problems. Recently, Shakir et al. [34] pushed this further by providing sharp bounds for ${\mathcal{H}}_2\left(2\right)$ in specific subclasses of analytic functions (see also [35,36,37,38]).

In this work, our main focus shifts to the third-order Hankel determinant:

$${\mathcal{H}}_3\left(1\right)=\left|\begin{array}{ccc}{c}_1& c_2& c_3\\ c_2& c_3& c_4\\ c_3& c_4& c_5\end{array}\right|.$$

Since $c_1=1$ for functions in $\mathrm{\Lambda }$, this reduces to

$${\mathcal{H}}_3\left(1\right)=c_3(c_2{c}_4-c_3^2)-c_4(c_4-c_2{c}_3)+c_5(c_3-c_2^2).$$

(4)

Using the triangle inequality, we get a useful upper bound:

$$|{\mathcal{H}}_3\left(1\right)|\le |c_3| |c_2{c}_4-c_3^2|+|c_4| |c_4-c_2{c}_3|+|c_5| |c_3-c_2^2|.$$

(5)

Throughout the paper, we focus on estimating this expression. To do that, we first study the sharp bounds of the quantities involved:

$$|c_3-c_2^2|, |c_2{c}_4-c_3^2|, |c_4-c_2{c}_3|, |c_3|, |c_4|, |c_5|.$$

These estimates play a key role in determining the behavior of ${\mathcal{H}}_3\left(1\right)$ in certain subclasses of analytic and bi-univalent functions. Special attention is also given to the second-order determinant ${\mathcal{H}}_2\left(2\right)$, due to its frequent appearance in recent coefficient-related studies.

2. Definition and Lemmas

The sine function, with its well-known analytic and oscillatory properties in the unit disk, provides a powerful tool for constructing and analyzing subclasses of analytic functions. In this study, we utilize the sine function as a dominant function in a subordination relationship to capture geometric features such as bounded boundary rotation and symmetry. Specifically, we consider the subordination $f^{\prime }\left(z\right)+\vartheta z{f}^{\prime \prime }\left(z\right)\prec 1+sin\left(z\right),$ where $\vartheta \ge 0$, to define new classes of functions whose behavior is controlled by the sine function. This approach allows us to investigate coefficient estimates and derive sharp bounds for Hankel determinants within these sine based subclasses.

Definition 1.

Let $f\in \mathsf{\Sigma }$, and let g be defined as in (2). The function f is said to belong to the class ${\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$ if the following subordination conditions hold:

$$f^{\prime }\left(z\right)+\vartheta z{f}^{\prime \prime }\left(z\right)\prec 1+sinz, z\in \mathcal{Q},$$

(6)

and

$$g^{\prime }\left(w\right)+\vartheta w{g}^{\prime \prime }\left(w\right)\prec 1+sinw, w\in \mathcal{Q},$$

(7)

where $\vartheta \ge 0$.

Figure 1 shows the image of the grid in the domain under the mapping $f\left(z\right)=1+sinz$, illustrating the corresponding structure in the co-domain.

Remark 1.

This remark presents two special cases for specific values of ϑ.

 (i) 

If $\vartheta =1$, then the function f is said to belong to the class ${\mathcal{T}}_{\mathsf{\Sigma }}\left(1\right)$, and the definition simplifies to

$$f^{\prime }\left(z\right)+z{f}^{\prime \prime }\left(z\right)\prec 1+sinz, \mathit{and} g^{\prime }\left(w\right)+w{g}^{\prime \prime }\left(w\right)\prec 1+sinw.$$

 (ii) 

If $\vartheta =0$, then the function f is said to belong to the class ${\mathcal{T}}_{\mathsf{\Sigma }}\left(0\right)$, and the subordination becomes

$$f^{\prime }\left(z\right)\prec 1+sinz, \mathit{and} g^{\prime }\left(w\right)\prec 1+sinw.$$

Remark 2.

The class ${\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$ is not empty, since the domain generated by the function

$$1+sinz$$

(corresponding to the yellow region in Figure 2) clearly contains other subordinating domains.

In particular, consider the function

$$\sqrt{1+tanhz},$$

whose image is the well-known bean-shaped domain (illustrated in blue in Figure 2). From the figure, it is evident that the blue bean-shaped region is entirely contained within the yellow domain of $1+sinz$.

Thus, the function $\sqrt{1+tanhz}$ belongs to the class ${\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, confirming that this class is non-empty. A detailed discussion on the mapping $1+sinz$ and bean-shaped domains can be found in [38,39].

Let $\mathbb{P}$ be the class of analytic functions $p\left(z\right)$ defined in the open unit disk $\mathcal{Q}$ that satisfy

$$p\left(0\right)=1 \mathrm{and} \Re \left(p\right(z\left)\right)>0.$$

(8)

Lemma 1.

(see [5])

Suppose $s\left(z\right)\in \mathbb{P}$ has the form

$$s\left(z\right)=1+s_{1}z+s_2{z}^2+s_3{z}^3+\cdots ,$$

then the following inequality holds:

$$|s_k|\le 2, \mathit{for} \mathit{all} k\in \mathbb{N}=\{1,2,3,\dots \}.$$

(9)

Lemma 2.

(see [40])

Let $s\left(z\right)\in \mathbb{P}$ and be written as

$$s\left(z\right)=1+s_{1}z+s_2{z}^2+s_3{z}^3+\cdots ,$$

then we have

$$2s_2=s_1^2+k(4-s_1^2),$$

(10)

and

$$4s_3=s_1^3+2s_1(4-s_1^2)k-s_1(4-s_1^2)k^2+2(4-s_1^2){(1-|k|}^2)z,$$

(11)

for some complex numbers k and z such that $\left|k\right|\le 1$ and $\left|z\right|\le 1$ and $s_1\ge 0$.

3. On the Second Hankel Determinant Associated with the Class ${\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$

Theorem 1.

Let $f\left(z\right)$ given by (1) belong to the class ${\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, where $\vartheta \ge 0$. Then the following holds:

$$\begin{array}{cc}\hfill \left|c_2{c}_4-c_3^2\right|& \le {\displaystyle \frac{5}{8(1+\vartheta )(1+3\vartheta )}}-{\displaystyle \frac{4+\vartheta \left(12+\vartheta (3+\vartheta )\right)}{48\left(1+3\vartheta \right){(1+\vartheta )}^4}}.\hfill \end{array}$$

(12)

Proof. 

Let $f\in \mathsf{\Sigma }(\vartheta ,sin)$. Then there exist two functions $t,s:\mathcal{Q}\to \mathcal{Q}$, both satisfying $t\left(0\right)=s\left(0\right)=0$ and $\left|t\right(z\left)\right|<1$, $\left|s\right(w\left)\right|<1$, such that

$$f^{\prime }\left(z\right)+\vartheta z{f}^{\prime \prime }\left(z\right)=1+sint\left(z\right),$$

(13)

and

$$g^{\prime }\left(w\right)+\vartheta w{g}^{\prime \prime }\left(w\right)=1+sins\left(w\right).$$

(14)

Assume that the functions $p\left(z\right)$ and $q\left(w\right)$ belong to the class $\mathbb{P}$, and take the forms

$$p\left(z\right)=1+p_{1}z+p_2{z}^2+\cdots ,$$

$$q\left(w\right)=1+q_{1}w+q_2{w}^2+\cdots .$$

Then, the functions $t\left(z\right)$ and $s\left(w\right)$ can be written as

$$t\left(z\right)={\displaystyle \frac{p\left(z\right)-1}{p\left(z\right)+1}}={\displaystyle \frac{1}{2}}\left[t_{1}z+\left(t_2-{\displaystyle \frac{t_1^2}{2}}\right)z^2+{\displaystyle \frac{1}{4}}\left(t_1^3-4t_1{t}_2+4t_3\right)z^3+\cdots \right],$$

(15)

$$s\left(w\right)={\displaystyle \frac{q\left(w\right)-1}{q\left(w\right)+1}}={\displaystyle \frac{1}{2}}\left[s_{1}w+\left(s_2-{\displaystyle \frac{s_1^2}{2}}\right)w^2+{\displaystyle \frac{1}{4}}\left(s_1^3-4s_1{s}_2+4s_3\right)w^3+\cdots \right].$$

(16)

By plugging (15) and (16) into Equations (13) and (14), we get the following expansions:

$$\begin{array}{cc}\hfill 1+sint\left(z\right)= & 1+{\displaystyle \frac{t_1}{2}}z+\left({\displaystyle \frac{t_2}{2}}-{\displaystyle \frac{t_1^2}{4}}\right)z^2+\left({\displaystyle \frac{5t_1^3}{48}}-{\displaystyle \frac{t_1{t}_2}{2}}+{\displaystyle \frac{t_3}{2}}\right)z^3\hfill \\ \hfill & +\left({\displaystyle \frac{t_4}{2}}-{\displaystyle \frac{t_1^4}{32}}+{\displaystyle \frac{5t_1^2{t}_2}{16}}-{\displaystyle \frac{t_2^2}{4}}-{\displaystyle \frac{t_1{t}_3}{2}}\right)z^4+\cdots \hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill 1+sins\left(w\right)= & 1+{\displaystyle \frac{s_1}{2}}w+\left({\displaystyle \frac{s_2}{2}}-{\displaystyle \frac{s_1^2}{4}}\right)w^2+\left({\displaystyle \frac{5s_1^3}{48}}-{\displaystyle \frac{s_1{s}_2}{2}}+{\displaystyle \frac{s_3}{2}}\right)w^3\hfill \\ \hfill & +\left({\displaystyle \frac{s_4}{2}}-{\displaystyle \frac{s_1^4}{32}}+{\displaystyle \frac{5s_1^2{s}_2}{16}}-{\displaystyle \frac{s_2^2}{4}}-{\displaystyle \frac{s_1{s}_3}{2}}\right)w^4+\cdots \hfill \end{array}$$

(18)

Since $f\in \mathsf{\Sigma }$, its Taylor expansion is given by (1), and the series for its inverse $g=f^{-1}$ is given in (2). Then, we compute

$$\begin{array}{cc}\hfill f^{\prime }\left(z\right)+\vartheta z{f}^{\prime \prime }\left(z\right)=& 1+2(1+\vartheta )c_{2}z+3(1+2\vartheta )c_3{z}^2\hfill \\ \hfill & +4(1+3\vartheta )c_4{z}^3+5(1+4\vartheta )c_5{z}^4+\cdots \hfill \end{array}$$

(19)

and

$$\begin{array}{cc}\hfill g^{\prime }\left(w\right)+\vartheta w{g}^{\prime \prime }\left(w\right)= & 1-2(1+\vartheta )c_{2}w+3(1+2\vartheta )(2c_2^2-c_3)w^2\hfill \\ \hfill & -4(1+3\vartheta )(5c_2^3-5c_2{c}_3+c_4)w^3\hfill \\ \hfill & +5(1+4\vartheta )(14c_2^4-21c_2^2{c}_3+3c_3^2+6c_2{c}_4-c_5)w^4+\cdots \hfill \end{array}$$

(20)

By comparing the coefficients of powers of z in Equations (17) and (19), we derive the following equations:

$$2(1+\vartheta )c_2={\displaystyle \frac{t_1}{2}},$$

(21)

$$3(1+2\vartheta )c_3={\displaystyle \frac{t_2}{2}}-{\displaystyle \frac{t_1^2}{4}},$$

(22)

$$4(1+3\vartheta )c_4={\displaystyle \frac{5t_1^3}{48}}-{\displaystyle \frac{t_1{t}_2}{2}}+{\displaystyle \frac{t_3}{2}},$$

(23)

and

$$\begin{array}{c}\hfill 5c_5(1+4\vartheta )={\displaystyle \frac{t_4}{2}}-{\displaystyle \frac{t_1^4}{32}}+{\displaystyle \frac{5t_1^2{t}_2}{16}}-{\displaystyle \frac{t_2^2}{4}}-{\displaystyle \frac{t_1{t}_3}{2}}.\end{array}$$

(24)

By comparing the coefficients of powers of w in Equations (18) and (20), we derive the following equations:

$$-2c_2(1+\vartheta )={\displaystyle \frac{s_1}{2}},$$

(25)

$$3(1+2\vartheta )(2c_2^2-c_3)={\displaystyle \frac{s_2}{2}}-{\displaystyle \frac{s_1^2}{4}},$$

(26)

$$-4(1+3\vartheta )(5c_2^3-5c_2{c}_3+c_4)={\displaystyle \frac{5s_1^3}{48}}-{\displaystyle \frac{s_1{s}_2}{2}}+{\displaystyle \frac{s_3}{2}},$$

(27)

and

$$\begin{array}{c}\hfill 5(1+4\vartheta )(14c_2^4-21c_2^2{c}_3+3c_3^2+6c_2{c}_4-c_5)={\displaystyle \frac{s_4}{2}}-{\displaystyle \frac{s_1^4}{32}}+{\displaystyle \frac{5s_1^2{s}_2}{16}}-{\displaystyle \frac{s_2^2}{4}}-{\displaystyle \frac{s_1{s}_3}{2}}.\end{array}$$

(28)

By comparing the Equations (21) and (25), we obtain

$$c_2={\displaystyle \frac{t_1}{4(1+\vartheta )}}={\displaystyle \frac{-s_1}{4(1+\vartheta )}},$$

(29)

and also

$$t_1=-s_1.$$

(30)

By subtracting Equations (22) and (26) and using Equation (30), we obtain:

$$c_3={\displaystyle \frac{t_2-s_2}{12(1+2\vartheta )}}+{\displaystyle \frac{t_1^2}{16{(1+\vartheta )}^2}}.$$

(31)

By subtracting Equations (23) and (27) and using Equations (29) and (30), we obtain

$$c_4={\displaystyle \frac{1}{384}}\left({\displaystyle \frac{20t_1(t_2-s_2)}{(1+\vartheta )(1+2\vartheta )}}+{\displaystyle \frac{5(t_1^3-s_1^3)-24t_1(t_2+s_2)+24(t_3-s_3)}{1+3\vartheta }}\right).$$

(32)

By using Equations (29)–(31), we obtain the following equation:

$$\begin{array}{cc}\hfill c_2{c}_4-c_3^2={\displaystyle \frac{1}{4608}}(& {\displaystyle \frac{-48t_1^2{t}_2+48s_2{t}_1^2}{{(1+\vartheta )}^2(1+2\vartheta )}}-{\displaystyle \frac{18t_1^4}{{(1+\vartheta )}^4}}-{\displaystyle \frac{32{(s_2-t_2)}^2}{{(1+2\vartheta )}^2}}\hfill \\ \hfill & +{\displaystyle \frac{3t_1}{1+\vartheta }}\left({\displaystyle \frac{20t_1(-s_2+t_2)}{(1+\vartheta )(1+2\vartheta )}}+{\displaystyle \frac{5(-s_1^3+t_1^3)-24t_1(s_2+t_2)+24(-s_3+t_3)}{1+3\vartheta }}\right))\hfill \end{array}$$

(33)

According to Lemma 2 and $t_1=-s_1$, we get

$$t_2-s_2={\displaystyle \frac{4-t_1^2}{2}}(x-y), t_2+s_2=t_1^2+{\displaystyle \frac{4-t_1^2}{2}}(x+y)$$

(34)

and

$$t_3-s_3={\displaystyle \frac{t_1^3}{2}}+{\displaystyle \frac{(4-t_1^2)t_1}{2}}(x+y)-{\displaystyle \frac{(4-t_1^2)t_1}{4}}(x^2+y^2)+{\displaystyle \frac{4-t_1^2}{2}}\left[{(1-|x|}^2{)z-(1-\left|y\right|}^2)w\right],$$

(35)

for some $x,y,z,w$ with $\left|x\right|\le 1$, $\left|y\right|\le 1$, and $\left|w\right|\le 1$.

Since $t\in \mathbb{P}$, it holds that $|t_1|\le 2$. By setting $t_1=t$, we can, without loss of generality, assume $t\in [0,2]$. Now, using the expressions in (34) and (35) and substituting them into (33), and by letting $\sigma =\left|x\right|\le 1$ and $\epsilon =\left|y\right|\le 1$, we obtain

$$|c_2{c}_4-c_3^2|\le {\mathbb{L}}_1+{\mathbb{L}}_2(\sigma +\epsilon )+{\mathbb{L}}_3({\sigma }^2+{\epsilon }^2)+{\mathbb{L}}_4{(\sigma +\epsilon )}^2=\mathbb{L}(\sigma ,\epsilon ),$$

where

$${\mathbb{L}}_1={\displaystyle \frac{t^4\left(4+\vartheta \left(12+\vartheta (3+\vartheta )\right)\right)}{768{(1+\vartheta )}^4(-1-3\vartheta )}}\ge 0,$$

(36)

$${\mathbb{L}}_2={\mathbb{L}}_2(\sigma +\epsilon )={\displaystyle \frac{t^2(-4+t^2)}{768{(1+\vartheta )}^2(-1-2\vartheta )}}\ge 0$$

(37)

$${\mathbb{L}}_3={\mathbb{L}}_3({\sigma }^2+{\epsilon }^2)={\displaystyle \frac{1}{256}}\left({\displaystyle \frac{t(8-4t-2t^2+6t^3)}{(1+\vartheta )(1+3\vartheta )}}\right)\le 0$$

(38)

$${\mathbb{L}}_4={\mathbb{L}}_4{(\sigma +\epsilon )}^2={\displaystyle \frac{1}{576}}\left({\displaystyle \frac{8t^2-16-t^4}{{(1+2\vartheta )}^2}}\right)\ge 0.$$

(39)

Next, we aim to find the maximum value of $\mathbb{L}(\sigma ,\epsilon )$ over the closed square $[0,1]\times [0,1]$, with the parameter $t\in [0,2]$. Given that ${\mathbb{L}}_3\le 0$ and ${\mathbb{L}}_3+2{\mathbb{L}}_2\ge 0$, it follows that $t\in (0,2)$, and the determinant of the Hessian, ${\mathbb{L}}_{\sigma \sigma } {\mathbb{L}}_{\epsilon \epsilon }-{\left({\mathbb{L}}_{\sigma \epsilon }\right)}^2$ is strictly negative. This implies that $\mathbb{L}$ cannot attain a local maximum in the interior of the square. Therefore, we analyze the maximum of $\mathbb{L}$ along the boundary.

Consider the case when $\sigma =0$ and $0\le \epsilon \le 1$, then

$$\mathbb{L}(0,\epsilon )=\psi \left(\epsilon \right)={\mathbb{L}}_1+{\mathbb{L}}_2\epsilon +({\mathbb{L}}_3+{\mathbb{L}}_4){\epsilon }^2.$$

Next, we consider two separate scenarios:

Case 1: Suppose ${\mathbb{L}}_3+{\mathbb{L}}_4\ge 0$. In this case, for all $\epsilon \in [0,1]$ and a fixed $t\in [0,2)$, the derivative

$${\psi }^{\prime }\left(\epsilon \right)={\mathbb{L}}_2+2({\mathbb{L}}_3+{\mathbb{L}}_4)\epsilon >0.$$

This implies that $\psi \left(\epsilon \right)$ is strictly increasing, so the maximum value is achieved at $\epsilon =1$. Thus,

$$max\psi \left(\epsilon \right)=\psi \left(1\right)={\mathbb{L}}_1+{\mathbb{L}}_2+{\mathbb{L}}_3+{\mathbb{L}}_4.$$

Case 2: Assume ${\mathbb{L}}_3+{\mathbb{L}}_4<0$. Given that $2({\mathbb{L}}_3+{\mathbb{L}}_4)+{\mathbb{L}}_2\ge 0$, and for $0<\epsilon <1$, it follows that

$$2({\mathbb{L}}_3+{\mathbb{L}}_4)+{\mathbb{L}}_2<2({\mathbb{L}}_3+{\mathbb{L}}_4)\epsilon +{\mathbb{L}}_2<{\mathbb{L}}_2.$$

Therefore, $\psi \left(\epsilon \right)>0$, and again the maximum occurs at $\epsilon =1$. Thus, we have:

$$\mathbb{L}(1,\epsilon )=\mathbb{G}\left(\epsilon \right)=({\mathbb{L}}_3+{\mathbb{L}}_4){\epsilon }^2+({\mathbb{L}}_2+2{\mathbb{L}}_4)\epsilon +{\mathbb{L}}_1+{\mathbb{L}}_2+{\mathbb{L}}_3+{\mathbb{L}}_4.$$

From both cases, we conclude that

$$max\mathbb{G}\left(\epsilon \right)=\mathbb{G}\left(1\right)={\mathbb{L}}_1+2{\mathbb{L}}_2+2{\mathbb{L}}_3+4{\mathbb{L}}_4.$$

Since $\psi \left(1\right)\le \mathbb{G}\left(1\right)$, it follows that the maximum value of $\mathbb{L}(\sigma ,\epsilon )$ on the boundary of the domain $[0,1]\times [0,1]$ is given by

$$max\mathbb{L}(\sigma ,\epsilon )=\mathbb{L}(1,1).$$

Define the real-valued function $\mathcal{H}$ on the interval $(0,1)$ by

$$max\mathcal{H}\left(t\right):=\mathbb{L}(1,1)={\mathbb{L}}_1+2{\mathbb{L}}_2+2{\mathbb{L}}_3+4{\mathbb{L}}_4.$$

By substituting the expressions of ${\mathbb{L}}_1,{\mathbb{L}}_2,{\mathbb{L}}_3,{\mathbb{L}}_4$ into $\mathcal{H}$, we obtain the desired bound.

$$\begin{array}{cc}\hfill \mathbb{L}(1,1)& ={\displaystyle \frac{t^2\left(-4+t^2\right)}{384\left(-1-2\vartheta \right){(1+\vartheta )}^2}}+{\displaystyle \frac{-16+8t^2-t^4}{144{(1+2\vartheta )}^2}}\hfill \\ \hfill & +{\displaystyle \frac{t\left(8-4t-2t^2+6t^3\right)}{128(1+\vartheta )(1+3\vartheta )}}+{\displaystyle \frac{t^4\left(4+\vartheta \left(12+\vartheta (3+\vartheta )\right)\right)}{768\left(-1-3\vartheta \right){(1+\vartheta )}^4}}.\hfill \end{array}$$

(40)

Now, due to the complexity of the explicit form of $\mathbb{L}(1,1)$, we illustrate its monotonicity numerically. Figure 3 shows the plot of $\mathbb{L}(1,1)$, which clearly demonstrates that the function attains its maximum at $t=2$. This figure was generated using Mathematica 14.3.

Therefore, the maximum value of the function $\mathcal{H}\left(t\right)$ occurs at $t=2$, giving

$$\begin{array}{c}\hfill max\mathcal{H}\left(t\right)={\displaystyle \frac{5}{8(1+\vartheta )(1+3\vartheta )}}-{\displaystyle \frac{4+\vartheta \left(12+\vartheta (3+\vartheta )\right)}{48\left(1+3\vartheta \right){(1+\vartheta )}^4}}.\end{array}$$

(41)

This completes the proof. □

Theorem 2.

Let $f\left(z\right)\in {\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, with $\vartheta \ge 0$. Then, we have

$$|c_2{c}_3-c_4|\le \left\{\begin{array}{cc}{\displaystyle \frac{1}{8{(1+\vartheta )}^3}}+{\displaystyle \frac{13}{24+72\vartheta }},\hfill & m\le t\le 2\hfill \\ {\displaystyle \frac{1}{4+12\vartheta }},\hfill & 0\le t\le m\hfill \end{array}\right..$$

(42)

where

$$m={\displaystyle \frac{-d_3\pm \sqrt{d_3^2-12d_2(d_1-d_2)}}{3(d_1-d_2)}},$$

(43)

$$d_1=-{\displaystyle \frac{957+2871\vartheta +2880{\vartheta }^2+960{\vartheta }^3}{768{(1+\vartheta )}^3(3+\vartheta )}},$$

$$d_2={\displaystyle \frac{3+4\vartheta }{-32(1+\vartheta )(1+2\vartheta )}},$$

and

$$d_3={\displaystyle \frac{-12}{1+3\vartheta }}.$$

Proof. 

From (29), (31), and (32), we obtain

$$\begin{array}{c}\hfill |c_2{c}_3-c_4|={\displaystyle \frac{1}{384}}|{\displaystyle \frac{6t_1^3}{{(1+\vartheta )}^3}}+{\displaystyle \frac{12t_1(s_2-t_2)}{(1+\vartheta )(1+2\vartheta )}}+{\displaystyle \frac{5(s_1^3-t_1^3)}{1+3\vartheta }}+{\displaystyle \frac{24t_1(s_2+t_2)}{1+3\vartheta }}+{\displaystyle \frac{24(s_3-t_3)}{1+3\vartheta }}|.\end{array}$$

(44)

By virtue of Lemma (2), we may assume, without loss of generality, that $t\in [0,2]$, where $t_1=t$. Hence, for $\gamma =\left|x\right|\le 1$ and $\zeta =\left|y\right|\le 1$, it follows that

$$|c_2{c}_3-c_4|\le {\mathbb{J}}_1+{\mathbb{J}}_2(\gamma +\zeta )+{\mathbb{J}}_3({\gamma }^2+{\zeta }^2)=\mathbb{M}(\gamma ,\zeta ),$$

(45)

where

$$\begin{array}{cc}\hfill {\mathbb{J}}_1= & {\displaystyle \frac{1}{384}}\left({\displaystyle \frac{26t^3}{1+3\vartheta }}+{\displaystyle \frac{6t^3}{{(1+\vartheta )}^3}}\right)\ge 0,\hfill \end{array}$$

(46)

$${\mathbb{J}}_2=\mathbb{J}(\gamma ,\zeta )={\displaystyle \frac{1}{384}}\left({\displaystyle \frac{24t_1(4-t^2)}{1+3\vartheta }}+{\displaystyle \frac{6t(4-t^2)}{(1+\vartheta )(1+2\vartheta )}}\right)\ge 0,$$

(47)

and

$${\mathbb{J}}_3=\mathbb{J}({\gamma }^2,{\zeta }^2)={\displaystyle \frac{1}{384}}\left({\displaystyle \frac{(6t-12)(-4+t^2)}{1+3\vartheta }}\right)\le 0.$$

(48)

By using the same method as in Theorem 2, the maximum occurs at $\gamma =1$ and $\zeta =1$ in the closed square $[0,2]$, leading to

$$\mathrm{\Psi }\left(t\right)=max\mathbb{M}(\gamma ,\zeta )={\mathbb{J}}_1+2({\mathbb{J}}_2+{\mathbb{J}}_3).$$

(49)

Substituting the values of ${\mathbb{J}}_1,{\mathbb{J}}_2$, and ${\mathbb{J}}_3$ in $\mathrm{\Psi }\left(t\right)$, we get

$$\mathrm{\Psi }\left(t\right)={\displaystyle \frac{1}{192}}\left({\displaystyle \frac{3t^3}{{(1+\vartheta )}^3}}+{\displaystyle \frac{6t(-4+t^2)}{1+\vartheta }}-{\displaystyle \frac{12t(-4+t^2)}{1+2\vartheta }}+{\displaystyle \frac{48+t\left(72-t(12+5t)\right)}{1+3\vartheta }}\right).$$

By simplifying slightly, we obtain

$$\mathrm{\Psi }\left(t\right)=d_1{t}^3+d_{2}t(4-t^2)-d_3(4-t^2).$$

(50)

where

$$d_1=-{\displaystyle \frac{957+2871\vartheta +2880{\vartheta }^2+960{\vartheta }^3}{768{(1+\vartheta )}^3(3+\vartheta )}},$$

$$d_2={\displaystyle \frac{3+4\vartheta }{-32(1+\vartheta )(1+2\vartheta )}},$$

and

$$d_3={\displaystyle \frac{-12}{1+3\vartheta }}.$$

We have

$${\mathrm{\Psi }}^{\prime }\left(t\right)=3(d_1-d_2)t^2+2d_{3}t+4d_2,$$

$${\mathrm{\Psi }}^{\prime \prime }\left(t\right)=6(d_1-d_2)p+2d_3.$$

If $d_1-d_3>0$, meaning $d_1>d_3$, then ${\mathrm{\Psi }}^{\prime }\left(t\right)>0$. Thus, the function $\mathrm{\Psi }\left(t\right)$ is increasing over the closed interval $[0,2]$, reaching its maximum value at $t=2$, which gives

$$|c_2{c}_3-c_4|\le \mathrm{\Psi }\left(2\right)={\displaystyle \frac{1}{8{(1+\vartheta )}^3}}+{\displaystyle \frac{13}{24+72\vartheta }}.$$

If $d_1-d_3<0$, solving ${\mathrm{\Psi }}^{\prime }\left(t\right)=0$ gives

$$p=m={\displaystyle \frac{-d_3\pm \sqrt{d_3^2-12d_2(d_1-d_2)}}{3(d_1-d_2)}},$$

For $m<p\le 2$, we find that ${\mathrm{\Psi }}^{\prime }\left(t\right)>0$, indicating that $\mathrm{\Psi }\left(t\right)$ is increasing throughout the interval $[0,2]$. Therefore, the maximum value of $\mathrm{\Psi }\left(t\right)$ occurs at $t=2$. On the other hand, if $\mathrm{\Psi }\left(t\right)$ is decreasing on $[0,2]$, then its maximum is attained at $t=0$. As a result, we conclude

$$|c_2{c}_3-c_4|\le \mathrm{\Psi }\left(0\right)={\displaystyle \frac{1}{4+12\vartheta }}.$$

This completes the proof. □

Remark 3.

During the proof, we computed ${\mathrm{\Psi }}^{\prime }\left(t\right)=3(d_1-d_2)t^2+2d_{3}t+4d_2$, which leads to a quadratic equation. Setting ${\mathrm{\Psi }}^{\prime }\left(t\right)=0$ gives the critical point m. Consequently, the inequality splits into two cases depending on the behavior of $\mathrm{\Psi }\left(t\right)$ over $[0,2]$, and we analyzed the value of t for each branch separately.

4. Third Hankel Determinant and Some Inequalities

In this section, we establish sharp upper bounds related to the Fekete–Szegö problem when the parameter $\eta =1$. In particular, we derive important inequalities involving the coefficients $c_2$ and $c_3$, which enable us to estimate the upper bounds for $|c_3-c_2^2|$ and $|c_3|$. These results are fundamental for bounding the coefficients $c_4$ and $c_5$.

Theorem 3.

Let $f\left(z\right)\in {\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, with $\vartheta \ge 0$. Then, the following inequalities hold:

$$|c_3-c_2^2|\le {\displaystyle \frac{1}{3(1+2\vartheta )}},$$

(51)

$$|c_3|\le {\displaystyle \frac{1}{3(1+2\vartheta )}}+{\displaystyle \frac{1}{4{(1+\vartheta )}^2}}.$$

(52)

Proof. 

By using (31) along with Lemma 1, we establish (52). The Fekete–Szegö functional, given $\eta \in \mathbb{C}$ and $f\in {\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, satisfies

$$c_3-\eta c_2^2={\displaystyle \frac{t_2-s_2}{12(1+2\vartheta )}}+{\displaystyle \frac{(1-\eta )t_1^2}{16{(1+\vartheta )}^2}}.$$

By applying Lemma 1, we obtain

$$|c_3-\eta c_2^2| \le {\displaystyle \frac{1}{3(1+2\vartheta )}}+{\displaystyle \frac{(1-\eta )}{4{(1+\vartheta )}^2}}.$$

For $\eta =1$, we derive inequality (51), completing the proof. □

Theorem 4.

Let $f\left(z\right)$, given by Equation (1), belong to the class ${\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, where $\vartheta \ge 0$. Then the following upper bounds hold for the coefficients $c_4$ and $c_5$:

$$|c_4|\le {\displaystyle \frac{1}{384}}\left({\displaystyle \frac{160}{(1+\vartheta )(1+2\vartheta )}}+{\displaystyle \frac{464}{1+3\vartheta }}\right),$$

(53)

$$|c_5|\le {\displaystyle \frac{5}{16{(1+\vartheta )}^4}}+{\displaystyle \frac{1}{6{(1+2\vartheta )}^2}}+{\displaystyle \frac{1}{2{(1+\vartheta )}^2(1+2\vartheta )}}+{\displaystyle \frac{4784}{5+40\vartheta +95{\vartheta }^2+60{\vartheta }^3}}.$$

(54)

Proof. 

Taking the subtraction of Equations (24) and (28) gives us

$$\begin{array}{cc}\hfill c_5= & 7c_2^4-{\displaystyle \frac{21}{2}}{c}_2^2{c}_3+{\displaystyle \frac{3}{2}}{c}_3^2+3c_2{c}_4\hfill \\ \hfill & +{\displaystyle \frac{s_1^4-10s_1^2{s}_2+8s_2^2+16s_1{s}_3-16s_4-t_1^4+10t_1^2{t}_2-8t_2^2-16t_1{t}_3+16t_4}{320+1280\vartheta }},\hfill \end{array}$$

(55)

by substituting Equations (29), (31), and (32) into Equation (55), we obtain

$$\begin{array}{cc}\hfill c_5={\displaystyle \frac{1}{512}}(& -{\displaystyle \frac{7t_1^4}{{(1+\vartheta )}^4}}+{\displaystyle \frac{8t_1^2(s_2-t_2)}{{(1+\vartheta )}^2(1+2\vartheta )}}+{\displaystyle \frac{t_1\left(5(-s_1^3+t_1^3)-24t_1(s_2+t_2)+24(-s_3+t_3)\right)}{(1+\vartheta )(1+3\vartheta )}}\hfill \\ & +{\displaystyle \frac{8\left(10(t_1^2{t}_2-s_1^2{s}_2)-8(t_2^2-s_2^2)+16(t_4+s_1{s}_3)-16(s_4+t_1{t}_3)\right)}{5+20\vartheta }}\hfill \\ & +{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{3t_1^2}{{(1+\vartheta )}^2}}+{\displaystyle \frac{4(-s_2+t_2)}{1+2\vartheta }}\right)}^2)\hfill \end{array}$$

By applying Lemma 2, we obtain the result (53). □

Theorem 5.

Let $f\left(z\right)\in {\mathcal{T}}_{\mathsf{\Sigma }}(\vartheta ,sin)$, where $\vartheta \ge 0$. Then, we have

$$|{\mathcal{H}}_3\left(1\right)|\le \left\{\begin{array}{cc}\mathcal{R}{\mathcal{R}}_1+{\mathcal{R}}_2\left({\displaystyle \frac{1}{8{(1+\vartheta )}^3}}+{\displaystyle \frac{13}{24+72\vartheta }}\right)+{\mathcal{R}}_3{\mathcal{R}}_4,\hfill & m\le c\le 2,\hfill \\ \mathcal{R}{\mathcal{R}}_1+{\displaystyle \frac{1}{4+12\vartheta }}{\mathcal{R}}_2+{\mathcal{R}}_3{\mathcal{R}}_4,\hfill & 0\le c\le m.\hfill \end{array}\right.$$

(56)

where $\mathcal{R},{\mathcal{R}}_1,{\mathcal{R}}_2,{\mathcal{R}}_3,{\mathcal{R}}_4$, and m are defined in (12), (42), (51), (52), (53), and (54), respectively.

Proof. 

Since

$$|{\mathcal{H}}_3\left(1\right)|\le |c_3| |c_2{c}_4-c_3^2|+|c_4| |c_4-c_2{c}_3|+|c_5| |c_3-c_2^2|,$$

applying the triangle inequality yields (56). □

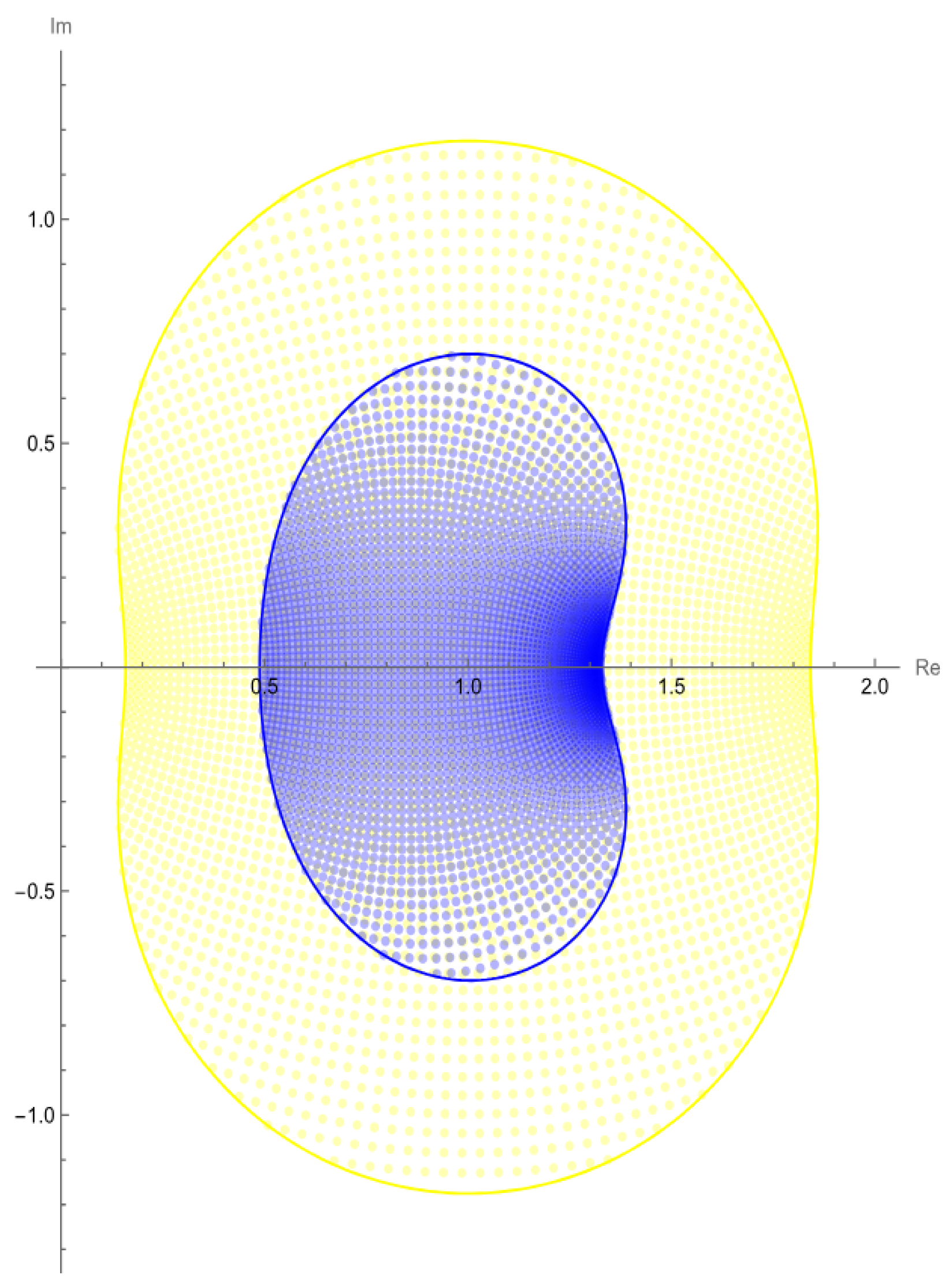
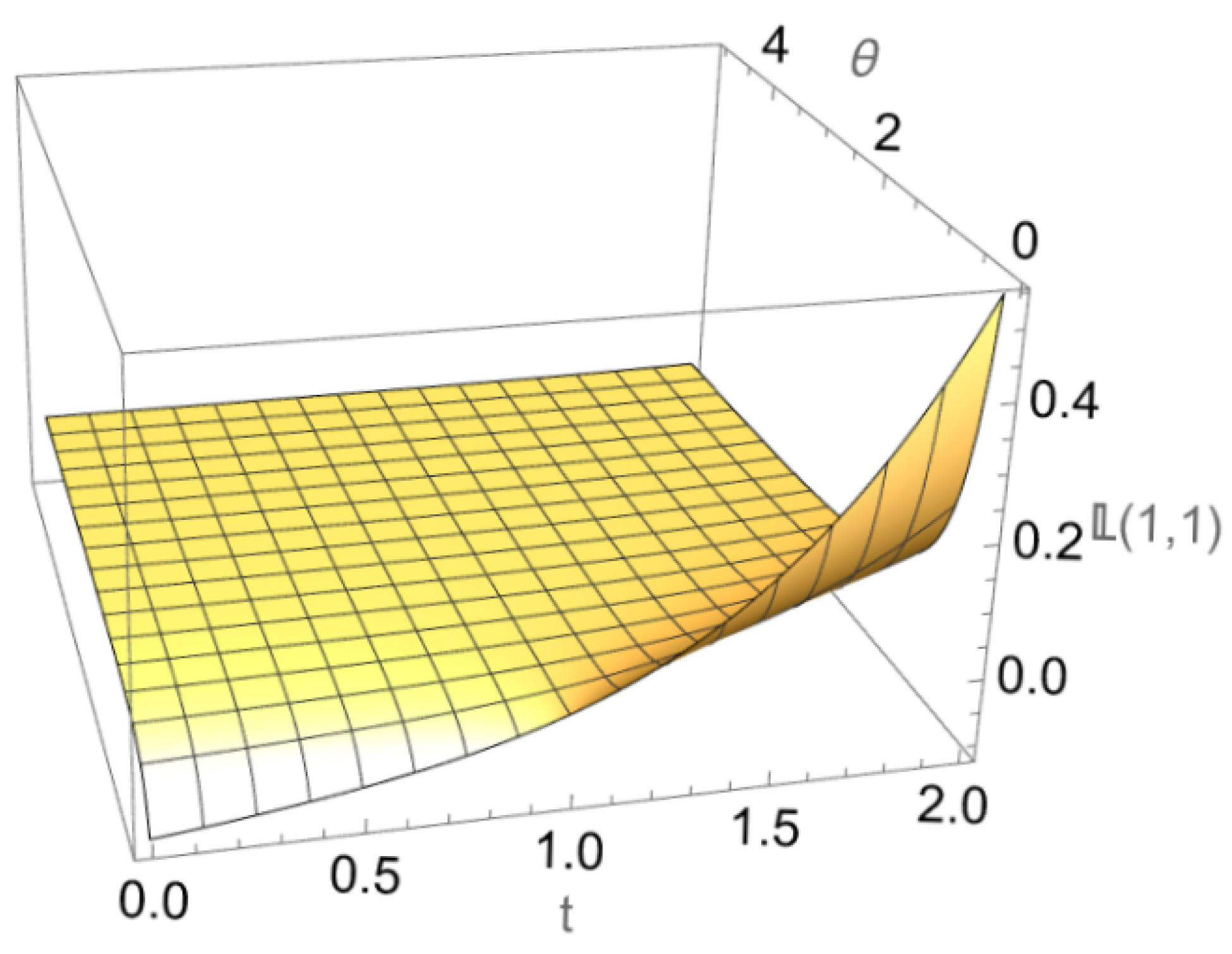
5. Examples of the Main Results

We present the special cases of the main theorems for $\vartheta =0$ and $\vartheta =1$, using the class notation introduced in the previous remark.

Example 1 (Case $\vartheta =0$: $f\in {\mathcal{T}}_{\mathsf{\Sigma }}\left(0\right)$).

The bounds are

$$\begin{array}{cc}\hfill |c_2{c}_4-c_3^2|& \le {\displaystyle \frac{5}{8}},\hfill \\ \hfill |c_2{c}_3-c_4|& \le \left\{\begin{array}{cc}{\displaystyle \frac{2}{3}},\hfill & m\le t\le 2,\hfill \\ {\displaystyle \frac{1}{4}},\hfill & 0\le t\le m,\hfill \end{array}\right.\hfill \\ \hfill |c_3-c_2^2|& \le {\displaystyle \frac{1}{3}}, \left|c_3\right|\le {\displaystyle \frac{7}{12}},\hfill \\ \hfill |c_4|& \le {\displaystyle \frac{5}{12}}, \left|c_5\right|\le {\displaystyle \frac{229867}{240}}.\hfill \end{array}$$

The corresponding bound for $|{\mathcal{H}}_3\left(1\right)|$ is

$$|{\mathcal{H}}_3\left(1\right)|\le \left\{\begin{array}{cc}{\displaystyle \frac{153553}{480}}\approx 319.90,\hfill & m\le c\le 2,\hfill \\ {\displaystyle \frac{460409}{1440}}\approx 319.73,\hfill & 0\le c\le m.\hfill \end{array}\right.$$

Example 2 (Case $\vartheta =1$: $f\in {\mathcal{T}}_{\mathsf{\Sigma }}\left(1\right)$).

The bounds are

$$\begin{array}{cc}\hfill |c_2{c}_4-c_3^2|& \le {\displaystyle \frac{5}{32}},\hfill \\ \hfill |c_2{c}_3-c_4|& \le \left\{\begin{array}{cc}{\displaystyle \frac{29}{192}},\hfill & m\le t\le 2,\hfill \\ {\displaystyle \frac{1}{16}},\hfill & 0\le t\le m,\hfill \end{array}\right.\hfill \\ \hfill |c_3-c_2^2|& \le {\displaystyle \frac{1}{9}}, \left|c_3\right|\le {\displaystyle \frac{25}{144}},\hfill \\ \hfill |c_4|& \le {\displaystyle \frac{41}{768}}, \left|c_5\right|\le {\displaystyle \frac{4147151}{172800}}.\hfill \end{array}$$

The corresponding bound for $|{\mathcal{H}}_3\left(1\right)|$ is

$$|{\mathcal{H}}_3\left(1\right)|\le \left\{\begin{array}{cc}{\displaystyle \frac{268920239}{99532800}}\approx 2.702,\hfill & m\le c\le 2,\hfill \\ {\displaystyle \frac{67112441}{24883200}}\approx 2.697,\hfill & 0\le c\le m.\hfill \end{array}\right.$$

6. Conclusions

In this paper, we explored a new subclass of bi-univalent analytic functions associated with the function $1+sinz$. Our main focus was to establish sharp estimates for the initial Taylor–Maclaurin coefficients, particularly the second- and third-order Hankel determinants. These findings contribute to the ongoing research in geometric function theory, especially in the area of bi-univalent functions. To confirm that the class is non-empty, we provided the example $\sqrt{1+tanhz}$, which maps the unit disk onto a bean-shaped domain. This example satisfies the conditions stated in Definition 1 and offers insight into the behavior of the class, and since this function belongs to the considered class, one can directly apply the main results to obtain the explicit coefficient estimates for this function. Overall, the results indicate that this class has meaningful properties deserving further investigation. Future research could consider more general cases, higher-order determinants, or extend the approach to other function classes.