Evolutionary Computation for Air Transportation: A Survey
Abstract
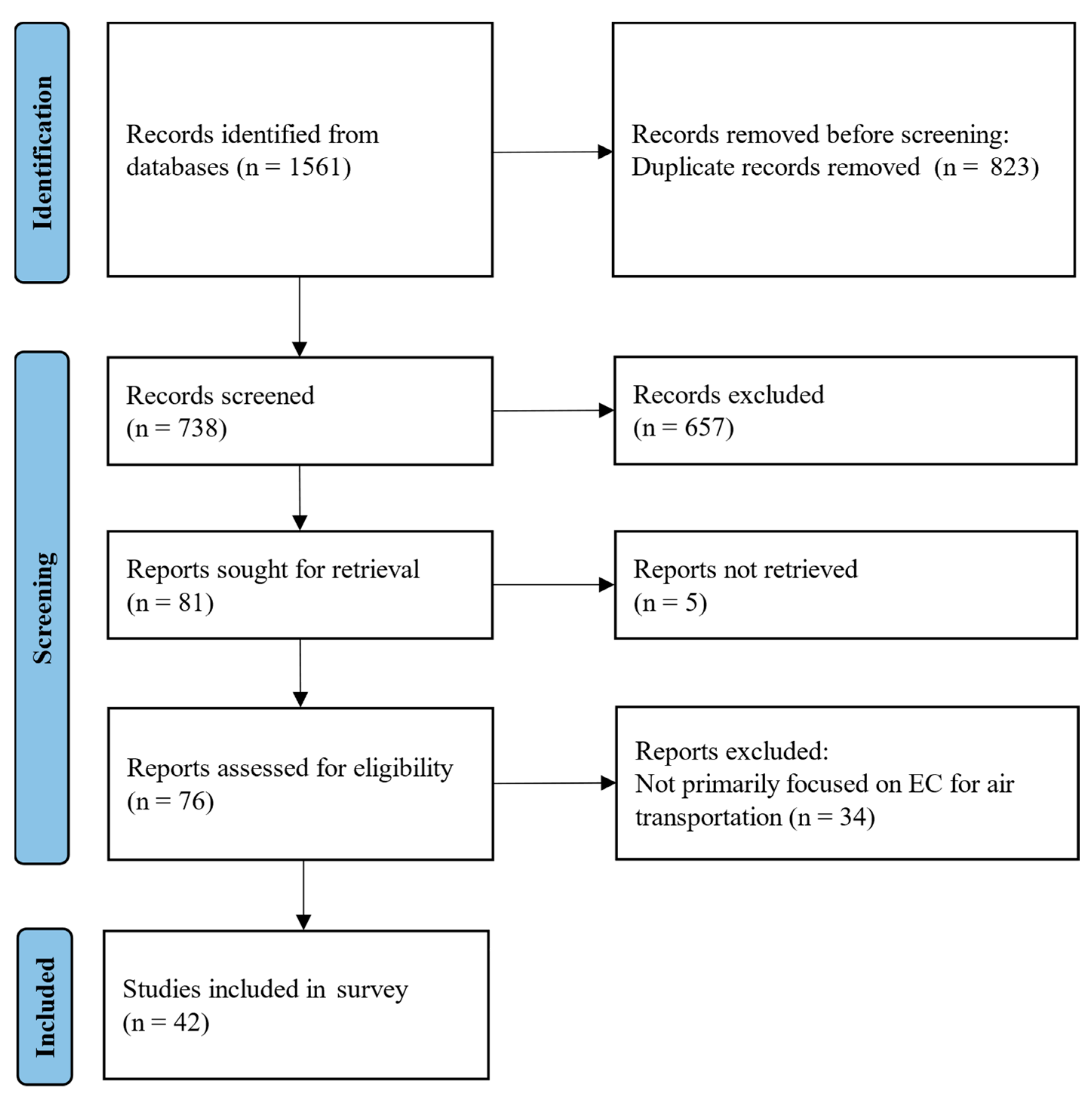
1. Introduction
2. Background
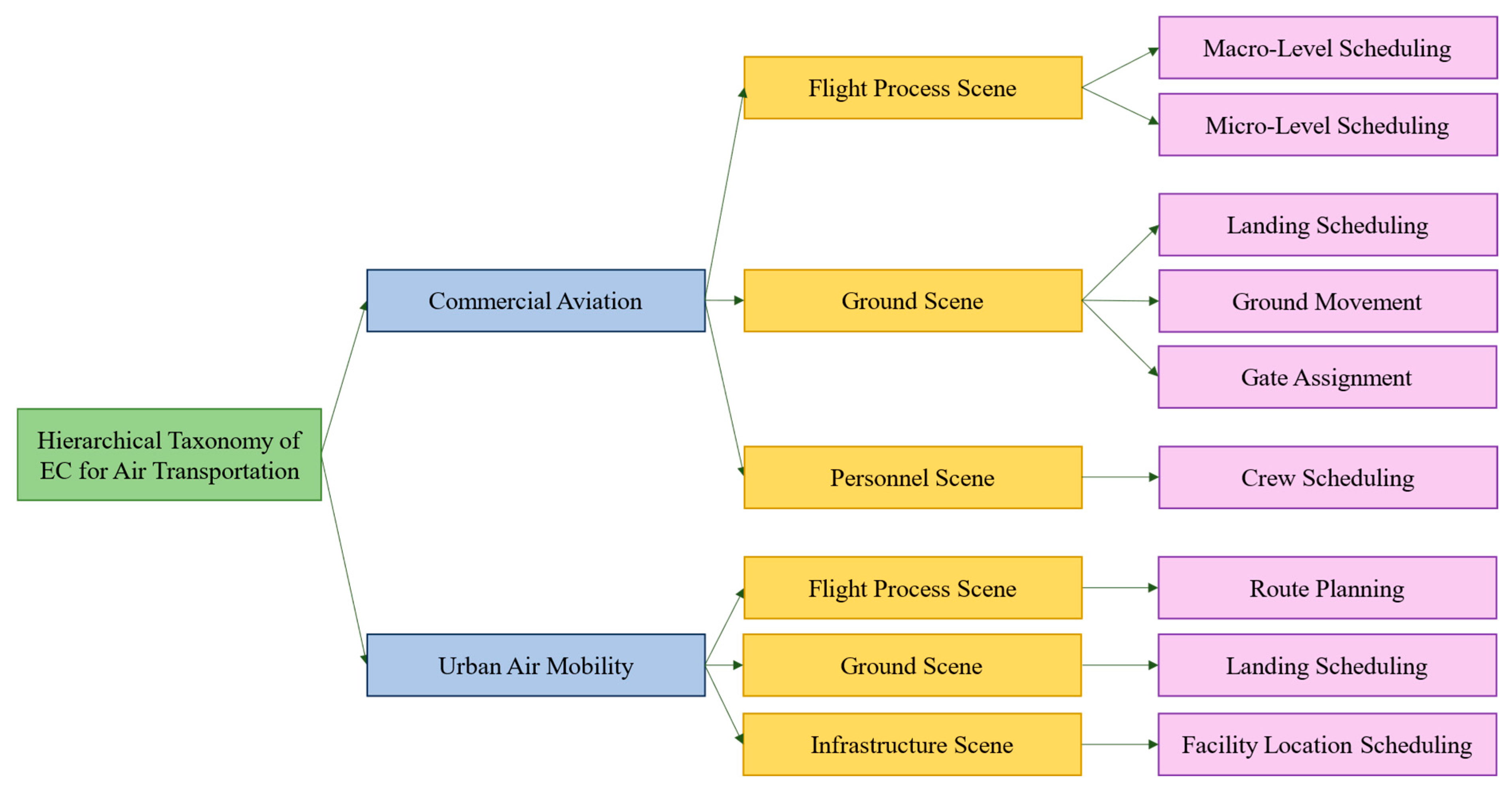
3. Evolutionary Computation for Commercial Aviation
3.1. Flight Process Scene
3.1.1. Macro-Level Scheduling
3.1.2. Micro-Level Scheduling
| Problem | References | Basic EC | Optimization Objectives | Data Source | Metrics |
|---|---|---|---|---|---|
| Macro-level flight process scheduling | Amara et al., 2023 [39] | GA | (1) Minimize flight conflicts (2) Minimize operational costs | Real-world data from Algerian airspace | Conflict resolution rate and operational indicator |
| Cai et al., 2022 [40] | GA and PSO | (1) Minimize the incremental risk of lateral collisions (2) Minimize the number of flights for flight level changing | Real-world data from Singapore airspace | HV | |
| Guo et al., 2022 [41] | GA | Minimize unfairness among airlines | Real data and simulation data | IGD | |
| Micro-level flight process scheduling | Xu et al., 2021 [43] | GA | Minimize number of conflicts | Real-world data from Chinese airspace | Conflict resolution effectiveness, adjustment costs, and running time |
| Oruc et al., 2024 [44] | GA and PSO | Minimize the error in predicted range values | Real-world data from jet-powered transport aircraft | Objective value | |
| Ntakolia et al., 2022 [45] | ACO | (1) Minimize ground delays (2) Minimize flight cancellations (3) Maximize airborne efficiency | Simulation data | Weighted objective value and running time | |
| Guo et al., 2024 [46] | GA | (1) Minimize total delays (2) Minimize flight conflict | Real-world data from Chinese airspace | HV and running time | |
| Guo et al., 2024 [47] | GA | (1) Minimize total delays (2) Minimize flight conflict | Real-world data from Chinese airspace | HV and running time | |
| Liu et al., 2022 [48] | GA and SA | (1) Minimize the cost of aircraft deviation (2) Minimize the cost specific to operations (3) Minimize the number of conflicts | Real-world data from Chinese airspace | HV, the diversity and convergence of solutions | |
| Xiao et al., 2025 [49] | GA | (1)Minimize air traffic control workload (2) Minimize total delays | Real-world data from Chinese airspace | HV, IGD, and spread | |
| Landing scheduling | Fernando et al., 2024 [50] | GA | Minimize pollution time | Real-world data from an American airport | Pollution time, number of constraint violations, and convergence |
| Xu et al., 2025 [51] | ACO | Minimize total delay time | Simulation data | Total delay time, algorithm stability, and running time | |
| Zhang et al., 2020 [52] | ICA | (1) Minimize total landing delay time (2) Minimize the aircraft’s airborne stay time in the terminal area | Simulation data | Objective values | |
| Zhang et al., 2024 [53] | HSEA | (1) Minimize makespan (2) Minimize the total flight time | Real-world data from Singapore airspace | Objective values and running time | |
| Shirini et al., 2024 [54] | GA | (1) Minimize operational costs (2) Minimize fuel consumption | Real-world data from a benchmark dataset | HV and IGD | |
| Bhattacharya et al., 2024 [55] | PSO | (1) Maximize coverage speed (2) Maximize coverage impact (3) Minimize cover-break cost | Real-world data from Indian airspace | Coverage efficiency and running time | |
| Ground movement | Sirigu et al., 2020 [56] | PSO | Minimize total cost of taxiing | Real-world data from an Italian airport | Objective values, convergence speed, and running time |
| Beke et al., 2024 [57] | MA | (1) Minimize total coasting time (2) Minimize total fuel consumption | Real data and simulation data | Cost saving, the number of non-dominated solutions, and running time | |
| Perea et al., 2023 [58] | GA | (1) Minimize total coasting time (2) Minimize total fuel consumption | Real-world data from a UK airport | Economic cost and running time | |
| Gate assignment | Deng et al., 2024 [59] | PSO and QEA | (1) Minimize the walking distance of passengers (2) Minimize idle time of gate (3) Maximize the utilization rate of gates | Real-world data from a Chinese airport | Convergence and weighted objective value |
| Nikolić et al., 2024 [60] | BCO | (1) Minimize total delay (2) Minimize the number of jet bridges used (3) Minimize total walking distance of passengers. | Real-world data from American airports | Quality and convergence of the solution | |
| Xia et al., 2024 [61] | GA | (1) Maximize utilization rate of gate (2) Minimize variance of idle time of gate | Real-world data from a Chinese airport | Prediction accuracy and objective values | |
| Zhu et al., 2024 [62] | GA | (1) Maximize utilization rate of gate (2) Minimize variance of idle time of gate | Real-world data from a Chinese airport | Prediction accuracy and gate assignment performance | |
| Gao et al., 2023 [63] | GA | (1) Minimize fuel consumption during taxiing (2) Maximize utilization rate of jet bridges (3) Minimize fuel consumption of tow trucks (4) Minimize the size of the tow truck fleet | Real-world data from a Chinese airport | Objective values and convergence | |
| Hsu et al., 2024 [64] | SFLA | Minimize total cost | Simulation data | Convergence and runtime | |
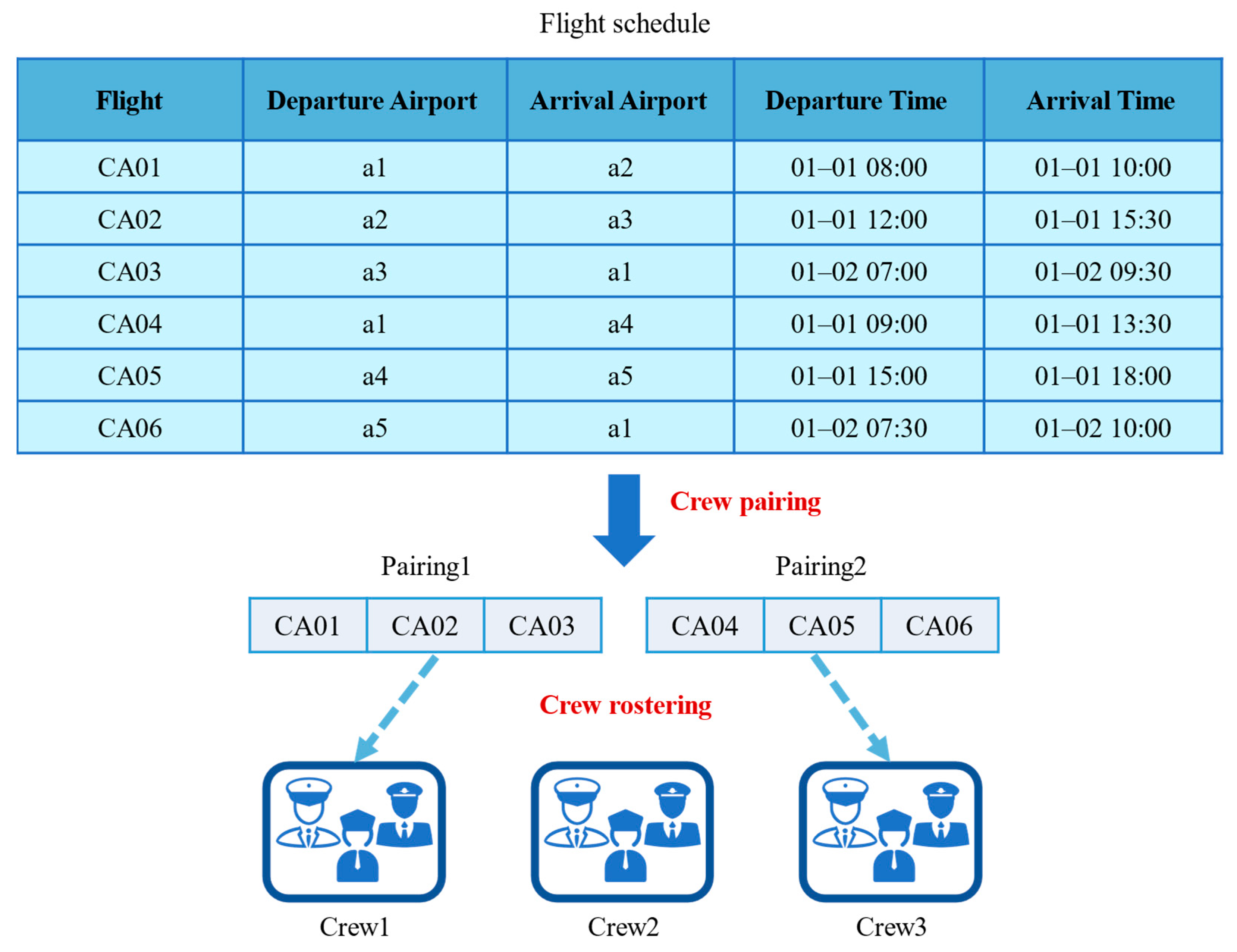
| Crew scheduling | Aggarwal et al., 2023 [65] | GA | Minimize total cost | Real-world data from an American airline | Objective value, the number of idle crew, and running time |
| Zeren et al., 2024 [66] | GA | (1) Minimize crew pairing cost (2) Minimize penalty cost | Real-world data from Turkish airlines | Cost saving, crew utilization rate, and running time | |
| Zhou et al., 2021 [67] | ACO | (1) Maximize fairness (2) Maximize satisfaction | Real-world data from north America airlines | HV, dominance rate, feasible rate, | |
| Zhang et al., 2021 [68] | GA | (1) Minimize cost (2) Maximize work time balance | Real-world data from Chinese airlines | Objective values | |
| Chutima 2020 [69] | GA | (1) Minimize cost (2) Maximize work time balance (3) Minimize unsatisfaction | Real-world data from a Thai airline | Convergence and diversity |
3.2. Ground Scene
3.2.1. Landing Scheduling
3.2.2. Ground Movement
3.2.3. Gate Assignment
3.3. Personnel Scene
Crew Scheduling
4. Evolutionary Computation for Urban Air Mobility
4.1. Flight Process Scene
Route Planning
4.2. Ground Scene
Landing Scheduling
4.3. Infrastructure Scene
Facility Location Scheduling
5. Future Research Directions and Open Issues
5.1. Real-Time Evolutionary Computation for Air Transportation
5.2. Surrogate-Assisted Evolutionary Computation for Air Transportation
5.3. Evolutionary Computation for Robust Air Transportation Optimization
5.4. Evolutionary Computation for Large-Scale Dynamic Multiobjective Air Transportation Optimization Problems
5.5. Evolutionary Computation Combined with Artificial Intelligence for Air Transportation Optimization Problems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1: Genetic Algorithm |
| Input: P, Gmax, pc, pm |
| Output: xbest |
| 1: t = 0 |
| 2: Initialize population Pt = {x1t, …, xpt} |
| 3: Evaluate fitness f(xit) for all xit ∈ Pt |
| 4: xbest = (f(xit)) |
| 5: while t < Gmax and stopping criteria not met do |
| 6: Poff = selection(Pt) |
| 7: for k = 1 to P/2 do |
| 8: Randomly select parents xa, xb ∈ Poff |
| 9: if rand() < pc then |
| 10: y1, y2 = crossover(xa, xb) |
| 11: else |
| 12: y1 = xa, y2 = xb |
| 13: end if |
| 14: Poff = Poff {y1, y2} |
| 15: end for |
| 16: Each individual in Poff mutates with probability pm |
| 17: Pt+1 = Poff |
| 18: Evaluate fitness f(xit) for all xit ∈ Pt+1 |
| 19: xtbest = (f(xit+1)) |
| 20: if f(xtbest) is better than f(xbest) |
| 21: xbest = xtbest |
| 22: t = t + 1 |
| 23: end while |
| 24: return xbest |
| end procedure |
Appendix B
- The departure time of each flight ti ∈ [timin, timax], i = 1, …, N.
- The route of each flight Ri = (ri1, ri2, …, ri|Ri|) = (aidep, wi1, wi2, …, aiarr) ∈ Πi, where wi1, wi2, …; are waypoints of the route Ri and two waypoints are connected to form a segment. Note that |Ri| represents the number of segments in Ri. aidep and aiarr represent the departure airport and the arrival airport of fi, respectively.
- The segment speed of selected route for each flight v(rij) ∈ V(rij), i = 1, …, N, j = 1, …, |Ri|.
| Notation | Definition |
|---|---|
| A | Set of airports |
| F | Set of flights |
| S | Set of sectors |
| Πi | Set of feasible routes of fi |
| a | An airport in A |
| fi | The i-th flight in F |
| ti | The departure time of fi |
| timin | The minimum departure time of fi |
| timax | The maximum departure time of fi |
| Ri | The selected flight route of fi |
| rij | The j-th segment of Ri |
| wig | The g-th waypoint of Ri |
| v(rij) | The speed of rij |
| V(rij) | The feasible speed set of rij |
| aidep | The departure airport of fi |
| aiarr | The arrival airport of fi |
| s | A sector of S |
| Ca | The maximum capacity of airport a |
| Cs | The maximum capacity of sector s |
| N | The number of flights in F |
| Tmax | The latest arrival time among all flights |
Appendix C
| Basic EC | References | Application Problem | The Type of Optimization Problem | Basic EC | References | Application Problem | The Type of Optimization Problem |
|---|---|---|---|---|---|---|---|
| GA | Amara et al., 2023 [39] | Macro-level flight process scheduling | Hybrid continuous and discrete | GA | Senthilnathan et al., 2025 [85] | Facility location scheduling in UAM | Discrete |
| GA | Guo et al., 2022 [41] | Macro-level flight process scheduling | Discrete | GA | Jiang 2025 [86] | Facility location scheduling in UAM | Discrete |
| GA | Xu et al., 2021 [43] | Micro-level flight process scheduling | Discrete | PSO | Bhattacharya et al., 2024 [55] | Landing scheduling | Discrete |
| GA | Guo et al., 2024 [46] | Macro-level flight process scheduling | Discrete | PSO | Sirigu et al., 2020 [56] | Ground Movement | Discrete |
| GA | Guo et al., 2024 [47] | Micro-level flight process scheduling | Discrete | PSO | Chan et al., 2023 [73] | Route planning in UAM | Hybrid continuous and discrete |
| GA | Xiao et al., 2025 [49] | Micro-level flight process scheduling | Hybrid continuous and discrete | PSO | Wang et al., 2024 [74] | Route planning in UAM | Hybrid continuous and discrete |
| GA | Fernando et al., 2024 [50] | Landing scheduling | Hybrid continuous and discrete | ACO | Ntakolia et al., 2022 [45] | Micro-level process flight scheduling | Hybrid continuous and discrete |
| GA | Shirini et al., 2024 [54] | Landing scheduling | Discrete | ACO | Xu et al., 2025 [51] | Landing scheduling | Hybrid continuous and discrete |
| GA | Perea et al., 2023 [58] | Ground Movement | Discrete | ACO | Zhou et al., 2021 [67] | Crew scheduling | Discrete |
| GA | Xia et al., 2024 [61] | Gate assignment | Discrete | ACO | Ge 2025 [83] | Landing scheduling in UAM | Discrete |
| GA | Zhu et al., 2024 [62] | Gate assignment | Discrete | BCO | Nikolić et al., 2024 [60] | Gate assignment | Discrete |
| GA | Gao et al., 2023 [63] | Gate assignment | Discrete | SA | Farazi et al., 2024 [78] | Route planning in UAM | Discrete |
| GA | Aggarwal et al., 2023 [65] | Crew scheduling | Discrete | ICA | Zhang et al., 2020 [52] | Landing scheduling | Discrete |
| GA | Zeren et al., 2024 [66] | Crew scheduling | Discrete | HSEA | Zhang et al., 2024 [53] | Landing scheduling | Discrete |
| GA | Zhang et al., 2021 [68] | Crew scheduling | Discrete | SFLA | Hsu et al., 2024 [64] | Gate assignment | Discrete |
| GA | Chutima 2020 [69] | Crew scheduling | Discrete | MA | Beke et al., 2024 [57] | Ground Movement | Discrete |
| GA | Ko et al., 2025 [75] | Route planning in UAM | Discrete | GA and PSO | Cai et al., 2022 [40] | Macro-level flight process scheduling | Discrete |
| GA | Hildemann 2023 [77] | Route planning in UAM | Discrete | GA and PSO | Oruc et al., 2024 [44] | Micro-level flight process scheduling | Continuous |
| GA | Farazi et al., 2024 [78] | Route planning in UAM | Discrete | GA and PSO | Kim et al., 2020 [76] | Route planning in UAM | Discrete |
| GA | Xie et al., 2021 [80] | Route planning in UAM | Hybrid continuous and discrete | GA and SA | Liu et al., 2022 [48] | Micro-level flight process scheduling | Discrete |
| GA | Zhang et al., 2025 [84] | Facility location scheduling in UAM | Discrete | PSO and QEA | Deng et al., 2024 [59] | Gate assignment | Discrete |
Appendix D
References
- Airports Council International. The Trusted Authority on Air Travel Demand Insights. Available online: https://aci.aero/2025/02/26/the-trusted-authority-on-air-travel-demand-insights/ (accessed on 26 February 2025).
- Cafieri, S.; Conn, A.R.; Mongeau, M. Mixed-integer nonlinear and continuous optimization formulations for aircraft conflict avoidance via heading and speed deviations. Eur. J. Oper. Res. 2023, 310, 670–679. [Google Scholar] [CrossRef]
- Yeung, T.; Zhang, C.; Jin, Z.; Ng, K.K. A joint stochastic programming approach for aircraft landing and terminal traffic flow problem under weather scenarios. J. Air Transp. Res. Soc. 2024, 3, 100046. [Google Scholar] [CrossRef]
- Hu, X.-B.; Chen, W.-H.; Di Paolo, E. Multiairport capacity management: Genetic algorithm with receding horizon. IEEE Trans. Intell. Transp. Syst. 2007, 8, 254–263. [Google Scholar] [CrossRef]
- Hu, X.-B.; Di Paolo, E. Binary-representation-based genetic algorithm for aircraft arrival sequencing and scheduling. IEEE Trans. Intell. Transp. Syst. 2008, 9, 301–310. [Google Scholar]
- Zhan, Z.-H.; Zhang, J.; Li, Y.; Liu, O.; Kwok, S.K.; Ip, W.H.; Kaynak, O. An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem. IEEE Trans. Intell. Transp. Syst. 2010, 11, 399–412. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Zhang, Z.; Yu, H. Multi-objectives optimization on flights landing sequence at busy airport. J. Transp. Syst. Eng. Inf. Technol. 2012, 12, 135–142. [Google Scholar] [CrossRef]
- Girish, G.B.S. An efficient hybrid particle swarm optimization algorithm in a rolling horizon framework for the aircraft landing problem. Appl. Soft Comput. 2016, 44, 200–221. [Google Scholar] [CrossRef]
- Yang, Z.; Fang, Z.; Li, P. Bio-inspired collision-free 4D trajectory generation for UAVs using tau strategy. J. Bionic Eng. 2016, 13, 84–97. [Google Scholar] [CrossRef]
- Jha, P.D.; Suchkov, A.; Subbu, R.V.; Lizzi, J.M.; Zhang, J.; Crook, I.; Tibichte, A.; Lockheed Martin Corp. Hybrid Heuristic National Airspace Flight Path Optimization. U.S. Patent US8185298B2, 2 May 2012. [Google Scholar]
- Luo, J.; Yu, L.S.; Luo, H.X.; Ou, G.Q. Airport Ground Resource Scheduling Method, Electronic Equipment and Computer Readable Storage Medium. Chinese Patent CN112163790A, 6 September 2024. [Google Scholar]
- Chen, Y.; Bi, H.; Zhang, F.; Song, Z.X. Method for Dynamically Dividing Sector Based on Airspace Traffic Characteristics. Chinese Patent CN103226899A, 23 December 2015. [Google Scholar]
- Song, Y.; Wen, M. Air Traffic Scheduling Method. Chinese Patent CN108630020A, 24 August 2021. [Google Scholar]
- Balakrishnan, H. Control and optimization algorithms for air transportation systems. Annu. Rev. Control 2016, 41, 39–46. [Google Scholar] [CrossRef]
- Chen, Z.-G.; Zhan, Z.-H.; Kwong, S.; Zhang, J. Evolutionary computation for intelligent transportation in smart cities: A survey. IEEE Comput. Intell. Mag. 2022, 17, 83–102. [Google Scholar] [CrossRef]
- Seymour, K.; Held, M.; Georges, G.; Boulouchos, K. Fuel estimation in air transportation: Modeling global fuel consumption for commercial aviation. Transp. Res. Part D Transp. Environ. 2020, 88, 102528. [Google Scholar] [CrossRef]
- Szenczuk, J.B.T.; Gomes, R.d.A. Level-offs in terminal areas and path stretches: Empirically estimating extra fuel burn rates in commercial aviation. J. Air Transp. Manag. 2022, 105, 102276. [Google Scholar] [CrossRef]
- Crouse, S.R.; Box, S.C.; Winter, S.R.; Rice, S. Support for green initiatives in aviation: A case study across American aviation consumers. J. Air Transp. Res. Soc. 2024, 2, 100020. [Google Scholar] [CrossRef]
- Reiche, C.; McGillen, C.; Siegel, J.; Brody, F. Are we ready to weather urban air mobility (UAM)? In Proceedings of the 2019 Integrated Communications, Navigation and Surveillance Conference (ICNS), Herndon, VA, USA, 9–11 April 2019; pp. 1–7. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar]
- Goldberg, D.E.; Deb, K. A comparative analysis of selection schemes used in genetic algorithms. In Foundations of Genetic Algorithms; Rawlins, G.J.E., Ed.; Elsevier: Amsterdam, The Netherlands, 1991; Volume 1, pp. 69–93. [Google Scholar] [CrossRef]
- Holland, J. Genetic algorithm. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, H.H.; Xue, Z.S.; Liu, X.Y.; Li, P.; Jiang, L.; Shi, G.M. Optimization of high-speed channel for signal integrity with deep genetic algorithm. IEEE Trans. Electromagn. Compat. 2022, 64, 1270–1274. [Google Scholar] [CrossRef]
- Jiang, J.; Sun, Z.; Lu, R.; Pan, L.; Peng, Z. Real relative encoding genetic algorithm for workflow scheduling in heterogeneous distributed computing systems. IEEE Trans. Parallel Distrib. Syst. 2025, 36, 1–14. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gao, D.; Pedrycz, W. Solving multiobjective fuzzy job-shop scheduling problem by a hybrid adaptive differential evolution algorithm. IEEE Trans. Ind. Inform. 2022, 18, 8519–8528. [Google Scholar] [CrossRef]
- Qin, H.; Bai, W.; Xiang, Y.; Liu, F.; Han, Y.; Wang, L. A self-adaptive collaborative differential evolution algorithm for solving energy resource management problems in smart grids. IEEE Trans. Evol. Comput. 2024, 28, 1427–1441. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Cai, J.; Ma, K.; Tan, T. Research on terminal distance index-based multi-step ant colony optimization for mobile robot path planning. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2321–2337. [Google Scholar] [CrossRef]
- Hu, L.; Lei, W.; Zhao, J.; Sun, X. Optimal weighting factor design of finite control set model predictive control based on multiobjective ant colony optimization. IEEE Trans. Ind. Electron. 2024, 71, 6918–6928. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Lin, H.; Tang, C. Analysis and optimization of urban public transport lines based on multiobjective adaptive particle swarm optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16786–16798. [Google Scholar] [CrossRef]
- Wang, H.; Cai, T.; Pedrycz, W. Kriging surrogate model-based constraint multiobjective particle swarm optimization algorithm. IEEE Trans. Cybern. 2025, 55, 1224–1237. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Tyagi, I.; Kumar, H.; Sharma, D. Tasks scheduling through hybrid genetic algorithm in real-time system on heterogeneous environment. SN Comput. Sci. 2022, 3, 75. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective optimisation using evolutionary algorithms: An introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Wang, L., Ng, A., Deb, K., Eds.; Springer: London, UK, 2011. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Jiang, S.; Ong, Y.-S.; Zhang, J.; Feng, L. Consistencies and contradictions of performance metrics in multiobjective optimization. IEEE Trans. Cybern. 2014, 44, 2391–2404. [Google Scholar] [CrossRef]
- Amara, R.; Aissa, M.B.; Kemcha, R.; Bougherara, M.; Louam, N. Geographical information system for air traffic optimization using genetic algorithm. GeoInformatica 2023, 27, 593–617. [Google Scholar] [CrossRef]
- Cai, Q.; Ang, H.; Alam, S. A multiobjective optimization approach for air traffic flow management for airspace safety enhancement. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–9. [Google Scholar]
- Guo, Y.; Hu, M.; Zou, B.; Hansen, M.; Zhang, Y.; Xie, H. Air traffic flow management integrating separation management and ground holding: An efficiency-equity bi-objective perspective. Transp. Res. Part B Methodol. 2022, 155, 394–423. [Google Scholar] [CrossRef]
- International Civil Aviation Organization Air Traffic Management Requirements and Performance Panel. Global TBO Concept. Available online: https://www.icao.int (accessed on 24 May 2025).
- Xu, M.; Hu, M.; Zhang, Y.; Zhou, Y. Strategic conflict resolution based on cooperative co-evolution algorithm. In Proceedings of the 6th International Conference on Information Science, Computer Technology and Transportation, Xishuangbanna, China, 26–28 November 2021; pp. 1–6. [Google Scholar]
- Oruc, R.; Baklacioglu, T. Cruise range modeling of different flight strategies for transport aircraft using genetic algorithms and particle swarm optimization. Energy 2024, 294, 130917. [Google Scholar] [CrossRef]
- Ntakolia, C.; Lyridis, D.V. An n-D ant colony optimization with fuzzy logic for air traffic flow management. Oper. Res. 2022, 22, 5035–5053. [Google Scholar] [CrossRef]
- Guo, T.; Mei, Y.; Tang, K.; Du, W. A knee-guided evolutionary algorithm for multi-objective air traffic flow management. IEEE Trans. Evol. Comput. 2024, 28, 994–1008. [Google Scholar] [CrossRef]
- Guo, T.; Mei, Y.; Tang, K.; Du, W. Cooperative co-evolution for large-scale multi-objective air traffic flow management. IEEE Trans. Evol. Comput. 2024, 28, 1644–1658. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J.; Zhu, Y.; Cai, K. Hierarchical four-dimensional trajectories planning method for manned and unmanned aircraft integrated airspace. J. Guid. Control Dyn. 2022, 45, 1017–1032. [Google Scholar] [CrossRef]
- Xiao, M.; Hong, C.; Cai, K. Optimizing the safety-efficiency trade-off on nationwide air traffic network flow using cooperative co-evolutionary paradigm. Sci. Rep. 2025, 15, 20377. [Google Scholar] [CrossRef]
- Guedan-Pecker, F.; Ramirez-Atencia, C. Airport take-off and landing optimization through genetic algorithms. Expert Syst. 2024, 41, e13565. [Google Scholar] [CrossRef]
- Xu, X.-X.; Jiang, Y.; Sang, H.-Y.; Gong, H.-L.; Ding, X.-Q.; Kwong, S.; Zhan, Z.-H. A receding horizon control-based holistic ant colony system approach for multi-runway aircraft arrival sequencing and scheduling. Memetic Comput. 2025, 17, 16. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, P.; Zhang, Y.; Dai, X.; Sui, D. Criteria selection and multi-objective optimization of aircraft landing problem. J. Air Transp. Manag. 2020, 82, 101734. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Zhang, Y.; Yin, Y. A study of TMA aircraft conflict-free routing and operation: With mixed integer linear programming, multi-agent path finding, and metaheuristic-based neighborhood search. IEEE Trans. Intell. Transp. Syst. 2024, 25, 13976–13990. [Google Scholar] [CrossRef]
- Shirini, K.; Aghdasi, H.S.; Saeedvand, S. Multi-objective aircraft landing problem: A multi-population solution based on non-dominated sorting genetic algorithm-II. J. Supercomput. 2024, 80, 25283–25314. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Pal, M. Covering of fuzzy graphs and its application in emergency aircraft landing using particle swarm optimization method. Appl. Soft Comput. 2024, 165, 112035. [Google Scholar] [CrossRef]
- Sirigu, G.; Clarke, J.-P.; Battipede, M.; Gili, P. Hybrid particle swarm optimization with parameter fixing: Application to automatic taxi management. J. Air Transp. 2020, 28, 36–48. [Google Scholar] [CrossRef]
- Beke, L.; Uribe, L.; Lara, A.; Coello, C.A.C.; Weiszer, M.; Burke, E.K.; Chen, J. Routing and scheduling in multigraphs with time constraints—A memetic approach for airport ground movement. IEEE Trans. Evol. Comput. 2024, 28, 474–488. [Google Scholar] [CrossRef]
- Perea, F.R.P.; Chen, J.; Weiszer, M.; Korna, J.; Cannon, R. Airport ground movement optimization revisited: Coupling airport runway spacing to multi-objective routing and scheduling through genetic algorithms. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Mexico City, Mexico, 5–8 December 2023; pp. 200–206. [Google Scholar]
- Deng, W.; Xu, J.; Zhao, H.; Song, Y. A novel gate resource allocation method using improved PSO-based QEA. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1737–1745. [Google Scholar] [CrossRef]
- Nikolić, M.; Rakas, J.; Teodorović, D. Formulation of the airport collaborative gate allocation problem and the bee colony optimization solution approach. Eng. Appl. Artif. Intell. 2024, 128, 107433. [Google Scholar] [CrossRef]
- Xia, L.; Wang, H.; Zhou, H.; Wang, Y. Research on the aircraft stands assignment based on two-stage genetic algorithm. In Proceedings of the IEEE 4th International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 26–28 May 2023; pp. 150–158. [Google Scholar]
- Zhu, Z.; Li, X.; Chen, H.; Zhou, X.; Deng, W. An effective and robust genetic algorithm with hybrid multi-strategy and mechanism for airport gate allocation. Inf. Sci. 2024, 654, 119892. [Google Scholar] [CrossRef]
- Gao, Y.; Tang, T.-Q.; Cao, F.; Zhang, J.; Wang, R. A two-phase total optimization on aircraft stand assignment and tow-tractor routing considering energy-saving and attributes. Sustain. Energy Technol. Assessments 2023, 57, 103237. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Yang, W.-F.; Vo, T.T.B.C. Dynamic airport gate assignment with improved shuffled frog-leaping algorithm and triangle membership function. Adv. Eng. Inform. 2024, 62, 102888. [Google Scholar] [CrossRef]
- Aggarwal, D.; Saxena, D.K.; Bäck, T.; Emmerich, M. Real-world airline crew pairing optimization: Customized genetic algorithm versus column generation method. In Proceedings of the Evolutionary Multi-Criterion Optimization, Leiden, The Netherlands, 20–24 March 2023; Springer: Cham, Switzerland; Volume 13970, pp. 518–531. [Google Scholar]
- Zeren, B.; Özcan, E.; Deveci, M. An adaptive greedy heuristic for large scale airline crew pairing problems. J. Air Transp. Manag. 2024, 114, 102492. [Google Scholar] [CrossRef]
- Zhou, S.-Z.; Zhan, Z.-H.; Chen, Z.-G.; Kwong, S.; Zhang, J. A multi-objective ant colony system algorithm for airline crew rostering problem with fairness and satisfaction. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6784–6798. [Google Scholar] [CrossRef]
- Zhang, C.; Gu, C.; Gong, M.; Wu, K.; Xia, H.; Zhang, F. An improved fast search multi-objective genetic algorithm for airline crew scheduling problems. In Proceedings of the 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 1900–1904. [Google Scholar]
- Chutima, P.; Arayikanon, K. Many-objective low-cost airline cockpit crew rostering optimisation. Comput. Ind. Eng. 2020, 150, 106844. [Google Scholar] [CrossRef]
- Korte, J.P.; Yorke-Smith, N. An aircraft and schedule integrated approach to crew scheduling for a point-to-point airline. J. Air Transp. Manag. 2025, 124, 102755. [Google Scholar] [CrossRef]
- Amazon Staff. Amazon Drones: Prime Air Expands Drone Deliveries after FAA Approval. Available online: https://www.aboutamazon.com/news/transportation/amazon-drone-prime-air-expanded-delivery-faa-approval (accessed on 30 May 2024).
- Meituan UAV. China’s First Cross-Border Drone Delivery Route Launches in Shenzhen, Enabling “Goods-to-Person” Service for Travelers. Available online: https://www.meituan.com/news/NN241023053008001 (accessed on 23 October 2024).
- Chan, Y.; Ng, K.K.; Lee, C.; Hsu, L.-T.; Keung, K. Wind dynamic and energy-efficiency path planning for unmanned aerial vehicles in the lower-level airspace and urban air mobility context. Sustain. Energy Technol. Assessments 2023, 57, 103202. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Yuan, Y.; Lai, C.S. Joint optimization of cost and scheduling for urban air mobility operation based on safety concerns and time-varying demand. Aerospace 2024, 11, 861. [Google Scholar] [CrossRef]
- Ko, J.; Ahn, J. On-demand urban air mobility scheduling with operational considerations. J. Aerosp. Inf. Syst. 2025, 22, 401–411. [Google Scholar] [CrossRef]
- Kim, S.H. Receding horizon scheduling of on-demand urban air mobility with heterogeneous fleet. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2751–2761. [Google Scholar] [CrossRef]
- Hildemann, M.; Verstegen, J.A. 3D-flight route optimization for air-taxis in urban areas with evolutionary algorithms and GIS. J. Air Transp. Manag. 2023, 107, 102356. [Google Scholar] [CrossRef]
- Farazi, N.P.; Zou, B. Planning electric vertical takeoff and landing aircraft (eVTOL)-based package delivery with community noise impact considerations. Transp. Res. Part E Logist. Transp. Rev. 2024, 189, 103661. [Google Scholar] [CrossRef]
- Wang, Z.; Delahaye, D.; Farges, J.-L.; Alam, S. Complexity optimal air traffic assignment in multi-layer transport network for urban air mobility operations. Transp. Res. Part C Emerg. Technol. 2022, 142, 103776. [Google Scholar] [CrossRef]
- Xie, Y.; Gardi, A.; Sabatini, R. Reinforcement learning-based flow management techniques for urban air mobility and dense low-altitude air traffic operations. In Proceedings of the IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–10. [Google Scholar]
- Espejo-Díaz, J.A.; Alfonso-Lizarazo, E.; Montoya-Torres, J.R. A heuristic approach for scheduling advanced air mobility aircraft at vertiports. Appl. Math. Model. 2023, 123, 871–890. [Google Scholar] [CrossRef]
- Pradeep, P.; Wei, P. Heuristic approach for arrival sequencing and scheduling for eVTOL aircraft in on-demand urban air mobility. In Proceedings of the IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–7. [Google Scholar]
- Ge, G. Research and design of eVTOL garage scheduling and management systems for urban air mobility. In Proceedings of the 4th International Signal Processing, Communications and Engineering Management Conference (ISPCEM), Montreal, QC, Canada, 28–30 November 2024; pp. 270–275. [Google Scholar]
- Zhang, C.; Du, W.; Guo, T.; Yu, R.; Song, T.; Li, Y. Multi-objective hub location for urban air mobility via self-adaptive evolutionary algorithm. Adv. Eng. Inform. 2025, 64, 102974. [Google Scholar] [CrossRef]
- Senthilnathan, V.P.; Singaravelu, M.; Rajendran, S.; Srinivas, S. A clustering-metaheuristic-simulation approach to determine air taxi operating site location. Transp. Res. Interdiscip. Perspect. 2025, 29, 101330. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Z.; Wang, Y.; Xue, Q. Vertiport location for eVTOL considering multidimensional demand of urban air mobility: An application in Beijing. Transp. Res. Part A Policy Pr. 2025, 192, 104353. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Chen, W.-N.; Guo, X.-Q.; Gong, Y.-J.; Zhang, J. A multiagent co-evolutionary algorithm with penalty-based objective for network-based distributed optimization. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 4358–4370. [Google Scholar] [CrossRef]
- Li, J.-Y.; Du, K.-J.; Zhan, Z.-H.; Wang, H.; Zhang, J. Distributed differential evolution with adaptive resource allocation. IEEE Trans. Cybern. 2023, 53, 2791–2804. [Google Scholar] [CrossRef]
- Zhang, M.; Li, H.; Pan, S.; Lyu, J.; Ling, S.; Su, S. Convolutional neural networks-based lung nodule classification: A surrogate-assisted evolutionary algorithm for hyperparameter optimization. IEEE Trans. Evol. Comput. 2021, 25, 869–882. [Google Scholar] [CrossRef]
- Wang, B.; Xue, B.; Zhang, M. Surrogate-assisted particle swarm optimization for evolving variable-length transferable blocks for image classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3727–3740. [Google Scholar] [CrossRef] [PubMed]
- Nishihara, K.; Nakata, M. Surrogate-assisted differential evolution with adaptation of training data selection criterion. In Proceedings of the 2022 IEEE Symposium Series on Computational Intelligence (SSCI), Singapore, 4–7 December 2022; pp. 1675–1682. [Google Scholar]
- Guo, T.; Mei, Y.; Zhang, M.; Sun, R.; Zhu, Y.; Du, W. Genetic programming with multi-fidelity surrogates for large-scale dynamic air traffic flow management. IEEE Trans. Evol. Comput. 2024; early access. [Google Scholar] [CrossRef]
- Yang, C.; Mao, J.; Qian, X.; Wei, P. Designing robust air transportation networks via minimizing total effective resistance. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2353–2366. [Google Scholar] [CrossRef]
- Yang, C.; Mao, J.; Qian, X.; Wu, E.Q. Robustness optimization of air transportation network with total route cost constraint. IEEE Trans. Autom. Sci. Eng. 2025, 22, 3280–3294. [Google Scholar] [CrossRef]
- Jun, L.Z.; Alam, S.; Dhief, I.; Schultz, M. Towards a greener extended-arrival manager in air traffic control: A heuristic approach for dynamic speed control using machine-learned delay prediction model. J. Air Transp. Manag. 2022, 103, 102250. [Google Scholar] [CrossRef]
- Gao, S.; Zuo, L.; Bao, S.X. UAV reconnaissance task allocation with reinforcement learning and genetic algorithm. In Proceedings of the 2022 International Conference on Automation, Robotics and Computer Engineering (ICARCE), Wuhan, China, 16 December 2022; pp. 1–3. [Google Scholar]
- Zhou, Q.; Wu, J.; Dai, H.; Yang, G.; Zhang, Y. An intelligent ride-sharing recommendation method based on graph neural network and evolutionary computation. IEEE Trans. Intell. Transp. Syst. 2025, 26, 569–578. [Google Scholar] [CrossRef]
| Problem | References | Basic EC | Optimization Objectives | Data Source | Metrics |
|---|---|---|---|---|---|
| Route planning | Chan et al., 2023 [73] | PSO | (1) Minimize flight distance (2) Minimize wind resistance energy consumption | Real-world data from a Chinese city | Objective values |
| Wang et al., 2024 [74] | PSO | (1) Maximize the number of passengers served (2) Minimize costs | Real-world data from six Chinese cities | Objective values | |
| Ko et al., 2025 [75] | GA | (1) Maximize operational profits (2) Minimize optimize service quality | Real-world data from Paris, France | Optimality gap and Average runtime | |
| Kim et al., 2020 [76] | GA and PSO | (1) Maximize operational profits (2) Maximize service quality | Simulation data | Optimality gap | |
| Hildemann 2023 [77] | GA | (1) Minimize flight time (2) Minimize energy consumption (3) Minimize noise pollution | Real-world data from New York and simulation data | Objective values | |
| Farazi et al., 2024 [78] | GA | (1) Minimize operational costs (2) Minimize noise impact | Real-world data from Chicago, USA | Objective values | |
| Wang et al., 2022 [79] | SA | Minimize the global complexity of the three-dimensional air transport network for UAM | Real-world data from Singapore | Objective value | |
| Xie et al., 2021 [80] | GA | (1) Minimize airspace overload time (2) Maximize operational efficiency | Simulation data | Airspace overload time, runtime, and convergence iterations | |
| Landing scheduling | Espejo-Díaz et al., 2023 [81] | Heuristic | (1) Maximize throughput (2) Minimize makespan | Simulation data | Computational efficiency |
| Pradeep et al., 2024 [82] | Heuristic | Minimize makespan | Simulation data | Solution quality and computational efficiency | |
| Ge 2025 [83] | ACO | (1) Maximize resource utilization (2) Minimize makespan | Simulation data | Task completion time reduction rate and gate utilization rate | |
| Facility location scheduling | Zhang et al., 2025 [84] | GA | (1) Minimize economic costs (2) Minimize security risks | Real-world data from Australia | HV |
| Senthilnathan et al., 2025 [85] | GA | (1) Maximize population coverage (2) Minimize rent and labor costs (3) Minimize passenger waiting time (4) Maximize vehicle utilization | Real-world data from New York, USA | Economic efficiency, coverage rate, and resource utilization rate | |
| Jiang et al., 2025 [86] | GA | (1) Maximize demand coverage (2) Maximize congestion relief (3) Minimize redundant coverage | Real-world data from Beijing, China | Regular shuttle coverage rate, on-demand mobility coverage rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Chen, Z.-G. Evolutionary Computation for Air Transportation: A Survey. Mathematics 2025, 13, 2867. https://doi.org/10.3390/math13172867
Huang R, Chen Z-G. Evolutionary Computation for Air Transportation: A Survey. Mathematics. 2025; 13(17):2867. https://doi.org/10.3390/math13172867
Chicago/Turabian StyleHuang, Rui, and Zong-Gan Chen. 2025. "Evolutionary Computation for Air Transportation: A Survey" Mathematics 13, no. 17: 2867. https://doi.org/10.3390/math13172867
APA StyleHuang, R., & Chen, Z.-G. (2025). Evolutionary Computation for Air Transportation: A Survey. Mathematics, 13(17), 2867. https://doi.org/10.3390/math13172867







