Thermal Stress of Fractured Rock Under Solar Radiation Based on a Typical Shape Function Method
Abstract
1. Introduction
2. Typical Function of Thermal Stress Field of Fractured Rocks Under Solar Radiation
3. Thermal Stress Field of Rocks Based on Typical Fracture Heat Source Functions
3.1. Thermal Stress Field of Rocks Based on Parabolic and Triangular Heat Source Functions
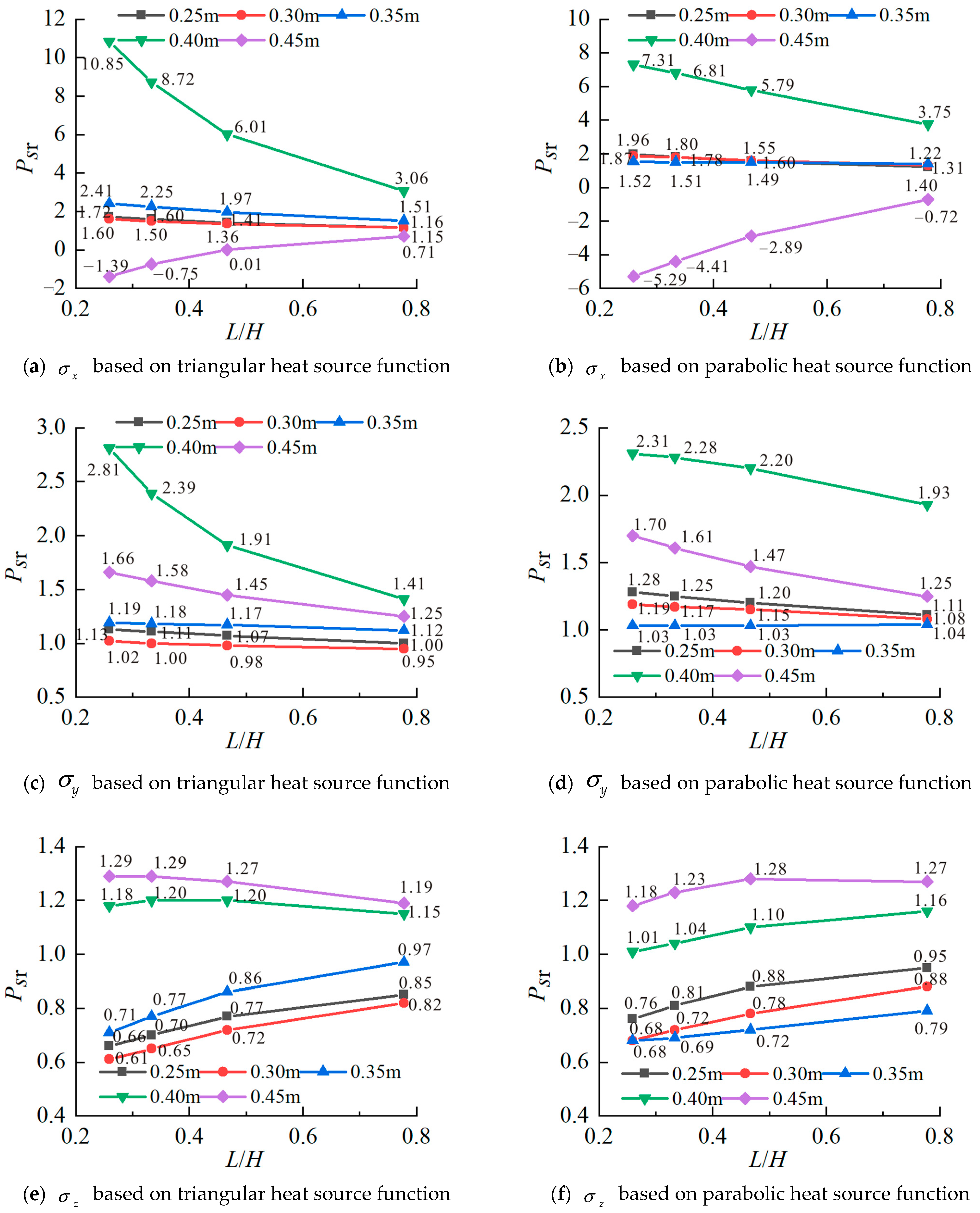
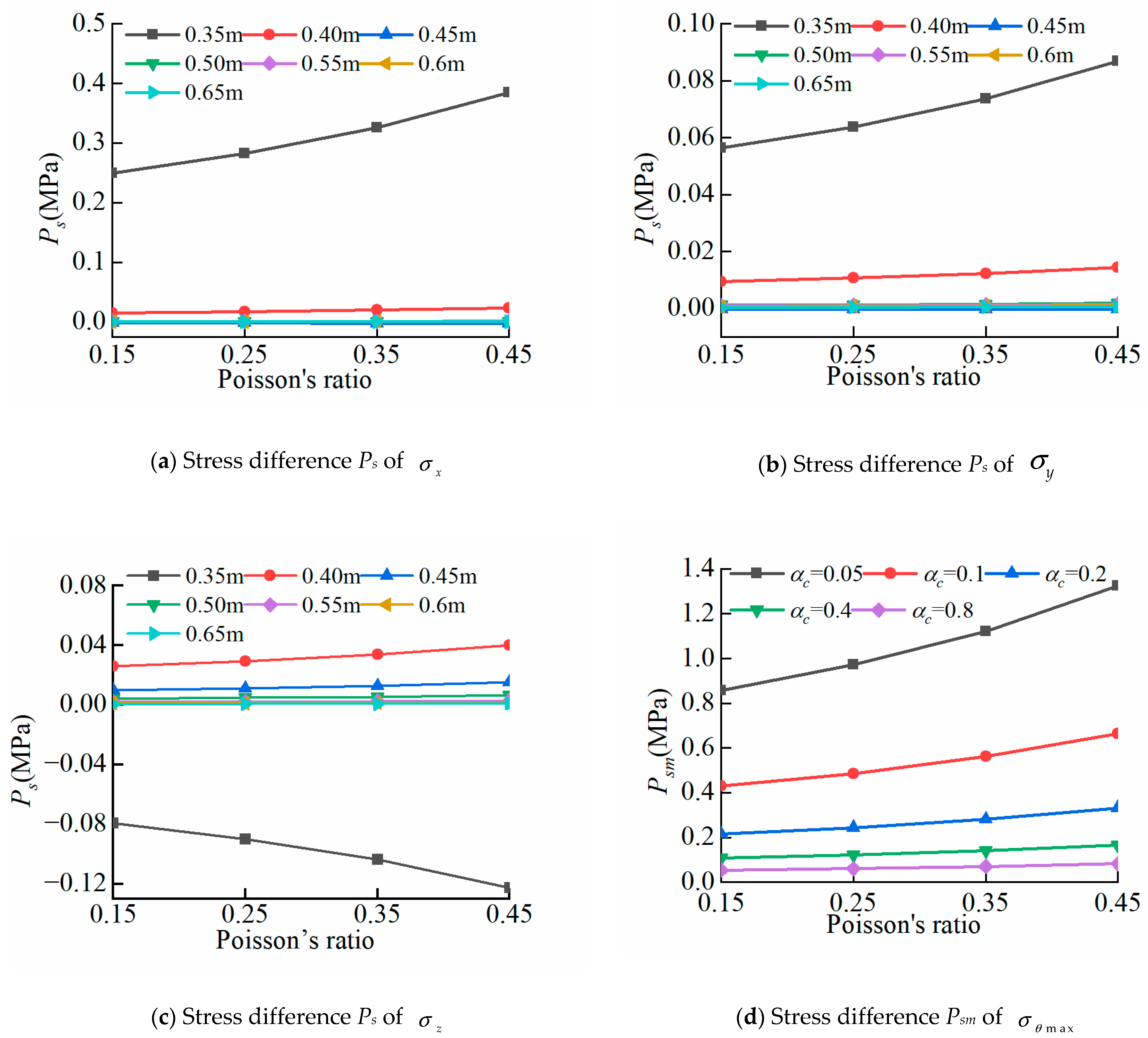
3.2. Influence of Geometric Parameters of Fracture Shape on Thermal Stress
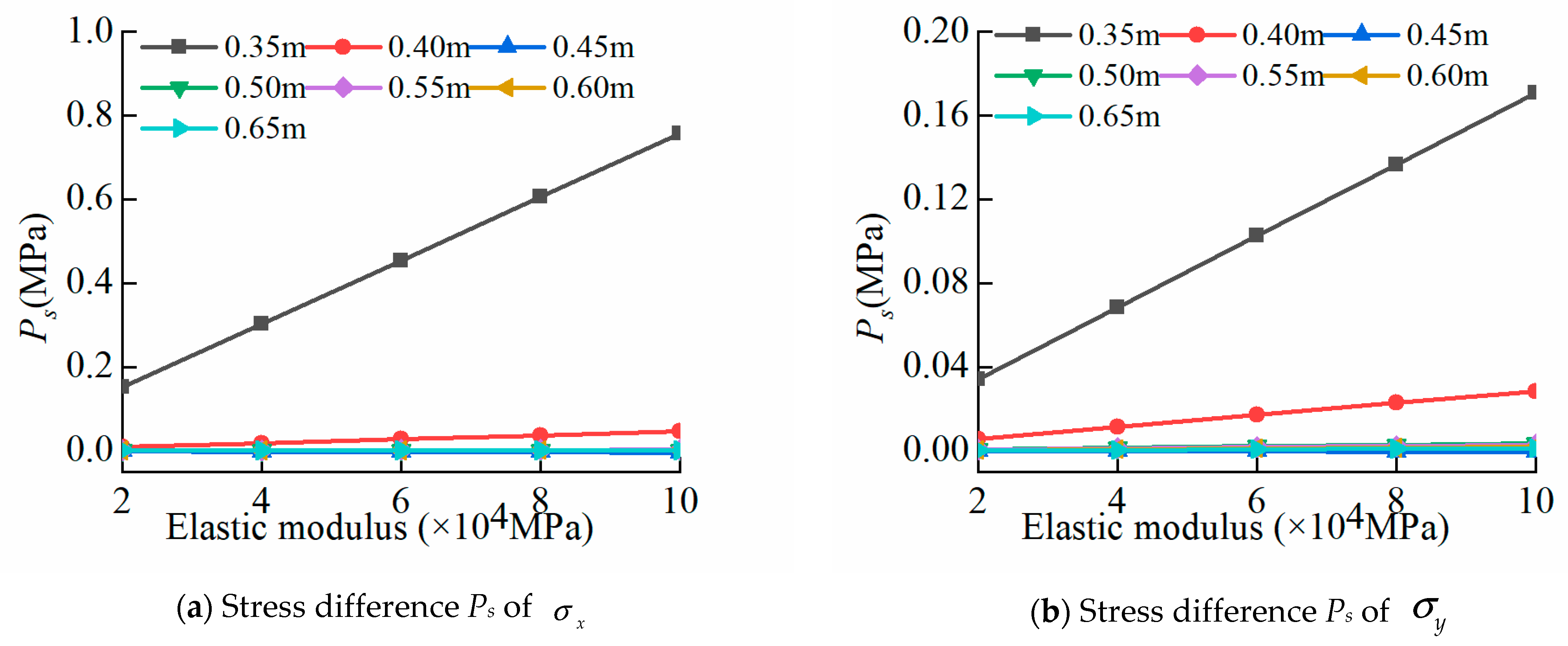
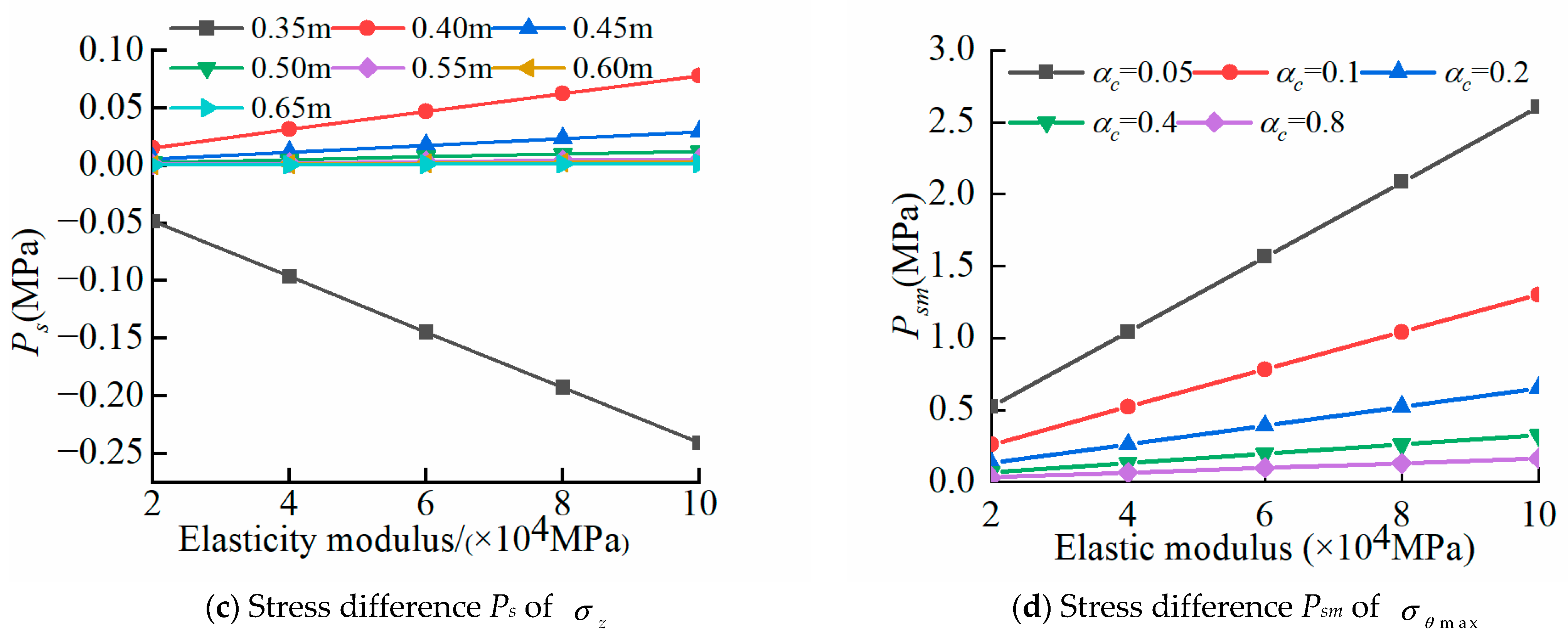
3.3. Applicability Analysis of Fracture Heat Source Functions
4. Finite Element Analysis of Thermal Stress Field of Rocks with Typical Fracture Heat Sources
4.1. Parameters of Finite Element Analysis
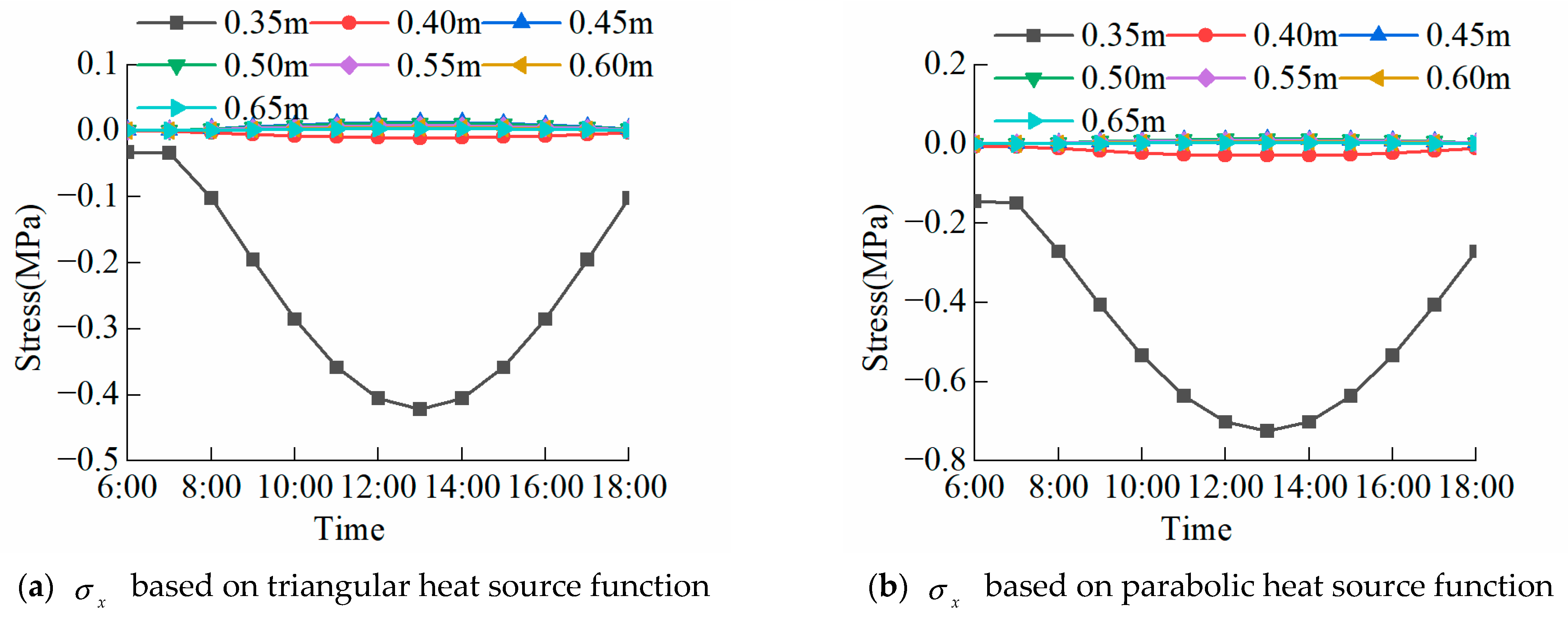
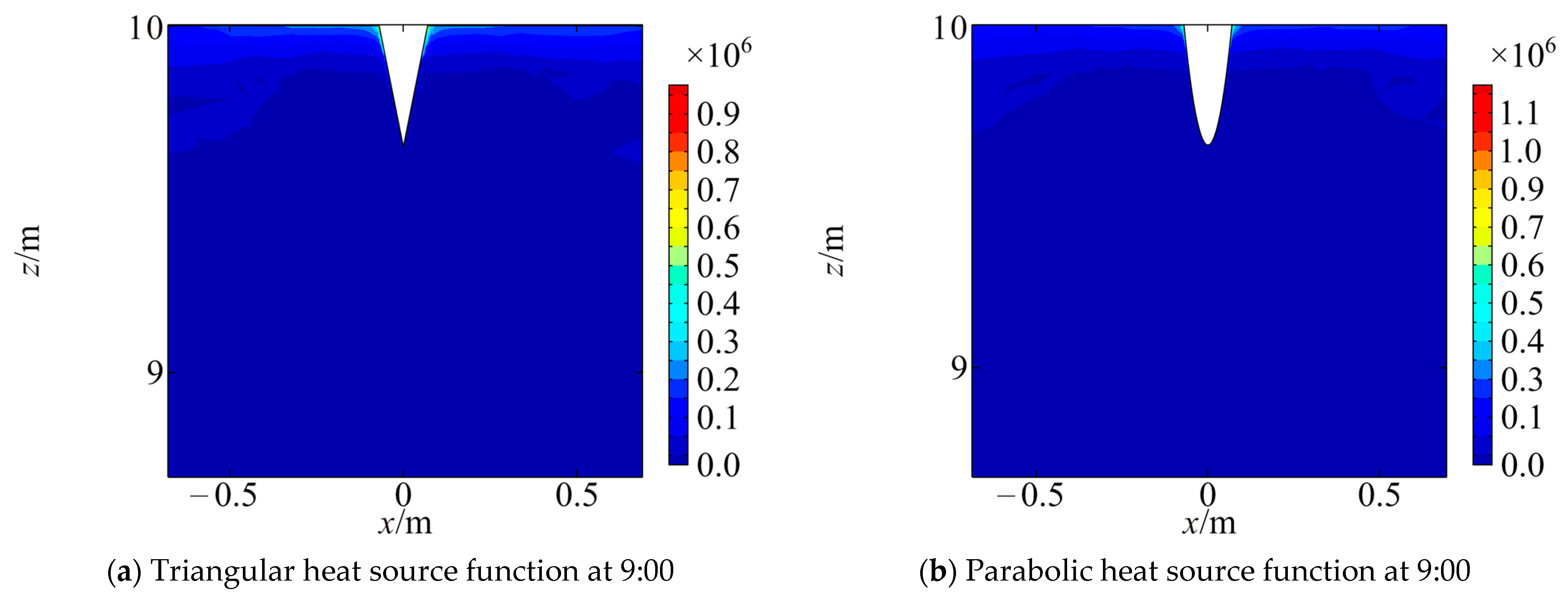
4.2. Thermal Stress Field of Fractured Rocks
5. Discussion
6. Conclusions
- (1)
- The daily variation trends in thermal stress based on triangular and parabolic heat source functions are consistent. Compared with the triangular heat source function, the values of thermal stress at fracture tip are larger, and the daily maximum increases by 8.14% when based on the parabolic heat source function. When analyzing thermal stability of fractured rocks under solar radiation, parabolic heat source function provides more conservative estimations of thermal stress.
- (2)
- Based on both heat source functions, the horizontal stresses and increase as the ratio of fracture length to fracture opening length (L/H) decreases, while the vertical stress decreases as L/H decreases, and the maximum circumferential tensile stress at fracture tip increases as L/H increases. Compared with parabolic heat source function, the thermal stress values based on triangular heat source function change larger as L/H increases, indicating that the variation in fracture shape geometric parameter L/H has a more significant effect on the thermal stress values based on the triangular heat source function.
- (3)
- The applicability of fracture heat source functions is analyzed. For soft rocks and those with good thermal conductivity and small thermal deformation, the parabolic heat source function is more reasonable. For hard rocks, the triangular heat source function is more appropriate. The parabolic fracture heat source function provides a valuable framework for analyzing the thermal stress field of rocks with diverse thermodynamic properties, which is a typical method for analyzing the thermal effects of fractured rocks under solar radiation.
- (4)
- Thermal stress fields of rocks with triangular and parabolic fracture heat sources under solar radiation are analyzed by numerical simulation. Results indicate an increase in thermal stress around the fracture. Compared with triangular heat source, the thermal stress at fracture tip is larger with parabolic heat source. As the depth increases, the thermal stress values of both functions approach each other.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guerin, A.; Jaboyedoff, M.; Collins, B.D.; Stock, G.M.; Derron, M.; Abellán, A.; Matasci, B. Remote thermal detection of exfoliation sheet deformation. Landslides 2020, 18, 865–879. [Google Scholar] [CrossRef]
- Loope, D.B.; Loope, G.R.; Burberry, C.M.; Rowe, C.M.; Bryant, G.C. Surficial fractures in the Navajo Sandstone, Southwestern USA: The roles of thermal cycles, rainstorms, granular disintegration, and iterative cracking. Earth Surf. Process. Landf. 2020, 45, 2063–2077. [Google Scholar] [CrossRef]
- Karoline, M.; Heather, V.; Jan-christoph, O.; Andreas, E.; Richard, D. Linking rock weathering, rockwall instability and rockfall supply on talus slopes in glaciated hanging valleys (Swiss Alps). Permafr. Periglac. Process. 2018, 29, 135–151. [Google Scholar] [CrossRef]
- Gunzburger, Y.; Merrirn-Soukatchoff, V. Near-surface temperatures and heat balance of bare outcrops exposed to solar radiation. Earth Surf. Process. Landf. 2011, 36, 1577–1589. [Google Scholar] [CrossRef]
- Smith, B.J.; Srinivasan, S.; Gomez-Heras, M.; Basheer, P.A.M.; Viles, H.A. Near-surface temperature cycling of stone and its implications for scales of surface deterioration. Geomorphology 2011, 130, 76–82. [Google Scholar] [CrossRef]
- Meier, J.; Bock, H. Stability of a block resting on an inclined plane—A classical problem revisited. Int. J. Rock Mech. Min. Sci. 2014, 70, 407–417. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Q.; Xun, X. Radiation and energy balance characteristics of asphalt pavement in permafrost regions. Environ. Earth Sci. 2016, 75, 221. [Google Scholar] [CrossRef]
- Aldred, J.; Eppes, M.C.; Aquino, K.; Deal, R.; Garbini, J.; Swami, S.; Tuttle, A.; Xanthos, G. The influence of solar-induced thermal stresses on the mechanical weathering of rocks in humid mid-latitudes. Earth Surf. Process. Landf. 2016, 41, 603–614. [Google Scholar] [CrossRef]
- Ding, W.; Chen, J.; Feng, X.; Zhou, H.; Wang, S. Study on weathering characteristics of surrounding rock in Longmen cavern. Rock Soil Mech. 2004, 25, 145–148. (In Chinese) [Google Scholar]
- Meng, Y.; Yan, Z.; Wang, J.; Ni, P.; Liu, Y. Research on solar radiation characteristics in Vairocana Buddha niche in Longmen Grottoes. J. Arid Land Resour. Environ. 2022, 36, 129–138. (In Chinese) [Google Scholar]
- Wang, Y.; Chen, W. Study on thermal stress field of triangle fracture of granite in high-temperature environment. Chin. J. Rock Mech. Eng. 2021, 40, 3074–3083. (In Chinese) [Google Scholar]
- Xu, D.; Gu, H.; Chen, W.; Liang, X.; Zhang, J.; Wang, Z. Characteristics of thermal stress and vulnerability assessment of Houxu Tablet in Yongyou Temple Mountain Resort. J. Northwest Univ. Nat. Sci. Ed. 2021, 51, 353–359. (In Chinese) [Google Scholar]
- Chen, J.; Wang, J.; Yan, S.; Fang, Y. Analysis on the Cracking Mechanism of the Surface Layer on Huashan Rock Painting in Ningming, Guangxi. J. Fudan Univ. Nat. Sci. 2021, 60, 157–165. (In Chinese) [Google Scholar]
- Collins, B.D.; Stock, G.M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 2016, 9, 395–400. [Google Scholar] [CrossRef]
- Wedekind, W.; Gross, C.J.; Hoffmann, A.; Siegesmund, S. Damage phenomenon and petrophysical properties of sandstones at the Phnom Bakheng Temple (Angkor, Cambodia): First investigations and possible conservation measures. Environ. Geol. 2018, 77, 735.1–735.36. [Google Scholar] [CrossRef]
- Amaral Vamaral, E.; Velloso, R.; Chavez, L.; Gusmão, L.; Amaral, C. On the Effect of Thermally Induced Stresses in Failures of Some Rock Slopes in Rio de Janeiro, Brazil. Rock Mech. Rock Eng. 2013, 46, 123–134. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W. Nonlinear temperature field of granite fracture tip induced by high natural environmental temperature based on fracture shape function. Rock Soil Mech. 2022, 43, 267–274. (In Chinese) [Google Scholar]
- Hu, J.; Li, S.; Li, L.; Shi, S.; Zhou, Z.; Liu, H.; He, P. Field, experimental, and numerical investigation of a rockfall above a tunnel portal in southwestern China. Bull. Eng. Geol. Environ. 2018, 77, 1365–1382. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, H.; Lin, J.S.; Zhang, X.; Ma, G. Tunnel stability assessment by 3D DDA-keyblock analysis. Tunn. Undergr. Space Technol. 2018, 71, 210–214. [Google Scholar] [CrossRef]
- Alam, M.R.; Munaswamy, K.; Swamidas, A.S.J. Experimental and numerical studies on dynamic crack growth in layered slate rock under wedge impact loads: Part II—Non-plane strain problem. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 915–931. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R. Determination of mode II fracture toughness for U-shaped notches using Brazilian disc specimen. Int. J. Solids Struct. 2010, 47, 454–465. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R. Brittle fracture in rounded-tip V-shaped notches. Mater. Des. 2010, 31, 60–67. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Wang, Z.X.; Lin, X.Y. Refinement for stress intensity factor solution for a parabolic-shaped crack from the perturbation method. Mech. Res. Commun. 2010, 37, 47–49. [Google Scholar] [CrossRef]
- Khojastehpour, M. Blunt crack-tip elastoplastic zone of mixed mode fracture. Acta Mech. Solid. Sin. 2014, 27, 531–541. [Google Scholar] [CrossRef]
- Zhao, K.; Stead, D.; Kang, H.; Gao, F.; Donati, D. Three-dimensional simulation of hydraulic fracture propagation height in layered formations. Environ. Earth Sci. 2021, 80, 435. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W. The shape function method of nonlinear thermal stress of granite fracture tips in a high-temperature environment. Sci. Rep. 2024, 14, 2736. [Google Scholar] [CrossRef] [PubMed]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Li, M. Thermal–Moisture Stress Analysis of Tunnel Portal Rock in High Temperature and Humidity. Ph.D. Dissertation, Beijing Jiaotong University, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Wang, Y.; Shao, M.; Zhang, J.; Li, L.; Wang, N. Quantitative evaluation of alteration and exfoliation in Jurassic sandstone, Chongqing Danzishi rock carvings, China. Eng. Geol. 2021, 292, 106277. [Google Scholar] [CrossRef]














| Density (kg·m−3) | Heat Capacity (J·kg−1·K−1) | Thermal Conductivity (W·m−1·K−1) | Elastic Modulus (MPa) | Poisson’s Ratio | Thermal Expansion Coefficient (K−1) |
|---|---|---|---|---|---|
| 2.6 × 103 | 1.1 × 103 | 2.8 | 4 × 104 | 0.3 | 8 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, W. Thermal Stress of Fractured Rock Under Solar Radiation Based on a Typical Shape Function Method. Mathematics 2025, 13, 2864. https://doi.org/10.3390/math13172864
Wang Y, Chen W. Thermal Stress of Fractured Rock Under Solar Radiation Based on a Typical Shape Function Method. Mathematics. 2025; 13(17):2864. https://doi.org/10.3390/math13172864
Chicago/Turabian StyleWang, Yang, and Wenhua Chen. 2025. "Thermal Stress of Fractured Rock Under Solar Radiation Based on a Typical Shape Function Method" Mathematics 13, no. 17: 2864. https://doi.org/10.3390/math13172864
APA StyleWang, Y., & Chen, W. (2025). Thermal Stress of Fractured Rock Under Solar Radiation Based on a Typical Shape Function Method. Mathematics, 13(17), 2864. https://doi.org/10.3390/math13172864





