Mathematical Modeling and Optimal Design for HRE-Free Permanent-Magnet-Assisted Synchronous Reluctance Machine Considering Electro-Mechanical Characteristics
Abstract
1. Introduction
2. Design of HRE-Free PMa-SynRM with Conventional IPMSM
2.1. Configuration and Specifications of Conventional IPMSM
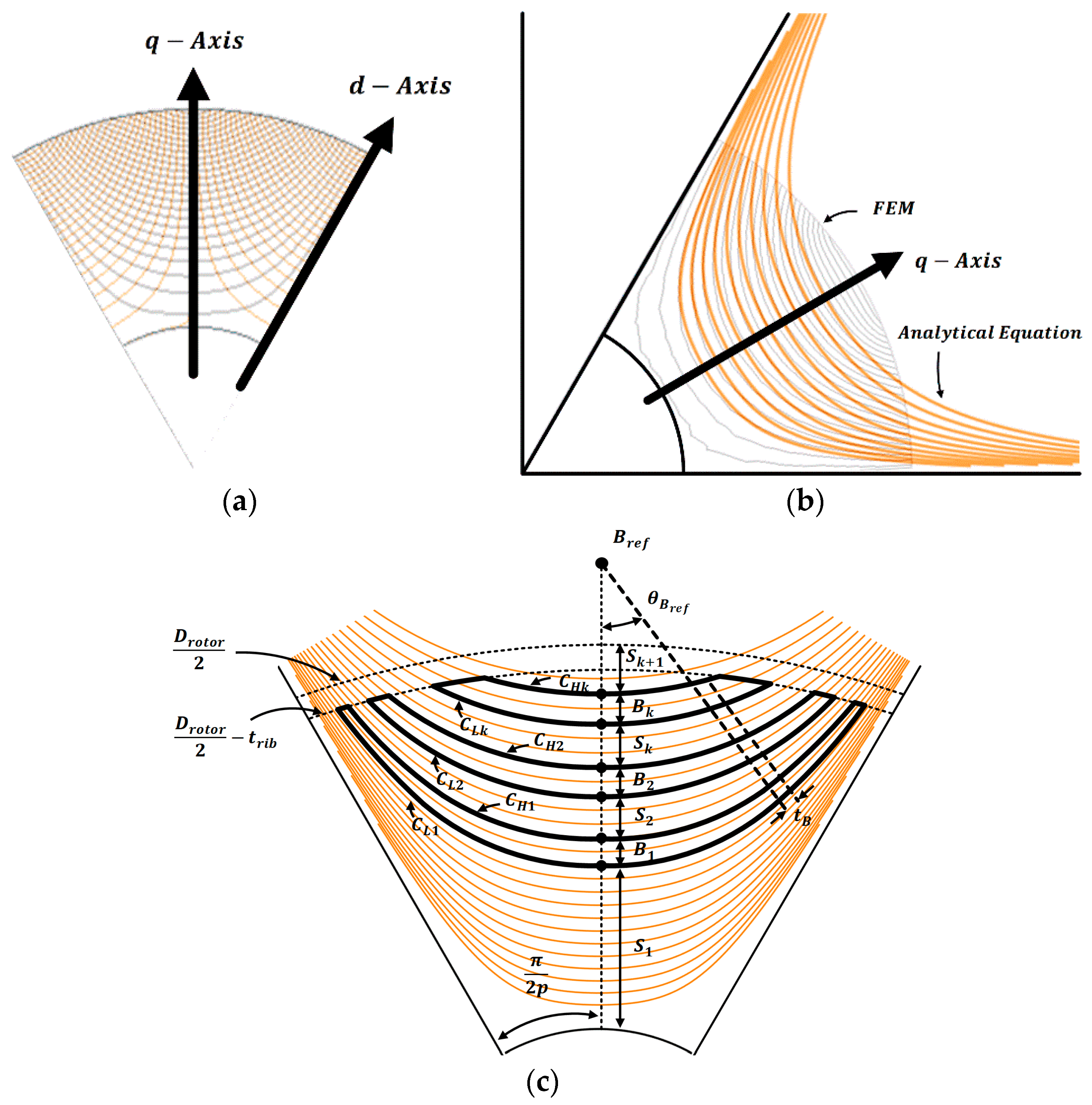
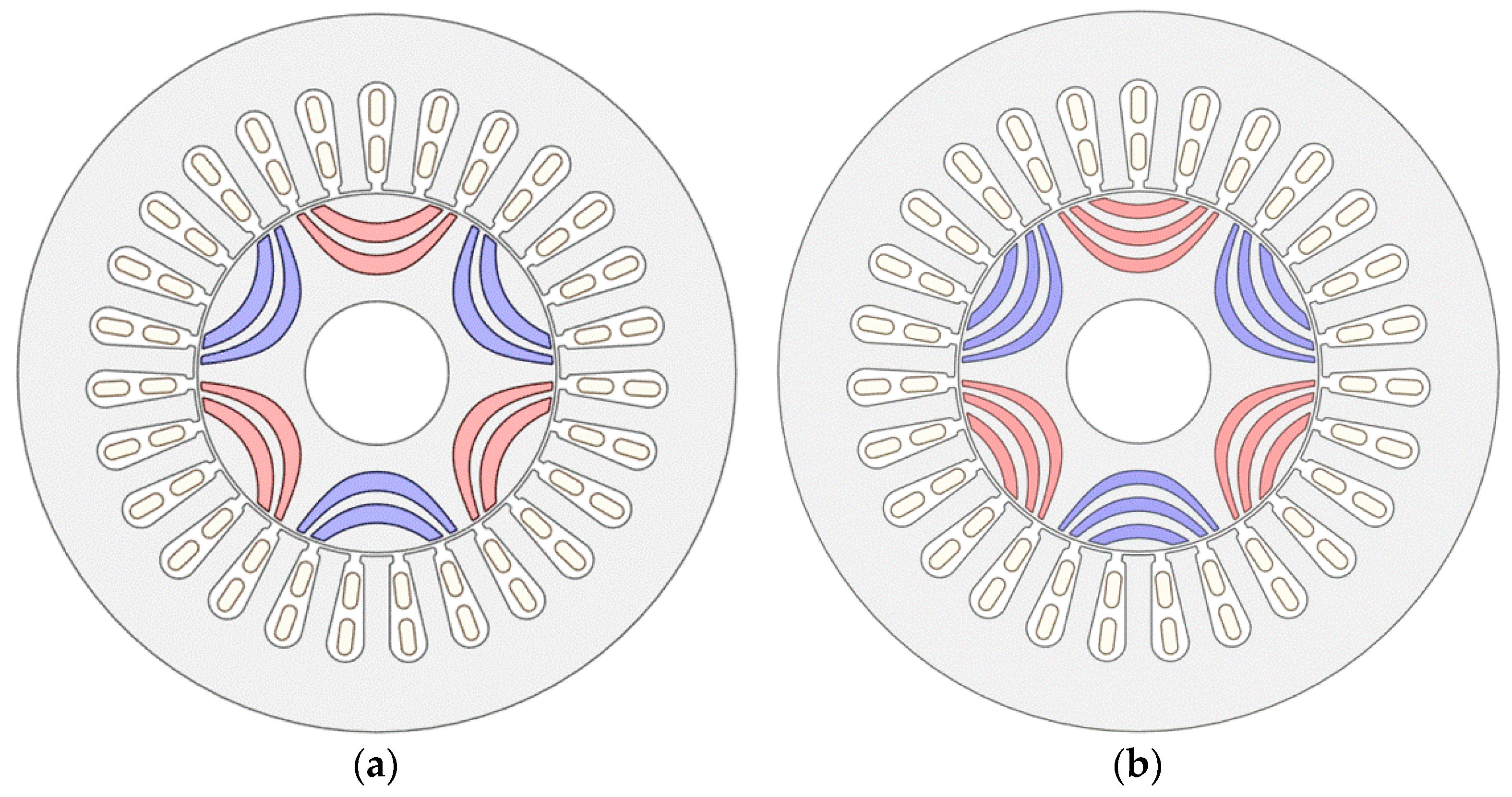
2.2. Modeling of Rotor Structure for HRE-Free PMa-SynRM
3. Robust Design Considering Electro-Mechanical Characteristics
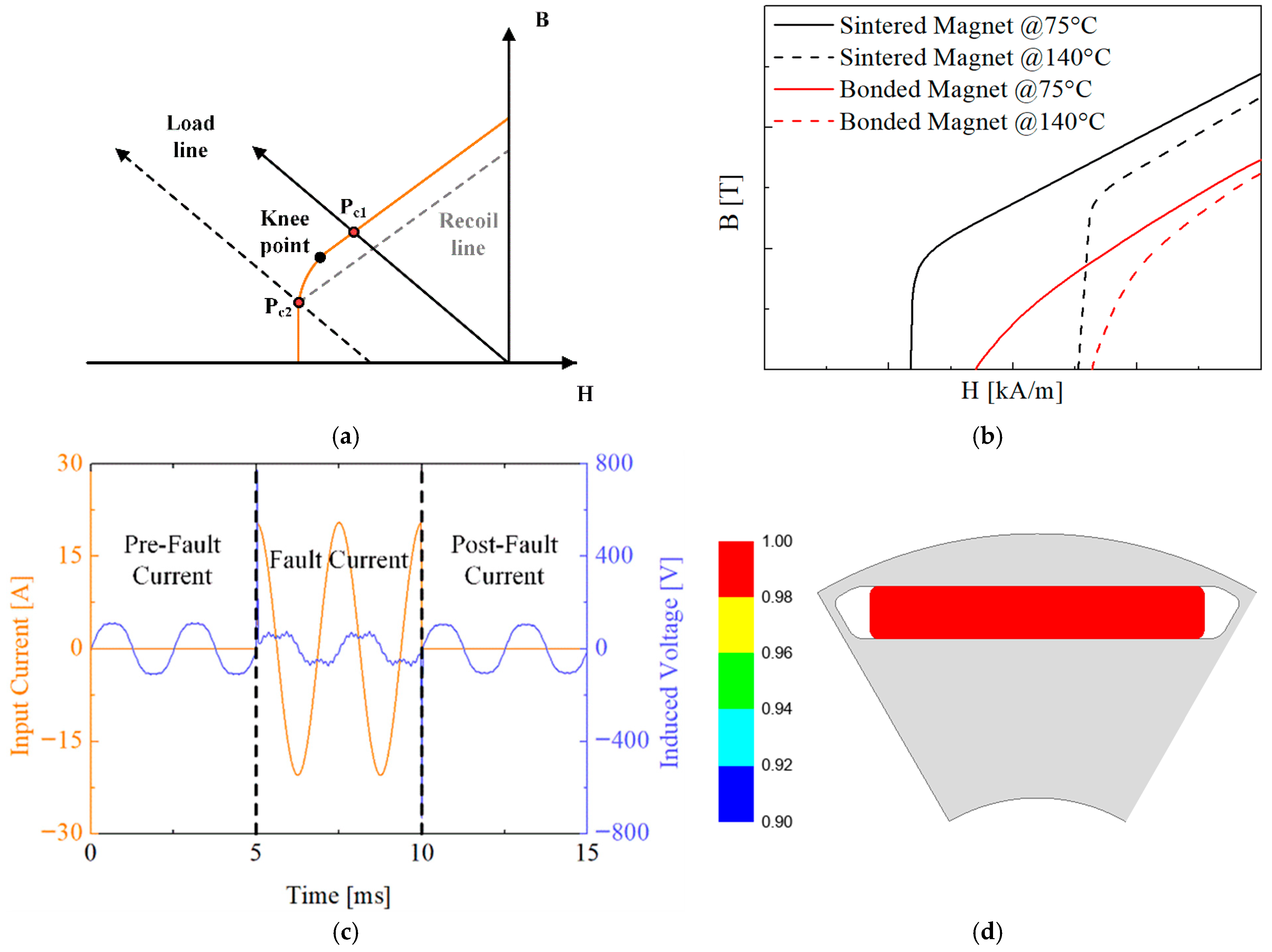
3.1. Criteria and Method of Irreversible Demagnetization Analysis
3.2. Rotor Mechanical Stress and Safety Factor
4. Multi-Objective Optimization
4.1. Optimization Framework for Multiple Variables and Objective
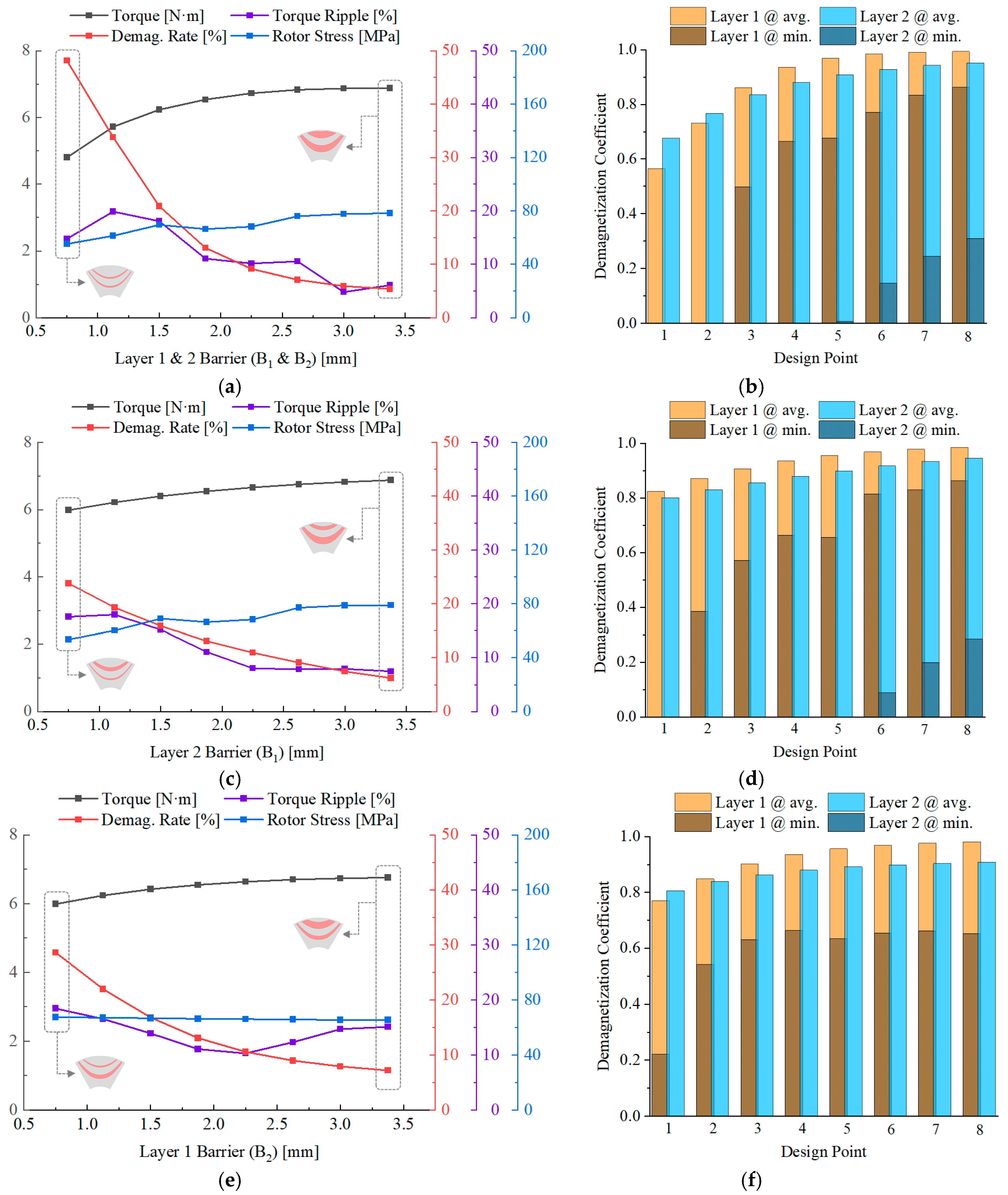
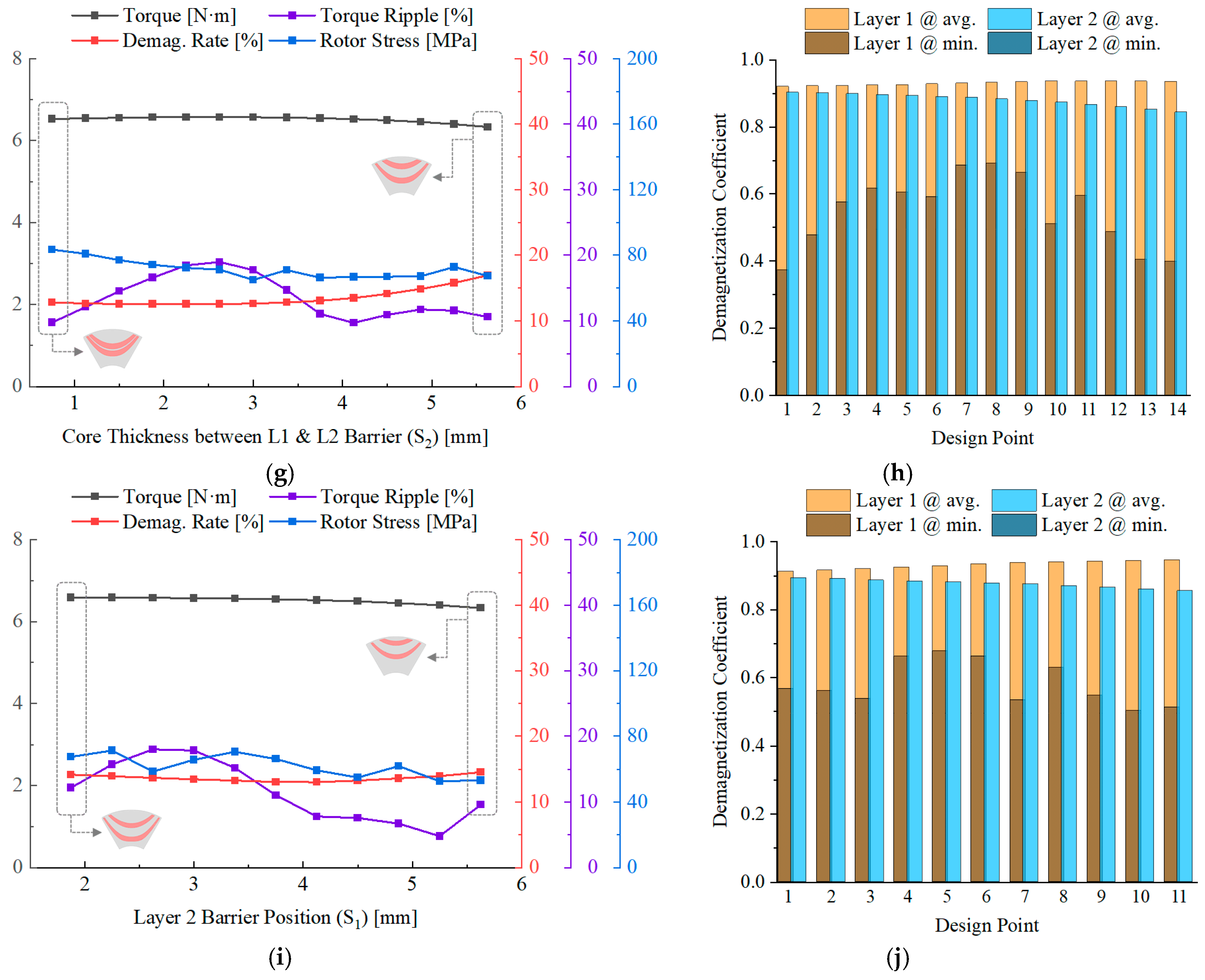
4.2. Sensitive Analysis with Design Variables
4.2.1. Barrier Position and Thickness
- The barrier thickness of each layer should not differ greatly;
- Magnets in the lower layer should be thicker;
- Barrier spacing is highly sensitive to torque ripple;
- Barrier position does not significantly affect performance, except for torque ripple;
- All irreversible demagnetization occurs at the ends of the barriers.
4.2.2. Bridge Position and Angle
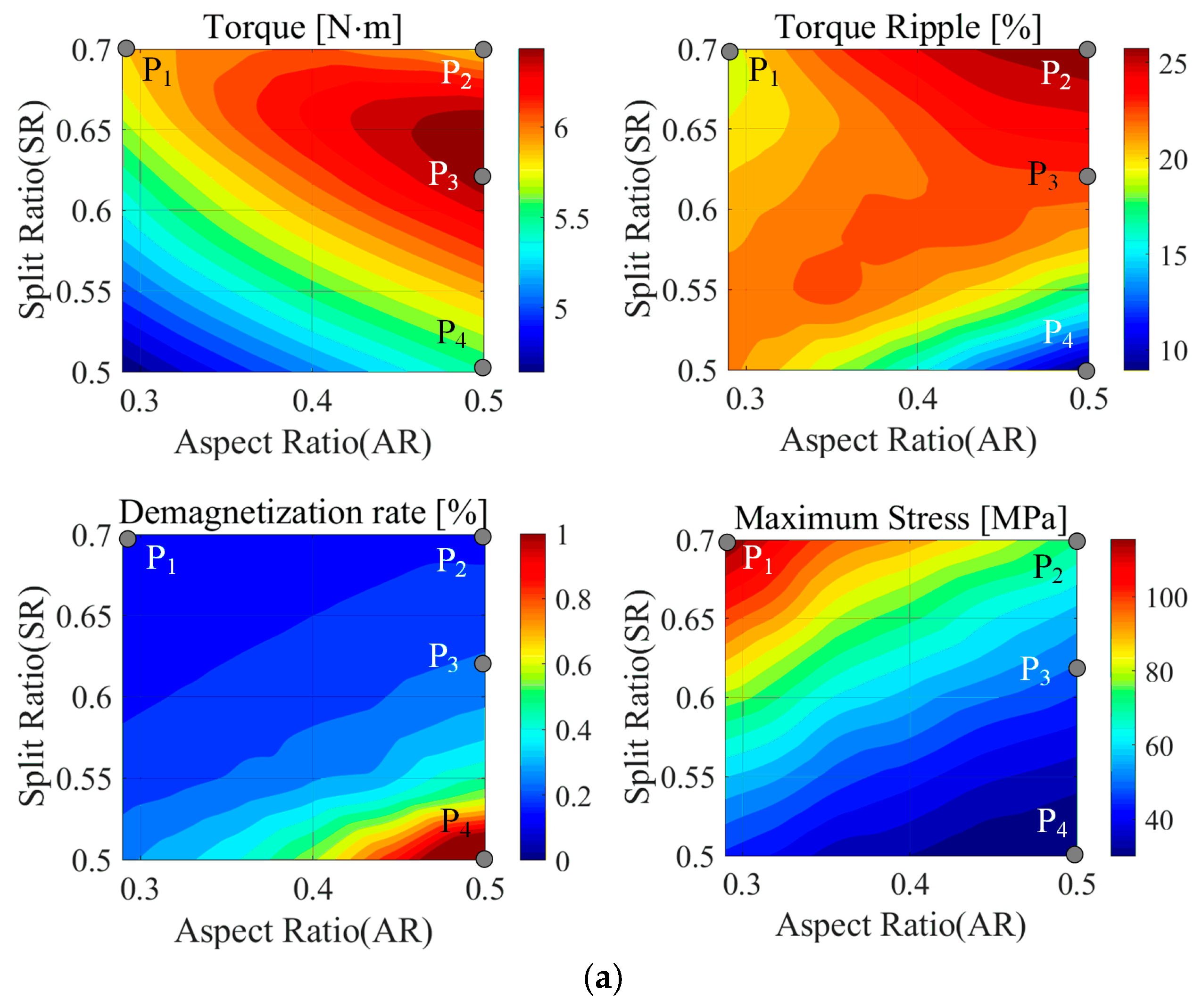
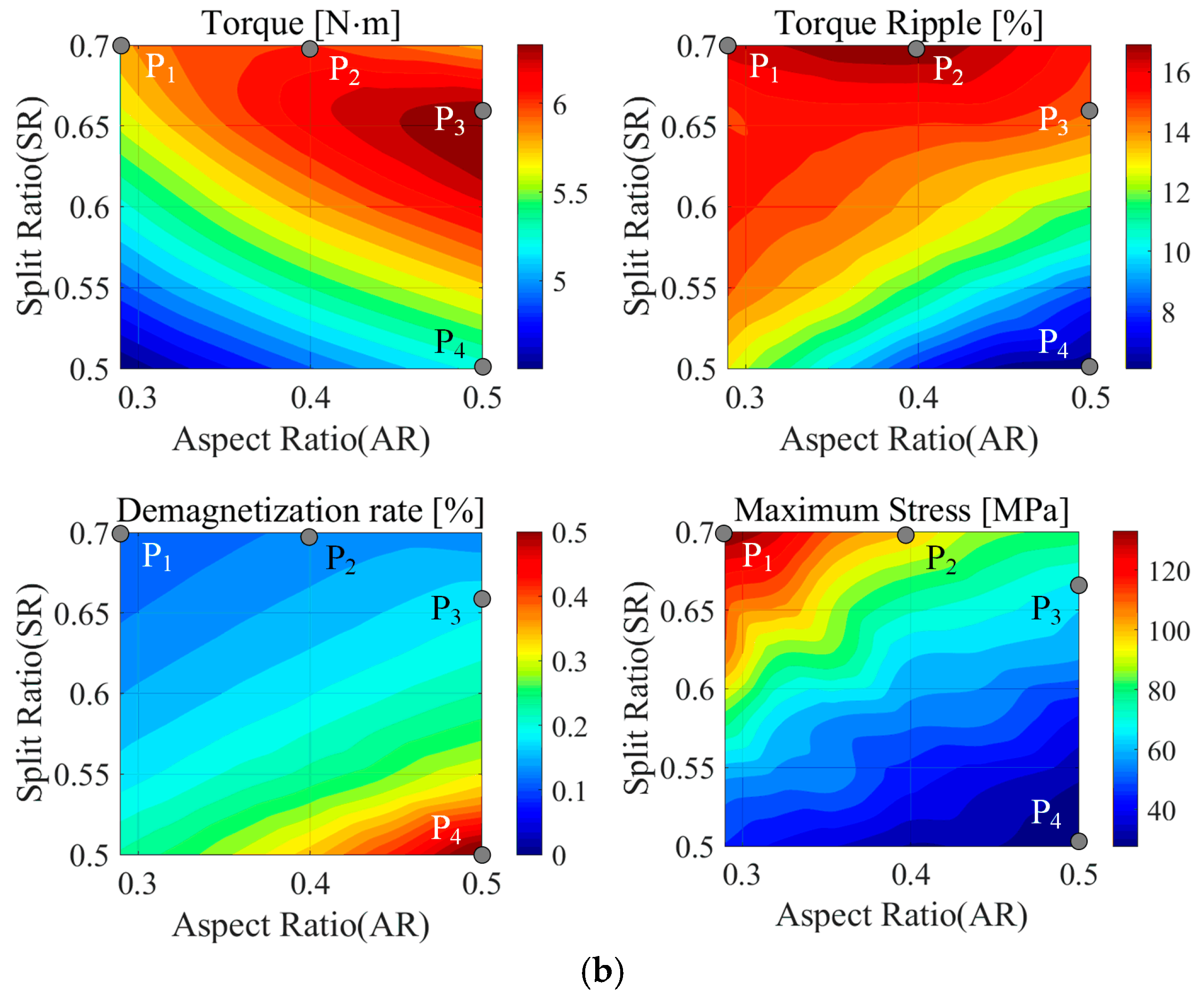
4.2.3. Split Ratio and Aspect Ratio
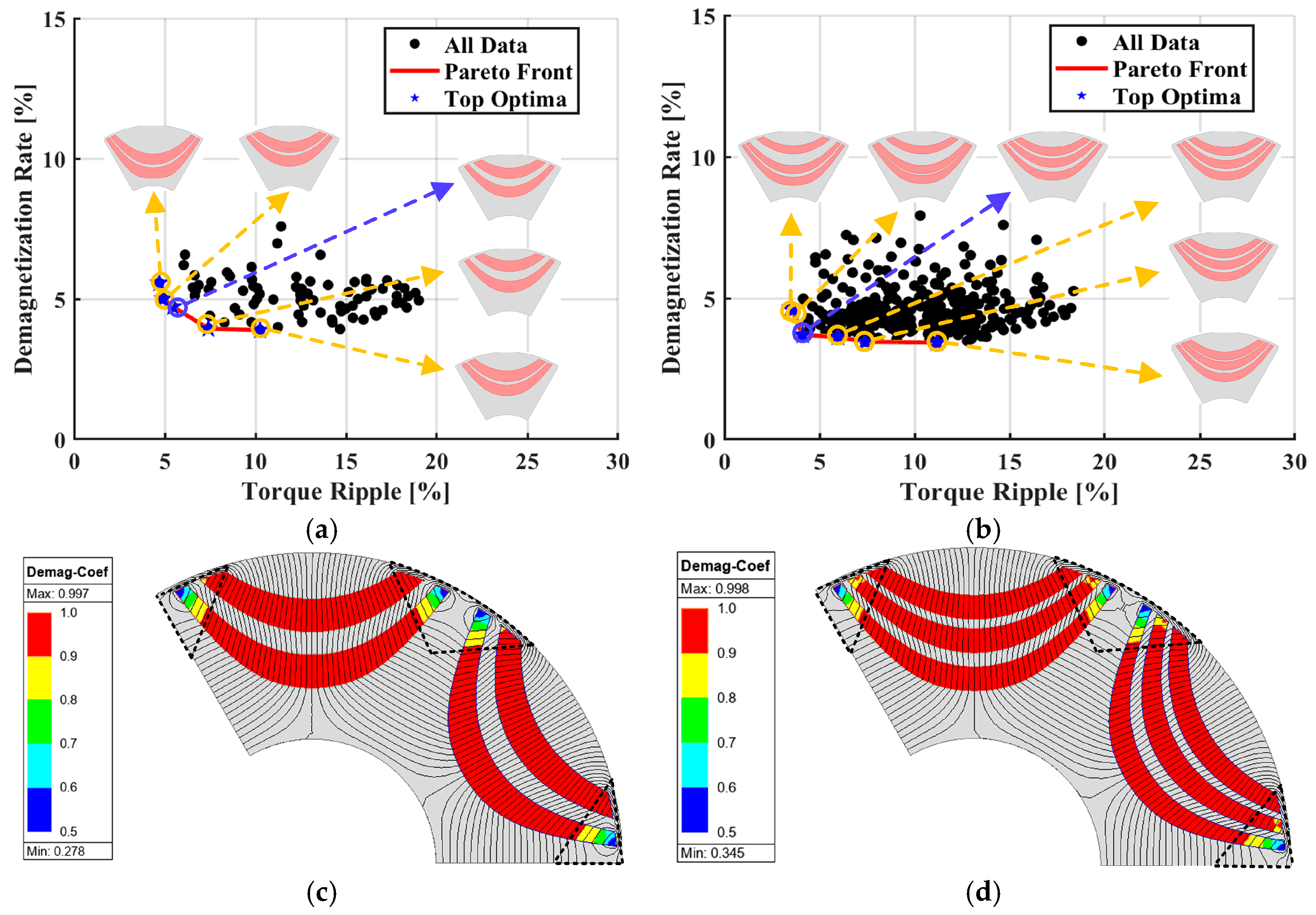
5. Results and Discussion
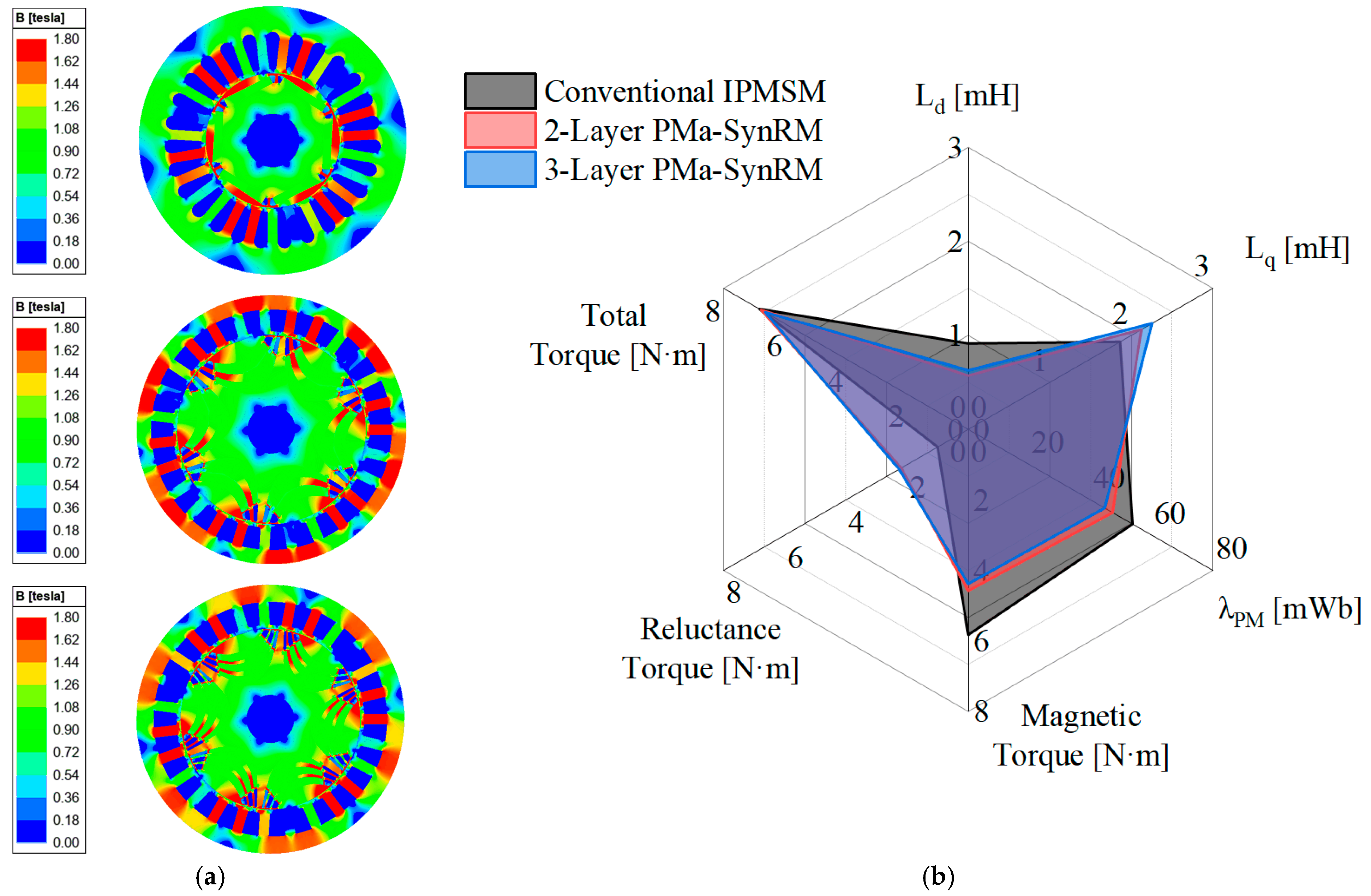
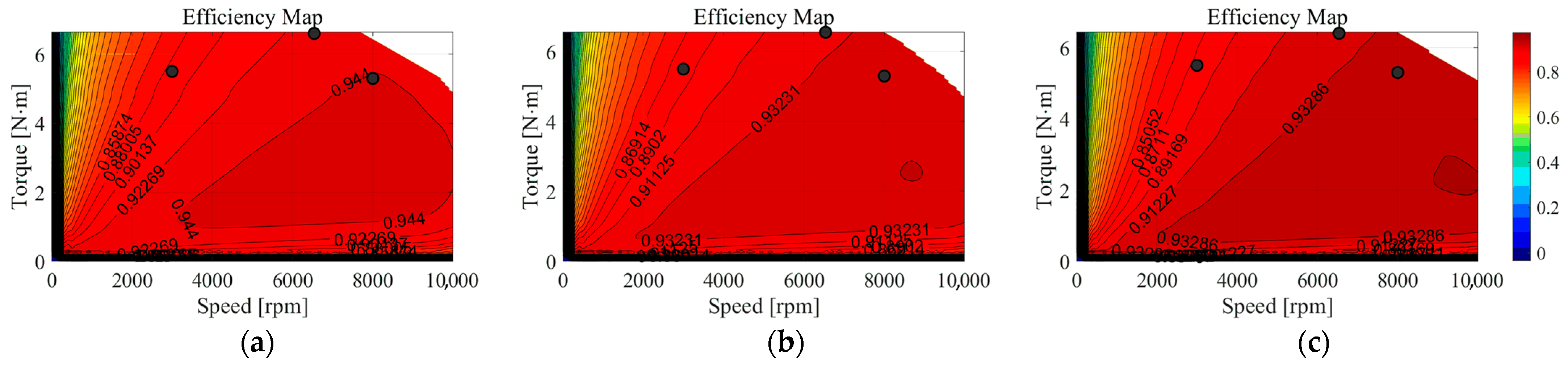
5.1. Comparison of Electromagnetic Performances with Conventional IPMSM
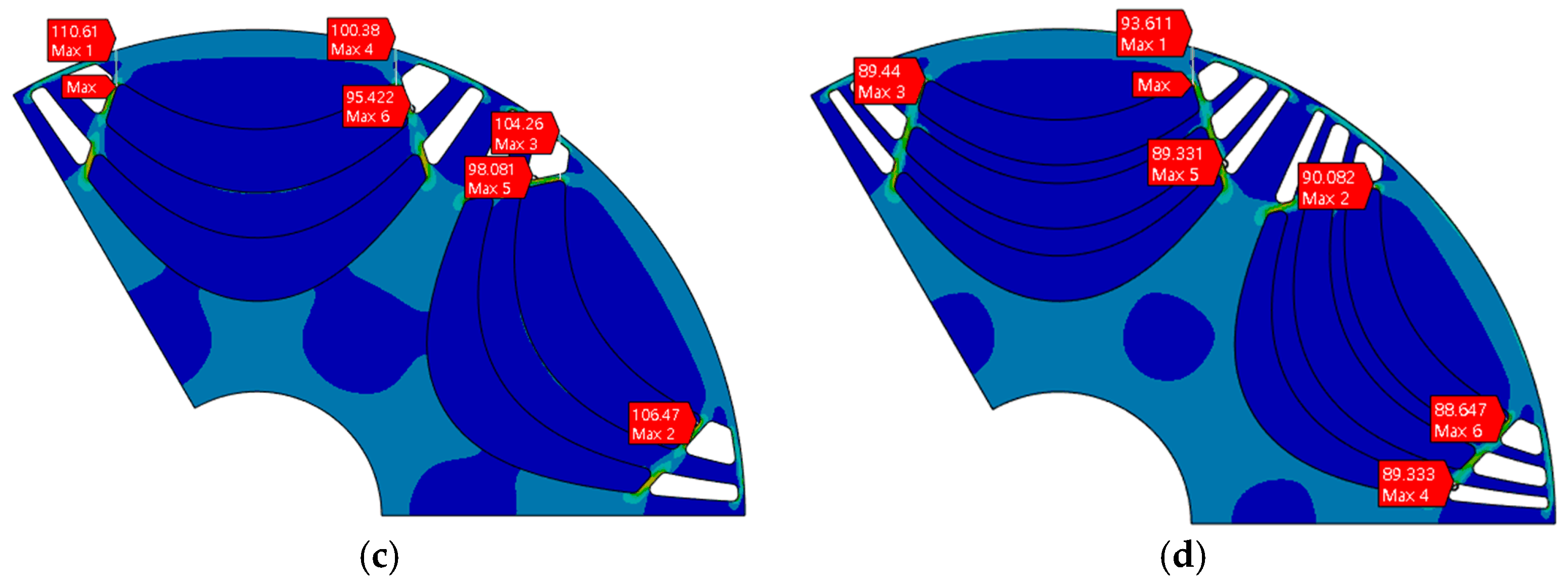
5.2. Analysis Results of Irreversible Demagnetization and Mechanical Stress
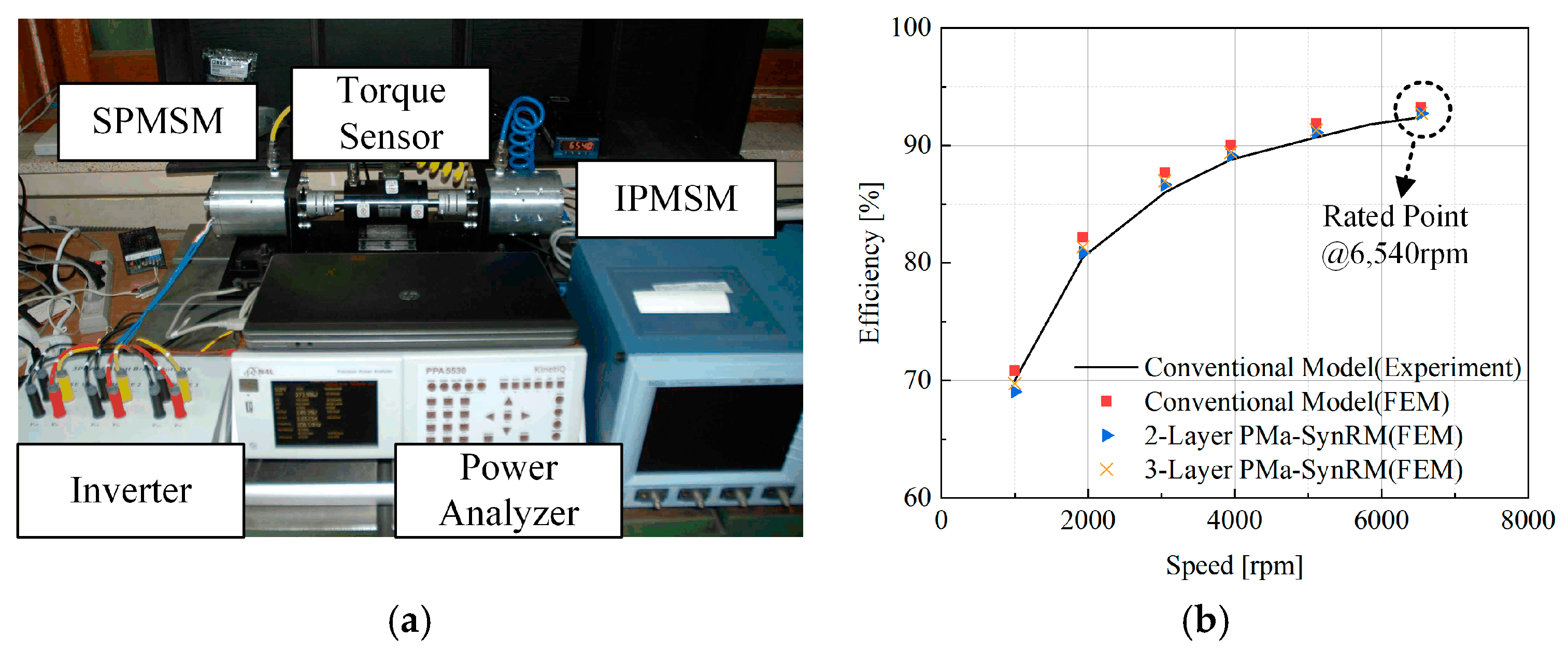
5.3. Experimental Validation
5.4. Techno-Economic Cost Analysis of Nd-Based vs. SmFeN-Based Designs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMa-SynRM | Permanent-Magnet-Assisted Synchronous Reluctance Motor |
| IPMSM | Interior Permanent Magnet Synchronous Motor |
| PM | Permanent Magnet |
| HRE | Heavy Rare Earth |
| FEM | Finite Element Method |
| EA | Evolutionary Algorithm |
| SF | Safety Factor |
| SR | Split Ratio |
| AR | Aspect Ratio |
References
- Zhu, S.; Hu, Y.; Liu, C.; Jiang, B. Shaping of the Air Gap in a V-Typed IPMSM for Compressed-Air System Applications. IEEE Trans. Magn. 2021, 57, 8103705. [Google Scholar] [CrossRef]
- Tao, X.; Takemoto, M.; Tsunata, R.; Ogasawara, S. Novel Rotor Structure Employing Large Flux Barrier and Disproportional Airgap for Enhancing Efficiency of IPMSM Adopting Concentrated Winding Structure. IEEE Access 2023, 11, 2848–2862. [Google Scholar] [CrossRef]
- Hao, Z.; Yang, Y.; Tian, Y.; Gong, Y.; Zhang, C.; Song, H.; Hao, Z.; Zhang, J. Phase Lead Compensation of a Phase-Locked Loop in an IPMSM for Air-Conditioner Compressors. IEEE Trans. Energy Convers. 2021, 36, 1090–1100. [Google Scholar] [CrossRef]
- Xu, R.; Shen, X.; Lin, X.; Liu, Z.; Xu, D.; Liu, J. Robust Model Predictive Control of Position Sensorless-Driven IPMSM Based on Cascaded EKF-LESO. IEEE Trans. Transp. Electrif. 2025, 11, 8824–8832. [Google Scholar] [CrossRef]
- Lin, X.; Liu, J.; Liu, Z.; Gao, Y.; Peretti, L.; Wu, L. Model-Free Current Predictive Control for PMSMs with Ultralocal Model Employing Fixed-Time Observer and Extremum-Seeking Method. IEEE Trans. Power Electron. 2025, 40, 10682–10693. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Yan, Q.; Huang, N.; Du, G. An Improved Model−Free Current Predictive Control of Permanent Magnet Synchronous Motor Based on High−Gain Disturbance Observer. Energies 2023, 16, 141. [Google Scholar] [CrossRef]
- Yoshida, Y.; Yoshida, R.; Sakurai, S.; Abe, M.; Tada, S.; Yamamoto, M.; Tajima, K. Study on Orientation and Magnetization Characteristics of Injection-Molded IPMSM Using Sm-Fe-N Bonded Magnets. In Proceedings of the IEEE Industry Applications Society Annual Meeting (IAS), Taipei, Taiwan, 15–20 June 2025; pp. 1–5. [Google Scholar]
- Yoshida, Y.; Yoshida, R.; Uwano, T.; Sakurai, S.; Abe, M.; Tada, S.; Yamamoto, M.; Tajima, K. Evaluation of an IPMSM Featuring a Rotor Core Directly Injection-Molded with Sm-Fe-N Bonded Magnets. In Proceedings of the 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024; pp. 2636–2639. [Google Scholar]
- Kim, K.-O.; Jung, Y.-H.; Park, J.-C.; Lim, M.-S. Comparative Study of Mechanical and Electrical Characteristics of High-Strength and Conventional Electrical Steel for EV Traction High-Speed Multilayer IPMSM Using Rare-Earth Free PM. IEEE Trans. Magn. 2023, 59, 8102205. [Google Scholar] [CrossRef]
- Jung, Y.-H.; Park, M.-R.; Kim, K.-O.; Chin, J.-W.; Hong, J.-P.; Lim, M.-S. Design of High-Speed Multilayer IPMSM Using Ferrite PM for EV Traction Considering Mechanical and Electrical Characteristics. IEEE Trans. Ind. Appl. 2021, 57, 327–339. [Google Scholar] [CrossRef]
- Kazemisangdehi, S.; Zhu, Z.Q.; Zhou, Y.; Chen, L.; Yang, L. Series Hybrid Rare-Earth and Ferrite Magnets Delta-Shape IPMSM with Split Ferrite Spoke. IEEE Trans. Ind. Appl. 2025, 1–12, early access. [Google Scholar] [CrossRef]
- Poudel, B.; Amiri, E.; Rastgoufard, P.; Mirafzal, B. Toward Less Rare-Earth Permanent Magnet in Electric Machines: A Review. IEEE Trans. Magn. 2021, 57, 900119. [Google Scholar] [CrossRef]
- Tahanian, H.; Aliahmadi, M.; Faiz, J. Ferrite Permanent Magnets in Electrical Machines: Opportunities and Challenges of a Non-Rare-Earth Alternative. IEEE Trans. Magn. 2020, 56, 900120. [Google Scholar] [CrossRef]
- Kobayashi, M.; Morimoto, S.; Sanada, M.; Inoue, Y. Performance Comparison between PMASynRM with Dy-Free Bonded Magnets and IPMSM with Sintered Magnets for Automotive Applications under Various Temperature Conditions. In Proceedings of the 21st European Conference on Power Electronics and Applications (EPE ‘19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–9. [Google Scholar]
- Kobayashi, M.; Morimoto, S.; Sanada, M.; Inoue, Y. Basic Study of PMASynRM with Bonded Magnet for Automotive Applications. In Proceedings of the 2018 International Power Electronics Conference (IPEC), Niigata, Japan, 20–24 May 2018; pp. 2802–2807. [Google Scholar]
- Xing, F.; Zhang, J.; Zuo, F.; Gao, Y. Optimization of an Asymmetric-Rotor Permanent Magnet-Assisted Synchronous Reluctance Motor for Improved Anti-Demagnetization Performance. Appl. Sci. 2024, 14, 11233. [Google Scholar] [CrossRef]
- Chuang, T.-S. A high-efficiency PM-assisted synchronous reluctance motor drive. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 3180–3185. [Google Scholar]
- Zhao, W.; Xing, F.; Wang, X.; Lipo, T.A.; Kwon, B.I. Design and Analysis of a Novel PM-Assisted Synchronous Reluctance Machine with Axially Integrated Magnets by the Finite-Element Method. IEEE Trans. Magn. 2017, 53, 8104104. [Google Scholar] [CrossRef]
- Liu, C.-T.; Luo, T.Y.; Shih, P.C.; Yen, S.C.; Lin, H.N.; Hsu, Y.W.; Hwang, C.C. On the Design and Construction Assessments of a Permanent-Magnet-Assisted Synchronous Reluctance Motor. IEEE Trans. Magn. 2017, 53, 2002104. [Google Scholar]
- Kong, Y.; Nicola, B.; Lin, M. Loss Functions and Efficiency Model of Permanent Magnet Assisted Synchronous Reluctance Machine. IEEE Trans. Energy Convers. 2023, 38, 53–63. [Google Scholar] [CrossRef]
- Cho, S.-K.; Jung, K.-H.; Choi, J.-Y. Design optimization of interior permanent magnet synchronous motor for electric compressors of air-conditioning systems mounted on EVs and HEVs. IEEE Trans. Magn. 2018, 54, 8204705. [Google Scholar] [CrossRef]
- Shin, H.-J.; Choi, J.-Y.; Cho, H.-W.; Jang, S.-M. Analysis on electromagnetic vibration source permanent magnet synchronous motor for compressor of electric vehicles. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference (VPPC), Seoul, Republic of Korea, 9–12 October 2012; pp. 200–203. [Google Scholar]
- Kobayashi, M.; Morimoto, S.; Sanada, M.; Inoue, Y. Investigation of PMASynRM with Dy-Free Bonded Magnets for Traction Applications Considering Irreversible Demagnetization. In Proceedings of the IEEE Energy Conv. Congress & EXPO (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1627–1632. [Google Scholar]
- Minoru, K. Reluctance Motor. Japan Patent JP 2004/096909 A, 25 March 2004. [Google Scholar]
- Germishuizen, J.J.; Van der Merwe, F.S.; Van der Westhuizen, K.; Kamper, M.J. Performance comparison of reluctance synchronous and induction traction drives for electrical multiple units. In Proceedings of the IEEE Industry Applications Conference, Conference Record, Rome, Italy, 8–12 October 2000; Volume 1, pp. 316–323. [Google Scholar]
- Moghaddam, R.R. Synchronous Reluctance Machine (SynRM) Design. Master’s Thesis, Royal Institute of Technology (KTH), Stockholm, Sweden, 2007. [Google Scholar]
- Kostko, J.K. Polyphase reaction synchronous motors. J. Am. Inst. Electr. Eng. 1923, 42, 1162–1168. [Google Scholar] [CrossRef]
- Uberti, F.; Frosini, L.; Szabó, L. A New Design Procedure for Rotor Laminations of Synchronous Reluctance Machines with Fluid Shaped Barriers. Electronics 2022, 11, 134. [Google Scholar] [CrossRef]
- Rajabi Moghaddam, R. Synchronous Reluctance Machine (SynRM) in Variable Speed Drives (VSD) Applications. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2011. [Google Scholar]
- Wang, Y.; Bacco, G.; Bianchi, N. Geometry Analysis and Optimization of PM-Assisted Reluctance Motors. IEEE Trans. Ind. Appl. 2017, 53, 4338–4347. [Google Scholar] [CrossRef]
- Mathews, J.H.; Howell, R.W. Complex Analysis for Mathematics and Engineering, 4th ed.; Jones and Bartlett Publishers: Sudbury, MA, USA, 2001; ISBN 0-7637-1425-9. [Google Scholar]
- Binns, K.J.; Lawrenson, P.J. The Analytical and Numerical Solution of Electric and Magnetic Fields; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Wilson, R.; Kumar, P.; El-Refaie, A. Minimization of Rare-Earth Permanent Magnets and Demagnetization Risk in PM-assisted Synchronous Reluctance Motor with Blended Magnets. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 4257–4264. [Google Scholar]
- Kumar, P.; Wilson, R.; Chowdhury, T.; El-Refaie, A. Electromagnetic and Mechanical Design Optimization of High-Speed PMASynRM Utilizing Different Magnet Combinations for EV Application. In Proceedings of the International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar]
- Lin, D.; Zhou, P.; Bracken, E. Generalized Algorithm to Deal with Temperature-Dependent Demagnetization Curves of Permanent Magnets for FEA. IEEE Trans. Magn. 2021, 57, 7402706. [Google Scholar] [CrossRef]
- Jeong, J.; Lee, H.; Orviz, M.; Bin Lee, S.; Reigosa, D.; Briz, F. Detection of Trailing Edge PM Demagnetization in Surface PM Synchronous Motors. IEEE Trans. Ind. Appl. 2023, 59, 3390–3399. [Google Scholar] [CrossRef]
- Rao, D.; Bagianathan, M. Selection of Optimal Magnets for Traction Motors to Prevent Demagnetization. Machines 2021, 9, 124. [Google Scholar] [CrossRef]
- Al-Qarni, A.; El-Refaie, A. Optimum Rotor Design for Rare-Earth Free High Performance Traction Applications Interior Permanent Magnet Motors Enabled by Iron Nitride Permanent Magnet. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), San Francisco, CA, USA, 15–18 May 2023; pp. 1–7. [Google Scholar]
- Kang, D.-W. Analysis of Vibration and Performance Considering Demagnetization Phenomenon of the Interior Permanent Magnet Motor. IEEE Trans. Magn. 2017, 53, 8210807. [Google Scholar] [CrossRef]
- Al-Qarni, A.; El-Refaie, A. Design and Optimization of High-Performance Rare-Earth Free Interior Permanent Magnet Motors for Electric Vehicles Enabled by Iron Nitride Magnets. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–November 2023; pp. 4082–4089. [Google Scholar]
- Yoon, K.-Y.; Hwang, K.-Y. Optimal Design of Spoke-Type IPM Motor Allowing Irreversible Demagnetization to Minimize PM Weight. IEEE Access 2021, 9, 65721–65729. [Google Scholar] [CrossRef]
- Hwang, K.-Y.; Yoon, K.-Y. Fault-Tolerant Design Process of Spoke-Type IPM Motor Considering Irreversible Demagnetization of PM in Integrated Electric Brake System. IEEE Trans. Magn. 2022, 58, 8206809. [Google Scholar] [CrossRef]
- Ni, R.; Xu, D.; Wang, G.; Ding, L.; Zhang, G.; Qu, L. Maximum efficiency per ampere control of permanent-magnet synchronous machines. IEEE Trans. Ind. Electron. 2015, 62, 2135–2143. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kumagai, M. Torque analysis of interior permanent magnet synchronous motors by considering cross-magnetization: Variation in torque components with permanent-magnet configurations. IEEE Trans. Ind. Electron. 2014, 61, 3192–3201. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Z.Q.; Ombach, G.; Chlebosz, W. Average torque improvement of interior permanent-magnet machine using third harmonic in rotor shape. IEEE Trans. Ind. Electron. 2014, 61, 5047–5057. [Google Scholar] [CrossRef]
- Chai, F.; Li, Y.; Liang, P.; Pei, Y. Calculation of the Maximum Mechanical Stress on the Rotor of Interior Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2016, 63, 3420–3432. [Google Scholar] [CrossRef]
- Barcaro, M.; Meneghetti, G.; Bianchi, N. Structural Analysis of the Interior PM Rotor Considering Both Static and Fatigue Loading. IEEE Trans. Ind. Appl. 2014, 50, 253–260. [Google Scholar] [CrossRef]
- Lee, S.-J.; Nguyen, M.-D.; Kwak, K.-W.; Kim, T.-S.; Eom, S.-H.; Choi, Y.-T.; Kim, Y.-J.; Shin, K.-H.; Choi, J.-Y. Characteristic Analysis and Improved Design of IPMSM for Automotive Compressor Through Tapering of Rotor Surface. IEEE Trans. Magn. 2025, 61, 8203105. [Google Scholar] [CrossRef]
- Chu, G.; Dutta, R.; Rahman, M.F.; Lovatt, H.; Sarlioglu, B. Analytical calculation of maximum mechanical stress on the rotor of interior permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2019, 56, 1321–1331. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H.; Li, D.; Qu, R. Calculation of the Rotor Mechanical Stress of Bridgeless Interior Permanent-Magnet Synchronous Machines with a High-Strength Sleeve. In Proceedings of the IEEE 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 185–190. [Google Scholar]
- Sahu, A.; Abdelrahman, A.; Al-Ani, D.; Bilgin, B. Fatigue life calculation and mitigation of bridge stresses in the rotor core of a delta-shape interior permanent magnet motor. In Proceedings of the IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 1–6. [Google Scholar]
- Chu, G.; Dutta, R.; Xiao, D.; Fletcher, J.E.; Rahman, M.F. Development and optimization of a mechanically robust novel rotor topology for very-high-speed IPMSMs. IEEE Trans. Energy Convers. 2023, 38, 1781–1792. [Google Scholar] [CrossRef]
- Monissen, C.; Arslan, M.E.; Krings, A.; Andert, J. Mechanical stress in rotors of permanent magnet machines—Comparison of different determination methods. Energies 2022, 15, 9169. [Google Scholar] [CrossRef]
- De Jong, K.A. Evolutionary Computation: A Unified Approach; MIT Press: Cambridge, MA, USA; London, UK, 2006. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; pp. 261–265. [Google Scholar]
- Yu, C.; Qu, R.; Xu, W.; Li, J. Analytical determination of optimal split ratio for interior permanent magnet synchronous motor. In Proceedings of the IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Hong, H.; Lee, J.-K.; Jung, D.-H.; Lee, J.; Kim, H. Comparative Study on Electromagnetic Performance of Slotted and Slotless PM Synchronous Motors According to Aspect Ratios. IEEE Trans. Magn. 2025, 61, 8201604. [Google Scholar] [CrossRef]
- Tsunata, R.; Takemoto, M.; Imai, J.; Saito, T.; Ueno, T. Comparison of Thermal Characteristics in Various Aspect Ratios for Radial-Flux and Axial-Flux Permanent Magnet Machines. IEEE Trans. Ind. Appl. 2023, 59, 3353–3367. [Google Scholar] [CrossRef]
- Cui, J.; Ormerod, J.; Parker, D.; Ott, R.; Palasyuk, A.; Mccall, S.; Paranthaman, M.P.; Kesler, M.S.; McGuire, M.A.; Nlebedim, I.C.; et al. Manufacturing Processes for Permanent Magnets: Part I—Sintering and Casting. JOM 2022, 74, 1279–1295. [Google Scholar] [CrossRef]
- Wang, H.; Lamichhane, T.N.; Paranthaman, M.P. Review of additive manufacturing of permanent magnets for electrical machines: A prospective on wind turbine. Mater. Today Phys. 2022, 24, 100675. [Google Scholar] [CrossRef]
- Kitco—Base Metals Prices. Available online: https://www.kitco.com/price/base-metals (accessed on 8 August 2025).
- Metal.com—Cold-Rolled Non-Oriented Silicon Steel–B35A250–0.35*1200*C–Shanghai–Baosteel. Available online: https://www.metal.com/en/prices/202403290002 (accessed on 8 August 2025).
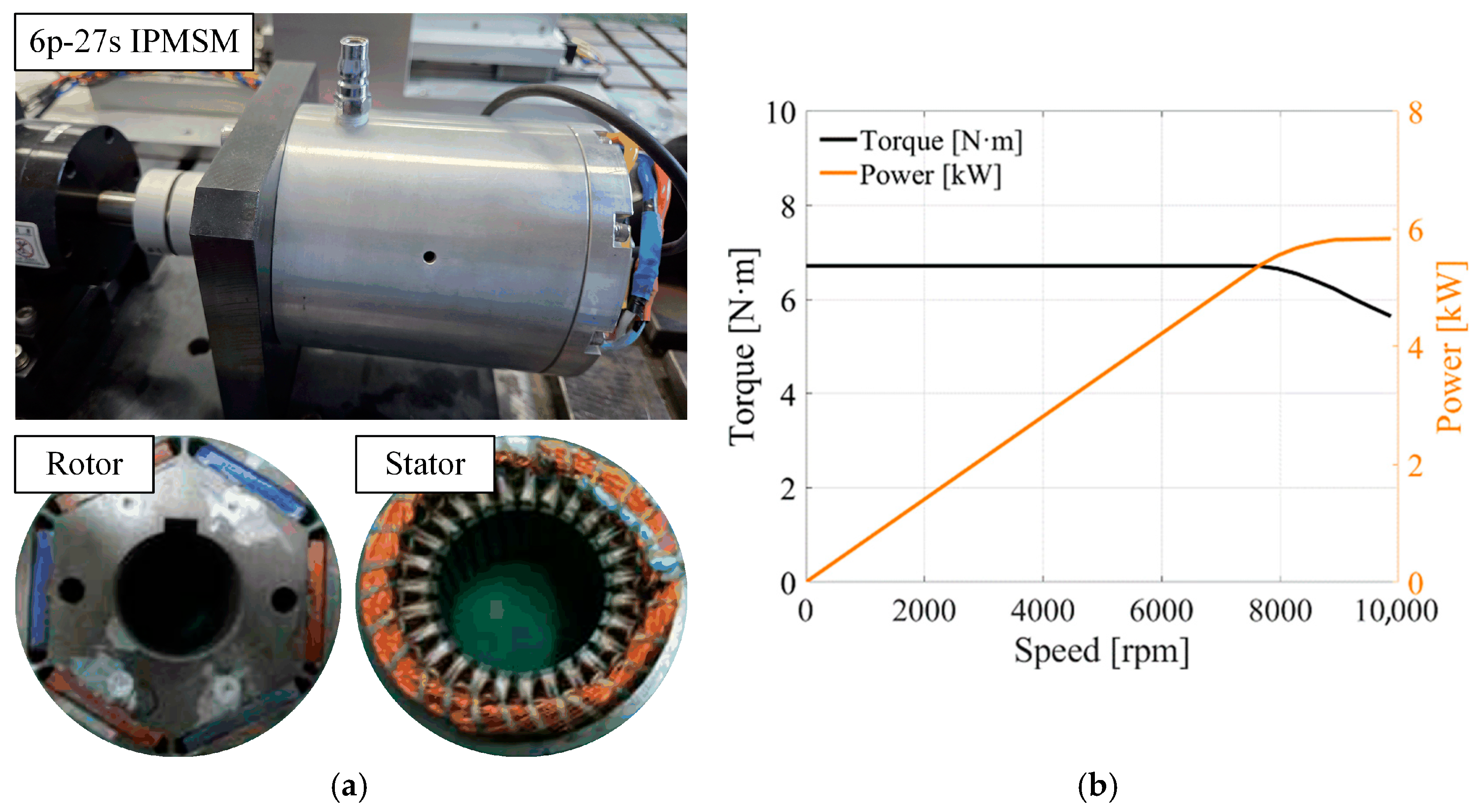

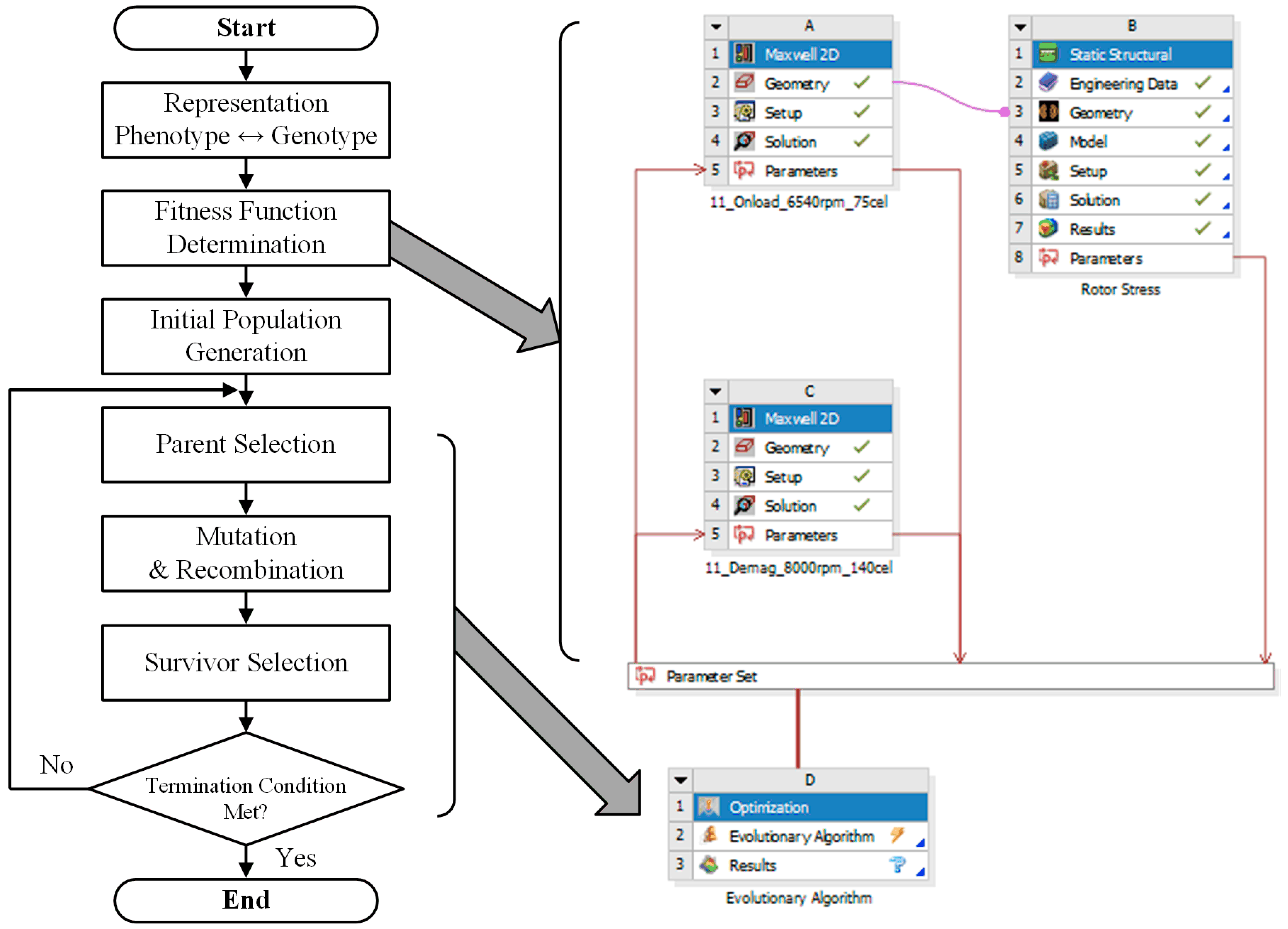

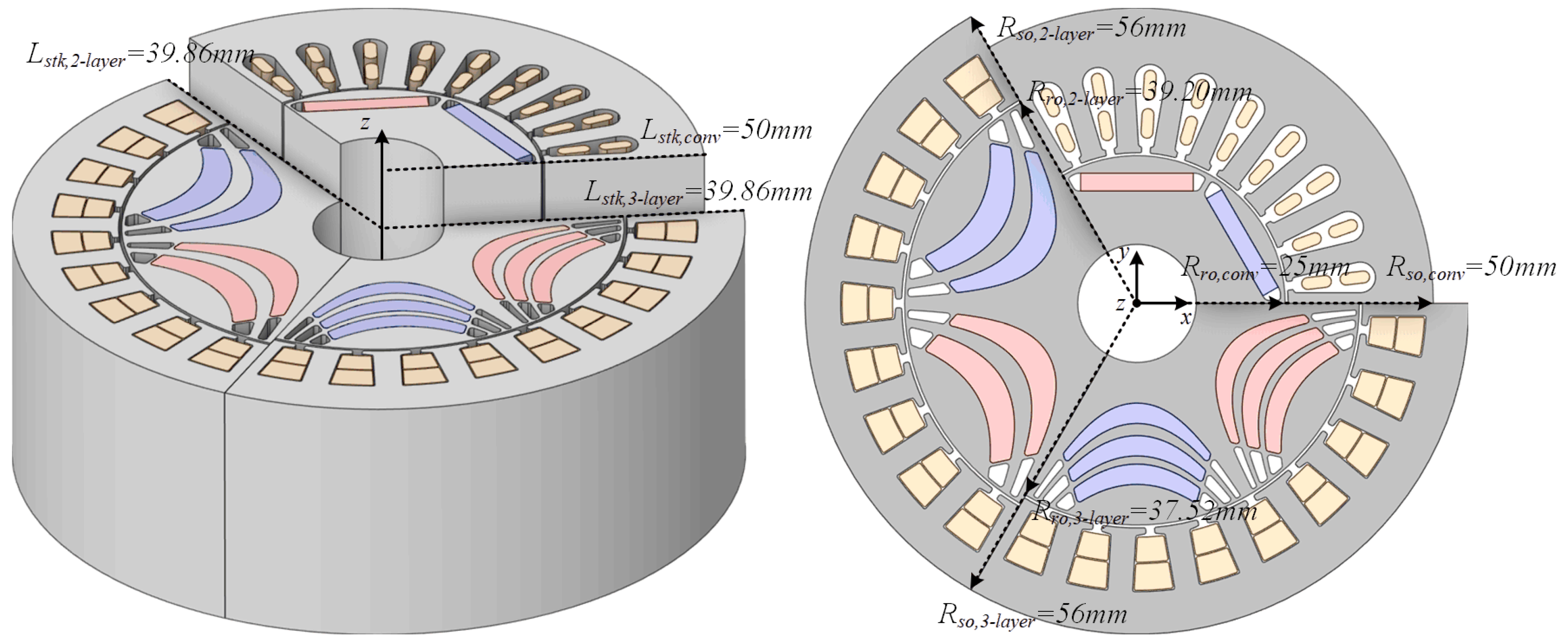

| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| Poles/slots | 6/27 | - | Rated speed | 6540 | rpm |
| Number of Phases | 3 | - | Maximum speed | 8000 | rpm |
| Stator outer diameter | 100 | mm | Input current | 26 | Amax |
| Rotor outer diameter | 50 | mm | Rated torque | 6.82 | N·m |
| Stator slot top diameter | 40.5 | mm | Output power | 4.674 | kW |
| Slot opening | 1.5 | mm | Efficiency | 92.90 | % |
| Tooth width | 3.6 | mm | Line-voltage limit | 288 | V |
| Air-gap length | 0.5 | mm | Grade of core | 35PN250 | - |
| Axial length | 50 | mm | Grade of PM | N42 | - |
| Analysis Condition | Analysis Result (Conventional IPMSM) | ||||
|---|---|---|---|---|---|
| Parameter | Value | Unit | Parameter | Value | Unit |
| Fault current | 20.08 | Amax | Induced voltage (1–2) | 85.40 | Vrms |
| Phase angle | 90 | Deg. | Induced voltage (5–6) | 85.26 | Vrms |
| Temperature | 140 | °C | Demag. rate | 0.16 | % |
| Item | Value | Unit | ||
|---|---|---|---|---|
| 35PN250 | N42 | SmFeN | ||
| Density | 7600 | 7500 | 5500 | kg/m3 |
| Poisson’s ratio | 0.3 | 0.24 | 0.36 | - |
| Yield strength | 370 | 78.4 | 27.3 | MPa |
| Item | Value | Unit | |
|---|---|---|---|
| 2-Layer PMa-SynRM | 3-Layer PMa-SynRM | ||
| Torque | 6.89 | 6.97 | N·m |
| Torque ripple | 8.87 | 4.12 | % |
| Magnet usage | 0.150 | 0.162 | kg |
| Maximum stress | 72.05 | 77.33 | MPa |
| P1 | P2 | P3 | P4 | ||
|---|---|---|---|---|---|
| 2-Layer PMa-SynRM |  | 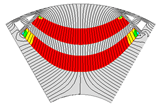 | 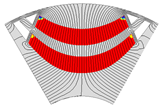 | 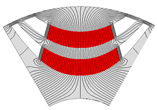 |  |
| Torque [N·m] | 5.90 | 5.53 | 4.43 | 5.66 | |
| Torque ripple [%] | 8.72 | 8.97 | 17.37 | 9.33 | |
| Demagnetization rate [%] | 2.00 | 1.36 | 0.35 | 2.15 | |
| Maximum stress [MPa] | 40.01 | 34.09 | 22.89 | 29.14 | |
| 3-Layer PMa-SynRM |  | 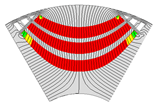 | 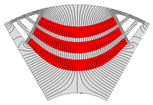 |  | 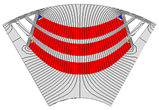 |
| Torque [N·m] | 5.96 | 5.28 | 4.37 | 5.42 | |
| Torque ripple [%] | 7.06 | 6.06 | 8.72 | 8.22 | |
| Demagnetization rate [%] | 1.59 | 0.54 | 0.32 | 4.42 | |
| Maximum stress [MPa] | 34.27 | 27.78 | 20.70 | 31.10 | |
| P1 | P2 | P3 | P4 | |
|---|---|---|---|---|
| 2-Layer PMa-SynRM |  | 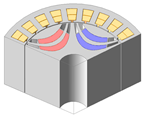 | 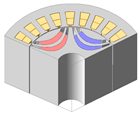 | 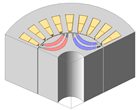 |
| AR/SR | 0.29/0.70 | 0.5/0.70 | 0.5/0.62 | 0.5/0.50 |
| Torque [N·m] | 5.89 | 5.86 | 6.48 | 5.53 |
| Torque ripple [%] | 19.39 | 26.60 | 23.13 | 8.96 |
| Demagnetization rate [%] | 0.12 | 0.15 | 0.25 | 1.36 |
| Maximum stress [MPa] | 127.21 | 73.52 | 51.40 | 30.22 |
| 3-Layer PMa-SynRM | 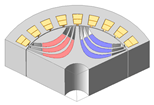 | 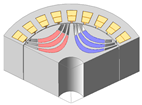 | 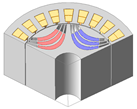 | 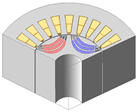 |
| AR/SR | 0.29/0.70 | 0.40/0.70 | 0.50/0.66 | 0.50/0.50 |
| Torque [N·m] | 5.84 | 6.05 | 6.38 | 5.28 |
| Torque ripple [%] | 16.71 | 17.42 | 14.76 | 6.06 |
| Demagnetization rate [%] | 0.11 | 0.14 | 0.18 | 0.54 |
| Maximum stress [MPa] | 138.39 | 102.29 | 67.14 | 27.78 |
| Item | Value | Unit | ||
|---|---|---|---|---|
| Conventional IPMSM | 2-Layer PMa-SynRM | 3-Layer PMa-SynRM | ||
| L-L voltage (FFT) | 225.4 | 213.45 | 216.06 | V |
| Cogging torque | 57.20 | 63.26 | 192.32 | mN·m |
| Torque | 6.82 | 6.76 | 6.64 | N·m |
| Torque ripple | 7.47 | 23.90 | 16.51 | % |
| Copper loss | 290.74 | 307.86 | 302.10 | W |
| Core loss | 44.65 | 54.94 | 52.89 | W |
| Magnet loss | 0.44 | 0.08 | 0.07 | W |
| Efficiency | 93.29 | 92.73 | 92.76 | % |
| Item | Efficiency | Unit | ||
|---|---|---|---|---|
| 3000 [rpm] | 6540 [rpm] | 8000 [rpm] | ||
| Conventional IPMSM | 89.39 | 93.29 | 94.92 | % |
| 2-Layer PMa-SynRM | 88.22 | 92.75 | 94.32 | |
| 3-Layer PMa-SynRM | 88.12 | 92.78 | 94.25 | |
| Item | Value | Unit | |
|---|---|---|---|
| 2-Layer PMa-SynRM | 3-Layer PMa-SynRM | ||
| Demagnetization rate | 0.30 | 0.26 | % |
| Maximum stress | 110.61 | 93.61 | MPa |
| SF | 3.35 | 3.95 | - |
| Item | Magnet Usage | Unit | Total Cost | Unit |
|---|---|---|---|---|
| Conventional IPMSM | 0.130 | kg | 1.00 | P.U. |
| 2-Layer PMa-SynRM | 0.303 | 0.54 | ||
| 3-Layer PMa-SynRM | 0.282 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.-T.; Kim, S.-M.; Lee, S.-J.; Jang, J.-H.; Kim, S.-W.; Park, J.-B.; Kim, Y.-S.; Lee, D.-H.; Choi, J.-Y.; Shin, K.-H. Mathematical Modeling and Optimal Design for HRE-Free Permanent-Magnet-Assisted Synchronous Reluctance Machine Considering Electro-Mechanical Characteristics. Mathematics 2025, 13, 2858. https://doi.org/10.3390/math13172858
Choi Y-T, Kim S-M, Lee S-J, Jang J-H, Kim S-W, Park J-B, Kim Y-S, Lee D-H, Choi J-Y, Shin K-H. Mathematical Modeling and Optimal Design for HRE-Free Permanent-Magnet-Assisted Synchronous Reluctance Machine Considering Electro-Mechanical Characteristics. Mathematics. 2025; 13(17):2858. https://doi.org/10.3390/math13172858
Chicago/Turabian StyleChoi, Yeon-Tae, Su-Min Kim, Soo-Jin Lee, Jun-Ho Jang, Seong-Won Kim, Jun-Beom Park, Yeon-Su Kim, Dae-Hyun Lee, Jang-Young Choi, and Kyung-Hun Shin. 2025. "Mathematical Modeling and Optimal Design for HRE-Free Permanent-Magnet-Assisted Synchronous Reluctance Machine Considering Electro-Mechanical Characteristics" Mathematics 13, no. 17: 2858. https://doi.org/10.3390/math13172858
APA StyleChoi, Y.-T., Kim, S.-M., Lee, S.-J., Jang, J.-H., Kim, S.-W., Park, J.-B., Kim, Y.-S., Lee, D.-H., Choi, J.-Y., & Shin, K.-H. (2025). Mathematical Modeling and Optimal Design for HRE-Free Permanent-Magnet-Assisted Synchronous Reluctance Machine Considering Electro-Mechanical Characteristics. Mathematics, 13(17), 2858. https://doi.org/10.3390/math13172858





