Construction of an Optimal Strategy: An Analytic Insight Through Path Integral Control Driven by a McKean–Vlasov Opinion Dynamics

Abstract

In this paper, we have constructed a closed-form optimal strategy within a social network using stochastic McKean–Vlasov dynamics. Each agent independently minimizes their dynamic cost functional, driven by stochastic differential opinion dynamics. These dynamics reflect agents’ opinion differences from others and their past opinions, with random influences and stubbornness adding to the volatility. To gain an analytic insight into the optimal feedback opinion, we employed a Feynman-type path integral approach with an appropriate integrating factor, marking a novel methodology in this field. Additionally, we utilized a variant of the Friedkin–Johnsen-type opinion dynamics to derive a closed-form optimal strategy for an agent and conducted a comparative analysis.

1. Introduction

In recent years, there has been a growing interest in the study of opinion dynamics, which explores how the beliefs of a typically large population of individuals evolve over time through repeated interactions within a social network [1]. In continuous opinion dynamics, beliefs (referred to interchangeably as opinions or beliefs) are depicted as scalar values or vectors, with each individual’s belief moving towards a weighted average of other agents’ beliefs, reflecting the influence of social interactions [2]. Traditional models generally suggest that, given a connected social network, consensus among agents will eventually be reached over time [3]. However, exceptions arise in bounded confidence models, where agents disregard the influence of others whose beliefs diverge significantly from their own, and in models featuring stubborn agents who resist changing their opinions but can still sway the opinions of others. These stubborn agents may represent leaders, political parties, or media sources aiming to influence the beliefs of the broader population [4]. Studies on scaling limits indicate that in a homogeneous population, as the population size increases, the observed distribution of beliefs tends to converge towards the solution of a specific deterministic mean-field differential equation in the space of probability measures. These findings align with the concept of the propagation of chaos in interacting particle systems [3]. It is a well understood fact that when agents interact, their opinions tend to converge towards an average [5]. Global interactions often lead to consensus, while local interactions typically result in clusters of similar opinions. This clustering happens when agents only engage with neighbors who share their views, avoiding those with differing opinions. To understand the differences in final opinion values, researchers have developed a Lagrangian model of dissensus, employing graph theory and stochastic stability theory [6].

Social networks exert significant influence on various aspects of behavior, such as educational attainment [7], employment opportunities [8], technology uptake [9], consumer habits [10], and even smoking habits [11,12]. Since social networks emerge from individual decisions, understanding the consensus plays a pivotal role in deciphering their formation. Despite extensive theoretical exploration of social networks, there has been minimal investigation into consensus as a Nash equilibrium within stochastic networks. Ref. [12] characterizes the network as a simultaneous-move game, where social ties are formed based on the utility effects from indirect connections. Ref. [12] also introduces a computationally feasible method for partially identifying large social networks. The statistical examination of network formation traces back to pioneering work [13], where a random graph is constructed with independent links governed by a fixed probability. Beyond the Erdös–Rényi model, numerous techniques have been devised to simulate graphs exhibiting characteristics like varying degree distributions, small-world properties, and Markovian traits. Model-based approaches are valuable if they can be effectively fitted and yield realistic simulations. The Exponential Random Graph Model (ERGM) is widely used due to its ability to capture observed network statistics [14,15,16,17]. However, the ERGM lacks micro foundations crucial for counterfactual analyses, and economists consider network analysis as the domain of rational agents seeking to optimize their utilities. Another popular framework involves viewing networks as evolving through stochastic processes, where the focus lies on the parameters governing the process rather than on individual network realizations [16].

A distinction should be drawn between the classical Nash equilibrium in finite-agent stochastic games and the Mean Field Game (MFG) equilibrium. In a Nash equilibrium, each of the n agents optimizes their cost functional given the strategies of all other agents, and no individual agent can unilaterally reduce their cost. The resulting strategies depend explicitly on the empirical distribution of the population. In contrast, an MFG equilibrium arises in the limit $n\to \infty$, where a representative agent optimizes against the distribution of the population, typically modeled by a McKean–Vlasov process. The MFG equilibrium is then defined by a fixed-point condition: the optimal strategy of the representative agent generates exactly the same distribution that the agent anticipates. This limiting framework was formalized by Lasry and Lions [18,19], and a rigorous probabilistic foundation was later developed by Carmona and Delarue [20,21]. In this paper, we derive the optimal strategy for each finite agent and interpret its limiting behavior as an approximation of the MFG equilibrium when the number of agents is large.

To provide intuition before introducing the technical framework, consider a simplified opinion dynamics model with $n=50$ agents. Each agent’s opinion is represented by a point on a one-dimensional line, where proximity reflects similarity in views. At each time step, agents adjust their opinions toward those of nearby agents, with closer opinions exerting stronger influence. Control inputs may be applied to selected agents to steer the group toward a consensus or desired configuration, while random fluctuations represent unpredictable external influences. 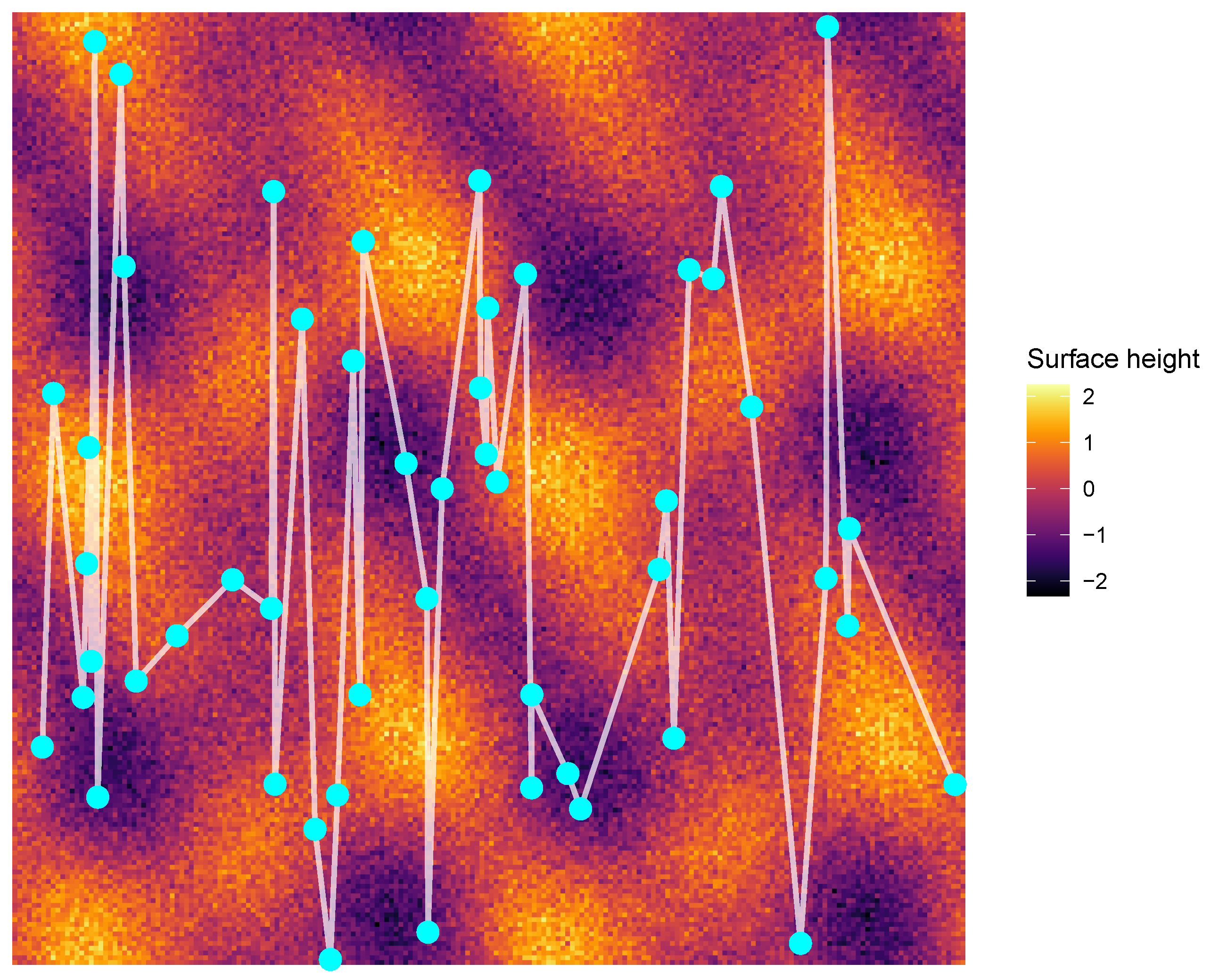Figure 1 illustrates a group of 50 agents represented as dots on a random surface. The surface indicates an underlying field that changes across space. Each agent is connected to other agents by lines (i.e., shares opinion). These lines show that every agent interacts with other agents. The colors of the surface reflect variation in the background opinion environment. The positions of the agents can change over time in response to these interactions and the environment.

In this paper, we propose an approach to opinion dynamics within the framework of McKean–Vlasov dynamics. We focus on a stochastic model with time-continuous beliefs comprising a homogeneous population of agents. Pioneering research into McKean–Vlasov equations was conducted by [22,23], where they examined uncontrolled Stochastic Differential Equations (SDEs) to establish chaos propagation outcomes. Kac’s work delved into mean-field SDEs driven by classical Brownian motion, offering deeper insights into the Boltzmann and Vlasov kinetic equations. Ref. Snitman [24] also contributed significantly to understanding this equation. While subsequent authors have expanded on this research, there has been a notable surge in interest over the past decade, largely due to its intersection with Mean Field Game (MFG) theory. This theory was independently introduced by [19,25]. The McKean–Vlasov equation is instrumental in analyzing scenarios where numerous identical agents, interacting via the empirical distribution of their state variables, aim for a Nash equilibrium. Conversely, for agents seeking a Pareto Equilibrium, stochastic control of McKean–Vlasov SDEs is considered. While these two equilibria are related, nuances exist, as highlighted by Carmona et al. [26]. Certainly, as indicated by these studies, as the number of agents tends towards infinity, it is anticipated that the individual agents’ opinions evolve independently. Each agent’s opinion is governed by a specific stochastic differential equation, where the coefficients are contingent upon the statistical distribution of their private state. The optimization of each agent’s objective function within the confines of this new dynamic state equates to the stochastic control of McKean–Vlasov dynamics, a mathematical conundrum not universally comprehended. Refer to [27] for an initial exploration in this direction. Returning to our original inquiry, one might question whether or not optimizing feedback strategies in this new control scenario yields a form of approximate equilibrium for the initial N-agent game. Regardless, if such a problem can be resolved, the crux lies in understanding how an optimal feedback strategy in this context aligns with the outcomes of the MFG theory.

Furthermore, it is possible to transform a class of non-linear HJB equations into linear equations through a logarithmic transformation. This technique dates back to the early days of quantum mechanics, where Schrödinger first used it to connect the HJB equation to the Schrödinger equation. Due to this linearity, backward integration of the HJB equation over time can be replaced by computing expectation values under a forward diffusion process, which involves stochastic integration over trajectories described by a path integral [28,29,30]. In more complex cases, such as the Merton–Garman–Hamiltonian system, finding a solution through the Pontryagin’s maximum principle is impractical, but the Feynman path integral method provides a solution. Previous works using the Feynman path integral method include its application in motor control theory by [31,32,33,34]. The use of Feynman path integrals in finance has been extensively discussed by [35]. Additionally, ref. [36] introduced a Feynman-type path integral to determine a feedback control.

Classical mean-field game theory, initiated by Lasry and Lions [18,19,37], provides a general framework for studying Nash equilibria in large populations of agents where the cost functional depends on the state distribution. In that setting, the analysis is typically conducted through a coupled system of HJB and Fokker–Planck (FP) equations. By contrast, the present work is based on controlled McKean–Vlasov dynamics, in which the emphasis is placed on the stochastic evolution of interacting particles and their empirical measure. This perspective avoids the need to solve the full PDE system and is closer to probabilistic methods for interacting diffusions. On the numerical side, a considerable body of work has focused on approximating mean-field equilibria using grid-based PDE solvers [38,39], as well as particle methods and deep learning approaches [40,41,42]. Our contribution is complementary to these developments: rather than approximating the Lasry–Lions equations directly, we formulate an optimal control problem over the particle system itself, with numerical implementation carried out through simulation of interacting agents. This approach allows us to capture finite-population effects and to design control strategies that remain interpretable in terms of agent-level interactions.

From a numerical standpoint, the literature on the mean-field approach has largely been developed along two complementary directions. On the one hand, finite-difference and related PDE-based solvers have been extensively applied to the Lasry–Lions system, yielding accurate approximations of the coupled HJB and FP equations on discretized grids [38,39]. While these approaches provide precise resolution in low-dimensional settings, their computational cost grows rapidly with the dimension of the state space, which limits their applicability in high-dimensional environments. On the other hand, simulation-based approaches, often leveraging interacting particle systems, provide a more scalable alternative. By directly evolving a large but finite set of controlled dynamics, such methods approximate the mean-field limit probabilistically and naturally incorporate stochasticity and finite-population effects. More recently, machine learning and deep reinforcement learning techniques [40,41,42] have extended this particle-based philosophy by introducing data-driven function approximations, enabling numerical treatment of high-dimensional and non-linear problems. The methodology developed in this paper belongs to this latter class; rather than discretizing PDEs, we simulate controlled particle systems and analyze their empirical distributions, thereby retaining interpretability at the agent level while avoiding the curse of dimensionality inherent in PDE solvers.

The rest of this paper is structured as follows: In Section 3, we formulate the opinion dynamics along with the cost functional. Section 4 outlines the assumptions and essential properties of stochastic McKean–Vlasov dynamics. In Section 5, we derive the deterministic Hamiltonian and stochastic Lagrangian for the system. Section 6 presents the main results related to Feynman-type path integral control and its applications to the Friedkin–Johnsen-type model. Finally, Section 7 concludes the paper and suggests possible future extensions.

2. Notations and Symbols

For convenience, the main notations and symbols used throughout the paper (including Appendix A) are summarized below.

Symbol	Description
n	Number of agents in the population.
$i,j$	Agent indices, $i,j\in \{1,\dots ,n\}$.
$s,t$	Continuous time variables.
$x^i\left(s\right)$	Opinion state of agent i at time s.
$x_0^i$	Initial opinion of agent i.
${\eta }_i$	Set of neighbors of agent i, defined as ${\eta }_i:=\{j\in N:(i,j)\in E\}$.
${\mathbb{A}}_i$	Neighborhood of agent i, i.e., $\left\{x^j\left(s\right)\right|\left|\right|x^i\left(s\right)-x^j\left(s\right)|{|}_2^2\le r\}$.
$\theta ={({\theta }_1,{\theta }_2)}^T$	Parameter vector of interaction kernel.
${\theta }_1$	Scale parameter of the kernel.
${\theta }_2$	Range parameter of the kernel.
${\varphi }_{\theta }\left(\beta \right)$	Interaction kernel governing influence between agents (Equation (7)).
$\alpha \left(s\right)$	Time-varying weight on self-opinion dynamics (decay rate).
$u^i\left(s\right)$	Control input of agent i at time s, $u^i\left(s\right)\in \mathcal{U}\left([0,t]\right)$.
$u^{i\ast }\left(s\right)$	Optimal control strategy of agent i (Equation (16)).
$h^i$	Feedback control function mapping agent states to admissible controls (Assumption 3).
${\sigma }^i$	Noise intensity (volatility) for agent i.
$B^i\left(s\right)$	Standard Brownian motion for agent i.
$\gamma$	Measure parameter in the mean-field formulation.
$w_{ij}$	Peer influence weight of agent j on agent i.
$k_i$	Stubbornness parameter of agent i.
$L^i(s,\mathit{x},u^i)$	Cost functional of agent i (Equation (1)).
$L_0,L_0^i$	Initial cost functional of society and of agent i, assumed concave (Assumption 4).
$\mathcal{U}$	Admissible control space (convex, open subset of ${\mathbb{R}}^n$).
$\mathcal{Z}$	Information (knowledge) space of the society (Assumption 4).
${\mathcal{Z}}_i$	Information subset available to agent i.
$\mathbb{E}[·]$	Expectation operator.
${\mathbb{E}}_0[·]$	Conditional expectation given initial state $x_0^i$.
$V^i(s,x)$	Value function of agent i solving the HJB equation.
${\lambda }^i\left(s\right)$	Adjoint (co-state) variable from stochastic optimal control.
$T_1,T_2,T_3$	Coefficients in quadratic formula representation of $u^{i\ast }\left(s\right)$ (Equation (16)).
${\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }$, ${\displaystyle \frac{d^2}{d{\left(x^i\right)}^2}}{\varphi }_{\theta }$	First and second derivatives of the kernel (used in optimality conditions).
$\mathcal{N}(0,1)$	Standard Gaussian distribution, used for noise terms.
$\mathcal{M}$	Set of probability measures on $\mathbb{R}$.
$\left|\right|·\left|\right|$	Euclidean norm.
$\mathrm{\Delta }$	Laplacian operator.
${\partial }_s$	Partial derivative with respect to time.
${\mathbb{P}}_{\left(x^i\right)}$	Probability law of agent i.

3. Construction of a Stochastic Differential Game of Opinion Dynamics

Following [43], consider a social network of n agents by a weighted directed graph $G=(N,E,w_{ij})$, where $N=\{1,...,n\}$ is the set of all agents. Let, $E\subseteq N\times N$ be the set of all ordered pairs of all connected agents, and $w_{ij}$ be the influence of agent j on agent i for all $(i,j)\in E$. There are two types of connections, one-sided or two-sided. For the principle–agent problem, the connection is one-sided (i.e., Stackelberg model), and for the agent–agent problem, it is two-sided (i.e., Cournot model). Suppose $x^i\left(s\right)\in [0,1]$ be the opinion of agent $i^{th}$ at time $s\in [0,t]$ with their initial opinion $x^i\left(0\right)=x_0^i\in [0,1]$. Then, $x^i\left(s\right)$ has been normalized into $[0,1]$, where $x^i\left(s\right)=0$ stands for a strong disagreement and $x^i\left(s\right)=1$ represents strong agreement and all other agreements stay in between. Let $\mathit{x}\left(s\right)={\left[x^1\left(s\right),x^2\left(s\right),\dots , x^n\left(s\right)\right]}^T\in {[0,1]}^n$ be the opinion profile vector of n agents at time s, where T represents the transposition of a vector. Following [43], define the cost function of agent i as

$$\begin{array}{cc}\hfill L^i(s,\mathit{x},u^i)& :=\mathbb{E}\left\{{\displaystyle \frac{1}{2}}{\int }_0^t\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(s\right)-x^j\left(s\right)\right]}^2+k_i{\left[x^i\left(s\right)-x_0^i\right]}^2+{\left[u^i\left(s\right)\right]}^2\right\}ds\right\},\hfill \end{array}$$

(1)

where $w_{ij}\in [0,\infty )$ is a parameter that weighs the susceptibility of agent j to influence agent i, $k_i\in [0,\infty )$ is agent i’s stubbornness, $u^i\left(s\right)\in \mathcal{U}\left([0,t]\right)$ is an adaptive control process of agent i taking values in a convex open set in ${\mathbb{R}}^n$, and set of all agents with whom i interacts is ${\eta }_i$ and defined as ${\eta }_i:=\{j\in N:(i,j)\in E\}$. In this paper, $u^i$ represents agent i’s control over their own opinion as well as influencing other agents’ opinions. The cost function $L^i(s,\mathit{x},u^i)$ is twice differentiable with respect to time in order to satisfy Wick rotation, is continuously differentiable with respect to $i^{th}$ agent’s control $u^i\left(s\right)$, non-decreasing in opinion $x^i\left(s\right)$, non-increasing in $u^i\left(s\right)$, and convex and continuous in all opinions and controls [44,45]. The opinion dynamics of agent i follow a McKean–Vlasov stochastic differential equation,

$$\begin{array}{cc}\hfill d{x}^i\left(s\right)& ={\mu }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]ds+{\sigma }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]d{B}^i\left(s\right),\hfill \end{array}$$

(2)

with the initial condition $x_0^i$, where ${\mu }^i$ and ${\sigma }^i$ are the drift and diffusion functions and ${\mathbb{P}}_{\left(x^i\right)}$ is the probability law the opinion of agent i with Brownian motion $B^i\left(s\right)=\left\{B^i\left(s\right),s\in [0,t]\right\}$. The reason behind incorporating Brownian motion in agent i’s opinion dynamics is because of Hebbian Learning, which states that neurons increase the synaptic connection strength between them when they are active together simultaneously, and this behavior is probabilistic in the sense that resource availability from a particular place is random [46,47]. For example, for a given stubbornness, and influence from agent j, agent i’s opinion dynamics have some randomness in opinion. Suppose from other resources agent i knows that the information provided by agent j’s influence is misleading. Apart from that, after considering humans as automatons, motor control and foraging for food become a big example of minimization of costs (or the expected return) [47]. As control problems like motor controls are stochastic in nature because there is a noise in the relation between the muscle contraction and the actual displacement with joints with the change of the information environment over time, we consider the Feynman path integral approach to determine the stochastic control after assuming the opinion dynamics; Equation (2) [48,49]. The coefficient of the control term in Equation (1) is normalized to 1, without loss of generality. The cost functional represented in Equation (1) is viewed as a model of the motive of agent i towards a prevailing social issue [43]. The aim of this paper is to characterize a feedback Nash equilibrium $u^{i\ast }\in \mathcal{U}\left([0,t]\right)$, such that

$$L^i\left(u^{i\ast }\right)=\underset{u^i\in \mathcal{U}\left([0,t]\right)}{argmin}{\mathbb{E}}_s\left\{L^i(s,\mathit{x},u^i)|{\mathcal{F}}_0^x\right\},$$

subject to the Equation (2), where ${\mathbb{E}}_0\left(L^i\right|{\mathcal{F}}_0^x)$ represents the expectation on $L^i$ at time 0 subject to agent i’s opinion filtration ${\mathcal{F}}_0^x$ generated by the Brownian motion $B^i$ starting at the initial time 0 for a complete probability space $(\mathrm{\Omega },\mathcal{F},{\mathcal{F}}_0^x,\mathbb{P})$. A solution to this problem is a feedback Nash equilibrium as the control of agent i is updated based on the opinion at the same time s.

4. Preliminaries

Let $t>0$ be a fixed finite horizon. Assume $B^i\left(s\right)={\left\{B^i\left(s\right)\right\}}_{s=0}^t$ is a 1-dimensional Brownian motion defined on a probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$, and ${\mathcal{F}}_s={\left\{{\mathcal{F}}_s^x\right\}}_{s=0}^t$ is its natural filtration augmented with an independent $\sigma$-algebra ${\mathcal{F}}_0^x$, where $\mathbb{P}$ is the probability law defined above. The McKean–Vlasov stochastic opinion dynamic of agent i is represented in Equation (2), where the drift and diffusion coefficients of opinion $x^i\left(s\right)$ are given by a pair of deterministic functions $({\mu }^i,{\sigma }^i):[0,t]\times \mathbb{R}\times {\mathcal{P}}_2\left(\mathbb{R}\right)\times \mathcal{U}\to \mathbb{R}\times \mathbb{R}$, and $u^i={\left\{u^i\left(s\right)\right\}}_{s=0}^t$ is the admissible control of agent i assumed to be a progressively measurable process with values in a measurable space $(\mathcal{U},{\mathcal{U}}^{*})$. In $(\mathcal{U},{\mathcal{U}}^{*})$, $\mathcal{U}$ is an open subset of an Euclidean space $\mathbb{R}$, and ${\mathcal{U}}^{*}$ is a $\sigma$-field induced by a Borel $\sigma$-field in the same Euclidean space [50]. For a metric space E, if $\mathcal{E}$ is its Borel $\sigma$-field, we use $\mathcal{P}\left(E\right)$ as the notation for the set of all probability measures on $(E,\mathcal{E})$. We further assume $\mathcal{P}\left(E\right)$ is endowed with the topology of weak convergence [51]. If E is a Polish space G, then for all $r\ge 1$ with metric $d_G$ define

$${\mathcal{P}}_r\left(G\right):=\left\{\gamma \in \mathcal{P}\left(G\right):{\int }_G{d}_G{(x_0^i,x^i)}^r\gamma \left(d{x}^i\right)<\infty \right\},$$

where $x_0^i\in G$ is arbitrary. For $r\ge 1$ Wasserstein distance $W_r(\gamma ,{\gamma }^{\prime })$ on $\mathcal{P}\left(E\right)$ define

$$W_r(\gamma ,{\gamma }^{\prime }):=inf{\left\{{\int }_{G\times G}{d}_G{(x^i,y^i)}^r\pi (d{x}^i,d{y}^i):\pi \in \mathcal{P}(G\times G)\mathrm{so}\mathrm{that}\pi (.\times G)=\gamma ,\mathrm{and}\pi (G\times .)={\gamma }^{\prime }\right\}}^{{\displaystyle \frac{1}{r}}},$$

for all $\gamma ,{\gamma }^{\prime }\in {\mathcal{P}}_r\left(G\right)$. The space $\left({\mathcal{P}}_r\left(G\right),W_r\right)$ is indeed a Polish space [51]. The term ‘non-linear’, used to describe Equation (2), does not mean the drift (${\mu }^i$) and diffusion (${\sigma }^i$) coefficients are non-linear functions of X, but instead they not only depend on the value of the unknown process $x^i\left(s\right)$ but also on its distributions ${\mathbb{P}}_{\left(x^i\right)}$ [50]. In the r-Wasserstein distance $W_r(\gamma ,{\gamma }^{\prime })$ the infimum is taken over all couplings $\pi \in \mathcal{P}(G\times G)$, such that the marginal laws

$$\pi (A\times G)=\gamma \left(A\right),\mathrm{and}\pi (G\times A)={\gamma }^{\prime }\left(A\right),\mathrm{for}\mathrm{all}\mathrm{Borel}\mathrm{sets}A\subseteq G$$

are satisfied. In other words, $\pi$ has marginals $\gamma$ and ${\gamma }^{\prime }$. The space $\left({\mathcal{P}}_r\left(G\right),W_r\right)$ is indeed a Polish space. To get rid of more symbols we represent “A” by “.” In this paper, $\gamma ={\mathbb{P}}_{\left(\mathit{x}\right)}$.

The set $\mathcal{U}$ of admissible controls $u^i$ as the set of $\mathcal{U}$-valued progressively measurable processes $u^i\in {\mathcal{H}}^{2,m}$, where ${\mathcal{H}}^{2,\tilde{m}}$ is a Hilbert space,

$${\mathcal{H}}^{2,\tilde{m}}:=\left\{y^i\in {\mathcal{H}}^{0,\tilde{m}};\mathbb{E}{\int }_0^t{\left|y^i\left(s\right)\right|}^{2}ds<\infty \right\}$$

with ${\mathcal{H}}^{0,\tilde{m}}$ being the collection of all ${\mathbb{R}}^{\tilde{m}}$-valued progressive measurable processes on $[0,t]$. Let $\mathcal{V}$ be a sub-$\sigma$-algebra of $\mathcal{F}$ so that the following assumption holds.

Assumption 1. (i). $\mathcal{V}$ and the filtration ${\mathcal{F}}_{\infty }$ generated by the Brownian motion of $i^{th}$ agent $B^i\left(s\right)$ are independent.

• (ii). $\mathcal{V}$ is “rich enough” by means of the following condition:

$$\begin{array}{c}{\mathcal{P}}_2\left(C([0,t],{\mathcal{H}}^{2,\tilde{m}})\right)=\{{\mathbb{P}}_{\left(Y\right)}\mathit{with}Y:[0,t]\times \mathrm{\Omega }\to {\mathcal{H}}^{2,\tilde{m}}\mathit{continuous}\mathit{and}\hfill \\ \hfill \mathcal{B}\left([0,t]\right)\otimes \mathcal{V}-\mathit{measurable}\mathit{process}\mathit{satisfying}\mathbb{E}{\int }_0^t{\left|y^i\left(s\right)\right|}^{2}ds<\infty \}.\end{array}$$

In other words, for all $\gamma \in {\mathcal{P}}_2\left(C([0,t],{\mathcal{H}}^{2,\tilde{m}})\right)$ there exists a continuous and Borel $\mathcal{B}\left(\right[0,t\left]\right)\otimes \mathcal{V}$-process $y^i:[0,t]\times \mathrm{\Omega }\to {\mathcal{H}}^{2,\tilde{m}}$, such that $\mathbb{E}{\int }_0^t{\left|y^i\left(s\right)\right|}^{2}d{s}^{<}\infty$, and Y has the law (distribution) equal to γ.

Lemma 1 

([51]). Let $\tilde{\mathcal{V}}$ be another sub-σ-algebra of $\mathcal{F}$ on the probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$. If Assumption 1 holds then the following statements are equivalent.

• (i). There exists a $\tilde{\mathcal{V}}$-measurable random variable $z^i:\mathrm{\Omega }\to \mathbb{R}$ with the Uniform distribution $[0,1]$.
• (ii). $\tilde{\mathcal{V}}$ is “rich enough” by means of the following condition:

$$\begin{array}{c}{\mathcal{P}}_2\left(C([0,t],{\mathcal{H}}^{2,\tilde{m}})\right)=\{{\mathbb{P}}_{\left(y^i\right)}\mathit{with}{y}^i:[0,t]\times \mathrm{\Omega }\to {\mathcal{H}}^{2,\tilde{m}}\mathit{continuous}\mathit{and}\hfill \\ \hfill \mathcal{B}\left([0,t]\right)\otimes \tilde{\mathcal{V}}-\mathit{measurable}\mathit{process}\mathit{satisfying}\mathbb{E}{\int }_0^t{\left|y^i\left(s\right)\right|}^{2}ds<\infty \}.\end{array}$$

Remark 1. 

Consider two sets of sub-σ-algebras $F_1\in \tilde{\mathcal{V}}$ and $F_2\in \tilde{\mathcal{V}}$ in the probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ so that $\mathbb{P}\left(F_1\right)>0$, and $F_1\subset F_2$ with $0<\mathbb{P}\left(F_1\right)<\mathbb{P}\left(F_2\right)$ (atomless space). Then, statements (i) and (ii) in Lemma 1 are equivalent.

Assumption 2. (i) There exists a linear, unbounded operator $O:\mathcal{D}\left(O\right)\subset {\mathcal{H}}^{2,\tilde{m}}\to {\mathcal{H}}^{2,\tilde{m}}$, which facilitates a $C_0$-semigroup of pseudo-contractions $\{exp(sO);s\ge 0$ in ${\mathcal{H}}^{2,\tilde{m}}$.

• (ii). The drift ${\mu }^i$ and the diffusion coefficients ${\sigma }^i$ are measurable.
• (iii). There exists a constant $C^{*}$, such that

$$\begin{array}{cc}\hfill |{\mu }^i(s,\gamma ,x^i,u^i)-{\mu }^i(s,{\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i\left(s\right)-x^{i^{\prime }}\left(s\right)|+|u^i\left(s\right)-u^{i^{\prime }}\left(s\right)\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i),({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U},\hfill \\ \hfill |{\sigma }^i(s,\gamma ,x^i,u^i)-\sigma (s,{\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i\left(s\right)-x^{i^{\prime }}\left(s\right)|+|u^i\left(s\right)-u^{i^{\prime }}\left(s\right)\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}\gamma ,{\gamma }^{\prime }\in {\mathcal{P}}_2\left(\mathbb{R}\right),\hfill \\ \hfill |L^i(s,\mathit{x},u^i)-L^i(s,{\mathit{x}}^{\prime },u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i\left(s\right)-x^{i^{\prime }}\left(s\right)|+|u^i\left(s\right)-u^{i^{\prime }}\left(s\right)\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i),({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}.\hfill \end{array}$$

• (iv). ${\sigma }^i$ is differentiable in $(\gamma ,x^i,u^i)\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}$, and the derivative ${\partial }_{\gamma }{\sigma }^i:{\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}\to \mathbb{R}\times \mathcal{U}$ is bounded Lipschitz continuous. Hence, there exists a positive constant $C^{*}$, such that

$$\begin{array}{cc}\hfill |{\partial }_{\gamma }{\sigma }^i(s,\gamma ,x^i,u^i)|& \le C^{*},\mathit{for}\mathit{all}(\gamma ,x^i,u^i)\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U},\hfill \\ \hfill |{\partial }_{\gamma }{\sigma }^i(s,\gamma ,x^i,u^i)-{\partial }_{\gamma }\sigma (s,\gamma ,x^{i^{\prime }},u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i\left(s\right)-x^{i^{\prime }}\left(s\right)|+|u^i\left(s\right)-u^{i^{\prime }}\left(s\right)\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i),({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}.\hfill \end{array}$$

• (v). Consider ${\omega }^i={\mu }^i$ and $L^i$. Therefore, ${\omega }^i$ is differentiable in $(\gamma ,x^i,u^i)\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}$ and the derivatives ${\partial }_{\gamma }{\omega }^i:{\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}\times (\mathbb{R}\times \mathcal{U})\to \mathbb{R}\times \mathcal{U}$, ${\partial }_x{\omega }^i:{\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}\to \mathbb{R}$, and ${\partial }_u{\omega }^i:{\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}\to \mathcal{U}$ are bounded and Lipschitz continuous. Hence, for a given $s\in [0,t]$, there exists a constant $C^{*}>0$, so that

$$\begin{array}{cc}\hfill |{\partial }_{\gamma }{\omega }^i(\gamma ,x^i,u^i)|+|{\partial }_x{\omega }^i(\gamma ,x^i,u^i)|& +|{\partial }_u{\omega }^i(\gamma ,x^i,u^i)|\le C^{*},\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i)\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}\times (\mathbb{R}\times \mathcal{U}),\hfill \\ \hfill |{\partial }_{\gamma }{\omega }^i(\gamma ,x^i,u^i)-{\partial }_{\gamma }{\omega }^i({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i-x^{i^{\prime }}|+|u^i-u^{i^{\prime }}\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i),({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}\times (\mathbb{R}\times \mathcal{U}),\hfill \\ \hfill |{\partial }_x{\omega }^i(\gamma ,x^i,u^i)-{\partial }_x{\omega }^i({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i-x^{i^{\prime }}|+|u^i-u^{i^{\prime }}\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i),({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U},\hfill \\ \hfill |{\partial }_u{\omega }^i(\gamma ,x^i,u^i)-{\partial }_u{\omega }^i({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})|& \le C^{*}(W_2(\gamma ,{\gamma }^{\prime })+|x^i-x^{i^{\prime }}|+|u^i-u^{i^{\prime }}\left|\right),\hfill \\ \hfill & \mathit{for}\mathit{all}(\gamma ,x^i,u^i),({\gamma }^{\prime },x^{i^{\prime }},u^{i^{\prime }})\in {\mathcal{P}}_2(\mathbb{R}\times \mathcal{U})\times \mathbb{R}\times \mathcal{U}.\hfill \end{array}$$

Assumption 3. 

Under a feedback control structure of a society, there exists a measurable function $h^i$ such that $h^i:[0,t]\times C([0,t];\mathbb{R})\times \mathcal{U}\to \mathcal{U}$, for which $u^i\left(s\right)=h^i[x^i\left(s\right),u^i]$ ensures that Equation (2) admits a solution.

Remark 2. 

This assumption is standard in stochastic control theory, where feedback (or closed-loop) controls guarantee measurability and admissibility of control strategies [52,53]. In the context of social networks, feedback-type control structures capture the fact that agents adjust their opinions dynamically based on their current state and the observed states of their neighbors. Empirical and theoretical studies in opinion dynamics also support this modeling choice, since adaptive responses to social influence are more realistic than open-loop strategies [1,54,55]. Such assumptions have also been employed in the control of mean-field models and networked systems, where measurable feedback ensures both tractability and real-world interpretability [56].

Assumption 4. (i) Let $\mathcal{Z}$ denote the information (or knowledge) space of the society, assumed to be a measurable space. For each agent i, we define an information set ${\mathcal{Z}}_i\subseteq \mathcal{Z}$, which represents the collection of signals or knowledge available to agent i at time $s\in [0,t]$. The family ${\left\{{\mathcal{Z}}_i\right\}}_{i=1}^n$ is such that ${\mathcal{Z}}_i\ne {\mathcal{Z}}_j$ whenever $i\ne j$, reflecting heterogeneity in access to information across agents. Moreover, we assume that each ${\mathcal{Z}}_i$ is non-empty, measurable, and evolves monotonically with respect to time, i.e., ${\mathcal{Z}}_i\left(s_1\right)\subseteq {\mathcal{Z}}_i\left(s_2\right)$, whenever $s_1<s_2$.

(ii) The initial cost functional of the society is given by

$$L_0:[0,t]\times \mathbb{R}\times \mathcal{U}⟶\mathbb{R},$$

which is concave in its arguments. For each agent i, the individual cost functional is denoted $L_0^i:[0,t]\times \mathbb{R}\times \mathcal{U}\to \mathbb{R}$, satisfying $L_0^i\subseteq L_0$, and the concavity of $L_0^i$ is assumed. This condition is equivalent to the Slater condition (see [57]), ensuring feasibility and dual attainability in the associated optimization problem.

(iii) For each admissible control $u^i(·)\in \mathcal{U}\left([0,t]\right)$, there exists $ϵ>0$ sufficiently small, such that the quadratic form

$${\mathbb{E}}_0\left[{\int }_0^t{\displaystyle \frac{1}{2}}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left(x^i\left(s\right)-x^j\left(s\right)\right)}^2+k_i{\left(x^i\left(s\right)-x_0^i\right)}^2+{\left(u^i\left(s\right)\right)}^2\right\}ds\right]\ge ϵ,$$

holds for all $i=1,\dots ,n$ with $i\ne j$, where ${\mathbb{E}}_0[·]=\mathbb{E}[·|x_0^i]$. This ensures a uniform coercivity condition on the expected quadratic cost.

Remark 3. 

Assumption 4 reflects the realistic heterogeneity of information across agents in social networks, a feature emphasized in the literature on bounded confidence models, and Bayesian learning in networks [1]. The monotonicity of information sets formalizes the idea that knowledge is non-decreasing over time, consistent with cumulative learning models [58]. The concavity of the cost functional $L_0$ and its agent-specific restrictions $L_0^i$ parallels standard convex optimization assumptions (e.g., Slater condition), ensuring well-posedness of equilibrium and duality [57]. Finally, the uniform coercivity condition in (iii) is common in quadratic cost formulations of stochastic control and mean-field games [20,56], guaranteeing the stability of optimal strategies and preventing degenerate solutions.

Remark 4. 

Assumption 3 guarantees the possibility of at least one fixed point in the knowledge space. It is important to note that the agent makes decisions based on all available information. Then, the following Lemma 2 shows that the fixed point is indeed unique. Assumption 4 implies that each agent has some initial cost functional $L_0^i$ at the beginning of $[0,t]$, and the conditional expected cost functional ${\mathbb{E}}_0\left\{L^i\right\}$ is positive throughout this time interval.

Lemma 2. 

Suppose $i^{th}$ agent’s initial opinion $x_0^i\in G$ is independent of $B^i\left(s\right)$, and ${\mu }^i$ and ${\sigma }^i$ satisfy Assumptions 1 and 2. Then there exists a unique solution to opinion dynamics represented by the Equation (2) in ${\mathcal{H}}^{2,\tilde{m}}$. Moreover, there exists some positive constant $\widehat{c}$ on time t and Lipschitz constants ${\mu }^i$ and ${\sigma }^i$; the unique solution satisfies

$$\mathbb{E}\left\{\underset{s\in [0,t]}{sup}{\left|x^i\left(s\right)\right|}^2\right\}\le \widehat{c}(1+\mathbb{E}|x_0^i{|}^2)exp\left(\widehat{c}t\right),$$

for all $i=1,2,\dots ,n$.

Proof. 

See Appendix A. □

Remark 5. 

Lemma 2 guarantees that the stochastic opinion dynamics shown in Equation (2) exhibits a unique fixed point, and the expectation is bounded in the polish space G.

Assume the set of admissible strategies $\mathcal{U}\left(\right[0,t\left]\right)$ is convex and $u^i\in \mathcal{U}\left([0,t]\right)$. Define $x^{i\ast }\left(s\right):=x^{i\ast }(s,u^{i\ast })$ as the optimal opinion, which is the solution of Equation (2) with the initial opinion $x_0^i$. The first objective is to determine the Gâteaux derivative of the cost functional $L^i(s,\mathit{x},u^i)$ at $u^i$ in all directions. Consider another strategy $v^i$ such that $v^i\left(s\right)=u^{i^{\prime }}\left(s\right)-u^i\left(s\right)$ for another admissible strategy $u^{i^{\prime }}\in \mathcal{U}\left([0,t]\right)$. Hence, $v^i\in \mathcal{U}\left([0,t]\right)$. $v^i$ can be considered as the direction of the Gâteaux derivative of $L^i(s,\mathit{x},u^i)$ [59]. For every $ϵ>0$ small enough, define a strategy $u^{iϵ}\left(s\right)=u^i\left(s\right)+ϵv^i\left(s\right)$, and the corresponding controlled opinion vector ${\mathit{x}}^{ϵ}:={\mathit{x}}^{ϵ}(s,u^i)$. Furthermore, define the variational process $\mathfrak{V}={\left\{{\mathcal{V}}^i\left(s\right)\right\}}_{s=0}^t$ as the solution of the equation

$$\begin{array}{c}d{\mathcal{V}}^i\left(s\right)=\left[{\displaystyle \frac{\partial }{\partial x^i}}{\mu }^i(s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)){\mathcal{V}}^i\left(s\right)+\zeta \left(s,{\mathbb{P}}_{(x^i,{\mathcal{V}}^i)}\right)+{\displaystyle \frac{\partial }{\partial u^i}}{\mu }^i(s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right))\right]ds\hfill \\ \hfill +\left[{\displaystyle \frac{\partial }{\partial x^i}}{\sigma }^i(s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)){\mathcal{V}}^i\left(s\right)+\widehat{\zeta }\left(s,{\mathbb{P}}_{(x^i,{\mathcal{V}}^i)}\right)+{\displaystyle \frac{\partial }{\partial u^i}}{\sigma }^i(s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right))\right]d{B}^i\left(s\right),\end{array}$$

(3)

where

$$\zeta (.)=\tilde{\mathbb{E}}\left\{{\displaystyle \frac{\partial }{\partial \gamma }}{\mu }^i(s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right))\left({\tilde{x}}^i\left(s\right)\right).{\widehat{\mathcal{V}}}^i\left(s\right){|}_{x^i=x^i\left(s\right),u^i=u^i\left(s\right)}\right\},$$

and

$$\widehat{\zeta }(.)=\tilde{\mathbb{E}}\left\{{\displaystyle \frac{\partial }{\partial \gamma }}{\sigma }^i(s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right))\left({\tilde{x}}^i\left(s\right)\right).{\widehat{\mathcal{V}}}^i\left(s\right){|}_{x^i=x^i\left(s\right),u^i=u^i\left(s\right)}\right\}$$

with $\{{\tilde{x}}^i\left(s\right),{\widehat{\mathcal{V}}}^i\left(s\right)\}$ being an independent copy of $\{x^i\left(s\right),{\mathcal{V}}^i\left(s\right)\}$. A Fréchet differentiability has been used to define $\tilde{\mathbb{E}}$. This type of functional analytic differentiability was introduced by Pierre Lions at the Collége de France [50,59]. This is a type of differentiability based on the lifting of functions ${\mathcal{P}}_2\left({\mathbb{R}}^n\right)\ni \gamma \hookrightarrow \mathcal{H}\left(\gamma \right)$ into functions $\widehat{\mathcal{H}}$ defined on Hilbert space ${\mathcal{H}}^{2,\tilde{m}}(\tilde{\mathrm{\Omega }};{\mathbb{R}}^n)$ on some probability space $(\tilde{\mathrm{\Omega }},\tilde{\mathcal{F}},\tilde{\mathbb{P}})$ after setting $\widehat{\mathcal{H}}\left(\tilde{\mathit{x}}\right)=\mathcal{H}\left({\tilde{\mathbb{P}}}_{\tilde{\mathit{x}}}\right)$ for all $\tilde{\mathit{x}}\in {\mathcal{H}}^{2,\tilde{m}}(\tilde{\mathrm{\Omega }};{\mathbb{R}}^n)$, with $\tilde{\mathrm{\Omega }}$ being a Polish space and $\tilde{\mathbb{P}}$ an atomless measure [50]. Since there are n number of agents in the system, such that $n\to \infty$, instead of considering the opinions of the other agents, agent i considers the distribution of all opinions in the system $\mathcal{H}\left({\tilde{\mathbb{P}}}_{\tilde{\mathit{x}}}\right)$ and makes their opinions. Therefore, in this case the distribution function of opinions $\mathcal{H}$ is said to be differentiable at $\overline{\gamma }\in {\mathcal{P}}_2\left({\mathbb{R}}^n\right)$ if there exists a set of random opinions ${\tilde{\mathit{x}}}_{*}$ with probability distribution $\overline{\gamma }$ (i.e., ${\tilde{\mathbb{P}}}_{{\tilde{\mathit{x}}}_{*}}=\overline{\gamma }$). The Fréchet derivative of $\widehat{\mathcal{H}}$ at ${\tilde{\mathit{x}}}_{*}$ is the element of Hilbert space ${\mathcal{H}}^{2,\tilde{m}}(\tilde{\mathrm{\Omega }};{\mathbb{R}}^n)$ by identifying itself and its dual [50]. One important aspect of the Fréchet differentiation in this type of environment is that the distribution of the derivative depends on $\overline{\gamma }$, not on ${\tilde{\mathit{x}}}_{*}$. The Fréchet derivative of $\mathcal{H}$ is

$$\mathcal{H}\left(\gamma \right)=\mathcal{H}\left(\widehat{\gamma }\right)+\left[D_f\widehat{\mathcal{H}}\right]\left({\tilde{\mathit{x}}}_{*}\right).(\tilde{\mathit{x}}-{\tilde{\mathit{x}}}_{*})+o\left(\parallel \tilde{\mathit{x}}-{\tilde{\mathit{x}}}_{*}{\parallel }_2\right),$$

where $\left[D_f\widehat{\mathcal{H}}\right]\left({\tilde{\mathit{x}}}_{*}\right)$ is the Fréchet derivative, the dot is the inner product of the Hilbert space over $(\tilde{\mathrm{\Omega }},\tilde{\mathcal{F}},\tilde{\mathbb{P}})$, and ${\parallel .\parallel }_2$ is a norm of that Hilbert space. For a deterministic function $\tilde{g}:{\mathbb{R}}^n\hookrightarrow {\mathbb{R}}^n$, it is well understood that the Fréchet derivative of the form $\tilde{g}\left({\tilde{\mathit{x}}}_{*}\right)$ is uniquely defined $\widehat{\gamma }$ almost everywhere in $\mathbb{R}$ [59,60]. The unique equivalence class of $\tilde{g}$ is denoted by ${\partial }_{\gamma }\mathcal{H}\left(\overline{\gamma }\right)$. ${\partial }_{\gamma }\mathcal{H}\left(\overline{\gamma }\right)$ is the partial derivative of $\mathcal{H}$ at $\overline{\gamma }$, such that

$${\partial }_{\gamma }\mathcal{H}\left(\overline{\gamma }\right)(.):{\mathbb{R}}^n\hookrightarrow {\partial }_{\gamma }\mathcal{H}\left(\overline{\gamma }\right)\left(y\right)\in {\mathbb{R}}^n.$$

The partial derivative ${\partial }_{\gamma }\mathcal{H}\left(\overline{\gamma }\right)$ allows one to express the Fréchet derivative $\left[D_f\widehat{\mathcal{H}}\right]\left({\tilde{\mathit{x}}}_{*}\right)$ as a function of any random variable ${\tilde{\mathit{x}}}_{*}$ with its law $\overline{\gamma }$, irrespective of the definition of ${\tilde{\mathit{x}}}_{*}$. If $\mathcal{H}\left(\gamma \right)={\int }_{{\mathbb{R}}^n}g\left(y\right)\gamma \left(dy\right)=\langle g,\gamma \rangle$ for some scalar differentiable function g on ${\mathbb{R}}^n$. Here, $\widehat{\mathcal{H}}\left(\tilde{\mathit{y}}\right)=\tilde{\mathbb{E}}\left[g\left(\tilde{\mathit{y}}\right)\right]$ and $D_f\widehat{\mathcal{H}}\left(\tilde{\mathit{y}}\right).\left(\tilde{\mathit{x}}\right)=\tilde{\mathbb{E}}[\partial g\left(\tilde{\mathit{y}}\right).\left(\tilde{\mathit{x}}\right)]$, where ${\partial }_{\gamma }\mathcal{H}\left(\gamma \right)$ is thought to be a deterministic function $\partial g$ [50].

Lemma 3. 

For a small $ϵ>0$, the admissible strategy $u^{iϵ}$ defined as $u^{iϵ}\left(s\right)=u^i\left(s\right)+ϵv^i\left(s\right)$, with the opinion of agent i as ${\mathit{x}}^{ϵ}:={\mathit{x}}^{ϵ}(s,u^i)$, the following condition holds

$$\underset{ϵ\to 0}{lim}\mathbb{E}\left\{\underset{s\in [0,t]}{sup}\left|{\mathcal{V}}^i\left(s\right)-{\displaystyle \frac{x^{iϵ}\left(s\right)-x^i\left(s\right)}{ϵ}}\right|\right\}=0,$$

where $x^{iϵ}\left(s\right)\in {\mathit{x}}^{ϵ}$ is agent i’s opinion at time s coming from the set of all opinions in the environment.

Proof. 

See Appendix A. □

Remark 6. 

Based on Assumptions 1–3, Lemma 3 guarantees the existence and the uniqueness of ${\mathcal{V}}^i\left(s\right)$. Furthermore, for any $\varrho \in [1,\infty )$ this ${\mathcal{V}}^i\left(s\right)$ satisfies $\mathbb{E}\left\{{sup}_{s\in [0,t]}{\left|{\mathcal{V}}^i\left(s\right)\right|}^{\varrho }\right\}<\infty$. Above Lemma 3 in some Hilbert space ${\mathcal{H}}^{2,\tilde{m}}$, ${\mathcal{V}}^i\left(s\right)$ is derivative of the opinion driven by $i^{th}$ agent’s strategy when the direction of the derivative $v^i\left(s\right)$ is changed.

Lemma 4. 

For $ϵ>0$ small enough and the time interval $[s,s+ϵ]\subset [0,t]$, there exists some $\delta \in [0,ϵ)$ so that the admissible strategy function of agent i denoted as $u^i\left(s\right)\hookrightarrow L^i(s,\mathit{x},u^i)$ is Gâteaux differentiable and

$${\displaystyle \frac{\partial }{\partial \delta }}{L}^i(s,\mathit{x},u^i){|}_{\delta =0}={\mathbb{E}}_s\left\{{\int }_s^{s+ϵ}\left[{\mathcal{V}}^i\left(\nu \right)\sum _{j\in {\eta }_i}\left(w_{ij}\left[x^i\left(\nu \right)-x^j\left(\nu \right)\right]+k_i\left[x^i\left(\nu \right)-x_0^i\right]\right)+u^i\left(\nu \right)v^i\left(\nu \right)\right]d\nu \right\},$$

where ${\mathbb{E}}_s\{.\}=\mathbb{E}\{.|x^i\left(s\right)\}$ for all $\nu \in [s,s+ϵ]$.

Proof. 

See Appendix A. □

Remark 7. 

The above Lemma determines the directional derivative of the cost functional $L^i(s,\mathit{x},u^i)$ for some $ϵ>0$ small enough, $[s,s+ϵ]\subset [0,t]$.

5. The Lagrangian and the Adjoint Processes

Let for $s\in [0,t]$, $g\left(s\right):[p,q]\to \mathcal{C}$ be an opinion dynamics of $i^{th}$ agent with initial and terminal points $g\left(p\right)$ and $g\left(q\right)$, respectively, such that the line path integral is ${\int }_{\mathcal{C}}f\left(\gamma \right)ds={\int }_p^{q}f\left(g\left(s\right)\right)\left|g^{\prime }\left(s\right)\right|ds$, where $g^{\prime }\left(s\right)=\partial g\left(s\right)/\partial s$. In this paper, a functional path integral approach is considered where the domain of the integral is assumed to be the space of functions [36]. In [61], theoretical physicist Richard Feynman introduced the Feynman path integral and popularized it in quantum mechanics. Furthermore, mathematicians developed the measurability of this functional integral, and in recent years it has become popular in probability theory [49]. In quantum mechanics, when a particle moves from one point to another, between those points it chooses the shortest path out of infinitely many paths, such that some of them touch the edge of the universe. After introducing n number of small intervals of equal length $[s,s+ϵ]\subset [0,t]$ with $ϵ>0$ small enough, and using the Riemann–Lebesgue lemma if at time s one particle touches the end of the universe, then at a later time point it would come back and go to the opposite side of the previous direction to make the path integral a measurable function [62]. Similarly, since agent i has infinitely many opinions, they choose the opinion associated with least cost given by the constraint explained in Equation (2). Furthermore, the Feynman approach is useful in both linear and non-linear stochastic differential equation systems where constructing an HJB equation numerically is quite difficult [35].

Definition 1. 

For a particle, let $\widehat{\mathcal{L}}[s,y\left(s\right),\dot{y}\left(s\right)]=(1/2)\widehat{m}\dot{y}{\left(s\right)}^2-\widehat{V}\left(y\right)$ be the Lagrangian in the classical sense in generalized coordinate y with mass $\widehat{m}$, where $(1/2)\widehat{m}{\dot{y}}^2$ and $\widehat{V}\left(y\right)$ are kinetic and potential energies, respectively. The transition function of the Feynman path integral corresponding to the classical action function $Z^{*}={\int }_0^t\widehat{\mathcal{L}}(s,y\left(s\right),\dot{y}\left(s\right))ds$ is defined as $\mathrm{\Psi }\left(y\right)={\int }_{\mathbb{R}}exp\left\{Z^{*}\right\}{\mathcal{D}}_Y$, where $\dot{y}=\partial y/\partial s$ and ${\mathcal{D}}_Y$ is an approximated Riemann measure that represents the positions of the particle at different time points s in $[0,t]$ [36].

Remark 8. 

Definition 1 describes the construction of the Feynman path integral in a physical sense. This definition is important to construct the stochastic Lagrangian of agent i.

From Equation (45) of [63] for agent i, the stochastic Lagrangian at time $s\in [0,t]$ is defined as

$$\begin{array}{c}{\widehat{\mathcal{L}}}^i\left(s,\mathit{x},{\mathbb{P}}_{\left(\mathit{x}\right)},{\lambda }^i,u^i\right)={\mathbb{E}}_0\{{\displaystyle \frac{1}{2}}{\int }_0^t\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(s\right)-x^j\left(s\right)\right]}^2+k_i{\left[x^i\left(s\right)-x_0^i\right]}^2+{\left[u^i\left(s\right)\right]}^2\right\}ds\hfill \\ \hfill +{\int }_0^t\left[x^i\left(s\right)-x_0^i-{\int }_0^s[{\mu }^i[\nu ,x^i\left(\nu \right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(\nu \right)]d\nu -{\sigma }^i[\nu ,x^i\left(\nu \right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(\nu \right)]d{B}^i\left(\nu \right)]\right]d{\lambda }^i\left(s\right)\},\end{array}$$

(4)

where ${\lambda }^i\left(s\right)$ is the Lagrangian multiplier and ${\mathbb{E}}_0=\mathbb{E}\{.|x_0^i\}$.

Proposition 1 

([63,64]). Suppose for agent i, $u^{i\ast }\left(s\right)$ is an admissible strategy and $x^{i\ast }\left(s\right)$ is the corresponding opinion. Furthermore, assume that there exists a progressively measurable Lagrangian multiplier ${\lambda }^{i\ast }\left(s\right)$ so that following two conditions hold:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathcal{L}}^i}{\partial x^i}}\left[s,{\mathit{x}}^{*}\left(s\right),{\mathbb{P}}_{\left({\mathit{x}}^{*}\right)},{\lambda }^{i\ast }\left(s\right),u^{i\ast }\left(s\right)\right]& =0,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathcal{L}}^i}{\partial u^i}}\left[s,{\mathit{x}}^{*}\left(s\right),{\mathbb{P}}_{\left({\mathit{x}}^{*}\right)},{\lambda }^{i\ast }\left(s\right),u^{i\ast }\left(s\right)\right]& =0.\hfill \end{array}$$

(6)

Moreover, assume that the mapping

$$(x^i,u^i)\mapsto L^i(s,\mathit{x},u^i)+{\mu }^i[\nu ,x^i,{\mathbb{P}}_{\left(x^i\right)},u^i]{\lambda }^{i\ast }\left(s\right)+{\sigma }^i[\nu ,x^i,{\mathbb{P}}_{\left(x^i\right)},u^i]{\displaystyle \frac{d{\lambda }^{i\ast }\left(s\right)dB\left(s\right)}{ds}},$$

(7)

is almost surely concave in $s\in [0,t]$. Therefore, the admissible strategy $u^{i\ast }\left(s\right)$ is an optimal strategy of agent i.

Remark 9. 

Following [63], we know that if $u^{i\ast }$ is the solution of the system represented by Equations (1) and (2) and Condition 7, then there exists a progressively measurable Itô process ${\lambda }^{i\ast }\left(s\right)$, such that Equations (5) and (6) hold. In Proposition 1, the Lagrangian multiplier ${\lambda }^{i\ast }\left(s\right)$ is indeed a progressively measurable process.

Since at the beginning of the continuous interval $[s,s+ϵ]$ for all $ϵ\downarrow 0$, agent i does not have any future information to build their opinion. Thus, ${\mathbb{E}}_{[s,s+ϵ]}\{.\}\simeq {\mathbb{E}}_s\{.\}=\mathbb{E}\{.|x^i\left(s\right)\}$. Furthermore, as $ϵ\downarrow 0$, the Lagrangian expressed in Equation (4) becomes

$$\begin{array}{cc}\hfill {\mathcal{L}}^i\left(s,\mathit{x},{\mathbb{P}}_{\left(\mathit{x}\right)},{\lambda }^i,u^i\right)& :=\underset{ϵ\downarrow 0}{lim}{\mathbb{E}}_s\{{\displaystyle \frac{1}{2}}{\int }_s^{s+ϵ}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(\nu \right)-x^j\left(\nu \right)\right]}^2+k_i{\left[x^i\left(\nu \right)-x_0^i\right]}^2+{\left[u^i\left(\nu \right)\right]}^2\right\}d\nu \hfill \\ \hfill & +{\int }_s^{s+ϵ}\left[x^i\left(\nu \right)-x_0^i-{\int }_s^{\nu }[{\mu }^i[\widehat{\nu },x^i\left(\widehat{\nu }\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(\widehat{\nu }\right)]d\widehat{\nu }-{\sigma }^i[\widehat{\nu },x^i\left(\widehat{\nu }\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(\widehat{\nu }\right)]d{B}^i\left(\widehat{\nu }\right)]\right]d{\lambda }^i\left(\nu \right)\}\hfill \\ \hfill & \approx {\mathbb{E}}_s\{{\displaystyle \frac{1}{2}}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(s\right)-x^j\left(s\right)\right]}^2+k_i{\left[x^i\left(s\right)-x_0^i\right]}^2+{\left[u^i\left(s\right)\right]}^2\right\}ds\hfill \\ \hfill & +\left[x^i\left(s\right)-x_0^i-{\mu }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]-{\sigma }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]\right]d{\lambda }^i\left(s\right)\},\hfill \end{array}$$

(8)

where $[s,\nu ]\subset [s,s+ϵ]$.

The adjoint process of the system is

$$d{\lambda }_1^i\left(s\right)=-\left[{\displaystyle \frac{\partial }{\partial x}}{\mu }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]{\lambda }_1^i\left(s\right)+{\displaystyle \frac{\partial }{\partial x}}{\sigma }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]{\lambda }_1^i\left(s\right)+{\displaystyle \frac{\partial }{\partial x}}{L}^i(s,\mathit{x},u^i)\right]ds+{\lambda }_2^i\left(s\right)d{B}^i\left(s\right),$$

(9)

where ${\lambda }_1^i\left(s\right)$ and ${\lambda }_2^i\left(s\right)$ are two new dual variables belong to the dual spaces of the spaces from where ${\mu }^i$ and ${\sigma }^i$ take their values, such that ${\lambda }_1^i\in \mathbb{R}$ like $x^i$, and that ${\lambda }_2^i\in {\mathbb{R}}^2$. Notice that the deterministic Hamiltonian of the system is

$$H^i\left(s,\mathit{x},{\mathbb{P}}_{\left(\mathit{x}\right)},{\lambda }_1^i,{\lambda }_2^i,u^i\right)=L^i(s,\mathit{x},u^i)+{\lambda }_1^i\left(s\right){\mu }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]+{\lambda }_2^i\left(s\right){\sigma }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)].$$

The differences between the above Hamiltonian and Equation (4) are the presence of $\mathrm{\Delta }{x}^i\left(s\right):=x^i\left(s\right)-x_0^i$, ${\lambda }^i\left(s\right)$, ${\mathbb{E}}_s\{.\}$, $ds$ and $d{B}^i\left(s\right)$. If $\mathrm{\Delta }{x}^i\left(s\right)\to 0$, under the deterministic case, the Hamiltonian and Lagrangian share a similar structure. Since the Feynman path integral approach has been used, $d{B}^i\left(s\right)$ determines the true fluctuation of ${\mathcal{L}}^i$, and further inclusion of ${\mathbb{E}}_s$ facilitates the conditional expectation of a forward looking process for $[s,s+ϵ]$. The Lagrangian used in Equation (4) is stochastic, but the usual Hamiltonian of the control theory is deterministic.

Definition 2. 

For a set of admissible strategies ${\mathit{u}}^i={\left\{u^i\left(s\right)\right\}}_{s=0}^t\in \mathcal{U}\left([0,t]\right)$ of agent i, denote ${\mathit{x}}^i\left(s\right)={\mathit{x}}^i(s,u^i)$ the set of corresponding controlled opinions, and let $({\mathit{\lambda }}_1^i,{\mathit{\lambda }}_2^i)={\{{\lambda }_1^i\left(s\right),{\lambda }_2^i\left(s\right)\}}_{s=0}^t$ be any coupled adjoint progressively measurable stochastics processes satisfying

$$d{\lambda }_1^i\left(s\right)=-{\partial }_x{H}^i(s,\mathit{x},{\mathbb{P}}_{\mathit{x}},{\lambda }_1^i,{\lambda }_2^i,u^i)+{\lambda }_2^i\left(s\right)d{B}^i\left(s\right)-\tilde{\mathbb{E}}\left[{\partial }_{\gamma }{\tilde{H}}^i(s,\tilde{\mathit{x}},{\mathbb{P}}_{\tilde{\mathit{x}}},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i)\right]\left[x^i\left(s\right)\right],$$

where $(\tilde{\mathit{x}},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i,{\tilde{\mathcal{L}}}^i)$ is the independent copy of $(\mathit{x},{\lambda }_1^i,{\lambda }_2^i,u^i,{\mathcal{L}}^i)$ and $\tilde{\mathbb{E}}$ is the expectation of the independent copy. In the adjoint equation, ${\partial }_x=\partial /\partial x$ and ${\partial }_{\gamma }=\partial /\partial \gamma$.

Remark 10. 

If ${\mu }^i$ and ${\sigma }^i$ are independent with the marginal distributions of the process, the extra terms appearing in the adjoint equation in Definition 2 vanishes, and indeed this equation becomes the classical adjoint equation.

In the present setup, the adjoint equation can be written as

$$\begin{array}{c}d{\lambda }_1^i\left(s\right)=-\left[{\partial }_x{\mu }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]{\lambda }_1^i\left(s\right)+{\partial }_x{\sigma }^i[s,x^i\left(s\right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(s\right)]{\lambda }_1^i\left(s\right)\right]ds+{\partial }_x{L}^i(s,\mathit{x},u^i)+{\lambda }_2^i\left(s\right)d{B}^i\left(s\right)\hfill \\ \hfill -\tilde{\mathbb{E}}\left\{\left[{\partial }_{\gamma }{\tilde{\mu }}^i\left((s,\tilde{\mathit{x}},\mathit{x},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i)\right)+{\partial }_{\gamma }{\tilde{\sigma }}^i(s,\tilde{\mathit{x}},\mathit{x},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i)\right]ds+{\partial }_{\gamma }{\tilde{L}}^i(s,\tilde{\mathit{x}},\mathit{x},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i){|}_{\mathit{x}=\mathit{x}\left(s\right)}\right\}.\end{array}$$

It is important to note that for a given admissible strategy $u^i\in \mathcal{U}\left([0,t]\right)$ and the controlled opinion $x^i$, despite the boundedness assumptions of the partial derivatives of ${\mu }^i$ and ${\sigma }^i$, and despite that the first part of the above adjoint equation is linear with respect to ${\lambda }_1^i\left(s\right)$ and ${\lambda }_2^i\left(s\right)$, the existence and uniqueness of a solution $\{{\mathit{\lambda }}_1^{i\ast },{\mathit{\lambda }}_2^{i\ast }\}$ of the adjoint equation cannot be determined by the standard process (for example, Theorem 2.2 in [59]). The main reason for this is that the joint distribution of the solution process appears in ${\mu }^i$ and ${\sigma }^i$ [50,59].

Lemma 5. 

Under (v) of Assumption 2, there exists a unique adapted solution $({\mathit{\lambda }}_1^{i\ast },{\mathit{\lambda }}_2^{i\ast })$ of the coupled adjoint progressively measurable stochastics processes, satisfying

$$d{\lambda }_1^i\left(s\right)=-{\partial }_x{\mathcal{L}}^i(s,\mathit{x},{\mathbb{P}}_{\left(\mathit{x}\right)},{\lambda }_1^i,{\lambda }_2^i,u^i)+{\lambda }_2^i\left(s\right)d{B}^i\left(s\right)-\tilde{\mathbb{E}}\left[{\partial }_{\gamma }{\tilde{\mathcal{L}}}^i(s,\tilde{\mathit{x}},{\mathbb{P}}_{\left(\tilde{\mathit{x}}\right)},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i)\right]\left[x^i\left(s\right)\right],$$

in ${\mathcal{H}}_{{\mathit{\lambda }}_1}^{2,\tilde{m}}⨂{\mathcal{H}}_{{\mathit{\lambda }}_2}^{2,\tilde{m}}$, where

$${\mathcal{H}}_{{\mathit{\lambda }}_1}^{2,\tilde{m}}:=\left\{{\mathit{\lambda }}_1^i\in {\mathcal{H}}_{{\mathit{\lambda }}_1}^{0,\tilde{m}};\mathbb{E}{\int }_0^t{\left|{\lambda }_1^i\left(s\right)\right|}^{2}ds<\infty \right\},$$

and

$${\mathcal{H}}_{{\mathit{\lambda }}_2}^{2,\tilde{m}}:=\left\{{\mathit{\lambda }}_2^i\in {\mathcal{H}}_{{\mathit{\lambda }}_1}^{0,\tilde{m}};\mathbb{E}{\int }_0^t{\left|{\lambda }_2^i\left(s\right)\right|}^{2}ds<\infty \right\}.$$

Sketch of Proof. 

Here we provide the sketch of the proof. Details are discussed in Appendix A. We first define the weighted norm,

$$\parallel ({\lambda }_1^i,{\lambda }_2^i){\parallel }_{\rho }^2:=\mathbb{E}\left[{\int }_0^t\left(|{\lambda }_1^i{\left(s\right)|}^2+{\left|{\lambda }_2^i\left(s\right)\right|}^2\right)exp\left(\rho s\right)ds\right],\rho >0.$$

For a candidate pair $({\lambda }_1^{i\#},{\lambda }_2^{i\#})\in {\mathcal{H}}^{2,\tilde{m}}$, Proposition 2.2 of [65] and Theorem 2.2 of [59] ensure the existence of a solution $({\lambda }_1^i,{\lambda }_2^i)$ to the adjoint equation

$$\begin{array}{c}d{\lambda }_1^i\left(s\right)=-{\partial }_x{\mathcal{L}}^i\left(s,\mathit{x},{\mathbb{P}}_{\mathit{x}},{\lambda }_1^{i\#},{\lambda }_2^{i\#},{\lambda }_1^i,{\lambda }_2^i,u^i\right)ds+{\lambda }_2^i\left(s\right)d{B}^i\left(s\right)\hfill \\ \hfill -\tilde{\mathbb{E}}\left[{\partial }_{\gamma }{\tilde{\mathcal{L}}}^i(s,\tilde{\mathit{x}},{\mathbb{P}}_{\tilde{\mathit{x}}},{\lambda }_1^{i\#},{\lambda }_2^{i\#},{\tilde{\lambda }}_1^i,{\tilde{\lambda }}_2^i,{\tilde{u}}^i)\right]\left[x^i\left(s\right)\right].\end{array}$$

This defines a mapping $M:({\lambda }_1^{i\#},{\lambda }_2^{i\#})\mapsto ({\lambda }_1^i,{\lambda }_2^i)$ on ${\mathcal{H}}^{2,\tilde{m}}$. To establish uniqueness, let $({\lambda }_1^{i1},{\lambda }_2^{i1})=M({\lambda }_1^{i\#1},{\lambda }_2^{i\#1})$ and $({\lambda }_1^{i2},{\lambda }_2^{i2})=M({\lambda }_1^{i\#2},{\lambda }_2^{i\#2})$. Denote the differences

$${\tilde{\lambda }}_1^i:={\lambda }_1^{i2}-{\lambda }_1^{i1},{\tilde{\lambda }}_2^i:={\lambda }_2^{i2}-{\lambda }_2^{i1},{\tilde{\lambda }}_1^{i\#}:={\lambda }_1^{i\#2}-{\lambda }_1^{i\#1},{\tilde{\lambda }}_2^{i\#}:={\lambda }_2^{i\#2}-{\lambda }_2^{i\#1}.$$

Applying Itô’s formula to $|{\tilde{\lambda }}_1^i{\left(s\right)|}^{2}exp\left(\rho s\right)$ yields the estimate

$$\mathbb{E}\left[{\int }_0^t{e}^{\rho s}\left(|{\tilde{\lambda }}_1^i{\left(s\right)|}^2+{|{\tilde{\lambda }}_2^i\left(s\right)|}^2\right)ds\right]\le {\displaystyle \frac{C}{\rho }}\mathbb{E}\left[{\int }_0^t{e}^{\rho s}\left(|{\tilde{\lambda }}_1^{i\#}{\left(s\right)|}^2+{|{\tilde{\lambda }}_2^{i\#}\left(s\right)|}^2\right)ds\right],$$

where $C>0$ depends on the Lipschitz constants of the derivatives of ${\mu }^i,{\sigma }^i,L^i$ from Assumption (v). Choosing $\rho$ sufficiently large ensures $\frac{C}{\rho }<1$, i.e., M is a contraction under ${\parallel ·\parallel }_{\rho }$.

By the Banach fixed point theorem, there exists a unique fixed point $({\mathit{\lambda }}_1^{i\ast },{\mathit{\lambda }}_2^{i\ast })\in {\mathcal{H}}_{{\mathit{\lambda }}_1}^{2,\tilde{m}}\otimes {\mathcal{H}}_{{\mathit{\lambda }}_2}^{2,\tilde{m}}$, which is the unique adapted solution of the adjoint system. □

Remark 11. 

Lemma 5 states that for each admissible strategy $u^i$, there exists a couple of adjoint processes $\left({\mathit{\lambda }}_1^i,{\mathit{\lambda }}_2^i\right)$ so that $\mathbb{E}\left\{{sup}_{s\in [0,t]}{\left|{\lambda }_1^i\left(s\right)\right|}^2\right\}+\mathbb{E}\left\{{\int }_0^t{\left|{\lambda }_2^i\left(s\right)\right|}^{2}ds\right\}$.

For a normalizing constant $L_{ϵ}^i>0$, define a transition function from s to $s+ϵ$ as

$${\mathrm{\Psi }}_{s,s+\epsilon }^i\left(x^i\right):={\displaystyle \frac{1}{L_{\epsilon }^i}}{\int }_{{\mathbb{R}}^n}exp[-\epsilon {\mathcal{A}}_{s,s+\epsilon }\left(x^i\right)]{\mathrm{\Psi }}_s^i\left(x^i\right)d{x}^i\left(s\right),$$

(10)

where ${\mathrm{\Psi }}_s^i\left(x^i\right)$ is the value of the transition function based on opinion $x^i$ at time s with the initial condition ${\mathrm{\Psi }}_0^i\left(x^i\right)={\mathrm{\Psi }}_0^i$. The penalization constant $L_{ϵ}^i$ is chosen in such a way that the right hand side of the expression (10) becomes unity. Therefore, the action function of agent i in time interval $[s,s+ϵ]$ is

$$\begin{array}{c}\hfill {\mathcal{A}}_{s,s+\epsilon }\left(x^i\right)={\int }_s^{s+\epsilon }{\mathbb{E}}_{\nu }\{{\displaystyle \frac{1}{2}}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(\nu \right)-x^j\left(\nu \right)\right]}^2+k_i{\left[x^i\left(\nu \right)-x_0^i\right]}^2+{\left[u^i\left(\nu \right)\right]}^2\right\}d\nu +h^i[\nu +\mathrm{\Delta }\nu ,x^i\left(\nu \right)+\mathrm{\Delta }{x}^i\left(\nu \right)]d{\lambda }^i\left(\nu \right)\},\end{array}$$

where $h^i[\nu +\mathrm{\Delta }\nu ,x^i\left(\nu \right)+\mathrm{\Delta }{x}^i\left(\nu \right)]\in C^2([0,t]\times \mathbb{R})$ is an Itô process so that,

$$h^i[\nu +\mathrm{\Delta }\nu ,x^i\left(\nu \right)+\mathrm{\Delta }{x}^i\left(\nu \right)]\approx x^i\left(\nu \right)-x_0^i-{\mu }^i[\nu ,x^i\left(\nu \right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(\nu \right)]d\nu -{\sigma }^i[\nu ,x^i\left(\nu \right),{\mathbb{P}}_{\left(x^i\right)},u^i\left(\nu \right)]d{B}^i\left(\nu \right).$$

It is important to note that the implicit form of the McKean–Vlasov SDE is replaced by an Itô process. The action ${\mathcal{A}}_{s,s+ϵ}\left(x^i\right)$ tells us that within $[s,s+ϵ]$ the action of agent i depends on their opinion $x^i$ under a feedback structure.

Definition 3. 

For optimal opinion $x^{i\ast }\left(s\right)$ there exists an optimal admissible control $u^{i\ast }\left(s\right)$, such that for all $s\in [0,t]$ the conditional expectation of the cost function is

$$\begin{array}{c}{\mathbb{E}}_0\left[{\int }_0^t{\displaystyle \frac{1}{2}}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^{i\ast }\left(s\right)-x^{j\ast }\left(s\right)\right]}^2+k_i{\left[x^{i\ast }\left(s\right)-x_0^i\right]}^2+{\left[u^{i\ast }\left(s\right)\right]}^2\right\}ds|{\mathcal{F}}_0^{x^{\ast }}\right]\hfill \\ \hfill \ge {\mathbb{E}}_0\left[{\int }_0^t{\displaystyle \frac{1}{2}}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(s\right)-x^j\left(s\right)\right]}^2+k_i{\left[x^i\left(s\right)-x_0^i\right]}^2+{\left[u^i\left(s\right)\right]}^2\right\}ds|{\mathcal{F}}_0^x\right],\end{array}$$

such that Equation (2) holds, where ${\mathcal{F}}_0^{x^{\ast }}$ is the optimal filtration satisfying ${\mathcal{F}}_0^{x^{\ast }}\subset {\mathcal{F}}_0^x$.

6. Main Results

Consider that, for an opinion space $X_0=\{\mathit{x}\left(s\right):s\in [0,t]\}$ and agent i’s control space $\mathcal{U}$, there exists an admissible control $u^i:[0,t]\times X_0\to \mathcal{U}$, and for all $i\in N$ define the integrand of the cost function $L^i(.)$ as

$$L^i(s,\mathit{x},u^i)=\mathbb{E}\left\{{\displaystyle \frac{1}{2}}{\int }_0^t\left(\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(s\right)-x^j\left(s\right)\right]}^2+k_i{\left[x^i\left(s\right)-x_0^i\right]}^2+{\left[u^i\left(s\right)\right]}^2\right)ds\right\}.$$

Proposition 2. 

For agent i

• (i). The feedback control $u^i(s,x^i):[0,t]\times \mathbb{R}\times \mathcal{U}\to \mathcal{U}$ is a continuously differentiable function,
• (ii). The cost functional $L^i(s,\mathit{x},u^i):[0,t]\times {\mathbb{R}}^n\times \mathbb{R}\to \mathbb{R}$ is smooth on $\mathbb{R}\times \mathcal{U}$.
• (iii). If $X_0=\{\mathit{x}\left(s\right),s\in [0,t]\}$ is an opinion trajectory of agent i, then the feedback Nash equilibrium $\left\{u^{i\ast }(s,x^i)\in \mathcal{U};i\in N\right\}$ would be the solution of the following equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial u^i}}{f}^i(s,\mathit{x},u^i){\left[{\displaystyle \frac{{\partial }^2}{\partial {\left(x^i\right)}^2}}{f}^i(s,\mathit{x},u^i)\right]}^2=2{\displaystyle \frac{\partial }{\partial x^i}}{f}^i(s,\mathit{x},u^i){\displaystyle \frac{{\partial }^2}{\partial x^i\partial u^i}}{f}^i(s,\mathit{x},u^i),\end{array}$$

(11)

where, for an Itô process $h^i(s,x^i)\in [0,t]\times {\mathcal{P}}_2\left(\mathbb{R}\right)\times \mathbb{R}$

$$\begin{array}{cc}\hfill f^i(s,\mathit{x},\gamma ,u^i)& =L^i(s,\mathit{x},u^i)+h^i(s,x^i)d{\lambda }^i\left(s\right)+\left[{\displaystyle \frac{\partial h^i(s,x^i)}{\partial s}}d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}{h}^i(s,x^i)\right]\hfill \\ \hfill & +{\displaystyle \frac{\partial h^i(s,x^i)}{\partial x^i}}{\mu }^i\left[s,x^i,{\mathbb{P}}_{\left(x^i\right)},u^i\right]d{\lambda }^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left[{\sigma }^i\left[s,x^i,{\mathbb{P}}_{\left(x^i\right)},u^i\right]\right]}^2{\displaystyle \frac{{\partial }^2{h}^i(s,x^i)}{\partial {\left(x^i\right)}^2}}d{\lambda }^i\left(s\right).\hfill \end{array}$$

(12)

Proof. 

See Appendix A. □

Remark 12. 

The central idea of Proposition 2 is to choose $h^i$ appropriately. Therefore, one natural candidate should be a function of the integrating factor of the stochastic opinion dynamics represented in Equation (2).

To demonstrate the preceding proposition, we present a detailed example to identify an optimal strategy in McKean–Vlasov SDEs and the corresponding systems of interacting particles. Specifically, we examine a stochastic opinion dynamics model involving six unknown parameters. To construct this example, we are going to combine the equations from [66,67,68]. Following [67], consider a one-dimensional stochastic opinion dynamics model, parameterized by $\theta ={({\theta }_1,{\theta }_2)}^T\in {\mathbb{R}}^2$ of the form

$$d{x}^i\left(s\right)=-\left[{\int }_{\mathbb{R}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]\gamma d\left(x^j\right)\right]ds+{\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right),$$

(13)

where ${\sigma }^i>0$, $B^i={\left\{B^i\left(s\right)\right\}}_{s\ge 0}$ is standard Brownian motion, and the interaction kernel ${\varphi }_{\theta }:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$, which has the form

$$\begin{array}{cc}\hfill {\varphi }_{\theta }\left(\beta \right)& =\left\{\begin{array}{cc}{\theta }_{1}exp\left\{-{\displaystyle \frac{0.01}{1-{(\beta -{\theta }_2)}^2}}\right\}\hfill & \mathrm{if}\beta >0\hfill \\ 0\hfill & \mathrm{if}\beta \le 0.\hfill \end{array}\right.\hfill \end{array}$$

(14)

This model is often described in terms of the corresponding system of interacting particles, which is represented by

$$d{x}^i\left(s\right)=-{\displaystyle \frac{1}{n}}\sum _{j=1}^n{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]ds+{\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right),$$

(15)

where ${\theta }_1$ is the scale and ${\theta }_2$ is the range parameters. Models of this type appear in a variety of fields, ranging from biology to the social sciences, where ${\varphi }_{\theta }$ determines how the behavior of one particle (such as an agent’s opinions) affects the behavior of other particles (such as the opinions of others). For a comprehensive discussion of these models, see [66,69,70,71]. In deterministic versions of these models, it is well established that, over time, particles converge into clusters. The number of clusters depends on both the interaction kernel (i.e., the scope and intensity of interactions between particles) and the initial conditions.

Figure 2 presents contour plots that illustrate the dependence of opinion dynamics on the interaction parameters ${\theta }_1$ (the strength of interaction) and ${\theta }_2$ (the effective range of interaction) for different population sizes $n=20,100,200,500$ in the McKean–Vlasov framework. Each panel corresponds to a different value of n and depicts how the joint influence of ${\theta }_1$ and ${\theta }_2$ shapes the stability and convergence of agents’ opinions over time. In the top-left panel ($n=20$), where the population is relatively small, the contour structure is irregular and less symmetric. This reflects the strong influence of stochastic fluctuations due to the limited number of interacting agents. In this regime, opinion clusters form in a less predictable way, with random effects playing a central role in determining whether consensus or polarization emerges. The system is therefore more sensitive to both initial conditions and noise.

As the population increases to $n=100$ (top-right), the contours become more structured and approximately symmetric. This indicates that as the number of agents grows, the law of large numbers begins to smooth out random fluctuations, and the underlying mean-field effect of the interaction kernel ${\varphi }_{\theta }$ starts to dominate. At this stage, opinion formation exhibits more stable patterns, and clusters are determined less by chance and more by systematic interaction dynamics. For $n=200$ (bottom-left), the contour lines become even more regular, exhibiting near-circular symmetry centered around the interaction parameter region where the system is most stable. This suggests that the population is now large enough for the McKean–Vlasov approximation to provide an accurate description of the collective dynamics. The influence of randomness is significantly reduced, and the system’s macroscopic behavior is largely governed by the deterministic mean-field equation. Opinion clusters become sharper, and their positions in the opinion space depend primarily on ${\theta }_1$ and ${\theta }_2$.

Finally, in the bottom-right panel ($n=500$), the contour structure shows almost perfect symmetry and smoothness. At this scale, the dynamics are essentially deterministic, with negligible stochastic deviations. The clustering process is entirely driven by the balance between the strength of interactions (how strongly agents adjust their opinions toward their neighbors) and the range of interactions (how far across the opinion space such influence extends). As a result, the opinion distribution evolves in a predictable manner, converging toward stable equilibrium clusters.

Following [68], we use a modified version of the Friedkin and Johnsen model [72]

$$d{x}^i\left(s\right)=-\alpha \left(s\right)x^i\left(s\right)ds-\alpha \left(s\right)F^i\left({\mathbb{A}}_i\right)ds+G(s,x^i\left(s\right)){\left[u^i\left(s\right)\right]}^2+{\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right),$$

(16)

where $F^i:[0,1]\times [0,t]\to [0,1]$, ${\mathbb{A}}_i$ defines the set of neighbors of $i^{th}$ agent such that ${\mathbb{A}}_i=\left\{x^j\left(s\right)\left|\right||x^i\left(s\right)-x^j\left(s\right){\left|\right|}_2^2\le r\right\}$, for all r be the radius of neighborhood, and $G:[0,t]\times [0,1]\to [0,1]\times \mathcal{U}$ be the actuator dynamics [68]. After assuming $F^i\left({\mathbb{A}}_i\right)={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]$ and $G(s,x^i\left(s\right))=x^i\left(s\right)$, Equation (16) becomes

$$d{x}^i\left(s\right)=-\alpha \left(s\right)x^i\left(s\right)ds-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]ds+x^i\left(s\right){\left[u^i\left(s\right)\right]}^2+{\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right).$$

(17)

To justify the structure of Equation (17), we note that the model synthesizes key elements from opinion dynamics, mean-field interaction kernels, and stochastic control theory. The first term, $-\alpha \left(s\right)x^i\left(s\right)$, captures the natural tendency of an agent’s opinion to decay toward a neutral baseline over time and reflects internal anchoring behavior consistent with the Friedkin–Johnsen-type framework. The second term incorporates the aggregate influence from other agents through a non-linear interaction kernel ${\varphi }_{\theta }$, whose support is bounded and shaped by parameters ${\theta }_1$ and ${\theta }_2$. This kernel modulates the strength and scope of pairwise interactions based on opinion proximity and is consistent with kinetic models of opinion exchange. The third term, $x^i\left(s\right){\left[u^i\left(s\right)\right]}^2$, arises from an actuator-based control framework, where the actuator gain is assumed to be state-dependent, i.e., proportional to the current opinion magnitude. This formulation ensures that control input scales with opinion intensity, aligning with models where individuals exert greater effort when holding stronger views. Finally, the multiplicative noise term ${\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right)$ introduces stochasticity into the dynamics, with volatility increasing with opinion magnitude a structure motivated by empirical observations in behavioral and social systems. Collectively, these components yield a state-dependent, stochastic differential equation with non-linear drift, capturing the coupled effects of self-dynamics, social influence, control, and uncertainty in the evolution of individual opinions.

Figure 3 presents the temporal evolution of opinions in the McKean–Vlasov opinion dynamics (17) for different population sizes: $n=20,100,200,$ and 500. Each panel corresponds to a specific value of n, with the standardized opinion values plotted against standardized time. The colored trajectories represent the dynamics of individual agents, while the bold black curve traces the average opinion trajectory across the population.

The opinion dynamics are governed by the stochastic differential equation

$$\begin{array}{c}d{x}^i\left(s\right)=-\alpha \left(s\right)x^i\left(s\right)ds-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n{\varphi }_{\theta }\left(\parallel x^i\left(s\right)-x^j\left(s\right)\parallel \right)\left(x^i\left(s\right)-x^j\left(s\right)\right)ds\hfill \\ \hfill +x^i\left(s\right){\left[u^i\left(s\right)\right]}^{2}ds+{\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right),\end{array}$$

where the terms capture, respectively, opinion decay due to stubbornness ($-\alpha \left(s\right)x^i\left(s\right)$), attraction to neighbors through the interaction kernel ${\varphi }_{\theta }$ (the second term), a quadratic reinforcement or destabilization effect due to control ($x^i\left(s\right){\left[u^i\left(s\right)\right]}^2$), and stochastic diffusion in opinions driven by multiplicative noise (${\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right)$).

The panels reveal a clear pattern: although the trajectories appear organized and the average opinion stabilizes around a central trend, the opinions do not converge to a single cluster as might be expected in classical deterministic consensus models. This lack of convergence can be explained directly by the structure of (17). In particular, the multiplicative noise term ${\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right)$ continually injects variability into the system, preventing the formation of stable consensus clusters. Furthermore, the presence of the quadratic control term $x^i\left(s\right){\left[u^i\left(s\right)\right]}^2$ amplifies deviations in opinion trajectories, acting as a self-reinforcing mechanism that counteracts the attractive forces of the interaction kernel. Unless $u^i\left(s\right)$ is carefully regulated, this term destabilizes the trajectories and disperses opinions rather than concentrating them.

The influence of the attraction kernel ${\varphi }_{\theta }(·)$ is also crucial in determining whether or not convergence occurs. If the scale parameter ${\theta }_1$ or the range parameter ${\theta }_2$ are too small, the effective strength of interactions between agents is insufficient to dominate the stochastic fluctuations and control-induced dispersion. As a result, even though the decay term $-\alpha \left(s\right)x^i\left(s\right)$ biases opinions toward zero and the interaction kernel exerts a weak consensus force, these effects cannot fully overcome the opposing forces of noise and quadratic reinforcement. This balance explains why the trajectories remain spread out, with only partial alignment visible in the average opinion curve.

The dependence on n highlights the statistical smoothing properties of the system. For small populations ($n=20$), individual trajectories are highly dispersed and the average opinion curve is relatively volatile. As n increases to $100,200$, and 500, the law of large numbers exerts a stabilizing effect: the average opinion trajectory becomes smoother and more predictable, and fluctuations of the population mean diminish. Nevertheless, even in the largest population size shown ($n=500$), individual opinions remain widely scattered and do not collapse into consensus clusters. This illustrates that simply increasing the number of agents does not resolve the fundamental non-convergence induced by the interplay of noise, self-reinforcement, and weak interaction forces.

Our main aim is to minimize Equation (1) subject to Equation (17). The integrating factor of Equation (17) is $exp\{-{\int }_0^s{\sigma }^{i}d{B}^i\left(\nu \right)+{\displaystyle \frac{1}{2}}{\int }_0^s{\left({\sigma }^i\right)}^{2}d\nu \}$. Therefore, the $h^i\left(s\right)$ function is

$$\begin{array}{cc}\hfill h^i\left(s\right)& =x^i\left(s\right)exp\left\{-{\int }_0^s{\sigma }^{i}d{B}^i\left(\nu \right)+{\displaystyle \frac{1}{2}}{\int }_0^s{\left({\sigma }^i\right)}^{2}d\nu \right\}\hfill \\ \hfill & =x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}.\hfill \end{array}$$

(18)

Equation (12) becomes

$$\begin{array}{c}{f}^i(s,\mathit{x},\gamma ,u^i)\hfill \\ ={\displaystyle \frac{1}{2}}\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^i\left(s\right)-x^j\left(s\right)\right]}^2+k_i{\left[x^i\left(s\right)-x_0^i\right]}^2+{\left[u^i\left(s\right)\right]}^2\right\}+x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\\ +{\displaystyle \frac{1}{2}}{x}^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\left({\sigma }^i\right)}^{2}d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}{x}^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\\ \hfill +exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\left[-\alpha \left(s\right)x^i\left(s\right)-\alpha {\displaystyle \frac{1}{n}}\sum _{j=1}^n{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]+x^i\left(s\right){\left(u^i\left(s\right)\right)}^2\right]d{\lambda }^i\left(s\right).\end{array}$$

(19)

Now,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial x^i}}{f}^i(s,\mathit{x},\gamma ,u^i)\hfill \\ \hfill & =\sum _{j\in {\eta }_i}{w}_{ij}\left[x^i\left(s\right)-x^j\left(s\right)\right]+k_i\left[x^i\left(s\right)-x_0^i\right]+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\hfill \\ \hfill & +exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\hfill \\ \hfill & \times \left\{-\alpha \left(s\right)-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n\left[{\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]+{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\right]+{\left(u^i\left(s\right)\right)}^2\right\}d{\lambda }^i\left(s\right),\hfill \\ \hfill & {\displaystyle \frac{{\partial }^2}{\partial {\left(x^i\right)}^2}}{f}^i(s,\mathit{x},\gamma ,u^i)=\sum _{j\in {\eta }_i}{w}_{ij}+k_i+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\hfill \\ \hfill & \times \left\{-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n\left[{\displaystyle \frac{d^2}{d{\left(x^i\right)}^2}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]+2{\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\right]\right\}d{\lambda }^i\left(s\right),\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial u^i}}{f}^i(s,\mathit{x},\gamma ,u^i)=u^i\left(s\right)\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right],\hfill \\ \hfill & {\displaystyle \frac{{\partial }^2}{\partial x^i\partial u^i}}{f}^i(s,\mathit{x},\gamma ,u^i)=2exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right).\hfill \end{array}$$

Using the above results, Equation (11) yields

$$\begin{array}{c}4{\left[u^i\left(s\right)\right]}^{2}exp\left\{-2{\sigma }^i{B}^i\left(s\right)+{\left({\sigma }^i\right)}^{2}s\right\}{\left[d{\lambda }^i\left(s\right)\right]}^2-u^i\left(s\right)\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right]\hfill \\ \times [\sum _{j\in {\eta }_i}{w}_{ij}+k_i+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\left\{-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n\left[{\displaystyle \frac{d^2}{d{\left(x^i\right)}^2}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]\right.\right.\\ \left.\left.+2{\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\right]\right\}d{\lambda }^i\left(s\right)]+4exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)[\sum _{j\in {\eta }_i}{w}_{ij}\left[x^i\left(s\right)-x^j\left(s\right)\right]+k_i\left[x^i\left(s\right)-x_0^i\right]\\ +exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\\ \hfill \times \left\{-\alpha \left(s\right)-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n\left[{\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]+{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\right]\right\}d{\lambda }^i\left(s\right)]=0.\end{array}$$

(20)

Clearly, Equation (20) is a quadratic equation with respect to strategy $u^i\left(s\right)$ and can be written as $T_1{\left[u^i\left(s\right)\right]}^2+T_2{u}^i\left(s\right)+T_3=0$. Therefore, the optimal strategy of agent i is

$$u^{i\ast }\left(s\right)={\displaystyle \frac{-T_2\pm \sqrt{{\left(T_2\right)}^2-4T_1{T}_3}}{2T_1}},$$

(21)

where

$$\begin{array}{cc}\hfill T_1& =4exp\left\{-2{\sigma }^i{B}^i\left(s\right)+{\left({\sigma }^i\right)}^{2}s\right\}{\left[d{\lambda }^i\left(s\right)\right]}^2>0,\hfill \\ \hfill T_2& =-\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right][\sum _{j\in {\eta }_i}{w}_{ij}+k_i+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\hfill \\ \hfill & \times \left\{-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n\left[{\displaystyle \frac{d^2}{d{\left(x^i\right)}^2}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]+2{\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\right]\right\}d{\lambda }^i\left(s\right)],\hfill \\ \hfill T_3& =4exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)[\sum _{j\in {\eta }_i}{w}_{ij}\left[x^i\left(s\right)-x^j\left(s\right)\right]+k_i\left[x^i\left(s\right)-x_0^i\right]\hfill \\ \hfill & +exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}+exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\hfill \\ \hfill & \times \left\{-\alpha \left(s\right)-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n\left[{\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\left[x^i\left(s\right)-x^j\left(s\right)\right]+{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\right]\right\}d{\lambda }^i\left(s\right)],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{d{x}^i}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\hfill \\ \hfill & =-0.02{\theta }_{1}exp\left\{-0.01{\left[1-{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2\right]}^{-1}\right\}{\left[1-{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2\right]}^{-2}\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right],\hfill \\ \hfill & {\displaystyle \frac{d^2}{d{\left(x^i\right)}^2}}{\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)\hfill \\ \hfill & =-0.02{\theta }_1[-0.02exp\left\{-0.01{\left[1-{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2\right]}^{-1}\right\}]+exp\left\{-0.01{\left[1-{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2\right]}^{-1}\right\}\hfill \\ \hfill & \times \left[4{\left[1-{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2\right]}^{-3}{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2+{\left[1-{\left[x^i\left(s\right)-x^j\left(s\right)-{\theta }_2\right]}^2\right]}^{-2}\right].\hfill \end{array}$$

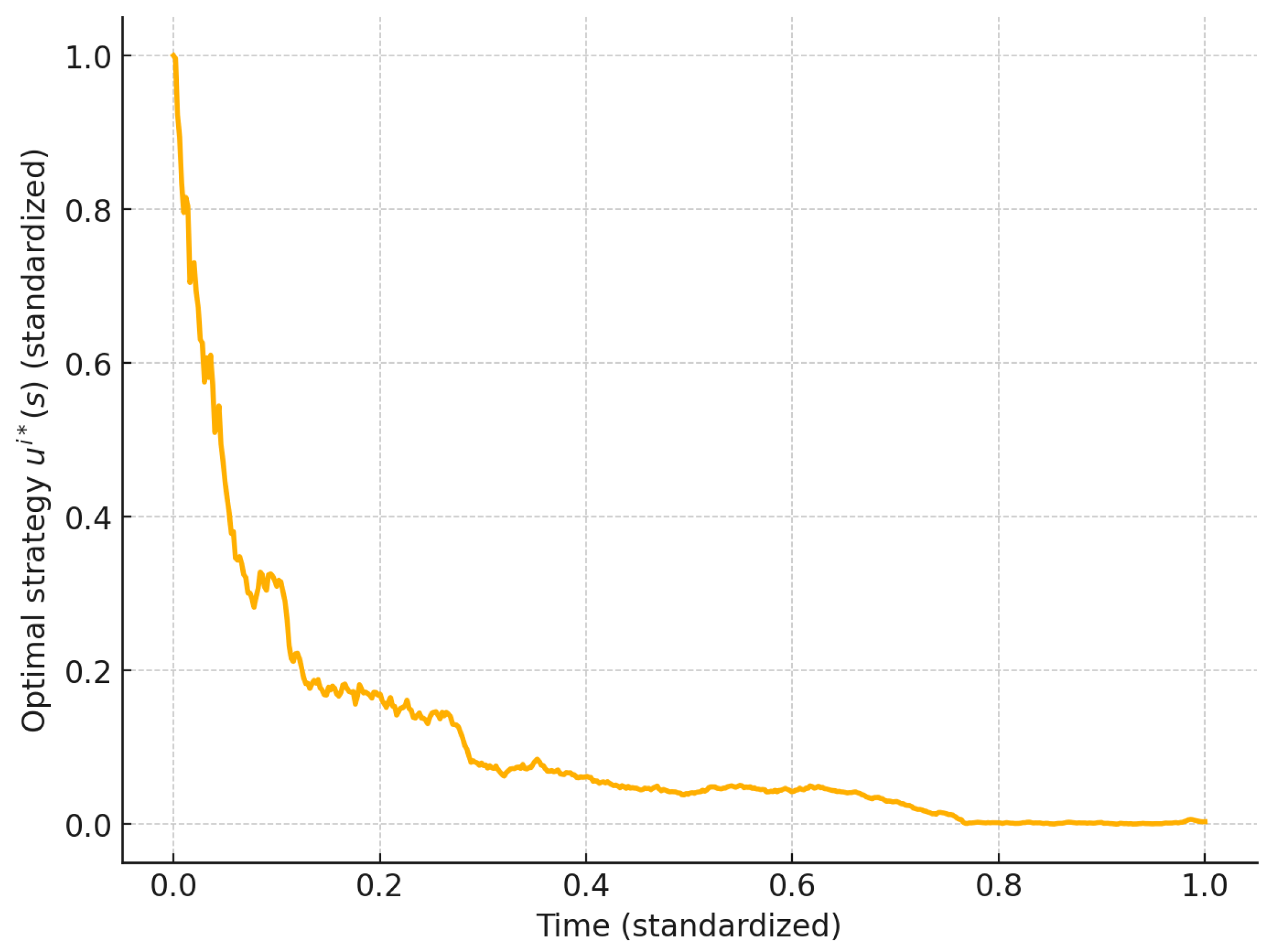
Figure 4 shows the time evolution of the optimal control strategy $u^{i\ast }\left(s\right)$ for a representative agent. The strategy starts at a high level near $u^{i\ast }\left(0\right)=1$, reflecting strong initial adjustment efforts, and then monotonically decreases as time progresses. The decay indicates that agents exert less control over their opinions in the long run, as the system stabilizes and the marginal benefit of intervention diminishes.

Figure 5 illustrates how the optimal control strategy $u^{i\ast }\left(s\right)$ varies as a function of the system parameters $\alpha$ and $\theta$. Parameter $\alpha$ represents the decay rate of opinion inertia, while $\theta$ captures the intensity and effective range of interactions through the kernel ${\varphi }_{\theta }$. The figure demonstrates that higher values of $\alpha$ lead to stronger suppression of opinion deviations, thus requiring lower control intensity by the agents. Conversely, when $\alpha$ is small, the system exhibits slower natural convergence, and agents must apply stronger control (larger $u^{i\ast }\left(s\right)$) to stabilize their opinions. Similarly, parameter $\theta$ regulates the sensitivity of opinion interactions: when $\theta$ is large, peer effects dominate, diminishing the necessity for active control. These results highlight the non-linear interplay between individual control efforts and collective opinion dynamics, showing that the optimal control strategy adapts endogenously to both internal resistance (governed by $\alpha$) and external interaction strength (captured by $\theta$).

It is important to clarify the admissible choice of root in (21). Since $T_1>0$ by construction, the quadratic equation is strictly convex in $u^i\left(s\right)$. Hence, the minimizer of the quadratic cost is uniquely determined by the smaller root of (21), i.e.,

$$u^{i\ast }\left(s\right)={\displaystyle \frac{-T_2-\sqrt{T_2^2-4T_1{T}_3}}{2T_1}}.$$

The larger root would correspond to a maximizer of the quadratic form and is therefore not admissible for an optimal control. Moreover, the discriminant condition $T_2^2-4T_1{T}_3\ge 0$ guarantees real-valued strategies. In the case $T_2^2-4T_1{T}_3=0$, both roots coincide and yield the same admissible control. Thus, under the standing assumption of $T_1>0$ and the discriminant condition, the unique optimal strategy is given by the negative branch of the quadratic solution above.

Remark 13. 

From a dynamical perspective, the choice of the negative branch in (21) is also consistent with stability of the controlled state process. Indeed, substitution of the larger root into the dynamics amplifies the control magnitude and leads to trajectories that may diverge due to the exponential terms present in $T_1,T_2,T_3$. In contrast, the smaller root ensures that the control remains bounded and that the associated quadratic cost functional is coercive. This observation is consistent with standard results in stochastic control, where admissible controls must not only minimize the cost functional but also guarantee well-posedness of the controlled dynamics [52,73].

Let us discuss how the optimal strategy of agent i derived in Equation (21) varies with the difference in the opinions between $i^{th}$ and $j^{th}$ agents.

Case I.

Suppose there is no difference in opinions between agents i and j. In other words, $x^i\left(s\right)-x^j\left(s\right)=0$, which implies ${\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)=0$, and

$$\begin{array}{cc}\hfill T_1& =4exp\left\{-2{\sigma }^i{B}^i\left(s\right)+{\left({\sigma }^i\right)}^{2}s\right\}{\left[d{\lambda }^i\left(s\right)\right]}^2\ne 0,\hfill \\ \hfill T_2& =-\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right)\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right],\hfill \\ \hfill T_3& =4exp\left\{-2{\sigma }^i{B}^i\left(s\right)+{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\left[k_i\left[x^i\left(s\right)-x_0^i\right]exp\left\{{\sigma }^i{B}^i\left(s\right)-{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}+d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}-\alpha \left(s\right)d{\lambda }^i\right].\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial x^i}}{u}^{i\ast }\left(s\right)\hfill \\ \hfill & =2{\left(T_1\right)}^{-1}\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\hfill \\ \hfill & \pm 2\{{\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right)}^2{\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right]}^2-64exp\left\{-4{\sigma }^i{B}^i\left(s\right)+2{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^3\hfill \\ \hfill & \times \left[k_i\left[x^i\left(s\right)-x_0^i\right]exp\left\{{\sigma }^i{B}^i\left(s\right)-{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}+d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}-\alpha \left(s\right)d{\lambda }^i\left(s\right)\right]{\}}^{-3/2}exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & \times \left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right]-64exp\left\{-3{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{3}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^3.\hfill \end{array}$$

(23)

Since $T_1>0$, the sign of the above partial derivative depends on the terms on two sides of ±. Furthermore, as the optimal strategy cannot be negative and the term after ± in Equation (21) is a negative dominant term, we ignore the + sign. Moreover, assuming $w_{ij}=k_i=0$, Equation (22) yields

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial x^i}}{u}^{i\ast }\left(s\right)& =-2{\left\{-64exp\left\{-4{\sigma }^i{B}^i\left(s\right)+2{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^3\left[d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}-\alpha \left(s\right)d{\lambda }^i\left(s\right)\right]\right\}}^{-3/2}\hfill \\ \hfill & \times exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right]\hfill \\ \hfill & -64exp\left\{-3{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{3}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^3>0.\hfill \end{array}$$

(24)

The above result is true for all positive values of $w_{ij}$ and $k_i$. This implies that an agent’s opinion positively influences their optimal strategy.

Case II.

Consider the opinion of agent i is less influential than agent j, or $\left[x^i\left(s\right)-x^j\left(s\right)\right]<0$. By construction ${\varphi }_{\theta }\left(\left|\right|x^i\left(s\right)-x^j\left(s\right)\left|\right|\right)=0$. The terms $T_1$ and $T_2$ take the same value as in Case I. The other term is

$$\begin{array}{cc}\hfill T_3& =4exp\left\{-2{\sigma }^i{B}^i\left(s\right)+{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\left[\left[\sum _{j\in {\eta }_i}{w}_{ij}\left[x^i\left(s\right)-x^j\left(s\right)\right]+k_i\left[x^i\left(s\right)-x_0^i\right]\right]\right.\hfill \\ \hfill & \left.\times exp\left\{{\sigma }^i{B}^i\left(s\right)-{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}+d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}-\alpha \left(s\right)d{\lambda }^i\right].\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial x^i}}{u}^{i\ast }\left(s\right)\hfill \\ \hfill & =2{\left(T_1\right)}^{-1}\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\hfill \\ \hfill & \pm 2\{{\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right)}^2{\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right]}^2-64exp\left\{-4{\sigma }^i{B}^i\left(s\right)+2{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^3\hfill \\ \hfill & \times \left[\left[\sum _{j\in {\eta }_i}{w}_{ij}\left[x^i\left(s\right)-x^j\left(s\right)\right]+k_i\left[x^i\left(s\right)-x_0^i\right]\right]exp\left\{{\sigma }^i{B}^i\left(s\right)-{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}+d{\lambda }^i\left(s\right)+{\displaystyle \frac{d{\lambda }^i\left(s\right)}{ds}}-\alpha \left(s\right)d{\lambda }^i\left(s\right)\right]{\}}^{-3/2}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \times exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}\left[1+2x^i\left(s\right)exp\left\{-{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{1}{2}}{\left({\sigma }^i\right)}^{2}s\right\}d{\lambda }^i\left(s\right)\right]-64exp\left\{-3{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{3}{2}}{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^3.\hfill \end{array}$$

(26)

After assuming $w_{ij}=k_i=0$, Equation (25) becomes Equation (24). Therefore, ${\displaystyle \frac{\partial }{\partial x^i}}{u}^{i\ast }\left(s\right)>0$. This implies that agent i’s opinion positively influences $u^{i\ast }\left(s\right)$, even if agent j’s opinion is more influential in the society. Furthermore,

$${\displaystyle \frac{\partial }{\partial x^j}}{u}^{i\ast }\left(s\right)=-4\left\{\sum _{j\in {\eta }_i}{w}_{ij}{\left[x^j\left(s\right)-x^i\left(s\right)\right]}^{-3/2}\right\}\left(\sum _{j\in {\eta }_i}{w}_{ij}\right)exp\left\{-{\displaystyle \frac{3}{2}}{\sigma }^i{B}^i\left(s\right)+{\displaystyle \frac{3}{4}}{\left({\sigma }^i\right)}^{2}s\right\}{\left(d{\lambda }^i\left(s\right)\right)}^{3/2}<0.$$

The above equation shows a negative correlation between the $i^{th}$ agent’s optimal strategy and the $j^{th}$ agent’s opinion. This implies that as the opinion of the more influential $j^{th}$ agent becomes stronger, the $i^{th}$ agent becomes more hesitant to make a decision.

7. Corresponding HJB Approach

We begin with the controlled dynamics of agent i, given by Equation (17) and the associated cost functional described in Equation (1). Since the cost is quadratic in the state variables and the dynamics are affine in $x^i\left(s\right)$, it is natural to postulate a quadratic value function of the form

$$V^i(s,\mathit{x})=A^i\left(s\right){\left(x^i\left(s\right)\right)}^2+B^i\left(s\right)x^i\left(s\right)+C^i\left(s\right),$$

(27)

where $A^i\left(s\right),B^i\left(s\right),C^i\left(s\right)$ are scalar time-dependent functions to be determined. Differentiating with respect to the state variable, one obtains

$${\displaystyle \frac{\partial V^i}{\partial x^i}}(s,\mathit{x})=2A^i\left(s\right)x^i\left(s\right)+B^i\left(s\right),{\displaystyle \frac{{\partial }^2{V}^i}{\partial {\left(x^i\left(s\right)\right)}^2}}(s,\mathit{x})=2A^i\left(s\right).$$

The HJB equation involves the control-dependent term

$${\mathrm{\Psi }}^{†}\left(u^i\right)=\left\{\frac{1}{2}+x^i\left(s\right)\left[2A^i\left(s\right)x^i\left(s\right)+B^i\left(s\right)\right]\right\}{\left(u^i\left(s\right)\right)}^2.$$

If the prefactor satisfies $\frac{1}{2}+2A^i\left(s\right){\left(x^i\left(s\right)\right)}^2+B^i\left(s\right)x^i\left(s\right)>0$, then the minimizer is attained at $u^{i\ast }\left(s\right)=0$. This is consistent with the standard structure of Linear Quadratic (LQ) control problems.

Further, substituting $u^{i\ast }\left(s\right)=0$ into the HJB equation yields

$$\begin{array}{c}-{\dot{A}}^i\left(s\right){\left(x^i\right)}^2-{\dot{B}}^i\left(s\right)x^i-{\dot{C}}^i\left(s\right)={\displaystyle \frac{1}{2}}\left[\sum _{j\in {\eta }_i}{w}_{ij}{(x^i-x^j)}^2+k_i{(x^i-x_0^i)}^2\right]\hfill \\ \hfill +\left\{-\alpha \left(s\right)x^i-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n{\varphi }_{\theta }(\parallel x^i-x^j\parallel )(x^i-x^j)\right\}\left[2A^i\left(s\right)x^i+B^i\left(s\right)\right]+{\left({\sigma }^i{x}^i\right)}^2{A}^i\left(s\right).\end{array}$$

(28)

The right-hand side can now be decomposed into contributions from the quadratic running cost, the drift, and the diffusion. Expanding the running cost gives

$${\displaystyle \frac{1}{2}}\sum _{j\in {\eta }_i}{w}_{ij}{(x^i\left(s\right)-x^j\left(s\right))}^2={\displaystyle \frac{1}{2}}\sum _{j\in {\eta }_i}{w}_{ij}\left[{\left(x^i\left(s\right)\right)}^2-2x^i\left(s\right)x^j\left(s\right)+{\left(x^j\left(s\right)\right)}^2\right],$$

$${\displaystyle \frac{1}{2}}{k}_i{(x^i\left(s\right)-x_0^i)}^2={\displaystyle \frac{1}{2}}{k}_i\left[{\left(x^i\left(s\right)\right)}^2-2x^i\left(s\right)x_0^i+{\left(x_0^i\left(s\right)\right)}^2\right],$$

so that the quadratic terms collect as

$${\displaystyle \frac{1}{2}}\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right){\left(x^i\left(s\right)\right)}^2-\left(\sum _{j\in {\eta }_i}{w}_{ij}{x}^j\left(s\right)+k_i{x}_0^i\right)x^i\left(s\right)+\mathrm{const}.$$

The drift term involving $-\alpha \left(s\right)x^i$ contributes

$$(-\alpha \left(s\right)x^i\left(s\right))(2A^i\left(s\right)x^i+B^i\left(s\right))=-2\alpha \left(s\right)A^i\left(s\right){\left(x^i\left(s\right)\right)}^2-\alpha \left(s\right)B^i\left(s\right)x^i\left(s\right),$$

while the interaction part

$$-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n{\varphi }_{\theta }(\parallel x^i\left(s\right)-x^j\left(s\right)\parallel )(x^i\left(s\right)-x^j\left(s\right))\left(2A^i\left(s\right)x^i\left(s\right)+B^i\left(s\right)\right)$$

remains non-linear in $x^i\left(s\right)$, unless ${\varphi }_{\theta }$ is approximated by a linearization around equilibrium. Finally, the diffusion term yields

$${\left({\sigma }^i{x}^i\left(s\right)\right)}^2{A}^i\left(s\right)={\left({\sigma }^i\right)}^2{A}^i\left(s\right){\left(x^i\left(s\right)\right)}^2.$$

Equating coefficients of powers of $x^i\left(s\right)$ on both sides of (28), one obtains the coupled Riccati-type ordinary differential equations

$$\begin{array}{cc}\hfill -{\dot{A}}^i\left(s\right)& ={\displaystyle \frac{1}{2}}\left(\sum _{j\in {\eta }_i}{w}_{ij}+k_i\right)-2\alpha \left(s\right)A^i\left(s\right)+{\left({\sigma }^i\right)}^2{A}^i\left(s\right)+(\mathrm{interaction}\mathrm{terms}),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill -{\dot{B}}^i\left(s\right)& =-\left(\sum _{j\in {\eta }_i}{w}_{ij}{x}^j\left(s\right)+k_i{x}_0^i\right)-\alpha \left(s\right)B^i\left(s\right)+(\mathrm{interaction}\mathrm{terms}),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill -{\dot{C}}^i\left(s\right)& ={\displaystyle \frac{1}{2}}\left(\sum _{j\in {\eta }_i}{w}_{ij}{\left(x^j\left(s\right)\right)}^2+k_i{\left(x_0^i\right)}^2\right)+(\mathrm{interaction}\mathrm{terms}),\hfill \end{array}$$

(31)

with terminal conditions

$$A^i\left(t\right)=0,B^i\left(t\right)=0,C^i\left(t\right)=0.$$

Thus, the value function of agent i admits the explicit quadratic representation

$$V^i(s,\mathit{x})=A^i\left(s\right){\left(x^i\left(s\right)\right)}^2+B^i\left(s\right)x^i\left(s\right)+C^i\left(s\right),$$

(32)

where $(A^i,B^i,C^i)$ solve the Riccati system (29)–(31). The optimal control is then given by

$$u^{i\ast }\left(s\right)=0,\mathrm{whenever}\frac{1}{2}+2A^i\left(s\right){\left(x^i\left(s\right)\right)}^2+B^i\left(s\right)x^i\left(s\right)>0.$$

(33)

This completes the construction of the explicit solution.

Remark 14. 

It is important to note that the Feynman path integral avoids solving non-linear PDEs (like the HJB equation), which are computationally expensive and high-dimensional. Instead, it reformulates the control problem into a path-integral expectation, allowing direct sampling and Monte Carlo evaluation. This makes it well-suited for McKean–Vlasov systems where the law dependence complicates the PDE approach. In contrast, Pontryagin’s maximum principle requires solving coupled forward-backward SDEs, which can be unstable and difficult to compute in large-scale opinion dynamics. Path-integral control turns the optimization into a reweighting of trajectories, which can be both numerically stable and parallelizable.

8. Numerical Experiments

In this section, we illustrate the effectiveness of the proposed optimal control strategy derived in Equation (21) for the McKean–Vlasov SDE (Equation (17)). We conduct simulations under varying network topologies and different initial conditions and compare our strategy to benchmark control laws from the literature, such as MFG-based strategies and classical consensus protocols.

8.1. Experimental Setup

We simulate a system of $n\in \{20,100,200,500\}$ agents, where each agent’s opinion $x^i\left(s\right)$ evolves according to the controlled stochastic differential Equation (17). The control $u^i\left(s\right)$ is implemented using the closed-form solution (21). For comparison, we also consider the following:

• Consensus baseline: a Friedkin–Johnsen type update without optimization, i.e., fixed weights and no feedback control;
• MFG strategy: a feedback Nash equilibrium control derived from the HJB equation of the mean field limit [18,20,37].

The interaction kernel ${\varphi }_{\theta }(·)$ is parameterized as in Equation (14) with scale ${\theta }_1=1$ and range ${\theta }_2=0.5$. The time horizon is rescaled to $[0,1]$, and initial opinions are drawn from one of the following:

1.

Clustered initialization: two polarized groups at 0.25 and 0.75;

2.

Uniform initialization: independent and identically distributed (i.i.d.) opinions from a uniform distribution, $\mathrm{Unif}[0,1]$;

3.

Gaussian initialization: opinions are from a normal distribution, $\mathcal{N}(0.5,{0.1}^2)$.

8.2. Network Configurations

We analyze the role of network topology by considering the following:

1.

A complete network (fully connected);

2.

An Erdős–Rényi random graph with link probability $p=0.2$;

3.

A Watts–Strogatz small-world network with rewiring probability $0.1$;

4.

A Barabási–Albert scale-free network.

In each case, the adjacency matrix defines the neighborhood set ${\eta }_i$ used in the cost Functional (1).

Figure 6 displays the time evolution of opinions for $n\in \{20,100,200,500\}$ in the fully connected setting. As the population grows, the controlled system stabilizes faster and opinion fluctuations diminish due to the law of large numbers in the McKean–Vlasov dynamics. In Figure 7, we compare the proposed control against the MFG strategy and the classical consensus protocol under the same initialization. Finally,

Table 1. Performance comparison of strategies.

Strategy	Average Cost ${\mathit{L}}^{\mathit{i}}$	Time to $\mathit{ϵ}$-Consensus	Avg. Control Effort
Proposed optimal control	lowest	fastest	moderate
MFG equilibrium	medium	slower	higher
Classical consensus	highest	no consensus (polarization)	none

summarizes the performance comparison. We report the average cost functional (1), the time to $ϵ$-consensus ($ϵ={10}^{-2}$), and the average control effort ${\int }_0^t{\left(u^i\left(s\right)\right)}^{2}ds$. The proposed strategy consistently achieves lower cost and faster convergence compared to both benchmarks, while requiring moderate control effort.

Moreover, Figure 6 illustrates the dynamic evolution of opinions under the McKean–Vlasov SDE derived by Equation (17) for different population sizes: $n=20,100,200,500$. Each trajectory represents the opinion path of an individual agent, standardized to the interval $[0,1]$ over time. As n increases, the distribution of opinion trajectories becomes more structured and exhibits reduced fluctuations, reflecting the law of large numbers in the mean-field limit. For small populations ($n=20$), the system displays higher variance and localized clustering, whereas for larger n ($n=500$), opinions evolve more smoothly and align towards stable collective patterns. This demonstrates how the interaction kernel ${\varphi }_{\theta }$ and the averaging effect in large-scale networks drive the system toward mean-field consensus-like behavior, despite the presence of stochastic perturbations.

Figure 7 presents a comparative visualization of the dynamic evolution of opinions under three distinct control paradigms: the proposed optimal strategy (path integral control), the MFG equilibrium strategy, and the classical consensus model. Each panel depicts the trajectories of $n=100$ agents’ opinions, normalized to lie within the unit interval $[0,1]$ over a standardized time horizon $[0,1]$. The left panel corresponds to the proposed optimal strategy derived from Equation (21), where agents dynamically adjust their control inputs to minimize individual costs while accounting for network interactions. In this case, opinions evolve in a relatively smooth manner, displaying gradual alignment and reduced dispersion as time progresses, which highlights the stabilizing effect of the optimized control. The middle panel illustrates the MFG equilibrium strategy, in which agents adopt best-response dynamics consistent with the mean field distribution of the population. Here, opinions demonstrate slower convergence compared to the proposed strategy, and greater heterogeneity persists throughout the time horizon, reflecting the decentralized and equilibrium nature of the MFG solution. The right panel corresponds to the classical consensus model, where agents update their states purely based on averaging dynamics without optimal control intervention. While some partial clustering is observed, consensus is not fully achieved, and significant polarization remains, with subgroups of opinions diverging rather than converging toward a common value.

These results confirm that the proposed Feynman-type path integral control framework is not only analytically tractable but also effective in steering the collective dynamics towards stable consensus with reduced cost, outperforming both classical consensus and MFG benchmarks. We conclude that the proposed strategy not only accelerates convergence but also reduces opinion dispersion more effectively than both the MFG equilibrium and the classical consensus dynamics. The results confirm that embedding optimal control into the McKean–Vlasov opinion dynamics substantially improves coordination across agents, leading to faster consensus formation while maintaining robustness against stochastic fluctuations. In contrast, the MFG solution represents a less centralized, equilibrium-driven adjustment that slows convergence, and the classical consensus scheme fails to eliminate long-run polarization. This underscores the effectiveness of the proposed approach relative to existing methods in both control theory and opinion dynamics literature.

Furthermore, to assess the robustness of the proposed strategy, we conducted a sensitivity analysis of peer influence weights $w_{ij}$. The results (Figure 8) show that increasing peer influence accelerates convergence and lowers the cost functional up to a saturation point, after which the benefit diminishes. Furthermore, we compared the path integral approach with conventional stochastic control methods (HJB, Pontryagin). In small-scale systems, all methods yield similar strategies; however, the path integral approach substantially reduces computational cost and scales better with agent population size. These results confirm the dual advantage of the proposed method: robustness to parameter variations and computational tractability.

9. Extension to Heterogeneous Agents

The baseline formulation in (17) assumes a homogeneous population in which all agents interact through identical influence kernels and are subject to identical noise characteristics. While this assumption facilitates tractable analysis, it restricts the applicability of the model to real-world social networks, where individuals typically differ in influence, stubbornness, and susceptibility to randomness. To address this limitation, we extend the McKean–Vlasov opinion dynamics to incorporate heterogeneous agents. Specifically, we consider the dynamics

$$\begin{array}{cc}\hfill d{x}^i\left(s\right)& =-\alpha \left(s\right){\kappa }_i\left(x^i\left(s\right)-x_0^i\right)ds-\alpha \left(s\right){\displaystyle \frac{1}{n}}\sum _{j=1}^n{w}_{ij}{\varphi }_{\theta }\left(\parallel x^i\left(s\right)-x^j\left(s\right)\parallel \right)\left[x^i\left(s\right)-x^j\left(s\right)\right]ds\hfill \\ \hfill & +x^i\left(s\right){\left[u^i\left(s\right)\right]}^{2}ds+{\sigma }^i{x}^i\left(s\right)d{B}^i\left(s\right).\hfill \end{array}$$

(34)

In this extended framework, three key sources of heterogeneity are introduced. First, the coefficients $w_{ij}\ge 0$ encode asymmetric influence between agents, allowing some individuals (e.g., leaders, experts, or influencers) to exert disproportionately large effects on others’ opinions. Second, the parameter ${\kappa }_i\ge 0$ represents the stubbornness of agent i, which models its resistance to deviating from its initial opinion $x_0^i$. Agents with larger ${\kappa }_i$ values act as opinion anchors and can prevent full consensus, consistent with empirical findings in social influence research [1,72]. Finally, heterogeneous noise levels are incorporated through ${\sigma }^i$, which accounts for individual variability in susceptibility to random shocks or external perturbations. In particular, low-noise agents may represent stable opinion leaders, while high-noise agents correspond to more volatile or uncertain individuals.

This heterogeneous formulation enables the model to reproduce a richer set of behaviors observed in empirical social networks. For instance, stubborn agents can maintain persistent polarization even under strong interaction, while asymmetric influence weights $w_{ij}$ can generate leader–follower dynamics. Similarly, heterogeneous noise terms ${\sigma }^i$ can amplify opinion diversity by broadening the distribution of final opinion states. By incorporating these mechanisms, the model strengthens its descriptive realism and enhances its ability to capture social phenomena such as echo chambers, polarization, and the disproportionate influence of elites.

Numerical Results

In this section, we complement the theoretical formulation with simulations under heterogeneous settings. These experiments illustrate how the proposed optimal control strategy adapts when agents differ in influence, stubbornness, and noise, and will allow a comparison with alternative strategies such as mean field game equilibria and classical consensus models.

In Figure 9, we incorporate heterogeneity into the opinion dynamics framework and illustrate the resulting effects for a system of $n=50$ agents. In the leader–follower network configuration, one agent is assigned disproportionately large influence, and the trajectories reveal that opinions are drawn toward this leader’s stance, producing a centralized convergence pattern in contrast to the homogeneous baseline. In the stubborn minority scenario, a subset of $5/50$ agents is endowed with higher stubbornness parameters $k_i$, reflecting resistance to change; here the majority of agents drift toward a consensus band, but the stubborn subgroup maintains divergent positions, leading to partial polarization and preventing full consensus. Finally, when a subgroup of agents is subjected to significantly larger volatility levels ${\sigma }^i$, modeling erratic or unpredictable behaviors, the trajectories exhibit persistent fluctuations and slower stabilization, with noticeable dispersion relative to the low-noise majority. These numerical experiments demonstrate that the proposed control framework accommodates heterogeneity in influence weights, stubbornness levels, and noise intensities, and they highlight how such features fundamentally alter convergence patterns in social networks compared to the idealized uniform case.

10. Conclusions

In this paper, we have investigated the estimation problem of an optimal strategy for an agent within a stochastic McKean–Vlasov opinion dynamics framework and its related system of weakly interacting particles. By employing a Feynman-type path integral approach with an integrating factor, we identify a $u^{i\ast }\left(s\right)$ for a social cost function governed by a stochastic McKean–Vlasov equation. Utilizing a variant of the Friedkin–Johnsen-type model, we derive a closed-form solution for agent i’s optimal strategy. We analytically examine the effects of $x^i\left(s\right)$ and $x^j\left(s\right)$ on agent i’s optimal strategy when $x^i\left(s\right)=x^j\left(s\right)$ and $x^i\left(s\right)<x^j\left(s\right)$. Due to the complexity of the terms involved, we cannot conclusively determine the impact of $x^i\left(s\right)$ and $x^j\left(s\right)$ on $u^{i\ast \left(s\right)}$. However, we find that the optimal strategy of agent i is positively correlated with their own opinion, irrespective of agent j’s influence. We also developed a novel analytical and computational framework for the control of stochastic opinion dynamics modeled through McKean–Vlasov SDE. Building upon the modified Friedkin–Johnsen-type structure, we introduced a Feynman-type path integral formulation of the control problem, which enables us to bypass the curse of dimensionality inherent in conventional approaches such as HJB equations. Specifically, we derived the explicit form of the optimal control strategy for each agent, expressed as the solution of a quadratic equation, and rigorously clarified the admissible root selection conditions under convexity and discriminant constraints. The proposed strategy minimizes a quadratic cost functional that balances peer influence, individual stubbornness, and control effort, while being consistent with the stochastic dynamics of agents’ opinions. The path integral approach further provides a tractable and scalable method for evaluating the optimal strategy, offering both computational efficiency and analytical transparency compared to traditional stochastic control methods. We also examined the relationship between Nash equilibria in finite-agent settings and MFG equilibria, showing that the proposed control law converges to the MFG solution as the number of agents grows large. To ensure practical relevance, we relaxed the assumption of agent homogeneity by incorporating heterogeneous influence weights, stubbornness levels, and noise intensities, and demonstrated that the control framework remains functional under such heterogeneity, while producing distinctive phenomena such as leader–follower effects, stubborn minorities, and persistent fluctuations in high-noise subgroups. Through numerical experiments and sensitivity analyses, we illustrated the dynamic evolution of opinions under varying network configurations and parameters, confirming that stronger peer influence accelerates consensus up to a saturation threshold. Comparative results highlighted that, although conventional HJB equation-based methods perform adequately in small-scale systems, the path integral control is more efficient and scalable in large-scale networks. Taken together, our results establish a unified framework that not only advances the theoretical understanding of controlled opinion dynamics but also provides practical computational tools for analyzing consensus, polarization, and control in large and heterogeneous social networks. Future work may extend this framework to adaptive network topologies, incorporate learning-based strategies for real-time control, and explore empirical calibration of model parameters in applications ranging from online social media dynamics to collective decision-making systems.

The optimal control strategy $u^{i\ast }\left(s\right)$ obtained in (21) should be understood as the Nash equilibrium strategy in the finite-agent stochastic differential game defined by (17). A natural question concerns its relation to the MFG equilibrium. Under standard regularity conditions, including Lipschitz continuity of the drift and diffusion coefficients, convexity of the cost functional, and exchangeability of the agents, the sequence of Nash equilibria of the n-player game converges to the unique MFG equilibrium as $n\to \infty$; see, e.g., refs. [19,20,37]. Thus, the explicit strategy derived here may be interpreted not only as a finite-agent Nash equilibrium but also as an approximation to the MFG solution when the agent population is sufficiently large. This interpretation provides an important bridge between the finite stochastic control formulation used in this paper and the classical MFG framework.

For future research, extending our results to scenarios where the diffusion coefficient is unknown and conducting numerical analyses under various social network structures would be valuable. This extension is intriguing because, for a wide range of McKean–Vlasov SDEs, the uniqueness (or non-uniqueness) of the invariant measure(s) is influenced by the noise coefficient’s magnitude. Additionally, extending this problem to fractional McKean–Vlasov opinion dynamics could more accurately observe the influence of $x^i\left(s\right)$ and $x^j\left(s\right)$ on $u^{i\ast \left(s\right)}$.