2.1. CRYSTALS-Dilithium
CRYSTALS-Dilithium is part of the cryptographic suite for the Algebraic Lattice digital signature schema. It operates on the hardness of the lattice problem over module lattices, making it a candidate for post-quantum cryptography standards. The security concept is that an adversary having access to a signing oracle cannot produce a signature of a message whose signature they have not yet seen, nor produce a different signature of a message that they already saw signed [
19]. It is a lattice-based digital signature based on the Fiat–Shamir paradigm [
13,
22,
23]. In Dilithium, the public key can be viewed as a special kind of lattice-based sample constructed over a polynomial ring, where operations are performed modulo both a prime number
q and a fixed polynomial. Conceptually, it consists of a matrix–vector relationship with two small secret vectors, sampled from a narrow, symmetric range around zero, which provides both efficiency and security [
13,
24]. Unlike other lattice-based cryptosystems, Dilithium uses a uniform distribution for generating error vectors, while most others rely on some form of truncated Gaussian distribution [
13].
2.1.1. Preliminaries
Before discussing the algorithms implemented by CRYSTALS-Dilithium, we will first introduce a few important mathematical prerequisites.
Rings and Fields
A ring is defined as a nonempty set R endowed with two binary operations, addition and multiplication , satisfying the following properties. First, forms an abelian group, meaning that for all , the operation of addition is associative, satisfying ; there exists an additive identity such that ; each element has an additive inverse such that ; and addition is commutative, so . Second, multiplication is associative, ensuring that for all . Third, multiplication distributes over addition, satisfying and for all . Unless explicitly stated, rings are not assumed to be commutative with respect to multiplication nor to possess a multiplicative identity.
A ring
R is classified as commutative if
for all
. It is unital, or a ring with unity, if there exists an element
, distinct from 0, such that
for all
. A ring is an integral domain if it is commutative, unital, and contains no zero divisors, meaning that for all
, if
, then either
or
. A division ring is a unital ring in which every nonzero element
has a multiplicative inverse
such that
. A field is a commutative division ring, combining commutativity with the existence of multiplicative inverses for all nonzero elements. In a ring, multiplicative inverses are not necessarily required to exist. A nonzero commutative ring in which every nonzero element has a multiplicative inverse is called a field. Further mathematical definition of the field is also given in the McEliece
Section 2.2.
Ideal of a Ring
An ideal of a ring is a distinguished subset that exhibits closure under specific algebraic operations. Formally, let R be a ring and I a subset of R. Then, I is an ideal of R if it satisfies the following conditions: for all , the elements and belong to I, ensuring closure under addition and subtraction; and for all and , the products and are in I, guaranteeing absorption under multiplication by any ring element.
Quotient Ring
A quotient ring, also referred to as a factor ring, arises from partitioning a ring by an ideal and defining operations on the resulting cosets. Formally, let R be a ring and I an ideal of R. The quotient ring is constructed as follows. The elements of are the cosets of I in R, denoted for any , such that . The operations of addition and multiplication on are defined by and , respectively, for all . These operations are well defined, as they are independent of the choice of coset representatives a and b for and .
Ring of Polynomials over a Finite Field
The ring denotes the ring of polynomials with coefficients in the finite field , where q is a prime power and represents the finite field of order q. For a prime p, the finite field consists of residue classes modulo p, given by , with addition and multiplication defined modulo p.
The ring comprises all polynomials of the form , where each coefficient for . In this ring, the arithmetic operations of addition, subtraction, and multiplication are performed with coefficients reduced modulo q, ensuring that all resulting coefficients remain in . This structure endows with the properties of a ring, facilitating the study of polynomial algebra over finite fields.
Lattice in a Vector Space
A lattice in a vector space is a discrete subgroup that spans the space over the real numbers. Formally, let V be a real vector space, typically , and a subset. The set is a lattice in V if it satisfies two conditions: first, is an additive subgroup of V, meaning that for all , the sum ; second, spans V over , such that any vector can be expressed as a linear combination , where and for .
Equivalently, a lattice L is a discrete set of points in generated by a basis . The lattice induced by is defined as . Thus, a lattice forms a periodic, grid-like structure of vectors in the vector space, characterized by its regular arrangement of points spanning the entire space.
Modules and Module Lattices
A module extends the concept of a vector space by allowing scalars to be elements of an arbitrary ring rather than a field. Formally, let
R be a ring, not necessarily commutative, and
M an abelian group under addition. An
R-module structure on
M is defined by a scalar multiplication operation
, mapping
, which satisfies the following properties: for all
and
, compatibility with ring multiplication holds, such that
, and distributivity is satisfied, such that
and
. Thus, an
R-module is an abelian group
M equipped with an
R-action generalizing the scalar multiplication of vector spaces. When
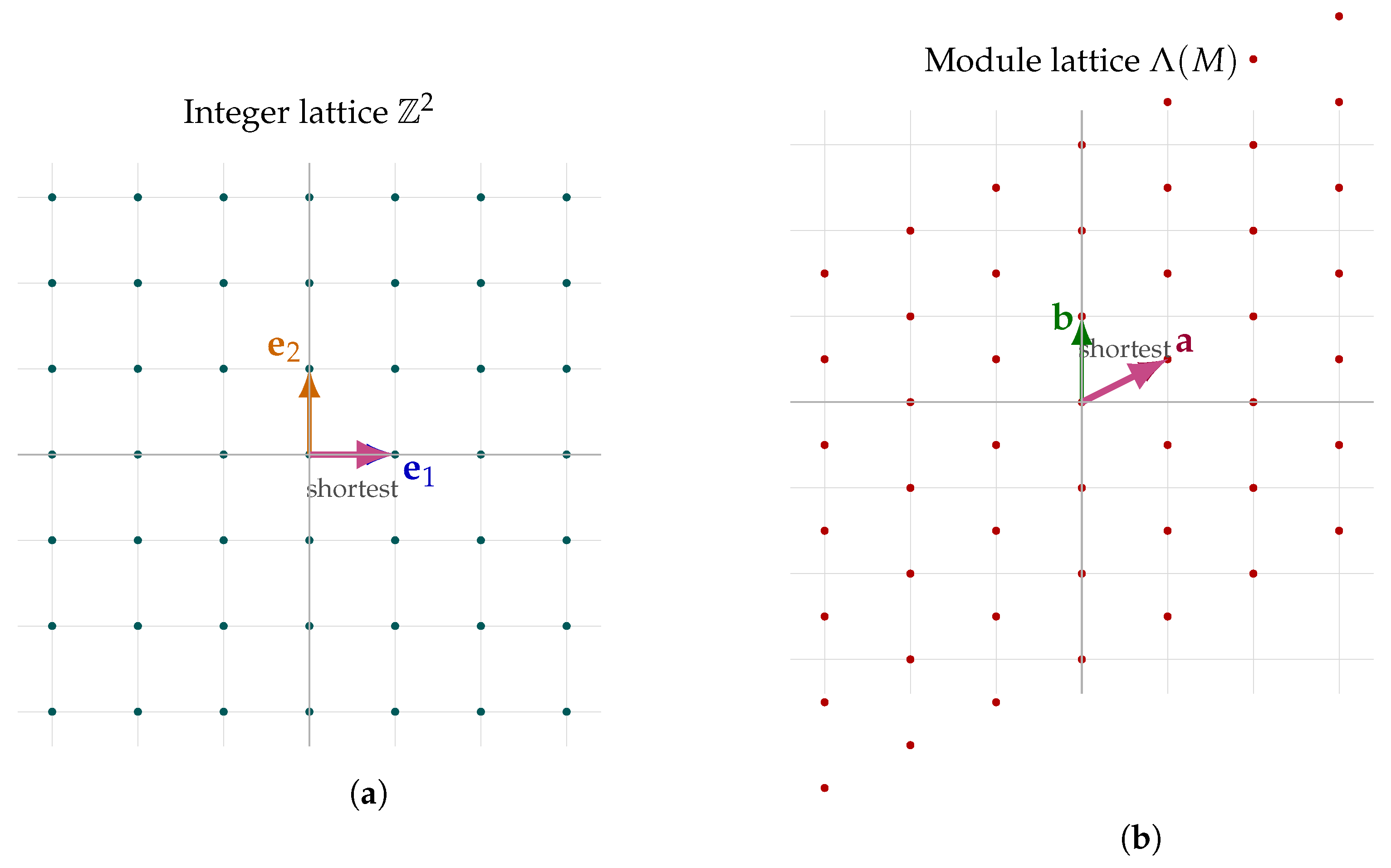
R is a field, the module becomes a vector space over that field. The example of a two-dimensional module lattice is shown in
Figure 1.
A module lattice is a submodule of an R-module that additionally possesses the structure of a lattice, integrating the algebraic properties of an R-module with the order-theoretic structure of a partially ordered set. Specifically, let M be an R-module and a submodule. The set is a module lattice if it is an additive subgroup of M, discrete with respect to a suitable topology on M (when applicable, e.g., for with R a topological ring like or ), and generates M as an R-module, such that . Additionally, forms a lattice in the geometric sense, often represented as for a basis of , when M is free of rank n. For instance, when and , a module lattice is a free abelian group of rank n, forming a grid-like structure. This interplay of algebraic and geometric properties positions module lattices as a significant object of study, bridging module theory and lattice theory.
The Polynomial Ring and the Quotient Ring
The ring , consisting of all polynomials with integer coefficients, is equipped with the standard operations of polynomial addition and multiplication. This commutative ring with unity extends the integers by incorporating an indeterminate x, thereby serving as a fundamental structure in algebra with applications across various mathematical domains.
A key construction derived from is the quotient ring , formed by factoring out the principal ideal generated by the polynomial . Elements of are equivalence classes of polynomials in , where two polynomials are equivalent if , meaning for some . The equivalence class of a polynomial is denoted .
Each element in has a unique representative polynomial of degree at most , expressible as , where for . The defining relation in the quotient ring allows higher powers of x to be reduced via . This algebraic structure, characterized by polynomial reduction modulo , renders particularly valuable in fields such as coding theory, lattice-based cryptography, and the arithmetic of cyclotomic fields.
2.1.2. Shortest Vector Problem (SVP) in Module Lattices
Let
M be a module over a ring
R, and let
denote the associated module lattice generated by a basis of
M. The Shortest Vector Problem (SVP) in
is formulated as follows:
Here, denotes a chosen norm on ; the Euclidean norm is most commonly employed due to its favorable geometric properties and well-established role in lattice-based cryptography.
The SVP in module lattices (a simple illustration is given in
Figure 2) generalizes the classical SVP in integer lattices by leveraging the additional algebraic structure of
R-modules. This generalization is of significant interest in cryptographic constructions, as it enables more compact key sizes and efficient algorithms while preserving hardness guarantees under well-studied assumptions. The presumed intractability of approximating SVP within certain factors under the Euclidean norm forms the security foundation of numerous post-quantum cryptosystems, including those based on the Learning With Errors (LWE) and Ring-LWE problems. Consequently, precise formulations and complexity analyses of SVP in module lattices are critical both for theoretical investigations in computational number theory and for practical evaluations of cryptographic resilience against classical and quantum adversaries.
Although Dilithium does not directly use SVP or CVP, it relies on the hardness assumption of these problems indirectly. Dilithium is based on the hardness of Module Learning with Errors (MLWE) problems. MLWE, a variant of the Learning with Errors (LWE) problem adapted to module lattices, involves solving systems of linear equations with noise—a difficult task for both classical as well as quantum computers [
24]. It involves solving a system of linear equations with noise, which is widely believed to be hard to solve efficiently for both classical as well as quantum computers.
Since this process leverages MLWE, formally given a public matrix
A, and a vector
b,
where
e is an error vector, and the goal of MLWE is to solve
s. The error vector
e makes it difficult to solve for
s.
2.1.3. NTT Domain Representation
Let
q be a modulus admitting a primitive 512-th root of unity
. In the cyclotomic ring
, the polynomial
factors as
which, by the Chinese Remainder Theorem [
25], induces an isomorphism between
and a direct product of finite fields, allowing multiplication to be carried out component-wise. This structural property underpins the Number Theoretic Transform (NTT), a finite-field analog of the Fast Fourier Transform (FFT), which enables asymptotically fast polynomial multiplication. Following the classical Cooley–Tukey decomposition [
26], the factorization
is applied recursively until degree-one factors are reached, enabling efficient evaluation through butterfly operations. As in the FFT, the standard output order of the NTT is bit-reversed. To fix a canonical ordering, we define the NTT domain representation of
as
where
and
denotes the bit-reversal permutation of an 8-bit integer. Under this convention, multiplication in
is performed as
where ⊙ denotes component-wise multiplication. For vectors or matrices over
, the NTT is applied element-wise, and the inverse transform maps the product back to coefficient form [
24].
2.1.4. Components
The Dilithium suite contains sets of components that are responsible for generating the key, signature creation, and verification. Key generation handles the generation of public as well as private keys. Let S be a set, and is a uniformly chosen random from S (in practical terms, S is a probability distribution).
A signature schema is a triplet of probabilistic polynomial time algorithms together with a message space M. The KeyGen algorithm generates two keys: public and private . The signing algorithm takes a secret key and a message to generate a signature . Finally, the deterministic algorithm takes a public key , a message m, and a signature , and outputs binary 0 or 1; in other words, it accepts or rejects.
If we let
denote a ring [
24],
We denote by
the natural reduction map sending each integer coefficient to its residue modulo
q. We work with the cyclotomic polynomial
(with
n a power of two) so that
R has degree
n and admits efficient Number-Theoretic Transform operations. Secrets and errors are drawn from the sparse ternary set
whose cardinality is
Finally, in key-generation and signing (or encryption), we sample
, compute
, and proceed with the standard Dilithium-style routines.
The value of
n originally used is 256 and
q is the prime,
[
13,
24].
For the CRYSTALS-Dilithium original version, we need a cryptographic hash function that hashes onto
, which has more than
elements. The Algorithm 1 shows the process for generating random elements. The algorithm used is also called the “inside-out” version of the Fisher–Yates method.
| Algorithm 1 Create a random 256-element array with 60 ’s and 196 0’s [24] |
- 1:
Initialize - 2:
for to 255 do - 3:
- 4:
- 5:
- 6:
- 7:
end for - 8:
return c
|
Expanding the Matrix
The function ExpandMatrix shown in the Algorithm 2 maps a uniform seed to a matrix in NTT domain representation. For each entry , it uses and the index as a domain separator to initialize either a SHAKE-128 instance or an AES256-CTR stream, depending on the implementation variant. The output stream is interpreted as a sequence of 23-bit integers obtained by reading three consecutive bytes in little-endian order, masking the highest bit of the third byte to zero. This ensures each parsed integer lies in the range . Integers greater than or equal to q are discarded via rejection sampling, and sampling continues until exactly n coefficients are obtained. Each polynomial produced in this manner is then transformed to the NTT domain, yielding . This process is repeated for all to obtain the full matrix in NTT form.
The choice of
in Dilithium satisfies
, which makes this sampling efficient. The use of
and
as domain separators ensures that each
is generated independently and deterministically, enabling the matrix to be reconstructed from
without storing it explicitly. This greatly reduces the public key size while preserving the uniformity and independence of matrix entries, which is essential for the Module-LWE security of the scheme.
| Algorithm 2 ExpandMatrix |
- 1:
Input: seed ; modulus ; degree n (e.g., 256); dimensions ; - 2:
Output: matrix in NTT domain - 3:
for to do - 4:
for to do - 5:
▹ two-byte domain separator - 6:
if then - 7:
- 8:
absorb the 32 bytes of ; absorb - 9:
else - 10:
- 11:
end if - 12:
Initialize polynomial with n coefficients (unset) - 13:
- 14:
while do - 15:
▹ three consecutive bytes - 16:
▹ zero highest bit of every third byte - 17:
▹ little-endian 23-bit integer - 18:
if then - 19:
; - 20:
end if - 21:
end while - 22:
▹ place in the scheme’s reference NTT order - 23:
end for - 24:
end for - 25:
return
|
Module LWE
Let l be a positive integer. The hard problem underlying the security of the scheme is the Module-LWE problem. The Module-LWE is a distribution on induced by pairs , where is uniform and , with common to all samples and fresh for every sample.
Module LWE consists in recovering from polynomially many samples chosen from the Module-LWE distribution such that,
We say that , the hardness assumption holds if no algorithm A running in at most t has an advantage greater than .
Key Generation
The first step of the overall suite key generation process works as below,
The key generation described in Algorithm 3 procedure produces a public/secret key pair
based on the Module-LWE problem over the polynomial ring
. It begins by sampling two independent uniform bitstrings
using a cryptographically secure pseudorandom number generator, where
is the security parameter. The value
is expanded via ExpandMatrix into a matrix
, ensuring that
can be reconstructed by anyone possessing
, thus reducing the public key size.
| Algorithm 3 KeyGen |
- Requires:
Security parameter , modulus q, dimension parameters , decomposition parameter d, hash function , seed expansion function - Returns:
Public key , secret key - 1:
▹ Uniform seeds for matrix and secret sampling - 2:
▹ - 3:
▹ Sample in and - 4:
▹ - 5:
▹ Decompose t into low- and high-bits - 6:
- 7:
- 8:
return
|
The secret key consists of two short vectors and sampled uniformly from a bounded discrete distribution , where is small (e.g., for recommended parameter sets). These distributions produce coefficients in , ensuring both efficiency and security against lattice-reduction attacks.
The vector
is computed as
which is essentially a Module-LWE sample with secret
. To enable compression and reduce public key size,
is decomposed into a high-order part
and a low-order part
using the Power2Round function:
where
d controls the number of bits truncated from each coefficient. The high-order bits
are included in the public key, while
is stored in the secret key to allow lossless reconstruction of
during verification. The final keys are:
The use of seeds instead of explicit matrices and randomness vectors significantly reduces storage requirements while maintaining reproducibility and security [
24].
Signature Creation
The signature algorithm (also described in Algorithm 4) progresses by having the signer generate a vector
y with entries from
, using the extendable output function
seeded by
r. The vector
w is computed as
, where
lies within
. The signer then calculates
and subsequently derives
. The algorithm restarts if any
z component is at least
, or if any coefficient of
exceeds
. This is to ensure the security of the signing process and to prevent any information leakage regarding
. The verification
is crucial for the correctness of the protocol. It is noted that if
, then
, and thus
. The probability of
being below
is designed to be high, ensuring the protocol’s security by making the chances of violation negligible. Nevertheless, this check is included to raise the probability of a verifier accepting a genuine signature to unity.
| Algorithm 4 Sign |
- 1:
- 2:
- 3:
- 4:
- 5:
- 6:
- 7:
- 8:
- 9:
- 10:
- 11:
if or or then - 12:
goto 4 - 13:
end if - 14:
- 15:
if or the number of 1’s in h is greater than then - 16:
goto 4 - 17:
end if - 18:
return
|
Provided all conditions are met and a restart is deemed unnecessary, one can assert that
. If the verifier had access to the complete
t and
,
could be independently ascertained after confirming that
and
. Yet, to reduce the size of the public key, the verifier is only acquainted with
. Consequently, the signer must provide a “hint” to enable the verifier to deduce
. This is the essence of Step 12. During Step 13, the verifier conducts a series of checks that infrequently result in failure (under 1% chance), which negligibly impacts the overall execution duration. Notably, Step 12’s primary function is to compress and it does not compromise the security of the scheme, assuming the verifier has full knowledge of
t. This assumption potentially renders the actual scheme even more robust in practical applications [
24].
Verification
Given a public key
, message
, and signature
, the verifier reconstructs the NTT-domain matrix
from the seed
in the public key. Using the hint
h, the function
recovers the high-order bits
from
modulo
q, where
is the challenge polynomial. The hint encodes which coefficients require rounding adjustments so that the verifier can deterministically recover the same high-order bits as computed during signing without transmitting the full
vector. This significantly reduces the signature size while preserving correctness. The Algorithm 5 shows the verfication process.
| Algorithm 5 Verify |
- 1:
- 2:
- 3:
if and and the number of 1’s in h is then - 4:
return 1 - 5:
else - 6:
return 0 - 7:
end if
|
Next, the verifier recomputes the challenge polynomial
and checks equality
. This step binds the signature to both the message and the public key, preventing forgery by ensuring that
corresponds to the actual
value for the claimed signer.
A crucial norm bound check
ensures that the signing vector
z remains within a narrow range, mitigating leakage of the secret key via lattice-reduction attacks. Additionally, the verifier enforces that the Hamming weight of
h does not exceed
, where
is derived from the masking strategy used in the signing process. This bound limits the number of coefficients in
that could have been adjusted, constraining an adversary’s ability to manipulate hints. Due to the structure of
and parameter selection in Dilithium, the probability of verification failure when a valid signature is presented is negligible, dominated by the rare carry-propagation events involving
coefficients. For the parameter sets recommended in [
24], the carry count exceeds
with probability below
, giving an empirical verification success rate above
.
2.1.5. Efficiency Trade-Offs
To optimize key size and efficiency, Dilithium’s signing and verification procedures reconstruct the matrix
(or its NTT-domain version
) from a short seed
[
24]. When memory constraints are relaxed,
can be precomputed and stored as part of the public or secret key, along with precomputed NTT forms of
to accelerate signing. Conversely, for minimal secret key size, only a compact seed
is retained, from which all necessary randomness for
is generated. Memory use during computations can also be reduced by retaining only the NTT components currently in use. Furthermore, the scheme supports both deterministic and randomized signatures: in the deterministic variant, the signing randomness seed
is derived from the message and key, producing identical signatures for the same message; in the randomized variant,
is chosen uniformly at random. While deterministic signing avoids randomness costs, randomized signing may be preferable when mitigating side-channel attacks or concealing the exact message being signed.
2.1.6. Parameter Sets for CRYSTALS-Dilithium
Table 3,
Table 4 and
Table 5 summarize the output sizes, core parameters, and estimated hardness levels for CRYSTALS-Dilithium across multiple security targets. The first two tables correspond to the parameter sets proposed for NIST security levels 2, 3, and 5, which align with
128,
192, and
256 bits of post-quantum security, respectively, under the Module-LWE and Module-SIS hardness assumptions. The third table extends this to include “challenge” parameter sets (1−−, 1−, 5+, 5++), designed to explore the margins of the scheme’s security.
Parameter Details
q: The modulus used for all polynomial coefficient arithmetic. For Dilithium, is a 23-bit prime supporting efficient NTTs.
d: The number of least significant bits dropped from each coefficient of during , used to compress the public key.
: The Hamming weight of the challenge polynomial c, i.e., the number of coefficients equal to .
Challenge entropy: bits; reflects the search space for valid challenges.
: Bound on the infinity norm of the vector in signing; higher values increase rejection probability but enlarge the range of signatures.
: Range parameter for the decomposition; impacts correctness and compression efficiency.
: Dimensions of the public matrix in ; jointly determine the Module-LWE dimension.
: Bound for secret key coefficients; small yields more efficient signing but affects hardness.
: Verification bound parameter, typically .
: Maximum allowed number of 1’s in the hint vector h; constrains information leakage.
Repetitions: Expected number of signing attempts (restarts) due to bound checks.
For the extended challenge parameter sets in
Table 5, the “1
” and “1−” levels correspond to parameter choices below the NIST level 1 target. The 1− set targets significantly reduced security (less than 60 bits of Core-SVP hardness) to act as a “canary” for improvements in lattice cryptanalysis: if such parameters can be broken in practice, it signals a need to reassess all higher levels. The 1− set retains roughly 90 bits of Core-SVP hardness and a BKZ block-size of
300, serving as a conservative low-end benchmark.
The “5+” and “5++” sets represent above NIST level 5 security, anticipating moderate advances in lattice algorithms. The 5+ set achieves slightly more than NIST level 5 hardness, while the 5++ set has roughly twice the Core-SVP security of level 3 (and well above level 5), making it a forward-looking choice if future cryptanalytic results begin to threaten current level 3 or level 5 parameters.
These extended sets help bound the safe operating range for Dilithium [
24]. On the low-security side, they offer an early warning indicator for practical breaks; on the high-security side, they show how the parameters would scale to preserve security in the face of improved attacks. Because the underlying lattice hardness dominates the overall security, these adjustments are made without altering the security of symmetric primitives, such as the hash functions or PRFs used internally.
2.1.7. Known Attacks and Security
The security of Dilithium depends on the standard hard problems: Module Learning with Errors (MLWE), Module Short Integer Solution (MSIS), and Self Target MSIS. The standard definition of these three problems has been taken from [
27]. This means that it suffices to show that the secret key can not be forged using the public key [
13]. Under another assumption, a variant of the Module-SIS, called SelfTargetMSIS [
27], Dilithium is strongly unforgeable [
13,
24]. The most well-known attacks against Dilithium, which do not take advantage of side-channels, are similar to other lattice-based approaches in that they involve using general algorithms to locate short vectors within lattices. For Dilithium, the core SVP security is roughly 124, 186, and 265 for NIST levels 2, 3, and 5, respectively [
13]. Ref. [
28] shows the single-trace side-channel attacks by exploiting some information leakage in the secret key. The authors of [
29] introduce two novel attacks on randomized/hedged Dilithium that include key recovery. The concept of fixing incorrect signatures after they have been signed underlies both attacks. The value of a secret intermediate carrying key information is obtained upon successful rectification. Once a large number of incorrect signatures and their matching rectification values have been gathered, the signing key can be found using either basic linear algebra or lattice-reduction methods. The common form of attacks on Dilithium are as follows: (i) Side-Channel attack which focuses on the strategy to recover the secret key by exploiting the underlying polynomial multiplication [
27,
29,
30,
31]; (ii) Fault Attack which makes the deterministic version of Dilithium vulnerable. In this type of attack, an adversary can inject a single random fault during the signature generation to a message
m, then let the
m be signed again without any breach. By doing this a fault-induced non-reuse scenario is achieved, making the key recovery trivial using a single faulty signature [
29,
32]. And [
33] extended this attack to the randomized version of Dilithum as well. Ref. [
29] introduced another variant of the skipping fault attack introduced by [
34]. Readers are suggested to read [
24,
27,
28,
30] for a more comprehensive security analysis.
Definition 1 (Module Learning with Errors (MLWE)). Let . The advantage of an algorithm for solving is defined as: Here, the notation
denotes
as a function of
x. We note that the MLWE problem is often phrased in other contexts with the short vectors
and
coming from a Gaussian, rather than a uniform, distribution. The use of a uniform distribution is one of the particular features of CRYSTALS-Dilithium [
27].
The second problem, MSIS, is concerned with finding short solutions to randomly chosen linear systems over .
Definition 2 (Module Short Integer Solution (MSIS)). Let . The advantage of an algorithm for solving is defined as: The third problem is a more complex variant of MSIS that incorporates a hash function H.
Definition 3 (SelfTargetMSIS). Let and , where is the set of polynomials with exactly τ coefficients in and all remaining coefficients are zero. The advantage of an algorithm for solving is defined as: From [
27,
35],
where all terms on the right-hand side of the inequality depend on parameters that specify Dilithium, and sEUF-CMA stands for strong unforgeability under chosen message attacks. The interpretation of Equation (
5) is: if there exists a quantum algorithm
that attacks the sEUF-CMA-security of Dilithium, then there exist quantum algorithms
for MLWE, SelfTargetMSIS, and MSIS that have advantages satisfying the inequality comparable to
. Equation (
5) implies that breaking the sEUF-CMA security of Dilithium is at least as hard as solving one of the MLWE, MSIS, or SelfTargetMSIS problems. MLWE and MSIS are known to be no harder than LWE and SIS, respectively [
27,
35].
2.1.8. Evolution of Dilithium on NIST Submission
Based on the submission details provided by CRYSTALS-Dilithium [
24] and the NIST submission report [
13], we note the major changes and updates that occurred in the core algorithms and related sub-processes in Dilithium suites in the
Figure 3.
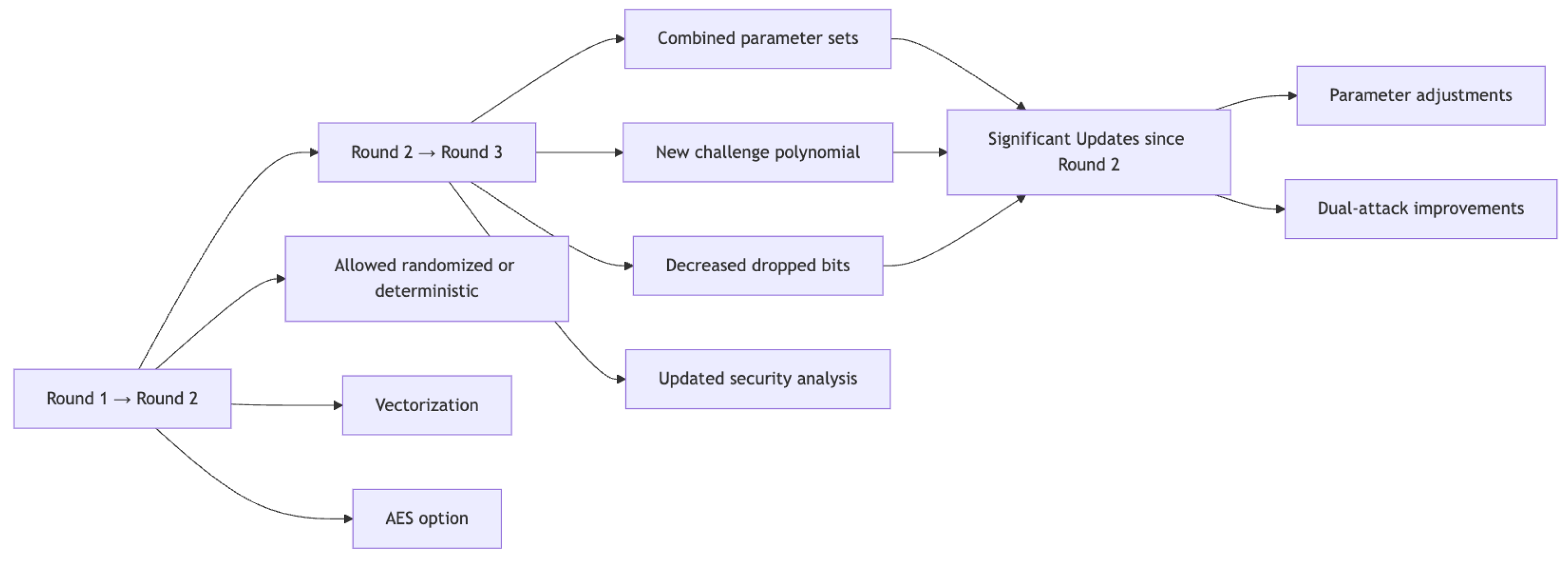
Important Updates (Round 1 → Round 2)
The primary conceptual design change was to allow the scheme to be either randomized or deterministic.
For the deterministic and randomized version, the function ExpandMask uses a 48-byte seed instead of a key and the message.
The nodes of various expansion functions for matrix A, masking vector y, and secret vectors are all 16-bit integers.
Implementation changes included vectorization and a simpler assembler NTT implementation using macros.
An optimized version using AES instead of SHAKE was introduced.
Important Updates (Round 2 → Round 3)
Combined the first two parameter sets into one NIST level 2 set and introduced a level 5 parameter set.
Now outputs challenges with 39 and 49 coefficients for security levels 2 and 3, respectively, instead of always outputting with 60 nonzero coefficients.
Decreased the number of dropped bits from the public key from 14 to 13, increasing SIS hardness.
The masking polynomial is now sampled from a range with power-of-2 possibilities.
Changed the challenge sampling and transmission method to use a 32-byte challenge seed.
Updated concrete security analysis based on recent progress and lattice algorithms.
Significant Updates Since Round 2
Changes and parameter set adjustments to better match NIST security levels.
Improvements to the dual attack proposed during the third round suggested lower estimated security in the RAM model than claimed, indicating two of the three-parameter sets fell slightly below the claimed security levels when memory access costs are considered.
2.2. McEliece Cryptosystem
In 1978, in the early history of public key cryptography, McEliece proposed using a generator matrix as a public key, and encrypting a code word (an element of code) by adding a specified number of errors to it [
16]. The McEliece cryptosystem [
36] is based on the concept of error correcting codes. The error-correcting codes are designed to detect and correct errors in transmitted messages. These codes can be in the form of vectors. The general approach is to add errors during the encoding and also add some extra information to the message, such that during decoding, some of the errors may be corrected using the supplied extra information. For example, let us assume we have a message ciphertext
c, and we add errors
e, which makes the final message
. Then, when the person on the receiving end receives this message, he/she has to work his/her way to recover from the error and reconstruct the original message that was intended to be received.
Right now, the McEliece cryptosystem is being considered as one of the candidates for the Round 4 standardization for KEM [
18]. To begin to understand this code-based cryptosystem, we need to describe some of the core mathematical concepts.
A field is a set F equipped with two binary operations, addition and multiplication, denoted and , satisfying the following properties for all . First, addition and multiplication are associative, such that and . Second, both operations are commutative, so and . Third, there exist distinct identity elements: an additive identity such that , and a multiplicative identity such that and . Fourth, for each , there exists an additive inverse such that , and for each with , there exists a multiplicative inverse such that . Finally, multiplication distributes over addition, so .
A finite field , also known as a Galois field and denoted , is a field with q elements, where is a prime power for some prime p and positive integer n. The prime p is the characteristic of the field.
An extension of a finite field is a Galois field of order , where p is a prime and k is a positive integer. The field is a field extension of degree k over , constructed as a vector space of dimension k over with operations defined modulo an irreducible polynomial of degree k in . This structure underpins many applications in algebra, number theory, and related fields.
The Hamming distance between two binary strings
and
of equal length
n is defined as the number of positions at which their corresponding bits differ. Formally, for binary strings
, the Hamming distance
is given by
where ⊕ denotes the exclusive OR operation, and
represent the
k-th bits of
and
, respectively.
For an error-correcting code
, the minimum Hamming distance of
C, denoted
, is the smallest Hamming distance between any pair of distinct codewords in
C. It is defined as
This quantity determines the error-correcting capability of the code, as a larger enables the detection and correction of more errors.
The Hamming weight of a codeword
, denoted
, is the number of nonzero entries (i.e., ones) in
. Mathematically,
To optimize error correction, codewords in C are designed to be maximally separated in terms of the Hamming distance. This is achieved by ensuring that legal codewords, those belonging to C and adhering to its structure, are sufficiently distinct from one another. Illegal codewords, which lie outside C and do not conform to its structure, are distributed to maximize the separation, thereby enhancing the minimum Hamming distance . This construction underpins the robustness of error-correcting codes in applications such as coding theory and data transmission.
Linear Codes
A linear code of dimension k and length n over a field F is a k-dimensional subspace of the vector space , which consists of all n-dimensional vectors over F. This code is referred to as an code. If the minimum Hamming distance of the code is d, then the code is called an code. A linear code C of dimension k and length n over a field F is a k-dimensional subspace of the vector space . The elements of C are called codewords. The parameters of the code are defined as follows:
Length n: The number of components in each codeword.
Dimension k: The number of linearly independent codewords in the code.
Minimum Hamming Distance d: The smallest Hamming distance between any two distinct codewords in the code.
The code
C can be described as an
code. If the minimum Hamming distance is
d, the code is described as an
code. Since a linear code is a vector space, each codeword within it can be expressed as a linear combination of basis vectors. This means that knowing a basis for the linear code is essential for describing all the codewords explicitly [
16].
Goppa Codes
A Goppa code is a linear, error-correcting code for message encryption and decryption. Let a Goppa polynomial be defined as a polynomial over
, that is,
with each
. Let
L be a finite subset of extension field
,
p being a prime number, say
such that
.
Now, given a codeword vector
over
, we have a function,
where
is the unique polynomial with
with a degree less than or equal to
. Then, a Goppa code
is made up of all code vectors
C such that
. This means that the polynomial
divides
.
A generator matrix G for a Goppa code is a matrix whose rows form a basis for the Goppa code. Here, k is the dimension of the code and n is the length of the code.
Given a Goppa code
with
and a Goppa polynomial
, the generator matrix
G is defined as follows:
where each row
(for
) is a basis of the Goppa code
.
To encode a message using Goppa codes, the message is multiplied by the generator matrix of the Goppa code, G. Specifically, the message is written as a block of k symbols. Each block is then multiplied by the generator matrix G, resulting in a set of codewords C.
Generator Matrix: Let
G be the
generator matrix for the Goppa code
:
Message Block: Let
be a message block of
k symbols:
Encoded Codeword: The encoded codeword
is obtained by multiplying the message block
by the generator matrix
G:
Resulting Codeword: The resulting codeword
is a row vector of length
n:
Decoding is performed by correcting the code using Patterson’s Algorithm [
37] (also presented in Algorithm 6, which essentially involves solving the system of
n equations with
k unknowns. For the message vector
, where
exactly at
r places. The process starts by locating the position of the error,
. After locating the position of the error, we then retrieve the value of the error
. To achieve this, we need two polynomials: a locator polynomial
and an error evaluator polynomial
. These polynomials have
j and
degree, respectively. We need to compute syndrome
, solve the equation
, then determine the error location
, then compute the error value using the position, and finally, the codeword sent is calculated by
or in vector form,
.
| Algorithm 6 Patterson’s Algorithm for decoding Goppa codes |
- 1:
Input: Received word - 2:
Output: Decoded codeword - 3:
Initialization: Let - 4:
Compute the Syndrome - 5:
Compute the syndrome : - 6:
Forming the Key Equation - 7:
Construct the syndrome polynomial from - 8:
- 9:
Solving the Key Equation - 10:
Use the Euclidean algorithm to solve for the error locator polynomial and the error evaluator polynomial - 11:
Finding Error Locations - 12:
Determine the error locations by finding the roots of :
where is the set of error positions - 13:
Step 5: Correcting Errors - 14:
Correct the errors at the identified positions in to obtain the decoded codeword - 15:
return
|
2.3. Classic McEliece KEM Algorithms
The Classic McEliece Key encapsulation mechanism presented in the NIST submission [
38] consists of algorithms as follows: irreducible-polynomial generation, field-ordering algorithm, key generation, fixed-weight vector generation, and finally, encapsulation and decapsulation. These algorithms are presented below:
The
Encode function (also given in the Algorithm 7) maps a weight-
t error vector
to a corresponding codeword
using the public key
T, an
matrix over
. The algorithm constructs the systematic form of the parity-check matrix
and computes the syndrome
in
. This transformation is linear and deterministic, enabling direct verification in the decoding stage.
| Algorithm 7 Encode |
- Requires:
with , public key - Returns:
Codeword - 1:
Define - 2:
- 3:
return C
|
The
Decode function (also presented in the Algorithm 8) attempts to recover the weight-
t error vector
e from a given codeword
using the private key information
. The private key includes
where
g is the Goppa polynomial and
are field elements used in the code definition. Decoding succeeds if, and only if, there exists a unique
e of weight
t such that
with
; otherwise the function returns ⊥. The uniqueness property of
e follows from the error-correcting capability of the Goppa code.
| Algorithm 8 Decode |
- Requires:
, secret key component - Returns:
Error vector e or ⊥ if decoding fails - 1:
Extend C to by appending k zeros - 2:
Find the unique such that:
If no such c exists, return ⊥
- 3:
- 4:
if and then return e - 5:
else return ⊥ - 6:
end if
|
The
Irreducible Algorithm 9 generates a monic irreducible polynomial
of degree
t, where
. The procedure begins by parsing the input bitstring into coefficients
, thereby constructing an element
in the extension field. The minimal polynomial
g of
over
is computed; this ensures that
g is the smallest-degree polynomial having
as a root. If the resulting degree is not exactly
t, the candidate is discarded and a new one is generated. This polynomial defines the Goppa code parameters and has a direct impact on the security of the scheme.
| Algorithm 9 Irreducible |
- Requires:
Random seed , parameters - Returns:
Monic irreducible polynomial of degree t - 1:
Parse into - 2:
- 3:
minimal polynomial of over - 4:
if then return failure - 5:
end if - 6:
return g
|
The
FieldOrdering Algorithm 10 deterministically maps a bitstring to an ordered sequence
of distinct elements in
. The input is interpreted as integers
, and uniqueness is verified. The elements are then sorted to produce a fixed ordering used in the evaluation of the Goppa code. Duplicate entries invalidate the ordering and trigger a restart.
| Algorithm 10 FieldOrdering |
- Requires:
Random seed , parameter m - Returns:
Ordered list - 1:
Parse into - 2:
if are not all distinct then return failure - 3:
end if - 4:
Sort lexicographically - 5:
Map each to - 6:
return
|
KeyGen (Algorithm 11) produces a public/secret key pair by first generating a master seed
and delegating to
SeededKeyGen (Algorithm 12). The seeded variant expands
into seeds for field ordering, Goppa polynomial generation, and matrix generation. The public key contains the systematic form of the parity-check matrix, while the private key stores
are needed for decoding. Failures in irreducibility checks, ordering uniqueness, or matrix formation trigger regeneration.
| Algorithm 11 KeyGen() |
- 1:
random seed - 2:
return SeededKeyGen
|
| Algorithm 12 SeededKeyGen |
- Requires:
Seed - Returns:
Public key , secret key - 1:
Expand into - 2:
FieldOrdering - 3:
Irreducible - 4:
MatGen - 5:
if any step fails then return failure - 6:
end if - 7:
- 8:
- 9:
return
|
The
MatGen function (Algorithm 13) constructs the public parity-check matrix from the Goppa polynomial and ordered field elements. A Gaussian elimination procedure attempts to reduce the matrix to systematic form. In semi-systematic cases, partial reduction with controlled column swaps is applied. The procedure may fail if the matrix is not full rank.
| Algorithm 13 MatGen |
- Requires:
, , seed - Returns:
Public matrix T, secret permutation S - 1:
Build H from g and - 2:
Attempt to reduce H to systematic form via Gaussian elimination - 3:
if reduction fails then return failure - 4:
end if - 5:
Output reduced T and permutation S
|
This Algorithm 14 samples a binary vector
with exactly
t ones, uniformly over all such vectors. It is implemented by selecting
t distinct indices without replacement and setting the corresponding positions to 1.
| Algorithm 14 FixedWeight |
- Requires:
Weight t, length n - Returns:
Vector with - 1:
- 2:
Choose t distinct positions uniformly at random - 3:
Set those positions in e to 1 - 4:
return e
|
Encap (Algorithm 15) creates a shared secret and corresponding ciphertext. A random error vector of weight
t is generated, encoded under the public key to produce the ciphertext, and hashed along with fixed domain separation to yield the session key.
| Algorithm 15 Encap |
- Requires:
Public key - Returns:
Ciphertext C, shared key K - 1:
FixedWeight - 2:
Encode - 3:
Hash - 4:
return
|
Decap (Algorithm 16) recovers the session key from the ciphertext. Using the private key, the ciphertext is decoded to retrieve
e. If decoding fails, a fallback secret is used to preserve CCA security.
| Algorithm 16 Decap |
- Requires:
Secret key , ciphertext C - Returns:
Shared key K - 1:
Decode - 2:
if decoding fails then - 3:
default secret - 4:
end if - 5:
Hash - 6:
return K
|
The overall process consists of three core stages: KeyGen (and its variant SeededKeyGen), Encap, and Decap, which together enable secure key establishment under the chosen code-based cryptosystem. During the KeyGen stage, a uniform random seed is generated, from which the public matrix A (or T in the McEliece context) and associated secret vectors are derived via deterministic expansion functions such as ExpandMatrix. The public key encapsulates the matrix seed and auxiliary high-bit components, while the private key stores the matrix seed, secret polynomials or vectors, and decomposition artifacts necessary for reconstruction and decoding. In the Encap stage, the sender selects a fixed-weight error vector (with ) uniformly at random, then computes the syndrome using the public parity-check matrix . This syndrome C forms the ciphertext (optionally concatenated with auxiliary components) and is used as input to a cryptographic hash function to derive the shared session key K. This ensures that the session key is computationally indistinguishable from random under the hardness of the underlying syndrome decoding problem. The Decap stage uses the private key to perform error recovery via the Decode subroutine, which applies the secret structure to correct the received codeword and retrieve the original error vector e. Integrity checks are applied by recomputing the syndrome and comparing it against the received ciphertext. If the verification passes, the same function is applied to C to reconstruct the session key K; otherwise, a pseudorandom fallback key is returned to preserve CCA-security. This design ensures that only holders of the private key can recover the legitimate session key, while adversaries without decoding capability cannot distinguish it from random.
2.3.1. Parameter Sets
In
Table 6 Coefficients of
lie in
; hence, terms like “
” denote field coefficients in
. A dash “—” indicates the public key is in full systematic form. The semi–systematic choice
follows the submission and adjusts the reduction shape of the parity-check matrix to improve robustness of key generation for those sets.
2.3.2. Known Attacks and Security
The security of McEliece like other code-based KEMs relies on the inherent difficulty of general and syndrome decoding problems [
13]. For any vector
, let
denote the Hamming weight of
v. These hard problems are defined as below [
13,
16,
39].
(Decisional Syndrome Decoding problem) Given an parity-check matrix H for C, a vector , and a target , determine whether there exists that satisfies and .
(Decisional Codeword Finding problem) Given an parity-check matrix H for C and a target , determine whether there exists that satisfies and .
The most common form of attacks on the code-based cryptographic algorithm are the Information-Set Decoding (ISD) attack originally introduced by Prange [
40] and many variants that have been studied afterward [
39,
41]. This approach ignores the structure of the binary code and seeks to recover the error vector based on its low Hamming weight [
13]. Given an
matrix
G over
, vector
, and error vector
of weight
t, we consider the ciphertext
. Select
k positions in
C, ensuring these positions in
e are all zero with probability
. If this set is error-free, then the selected positions in
C match those in
. Recover
a from these positions using linear algebra. Verify success by checking if
has weight
t; otherwise, choose a new set. The
matrix formed by selecting these positions in
G may not be invertible. To handle this, choose an “information set” where the resulting matrix is invertible, retrying as needed. This is the original form of information-set decoding [
39,
40]. Moving forward after Prange, the ISD attacks were improved by Lee-Brikell [
39,
42] by assuming multiple errors in the information set rather than the original 0 case. Later the attack was further improved by Leon’s work [
43], which instead of computing all positions of
, just proposed checking if
has weight
t, from the information set
a [
39]. Later on, Stern, and more lately Becker et al., showed a more sophisticated version of this attack by leveraging the combinatorial searches for errors in the given information set [
39,
44,
45].
Alternatively, the scheme’s security can be based on the assumptions that row-reduced parity check matrices for binary Goppa codes in Classic McEliece are indistinguishable from those of random linear codes of the same dimensions and that the syndrome decoding problem is hard for such random codes. Current cryptanalysis supports these assumptions [
13]. It has also been shown as IND-CCA2 secure against all ROM attacks [
13,
39,
46,
47].
2.3.3. Major Updates in McEliece KEM NIST Submission [13,47]
Security Stability: The security level of the McEliece system has remained stable over 40 years despite numerous attack attempts; it was originally designed for security but is scalable to counter advanced computing technologies, including quantum computing.
Efficiency Improvements: Significant follow-up work has improved the system’s efficiency while preserving security, including a “dual” PKE proposed by Niederreiter, and various software and hardware speedups.
KEM Conversion: The method to convert an OW-CPA PKE into a KEM that is IND-CCA2 secure against all ROM attacks is well known and tight, preserving security level with no decryption failures for valid ciphertexts.
Handling QROM Attacks: Recent advances have extended security to handle a broader class of attacks, including QROM attacks, by using a high-security, unstructured hash function.
Classic McEliece (CM) Design: The NIST submission for Classic McEliece (CM) aims for IND-CCA2 security at a very high level, even against quantum computers, leveraging Niederreiter’s dual version using binary Goppa codes.
2.4. BIKE: Bit Flipping Key Encapsulation
A bit flipping key encapsulation (BIKE) is a public key encapsulation technique [
48] also known widely as a KEM technique, which is also based on coding theory. It is also one of the finalized candidate post-quantum algorithms in the NIST PQC standardization competition and is currently being considered for the Round 4 competition [
49]. The design of BIKE is based on the Niederreiter-based KEM instantiated with QC-MDPC codes and leverages the Black-Gray-Flip Decoder implemented in constant times [
48,
49]. In other words, it is the McEliece schema instantiated with QC-MDPC and relies on the hardness of quasi-cyclic variants of the hard problems from coding theory [
49].
2.4.1. Preliminaries
: The binary finite field, consisting of two elements {0, 1} with addition and multiplication defined modulo 2. Usage: Used for defining elements in binary operations and polynomial arithmetic.
: A cyclic polynomial ring, specifically, . Here, is a polynomial of degree r, and the operations are performed modulo this polynomial. Usage: Represents the set of polynomials used in encoding and decoding processes.
: The private key space consisting of pairs of sparse polynomials in such that the Hamming weights of and are each . Usage: Used to generate private keys in the BIKE scheme.
: The error space, consisting of pairs of polynomials in where the sum of their Hamming weights is t. Usage: Represents the error vectors used in the encoding process.
: The Hamming weight of a binary polynomial g in , defined as the number of nonzero coefficients in g. Usage: Used to measure the sparsity of polynomials.
: Denotes that the variable u is sampled uniformly at random from the set U. Usage: Used in key generation and error vector selection processes.
⊕: The exclusive OR (XOR) operation, performed component-wise when applied to vectors. Usage: Used in bitwise operations within the encoding and decoding algorithms.
2.4.2. QC-MDPC Code
BIKE is based on the Quasi-Cyclic Moderate Density Parity Check (QC-MDPC) codes, which are also related to the Low Density Parity Check (LDPC) codes [
50]. A Quasi-Cyclic Moderate Density Parity Check code of index 2, length
n, and row weight
w is defined as a pair of sparse parity polynomials
. These polynomials form the private key used in the encoding and decoding processes. Decryption in BIKE is performed by decoding a QC-MDPC code, which is usually performed using a variant of the bit-flipping algorithm [
50].
Mathematically, a QC-MDPC code is defined by its parity-check matrix [
51]
H, which has the following properties:
H is composed of two circulant blocks, each of size .
The matrix can be written as:
where
and
are circulant matrices derived from the polynomials
and
, respectively.
Each row of and contains exactly ones, reflecting the sparsity condition.
A codeword
c in the QC-MDPC code satisfies the equation:
where
c is a binary vector of length
n.
2.4.3. Decoder
Let
be the ring of binary circulant polynomials of degree
. The private key consists of two sparse parity polynomials
, each of Hamming weight
w, and the public key is
. The decoder is required to satisfy the correctness condition that for any error pair
with
,
Equivalently, given a syndrome and the secret support , the decoder recovers the unique of weight at most t. In practice, BIKE instantiates the decoder with an iterative bit-flipping procedure on the QC-MDPC code defined by .
2.4.4. Algorithms for BIKE-KEM
Key Generation
The key generator (Algorithm 17) samples two weight-
w polynomials
uniformly from
and computes the public key
in
(the inverse exists with overwhelming probability for BIKE parameters). A random seed
is stored for FO-style fallback during decapsulation.
| Algorithm 17 Key Generation (KeyGen) |
- 1:
Input: None - 2:
Output: , - 3:
- 4:
- 5:
|
Encapsulation
To encapsulate (Algorithm 18, the sender draws
, hashes it to a sparse error pair
of total weight
t, and forms the ciphertext
with
and
, where
is a leakage-resistant linearization of the error (typically a compression of its support positions). The session key is
via a KDF.
| Algorithm 18 Encapsulation (Encaps) |
- 1:
Input: - 2:
Output: - 3:
- 4:
- 5:
- 6:
|
Decapsulation
The receiver uses the secret parity pair
to decode the first ciphertext component and recover an error estimate
. The message is then reconstructed from
by inverting
. If
holds (consistency check tying the recovered message to its error), the legitimate key
is returned; otherwise the FO-fallback
is derived to preserve CCA security. The algorithm is decribed in Algorithm 19.
| Algorithm 19 Decapsulation (Decaps) |
- 1:
Input: , - 2:
Output: - 3:
- 4:
▹ with the convention - 5:
if then - 6:
- 7:
else - 8:
- 9:
end if
|
Iterative Bit-Flipping Decoder
BIKE instantiates
(Algorithm 20) with a hard-decision, majority-logic bit-flipping algorithm over the QC-MDPC code defined by the
parity-check matrix
induced by
. Starting from the syndrome
, the algorithm repeatedly (i) counts unsatisfied checks per code bit, (ii) flips bits whose counters exceed an iteration-dependent threshold, and (iii) updates the running syndrome. The number of iterations (
NbIter) and threshold schedule are selected to balance decoding success and constant-time behavior.
| Algorithm 20 BIKE Decoder |
- 1:
Input: () - 2:
- 3:
for do - 4:
- 5:
for do - 6:
▹ unsatisfied-check counter for bit j - 7:
end for - 8:
for do - 9:
if then - 10:
- 11:
- 12:
end if - 13:
end for - 14:
end for - 15:
return
|
Adaptive Threshold Schedule
The function
THRESHOLD (Algorithm 21) chooses the flipping threshold as a convex combination of (i) an “optimal” value
predicted from the syndrome weight, and (ii) the majority value
, where
d is the row weight of
H (approximately the MDPC density). The additive margin
enforces robustness and constant-time behavior. The final threshold is lower-bounded by
to avoid over-flipping late in the decoding.
| Algorithm 21 Function THRESHOLD |
- 1:
function THRESHOLD() - 2:
▹ syndrome-weight heuristic - 3:
▹ majority threshold - 4:
if then - 5:
- 6:
else if then - 7:
- 8:
else if then - 9:
- 10:
else - 11:
- 12:
end if - 13:
return - 14:
end function
|
Key generation samples and publishes . Encapsulation hashes a fresh m into a weight-t error pair , forms , protects m as , and derives . Decapsulation computes and ; if the session key is output, else the fallback is returned. Under the decoder correctness condition and for , we have and , implying and consistent key derivation on both sides; the FO-style fallback ensures CCA security for invalid ciphertexts.
2.4.5. BIKE Parameters
The BIKE Key Encapsulation Mechanism (BIKE-KEM) is parameterized to meet the NIST security categories corresponding to the classical security levels of AES-128, AES-192, and AES-256, referred to as Levels 1, 3, and 5, respectively. The parameter set for BIKE is defined as a triple
, where
r denotes the code length parameter (half the code length in bits),
w is the Hamming weight of each secret key polynomial, and
t is the maximum number of errors that can be corrected during decapsulation. For all security levels, the key length is fixed to
, and the target Decoding Failure Rate (DFR) is chosen to be negligible relative to the claimed security level—
,
, and
for Levels 1, 3, and 5, respectively, as shown in
Table 7. The values of
are carefully selected to balance decoding performance, security against information-set decoding (ISD) attacks, and resistance to structural attacks on quasi-cyclic codes. Additionally, the decoding process employs the Bit-Guess-and-Flip (BGF) algorithm, whose performance is tuned through parameters such as the number of decoding iterations (
), the threshold adaptation parameter
, and a level-specific linear threshold function
based on the syndrome weight
S. These parameters ensure that decoding remains both efficient and secure, while maintaining a decoding failure probability well below the security margin mandated by NIST. The configuration for Decoder is given in
Table 8.
2.4.6. Known Attacks and Security
The security of BIKE relies on the hardness of two hard coding theory problems: the Hardness of QCSD (Quasi-Cyclic Syndrome Decoding) and hardness of QCCF (Quasi-Cyclic Codeword Finding). The complete definitions of these problems are given below. It also has another security assumption which is the Correctness of Decoder
: a KEM is
correct if the decapsulation fails with probability at most
on average over all keys and messages [
49]).
Let the element of
is odd and even weights are denoted as
and
. For any integer
t, the parity is denoted as
, then the standard hard problems of QCSD and QCCF are [
13,
49].
QC Syndrome Decoding-QCSD)
Given and an integer , determine if there exists such that .
Codeword Finding-QCCF)
Given and an even integer with odd, determine if there exists such that .
While there is a known search-to-decision reduction for the general syndrome decoding problem, no such reduction exists for the quasi-cyclic case, and the best solvers for quasi-cyclic problems, which are based on Information Set Decoding (ISD), perform similarly for both search and decision problems [
49]. The best-known attacks against BIKE’s KEM are Information Set Decoding and its variants, as in the case of any code-based KEM, such as McEliece [
13]. Further the Quasi-Cyclic structure of the quasi-cyclic code can be exploited; it makes both codeword finding and decoding relatively easier. The details of these are given in [
49]. But different sets of parameters can be chosen to adapt to these challenges and BIKE still is IND-CAP and IND-CCA proven [
13,
49]. In the purposed cryptosystem, the key-pair should not be reused [
49], but if they are ever, then it becomes vulnerable to decoding failure attacks such as GJS rejection attacks [
52].
BIKE targets IND-CCA security by requiring decoders with extremely low decryption failure rates (DFRs)—specifically, of the order of
,
, and
for NIST Security Levels 1, 3, and 5, respectively [
49]. However, more recent empirical analysis indicates that the real-world average DFR for Level 1 may be closer to
, falling short of the design goal [
53]. This discrepancy has implications for security because multi-target key recovery attacks become more feasible when decryption failures exceed expected thresholds. Consequently, BIKE’s specification has evolved to adjust decoder thresholds and incorporate mitigations, such as weak-key filtering, to reduce DFR and preserve IND-CCA security under more realistic operational conditions [
49,
54].
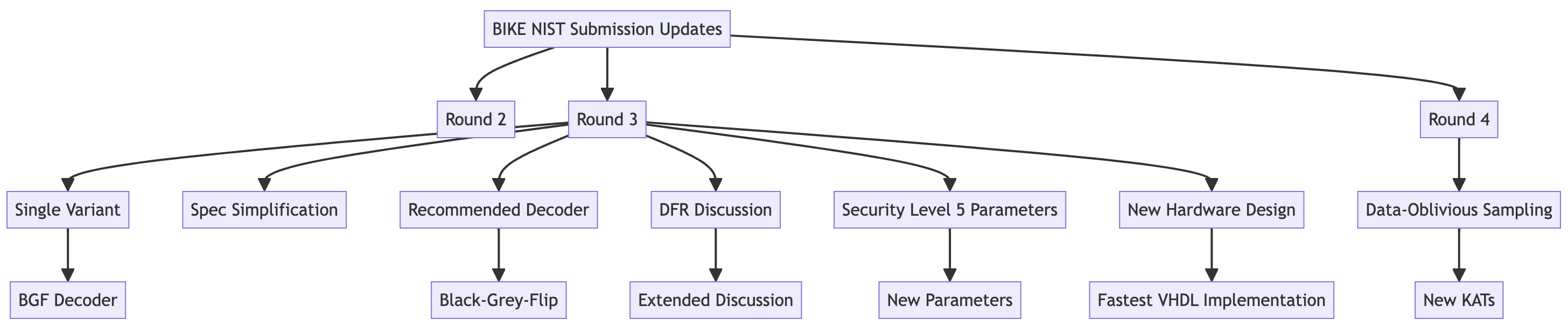
2.4.7. Major Updates in BIKE KEM NIST Submission [13,49]
Single Variant: The BIKE team narrowed down various versions of the algorithm to a single variant using the Black-Grey-Flip (BGF) decoder for enhanced security and efficiency.
Security Enhancements: Security category 5 parameters were added, and all random oracles were updated to SHA-3-based constructions to improve hardware performance and avoid IP issues.
Specification Simplification: The document structure was significantly simplified, with most mathematical background moved to the appendix.
IND-CCA Security Claim: BIKE now claims IND-CCA security with additional analysis supporting this claim.
Data-Oblivious Sampling: Introduced a data-oblivious sampling technique to mitigate side-channel attacks, generating new Known Answer Tests (KATs).
Figure 4 shows the major updates in BIKE algorithms throughout the multiple rounds of submissions.
2.5. Hamming Quasi-Cycle Cryptosystem
The Hamming Quasi-Cycle Cryptosystem is another KEM candidate currently under consideration for the 4th round of the NIST post-quantum standardization effort. HQC was motivated by the schema introduced by Alexhnovich [
55]. The trapdoor, also known as the secret key, in the [
55] schema is a random error vector that has been combined with a random codeword of a random code. Hence, finding the secret key is similar to finding out how to decode a random code that has no hidden structure [
56]. The HQC cryptosystem uses two codes: a known efficient decoding code
and a
random double-circulant code
H in systematic form to generate noise. The public key consists of the generator matrix
and the syndrome
, where
form the secret key. To encrypt a message
m, it is encoded with
, combined with
s and a short vector
, resulting in the ciphertext
. The recipient uses the secret key to decode
and retrieve the plaintext [
56].
This system does not rely on the error term being within the decoding capability of the code. In traditional McEliece approaches, the error term added to the encoding of the message must be less than or equal to the decoding capability of the code to ensure correctness. However, in this construction, this assumption is no longer required. The correctness of this cryptosystem is guaranteed as the legitimate recipient can remove enough errors from the noisy encoding
of the message using the secret key
[
13,
56].
Most of the preliminaries of HQC have been covered in the earlier sections of McEliece and BIKE; hence, here we list only the aspects that were not already covered.
Circulant Matrix [
56] Let
, the circulant matrix induced by
x is defined by,
Quasi-Cyclic Codes [
56] View a vector
of
as
s successive blocks (
n-tuples). An
linear code
is Quasi-Cyclic (QC) of index
s if, for any
, the vector obtained after applying a simultaneous circular shift to every block
is also a codeword.
More formally, by considering each block as a polynomial in , the code is QC of index s if for any it holds that .
Systematic Quasi-Cyclic Codes [
56] A systematic Quasi-Cyclic
code of index
s and rate
is a quasi-cyclic code with an
parity-check matrix of the form:
The HQC schema consists of our polynomial time algorithms. Setup: generates the global parameters needed for the algorithms; KeyGen(params): generates the public and private key . Then, Encrypt(pk, m): takes the public key and message and generates the chipertext c. Finally, Decode(sk, c): uses the private key of the receiving party and ciphertext to reconstruct the original message.
HQC uses two types of codes: a decodable
code
C, generated by
and which can correct at least
errors via an efficient algorithm
; and a random double-circulant
code, of the parity-check matrix
[
57].
The Setup (Algorithm 22) procedure derives the global coding and masking parameters from the security parameter
. The tuple
fixes the ambient ring
, the public generator matrix
of the underlying code
C, the masking/truncation length
ℓ, and the Hamming–weight constraints for secrets (
w), ephemeral randomness (
), and encryption noise (
). The decoding radius
captures the designed error-correction capability of
C used in Decrypt.
| Algorithm 22 Setup |
- 1:
Input: Security parameter - 2:
Output: Global parameters
|
Given param, KeyGen (Algorithm 23) samples a public ring element
and secret vectors
of prescribed weights
w and
, respectively. It computes
and publishes
together with the public generator
of
C. The secret key stores
. Correctness follows since, under the designed weights, decryption will subtract the structured interference
and leave a codeword plus small error within the decoding radius.
| Algorithm 23 KeyGen |
- 1:
Input: param - 2:
Sample - 3:
Generate the matrix of C - 4:
Sample - 5:
Set - 6:
Set - 7:
Output: ()
|
Encrypt (Algorithm 24) samples an encryption error
of weight
and an ephemeral pair
of weight
each. It masks a message
by forming
and
, where the truncation operator reduces bandwidth while retaining sufficient redundancy for reliable decoding. The ciphertext is
.
| Algorithm 24 Encrypt |
- 1:
Input: - 2:
Generate - 3:
Sample - 4:
Set - 5:
Set - 6:
Output:
|
Decrypt (Algorithm 25) cancels the structured mask by computing
, which ideally equals
for a noise
within the decoding radius
. Applying the decoder
recovers
m (or outputs
⊥ on failure). Correctness hinges on the weight design
and the code’s guaranteed decoding capability.
| Algorithm 25 Decrypt |
- 1:
Input: - 2:
Output:
|
From PKE to KEM. HQC-KEM wraps the above PKE with a Fujisaki–Okamoto-style transform. A fresh salt ensures domain separation and nonces the KDF/PRG, enabling deterministic re-encryption during decapsulation for robust CCA checks.
The KEM’s Setup (Algorithm 26) simply exposes the global tuple param for all parties and implementations, ensuring consistent code, weights, and truncation length across Encapsulate/Decapsulate
| Algorithm 26 Setup() |
- 1:
Outputs the global parameters .
|
KEM KeyGen (Algorithm 27) augments the PKE key pair with a uniformly random commitment string
, used as FO fallback material in case re-encryption checks fail during decapsulation. The public key remains
.
| Algorithm 27 KeyGen(param) |
- 1:
Samples . - 2:
Samples . - 3:
Generates the matrix of C. - 4:
Samples . - 5:
Sets . - 6:
Sets . - 7:
Returns .
|
Encapsulate (Algorithm 28) samples a session seed
and a 128-bit salt, derives PRG output
, and deterministically generates
with target weights
. It then constructs
exactly as in PKE and outputs the ciphertext
together with the session key
. Binding
K to both
m and
prevents key-mismatch and contributes to CCA resilience.
| Algorithm 28 Encapsulate(pk) |
- 1:
Generates . - 2:
Generates . - 3:
Derives randomness . - 4:
Uses to generate such that and . - 5:
Sets . - 6:
Sets . - 7:
Sets . - 8:
Computes . - 9:
Returns .
|
Decapsulate (Algorithm 29) first decrypts to
. It derives
, re-encrypts deterministically to
, and checks
. On success, it outputs
; otherwise, it returns the FO fallback
. This re-encryption check thwarts invalid-ciphertext and reaction attacks and ensures that only ciphertexts consistent with
lead to the “real” key.
| Algorithm 29 Decapsulate() |
- 1:
Decrypts . - 2:
Computes randomness . - 3:
Re-encrypts by using to generate such that and . - 4:
Sets . - 5:
Sets . - 6:
Sets . - 7:
if or then - 8:
. - 9:
else - 10:
. - 11:
end if
|
The HQC-KEM scheme operates through a structured sequence of steps involving setup, key generation, encapsulation, and decapsulation. In the Setup phase, global parameters are established, defining the code length, dimension, decoding threshold, and weight parameters for error vectors and random vectors. The KeyGen algorithm samples a random public vector h from , generates the generator matrix of the underlying linear code C, and selects secret vectors and of the prescribed Hamming weights, forming the secret key sk and public key pk. The procedure Encapsulate begins by sampling a random message m and a salt value, from which the randomness is derived using a hash-based function . Using , the sender generates an error vector and two random vectors , encodes them into a pair using the public key, and outputs the ciphertext along with the session key . In the Decapsulate phase, the receiver uses the secret key to decode from the ciphertext, regenerates the randomness and corresponding vectors, and verifies the ciphertext by recomputation. If the integrity check passes, the original session key is recomputed; otherwise, a fallback key derived from the secret seed is used.
2.5.1. HQC Parameters
Table 9 summarizes the main parameters of HQC across its three recommended NIST security levels 1, 3, 5 (128, 192, and 256 bits). The table presents public key sizes, ciphertext sizes, and computational costs for key generation, encapsulation, and decapsulation. Notably, the DFR is also included, which represents the probability that a legitimate ciphertext fails to decrypt correctly under normal conditions.
Although decryption failures can occur due to the probabilistic nature of code-based decoding, HQC ensures that the DFR remains negligibly small, well below the classical brute-force attack thresholds at each security level (, , , respectively). This makes HQC highly reliable in practical deployments, where such rare failures are statistically insignificant over the expected system lifetime.
2.5.2. Known Attacks and Security
The security of HQC, as in other code-based cryptosystems, relies on the decoding problem. Specifically, HQC relies on Quasi-Cycle Syndrome Decoding (QCSD) with parity problem. The Fujsaki–Okamoto transform has been applied to CPS-secure public key to achieve an IND-CCA KEM [
13]. These problems are called 2-QCSD-P and 3-QCSD-P problems; we borrow the definition from [
57].
2-DQCSD-P Problem Let n, w, be positive integers and . Given , the Decisional 2-Quasi-Cyclic Syndrome Decoding with Parity Problem 2-DQCSD-P() asks to decide with non-negligible advantage whether came from the 2-QCSD-P() distribution or the uniform distribution over .
3-QCSD-PT Distribution Let n, w, , , ℓ be positive integers and . The 3-Quasi-Cyclic Syndrome Decoding with Parity and Truncation Distribution 3-QCSD-PT() samples and such that , computes where and outputs .
Both of these problems are believed to be hard [
57] and as in other code-base KEM, the best-known attacks are ISD attacks and their variants [
13]. Although Combinatorial and Algebraic attacks are studied [
56] still the most promising attack, if there are any, remains the ISD.
2.5.3. Major Updates in HQC KEM NIST Submission [13,57]
Parameter Set Reduction:
- –
Initially included three parameter sets for security category 5 (HQC-256-1, HQC-256-2, HQC-256-3) targeting different decryption failure rates.
- –
HQC-256-1 was broken during the second round.
- –
Now only contains one parameter set per security category with low decryption failure rates.
Side-Channel Attack Mitigation:
- –
Implementations now run in constant time and avoid secret-dependent memory access to counter side-channel attacks.
Removal of BCH-Repetition Decoder:
- –
Removed due to overall improvements from the RMRS decoder.
Security Proof and Implementation Updates:
- –
Updated IND-CPA and IND-CCA2 security proofs and definitions.
- –
Incorporated HHK transform with implicit rejection, enhancing IND-CCA2 security.
- –
Replaced modulo operator with Barrett reduction to counter timing attacks.
Handling Multi-Ciphertext Attacks:
- –
Modified HQC-128 to include a public salt value in the ciphertext to counter multi-ciphertext attacks.
- –
Added counter-measures for key-recovery timing attacks [
58] based on Nicolas Sendrier’s approach [
59].
- –
Implemented a constant-time C implementation to improve security.