Abstract
Federated Learning (FL) enables collaborative model training across distributed users, while preserving data privacy by only sharing model updates. However, secure aggregation, which is essential to prevent data leakage during this process, often incurs significant communication and computational costs. Moreover, existing schemes rarely consider whether they can resist quantum attacks. To address these challenges, we propose an efficient, post-quantum aggregation protocol based on a Key Homomorphic Pseudo-Random Function (KHPRF). Our non-interactive mask elimination mechanism reduces aggregation to a single round, significantly minimizing the communication overhead. Furthermore, the KHPRF keys are reusable, enabling multiple aggregations with a one-time initialization, thereby enhancing efficiency in cross-silo federated learning. Compared to existing schemes, our approach achieves quantum-resistant aggregation with improved efficiency.
Keywords:
cross-silo federated learning; pseudo-random functions; secure aggregation; secret sharing MSC:
81P94
1. Introduction
With the tightening of data privacy regulations, such as the EU’s General Data Protection Regulation [1] and China’s Cybersecurity Law, institutions can no longer directly share raw data, due to concerns over data sovereignty and privacy. This exacerbates the “data silos” problem, where sensitive data—such as healthcare and financial records—remain fragmented across institutions, preventing centralized training. Federated learning addresses this challenge by following the principle of “data remain local, models are shared”. Instead of exchanging raw data, institutions train models locally and share only encrypted parameters (gradients/weights) for privacy-preserving collaboration. Cross-silo federated learning is particularly suited for multi-domain cooperation, such as collaborative disease diagnosis model training among healthcare providers or joint risk assessment model optimization by banks and e-commerce firms.
While federated learning mitigates the risk of direct data exposure, it remains vulnerable to various privacy threats, including membership inference attacks, gradient leakage, and data poisoning. In this work, we focus on gradient leakage attacks [2], where gradients may inadvertently reveal sensitive features of data. Attackers can exploit this information to reconstruct the original data through reverse engineering techniques, such as Generative Adversarial Network (GAN)-based attacks.
To enhance privacy in federated learning, various cryptographic techniques have been adopted, including differential privacy [3,4], homomorphic encryption [5,6], and secure multi-party computation [7,8]. However, these approaches face several challenges. While differential privacy guarantees security, it reduces the accuracy of the model. Homomorphic encryption incurs significant computational overhead, while secure multi-party computation-based privacy-preserving federated learning suffers from high computational and communication costs, particularly when transmitting high-dimensional gradients. Traditional federated learning relies on homomorphic encryption or secure multi-party computation, but these approaches face a dramatic increase in computational overhead as the model complexity increases. The differential advantage of neural cryptography provides a new solution to this problem: during the local training phase of federated learning, nodes can dynamically generate cryptographic functions for the current data distribution via an adversarial generative network GAN, while identifying the key feature dimensions to be protected via an attention mechanism. Pleshakova et al. [9] proposed a autonomous large-language model agent swarm architecture that allows for collaborative optimization of cryptographic strategies through a decentralized negotiation mechanism, maintaining model utility, while safeguarding security goals.
In addition, current privacy-preserving federated learning systems still heavily rely on quantum-vulnerable algorithms, such as traditional public-key encryption and Diffie–Hellman key exchange, whose security relies on the hardness of large integer factorization or discrete logarithm problems. Quantum computers can solve integer factorization and discrete logarithm problems in polynomial time using Shor’s algorithm. The National Institute of Standards and Technology (NIST) has set an official deadline for transitioning away from legacy encryption algorithms: by 2030, RSAECDSA, EdDSA, DH, and ECDH will be deprecated, and by 2035, they will be completely disallowed [10]. This impending quantum threat poses a significant challenge to current privacy-preserving federated learning, necessitating the development of post-quantum security mechanisms.
We propose a quantum-resistant secure aggregation scheme that minimizes the communication overhead and rounds, while avoiding the introduction of excessive noise. Our approach significantly enhances performance by reducing round complexity through a round-free, non-interactive mask elimination mechanism. This distinguishes it from prior cross-device federated learning studies, such as the recent work by Ma et al. [11,12], which, despite sharing similar objectives, relied on a Trusted Third Party (TTP) and incurred high communication overheads. Additionally, the proposed approach employs reusable aggregation parameters, making it an efficient, iterative scheme, rather than a one-time-use model. The proposed approach includes a high-cost initial setup, followed by multiple lightweight summations during training. Each global training iteration is securely aggregated using pre-established masks and intermediate parameters, thereby significantly reducing computational overhead in the aggregation phase.
Beyond performance improvements, our scheme enhances security by ensuring privacy-preserving federated learning with quantum-resistant guarantees. This is achieved through post-quantum cryptographic techniques, including the Kyber Key Encapsulation Mechanism (KEM) [13] and an implementation of KHPRF based on the Ring Learning With Rounding (RLWR) problem. We use the former for quantum-resistant key exchange and the latter to speed up the batch generation of masks for each model parameter that needs to be uploaded, as well as to guarantee the quantum-resistant security of the blinding process. In addition, the secret sharing scheme itself has a post-quantum property, so that the proposed secure aggregation process has full quantum-resistant properties. These cryptographic primitives provide robust protection against quantum attacks, securing federated learning against future adversarial threats.
We focus on designing a secure aggregation scheme for privacy-preserving federated learning, and our main contributions are as follows:
- 1.
- We introduce a novel post-quantum secure aggregation scheme with low communication overhead, low communication rounds, and no TTP. This approach provides a new entry point for constructing privacy-preserving federated learning systems. Furthermore, our scheme is adaptable to various application domains, including smart grids and sensor networks.
- 2.
- We construct privacy-preserving cross-silo federated learning using the aforementioned secure aggregation scheme based on secret sharing scheme and KHPRF. By exploiting the key homomorphism property of KHPRF, we optimize the mask-based secure aggregation mechanism, significantly reducing the round complexity compared to classical double-masking schemes. Our approach achieves the minimal round complexity of just one round (the same round complexity as federal learning without privacy protection) in the aggregation phase. Additionally, it supports multiple aggregations, without requiring repeated initialization, making it highly efficient for cross-silo federated learning.
The remainder of this article is composed of the following sections: In Section 2, we review related works. Section 3 introduces the notations and necessary background definitions. Section 4 proposes our privacy-preserving aggregation method, detailing its core mechanisms. A comprehensive security analysis, including formal proofs and correctness verification, is provided in Section 5. Section 6 analyzes the theoretical and experimental results, with comparisons to existing approaches. In Section 7, we discusses the findings, including a summary of the results, quantitative comparison, and applicability limits. Finally, the conclusions and future work are summarized in Section 8.
2. Related Works
Machine learning models increasingly leverage user and enterprise data to enhance service quality in real-world applications. However, this reliance on, often sensitive, data raises significant concerns regarding potential exposure and security risks. Consequently, balancing data privacy requirements with the need for high-quality, data-driven services remains a central challenge. This challenge is amplified when training is outsourced to third parties, making robust data privacy during the training process critical. Various privacy-enhancing technologies, including differential privacy, homomorphic encryption, and secret sharing schemes, have been developed to address these concerns in the context of federated learning.
2.1. Classical Secure Federated Learning
Classical approaches aim to secure federated learning using established cryptographic and privacy techniques.
- Differential Privacy: Differential privacy introduces noise into data or model updates to provide formal privacy guarantees. Wang et al. [3] introduced a local differential privacy mechanism transforming user data into randomized bit strings, reconstructed later by an edge server. While safeguarding user privacy and maintaining data usability to some extent, this method incurs significant computational complexity for data reconstruction. Similarly, Tran et al. [4] proposed a privacy-preserving FL framework employing differential privacy techniques (including DP-GANs) and optimized model-agnostic meta-learning algorithms. Their goal was to achieve client instance-level privacy and support personalized model training. However, this framework suffers from high computational and communication overheads, and faces difficulties in optimally balancing privacy guarantees with model performance.
- Homomorphic Encryption: Homomorphic encryption allows computations on encrypted data, enabling secure aggregation, without exposing raw model updates. Zhang et al. [5] designed BatchCrypt for cross-silo federated learning, utilizing quantization, encoding, and batch encryption to reduce encryption and communication overheads, accelerate training, and maintain model quality. Nonetheless, BatchCrypt has limitations regarding synchronization requirements, scalability to very large models, and applicability in vertical-federated learning settings. Liu et al. [7] introduced the DHSA scheme, which integrates multi-key homomorphic encryption with a seeded homomorphic pseudo-random number generator. DHSA offers strong security guarantees, notably defending against collusion threats involving up to participants and the aggregator. While minimizing the computational/communication overhead and reducing round complexity, DHSA is limited by its inability to support one-time initialization and its applicability being restricted to specific scenarios. Zhang et al. [14] proposed the QPFFL framework, integrating functional encryption and homomorphic encryption techniques alongside a privacy-preserving reputation mechanism. This aimed to achieve privacy preservation, fairness guarantees, and robustness enhancement. However, QPFFL relies on a TTP, incurs high computational and communication overheads, and makes certain idealized assumptions.
- Secret Sharing Schemes: A secret sharing scheme distributes shares of a secret (e.g., model updates) among multiple parties, such that only authorized subsets can reconstruct it. This technique is often used for secure aggregation. Building upon the classic double-mask scheme proposed by Bonawitz et al. [8], Bell et al. [15] introduced BBGLR, which employs graph-theory based communication structures, multiple cryptographic primitives, and secret sharing for efficient and secure aggregation. Despite its advancements, BBGLR’s overheads offer room for improvement, it does not handle adaptive adversaries, and requires re-initialization for each aggregation round. Kadhe et al. [16] proposed FastSecAgg, aiming for low-overhead secure aggregation using an SSS based on the Fast Fourier Transform and Chinese Remainder Theorem, combined with authenticated encryption. However, it exhibits lower resistance to collusion compared to certain other schemes and faces practical deployment challenges. So et al. [17] presented LightSecAgg, a lightweight protocol that reconfigures one-time aggregation masks using encoding/decoding techniques. This significantly reduces server-side computation, while preserving privacy and fault-tolerance guarantees similarly to existing protocols. However, its design and implementation are relatively complex, it introduces additional communication overhead, and relies on an ‘honest-but-curious’ threat model, potentially limiting its security in the face of malicious attackers. Tran and Hu et al. [18] utilized a secret sharing scheme to develop a two-layer encryption scheme, avoiding reliance on a TTP or multiple non-colluding servers. Their approach supports dynamic client participation but requires five communication rounds for aggregation and lacks support for one-time initialization.
In summary, classical security techniques provide foundational methods for privacy-preserving federated learning, but often involve trade-offs between security strength, computational/communication efficiency, system complexity, and underlying trust assumptions.
2.2. Quantum-Resistant Federated Learning
The advent of powerful quantum computers poses a significant threat to classical cryptographic schemes based on problems like large integer factorization or discrete logarithms (e.g., traditional homomorphic encryption, Diffie–Hellman). This has motivated the development of post-quantum federated learning frameworks.
Xu et al. [19] pioneered the integration of post-quantum security into federated learning with LaF. LaF utilizes a lattice-based multipurpose secret sharing scheme to achieve post-quantum secure aggregation, with lower communication costs than the scheme of Bonawitz et al. [8], albeit at the cost of higher computation. Zhang et al. [14], in their QPFFL framework (also mentioned in Section 2.1), specifically employed the lattice-based BFV homomorphic encryption scheme alongside functional encryption to achieve efficient post-quantum secure aggregation, while also incorporating fairness and robustness mechanisms. However, as noted earlier, the framework’s reliance on a TTP remains a significant practical limitation. Gharavi et al. [20] proposed PQBFL, aiming for a quantum-attack-resistant, efficient, and scalable framework. It combines the lattice-based Kyber algorithm with Elliptic Curve Diffie–Hellman (potentially in a hybrid approach) via dual key exchange and incorporates a dynamic key rotation mechanism managed through a blockchain for transparency. Potential limitations stem from the inherent latencies and scalability challenges associated with blockchain technology. Zhang et al. [21] designed Improved-Pilaram, a lattice-based multi-stage secret sharing scheme, which formed the basis for their PQSF framework for post-quantum secure federated learning. Notably, similar to the objective of our work, their scheme supports a single initialization followed by multiple aggregation operations. Nevertheless, PQSF still incurs high computational, communication, and rounding overheads.
3. Preliminaries
This section introduces the basic cryptographic primitives used in our construction. The notations used in this paper are defined in Appendix A.
3.1. Key-Homomorphic Pseudo-Random Functions (KHPRFs)
3.1.1. PRF and KHPRF
The concept of a Pseudo-Random Function (PRF) was first introduced by Goldreich, Goldwasser, and Micali in 1986 [22], in which they also proposed a construction for a pseudo-random number generator.
To begin with, we briefly introduce the concept of a PRF: A PRF is a deterministic function denoted as . It takes two inputs: a key k (), and a data block x (). Typically, a fixed key k is chosen to define the function , allowing it to be used as a single-input function. The formal definition is as follows:
Then, we define the KHPRF: Let be a secure PRF and suppose that the key space has a group structure, where ⊕ denotes the group action, and the output space has a group structure, where ⊗ denotes its group action. We say that F is key homomorphic if, given and , there is an efficient procedure that outputs , which means that the homomorphic property of KHPRF is related to keys.
Definition 1
(KHPRF). Consider an efficiently computable function such that () and () are both groups. We say that the tuple () is a KHPRF if the following two properties hold:
- 1.
- F is a secure PRF.
- 2.
- For every , and every .
For notation simplicity, we will write hereafter, using “+” to denote the group actions in, respectively, the group and the group .
3.1.2. LWE-Based and LWR-Based KHPRF
Learning With Errors (LWEs) is a core hard problem in lattice theory cryptography, proposed by Oded Regev [23], and is considered one of the cornerstones for building post-quantum cryptosystems. The core idea is to recover secret vectors in a noisy system of linear equations, ensuring that even if an attacker obtains some of the information, it cannot be effectively cracked. Ring Learning With Errors (RLWEs) is an extension of the LWE problem over a polynomial ring, and its core idea is to ensure security for cryptographic protocols through the intractability of systems of noisy linear equations.
The first standard-model construction of KHPRF, proposed by Boneh et al. [24], built on the LWE assumption and extended the lattice-based PRF framework of Banerjee et al. [25]. Subsequent improvements by Banerjee and Peikert [26] strengthened security guarantees under refined lattice assumptions. LWE-based KHPRF achieves approximate key homomorphism, where the relation
holds for a small error in an appropriate norm. This property suffices for applications like distributed key distribution and updatable encryption.
Definition 2
(LWE-Based KHPRF). Let be random binary matrices. For modulus q, a secret key , and input , the LWE-based KHPRF is
where denotes rounding to . The approximate homomorphism satisfies
A parallel construction in the random oracle model, proposed by Boneh et al. [24], utilizes the Learning With Rounding (LWR) problem [25]. As a variant of LWE, LWR improves computational efficiency by introducing deterministic rounding operations in place of random noise, while maintaining security, especially in resource-constrained scenarios.
Definition 3
(LWR-Based KHPRF). For primes , let be a random oracle. The LWR-based KHPRF is
where maps to via scaling and rounding. The approximate homomorphism yields
3.1.3. Ring-LWR-Based KHPRF
To enhance efficiency in federated learning scenarios requiring vector operations, we use the ring version of LWR. Similar to the LWR problem, RLWR is a deterministic variant of the LWE problem whose security is rooted in hard problems in lattice cryptography, particularly the ring version of the shortest vector problem. There are no known quantum algorithms that efficiently solve the approximate shortest vector problem on the lattice or related ring variants. Under appropriate parameters, the security of RLWR can be reduced to RLWE [25], which has been shown to be a hard problem [27] under quantum computing models.
Let and for prime moduli . The RLWR problem and RLWR-based KHPRF are defined as follows:
Definition 4
(RLWR Problem). For , the RLWR distribution samples uniformly and outputs .
Definition 5
(RLWR-Based KHPRF). Given a random oracle , the RLWR-based KHPRF is:
It retains the approximate homomorphism of its LWR counterpart. This construction reduces the communication and computation costs in federated learning by leveraging polynomial ring arithmetic, while maintaining security under the RLWR assumption [25,27].
The computational burden of the LWR variant is the lowest in the lattice-based KHPRF. The rounding-induced error is negligible in comparison to the noise injection in the differential privacy scheme. However, the RLWR variant facilitates superior batch processing and is more applicable in cross-silo federated learning scenarios.
3.2. Key Exchange Protocol
Key Exchange (KE) allows two entities to negotiate a key over a public channel. The key is only known to the two parties, and an adversary cannot obtain any information about the key from the communication. The Diffie–Hellman key agreement, a well-known KE [28], guarantees key security based on the discrete logarithm problem. In a classical computing environment, the problem requires a super-polynomial time solution, but a quantum computer can crack the discrete logarithm problem in polynomial time using the Shor algorithm. Therefore, we choose a CCA-secure KEM Kyber [13] as our post-quantum key exchange protocol. We chose Kyber over Newhope or other solutions for our key exchange protocol because it was one of the final algorithms screened by the NIST Post-Quantum Cryptography Competition as providing secure key exchange and encapsulation capabilities that can withstand attacks from quantum computers.
Kyber consists of a tuple of algorithms (KeyGen, Enc, Dec). We employed CCA-secure KEM Kyber to construct a key exchange protocol Kyber.KE. Kyber.KE is shown in Figure 1.
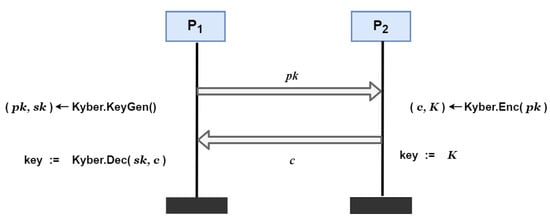
Figure 1.
Kyber.KE—post-quantum key exchange protocol.
3.3. Lagrange Interpolation
We employ Lagrange interpolation, the mathematical foundation of the secret sharing scheme [29], to establish a non-interactive masking mechanism with low communication overhead. This section details the Lagrange interpolation framework and its integration with the secret sharing scheme.
Given distinct points , there exists a unique interpolating polynomial of at most t degree satisfying for all . In secret sharing scheme construction,
- 1.
- A degree-t polynomial is generated with as the secret.
- 2.
- n shares are distributed to participants ().
- 3.
- Secret recovery requires at least shares to reconstruct :
where denotes the Lagrange basis polynomial:
The basis polynomials satisfy the Kronecker delta property:
The Lagrangian Interpolation Coefficient (LIC) is defined as :
The secret S is recovered via
This formulation underpins our encryption key construction.
3.4. Threshold Secret Sharing Scheme
The secret sharing scheme was first introduced by Shamir et al. [29] and Blakley et al. [30] in 1979. Throughout this paper, threshold secret sharing scheme refers to Shamir’s scheme. The quantum-resistant security of the Shamir secret sharing scheme is essentially due to its information-theoretic security design, which achieves unconditional security through an algebraic structure of polynomial interpolation. Its core property ensures that if the number of participants is less than a threshold t, i.e., if or less shares are obtained, these shares do not provide any information about the secret value S. Security is guaranteed by the mathematical structure, not by the assumption that it is “computationally hard to break”. While quantum computers can solve certain computationally hard problems, such as the Shor algorithm for breaking RSA and ECC, they cannot break the bounds of information-theoretic security. Informationally secure schemes are theoretically secure against any computational power, including quantum computers, because their security does not depend on the limits of the attacker’s computational resources. In the secret sharing scheme, a secret value S is split into n shares, each distributed to a participant. Reconstruction requires at least t participants, while fewer than t reveal no information about S.
The secret sharing scheme with Binary Reconstruction [31] is a specialized form of linear-threshold secret sharing scheme, where reconstruction coefficients are limited to 0 and 1. Here, the secret is a field element, and shares consist of sets of field elements. Any t participants can reconstruct the secret via a linear combination of their shares, while fewer than t gain no information.
A simple construction involves bit-decomposing the secret sharing scheme. Given a secret s, a random polynomial p satisfying is chosen, and the i-th share is . In the improved scheme, each share s is decomposed as . During reconstruction, a coefficient is expressed as , leading to for binary reconstruction.
We apply this binary reconstruction secret sharing scheme to mitigate errors in our secure aggregation for privacy-preserving federated learning.
4. Methods
4.1. Overview
The proposed scheme facilitates data aggregation across multiple rounds without necessitating a separate configuration for each round, thereby streamlining the process. The primary objective of the scheme is to mask the client weight data and ensure that sensitive information is not extrapolated from the weights by external entities, including servers and other clients. Concurrently, it guarantees that the Center Server (CS) can accurately decrypt the aggregated data, specifically by obtaining the sum through removing the masking factors in a secure manner. The workflow illustrating the secure aggregation scheme is provided in Figure 2. Algorithm 1 outlines the complete procedure of the proposed post-quantum cross-silo federated learning from the client side and the server side. This work is founded on two key ideas:
| Algorithm 1 Proposed Post-Quantum Cross-Silo federated learning Algorithm. |
|
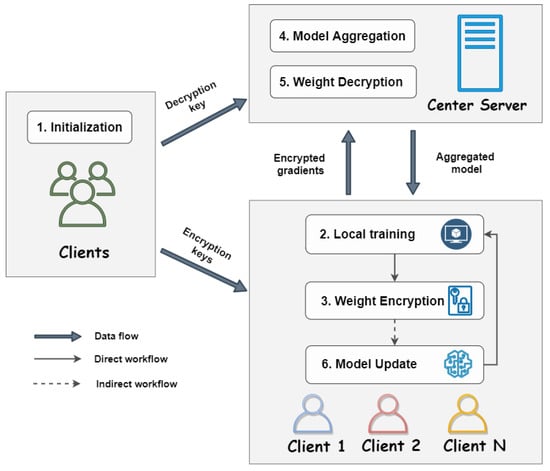
Figure 2.
Workflow of proposed scheme.
- 1.
- Reusable PRF Key FactorsOne of our primary objectives is to eliminate the need for a separate initialization in each aggregation round. This is achieved by reusing the materials generated during the initial setup across the subsequent aggregation phases. The KHPRF provides the necessary functionality to accomplish this objective. During the initialization phase, we generate and distribute the key factors , along with the decryption key required for the server side. These values are then persistently used in all subsequent aggregation rounds. In particular, the output of the KHPRF serves as a masking to blind (or encrypt) the data on the client side before aggregation. To ensure fresh masking in each round, we use time-dependent random values as inputs to the KHPRF. Regarding the PRF key structure, part of it is fixed as , while the remaining portion is a constant associated with the current set of online clients. The fixed component , which is a reusable part of the PRF key, is referred to as the key factor.
- 2.
- Non-interactive mask elimination Another main objective of our research on secure aggregation is to minimize the number of communication rounds required between the client and the server in a single aggregation process. The implementation of the KHPRF plays a pivotal role in achieving this goal, as its key-homomorphic property helps to construct a mask removal mechanism that does not require communication and interaction among the participating entities. Analogous to classical double-masking, we can implement KHPRF-based dual masks via a single mechanism, where both masks are derived from the same KHPRF but serve distinct functions. Our scheme achieves equivalent security guarantees with a single-mask design, halving the computational overhead for both clients and servers. During aggregation, the server efficiently eliminates dual masks through lightweight computations, provided all clients remain active. In the context of cross-silo federated learning, given the relatively limited number of participating entities and the absence of variability in this parameter, the scenario of client disconnections is not a concern.
4.2. Initialization
The initialization process is responsible for preparing the PRF keys for the clients and the . The total number of clients is denoted by N, and A denotes the full set of clients. The update client ’s data, represented by , we first compute
and set the encryption modulus as follows: Choose a prime number p slightly larger than E as the encryption modulus. The following are the detailed steps of the initialization phase:
- 1.
- Public Parametersgenerates the necessary parameters: , determine the composition of a client full set A, denote as the clients’ unique position to share the secret; choose a RLWR based KHPRF , where the hash function is as follows , . Then, the publishes as public parameters.
- 2.
- Key Exchange and Secure Channel EstablishmentTo facilitate secure communication throughout the protocol, we employ the quantum-resistant key exchange mechanism Kyber, which is based on the Kyber KEM detailed in Section 3.2. The standard execution details of Kyber are omitted for brevity. Secure channels are established as follows:
- (a)
- Client-Server Channels: Each client executes the Kyber.KE protocol with the CS. This ensures confidential and authenticated communication for exchanging parameters, submitting aggregated results, and potentially other server interactions.
- (b)
- Client–Client Channels: Crucially, for the subsequent secret sharing phase (Step 3), each pair of distinct clients (, ) must also establish a pairwise secure channel. This is achieved by executing Kyber.KE between them. These channels are essential to protect the confidentiality and integrity of the secret shares () exchanged directly between clients.
- 3.
- Computing Key Factors:
- (a)
- For each client , a random number is chosen and used as the secret value for the secret sharing scheme. Specifically, additional random numbers are selected to generate the following polynomial:where the constant term is the previously chosen random secret value .
- (b)
- Subsequently, the client can calculate the share values for the remaining participants, where , and also holds . Then, the client transmits the value to , where is at a specific sharing position denoted by .
- (c)
- After that, the client receives values from other clients and calculatesthereby obtaining the KHPRF key factor of client , and then locally computing
The schematic diagram for calculating the key factor is shown in Figure 3. As shown in the figure, each client locally generates a random number and then performs secret sharing with the remaining clients (including themselves). The client adds up all the shared values received and the resulting sum is , which is used to compute the KHPRF key.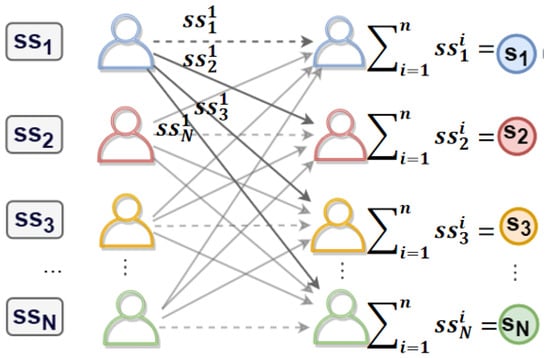 Figure 3. Computation of key factors.
Figure 3. Computation of key factors. - 4.
- Computing the Decryption Key:Since we do not consider client drops during the aggregation process, the server needs to subtract the total mask from all the received ciphertexts. To calculate the total mask, the server needs to obtain the total PRF key, using the following relation:Each client can send the random number generated at the start of the initialization process to the server-side. The server then calculates the decryption key S according to Equation (11). That is, the PRF key required to calculate the total mask can be obtained in this way without revealing the key factor of any client.Due to the additive homomorphic property of the secret sharing scheme, after using the secret sharing scheme on , the sum of the share values held by each client, is the share value of S. Therefore, we have
4.3. Aggregation Phase
In the aggregation phase, clients encrypt their vectors and upload them to the server. Upon receipt, the server aggregates these ciphertexts. Subsequently, it uses the decryption key to calculate the PRF mask and decrypt the aggregated data. This aggregation phase is crucial as it involves client-side inputs. In the context of federated learning, multiple rounds of uploading are frequently observed. The proposed scheme exhibits the benefit of being capable of executing this aggregation phase on multiple occasions following a single initialization.
4.3.1. Encryption
: encrypt the weight , which includes the following steps:
- 1.
- Following the initialization phase, the client is required to calculate the mask using the key of the KHPRF, which is obtained during the initialization phase and is formed by multiplying by :then, follow the steps below to encrypt:
- 2.
- A mask is computed for each client participating in the current aggregation round:we use a synchronization timestamp as a random input to the PRF, and the above computation of the mask ensures the reusability of the PRF key factor at each round of subaggregation.
- 3.
- Merge the calculated mask into the plain-text update data to complete the blinding process, which is also the encryption process within the scheme. After the encryption phase is completed, each participant obtains the ciphertext form of the client-side updated data, as follows:
Once the initialization phase is completed, clients obtain sufficient information to start the encryption process. As previously mentioned, our scheme is based on a masking mechanism. In this mechanism, the private data of clients (which are usually parameters such as gradients or weights in federated learning) will be masked with a masking value, which is in the form of the output of the KHPRF.
4.3.2. Aggregation
Upon encryption, every participant transmits the resulting encrypted data to the central aggregation collector . The primary responsibility of the collector is to aggregate the ciphertexts contributed by each online participant . This is achieved by summing the individual ciphertexts to compute the cumulative ciphertext, which can be expressed as
Specifically, the aggregated ciphertext is derived through the computation detailed by the following expression:
4.3.3. Decryption
: decrypt the weight as follows:
The only needs to calculate
to obtain the aggregated plaintext value M.
As shown in Equation (23), the only difference between the sum of the ciphertexts C (the aggregated ciphertexts from each client) and the sum of the plaintexts M (the aggregated plaintext data, represented as , the total sum of all individual plaintext values) is the value of . This is the result of our proposed non-interactive mask construction mechanism and also the result of the data requested by the server .
It should be noted that, at this moment, the already has the PRF key S required for the final decryption. This enables it to easily generate the final mask and subtract it from the sum of the ciphertexts C, which is the aggregated ciphertext collected from the online clients. The aggregated plaintext obtained through this process is exactly what the needs to update the global federated learning model.
In our scheme, we set all values to zero. This approach does not compromise security, since each client selects a unique set of random numbers, resulting in distinct polynomials and calculated sharing values. Consequently, clients avoid sending any values to the server, thereby reducing the communication overhead. Additionally, since the output of the KHPRF is zero when the key is zero, that means the total sum of the masks is also zero. That is
as a result, the server need not compute any masks or perform any computations on the aggregated ciphertext value to obtain the aggregated plaintext value. This is because the mask is “automatically” eliminated when the zero value is set as described above.
5. Security Analysis
5.1. Security Proof
We consider a semi-honest adversary , let U be the set of clients. Let denote our masking protocol, and denote the ideal functionality that computes the sum of the clients’ inputs , while revealing nothing except the aggregated result.
Theorem 1.
For a semi-honest adversary who can corrupt at most clients and the server, our protocol Π securely realizes , i.e., there exists a PPT simulator such that
Proof.
1. Hybrid (Real Protocol)
This hybrid is a random variable distributed exactly like . generate keys via the initialization setup. Clients compute , then CS aggregates .
- 2.
- Hybrid (Key Replace)Sim replace with random values . Clients compute , then CS aggregates . The secret key is generated based on the Shamir secret sharing scheme. Since the secret sharing scheme performed during the initialization phase is based on randomly generated polynomials for the distribution of the shared value, as long as the adversary corrupts less than t clients, the key is indistinguishable from the random number . Therefore, and are computationally indistinguishable.
- 3.
- Hybrid (Mask Replace)Sim replace with random masks . Clients compute , then CS aggregates . Since F is a KHPRF based on the RLWR problem, the security of the KHPRF used in this paper can be reduced to the RLWR problem. According to the properties of the PRF, for any polynomial-time predicate D, the probability of distinguishing from a random vector is negligible. Therefore, and are computationally indistinguishable.
- 4.
- Hybrid (Result Replace)CS returns random vector instead of Since the sum of the ciphertexts is also a random number, we cannot distinguish the sum of the ciphertexts from another random number V; therefore, and are computationally indistinguishable.
By transitivity of indistinguishability:
Since outputs a random , the real protocol is indistinguishable from the ideal functionality. □
5.2. Correctness
This section will assess and substantiate the correctness of the scheme proposed in this paper. The primary objective is to demonstrate that, in a cross-silo scenario, the aggregated outcome obtained through decryption in accordance with the scheme is the sum of all plaintexts. Prior to elucidating the validity of the secure aggregation scheme, the following theorem is introduced:
Theorem 2.
In the aggregation phase of the scheme proposed above, the following equation holds:
Proof.
In the scheme proposed in this paper, clients ultimately use the product for encryption. Here, is the sum of the share values of the local random numbers (, where ) of all other clients at the special position of client i during the initialization phase. Due to the additive homomorphic property of the secret sharing scheme, is equivalent to , which is the share value of S. The value of S can be reconstructed through the Lagrange interpolation formula. Therefore, . □
Based on the abovementioned theorem, the correctness of the normal aggregation phase can be deduced as follows:
according to Equation (29), if we attempt to prove Formula (24), this is also equivalent to proving that
due to the Theorem (2), is established, so Equation (24) is proved. Then, is established, so the correctness is proven.
6. Performance Analysis
6.1. Asymptotic Performance
Table 1 shows a comparison of the different qualities of certain classic and recent works. Among them, our scheme enables multiple lightweight aggregation operations after a slightly expensive initialization, without relying on a TTP. Other works such as Flamingo and MicroSecAgg also provide this functionality, mainly for the cross-device federated learning scenario, but cannot provide post-quantum properties. And PKI is required in Flamingo to implement some key features. The remaining scenarios have limitations for multiple rounds or collusion resistance. We also compare our scheme against contemporary post-quantum secure frameworks, to ensure a fair evaluation. Notably, we examine the PQSF [21], which leverages secret sharing, and QPFFL [14], another relevant protocol based on homomorphic encryption. While both provide post-quantum security, their suitability for cross-silo scenarios differs from ours due to specific design choices. QPFFL mandates a TTP for key management and distribution—a potential hurdle for typical cross-silo deployments—in exchange for stronger collusion resistance (tolerating colluding clients). The PQSF, like our scheme, operates without a TTP, aligning better with the decentralized trust models common in cross-silo settings, but provides a collusion resistance level () identical to ours.

Table 1.
Comparison of secure aggregation schemes.
Table 2 compares the communication and computational costs of clients and the server over T global training iterations (T aggregation operations) in the proposed scheme, cross-silo federated learning, and several classic approaches. It includes the communication costs and computational costs of the server and clients, as well as the relevant information on round-complexity. Next, an analysis of the relevant overheads involved in this work will be carried out:

Table 2.
Communication and complexity cost of privacy-preserving federated learning schemes.
- 1.
- Client Computation
- Initialization: .The primary overhead in the initialization phase is determined by the computations during secret sharing scheme. Each client locally selects a polynomial of degree and then computes the values of l polynomials for the remaining clients. In total, it needs to calculate the values of polynomials.When computing the value of a single polynomial, multiplications and additions are required. Since the value of t is restricted by N, the overall complexity of computing the value of a single polynomial is . Consequently, the complexity of computing the values of polynomials is , and the average complexity per client is .Key generation and encapsulation for Kyber-512 requires operations, and decapsulation requires , where , n is the polynomial dimension. Therefore, the computational overhead of key negotiation using Kyber is a fixed 8196.
- Aggregation: .During the aggregation phase, the computational overhead of RLWR-KHPRF depends on the polynomial multiplication, which is nlogn under NTT acceleration with an n of 256, and this results in a constant of 2048, which is much smaller than the length of the model parameter l in cross-silo scenarios, and thus can be ignored. Each client only needs to perform one addition operation between the mask and the original data, with a complexity of . Therefore, the total computational overhead generated is .
- 2.
- Client Communication:
- Initialization: .Each client shares the share values (i.e., polynomial values) computed during the initialization phase with every other client, generating a communication volume of in this process.Kybey-512’s communication overhead is fixed at 1568 bytes.
- Aggregation: .The overhead of sending the encrypted vectors is , and the output size of RLWR-KHPRF is , and p is the RLWR output modulus.
- 3.
- Server Computation:
- Initialization: .When computing the decryption key, addition operations are required, which incurs a computation overhead on the server side.Key generation and encapsulation for Kyber-512 requires operations, and decapsulation requires , where k = 2. Therefore, the computational overhead for key negotiation using Kyber is a fixed 8196.
- Aggregation: .Summing up the ciphertext vectors from N clients incurs an overhead of .
- 4.
- Server Communication:
- Initialization: .Receiving a total of random values from N clients generates a communication volume of .Kybey-512’s communication overhead is fixed at 1568 bytes.
- Aggregation: .Receiving the ciphertext vectors from N clients also results in a communication volume of , and the output size of RLWR-KHPRF is , and p is the RLWR output modulus.
In summary, our round complexity is the lowest among all schemes. We reduces the number of communication rounds after the initial setup from 6 to 1, reducing the overhead of the entire aggregation phase by 83.3% compared to Bell’s double-mask-based approach BBGLR. In addition, among similar schemes that can be initialized once and run multiple times, our scheme also has the lowest communication overhead and computation overhead in the aggregation phase.
6.2. Experimental Performance
We evaluated the performance of the schemes proposed in this paper by simulating the computational and communication overheads, and we compared several schemes similar to our work, in order to evaluate the performance of these schemes as comprehensively as possible.
The settings were as follows: , l = 100,000, and modulo p = 2,147,483,659 in PRG, also in the RLWR-KHPRF of the scheme proposed in this paper, and each element in the model parameters was an integer of type uint32. The computational overhead of RLWR-KHPRF depends on the polynomial multiplication, which is under NTT acceleration, where the polynomial order . The output size of the RLWR-KHPRF is , and p is the RLWR output modulus.
We compared with the communication and computational overheads of two recent works, also for the cross-silo federated learning scenario, the work proposed by Tran et al. [18] in 2023, and the DHSA proposed by Liu et al. [7]. The former combines the two-layer encryption proposed by the secret sharing scheme, which performs well in both federated learning scenarios and smart grids, and the latter is based on the Multi-Key Homomorphic Encryption protocol.
6.2.1. Accuracy and Loss
An accuracy and loss comparison between our proposed scheme, the classical work BIKMM [8], and the benchmark experiment (i.e., federated learning without privacy protection) is illustrated in Figure 4 and Figure 5. In Figure 4, the number of global training rounds (Epochs) was set to 20, the number of local training rounds was 3, the federated learning model employed was ResNet-18, and the dataset used was CIFAR-10. The accuracy ranged from 68% to 83%. Notably, the accuracy started at 68% in the first round, which was attributed to the pretraining process. Specifically, we initialized the model using a pretrained ResNet available in the ‘models’ module of ‘torchvision’.
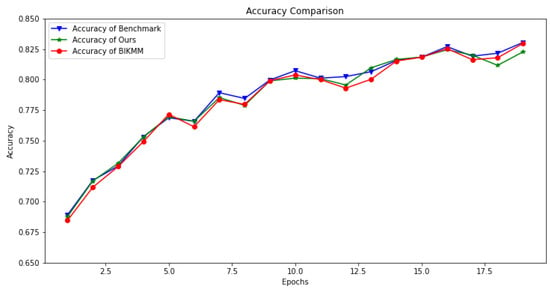
Figure 4.
Accuracy comparison for classification task.
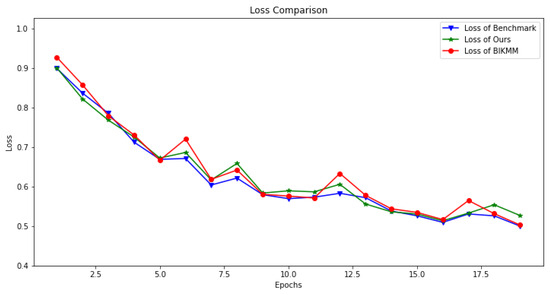
Figure 5.
Loss comparison for classification task.
The green star-marked curve in Figure 4 represents the accuracy trend of our privacy-preserving federated learning scheme with mask protection. Throughout the training process, our accuracy curve largely overlaps with the benchmark experiment (red circular-marked curve) and the BIKMM scheme (blue triangular-marked curve). Although minor fluctuations and slight deviations appear in the middle, these variations are within the normal range of training fluctuations. This demonstrates that our proposed privacy-preserving secure aggregation scheme did not have a significant impact on model training, effectively maintaining a comparable accuracy level to conventional federated learning.
Similarly, Figure 5 presents a loss comparison under the same experimental settings as Figure 4. The loss values range from 0.92 to 0.50. Over the course of 20 global training rounds, the loss trend of our proposed scheme (green star-marked curve) remained closely aligned with the benchmark experiment (blue triangular-marked curve). In contrast, the loss curve of BIKMM (red circular-marked curve) exhibits a greater fluctuation than our approach. This indicates that our mask-based privacy-preserving scheme had minimal impact on the stability of federated learning and maintained a more consistent training performance across the 20 global rounds.
6.2.2. Communication Costs
Figure 6 shows the communication overhead of our proposed scheme, as well as the compared schemes, on the client and server side. In comparison, our communication overhead was slightly higher on the client side, due to the extra overhead of RLWR-KHPRF, than the client communication of the work of Tran et al. with a corresponding extra overhead on the server side. The scheme of DHSA, on the other hand, had a higher overhead than our scheme on both the client and the server sides, due to the additional overhead associated with the individual public keys it transmits in its masking seed agreement [7] protocol, as well as messages such as the ciphertexts of masking seeds. We chose the parameter settings of as mentioned in the DHSA [7]. In comparison with DHSA, our communication overhead was reduced by 97.6% and 96.7% on the client and server sides.
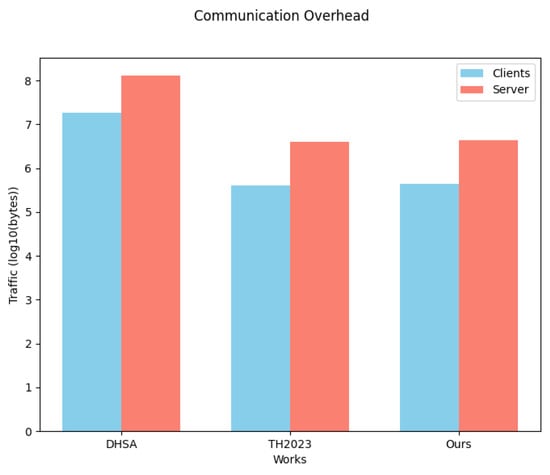
Figure 6.
Communication overhead comparison for both client and server sides.
6.2.3. Computation Costs
Figure 7 shows the computation overhead of our work, as well as the comparison works. It can be observed that our scheme was similar to the other two schemes in terms of client-side computational overhead; i.e., the overhead of computing a mask of the form RLWR-KHPRF in our scheme was similar to the total overhead of key generation and encryption in DHSA. Since the computational complexity of the RLWE-based BFV homomorphic encryption algorithm it uses comes from the dimension n of the polynomial ring, we set this to be of the same dimension as the RLWR in the scheme of this paper.
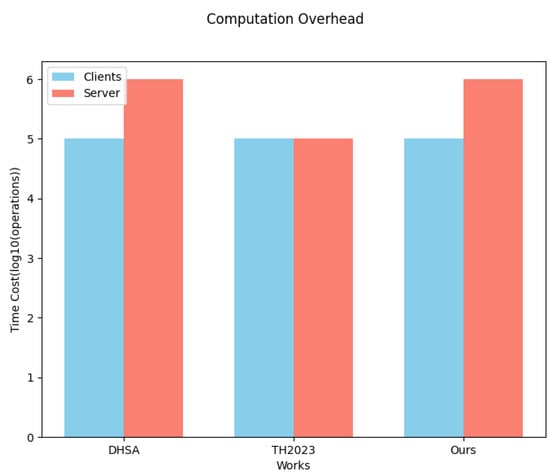
Figure 7.
Computation overhead comparison on client and server sides.
The computational overhead of TH on the server side is mainly from decrypting the aggregated model at each iteration, with a complexity of , where l is the length of the model and is the overhead of having to reconstruct the secret in the presence of a client dropout. However in cross-silo federated learning, there is no need to consider the overhead of a client dropout, and thus only is required, which is the same as the overhead of a client encrypting the local model parameters. This is less than our server-side overhead. Furthermore, an analysis of the server-side computational overhead of the DHSA scheme reveals a similar overhead to that observed in our scheme. Our computational overhead was slightly higher than TH, by 2%, on the server side.
In conclusion, the preceding analysis demonstrates that the proposed scheme did not compromise the accuracy and loss of federated learning training. Furthermore, it exhibited a reduced communication overhead and communication rounds in comparison to recent work, whilst exhibiting a marginally elevated computational overhead due to the additional computation associated with the quantum-resistant RLWR-KHPRF. However, this is a requisite sacrifice in order to achieve a quantum-resistant secure aggregation scheme.
7. Discussion
Our proposed cross-silo federated learning scheme introduces a quantum-resistant secure aggregation mechanism with significantly improved communication efficiency. This is achieved through two primary innovations: (1) A KHPRF-enhanced mask aggregation technique reduces the communication rounds required after initial setup, from six to just one, yielding an 83.3% reduction in round complexity in aggregation phase overhead compared to conventional double-masking approaches like Bell’s. (2) Our RLWR-KHPRF co-design further optimizes single-round communication costs, demonstrating reductions of 97.6% (client-side) and 96.7% (server-side) compared to recent comparable works at a 100-client scale.
The scheme is intentionally designed for cross-silo environments, where high client reliability (over 99%, implying <1% dropout probability) is typical and assumed. However, readers should be aware of three key considerations:
- Security Assumptions: The protocol’s security relies on a semi-honest (“honest but curious”) server model and assumes reliable network connectivity; its current design offers limited resilience to client dropouts during aggregation rounds.
- Computational Overhead: While communication-efficient, the necessary cryptographic operations, especially the RLWR-based (for the sake of quantum resistance) KHPRF evaluation, introduce computational costs exceeding those of non-secure FL protocols, potentially impacting resource-constrained settings.
- Scenario Specificity: The current design is optimized for cross-silo deployments and would require adaptation to effectively handle the scale and frequent client dropouts characteristic of cross-device scenarios.
8. Conclusions and Future Work
We have presented a cross-silo federated learning scheme providing resistance against quantum attacks. Our approach integrates the NIST post-quantum standard Kyber-KEM with an RLWR-based KHPRF to build a novel secure aggregation mechanism. Combined with a secret sharing scheme, this enables efficient multi-round aggregation after a single initialization phase. The resulting framework significantly reduces communication costs by over 90% compared to similar secure federated learning schemes, while maintaining strong privacy and security guarantees for the aggregation process. This work offers a practical and efficient pathway towards post-quantum secure federated learning in cross-silo settings.
To further enhance the robustness and applicability of our scheme, we propose the following directions for future research:
- Strengthening Server Trust Model: Extend the security framework beyond the current semi-honest server assumption to defend against actively malicious adversaries, potentially by incorporating verifiable computation techniques or other cryptographic primitives.
- Enabling Dynamic Client Participation: Develop mechanisms to smoothly handle client dropouts and support dynamic client availability during the learning process. While the core cryptographic components offer potential extension points, robust management of varying client sets requires dedicated design and analysis.
- Developing Lightweight Protocols: Address the computational overhead for highly resource-constrained environments. This involves exploring and integrating lightweight cryptographic primitives and potentially leveraging hardware acceleration to minimize latency and energy consumption, without compromising security guarantees.
Author Contributions
Conceptualization, X.Q. and R.X.; methodology, X.Q.; software, X.Q.; validation, X.Q. and R.X; formal analysis, X.Q.; investigation, X.Q.; resources, X.Q.; data curation, X.Q.; writing—original draft preparation, X.Q.; writing—review and editing, X.Q. and R.X; visualization, X.Q.; supervision, R.X.; project administration, R.X.; funding acquisition, R.X. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented in this paper was supported in part by the National Natural Science Foundation of China under Grant No. 61802354, and Open Research Project of The Hubei Key Laboratory of Intelligent Geo-Information Processing under Grant No. KLIGIP 2021B07.
Data Availability Statement
This section provides a link to the repository https://github.com/obuchishin-baby/KHAgg.git (accessed on 19 April 2025) containing the source code used for the computational experiments, which allows for the reproducibility of our results. Our code implementation references the relevant code in the book Practicing Federated Learning [32].
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
List of Notations.
Table A1.
List of Notations.
| Notation | Definition |
|---|---|
| The i′th client in a specific training phase | |
| Center Server, the party that gets the aggregate result | |
| A | The set of all clients |
| q | key modulus, prime |
| p | mask modulus, prime who less than q |
| Random number locally chosen by client , secret for secret sharing scheme | |
| Share values of , held by client | |
| The product factor of KHPRF key, is the sum of the shared values of | |
| all other clients | |
| S | The decryption key |
| The KHPRF used in this work | |
| Lagrange basis | |
| Lagrangian interpolation coefficient, a constant value related to the client set A | |
| Encrypted data of | |
| N | Total number of clients(length of A) in full federated learning training |
| T | Total number of summations/epochs in full federated learning training |
| Summation of all encrypted data for the round of training | |
| Random input to KHPRF for the round of training | |
| t | The threshold of secret sharing scheme for our scheme |
References
- Voigt, P.; Von dem Bussche, A. The eu general data protection regulation (gdpr). In A Practical Guide, 1st ed.; Springer International Publishing: Cham, Switzerland, 2017; Volume 10. [Google Scholar]
- Zhu, L.; Liu, Z.; Han, S. Deep leakage from gradients. Adv. Neural Inf. Process. Syst. 2019, 32, 14747–14756. [Google Scholar]
- Wang, C.; Wu, X.; Liu, G.; Deng, T.; Peng, K.; Wan, S. Safeguarding cross-silo federated learning with local differential privacy. Digit. Commun. Netw. 2022, 8, 446–454. [Google Scholar] [CrossRef]
- Tran, V.T.; Pham, H.H.; Wong, K.S. Personalized privacy-preserving framework for cross-silo federated learning. IEEE Trans. Emerg. Top. Comput. 2024, 12, 1014–1024. [Google Scholar] [CrossRef]
- Zhang, C.; Li, S.; Xia, J.; Wang, W.; Yan, F.; Liu, Y. BatchCrypt: Efficient homomorphic encryption for Cross-Silo federated learning. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC 20), Online, 15–17 July 2020; pp. 493–506. [Google Scholar]
- Jiang, Z.; Wang, W.; Liu, Y. Flashe: Additively symmetric homomorphic encryption for cross-silo federated learning. arXiv 2021, arXiv:2109.00675. [Google Scholar]
- Liu, Z.; Chen, S.; Ye, J.; Fan, J.; Li, H.; Li, X. DHSA: Efficient doubly homomorphic secure aggregation for cross-silo federated learning. J. Supercomput. 2023, 79, 2819–2849. [Google Scholar] [CrossRef]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar]
- Pleshakova, E.; Osipov, A.; Gataullin, S.; Gataullin, T.; Vasilakos, A. Next gen cybersecurity paradigm towards artificial general intelligence: Russian market challenges and future global technological trends. J. Comput. Virol. Hacking Tech. 2024, 20, 429–440. [Google Scholar] [CrossRef]
- Moody, D.; Perlner, R.; Regenscheid, A.; Robinson, A.; Cooper, D. Transition to Post-Quantum Cryptography Standards; Technical report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024.
- Guo, Y.; Polychroniadou, A.; Shi, E.; Byrd, D.; Balch, T. MicroSecAgg: Streamlined Single-Server Secure Aggregation. Cryptology ePrint Archive. 2022. Available online: https://eprint.iacr.org/2022/714 (accessed on 30 September 2024).
- Ma, Y.; Woods, J.; Angel, S.; Polychroniadou, A.; Rabin, T. Flamingo: Multi-round single-server secure aggregation with applications to private federated learning. In Proceedings of the 2023 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–24 May 2023; pp. 477–496. [Google Scholar]
- Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Kyber: A CCA-secure module-lattice-based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar]
- Zhang, R.; Li, H.; Qian, X.; Liu, X.; Jiang, W. QPFFL: Advancing Federated Learning with Quantum-Resistance, Privacy, and Fairness. In Proceedings of the GLOBECOM 2024—2024 IEEE Global Communications Conference, Cape Town, South Africa, 8–12 December 2024; pp. 4994–4999. [Google Scholar]
- Bell, J.H.; Bonawitz, K.A.; Gascón, A.; Lepoint, T.; Raykova, M. Secure single-server aggregation with (poly) logarithmic overhead. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, 9–13 November 2020; pp. 1253–1269. [Google Scholar]
- Kadhe, S.; Rajaraman, N.; Koyluoglu, O.O.; Ramchandran, K. Fastsecagg: Scalable secure aggregation for privacy-preserving federated learning. arXiv 2020, arXiv:2009.11248. [Google Scholar]
- So, J.; He, C.; Yang, C.S.; Li, S.; Yu, Q.; E Ali, R.; Guler, B.; Avestimehr, S. Lightsecagg: A lightweight and versatile design for secure aggregation in federated learning. Proc. Mach. Learn. Syst. 2022, 4, 694–720. [Google Scholar]
- Tran, H.Y.; Hu, J.; Yin, X.; Pota, H.R. An efficient privacy-enhancing cross-silo federated learning and applications for false data injection attack detection in smart grids. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2538–2552. [Google Scholar] [CrossRef]
- Xu, P.; Hu, M.; Chen, T.; Wang, W.; Jin, H. LaF: Lattice-Based and Communication-Efficient Federated Learning. IEEE Trans. Inf. Forensics Secur. 2022, 17, 2483–2496. [Google Scholar] [CrossRef]
- Gharavi, H.; Granjal, J.; Monteiro, E. PQBFL: A Post-Quantum Blockchain-based Protocol for Federated Learning. arXiv 2025, arXiv:2502.14464. [Google Scholar]
- Zhang, X.; Deng, H.; Wu, R.; Ren, J.; Ren, Y. PQSF: Post-quantum secure privacy-preserving federated learning. Sci. Rep. 2024, 14, 23553. [Google Scholar] [CrossRef] [PubMed]
- Goldreich, O.; Goldwasser, S.; Micali, S. How to construct random functions. J. ACM (JACM) 1986, 33, 792–807. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM (JACM) 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Boneh, D.; Lewi, K.; Montgomery, H.; Raghunathan, A. Key homomorphic PRFs and their applications. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2013; pp. 410–428. [Google Scholar]
- Banerjee, A.; Peikert, C.; Rosen, A. Pseudorandom functions and lattices. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2012; pp. 719–737. [Google Scholar]
- Banerjee, A.; Peikert, C. New and Improved Key-Homomorphic Pseudorandom Functions. Cryptology ePrint Archive, Paper 2014/074. 2014. Available online: https://eprint.iacr.org/2014/074 (accessed on 30 September 2024).
- Lyubashevsky, V.; Peikert, C.; Regev, O. On ideal lattices and learning with errors over rings. In Proceedings of the Advances in Cryptology–EUROCRYPT 2010: 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; pp. 1–23. [Google Scholar]
- Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; pp. 313–318. [Google Scholar] [CrossRef]
- Ball, M.; Çakan, A.; Malkin, T. Linear threshold secret-sharing with binary reconstruction. In Proceedings of the 2nd Conference on Information-Theoretic Cryptography (ITC 2021), Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Virtual, 24–26 July 2021. [Google Scholar]
- Yang, Q.; Huang, A.; Liu, Y.; Chen, T. Practicing Federated Learning; Publishing House of Electronics and Industry: Beijing, China, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).