Hidden Attractors in a New 4D Memristor-Based Hyperchaotic System: Dynamical Analysis, Circuit Design, Synchronization, and Its Applications
Abstract
1. Introduction
- (1)
- Ensuring the presence of multiple positive Lyapunov exponents;
- (2)
- Minimizing the number of terms in the system for simplicity;
- (3)
- Maximizing the Kaplan–Yorke dimension to achieve higher system complexity.
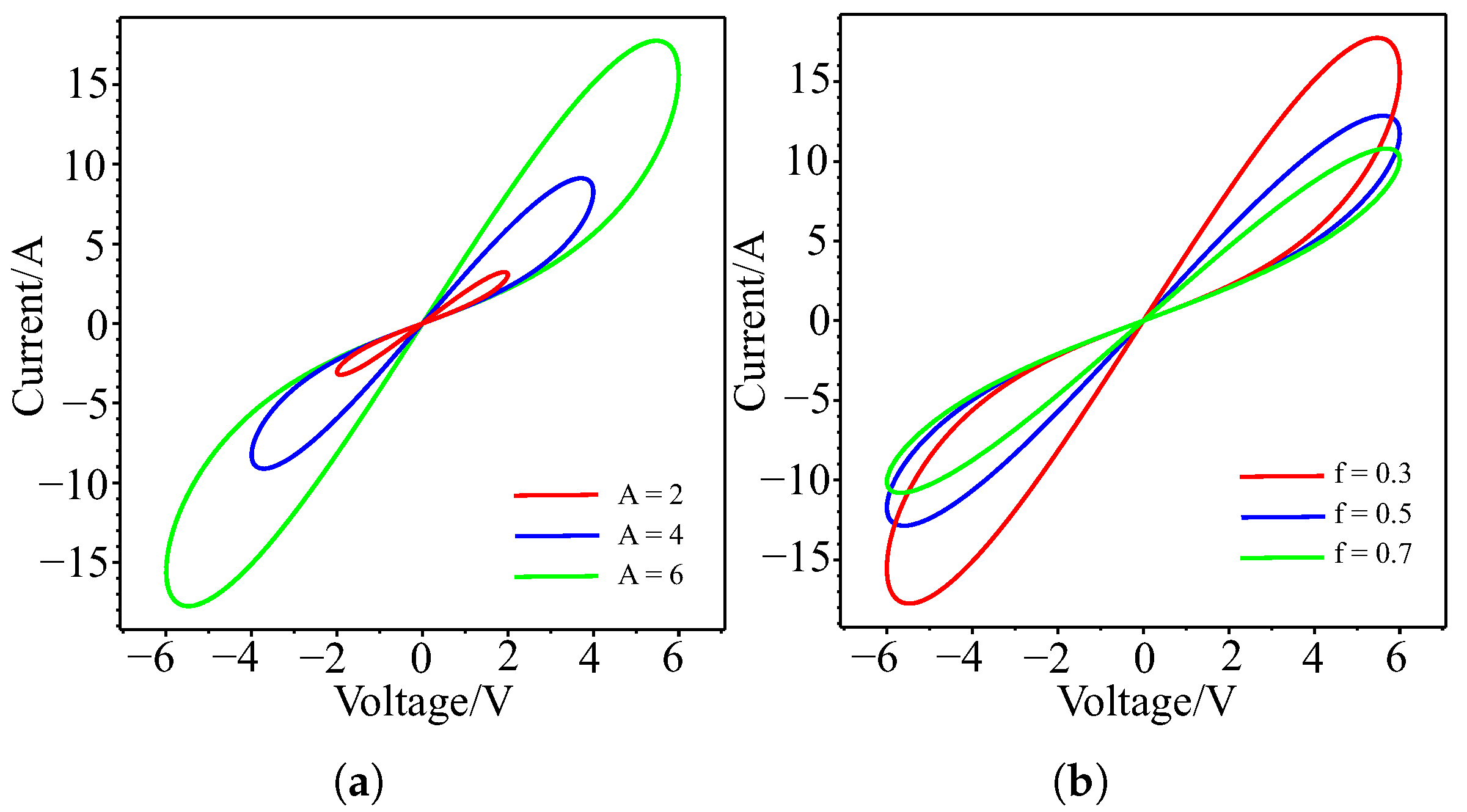
2. A New 4D Memristive Dynamical System: Derivation and Key Properties
3. Dynamical Analysis
3.1. Symmetry and Dissipative
3.2. Equilibrium Points
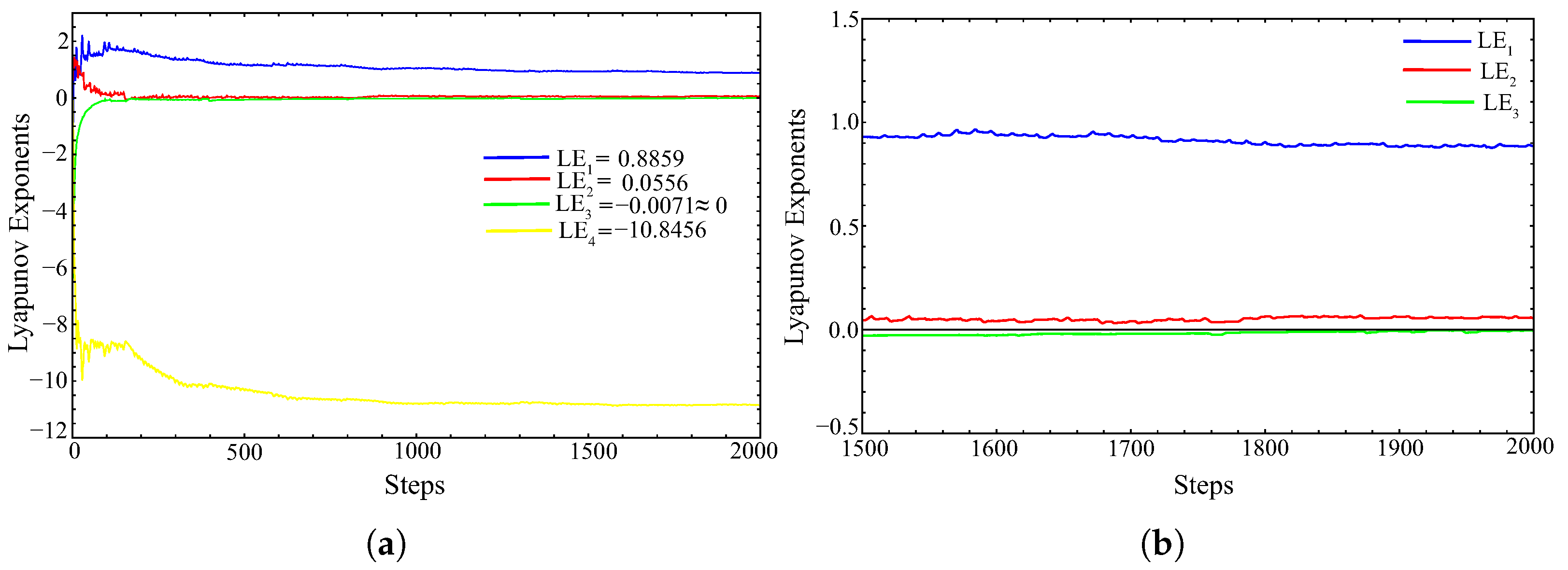
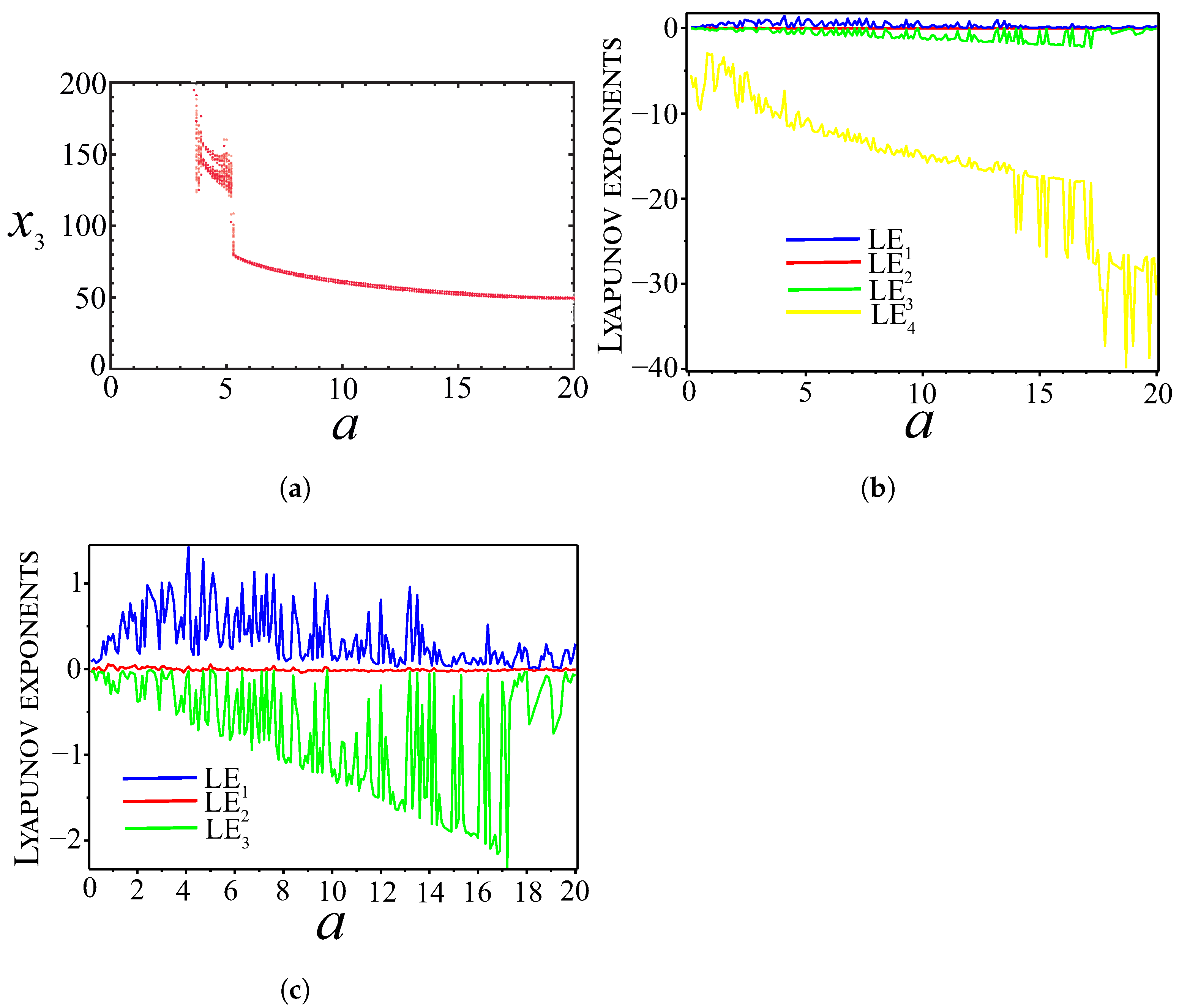
3.3. Lyapunov Exponents and Kaplan–Yorke Dimension
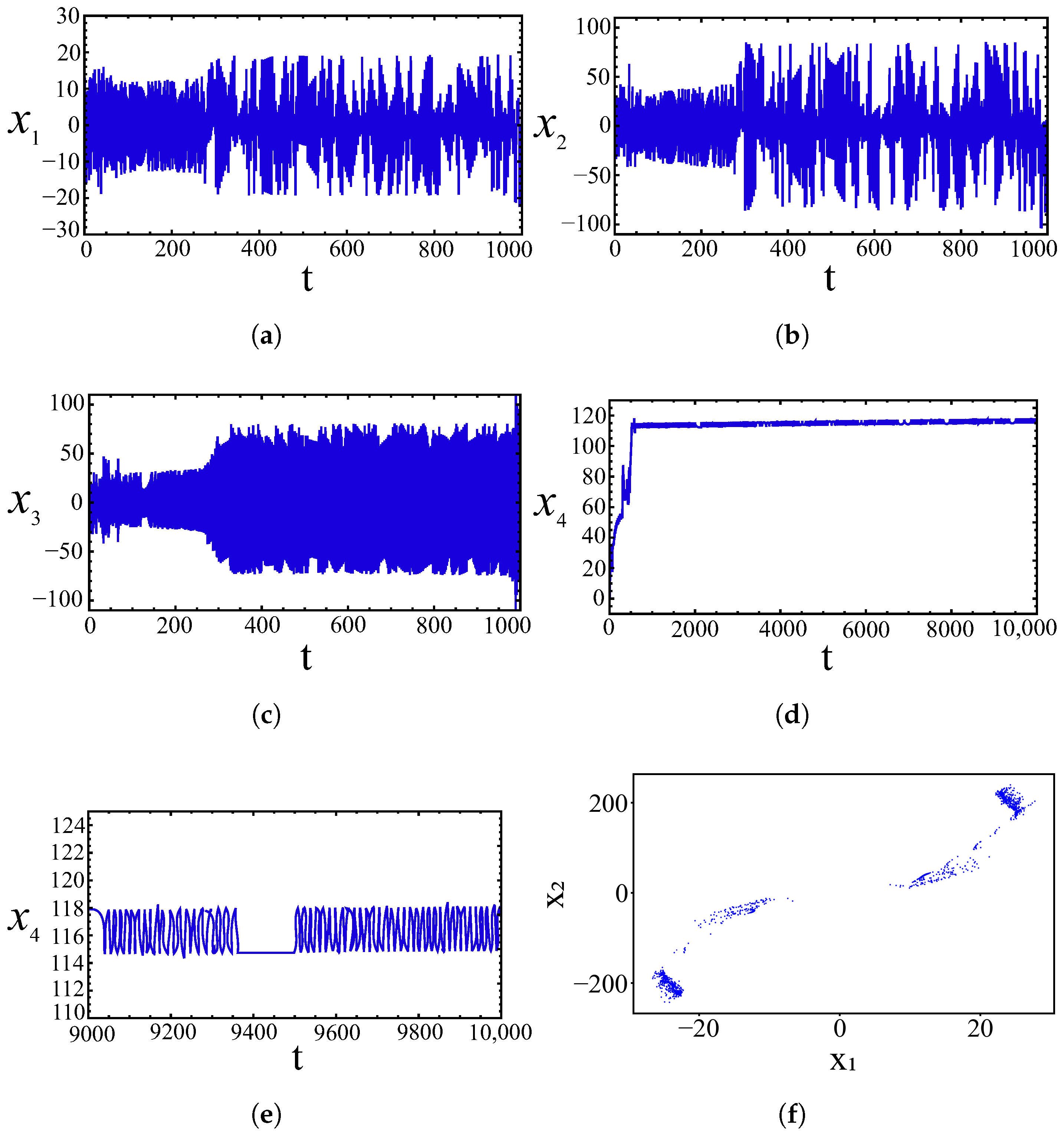
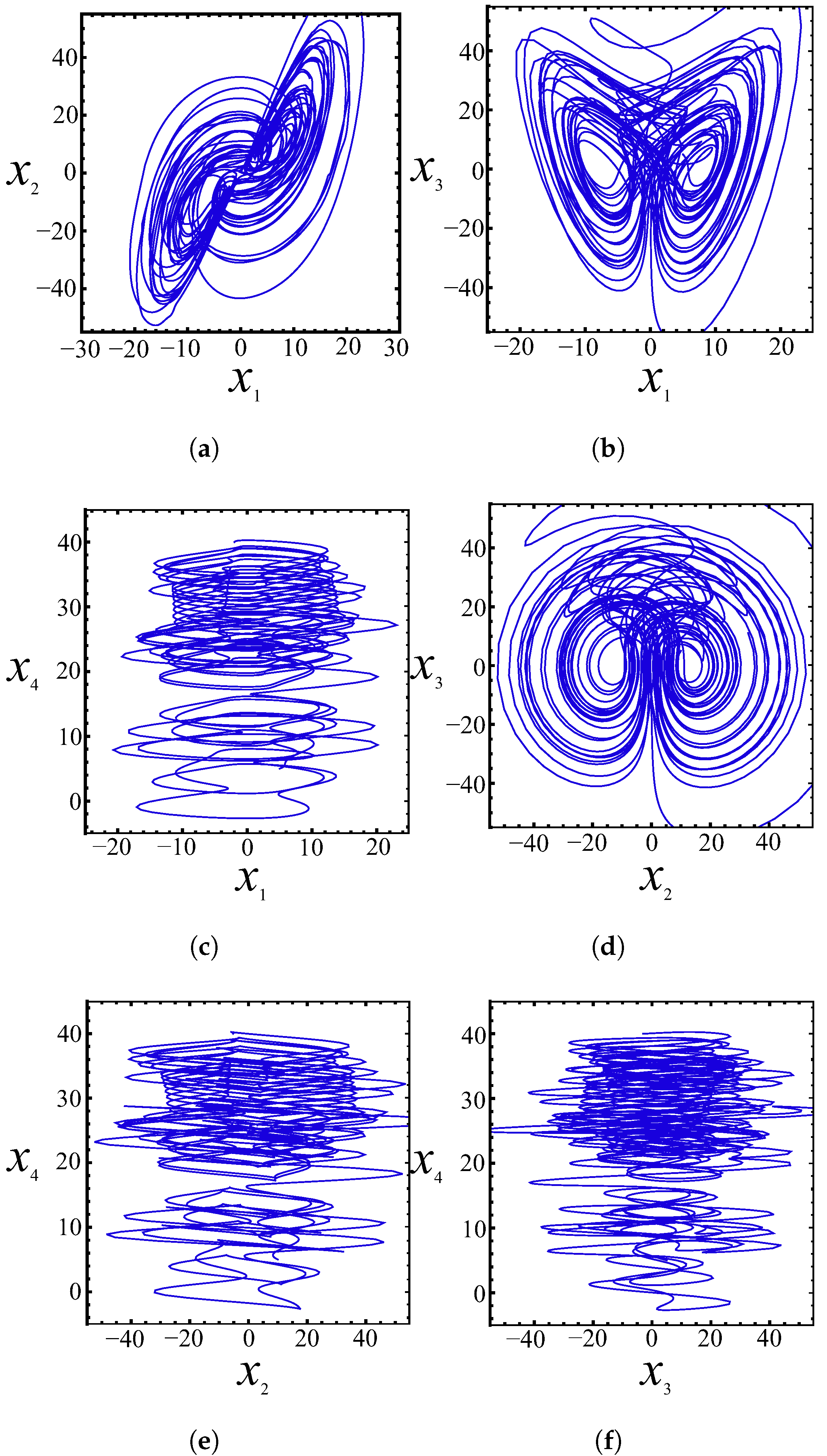
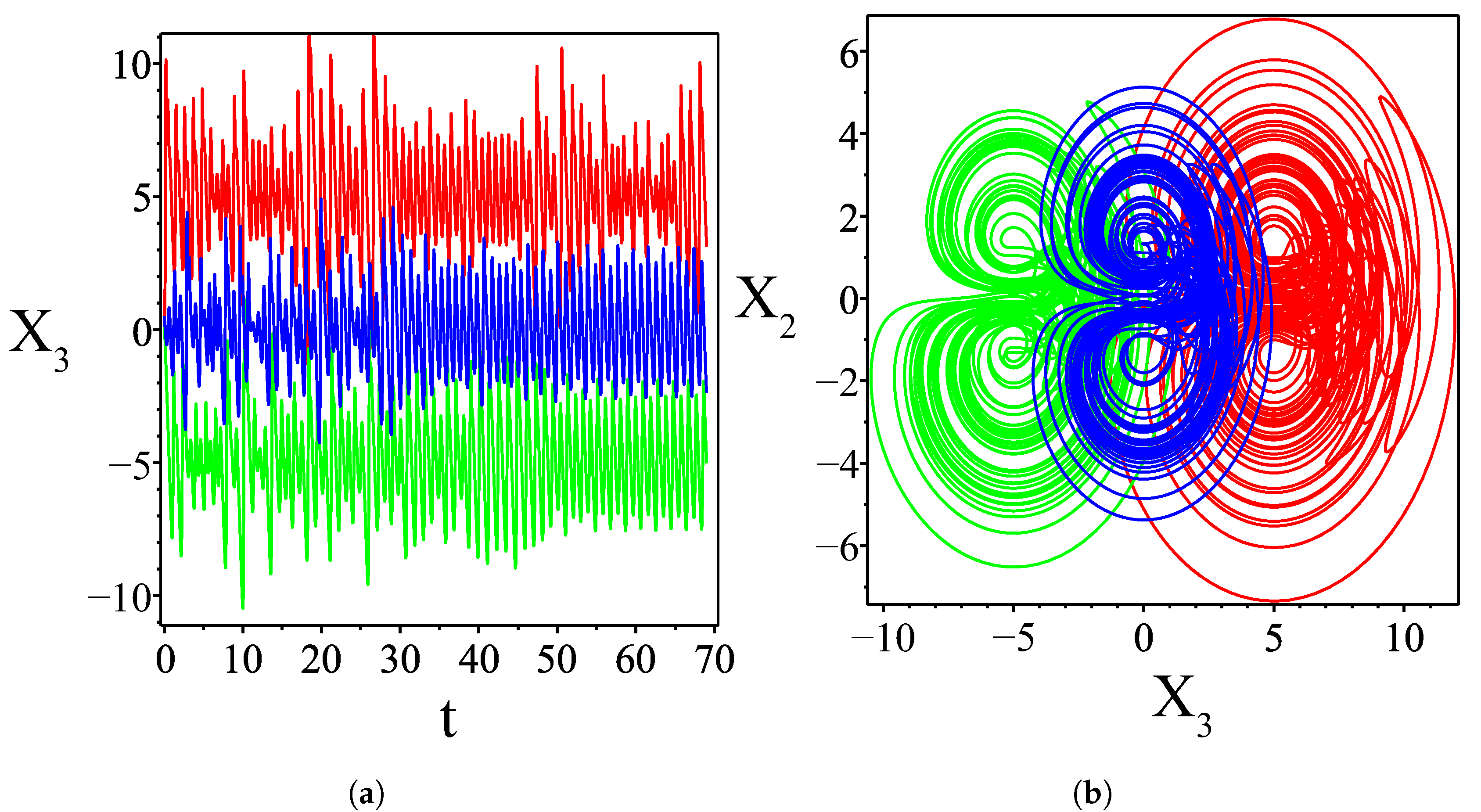
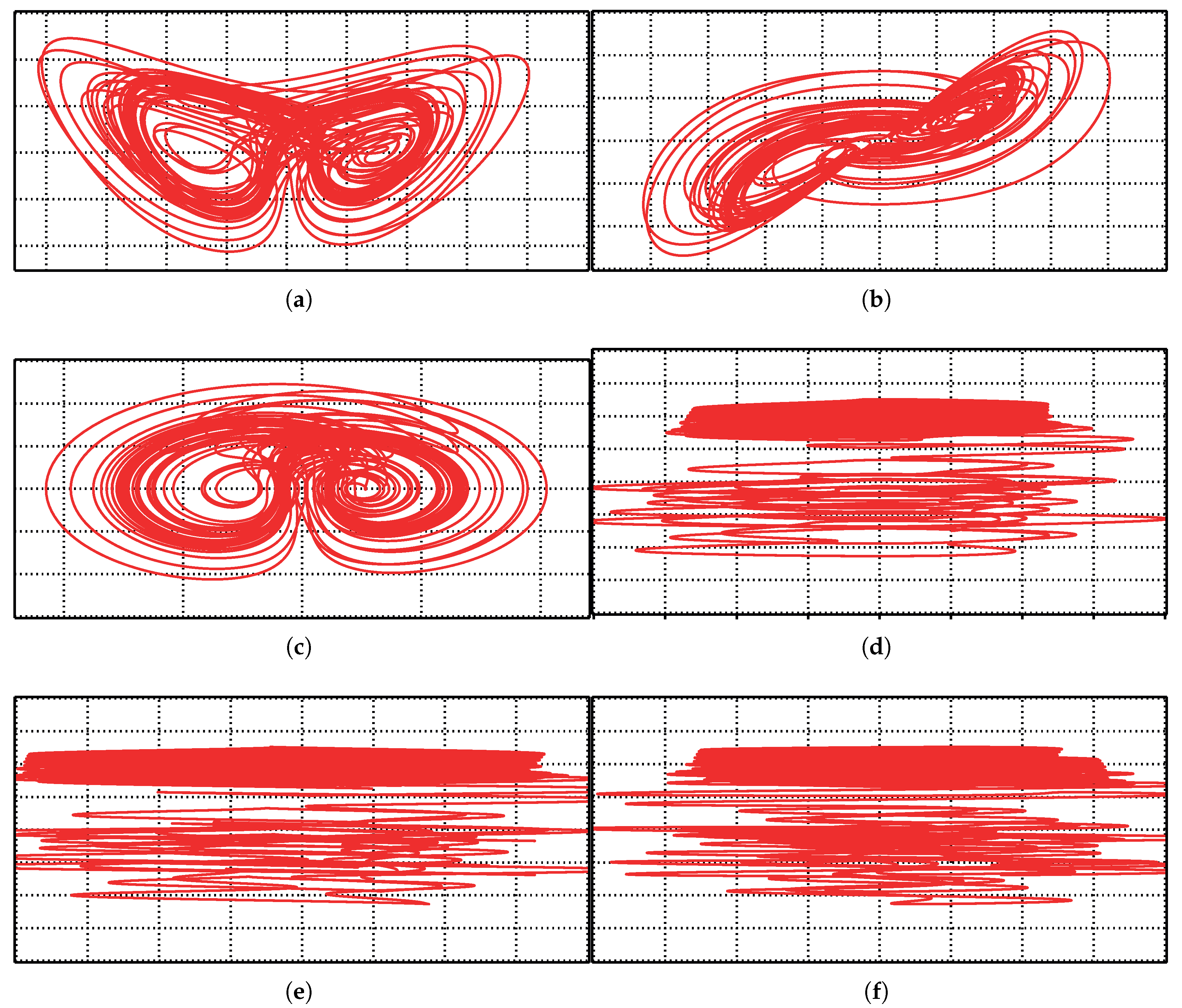
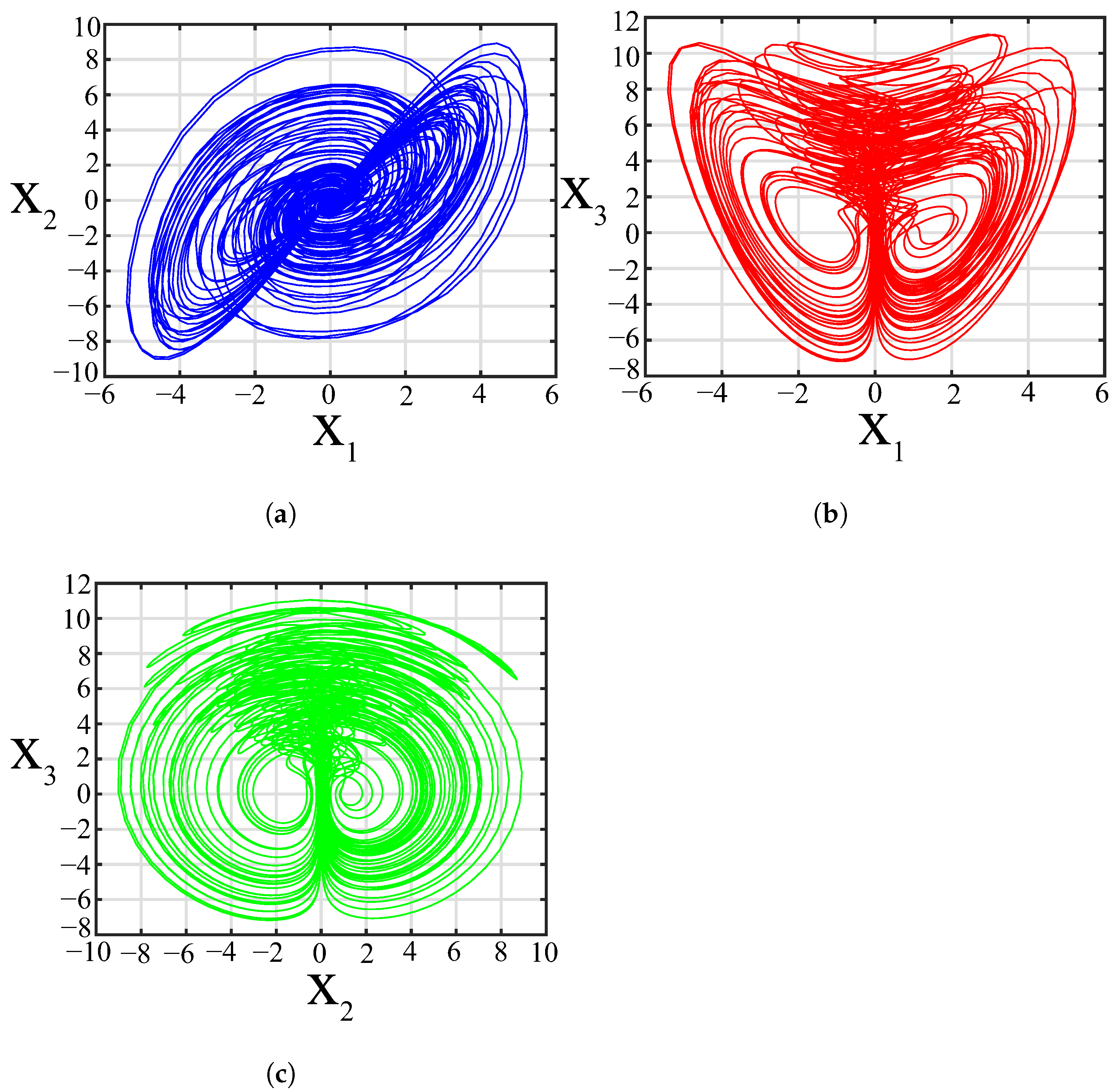
3.4. Temporal Diagrams and Phase Portraits
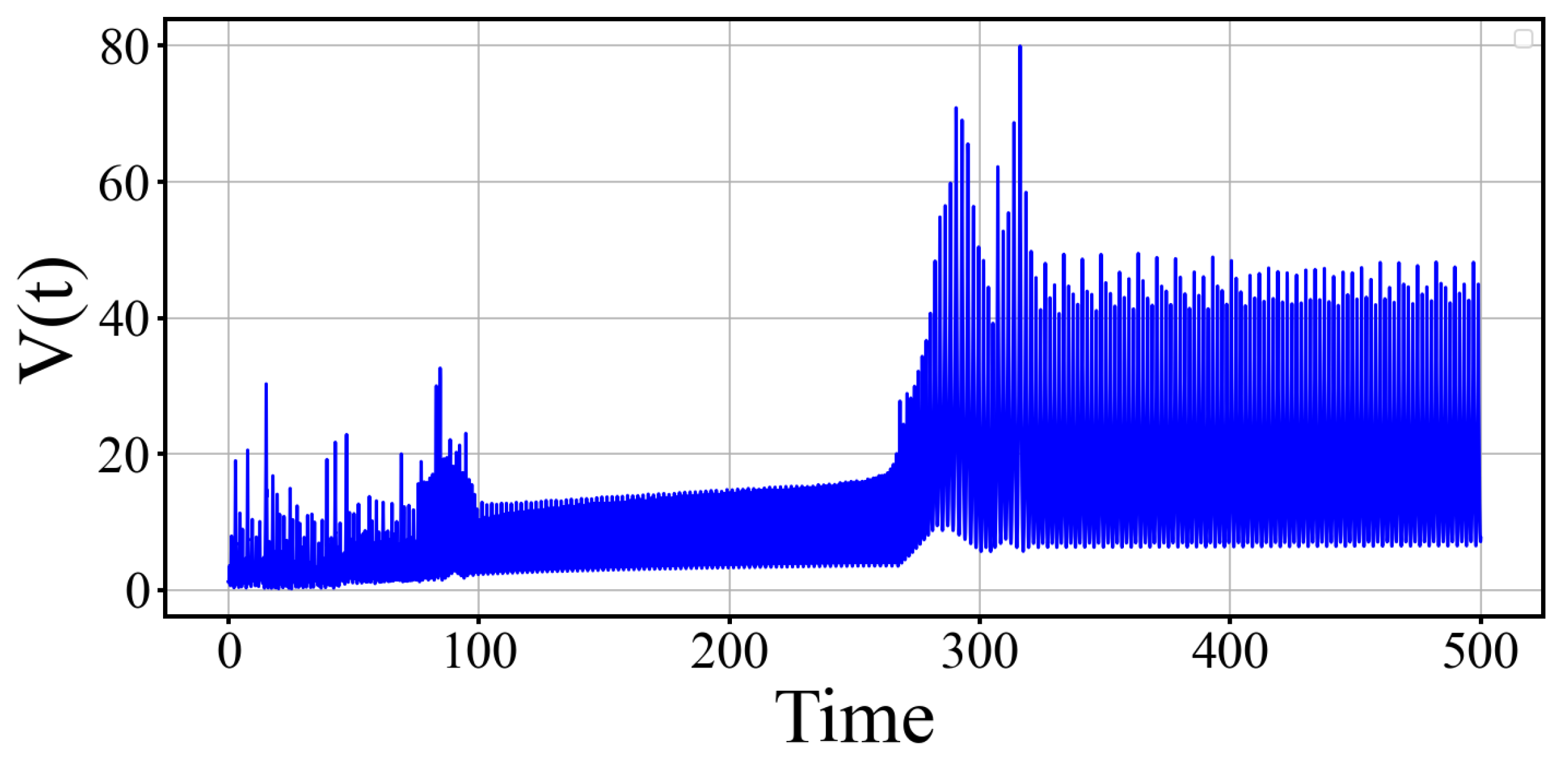
3.5. Stability Analysis via the Lyapunov Function
3.6. Sensitivity Analysis
3.7. Testing the Randomness of Chaotic Sequences
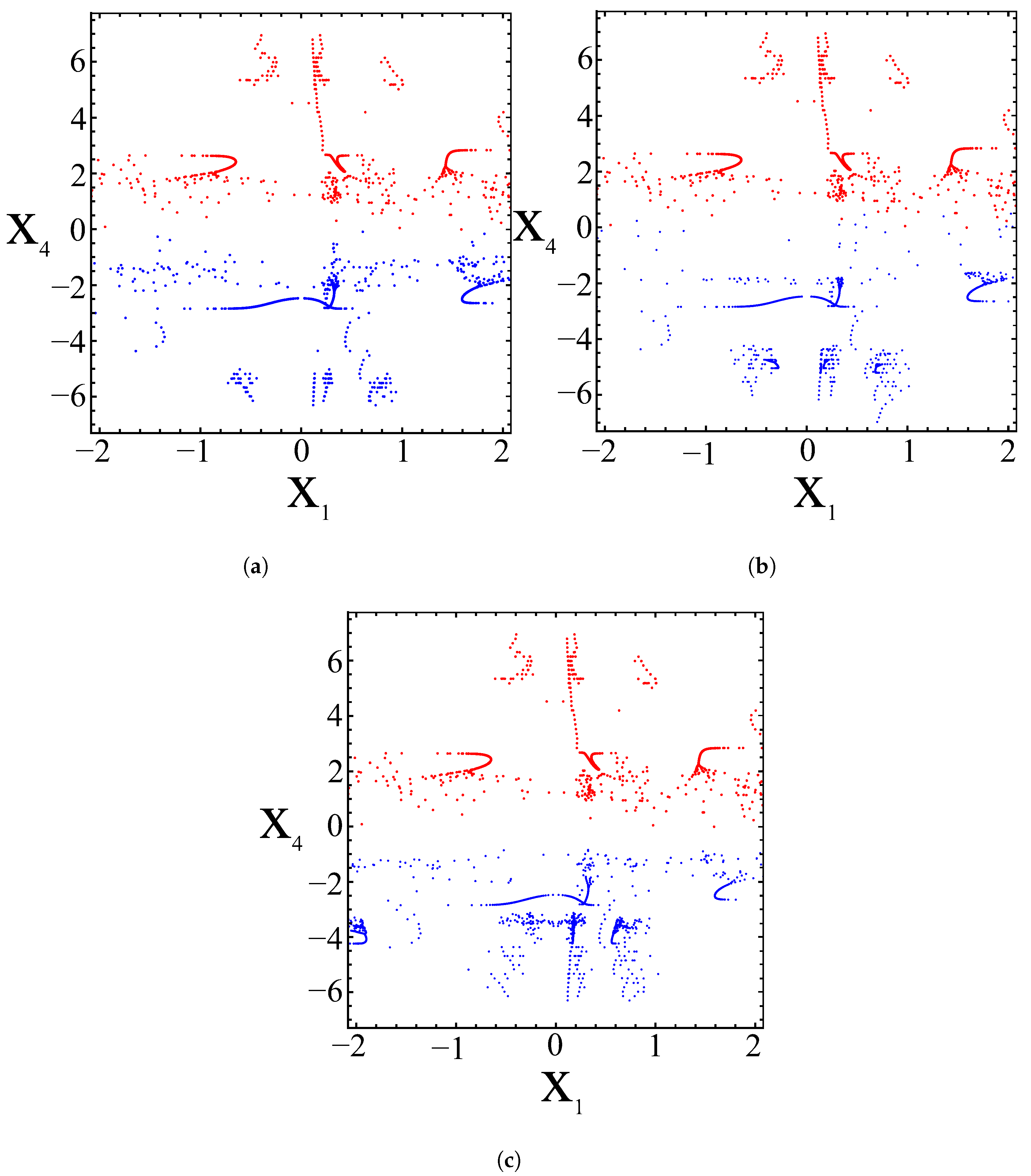
3.8. Multistability and Offset Boosting Control
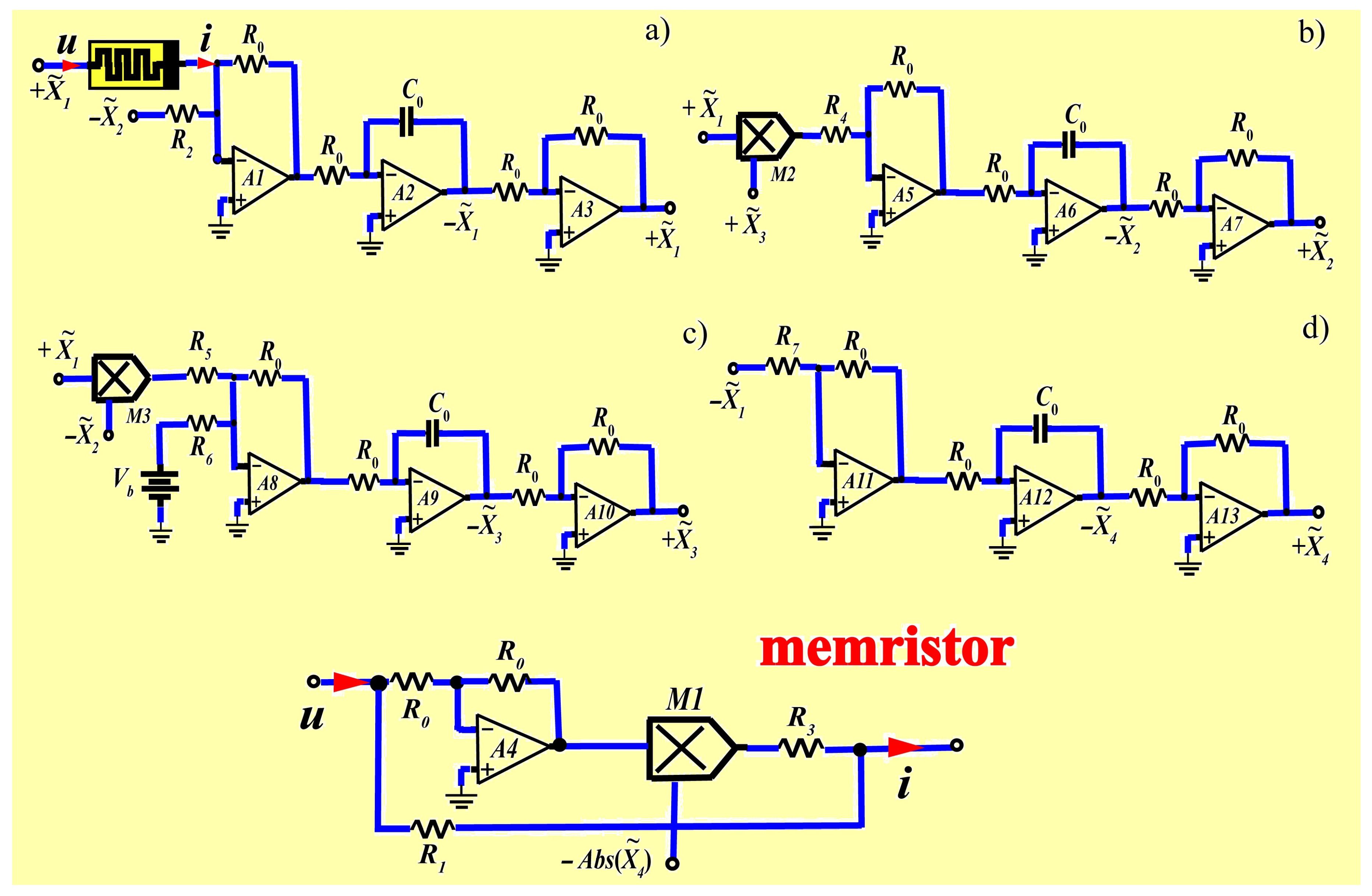
4. Electronic Circuit Implementation of the New Hyperchaotic System
5. Control and Synchronization Mechanisms for a New Hyperchaotic System
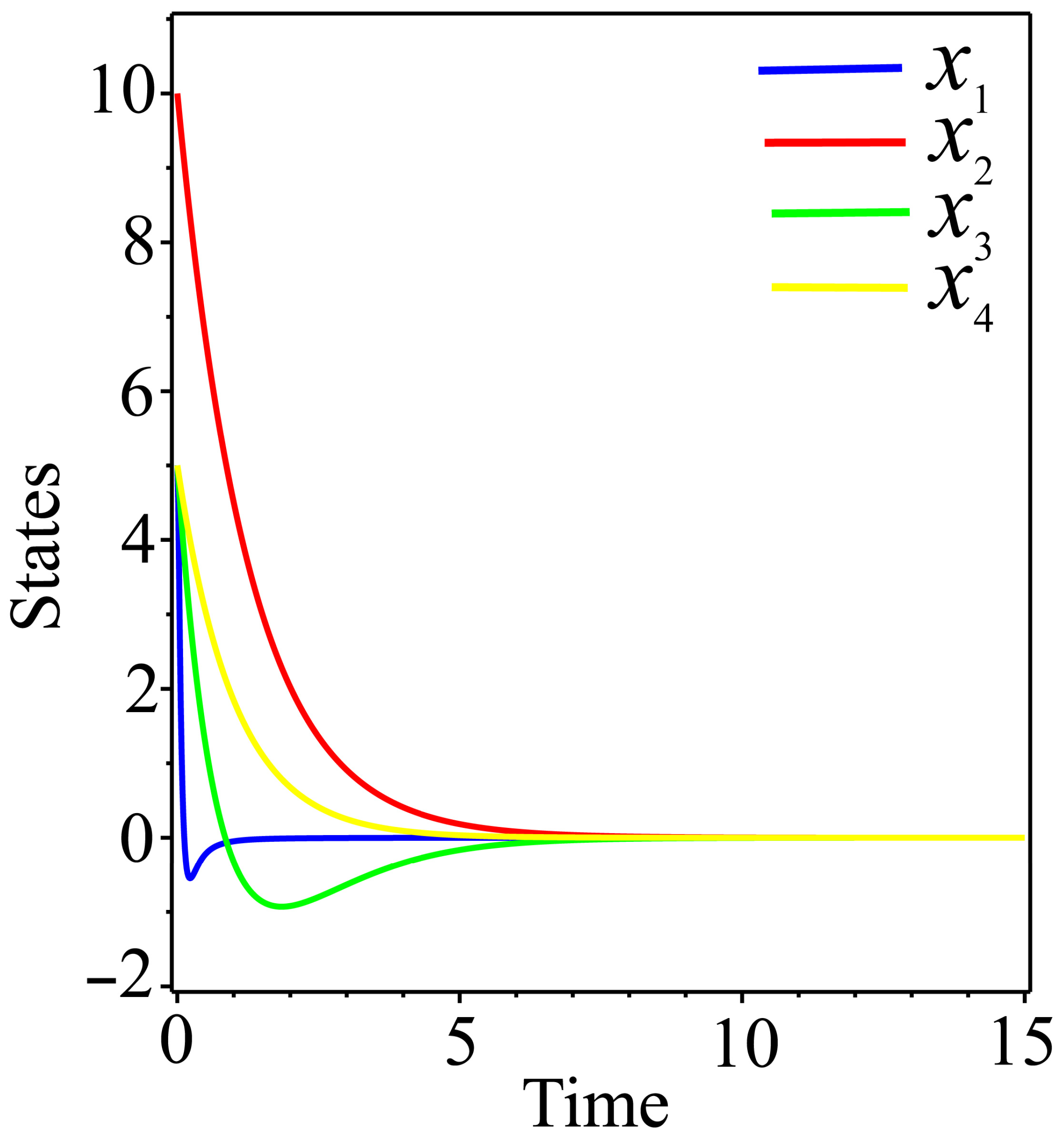
5.1. Adaptive Control
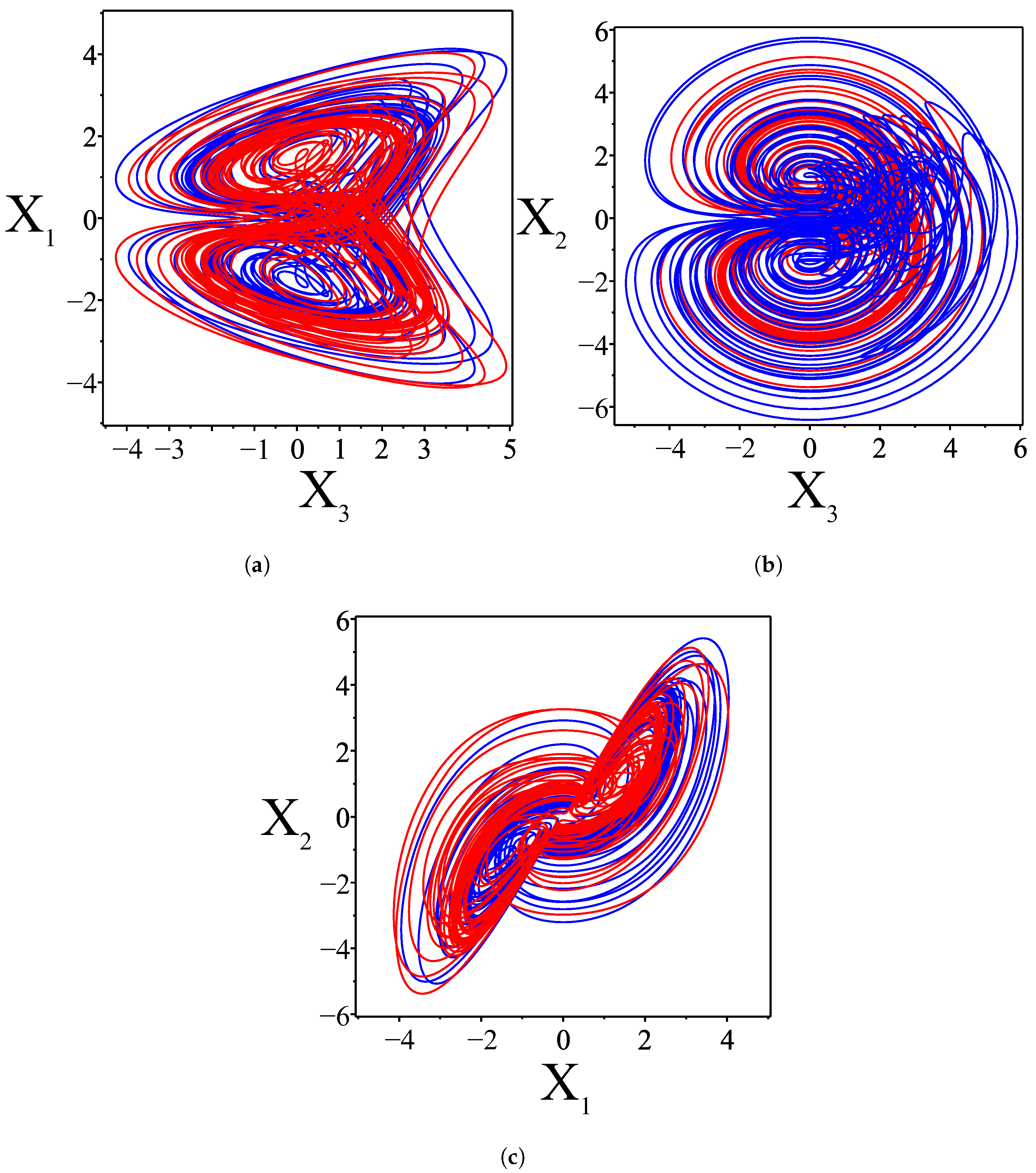
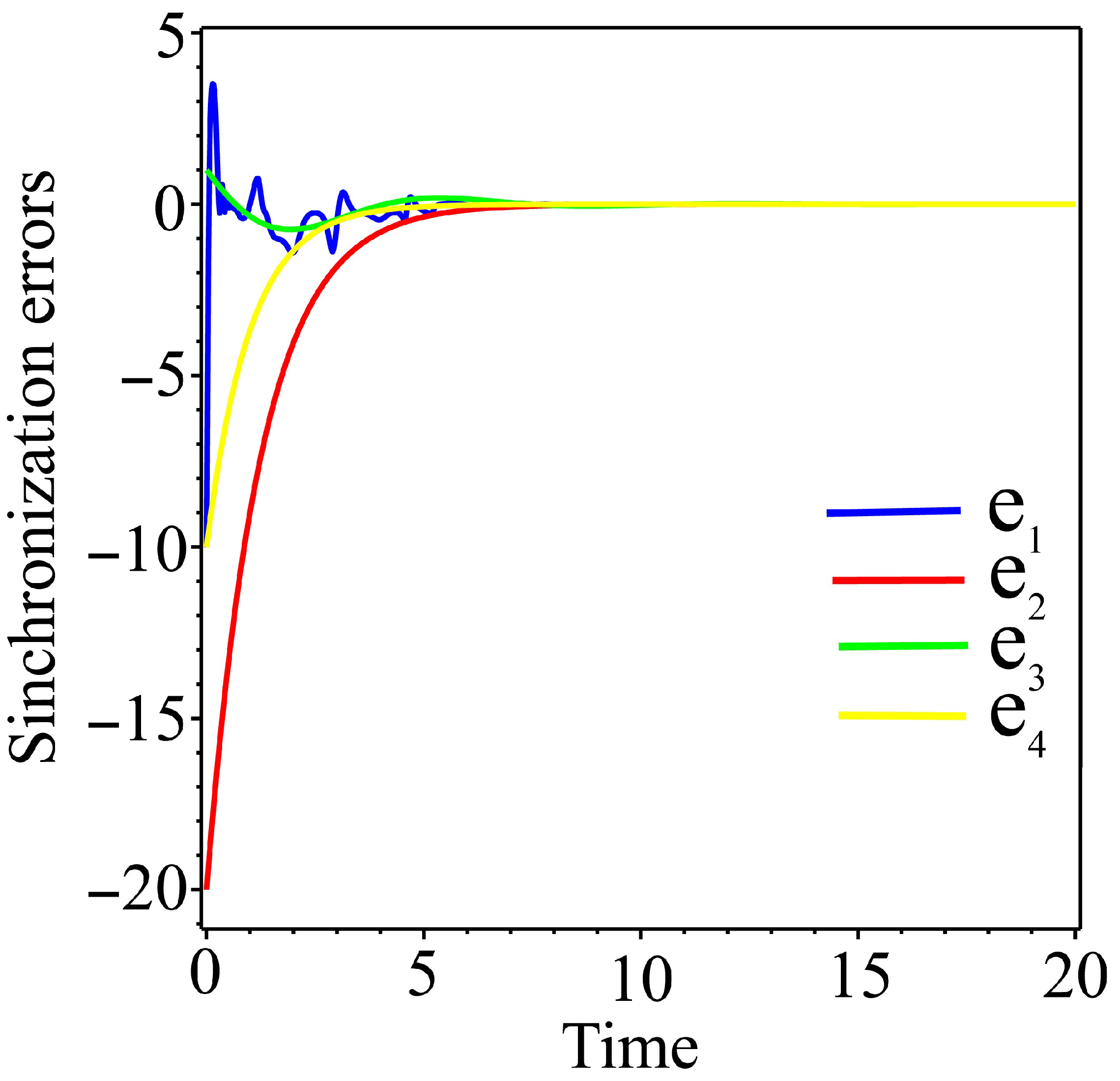
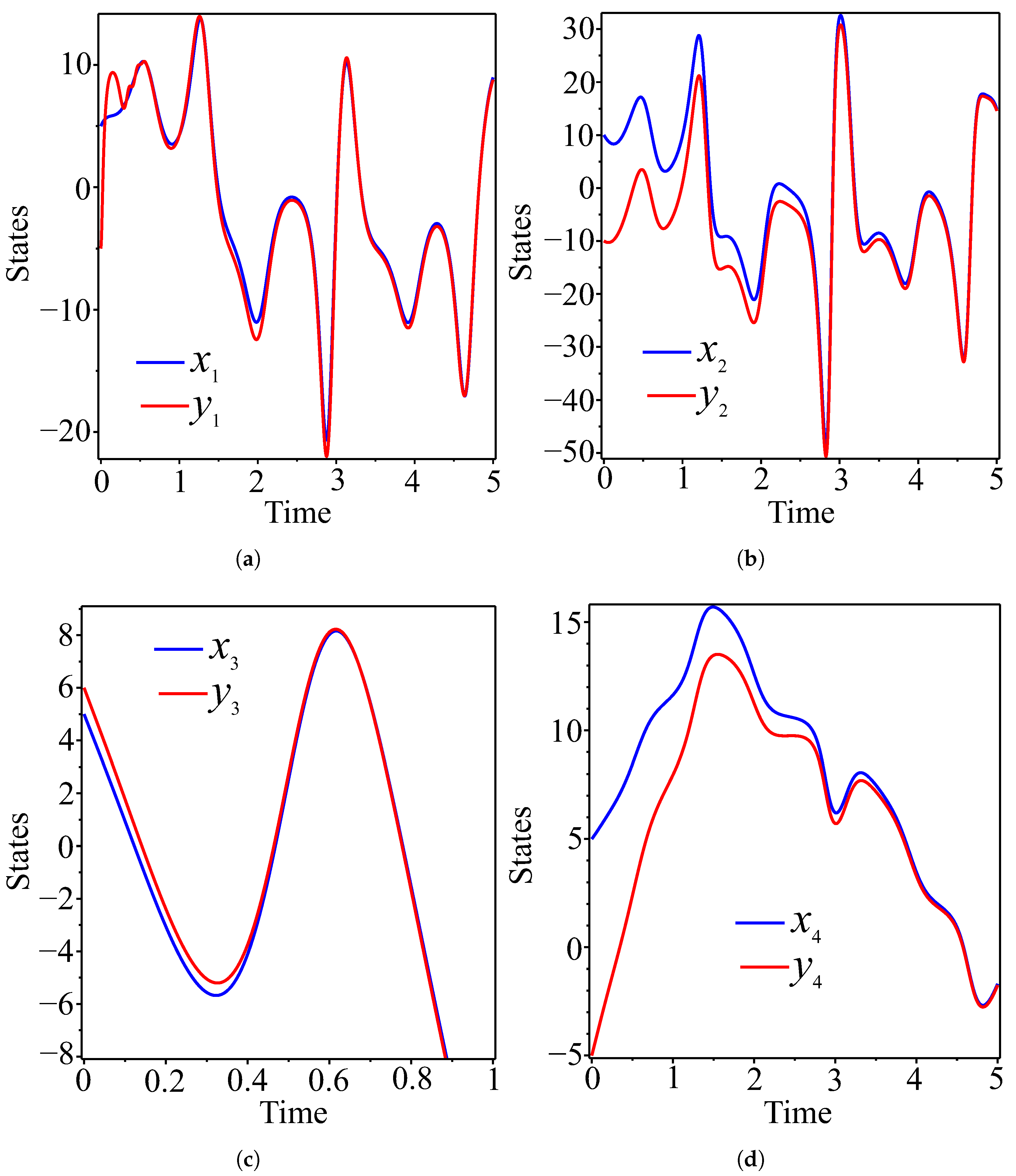
5.2. Adaptive Synchronization
6. Adaptive Control Method for Chaotic Masking and Decoding Useful Signals
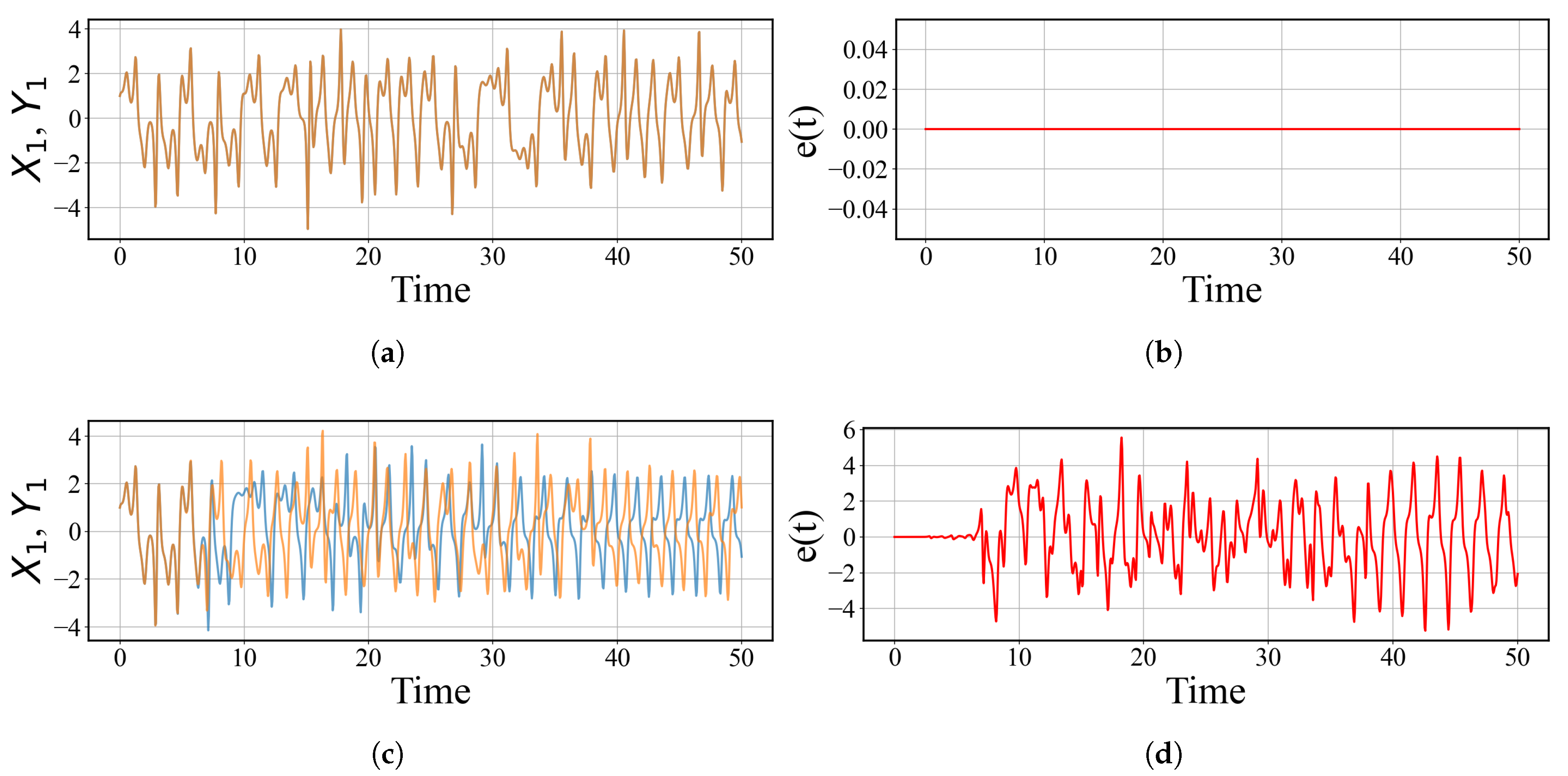
7. Application of Complete Synchronization of Hyperchaotic Systems to Detect Weak Signals
7.1. Numerical Results
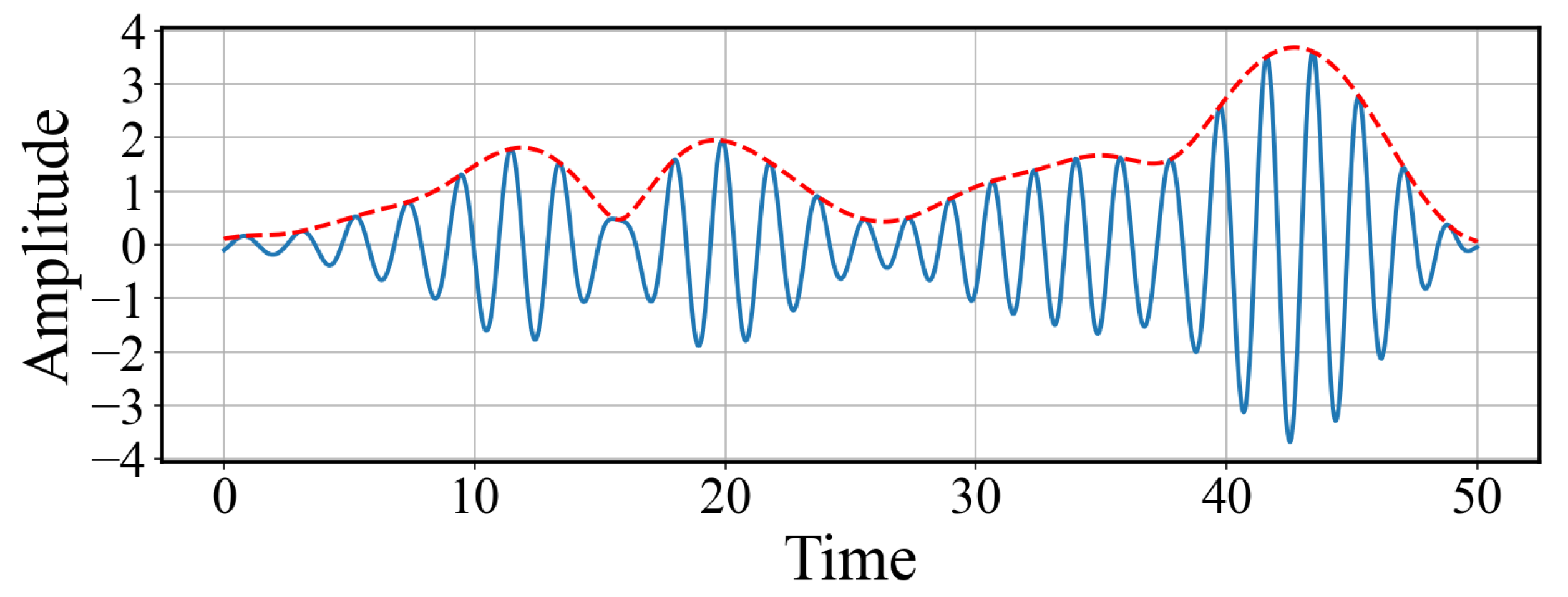
7.2. Filtering the Synchronization Error near Frequency
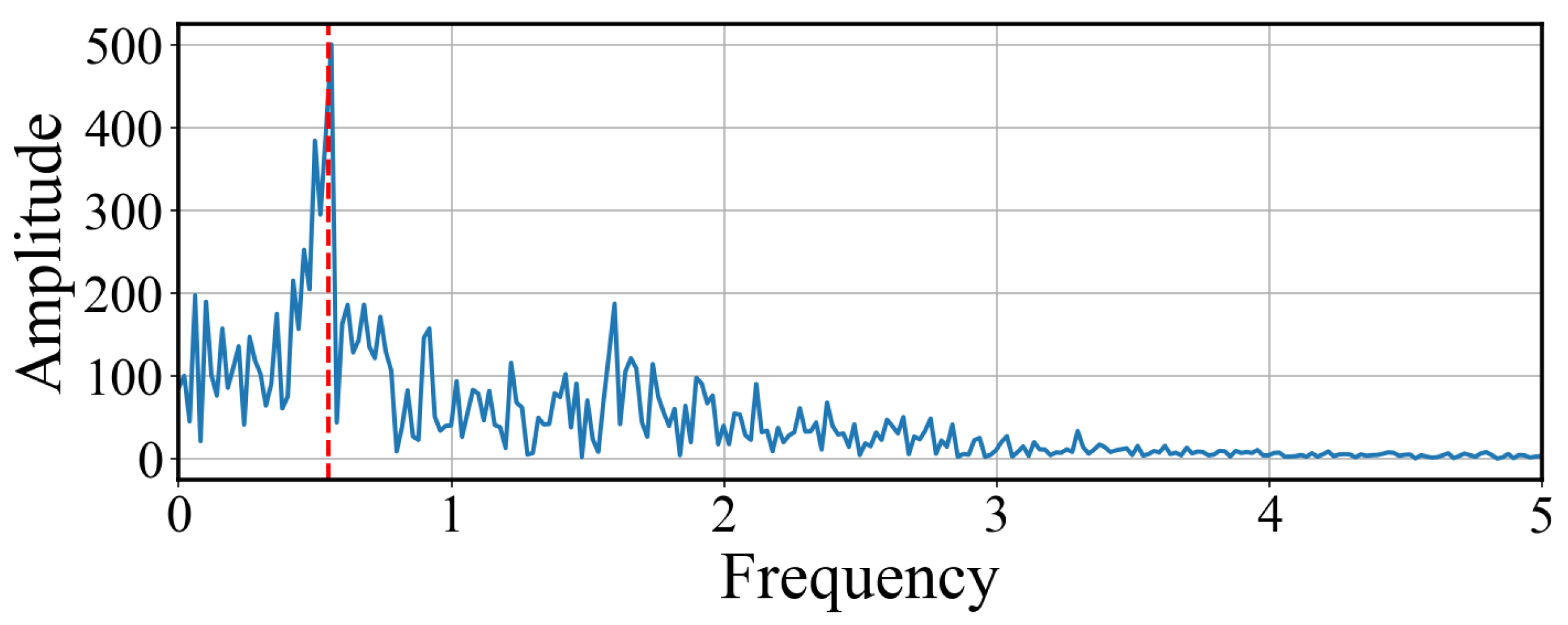
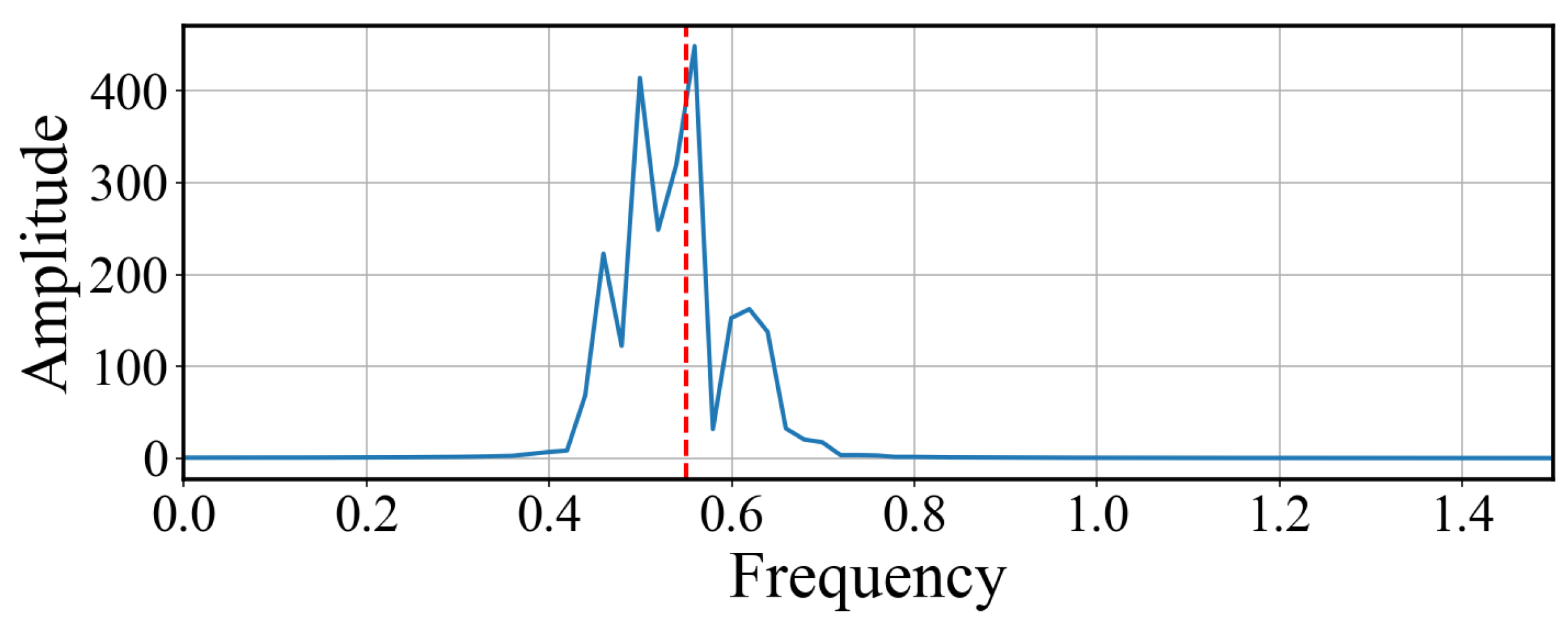
7.3. Spectral Detection of the Weak Signal
8. Practical Implementation of a 4D Memristor-Based Hyperchaotic System on Arduino UNO
8.1. Chaotic Dynamic Based on Arduino-Generated Chaotic Sequences
8.2. Image Encryption and Decryption Using Arduino-Generated Chaotic Sequences
| Algorithm 1: Chaos generation on Arduino (see system (10), initial conditions (11)) |
Input: Initial state , step size h, iterations N Output: Chaotic bytes  |
| Algorithm 2: Image encryption and decryption in MATLAB |
Input: Grayscale image I, chaotic byte stream Output: Encrypted image E, decrypted image 1 Flatten I into vector 2 Receive chaotic sequence of same length 3 Generate permutation by sorting 4 Apply permutation: 5 Encrypt: 6 Decrypt: 7 Recover original order: 8 Reshape into image |
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hashemi, S.; Pourmina, M.A.; Mobayen, S.; Alagheband, M.R. Multiuser wireless speech encryption using synchronized chaotic systems. Int. J. Speech Technol. 2021, 24, 651–663. [Google Scholar] [CrossRef]
- Shahna, K.U. Novel chaos based cryptosystem using four-dimensional hyper chaotic map with efficient permutation and substitution techniques. Chaos Solitons Fractals 2023, 170, 113383. [Google Scholar] [CrossRef]
- Ponnambalam, M.; Ponnambalam, M.; Ghazalah, S.A.; Sambas, A. Hybrid inter woven scrambling with spiral shell 3D hyperchaotic diffusion for secure color image encryption. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]
- Ye, C.J.; Sharpe, Z.; Heng, H.H. Origins and consequences of chromosomal instability: From cellular adaptation to genome chaos-mediated system survival. Genes 2020, 11, 1162. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Kozlovska, O.; Sadyrbaev, F.; Samuilik, I. A New 3D Chaotic Attractor in Gene Regulatory Network. Mathematics 2024, 12, 100. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, K.; Wang, H.; Yao, Z. Coexisting hyperchaos and multistability in a discrete memristor-coupled bi-neuron model. Nonlinear Dyn. 2024, 112, 9547–9561. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Sprott, J.C. Simplest dissipative chaotic flow. Phys. Lett. 1997, 228, 271–274. [Google Scholar] [CrossRef]
- der Schrier, G.V.; Maas, L.R.M. The diffusionless Lorenz equations; Shil’nikov bifurcations and reduction to an explicit map. Phys. D Nonlinear Phenom. 2000, 141, 19–36. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Ozoguz, S.; Kennedy, M.P. Creation of a complex butterfly attractor using a novel Lorenz-Type system. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 527–530. [Google Scholar] [CrossRef]
- Toncharoen, C.; Srisuchinwong, B. A heart-sound-like chaotic attractor and its synchronization. In Proceedings of the 6th International Conference on Telecommunications and Information Technology (ECTI-CON 2009), Chonburi, Thailand, 6–9 May 2009; Volume 1, pp. 407–410. [Google Scholar] [CrossRef]
- Munmuangsaen, B.; Srisuchinwong, B. A new five-term simple chaotic attractor. Phys. D Phys. Lett. 2009, 373, 4038–4043. [Google Scholar] [CrossRef]
- Chang, P.H.; Kim, D. Introduction and synchronization of a five-term chaotic system with an absolute-value term. Nonlinear Dyn. 2013, 73, 311–323. [Google Scholar] [CrossRef]
- Tamba, V.K.; Pham, V.T.; Hoang, D.V.; Jafari, S.; Alsaadi, F.E.; Alsaadi, F.E. Dynamic system with no equilibrium and its chaos anti-synchronization. Automatika 2018, 59, 35–42. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Kocamaz, U.E.; Uyaroglu, Y.; Calgan, H. A novel five-term 3D chaotic system with cubic nonlinearity and its microcontroller-based secure communication implementation. Int. J. Electron. Commun. 2023, 160, 154497. [Google Scholar] [CrossRef]
- Sprott, J.C. Elegant Automation; World Scientific: Singapore, 2023; 348p. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Radwan, A.G.; Fouda, M.E. On the Mathematical Modeling of Memristor, Memcapacitor, and Meminductor; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Gambuzza, L.V. A memristive hyperchaotic system without equilibrium. Sci. World J. 2014, 2014, 368986. [Google Scholar] [CrossRef]
- Rajagopal, K.; Bayani, A.; Khalaf, A.J.M.; Namazi, H.; Jafari, S.; Pham, V.T. A no-equilibrium memristive system with four-wing hyperchaotic attractor. Int. J. Electron. Commun. (AEU) 2018, 95, 207–215. [Google Scholar] [CrossRef]
- Singh, P.P.; Roy, B.K.; Volos, C. Chapter 9—Memristor-based novel 4D chaotic system without equilibria. In Advances in Nonlinear Dynamics and Chaos (ANDC), Mem-Elements for Neuromorphic Circuits with Artificial Intelligence Applications; Volos, C., Pham, V.-T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 183–205. [Google Scholar] [CrossRef]
- Tamba, V.K.; Tagne, F.K.; Biamou, A.L.M.; Nkeing, M.C.; Takougang, A.N. Chapter 7—Hidden extreme multistability generated from a novel memristive two-scroll chaotic system. In Advances in Nonlinear Dynamics and Chaos (ANDC), Mem-Elements for Neuromorphic Circuits with Artificial Intelligence Applications; Volos, C., Pham, V.-T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 147–164. [Google Scholar] [CrossRef]
- Irfan, A. Simple Chaotic Jerk, Hyperjerk, and Hyperchaotic Hyperjerk Circuits and Systems: Families of Self-Excited and Hidden Attractors. Ph.D. Thesis, Thammasat University, Bangkok, Thailand, 2020. [Google Scholar]
- Zhang, H.; Zhang, W.; Zhao, Y.; Ji, M. Adaptive state observers for incrementally quadratic nonlinear systems with application to chaos synchronization. Circuits Syst. Signal Process. 2020, 39, 1290–1306. [Google Scholar] [CrossRef]
- Tohidi, S.; Yildiz, Y.; Kolmanovsky, I. Adaptive control allocation for constrained systems. Automatica 2020, 121, 109161. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.K.; Pham, V.T. Hyperchaos, adaptive control and synchronization of a novel 5-D hyperchaotic system with three positive Lyapunov exponents and its SPICE implementation. Arch. Control Sci. 2014, 24, 409–446. [Google Scholar]
- Vaidyanathan, S.; Volos, C.K. Analysis and adaptive control of a novel 3-D conservative no-equilibrium chaotic system. Arch. Control Sci. 2015, 25, 333–353. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.Y.; Li, P.; Yan, H. A new Lorentz chaotic system and its circuit implementation. In Proceedings of the 8th EAI International Conference on Green Energy and Networking, GreeNets 2021, Dalian, China, 6–7 June 2021. [Google Scholar]
- Silva, C.P. Shil’nikov’s theorem—A tutorial. IEEE Trans. Circuits Syst. 1993, 40, 675–682. [Google Scholar] [CrossRef]
- Pareschi, J.F.; Rovatti, R.; Setti, G. On statistical tests for randomness included in the NIST SP800-22 test suite and based on the binomial distribution. IEEE Trans. Inf. Forensics Secur. 2012, 7, 491–505. [Google Scholar] [CrossRef]
- Wen, J.; Feng, Y.; Tao, X.; Cao, Y. Dynamical Analysis of a New Chaotic System: Hidden Attractor, Coexisting-Attractors, Offset Boosting, and DSP Realization. IEEE Access 2021, 9, 167920–167927. [Google Scholar] [CrossRef]
- Sedra, A.S.; Smith, K.C. Microelectronics Circuits, 4th ed.; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Khalil, H.K. Nonlinear System; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Li, G.; Zhang, B. A Novel Weak Signal Detection Method via Chaotic Synchronization Using Chua’s Circuit. IEEE Trans. Ind. Electron. 2017, 64, 2255–2265. [Google Scholar] [CrossRef]
- Haykin, S.; Li, X.B. Detection of signals in chaos. Proc. IEEE 1995, 83, 95–122. [Google Scholar] [CrossRef]
- Dwivedi, A.; Mittal, A.K.; Dwivedi, S. Chaotic communication using Pecora Carroll complete replacement and parameter modulation without controller. In Proceedings of the 2014 Students Conference on Engineering and Systems, Allahabad, India, 28–30 May 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, G.; Chen, D.; Lin, J.; Chen, X. The application of chaotic oscillators to weak signal detection. IEEE Trans. Ind. Electron. 1999, 46, 440–444. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L.; Johnson, G.A.; Mar, D.J.; Heagy, J.F. Fundamentals of synchronization in chaotic systems, concepts, and applications. Chaos 1997, 7, 520–543. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.J. Chaotic system for the detection of periodic signals under the background of strong noise. Chin. Sci. Bull. 2003, 48, 508–510. [Google Scholar] [CrossRef]







| Reference | Terms | Attractor | Equilibria | No. of NL Terms |
|---|---|---|---|---|
| Pham et al. [20] | 12 | Chaotic/hyperchaotic | None | 5 |
| Rajagopal et al. [21] | 11 | Chaotic/hyperchaotic | None or line | 5 |
| Singh et al. [22] | 9 | Chaotic | None | 2 |
| Tamba et al. [23] | 7 | Two-scroll chaos | None | 3 |
| Irfan [24] | 7 | Hyperchaotic | Line equilibrium | 1 |
| This work | 7 | Hyperchaotic | None | 3 |
| a | |||
|---|---|---|---|
| 2 | |||
| 3 | |||
| 5 | |||
| 10 |
| No. | Test Name | p-Value | Result |
|---|---|---|---|
| 1 | Frequency (Monobit) Test | 1.00000 | PASS |
| 2 | Block Frequency Test | 0.96718 | PASS |
| 3 | Runs Test | 0.13887 | PASS |
| 4 | Cumulative Sums Test (Forward) | 0.55996 | PASS |
| 5 | Cumulative Sums Test (Backward) | 0.55996 | PASS |
| 6 | Discrete Fourier Transform (Spectral) Test | 0.14203 | PASS |
| 7 | Approximate Entropy Test | 0.88952 | PASS |
| 8 | Serial Test | 0.72385 | PASS |
| 9 | Longest Run of Ones in a Block Test | 0.40256 | PASS |
| 10 | Rank Test | 0.37439 | PASS |
| 11 | Non-overlapping Template Matching Test | 0.29135 | PASS |
| 12 | Overlapping Template Matching Test | 0.96518 | PASS |
| 13 | Universal Statistical Test (Maurer’s Test) | 0.94858 | PASS |
| 14 | Linear Complexity Test | 0.27652 | PASS |
| 15 | Random Excursions (Variant) Test: | ||
| State −4: | 0.85648 | PASS | |
| State −3: | 0.91479 | PASS | |
| State −2: | 0.58058 | PASS | |
| State −1: | 0.33856 | PASS | |
| State 1: | 0.86431 | PASS | |
| State 2: | 0.55385 | PASS | |
| State 3: | 0.55109 | PASS | |
| State 4: | 0.78617 | PASS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopp, M.I.; Samuilik, I. Hidden Attractors in a New 4D Memristor-Based Hyperchaotic System: Dynamical Analysis, Circuit Design, Synchronization, and Its Applications. Mathematics 2025, 13, 2838. https://doi.org/10.3390/math13172838
Kopp MI, Samuilik I. Hidden Attractors in a New 4D Memristor-Based Hyperchaotic System: Dynamical Analysis, Circuit Design, Synchronization, and Its Applications. Mathematics. 2025; 13(17):2838. https://doi.org/10.3390/math13172838
Chicago/Turabian StyleKopp, M. I., and I. Samuilik. 2025. "Hidden Attractors in a New 4D Memristor-Based Hyperchaotic System: Dynamical Analysis, Circuit Design, Synchronization, and Its Applications" Mathematics 13, no. 17: 2838. https://doi.org/10.3390/math13172838
APA StyleKopp, M. I., & Samuilik, I. (2025). Hidden Attractors in a New 4D Memristor-Based Hyperchaotic System: Dynamical Analysis, Circuit Design, Synchronization, and Its Applications. Mathematics, 13(17), 2838. https://doi.org/10.3390/math13172838







