Estimate-Based Dynamic Memory-Event-Triggered Control for Nonlinear Networked Control Systems Subject to Hybrid Attacks

Abstract

Within the framework of a dynamic memory-event-triggered mechanism (DMETM), this paper proposes an estimate-based secure control algorithm for nonlinear networked control systems (NNCSs) that suffer from hybrid attacks. Firstly, a sampled-data observer is employed utilizing the output signals to estimate the states. Secondly, due to the limitation of data transmission capacity in NNCSs, a novel DMETM with auxiliary variable is proposed, which effectively leverages the benefits of historical sampled data. In the process of network data transmission, a hybrid attack model that simultaneously considers the impact of both deception and denial of service (DoS) attacks is introduced, which can undermine signal integrity and disrupt data transmission. Then, a memory-event-triggered controller is developed, and the mean square stability of the NNCSs can be ensured by selecting some appropriate values. Finally, a numerical simulation and a practical example are given to illustrate the meaning of the designed dynamic memory-event-triggered control (DMETC) algorithm.

1. Introduction

It is well known that nonlinear networked control systems (NNCSs) gained considerable interest because of their efficient integration of nonlinear dynamics and network communication capabilities. These systems are widely applied in various fields, including industrial automation, smart grids, robotics, and intelligent transportation systems [1,2,3,4]. In general, the use of networked communication facilitates remote control and real-time adjustments, which significantly enhances the system reliability and efficiency [5,6,7]. Despite these advantages, NNCSs can be limited by constrained bandwidth and potential cyber-attacks, which necessitate the development of advanced control strategies to maintain system stability and performance.

The traditional time-triggered mechanism results in the transmission of redundant signals, even when the system has already achieved the desired control objective, thereby causing unnecessary resource consumption. To overcome this issue, an event-triggered mechanism (ETM) that can reduce the signal transmission rate has garnered significant attention from researchers [8,9,10,11]. Recent advancements in event-triggered control have achieved significant results in several areas, including predictive control, $H_{\infty }$ control, and output feedback control [12]. Based on these developments, a memory-event-triggered mechanism is introduced to improve communication resource utilization by utilizing historical sampled data [13,14]. Compared to traditional ETM, the memory-event-triggered scheme can reduce unnecessary data transmission during unexpected system fluctuations and improve data update efficiency when changes are smooth near critical troughs. For example, a memory event-triggered finite-time lane-keeping control strategy was designed for autonomous heavy trucks in [15]. A load frequency control problem of power systems is addressed in [16], where the adaptive-memory ETM was presented to optimize resource utilization. Moreover, dynamic ETM can further reduce bandwidth usage by adjusting the auxiliary variable or dynamic threshold [17,18,19,20]. For instance, a data-driven control of nonlinear systems under dual-channel memory ETM was studied in [21]. An anti-disturbance control method for switched cyber-physical systems was proposed in [22], where DMETM was considered. It should be noted that studying DMETM is crucial for optimizing resource utilization while maintaining system stability and performance.

In NNCSs, data transmission is not only constrained by limited bandwidth resources but also potentially threatened by cyber-attacks, both of which collectively impact the stability and security of the systems. Concerning cyber-attacks, the recent literature introduces most security control methods for NNCSs [23,24,25,26]. Cyber-attacks on NNCSs are generally divided into three main primary types: DoS attacks, replay attacks, and deception attacks [27]. Specifically, DoS attacks aim to disrupt data transmission by intentionally dropping or blocking data packets during the communication process, thereby preventing the normal exchange of information between system components. Replay attacks involve the interception and retransmission of previously captured data packets, which can mislead the system into making incorrect decisions based on outdated information. Deception attacks involve the injection of false or malicious data into the system, potentially leading to severe safety hazards. Despite these advancements, most existing research primarily focuses on addressing a single type of attack, with limited attention given to the more complex and realistic scenario of hybrid attacks, where multiple attack types may occur simultaneously or sequentially [28,29]. For example, the problem of discrete proportion–integration–differentiation control was coped with in [29] for interconnected power systems with hybrid attacks. In [30], a cooperative resilient control strategy was designed for energy storage systems with hybrid attacks, where false data injection and DoS attacks were taken into account.

Based on the above discussion, in the presence of hybrid attacks, two key challenges should be tackled: (1) how to jointly develop a DMETM and observer to estimate the output signals when the full system states are unavailable; (2) how to formulate the estimate-based dynamic memory-event-triggered control (DMETC) approach to obtain the mean square stability of NNCSs when the communication network is subjected to hybrid attacks. To overcome these challenges, an estimate-based DMETC is designed in this paper for NNCSs subject to hybrid attacks. The main contributions are summarized as follows:

• By virtue of auxiliary variable and past sampled-data, this paper proposes DMETM, which offers a more effective balance between communication utilization and control performance in comparison to the traditional ETM with fixed threshold [8,9,10].
• This paper considers a hybrid attack model that incorporates both DoS attacks and deception attacks. This control approach is more general than those considered in previous works [26,27], which primarily focused on single-attack scenarios.
• Both the designed DMETM and memory-event-triggered output feedback controller are formulated in discrete time. This means that only the system output data are necessary for the joint design of the memory-event-triggered controller and the DMETM, which makes the approach more practical and applicable to the actual system.

The structure of this paper is outlined as follows: Section 2 and Section 3 present the problem formulation and the procedure for designing the estimate-based DMETC. Section 4 provides the stability analysis, and Section 5 demonstrates the effectiveness of the designed estimate-based DMETC approach through two examples. Section 6 reaches the conclusion of the designed results.

Notations: $\mathbb{N}$ and $\mathbb{R}$ stand for the sets of non-negative numbers and real numbers. $W\in {\mathbb{R}}^{n\times m}$ and $W^T$ refer to the set of the $n\times m$ real matrix and the transpose of W. When $W=W^T\in {\mathbb{R}}^{m\times m}$, ${\lambda }_{\min }\left(W\right)$ and ${\lambda }_{\max }\left(W\right)$ denote the minimum and the maximum eigenvalues of W, respectively. $\parallel ·\parallel$ and I represent the 2-norm and the identity matrix.

2. Problem Formalization

As illustrated in Figure 1, the proposed estimate-based DMETC framework integrates the plant, the sampled-data state observer, the DMETM, and the memory-event-triggered controller. The DMETM exploits historical sampled data to reduce communication load, while hybrid attacks, including deception and DoS attacks, are modeled on the communication channel to represent threats to signal integrity and reliability.

System Model

Consider an NNCS as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_i=x_{i+1}+f_i\left({\tilde{x}}_i\right),1\le i\le n-1,\hfill \\ {\dot{x}}_n=u+f_n\left(x\right),\hfill \\ y=x_1\hfill \end{array}\right.\end{array}$$

(1)

where $x={\left[x_1,\dots ,x_n\right]}^T\in {\mathbb{R}}^n$, ${\tilde{x}}_i={\left[x_1,\dots ,x_i\right]}^T\in {\mathbb{R}}^i$, $u\in \mathbb{R}$, and $y\in \mathbb{R}$ refer to the state, control input, and system output; $f_i,i=1,2,\dots ,n$ stands for the nonlinear terms.

Motivated by [31], the following assumption on nonlinear uncertain terms is used.

Assumption 1.

For the nonlinear uncertain terms $f_i\left(t\right),i=1,2,\dots ,n$, there exists a constant $c_0>0$ such that

$$|f_i\left({\tilde{x}}_i\right)|\le c_0\left(\left|x_1\right|+\cdots +\left|x_i\right|\right).$$

(2)

Based on Assumption 1, this paper addresses the estimate-based DMETC issue for system (1) subject to hybrid attacks when only the output signals are available. By establishing sufficient conditions, the mean square stability of the NNCSs can be guaranteed while simultaneously minimizing the number of events to the greatest extent possible.

Define the following variables:

$$\begin{array}{c}\hfill z_i={\displaystyle \frac{x_i}{{\iota }^{i-1}}},v={\displaystyle \frac{u}{{\iota }^n}},i=1,2,\dots ,n.\end{array}$$

Then, (1) can be further described as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{z}=\iota A_{0}z+\iota B_{0}v+\tilde{f}\left(z\right),\hfill \\ y=C_{0}z\hfill \end{array}\right.\end{array}$$

(3)

where $z={[z_1,\dots ,z_n]}^T$, $\tilde{f}\left(z\right)={[{\displaystyle \frac{f_1}{{\iota }^0}},\dots ,{\displaystyle \frac{f_n}{{\iota }^{n-1}}}]}^T$, $A_0=\left[\begin{array}{cc}{0}_{(n-1)\times 1}& I_{(n-1)\times (n-1)}\\ 0& 0_{1\times (n-1)}\end{array}\right]$, $B_0=\left[\begin{array}{c}{0}_{(n-1)\times 1}\\ 1\end{array}\right]$, $C_0=\left[\begin{array}{cc}1& 0_{1\times (n-1)}\end{array}\right]$.

3. Estimate-Based DMETC Design Against Hybrid Attacks

In this section, the aim of this study is to develop an estimate-based DMETC strategy for NNCSs (3), which includes three parts: (1) A sampled-data observer is presented to estimate the output, and a DMETM with dynamic variable is established to alleviate bandwidth pressure. (2) A hybrid attacks model encompassing DoS and deception attacks is considered, which has an impact on the transmission signals. (3) According to the hybrid attacks and the DMETM, a memory-event-triggered output feedback tracking controller is proposed.

3.1. Sampled-Data Observer Design

Let h, ${\left\{t_{k}h\right\}}_{k\in \mathbb{N}}$, and $t_{k,g}h=t_{k}h+gh$, $g=1,2,\dots$ be the sampling period, the set of event-triggered instants, and the sampling instants, respectively. Based on (3), a sampled-data observer is built for $t\in [t_{k,g}h,t_{k,g+1}h)$

$$\begin{array}{c}\hfill \dot{\widehat{z}}\left(t\right)=\iota A_0\widehat{z}\left(t\right)+\iota B_{0}v\left(t\right)+\iota H(y\left(t_{k,g}h\right)-C_0\widehat{z}\left(t\right))\end{array}$$

(4)

where $\widehat{z}\left(t\right)={[{\widehat{z}}_1\left(t\right),\dots ,{\widehat{z}}_n\left(t\right)]}^T$ stands for the estimate of $z\left(t\right)$, and $H={[h_1,\dots ,h_n]}^T$ refers to the observer parameters.

Define the following estimation error: $e_i=z_i-{\widehat{z}}_i,i=1,\dots ,n$. With help of (3) and (4), the estimation error system is expressed as

$$\begin{array}{cc}\hfill \dot{e}\left(t\right)=& \iota A_{0}e\left(t\right)+\tilde{f}\left(z\left(t\right)\right)-\iota H(y\left(t_{k,g}h\right)-C_0\widehat{z}\left(t\right)),t\in [t_{k,g}h,t_{k,g+1}h)\hfill \end{array}$$

(5)

where $e={[e_1,\dots ,e_n]}^T$.

3.2. DMETM Design

By applying the average of historical system output, a DMETM is employed to decide whether the estimated signals should be released to a remote controller. Define

$$\begin{array}{cc}\hfill & \mathbb{M}\left(t\right)=\sum _{m=1}^{\tilde{m}}\parallel {\theta }_m{ϵ}_m\left(t\right)\parallel -{\displaystyle \frac{\sigma }{\iota }}\parallel \widehat{z}\left(t_{k,g}h\right)\parallel -{\displaystyle \frac{\eta }{\iota }}\gamma \left(t_{k,g}h\right),\hfill \\ \hfill & {ϵ}_m\left(t\right)=\widehat{z}\left(t_{k,g}h\right)-\widehat{z}\left(t_{k-m+1}h\right)\hfill \end{array}$$

where $\tilde{m}$ and $t_{k-m+1}h,m=1,2,\dots ,\tilde{m}$ stand for the maximum value of the historical event-triggered instant and the past event-triggered instant; ${\theta }_m$ denotes the weight of historical signals at instant $t_{k-m+1}h$; $\sigma \ge 0$, $\eta >0$, $\gamma \left(t_{k,g}h\right)$ refers to the dynamic variable and satisfies the following adaptive law:

$$\dot{\gamma }\left(t\right)=-\overline{\eta }\gamma \left(t\right)+{\displaystyle \frac{\sigma }{\iota }}\parallel \widehat{z}\left(t_{k,g}h\right)\parallel -\sum _{m=1}^{\tilde{m}}\parallel {\theta }_m{ϵ}_m\left(t\right)\parallel$$

(6)

where $t\in [t_{k,g}h,t_{k,g+1}h)$, $\overline{\eta }>0$, and $\gamma \left(0\right)\ge 0$ denote the initial condition. Then, the next triggered instant is determined by

$$\begin{array}{c}\hfill t_{k+1}h=t_{k}h+\underset{g\ge 1}{\min }\left\{gh\left|\mathbb{M}\right(t)\ge 0\right\}.\end{array}$$

(7)

Remark 1.

Different from memoryless ETM [17], the proposed DMETM (7) employs the average value of past data ${\sum }_{m=1}^{\tilde{m}}\parallel {\theta }_m{ϵ}_m\left(t\right)\parallel$ with pre-assigned constant historical weights ${\theta }_m$, where more recent event-triggered data are assigned larger weights, and older data receive smaller weights. This design emphasizes the influence of recent information, helping reduce unnecessary data transmissions caused by sudden changes in the system state while avoiding excessive sensitivity to outdated data. It should be noted that the historical information $\widehat{z}\left(t_{k-m+1}h\right)$ is utilized in (7) to avoid unnecessary transmissions influenced by external factors.

The subsequent lemma is employed to represent the key characteristics of the auxiliary variable $\gamma \left(t\right)$.

Lemma 1.

Consider the rule (6) with $\gamma \left(0\right)\ge 0$; if $\eta >0$ and $\overline{\eta }>0$, the sampling period h satisfies

$$\begin{array}{c}\hfill h<{\displaystyle \frac{1}{\overline{\eta }}}ln\left({\displaystyle \frac{\iota \overline{\eta }}{\eta }}+1\right),\end{array}$$

(8)

then, for all $t\in [0,\infty )$, $\gamma \left(t\right)\ge 0$ holds.

Proof. 

Based on the DMETM (7) that $\parallel {\sum }_{m=1}^{\tilde{m}}{\theta }_m{ϵ}_m\left(t\right)\parallel \le {\displaystyle \frac{\sigma }{\iota }}\parallel \widehat{z}\left(t_{k,g}h\right)\parallel +{\displaystyle \frac{\eta }{\iota }}\gamma \left(t_{k,g}h\right)$, $\forall t\in [t_{k,g}h,t_{k,g+1}h)$. Integrating (6) from $t_{k,g}h$ to $t\in [t_{k,g}h,t_{k,g+1}h)$, one has

$$\begin{array}{cc}\hfill \gamma \left(t\right)=& e^{-\overline{\eta }(t-t_{k,g}h)}\gamma \left(t_{k,g}h\right)+{\int }_{t_{k,g}h}^t{e}^{-\overline{\eta }(t-v)}dv\left({\displaystyle \frac{\sigma }{\iota }}\parallel \widehat{z}\left(t_{k,g}h\right)\parallel -\parallel \sum _{m=1}^{\tilde{m}}{\theta }_m{ϵ}_m\left(t\right)\parallel \right)\hfill \\ \hfill \ge & e^{-\overline{\eta }(t-t_{k,g}h)}\gamma \left(t_{k,g}h\right)-{\int }_{t_{k,g}h}^t{e}^{-\overline{\eta }(t-v)}dv{\displaystyle \frac{\eta \gamma \left(t_{k,g}h\right)}{\iota }}\hfill \\ \hfill \ge & \left(e^{-\overline{\eta }h}-{\displaystyle \frac{\eta (1-e^{-\overline{\eta }h})}{\iota \overline{\eta }}}\right)\gamma \left(t_{k,g}h\right).\hfill \end{array}$$

(9)

Taking (9) into consideration, it can be obtained that $\gamma \left(t\right)\ge 0$, where $t\in [t_{k,g}h,t_{k,g+1}h)$. Moreover, since $\gamma \left(t\right)$ is a continuous function, $\gamma \left(t_{k,g+1}^{-}h\right)=\gamma \left(t_{k,g+1}h\right)$, which implies that $\gamma \left(t_{k,g+1}h\right)\ge 0$. Obviously, it follows that $\gamma \left(t\right)\ge 0$, $\forall t\in [0,\infty )$. □

Remark 2.

For the proposed DMETM in (7), the inclusion of the dynamic variable γ enables potential noise attenuation, since the γ value can be interpreted as a filtered parameter of the error function ${ϵ}_m$. Unlike the traditional ETM with a fixed threshold [8,27], the DMETM (7) employs a more sophisticated triggering condition. This condition is inherently more challenging to satisfy due to the presence of the term ${\displaystyle \frac{\eta }{\iota }}\gamma \left(t_{k,g}h\right)$, which is always non-negative. As a result, the DMETM ensures that events are triggered only when significant changes occur, thereby reducing unnecessary transmissions and saving limited network resources.

Remark 3.

In contrast to certain existing memory ETM approaches [13,14], the DMETM (7) in this paper is constructed based on the state estimates rather than relying on full states. The designed DMETM (7) incorporates three adjustable parameters: σ, η, and $\overline{\eta }$. By setting $\eta =0$, the designed DMETM (7) simplifies to the conventional ETM [8]. Furthermore, when both σ and η are set to 0, the designed DMETM (7) simplifies to the time-triggered mechanism. Generally, smaller values of σ and η typically result in a higher transmission frequency, thereby improving the control performance. Therefore, it is crucial to carefully adjust these parameters to achieve an optimal trade-off between the transmission rate and the desired control performance.

3.3. Hybrid Attacks

As depicted in Figure 1, the hybrid attacks studied in this paper consist of both deception and DoS attacks. Specifically, the deception attacks can tamper with the transmitted data and damage their integrity, while the DoS attacks can block the packets transmission, resulting in sampled signals being unable to reach the controller. When these two attacks occur simultaneously, the impact of the hybrid attacks exceeds that of a single attack, as it not only compromises the accuracy of the data but also disrupts its transmission.

The transmission signal affected by the hybrid attacks model is presented as

$$\begin{array}{c}\hfill \tilde{z}\left(t_{k}h\right)={\beta }_k\left(t\right)[{\alpha }_k\left(t\right)\widehat{z}\left(t_{k}h\right)+(1-{\alpha }_k\left(t\right))g\left(\widehat{z}\left(t_{k}h\right)\right)]\end{array}$$

(10)

where $g\left(\widehat{z}\left(t_{k}h\right)\right)$ stands for the nonlinear function created by deception attacks and satisfies $\parallel g\left(\widehat{z}\left(t_{k}h\right)\right)\parallel \le c\parallel \widehat{z}\left(t_{k}h\right)\parallel$, with $c>0$. ${\alpha }_k\left(t\right)\in \{0,1\}$ and ${\beta }_k\left(t\right)\in \{0,1\}$ denote the Bernoulli distributed variable, with the associated probabilities given by

$$\begin{array}{cc}\hfill Pr\{{\alpha }_k\left(t\right)=1\}& ={\overline{\alpha }}_k,Pr\{{\alpha }_k\left(t\right)=0\}=1-{\overline{\alpha }}_k,\hfill \\ \hfill Pr\{{\beta }_k\left(t\right)=1\}& ={\overline{\beta }}_k,Pr\{{\beta }_k\left(t\right)=0\}=1-{\overline{\beta }}_k\hfill \end{array}$$

(11)

with $0\le {\overline{\alpha }}_k<1$, and $0\le {\overline{\beta }}_k<1$.

Remark 4.

According to (10), if ${\beta }_k\left(t\right)=0$, this indicates that the sampled output suffers from DoS attacks. If ${\beta }_k\left(t\right)=1$ and ${\alpha }_k\left(t\right)=0$, the estimated signal $\widehat{z}\left(t_{k}h\right)$ suffers from deception attacks, and the actual signal received by the controller is $g\left(\widehat{Z}\left(t_{k}h\right)\right)$. If ${\beta }_k\left(t\right)=1$ and ${\alpha }_k\left(t\right)=1$, this implies that the data are unaffected by the hybrid attacks and can reach the controller on time while maintaining its integrity.

3.4. Output Feedback Controller Design

Based on (4) and (10), the control input $v\left(t\right)$ is defined by

$$\begin{array}{c}\hfill v\left(t\right)={\iota }^{n}u\left(t_{k}h\right)=-{\iota }^n\sum _{m=1}^{\tilde{m}}K\tilde{z}\left(t_{k-m+1}h\right),t\in [t_{k}h,t_{k+1}h)\end{array}$$

(12)

where $K=[k_1,\dots ,k_n]$ denotes the controller parameters to be designed.

With the DMETM (7) and the hybrid attacks model (10) in mind, the event-triggered controller (12) is redesigned as

$$\begin{array}{c}\hfill v\left(t\right)=-\sum _{m=1}^{\tilde{m}}\left[K{\beta }_k\left(t\right){\alpha }_k\left(t\right)(\widehat{z}\left(t_{k,g}h\right)-{ϵ}_m\left(t\right))+K{\beta }_k\left(t\right)(1-{\alpha }_k\left(t\right))g\left(\widehat{z}\left(t_{k-m+1}h\right)\right)\right]\end{array}$$

(13)

where $t\in [t_{k,g}h,t_{k,g+1}h)$.

Then, combining (3) and (5), a closed-loop system is designed as

$$\begin{array}{cc}\hfill \dot{\rho }\left(t\right)=& \iota {\Xi }_1\rho \left(t\right)+\iota {\Xi }_2\sum _{m=1}^{\tilde{m}}{\beta }_k\left(t\right){\alpha }_k\left(t\right){ϵ}_m\left(t\right)+F\left(z\left(t\right)\right)\hfill \\ \hfill & -\iota {\Xi }_2\sum _{m=1}^{\tilde{m}}{\beta }_k\left(t\right)(1-{\alpha }_k\left(t\right))g\left(\widehat{z}\left(t_{k-m+1}h\right)\right)\hfill \\ \hfill & +\iota {\Xi }_3{\beta }_k\left(t\right){\alpha }_k\left(t\right)\rho \left(t_{k,g}h\right))+\iota {\Xi }_4(z\left(t\right)-z\left(t_{k,g}h\right))\hfill \end{array}$$

(14)

where $t\in [t_{k,g}h,t_{k,g+1}h)$, $\rho ={[z^T,e^T]}^T$, ${\Xi }_1=\left[\begin{array}{cc}{A}_0& 0\\ 0& A_0-H{C}_0\end{array}\right]$, ${\Xi }_2=\left[\begin{array}{c}{B}_{0}K\\ 0\end{array}\right]$, ${\Xi }_3=\left[\begin{array}{c}{B}_{0}K\\ -B_{0}K\end{array}\right]$, ${\Xi }_4=\left[\begin{array}{c}0\\ H{C}_0\end{array}\right]$, $F\left(z\left(t\right)\right)=\left[\begin{array}{c}\tilde{f}\left(z\left(t\right)\right)\\ \tilde{f}\left(z\left(t\right)\right)\end{array}\right]$.

4. Stability Analysis

To establish the stability analysis for the NNCSs, the following lemma is presented.

Lemma 2

([31]). Let $\vartheta :{\mathbb{R}}^n\times {\mathbb{R}}^n⟶{\mathbb{R}}^n$. Consider the following differential equation:

$$\begin{array}{c}\hfill \dot{\vartheta }\left(j\right)=\mu (\vartheta \left(j\right),\vartheta \left(j_k\right)),\forall j\in [j_k,j_{k+1}),j_k=t_{k}h,k\in \mathbb{N}.\end{array}$$

(15)

If $\mu (\vartheta \left(j\right),\vartheta \left(j_k\right))$ satisfies

$$\begin{array}{c}\hfill \parallel \mu (\vartheta \left(j\right),\vartheta \left(j_k\right))\parallel \le b_1(\parallel \vartheta \left(j\right)-\vartheta \left(j_k\right)\parallel +\parallel \vartheta \left(j_k\right)\parallel )\end{array}$$

(16)

where $b_1$ denotes a positive constant; then, it holds that

$$\begin{array}{cc}\hfill \parallel \mu (\vartheta \left(j\right),\vartheta \left(j_k\right))\parallel \le & (e^{b_1(j-j_k)}-1)\parallel \vartheta \left(j_k\right)\parallel ,\forall j\in [j_k,j_{k+1}),k\in \mathbb{N}.\hfill \end{array}$$

According to (14), there exists a positive matrix $P=P^T\in {\mathbb{R}}^{n\times n}$ such that ${\Xi }_1^{T}P+P{\Xi }_1=-I$ holds, where ${\Xi }_1$ is a Hurwitz matrix. Then, the following theorem is presented to demonstrate the stability of NNCSs (14) under hybrid attacks.

Theorem 1.

Under Assumption 1, consider the NNCSs (3) subject to hybrid attacks and DMETM (7). If ι and h satisfy

$$\begin{array}{cc}\hfill \overline{\omega }=& {\omega }_1{\lambda }_{\min }\left(P\right)-2\tilde{m}\parallel P{\Xi }_2\parallel {\overline{\beta }}_k({\overline{\alpha }}_k+c(1-{\overline{\alpha }}_k))(\sigma +\eta )-2\sigma >0,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill h<& \left\{{\displaystyle \frac{1}{\overline{\eta }}}ln\left({\displaystyle \frac{\iota \overline{\eta }}{\eta }}+1\right),{\displaystyle \frac{1}{a_2}}ln\left(1+{\displaystyle \frac{\overline{\omega }}{{\overline{\omega }}_1}}\right)\right\},\hfill \end{array}$$

(18)

where $a_1={\displaystyle \frac{\eta \parallel {\Xi }_4\parallel }{a_2}}$, $a_2=\max \{\iota \parallel {\Xi }_1\parallel +\iota \parallel {\Xi }_2\parallel +c_1,\iota \parallel {\Xi }_1\parallel +\sigma \parallel {\Xi }_2\parallel +c_1\}$,

$$\begin{array}{cc}\hfill {\overline{\omega }}_1=& \sqrt{2}c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel (\iota +\sigma ))(1+a_1)+2(\sqrt{2}\tilde{m}\sigma \parallel P{\Xi }_2\parallel {\overline{\beta }}_k{\overline{\alpha }}_k+\iota \parallel P{\Xi }_4\parallel ,\hfill \\ \hfill {\omega }_1=& \min \{2\overline{\eta },{\displaystyle \frac{\iota -2c_1\parallel P\parallel -2\sqrt{2}\tilde{m}\sigma \parallel P{\Xi }_2\parallel {\overline{\beta }}_k{\overline{\alpha }}_k}{{\lambda }_{\max }\left(P\right)}}-{\displaystyle \frac{2\sqrt{2}c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel (\iota +\sigma )}{{\lambda }_{\max }\left(P\right)}}\}>0,\hfill \\ \hfill {\omega }_2=& {\displaystyle \frac{2(\sqrt{2}\tilde{m}\sigma \parallel P{\Xi }_2\parallel {\overline{\beta }}_k{\overline{\alpha }}_k+\iota \parallel P{\Xi }_4\parallel )(1+a_1)(e^{a_{2}h}-1)}{{\lambda }_{\min }\left(P\right)}}\hfill \\ \hfill & +{\displaystyle \frac{2\sqrt{2}c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel (\iota +\sigma )(1+a_1)(e^{a_{2}h}-1)}{{\lambda }_{\min }\left(P\right)}}\hfill \\ \hfill & +{\displaystyle \frac{2\tilde{m}\parallel P{\Xi }_2\parallel {\overline{\beta }}_k\eta ({\overline{\alpha }}_k+c(1-{\overline{\alpha }}_k))+2\sigma 2\iota {\overline{\beta }}_k{\overline{\alpha }}_k\parallel P{\Xi }_3\parallel }{{\lambda }_{\min }\left(P\right)}},\hfill \end{array}$$

then, the system (14) is mean square stable.

Proof. 

For the system (14), construct the following Lyapunov function:

$$\begin{array}{c}\hfill V\left(\tilde{\rho }\right)={\rho }^{T}P\rho +{\gamma }^2\end{array}$$

(19)

where $\tilde{\rho }={[{\rho }^T,\gamma ]}^T$. Taking the mathematical expectation and derivation of $V\left(\tilde{\rho }\left(t\right)\right)$ with respect to the (14) in the time interval $t\in [t_{k,g}h,t_{k,g+1}h)$ yields

$$\begin{array}{cc}\hfill E\left\{\mathfrak{L}V\left(\tilde{\rho }\left(t\right)\right)\right\}\le & -{\iota \parallel \rho \left(t\right)\parallel }^2+2\iota {\rho }^T\left(t\right)P{\Xi }_2\sum _{m=1}^{\tilde{m}}{\beta }_k\left(t\right){\alpha }_k\left(t\right){ϵ}_m\left(t\right)\hfill \\ \hfill & +2{\rho }^T\left(t\right)PF\left(z\left(t\right)\right)+2\iota {\rho }^T\left(t\right)P{\Xi }_4(z\left(t\right)-z\left(t_{k,g}h\right))\hfill \\ \hfill & -2\iota {\rho }^T\left(t\right)P{\Xi }_2\sum _{m=1}^{\tilde{m}}{\beta }_k\left(t\right)(1-{\alpha }_k\left(t\right))g\left(\widehat{z}\left(t_{k-m+1}h\right)\right)\hfill \\ \hfill & -2\overline{\eta }{\gamma }^2\left(t\right)+{\displaystyle \frac{2\sigma }{\iota }}\parallel z\left(t_{k,g}h\right)\parallel \gamma \left(t\right)-2\sum _{m=1}^{\tilde{m}}\parallel {\theta }_m{ϵ}_m\left(t\right)\parallel \gamma \left(t\right)\hfill \\ \hfill & +2\iota {\rho }^T\left(t\right)P{\Xi }_3{\beta }_k\left(t\right){\alpha }_k\left(t\right)\rho (t_{k,g}h)).\hfill \end{array}$$

(20)

According to the DMETM (7) and Lemma 1, one can get

$$\begin{array}{cc}\hfill \iota \sum _{m=1}^{\tilde{m}}\parallel {ϵ}_m\left(t\right)\parallel \le & \tilde{m}(\sigma \parallel \widehat{z}\left(t_{k,g}h\right)\parallel +\eta \parallel \gamma \left(t_{k,g}h\right)\parallel )\hfill \\ \hfill \le & \tilde{m}(\sigma \parallel e\left(t\right)-e\left(t_{k,g}h\right)\parallel +\sigma \parallel e\left(t\right)\parallel \hfill \\ \hfill & +\sigma \parallel z\left(t\right)\parallel +\sigma \parallel z\left(t\right)-z\left(t_{k,g}h\right)\parallel +\eta \parallel \gamma \left(t_{k,g}h\right)\parallel )\hfill \\ \hfill \le & \sqrt{2}\tilde{m}\sigma (\parallel \rho \left(t\right)-\rho \left(t_{k,g}h\right)\parallel +\parallel \rho \left(t\right)\parallel )+\tilde{m}\eta \parallel \gamma \left(t_{k,g}h\right)\parallel .\hfill \end{array}$$

(21)

Based on the definition of the hybrid attacks model (11), one has

$$\begin{array}{cc}\hfill & E\left[2\iota {\rho }^T\left(t\right)P{\Xi }_2\sum _{m=1}^{\tilde{m}}{\beta }_k\left(t\right)(1-{\alpha }_k\left(t\right))g\left(\widehat{z}\left(t_{k-m+1}h\right)\right)\right]\hfill \\ \hfill \le & 2\iota c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel \parallel \rho \left(t\right)\parallel \parallel \widehat{z}\left(t_{k}h\right)\parallel \hfill \\ \hfill \le & 2\iota c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel \parallel \rho \left(t\right)\parallel (\parallel {ϵ}_m\left(t\right)\parallel +\parallel \widehat{z}\left(t_{k,g}h\right)\parallel ).\hfill \end{array}$$

(22)

By (21), (22) is equivalent to the following inequality:

$$\begin{array}{cc}\hfill & E\left[2\iota {\rho }^T\left(t\right)P{\Xi }_2\sum _{m=1}^{\tilde{m}}{\beta }_k\left(t\right)(1-{\alpha }_k\left(t\right))g\left(\widehat{z}\left(t_{k-m+1}h\right)\right)\right]\hfill \\ \hfill \le & 2\iota c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel \parallel \rho \left(t\right)\parallel (\parallel {ϵ}_m\left(t\right)\parallel +\parallel z\left(t_{k,g}h\right)\parallel +\parallel e\left(t_{k,g}h\right)\parallel )\hfill \\ \hfill \le & 2\iota c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel \parallel \rho \left(t\right)\parallel (\parallel {ϵ}_m\left(t\right)\parallel +\sqrt{2}\parallel \rho \left(t\right)\parallel +\sqrt{2}\parallel \rho \left(t\right)-\rho \left(t_{k,g}h\right)\parallel ).\hfill \end{array}$$

(23)

With Assumption 1 in mind, one can get

$$\begin{array}{c}\hfill 2{\rho }^T\left(t\right)PF\left(z\left(t\right)\right)\le 2c_1{\parallel P\parallel \parallel \rho \left(t\right)\parallel }^2\end{array}$$

(24)

where $c_1=c_0\sqrt{2n(n+1)}$.

According to Lemma 2 and the Gronwall–Bellman inequality in [32], $\forall t\in [t_{k,g}h,t_{k,g+1}h)$, it holds that

$$\begin{array}{cc}\hfill ∥z\left(t\right)-z\left(t_{k,g}h\right)∥\le & ∥\rho \left(t\right)-\rho \left(t_{k,g}h\right)∥\hfill \\ \hfill \le & {\int }_{t_{k,g}h}^t∥\dot{\rho }\left(v\right)∥dv\hfill \\ \hfill \le & (e^{a_2(t-t_{k,g}h)}-1)(\parallel \rho \left(t_{k,g}h\right)\parallel +a_1\gamma \left(t_{k,g}h\right))\hfill \end{array}$$

(25)

where $a_1={\displaystyle \frac{\eta \parallel {\Xi }_4\parallel }{a_2}}$, $a_2=\max \{\iota \parallel {\Xi }_1\parallel +\iota \parallel {\Xi }_2\parallel +c_1,\iota \parallel {\Xi }_1\parallel +\sigma \parallel {\Xi }_2\parallel +c_1\}$.

For $\forall t\in [t_{k,g}h,t_{k,g+1}h)$, substituting (21)–(25) into (20) results in

$$\begin{array}{cc}\hfill E\left\{\mathfrak{L}V\left(\tilde{\rho }\left(t\right)\right)\right\}\le & -(\iota -2c_1{\parallel P\parallel )\parallel \rho \left(t\right)\parallel }^2-2\overline{\eta }{\gamma }^2\left(t\right)+{\displaystyle \frac{2\sigma }{\iota }}\parallel z\left(t_{k,g}h\right)\parallel \gamma \left(t\right)\hfill \\ \hfill & +2\tilde{m}\parallel P{\Xi }_2\parallel {\overline{\beta }}_k{\overline{\alpha }}_k\parallel \rho \left(t\right)\parallel \left[\eta \parallel \gamma \left(t_{k,g}h\right)\parallel +\sqrt{2}\sigma \left(\parallel \rho \left(t\right)-\rho \left(t_{k,g}h\right)\parallel +\parallel \rho \left(t\right)\parallel \right)\right]\hfill \\ \hfill & +2\iota \parallel P{\Xi }_4\parallel \parallel \rho \left(t\right)\parallel (\parallel \rho \left(t_{k,g}h\right)\parallel +a_1\parallel \gamma \left(t_{k,g}h\right)\parallel )(e^{a_{2}h}-1)\hfill \\ \hfill & +2\iota {\overline{\beta }}_k{\overline{\alpha }}_k\parallel P{\Xi }_3\parallel \parallel \rho \left(t\right)\parallel \parallel \rho \left(t_{k,g}h\right))\parallel +2\iota c\tilde{m}{\overline{\beta }}_k(1-{\overline{\alpha }}_k)\parallel P{\Xi }_2\parallel \parallel \rho \left(t\right)\parallel \hfill \\ \hfill & \times (\parallel {ϵ}_m\left(t\right)\parallel +\sqrt{2}\parallel \rho \left(t\right)\parallel +\sqrt{2}\parallel \rho \left(t\right)-\rho \left(t_{k,g}h\right)\parallel ).\hfill \end{array}$$

(26)

By assigning $\iota >2c_1\parallel P\parallel$, it follows from (26) that

$$\begin{array}{cc}\hfill E\left\{\mathfrak{L}V\left(\tilde{\rho }\left(t\right)\right)\right\}\le & -{\omega }_{1}E\left\{V\left(\tilde{\rho }\left(t\right)\right)\right\}+{\omega }_{2}E\left\{\sqrt{V\left(\tilde{\rho }\left(t\right)\right)V\left(\tilde{\rho }\left(t_{k,g}h\right)\right)}\right\}\hfill \end{array}$$

(27)

where ${\omega }_1$ and ${\omega }_2$ are given in Theorem 1.

It can be derived from (27) that

$$\begin{array}{c}E\{\mathfrak{L}\sqrt{V\left(\tilde{\rho }\left(t\right)\right)}\}\le -{\displaystyle \frac{{\omega }_1}{2}}E\left\{\sqrt{V\left(\tilde{\rho }\left(t\right)\right)}\right\}+{\displaystyle \frac{{\omega }_2}{2}}E\left\{\sqrt{V\left(\tilde{\rho }\left(t_{k,g}h\right)\right)}\right\},t\in [t_{k,g}h,t_{k,g+1}h).\end{array}$$

(28)

By integrating $\sqrt{V\left(\tilde{\rho }\left(t\right)\right)}$ from $t_{k,g}h$ to $t_{k,g+1}h$, one has

$$\begin{array}{c}\hfill E\left\{\sqrt{V\left(\tilde{\rho }\left(t_{k,g+1}h\right)\right)}\right\}\le {\omega }_{3}E\left\{\sqrt{V\left(\tilde{\rho }\left(t_{k,g}h\right)\right)}\right\}\end{array}$$

(29)

where ${\omega }_3={\displaystyle \frac{{\omega }_2}{{\omega }_1}}(1-e^{-{\displaystyle \frac{{\omega }_2}{2}}h})+e^{-{\displaystyle \frac{{\omega }_1}{2}}h}$.

It can be concluded from (29) that when $t_{k,g}h$ tends to infinity, one can obtain that $\tilde{\rho }\left(t_{k,g+1}h\right))$ asymptotically converges to zero. Furthermore, if the conditions (17) and (18) are met, the NNCSs (3) under hybrid attacks and DMETM (7) have mean square stability. This completes the proof of the theorem. □

Remark 5.

The stability conditions (17) and (18) in Theorem 1 constitute sufficient but not necessary and sufficient conditions for system stability. Hence, these conditions are inherently conservative to some extent. Deriving necessary and sufficient stability conditions for secure control under hybrid attacks is a challenging problem due to the inherent complexity and uncertainty of the NNCSs. Therefore, developing less conservative or tighter stability criteria remains a significant topic for future research.

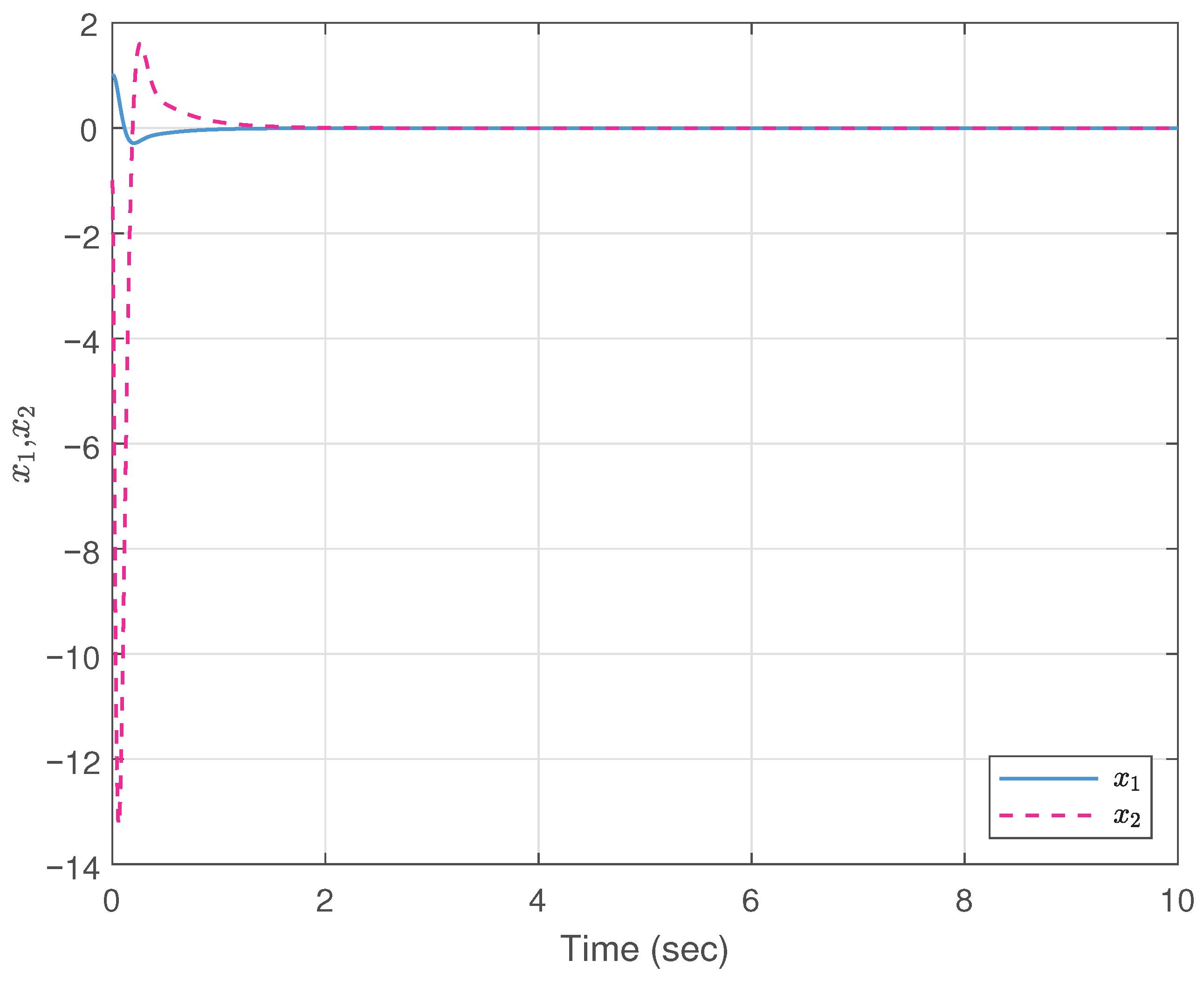
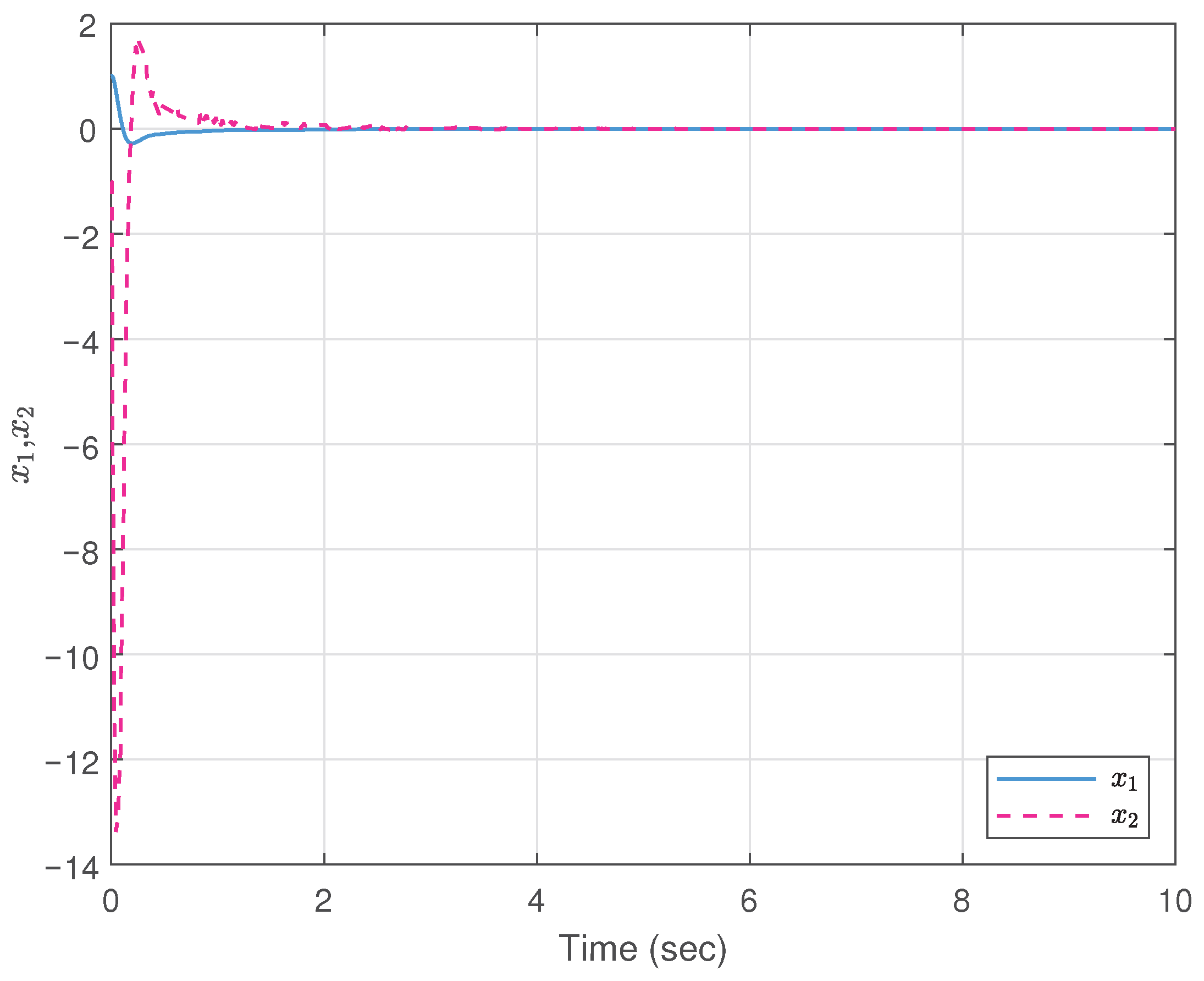
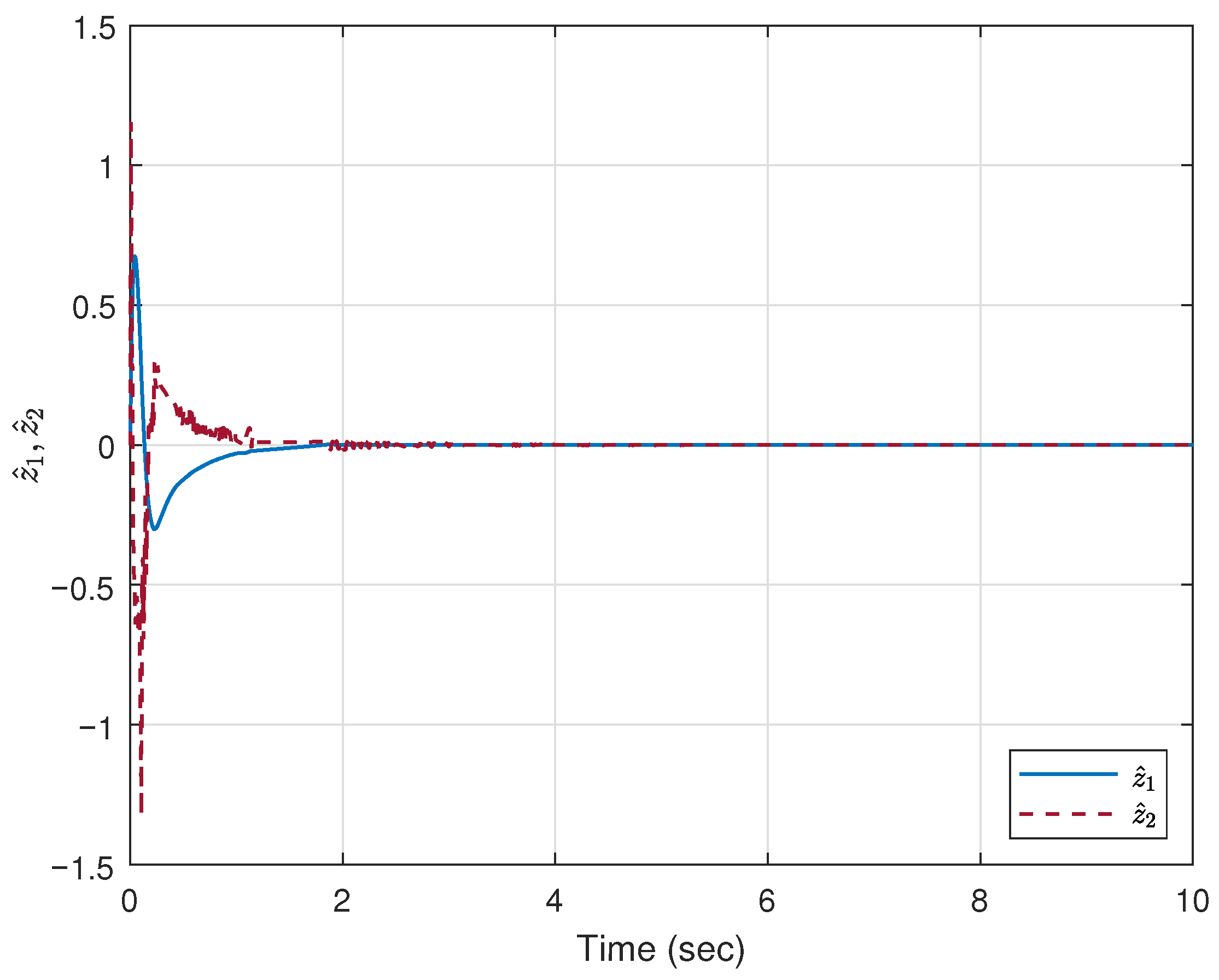
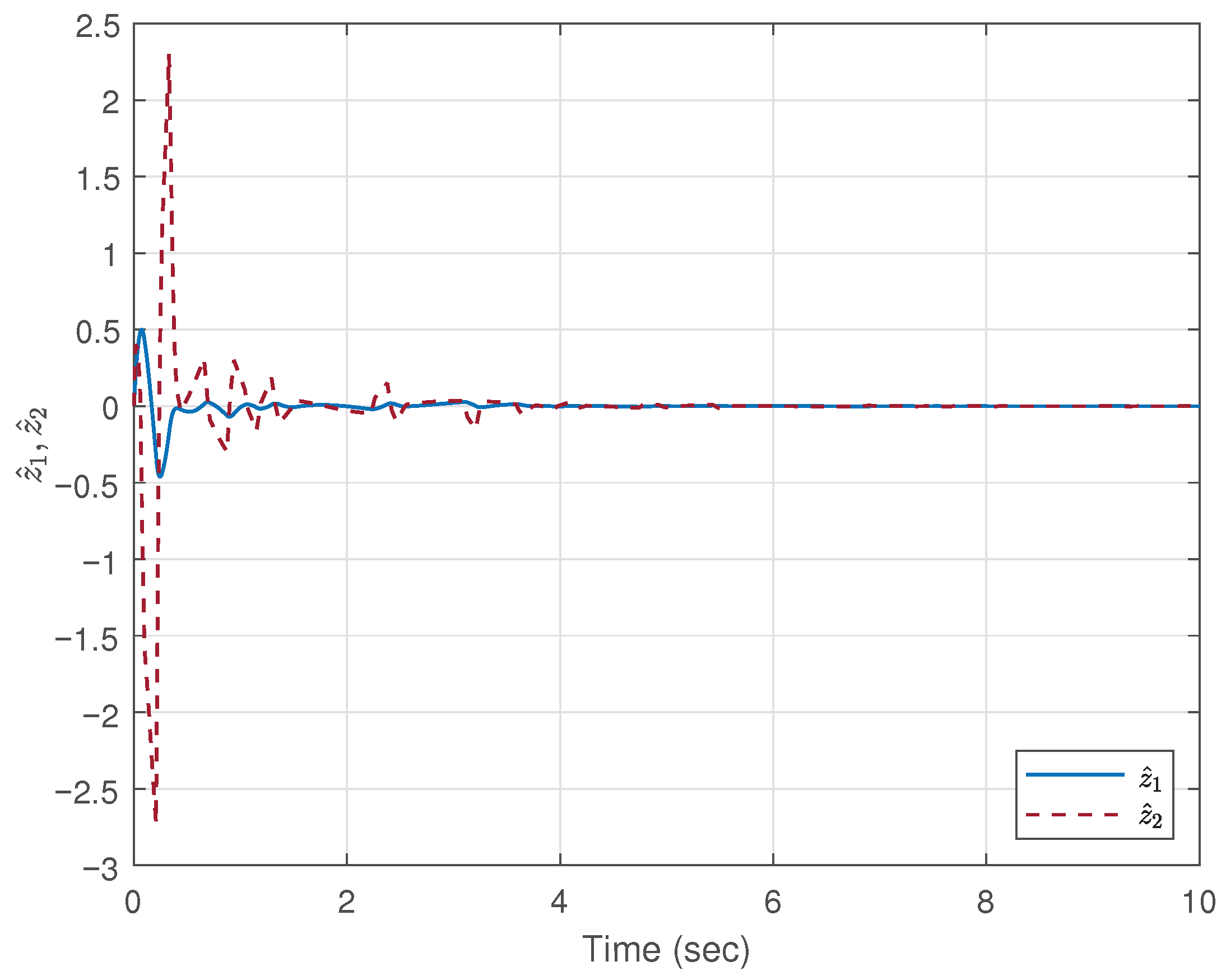
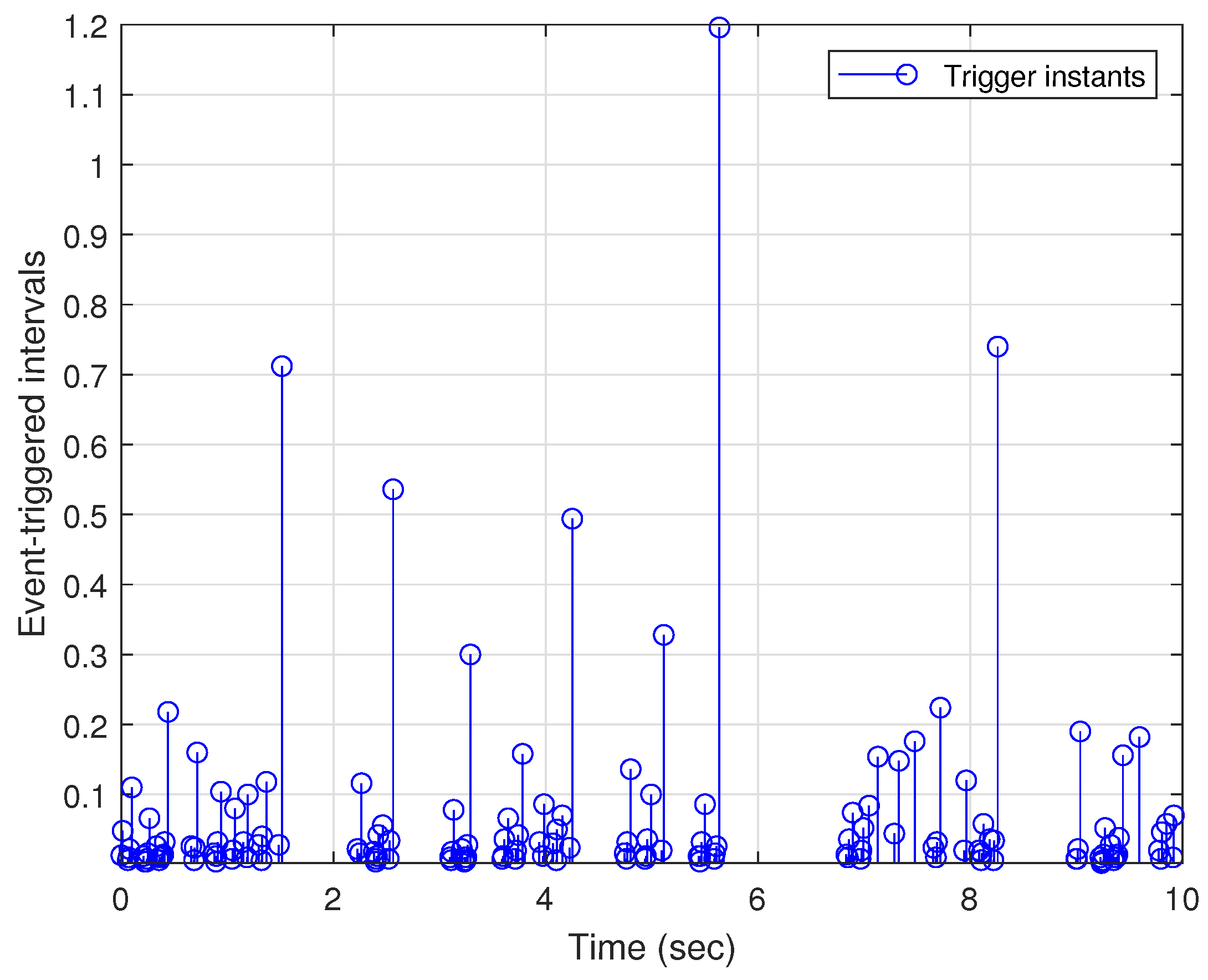
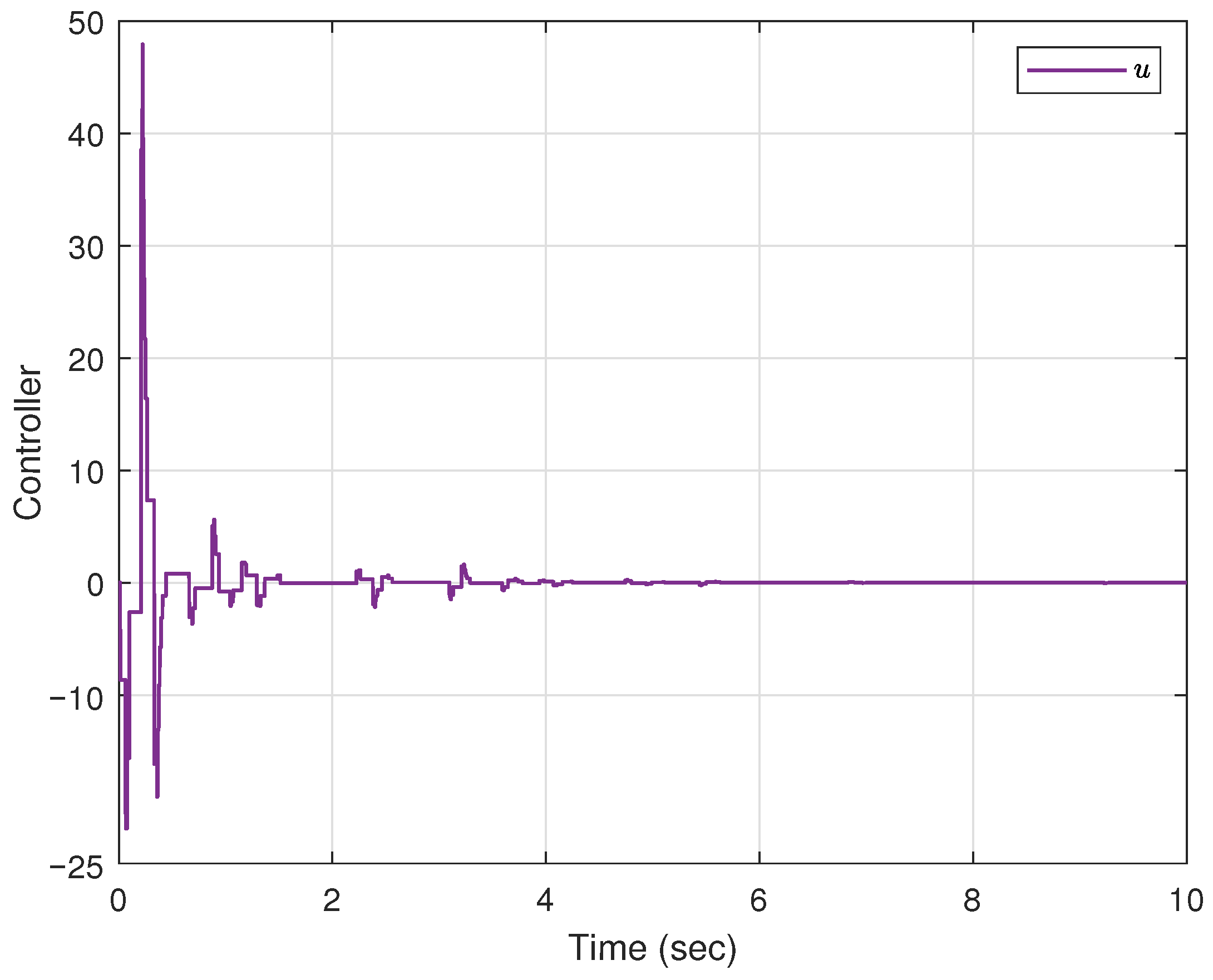
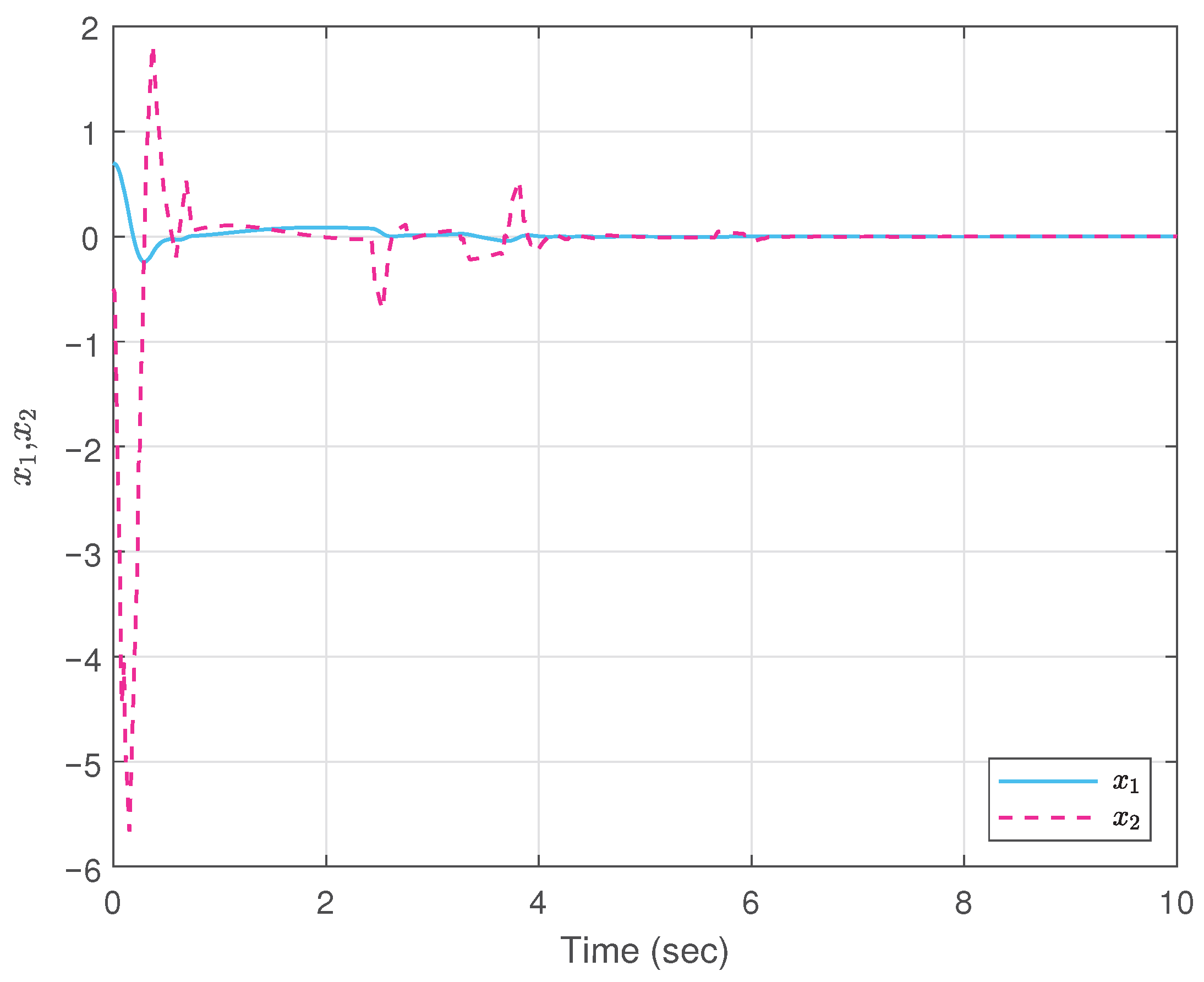
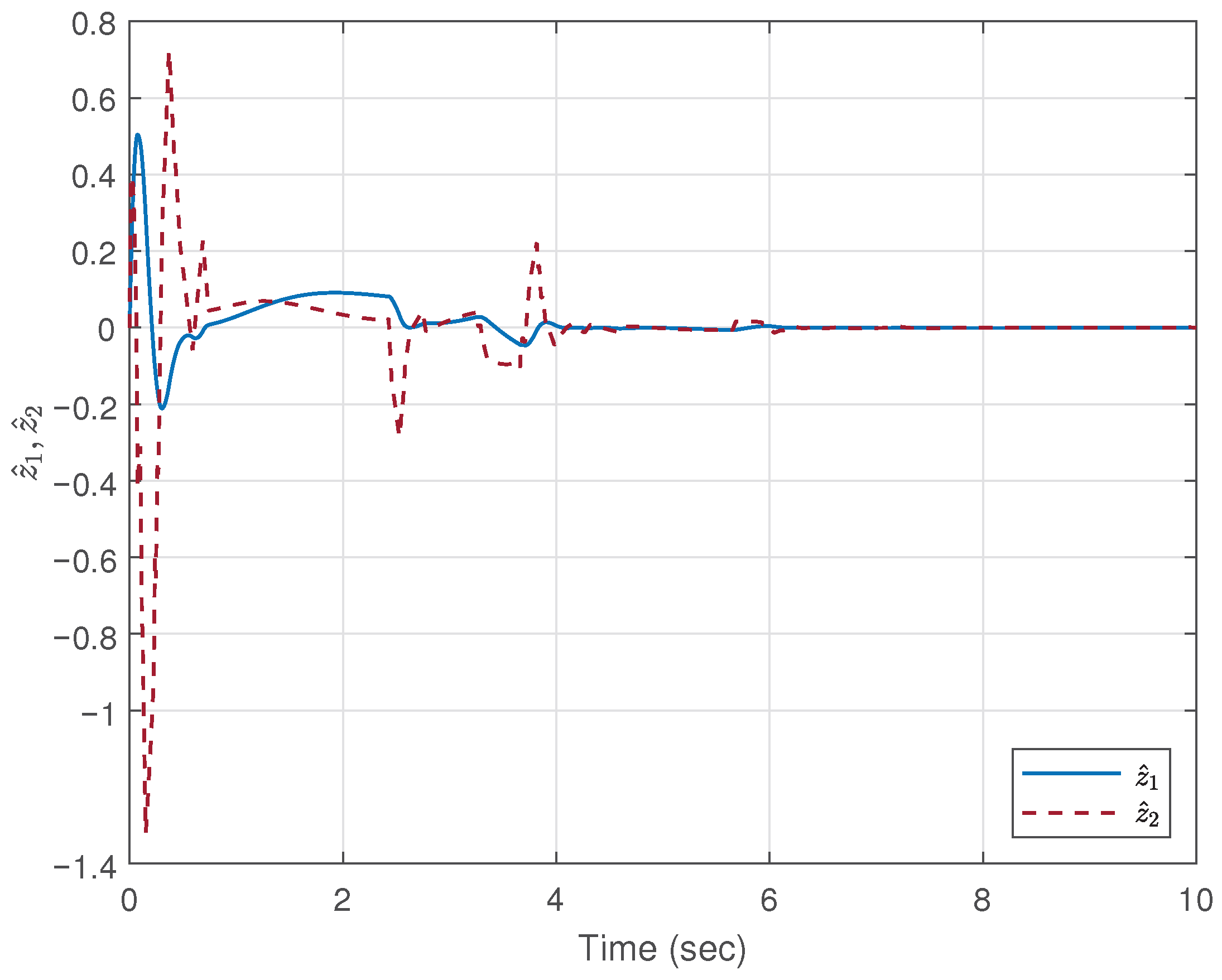
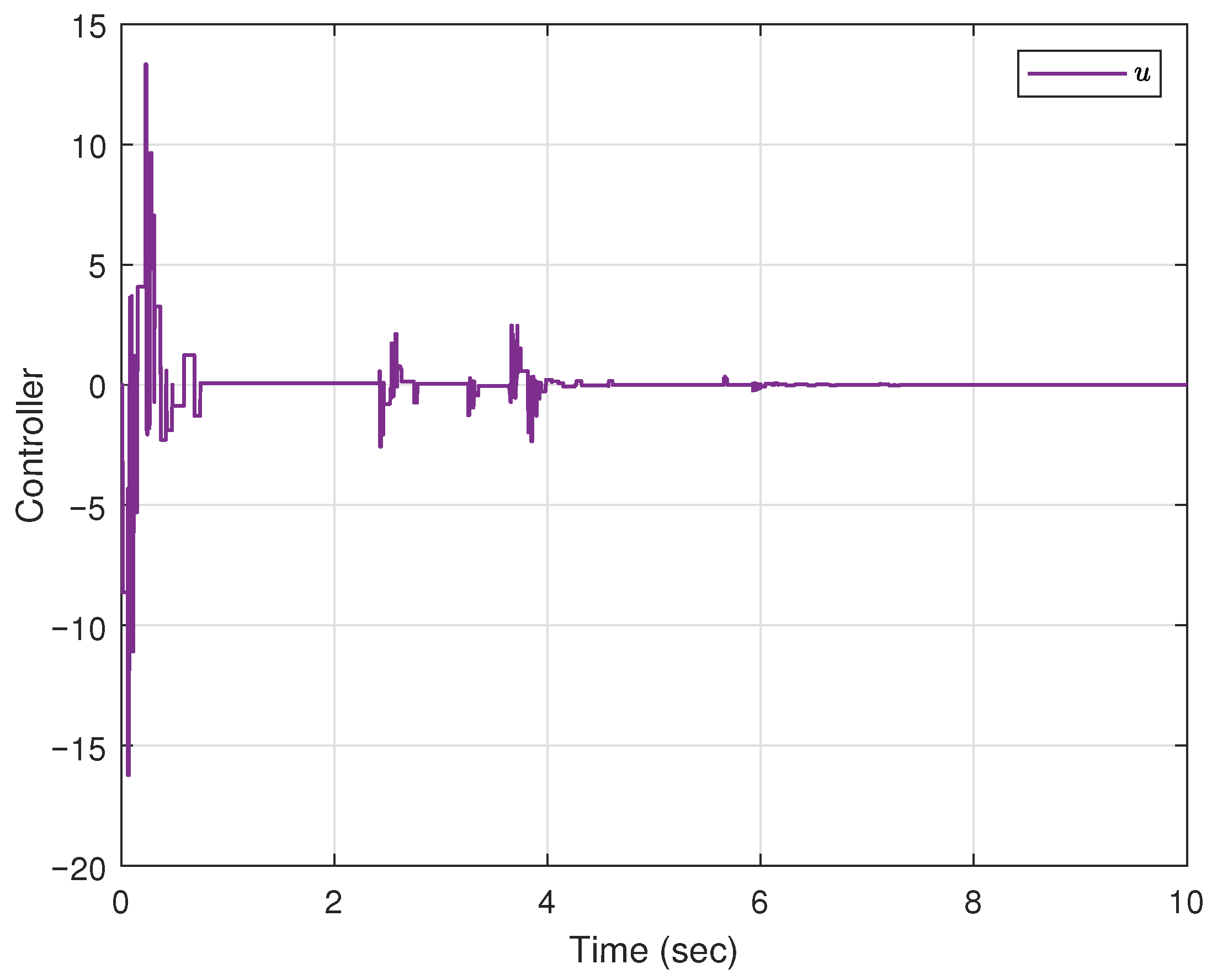
5. Simulation Example

In this section, a numerical simulation and a practical example of a single-link robot arm system are utilized to demonstrate the superiority of the designed DMETC strategy.

Example 1.

Consider the following system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_1=x_2+2sin\left(x_1\right)\hfill \\ {\dot{x}}_2=u-ln(1+x_1^2)-sin\left(t\right)x_2\hfill \\ y=x_1\hfill \end{array}\right.\end{array}$$

(30)

The controller and observer parameters are chosen as $K=[26,31]$, $H={[11,59]}^T$, and $\iota =3$. The sampling period is selected as $h=0.002s$. For hybrid attacks, the nonlinear function is set as $g\left(\widehat{z}\left(t_{k}h\right)\right)=-tanh\left(0.6\widehat{z}\left(t_{k}h\right)\right)$, ${\overline{\alpha }}_k=0.3$, and ${\overline{\beta }}_k=0.6$. The initial values of the system and observer states are given by $x={[1,-1]}^T$ and $\widehat{z}={[0,0]}^T$. For the designed DMETM, $\sigma =0.2$, $\eta =0.2$, $\overline{\eta }=0.8$, ${\theta }_1=0.5$, ${\theta }_2=0.3$, ${\theta }_3=0.2$, and $\gamma \left(0\right)=1$.

The response curves of the state x and observer $\widehat{z}$ are depicted in Figure 2 and Figure 3. Figure 4 presents the event instants and intervals under the Conventional ETM [8], where the numbers of triggered data are 999. The trajectories of the state x are illustrated in Figure 5, from which one can discern that the designed controller stabilizes the system under hybrid attacks. The response curves of observer $\widehat{z}$ are illustrated in Figure 6. Figure 7 presents the event instants and intervals under the DMETM, where the numbers of event are 613. Figure 8 depicts the evolution of the controller.

The effectiveness of the designed DMETC strategy has been validated through a table by comparing it with the time-triggered mechanism and the conventional ETM [8]. The numbers of event-triggered packets under different communication mechanisms are presented in

Table 1. Event-triggered numbers under different mechanism.

Method	Event-Triggered Packets	$\mathfrak{R}$
Time-triggered mechanism	5000	100%
Conventional ETM	999	19.98%
DMETM (7)	613	12.26%

, in which $\mathfrak{R}$ refers to the ratio between data packets under different ETMs and the time-triggered numbers. As shown in this table, the proposed DMETM (7) significantly reduces the number of transmission signals compared to the conventional ETM and time-triggered mechanism. Specifically, the proposed DMETM (7) decreases the network bandwidth consumption by $87.74\%$ compared to the time-triggered method and by $7.72\%$ compared to the conventional ETM.

Example 2.

Consider the following robot arm system [33]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_1=x_2\hfill \\ {\dot{x}}_2=u-{\displaystyle \frac{M\overline{g}\overline{h}}{G}}sin\left(x_1\right)-{\displaystyle \frac{J}{G}}{x}_2\hfill \\ y=x_1\hfill \end{array}\right.\end{array}$$

(31)

where $M=1.1$ kg, and $\overline{h}=0.6$ m stands for the mass and the length of the arm; $\overline{g}=9.81$   ${m/s}^2$, $G=1$ kg·$m^2$, and $J=2$ N·m·s/rad refer to the gravity acceleration, the viscous friction coefficients, and the moment of inertia, respectively.

The values for the control strategy are selected as follows: the sampling period $h=0.002$ s, the observer parameters $\iota =2.5$ and $H={[8,20]}^T$, and the controller parameter $K=[16,5]$. For hybrid attacks, the nonlinear function is given by $g\left(\widehat{z}\left(t_{k}h\right)\right)=-tanh\left(0.2\widehat{z}\left(t_{k}h\right)\right)$, ${\overline{\alpha }}_k=0.5$, and ${\overline{\beta }}_k=0.5$. The initial values are defined by $x={[0.7,-0.5]}^T$ and $\widehat{z}={[0,0]}^T$. For the designed DMETM, $\sigma =0.3$, $\eta =0.3$, $\overline{\eta }=0.8$, ${\theta }_1=0.5$, ${\theta }_2=0.3$, ${\theta }_3=0.2$, and $\gamma \left(0\right)=0.9$.

In the absence of hybrid attacks, the trajectory of the state x is shown in Figure 9, and the trajectory of observer $\widehat{z}$ is presented in Figure 10. The event instants and intervals are given in Figure 11, where the event-triggered numbers generated by DMETM are 156. Figure 12 displays the curves of the controller. Figure 13 and Figure 14 depict the trajectories of the state x and observer $\widehat{z}$ under hybrid attacks. Figure 15 shows the event instants and intervals, where the event-triggered packets generated by DMETM are 326. The evolution of the controller is presented in Figure 16. According to Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, compared with the attack-free scenario, the hybrid attacks inevitably introduce certain performance degradations to the system. Nevertheless, the designed DMETC strategy effectively compensates for these adverse effects, enabling the system to achieve superior steady-state performance even under the influence of hybrid attacks. This highlights the capability of the designed strategy to maintain system stability and performance in the presence of hybrid attacks threats.

6. Conclusions

In this paper, the estimate-based DMETC issue has been presented for a class of NNCSs under hybrid attacks. When only the measurable signals are available, the sampled-data observer has been utilized to estimate the system output. To save the bandwidth resources, the DMETM and the auxiliary variable update law have been developed, which effectively utilize the advantages of historical sampled-data estimates. The hybrid attack model that accounts for the combined effects of both deception and DoS attacks has been put forward to describe the potential threats during network data transmission. Then, the memory-event-triggered output feedback controller has been designed to ensure that the NNCSs can achieve the mean square stability. Finally, the results of two examples have been given, which illustrate that the estimate-based DMETC method can be validated under hybrid attacks. A potential research for future work is to expand the developed DMETC method to disturbance rejection control, and finite-time security control will also be investigated.