General Runge–Kutta–Nyström Methods for Linear Inhomogeneous Second-Order Initial Value Problems

Abstract

In this paper, general Runge–Kutta–Nyström (GRKN) methods are developed and analyzed, tailored for second-order initial value problems of the form $y^{″}=L{y}^{\prime }+My+g\left(t\right)$, where $L,M\in {\mathbb{R}}^{n\times n}$ are constant matrices with $n\ge 1$. The construction of embedded pairs of orders $6\left(4\right)$ and $7\left(5\right)$, suitable for adaptive integration strategies, is emphasized. By utilizing rooted tree theory and recent simplifications for linear inhomogeneous systems, symbolic order conditions are derived, and efficient schemes are designed through algebraic and evolutionary techniques. Numerical tests verify the superiority of our new derived pairs. In particular, this work introduces novel embedded GRKN pairs with reduced-order conditions that exploit the linearity and structure of the underlying system, enabling the construction of low-stage, high-accuracy integrators. The methods incorporate FSAL (First Same As Last) formulations, making them computationally efficient. They are tested on representative physical systems in one, two, and three dimensions, demonstrating notable improvements in efficiency and accuracy over existing high-order RKN methods.

1. Introduction

Initial value problems (IVPs) involving second-order differential equations arise in numerous applications, from classical mechanics to electrical circuits and structural dynamics. When the system is expressed in the general form

$$y^{″}=f(x,y,y^{\prime }),$$

(1)

it is natural to employ specialized integrators that preserve the second-order structure for efficiency and accuracy. Among these, the Runge–Kutta–Nyström (RKN) family of methods, originally devised for equations of the form $y^{″}=f(x,y)$, has proven particularly effective.

However, many real-world problems require addressing the more general case where f also depends on $y^{\prime }$, as in (1). To tackle this, Generalized Runge–Kutta–Nyström (GRKN) methods have been proposed. Unlike classical RKN schemes, these accommodate velocity dependence, at the cost of more intricate order conditions.

Previous work includes the foundational NASA report by E. Fehlberg [1], who developed several high-order methods for such problems. Later, J.M. Fine [2] introduced embedded RKNG pairs of orders $3\left(4\right)$ and $4\left(5\right)$, emphasizing practical applicability and error control.

Kovalnogov et al. [3] derived Runge–Kutta–Nyström pairs for inhomogeneous linear problems of the $y^{″}=f(x,y)$, showing that simplifications in the rooted tree framework can significantly reduce the number of necessary order conditions, particularly for linear systems with constant coefficients.

In this work, we focus on the special variation of the problem (1) with the form

$$y^{″}=L{y}^{\prime }+My+g\left(t\right),$$

and constant matrices $L,M\in {\mathbb{R}}^{n\times n},n\ge 1$. We construct GRKN methods for such linear inhomogeneous systems, targeting embedded pairs of orders $6\left(4\right)$ and $7\left(5\right)$. These methods are especially relevant in contexts where error control and adaptivity are critical.

GRKN methods target initial value problems; applying them to boundary value problems requires shooting methods, adding complexity and reducing direct applicability.

2. General Runge–Kutta–Nyström Methods and Order Conditions

We consider the general second-order IVP system:

$$y^{″}\left(x\right)=f(x,y\left(x\right),y^{\prime }\left(x\right)),y\left(x_0\right)=y_0,y^{\prime }\left(x_0\right)=y_0^{\prime },$$

with $f:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$. In the linear inhomogeneous case,

$$y^{″}\left(x\right)=f(x,y,y^{\prime })=L{y}^{\prime }+My+g\left(t\right),y\left(x_0\right)=y_0,y^{\prime }\left(x_0\right)=y_0^{\prime }$$

(2)

where $L,M\in {\mathbb{R}}^{n\times n}$, $g\left(t\right)$ is a known function and $y\left(x_0\right)=y_0,y^{\prime }\left(x_0\right)=y_0^{\prime }$ the initial values.

A general GRKN method with s stages is defined by:

$$\begin{array}{cc}\hfill Y_i& =y_n+c_i{h}_n{y}_n^{\prime }+h_n^2\sum _{j=1}^s{\overline{a}}_{ij}{f}_j,\hfill \\ \hfill Y_i^{\prime }& =y_n^{\prime }+h_n\sum _{j=1}^s{a}_{ij}{f}_j,\hfill \\ \hfill f_i& =f(x_n+c_i{h}_n,Y_i,Y_i^{\prime }),\hfill \\ \hfill y_{n+1}& =y_n+h_n{y}_n^{\prime }+h_n^2\sum _{i=1}^s{d}_i{f}_i,\hfill \\ \hfill y_{n+1}^{\prime }& =y_n^{\prime }+h_n\sum _{i=1}^s{b}_i{f}_i\hfill \end{array}$$

(3)

and advances the solution from $x_n,y_n,y_n^{\prime }$ to $x_{n+1},y_{n+1},y_{n+1}^{\prime }$.

The coefficients $a_{ij},{\overline{a}}_{ij},b_i,d_i,c_i$ form the method’s Butcher tableau.

2.1. Butcher Tableau for GRKN Methods

A general tableau for a GRKN method has the structure:

$$\begin{array}{ccccc}{c}_1& a_{11}& a_{12}& \dots & a_{1s}\\ c_2& a_{21}& a_{22}& \dots & a_{2s}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ c_s& a_{s1}& a_{s2}& \dots & a_{ss}\\ & {\overline{a}}_{11}& {\overline{a}}_{12}& \dots & {\overline{a}}_{1s}\\ & {\overline{a}}_{21}& {\overline{a}}_{22}& \dots & {\overline{a}}_{2s}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ & {\overline{a}}_{s1}& {\overline{a}}_{s2}& \dots & {\overline{a}}_{ss}\\ & b_1& b_2& \dots & b_s\\ & d_1& d_2& \dots & d_s\end{array}$$

and in compact form using matrices

$$\begin{array}{cc}c& A\\ & \overline{A}\\ & b\\ & d\end{array}$$

Here, we deal with explicit methods and $A,\overline{A}$ are strictly lower triangular. Then, $f_i$’s are evaluated explicitly i.e., sequentially. The method provides approximations sequentially in the points $x_1=x_0+h_1$, $x_2=x_1+h_2$, etc.

Relatively few Runge–Kutta–Nyström–Gear (RKNG) pairs have been developed in the literature. Fehlberg [1] proposed several classes of such methods, including 5(6), 6(7), and 7(8) pairs. In all these pairs the solution advances with the lower-order formula. In addition they do not incorporate a higher-order formula for $y^{\prime }$, which limits their ability to control the local error in the derivative. The respective methods involve nine, eleven, and fourteen stages; however, the final stage in each step is reused as the initial stage in the subsequent step, effectively reducing the number of function evaluations per step to eight, ten, and thirteen. This tecnique is FSAL (First Stage As Last).

In a separate contribution, Fine [2] introduced a class of 5(4) pairs that require six stages, as well as a class of 4(3) pairs with four stages.

2.2. Rooted Trees and Order Conditions

To derive order conditions for GRKN methods, we use a rooted tree formalism, originally developed by Butcher [4,5] and extended by Hairer et al. [6,7] for general second-order systems. Each rooted tree corresponds to an elementary differential of the solution, and its associated order condition ensures that the GRKN method reproduces the corresponding Taylor expansion term up to a desired order.

In linear inhomogeneous problems, the structure of f dramatically simplifies the set of rooted trees. Specifically, all higher-order derivatives of f vanish, except those that involve the first derivatives of y and $y^{\prime }$. As a result, only a subset of the full-order conditions is needed to ensure high-order accuracy.

For example, Fine [2] showed that for a sixth-order method, only 34 order conditions are necessary (compared to more than 200 in the general case), and these can be grouped and handled systematically. Similarly, Simos and Tsitouras [8] derived simplified symbolic forms of order conditions using Frechet derivatives and Taylor expansion matching, facilitating the design of new RK pairs with fewer stages.

2.3. Embedded Pairs and Linear Problems

In adaptive solvers, embedded pairs of the form 6(4) are commonly used. These include:

-

A primary method of order $p=6$ for accuracy.

-

A secondary method of order $q=4$ for error estimation.

For the lower-order formula, we simply need two additional weight vectors $\widehat{b}\ne b$ and $\widehat{d}\ne d$. Then, using the same functions $f_i,i=1,2,\dots ,s$ we may have the fourth-order approximations $\widehat{y}$ and ${\widehat{y}}^{\prime }$.

For the linear inhomogeneous problem (2), the algebraic structure allows for simplifications:

-

Many elementary differentials vanish due to linearity.

-

This reduces the number of conditions and parameters needed.

-

Evolutionary optimization (e.g., Differential Evolution) can be employed to search for coefficients satisfying the order conditions while minimizing local error [8].

In the following, we aim to derive

• a six-stage GRKN pair of orders $6\left(4\right)$,
• an eight-stage GRKN pair of orders $7\left(5\right)$,

exploiting these simplifications to construct efficient schemes. At each integration step, a local error estimate, denoted as $ϵ$, is computed. This estimate is typically defined as the maximum absolute difference between the numerical solution and a more accurate reference solution (or an estimate thereof) for both position and velocity components, i.e., $ϵ=max\{\parallel y_{n+1}-{\widehat{y}}_{n+1}{\parallel }_{\infty },\parallel y_{n+1}^{\prime }-{\widehat{y}}_{n+1}^{\prime }{\parallel }_{\infty }\}$, where $y_{n+1}$ is the current step’s numerical approximation and ${\widehat{y}}_{n+1}$ is a higher-order or more refined approximation used for error control. Given a user-specified error tolerance, $TOL$, the current step is accepted, and the integration proceeds if $ϵ<TOL$. Conversely, if $ϵ\ge TOL$, the step is rejected, and the integration is reattempted with a reduced step size. In either scenario (acceptance or rejection), the step size for the subsequent integration, $h_{n+1}$, is adjusted based on the observed error and the desired tolerance using the formula:

$$h_{n+1}=0.9h_n{\left({\displaystyle \frac{TOL}{ϵ}}\right)}^{{\displaystyle \frac{1}{q+1}}}.$$

(4)

Here, $h_n$ is the current step size, q is the magnitude of the lower order of the pair, and the factor of $0.9$ is a safety margin. In the event of a rejected step, the calculated $h_{n+1}$ value serves as the new reduced step size for recomputing the current step. The procedure in a flow chart is given as Algorithm 1.

Algorithm 1 Adaptive embedded GRKN method

Require: Initial values $x_0,y_0,y_0^{\prime }$, step size h, tolerance TOL, coefficients $a_{ij},{\overline{a}}_{ij},b_i,{\widehat{b}}_i,d_i,{\widehat{d}}_i,c_i$ Ensure: Approximate values $y_1,y_1^{\prime }$ at $x_1=x_0+h$   1: Set $x_0\leftarrow \mathrm{initial}\mathrm{time}$   2: repeat   3:     for $i=1$ to s do   4:         Evaluate $g_i=g(x_0+c_{i}h)$   5:         Compute $f_i=L{Y}_i^{\prime }+M{Y}_i+g_i$   6:         Compute stage values: $$Y_i\&Y_i^{\prime }\mathrm{as}\mathrm{shown}\mathrm{in}\left(3\right)$$   7:     end for   8:     Compute main solution: $$y_1=y_0+h{y}_0^{\prime }+h^2\sum _{i=1}^s{d}_i{f}_i,y_1^{\prime }=y_0^{\prime }+h\sum _{i=1}^s{b}_i{f}_i$$   9:     Compute embedded solution: $${\widehat{y}}_1=y_0+h{y}_0^{\prime }+h^2\sum _{i=1}^s{\widehat{d}}_i{f}_i,{\widehat{y}}_1^{\prime }=y_0^{\prime }+h\sum _{i=1}^s{\widehat{b}}_i{f}_i$$ 10:     Estimate error: $$ϵ=max\{\parallel y_{n+1}-{\widehat{y}}_{n+1}{\parallel }_{\infty },\parallel y_{n+1}^{\prime }-{\widehat{y}}_{n+1}^{\prime }{\parallel }_{\infty }\}$$ 11:     if $ϵ\le$ TOL then 12:         Accept step: $$x_0\leftarrow x_0+h,y_0\leftarrow y_1,y_0^{\prime }\leftarrow y_1^{\prime }$$ 13:     else 14:         Reject step 15:     end if 16:     Update step size (for both cases): $$h\leftarrow 0.9h{\left({\displaystyle \frac{TOL}{ϵ}}\right)}^{{\displaystyle \frac{1}{q+1}}}$$ 17: until end of integration interval

A forthcoming section will outline the algorithmic generation of such schemes using symbolic computation and optimization.

3. Method Derivation and Symbolic Conditions for Linear Problems

The scope of this work is deliberately restricted to the integration of linear inhomogeneous second-order initial value problems of the form (2), which allows us to exploit the structure of the problem and derive reduced-order conditions. While the proposed methodology can, in principle, be extended to nonlinear problems or systems with time-dependent coefficients, such generalizations would require solving a fundamentally different and significantly more complex set of order conditions. Moreover, nonlinear cases typically demand a greater number of stages to achieve comparable accuracy, thereby increasing computational cost. These aspects are beyond the present study’s focus and are reserved for future investigation. This will be clear below.

In [6], a general theory linking elementary differentials and rooted trees theory was introduced enhancing the relevant connection remarked by Butcher for conventional Runge–Kutta methods.

3.1. Summary: A Theory for General Nyström Methods

In [6], it was proposed that these direct methods offer a more general and flexible approach compared to the common practice of transforming second-order ODEs into a doubled-dimension system of first-order equations. This increased generality provides greater freedom for enhancing both stability and accuracy in numerical solutions, particularly for methods like the General Runge–Kutta–Nyström (GRKN) scheme.

The paper’s core contribution lies in developing a theory that extends concepts from first-order equations to the more complex domain of second-order ODEs. This theory is applicable to the study of a wide range of numerical methods for such problems. While the fundamental theory is often presented for autonomous systems $y^{″}=f(y,y^{\prime })$, non-autonomous systems (where f depends explicitly on the independent variable x, as often seen in GRKN methods) can typically be made autonomous by extending the dimension of the system. This extension is built upon the novel concept of “Nyström-trees” (N-trees). These specialized trees, along with their “fat” and “meagre” nodes, provide a graphical representation of the terms arising from repeated differentiation of the ODE solution. Specifically, each “fat” node represents “f” (the function $f(y,y^{\prime })$ or its autonomous equivalent), and each branch leaving this node represents a derivative: $D_2$ if the subsequent node is “fat,” and $D_1$ if the adjacent node is “meagre.” Meagre nodes have no ramifications and each adjacent node must be fat. The labels on the trees indicate the order of generation of these nodes following this procedure. The set of trees which appear in this way are the monotonically labeled Nyström-trees, denoted by LNT.

Central to the theory is the recursive definition of “Elementary Differentials” ($F\left(\mathrm{tree}\right):E\times E\to E$) for every N-tree ‘tree’ $\in NT$. These differentials correspond directly to the terms in the Taylor expansion of the solution. For instance, $F(\varnothing )(y,y^{\prime })=y$, $F\left({\tau }_1\right)(y,y^{\prime })=y^{\prime }$, and $F\left({\tau }_2\right)(y,y^{\prime })=f(y,y^{\prime })$. For a composite N-tree ‘tree’ $=[{\mathrm{tree}}_1,\dots ,{\mathrm{tree}}_k;{\mathrm{tree}}_{k+1},\dots ,{\mathrm{tree}}_m]$, the elementary differential is defined as:

$$F\left(\mathrm{tree}\right)(y,y^{\prime })=D_1^k{D}_2^{m-k}f·(F\left({\mathrm{tree}}_1\right),\dots ,F\left({\mathrm{tree}}_k\right),F\left({\mathrm{tree}}_{k+1}\right),\dots ,F\left({\mathrm{tree}}_m\right))$$

This allows for the introduction of “Nyström-series,” a powerful tool akin to Butcher-series for first-order methods. A Nyström-series is defined with a mapping $a:NT\to \mathbb{R}$ as:

$$N(a,y_0,y_0^{\prime })=\sum _{\mathrm{tree}\in LNT}a\left(\mathrm{tree}\right)F\left(\mathrm{tree}\right)(y_0,y_0^{\prime }){\displaystyle \frac{h^{e\left(\mathrm{tree}\right)}}{e\left(\mathrm{tree}\right)!}}$$

Its derivative is $N^{\prime }(a,y_0,y_0^{\prime })={\sum }_{\mathrm{tree}\in LNT}a\left(\mathrm{tree}\right)F\left(\mathrm{tree}\right)(y_0,y_0^{\prime }){\displaystyle \frac{h^{e\left(\mathrm{tree}\right)-1}}{\left(e\right(\mathrm{tree})-1)!}}$. The exact solution of the differential equation is an N-series $N(p,y_0,y_0^{\prime })$ with $p\left(\mathrm{tree}\right)=1$ for all ‘tree’ $\in NT$. A significant aspect is that the coefficients $a\left(\mathrm{tree}\right)$ in these Nyström-series are uniquely determined.

Ultimately, the theoretical machinery developed, particularly the concept of Nyström-trees and Nyström-series, enables the systematic derivation of order conditions for the parameters of various Nyström methods. These conditions are obtained by comparing the Taylor series expansions of a numerical method’s solution (e.g., $y_{n+1}$ and $y_{n+1}^{\prime }$ from a GRKN method) with the exact Nyström-series expansions for the true solution $y\left(x_{n+1}\right)$ and its derivative $y^{\prime }\left(x_{n+1}\right)$. For a method to be of a certain order, its coefficients must satisfy a set of algebraic equations that ensure the numerical solution matches the exact solution’s Nyström-series up to that specific order. This theoretical framework provides not only the correct equations of conditions but also an insight into the structure of methods useful for choosing good formulas. By providing a unified and rigorous theoretical foundation, this work validates the benefits of direct Nyström methods and offers a powerful tool for their design, analysis, and optimization in the numerical solution of second-order differential equations.

We now derive a class of general Runge–Kutta–Nyström (GRKN) methods for second-order initial value problems of the form (2). We aim to construct embedded pairs of order $6\left(4\right)$ and $7\left(5\right)$, exploiting the linear and inhomogeneous structure of the problem to simplify the set of order conditions.

3.2. Order Conditions for GRKN Methods

The local truncation error (LTE) of a numerical method of order p behaves as

$$\mathrm{LTE}=\mathrm{\Delta }{h}^{p+1}+\mathcal{O}\left(h^{p+2}\right),$$

where $\mathrm{\Delta }$ is a constant depending on the solution and its derivatives, and h is the step size.

i.e., for a 7th-order method, the LTE satisfies:

$$\mathrm{LTE}={\mathrm{\Delta }}_7{h}^8+\mathcal{O}\left(h^9\right),$$

with ${\mathrm{\Delta }}_7$ involving derivatives of the true solution up to order eight.

In our implementation, the error is estimated using an embedded pair of order $7\left(5\right)$, and the error estimator is computed via

$$ϵ=max\left(\parallel h^2(\widehat{d}-d){f\parallel }_{\infty },{\parallel h(\widehat{b}-b)f\parallel }_{\infty }\right),$$

which effectively gives an estimate of the local error of order $\mathcal{O}\left(h^6\right)$, since it reflects the difference between the 7th- and 5th-order methods.

Therefore, the key characteristics are:

• True local error of the 7th-order method:

  $$\mathrm{LTE}\le C_7{h}^8.$$
• Estimated local error (from the embedded pair):

  $$\mathrm{Estimated}\mathrm{Error}\approx \mathcal{O}\left(h^6\right).$$
• Global error (accumulated over $N=\mathcal{O}(1/h)$ steps):

  $$\mathrm{Global}\mathrm{Error}\approx \mathcal{O}\left(h^7\right).$$

This analysis confirms the high accuracy of the method, particularly for smooth problems with controlled step sizes.

In conclusion, the behavior of numerical methods can be encoded using rooted trees, where each node corresponds to a derivative in the Taylor expansion. For general $f(t,y,y^{\prime })$, we must consider both partial derivatives with respect to y and $y^{\prime }$, leading to a large tree set.

Fehlberg [1] presented the equations of condition in an elaborate form, employing indices and dummy inner variables. Here, in 

Table 1. Equations of condition for $y^{\prime }$ for orders 1–6. Whenever ^† does not appear to the left of an equation, then it is not valid for problem (2).

†$b·e=1$	† $b·c=\frac{1}{2}$	† $b·c^2=\frac{1}{3}$
† $b·A·c={\displaystyle \frac{1}{6}}$	† $b·c^3={\displaystyle \frac{1}{4}}$	$b·(c\odot A·c)={\displaystyle \frac{1}{8}}$
† $b·\overline{A}·c={\displaystyle \frac{1}{24}}$	† $b·A·c^2={\displaystyle \frac{1}{12}}$	† $b·A·A·c={\displaystyle \frac{1}{24}}$
† $b·c^4={\displaystyle \frac{1}{5}}$	$b·(c^2\odot A·c)={\displaystyle \frac{1}{10}}$	$b·(c\odot \overline{A}·c)={\displaystyle \frac{1}{30}}$
$b·(c\odot A·c^2)={\displaystyle \frac{1}{15}}$	† $b·\overline{A}·c^2={\displaystyle \frac{1}{60}}$	† $b·A·c^3={\displaystyle \frac{1}{20}}$
$b·{(A·c)}^2={\displaystyle \frac{1}{20}}$	$b·(c\odot A·A·c)={\displaystyle \frac{1}{30}}$	† $b·\overline{A}·A·c={\displaystyle \frac{1}{120}}$
$b·A·(c\odot A·c)={\displaystyle \frac{1}{40}}$	† $b·A·\overline{A}·c={\displaystyle \frac{1}{120}}$	† $b·A·A·c^2={\displaystyle \frac{1}{60}}$
† $b·A·A·A·c={\displaystyle \frac{1}{120}}$	† $b·c^5={\displaystyle \frac{1}{6}}$	$b·(c^3\odot A·c)={\displaystyle \frac{1}{12}}$
$b·(c^2\odot \overline{A}·c)={\displaystyle \frac{1}{36}}$	$b·(c^2\odot A·c^2)={\displaystyle \frac{1}{18}}$	$b·(c\odot \overline{A}·c^2)={\displaystyle \frac{1}{72}}$
$b·(c\odot A·c^3)={\displaystyle \frac{1}{24}}$	$b·(c\odot {(A·c)}^2)={\displaystyle \frac{1}{24}}$	† $b·\overline{A}·c^3={\displaystyle \frac{1}{120}}$
$b·(A·c\odot \overline{A}·c)={\displaystyle \frac{1}{72}}$	† $b·A·c^4={\displaystyle \frac{1}{30}}$	$b·(A·c^2\odot A·c)={\displaystyle \frac{1}{36}}$
$b·(c^2\odot A·A·c)={\displaystyle \frac{1}{36}}$	$b·(c\odot \overline{A}·A·c)={\displaystyle \frac{1}{144}}$	$b·(c\odot A·(c\odot A·c))={\displaystyle \frac{1}{48}}$
$b·(c\odot A·\overline{A}·c)={\displaystyle \frac{1}{144}}$	$b·(c\odot A·A·c^2)={\displaystyle \frac{1}{72}}$	$b·\overline{A}·(c\odot A·c)={\displaystyle \frac{1}{240}}$
† $b·\overline{A}·\overline{A}·c={\displaystyle \frac{1}{720}}$	† $b·\overline{A}·A·c^2={\displaystyle \frac{1}{360}}$	$b·A·(c^2\odot A·c)={\displaystyle \frac{1}{60}}$
$b·A·(c\odot \overline{A}·c)={\displaystyle \frac{1}{180}}$	$b·A·(c\odot A·c^2)={\displaystyle \frac{1}{90}}$	† $b·A·\overline{A}·c^2={\displaystyle \frac{1}{360}}$
† $b·A·A·c^3={\displaystyle \frac{1}{120}}$	$b·A·{(A·c)}^2={\displaystyle \frac{1}{120}}$	$b·(A·c\odot A·A·c)={\displaystyle \frac{1}{72}}$
$b·(c\odot A·A·A·c)={\displaystyle \frac{1}{144}}$	† $b·\overline{A}·A·A·c={\displaystyle \frac{1}{720}}$	$b·A·(c\odot A·A·c)={\displaystyle \frac{1}{180}}$
† $b·A·\overline{A}·A·c={\displaystyle \frac{1}{720}}$	$b·A·A·(c\odot A·c)={\displaystyle \frac{1}{240}}$	† $b·A·A·\overline{A}·c={\displaystyle \frac{1}{720}}$
† $b·A·A·A·c^2={\displaystyle \frac{1}{360}}$	†  $b·A·A·A·A·c={\displaystyle \frac{1}{720}}$

and

Table 2. Equations of condition for y for orders 1–6. For ^† see explanation in previous Table.

† $d·e=\frac{1}{2}$	† $d·c=\frac{1}{6}$	† $d·c^2=\frac{1}{12}$
† $d·A·c={\displaystyle \frac{1}{24}}$	† $d·c^3={\displaystyle \frac{1}{20}}$	$d·(c\odot A·c)={\displaystyle \frac{1}{40}}$
† $d·\overline{A}·c={\displaystyle \frac{1}{120}}$	† $d·A·c^2={\displaystyle \frac{1}{60}}$	† $d·A·A·c={\displaystyle \frac{1}{120}}$
† $d·c^4={\displaystyle \frac{1}{30}}$	$d·(c^2\odot A·c)={\displaystyle \frac{1}{60}}$	$d·(c\odot \overline{A}·c)={\displaystyle \frac{1}{180}}$
$d·(c\odot A·c^2)={\displaystyle \frac{1}{90}}$	† $d·\overline{A}·c^2={\displaystyle \frac{1}{360}}$	† $d·A·c^3={\displaystyle \frac{1}{120}}$
$d·{(A·c)}^2={\displaystyle \frac{1}{120}}$	$d·(c\odot A·A·c)={\displaystyle \frac{1}{180}}$	† $d·\overline{A}·A·c={\displaystyle \frac{1}{720}}$
$d·A·(c\odot A·c)={\displaystyle \frac{1}{240}}$	† $d·A·\overline{A}·c={\displaystyle \frac{1}{720}}$	† $d·A·A·c^2={\displaystyle \frac{1}{360}}$
† $d·A·A·A·c={\displaystyle \frac{1}{720}}$

, we consolidate the equations of condition for the weights b and d, up to the sixth algebraic order (i.e., Taylor matching). Our approach, however, adopts a more straightforward implementation utilizing only matrices and vectors. In these tables, the symbol “·” denotes the classical dot product, whereas “⊙” represents the component-wise (Hadamard) multiplication of vectors. For instance, if $v,u\in {\mathbb{R}}^s$, then

$$v\odot u=[v_1{u}_1,v_2{u}_2,\dots ,v_s{u}_s].$$

This operation has the lowest precedence among operators. For example, in the expression $c\odot A·c$, the dot product is evaluated first, followed subsequently by the component-wise multiplication.

Additionally, we define as $c^2=c\odot c$, $c^3=c\odot c^2,\dots$. As an exception, this operation has first priority. In the first equation of these Tables, we observe that $e=[1,1,1,\dots ,1]\in {\mathbb{R}}^s$.

3.3. Order Conditions for Linear Inhomogeneous Problems

However, for linear inhomogeneous problems, the right-hand side in (2) has the following properties:

• All higher-order derivatives $f_{yy},f_{y^{\prime }{y}^{\prime }},f_{y{y}^{\prime }},\dots$ vanish.
• Nonlinear combinations of trees reduce to simpler linear combinations.
• Many trees collapse into equivalent forms.

The symmetry of the trees allows for reuse and simplification of these terms. For example, many trees result in identical algebraic expressions for linear systems, which reduces redundancy. In Table 1 and Table 2, we mark the equations of condition for the case of interest here by using ^† in the upper left of the equation.

The order conditions can now be formulated through the following couple of equations:

$$b·\mathsf{\Psi }(A,\overline{A})·c^j={\displaystyle \frac{j!}{p!}},\mathrm{for}p-1\ge j\ge 1,p\ge 1,$$

(5)

$$d·\overline{\mathsf{\Psi }}(A,\overline{A})·c^j={\displaystyle \frac{j!}{p!}},\mathrm{for}p-1\ge j\ge 1,p\ge 2,$$

(6)

where $\mathsf{\Psi }(A,\overline{A})$ and $\overline{\mathsf{\Psi }}(A,\overline{A})$ denote matrix products involving A and $\overline{A}$.

To facilitate the analysis, we define the RKN-rank of matrix A to be 1, and the RKN-rank of matrix $\overline{A}$ to be 2. The sum-RKN-rankr of an expression involving $\mathsf{\Psi }$ or $\overline{\mathsf{\Psi }}$ is then defined as the total sum of the individual RKN-ranks of the matrices appearing in the corresponding matrix product. For example, the expression $\overline{A}·A·A$ has a sum-RKN-rank of $r=4$.

To achieve a method of order p for the derivative $y^{\prime }$, the condition $r+j=p-1$ must be satisfied. In contrast, to achieve the same order p for the function y, the condition becomes $r+j=p-2$.

For instance, consider the condition

$$b·A·\overline{A}·A·c={\displaystyle \frac{1}{720}},$$

where we identify $r=4$, $j=1$, and thus infer that $p=6$ for $y^{\prime }$, i.e., Equations (5).

Similarly, for the condition

$$d·A·\overline{A}·A·c={\displaystyle \frac{1}{5040}},$$

we again have $r=4$, $j=1$, which corresponds to $p=7$ for y, i.e., Equations (6).

3.4. Producing the New Methods

For a conventional pair of order $6\left(4\right)$, we have 56, 22, 9, and 4 equations of condition for b, d, $\widehat{b}$, and $\widehat{d}$, respectively. Indeed, only the first three rows in Table 1 suffice for deducing the fourth-order conditions for $\widehat{b}$, where it is enough to replace b with $\widehat{b}$.

However, in the context of linear inhomogeneous problems, analysis of the tables confirms that only 27, 15, 8, and 4 equations of condition remain valid for b, d, $\widehat{b}$, and $\widehat{d}$, respectively. Consequently, we arrive at a total system comprising 54 equations.

We proceed by selecting $s=7$ and employing the FSAL (First Same As Last or First Stage As Last) principle, i.e., $a_{sj}=b_j$ and ${\overline{a}}_{sj}=d_j$ for $1\le j\le s$. This implies that the method requires only six stages per step. Furthermore, we impose the simplifications $A·e=c$ and $\overline{A}·e=A·c$, thereby determining the first column of A and $\overline{A}$.

For the new pair of orders $7\left(5\right)$, we choose $s=9$ and again employ the FSAL strategy, resulting in a method that utilizes eight stages per step. From Equations (5) and (6), it follows that, under the linear inhomogeneous problem framework, there now exist 47, 27, 15, and 8 conditions to be satisfied for b, d, $\widehat{b}$, and $\widehat{d}$, respectively.

To address the determination of coefficients for the two problems described above, we employed the Differential Evolution (DE) technique [9]. DE is an iterative procedure in which, at each iteration (referred to as generation g), we maintain a population of individuals—namely, the free parameters

$$\left(c_2^{\left(g\right)},c_3^{\left(g\right)},\dots ,{\widehat{d}}_{s-1}^{\left(g\right)},{\widehat{d}}_s^{\left(g\right)}\right),i=1,2,\dots ,N,$$

where N denotes the population size. An initial population

$$\left(c_2^{\left(0\right)},c_3^{\left(0\right)},\dots ,{\widehat{d}}_{s-1}^{\left(0\right)},{\widehat{d}}_s^{\left(0\right)}\right),i=1,2,\dots ,N,$$

is randomly generated at the outset of the algorithm. Subsequently, we define a fitness function to minimize, ideally driving it to zero. Specifically, this function is defined as the square root of the sum of squared residuals

$$T={\left({(b·e-1)}^2+{(b·c-\frac{1}{2})}^2+\dots +{(d·e-1)}^2+\dots +{(\widehat{b}·e-1)}^2+\dots \right)}^{0.5}.$$

This fitness function is then evaluated for each member of the initial population. The DE procedure proceeds through three sequential phases—Differentiation, Crossover, and Selection—updating all individuals in the population at each generation g.

For implementing this optimization approach, we utilized the MATLAB [10] software DeMat [11]. Recent studies, such as [12], demonstrate the broad applicability of hybrid metaheuristic strategies in computational mathematics and engineering contexts, further supporting the use of evolutionary approaches like Differential Evolution in the present work. Accordingly, Tsitouras and Famelis [13], demonstrate the effectiveness of leveraging symbolic computation—particularly rooted tree expansions—for automating and streamlining the derivation of order conditions in the design of efficient numerical integrators.

As a result, we successfully constructed two methods, whose coefficients are presented in

Table 3. Coefficients of the 6(4) pair.

c	A
0	0	0	0	0	0	0
${\displaystyle \frac{137878459}{588903905}}$	${\displaystyle \frac{137878459}{588903905}}$	0	0	0	0	0
${\displaystyle \frac{7491243902}{8820050637}}$	$-{\displaystyle \frac{6912565003}{2383548425}}$	${\displaystyle \frac{3549781859}{946745408}}$	0	0	0	0
${\displaystyle \frac{1255892843}{1981008397}}$	$-{\displaystyle \frac{332863433}{671077243}}$	${\displaystyle \frac{624923549}{584067693}}$	${\displaystyle \frac{19931549}{332029333}}$	0	0	0
${\displaystyle \frac{828617034}{877777573}}$	${\displaystyle \frac{1447820040}{569227477}}$	$-{\displaystyle \frac{4577789031}{1550725129}}$	$-{\displaystyle \frac{612583895}{977387216}}$	${\displaystyle \frac{1801563031}{910202194}}$	0	0
${\displaystyle \frac{251309330}{527492149}}$	${\displaystyle \frac{225803829}{522734068}}$	${\displaystyle \frac{440925161}{301931773}}$	${\displaystyle \frac{1367472924}{733541063}}$	$-{\displaystyle \frac{1664626223}{450640808}}$	${\displaystyle \frac{1241932216}{3001210703}}$	0
1	${\displaystyle \frac{92306947}{1303649843}}$	${\displaystyle \frac{429325261}{1225378013}}$	${\displaystyle \frac{221851245}{3287539774}}$	${\displaystyle \frac{420269659}{1217598825}}$	${\displaystyle \frac{740841171}{5528332403}}$	${\displaystyle \frac{31129404}{967389425}}$
	0	0	0	0	0	0
	0	0	0	0	0	0
	${\displaystyle \frac{209798341}{238991032}}$	0	0	0	0	0
$\overline{A}\to$	${\displaystyle \frac{55984799}{732668533}}$	${\displaystyle \frac{204286275}{907624337}}$	0	0	0	0
	${\displaystyle \frac{166571266}{1150705629}}$	$-{\displaystyle \frac{53953832}{232314825}}$	${\displaystyle \frac{183479015}{1544223716}}$	0	0	0
	$-{\displaystyle \frac{1255284611}{575881630}}$	${\displaystyle \frac{2556741844}{1407985387}}$	$-{\displaystyle \frac{354912741}{737708101}}$	${\displaystyle \frac{861639665}{1051992621}}$	0	0
	${\displaystyle \frac{139623777}{1998501059}}$	${\displaystyle \frac{151075790}{551923941}}$	$-{\displaystyle \frac{5431732}{1654707983}}$	${\displaystyle \frac{57784943}{394768749}}$	${\displaystyle \frac{16965417}{1274071093}}$	0
$b\to$	${\displaystyle \frac{92306947}{1303649843}}$	${\displaystyle \frac{429325261}{1225378013}}$	${\displaystyle \frac{221851245}{3287539774}}$	${\displaystyle \frac{420269659}{1217598825}}$	${\displaystyle \frac{740841171}{5528332403}}$	${\displaystyle \frac{31129404}{967389425}}$
$\widehat{b}\to$	${\displaystyle \frac{36719078}{466615877}}$	${\displaystyle \frac{208071437}{627991452}}$	${\displaystyle \frac{7005164}{483157681}}$	${\displaystyle \frac{1928335569}{4601595221}}$	${\displaystyle \frac{125234026}{1338671715}}$	${\displaystyle \frac{21346033}{1658393989}}$	${\displaystyle \frac{1}{20}}$
$d\to$	${\displaystyle \frac{139623777}{1998501059}}$	${\displaystyle \frac{151075790}{551923941}}$	$-{\displaystyle \frac{5431732}{1654707983}}$	${\displaystyle \frac{57784943}{394768749}}$	${\displaystyle \frac{16965417}{1274071093}}$
$\widehat{d}\to$	${\displaystyle \frac{102105254}{1366647511}}$	${\displaystyle \frac{153643847}{584456494}}$	$-{\displaystyle \frac{3997442}{654400525}}$	${\displaystyle \frac{207616691}{1340523277}}$	${\displaystyle \frac{12972367}{1078624536}}$	${\displaystyle \frac{752567}{467741276}}$

and

Table 4. Coefficients of the 7(5) pair.

c	A
0	0	0	0	0	0	0	0	0
${\displaystyle \frac{1}{8}}$	${\displaystyle \frac{1}{8}}$	0	0	0	0	0	0	0
${\displaystyle \frac{1}{5}}$	${\displaystyle \frac{53349690}{603180907}}$	${\displaystyle \frac{202053157}{1811278965}}$	0	0	0	0	0	0
${\displaystyle \frac{2}{5}}$	$-{\displaystyle \frac{6018455}{1047543353}}$	$-{\displaystyle \frac{331258825}{1424686717}}$	${\displaystyle \frac{1575913757}{2469082868}}$	0	0	0	0	0
${\displaystyle \frac{1}{2}}$	$-{\displaystyle \frac{34276137}{600042728}}$	$-{\displaystyle \frac{119693677}{470929744}}$	${\displaystyle \frac{456514532}{673786419}}$	${\displaystyle \frac{91782119}{686213876}}$	0	0	0	0
${\displaystyle \frac{3}{5}}$	${\displaystyle \frac{104326539}{715754762}}$	$-{\displaystyle \frac{528081604}{478040477}}$	${\displaystyle \frac{232828616}{145770633}}$	$-{\displaystyle \frac{346503067}{803949037}}$	${\displaystyle \frac{458528309}{1167636595}}$	0	0	0
${\displaystyle \frac{4}{5}}$	${\displaystyle \frac{164370736}{719166091}}$	${\displaystyle \frac{287836583}{475340755}}$	$-{\displaystyle \frac{434202437}{787748133}}$	${\displaystyle \frac{776183737}{2072773349}}$	$-{\displaystyle \frac{359707736}{568196253}}$	${\displaystyle \frac{297706885}{383789789}}$	0	0
${\displaystyle \frac{5}{6}}$	${\displaystyle \frac{571234282}{1292256085}}$	$-{\displaystyle \frac{163644024}{598795985}}$	${\displaystyle \frac{434129672}{1024184363}}$	$-{\displaystyle \frac{458249359}{1591656232}}$	$-{\displaystyle \frac{226893932}{1525451613}}$	${\displaystyle \frac{720660496}{1154927353}}$	${\displaystyle \frac{70287235}{1317288008}}$	0
1	${\displaystyle \frac{84500844}{419992723}}$	$-{\displaystyle \frac{577927735}{469547576}}$	${\displaystyle \frac{15167575312}{6875238419}}$	$-{\displaystyle \frac{1847505748}{646735723}}$	${\displaystyle \frac{2648529023}{782098598}}$	$-{\displaystyle \frac{1167018767}{1234225733}}$	$-{\displaystyle \frac{1515995803}{1684134096}}$	${\displaystyle \frac{924250955}{811144576}}$
	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0
	${\displaystyle \frac{6718965}{481850228}}$	0	0	0	0	0	0	0
	${\displaystyle \frac{54942235}{2006066137}}$	${\displaystyle \frac{15472181}{217307372}}$	0	0	0	0	0	0
$\overline{A}\to$	${\displaystyle \frac{13577792}{495771991}}$	${\displaystyle \frac{22050438}{495716135}}$	${\displaystyle \frac{283627865}{3322412337}}$	0	0	0	0	0
	$-{\displaystyle \frac{14180539}{845563863}}$	${\displaystyle \frac{27053183}{151491698}}$	$-{\displaystyle \frac{13187092}{1461421841}}$	${\displaystyle \frac{14285958}{271989619}}$	0	0	0	0
	${\displaystyle \frac{21160793}{121602384}}$	$-{\displaystyle \frac{85686929}{101458060}}$	${\displaystyle \frac{250790469}{239063945}}$	$-{\displaystyle \frac{36154403}{86286747}}$	${\displaystyle \frac{49695151}{163139864}}$	0	0	0
	${\displaystyle \frac{8462875}{72563974}}$	$-{\displaystyle \frac{79891174}{158211209}}$	${\displaystyle \frac{36044633}{52796893}}$	$-{\displaystyle \frac{47016078}{174876551}}$	${\displaystyle \frac{27008407}{127844653}}$	${\displaystyle \frac{4837109}{116867752}}$	0	0
	${\displaystyle \frac{67824649}{2783623662}}$	${\displaystyle \frac{48741640}{205101599}}$	$-{\displaystyle \frac{23811983}{397137837}}$	${\displaystyle \frac{17380466}{88975787}}$	${\displaystyle \frac{16168641}{556147049}}$	${\displaystyle \frac{7125373}{559402722}}$	${\displaystyle \frac{64065334}{1053745503}}$	0
$b\to$	${\displaystyle \frac{84500844}{419992723}}$	$-{\displaystyle \frac{577927735}{469547576}}$	${\displaystyle \frac{15167575312}{6875238419}}$	$-{\displaystyle \frac{1847505748}{646735723}}$	${\displaystyle \frac{2648529023}{782098598}}$	$-{\displaystyle \frac{1167018767}{1234225733}}$	$-{\displaystyle \frac{1515995803}{1684134096}}$	${\displaystyle \frac{924250955}{811144576}}$
$\widehat{b}\to$	$-{\displaystyle \frac{320560198}{1387413679}}$	${\displaystyle \frac{3304935953}{2148629380}}$	$-{\displaystyle \frac{934978493}{716035472}}$	${\displaystyle \frac{119856567}{781419025}}$	${\displaystyle \frac{3541196691}{4411805198}}$	$-{\displaystyle \frac{498658693}{2238995507}}$	$-{\displaystyle \frac{278833107}{894718040}}$	${\displaystyle \frac{239425724}{454342689}}$	${\displaystyle \frac{1}{20}}$
$d\to$	${\displaystyle \frac{67824649}{2783623662}}$	${\displaystyle \frac{48741640}{205101599}}$	$-{\displaystyle \frac{23811983}{397137837}}$	${\displaystyle \frac{17380466}{88975787}}$	${\displaystyle \frac{16168641}{556147049}}$	${\displaystyle \frac{7125373}{559402722}}$	${\displaystyle \frac{64065334}{1053745503}}$
$\widehat{d}\to$	${\displaystyle \frac{17896581}{105671711}}$	$-{\displaystyle \frac{83237081}{155999235}}$	${\displaystyle \frac{234468734}{296248719}}$	$-{\displaystyle \frac{29643419}{142582240}}$	${\displaystyle \frac{7438697}{37050289}}$	${\displaystyle \frac{13041803}{327653383}}$	$-{\displaystyle \frac{14651331}{867442538}}$	${\displaystyle \frac{25835861}{453483297}}$

.

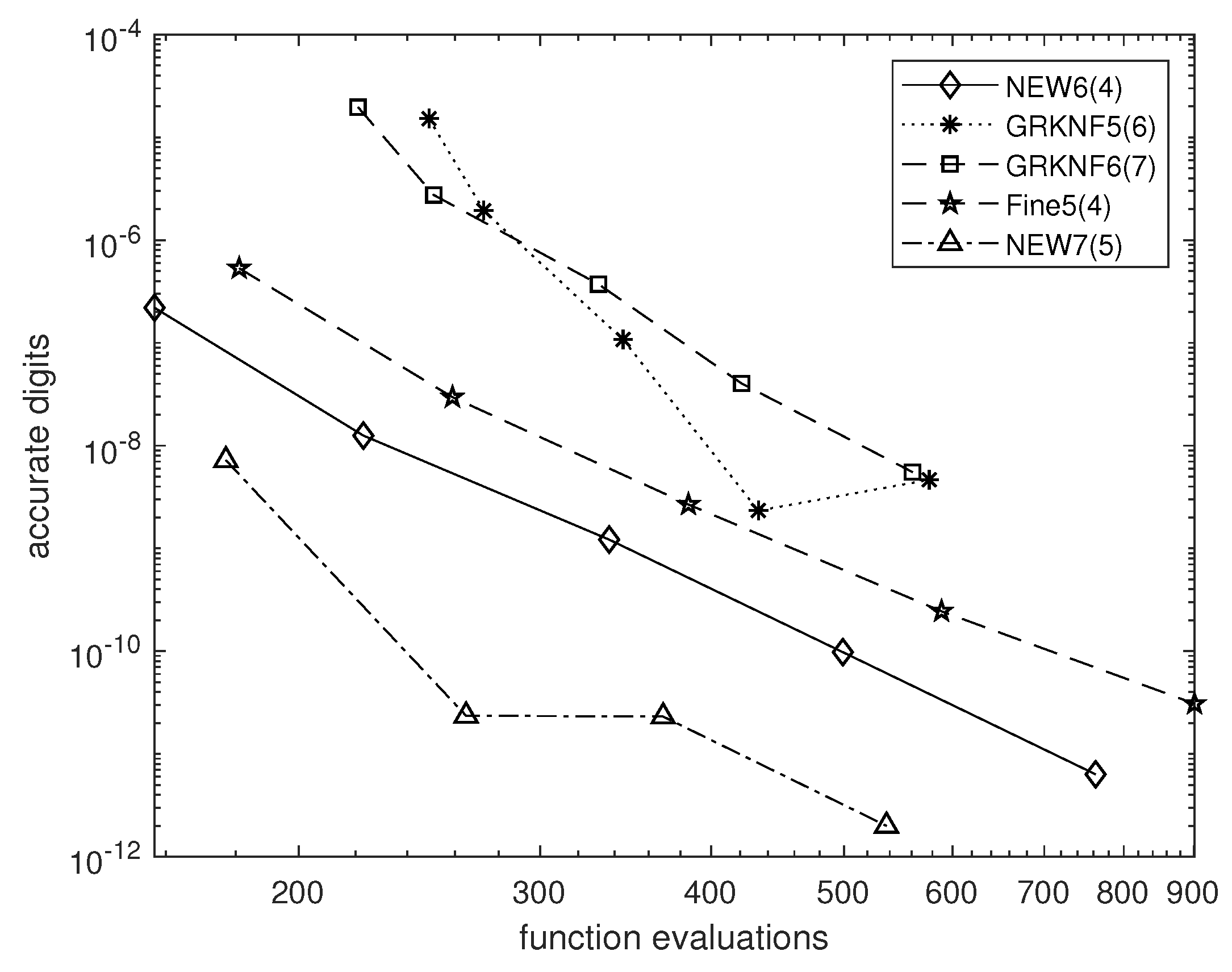
4. Numerical Tests

The methods considered for tests are three already known pairs from the literature and both pairs given above. Namely,

• GRKNF5(6), a fifth-order method, effectively using six stages pair step, appeared in [1]
• GRKNF6(7), a sixth-order method, effectively using ten stages pair step, appeared in [1].
• Fine5(4), an FSAL fifth-order method, effectively using six stages pair step, appeared in [2].
• NEW6(4), the FSAL pair constructed here, effectively using six stages pair step.
• NEW7(5), the FSAL pair constructed here, effectively using eight stages pair step.

The order of the pairs is included in their names. e.g., Fine5(4) is a pair using orders five and four. The solution advances with the fifth-order formula. GRKNF5(6) is a fifth-order formula since the solution advances with the fifth-order formula. The sixth-order formula is accompanying only solution in y and not in $y^{\prime }$, i.e., in the notation given here, there are only vectors $b,\widehat{b},\widehat{d}$ and the solution propagates through $\widehat{b},\widehat{d}$. Similar logic holds for GRKNF6(7).

To evaluate the performance of Runge–Kutta–Nyström (RKN) methods designed for systems of the form (2) with $L,M\in {\mathbb{R}}^{n\times n}$, we consider three test cases that arise from relevant physical and engineering applications. These problems are linear and inhomogeneous, providing structured challenges that are well suited for the development and testing of high-order RKN methods.

4.1. Damped Harmonic Oscillator with External Forcing ($n=1$)

The classic damped harmonic oscillator with external forcing is given by:

$$y^{″}\left(t\right)+\lambda y^{\prime }\left(t\right)+{\omega }^{2}y\left(t\right)=g\left(t\right).$$

Rewriting in standard form yields:

$$y^{″}\left(t\right)=-\lambda y^{\prime }\left(t\right)-{\omega }^{2}y\left(t\right)+g\left(t\right),$$

with

$$L=-\lambda ,M=-{\omega }^2,g\left(t\right)=Asin\left(\nu t\right).$$

We consider a numerical example with parameters:

$$\lambda =5,\omega =1,A=1,\nu ={\displaystyle \frac{1}{10}},$$

and initial conditions:

$$y\left(0\right)=0,y^{\prime }\left(0\right)=0.$$

This problem is representative of mechanical systems with damping and periodic excitation, such as vibrating beams or mass–spring–damper systems under sinusoidal forcing [14]. All computations were carried out over the interval $[0,10]$. Using the known value

$$y\left(10\right)\approx 0.50814725856006851284$$

as a reference, we measured the number of function evaluations required by each of the five pairs in relation to their corresponding endpoint errors. The resulting efficiency comparison is displayed in Figure 1. In Appendix A, we include a MATLAB script that contains the coefficients of the pair $7\left(5\right)$. By running it, we may reproduce the lowermost line of this figure.

4.2. Coupled Oscillators in a 2D Framework ($n=2$)

We next examine a two-mass system with coupling, damping, and time-varying forcing. The parameters from (2) take the form:

$$L=\left(\begin{array}{cc}-4& 0\\ 0& -0.3\end{array}\right),M=\left(\begin{array}{cc}-2& 1\\ 1& -3\end{array}\right),g\left(t\right)=\left(\begin{array}{c}sin\left(t\right)\\ cos\left(t\right)\end{array}\right),$$

while the initial values are:

$$y\left(0\right)=\left(\begin{array}{c}1\\ 0\end{array}\right),y^{\prime }\left(0\right)=\left(\begin{array}{c}0\\ 1\end{array}\right).$$

This system models two coupled masses subject to damping and external excitation. Such models appear in robotic manipulators, seismology, and mechanical vibrations of plates or membranes with interacting modes [15]. All computations were performed on the interval $[0,10]$. The known approximation

$$y\left(10\right)\approx \left[\begin{array}{c}0.1566961779698483\\ -0.4529092672497892\end{array}\right],$$

was employed as a reference solution. For each of the five method pairs, the number of function evaluations required to achieve their respective endpoint errors was recorded. The resulting comparison of computational efficiency is illustrated in Figure 2.

4.3. Multi-Mass Coupled Oscillators with Damping and Forcing ($n=3$)

A more complex example involves three masses connected via springs and dampers, a system common in structural and control applications. Now, the parameters from (2) take the form:

$$L=\left(\begin{array}{ccc}-6& 0.2& 0\\ 0.1& -7& 0.1\\ 0& 0.3& -5\end{array}\right),M=\left(\begin{array}{ccc}-5& 2& 0\\ 2& -6& 2\\ 0& 2& -5\end{array}\right),g\left(t\right)=\left(\begin{array}{c}sin\left(t\right)\\ cos\left(2t\right)\\ e^{-t}\end{array}\right),$$

and the initial values are:

$$y\left(0\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),y^{\prime }\left(0\right)=\left(\begin{array}{c}1\\ 0\\ -1\end{array}\right).$$

Such configurations occur in rail vehicle suspensions, aerospace structure control, and biomechanical systems where joint dynamics are modeled using second-order linear systems with coupling [16,17,18].

All computations were conducted over the interval $[0,10]$. The following known approximation was utilized as a reference solution:

$$y\left(10\right)\approx \left[\begin{array}{c}0.0622697554888544436\\ 0.09716732533321522028\\ 0.0103120325178873458\end{array}\right].$$

For each of the five pairs of methods, the number of function evaluations necessary to achieve their respective endpoint errors was recorded. A comparative analysis of the computational efficiency is presented in Figure 3.

Interpreting the results, it is evident that the NEW7(5) pair exhibits superior efficiency compared to all other methods. The NEW6(4) pair follows as the second most efficient. This enhanced performance can be attributed to the reduced number of stages required in their construction, as both methods are specifically tailored for problems of the form (2).

5. Conclusions

This study introduces novel embedded General Runge–Kutta–Nyström (GRKN) methods specifically designed for linear inhomogeneous second-order systems, with a focus on constructing efficient pairs of orders $6\left(4\right)$ and $7\left(5\right)$. A key contribution lies in the symbolic derivation of order conditions tailored to the linear structure, which allows for low-stage, high-accuracy schemes. The incorporation of FSAL properties and the use of evolutionary techniques for parameter optimization further enhance computational performance. The proposed methods exhibit clear advantages over existing RKN-type integrators, especially in high-dimensional and tightly coupled systems. Future research may explore extensions to nonlinear or variable coefficient problems.