A Mathematical Methodology for the Detection of Rail Corrugation Based on Acoustic Analysis: Toward Autonomous Operation
Abstract
1. Introduction
2. Research Methodology
2.1. Data Capture
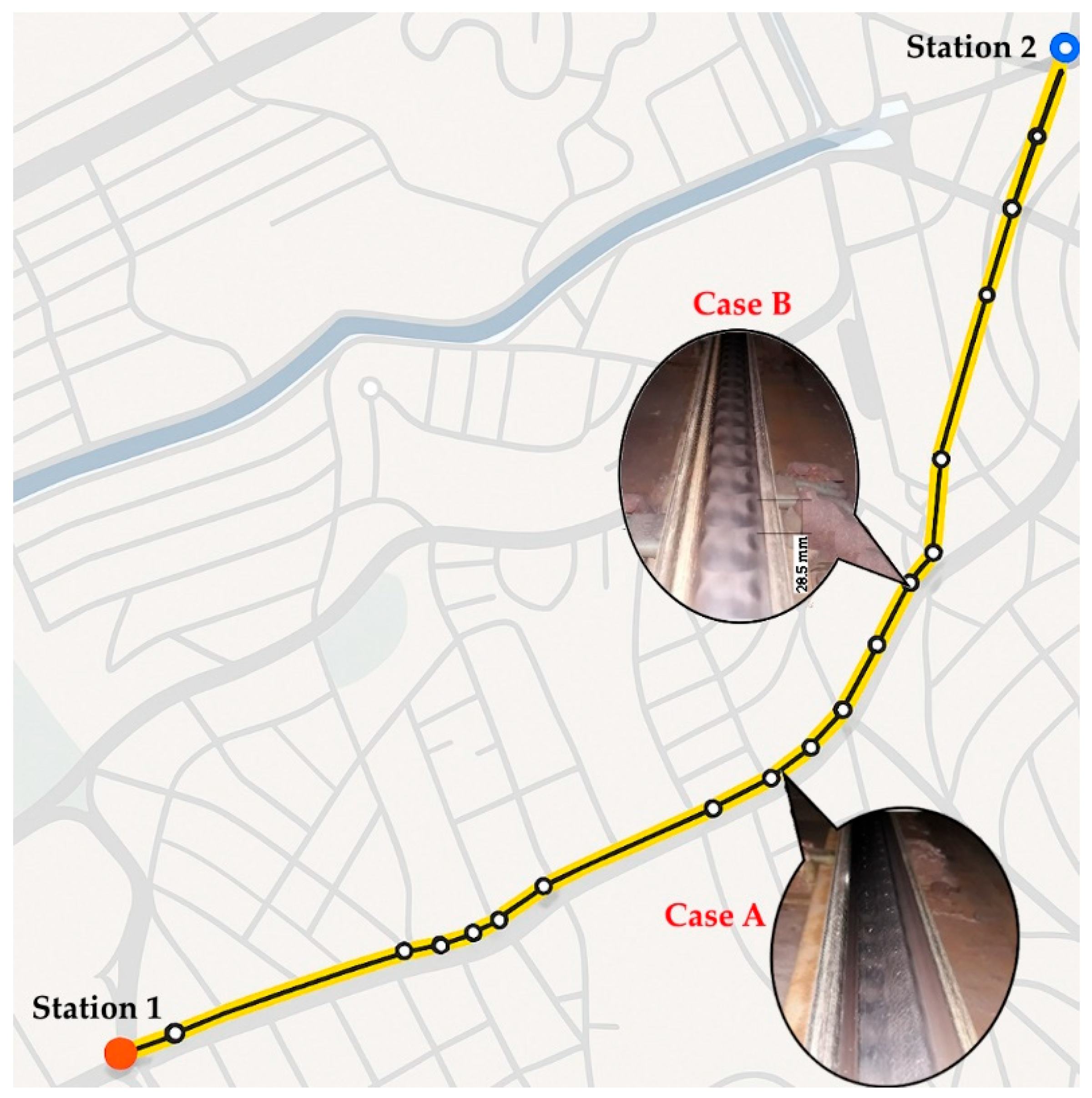
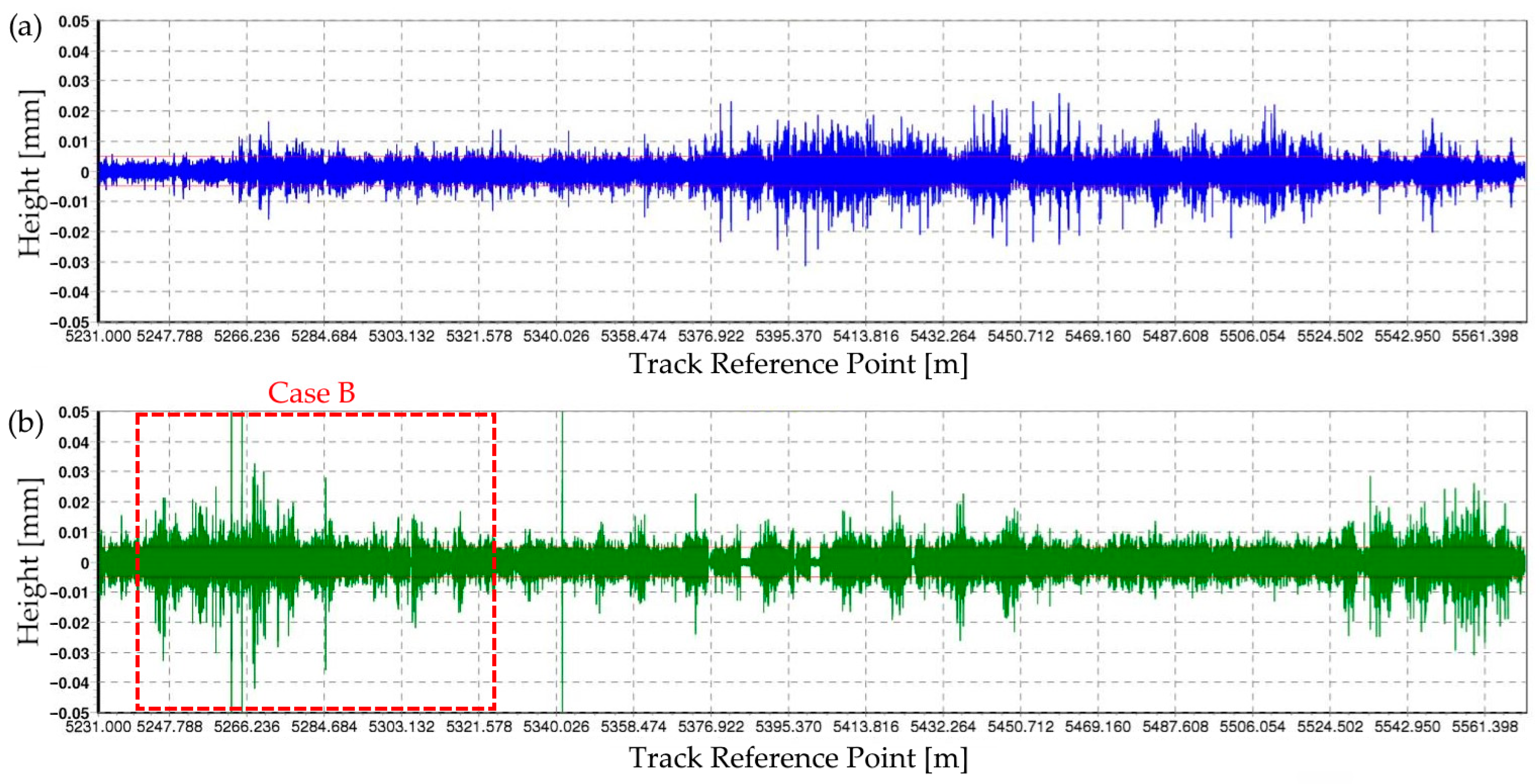
2.1.1. Experimental Design
2.1.2. Instrumentation and Data Acquisition
2.1.3. Kilometer Position Estimation
2.2. Preliminary Pattern Identification
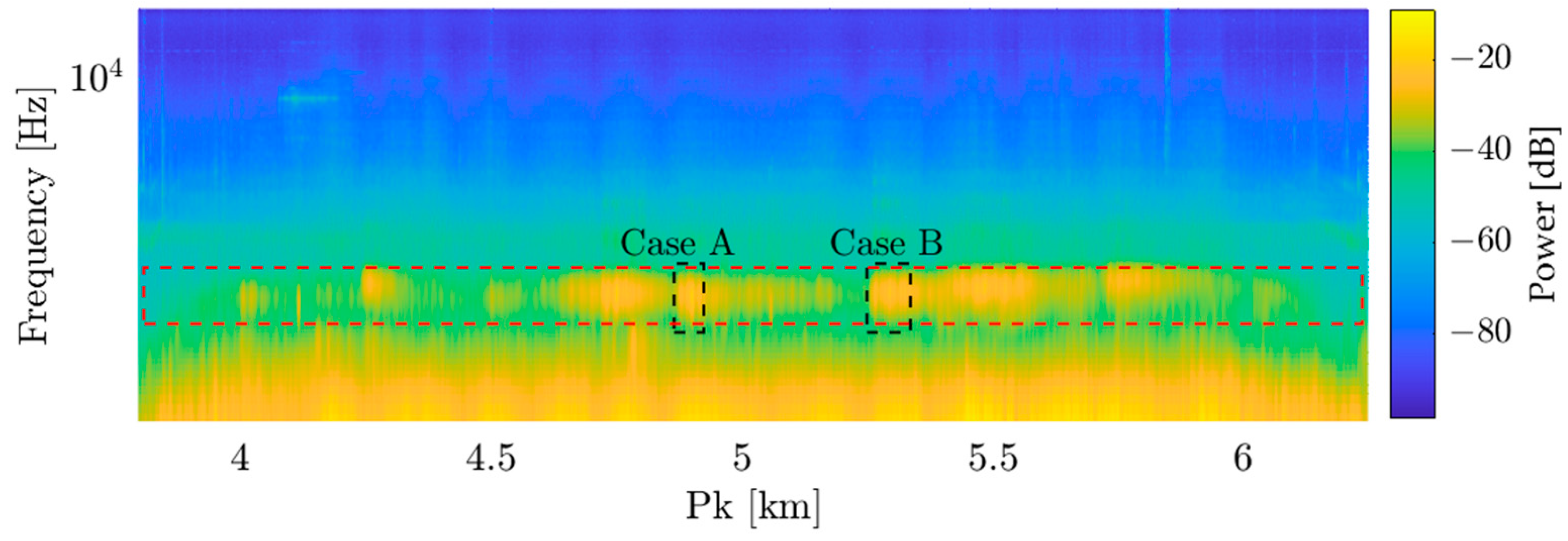
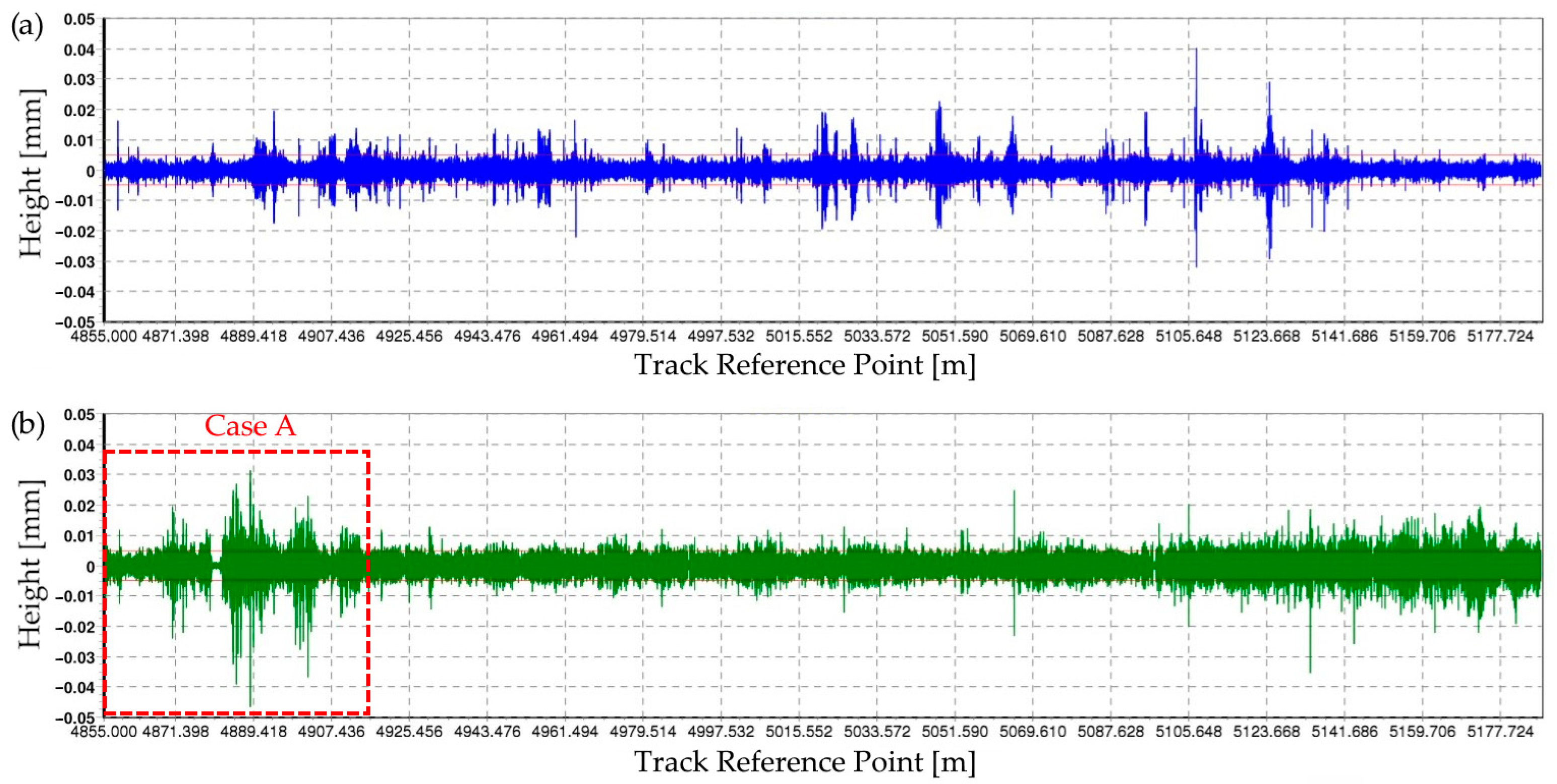
2.2.1. Physical Inspection and Fault Location
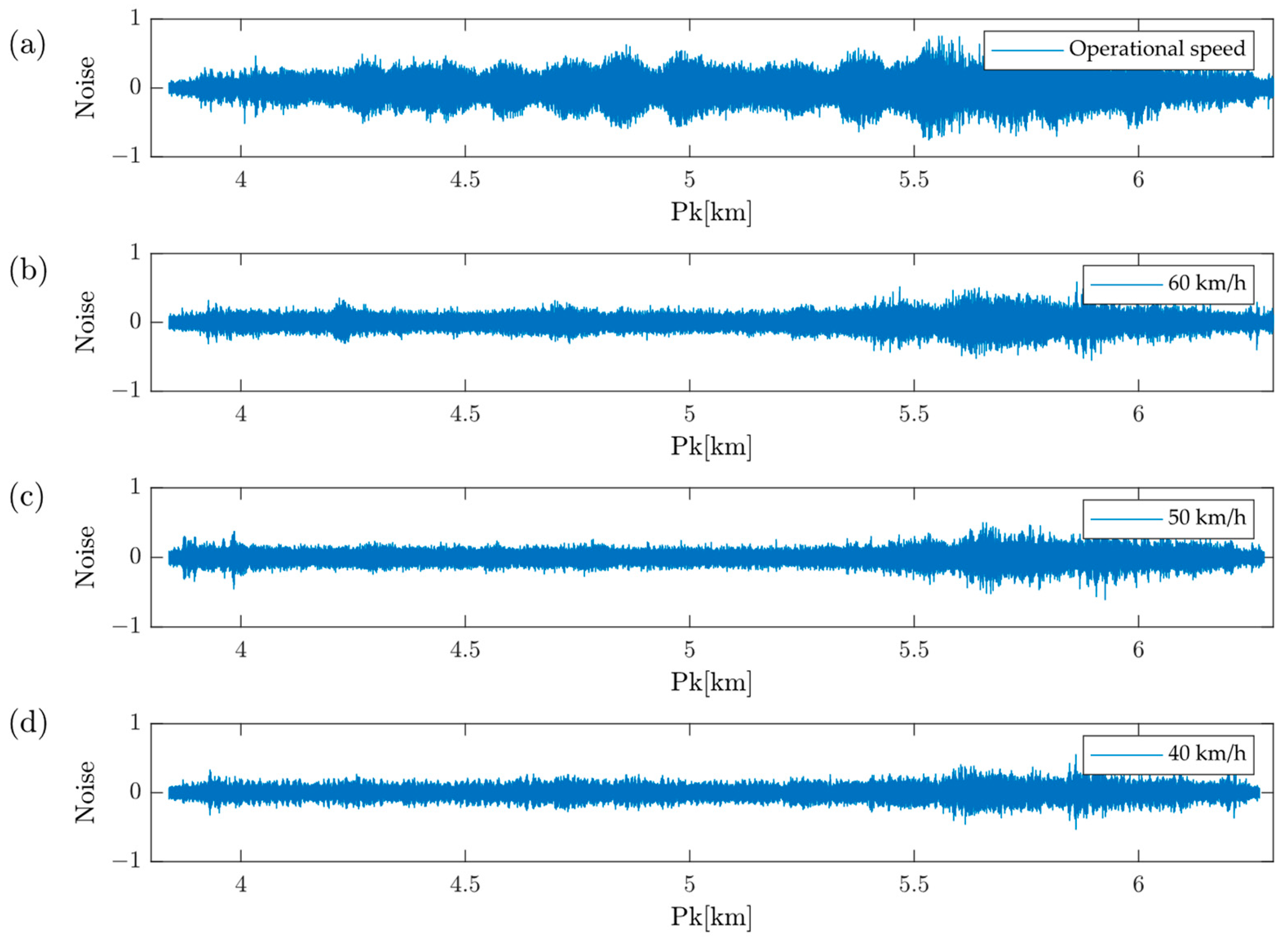
2.2.2. Detection of Annoying Noise
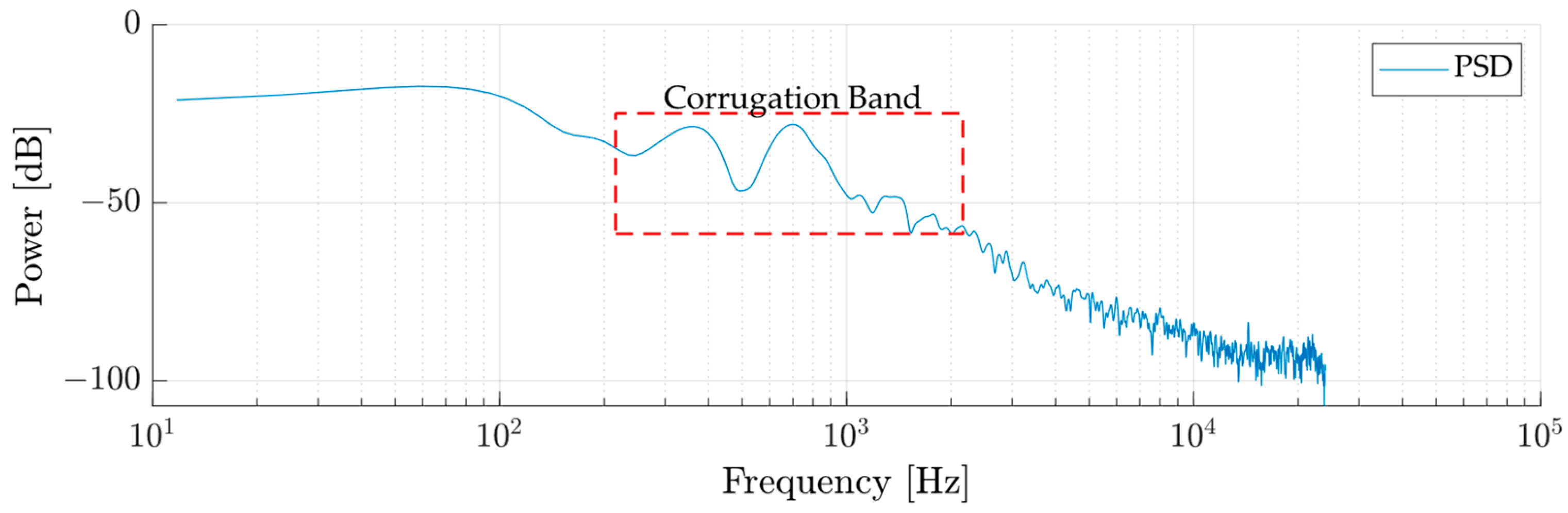
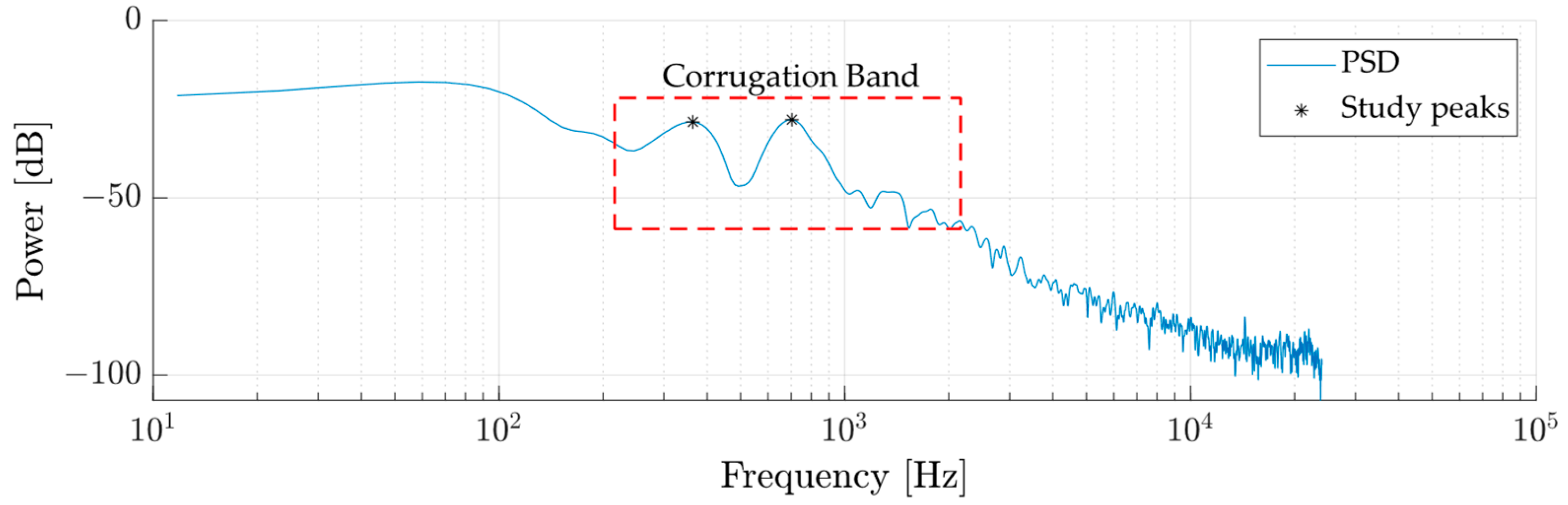
2.2.3. Spectral Processing—PSD
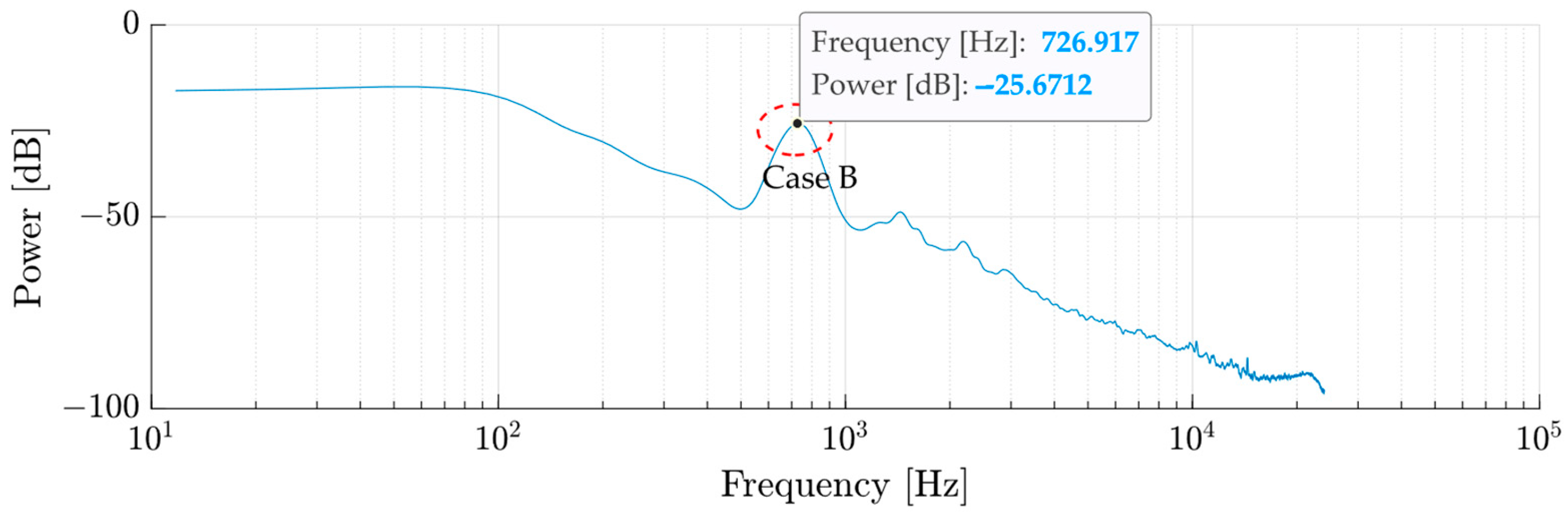
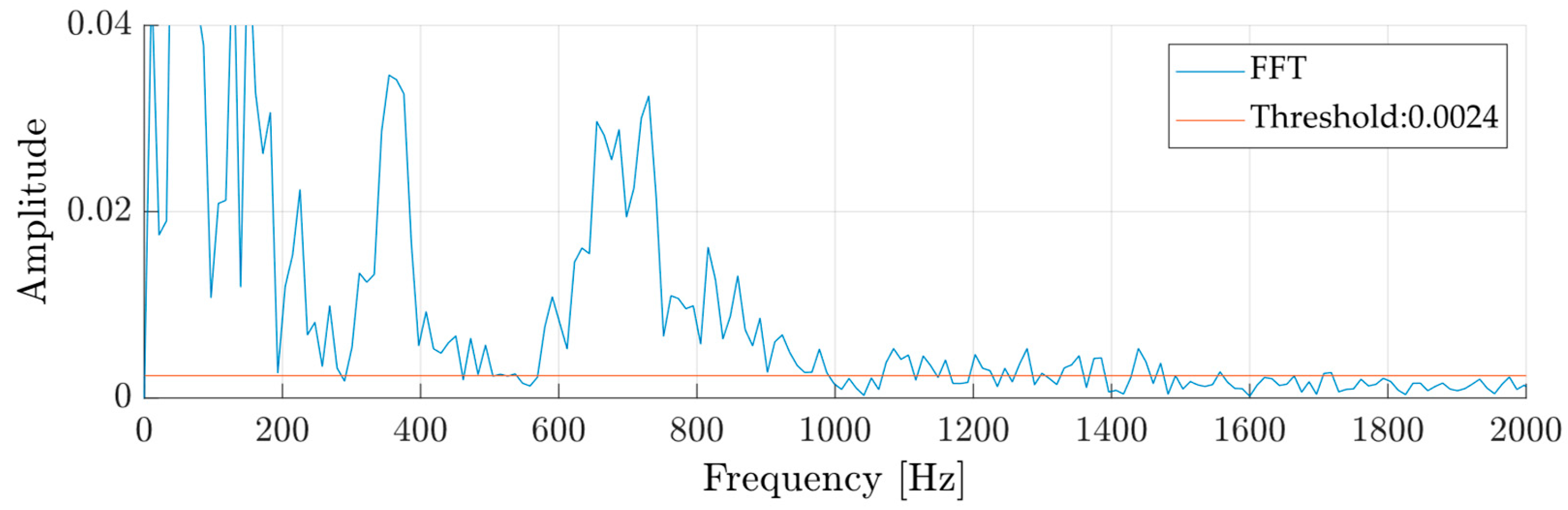
2.2.4. Spectral Processing—FFT
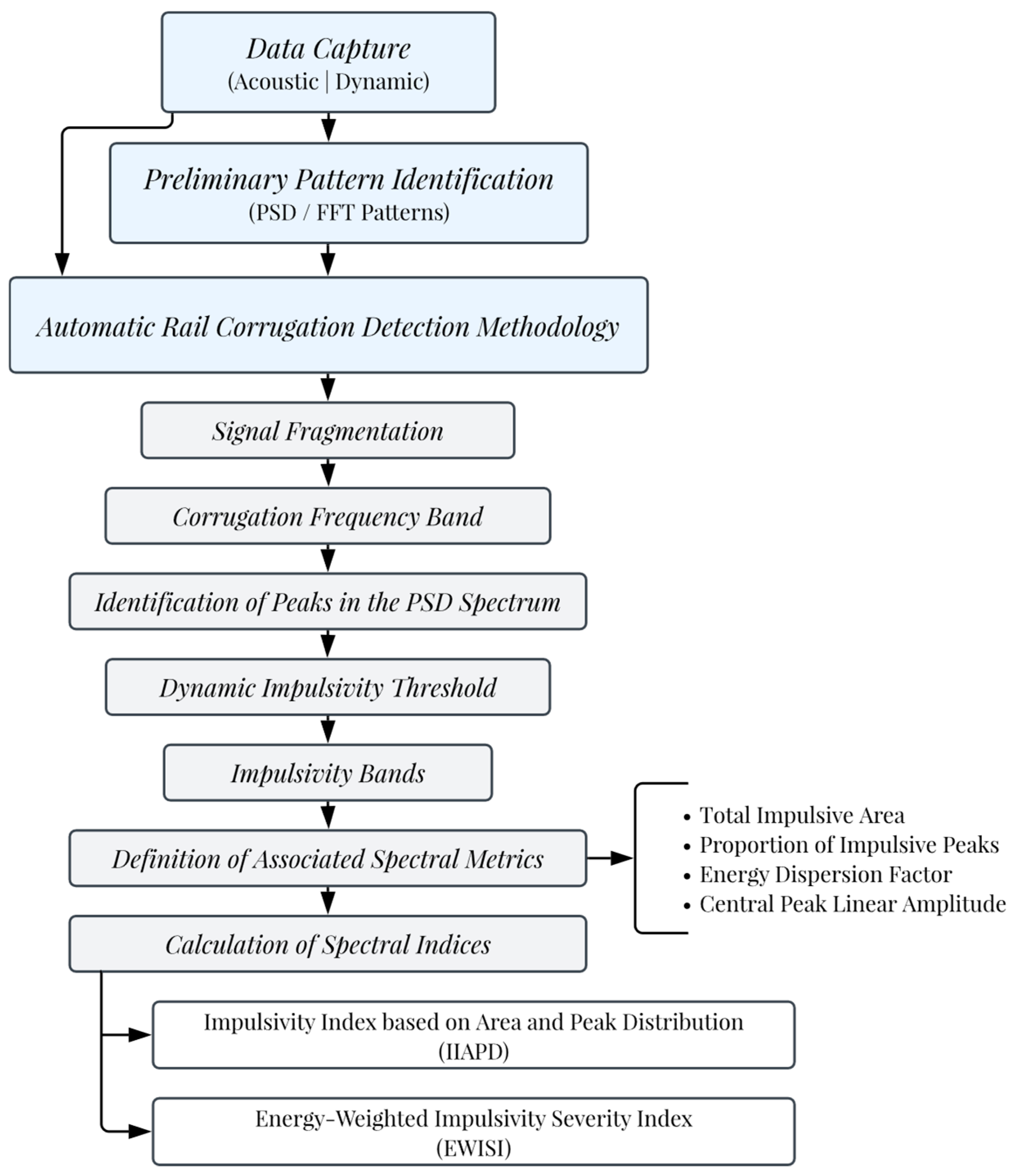
2.3. Proposed Index for Automatic Corrugation Detection
2.3.1. Signal Fragmentation
2.3.2. Definition of the Corrugation Frequency Band
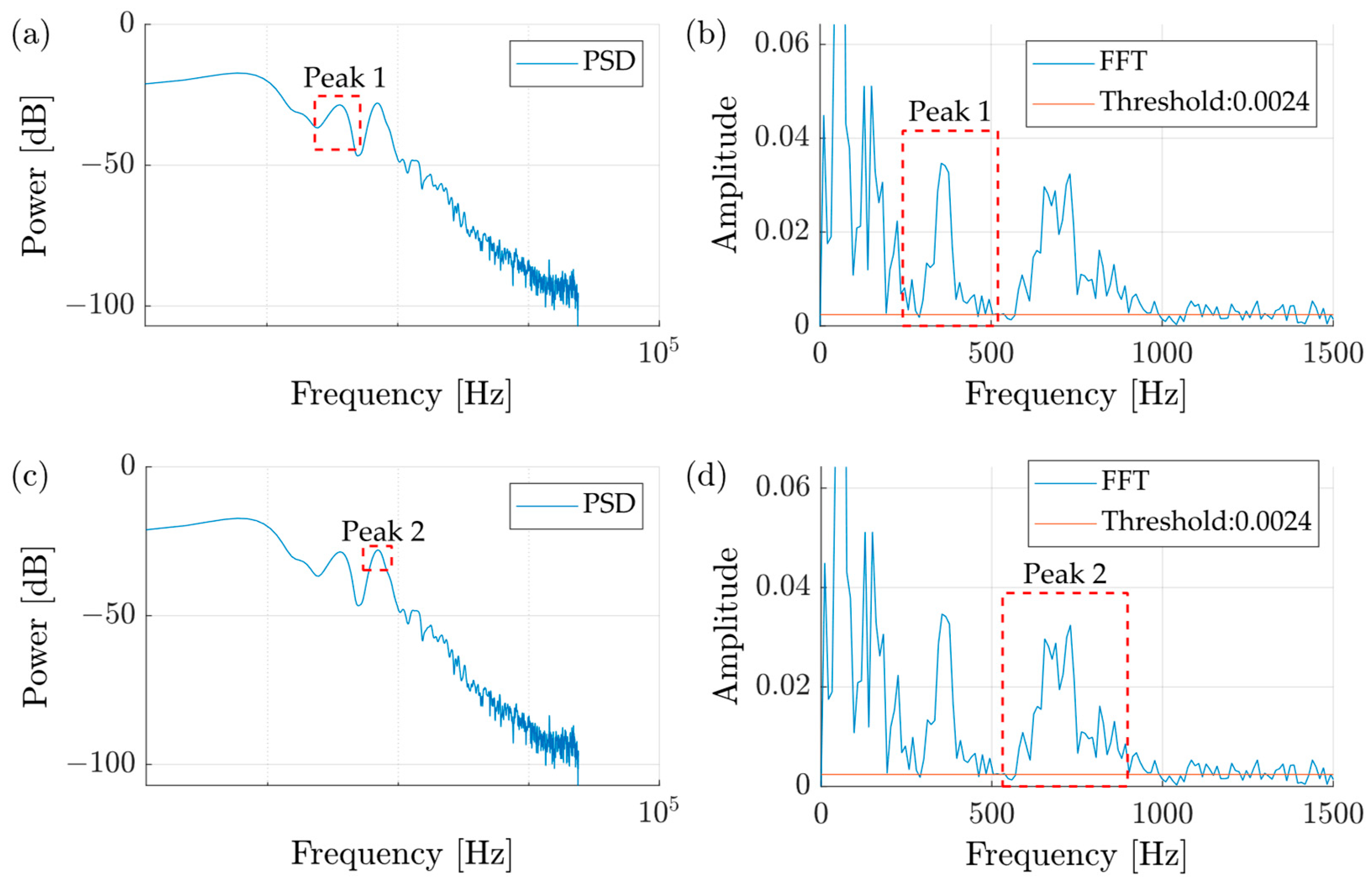
2.3.3. Preliminary Identification of Peaks in the PSD Spectrum
- A minimum height greater than –40 dB (–50 dB is allowed if no valid peaks are found).
- A minimum prominence dynamically adjusted according to the average speed, as expressed in Equation (4)where Kspeed is the average speed in km/h of the segment under analysis. This adaptive criterion compensates for spectral energy level variations caused by speed.
2.3.4. Dynamic Impulsivity Threshold
2.3.5. Definition of Impulsivity Bands
2.3.6. Definition of Associated Spectral Metrics
- Total impulsive area (AT): area under the curve of the spectrum within the impulsiveness band [, ], considering only amplitude values that exceed the dynamic impulsiveness threshold Timp.
- Proportion of impulsive peaks (PPeak): ratio between the number of spectral peaks in , within the impulsiveness band [, ], that exceed the threshold Timp, and the total number of spectral points contained in that band.
- Energy dispersion factor (1 − DP): penalization coefficient that evaluates the distribution of spectral energy in , within the impulsiveness band, calculated according to Equation (6).
- Central peak linear amplitude (AL): linear-scale value of the amplitude at the central frequency previously identified in , obtained by converting it from decibels.
2.3.7. Calculation of Spectral Indices
Impulsivity Index Based on Area and Peak Distribution (IIAPD)
Energy-Weighted Impulsivity Severity Index (EWISI)
Conceptual Comparison of the IIAPD and EWISI
- The IIAPD is more sensitive to the distribution of impulsive content. It is ideal for identifying recurring or distributed defects, even when the individual amplitude is not high.
- The EWISI, on the other hand, prioritizes defects with high amplitude at the central frequency. This index is suitable for areas with severe and localized corrugation, where the spectral energy is significant.
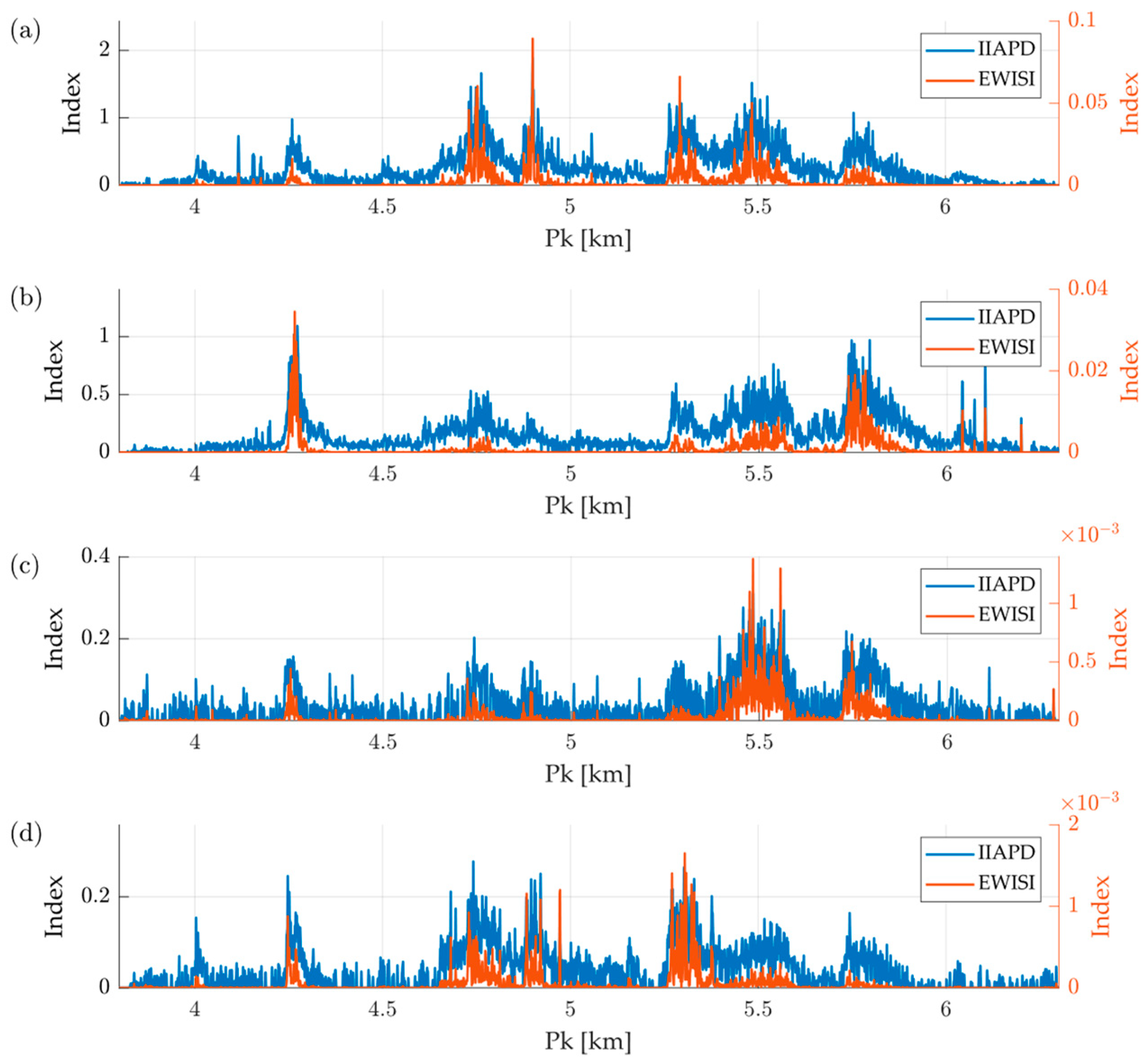
3. Results
- (a)
- Speed profile;
- (b)
- Severity estimation according to the methodology of Bocciolone;
- (c)
- Results of the proposed indices, the IIAPD and EWISI;
- (d)
- Spectrogram according to the methodology of De Rosa.
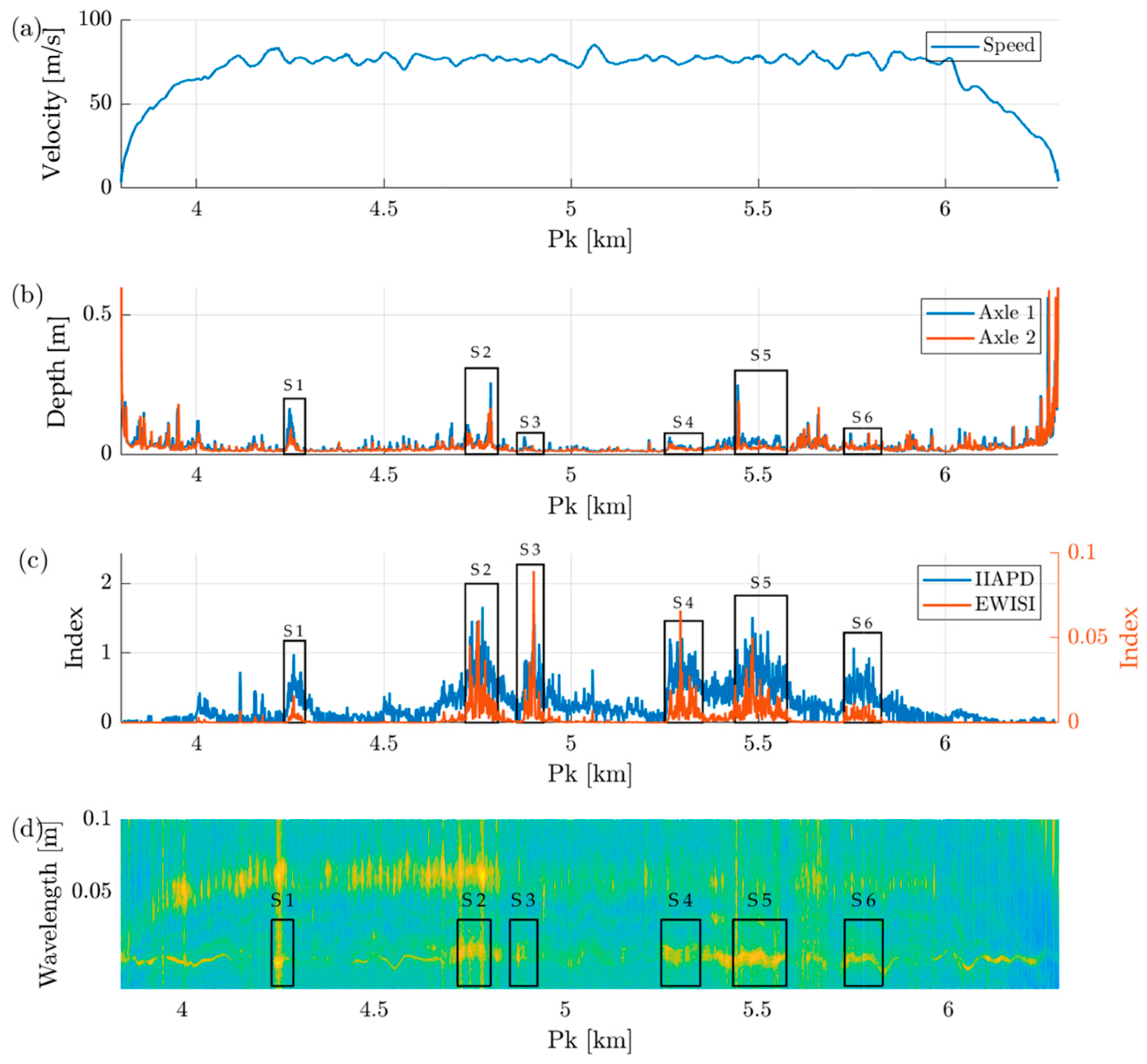
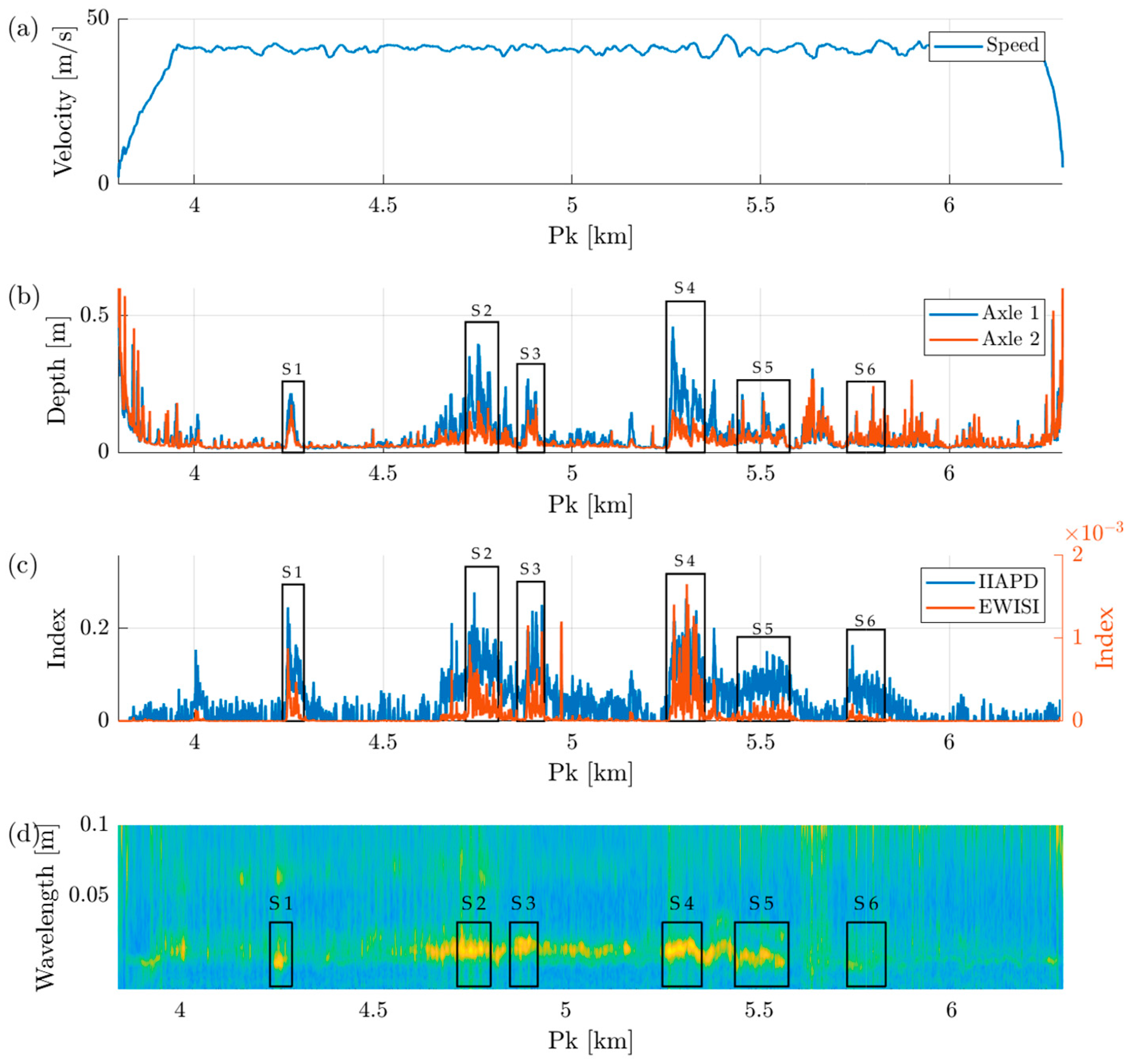
3.1. Results at the Operating Speed (75 km/h)
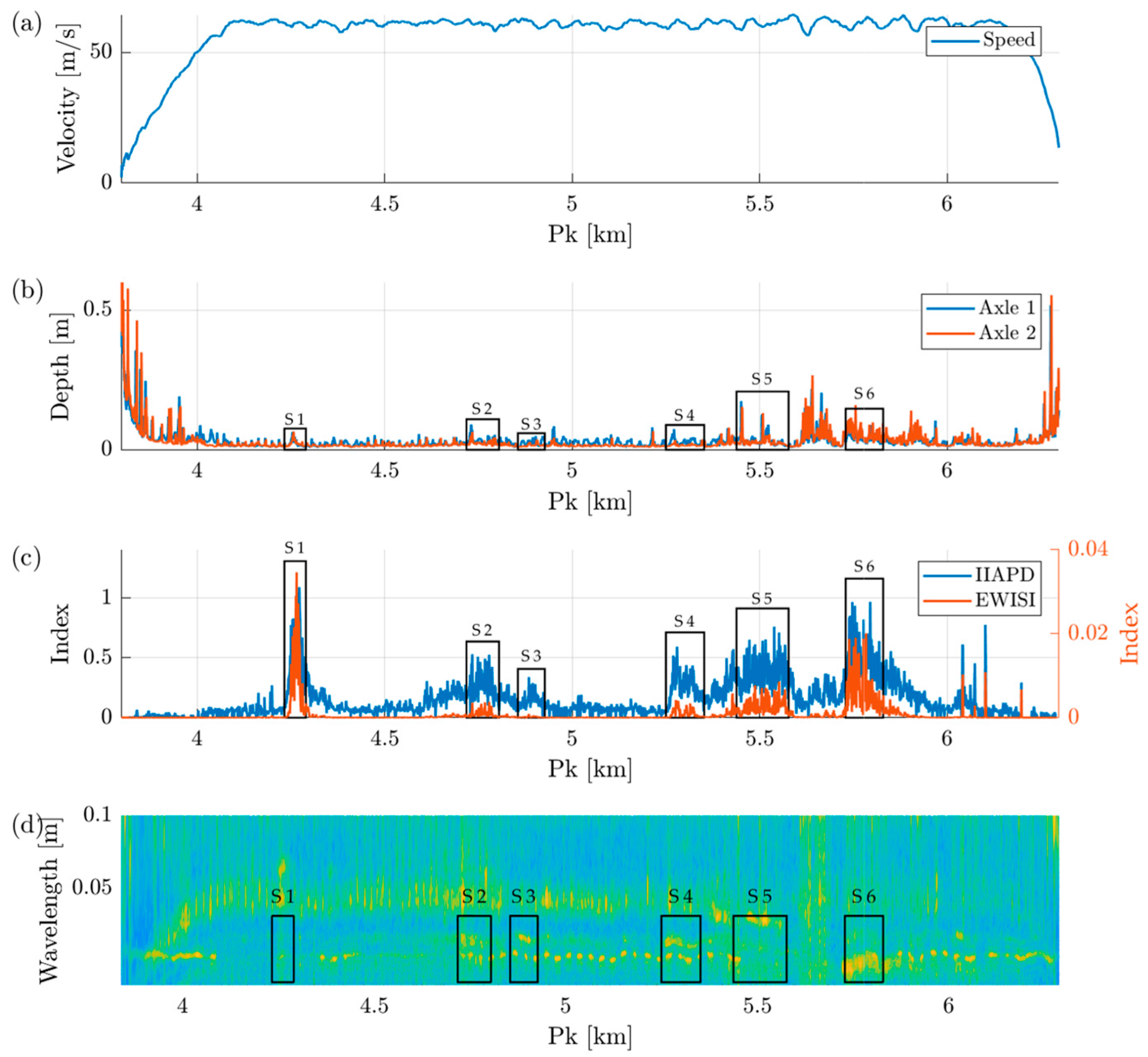
3.2. Results at 60 km/h
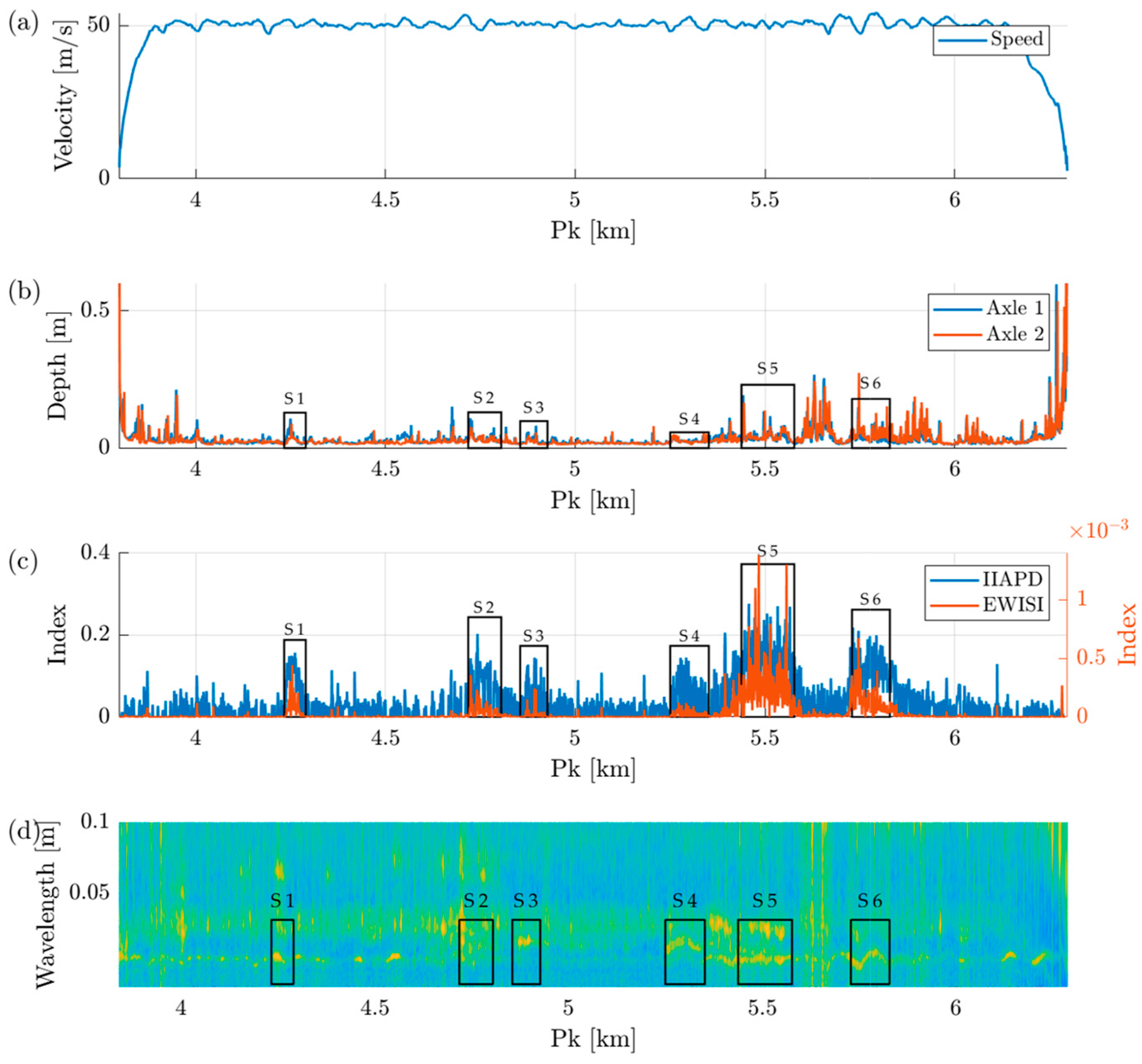
3.3. Results at 50 km/h
3.4. Results at 40 km/h
3.5. Comparative Accuracy with Reference Methodologies
3.6. Validation Through Trolley-Based Measurement
4. Discussion
4.1. Comparative Analysis by Speed: Robustness and Diagnostic Capability
- Bocciolone et al. [32]: The index shows high variability during acceleration and braking, which reduces its reliability. At low speeds, its sensitivity decreases drastically. Finally, normalization by quadratic speed introduces distortions that affect the coherence between recordings.
- De Rosa et al. [30]: The spectrogram reveals areas with energy patterns compatible with corrugation, especially at high speeds. However, its interpretation requires prior experience, and at low speeds, key responses are lost (such as S5 at 60 km/h or S6 at 40 km/h).
- Proposed methodology: Both the IIAPD and EWISI show consistent detections across the six identified sections, with greater sensitivity at 75 km/h and acceptable stability even at 40 km/h. The IIAPD highlights moderate and distributed defects, while the EWISI discriminates zones with greater spectral severity. The dual logic enables precise and tiered diagnosis, without relying on fixed thresholds or subjective interpretation.
4.2. Influence of Travel Direction and Dynamic Conditions
- Bocciolone shows strong dependence on train dynamics. During acceleration or braking phases, it generates responses that exceed the amplitudes of confirmed defective zones, affecting coherence between travel directions.
- De Rosa offers greater stability in runs with similar conditions but loses detection capability in the reverse direction, especially at low speed. Additionally, the presence of energy in bands not associated with corrugation issues compromises its interpretation.
- The proposed methodology (IIAPD and EWISI) presents a structured response by the direction of travel, with consistent spectral patterns aligned with kilometer position. The response is not affected by speed changes, and the indices maintain their selectivity without generating false positives during transitional phases. This resilience confirms their robustness against variable dynamic conditions and their applicability in real-world environments.
4.3. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhai, W.; Jin, X.; Wen, Z.; Zhao, X. Wear Problems of High-Speed Wheel/Rail Systems: Observations, Causes, and Countermeasures in China. Appl. Mech. Rev. 2020, 72, 060801. [Google Scholar] [CrossRef]
- Jin, X. Research Progress of High-Speed Wheel–Rail Relationship. Lubricants 2022, 10, 248. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.; Li, Z. Short Pitch Corrugation Mitigation by Rail Constraint Design. Int. J. Mech. Sci. 2023, 243, 108037. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.; Dollevoet, R.; Li, Z. Parametric Investigation of Railway Fastenings into the Formation and Mitigation of Short Pitch Corrugation. Rail. Eng. Sci. 2024, 32, 286–306. [Google Scholar] [CrossRef]
- Wang, Q.-A.; Huang, X.-Y.; Wang, J.-F.; Ni, Y.-Q.; Ran, S.-C.; Li, J.-P.; Zhang, J. Concise Historic Overview of Rail Corrugation Studies: From Formation Mechanisms to Detection Methods. Buildings 2024, 14, 968. [Google Scholar] [CrossRef]
- Wu, B.; Wang, W.; Pan, J.; Hu, Y.; Xu, R.; Ye, D.; Yan, W.; Zhang, R. Study on Corrugated Wear on High-Speed Railways Based on an Improved Finite Element Model of Wheel-Rail Rolling Contact. Tribol. Int. 2023, 179, 108199. [Google Scholar] [CrossRef]
- Ma, C.; Gao, L.; Xin, T.; Cai, X.; Nadakatti, M.M.; Wang, P. The Dynamic Resonance under Multiple Flexible Wheelset-Rail Interactions and Its Influence on Rail Corrugation for High-Speed Railway. J. Sound Vib. 2021, 498, 115968. [Google Scholar] [CrossRef]
- Bao, P.; Cui, X.; Ding, H.; Yin, Y.; Du, Z.; Yang, Z. Influences of Friction Self-Excited Vibration Characteristics of Various Types of High-Speed Trains on Rail Corrugations in Braking Sections. Eng. Fail. Anal. 2022, 134, 106087. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, P.; Wang, Q.; Chen, Z.; He, Q. Using Vehicle Interior Noise Classification for Monitoring Urban Rail Transit Infrastructure. Sensors 2020, 20, 1112. [Google Scholar] [CrossRef]
- Soeta, Y.; Shimokura, R. The Impact of External Environments and Wheel-Rail Friction on Noise inside a Train Car. Noise Vib. Worldw. 2012, 43, 9–22. [Google Scholar] [CrossRef]
- Jeong, W.; Jeong, D. Acoustic Roughness Measurement of Railhead Surface Using an Optimal Sensor Batch Algorithm. Appl. Sci. 2020, 10, 2110. [Google Scholar] [CrossRef]
- Xin, T.; Wang, S.; Gao, L.; Huo, H.; Ding, Y.; Wang, P.; Chen, P.; Liu, P. Field Measurement of Rail Corrugation Influence on Environmental Noise and Vibration: A Case Study in China. Measurement 2020, 164, 108084. [Google Scholar] [CrossRef]
- Lei, X. Methods for Predicting the Ambient Vibration and Noise Resulting from Rail Transit. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 1054–1067. [Google Scholar] [CrossRef]
- Tsai, K.-T.; Lin, M.-D.; Lin, Y.-H. Noise Exposure Assessment and Prevention around High-Speed Rail. Int. J. Environ. Sci. Technol. 2019, 16, 4833–4842. [Google Scholar] [CrossRef]
- Sadeghi, J.; Hasheminezhad, A. Correlation between Rolling Noise Generation and Rail Roughness of Tangent Tracks and Curves in Time and Frequency Domains. Appl. Acoust. 2016, 107, 10–18. [Google Scholar] [CrossRef]
- Thompson, D.J.; Hemsworth, B.; Vincent, N. Experimental Validation of the Twins Prediction Program for Rolling Noise, Part 1: Description of the Model and Method. J. Sound Vib. 1996, 193, 123–135. [Google Scholar] [CrossRef]
- Thompson, D.J.; Fodiman, P.; Mahé, H. Experimental Validation of the Twins Prediction Program for Rolling Noise, Part 2: Results. J. Sound Vib. 1996, 193, 137–147. [Google Scholar] [CrossRef]
- Thompson, D.J.; Jones, C.J.C. A review of the Modelling of Wheel/Rail Noise Generation. J. Sound Vib. 2000, 231, 519–536. [Google Scholar] [CrossRef]
- Prakash, A.; Tadepalli, T. A Review of Acoustic Signal-Based Detection of Damage in Railway Tracks. In Proceedings of the 2024 IEEE Conference on Engineering Informatics (ICEI), Melbourne, Australia, 20–28 November 2024; pp. 1–13. [Google Scholar]
- Yao, S.; Yue, L.; Xie, W.; Zheng, S.; Tang, S.; Liu, J.; Wang, W. Investigating the Influence of Non-Uniform Characteristics of Layered Foundation on Ground Vibration Using an Efficient 2.5D Random Finite Element Method. Mathematics 2024, 12, 1488. [Google Scholar] [CrossRef]
- UNE-EN 15610; Aplicaciones Ferroviarias. Acústica. Medición de la Rugosidad de los Carriles y de las Ruedas Relacionada con la Generación de Ruido de Rodadura. Asociación Española de Normalización: Madrid, Spain, 2020.
- Grassie, S.L. Rail Irregularities, Corrugation and Acoustic Roughness: Characteristics, Significance and Effects of Reprofiling. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 542–557. [Google Scholar] [CrossRef]
- Mori, H.; Tsunashima, H.; Kojima, T.; Matsumoto, A.; Mizuma, T. Condition Monitoring of Railway Track Using In-Service Vehicle. J. Mech. Syst. Transp. Logist. 2010, 3, 154–165. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, J.; Zhang, Z. A Heavy-Haul Railway Corrugation Diagnosis Method Based on WPD-ASTFT and SVM. Shock. Vib. 2022, 2022, 8370796. [Google Scholar] [CrossRef]
- Han, J.; Xiao, X.; Wu, Y.; Wen, Z.; Zhao, G. Effect of Rail Corrugation on Metro Interior Noise and Its Control. Appl. Acoust. 2018, 130, 63–70. [Google Scholar] [CrossRef]
- UNE-EN ISO 3095; Acústica. Aplicaciones Ferroviarias. Medición Del Ruido Emitido Por Vehículos Que Circulan Sobre Carriles. Asociación Española de Normalización: Madrid, Spain, 2014.
- Shafique, R.; Siddiqui, H.-U.-R.; Rustam, F.; Ullah, S.; Siddique, M.A.; Lee, E.; Ashraf, I.; Dudley, S. A Novel Approach to Railway Track Faults Detection Using Acoustic Analysis. Sensors 2021, 21, 6221. [Google Scholar] [CrossRef]
- Siddiqui, H.U.R.; Saleem, A.A.; Raza, M.A.; Zafar, K.; Munir, K.; Dudley, S. IoT Based Railway Track Faults Detection and Localization Using Acoustic Analysis. IEEE Access 2022, 10, 106520–106533. [Google Scholar] [CrossRef]
- Sfayyih, A.H.; Sabry, A.H.; Jameel, S.M.; Sulaiman, N.; Raafat, S.M.; Humaidi, A.J.; Kubaiaisi, Y.M.A. Acoustic-Based Deep Learning Architectures for Lung Disease Diagnosis: A Comprehensive Overview. Diagnostics 2023, 13, 1748. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, A.; Luber, B.; Müller, G.; Fuchs, J. Methodology to Detect Rail Corrugation from Vehicle On-Board Measurements by Isolating Effects from Other Sources of Excitation. Appl. Sci. 2024, 14, 8920. [Google Scholar] [CrossRef]
- Thompson, D.J. On the Relationship between Wheel and Rail Surface Roughness and Rolling Noise. J. Sound Vib. 1996, 193, 149–160. [Google Scholar] [CrossRef]
- Bocciolone, M.; Caprioli, A.; Cigada, A.; Collina, A. A Measurement System for Quick Rail Inspection and Effective Track Maintenance Strategy. Mech. Syst. Signal Process. 2007, 21, 1242–1254. [Google Scholar] [CrossRef]
- Li, S.; Núñez, A.; Li, Z.; Dollevoet, R. Automatic Detection of Corrugation: Preliminary Results in the Dutch Network Using Axle Box Acceleration Measurements. In Proceedings of the JRC2015, San Jose, CA, USA, 23–26 March 2015; American Society of Mechanical Engineers Digital Collection: San Jose, CA, USA, 2015. [Google Scholar]
- Hsu, W.-L.; Chang, C.-M. Rail Corrugation Index Development by Sound-Field Excitation on the Carriage Floor of In-Service Train. Sensors 2023, 23, 7539. [Google Scholar] [CrossRef]
- Jeong, W. Spectral Characteristics of Rail Surface by Measuring the Growth of Rail Corrugation. Appl. Sci. 2021, 11, 9568. [Google Scholar] [CrossRef]
- Han, J.; Wang, H.; Zhao, G.; Liu, X.; Xiao, X.; He, Y. Indirect Detection of Short-Pitch Rail Corrugation Using Acoustic Signal. IEEE Trans. Instrum. Meas. 2025, 74, 1–13. [Google Scholar] [CrossRef]
- Khan, D.; Burdzik, R. Measurement and Analysis of Transport Noise and Vibration: A Review of Techniques, Case Studies, and Future Directions. Measurement 2023, 220, 113354. [Google Scholar] [CrossRef]
- Zhou, W.; Li, X.; Shi, X. Joint Optimization of Time-Dependent Line Planning and Differential Pricing with Passenger Train Choice in High-Speed Railway Networks. Mathematics 2023, 11, 1290. [Google Scholar] [CrossRef]
- Cano-Moreno, J.D.; de Pedro, J.M.M.S.; Villagrá, M.R.; González, R.G. Design and Development of a Data Acquisition System to Monitor Comfort and Safety in Railways. Insight—Non-Destr. Test. Cond. Monit. 2021, 63, 47–54. [Google Scholar] [CrossRef]
- Donkoh, E.K.; Opoku, A.A. Optimal Geometric Disks Covering Using Tessellable Regular Polygons. JMR 2016, 8, 25. [Google Scholar] [CrossRef]
- UNE-EN 13231-5; Aplicaciones Ferroviarias. Vía. Recepción de Trabajos. Parte 5: Procedimientos Para El Reperfilado de Carril En Plena Vía, Interruptores, Cruces y Dispositivos de Expansión. Asociación Española de Normalización: Madrid, Spain, 2019.
- Zhao, Y.; Zhao, C.; Wang, L.; Wang, P. A Rail Corrugation Evaluation Method Using Fractal Characterization Based on Structure Function Method. Wear 2022, 506–507, 204454. [Google Scholar] [CrossRef]
- Soto Ocampo, C.R. Desarrollo de un Sistema de Diagnóstico de Maquinaria Rotativa: Aplicación a Rodamientos de Apoyo de ejes Ferroviarios. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2023. [Google Scholar]

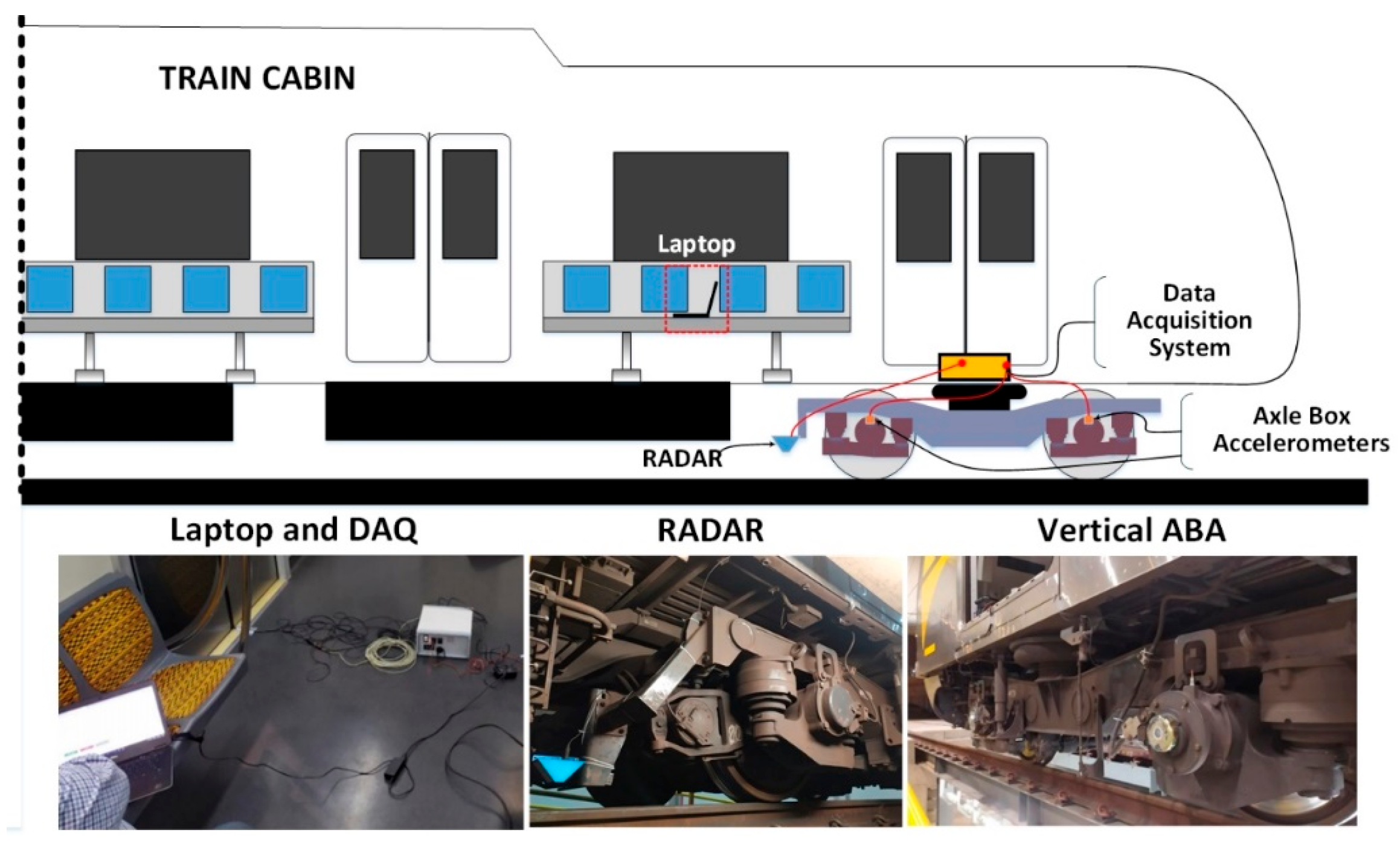


| Variables | Number | Locations | Sensors | Images |
|---|---|---|---|---|
| Vertical Acceleration | 2 | Axle box (one per axle) | Accelerometer ICP 100 mV/g, range ±60 g [KS-76C-100] |  |
| Signal conditioner IEPE [M33] |  | |||
| Low-Pass Filter 10 kHz [M29] | ||||
| Linear Speed | 1 | Bogie frame | RADAR based on Doppler effect [GSS15C] |  |
| Case | Mean Speed [km/h] | fmin [Hz] | fmax [Hz] |
|---|---|---|---|
| 1 | 75 | 203 | 2032 |
| 2 | 60 | 167 | 1667 |
| 3 | 50 | 139 | 1389 |
| 4 | 40 | 111 | 1111 |
| Section | Initial Pk [km] | Final Pk [km] |
|---|---|---|
| S1 | 4.243 | 4.300 |
| S2 | 4.718 | 4.805 |
| S3 | 4.855 | 4.927 |
| S4 | 5.250 | 5.352 |
| S5 | 5.438 | 5.577 |
| S6 | 5.729 | 5.829 |
| Speed | Section 1 | Section 2 | Section 3 | Section 4 | Section 5 | Section 6 |
|---|---|---|---|---|---|---|
| Operation | 809 (26.2) [−29] | 715 (30.1) [−25] | 692 (30.4) [−26] | 727 (29) [−26] | 774 (27.5) [−26] | 844 (25.5) [−29] |
| 60 km/h | 645 (26.1) [−25] | 610 (27.6) [−32] | 598 (28.4) [−37] | 586 (28.6) [−31] | 645 (26.4) [−28] | 692 (24.4) [−26] |
| 50 km/h | 539 (26) [−39] | 481 (29.1) [−38] | 457 (30.7) [−41] | 469 (29.8) [−40] | 516 (27.2) [−34] | 563 (25.1) [−36] |
| 40 km/h | 434 (25.8) [−35] | 387 (29.6) [−34] | 375 (30.8) [−35] | 375 (30.1) [−33] | 410 (27.3) [−37] | 446 (25.4) [−39] |
| Speed | Proposed (IIAPD + EWISI) | De Rosa [30] | Bocciolone [32] |
|---|---|---|---|
| 75 km/h | 6/6 (100%) | 6/6 (100%) | 3/6 (50%) |
| 60 km/h | 5.5/6 (91.66%) | 4/6 (66.6%) | 2/6 (33.3%) |
| 50 km/h | 6/6 (100%) | 4/6 (66.6%) | 3/6 (50%) |
| 40 km/h | 6/6 (100%) | 5/6 (83.3%) | 6/6 (100%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto-Ocampo, C.R.; Cano-Moreno, J.D.; Maroto, J.; Mera, J.M. A Mathematical Methodology for the Detection of Rail Corrugation Based on Acoustic Analysis: Toward Autonomous Operation. Mathematics 2025, 13, 2815. https://doi.org/10.3390/math13172815
Soto-Ocampo CR, Cano-Moreno JD, Maroto J, Mera JM. A Mathematical Methodology for the Detection of Rail Corrugation Based on Acoustic Analysis: Toward Autonomous Operation. Mathematics. 2025; 13(17):2815. https://doi.org/10.3390/math13172815
Chicago/Turabian StyleSoto-Ocampo, César Ricardo, Juan David Cano-Moreno, Joaquín Maroto, and José Manuel Mera. 2025. "A Mathematical Methodology for the Detection of Rail Corrugation Based on Acoustic Analysis: Toward Autonomous Operation" Mathematics 13, no. 17: 2815. https://doi.org/10.3390/math13172815
APA StyleSoto-Ocampo, C. R., Cano-Moreno, J. D., Maroto, J., & Mera, J. M. (2025). A Mathematical Methodology for the Detection of Rail Corrugation Based on Acoustic Analysis: Toward Autonomous Operation. Mathematics, 13(17), 2815. https://doi.org/10.3390/math13172815







