Dynamic Stochastic Game Models for Collaborative Emergency Response in a Two-Tier Disaster Relief System
Abstract
1. Introduction
2. Problem Formulation and Assumptions
2.1. Problem Formulation
2.2. Basic Assumption
- (1)
- The disaster relief system primarily consists of the government and social organizations, where the latter refers to diverse non-governmental groups formed organically by different societal segments to address natural disasters [29].
- (2)
- According to prior studies [30,31], the costs associated with post-disaster relief efforts are generally positively correlated with the intensity of response efforts. In this study, we adopt the quadratic function commonly used in differential game models, i.e.,where represent the total costs incurred by the government and social organizations when carrying out emergency responses. denote their corresponding response efforts, such as the scale of emergency procurement, logistics deployment, or personnel mobilization. and are the marginal cost coefficients: a larger or means that each additional unit of effort requires disproportionately higher spending, reflecting increasing marginal costs. Such cost function not only satisfies the fundamental assumption of increasing marginal costs but also ensures the convexity of the objective function, thereby facilitating the derivation of closed-form equilibrium solutions via the Hamilton–Jacobi–Bellman (HJB) equation.
- (3)
- Emergency resource availability is dynamic and influenced by various uncertain factors such as technological shifts, policy changes, and sudden external shocks. Traditional static or deterministic models often overlook the complexity and volatility of real-time decision making in such environments. To address this issue, we introduce a stochastic differential equation to capture uncertainty in the decision-making process. Specifically, inspired by the classical Nerlove–Arrow goodwill model [32] and its stochastic extensions [24,26,27,28], we describe as a stochastic process, i.e.,where denote the marginal effectiveness of governmental and societal response efforts, respectively. More intuitively, measures how efficiently governmental actions are converted into available resources. Such actions include emergency procurement and the release of national stockpiles. In contrast, reflects the contribution efficiency of societal forces, which may involve public donations, volunteer logistics support, and mobilization of the private sector. The parameter is the natural decay rate of emergency supplies, capturing loss from consumption, spoilage, or expiration. represents the additional depletion rate caused by infrastructure damage such as blocked transportation or destroyed storage facilities. The term represents a standard Brownian motion capturing random environmental disturbances, such as sudden policy changes, extreme weather events, or secondary disasters. And, quantifies the intensity of these stochastic shocks. A larger value of indicates greater volatility in resource availability.Specifically, the diffusion term ensures the non-negativity of , thereby avoiding unrealistic scenarios such as negative emergency supplies. Moreover, it captures the state-dependent nature of uncertainty: when resources are abundant, the complexity of allocation and management increases, leading to higher volatility. Conversely, as , the diffusion term diminishes, and without external input, the system may fall into prolonged stagnation. Such a nonlinear stochastic equation effectively integrates endogenous strategic behavior with exogenous environmental uncertainty and has been widely applied in related studies.
- (4)
- The willingness and ability of organizations to engage in collaboration are fundamentally shaped by their access to resources and operational competencies. Institutions with limited assets or minimal influence often exhibit lower levels of engagement in joint initiatives. Furthermore, the effectiveness of emergency responses is closely tied to both the adequacy of response measures and the availability of necessary emergency resources, i.e.,This linear additive form is chosen to capture the separable and cumulative impacts of each input factor and to facilitate closed-form analytical derivations within the HJB framework. Here, represents the emergency response efficacy function, while and denote the marginal effectiveness of governmental and societal intervention efforts, respectively. The parameter captures the incremental influence of resource accessibility.
- (5)
- Non-governmental groups primarily rely on government funding and donations from the public for their operational finances. The effectiveness of these organizations in responding to disasters influences their overall influence and the amount of donations. Additionally, the emergency response efforts of social organizations can enhance their reputation in the community. Hence, the reputation function D can be constructed asThis formulation reflects the independent and complementary contributions of social effort and resources to the evolution of reputation and also aligns with existing works in cooperative decision making. Where are the marginal impact coefficients of social organizations’ response efforts and resource availability.
3. Preliminary
3.1. Stochastic Foundation
- Consistency under permutations:for any permutation π of ;
- Projective consistency:for all .
3.2. Hamilton–Jacobi–Bellman Equation for the Stochastic Control Problem
4. Centralized Decision Making for Collusive Emergency Response
5. Decentralized Emergency Response Without a Cost-Sharing Contract
6. Decentralized Emergency Response with a Cost-Sharing Contract
7. Comparative Analysis of Equilibrium Results
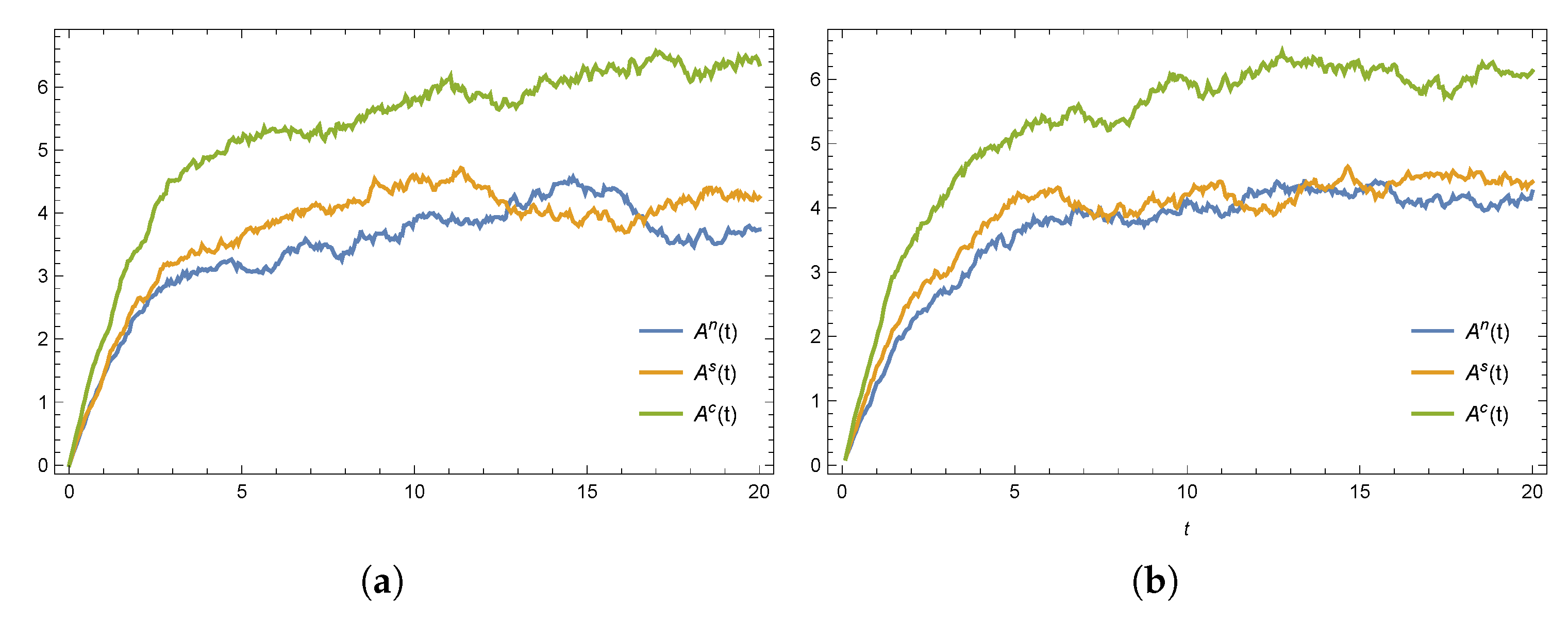
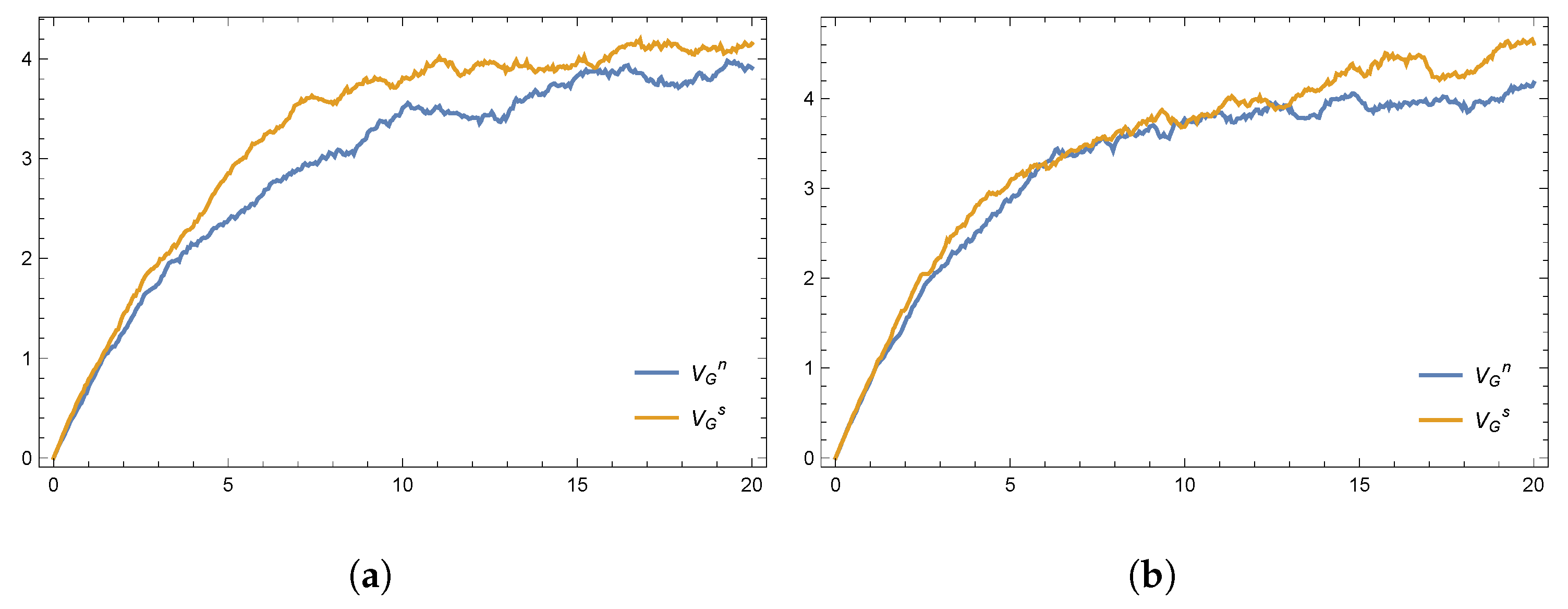
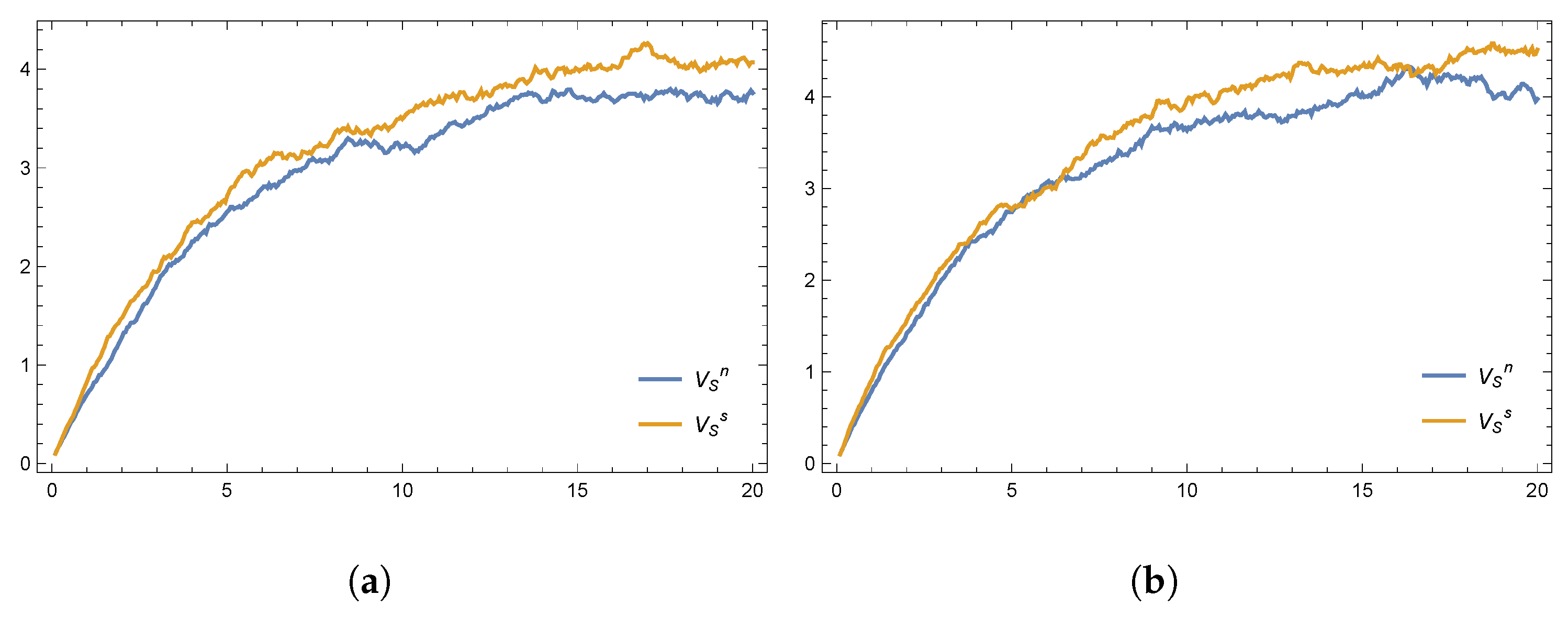
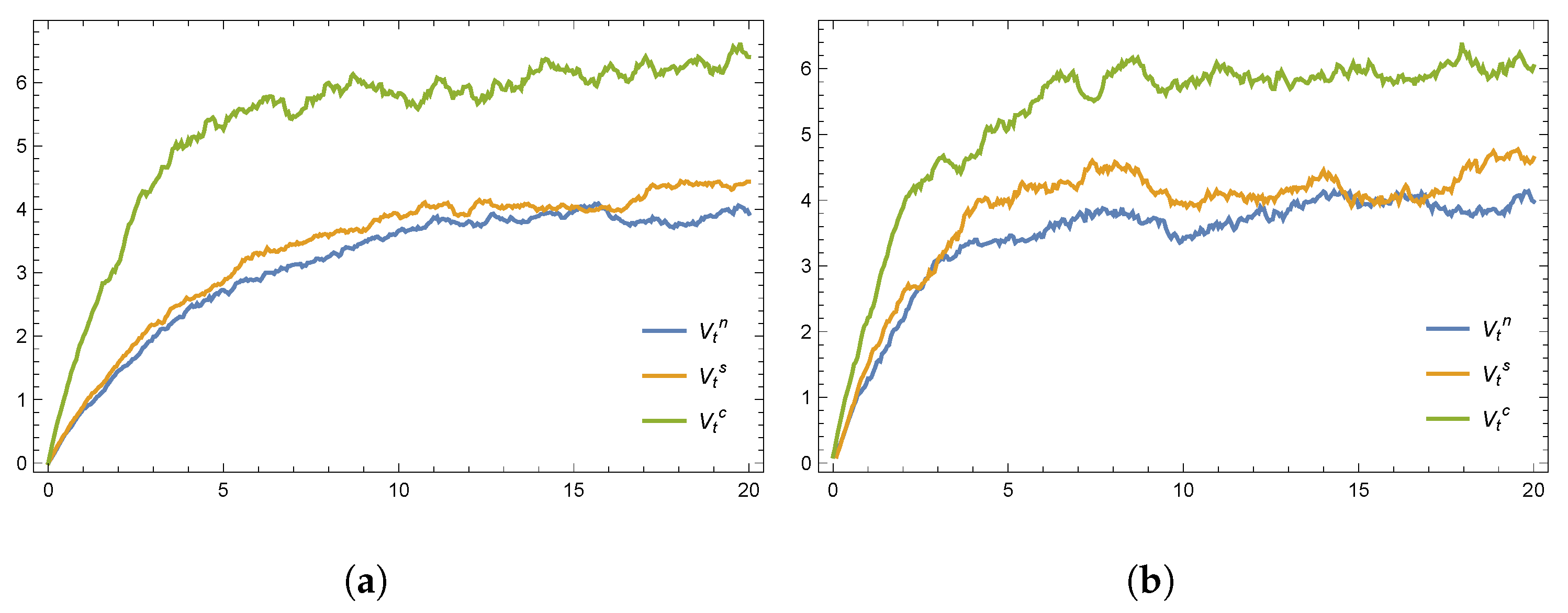
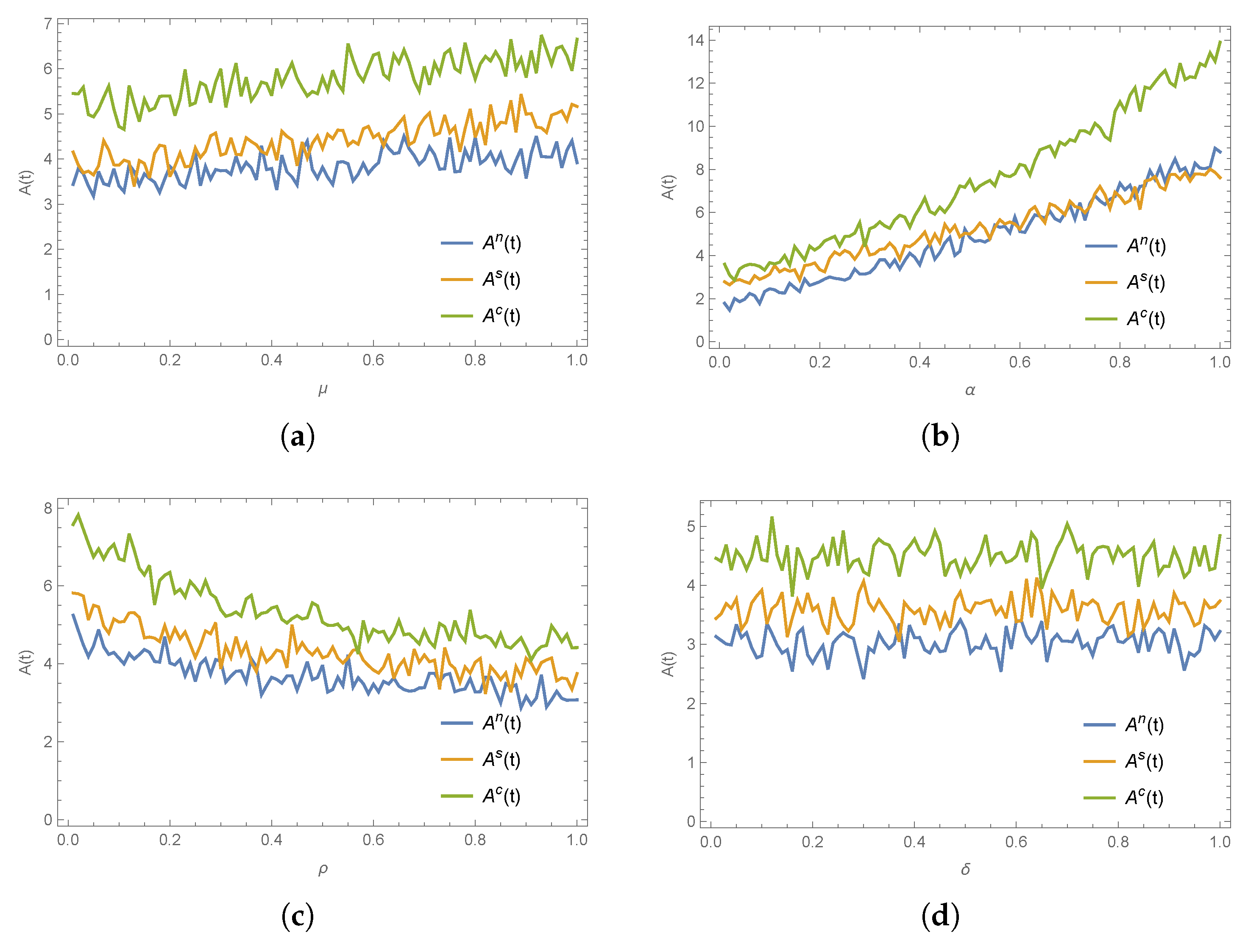
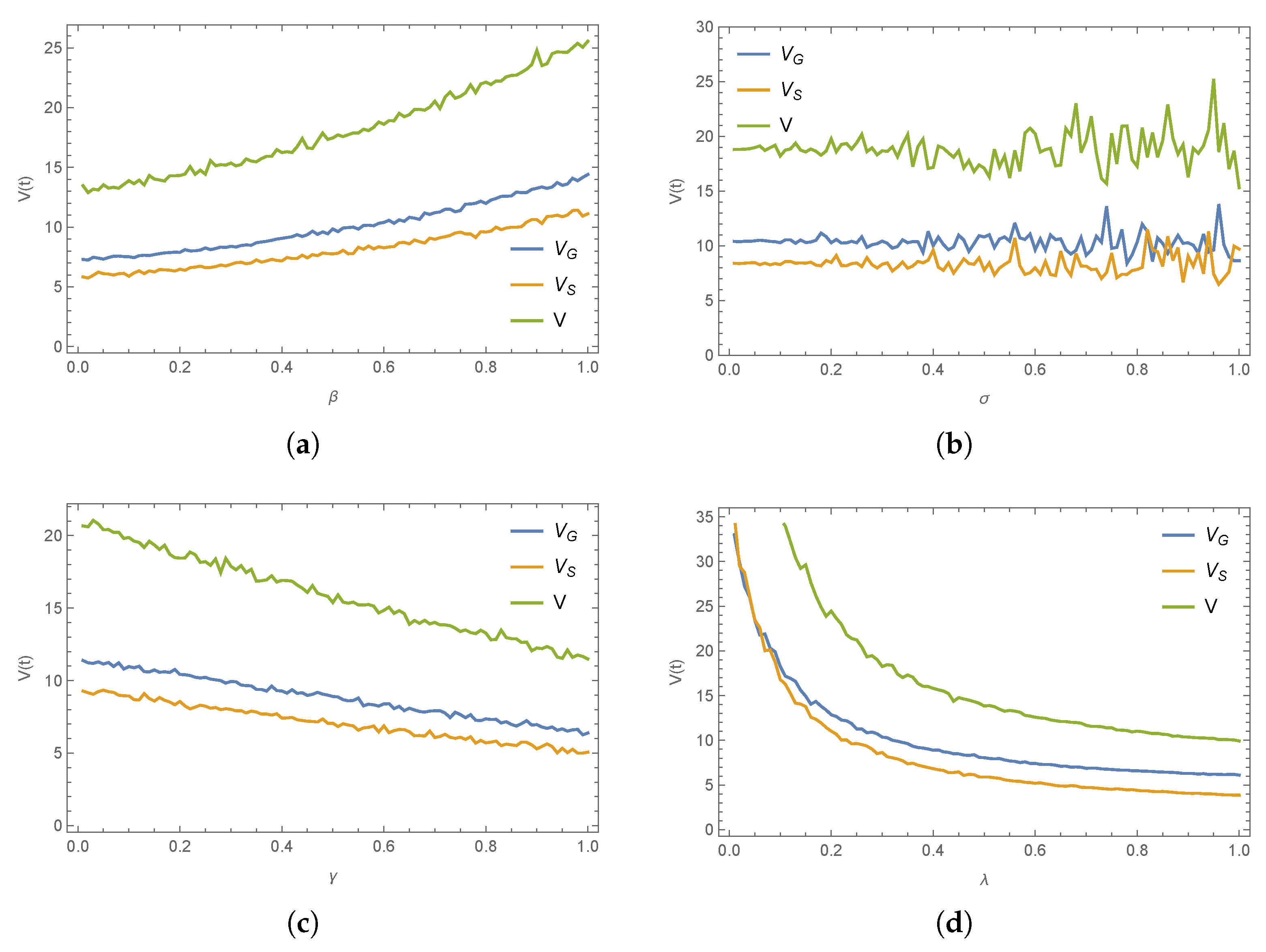
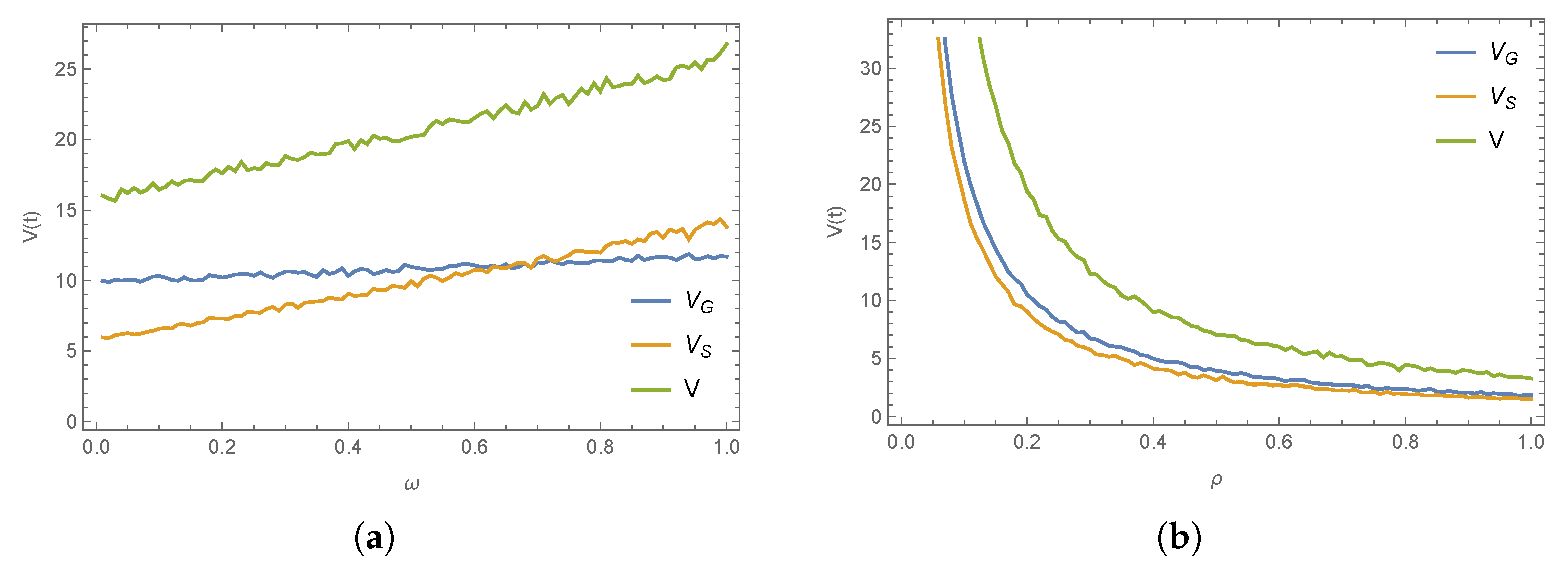
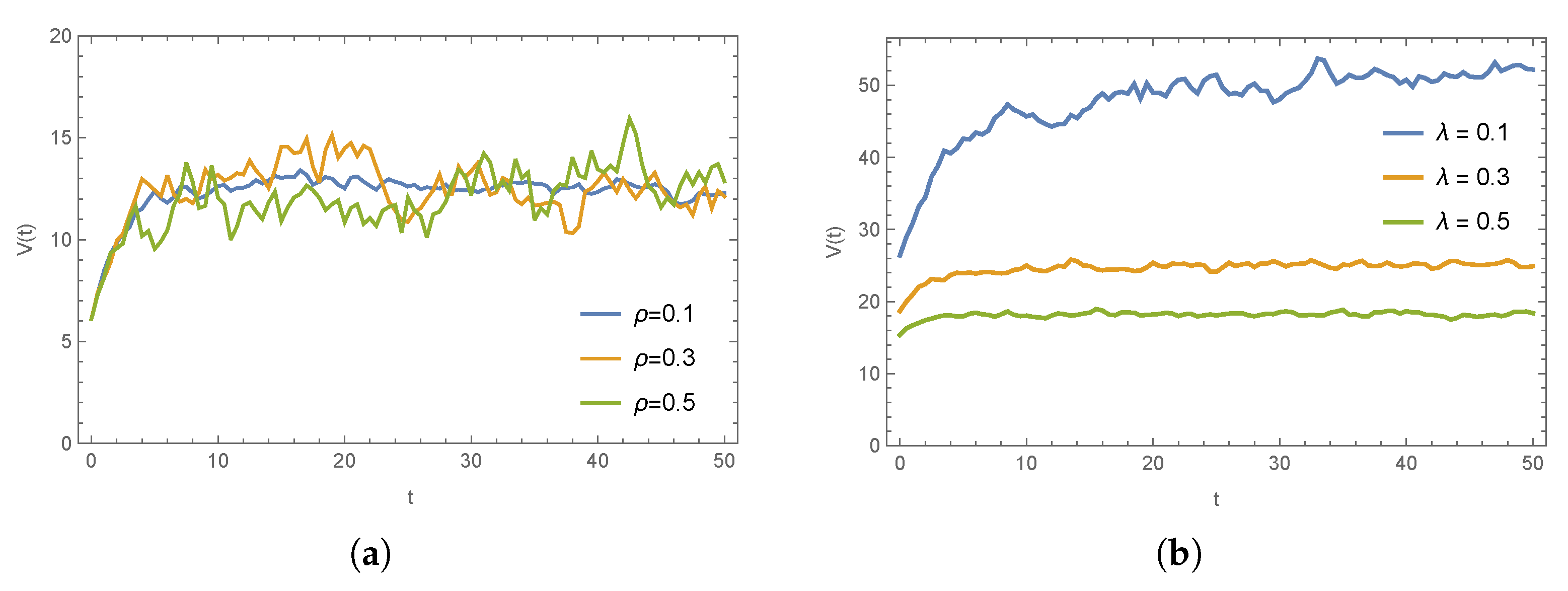
8. Numerical Simulations
9. Conclusions
- (1)
- Across all three scenarios, the collusive decision-making model enables the government and social organizations to achieve the highest emergency response efforts.
- (2)
- Introducing a cost-sharing mechanism into a decentralized game can motivate the other participants to engage more proactively in the establishment of a disaster relief system, achieving a Pareto-efficient outcome.
- (3)
- As all participants work together to enhance emergency supply capacity, the optimal evolution path of emergency resource availability increases over time, eventually stabilizing. Compared to the scenario without cost sharing, a cost-sharing contract yields a higher expected availability but also introduces greater fluctuations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Proposition 1
Appendix A.3. Proof of Theorem 2
Appendix A.4. Proof of Theorem 3
References
- Khan, M.T.I.; Anwar, S.; Sarkodie, S.A.; Yaseen, M.R.; Nadeem, A.M. Do natural disasters affect economic growth? The role of human capital, foreign direct investment, and infrastructure dynamics. Heliyon 2023, 9, e12911. [Google Scholar] [CrossRef]
- Jemli, R. The importance of natural disasters’ governance for macroeconomic performance and countries resilience. Int. J. Disaster Resil. Built. Environ. 2021, 12, 387–399. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Yi, X.; Jia, H.; Zhu, L. The regionalization of urban natural disasters in China. Nat. Hazards 2008, 44, 169–179. [Google Scholar] [CrossRef]
- Wang, D.; Qi, C.; Wang, H. Improving emergency response collaboration and resource allocation by task network mapping and analysis. Saf. Sci. 2014, 70, 9–18. [Google Scholar] [CrossRef]
- Sun, L.; Cao, X.; Alharthi, M.; Zhang, J.; Taghizadeh-Hesary, F.; Mohsin, M. Carbon emission transfer strategies in supply chain with lag time of emission reduction technologies and low-carbon preference of consumers. J. Clean. Prod. 2020, 264, 121664. [Google Scholar] [CrossRef]
- Kang, Y.; Dong, P.; Ju, Y.; Zhang, T. Differential game theoretic analysis of the blockchain technology investment and carbon reduction strategy in digital supply chain with government intervention. Comput. Ind. Eng. 2024, 189, 109953. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, Q.; Liang, L.; Huang, Z. Supply chain coordination through cooperative advertising with reference price effect. Omega-Int. J. Manag. S. 2013, 41, 345–353. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, L. Altruistic mode selection and coordination in a low-carbon closed-loop supply chain under the government’s compound subsidy: A differential game analysis. J. Clean. Prod. 2022, 366, 132863. [Google Scholar] [CrossRef]
- Xiao, L.; Liu, J.; Ge, J. Dynamic game in agriculture and industry cross-sectoral water pollution governance in developing countries. Agric. Water Manag. 2021, 243, 106417. [Google Scholar] [CrossRef]
- Xu, H.; Tan, D. Optimal Abatement Technology Licensing in a Dynamic Transboundary Pollution Game: Fixed Fee Versus Royalty. Comput. Econ. 2023, 61, 905–935. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, J. The progress of emergency response and rescue in China: A comparative analysis of Wenchuan and Lushan earthquakes. Nat. Hazard. 2014, 74, 421–444. [Google Scholar] [CrossRef]
- Zhao, L.; Li, C.; Guo, X. Research of cooperative relief strategy between government and enterprise based on differential game. Syst. Eng. Pract. 2018, 38, 885–899. [Google Scholar]
- Li, B.; Li, H.; Sun, Q.; Lv, R. Optimal control of false information clarification system under major emergencies based on differential game theory. Comput. Intel. Neurosc. 2022, 2022, 7291735. [Google Scholar] [CrossRef]
- Chen, T.; Huang, J. Exploratory research on the system of China relief reserve. Syst. Eng. 2012, 5, 99–106. [Google Scholar] [CrossRef]
- Zhang, M.; Kong, Z. A tripartite evolutionary game model of emergency supplies joint reserve among the government, enterprise and society. Comput. Ind. Eng. 2022, 169, 108132. [Google Scholar] [CrossRef]
- Qiu, Y.; Shi, M.; Zhao, X.; Jing, Y. System dynamics mechanism of cross-regional collaborative dispatch of emergency supplies based on multi-agent game. Complex. Intell. Syst. 2023, 9, 2321–2332. [Google Scholar] [CrossRef]
- Du, L.; Qian, L. The government’s mobilization strategy following a disaster in the Chinese context: An evolutionary game theory analysis. Nat. Hazards 2016, 80, 1411–1424. [Google Scholar] [CrossRef]
- Dutta, P.K. A folk theorem for stochastic games. J. Econ. Theory 1995, 66, 1–32. [Google Scholar] [CrossRef]
- Peter, S.; Ibrahim, B. Intuitive innovation: Unconventional modeling and systems neurology. Mathematics 2023, 11, 1–22. [Google Scholar] [CrossRef]
- Saburov, M. The discrete-time Kolmogorov systems with historic behavior. Mathematics 2023, 11, 3456. [Google Scholar] [CrossRef]
- Fan, Z.; Xu, W.; Zhang, W. Research on digital transformation strategy and subsidy mechanism of manufacturing supply chain based on differential game. AIMS Math. 2023, 8, 23850–23870. [Google Scholar] [CrossRef]
- Li, H.; Xiang, S.; Yang, Y.; Liu, C. Differential evolution particle swarm optimization algorithm based on good point set for computing Nash equilibrium of finite noncooperative game. AIMS Math. 2021, 6, 1309–1323. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, X. Uncertain stochastic hybrid differential game system with V-n jumps: Saddle point equilibrium strategies and application to advertising duopoly game. Chaos Solitons Fractals 2023, 171, 113490. [Google Scholar] [CrossRef]
- Wang, K.; Wu, P.; Zhang, W. Stochastic differential game of joint emission reduction in the supply chain based on CSR and carbon cap-and-trade mechanism. J. Franklin. Inst. 2024, 361, 106719. [Google Scholar] [CrossRef]
- Hashemi, D.H.; Khalilpourazari, S. Stochastic weekly operating room planning with an exponential number of scenarios. Ann. Oper. Res. 2023, 328, 643–664. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, L.; Wang, J.; Wang, C. Payments for environmental services strategy for transboundary air pollution: A stochastic differential game perspective. Sci. Total Environ. 2022, 852, 158286. [Google Scholar] [CrossRef]
- Zou, Y.; He, D.; Sun, R. Research on the Mechanism of Collaborative Innovation in Green Technology among Supply Chain Enterprises Based on Cost Sharing and Market Competition. Sustainability 2024, 16, 6295. [Google Scholar] [CrossRef]
- Sun, R.; He, D.; Yan, J. Dynamic analysis of green technology innovation in products and processes under supply chain competition scenarios—A study based on stochastic differential game model. J. Environ. Manag. 2025, 373, 123545. [Google Scholar] [CrossRef]
- Meding, J.K.V.; Oyedele, L.; Cleland, D.; Spillane, J.; Konanahalli, A. Mapping NGO competency to reduce human vulnerability in post-disaster communities: Comparing strategies in Sri Lanka and Bangladesh. Int. J. Humanit. 2011, 8, 119–138. [Google Scholar] [CrossRef]
- Breton, M.; Zaccour, G.; Zahaf, M. A differential game of joint implementation of environmental projects. Automatica 2005, 41, 1737–1749. [Google Scholar] [CrossRef]
- Hartman, R.; Wheeler, D.; Singh, M. The cost of air pollution abatement. Appl. Econ. 1997, 29, 759–774. [Google Scholar] [CrossRef]
- Nerlove, M.; Arrow, K.J. Optimal advertising policy under dynamic conditions. Economica 1962, 114, 129–142. [Google Scholar] [CrossRef]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Morton, I.K.; Nancy, L.S. Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management; Elsevier: New York, NY, USA, 1981. [Google Scholar]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]

| Variable | Description | |
|---|---|---|
| Decision variable | The response effort of the government | |
| The response effort of social organizations | ||
| State variable | The emergency resource availability | |
| Model parameters | The cost coefficients of the government and social organizations | |
| The cost of the government and social organizations | ||
| The marginal impact of in Equation (1) | ||
| The natural decay rate of emergency supplies | ||
| The marginal impact of infrastructure impairment | ||
| The emergency response efficacy of organizations | ||
| The marginal impact of on | ||
| The incremental influence of A on | ||
| D | The reputation of organizations | |
| The marginal impact of on D | ||
| The marginal impact of A on D | ||
| r | The discount rate | |
| The marginal profit coefficient of the government | ||
| The indirect profit of social organizations |
| V | ||||
|---|---|---|---|---|
| Euler method | ||||
| Milstein method |
| r | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| model n | + | + | ∼ | + | + | + | + | + | - | - | ∼ | ∼ | |
| + | + | ∼ | + | + | + | + | + | - | - | - | - | ||
| + | + | ∼ | + | + | + | + | + | - | - | - | - | ||
| V | + | + | ∼ | + | + | + | + | + | - | - | - | - | |
| model s | + | + | ∼ | + | + | + | ∼ | ∼ | - | - | ∼ | ∼ | |
| + | + | ∼ | + | + | + | + | + | - | - | - | - | ||
| + | + | ∼ | + | + | + | + | + | - | - | - | - | ||
| V | + | + | ∼ | + | + | + | + | + | - | - | - | - | |
| model c | + | + | ∼ | + | + | + | + | + | - | - | ∼ | ∼ | |
| V | + | + | ∼ | + | + | + | + | + | - | ∼ | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Wu, J.; Zhu, M.; Wang, M. Dynamic Stochastic Game Models for Collaborative Emergency Response in a Two-Tier Disaster Relief System. Mathematics 2025, 13, 2780. https://doi.org/10.3390/math13172780
Nie Y, Wu J, Zhu M, Wang M. Dynamic Stochastic Game Models for Collaborative Emergency Response in a Two-Tier Disaster Relief System. Mathematics. 2025; 13(17):2780. https://doi.org/10.3390/math13172780
Chicago/Turabian StyleNie, Yifan, Jingyu Wu, Minting Zhu, and Mancang Wang. 2025. "Dynamic Stochastic Game Models for Collaborative Emergency Response in a Two-Tier Disaster Relief System" Mathematics 13, no. 17: 2780. https://doi.org/10.3390/math13172780
APA StyleNie, Y., Wu, J., Zhu, M., & Wang, M. (2025). Dynamic Stochastic Game Models for Collaborative Emergency Response in a Two-Tier Disaster Relief System. Mathematics, 13(17), 2780. https://doi.org/10.3390/math13172780





