Abstract
Finite-difference methods are widely used to solve partial differential equations in diverse practical applications. Despite their prevalence, the computational efficiency of these methods encounters limitations due to the need to solve linear equation systems through matrix inversion or iterative solver, which is particularly challenging in scenarios involving high dimensions. The demand for numerical methods with high accuracy and fast computational speed is steadily increasing. To address this challenge, we present an efficient and accurate algorithm for high-dimensional numerical modeling. This approach combines a central finite-difference method with the discrete Sine transform (DST) scheme to solve the Poisson equation under Dirichlet boundary conditions (DBCs). To balance numerical accuracy and computation, the DST scheme is applied along one direction in the 2D case and two directions in the 3D case. This strategy effectively reduces problem complexity while maintaining low computational cost. The hybrid DST-accelerated finite-difference approach substantially lowers the computational cost associated with solving the Poisson equation on large grids. Comprehensive numerical experiments for 2D and 3D Poisson equations with DBCs have been conducted. The obtained numerical results demonstrate that the proposed hybrid method not only significantly reduces the computational expenses, but also maintains the central finite-difference accuracy.
Keywords:
Poisson equation; Dirichlet boundary conditions (DBCs); finite-difference method; discrete sine transform (DST) MSC:
65M06
1. Introduction
The Poisson equation is classified as a special type of elliptic partial differential equation (PDE). Numerical solutions of the Poisson equation (or its special case, such as Laplace equation) are crucial for dealing with various mathematical and physical problems. For numerically solving the boundary value problem associated with the Poisson equation, the main methods include the finite-difference method [1,2,3,4,5], finite-volume method [6,7,8,9,10], boundary-element method [11,12,13,14], finite-element method [15,16,17,18,19], spectral method [20,21,22], and spectral-element method [23,24,25,26]. The finite-difference method is widely employed among various numerical methods for approximating solutions to partial differential equations, particularly in the fields of electrostatics, mechanical engineering, and theoretical physics [27]. It is especially favored when dealing with uncomplicated boundary conditions.
The prevalent technique in numerical computations for high-dimensional Poisson equations on uniform boundaries is the finite-difference method, as indicated in contrast to alternative numerical methods [28]. By employing differential operators to approximate partial derivatives within PDE, this method facilitates the computation of numerical solutions for the resulting system [29]. The accuracy of the finite-difference method depends on the ability of a fine grid to approximate the continuous problem, and errors can be arbitrarily minimized by increasing the number of mesh points. Substantial advancements have been well developed in enhancing the efficiency and accuracy of the finite-difference approach for solving Poisson equations in two or three dimensions [30,31]. Although the finite-difference scheme is relatively simple and can achieve high accuracy, it is implicit and typically requires matrix inversion or an iterative solver for the linear system. The computational cost of solving large linear or non-linear systems through the matrix inversion method or an iterative solver is substantial, necessitating the exploration of alternative techniques that can yield solutions more efficiently. Therefore, in order to enhance the efficiency of the finite-difference method, it is essential to avoid matrix inversion or an iterative solver, especially for large-scale linear systems.
Fourier-related transforms play a crucial role in solving PDE problems [32,33,34,35]. Many PDE problems, including Poisson equations with constant coefficient and variable coefficient, can be solved efficiently using Fourier-related transforms. These transforms can be categorized into two types based on time continuity, discreteness, and periodicity: the discrete-time Fourier transform (DFT) and the continuous-time Fourier transform (CFT). The rapid development of digital technology, particularly computer hardware and software, has provided abundant resources for discrete signal processing. Notably, the fast Fourier transform (FFT) stands out as a prevalent tool for computing the DFT, which calculates the discrete-time Fourier series for periodic signals. Fourier-related transforms can be effective for solving the Poisson equation under a range of boundary conditions, such as periodic, Dirichlet, and Neumann boundary conditions [36]. Utilizing the finite difference method enables the derivation of solutions via distinct discrete Fourier transformations (DFTs). For example, the discrete Sine transform (DST) is suitable for addressing Dirichlet boundary conditions (DBCs), while the discrete Cosine transform (DCT) is applicable to Neumann boundary conditions (NBCs) [37]. Previously, these transforms have been utilized to efficiently solve the linear systems resulting from a finite-difference approach in the resolution of the Poisson equation, instead of using matrix inversion techniques or an iterative solver [38].
The DST approach is a highly efficient spectral technique for accelerating the finite difference solution of boundary value problems, especially those with Dirichlet boundary conditions [39,40]. The core idea is that, for a standard second-order finite difference discretization on a uniform grid, the coefficient matrix displays a specific eigenstructure. Importantly, the eigenvectors of this matrix align precisely with the basis functions of the DST. Consequently, applying a forward DST to the right-hand-side vector of the system effectively projects onto the eigenspace of the difference matrix. This paper aims to develop a computationally efficient numerical approach, leveraging the advantages of finite-difference methods, for solving high-dimensional Poisson equations with DBCs, using a DST-accelerated technique. In order to balance the accuracy and efficiency in finite-difference numerical computation, the DST scheme is employed along one direction in the 2D case and two directions in the 3D case, effectively reducing the problem complexity at low cost.
The layout of this paper is structured in the following manner. In Section 2, we provide a comprehensive review of Sine series and the associated DST. Section 3 details the implementation of the hybrid DST-accelerated finite-difference algorithm for high-dimensional Poisson equations with homogeneous DBCs. In Section 4, we present the numerical experiments for Poisson equations in 2D and 3D cases using the proposed hybrid method. Section 5 discusses 2D Poisson equations with non-homogeneous DBCs. In Section 6, the main conclusions are ultimately outlined.
2. Sine Series and the Associated Discrete Sine Transform
This section provides a concise overview of the Sine series and its associated discrete transform. Additional significant findings related to them can be found in Reference [41].
Let be a function defined on [0, L] and satisfying certain conditions:
Within the framework of Fourier series, can be represented as follows:
where is the Sine series coefficient. According to the Formula (2), we have
In the field of mathematics, the DST is a Fourier-related transform that exhibits similarities with the DFT. This transform corresponds to the imaginary components of a DFT of approximately twice the length and effectively handles real data with odd symmetry [42]. The DST technique utilized in this paper corresponds to the first type (I).
The DST-I for a given data sequence , , is defined by
The corresponding inverse DST-I is defined by
3. Hybrid DST-Accelerated Finite-Difference Scheme
This section illustrates the use of a central finite-difference technique for solving the Poisson equation with homogeneous DBCs in 2D and 3D cases. To reduce computational expense, we propose a hybrid DST-accelerated finite-difference approach.
3.1. Two-Dimensional Poisson Equation with Homogeneous DBCs
Firstly, we focus on the application of the hybrid DST-accelerated finite-difference approach to solving the 2D Poisson equation with homogeneous DBCs. Consider the following 2D boundary value problem:
where are constants, denotes a given source function, and represents an unknown solution.
The numerical solution for Equation (6) can be obtained using the five-point finite-difference approach. The computational domain is discretized into and rectangular elements, aligned parallel to the x- and y-axis, respectively, as depicted in Figure 1. The discrete nodes along the x-direction are indexed by , while those on the y-direction are indexed by . The nodal intervals are and . Additionally, and are represented as approximations for and , respectively. For an interior discrete node (i, j) that maintains equal grid spacing along both the x and y axes, the central-difference approach of the Poisson equation in Equation (6) can be written as follows:
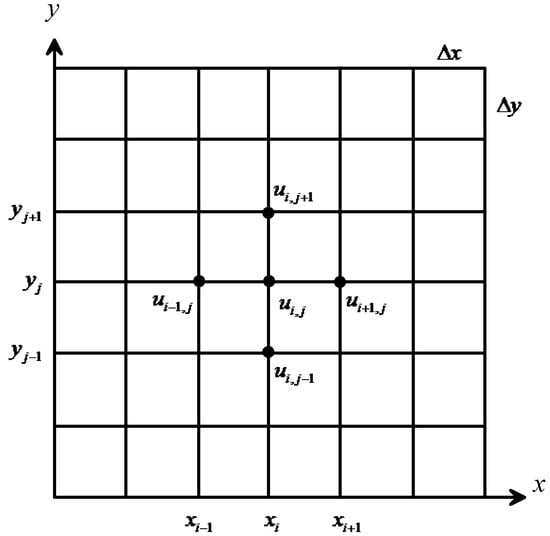
Figure 1.
Uniform rectangular grid stencil (five-point cross) for 2D Poisson equation.
Using the Kronecker tensor product , Equation (7) can be reformulated into the following algebraic equation form:
where and are identity matrix, respectively. with the following forms:
The vector u is the solution of the interior mesh nodes, and the vector f is related to the non-homogeneous term of the Poisson equation:
The direct utilization of Equation (8) to solve the 2D Poisson equation with homogeneous DBCs is a feasible approach. However, the computational cost will increase as the number of discrete rectangular meshes is augmented. In the following, we solely perform DST in the x-direction and solve the above 2D finite-difference discretization with the hybrid DST-accelerated finite-difference approach. We note the one-dimensional DST for the space-domain solution and its corresponding inverse transform for the hybrid wavenumber domain solution . They are defined as follows:
where , and .
At any interior node , applying the one-dimensional DST technique in the x-direction and the second-order central-difference approach, the partial derivative in Equation (6) can be expressed as follows:
Here we define modified wavenumber , then
Applying the one-dimensional DST technique in x-direction, the second-order central-difference approximation of partial derivative in Equation (6) can be expressed as follows:
Meanwhile,
where , and .
Substituting Equations (11)–(13) into Equation (7), and applying the homogeneous DBCs, a linear system for the hybrid space–wavenumber domain is expressed as follows
Solving the linear system in Equation (14), we can obtain the approximate solutions in the hybrid space–wavenumber domain. Furthermore, by applying the 1D inverse DST approach, we obtain the corresponding approximate solutions in the space domain, for all , and in Equation (6).
The procedure of the hybrid DST-accelerated finite-difference solver for the 2D Poisson equation with homogeneous DBCs is summarized in Algorithm 1.
| Algorithm 1 Hybrid DST-accelerated finite-difference solver for 2D Poisson equation with homogeneous DBCs |
| Required: , , , , and . 1: Compute wavenumber . 2: Compute modified wavenumber . 3: Compute with the 1D DST, defined by Equation (13). 4: Solve , defined by Equation (14) 5: Apply the 1D inverse DST on to obtain . |
3.2. Three-Dimensional Poisson Equation with Homogeneous DBCs
This subsection focuses on the application of the hybrid DST-accelerated finite-difference approach to solve the 3D Poisson problem in the case of homogeneous DBCs. Consider the 3D boundary value problem given below:
where represents an unknown solution, , and denotes a given source function.
To solve the boundary value problem (15) using the finite-difference approach, we discretize the 3D computational domain into rectangular meshes defined by the dividing planes , , and . The nodal intervals are , , and , as shown in Figure 2. In addition, and are represented as approximations of and , respectively. At any interior node with uniform meshes in x, y, and z axes, the 3D Poisson equation in Equation (15) is expressed using the central-difference approach as follows:
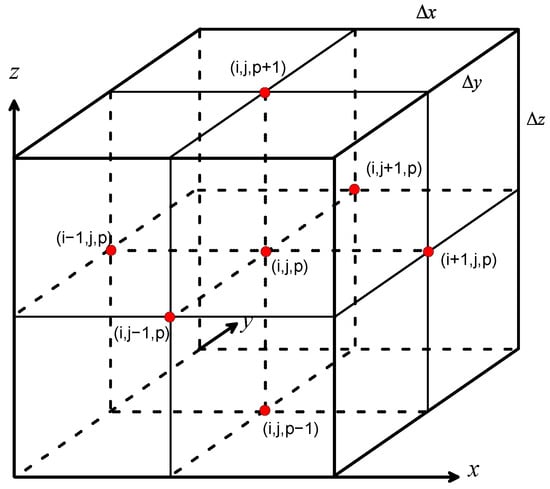
Figure 2.
Three-Dimensional numerical grid stencil (seven-point cross) used for formulating the Poisson equation using the finite-difference approach.
In the following, we perform DST technology in both the x-direction and the y-direction, and solve the aforementioned 3D finite-difference discretization using the hybrid DST-accelerated finite-difference approach. The 2D DST for and its corresponding inverse transform for are defined as
where , , and .
At any interior node (i, j, p), the partial derivative in Equation (15) can be expressed using the second-order central-difference technique as follows:
Here we define , then
At any interior node (i, j, p), the second-order partial derivative in Equation (15) can be expressed as follows:
Then,
where .
Appling 2D DST on the second-order central finite-difference approximation of the partial derivative in Equation (15) can be expressed as follows:
Meanwhile,
where , , and .
Substituting Equations (19)–(22) into Equation (16), we obtain
Applying the homogeneous DBCs, the linear system in the hybrid space–wavenumber domain can be written as
By solving the linear system in Equation (23), we obtain the approximate numerical solutions in the hybrid space–wavenumber domain. Additionally, by applying the 2D inverse DST approach, we obtain the corresponding approximate solutions in the space domain, for all , , and in Equation (15).
The procedure of the hybrid DST-accelerated finite-difference solver for the 3D Poisson equation with homogeneous DBCs is summarized in Algorithm 2.
| Algorithm 2 Hybrid DST-accelerated finite-difference solver for 3D Poisson equation with homogeneous DBCs |
| Required: , , , , , , and . 1: Compute wavenumber and . 2: Compute modified wavenumber and . 3: Compute with the 2D DST, defined by Equation (22). 4: Solve , defined by Equation (23) 5: Apply the 2D inverse DST on to obtain . |
4. Numerical Experiments
To enhance the understanding of how the hybrid DST-accelerated finite-difference solver is applied to solve high-dimensional (2D and 3D) Poisson equations with homogeneous DBCs, we carried out several numerical experiments on accuracy and efficiency in this section. Our numerical simulations were executed on a desktop computer featuring a 12th Gen Intel Core (TM) i7-12700F processor operating at 2.1 GHz with 32 GB DDR RAM.
4.1. Two-Dimensional Example
In this numerical experiment, we solve a 2D Poisson equation with homogeneous DBCs:
The analytical solution for this boundary value problem on the computational domain [0, 2] × [0, 2] is expressed as . Assuming , the numerical solution reveals strong agreement between the hybrid DST-accelerated finite-difference numerical solution and the corresponding analytical solution at all discrete nodes , as illustrated in Figure 3. The maximum absolute error observed of this numerical solution is equal to 0.0032.
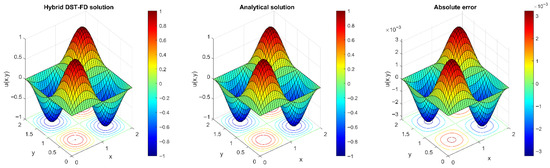
Figure 3.
A comparison of the hybrid DST-accelerated finite-difference approximate solution with the analytical solution in case of the 2D problem with homogeneous DBCs.
Moreover, numerical error statistics for this 2D problem have been conducted, as presented in Table 1. In this table, the computational error is defined using the discrete L2 norm as [43]:
where and represent the approximate numerical solution in 2D and the analytical solution, respectively. Increasing the number of rectangular mesh cells in this numerical experiment leads to a reduction in computational error. This reduction, in turn, enhances the stability of both our proposed hybrid scheme and the traditional finite-difference method. In addition, both our method and the traditional finite-difference method achieve comparable levels of precision. The numerical results indicate that our hybrid DST-accelerated finite-difference solver provides high accuracy in the case of the 2D problem with homogeneous DBCs.

Table 1.
Computational errors of our proposed hybrid solver compared to the traditional central finite-difference scheme for the 2D Poisson equation.
Additionally, we assess the computational time required by our proposed approach in comparison with the conventional central finite-difference method, as presented in Table 2. This table reveals that our hybrid DST-accelerated finite-difference method necessitates significantly less computational time, even when the mesh size is considered. In contrast, the traditional finite-difference method requires additional computational time to solve the 2D Poisson equation. The longer wall-clock time of the traditional finite-difference scheme in Table 2 is from two cumulative costs: (1) Large-scale assembly cost: The finite-difference method forms the discrete operator and right-hand side through nested loops over the grid to apply stencils, enforce boundary conditions, and update coefficients. This loop-based assembly to build the large sparse linear system is nontrivial and scales with the number of degrees of freedom. (2) Large-scale solve cost: Once assembled, the large sparse system must be solved using either a direct approach or an iterative solver. As the mesh is refined, both the assembly time (more grid points) and the solve time increase sharply.

Table 2.
Comparison of the computational time between our proposed hybrid solver and the traditional central finite-difference technique for the 2D problem.
4.2. Three-Dimensional Example
In this numerical experiment, we examine a 3D Poisson equation with homogeneous DBCs, defined as follows:
The analytical solution for this boundary value problem on the computational domain [0, 2] × [0, 2] × [0, 2] is given by . Assuming , the numerical computation is shown in Figure 4. We find that both the hybrid DST-accelerated finite-difference approximate numerical solutions and exact analytical solutions at all discrete nodes agree very well. The maximum absolute error is 0.0021.
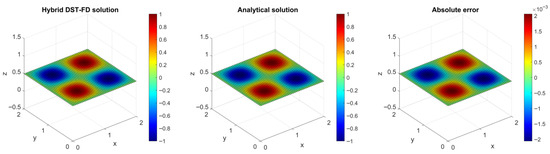
Figure 4.
Comparison of the hybrid DST-accelerated finite-difference approximate solution with the analytical solution in the case of the 3D problem featuring homogeneous DBCs on the face at z = 0.5.
In addition, a numerical error analysis has been conducted, as depicted in Table 3. In this table, the computational error is defined according to the discrete L2 norm as [44,45]:
where and represent the 3D numerical and analytical solutions, respectively. In this numerical experiment, consistent with previous findings, an increase in the number of rectangular meshes leads to a reduction in the computational error, thereby confirming the stability of both our proposed hybrid solver and the traditional central finite-difference method. Our approach, alongside the conventional finite-difference method, demonstrates equal numerical precision. These findings suggest that our hybrid DST-accelerated finite-difference solver ensures high precision when tackling the 3D Poisson equation under homogeneous DBCs.

Table 3.
Computational error of our proposed hybrid solver and the traditional central finite-difference approach for 3D Poisson equation.
The computational time of our proposed solver is further compared with that of the traditional central finite-difference scheme, as shown in Table 4. The table demonstrates that our hybrid DST-accelerated finite-difference solver exhibits a significantly reduced computational time requirement, particularly when the mesh size . The traditional central finite-difference method, however, requires a longer computational time to solve this 3D Poisson equation.

Table 4.
Comparison of computational efficiency between the proposed hybrid solver and the traditional central finite-difference approach in the case of the 3D problem.
5. Discussion
The numerical experiments described above used the hybrid DST-accelerated finite-difference technique to solve the Poisson equations, which is subject to homogeneous DBCs. In order to address problems with non-homogeneous DBCs, Wang et al. [38] utilized a variable transformation method to transform the specified non-homogeneous DBCs into a homogeneous form. However, the efficacy of this approach diminishes when an analytical solution is non-existent or difficult to attain. The subsequent discussion focuses on an efficient approach to handling non-homogeneous DBCs, with specific emphasis on the 2D Poisson equation as an illustrative example.
5.1. Non-Homogeneous DBCs in Non-DST Direction
If the non-homogeneous boundary is not in the DST direction, we only need to implement the DST on the non-homogeneous boundary, and Equation (14) should be modified with the imposed boundary conditions. By solving the corresponding linear system of Equation (14), we obtain the approximate solutions in the hybrid space–wavenumber domain.
For the purpose of a numerical example discussion, the non-homogeneous DBCs in the y-direction are considered as follows:
The analytical solution for this problem on the region [0, 1] × [0, 2] is . The Poisson equation in the x-direction is solved using the DST, and the DST is applied to the non-homogeneous boundaries. The 2D finite-difference discretization problem is then solved using the hybrid DST-accelerated finite-difference solver. Assuming , the numerical results are presented in Figure 5. We observe strong alignment between the hybrid DST-accelerated finite-difference approximate solutions and the related exact solutions at all discrete nodes . The maximum absolute error observed of this numerical solution is equal to 0.0027.
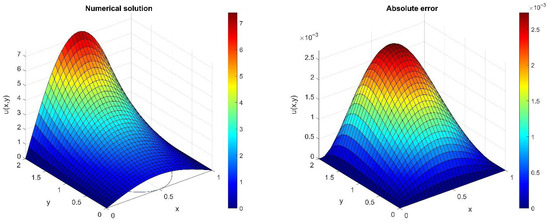
Figure 5.
Numerical solution and absolute error for the 2D Poisson equation under non-homogeneous DBCs in y-direction.
5.2. Non-Homogeneous DBCs in DST Direction
If the non-homogeneous boundary lies in the DST direction, we should revise the non-homogeneous term of the Poisson equation based on the non-homogeneous boundaries. As a numerical example discussion, we consider the non-homogeneous DBCs in the x-direction, defined as follows:
The analytical solution for this problem on the computational domain [0, 2] × [0, 1] is given by . The non-homogeneous DBCs can be implemented as
and
Assuming , the numerical results are shown in Figure 6, which reveal a high level of agreement between the hybrid DST-accelerated finite-difference approximate solutions and the associated exact solutions at all discrete nodes . The maximum absolute error observed of numerical solution is 0.0027.
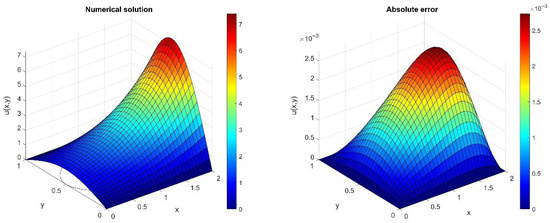
Figure 6.
Numerical solution and absolute error for the 2D non-homogeneous DBCs problem in x-direction.
Statistics of computational time and numerical error for the Poisson equation with non-homogeneous DBCs are represented in Table 5. As the number of rectangular mesh cells increases, the computational error decreases, which in turn enhances the stability of both the proposed hybrid scheme and the conventional finite-difference method. Both approaches achieve comparable accuracy. The results indicate that our hybrid DST-accelerated finite-difference solver attains high accuracy for the 2D problem with non-homogeneous DBCs, while requiring substantially less computational time—even on fine meshes—whereas the conventional finite-difference method incurs noticeably higher computational costs for the 2D Poisson equation with non-homogeneous DBCs.

Table 5.
Comparison of computational time and error between the proposed hybrid solver and the traditional finite-difference scheme for the 2D problem with non-homogeneous DBCs.
6. Conclusions
The present study proposes and implements a novel numerical scheme, namely the hybrid DST-accelerated finite-difference method, to address the limitations of the conventional central finite-difference approximation in solving high-dimensional Poisson equations. This approach aims to strike a balance between accuracy and computational efficiency. The hybrid DST-accelerated finite-difference approach, in comparison to the traditional finite-difference method, incorporates DST technology to independently convert 3D finite-difference problems into one-dimensional problems along the vertical direction. Despite requiring an additional inverse DST during the reduction of the research problem’s dimensionality, the proposed method can avoid the challenges associated with large-scale matrix inversion. The effectiveness and accuracy of the hybrid DST-accelerated finite-difference solver are illustrated by solving 2D and 3D Poisson problems with homogeneous DBCs. Results from numerical experiments indicate that this approach can significantly reduce computational cost while delivering highly accurate approximate solutions, with absolute errors on the order of 1 × 10−3, aligning closely with the exact analytical results.
The hybrid DST-accelerated finite-difference algorithm described in this paper primarily addresses high-dimensional Poisson equations with homogeneous DBCs. However, we demonstrate that the numerical method can also effectively tackle Poisson equations with non-homogeneous DBCs through appropriate treatment. Furthermore, our efficient solver can be readily adapted to address the associated discretized problems. This capability is especially beneficial for central finite-difference schemes employed in the discretization of PDEs, including the acoustic wave and heat conduction equations, where solving Poisson-type equations becomes necessary.
Author Contributions
Conceptualization, J.P. and X.T.; formal analysis, X.T.; funding acquisition, X.T.; methodology, J.P. and X.T.; project administration, J.P.; visualization, X.T.; supervision, J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was supported by the National Key R&D Program of China (Grant No. 2023YFF0718000).
Data Availability Statement
Data associated with this research are available and can be obtained by contacting the corresponding author.
Acknowledgments
The authors would like to thank Ya Sun, who modified this manuscript to improve the English writing quality and gave helpful discussions about the results of the models. We would also like to thank the editors and the reviewers for providing comments that substantially improved the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feng, Q.; Han, B.; Minev, P. Sixth order compact finite differences schemes for Poisson interface problems with singular sources. Comput. Math. Appl. 2021, 99, 2–25. [Google Scholar] [CrossRef]
- Abide, S. Finite difference preconditioning for compact scheme discretizations of the Poisson equation with variable coefficients. J. Comput. Appl. Math. 2020, 379, 112872. [Google Scholar] [CrossRef]
- Raeli, A.; Bergmann, M.; Iollo, A. A finite-difference method for the variable coefficient Poisson equation on hierarchical Cartesian meshes. J. Comput. Phys. 2018, 355, 59–77. [Google Scholar] [CrossRef]
- Mohanty, R.K.; Niranjan. A class of new implicit compact sixth-order approximations for Poisson equations and the estimates of normal derivatives in multi-dimensions. Results Appl. Math. 2024, 22, 100454. [Google Scholar] [CrossRef]
- Jomaa, Z.; Macaskill, C. The Shortley-Weller embedded finite-difference method for the 3D Poisson equation with mixed boundary conditions. J. Comput. Phys. 2010, 229, 3675–3690. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Bartoszek, K. Convergence of finite volume scheme for a three-dimensional Poisson equation. J. Math. Sci. 2014, 202, 130–153. [Google Scholar] [CrossRef]
- Bonnafont, T.; Bessieres, D.; Paillol, J. A finite volume method to solve the Poisson equation with jump conditions and surface charges: Application to electroporation. J. Comput. Phys. 2024, 504, 112862. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids. Geophysics 2013, 78, 69–80. [Google Scholar] [CrossRef]
- Yu, C.; Wang, Y.; Li, Y. The finite volume element methods for Poisson equation based on Adini’s element. Appl. Math. Comput. 2013, 219, 5537–5549. [Google Scholar] [CrossRef]
- Zapata, M.U.; Bang, D.P.V.; Nguyen, K.D. An unstructured finite volume technique for the 3D Poisson equation on arbitrary geometry using a σ-coordinate system. Int. J. Numer. Methods Fluids 2014, 76, 611–631. [Google Scholar] [CrossRef]
- Yu, B.; Jing, R. SCTBEM: A scaled coordinate transformation boundary element method with 99-line MATLAB code for solving Poisson’s equation. Comput. Phys. Commun. 2024, 300, 109185. [Google Scholar] [CrossRef]
- Dargush, G.F.; Banerjee, P.K. A boundary element method for axisymmetric soil consolidation. Int. J. Solids Struct. 1991, 28, 897–915. [Google Scholar] [CrossRef]
- Ramos, V.E.S.; Loeffler, C.F.; Mansur, W.J. A boundary element method recursive procedure applied to Poisson’s problems. Eng. Anal. Bound. Elem. 2017, 82, 104–110. [Google Scholar] [CrossRef]
- Desiderio, L.; Falletta, S.; Ferrari, M.; Scuderi, L. CVEM-BEM coupling with decoupled orders for 2D exterior Poisson problems. J. Sci. Comput. 2022, 92, 96. [Google Scholar] [CrossRef]
- Solin, P. Partial Differential Equations and the Finite Element Method; Blackwell Science Publishing: Oxford, UK, 2006. [Google Scholar]
- Pande, S.; Papadopoulos, P.; Babuska, I. A cut-cell finite element method for Poisson’s equation on arbitrary planar domains. Comput. Methods Appl. Mech. Eng. 2021, 383, 113875. [Google Scholar] [CrossRef]
- Guan, Q. Weak Galerkin finite element method for Poisson’s equation on polytopal meshes with small edges or faces. J. Comput. Appl. Math. 2020, 368, 112584. [Google Scholar] [CrossRef]
- Goona, N.K.; Parne, S.R. Distributed source scheme for Poisson equation using finite element method. J. Comput. Sci. 2023, 72, 102103. [Google Scholar] [CrossRef]
- Romao, E.C.; Campos, M.D.; Moura, L.F.M. Application of the Galerkin and least-squares finite element methods in the solution of 3D Poisson and Helmholtz equations. Comput. Math. Appl. 2011, 62, 4288–4299. [Google Scholar] [CrossRef][Green Version]
- Shen, J.; Tang, T. Spectral and High-Order Methods with Applications; Science Press: Beijing, China, 2006. [Google Scholar]
- Boyd, J.P.; Yu, F. Comparing seven spectral methods for interpolation and for solving the Poisson equation in a disk: Zernike polynomials, Logan–Shepp ridge polynomials, Chebyshev–Fourier Series, cylindrical Robert functions, Bessel–Fourier expansions, square-to-disk conformal mapping and radial basis functions. J. Comput. Phys. 2011, 230, 1408–1438. [Google Scholar] [CrossRef]
- Kong, W.; Wu, X. Chebyshev tau matrix method for Poisson-type equations in irregular domain. J. Comput. Appl. Math. 2009, 228, 158–167. [Google Scholar] [CrossRef][Green Version]
- Pan, J.; Li, H. A penalized weak Galerkin spectral element method for second order elliptic equations. J. Comput. Appl. Math. 2021, 386, 113228. [Google Scholar] [CrossRef]
- Caforio, F.; Imperiale, S. A high-order spectral element fast Fourier transform for the Poisson equation. SIAM J. Sci. Comput. 2019, 41, 2747–2771. [Google Scholar] [CrossRef]
- Gharti, H.N.; Tromp, J.; Zampini, S. Spectral-infinite-element simulations of gravity anomalies. Geophys. J. Int. 2018, 215, 1098–1117. [Google Scholar] [CrossRef]
- Tong, X.; Sun, Y. Spectral-element simulations of gravity anomalies for 3-D topography model. IEEE Geosci. Remote Sens. Lett. 2024, 21, 7503705. [Google Scholar] [CrossRef]
- Qu, W.; Gu, Y.; Fan, C.M. A stable numerical framework for long-time dynamic crack analysis. Int. J. Solids Struct. 2024, 293, 112768. [Google Scholar] [CrossRef]
- Goona, N.K.; Parne, S.R.; Sashidhar, S. Distributed source scheme to solve the classical form of Poisson equation using 3-D finite-difference method for improved accuracy and unrestricted source position. Math. Comput. Simul. 2021, 190, 965–975. [Google Scholar] [CrossRef]
- Zapata, M.U.; Balam, R.I. High-order implicit finite difference schemes for two-dimensional Poisson equation. Appl. Math. Comput. 2017, 309, 222–244. [Google Scholar] [CrossRef]
- Feng, X.; He, R.; Chen, Z. H1-superconvergence of finite difference method based on Q1-element on quasi-uniform mesh for the 3D Poisson equation. Numer. Methods Partial Differ. Equ. 2020, 36, 29–48. [Google Scholar] [CrossRef]
- Reimer, A.S.; Cheviakov, A.F. A Matlab-based finite-difference solver for the Poisson problem with mixed Dirichlet-Neumann boundary conditions. Comput. Phys. Commun. 2013, 184, 783–798. [Google Scholar] [CrossRef]
- Jodra, J.L.; Gurrutxaga, I.; Muguerza, J.; Yera, A. Solving Poisson’s equation using FFT in a GPU cluster. J. Parallel Distrib. Comput. 2017, 102, 28–36. [Google Scholar] [CrossRef]
- Schumann, U.; Sweet, R.A. Fast Fourier transforms for direct solution of Poisson’s equation with staggered boundary conditions. J. Comput. Phys. 1988, 75, 123–137. [Google Scholar] [CrossRef]
- Ren, Y.; Feng, H.; Zhao, S. A FFT accelerated high order finite difference method for elliptic boundary value problems over irregular domains. J. Comput. Phys. 2022, 448, 110762. [Google Scholar] [CrossRef]
- Feng, H.; Zhao, S. FFT-based high order central difference schemes for three-dimensional Poisson’s equation with various types of boundary conditions. J. Comput. Phys. 2020, 410, 109391. [Google Scholar] [CrossRef]
- Costa, P. A FFT-accelerated multi-block finite-difference solver for massively parallel simulations of incompressible flows. Comput. Phys. Commun. 2022, 271, 108194. [Google Scholar] [CrossRef]
- Galbert, L. FFT-based simulations of heterogeneous conducting materials with combined non-uniform Neumann, periodic and Dirichlet boundary conditions. Eur. J. Mech. -A/Solids 2024, 105, 105248. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Ma, X.; Qiu, J.; Liang, Y. An efficient implementation of fourth-order compact finite difference scheme for Poisson equation with Dirichlet boundary conditions. Comput. Math. Appl. 2016, 71, 1843–1860. [Google Scholar] [CrossRef]
- Gatiso, A.H.; Belachew, M.T.; Wolle, G.A. Sixth-order compact finite difference scheme with discrete sine transform for solving Poisson equations with Dirichlet boundary conditions. Results Appl. Math. 2021, 10, 100148. [Google Scholar] [CrossRef]
- Tong, C.; Tong, X.; Wei, K. An efficient accelerating algorithm for 3D gravity anomalies forward modeling using discrete sine transform. J. Appl. Geophys. 2025, 241, 105831. [Google Scholar] [CrossRef]
- Morin, L.; Paxus, J. A fast numerical method for the conductivity of heterogeneous media with Dirichlet boundary conditions based on discrete sine-cosine transforms. Comput. Methods Appl. Mech. Eng. 2024, 421, 116772. [Google Scholar] [CrossRef]
- Britani, V.; Yip, P.C.; Rao, K.R. Discrete Cosine and Sine Transforms: General Properties, Fast Algorithm and Integer Approximations; Academic Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wang, X.; Zhao, D.; Liu, J.; Zhang, Q. Efficient 2D modelling of magnetic anomalies using NUFFT in the Fourier domain. Pure Appl. Geophys. 2022, 179, 2311–2325. [Google Scholar] [CrossRef]
- Wu, L. Efficient modelling of gravity effects due to topographic masses using the Gauss-FFT method. Geophys. J. Int. 2016, 205, 160–178. [Google Scholar] [CrossRef]
- Pan, K.; Zhang, Z.; Hu, S.; Ren, Z.; Guo, R.; Tang, J. Three-dimensional forward modelling of gravity field vector and its gradient tensor using the compact difference schemes. Geophys. J. Int. 2021, 224, 1272–1286. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).