1. Introduction
Regular Bessel functions
usually appear in important applications in Physics, Electrodynamics, and Engineering [
1,
2,
3,
4,
5,
6,
7], including works that employ
to obtain magnetic fields [
8], as well as others where both
and
functions arise; for example, in the modeling of antenna structures [
9] and in thermal phenomena of superconducting wires [
10]. Their power series and asymptotic expansions are well known [
11], and the calculation for small values of the variable
x is straightforward. However, the power series converges slowly when
x increases, requiring a large number of terms to achieve an acceptable accuracy. On the other hand, the asymptotic expansions are only valid for sufficiently large
x, and they lose precision in intermediate ranges. As a result, obtaining reliable numerical values of
for the values commonly needed in applications is not trivial, and motivates the search for alternative representations and efficient approximation schemes.
In this work, an analytical approximation for the aforementioned functions is presented, valid for any value of the variable
x and for orders
within the range
. The technique we used is an extension of the Multipoint Quasirational Approximation (MPQA) method, which has been the subject of several previous works [
12,
13,
14,
15,
16]. In this case, the accuracy of the approximation is exact for
,
, and
. Furthermore, the precision remains high for most values of the order
within the interval considered.
In the present method, both power series and asymptotic expansions are employed, and rational functions are combined with other elementary functions. This distinguishes the present technique from the Padé approximation, as the rational functions must be combined with other elementary functions due to the use of asymptotic expansions. Consequently, the usual issues associated with Padé approximations [
17,
18] as the so-called defects (a zero in the denominator with another zero nearby in the numerator) have been avoided in the present work. This paper is organized as follows: theoretical analysis is presented in
Section 2, and the results are presented in
Section 3. Finally, the last section will be devoted to the conclusions.
2. Theoretical Analysis
The power series of the Regular Bessel functions [
11] are given by
which can also be written as follows:
where
, with
the rising factorial (Pochhammer symbol). Thus, we can express
,
The corresponding asymptotic expansions of these functions are expressed as follows [
11]:
where
To simplify the notation, the following constants and variables are introduced as follows:
where
is the integer part of
. Additionally, it is well-known that
The bridge approximation function, which connects the power and asymptotic expansions, is constructed as follows:
To explain the derivation of this structure, the following points are highlighted:
- 1.
From the power series, it is evident that the approximation must include only the even powers of the variable x, in order to preserve the symmetry.
- 2.
The asymptotic behavior indicates that the approximation should incorporate and combined with . This is achieved because the power term is compensated for by , and the factor simplifies with , resulting in the required . For , the additional power of x is taken into account for the numerator function, to preserve symmetry.
- 3.
From the power series, it is known that is multiplied by even power series. This property is also presented in the approximate function .
- 4.
The approximation must reproduce the exact forms of and when the parameters are appropriately determined. To ensure this, the term involving , must reduce to unity, as happens because and .
The next step involves determining the parameters , , , , , and using the power series and asymptotic expansions. It is worth noting that to avoid complications, the parameters are determined through linear equations, bypassing the challenges of nonlinear relationships. This is achieved by first multiplying the power series of by , and then equating terms.
From the above, six linear equations are obtained for the parameters
,
,
,
,
, and
. Consequently, there are six parameters and six equations. Thus, it is possible to determine all
and to compute the maximum absolute errors as follows:
Relative errors cannot be computed for the entire range of
x in this case, since the functions
have zeros. However, we present an example of its behavior in
Appendix B.
In this work, four equations are obtained from the power series and two from the asymptotic expansions. The expansions used for the power series are
which are combined with the additional power series
In this way, the following four equations for the parameters are obtained:
Two additional equations are obtained from the asymptotical expansions [details are given in
Appendix A].
In this way six equations are obtained for the six parameters , , , , , and .
3. Results
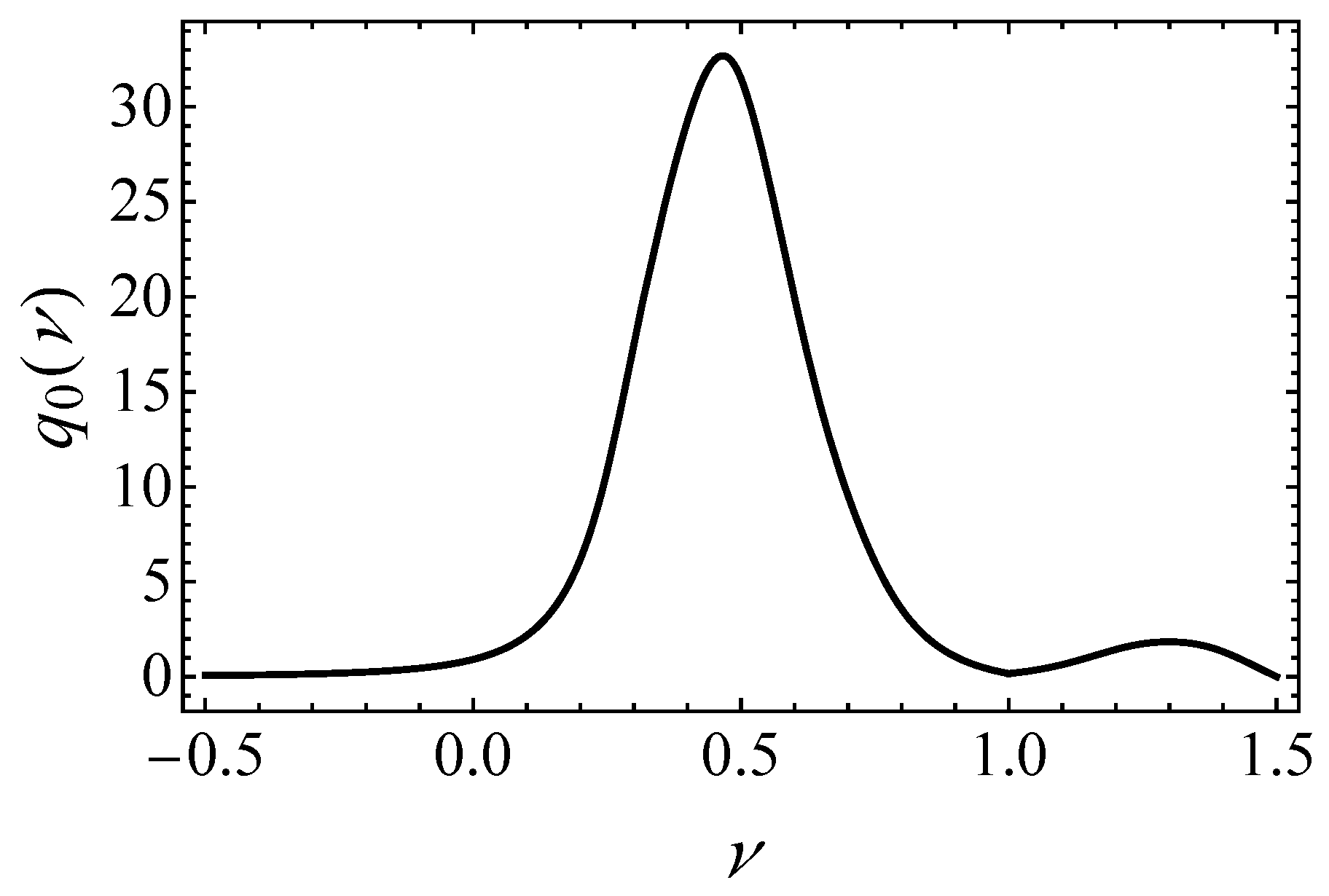
From the previous equations all the parameters are determined. The first parameter to determine is
, obtaining
where
and
An important point about this parameter is that it must be positive to avoid zeros in the denominator, i.e., the so-called
defects in the Padé treatments. This condition is verified in
Figure 1 for
in the interval (−1/2, 3/2), but later
becomes negative and the approximation is no longer useful. This is the reason why the present work is restricted to the mentioned interval.
The results for the other parameters are given by the following equations:
Finally,
and
have already been given in Equations (
25) and (
26), written here as follows:
For some particular values of
, the parameters are calculated and given in
Table 1.
Now it is clear how each approximate function is determined for each
, and how to compare it with the exact one. The point is to find the approximate function for the values
,
, and
. It is clear that
,
, and then the complete result is as follows:
That is, the result is exact.
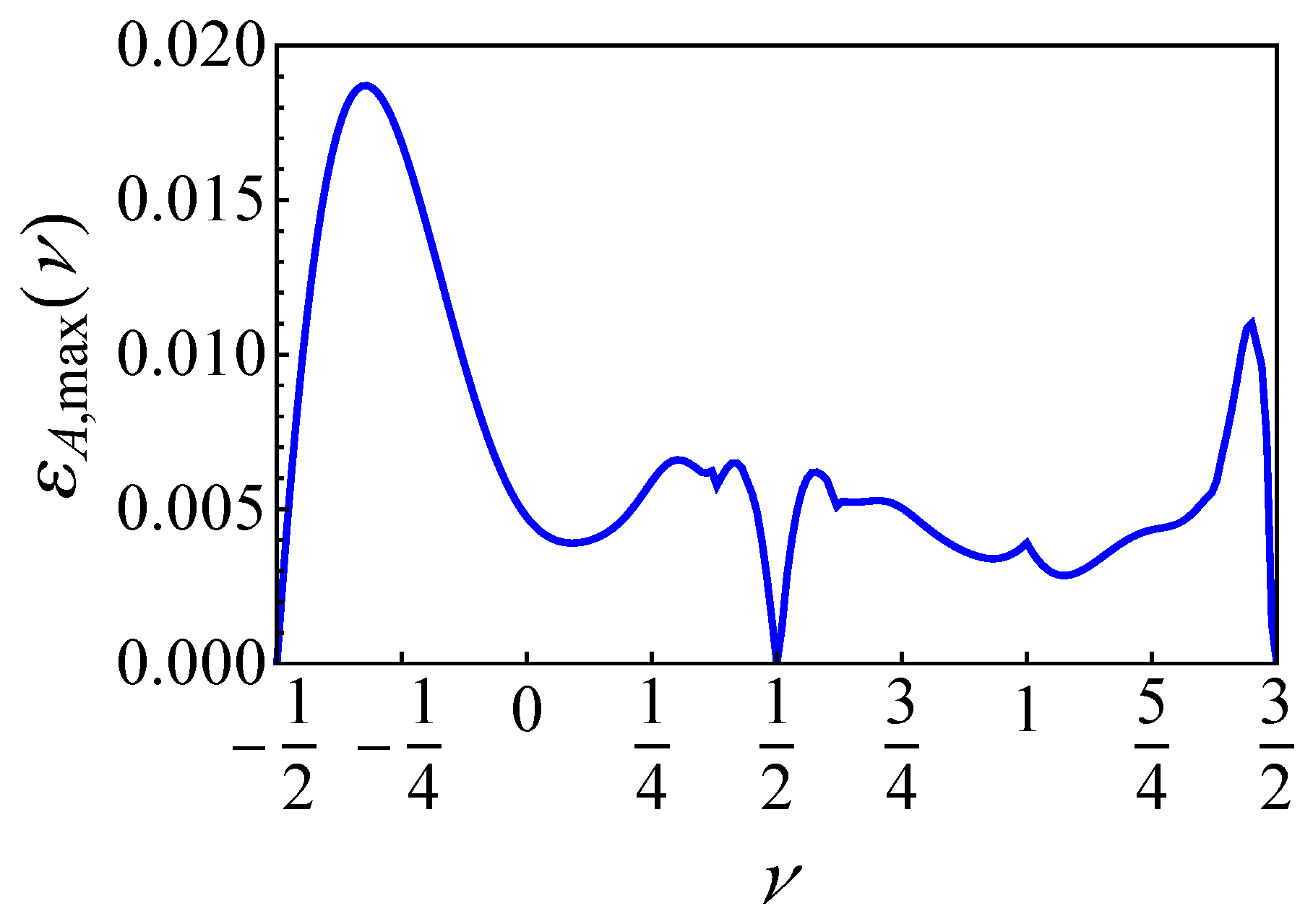
Another important point is to determine the maximum absolute error for each
(the maximum relative errors are always infinity, as was explained in the
Section 2). The maximum absolute errors are well defined for
. A plot of the maximum absolute errors is shown in
Figure 2. From the latter, it is observed that the maximum difference between the exact and approximated function is less than 0.02 in the entire interval.
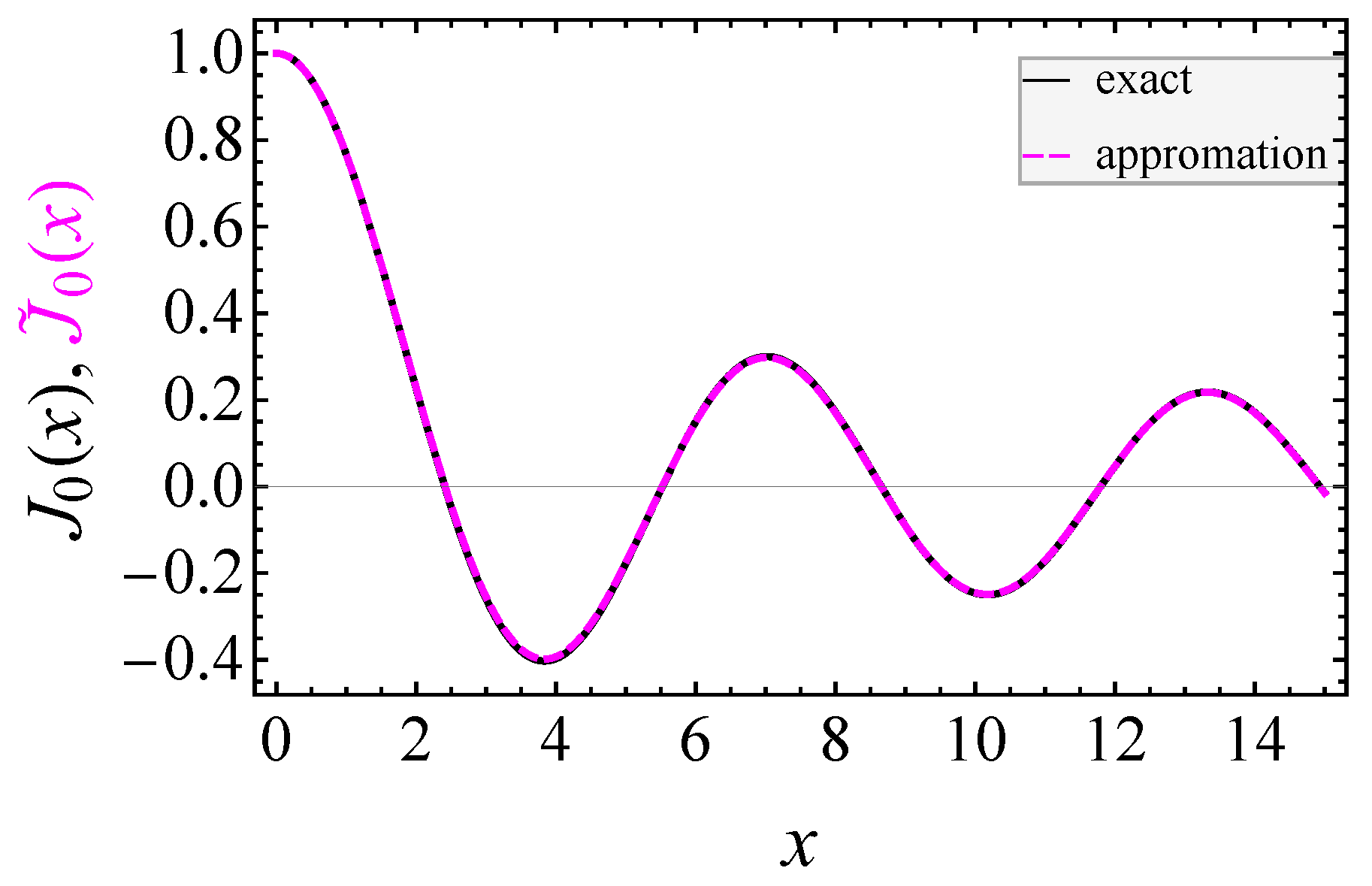
To show the effectiveness of the described technique, let us focus on the details of the results obtained for the orders
and
. These are shown in the following
Figure 3 and
Figure 4, respectively. In all cases, the exact and approximate functions are represented by solid and dashed lines, respectively. From the direct comparison, it is clear that the approximated function follows with good accuracy the shape of the exact one, obtaining the value
at
for
, and
at
for
. Note that a better accuracy between both functions is obtained as
x increases.
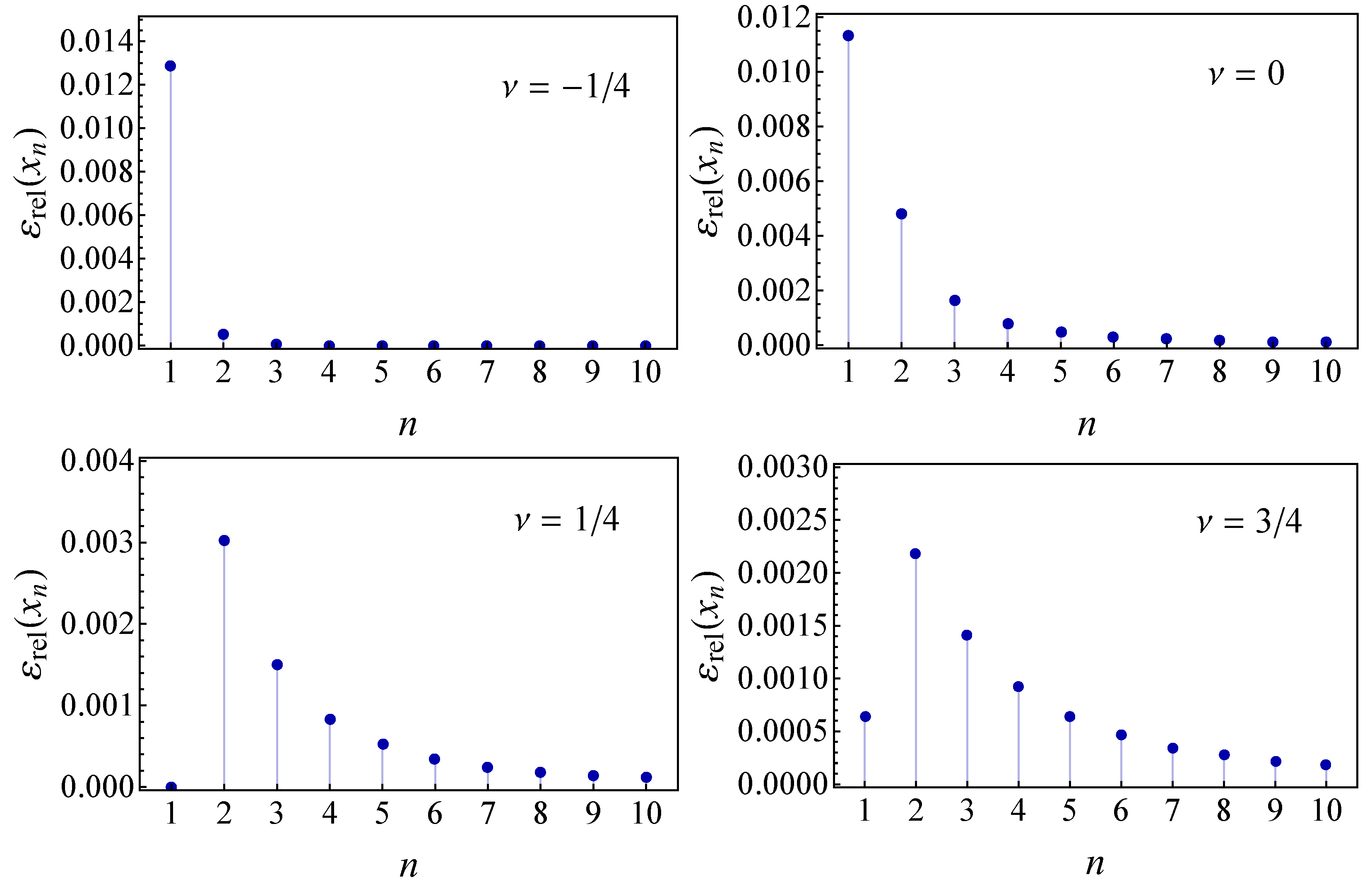
In order to give more details of the accuracy of the results, the relative error for the zeros obtained using the approximated function it is studied. The formula for these relative errors is given by
where
is the
n-zero of
and
the corresponding one of
. The relative errors of the zeros of the Bessel functions for some values of
are give in
Figure 5.
As it is clear from these graphs (
Figure 5), the error decreases always with the increasing of the values of
x, for all values of
.
4. Conclusions
An analytic approximation for the first kind Bessel functions (function ) has been determined for any positive value of the variable x and any value of in the interval . The procedure followed here is novel, as it resembles finding approximations for functions of two variables, although in this case, one of the variables is the order of the Bessel function. The approach employed simultaneously utilizes the power series and the asymptotic expansions of the corresponding functions, as in the Multipoint Quasi-rational Approximation (MPQA) technique. However, the presence of two variables complicates the search for the structure of the approximated function.
The accuracy of the approximations is very good for all the values of inside the considered interval. Furthermore, the approximation coincides with the exact functions in cases where the functions are simpler, such as for , , and . The maximum errors for each typically occur between integer values of congruents with 1/2. After these points, the errors decrease rapidly. The six parameters of the proposed approximation are determined precisely through six corresponding linear equations. The parameters are not left to be determined via numerical computation, as it is often the case with traditional approximations of the Bessel functions in the interval .
Given the very small errors observed, it appears that the present approximation will be useful for most applications involving the first-kind Bessel functions.
For context, we include a short comparison with Chebyshev-based approximations. These methods perform very well on fixed interval of
x and, with rational mappings or by factoring the leading asymptotics, can achieve high accuracy. However, attaining comparable uniform accuracy simultaneously in
x and
typically requires higher polynomial degree or piecewise expansions. By contrast, the MPQA technique used here enforces both the polinomial series and asymptotics expansions, yielding a single closed form expression that is uniform in
x and
and has lower evaluation cost [
19,
20,
21,
22].
Author Contributions
Conceptualization, P.M.; both authors contribute equally to the methodology, software, validation, formal analysis, investigation, writing—original draft preparation, writing—review, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
J.P.R.-A. is grateful for the financial support of FONDECYT Iniciación grant No. 11240637.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We thank posthumously the collaboration of the late Fernando Maass, a distinguished scientist and former head of the Physics Department at the University of Antofagasta, Chile.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| MPQA | Multipoint Quasi-rational Approximation |
Appendix A. Derivation of the Relations for p 2 and p 3
The approximated function
given in Equation (
14) for
it is expressed as follows:
By direct comparison with Equation (
6), the following relations are obtained as follows:
Then,
since
[Equation (
9)]. Thus, we obtained Equations (
25) and (
26) as follows:
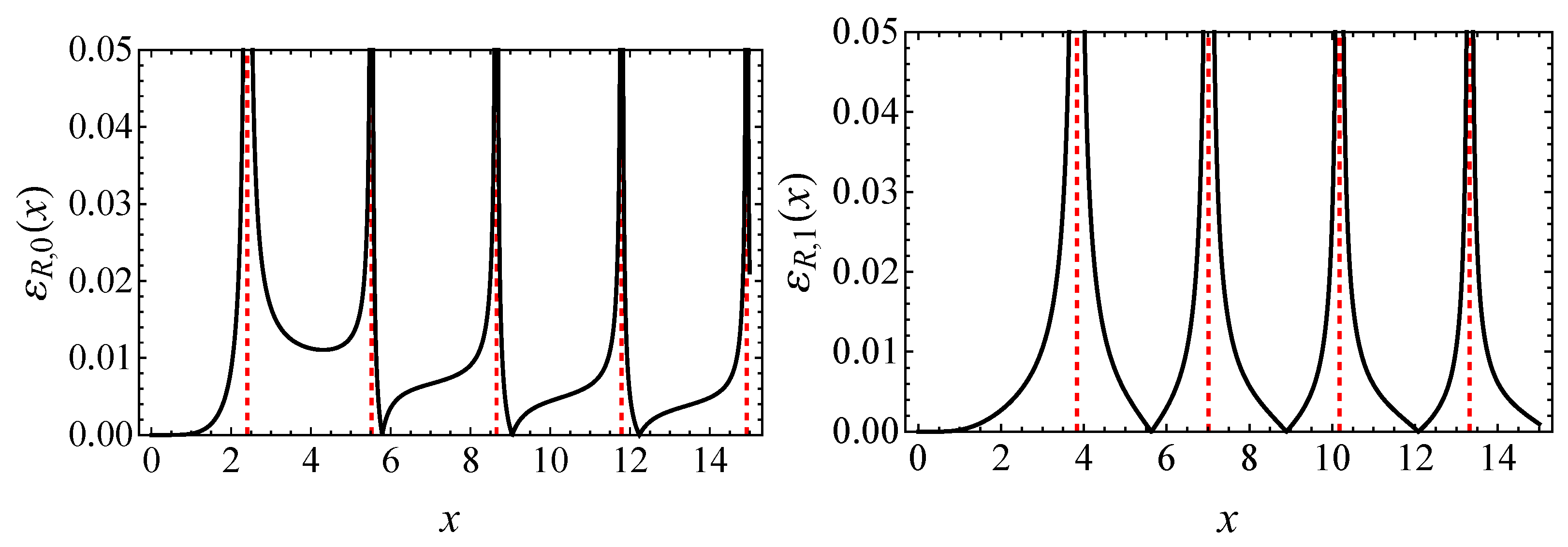
Appendix B. Relative Errors
As noted in the main text, the relative error of the approximation, defined as follows:
diverges near the zeros of
. Nevertheless, we display it explicitly for
and
in the
Figure A1 below. In both cases, it is clear that the relative error remains below
over most of the
x-interval considered, except in a narrow range of the
j-th zero, indicated by vertical red dashed lines.
Figure A1.
(Left) Relative error for . (Right) Relative error for . The solid black lines represent the relative error, while the red dashed vertical lines indicate the locations of the function’s zeros.
Figure A1.
(Left) Relative error for . (Right) Relative error for . The solid black lines represent the relative error, while the red dashed vertical lines indicate the locations of the function’s zeros.
References
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Willey and Sons, Inc.: New York, NY, USA, 1998; pp. 112–119. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1966; pp. 85–224. [Google Scholar]
- Rothwell, E.J. Exponential Approximation of the Bessel functions I0(x), I1(x), J0(x), J1(x),Y0(x) and H0(x) with applications to electromagnetic scattering, radiation and diffraction [EM Programmer’s Notebooks]. IEEE Antennas Propag. Mag. 2009, 51, 138–147. [Google Scholar] [CrossRef]
- Khosravian-Arab, H.; Dehghan, M.; Eslahchi, M.R. Generalized Bessel functions: Theory and their applications. Math. Methods Appl. Sci. 2017, 40, 6389–6410. [Google Scholar] [CrossRef]
- Guo, L.; Liang, P. Condensed matter physics in time crystals. New J. Phys. 2020, 22, 075003. [Google Scholar] [CrossRef]
- Ahumada, M.; Valderrama-Quinteros, N.; Romero, G. Floquet-engineered system-reservoir interaction in the transverse field Ising model. arXiv 2025, arXiv:2501.07527. [Google Scholar]
- Chen, K.; Li, J.; Zhu, G.; Zhang, W.; He, Z.; Zheng, G.; Li, Z. Phase-assisted angular-multiplexing nanoprinting based on the Jacobi-Anger expansion. Opt. Express 2022, 30, 46552–46559. [Google Scholar] [CrossRef] [PubMed]
- Collomb, D.; Bending, S.J.; Koshelev, A.E.; Smylie, M.P.; Farrar, L.; Bao, J.-K.; Chung, D.Y.; Kanatzidis, M.G.; Kwok, W.-K.; Welp, U. Observing the Suppression of Superconductivity in RbEuFe4As4 by Correlated Magnetic Fluctuations. Phys. Rev. Lett. 2021, 126, 157001. [Google Scholar] [CrossRef] [PubMed]
- Shaban, M. Development and Implementation of High-Gain, and High-Isolation Multi-Input Multi-Output Antenna for 5G mmWave Communications. Telecom 2025, 6, 14. [Google Scholar] [CrossRef]
- Khan, Z.; Pradhan, S.; Ahmed, I. Temperature Instability in High-Tc Superconducting Wire Exposed to Thermal Disturbance. Procedia Mater. Sci. 2014, 6, 249–255. [Google Scholar] [CrossRef]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Ninth Printing; Dover Books: New York, NY, USA, 1970; pp. 355–379. [Google Scholar]
- Martin, P.; Castro, E.; Paz, J.L.; De Freitas, A. Chapter 4: Multipoint quasi-rational approximations in Quantum Chemistry. In New Developments in Quantum Chemistry; Paz, J.L., Hernandez, J.A., Eds.; Transworld Research Network: Kerala, India, 2009; Chapter 3; pp. 55–76. [Google Scholar]
- Martin, P.; Ramos-Andrade, J.P.; Caro-Pérez, F.; Lastra, F. Accurate Analytical Approximation for the Bessel Function J2(x). Math. Comput. Appl. 2024, 29, 63. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P.; Olivares, J. Analytic Approximation to the Bessel function J0(x). Comput. Appl. Math. 2020, 39, 222. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P. Precise analytic Approximations for the Bessel function J1(x). Results Phys. 2018, 8, 1234–1238. [Google Scholar] [CrossRef]
- Martin, P.; Rojas, E.; Olivares, J.; Sotomayor, A. Quasi-rational analytic approximation for the modified Bessel function I1(x) with high accuracy. Symmetry 2021, 13, 741–742. [Google Scholar] [CrossRef]
- Baker, G.A., Jr.; Travers-Morris, P. Padé Approximants; Cambrige U.P.: Cambrige, UK, 1996. [Google Scholar]
- Peker, H.A. An Introduction to Padé Approximation. In Current Studies in Basic Sciences, Engineering and Tecnology; ISRES Publishing: Konya, Turkey, 2021; pp. 143–155. [Google Scholar]
- Trefethen, L.N. Approximation Theory and Approximation Practice; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Boyd, J.P. Orthogonal rational functions on a semi-infinite interval. J. Comput. Phys. 1987, 70, 63–88. [Google Scholar] [CrossRef]
- Gil, A.; Segura, J.; Temme, N.M. Numerical Methods for Special Functions; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).