Nonlocal Modeling and Inverse Parameter Estimation of Time-Varying Vehicular Emissions in Urban Pollution Dynamics
Abstract
1. Introduction
- (1)
- We systematically investigate how replacing the classical time and spatial derivatives in the convection–diffusion-reaction equation with fractional Caputo and Riesz derivatives, respectively, affects the dispersion of atmospheric pollutants. This analysis is carried out in a realistic setting involving dynamic line sources associated with vehicle motion, providing new insights into the memory and non-local transport effects that can be captured by fractional models.
- (2)
- We propose and evaluate a parameter estimation method for solving an inverse problem aimed at recovering unknown coefficients on the right-hand side of the governing equation. These coefficients modulate time-dependent pollutant emissions and are derived from realistic synthetic concentration measurements from spatially distributed observation points. Our results demonstrate the ability of the method to efficiently recover emission time profiles, even under model uncertainty caused by stochastic vehicle motion and fractional dynamics.
2. Materials and Methods
2.1. Problem Statement
2.1.1. Statement of the Forward Problem
2.1.2. Statement of the Inverse Problem
2.2. Solution Method
2.2.1. Method of Solving the Deterministic Forward Problem
2.2.2. Method for Solving the Stochastic Forward Problem
2.2.3. Method for Solving the Inverse Problem
2.2.4. Computational Algorithm
| Algorithm 1 Algorithm for solving the inverse problem |
|
3. Results
3.1. Analysis of the Forward Problem
3.1.1. Comparison of the Classical Convection–Diffusion Model with the Fractional Differential Model
3.1.2. Observation of Changes in Concentration at Stations: Transition from the Classical Model to the Fractional-Order Model
3.1.3. Analysis of the Influence of Lower Orders of Fractional Derivative on the Pollutant Dispersion Process
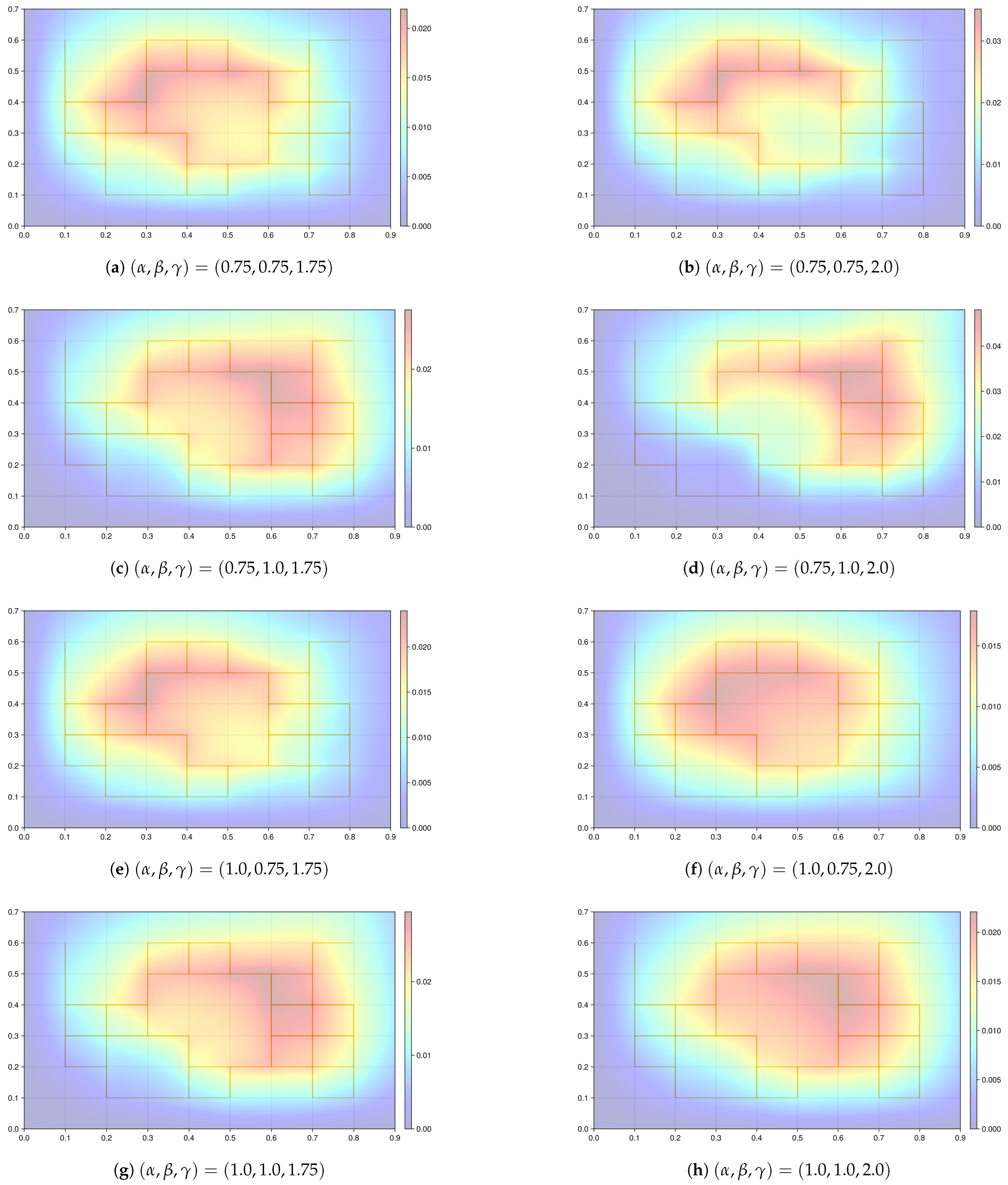
3.1.4. Influence of Parameters on the Spread of a Pollutant
3.2. Stability and Convergence of the Numerical Method
3.3. Evaluation of the Efficiency of the Algorithm for Solving the Inverse Problem
3.3.1. Convergence Behavior
3.3.2. Accuracy of the Derived Coefficients
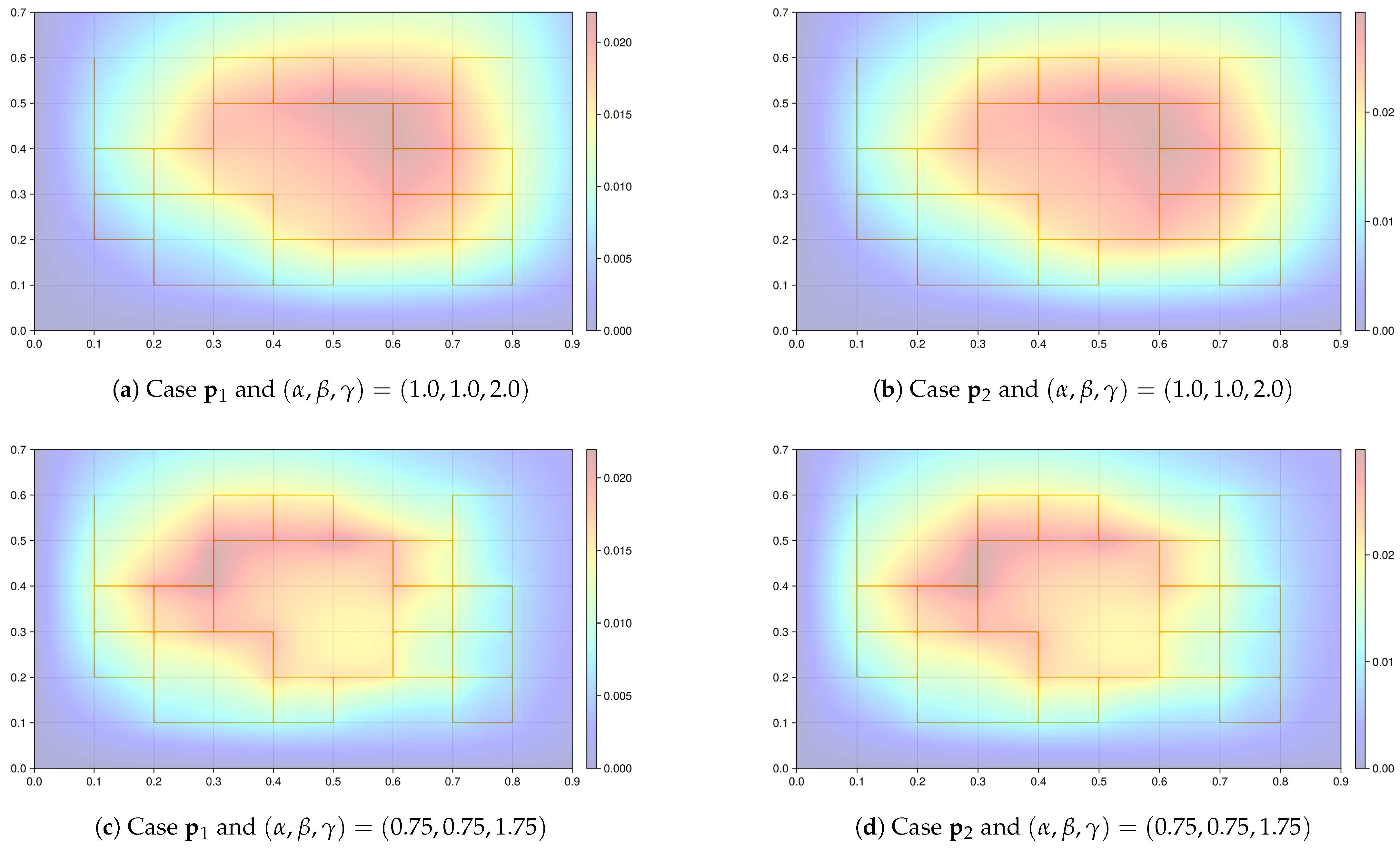
3.3.3. Scatter Plot of Actual and Expected Coefficients
3.3.4. Violin Plot of Accuracy Depending on the Parameter
3.4. Sensitivity to Parameters Initialization
3.4.1. Histogram of the Number of Iterations
3.4.2. Histogram of Inference Accuracy
3.4.3. Violin Plot of Parameter-Specific Accuracy
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the spatial domain [] | |
| the finite difference grid introduced in the spatial domain | |
| the Caputo fractional differentiation operator | |
| the Riemann-Liouville fractional differentiation operator | |
| the set of edges | |
| the -algebra | |
| the directed graph | |
| the unit matrix | |
| h | the discretization parameter of the spatial domain |
| L | the side length of the spatial domain [m] |
| M | the number of vehicles |
| the number of nodes in each direction of the finite difference grid | |
| the number of nodes in the uniform partition of the time interval | |
| the probability measure | |
| the vector of parameters | |
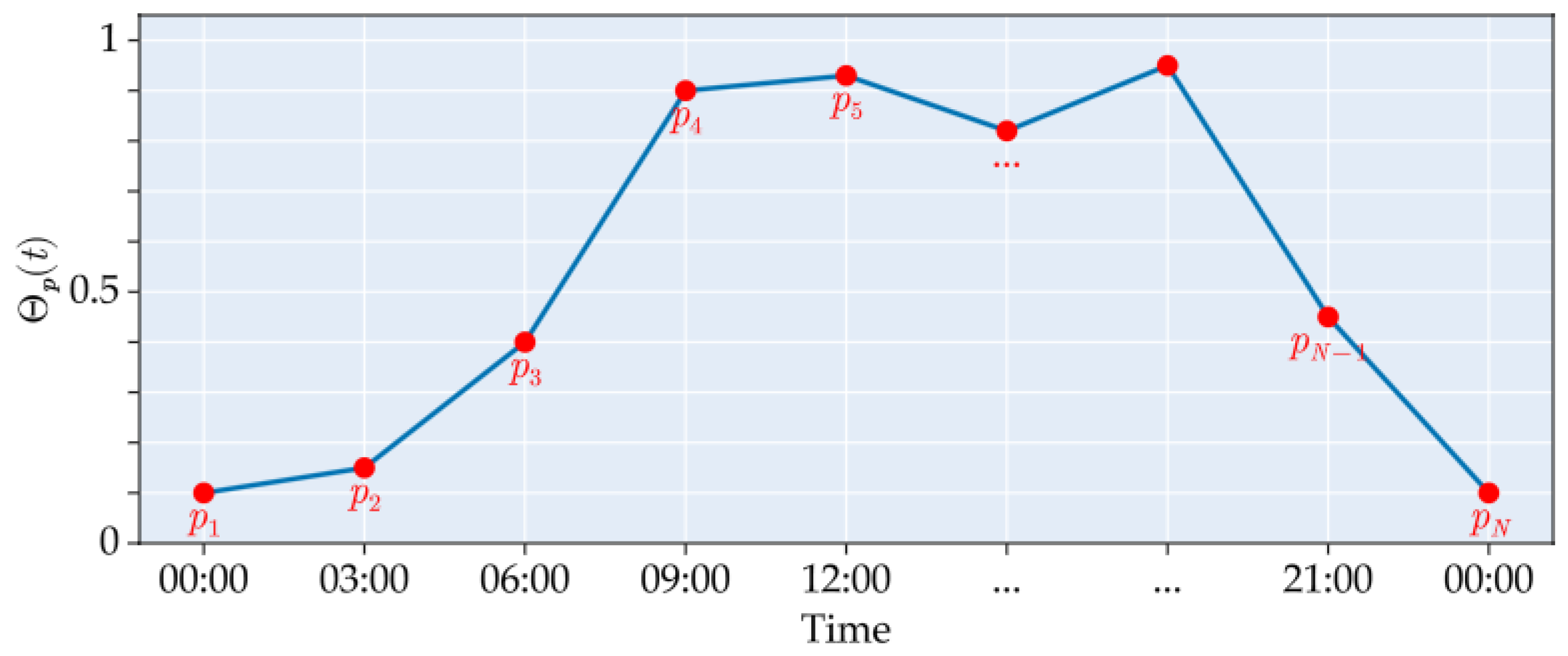
| the parameter indicating the empirical representation of the temporal change in emission activity [dimensionless] | |
| T | the final time [s] |
| a uniform partition of the time interval | |
| the Toeplitz matrix with the first column and the first row | |
| the wind velocity field [m/s] | |
| the set of nodes | |
| the position of the mth vehicle | |
| the node of the finite difference grid | |
| the vector of internal nodes of the finite difference grid | |
| the order of the temporal Caputo fractional derivative | |
| the order of the spatial Riesz fractional derivative | |
| the order of the spatial Riesz fractional derivative | |
| the atmospheric diffusion coefficient [] | |
| the wind pressure [Pa] | |
| the pollutant emission rate of the mth vehicle [kg/s] | |
| the contaminant concentration [] | |
| the grid function representing the contaminant concentration | |
| the discretization parameter of the time segment (time step) | |
| the modulation function [dimensionless] | |
| the finite difference grid introduced in the segment | |
| the sample space | |
| a sample | |
| ⊗ | the Kronecker product |
| ⊕ | the Kronecker sum |
References
- Seesaard, T.; Kamjornkittikoon, K.; Wongchoosuk, C. A comprehensive review on advancements in sensors for air pollution applications. Sci. Total Environ. 2024, 951, 175696. [Google Scholar] [CrossRef]
- Samsudin, M.S.; Azid, A.; Razik, M.A.; Zaudi, M.A.; Shaharudin, S.M. Source of apportionment of air quality parameters at federal port of Malaysia with emphasis on ship emission. IOP Conf. Ser. Earth Environ. Sci. 2021, 810, 012052. [Google Scholar] [CrossRef]
- Sokhi, R.; Baklanov, A.; Mahura, A. Integrated Systems of Meso-Meteorological and Chemical Transport Models; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Stockie, J.M. The mathematics of atmospheric dispersion modeling. SIAM Rev. 2011, 53, 349–372. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Gireesh Kumar, P.; Lekhana, P.; Tejaswi, M.; Chandrakala, S. Effects of vehicular emissions on the urban environment—A state of the art. Mater. Today Proc. 2021, 45, 6314–6320. [Google Scholar] [CrossRef]
- Hassan, N.A.; Hashim, J.H.; Wan Puteh, S.E.; Wan Mahiyuddin, W.R.; Mohd, M.S.F.; Shaharudin, S.M.; Mohammad Aidid, E.; Sapuan, I. Investigation of the impacts of climate change and rising temperature on food poisoning cases in Malaysia. PLoS ONE 2023, 18, e0283133. [Google Scholar] [CrossRef]
- Ferragut, L.; Asensio, M.I.; Cascón, J.M.; Prieto, D.; Ramírez, J. An efficient algorithm for solving a multi-layer convection–diffusion problem applied to air pollution problems. Adv. Eng. Softw. 2013, 65, 191–199. [Google Scholar] [CrossRef]
- Ruhiat, Y.; Guntara, Y. Regional detection polluted with diffusion and convection models in Banten province. J. Phys. Conf. Ser. 2020, 1428, 012051. [Google Scholar] [CrossRef]
- Habingabwa, M.E.N.; Ndahayo, F.; Berntsson, F. Air pollution tracking using PDEs. Rwanda J. 2012, 27. [Google Scholar] [CrossRef]
- Ioannidis, G.; Li, C.; Tremper, P.; Riedel, T.; Ntziachristos, L. Application of CFD modelling for pollutant dispersion at an urban traffic hotspot. Atmosphere 2024, 15, 113. [Google Scholar] [CrossRef]
- Kafle, J.; Adhikari, K.P.; Poudel, E.P. Air pollutant dispersion using advection-diffusion equation. Nepal J. Environ. Sci. 2024, 12, 1–6. [Google Scholar] [CrossRef]
- Temirbekov, N.; Malgazhdarov, Y.; Tokanova, S.; Amenova, F.; Baigereyev, D.; Turarov, A. Information technology for numerical simulation of convective flows of a viscous incompressible fluid in curvilinear multiply connected domains. J. Theor. Appl. Inf. Technol. 2019, 97, 3166–3177. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bottoni, M. Numerical Methods for the Solution of the Convection-Diffusion Equation and QUICK Algorithm; Springer International Publishing: Cham, Switzerland, 2021; pp. 155–215. [Google Scholar] [CrossRef]
- Lapina, O.N.; Nesterenko, A.G.; Nikitin, Y.G.; Pavlova, A.V. Modelling of the diffusion-convection process of a pollutant with a periodic source. Ecol. Bull. Res. Centers Black Sea Econ. Coop. 2022, 19, 26–35. [Google Scholar] [CrossRef]
- Issakhov, A.; Alimbek, A.; Abylkassymova, A. Numerical modeling of water pollution by products of chemical reactions from the activities of industrial facilities at variable and constant temperatures of the environment. J. Contam. Hydrol. 2023, 252, 104116. [Google Scholar] [CrossRef]
- Li, L.; Yin, Z. Numerical simulation of groundwater pollution problems based on convection diffusion equation. Am. J. Comput. Math. 2017, 7, 350–370. [Google Scholar] [CrossRef]
- Rashidinia, J.; Momeni, A.; Molavi-Arabshahi, M. Solution of convection-diffusion model in groundwater pollution. Sci. Rep. 2024, 14, 2075. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lu, W.; Huang, J. Monitoring, diffusion and source speculation model of urban soil pollution. Processes 2020, 8, 1339. [Google Scholar] [CrossRef]
- Konshin, O.V. Applicability of the convection-diffusion mechanism for modeling migration of 137cs and 90sr in the soil. Health Phys. 1992, 63, 291–300. [Google Scholar] [CrossRef]
- Thenmozhi, D.; Eswara Rao, M.; Renuka Devi, R.L.V.; Nagalakshmi, C.; Selvi, P.D. Dynamics of heat transfer in complex fluid systems: Comparative analysis of Jeffrey, Williamson and Maxwell fluids with chemical reactions and mixed convection. Int. J. Thermofluids 2024, 24, 100896. [Google Scholar] [CrossRef]
- Zhao, B. Fundamental heat and entropy transfer mechanisms of convection underlying the first and second laws for an unsteady multiport system and their applications in parallel flow heat exchangers. Int. J. Heat Fluid Flow 2024, 107, 109400. [Google Scholar] [CrossRef]
- Meng, X.; Huang, M.; Wang, B.; Ouyang, X.; Huang, Y.; Chen, D.; Cheng, Y.; Li, Y. A numerical method for two-dimensional transient nonlinear convection-diffusion equations. Ann. Nucl. Energy 2024, 205, 110604. [Google Scholar] [CrossRef]
- Kanatani, K. Effects of convection and diffusion of the vapour in evaporating liquid films. J. Fluid Mech. 2013, 732, 128–149. [Google Scholar] [CrossRef]
- Kirsch, V.A. Numerical simulation of convective diffusion of point particles in a laminar flow past a row of profiled hollow fibers. Fibers 2022, 10, 77. [Google Scholar] [CrossRef]
- Pope, C.A.; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Tarasov, V. Fractional Dynamics: Application of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: London, UK; New York, NY, USA, 2011. [Google Scholar]
- Baigereyev, D.; Alimbekova, N.; Berdyshev, A.; Madiyarov, M. Convergence analysis of a numerical method for a fractional model of fluid flow in fractured porous media. Mathematics 2021, 9, 2179. [Google Scholar] [CrossRef]
- Alimbekova, N.; Berdyshev, A.; Baigereyev, D. Parallel implementation of the algorithm for solving a partial differential equation with a fractional derivative in the sense of Riemann-Liouville. In Proceedings of the 2021 IEEE International Conference on Smart Information Systems and Technologies (SIST), Nur-Sultan, Kazakhstan, 28–30 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Moreira, D.; Xavier, P.; Palmeira, A.; Nascimento, E. New approach to solving the atmospheric pollutant dispersion equation using fractional derivatives. Int. J. Heat Mass Transf. 2019, 144, 118667. [Google Scholar] [CrossRef]
- Troparevsky, M.I.; Muszkats, J.P.; Seminara, S.A.; Zitto, M.E.; Piotrkowski, R. Modeling particulate pollutants dispersed in the atmosphere using fractional turbulent diffusion. Phys. A Stat. Mech. Its Appl. 2022, 599, 127478. [Google Scholar] [CrossRef]
- Palmeira, A.; Xavier, P.; Moreira, D. Simulation of atmospheric pollutant dispersion considering a bi-flux process and fractional derivatives. Atmos. Pollut. Res. 2020, 11, 57–66. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J.; Sokolov, I.M. Anomalous transport in external fields: Continuous time random walks and fractional diffusion equations extended. Phys. Rev. E 1998, 58, 1621–1633. [Google Scholar] [CrossRef]
- Kallianpur, G.; Xiong, J. Stochastic models of environmental pollution. Adv. Appl. Probab. 1994, 26, 377–403. [Google Scholar] [CrossRef]
- Cheng, K.-C.; Acevedo-Bolton, V.; Jiang, R.-T.; Klepeis, N.E.; Ott, W.R.; Kitanidis, P.K.; Hildemann, L.M. Stochastic modeling of short-term exposure close to an air pollution source in a naturally ventilated room: An autocorrelated random walk method. J. Expo. Sci. Environ. Epidemiol. 2013, 24, 311–318. [Google Scholar] [CrossRef][Green Version]
- Calvert, S.C. Stochastic Macroscopic Analysis and Modelling for Traffic Management. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener—Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Li, W.; Duan, Q.; Miao, C.; Ye, A.; Gong, W.; Di, Z. A review on statistical postprocessing methods for hydrometeorological ensemble forecasting. WIREs Water 2017, 4, W01411. [Google Scholar] [CrossRef]
- Buyo, N.; Sheikh-Akbari, A.; Saleem, F. An ensemble approach to predict a sustainable energy plan for London households. Sustainability 2025, 17, 500. [Google Scholar] [CrossRef]
- Baishemirov, Z.; Berdyshev, A.; Baigereyev, D.; Boranbek, K. Efficient numerical implementation of the time-fractional stochastic Stokes–Darcy model. Fractal Fract. 2024, 8, 476. [Google Scholar] [CrossRef]
- Wu, H.; Levinson, D. The ensemble approach to forecasting: A review and synthesis. Transp. Res. Part C Emerg. Technol. 2021, 132, 103357. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Vardoulakis, S.; Fisher, B.E.A.; Pericleous, K.; Gonzalez-Flesca, N. Modelling air quality in street canyons: A review. Atmos. Environ. 2003, 37, 155–182. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Hussain, A.; Zheng, Z.; Eyaya, F.A. Numerical solution of convection-dominated diffusion problem using modified upwind finite volume method. Authorea 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H. High-order finite difference Hermite weighted essentially nonoscillatory method for convection–diffusion equations. Math. Comput. Appl. 2025, 30, 3. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Hassan, S.K.; Ali Alazzawi, S.N.; Ibrahem, N.M.J. Some results in Grűnwald-Letnikov fractional derivative and its best approximation. J. Phys. Conf. Ser. 2021, 1818, 012020. [Google Scholar] [CrossRef]
- Stynes, M. A survey of the L1 scheme in the discretisation of time-fractional problems. Numer. Math. Theory Methods Appl. 2022, 15, 1173–1192. [Google Scholar] [CrossRef]
- Xiao, J.; Chen, Y.; Zeng, F.; Zhang, Z. L1 schemes for time-fractional differential equations: A brief survey and new development. Numer. Math. Theory Methods Appl. 2025, 18, 544–574. [Google Scholar] [CrossRef]
- Dimitrov, Y.; Georgiev, S.; Todorov, V. Approximation of Caputo fractional derivative and numerical solutions of fractional differential equations. Fractal Fract. 2023, 7, 750. [Google Scholar] [CrossRef]
- Ali, M.S.; Shamsi, M.; Khosravian-Arab, H.; Torres, D.F.M.; Bozorgnia, F. A space–time pseudospectral discretization method for solving diffusion optimal control problems with two-sided fractional derivatives. J. Vib. Control 2018, 25, 1080–1095. [Google Scholar] [CrossRef]
- Oloniiju, S.D.; Mukwevho, N.; Tijani, Y.O.; Otegbeye, O. Chebyshev pseudospectral method for fractional differential equations in non-overlapping partitioned domains. AppliedMath 2024, 4, 950–974. [Google Scholar] [CrossRef]
- Goulart, A.G.O.; Lazo, M.J.; Suarez, J.M.S.; Moreira, D.M. Fractional derivative models for atmospheric dispersion of pollutants. Phys. A Stat. Mech. Its Appl. 2017, 477, 9–19. [Google Scholar] [CrossRef]
- Zhang, Y.-N.; Sun, Z.-Z.; Liao, H.-L. Finite difference methods for the time fractional diffusion equation on non-uniform meshes. J. Comput. Phys. 2014, 265, 195–210. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Temirbekov, N.; Malgazhdarov, Y.; Tamabay, D.; Temirbekov, A. Mathematical and computer modeling of atmospheric air pollutants transformation with input data refinement. Indones. J. Electr. Eng. Comput. Sci. 2023, 32, 1405. [Google Scholar] [CrossRef]
- Berdyshev, A.; Baigereyev, D.; Boranbek, K. Numerical method for fractional-order generalization of the stochastic Stokes–Darcy model. Mathematics 2023, 11, 3763. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Madiyarov, M.; Temirbekov, N.; Alimbekova, N.; Malgazhdarov, Y.; Yergaliyev, Y. A combined approach for predicting the distribution of harmful substances in the atmosphere based on parameter estimation and machine learning algorithms. Computation 2023, 11, 249. [Google Scholar] [CrossRef]
- Powell, M.J.D. The NEWUOA software for unconstrained optimization without derivatives. In Large-Scale Nonlinear Optimization. Nonconvex Optimization and Its Applications; Di Pillo, G., Roma, M., Eds.; Springer: Boston, MA, USA, 2006; Volume 83. [Google Scholar] [CrossRef]
- Powell, M.J.D. The BOBYQA Algorithm for Bound Constrained Optimization Without Derivatives; Technical Report NA2009/06; Department of Applied Mathematics and Theoretical Physics, University of Cambridge: Cambridge, UK, 2009. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Beybalaev, V.D.; Abduragimov, E.I.; Yakubov, A.Z.; Meilanov, R.R.; Aliverdiev, A.A. Numerical research of non-isothermal filtration process in fractal medium with non-locality in time. Therm. Sci. 2021, 25, 465–475. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Lukashchuk, S.Y. Fractional differential approach to modeling filtration processes in complex inhomogeneous porous media. Vestn. UGATU 2017, 21, 104–112. (In Russian) [Google Scholar]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Goulart, A.G.; Lazo, M.J.; Suarez, J.M.S. A deformed derivative model for turbulent diffusion of contaminants in the atmosphere. Phys. A Stat. Mech. Its Appl. 2020, 557, 124847. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of fractional models of dispersion contaminants in the planetary boundary layer. Mathematics 2023, 11, 2040. [Google Scholar] [CrossRef]
- Sun, L.; Qiu, H.; Wu, C.; Niu, J.; Hu, B.X. A review of applications of fractional advection–dispersion equations for anomalous solute transport in surface and subsurface water. WIREs Water 2020, 7, e1448. [Google Scholar] [CrossRef]
- Vautard, R.; Beekmann, M.; Menut, L. Applications of adjoint modelling in atmospheric chemistry: Sensitivity and inverse modelling. Environ. Model. Softw. 2000, 15, 703–709. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, Y.; Knievel, J.C.; Zhai, Z. A city-scale inverse modelling method for air pollutant source determination. Sustain. Cities Soc. 2022, 87, 104248. [Google Scholar] [CrossRef]
- Wu, H.; Tang, X.; Wang, Z.; Wu, L.; Li, J.; Wang, W.; Yang, W.; Zhu, J. High-spatiotemporal-resolution inverse estimation of CO and NOx emission reductions during emission control periods with a modified ensemble Kalman filter. Atmos. Environ. 2020, 236, 117631. [Google Scholar] [CrossRef]
- Zhang, H.-L.; Li, B.; Shang, J.; Wang, W.-W.; Zhao, F.-Y. Source term estimation for continuous plume dispersion in Fusion Field Trial-07: Bayesian inference probability adjoint inverse method. Sci. Total Environ. 2024, 915, 169802. [Google Scholar] [CrossRef] [PubMed]
- Kasenov, S.; Tleulesova, A.; Temirbekov, A.; Bektemessov, Z.; Asanova, R. Numerical solution of the inverse thermoacoustics problem using QFT and gradient method. Fractal Fract. 2025, 9, 370. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]





| -Error | Order | h | -Error | Order | |
|---|---|---|---|---|---|
| 1/100 | - | 1/20 | - | ||
| 1/200 | 1.24 | 1/40 | 0.98 | ||
| 1/400 | 1.22 | 1/80 | 0.99 | ||
| 1/800 | 1.21 | 1/160 | 0.99 |
| Parameter No. | Value | Parameter No. | Value |
|---|---|---|---|
| 1 | 0.070064190535697 | 4 | 0.1963325132242003 |
| 2 | 0.278814378576473 | 5 | 0.4738792967134109 |
| 3 | 0.699921731580088 | 6 | 0.8701213766070134 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madiyarov, M.; Alimbekova, N.; Bakishev, A.; Mukhamediyev, G.; Yergaliyev, Y. Nonlocal Modeling and Inverse Parameter Estimation of Time-Varying Vehicular Emissions in Urban Pollution Dynamics. Mathematics 2025, 13, 2772. https://doi.org/10.3390/math13172772
Madiyarov M, Alimbekova N, Bakishev A, Mukhamediyev G, Yergaliyev Y. Nonlocal Modeling and Inverse Parameter Estimation of Time-Varying Vehicular Emissions in Urban Pollution Dynamics. Mathematics. 2025; 13(17):2772. https://doi.org/10.3390/math13172772
Chicago/Turabian StyleMadiyarov, Muratkan, Nurlana Alimbekova, Aibek Bakishev, Gabit Mukhamediyev, and Yerlan Yergaliyev. 2025. "Nonlocal Modeling and Inverse Parameter Estimation of Time-Varying Vehicular Emissions in Urban Pollution Dynamics" Mathematics 13, no. 17: 2772. https://doi.org/10.3390/math13172772
APA StyleMadiyarov, M., Alimbekova, N., Bakishev, A., Mukhamediyev, G., & Yergaliyev, Y. (2025). Nonlocal Modeling and Inverse Parameter Estimation of Time-Varying Vehicular Emissions in Urban Pollution Dynamics. Mathematics, 13(17), 2772. https://doi.org/10.3390/math13172772






