From Heuristics to Multi-Agent Learning: A Survey of Intelligent Scheduling Methods in Port Seaside Operations

Abstract

Port seaside scheduling, involving berth allocation, quay crane, and tugboat scheduling, is central to intelligent port operations. This survey reviews and statistically analyzes 152 academic publications from 2000 to 2025 that focus on optimization techniques for port seaside scheduling. The reviewed methods span mathematical modeling and exact algorithms, heuristic and simulation-based approaches, and agent-based and learning-driven techniques. Findings show deterministic models remain mainstream (77% of studies), with uncertainty-aware models accounting for 23%. Heuristic and simulation approaches are most commonly used (60.5%), followed by exact algorithms (21.7%) and agent-based methods (12.5%). While berth and quay crane scheduling have historically been the primary focus, there is growing research interest in tugboat operations, pilot assignment, and vessel routing under navigational constraints. The review traces a clear evolution from static, single-resource optimization to dynamic, multi-resource coordination enabled by intelligent modeling. Finally, emerging trends such as the integration of large language models, green scheduling strategies, and human–machine collaboration are discussed, providing insights and directions for future research and practical implementations.

1. Introduction

Ports serve as vital hubs in the global supply chain and international trade network, responsible for the aggregation, transshipment, and distribution of maritime cargo. With the ongoing advancement of economic globalization, ports play an irreplaceable role in linking national and regional economies. According to the International Maritime Organization (IMO), approximately 80% of global trade is carried by sea, making port efficiency a critical determinant of transportation timeliness, costs, and overall economic development [1].

In recent years, the steady growth of global trade volumes and the trend toward larger vessels have imposed increasing demands on port operational efficiency and service quality. Traditional port management models are becoming inadequate for complex and dynamic business environments, catalyzing the emergence of the smart port concept. By integrating automated equipment, intelligent scheduling systems, and big data analytics, smart ports can significantly enhance operational efficiency and resource utilization, underpinning both sustainable development and competitiveness. Among the core technologies enabling smart port operations, Terminal Operating Systems (TOSs) have been widely adopted to support landside functions such as yard planning, quay crane allocation, and container truck dispatching. These systems provide centralized control and real-time visibility, driving significant gains in landside operational efficiency. More importantly, the application of intelligent models and optimization algorithms relies on the data availability, system integration, and automation level found primarily in smart or automated terminals. In contrast, conventional manually operated terminals often lack the necessary infrastructure to support such advanced techniques, making smart terminals the natural foundation for intelligent scheduling solutions.

However, the seaside domain—comprising vessel arrival, berthing, cargo handling, and departure—is equally crucial to overall port performance. Efficient scheduling of these processes directly influences vessel turnaround time, port throughput, and the flow of the entire logistics chain. While landside systems have benefited from extensive research and digital transformation, the optimization of seaside operations remains comparatively underexplored. In response to these challenges, an expanding body of review literature has emerged. Early reviews provided comprehensive overviews of terminal operations and decision-making processes from a holistic perspective, establishing foundational knowledge for subsequent research efforts [2]. With the advancement of automation and intelligent technologies, scholarly attention has gradually expanded to landside operations and yard management, with detailed analyses of yard layout, equipment deployment, and AGV management highlighting the central role of landside systems [3]. Systematic reviews have also addressed the overall architecture of port operations, classifying activities into landside and quayside domains and emphasizing the growing roles of integration, artificial intelligence, and sustainability in future port development [4]. The need for coordinated optimization across yard and quayside resources is increasingly recognized, with the importance of integrated scheduling approaches being highlighted in recent surveys [5].

Within the domain of seaside operation optimization, berth allocation has remained a central research focus, with multiple comprehensive reviews summarizing its development, prevailing models, and key trends [6,7]. Quay crane assignment and scheduling are frequently examined alongside berth allocation, and recent surveys have synthesized advances in models, algorithms, and integrated optimization methods for these core problems [8,9,10]. Beyond individual resources, research on multi-resource coordinated optimization and system integration has intensified, with recent reviews identifying both mainstream models and critical research gaps in the coordination of berths, quay cranes, AGVs, and yards [11]. The growing complexity of real-world port environments has also driven the classification and analysis of scheduling under uncertainty, yielding valuable methodological frameworks for robust and adaptive scheduling [10,12].

Nevertheless, the majority of existing surveys have focused primarily on landside and quayside optimization, with relatively limited coverage of critical seaside operations—particularly tugboat scheduling, pilot assignment, and channel-constrained vessel scheduling. A recent review [13] provides an overview of current trends in addressing seaside terminal problems, with a particular focus on operations research, machine learning, and their integration as decision support tools. While their work highlights methodological advances, it concentrates mainly on berth and quay crane operations and offers limited discussion of scheduling problems involving other dynamic seaside resources such as tugboats, pilots, and navigational channels. In addition, the coordination and integrated optimization of these interdependent resources are not thoroughly addressed. In practice, the coordination of tugboats, pilots, and navigation within restricted channels is essential to vessel entry and departure, often serving as bottlenecks that directly impact port performance and downstream logistics operations. The optimization of these processes is thus of central importance to the overall efficiency and reliability of port systems.

To address these gaps, the present review concentrates on scheduling optimization within the seaside segment of ports. This paper systematically synthesizes research progress on tugboat scheduling, pilot assignment, channel-constrained vessel scheduling, and the integrated optimization of berths and quay cranes. In addition to problem-level analysis, we emphasize mathematical modeling under uncertainty and recent advances in reinforcement learning and agent-based methods, offering a comprehensive and forward-looking reference for future research in intelligent port scheduling.

This study aims to provide a systematic and comprehensive review of scheduling optimization methods specifically for port seaside operations, encompassing berth allocation, quay crane scheduling, tugboat scheduling, pilot assignment, and channel-constrained vessel scheduling. While landside operations in ports have been widely studied, seaside operations remain comparatively underexplored despite their critical impact on vessel turnaround times and overall port performance. Addressing this gap is essential for advancing smart port development, achieving higher operational efficiency, and enhancing the coordination between maritime and port resources. This work not only synthesizes the current state of research but also identifies key challenges and emerging trends, providing a valuable reference for both academia and industry.

To guide the review, the following research questions are addressed:

RQ1: What are the core components, resources, and operational processes involved in the seaside operation system of ports?

RQ2: What key performance indicators (KPIs) define operational efficiency in seaside scheduling, and how are they used to guide optimization?

RQ3: How can the main scheduling problems in seaside operations be classified, and what methodological approaches have been adopted to solve them?

RQ4: What are the major research gaps in the field, and what emerging trends and technologies are shaping future directions?

Building on these questions, the remainder of the paper is structured as follows. Section 2 outlines the research methodology and literature selection process. Section 3 presents the architecture and operational process of port seaside systems, including the definition of key resources and optimization metrics. Section 4 and Section 5 review mathematical models, exact algorithms, heuristic methods, and simulation approaches for seaside scheduling optimization. Section 6 discusses the application of agent-based methods and large language models. Section 7 provides a comparative analysis, highlights research trends, and offers future perspectives. Finally, Section 8 summarizes the main findings and potential research directions.

2. Research Methodology

2.1. Literature Identification and Selection Process

Due to the significance of scheduling problems in port seaside operation systems, a considerable number of scholars have conducted research and published papers in this field in recent years. In this survey, a two-step approach was adopted to identify and analyze the relevant literature.

First, a targeted keyword search was performed in major academic databases, including IEEE, ScienceDirect, Elsevier, and Web of Science, to capture pertinent studies. Given that the port seaside operation system encompasses multiple processes, the search strategy was designed to comprehensively review optimization research related to port seaside scheduling. The following core terms were used as the basis for retrieval: “port operation,” “container terminal,” “scheduling,” and “optimization.” These were further combined with typical process-specific keywords such as “berth allocation,” “quay crane scheduling,” “quay crane assignment,” “tugboat scheduling,” “pilotage scheduling,” “vessel scheduling AND channel,” and “vessel traffic scheduling.” The search focused primarily on studies concerning the scheduling and optimization of critical resources, including berths, quay cranes, tugboats, pilots, and channel constraints.

The inclusion criteria for literature selection were as follows: (1) any article that addresses port scheduling optimization; and (2) papers published between 2000 and 2025. Exclusion criteria included the following: (1) articles discussing and analyzing scenarios outside of port seaside operations; (2) papers unrelated to port scheduling optimization problems; and (3) books and review articles.

In the second step, the initially selected papers were further refined through careful reading and analysis to avoid potential bias stemming from keyword-based searches, since keyword-driven interest and preferences may yield different proportions of relevant literature. The screening process is illustrated in Figure 1. Based on the above criteria and procedures, a total of 152 papers were ultimately included in this survey.

2.2. Preliminary Statistical Overview

To comprehensively understand the current research status and development trends of port seaside scheduling problems, a systematic statistical analysis was conducted on the types, research scenarios, and temporal distribution of the collected literature. As shown in Figure 2, journal articles account for 92.8% of the total literature, while conference papers make up 7.2%. Among them, journal articles represent the overwhelming majority.

The optimization of port seaside scheduling problems encompasses several key resources, including berths (B), quay cranes (QC), tugboats (T), pilots (P), and channels (C). Given that different studies emphasize various resources and scheduling priorities, this paper categorizes port seaside scheduling problems based on the types of resources addressed in the scheduling models. The problems are classified into the following categories: (1) B; (2) QC; (3) T; (4) P; (5) Co-S (coordinated scheduling); and (6) M (multi-resource scheduling). Among them, Co-S refers to integrated scheduling models constructed for the coordination of multiple core resources in ports—such as tugboats, channels, and pilots—while M further extends to multi-level, comprehensive scheduling scenarios involving additional resources such as yard equipment.

As shown in Figure 3a, the pie chart on the left presents the distribution of different resource types in current research on port seaside scheduling. It can be observed that the berth allocation problem (BAP) still holds a dominant position, accounting for a large proportion of single-resource scheduling studies and remaining the main focus in the literature. In contrast, research involving auxiliary resources such as tugboats (T), pilots (P), and channels (C) remains relatively limited and is still in its early stages of development. In recent years, there has been a notable increase in studies on coordinated scheduling (Co-S) and multi-resource scheduling (M), reflecting a growing emphasis in the field on complex resource coupling and systematic optimization.

The sub-pie chart on the right further details the specific resource combinations addressed in the literature on coordinated scheduling (Co-S). The statistics indicate that integrated scheduling of berths and quay cranes (B+QC) is still the predominant research type, accounting for more than half of the relevant studies. Research focusing on combinations such as channel constraints, tugboat–pilot coordination, and other joint scheduling scenarios has also increased, though the overall proportion remains limited. This suggests considerable potential for further development in these directions.

Figure 3b illustrates the annual publication trends for different resource scheduling problems from 2001 to 2025. It is evident that between 2001 and 2010, the number of publications was relatively low, with primary attention devoted to berths (B) and quay cranes (QC). Since 2011, alongside advances in port automation and intelligent technologies, research interest has gradually intensified, and, in particular, the number of publications has increased significantly since 2019. In recent years, driven by growing demands for system integration and resource coordination, research on multi-resource scheduling (M) and coordinated scheduling (Co-S) has surged, becoming new growth points. At the same time, the scheduling of auxiliary resources such as tugboats (T), pilots (P), and channels (C) has attracted increasing attention and exploration.

In summary, research on port seaside scheduling optimization has evolved from an early focus on individual core resources such as berths and quay cranes to the coordinated optimization of multiple resources, including tugboats, channels, and pilots. This area is now advancing toward more complex resource coupling and system-integrated scheduling. Such a trend not only reflects the increasing complexity and intelligence of port operations but also demonstrates the field’s promising prospects for both theoretical innovation and practical application.

3. System Architecture and Performance Metrics of Port Seaside Operation System

3.1. Research Scope

The overall layout design of smart ports aims to achieve efficient operations, optimized resource utilization, and environmental sustainability. Modern ports are typically divided into two main functional zones: the seaside (water-side) and the landside. While each has its distinct roles, they together form an integrated port operation system.

The seaside zone primarily includes port waters, anchorages, berths, quay cranes, and other facilities related to vessel operations. As the critical interface between maritime transport and port infrastructure, this zone is responsible for vessel traffic management, cargo handling operations, and maritime traffic control. In smart ports, this area emphasizes high-precision channel planning, the integration of automated handling equipment, and the application of intelligent navigation systems to enhance operational safety and maximize efficiency.

In contrast, the landside zone mainly consists of container yards, truck operation areas, cargo transshipment facilities, logistics centers, and intermodal connections to rail and road networks. Its design focuses on improving the efficiency of logistics connectivity between the port and inland regions, ensuring smooth cargo flow across the supply chain.

Although the seaside and landside zones complement each other and jointly support overall port operations, this study will primarily focus on the seaside segment. Specifically, it explores how to optimize vessel inbound and outbound scheduling and operational workflows in the context of smart port development, aiming to improve overall operational efficiency and service quality.

This review centers on the seaside zone, systematically examining key issues such as berth allocation, quay crane scheduling, tugboat and pilot assignment, and vessel scheduling under channel constraints. It also briefly outlines the functional positioning of the landside zone to reflect the integrity and coordination of the port system.

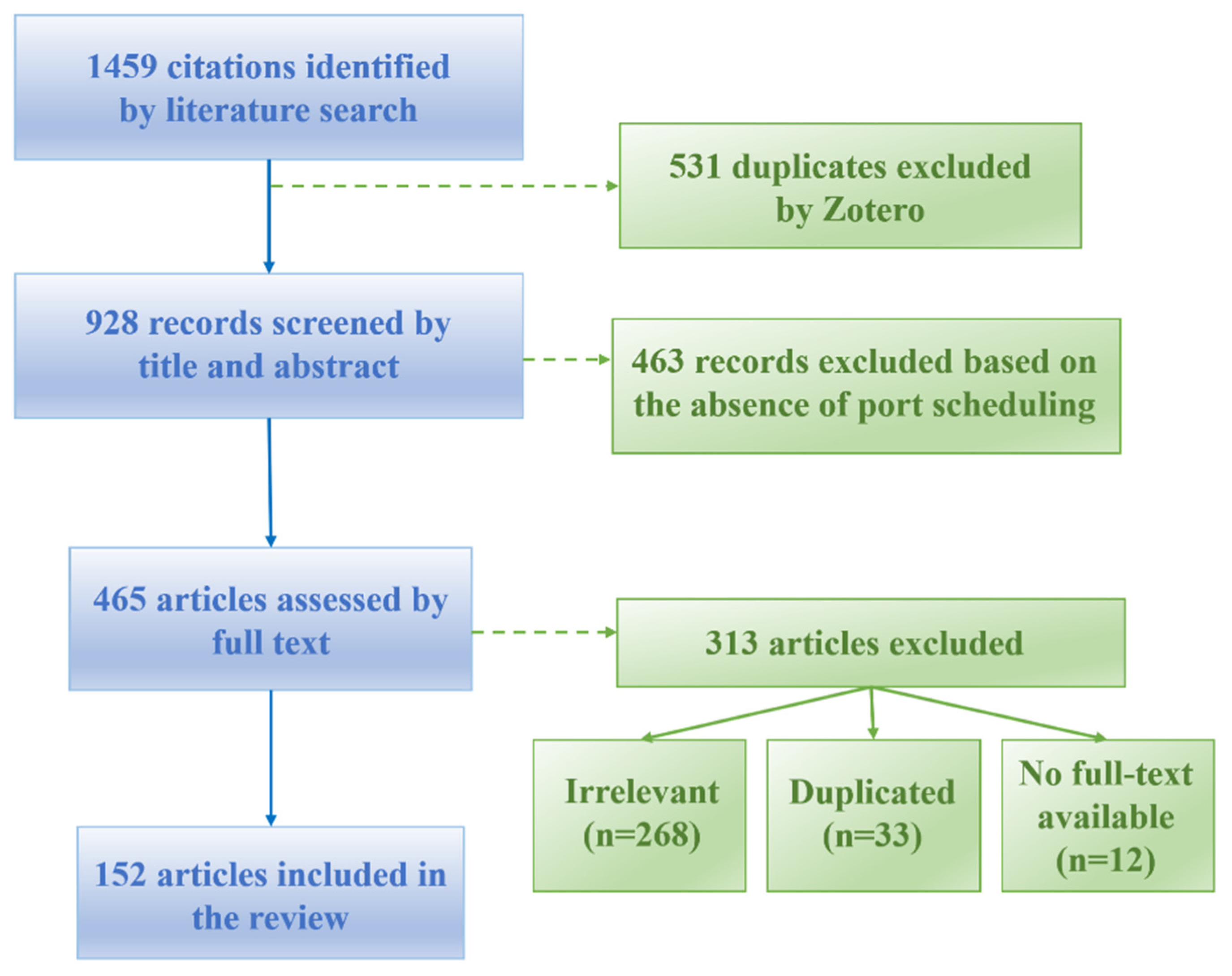
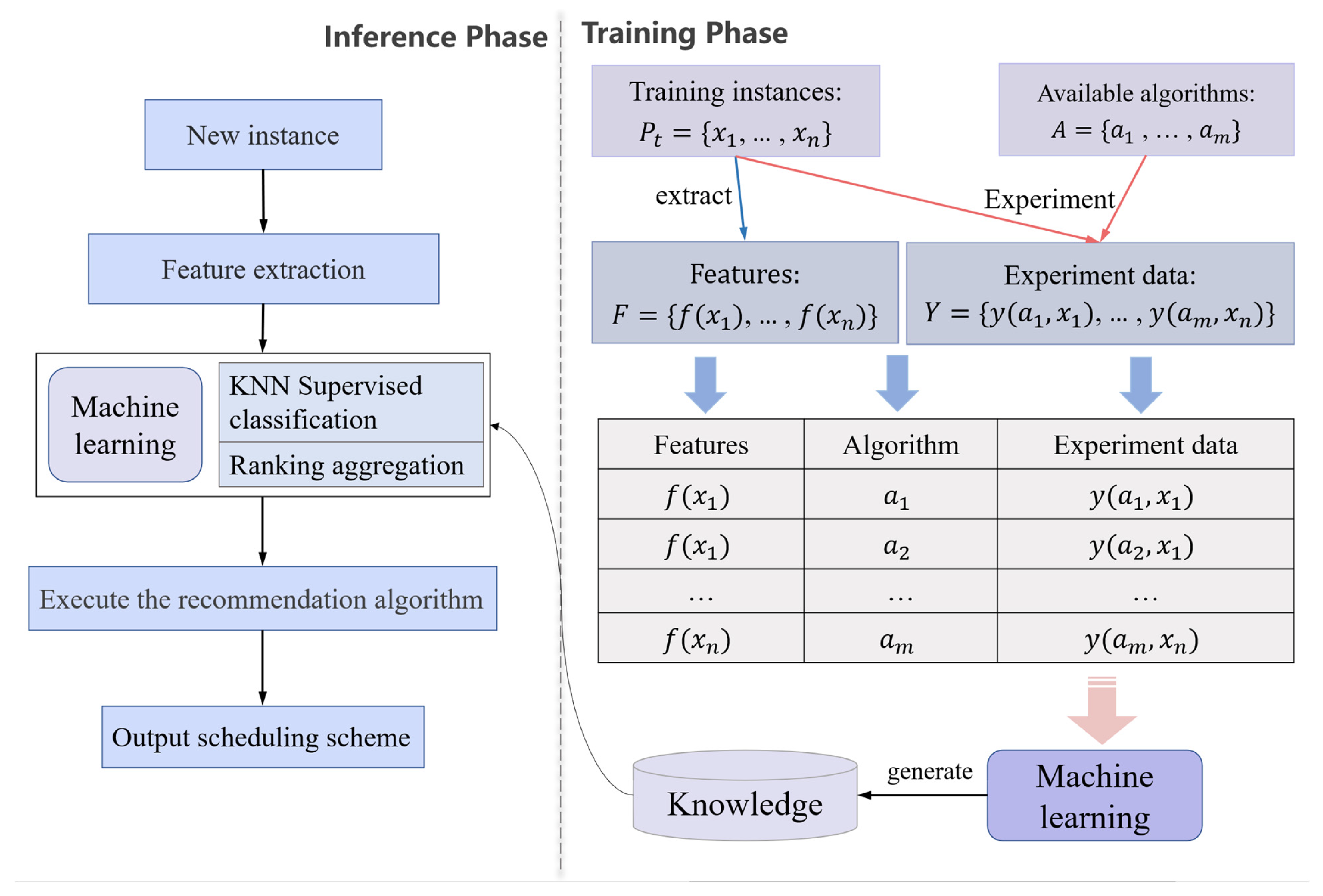
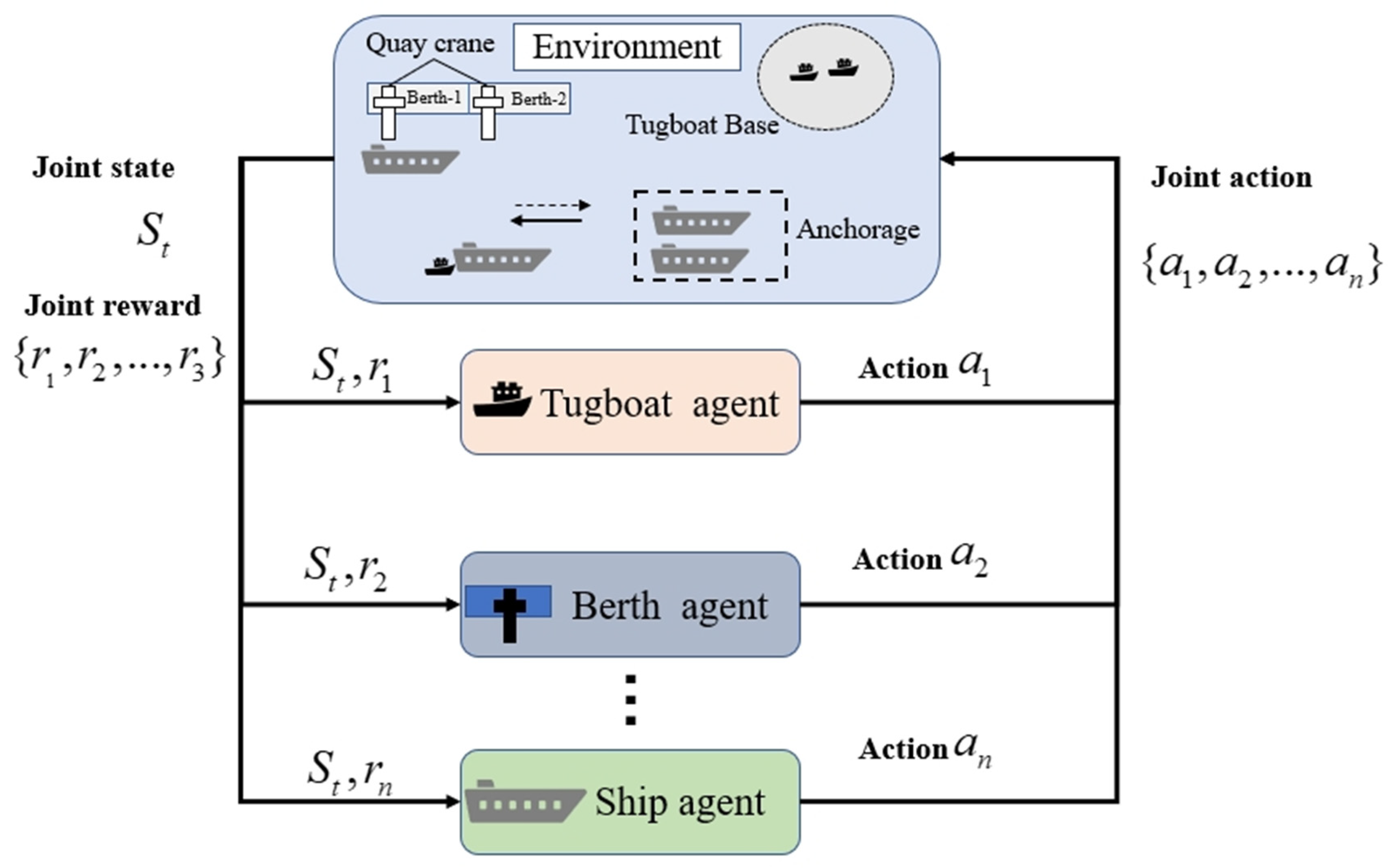
3.2. Components and Workflow of Seaside Operations

Seaside Operations primarily correspond to the process of vessel inbound and outbound operations, which are typically complex and intricate, involving multiple stages and stakeholders, with the aim of ensuring that vessels complete their entry and departure safely and efficiently. The typical scenario for vessel inbound and outbound operations is illustrated in Figure 4.

Based on the layouts and vessel inbound and outbound procedures documented for actual ports in the literature—including Tianjin Port [14,15,16], Shanghai Waigaoqiao Port [17], Tangshan Jingtang Port [18,19], Zhoushan Port and Rotterdam Port [20], Singapore Port [21,22], Guangzhou Port [23], and Bofa Port [24]—the following general process for vessel entry and departure can be summarized.

First, as a vessel approaches the port, it typically waits at an anchorage area located at a certain distance from the port. The port control center assigns an appropriate berth and arranges tugboats and pilots to assist with berthing, based on real-time data and vessel type. Tugboats are usually on standby at the “tugboat base” before the vessel enters port waters, ensuring they can promptly assist the vessel in safely approaching the berth when needed. In addition, pilots initially wait in the port area; when pilotage services are required, the port dispatches a pilot by pilot boat or helicopter to the anchorage, where the pilot boards the arriving vessel to provide guidance. As the vessel enters port waters, its speed is reduced to ensure safe maneuvering within the narrow channel.

Upon arrival at the designated berth, quay cranes are prepared, including the inspection of handling equipment and personnel. Meanwhile, the quayside operations team readies itself to enable the rapid and smooth loading and unloading of cargo. The handling process typically consists of two main stages: first, discharging, in which appropriate vehicles are arranged for cargo transfer according to cargo type and destination; and second, loading, which ensures that cargo is stowed in the prescribed order and manner to maintain vessel stability and safety.

After cargo operations are completed, the vessel begins the departure process. At this stage, tugboats and pilots are again mobilized to assist the vessel in safely leaving the berth. As the vessel navigates toward the port exit, it follows specific channel guidance to avoid interfering with other vessel traffic.

Finally, once the vessel leaves port waters, the captain continues to maintain contact with the navigation control center to ensure safe passage to the next destination. The entire inbound and outbound operation involves close coordination and cooperation among multiple parties and stages, requiring not only efficient port facilities but also effective information sharing and communication, so as to ensure overall port operational efficiency and safety.

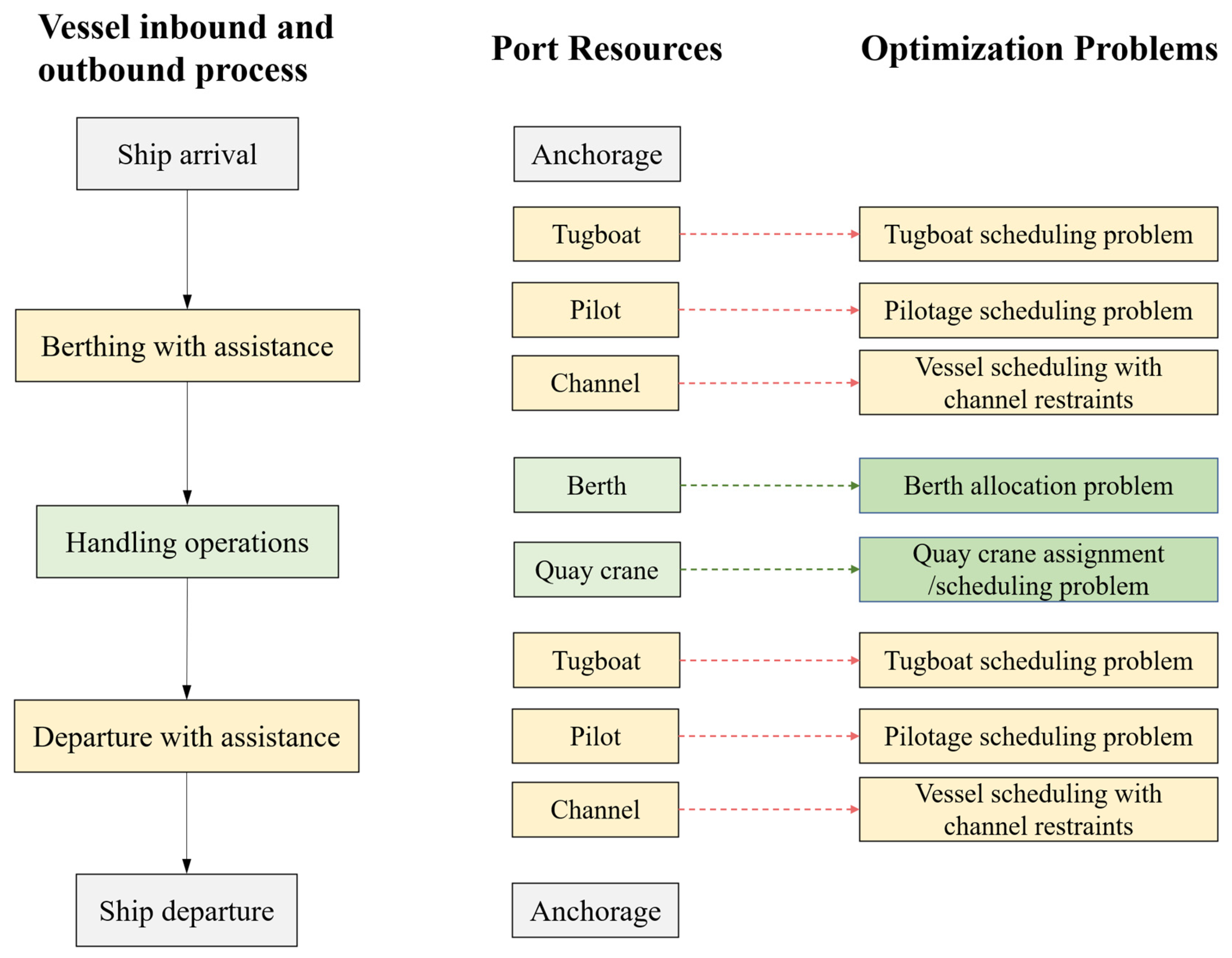
To further clarify the overall structure of port seaside operations, Figure 5 presents a comprehensive block diagram that maps the entire vessel inbound and outbound process, associated port resources, and corresponding optimization problems. This visualization provides an integrated perspective on the coordination of tugboats, pilots, channels, berths, and quay cranes, alongside the scheduling challenges inherent in each phase.

In summary, this section provides an overview of vessel inbound and outbound operations in seaside port systems, outlining the associated resources and their coordination, and illustrating how these elements relate to corresponding optimization problems.

3.3. Mathematical Formulations for Main Problems in Seaside Port Operations

As discussed in the previous section, the seaside port operation system comprises a series of interrelated processes with corresponding optimization problems, each characterized by limited resources, strict time constraints, and complex interdependencies. To effectively address these challenges, it is essential to construct mathematical formulations that clearly define decision variables, objectives, and operational constraints, thereby enabling systematic analysis and optimization through appropriate solution methods.

In the following, mathematical models for the main optimization problems in the seaside port operation system are presented, providing a formal basis for performance evaluation and the design of effective scheduling algorithms.

(1) Berth allocation problem

The berth allocation problem (BAP) is one of the most fundamental and extensively studied issues in port seaside operations. It focuses on determining the optimal assignment of vessels to specific berthing positions and time intervals along the quay, with the objective of improving berth utilization and minimizing vessel turnaround time. BAP directly affects downstream operations such as quay crane scheduling and yard logistics, and is subject to constraints including berth length, vessel draft requirements, and arrival–departure time windows. Depending on the spatial and temporal representation of berths, BAP can be categorized into discrete, continuous, and hybrid forms, each reflecting different levels of operational flexibility and complexity. In practical applications, BAP models may also incorporate tidal restrictions, channel accessibility, and environmental objectives, making it a critical decision-making problem in integrated port scheduling.

A typical BAP model was proposed by Imai et al. [25], which extended the static BAP to the Dynamic BAP (DBAP) and has made a significant contribution to subsequent BAP research. In this problem setting, it is assumed that berths are discrete and that each berth can serve only one vessel at a time, without considering other operational constraints. Suppose that a port has $m$ berths (set $B$), n vessels awaiting berthing (set $V$), and a set $P$ representing the service order of vessels. Let the arrival time of vessel $j$ be $A_j$, the handling time of vessel $j$ at berth $i$ be $H_{ij}$, and $D_i$ represent the time when berth $i$ becomes idle for berth allocation planning. The decision variable is a binary variable $x_{ijk}$, which equals 1 if vessel $j$ is serviced as the $k$th vessel at berth $i$, and 0 otherwise. Based on the above parameters, a static BAP mathematical model can be formulated as follows:

$$\mathrm{Minimize} {\displaystyle \sum _{i\in B}{\displaystyle \sum _{j\in V}{\displaystyle \sum _{k\in P}\left\{(n-k+1)H_{ij}+D_i-A_j\right\}}}}{x}_{ijk}$$

(1)

subject to

$${\displaystyle \sum _{i\in B}{\displaystyle \sum _{k\in P}{x}_{ijk}}}=1\hspace{1em}\forall j\in V$$

(2)

$${\displaystyle \sum _{j\in V}{x}_{ijk}}⩽1\hspace{1em}\forall i\in B,\hspace{0.33em}k\in P$$

(3)

$$x_{ijk}\in \{0,1\}\hspace{1em}\forall i\in B,\hspace{0.33em}j\in V,\hspace{0.33em}k\in P$$

(4)

The objective function (1) of this model aims to minimize the total service time and waiting time of all vessels. Constraint (2) ensures that each vessel is served at exactly one berth, and constraint (3) guarantees that at most one vessel can be served at the same berth at any given time. In the static BAP described above, it is assumed that all vessels arrive before the start of the planning horizon, i.e., $D_i\ge A_j$. However, according to the analysis of Imai et al. [25], vessels may arrive after the beginning of the planning horizon. Therefore, the corresponding DBAP model was proposed.

In this model, a set $V_i$ is introduced to represent vessels arriving after the start of berth planning (i.e., $A_j\ge S_i$), which is a subset of the vessel set $V$. In addition, a set $P_k=\left\{q\right|q<k\in P\}$ is defined to represent the service sequence prior to the $k$, which is a subset of $P$. Furthermore, an additional decision variable $y_{ijk}$ is introduced, representing the idle time of berth $i$ between the departure of the $k-1$th vessel and the arrival of the $k$th vessel when vessel $j$ is serviced as the $k$th vessel at berth $i$. Based on the above notation, the mathematical formulation of the DBAP can be expressed as follows:

$$\mathrm{Minimize} {\displaystyle \sum _{i\in B}{\displaystyle \sum _{j\in V}{\displaystyle \sum _{k\in P}\left\{(n-k+1)H_{ij}+D_i-A_j\right\}}}}{x}_{ijk}+{\displaystyle \sum _{i\in B}{\displaystyle \sum _{j\in V_i}{\displaystyle \sum _{k\in P}(n-k+1)}}}{y}_{ijk}$$

(5)

subject to constraints (2)–(4) and

$${\displaystyle \sum _{l\in V}{\displaystyle \sum _{q\in P_k}(H_{il}{x}_{ilq}+y_{ilq})}}+y_{ijk}⩾(A_j-D_i)x_{ijk}\hspace{1em}\forall i\in B,\hspace{0.33em}j\in V_i,\hspace{0.33em}k\in P$$

(6)

$$y_{ijk}⩾0\hspace{1em}\forall i\in B,\hspace{0.33em}j\in V,\hspace{0.33em}k\in P$$

(7)

The objective function (5) still aims to minimize the total handling time and waiting time of all vessels. The additional constraint (6) ensures that all vessels must begin service only after their arrival. This mathematical model represented a significant breakthrough in the early research on the BAP, and many subsequent studies [26,27] have built upon it for further improvements and extensions. Overall, this mathematical model captures the dynamic nature of vessel arrivals and berth availability, providing a more realistic framework for berth allocation in practical port operations.

Building on the above, the BAP has become one of the most extensively studied problems in seaside port operations, giving rise to a diverse range of mathematical formulations. These include discrete, continuous, and hybrid spatial representations, as well as deterministic, stochastic, and robust optimization frameworks, each tailored to different operational contexts and uncertainty conditions. A detailed and comparative overview of these formulations can be found in the review [6,10].

(2) BACAP

Following berth allocation, the efficient assignment and scheduling of quay cranes (QC) is critical to minimizing vessel turnaround time and maximizing berth productivity. The Quay Crane Assignment/Scheduling Problem (QCAP/QCSP) determines not only how many cranes should be assigned to each vessel but also the sequence and timing of their operations, subject to operational constraints such as non-crossing rules, safety margins, and interference avoidance between adjacent cranes. As a core component of seaside operations, this problem is inherently interdependent with berth allocation decisions and has been extensively studied through various mathematical formulations, ranging from deterministic mixed-integer programming models to stochastic and robust optimization frameworks. The following presents a representative mathematical model for the QC assignment and scheduling problem.

Kim and Park [28] developed an MIP model for the QCSP focusing on a single vessel, with the objective of minimizing the weighted sum of the makespan and the total completion time of QC. The primary aim of this model is to determine the sequence in which multiple quay cranes perform loading and unloading operations according to the vessel’s stowage plan, while considering constraints such as crane availability, precedence relationships between tasks, the non-crossing rule between cranes, and restrictions on tasks that cannot be executed simultaneously. This work laid the foundation for subsequent studies on quay crane scheduling and remains a benchmark for modeling operational constraints in port seaside resource management. Furthermore, different mathematical modeling frameworks for the QCSP have been summarized and discussed in detail in the review [5], providing a comprehensive overview of the problem’s diverse formulations.

In practice, berth allocation and quay crane scheduling are highly interdependent, and optimizing them separately may lead to suboptimal overall performance. This has given rise to the berth and quay crane assignment problem (BACAP), an integrated scheduling problem that jointly determines berth positions, vessel berthing times, and quay crane allocations. With the growing complexity of port operations and the increasing emphasis on resource coordination, BACAP has become a research hotspot, attracting significant attention for its potential to improve vessel turnaround times and enhance overall terminal productivity. Building on the BAP framework [25], Imai et al. [29] proposed a widely cited mathematical model for BACAP, which extends berth allocation to simultaneously determine optimal quay crane assignments under realistic operational constraints.

The model minimizes the total service time of all vessels while considering the required number of cranes per vessel, crane availability constraints, and detailed crane movement restrictions. By coupling berth allocation with quay crane assignment, this formulation captures the interdependence between the two resources more effectively than separate optimization, making it a key reference for coordinated scheduling in seaside port operations.

In the BACAP model, the berth set $B$, vessel set $V$, and service order set $P$ defined in the previous BAP model are retained, along with the parameters $D_i$, $A_j$, $H_{ij}$, and the decision variable $x_{ijk}$. Building on this foundation, the following additional parameters and variables are introduced: $M$ denotes a sufficiently large constant; $R_j$ represents the number of cranes required by vessel $j$; $Q_i$ denotes the number of cranes initially assigned to berth $i$ in the planning horizon; and $TQ$ is the total number of available quay cranes. In addition to $x_{ijk}$, new decision variables $s_{ijk}$ and $f_{ijk}$ are defined to represent, respectively, the start time and finish time of serving vessel $j$ at berth $i$ as the $k$th vessel.

For QC movement–related parameters, three additional decision variables are introduced: $e_{ik}$ denotes the number of cranes at berth $i$ immediately after serving the $k$th vessel, including cranes transferred from neighboring berths; $w_{i^{\prime }i{k}^{\prime }k}$ represents the number of cranes transferred from berth $i^{\prime }$ after serving its $k^{\prime }$th vessel to berth $i$ (the next to $i^{\prime }$) after serving its $k$th vessel; and $z_{ik}$ indicates the number of cranes allocated to berth $i$ for the $k$th vessel, including those in an idle state. In addition, three auxiliary variables—${\delta }_{i{i}^{\prime }k{k}^{\prime }}$, ${\varphi }_{i{i}^{\prime }k{k}^{\prime }}$, and ${\gamma }_{i{i}^{\prime }k{k}^{\prime }}$—are introduced to describe the temporal relationships in quay crane transfers between adjacent berths, ensuring the model can accurately distinguish between different crane movement scenarios; the detailed definitions of these variables can be found in [29]. The BACAP model is formulated as follows:

$$\mathrm{Minimize} {\displaystyle \sum _{j\in V}\left\{{\displaystyle \sum _{i\in B}{\displaystyle \sum _{k\in P}{f}_{ijk}}}-A_j\right\}}$$

(8)

subject to constraints (2)–(4) and

$${\displaystyle \sum _{i\in B}{\displaystyle \sum _{k\in P}{s}_{ijk}}}⩾A_j\hspace{1em}\forall j\in V$$

(9)

$${\displaystyle \sum _{j\in V}{s}_{ijk}}⩾{\displaystyle \sum _{j\in V}{f}_{ijk-1}}\hspace{1em}\forall i\in B,\hspace{0.33em}k\in P$$

(10)

$$s_{ijk}⩽M{x}_{ijk}\hspace{1em}\forall i\in B,\hspace{0.33em}j\in V,\hspace{0.33em}k\in P$$

(11)

$$s_{ijk}+H_{ij}{x}_{ijk}=f_{ijk}\hspace{1em}i\in B,\hspace{0.33em}j\in V,\hspace{0.33em}k\in P$$

(12)

$${\displaystyle \sum _{j\in V}{f}_{ij0}}=D_i\hspace{1em}i\in B$$

(13)

$${\displaystyle \sum _{j\in V}{R}_j}{x}_{ijk}⩽z_{ik}\hspace{1em}\forall i\in B,\hspace{0.33em}k\in P$$

(14)

$$e_{ik}=z_{ik}+{\displaystyle \sum _{i^{\prime }=(i-1,i+1)\in B}{\displaystyle \sum _{k^{\prime }\in P}{w}_{i^{\prime }i{k}^{\prime }k}}}\hspace{1em}\forall (i\ne 1,m)\in B,\hspace{0.33em}k\in P$$

(15)

$$e_{ik}=z_{ik+1}+{\displaystyle \sum _{i^{\prime }=(i-1,i+1)\in B}{\displaystyle \sum _{k^{\prime }\in P}{w}_{i{i}^{\prime }k{k}^{\prime }}}}\hspace{1em}\forall i(\ne 1,m)\in B,\hspace{0.33em}k\in P$$

(16)

$$e_{ik}=z_{ik}+{\displaystyle \sum _{k^{\prime }\in P}{w}_{i+1,i,k^{\prime }k}}\hspace{1em}\forall i(=1)\in B,\hspace{0.33em}k\in P$$

(17)

$$e_{ik}=z_{ik+1}+{\displaystyle \sum _{k^{\prime }\in P}{w}_{i,i+1,k{k}^{\prime }}}\hspace{1em}\forall i(=1)\in B,\hspace{0.33em}k\in P$$

(18)

$$e_{ik}=z_{ik}+{\displaystyle \sum _{k^{\prime }\in P}{w}_{i-1,i,k^{\prime }k}}\hspace{1em}\forall i(=m)\in B,\hspace{0.33em}k\in P$$

(19)

$$e_{ik}=z_{ik+1}+{\displaystyle \sum _{k^{\prime }\in P}{w}_{i,i-1,k{k}^{\prime }}}\hspace{1em}\forall i(=m)\in B,\hspace{0.33em}k\in P$$

(20)

$${\displaystyle \sum _{j^{\prime }(\ne j)\in V}{f}_{i^{\prime }{j}^{\prime }{k}^{\prime }}}-({\delta }_{i{i}^{\prime }k{k}^{\prime }}-1)M⩾{\displaystyle \sum _{j\in V}{f}_{ijk}}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(21)

$${\displaystyle \sum _{j\in V}{f}_{ijk}}-({\delta }_{i{i}^{\prime }k{k}^{\prime }}-1)M⩾{\displaystyle \sum _{j^{\prime }(\ne j)\in V}{s}_{i^{\prime }{j}^{\prime }{k}^{\prime }}}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(22)

$$w_{i{i}^{\prime }k{k}^{\prime }}-({\delta }_{i{i}^{\prime }k{k}^{\prime }}-1)M⩾0\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(23)

$${\displaystyle \sum _{j\in V}{f}_{ijk}}-({\varphi }_{i{i}^{\prime }k{k}^{\prime }}-1)M⩾{\displaystyle \sum _{j^{\prime }(\ne j)\in P}{f}_{i^{\prime }{j}^{\prime }{k}^{\prime }}}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(24)

$${\displaystyle \sum _{j^{\prime }(\ne j)\in V}{s}_{i^{\prime }{j}^{\prime }(k^{\prime }+1)}}-({\varphi }_{i{i}^{\prime }k{k}^{\prime }}-1)M⩾{\displaystyle \sum _{j\in V}{f}_{ijk}}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(25)

$$w_{i{i}^{\prime }k{k}^{\prime }}-({\varphi }_{i{i}^{\prime }k{k}^{\prime }}-1)M⩾0\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(26)

$$w_{i{i}^{\prime }k{k}^{\prime }}-(1-{\gamma }_{i{i}^{\prime }k{k}^{\prime }})M⩽0\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(27)

$${\delta }_{i{i}^{\prime }k{k}^{\prime }}+{\varphi }_{i{i}^{\prime }k{k}^{\prime }}+{\gamma }_{i{i}^{\prime }k{k}^{\prime }}=1\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(28)

$${\displaystyle \sum _{i^{\prime }\in B}{\displaystyle \sum _{k^{\prime }\in P}{w}_{i{i}^{\prime }k{k}^{\prime }}}}⩽M{\displaystyle \sum _{j\in V}{x}_{ijk}}\hspace{1em}\forall i\in B,\hspace{0.33em}k\in P$$

(29)

$$z_{i1}=Q_i\hspace{1em}\forall i\in B$$

(30)

$$\mathrm{TQ}={\displaystyle \sum _{i\in B}{Q}_i}$$

(31)

$$w_{i{i}^{\prime }k{k}^{\prime }}⩽z_{ik}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(32)

$$w_{i^{\prime }i{k}^{\prime }k}⩽e_{ik}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(33)

$${\displaystyle \sum _{i\in B}{z}_{ik}}={\displaystyle \sum _{i\in B}{Q}_i}\hspace{1em}\forall k\in P$$

(34)

$$s_{ijk},f_{ijk}⩾0\hspace{1em}\forall i\in B,\hspace{0.33em}j\in V,\hspace{0.33em}k\in P$$

(35)

$${\delta }_{i{i}^{\prime }k{k}^{\prime }}\in \{0,1\}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(36)

$${\varphi }_{i{i}^{\prime }k{k}^{\prime }}\in \{0,1\}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(37)

$${\gamma }_{i{i}^{\prime }k{k}^{\prime }}\in \{0,1\}\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(38)

$$z_{ik}⩾0\hspace{1em}\forall i\in B,\hspace{0.33em}k\in P$$

(39)

$$e_{ik}⩾0\hspace{1em}\forall i\in B,\hspace{0.33em}k\in P$$

(40)

$$w_{i{i}^{\prime }k{k}^{\prime }}⩾0\hspace{1em}\forall i,i^{\prime }\in B,\hspace{0.33em}k,k^{\prime }\in P$$

(41)

The objective function (8) is the minimization of the total service time.

Constraints (2)–(4) and (9)–(13) correspond to the BAP-related constraints and are therefore not repeated here. Constraint (14) ensures that each vessel is allocated a sufficient number of quay cranes to perform loading and unloading operations. Constraint sets (15)–(20) define the flow conservation rules governing crane movements, while constraints (21)–(28) specify flow conservation for crane transfers between two specific adjacent berths. Constraint (29) ensures that if vessel $j$ is served at a berth other than berth $i$, then no crane flow associated with vessel $j$ is generated at berth $i$. Constraint (30) links the initial number of cranes at each berth to the number of cranes assigned to the first vessel served at that berth. Equation (31) guarantees that all available quay cranes are allocated across all berths. Constraints (32) and (33) describe, for a given berth, the relationship between crane movements, a hypothetical crane-move node, and the number of cranes located at the berth immediately before the node. Equalities (34) ensure that, at any stage of the planning horizon, the total number of quay cranes distributed among all berths equals the total number available in the system. Finally, constraints (35)–(41) define the domains and admissible ranges of the decision variables. For further details and a complete description of the model, readers are referred to [29].

In summary, the BACAP model integrates berth allocation and quay crane assignment within a single optimization framework, capturing the spatial and temporal interdependencies between the two resources. This type of mathematical modeling framework for BACAP/BACASP has been well summarized and discussed in several review studies [8,9], reflecting the richness and diversity of research in this area. By combining vessel scheduling decisions with detailed crane allocation and movement constraints, the model provides a realistic and comprehensive representation of seaside port operations, offering a solid foundation for developing coordinated scheduling strategies that can significantly improve terminal efficiency.

(3) Tugboat scheduling problem

The tugboat scheduling problem is a critical component of seaside port operations, involving the allocation and scheduling of tugboats to assist vessels during berthing and unberthing maneuvers. Tugboats are essential for guiding vessels safely through harbor channels, positioning them at berths, and ensuring efficient departure procedures, particularly for large container ships and tankers that have limited maneuverability. The problem typically aims to minimize vessel waiting times, tugboat idle times, or total operational costs, while satisfying constraints related to tugboat availability, travel times between locations, required tug capacity for different vessel sizes, and service time windows. Due to the dynamic nature of vessel arrivals, varying tugboat assignments, and the tight coordination required with other port resources, the tugboat scheduling problem is inherently complex and has been widely studied using mathematical optimization and heuristic approaches.

A mathematical model for tugboat scheduling is presented in [30], designed to capture the key operational characteristics of tug allocation in port operations. In this model, it is assumed that the port operates with $l$ tugboats (set $G$) and $n$ vessels awaiting towage services (set $V$), with the set of service sequences denoted by $P$ and indexed by $k$. To simplify the problem description, a First-Come-First-Served (FCFS) rule is applied, meaning that vessels are towed in the order of their arrival. The matching rules between tugboat availability, horsepower, and vessel length, as well as the corresponding operation durations, are assumed to be predefined. The parameter $A_j$ denotes the arrival time of vessel $j$, $O_j$ represents the towage operation time for vessel $j$, $S_{jk}$ indicates the start time of vessel $j$ for the $k$th job, and $F_{jk}$ represents its completion time. Tugboat $i$ has a horsepower $H_i$, while vessel $j$ requires a minimum horsepower $L_j$. The decision variable $x_{ij}$ is defined to be 1 if tugboat $i$ is assigned to vessel $j$, and 0 otherwise. Based on the above definitions, the mathematical model can be formulated as follows:

$$\min (\max \{F_{j_{(1)}1},\dots ,F_{j_{(k)}k},\dots ,F_{j_{(l)}l}\})$$

(42)

subject to

$$1\le {\displaystyle \sum _{j\in V}{x}_{ij}}\le 2\hspace{1em}\forall i\in G$$

(43)

$${\displaystyle \sum _{i\in G}{x}_{ij}{H}_i}\ge L_j\hspace{1em}\forall j\in V$$

(44)

$$F_{jk}=S_{jk}+O_j\hspace{1em}\forall j\in V,\hspace{0.33em}k\in P$$

(45)

$$S_{jk}=\max \{A_j,F_{j_{(1)}{k}_{(1)}},F_{j_{(2)}{k}_{(2)}},\dots ,F_{j_{(j)}{k}_{(j)}}\},k_{(1)}, k_{(2)},\dots ,k_{(j)}<k$$

(46)

$$x_{ij}\in \{0,1\}\hspace{1em}\forall i\in G,\hspace{0.33em}j\in V$$

(47)

The objective function (42) minimizes the maximum completion time of all the vessels. Constraints (43) and (44) specify that the number and horsepower of tugboats assigned to each vessel must satisfy the assignment rules. Equality (45) calculates the completion time of vessel $j$ for the $k$th job as the sum of its start time and operation time. Equality (46) states that the start time of a vessel’s operation depends on the later of its arrival time and the completion time of its preceding task. Through these formulations, the mathematical model provides a concise yet effective representation of the key characteristics of the tugboat scheduling problem, capturing both resource matching requirements and temporal dependencies in service operations.

In summary, the presented mathematical model offers a straightforward yet representative framework for describing the tugboat scheduling problem, effectively capturing its core operational constraints and timing relationships. Subsequent studies have extended this modeling approach to incorporate additional practical considerations; for example, Kang et al. [31] account for the uncertainty in vessel arrival and tugging process time, further enhancing the applicability of tugboat scheduling models in dynamic port environments.

(4) Other problems

In addition to the BAP, BACAP, and tugboat scheduling problems discussed above, the seaside port operation system also involves several scheduling and optimization problems that have only recently begun to attract research attention. Examples include the vessel scheduling problem with channel restrictions and the pilotage scheduling problem, both of which were also mentioned in the inbound and outbound operation process described in the previous section. These problems, while less extensively studied than the classical models, play a critical role in ensuring safe, efficient, and coordinated port operations. In this subsection, we briefly introduce the main characteristics and core constraints of these two problems.

The vessel scheduling problem under channel restrictions is critical for ports with narrow channels, where limited navigational capacity can lead to vessel congestion and delays if not properly managed. In Zhang et al. [32], the case of a one-way channel is considered, and a mathematical model is proposed to minimize the total waiting time of vessels by jointly determining their entry and exit times while ensuring navigational safety. The model incorporates vessel time windows, channel transit times, and safety separation constraints for both same-direction and opposite-direction traffic, as well as berth availability, vessel speed and length, and berth position dependencies. This coordinated channel–berth scheduling framework ensures conflict-free vessel movements and adherence to port navigation rules. Building on this problem setting, subsequent studies have extended the one-way channel assumption to two-way channels, compound channel systems, and other more complex restricted channels [33,34,35,36,37].

Pilots, as another essential resource alongside tugboats in assisting vessel entry and departure, have only recently begun to attract research attention in the context of seaside port operations, and their scheduling is often studied in conjunction with other resources. Wu et al. [38] formulated the pilotage planning problem in seaports as an MIP model that jointly determines vessel scheduling through the channel, pilot shift assignments, and pilot routing. The model incorporates constraints on channel capacity for inbound and outbound traffic, vessel service time windows, pilot working time regulations, and travel times between pilots’ locations and vessels, ensuring feasible and efficient pilotage schedules that meet both navigational and labor requirements.

In summary, all the optimization problems discussed in this paper revolve around the core scheduling challenges illustrated in the diagram, which comprehensively represent the port seaside operation system. Specifically, the research scope of this study—focusing on berth allocation, quay crane scheduling, tugboat scheduling, pilot assignment, and channel-constrained vessel scheduling—aligns with the corresponding stages and resources mapped in the process. This structured overview provides a consistent foundation for the subsequent analysis and classification of optimization methods within the port seaside operations context.

3.4. Optimization Objectives and Performance Indicators of Port Seaside Operation Systems

In port seaside operation systems, optimization metrics are crucial for enhancing overall port efficiency. These metrics not only determine operational costs and resource utilization but also directly impact service quality and the achievement of environmental objectives. The following section discusses several key optimization metrics and illustrates how ports can achieve optimization through intelligent scheduling systems and advanced technologies.

(1) Time

Vessel turnaround time plays a vital role in port seaside operation systems. Prolonged turnaround times can lead to port congestion, delay subsequent vessel operations, and negatively affect overall logistics efficiency. To optimize this metric, ports employ intelligent scheduling systems to arrange vessel entry and departure sequences and adjust tugboat deployment in real time, ensuring that vessels can complete each operational stage swiftly and safely. In addition, efficient quay crane operations are essential for minimizing vessel berth time, while real-time monitoring and data analysis further support optimal resource allocation and high operational efficiency.

Based on a review and classification of the retrieved literature, time-related performance indicators in this study are divided into four categories: completion time, waiting time, delay/deviation time, and total turnaround time. Each type of objective emphasizes different aspects, as summarized in

Table 1. Classification of time-related optimization metrics.

Optimization Metric Category	Representative Objective (Examples)	Description	Ref
Completion Time	Minimize Makespan	Emphasizes shortening the overall operation cycle to improve port processing speed and throughput capacity.	[16,19,28,30,39,40,41,42,43]
	Minimize Maximum Completion Time
Vessel Waiting/Delay Time	Minimize Total Waiting Time	Focuses on the waiting time of vessels or equipment before operations and the punctuality of operation execution, aiming to improve responsiveness, service reliability, and scheduling fairness.	[32,44,45,46,47,48,49,50,51,52,53]
	Minimize Delay Time
Total Turnaround Time	Minimize Total Turnaround Time	Targets the total time vessels spend in port, aiming to enhance port flow efficiency and reduce resource occupancy duration.	[24,25,29,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75]
	Minimize Service Time

.

Minimizing completion time targets reducing the overall duration of port operations, commonly expressed as makespan or maximum completion time, thereby enhancing operational efficiency and resource utilization. For example, Tasoglu and Yildiz [39] focused on minimizing vessel departure times in integrated berth and quay crane scheduling. Liu et al. [16] addressed the expected weighted completion time considering uncertainties in vessel arrivals and handling times. Additional studies also emphasized completion time reduction across berth allocation, quay crane, and tugboat scheduling problems, highlighting its critical role in port efficiency [19,28,30,40,41,42,43].

Minimizing vessel waiting/delay time addresses the idle or delayed periods experienced by vessels or equipment due to resource conflicts or scheduling uncertainties, such as waiting for berths, quay cranes, or tugboats. Abou Kasm et al. [44] optimized the maximum vessel waiting time involving pilotage and tugboat operations, while Lv et al. [45] addressed weighted average vessel waiting time within dynamic berth allocation scenarios. Other studies further explored specific delays, including mooring, unberthing, and deballasting delays, underscoring their significant impact on operational efficiency and resource utilization [46,47].

Minimizing total vessel turnaround time concerns the entire duration of a vessel’s stay at port from arrival until departure, typically encompassing waiting, service, and operational delays. Li et al. [54] considered uncertainties in quay crane maintenance activities to effectively reduce vessel dwell time. Liang et al. [55] optimized total operational, waiting, and delay durations through dynamic quay crane scheduling. Additional research concentrated on minimizing vessel service time, further demonstrating the importance of reducing overall turnaround time for improved port throughput and resource efficiency [56,57].

(2) Cost

Operating cost is another core metric in port seaside operation systems. Excessive operational costs not only increase the financial burden on ports but may also undermine their market competitiveness, particularly in an unstable global economic environment. To reduce operating costs, ports optimize operational processes through intelligent scheduling systems to maximize resource utilization and avoid equipment and labor idleness or overuse. In addition, optimizing vessel entry and departure routes and introducing automated, energy-efficient equipment—such as electric tugboats and automated quay cranes—not only reduces energy consumption but also improves operational efficiency, thereby lowering operating costs and enhancing overall port competitiveness.

Based on a review of the literature related to cost metrics, optimization indicators in this category can generally be classified into four groups: resource utilization cost, waiting/delay/deviation cost, energy and emission cost, and comprehensive operating cost, as summarized in

Table 2. Classification of cost-related optimization metrics.

Optimization Metric Category	Representative Objectives (Examples)	Description	Ref
Resource Utilization Cost	Minimize tugboat operating cost	Focuses on the utilization and expenditure of port operation equipment (e.g., tugboats, quay cranes) during scheduling; emphasizes high resource utilization and scheduling economy.	[21,22,76,77]
	Minimize berth or quay crane usage costs Minimize vessel berthing cost
Waiting/Delay/Deviation Cost	Minimize vessel waiting cost	Mainly covers the loss incurred by vessels waiting for berths or tugboat resources and delay losses during scheduling; also includes the economic impact of deviations from uncertain or rescheduled plans. Emphasizes time loss valuation and robustness assurance.	[78,79,80,81,82,83,84,85,86]
	Minimize penalty cost for deviation between actual scheduling and baseline plan
Energy and Emission Cost	Minimize fuel consumption cost	Focuses on green port and energy optimization, emphasizing energy efficiency during operations and environmental sustainability.	[87,88,89,90,91]
	Minimize port carbon emission cost
Comprehensive Operating Cost	Minimize weighted sum of multiple costs (e.g., operation, delay, energy, equipment, etc.)	Considers multiple cost factors and builds a unified cost function, suitable for scenarios involving multi-resource coordination and overall operational optimization.	[91,92,93,94,95,96,97,98,99,100,101,102,103,104]

.

Resource utilization cost primarily aims to minimize the operational costs associated with tugboat, quay crane, or pilot deployment during port activities. For example, Wei et al. [21] focused on minimizing the tugboat operation cost through optimized scheduling. Building on this, subsequent studies have further incorporated both sailing costs and fixed costs of tugboats into the optimization objective, thus providing a more comprehensive evaluation of tugboat assignment expenses [22,76]. In addition, Xiao et al. [77] addressed minimization of total pilot service cost, including mobilization, fixed, and delay-related penalties.

Waiting/delay/deviation cost reflects economic losses from vessel waiting times and schedule deviations, emphasizing scheduling timeliness and robustness. In the context of BACAP, previous studies have minimized total costs comprising berth section deviation, late berthing, and late departure for each vessel [78,79,80]. Kolley et al. [81] addressed penalty costs from potential waiting time, spatial deviation, and non-robust or postponed assignments using a robust optimization model with vessel-specific priorities. Xie et al. [82] considered the weighted sum of deviations from expected berthing locations and times, optimizing both spatial and temporal assignments.

Energy and emission cost has also received attention in the recent literature. For example, Mao et al. [87] investigated berth allocation in a port multi-energy system, where the energy supply costs include the power generation unit’s fuel cost, start-up cost, and the cost of procuring electricity from the bulk power grid. Tang et al. [88] decompose terminal energy into operating, transport, and standby parts and show that layout-driven coordination cuts consumption. Iris & Lam [90] integrate PV-battery storage with time-of-use pricing and load shifting for further savings. Chargui et al. [91] embed robust optimization in berth–QC scheduling, hedging against uncertain arrival and processing times while tracking spot electricity prices, proving that simultaneous operational flexibility and price awareness can still shrink energy-emission expenditure.

Comprehensive operating cost encompasses multiple cost types, including equipment operation, vessel waiting and delay, and energy-related expenses, providing a holistic perspective more aligned with actual port operations. For instance, Wang et al. [92] minimized total costs involving vessel waiting, delay penalties, position deviation, and quay crane operation by jointly optimizing berth and crane allocation. Venturini et al. [93] considered idle time, operating, delay, and fuel costs for multi-port berth allocation, also optimizing vessel speed. He et al. [94] included quay crane operator performance and wage costs, while Yang et al. [95] focused on the integrated optimization of berths, tugboats, and quay cranes, considering costs related to in-port time, extra truck distance, tugboat use, and crane handling. Chargui et al. [91] further incorporated energy consumption costs and the potential revenue from vessels arriving ahead of schedule.

(3) Other

In addition to time- and cost-related metrics, optimization research in port seaside operation systems increasingly emphasizes energy consumption, resource utilization, service level, and indicators specific to quay crane operations, as summarized in

Table 3. Other optimization metrics.

Metric Category	Description	Ref
Energy Consumption	Energy/fuel consumption of equipment during operations	[23,88,105]
Resource Utilization Rate	Utilization rate of equipment	[106]
Service Level	Customer satisfaction	[107,108]
Quay Crane Related	Quay crane travel distance	[109]
	Movements of quay cranes	[110,111]
	Number of dual-cycle operations	[112]

.

With growing emphasis on global green development, optimizing energy consumption has become a crucial research direction. By integrating energy-efficient equipment and refining operational processes, ports can significantly lower energy use and environmental impact. The adoption of electric tugboats and automation technology has been shown to reduce the consumption associated with traditional fuel-driven equipment. Intelligent scheduling further optimizes vessel routing and operations, minimizing sailing and waiting times to enhance overall energy efficiency and support sustainability goals. Recent studies have addressed energy consumption in multi-resource scheduling scenarios [88], green tugboat operations [23], and overall port fuel consumption [105], collectively advancing energy conservation and emission reduction within port environments.

Resource utilization rate serves as a key indicator for evaluating the efficiency of equipment deployment, with implications for capacity enhancement, cost reduction, and scheduling flexibility. For example, Lassoued and Elloumi [106] investigated the joint berth and quay crane assignment problem and proposed a two-level model aimed at maximizing the number of available quay cranes to improve utilization rates.

Service level indicators, which assess punctuality, reliability, and customer satisfaction, are increasingly integrated into multi-objective port scheduling models. Notably, Xiang et al. [107] introduced a robust optimization framework that jointly minimizes total berth allocation cost and maximizes customer satisfaction under uncertainty. Similarly, Xu et al. [108] considered customer service improvements by targeting reductions in vessel delay and increases in buffer times to strengthen the robustness of berth planning.

Quay crane operation metrics, such as minimizing travel distance [109] and crane movements [110,111], are also frequently optimized, as they directly affect the efficiency and energy usage of cargo handling processes. Improvements in these areas not only reduce unnecessary movements and operational time but also decrease equipment wear and energy consumption. Further, Zhang and Kim [112] advanced dual-cycle operation strategies for quay crane assignment, aiming to maximize dual-cycle operations and thus minimize the number of operational cycles required.

In summary, these diverse optimization metrics are highly interrelated. Coordinated optimization across these areas not only boosts operational efficiency and cost-effectiveness but also strengthens port competitiveness and sustainability. The continued adoption of intelligent scheduling and automation technologies promises further gains in cost reduction, resource efficiency, service quality, and environmental performance.

4. Mathematical Models and Exact Solution Methods for Seaside Scheduling

4.1. Deterministic Models

Deterministic mathematical models have always played a fundamental role in research on port seaside scheduling optimization. Built on the premise of known and stable input data, these models—often formulated as mixed-integer programming (MIP) or Integer Programming (IP)—precisely capture the relationships among scheduling entities, resource allocation, and operational constraints, enabling the derivation of optimal solutions within a controllable framework. As scheduling systems have grown in complexity and management objectives have diversified, deterministic models have gradually evolved from representing single-resource problems to addressing multi-resource coordinated scheduling and dynamic scheduling scenarios, highlighting their adaptability and extensibility.

In the early stages of research, scholars mainly developed single-resource models for port scheduling tasks. For tugboat scheduling, Wang et al. [30] proposed an MIP model to minimize the maximum vessel service completion time, considering tugboat numbers, horsepower, and service times. Later studies introduced a multiple services from multiple waypoints (MSMW) approach and enhanced inequality constraints to improve schedule compactness and cost control [113], while network-based IP was employed to integrate tugboat point demand with vessel planning, achieving a coordinated balance between tugboat operating costs and vessel delay times [96].

BAP has long been a key topic in port scheduling research. Early studies mainly focused on discrete berth allocation, assigning vessels to fixed positions along the quay [25,56]. Later, continuous berth allocation models were developed, allowing vessels to berth flexibly along the quay and improving space utilization [114,115]. As research progressed, modeling approaches began to account for practical complexities such as tidal constraints and time-dependent berth accessibility [68] as well as dynamic vessel arrivals and real-time assignment [25]. Recent models further incorporate multi-port coordination and environmental objectives, including emission and fuel consumption reduction [93]. Optimizing vessel arrival times has also been recognized as a strategy for reducing port emissions and schedule delays within discrete dynamic BAPs [47]. These advances reflect the transition of BAP modeling from static deterministic formulations to frameworks that address operational, environmental, and collaborative challenges.

As another key issue in port operations, the quay crane assignment and scheduling problem has attracted significant attention and is often formulated as a deterministic model. Kim and Park [28] developed a mixed-integer programming model considering operation sequences, crane availability, and interference constraints to minimize vessel processing time. On this basis, Abou Kasm and Diabat [43] further incorporated non-crossing and safety distance constraints, using an improved integer programming model and branch-and-price strategy to more precisely control crane scheduling and effectively address interference during large vessel berthing.

Channel constraints during vessel inbound and outbound operations have made channel-constrained vessel scheduling an important topic in port research. To address these challenges, Li and Jia [116] and Jia et al. [117] incorporated channel limitations into their models and developed corresponding MILP formulations to minimize berthing and departure delays as well as costs from unmet vessel service. Subsequent studies have further examined the unique characteristics of port channels by proposing scheduling models tailored to one-way, two-way, and compound channels, with the goal of minimizing total vessel waiting time [35,37,118].

In addition, some studies have addressed pilot scheduling during vessel inbound operations by developing mathematical models. For instance, Wu et al. [38] formulated the pilot planning problem in seaports as an MIP model, using a branch-and-price algorithm to minimize pilotage operation costs through optimal pilot shift and assignment decisions.

As scheduling tasks have become more interdependent, research has advanced toward integrated models that optimize multiple port resources, such as berth allocation, quay crane assignment, and tugboat scheduling, within a unified framework. Joint optimization of berth and quay crane allocation has been widely studied; Imai et al. [29] first proposed a mathematical model for their simultaneous assignment to minimize total service time. The BACAP has since evolved, with Han et al. [110] introducing a two-stage continuous berth model that considers berthing time, position deviation, and optimized quay crane usage. Lassoued and Elloumi [106] developed a bi-level model linking berth allocation and quay crane assignment in an interactive mechanism. More comprehensive models, like the BACASP by Malekahmadi et al. [64], further include quay crane scheduling and constraints such as water depth, tidal effects, and crane safety distances. Some studies have extended these models to incorporate tugboat scheduling [52,95], while others focus on the coordination between berth allocation and channel scheduling to address navigational constraints [32,49].

In recent years, multi-objective optimization has been increasingly adopted in deterministic models to better address the complex demands of port operations. For vessel scheduling in unidirectional channels, Zhang et al. [72] minimized both total schedule time and total vessel waiting time—objectives frequently seen in channel-related scheduling studies [14,33]. Beyond time, fuel consumption is often included as an optimization goal; for example, Zhong et al. [23] designed a bi-objective model for green tugboat scheduling in tidal ports to minimize both makespan and fuel use. Yu et al. [119], under vessel service differentiation, proposed a bi-level multi-objective model for vessel speed and berth–quay crane coordination, integrating service delay and fuel costs to enhance customer satisfaction. Additional objectives have also been introduced, such as in Yao et al. [120], who considered maximum tugboat operational time, fuel costs, and overflow power for a more realistic tugboat scheduling model. These developments have greatly expanded the capability of deterministic port scheduling models.

In addition, deterministic models have been utilized for time-driven scheduling scenarios, enabling the handling of dynamic vessel arrivals and rolling task updates without relying on probabilistic or fuzzy methods. For instance, Sun et al. [20] introduced a task-triggered model for tugboat scheduling in large multi-terminal ports, employing a rolling genetic algorithm based on task phase segmentation to dynamically generate and allocate tugboat tasks over time. Similarly, Liang et al. [55] developed a dynamic scheduling model for quay cranes in multi-user container terminals, which incorporates vessel arrival times and crane usage plans to optimize vessel waiting, delay, and operation times, thereby significantly enhancing the efficiency of dynamic port scheduling.

In summary, deterministic models have consistently played a dominant role in port scheduling optimization. Their clear structure and controllable solution process make them widely applicable in both theoretical modeling and engineering practice. The evolution from single-problem models to multi-task collaborative models, as well as the integration of multi-objective and dynamic time mechanisms, demonstrates the ongoing potential of deterministic modeling for further development and extension. Future research can continue to enhance modeling capabilities in areas such as integrated scheduling and algorithmic synergy, in order to better address the increasingly complex scheduling demands of port systems.

4.2. Uncertainty Models

In port seaside operation systems, scheduling efficiency and the stability of plan execution are affected by a variety of uncertainty factors. Among these, uncertainty in vessel arrival times is the most common, as arrival is influenced by weather conditions, channel congestion, tidal fluctuations, and delays at previous ports. Additionally, handling times can fluctuate due to factors such as cargo type, equipment performance, operator experience, and unexpected malfunctions. Other sources of uncertainty include equipment maintenance schedules, fluctuations in energy prices, and changes in berth water depth, all of which can disrupt the execution of scheduling plans. Such factors are often difficult to predict accurately during the planning stage, resulting in the need for frequent adjustments to predetermined operation sequences and resource allocation schemes.

To address these uncertainty issues, researchers have gradually introduced uncertainty optimization models to enhance the robustness and adaptability of scheduling solutions in practical operations. These models have been widely applied to key scheduling tasks such as berth allocation, quay crane scheduling and assignment, and tugboat scheduling, with the goal of improving the operational efficiency and resource utilization of port systems under complex environments. By modeling the fluctuation ranges, probability distributions, or representative scenarios of uncertain parameters, related studies provide strong theoretical support and decision-making foundations for intelligent port scheduling.

In the context of berth and quay crane scheduling in ports, strategies for handling uncertainty can be categorized into three main types: proactive approaches, reactive approaches, and proactive/reactive approaches. This classification framework is widely used for modeling and solving scheduling problems under uncertainty, and it possesses a solid theoretical foundation as well as strong practical applicability [10].

(1) Proactive approaches address uncertainty in port scheduling by incorporating information on parameter variability before execution, aiming to generate robust schedules that perform well under a range of scenarios. For example, Han et al. [69] applied genetic algorithms combined with Monte Carlo simulation to proactively account for uncertain vessel arrival and handling times in integrated berth and quay crane scheduling. Similarly, Golias [121] adopted a bi-objective formulation and risk measures to proactively model handling time uncertainty, thereby improving schedule stability and throughput.

(2) Reactive approaches implement adjustments after uncertainty events occur (such as vessel arrival delays), re-constructing scheduling plans to mitigate the impact of disturbances. For instance, Zeng et al. [100] proposed a berth–quay crane disruption recovery model and used a tabu search algorithm for rapid repair; Umang et al. [97] adopted a rolling horizon planning strategy to process real-time arrival information and achieve continuous optimization.

(3) Proactive/reactive approaches combine robust planning with adaptive adjustments during execution to address uncertainty in port scheduling. Typically, these methods establish a baseline schedule that incorporates flexibility—such as buffer times or adjustable decisions—and implement strategies for recovery or rescheduling when disruptions occur. For example, Wang et al. [122] proposed a model that integrates buffer times into the initial plan and optimizes schedule adjustments in response to disturbances, while Rodrigues and Agra [41] developed a two-stage robust framework that allows certain decisions to be revised after the realization of uncertainty, thereby enhancing overall schedule adaptability

To address uncertainty in port scheduling, researchers have developed mathematical models extending traditional optimization frameworks. Stochastic programming assumes uncertain parameters follow known probability distributions and typically employs two-stage or multi-stage models to minimize expected costs or optimize system performance. This approach is well suited for uncertainties with statistical regularities, such as vessel arrival and handling times. In contrast, robust optimization does not depend on probabilistic information but instead aims for solutions that remain feasible across all scenarios within a defined uncertainty set, focusing on stability and worst-case performance. Both approaches are widely used in berth allocation, quay crane scheduling, and tugboat scheduling, and form key theoretical foundations for uncertainty modeling in ports.

4.2.1. Stochastic Programming

Stochastic programming has emerged as a powerful approach for handling uncertainty in port scheduling problems, particularly for variables such as vessel arrival times, handling durations, and resource availability. Rather than assuming deterministic data, these models explicitly consider uncertainty by representing key parameters as random variables or scenarios, aiming to optimize system performance under various possible outcomes.

For instance, in the context of integrated berth and channel planning, Liu et al. [16] develop a two-stage stochastic mixed-integer linear programming model that minimizes the expected total weighted completion time of vessels under uncertain arrivals and handling durations. Their approach coordinates berth allocation decisions made in the first stage with channel and tugboat assignments in the second stage, after uncertainties have been realized, providing a more robust framework for real-world operations. Similarly, Han et al. [69] address uncertainty in both vessel arrivals and handling times by formulating a stochastic mixed-integer programming model for berth and quay crane assignment, utilizing simulation-based genetic algorithms to generate robust schedules that reduce both expected completion times and variability.

Further extending the application of stochastic programming, Ji et al. [123] employ an Enhanced Non-dominated Sorting Genetic Algorithm (ENSGA-II) with scenario generation for berth and quay crane scheduling under uncertain arrivals, transforming constraint handling into a bi-objective optimization problem to enhance solution reliability and efficiency. In addition, Li et al. [54] consider the impact of random quay crane maintenance activities, establishing a stochastic integer linear programming model solved via sample average approximation to minimize expected vessel turnaround times, demonstrating practical value for integrated berth and quay crane assignment.

Beyond operational efficiency, the integration of sustainability objectives is also reflected in the literature. Zhen et al. [124] present a stochastic programming model for low-carbon berth allocation, incorporating uncertainties in arrival and handling times and leveraging column generation to optimize both carbon emissions and schedule reliability in dynamic environments. Risk-based approaches have also been proposed: Golias [121] formulates the berth allocation problem as a bi-objective mixed-integer program, jointly optimizing total vessel service time and the reliability of schedules under stochastic handling times, using risk measures to improve the robustness and stability of berth schedules beyond traditional deterministic models.

Collectively, these studies demonstrate the versatility and effectiveness of stochastic programming in capturing and mitigating various uncertainties inherent in port operations. By integrating scenario-based decision-making, risk measures, and multi-objective formulations, the models discussed provide robust theoretical and algorithmic foundations for optimizing complex port scheduling tasks under uncertainty, thereby enhancing both operational efficiency and resilience.

4.2.2. Robust Optimization

Robust optimization (RO) is a key method for addressing uncertainty in port scheduling, notable for its independence from precise probability distributions and its focus on both feasibility and robustness across diverse scenarios. In port seaside scheduling, RO models are generally categorized as either static or adjustable, based on whether decision variables can be adapted after uncertainty is realized.

Static robust models fix all decisions before execution and absorb disturbances by designing appropriate buffers. For example, Zhen and Chang [125] introduced time buffers into a bi-objective berth allocation model to minimize costs and improve robustness, using the weighted sum of buffer times as a key metric. Xu et al. [108] adopted a similar approach, confirming through sensitivity analysis the positive impact of buffer times on service levels and robustness. This strategy is especially useful in settings with low uncertainty or high adjustment costs. Zhen [86] further compared robust optimization and stochastic programming for berth allocation under uncertain handling times, finding that robust methods can yield high-quality solutions close to stochastic models, while providing strong worst-case guarantees.

Adjustable robust models increase flexibility by permitting certain decisions to be modified as uncertainty unfolds, often via scenario-based uncertainty sets. Xiang et al. [107] developed a bi-objective robust berth allocation model that incorporates deviation variables and penalty terms, allowing the schedule to be adjusted based on actual deviations during execution. Rodrigues and Agra [41] advanced this concept with a two-stage robust MIP model, where initial berth allocation is followed by quay crane scheduling adjustments according to realized vessel arrivals.

Recent developments have broadened the scope of robust optimization in port scheduling. Chargui et al. [91] included energy price fluctuations as well as time and operational uncertainties in their model, optimizing for both energy and delay costs. Wang et al. [122] proposed a proactive–reactive hybrid model that uses time buffers for minor disruptions and dynamic adjustments for larger delays, achieving a balance between robustness and flexibility. In another extension, Wang et al. [84] integrated prospect theory into a two-stage robust framework, capturing port managers’ behavioral responses to schedule deviations and enhancing model scalability.

In summary, static RO models control uncertainty with simple buffer mechanisms and are suitable for environments with predictable disturbances, while adjustable models allow dynamic adaptation to complex uncertainty. Together, these approaches offer robust theoretical and practical tools for enhancing efficiency and adaptability in port scheduling.

4.2.3. Literature Classification

Table 4. Classification of uncertainty models.

Ref	Resource					Approach			Model			Uncertainty
	B	QC	T	P	C	P	PR	R	SP	RO	D	AT	HT	DT	TT	CB	V	W	G
[54]	√	√					√		√							√
[123]	√	√				√			√			√
[16]	√				√	√			√			√	√
[124]	√						√		√			√	√
[69]	√	√				√			√			√	√
[31]			√				√		√			√			√
[121]	√					√			√				√
[85]	√						√		√			√	√
[126]	√						√		√			√	√			√	√	√
[127]	√					√			√				√
[77]				√		√			√						√
[107]	√						√			√		√	√
[41]	√	√					√			√		√
[125]	√					√				√		√	√
[91]	√	√					√			√		√	√
[108]	√					√				√		√	√
[84]	√	√					√			√		√	√
[122]	√	√					√			√		√				√
[86]	√					√			√	√			√
[128]	√					√				√		√	√
[129]					√		√			√				√
[130]	√	√					√			√		√	√
[97]	√							√			√	√	√
[20]			√					√			√	√			√
[100]	√	√						√			√	√							√
[131]	√	√						√			√	√	√			√	√
[102]	√					√					√		√
[81]	√					√					√	√

presents a classification of the literature addressing uncertainty issues in port seaside scheduling systems. The classification is organized by key scheduling resources in port seaside operations (including B: berth, QC: quay crane, T: tugboat, P: pilot, C: channel), approaches to handling uncertainty (P: proactive, PR: proactive/reactive, R: reactive), model types (SP: stochastic programming, RO: robust optimization), and the specific uncertainty factors considered in the literature (AT: arrival time, HT: handling time, TT: tugging time or pilotage duration, DT: departure time, CB: quay crane breakdowns or maintenance, V: calling of unscheduled vessels or change in the number of berthing vessels, W: weather, G: general disruptions).

A review of the existing literature reveals that research on uncertainty issues in port seaside scheduling systems has primarily focused on the scheduling of berth (B) and quay crane (QC) resources. Some studies have further extended the scope beyond berths and quay cranes to include the scheduling of tugboats (T) and channels (C), reflecting growing attention to multi-resource integrated scheduling in port seaside operations. However, the number of publications addressing tugboat and channel scheduling remains relatively limited, indicating that this area is still in the early stages of research.

In terms of uncertainty handling strategies, most studies employ proactive (P) or proactive–reactive hybrid (PR) approaches, reflecting the strong adaptability and practicality of strategies that anticipate potential disruptions and allow flexible adjustments when disturbances occur in port scheduling. Pure reactive (R) methods are less commonly used, possibly because single-response strategies are limited in their effectiveness under complex and dynamic environments.

In terms of model types, stochastic programming (SP) and robust optimization (RO) are the two most commonly used modeling frameworks. Early studies relied more on probabilistic information and adopted stochastic programming models. However, as it has become increasingly difficult to obtain accurate probability information in practical applications, the proportion of studies employing robust optimization models has gradually increased, making RO an important approach for uncertainty management. Particularly in situations involving multiple sources of uncertainty or incomplete probability information, robust optimization has become the preferred choice in many studies due to its advantages—such as not requiring precise probability data and its ability to control performance loss in worst-case scenarios.

With regard to uncertainty factors, most studies commonly consider uncertainties in vessel arrival time (AT) and handling time (HT), as these are the two factors with the greatest impact on scheduling execution. Arrival time is easily affected by factors such as weather and channel congestion and directly determines the actual berthing time of vessels; uncertainty in handling time reflects variations in loading and unloading efficiency and equipment condition, impacting vessel departure times and the turnover of berth resources. Deviations in AT and HT can result in vessel waiting, resource conflicts, and overall operational delays, thereby reducing port operational efficiency. As a result, most studies prioritize these two key factors and explicitly address them in optimization models. Some research has further incorporated more complex uncertainty factors, such as quay crane breakdowns or maintenance (CB) and weather (W), reflecting a growing academic interest in multidimensional uncertainty scenarios. However, research on tugboat and channel scheduling remains relatively limited, and studies addressing dynamic vessel changes (V) and general disruptions (G) are also scarce in current models, indicating that these areas offer substantial potential for further exploration.

In summary, existing studies exhibit several trends: a concentration on specific resource types, a tendency toward hybrid methods, an increasing preference for robust optimization models, and diversification in the consideration of uncertainty factors. Nevertheless, research on tugboat and channel scheduling, as well as dynamic adaptive modeling under complex disruptions, remains relatively underdeveloped. Future progress can be expected in the comprehensive modeling of uncertainty factors, the design of flexible scheduling mechanisms, and the application of intelligent solution algorithms.

4.3. Exact Algorithms

Scheduling problems in port seaside inbound and outbound operations are typically complex and subject to stringent constraints, particularly for tasks such as berth allocation, quay crane scheduling, tugboat scheduling, channel-constrained vessel scheduling, and pilot scheduling. Exact algorithms, as a major class of traditional optimization methods, can theoretically yield globally optimal solutions for well-structured models within finite computation time. Approaches such as MILP and Nonlinear Programming (NLP) remain indispensable for validating small- and medium-sized instances, guiding model formulation, and evaluating the performance of more scalable algorithms, despite limited applicability to large-scale problems.

Many studies utilize commercial solvers directly to obtain optimal solutions for formulated mathematical models. For example, Basri and Zainuddin [66] minimized total vessel dwell time in continuous berth and quay crane scheduling without interference constraints, showing with LINGO that their model outperformed FCFS (First-Come-First-Served) rules on small-scale instances. Similarly, Nikghadam et al. [132] developed an MILP model for joint scheduling of vessels and service providers under several strategies, and demonstrated using Python and Gurobi that joint optimization can significantly improve operational efficiency.

To tackle the scalability limitations of exact methods, recent studies have focused on preprocessing and reformulation strategies to improve computational efficiency. Tan et al. [133] addressed transshipment port berth allocation by applying linearization to remove big-M constraints before solving with CPLEX, effectively enhancing vessel connectivity at high berth utilization rates. Likewise, Hu et al. [105] converted a nonlinear multi-objective berth and quay crane scheduling model into a second-order cone programming (SOCP) form, applying a normalized weighted algorithm to mitigate computational challenges. In the area of tugboat scheduling, Wang et al. [30] introduced an enumeration algorithm based on the FCFS principle to identify optimal tugboat assignments, although such methods are generally practical only for small-scale cases due to low efficiency.

Recognizing the challenges posed by real-world, large-scale, and highly constrained scheduling problems, scholars have increasingly adopted relaxation and decomposition techniques within the exact algorithm framework. Relaxation strategies reduce model complexity and generate solution bounds, while decomposition breaks complex problems into manageable subproblems, enabling improved solvability and computational performance. These advancements have been widely applied across various port scheduling contexts, enhancing the practical value and adaptability of exact algorithms in both research and real-world applications.

(1) Relaxation Techniques

To improve the solvability of port scheduling models with large variable sets and complex constraints, relaxation techniques such as Lagrangian relaxation and cutting plane methods are widely used. Lagrangian relaxation works by embedding certain constraints into the objective function through multipliers, producing lower bounds for the original problem and iteratively updating these multipliers to approach optimality. For example, Fu and Diabat [134] applied Lagrangian relaxation and a genetic algorithm to a quay crane scheduling MIP model, efficiently generating bounds and delivering fast approximate solutions even for large-scale cases. Similarly, Imai et al. [25] combined Lagrangian relaxation with the subgradient method in a heuristic for public berth systems.

Building on these approaches, Al-Dhaheri and Diabat [42] tackled multi-vessel quay crane scheduling by relaxing constraints with Lagrangian multipliers and refining solutions using the cutting plane method, demonstrating rapid convergence and high performance. The cutting plane technique itself starts from a continuous relaxation and iteratively introduces cutting planes to move closer to an integer solution; this was effectively used by Türkoğulları et al. [78] to solve large-scale BACASP models.

Further, Liu et al. [83] addressed quay crane rescheduling under failure scenarios with a two-stage approach: an initial solution was found using a relax-and-fix MIP algorithm, and dynamic programming was then employed to manage interruptions. To further enhance real-world adaptability, they also incorporated behavioral perception modeling based on prospect theory.

(2) Decomposition Techniques

Decomposition methods, such as Benders decomposition and column generation (CG), are widely used to enhance the solution efficiency of complex port scheduling problems. By breaking large models into smaller, more manageable subproblems, these techniques enable faster convergence and better scalability. For example, Jia et al. [96] tackled the tugboat scheduling problem using Benders decomposition, separating vessel berthing and unberthing times (master problem) from tugboat routing (subproblem), and further improved convergence by integrating Lagrangian relaxation and several enhancement strategies.

CG has also proven effective in large-scale berth and vessel scheduling. Liu et al. [19] transformed an MILP model into a set partitioning formulation and employed an enhanced CG algorithm to iteratively generate high-quality solutions, demonstrating clear advantages over traditional approaches. Similarly, Iris et al. [135] proposed novel set partitioning models for the BACAP, incorporating column reduction strategies and providing significantly improved computational performance compared with previous compact formulations. Chargui et al. [91] applied decomposition to a robust BACASP model with energy price uncertainty, integrating multiple enhancement techniques to efficiently solve large instances. Additionally, Rodrigues and Agra [41] addressed vessel arrival uncertainty using a two-stage robust model, combining warm-start and scenario reduction strategies within the decomposition framework to reduce iteration counts and improve solution stability.

(3) Hybrid Methods

To overcome the computational bottlenecks of single exact algorithms in large-scale or highly complex port scheduling problems, many studies have adopted hybrid approaches. These methods combine exact algorithms with other optimization strategies or integrate different types of exact techniques to enhance both efficiency and solution quality.

For example, Wei et al. [113] developed a MILP model for tugboat scheduling and incorporated custom inequalities within a branch-and-cut framework, outperforming general-purpose MILP solvers. Türkoğulları et al. [79] proposed a cutting plane algorithm based on decomposition for the time-dependent BACASP model, splitting the problem into master and subproblems, where quay crane scheduling was solved using layered networks and flow-based methods, supplemented by heuristics for greater efficiency.

Hybrid methods have also proved effective in pilot scheduling, where Wu et al. [38] and Xiao et al. [77] applied the branch-and-pricing (B&P) algorithm—combining column generation with branching—to efficiently address large-scale problems with resource and time window constraints. For vessel scheduling involving both pilotage and tugboat operations, Abou Kasm et al. [44] used constraint separation, heuristics, relaxation, and branch-and-cut techniques to deliver high-quality solutions beyond those of standard solvers.

Further advances include the Column-and-Constraint Generation (C&CG) algorithm for two-stage robust integrated berth and quay crane scheduling, which used scenario simplification to reduce computation time [84]. Additional hybrid frameworks, such as the container division and combination plus branch-and-pricing method [43], and the branch-and-pricing approach based on Dantzig–Wolfe decomposition, have demonstrated significant performance gains in quay crane scheduling and integrated assignment problems [82].

Notably, Korekane et al. [74] introduced a Neural Network-assisted Branch-and-Bound (NNBB) framework, where deep learning predicts optimal branching paths for berth allocation, improving computational efficiency by 63% while maintaining solution quality. These results highlight the promise of combining learning models with exact algorithms for efficient, intelligent port scheduling.

In summary, exact algorithms remain important for optimizing port seaside scheduling, especially when model structures are clear and high solution accuracy is needed. They offer theoretical guarantees for tasks such as berth allocation, quay crane scheduling, tugboat scheduling, channel-constrained vessel scheduling, and pilot scheduling. However, as problem size and complexity grow, single solvers or exact methods alone often struggle to meet computational requirements. To address this, researchers have increasingly used structural optimization techniques like relaxation and decomposition, as well as hybrid approaches that combine exact and heuristic methods. These advancements have improved convergence and efficiency in a variety of port scheduling scenarios, supporting the development of practical and effective port operation systems.

To further clarify the research pathways and technological evolution of exact algorithms in the current literature, the related studies are classified in

Table 5. Statistics of literature on exact algorithms.

Ref	Resource					Solution
	B	QC	T	P	C
[44]			√	√		CS
[87]	√					GUROBI
[93]	√					CPLEX
[124]	√					CG
[41]	√	√				DA
[91]	√	√				DCP
[66]	√	√				LINGO
[132]			√	√		GUROBI
[133]	√					CPLEX
[105]	√	√				SOCP, CPLEX
[30]			√			ES
[134]		√				LR
[25]	√					LR
[42]		√				LR
[78]	√	√				CP
[83]	√	√				MIP-based relax-and-fix algorithm
[96]			√			LR, Benders decomposition
[19]	√				√	CG
[79]	√	√				CP
[84]	√	√				C&CG
[43]		√				Container division and combination (CDC), B&P
[82]	√	√				B&P
[77]				√		B&P
[38]				√		B&P
[116]					√	CG
[17]				√	√	LR
[117]					√	LR
[80]	√	√				LR
[113]			√			B&C
[74]	√					B&B
[28]		√				B&B
[106]	√	√				CPLEX

CS: constraint separation; CG: column generation; DA: decomposition algorithm; DCP: decomposition algorithm; SOCP: second-order cone programming; ES: Exhaustive Search; LR: Lagrangian relaxation; CP: cutting plane; C&CG: Column-and-Constraint Generation; B&P: branch-and-price; B&C: branch-and-cut; B&B: Branch-and-Bound.

according to scheduling scenarios, model types, and solution methods, facilitating systematic comparison and subsequent analysis.

From the perspective of literature distribution and methodological development, exact algorithms remain widely applicable and hold significant research value in port seaside scheduling problems. Early studies often utilized commercial solvers such as CPLEX, Gurobi, and LINGO to validate models and conduct comparative analyses on small-scale instances, providing intuitive evaluations of model effectiveness and the achievement of optimization objectives. In recent years, as the dimensionality and structural complexity of problems have increased, research has gradually shifted from relying solely on single solvers to a deeper exploration of model structures and strategic method optimization. In particular, for scenarios characterized by tightly coupled constraints or coordinated resource scheduling, researchers increasingly adopt combined decomposition and relaxation strategies to enhance both solution efficiency and solver adaptability.

In terms of scheduling resources, berth and quay crane problems have always been the mainstream research topics, with relatively mature models and well-developed algorithms. However, in recent years, with the advancement of port automation, tugboat scheduling, pilot scheduling, and channel-constrained vessel scheduling have gradually become research hotspots. These problems are generally characterized by high resource dynamism, strong operational sequence dependencies, and tight scheduling windows, which significantly increase the complexity of both modeling and algorithmic solutions. As a result, research in this area is advancing toward multi-task coordinated scheduling, real-time feedback mechanisms, and robust modeling under uncertainty.

In terms of solution method development, traditional approaches such as MILP and NLP remain effective for small-scale problems but face bottlenecks such as long computation times and high memory consumption in complex scenarios. Consequently, researchers have gradually introduced exact algorithmic strategies with structural advantages, including the following:

(1) Relaxation methods (such as LR and cutting plane methods), which relax certain complex constraints to obtain upper and lower bounds for the problem;

(2) Decomposition methods (such as Benders decomposition and CG), which decompose complex models into structurally independent or hierarchically organized subproblems for parallel or iterative solution;

(3) Hybrid exact algorithms (such as B&P and C&CG), which combine multiple strategies to balance solution quality and computational tractability, and are particularly suitable for high-complexity scenarios such as pilot scheduling, integrated berth and quay crane scheduling, and energy cost-sensitive scheduling.

It is worth emphasizing that as scheduling problems become increasingly aligned with real-world engineering scenarios, the research focus has shifted from static model construction and optimal solution acquisition to enhancing the capability and adaptability of algorithms in handling complex constraints, real-time dynamics, and uncertain environments. An increasing number of studies are dedicated to exploring structurally controllable, strategically flexible, and computationally efficient exact solution frameworks to better support the practical deployment and operation of scheduling systems in intelligent ports.

In summary, exact algorithms not only play a fundamental role in port scheduling optimization but are also evolving toward structurally driven, integrated, and intelligent paradigms. Future research trends will focus on the following aspects: first, developing exact solution frameworks that combine enhanced robustness with real-time capabilities; second, promoting the deep integration of exact algorithms with intelligent scheduling systems; and third, building multi-resource coordinated scheduling platforms tailored to the operational characteristics of real-world ports. Exact algorithms will continue to play a pivotal role in supporting the construction of intelligent decision-making systems for smart ports.

5. Heuristic-Based Scheduling Optimization for Port Seaside Systems

In research on port seaside scheduling optimization problems, effectively solving complex scheduling models has always been one of the core challenges. Due to the diversity and dynamic nature of port operations—such as fluctuations in vessel arrival times, variations in equipment capabilities, and sudden resource failures—real-world scheduling problems are typically highly combinatorial and nonlinear, making it difficult to obtain optimal solutions within reasonable time frames using traditional exact algorithms. As a result, both academia and industry have widely adopted heuristic algorithms as solution tools to balance solution quality and computational efficiency.

The scheduling optimization of port seaside systems involves complex dynamic environments and multiple constraints, where traditional exact algorithms often face challenges such as high computational complexity and difficulty in meeting real-time decision-making requirements, especially for large-scale problems. Against this backdrop, heuristic algorithms—by designing problem-driven rules or simulating natural optimization mechanisms—can generate high-quality feasible solutions within reasonable time frames, making them effective tools for solving vessel inbound and outbound scheduling problems. Compared to exact algorithms, heuristic algorithms offer greater flexibility and computational efficiency, and are particularly well suited to scenarios with strong spatiotemporal coupling, such as tugboat scheduling and berth allocation.

Heuristic algorithms are approaches that seek approximate solutions to problems by employing heuristic rules or experience-based strategies. These algorithms are commonly used to solve complex problems, particularly when the problem scale is large or the problem itself is NP-hard.

In intelligent port seaside system scheduling, the strong spatiotemporal coupling constraints among resources such as tugboats, berths, and quay cranes, along with dynamic environments and large-scale characteristics, often render the problem NP-hard. Although traditional exact algorithms can guarantee theoretically optimal solutions, they are often impractical in real-world scenarios due to high computational costs and poor real-time responsiveness, making it difficult to cope with dynamic disruptions such as vessel arrival fluctuations and tidal window limitations. Against this backdrop, heuristic algorithms—using problem-driven rules (e.g., priority sequencing, greedy selection) or by simulating natural mechanisms (e.g., genetic algorithms, simulated annealing)—can produce feasible solutions within reasonable time frames. These methods emphasize “approximate solutions over exact solutions, and real-time performance over optimality” as core principles, and through flexible adaptation to complex constraints and dynamic changes, have become indispensable for solving high-complexity subproblems such as tugboat collaborative routing and berth continuity allocation, effectively balancing solution quality and computational efficiency.

5.1. Priority Rules and Dispatching Heuristics

Simple heuristic methods typically rely on predefined rules or experience-based strategies, simplifying the modeling of problem structures to quickly generate feasible solutions. These methods offer advantages such as simplicity in algorithmic structure, high computational efficiency, and ease of implementation, and have been widely applied in port seaside scheduling optimization problems. Based on their strategic features, common simple heuristic methods include priority rules, greedy algorithms, and composite rules.

(1) Priority rules

Priority rules determine the operation sequence through empirical ranking and are widely used in vessel scheduling. The most commonly adopted rules include FCFS and Weighted Shortest Processing Time (WSPT). The FCFS rule serves not only as a common strategy in actual port operations [63] but is also frequently used to generate initial vessel queues, reducing problem complexity and improving computational efficiency [48,55,67,136]. Corry and Bierwirth [49] conducted research on applying FCFS and Earliest Completion Time (ECT) rules to construct a heuristic algorithm for berth allocation problems with channel constraints, enabling the algorithm to rapidly generate high-quality solutions. On the basis of modeling the berth allocation problem as a parallel machine scheduling problem, Xu et al. [68] introduced a heuristic algorithm based on the WSPT rule. Although this approach can quickly generate effective solutions, the solution quality tends to decline as the problem scale increases. Other common rules include ECT and STW (Shortest Time Window Length). Despite their limited optimality in complex dynamic environments, these rules are widely used as benchmark methods to validate the performance of more sophisticated algorithms.

(2) Greedy algorithms

Greedy algorithms are a category of constructive heuristic methods that make locally optimal choices at each step without considering global impacts. In port seaside scheduling, greedy algorithms can rapidly respond to real-time conditions and generate feasible solutions with low computational costs. For example, Abou Kasm et al. [53] designed a constructive greedy heuristic that sequentially assigns start times to unscheduled vessels, achieving favorable scheduling performance. Lalla-Ruiz et al. [63] proposed three greedy heuristics (random greedy, FCFS greedy, and STW greedy) and compared them with the simulated annealing (SA) algorithm, demonstrating that while greedy methods are computationally fast, their solution quality may be constrained. Umang et al. [97] further developed an intelligent greedy algorithm, which exhibited superior performance in berth allocation problems. Additionally, greedy algorithms are often used as initial solution generators or subroutines for more complex algorithms. For instance, Martin-Iradi et al. [98] applied greedy strategies to generate initial solutions in an Adaptive Large Neighborhood Search algorithm; Zhang et al. [80] employed greedy insertion to handle subproblems in Lagrangian relaxation; and Kim and Park [28] integrated greedy strategies into the GRASP algorithm to enhance the solution efficiency for large-scale quay crane scheduling problems.

(3) Composite rules

Composite rules combine multiple heuristic strategies to improve solution quality and adaptability. For instance, Zhang and Kim [112] addressed the quay crane scheduling problem by proposing a mixed-integer programming model that aims to minimize handling cycles and maximize the number of dual-cycle operations. They applied the Johnson rule for intra-bay and inter-bay sequencing and incorporated gap-based neighborhood local search techniques for further optimization. Empirical studies demonstrated that this approach achieves near-optimal solutions with short computation times.

In summary, simple heuristic methods can effectively simplify the solution process for port seaside scheduling problems and hold significant value in both practical applications and theoretical research. However, as problem sizes grow and dynamic complexity increases, single heuristic approaches often struggle to obtain satisfactory solutions. Consequently, researchers have progressively explored the combination of heuristic methods with metaheuristic algorithms or other advanced techniques to further enhance solution quality and algorithmic adaptability.

5.2. Metaheuristic Algorithms

As the scale and complexity of port seaside scheduling problems continue to increase—particularly with the growing challenges of resource coupling, multi-objective optimization, and dynamic uncertainty—metaheuristic algorithms have emerged as important solution methods due to their strong global search capabilities, ability to escape local optima, and adaptability to complex search spaces. Compared to simple heuristic methods that rely on experience or rules, metaheuristic algorithms can better balance solution quality and computational efficiency across a much broader search space.

Figure 6 illustrates the general process of a metaheuristic optimization algorithm. The process begins with initializing algorithm parameters and computing the initial solution, which is set as the current best. In each iteration, a new solution is generated and compared with the current best one; the better solution is retained. The current solution is then updated based on a predefined strategy. This loop continues until a termination condition is met. This flow reflects the key characteristics of metaheuristic methods—such as being problem-independent, capable of global search, and suitable for solving complex, large-scale scheduling problems without relying on problem-specific knowledge.

According to their search mechanisms and design principles, metaheuristic algorithms applied to port seaside scheduling problems can be classified into five categories: evolutionary algorithms, swarm intelligence algorithms, local search-based algorithms, hybrid algorithms, and innovative algorithms.

(1) Evolutionary Algorithms

Genetic Algorithms (GA), as one of the most widely used metaheuristic methods, play an important role in port seaside scheduling optimization due to their flexible encoding schemes, strong global search capabilities, and adaptability to complex constraints. GA has been applied to dynamic berth allocation, quay crane scheduling, tugboat scheduling, and multi-resource coordinated optimization problems [20,29,48,55,56]. To improve algorithm performance, researchers have conducted various innovative studies on encoding design, operator improvement, and integration with uncertainty management. For example, Golias et al. carried out research on introducing a two-level encoding and taboo mutation mechanism to enhance search efficiency. On this basis, Bacalhau et al. [62] further proposed hybrid algorithms with state space reduction (GASSR, MASSR), significantly improving the solution quality for large-scale instances. Some studies have combined GA with simulation models, using feedback mechanisms to dynamically evaluate scheduling outcomes, so as to adapt to the randomness and volatility of vessel arrivals and operation durations in ports [61,69,109].

For complex multi-objective optimization requirements, researchers widely employ the Non-dominated Sorting Genetic Algorithm II (NSGA-II) and its variants, which achieve an effective balance among conflicting objectives through non-dominated sorting and crowding distance mechanisms [72,115,123]. These algorithms perform well in simultaneously optimizing multiple objectives—such as operation time, resource utilization, and operational cost—and can generate balanced Pareto-optimal solution sets, making them widely applicable to berth allocation, quay crane assignment, and tugboat scheduling problems.

(2) Swarm Intelligence Algorithms

Swarm intelligence algorithms such as Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Gray Wolf Optimizer (GWO) simulate collective behaviors and show strong parallelism and search performance. PSO has been widely applied to berth allocation and quay crane scheduling due to its fast convergence characteristics [59,110]. To enhance the adaptability of PSO to complex constraints and specific port scenarios, some studies have further optimized its structure and mechanisms. For example, Malekahmadi et al. [64] conducted research on proposing RTPSO, a PSO based on random topology structure, which improves information dissemination, solution quality, and scalability. Wang and Zou et al. [99] introduced an immune mechanism into PSO and designed the IAPSO algorithm to optimize the coordinated scheduling of shore power and tugboat operations, balancing system resources and environmental constraints. These studies demonstrate the potential of PSO in structural optimization and practical application extension.

ACO is often used for berth sequencing and path selection. For instance, Yu et al. [70] carried out research on proposing a Parallel Search Structure Enhanced Ant Colony Algorithm (PACO) to improve search efficiency and stability in dynamic berth allocation.

GWO, due to its simple structure and strong global search ability, has been increasingly applied in port scheduling. Xiang et al. [107] constructed a robust berth scheduling model targeting economic efficiency and customer satisfaction and proposed an Adaptive GWO (AGWO) by incorporating mutation and local search to improve performance. Yao et al. [120] further applied the Improved GWO (IGWO) to multi-objective tugboat scheduling, enhancing the search ability through cosine convergence parameters, dynamic weights, and opposition-based learning strategies, thus showing advantages in solution accuracy and convergence speed.

(3) Local Search-Based Metaheuristics

Local search-based metaheuristics such as simulated annealing (SA), Tabu Search (TS), Variable Neighborhood Search (VNS), and Adaptive Large Neighborhood Search (ALNS) enhance solution quality through flexible neighborhood move strategies and acceptance criteria. SA has been widely applied to berth and channel scheduling problems. For example, Zhen et al. [85] constructed baseline and recovery models and applied SA to improve scheduling stability under uncertainty. Lalla-Ruiz et al. [63] combined SA with greedy algorithms and 2-opt neighborhood search to optimize channel vessel sequencing. Tasoglu and Yildiz [39] embedded SA in a simulation–optimization system to reduce the latest vessel departure time. TS is used to solve terminal resource disruptions and improve the efficiency of berth and quay crane rescheduling [100]. Iris et al. [137] developed improved formulations and an ALNS heuristic for the integrated berth allocation and quay crane assignment problem. VNS and ALNS optimize multi-stage scheduling through dynamic adjustment strategies, which have proven their superiority in berth allocation, tugboat, and quay crane scheduling [24,60,76,98,138].

(4) Hybrid Algorithms

Hybrid algorithms improve convergence speed and solution stability by integrating multiple optimization strategies, making them suitable for problems with complex constraints and multi-objective conflicts. For example, Fatemi-Anaraki et al. [40] combined GA, Differential Evolution, and GWO to optimize multi-resource scheduling in ports; Zhang et al. [32] proposed the SAMPGA algorithm, which integrates simulated annealing with multi-population GA, significantly improving vessel scheduling efficiency. Li et al. [65] further introduced reinforcement learning and proposed the GSAA-RL (Q-learning-based adaptive genetic simulated annealing algorithm), which uses a Markov decision process to dynamically adjust parameters, significantly reducing vessel port time and demonstrating strong adaptability and optimization capability. Moreover, Tang et al. [126] proposed a proactive berth allocation model considering multiple disruption scenarios and developed a multi-stage metaheuristic framework centered on GA, incorporating an Adaptive Hyperbox Algorithm (AHA) for local search and a Rolling Horizon Heuristic (RHH) for repair, to solve large-scale uncertain berth allocation problems.

(5) Innovative Algorithms

In recent years, researchers have explored novel or innovative metaheuristic algorithms to address specific challenges in port scheduling. Chemical Reaction Optimization (CRO) and Bee Colony Optimization (BCO), inspired by natural reactions and swarm behaviors, have demonstrated strong performance in maintaining solution diversity and convergence [71,101]. Chaotic Quantum Optimization Algorithms (such as CQASBO and CQWOA), which combine quantum computing and chaotic mapping mechanisms, have shown strong adaptability in integrated berth and quay crane scheduling as well as in tide-affected scenarios [95,111]. Additionally, Tang et al. [88] proposed the Collaborative Learning Imperialist Competitive Algorithm (CLICA) for multi-resource terminal scheduling, integrating sliding window optimization, time-varying assimilation, and collaborative learning mechanisms to balance solution quality and convergence efficiency, making it suitable for scheduling optimization in energy-constrained environments.

As shown in

Table 6. Classification of metaheuristic algorithm literature.

Ref	Resource				Algorithm
	B	QC	T	C
[55]		√			GA
[94]	√	√			GA
[109]	√				GA + Simulation
[56]	√				GA
[29]	√	√			GA
[62]	√				GA
[69]	√	√			GA + Simulation
[47]	√				GA
[57]	√				GA
[122]	√	√			GA
[20]			√		GA
[61]	√				GA + Simulation
[58]		√			GA
[67]	√				GA
[48]	√				GA
[34]	√		√	√	GA
[139]	√	√		√	GA
[35]				√	GA
[15]				√	GA
[118]				√	GA
[37]				√	GA
[128]	√	√			GA
[140]	√	√			GA
[72]				√	MOGA
[115]	√				NSGA-II
[123]	√	√			NSGA-II
[119]	√	√			NSGA-II
[23]			√		NSGA-II
[36]	√			√	NSGA-II
[141]	√			√	NGSA-III
[14]	√			√	NSGA-III
[64]	√	√			PSO
[110]	√	√			PSO
[99]	√		√		PSO
[59]	√				PSO
[142]			√		PSO
[143]			√		PSO
[63]				√	SA
[85]	√				SA
[39]	√	√			SA + Simulation
[144]				√	SA
[100]	√	√			TS
[70]	√				ACO
[120]			√		GWO
[107]	√				GWO
[24]			√		VNS
[60]	√	√			VNS
[145]	√	√		√	VNS
[146]	√				VNS + ML
[76]			√		ALNS
[98]	√				ALNS
[18]	√			√	ALNS
[137]	√	√			ALNS
[130]	√	√			ALNS
[111]	√	√			CQWOA
[101]	√				CRO
[71]	√				BCO
[95]	√	√	√		CQASBO
[125]	√				SWO
[40]	√	√		√	GA, DDE, GWO
[32]	√			√	SAMPGA
[147]	√			√	NSGA-II, VNS
[129]				√	MA, VNS
[33]				√	NSGA-II, TS
[148]			√		SA, ACO
[126]	√				GA, AHA, RHH
[86]	√				SWO, CSNS
[108]	√				SA, B&B
[92]	√	√			GA, ACO
[65]	√			√	GA, SA, RL

CSNS: Critical Shaking Neighborhood Search.

, genetic algorithms and their multi-objective extensions occupy a dominant position across various port scheduling problems, demonstrating outstanding performance, particularly in complex and multi-objective scenarios such as berth allocation, quay crane scheduling, and tugboat scheduling. Swarm intelligence algorithms are widely applied to large-scale and highly time-sensitive scheduling problems due to their superior parallel search capabilities and fast convergence. Local search-based metaheuristics effectively improve solution quality through flexible neighborhood move strategies, making them suitable for problems characterized by frequent dynamic disturbances or complex constraints. Meanwhile, research on innovative algorithms is gradually increasing, reflecting the academic community’s growing emphasis on algorithm integration and the introduction of new mechanisms. These methods exhibit strong potential for enhancing algorithm performance, adaptability, and multi-objective trade-offs, enabling better fulfillment of practical needs for real-time, dynamic, and complex coordinated optimization in port operations.

5.3. Simulation-Based and Hybrid Approaches

Port scheduling simulation constructs digital models to replicate port operations, providing quantitative analysis tools for resource optimization, energy consumption control, and decision support. In recent years, with the integration of intelligent algorithms, multidisciplinary modeling, and digital technologies, related research has achieved significant progress in areas such as equipment scheduling, berth allocation, and multimodal transport optimization.

As a core issue in port scheduling, berth allocation research has formed systematic outcomes. Yıldırım et al. [149] proposed a simulation-optimization approach based on the Artificial Bee Colony (ABC) optimization algorithm, constructing the Single-Queue Model (SQM) and Multi-Queue Model (MQM). The results verified the advantages of dynamic berth allocation strategies and Hybrid Queue Priority (HQP) rules in reducing vessel waiting time and improving berth utilization. On this basis, Ilati et al. [52] further integrated berth allocation, tugboat scheduling, and quay crane assignment, developing an Evolutionary Path Re-linking (EvoPR) algorithm. In the case study of Iran’s RAJAEE Port, the model effectively handled uncertainties in vessel arrival times and showed that fluctuations in berth operation times had a limited impact on the objective function, providing an integrated optimization framework for complex resource coordination. Additionally, Jia and Zeng [150] constructed an optimization model for port logistics decision systems based on the ACO algorithm. Simulation results verified the system’s effectiveness in enhancing operational efficiency and economic performance, expanding the application scenarios of intelligent algorithms in multi-objective scheduling.

In the field of equipment scheduling and energy management, addressing the inbound container dispatching problem for reach stackers at small terminals, Sarmiento et al. [151] compared the Shortest Processing Time (SPT) and FCFS rules, providing low-cost optimization strategies for micro-level operational scheduling in small and medium-sized terminals. In another study, Tang et al. [152] focused on peak electricity consumption in quay crane dual-cycle operations and evaluated peak-shaving strategies using an agent-based simulation model. This was the first to incorporate equipment energy consumption optimization into the port scheduling simulation framework, expanding the research dimension of green port operations.

Regarding the coordination between ports and inland transportation, Muravev et al. [153] developed a hybrid simulation model on the AnyLogic platform, integrating multi-agent modeling, system dynamics, and discrete-event simulation. They proposed a two-stage optimization framework that significantly improved system operational efficiency and financial performance in the parameter optimization of the dry port of Ningbo-Zhoushan Port, providing methodological support for resource allocation at multimodal transport nodes. In subsequent research, Kotachi et al. [154] constructed a discrete-event simulation model encompassing various resource types to quantitatively analyze the relationships among throughput, resource utilization, and waiting times in multimodal systems, revealing the impact mechanisms of input parameter variations on complex port operations and offering a simulation tool for multimodal transport coordination. Furthermore, Frazzon et al. [155] proposed the concept of “intelligent port–inland integration” and demonstrated through a Brazilian port case study that intelligent logistics systems can effectively improve the efficiency and reliability of port–inland interfaces, reduce supply chain disruption risks, and promote the simulation research on port–hinterland coordination toward more systematic and intelligent development.

With the application of digital technologies, Ding et al. [156] designed a Decision Support System (DSS) based on digital twin and big data technologies. Focusing on the Phase IV automated terminal at Shanghai Yangshan Port, they integrated discrete-event simulation and combinatorial optimization models to achieve full lifecycle resource optimization from macro-level planning to micro-level operations, significantly reducing operational delays and improving vessel service quality. This marks the entry of port scheduling simulation into the era of real-time and precise optimization. In another study, An et al. [157] addressed closed-loop vessel scheduling in the Middle East, considering uncertainties such as weather conditions. By comparing new and old scheduling policies through optimization models, they demonstrated the advantages of the new policy in terms of total cost and environmental impact, providing risk management strategies for dynamic scheduling in complex environments.

The aforementioned studies, through a variety of simulation methods and optimization algorithms, have addressed key aspects of port scheduling, including equipment, berths, intermodal operations, and decision support. These works not only demonstrate the effectiveness of simulation technologies in modeling complex systems but also provide practical approaches for ports to manage operational uncertainty and enhance resource efficiency. Future research can further explore the integration of multiple technologies (such as digital twins and reinforcement learning), end-to-end coordinated optimization (such as dynamic coupling of production maintenance and vessel speed), and low-carbon scheduling strategies, thereby promoting the development of port scheduling simulation toward greater intelligence and sustainability.

6. Intelligent Scheduling: Agent-Based Methods and Emerging Technologies

With the rapid development of artificial intelligence technologies, machine learning is gradually extending from tasks such as perception and predictive modeling to more complex areas of decision optimization. In port seaside scheduling problems, although traditional heuristic and metaheuristic methods have achieved substantial results in model construction and computational efficiency, they still face challenges such as limited adaptability and reliance on human expertise when addressing large-scale, highly dynamic, and uncertain scenarios. Consequently, intelligent scheduling approaches based on autonomous learning and environment interaction have become an important direction for current research. In contrast to heuristic and metaheuristic methods—which typically operate based on explicitly defined problem structures and tailored search strategies, often leveraging problem-specific expertise to balance solution quality and computational efficiency—machine learning approaches rely on data-driven patterns and continuous adaptation to handle uncertainty and dynamic changes. While heuristics provide reliability and interpretability in well-structured problems, learning-based methods excel in adaptability and scalability, especially in complex and uncertain seaside environments. Their complementary strengths suggest that hybrid strategies, such as reinforcement learning combined with metaheuristic search, hold great promise for advancing intelligent port scheduling.

Machine Learning (ML) has emerged as a powerful complement to traditional optimization methods in port scheduling. Unlike heuristics and exact models that rely on explicitly defined problem structures, ML leverages data-driven insights, continuous adaptation, and predictive capabilities to tackle the high dynamism and uncertainty of port operations. Its ability to learn from historical and real-time data makes it particularly suitable for tasks involving uncertain environments, large-scale decision-making, and the design of adaptive scheduling strategies.

In recent years, ML has been widely applied to key tasks in port scheduling, such as parameter prediction, algorithm selection, and the integration with metaheuristic algorithms for parameter optimization. A substantial body of literature has addressed vessel arrival time forecasting [158,159,160]. In the optimization problems addressed in this paper, some studies have also considered vessel arrival time forecasting in conjunction with the BAP. For example, Kolley et al. [81] combined AIS data with four machine learning algorithms to estimate vessel arrival times and introduced a dynamic buffering mechanism to enhance scheduling robustness. Beyond vessel arrival predictions, ML has also been employed to estimate other key operational parameters that affect scheduling efficiency. Guo et al. [102] used a BP neural network to predict operation times under weather influences and embedded the results into a berth and quay crane collaborative scheduling model. For algorithm recommendation, de León [73] utilized KNN classification and the Borda ranking aggregation mechanism to dynamically recommend optimal algorithm combinations for berth scheduling at bulk terminals. For large BAP, Wawrzyniak et al. [161] also adopted a similar algorithmic selection framework. Finally, in the integration of ML with metaheuristic algorithms, Cheimanoff et al. [146] applied a random forest regression to predict effective hyper-parameter combinations for a VNS metaheuristic, achieving superior performance compared with several classical approaches. In summary, ML has been applied in port scheduling for arrival forecasting, parameter prediction, algorithm selection, and metaheuristic integration, enhancing both robustness and efficiency under uncertainty.

The machine learning-based algorithm recommendation framework in Figure 7 is derived from reference [73]. This framework consists of a training phase and an inference phase. In the training phase, first, features $F$ are extracted based on the training instance set $P_t$. Then, by executing algorithms in set $A$ on instances, experimental data $Y$ is obtained, where $y(a,x)$ corresponds to the objective function value from running algorithm $a$ on instance $x$. Features, algorithms, and experimental data are integrated into a table, which is input to a machine learning algorithm to generate a knowledge base for recommendations. In the inference phase, for a new instance, features are first extracted. Then, using KNN supervised classification and ranking aggregation in machine learning, a recommended algorithm is obtained and executed, and a scheduling scheme is output. This approach demonstrates the advantage of machine learning in adapting to different problem instances and enabling data-driven decision-making for scheduling optimization.

Building on the advancements of machine learning in port scheduling, research has increasingly turned toward agent-based methods that emphasize autonomous decision-making and adaptive coordination. Unlike purely data-driven models, agent-based approaches explicitly model the interactions among heterogeneous port resources, enabling more realistic and dynamic representations of seaside operations. In particular, Reinforcement Learning (RL) focuses on single agents learning optimal strategies through trial-and-error interaction with the environment, making it especially suitable for scheduling sequence optimization and rolling decision control under uncertainty. Extending this framework, Multi-Agent Reinforcement Learning (MARL) addresses the collaborative and interactive relationships among multiple agents—such as vessels, tugboats, pilots, and quay cranes—allowing them to learn strategies not only in response to the environment but also through coordination or competition with each other. MARL supports distributed and parallel scheduling, captures game-theoretic dynamics, and enhances adaptability in complex and uncertain port environments. These features make RL and MARL powerful complements to traditional heuristics and machine learning in the development of intelligent seaside scheduling systems.

In addition, with the rapid advancement of large language models (LLMs), the application of pre-trained language models to scheduling strategy modeling, knowledge reasoning, and human–machine interaction is also revealing new possibilities for scheduling optimization.

6.1. Agent-Based Scheduling Optimization Methods

As the need for port scheduling systems to adapt to dynamic environmental changes continues to grow, reinforcement learning methods based on Markov Decision Processes (MDPs) have gradually become an important research direction in scheduling optimization. MDPs explicitly define the structure of states, actions, and rewards, capturing the dynamic evolution of the scheduling environment and the agent’s decision-making process. This enables the scheduling system to learn and optimize strategies through continuous interaction, thereby achieving adaptive and intelligent scheduling.

As shown in Figure 8, in the reinforcement learning framework, the agent selects actions based on the current environmental state, receives rewards and new states from the environment, and iteratively optimizes its strategy to gradually improve scheduling performance. This approach has been widely applied to typical scenarios such as berth allocation, tugboat scheduling, and channel traffic control, demonstrating significant potential in practical engineering applications.

In berth and handling equipment scheduling, Dai et al. [50] modeled integrated berth and quay crane scheduling as a multi-stage MDP problem. By adopting a Dueling DQN architecture and separating advantage functions, they improved the accuracy of complex state evaluation and job prioritization, enabling the system to handle high-pressure scenarios such as dense vessel arrivals. In a multi-terminal environment, Li et al. [104] further introduced the D3QN algorithm, integrating berth status, vessel priority, and transshipment costs to achieve efficient policy learning in complex state spaces, thereby effectively reducing the total vessel port time. In addition, Wang et al. [75] used a DQN network to directly control berthing sequences, achieving better performance in reducing waiting times and avoiding berth conflicts compared to traditional heuristic algorithms.

For bulk terminal operation scheduling, Ai et al. [162] proposed the PS-D3QN algorithm, which is based on prioritized experience replay and the Softmax strategy, to efficiently optimize integrated berth and yard scheduling. Through autonomous learning, the agent not only improved resource allocation efficiency but also reduced manual scheduling errors. Similarly, Rida [163] modeled container terminal handling operations as an MDP and optimized the dynamic allocation of quay cranes and vehicles, significantly reducing operation waiting times and validating the effectiveness of reinforcement learning in practical terminal scenarios.

For bulk terminals handling coal and other commodities, Li et al. [164] incorporated yard status, equipment status, and vessel demand into an MDP model and used Double DQN for training, enabling the autonomous generation of high-quality loading operation plans under highly stochastic task and yard conditions. This approach demonstrated strong generalization capability and fast convergence. In port disruption management, Li et al. [165] addressed extreme weather events by proposing a non-homogeneous MDP model combined with a rolling horizon and evolutionary algorithm, achieving dynamic adjustment of vessel operation rates and port selection, thus enhancing scheduling flexibility and robustness.

At the same time, many researchers have focused on enhancing model adaptability to real-world environmental disturbances. For example, Zhou et al. [51] improved the convergence of the D3QN policy under ETA uncertainty by introducing prioritized experience replay and state buffering mechanisms. Lv et al. [45] incorporated scheduling rule selection into the action space, enabling state-aware, multi-level coordinated scheduling optimization. In addition, the integration of Approximate Dynamic Programming (ADP) with rolling horizon evaluation and tabu search Wei et al. [22] has improved scheduling optimization efficiency without relying on deep neural networks. For complex scenarios involving multiple objectives and constraints, Wang et al. [46] applied a PPO deep policy network to investigate channel scheduling strategies under tidal window and emission constraints.

In summary, recent advancements in reinforcement learning-based scheduling optimization methods grounded in MDP have increasingly integrated multi-layered policy networks, experience replay mechanisms, and innovations in deep architectures. This has significantly enhanced the adaptability and generalization capability of these methods to high-dimensional and dynamic port operation environments. Such research has facilitated the practical deployment and iterative improvement of scheduling agent frameworks in engineering, providing strong support for the evolution of port intelligent scheduling systems toward greater autonomy and robustness.

6.2. Multi-Agent Reinforcement Learning (MARL)

With the continuous expansion of port operation systems and the increasing level of automation, scheduling optimization has gradually evolved from local optimization of single resources and single objectives to global optimization involving multi-resource and multi-stage coordination. While single-agent reinforcement learning methods can iteratively improve scheduling strategies through interactions with the environment, real-world port environments often require the simultaneous participation of various resources—such as quay cranes, tugboats, and vessels—in scheduling decisions. In such cases, the local perspective of a single agent is insufficient to address complex issues such as distributed resources, concurrent tasks, and dynamic collaboration within the system.

To address these challenges, MARL has been introduced into the field of port scheduling optimization. As illustrated in Figure 9, different types of equipment and operational entities in the port environment can be modeled as separate agents. These agents independently make decisions based on the environmental state and collaboratively drive the overall optimization of the system. All agents interact and compete within the same environment, continually adjusting their strategies to achieve efficient and intelligent scheduling under multiple objectives. This approach significantly improves resource utilization and system adaptability, providing strong theoretical and technical support for the efficient operation of complex port systems.

In port seaside loading, unloading, and transportation scheduling, MARL technology has been widely applied to the coordinated optimization of key equipment such as quay cranes and AGVs. For example, in quay crane scheduling, Longet al. [166] addressed the sequencing and conflict constraints of multiple quay cranes by proposing a multi-agent deep reinforcement learning approach based on the PPO algorithm. By utilizing a shared actor–critic architecture to simulate joint scheduling of multiple quay cranes, this method effectively improved operational efficiency and system flexibility in complex task environments. The results demonstrated that the MARL approach outperformed traditional metaheuristic algorithms and single-agent solutions in multi-agent scenarios, making it well suited for large-scale and highly dynamic port operation systems.

In automated container terminals, Automated Guided Vehicles (AGVs) serve as core equipment for horizontal transportation, and their scheduling optimization has long been a focus of academic research. Che et al. [167] addressed the real-time scheduling problem of electric AGVs under battery limitations and charging station capacity constraints by proposing a deep reinforcement learning framework based on heterogeneous graph neural networks and Multi-Agent Proximal Policy Optimization (MAPPO). This model effectively coordinates the complex relationships between vehicles and charging resources, achieving efficient and highly generalizable collaborative scheduling. In addition, Gong et al. [89] focused on energy optimization in actual container yard operations and employed the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm to realize real-time AGV scheduling under multiple constraints, including energy consumption, conflict, and charging. This approach significantly improved both the energy efficiency and operational effectiveness of the port yard.

In addition to quay cranes and AGVs, the scheduling of unmanned shipment vessels (USVs) in ports is also well suited to multi-agent reinforcement learning frameworks. Zhu et al. [103] developed a USV scheduling optimization model that considers energy supply, time windows, and berthing constraints, and proposed a MARL algorithm with multi-attention mechanisms. This approach not only achieved path conflict avoidance but also significantly reduced transportation delays and enhanced the intelligence level of waterborne transport, contributing positively to the overall throughput capacity of the port.

In equipment maintenance and management, MARL has also demonstrated significant potential. Yao et al. [168] addressed the problem of state-aware maintenance and maintenance resource management for port quay crane clusters by proposing an Evolutionary Multi-head Attention Critic with Adaptive Strategy–Multi-Agent Deep Deterministic Policy Gradient (EMACAS-MADDPG) algorithm. Through collaborative learning and division of labor among multiple agents, this model effectively reduced maintenance costs, improved equipment availability, and enhanced the overall robustness of port operations.

External port traffic and channel management also require collaborative optimization among multiple agents. Singh et al. [169] focused on vessel traffic control in busy waterways and adopted a hierarchical MARL approach, enabling large-scale vessels to make autonomous decisions and ensuring global safety management in dynamic environments. This provides a scalable, intelligent scheduling solution for practical port channel management systems. In addition, Zhao and Wu [170] addressed large-scale distributed cluster scheduling by integrating MARL with graph neural networks, achieving efficient collaboration and resource allocation among multiple agents within complex network structures. These studies highlight the scalability and generalization capabilities of MARL methods in highly complex systems.

It is worth noting that, although port scheduling optimization has mainly focused on operational equipment and transportation resources such as quay cranes, AGVs, and USVs, multi-agent reinforcement learning research on logistics–energy coordination is also opening new directions for intelligent port systems. Huang et al. [171] proposed an adaptive large-scale MARL model that enables the joint scheduling of all-electric vessels, quay cranes, AGVs, and port distribution networks, exploring novel theoretical and practical approaches for integrated energy management and intelligent decision-making in ports. This method, leveraging a super-network structure and hierarchical strategies, offers strong adaptability and computational efficiency, enabling it to handle daily variations in operational scale and scenarios while providing technological support for green and low-carbon port operations.

Table 7. Summary of literature on MARL.

Reference	Problem and Scenario	Main Framework/Algorithm
[166]	Quay crane scheduling	MAPPO
[167]	AGV scheduling and recharging	MAPPO, heterogeneous GNN
[89]	Energy-efficient AGV scheduling	MADDPG
[103]	USV scheduling	Multi-attention MARL
[168]	Gantry crane maintenance management	EMACAS-MADDPG
[169]	Maritime traffic management	Hierarchical MARL
[170]	ML cluster scheduling	MARL, hierarchical GNN
[171]	Logistics–energy spatiotemporal coordination	MARL, hierarchical policy network

systematically summarizes the representative literature, application scenarios, and major algorithmic frameworks of mainstream MARL in port and related scheduling optimization fields. As can be seen, these studies cover a wide range of aspects, including quay crane scheduling, AGV energy-efficient transport, unmanned vessel scheduling, equipment maintenance, port traffic management, and intelligent resource coordination. The adopted methods encompass a variety of mainstream reinforcement learning and agent system architectures, such as MAPPO, MADDPG, MARL-GNN, and EMACAS-MADDPG, fully demonstrating the breadth of MARL applications and algorithmic innovation in complex port systems.

Overall, current research on multi-agent reinforcement learning (MARL) for scheduling optimization is primarily focused on the landside of ports—such as yard operations, horizontal transportation, and equipment coordination—while MARL modeling and scheduling for seaside resources, including anchorage areas, berths, and port waterway traffic, remain relatively limited. In the future, as the digitalization and intelligence of port processes continue to advance, expanding MARL applications to the seaside and ultimately to the coordination of all resources throughout the entire port operation will be a key development direction. Achieving more refined and globally optimized intelligent scheduling for ports will become an important focus in this field.

6.3. Integration of Large Language Models (LLMs) for Decision Support

Large language models (LLMs), as a core technology in recent natural language processing research, possess strong semantic understanding, knowledge integration, and task reasoning capabilities, and have been widely applied to scenarios such as code generation, logical reasoning, and decision support. Compared with traditional optimization modeling approaches, LLMs can take natural language as input and automatically perform problem comprehension, model construction, and even preliminary solution processes, offering more intelligent and interactive solutions for complex tasks [172].

In scheduling optimization research, some studies have explored the introduction of LLMs to assist with modeling and strategy generation, particularly in areas such as job-shop scheduling, intelligent manufacturing, and urban transportation. Zeng et al. [173] proposed an LLM–reinforcement learning framework combined with human feedback mechanisms, which effectively improved the convergence efficiency and generalization capability of scheduling strategies. Mostajabdaveh et al. [174] developed a multi-agent LLM architecture that enables the automated process from natural language descriptions to optimization model construction and validation, demonstrating the great potential of LLMs in modeling automation. In addition, other studies have used LLMs to realize information parsing and task allocation for multi-vehicle scheduling and navigation tasks, enhancing scheduling decision-making capabilities in complex environments [175].

Although there is currently no literature directly applying LLMs to port seaside scheduling problems, the aforementioned achievements provide valuable references for future research. Port scheduling involves diverse tasks, complex constraints, and frequent dynamic changes; LLMs show promising potential in areas such as natural language parsing of scheduling instructions, multi-resource scheduling modeling, and expert knowledge supplementation. Future research may focus on LLM-driven automation of port scheduling modeling and language-based dynamic instruction response mechanisms, thereby advancing scheduling optimization systems toward greater intelligence and human–machine collaboration.

7. Analysis and Perspectives

7.1. Statistical Analysis of Reviewed Articles

To comprehensively review the current modeling and solution methods in port seaside scheduling optimization research, we classified and analyzed the core literature retrieved from our search from a methodological perspective. Specifically, based on the types of algorithms employed, the literature was divided into four main categories: exact algorithms, metaheuristic algorithms, agent-based methods, and other approaches. Their distribution is shown in Figure 10.

As shown in Figure 10, research on port seaside scheduling optimization is dominated by heuristic algorithms and simulation methods, which account for 60.5% of all the literature. This indicates that, in dealing with the highly coupled resources and dynamic changes characteristic of real-world port scenarios, heuristic methods have become the mainstream choice due to their high computational efficiency and flexibility. Exact algorithms represent 21.7% of the studies. Although they can provide optimal solutions for some problems, their application is relatively limited by the computational burden of large-scale and complex cases. Agent-based methods account for 12.5%, including the rapidly developing reinforcement learning and multi-agent reinforcement learning approaches in recent years. These methods, through autonomous decision-making and collaborative optimization among agents, are better suited to handle the dynamism and uncertainty of port systems. In addition, other innovative methods—such as data-driven and hybrid approaches—comprise 5.3%. Although currently a small proportion, they reveal promising directions for future theoretical and methodological innovations. Overall, research paradigms in this field are evolving toward greater diversity and intelligence.

Table 8. Comparison of different methods.

Method Type	Advantages	Limitations	Applicable Problem Scale and Dynamics
Exact Methods	Theoretical guarantee of solution optimality; suitable for problems with clear structure	High computational complexity, difficult to handle large-scale or dynamic changes	Suitable for small-scale, static problems, such as single berth allocation, fixed task quay crane scheduling, etc.
Heuristic Methods	Easy to implement, fast computation, flexible modeling	Easily trapped in local optima, lacking theoretical guarantees of convergence	Suitable for medium-scale or moderately dynamic problems, such as initial tugboat allocation, fast berth reassignment, etc.
Agent-Based Methods	Supports dynamic adaptation, autonomous learning, and distributed coordination; suitable for complex system modeling	Complex model construction, high training cost, strong dependence on the environment	Suitable for large-scale, highly dynamic systems, such as collaborative scheduling of multi-vessel resources, real-time event-driven scheduling, etc.

presents a comparison of these three methods and their applicability.

Table 8 provides a concise comparison of exact, heuristic, and agent-based methods in terms of their advantages, limitations, and suitable application contexts. Exact methods offer optimality guarantees but are computationally intensive and best suited for small-scale, static problems. Heuristic methods are flexible and computationally efficient but may lack global optimality, making them more appropriate for medium-scale or moderately dynamic problems. Agent-based methods excel in modeling complex, highly dynamic systems through adaptive and distributed coordination, though they require high development effort and are environment-dependent. This comparison highlights the trade-offs among different approaches and offers guidance for selecting methods based on problem scale and dynamics.

To examine the commonly used modeling strategies in port seaside scheduling optimization, we classified the mathematical models found in the literature into two categories: deterministic models and uncertainty models. Their distribution is shown in Figure 11.

The results show that deterministic models account for as much as 77%, remaining the mainstream approach in current research. These models assume that system parameters are fully known and do not vary over time, with clear model structures that facilitate the use of exact or heuristic solution methods. They are well suited to static or short-term planning problems, such as berth allocation or quay crane scheduling under fixed operational time windows. Uncertainty models account for 23% and enhance the adaptability of the models to real-world uncertainties—such as vessel delays, equipment failures, or weather impacts—by incorporating disturbances, fluctuations, or fuzziness. Common approaches include stochastic optimization, robust optimization, and fuzzy optimization. Although these methods are currently less prevalent, they have distinct advantages in improving the robustness of scheduling systems and coping with unexpected events, and the research interest in this area has been increasing year by year.

In addition, the statistical results indicate that 12 publications in the field of traditional mathematical modeling have explicitly considered the dynamic characteristics of port seaside operations, proposing modeling frameworks such as the Dynamic Berth Allocation Problem (Dynamic BAP) and Dynamic Tugboat Scheduling. These studies move beyond static assumptions by introducing rolling horizon approaches, real-time feedback, or event-driven mechanisms to enhance the practical adaptability and responsiveness of the models. This reflects a clear trend in the field toward the gradual evolution from static to dynamic scheduling.

In summary, current research is predominantly based on deterministic modeling, while uncertainty and dynamic modeling are gradually gaining importance as complementary directions. In the context of rapid advances in smart ports and automated systems, more flexible and real-time modeling approaches are expected to become important research directions in the future.

To further understand the application of metaheuristic algorithms in port seaside scheduling, we classified and analyzed the algorithm types used in the relevant literature. The results are shown in Figure 12.

Among these, evolutionary algorithms account for the largest proportion at 44%, with GA being the most representative. These are widely used for problems such as berth allocation and tugboat scheduling due to their strong global search capability and adaptability. Swarm intelligence algorithms account for 21%, which excel at complex combinatorial optimization. Local search-based metaheuristics represent 13%, with approaches such as SA, TS, VNS, and ALNS being well suited for local optimization and solution refinement. Hybrid algorithms make up 7%, reflecting a growing trend toward combining multiple strategies to enhance algorithm performance. Innovative algorithms account for 15%, representing the emergence of newer metaheuristic strategies in this field. Overall, evolutionary algorithms remain the most representative metaheuristic methods for port seaside scheduling problems, with swarm intelligence and local search strategies serving as key complementary approaches. The rise in hybrid and innovative methods further demonstrates that algorithm integration and adaptive mechanisms have become important trends in this field.

Systematic statistics on the methods and models in the literature reveal a clear trend in port seaside scheduling optimization research: a transition from traditional approaches toward intelligent solutions. In terms of modeling, although deterministic models still dominate, increasing attention is being paid to uncertainty and dynamic modeling methods, reflecting a response to the complexity and variability of real operational environments. Regarding solution approaches, metaheuristic algorithms have become mainstream, demonstrating strong adaptability and scalability; at the same time, exact methods continue to play a fundamental role in well-structured problems, and agent-based intelligent methods have shown unique advantages in dynamic, multi-agent collaborative scheduling scenarios. Overall, current research is moving toward greater flexibility, intelligence, and real-time responsiveness, providing a diverse foundation for future algorithm design and model development.

7.2. Future Perspectives

(1) Robust Optimization and Adaptive Algorithms in Dynamic Environments

Port seaside scheduling must cope with dynamic changes such as vessel delays and extreme weather, for which traditional static models often fail to meet real-time requirements. In the future, robust optimization and stochastic programming can be used to build resilient scheduling frameworks—for example, by introducing Distributionally Robust Optimization (DRO) to simultaneously address uncertainties such as tidal fluctuations and tugboat failures, thereby generating berth allocation schemes that balance safety and efficiency. In addition, Deep Reinforcement Learning (DRL) can dynamically adjust tugboat routing based on real-time data (e.g., AIS vessel trajectories) and continuously optimize response strategies through online learning. Moreover, digital twin technology can simulate extreme scenarios, such as typhoons and equipment failures, enabling pre-evaluation of scheduling feasibility and rapid iterative optimization, thus enhancing the system’s adaptability and resilience to risks.

(2) Intelligent Scheduling Models Driven by Green Energy

In pursuit of carbon neutrality, port scheduling must deeply integrate energy constraints with operational efficiency. For scenarios involving the mixed use of electric and fuel-powered tugboats, multi-objective optimization models should be designed to incorporate parameters such as battery capacity and charging time windows. For example, deploying electric tugboats preferentially during tidal windows can reduce energy consumption, while utilizing port microgrids can help balance energy supply and demand. Carbon footprint tracking technology can quantify carbon emission costs as part of the objective function—for instance, allocating berths closer to shore power facilities for vessels using shore power, thereby reducing reliance on fossil fuels. Additionally, Life Cycle Assessment (LCA) can help quantify the environmental impact of different scheduling schemes, promoting the transition of port operations toward low-carbon practices.

(3) Integration of Intelligent Algorithms and Improvement of Ultra-Large-Scale Solution Efficiency

As port scales increase, traditional algorithms face the “curse of dimensionality.” Hybrid intelligent optimization algorithms, which combine the global search capabilities of genetic algorithms with the rapid prediction abilities of neural networks, can filter out inefficient solution spaces—for example, by pre-screening feasible solutions in berth allocation and then refining them through genetic algorithm-based iteration. For ultra-large-scale problems (such as scheduling thousands of vessels), quantum-inspired algorithms can transform combinatorial optimization into quantum annealing models, significantly reducing solution time. For instance, by mapping the berth allocation problem to quantum bit states and leveraging quantum parallelism, near-optimal solutions can be rapidly generated to support real-time decision-making.

(4) Intelligent Scheduling Systems Empowered by LLMs

With the continuous improvement of LLMs in natural language understanding and task reasoning, their application prospects in port scheduling optimization are becoming increasingly promising. In the future, LLMs can serve as intelligent decision-making cores, automatically parsing natural language scheduling instructions and enabling end-to-end optimization—from requirement description to scheduling model construction, constraint identification, and parameter completion. For example, dispatchers can issue complex instructions such as multi-resource integrated scheduling or green operation priorities using natural language, and the LLMs will automatically translate them into executable mathematical models and scheduling strategies. By integrating real-time data, LLMs can dynamically adjust scheduling plans and support human–machine collaborative decision-making. With further integration with knowledge graphs and reinforcement learning, LLMs will advance port scheduling systems toward higher levels of intelligence, automation, and interpretability, providing a new paradigm for multi-objective collaborative optimization and the accumulation of expert knowledge in complex scenarios.

In summary, future port scheduling will be characterized by “real-time responsiveness, zero-carbon priority, intelligent computation, and knowledge integration.” Dynamic optimization technologies will ensure operational resilience, green models will drive sustainable development, new algorithms will overcome scale bottlenecks, and large models will reshape decision-making paradigms. However, the implementation of these technologies must overcome challenges such as data privacy protection, algorithm interpretability, and cross-system integration. With the continuous evolution of AI and energy technologies, port seaside systems are expected to transition from traditional operation modes to become intelligent core nodes of the global supply chain, leading a new era of efficiency and sustainability in the maritime industry.

8. Conclusions

In recent years, the optimization of port seaside scheduling has emerged as a prominent research frontier in the advancement of smart ports, driven by the intricate coupling of resources, dynamic operating conditions, and multi-objective requirements. This paper presents a comprehensive review of major research directions in port seaside scheduling, focusing on the modeling and coordination of key resources such as berths, quay cranes, tugboats, pilots, and navigational channels. Core modeling and solution strategies—including exact algorithms, metaheuristics, agent-based approaches, and large language models—are examined in depth. The literature indicates a clear shift from deterministic, static modeling toward dynamic, uncertainty-aware, and intelligent adaptive frameworks. Likewise, scheduling methods are evolving from conventional heuristics and exact techniques to reinforcement learning, multi-agent coordination, and data-driven intelligent systems. The practical application of these intelligent scheduling methods enhances not only operational efficiency but also the resilience and sustainability of port systems under complex and uncertain conditions.

Through a detailed analysis of 152 publications, several key findings have been identified. First, deterministic models still dominate the field, yet they are increasingly complemented by stochastic and robust optimization approaches to address operational uncertainties. Second, while heuristic and metaheuristic algorithms remain the most widely applied due to their flexibility and efficiency, exact algorithms continue to provide valuable benchmarks for model validation in small- to medium-scale scenarios. Third, agent-based methods and reinforcement learning have emerged as promising avenues for handling dynamic, multi-agent coordination problems, though their practical applications in ports are still in the early stages. Lastly, the review reveals a research gap in the integrated optimization of auxiliary resources such as tugboats, pilots, and channel scheduling, which are crucial for improving overall system performance but remain underexplored.

Looking forward, port scheduling optimization is expected to place greater emphasis on multi-objective coordination, environmentally sustainable operations, and intelligent system development. The next generation of models will integrate advanced technologies such as big data analytics, artificial intelligence, reinforcement learning, and large language models to support human–machine collaboration, knowledge-driven modeling, and interpretable decision-making. Despite ongoing challenges—including data privacy, algorithm transparency, and system interoperability—continued theoretical innovation and engineering advancements are poised to transform port seaside systems into intelligent and resilient hubs at the core of global maritime logistics, driving the sector’s transition toward efficiency and sustainability.