Hermite Finite Difference Through Kernel Approximations to Efficiently Solve Nonlinear Black-Scholes Model

Abstract

We develop a high-order compact numerical scheme for solving a nonlinear Black–Scholes equation arising in option pricing under transaction costs. By leveraging a Hermite-enhanced Radial Basis Function-Finite Difference (RBF-HFD) method with three-point stencils, we achieve fourth-order spatial accuracy. The fully nonlinear PDE, driven by Gamma-dependent volatility models, is discretized via RBF-HFD in space and integrated using an explicit sixth-order Runge–Kutta scheme. Numerical results confirm the proposed method’s accuracy, stability, and its capability to capture sharp gradient behavior near strike prices.

1. Introduction and Numerical Challenges

1.1. Background

Options are often traded over-the-counter (OTC), particularly among large financial institutions [1], and these instruments are frequently customized to meet the specific needs of contracting parties. An asset, in this context, typically refers to a tradable financial instrument—such as equities, currencies, or commodities—whose current price is observable but inherently uncertain in the future [2].

Among the various types of options, the European call option gives its holder (not an obligation) the right to obtain an underlying asset at a given strike price on a fixed expiry date. The cornerstone of classical option pricing theory is the celebrated Black–Scholes (BS) dynamic, which derives a partial differential equation (PDE) under the assumptions of no arbitrage, frictionless trading, and constant volatility [3]. These assumptions, while simplifying mathematical analysis, are often challenged in real markets, necessitating model generalizations. The standard BS PDE is expressed as (q is the continuous dividend yield):

$$U_t+{\displaystyle \frac{1}{2}}{\sigma }^2{Y}^2{U}_{YY}+(r-q)Y{U}_Y-rU=0,$$

(1)

where $U(Y,t)$ shows the option’s price at time t and underlying asset price Y, r is the interest rate without risk, and $\sigma$ is the constant volatility of returns.

The terminal payoff conditions for standard European options are:

$$U(Y,T)=\max \{K-Y,0\},(\mathrm{put}\mathrm{option}),$$

(2)

$$U(Y,T)=\max \{Y-K,0\},(\mathrm{call}\mathrm{option}),$$

(3)

with K representing the strike price and T the maturity date.

Despite its widespread use, the BS model has well-documented limitations. It considers that asset prices pursue a geometric Brownian motion with constant volatility and neglects several market frictions such as transaction costs, liquidity constraints, and large investor impacts. In reality, market volatility is stochastic, and trading activities incur costs that significantly alter optimal hedging strategies [4]. Transaction costs are generally categorized into fixed costs (e.g., brokerage fees, modeled as linear or piecewise-linear functions of trade volume) and impact costs (arising from the trader’s influence on market prices, typically nonlinear).

1.2. Nonlinear BS PDE

To incorporate such effects, the classical BS framework is extended to nonlinear models. In this work, we consider the Barles–Soner model, which modifies the volatility term to depend nonlinearly on the option’s second derivative (Gamma) [5], thus giving rise to a fully nonlinear PDE:

$$U_t+{\displaystyle \frac{1}{2}}{\sigma }^2(Y,t,U_Y,U_{YY})Y^2{U}_{YY}+(r-q)Y{U}_Y-rU=0.$$

(4)

A widely studied nonlinear volatility formulation is:

$${\sigma }^2={\sigma }_0^2\left(1+\mathsf{\Psi }\left({\displaystyle \frac{e^{r(T-t)}}{a^2}}{Y}^2{U}_{YY}\right)\right),$$

(5)

where $\mathsf{\Psi }(·)$ is a nonlinear auxiliary function solving a specific ordinary differential equation (ODE), and $a=\mu /\sqrt{c\mathcal{N}}$ encodes market impact parameters, including risk aversion $\beta$, number of traded options $\mathcal{N}$, and investor behavior [6].

1.3. Overview of RBF-FD Formulation

While Monte Carlo methods are traditionally employed in linear pricing problems, they face notable difficulties when applied to nonlinear PDEs due to complications in simulating nonlinear expectations and path-dependence. Thus, deterministic approaches, such as finite difference (FD) schemes or meshfree techniques like radial basis function (RBF) collocation, offer more tractable and efficient alternatives.

Recently, meshfree methods—particularly the RBF-FD method [7,8]—have emerged as powerful solvers for PDEs in computational finance. Let $\phi :{\mathbb{R}}^d\to \mathbb{R}$ be an RBF defined as $\phi \left(r\right)$, where $r=\parallel \mathbf{y}-{\mathbf{y}}_k{\parallel }_2$ is the radius in Euclidean distance. In classical RBF-FD, the linear differential operator $\mathcal{L}v$ at a center node ${\mathbf{x}}_c\in {\mathbb{R}}^d$ is numerically valued via a linear mix of functional values at m neighboring nodes:

$$\mathcal{L}v{|}_{{\mathbf{x}}_c}\approx \sum _{i=1}^m{a}_{i}v\left({\mathbf{y}}_i\right),$$

(6)

where the weights $a_i$ are computed by incorporating the interpolating condition using RBFs centered at nearby stencil points.

Infinitely smooth RBFs such as the Gaussian (GA) and multiquadric (MQ) functions are commonly used [9]:

$${\phi }_{\mathrm{MQ}}\left(r\right)=\sqrt{{\beta }^2+r^2},{\phi }_{\mathrm{GA}}\left(r\right)=\exp \left(-{\left({\displaystyle \frac{r}{\beta }}\right)}^2\right),$$

where $\beta >0$ is the shape parameter.

Incorporating RBF-FD into option pricing allows for a flexible, high-accuracy numerical discretization of the spatial derivatives. By constructing local RBF interpolants over stencil points, differentiation matrices can be computed without relying on structured meshes. This facilitates modeling under complex market conditions, including those with transaction costs or liquidity constraints. The procedure proves especially valuable when paired with high-order time integration schemes.

1.4. Hermite Interpolation in Meshfree Numerical Methods

An advancement in meshfree numerical schemes, particularly in the context of solving PDEs with high-order accuracy, stems from the adoption of Hermite-type interpolation. Unlike classical RBF interpolation, which uses only function values at scattered nodes, the Hermite approach incorporates both function values and their derivatives at each node to construct the interpolant [10,11]. This extension enriches the interpolation space and yields more compact and accurate approximations with fewer stencil points.

In one dimension, given nodes ${\left\{x_i\right\}}_{i=1}^m\subset \mathbb{R}$ and RBF $\phi \left(r\right)$, the classical RBF interpolant for a smooth function $f\left(x\right)$ takes the form [12,13]:

$$s\left(x\right)=\sum _{i=1}^m{\lambda }_i\phi \left(\right|x-x_i\left|\right),$$

where the weights ${\lambda }_i$ are computed by satisfying the interpolating conditions

$$s\left(x_j\right)=f\left(x_j\right),$$

for all $j=1,2,\dots ,m$. The Hermite interpolation generalizes this by additionally matching derivative data. If $f\left(x\right)$ is known along with its derivative $f^{\prime }\left(x\right)$ at the interpolation nodes, the Hermite RBF interpolant becomes:

$$s\left(x\right)=\sum _{i=1}^m{\lambda }_i\phi \left(\right|x-x_i\left|\right)+\sum _{j=1}^m{\overline{\lambda }}_j{\phi }^{\prime }\left(\right|x-x_j\left|\right),$$

with the coefficients ${\lambda }_i$ and ${\overline{\lambda }}_j$ now satisfying a larger linear system derived from both:

$$s\left(x_k\right)=f\left(x_k\right),s^{\prime }\left(x_k\right)=f^{\prime }\left(x_k\right),\mathrm{for}k=1,2,\dots ,m.$$

This Hermite-enhanced interpolant provides two critical benefits for PDE solvers [14]:

• It enables compact FD formulas with higher-order convergence using smaller stencils.
• It maintains geometric flexibility, essential for pricing problems where adaptive spatial resolution near singularities (e.g., strike points) is critical.

In the realm of RBF-FD methods, the Hermite idea leads to the so-called RBF-HFD scheme. This method uses Hermite interpolation to derive local differentiation weights that approximate derivatives of the solution. The result is a high-order accurate discretization suitable for nonlinear equations like the BS model with Gamma-dependent volatility. It is especially beneficial in option pricing problems, where sharp transitions in the solution require refined resolution near boundaries, yet excessive stencil growth is computationally undesirable [15].

In this work, we tackle the original nonlinear BS PDE (4) directly using a meshfree RBF-HFD discretization utilizing three nodes to gain higher order while keeping the sparsity of the differentiation matrices as much as possible. The spatial semi-discretization results in a set of nonlinear ODEs, which are then integrated in time via a high-order Runge–Kutta (RK) scheme following the method-of-lines approach [16].

1.5. Motivation and Novelty

In realistic market settings, several phenomena—such as transaction costs, uncertain volatility, large trader effects, and risk-adjusted valuation measures—introduce significant nonlinearities into the pricing models for financial derivatives.

While it is true that model parameters in finance (such as volatility, interest rates, and asset drift) are often uncertain or noisy, the presence of nonlinearity in the governing PDE amplifies the effects of any discretization error or local inaccuracy in the numerical scheme. Specifically, nonlinear feedback mechanisms may result in solution blow-up, loss of monotonicity, or convergence to incorrect equilibrium values if low-accuracy methods are used. Therefore, the use of a high-order numerical method is not only mathematically desirable but also essential to ensure the robustness and fidelity of the solution.

In this paper, we extend the meshless RBF-FD framework by constructing high-order Hermite-type discrete differential operators based on three-point uniform stencils for both first- and second-order derivatives. Unlike many earlier studies that relied on wide stencil configurations to achieve high accuracy, we investigate a compact and efficient discretization using uniformly spaced nodes, which simplifies implementation and analysis while preserving high-order accuracy.

This work is distinct from our previous study [17], which focused on a time-fractional BS model. The current paper, in contrast, targets fully nonlinear BS PDEs, where the nonlinearity often appears in the volatility or reaction terms and is treated directly within the RBF-HFD scheme without relying on linearization or perturbative methods. The new methodology proposed here is specifically tailored for such nonlinear problems and achieves excellent accuracy, as validated through rigorous convergence studies and benchmark numerical tests in Section 5. While the construction of the RBF-HFD weights was addressed in our prior work, its application to nonlinear financial PDEs with fractional time derivatives is novel. To the best of our knowledge, this is the first instance in which a compact, high-order RBF-HFD method is applied to such a model, yielding superior accuracy and flexibility compared to classical mesh-based approaches.

In practice, the calibration of option pricing models involves fitting the model to market data, which are inherently noisy. However, once the parameters are calibrated, solving the pricing equation with high numerical accuracy ensures that errors due to discretization are minimized, avoiding compounding uncertainties introduced by the calibration process. To summarize, the main contributions of this work are as follows:

• Although high-order methods may seem more complex, the RBF-HFD approach offers a favorable computational cost-versus-accuracy tradeoff due to its meshless structure and the use of compact stencils.
• We use a high-order RBF-HFD scheme based on compact three-point uniform stencils, offering computational efficiency.
• The method is applied to solve the nonlinear BS PDE, which is known for its nonlinearity.
• We discuss that the proposed method achieves rapid convergence using a small number of stencil points.

We believe that this study provides a methodological advancement in the numerical solution of nonlinear BS PDE, particularly in cases where classical FD or low-order meshless schemes fall short due to insufficient accuracy.

1.6. Our Structure

The remainder of this article is structured as follows. Section 2 further furnishes the mathematical formulation of the nonlinear pricing problem. In Section 3, we develop the RBF-HFD discretization scheme, including stencil construction and weight computation for uniform nodes. Section 4 describes the temporal discretization strategy, based on explicit RK integrators and stability analysis. Section 5 provides numerical simulations to validate the accuracy, convergence, and stability of the furnished method. Finally, concluding remarks are provided in Section 6.

2. Modeling Transaction Costs

A nonlinear model was presented by [18], incorporating market feedback mechanisms via the Gamma of the option. The volatility is modeled as:

$${\sigma }^2={\sigma }_0^2\left(1+\vartheta {\left(Y{U}_{YY}\right)}^{1/3}\right),$$

(7)

where

$$\vartheta =3{\left({\displaystyle \frac{{\zeta }^2\theta }{2\pi }}\right)}^{1/3},$$

(8)

with $\theta$ and $\zeta$ representing the investor’s risk tolerance and transaction cost parameter, respectively. This model captures the increased volatility sensitivity to large Gamma values, particularly relevant in options near expiration or at-the-money.

The nonlinear term in these models arises due to the breakdown of the idealized continuous hedging framework assumed in classical financial theory. In real markets, frequent rebalancing incurs costs, making the continuous-time self-financing replication infeasible. This discrepancy between theoretical and practical strategies introduces additional variance, which must be embedded into the pricing model. The function $U_{YY}$, known as Gamma, quantifies the convexity of the option price in terms of the underlying asset and thus reflects the sensitivity of hedge ratios. A large Gamma implies greater hedging frequency and higher associated costs, thereby motivating a volatility correction that increases with $U_{YY}$.

A seminal contribution by [5] adopted a different perspective by deriving a nonlinear pricing PDE from an investor utility maximization framework under exponential preferences. The resulting volatility is given by:

$${\sigma }^2={\sigma }_0^2\left(1+\mathsf{\Psi }\left(e^{r(T-t)}{a}^2{Y}^2{U}_{YY}\right)\right),$$

(9)

where $a=\mu \sqrt{\gamma \mathcal{N}}$ incorporates the transaction cost parameter $\mu$, risk aversion coefficient $\gamma$, and the number of shorted options $\mathcal{N}$. The auxiliary function $\mathsf{\Psi }\left(x\right)$, encoding the nonlinear transaction cost effect, satisfies the following first-order nonlinear ODE:

$$\left\{\begin{array}{cc}{\mathsf{\Psi }}^{\prime }\left(x\right)={\displaystyle \frac{1+\mathsf{\Psi }\left(x\right)}{2\sqrt{x\mathsf{\Psi }\left(x\right)}-x}},\hfill & x\ne 0,\hfill \\ \mathsf{\Psi }\left(0\right)=0,\hfill \end{array}\right.$$

(10)

and has the implicit solution [19]:

$$\left\{\begin{array}{cc}x={\left(-{\displaystyle \frac{\mathrm{arcsinh}\left(\sqrt{\mathsf{\Psi }}\right)}{\sqrt{1+\mathsf{\Psi }}}}+\sqrt{\mathsf{\Psi }}\right)}^2,\hfill & \mathsf{\Psi }>0,\hfill \\ x=-{\left({\displaystyle \frac{\arcsin \left(\sqrt{-\mathsf{\Psi }}\right)}{\sqrt{1+\mathsf{\Psi }}}}-\sqrt{-\mathsf{\Psi }}\right)}^2,\hfill & -1<\mathsf{\Psi }<0.\hfill \end{array}\right.$$

(11)

From a theoretical standpoint, Barles and Soner established the existence and uniqueness of a viscosity solution for the nonlinear PDE (1) and (9), confirming the well-posedness of the model in the presence of transaction costs.

Formulation (9), therefore, provides a nonlinear and state-dependent volatility structure that encapsulates both market risk and transaction-induced risk.

The numerical treatment of such a PDE demands robust, stable, and high-order accurate discretization methods. In contrast to linear PDEs, the model (9) cannot be linearized trivially due to the nonlinear coupling of the volatility. By employing a three-point Hermite-based FD structure within the RBF-FD framework, we achieve fourth-order spatial accuracy while maintaining computational compactness. This is especially advantageous for solving degenerate, nonlinear PDEs like (9), where capturing the behavior near critical regions is paramount.

Why Nonlinearity Arises in the Volatility Term

These transaction costs—whether proportional, fixed, or market-impact based—are particularly sensitive to the Gamma of the option, $U_{YY}$, since this second derivative quantifies the convexity of the option price with respect to the asset price. A higher Gamma necessitates more frequent rebalancing of the hedge, thereby increasing trading costs. As a result, the trader seeks to optimize the hedging strategy not solely for risk minimization but also to balance costs. Assuming an investor with exponential utility and incorporating transaction costs into the optimization problem, they derived a nonlinear PDE whose volatility term depends on Gamma, as seen in (9). The function $\mathsf{\Psi }(·)$ captures the nonlinear correction introduced by trading frictions and satisfies the nonlinear ODE (10) with the implicit solution (11).

From a modeling perspective, this structure means that the volatility is no longer a constant but a dynamic quantity that increases with the curvature of the option price. The higher the local convexity (i.e., the Gamma), the larger the required hedge adjustments, and consequently, the more pronounced the transaction cost effects. This justifies embedding the nonlinearity directly into the volatility term of the PDE.

To illustrate this further, recall that in the original BS model, the variance component is:

$${\displaystyle \frac{1}{2}}{\sigma }^2{Y}^2{U}_{YY}.$$

In the transaction cost-aware model, this becomes:

$${\displaystyle \frac{1}{2}}{\sigma }_0^2\left(1+\mathsf{\Psi }\left(e^{r(T-t)}{a}^2{Y}^2{U}_{YY}\right)\right)Y^2{U}_{YY},$$

which clearly introduces a nonlinearity due to the dependence of $\sigma$ on $U_{YY}$.

3. RBF-HFD Spatial Discretization

The RBF-HFD method extends classical FD frameworks to allow accurate and stable discretization of PDEs using scattered node sets. This is particularly useful in financial PDEs where localized steep gradients (e.g., near the strike price) demand geometric flexibility.

3.1. Hermite Extension: The RBF-HFD Approach

While increasing stencil size improves accuracy, it may result in computational overhead and instability. To overcome this, Wright and Fornberg [20] proposed the RBF-HFD method–a compact FD scheme that includes both function values and derivative data within the stencil. For example, using a 3-point stencil, the RBF-HFD scheme achieves fourth-order accuracy by incorporating Hermite interpolation.

Let $\{y_{i-1},y_i,y_{i+1}\}=\{y_i-h,y_i,y_i+h\}$ be equidistant nodes with spacing $h>0$, the RBF-HFD approximation of $v^{\prime }\left(y_i\right)$ is defined as:

$$v^{\prime }\left(y_i\right)\approx {\alpha }_{i-1}v\left(y_{i-1}\right)+{\alpha }_{i}v\left(y_i\right)+a_{i+1}v\left(y_{i+1}\right)+{\delta }_{i-1}{v}^{\prime }\left(y_{i-1}\right)+{\delta }_{i+1}{v}^{\prime }\left(y_{i+1}\right)={\widehat{v}}^{\prime }\left(y_i\right).$$

(12)

3.2. Weight Construction via Hermite RBF Interpolation

Let the approximant be constructed as:

$$v\left(y\right)=\sum _{i=1}^{m_1}{\lambda }_i\phi (\parallel y-y_i\parallel )+\sum _{p=1}^{m_2}{\overline{\lambda }}_p\mathcal{L}\left[\phi \right(\parallel y-y_p\parallel \left)\right],$$

(13)

where $m_1=3$, $m_2=2$, and the weights ${\alpha }_i,{\delta }_i$ are determined by enforcing interpolation conditions at stencil points [21]. We employ the cubic MQ RBF:

$$\phi \left(r\right)={({\beta }^2+r^2)}^{3/2},$$

(14)

which enables compact analytic derivations of weights.

3.3. RBF-HFD Approximation of First Derivative

Theorem 1.

Let $\phi \left(r\right)$ be the cubic MQ kernel. Then the RBF-HFD scheme (12) achieves fourth-order convergence for $v^{\prime }\left(y_i\right)$ on uniform grids.

Proof. 

Enforcing Equation (12) at the three stencil nodes but considering all five assumptions, with two of them coming from the Hermite idea, leads to Algorithm 1 and the following set of equations (see also [17]):

$$\begin{array}{cc}\hfill & {\beta }^3{\alpha }_{i+1}+{\alpha }_i{\left({\beta }^2+h^2\right)}^{3/2}+{\alpha }_{i-1}{\left({\beta }^2+4h^2\right)}^{3/2}+3h\sqrt{h^2+{\beta }^2}=6h{\delta }_{i-1}\sqrt{{\beta }^2+4h^2},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \sqrt{h^2+{\beta }^2}\left({\alpha }_{i+1}\left(h^2+{\beta }^2\right)+3h\left({\delta }_{i+1}-{\delta }_{i-1}\right)\right)+{\beta }^3{\alpha }_i+{\alpha }_{i-1}{\left(h^2+{\beta }^2\right)}^{3/2}=0,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & 3h\sqrt{h^2+{\beta }^2}=\sqrt{{\beta }^2+4h^2}\left({\alpha }_{i+1}\left({\beta }^2+4h^2\right)+6h{\delta }_{i+1}\right)+{\beta }^3{\alpha }_{i-1}+{\alpha }_i{\left({\beta }^2+h^2\right)}^{3/2},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & 6h{\alpha }_{i-1}\sqrt{{\beta }^2+4h^2}+{\displaystyle \frac{3\left(h{\alpha }_i\left({\beta }^2+h^2\right)+{\beta }^2+2h^2\right)}{\sqrt{{\beta }^2+h^2}}}={\displaystyle \frac{3{\delta }_{i-1}\left({\beta }^2+8h^2\right)}{\sqrt{{\beta }^2+4h^2}}}+3\beta {\delta }_{i+1},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{3\left({\beta }^2+2h^2\right)}{\sqrt{{\beta }^2+h^2}}}=3\left(h{\alpha }_i\sqrt{h^2+{\beta }^2}+2h{\alpha }_{i+1}\sqrt{{\beta }^2+4h^2}+{\displaystyle \frac{{\delta }_{i+1}\left({\beta }^2+8h^2\right)}{\sqrt{{\beta }^2+4h^2}}}+\beta {\delta }_{i-1}\right).\hfill \end{array}$$

(19)

which yields:

$$\begin{array}{cc}\hfill {\alpha }_i& =0,{\alpha }_{i-1}=-{\alpha }_{i+1}=-{\displaystyle \frac{3h}{16{\beta }^2}}-{\displaystyle \frac{3}{4h}},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\delta }_{i-1}={\delta }_{i+1}& =-{\displaystyle \frac{3h^2}{16{\beta }^2}}-{\displaystyle \frac{1}{4}}.\hfill \end{array}$$

(21)

We now need to impose the obtained weights back into the RBF-HFD approximation and simplify the whole procedure utilizing Taylor expansions, which finally leads to the local truncation error:

$$e_1\left(y_i\right)={\widehat{v}}^{\prime }\left(y_i\right)-v^{\prime }\left(y_i\right)=\left(-{\displaystyle \frac{v^{\left(3\right)}\left(y_i\right)}{8{\beta }^2}}-{\displaystyle \frac{1}{120}}{v}^{\left(5\right)}\left(y_i\right)\right)h^4+\mathcal{O}\left(h^5\right),$$

which confirms fourth-order accuracy. □

Algorithm 1 RBF-HFD for $v^{\prime }\left(y_i\right)$ using 3-point stencil

1: Given nodes $y_{i-1},y_i,y_{i+1}$ with spacing h and shape parameter $\beta$   2: Construct RBF interpolant with derivative terms   3: Solve the system derived from Taylor expansions or exact RBF evaluations   4: Compute and store weights ${\alpha }_{i-1},{\alpha }_i,{\alpha }_{i+1},{\delta }_{i-1},{\delta }_{i+1}$   5: Compute $v^{\prime }\left(y_i\right)$ using Equation (12)

3.4. RBF-HFD Approximation of the Second Derivative

Analogously, for the second derivative, we write

$$v^{\prime \prime }\left(y_i\right)\approx l_{i-1}v\left(y_{i-1}\right)+l_{i}v\left(y_i\right)+l_{i+1}v\left(y_{i+1}\right)+q_{i-1}{v}^{\prime \prime }\left(y_{i-1}\right)+q_{i+1}{v}^{\prime \prime }\left(y_{i+1}\right)={\widehat{v}}^{\prime \prime }\left(y_i\right).$$

(22)

Theorem 2.

The RBF-HFD scheme using Equation (22) achieves fourth-order convergence for $v^{\prime \prime }\left(y_i\right)$ over uniform nodes.

Proof. 

Now, another system of equations can be constructed at the nodal points by imposing the RBF-FD and Hermite conditions, as follows (see also Algorithm 2):

$$\begin{array}{cc}\hfill & {\displaystyle \frac{3\left({\beta }^2+2h^2\right)}{\sqrt{h^2+{\beta }^2}}}={\beta }^3{l}_{i+1}+{\left(h^2+{\beta }^2\right)}^{3/2}{l}_i+{\left({\beta }^2+4h^2\right)}^{3/2}{l}_{i-1}+{\displaystyle \frac{3\left({\beta }^2+8h^2\right)q_{i-1}}{\sqrt{{\beta }^2+4h^2}}}+3\beta q_{i+1},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & 3\beta ={\displaystyle \frac{{\left(h^2+{\beta }^2\right)}^2{l}_{i-1}+{\left(h^2+{\beta }^2\right)}^2{l}_{i+1}+3\left({\beta }^2+2h^2\right)q_{i-1}+3\left({\beta }^2+2h^2\right)q_{i+1}+{\beta }^3\sqrt{h^2+{\beta }^2}{l}_i}{\sqrt{h^2+{\beta }^2}}},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{3\left({\beta }^2+2h^2\right)}{\sqrt{h^2+{\beta }^2}}}={\beta }^3{l}_{i-1}+{\left(h^2+{\beta }^2\right)}^{3/2}{l}_i+{\left({\beta }^2+4h^2\right)}^{3/2}{l}_{i+1}+{\displaystyle \frac{3\left({\beta }^2+8h^2\right)q_{i+1}}{\sqrt{{\beta }^2+4h^2}}}+3\beta q_{i-1},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & 6h\sqrt{{\beta }^2+4h^2}{l}_{i-1}+3h\sqrt{h^2+{\beta }^2}{l}_i+{\displaystyle \frac{6\left(3{\beta }^{2}h+8h^3\right)q_{i-1}}{{\left({\beta }^2+4h^2\right)}^{3/2}}}={\displaystyle \frac{9{\beta }^{2}h+6h^3}{{\left(h^2+{\beta }^2\right)}^{3/2}}},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{9{\beta }^{2}h+6h^3}{{\left(h^2+{\beta }^2\right)}^{3/2}}}={\displaystyle \frac{6h\left({\left({\beta }^2+4h^2\right)}^2{l}_{i+1}+\left(3{\beta }^2+8h^2\right)q_{i+1}\right)}{{\left({\beta }^2+4h^2\right)}^{3/2}}}+3h\sqrt{h^2+{\beta }^2}{l}_i.\hfill \end{array}$$

(27)

This finally yields the following collection of compact differential weights for the second derivative:

$$\begin{array}{cc}\hfill l_{i-1}& =l_{i+1}={\displaystyle \frac{294h^2}{125{\beta }^4}}+{\displaystyle \frac{9}{50{\beta }^2}}+{\displaystyle \frac{6}{5h^2}},\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill l_i& ={\displaystyle \frac{3}{125}}\left(-{\displaystyle \frac{196h^2}{{\beta }^4}}-{\displaystyle \frac{15}{{\beta }^2}}-{\displaystyle \frac{100}{h^2}}\right),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill q_{i-1}=q_{i+1}& =-{\displaystyle \frac{9h^2}{100{\beta }^2}}-{\displaystyle \frac{1}{10}}.\hfill \end{array}$$

(30)

In a similar fashion to the proof of Theorem 1, the local error is given by:

$$e_2\left(y_i\right)={\widehat{v}}^{\prime \prime }\left(y_i\right)-v^{\prime \prime }\left(y_i\right)=\left({\displaystyle \frac{2352v^{\prime \prime }\left(y_i\right)}{1000{\beta }^4}}-{\displaystyle \frac{75v^{\left(4\right)}\left(y_i\right)}{1000{\beta }^2}}-{\displaystyle \frac{5v^{\left(6\right)}\left(y_i\right)}{1000}}\right)h^4+\mathcal{O}\left(h^5\right),$$

indicating a quartic convergence rate. □

Algorithm 2 RBF-HFD for $v^{\prime \prime }\left(y_i\right)$ using 3-point stencil

1: Given equidistant stencil and shape parameter $\beta$   2: Use Hermite-based RBF interpolation with derivatives   3: Solve resulting system to obtain $l_i$ and $q_i$   4: Evaluate the approximation of $v^{\prime \prime }\left(y_i\right)$

The RBF-HFD method achieves high-order accuracy while relying on compact stencils, thus enhancing computational efficiency.

The choice of shape parameter $\beta$ significantly affects the stability and accuracy of the method. Too-small values lead to ill-conditioning; too-large values reduce approximation quality. Following [15], we recommend adaptive tuning based on the node spacing h. Extremely small values render the interpolation matrix ill-conditioned, whereas overly large values reduce accuracy. One mitigation approach is to employ the RBF-QR or Contour-Padé techniques, which decouple the ill-conditioning from the interpolation structure [22]. Alternatively, adaptive shape parameter selection strategies based on local nodal spacing h can provide a balance between accuracy and stability, especially in regions with steep solution gradients.

A differentiation matrix maps function values at discrete points to approximations of their derivatives at those same points. Specifically, for a vector $\mathbf{w}$ representing the values of a function sampled at node locations, the derivative is approximated as:

$${\displaystyle \frac{\partial }{\partial Y}}\mathbf{w}\approx D_1\mathbf{w},$$

(31)

where $D_1$ is the first-order differentiation matrix. Similarly, a second-order matrix can be constructed using the proposed approximations in Equations (20), (21), (29), and (30). These matrices are assembled by systematically applying the analytically derived RBF-HFD stencil weights.

4. Full Discretization

To facilitate temporal integration, we apply the transformation [23]:

$$\tau =T-t,F(Y,\tau ):=U(Y,t),$$

which rewrites the original nonlinear PDE (9) as:

$$\left\{\begin{array}{c}{F}_{\tau }={\displaystyle \frac{1}{2}}{\sigma }_0^2\left(1+\mathsf{\Psi }\left(e^{r\tau }{a}^2{Y}^2{F}_{YY}\right)\right)Y^2{F}_{YY}+(r-q)Y{F}_Y-rF,\hfill \\ Y>0,\tau \in [0,T),\hfill \\ F(Y,0)=\mathrm{payoff}.\hfill \end{array}\right.$$

(32)

This equation is degenerate near $Y=0$, and the volatility becomes strongly nonlinear in regions where $F_{YY}$ is large, potentially leading to numerical stiffness. In practical computations, the infinite domain $Y\in [0,\infty )$ must be truncated [24]. We therefore define the computational domain as:

$$(Y,\tau )\in [0,Y_{\max }]\times (0,T],$$

(33)

where $Y_{\max }\gg K$ is selected to ensure that truncation does not significantly distort the solution in the region of interest. For European call options, the boundary conditions are:

$$\left\{\begin{array}{c}F(0,\tau )=0,\hfill \\ F(Y_{\max },\tau )=Y_{\max }-K{e}^{-r\tau },\hfill \end{array}\right.$$

(34)

which reflect the limiting behavior of deep in-the-money and out-of-the-money options.

Let us consider n distinct discretization nodes along the Y variable. The DM for the first derivative can be written compactly as:

$$D_1={(I-M_{1,1})}^{-1}{M}_{1,2},$$

(35)

where

$$M_{1,2}=\left\{\begin{array}{cc}{\alpha }_{i,j}\mathrm{from}\left(20\right),\hfill & |i-j|=1\&i=j,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(36)

and

$$M_{1,1}=\left\{\begin{array}{cc}{\delta }_{i,j}\mathrm{from}\left(21\right),\hfill & |i-j|=1,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(37)

In a similar fashion, the DM for the second derivative can be written compactly as:

$$D_2={(I-M_{2,1})}^{-1}{M}_{2,2},$$

(38)

where

$$M_{2,2}=\left\{\begin{array}{cc}{l}_{i,j}\mathrm{from}\left(29\right),\hfill & |i-j|=1\&i=j,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(39)

and

$$M_{2,1}=\left\{\begin{array}{cc}{q}_{i,j}\mathrm{from}\left(30\right),\hfill & |i-j|=1,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(40)

Here, we construct the set of semi-discretized ODEs corresponding to the nonlinear BS model (32) using the newly developed RBF-HFD weights in Section 3. The construction is based on the application of differentiation matrices that encode the diffusion and convection terms. For further theoretical foundations, we refer the reader to [25].

After incorporating boundary conditions, the resulting semi-discretized ODE system takes the compact form:

$$\begin{array}{cc}\hfill F_{\tau }& =B\left(\tau \right)F\left(\tau \right),\hfill \\ \hfill F\left(0\right)& =\mathrm{payoff}\mathrm{function},\hfill \end{array}$$

(41)

where $B\left(\tau \right)$ is a time-dependent matrix incorporating the nonlinear volatility effects, and $F\left(\tau \right)$ is the vector of numerical approximations to the solution at time $\tau$.

We now recall the general s-stage RK method introduced in [26], which provides an approximate numerical solution to an initial value problem evaluated at ${\tau }_{\iota +1}={\tau }_{\iota }+\mathsf{\Theta }$, for indices satisfying $0\le \iota \le k$. The formulation is given by:

$$\begin{array}{ccc}{g}_i& =& {\displaystyle {\mathbf{v}}_{\iota }+\mathsf{\Theta }\sum _{j=1}^s{a}_{i,j}{k}_j,}\\ k_i& =& {\displaystyle f\left(\mathsf{\Theta }{\beta }_i+{\tau }_{\iota },g_i\right),}\\ {\mathbf{v}}_{\iota +1}& =& {\displaystyle {\mathbf{v}}_{\iota }+\mathsf{\Theta }\sum _{i=1}^s{\delta }_i{k}_i,}\end{array}$$

(42)

where the vector-valued function $f(·,·)$ satisfies the relation $f(·,·)=B\left(\tau \right)F\left(\tau \right)$. A standard assumption underlying this formulation is that the so-called row-sum conditions must hold:

$${\beta }_i=\sum _{j=1}^s{a}_{i,j},i=1,2,\dots ,s,$$

(43)

which define the temporal locations at which the function is sampled within the integration process. In the specific case of explicit RK methods, the coefficient matrix $P=\left[a_{i,j}\right]$ is required to be strictly lower triangular. Based on this criterion, one can construct an explicit sixth-order RK method (denoted by RK6), as developed in [27], given by:

$$P=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0\\ {\displaystyle \frac{3}{8}}& {\displaystyle \frac{1}{8}}& 0& 0& 0& 0& 0\\ {\displaystyle \frac{8}{27}}& {\displaystyle \frac{2}{27}}& {\displaystyle \frac{8}{27}}& 0& 0& 0& 0\\ {\displaystyle \frac{3(3\overline{q}-7)}{392}}& {\displaystyle \frac{\overline{q}-7}{49}}& {\displaystyle \frac{-6(\overline{q}-7)}{49}}& {\displaystyle \frac{3(\overline{q}-21)}{392}}& 0& 0& 0\\ {\displaystyle \frac{-3(17\overline{q}+77)}{392}}& {\displaystyle \frac{-\overline{q}-7}{49}}& {\displaystyle \frac{-8\overline{q}}{49}}& {\displaystyle \frac{3(121\overline{q}+21)}{1960}}& {\displaystyle \frac{\overline{q}+6}{5}}& 0& 0\\ {\displaystyle \frac{7\overline{q}+22}{12}}& {\displaystyle \frac{2}{3}}& {\displaystyle \frac{2(7\overline{q}-5)}{9}}& {\displaystyle \frac{-7(3\overline{q}-2)}{20}}& {\displaystyle \frac{-7(9\overline{q}+49)}{90}}& {\displaystyle \frac{-7(\overline{q}-7)}{18}}& 0\end{array}\right),$$

(44)

with associated coefficient vectors

$$b=\left({\displaystyle \frac{9}{180}},0,{\displaystyle \frac{64}{180}},0,{\displaystyle \frac{49}{180}},{\displaystyle \frac{49}{180}},{\displaystyle \frac{9}{180}}\right),$$

and

$$C=\left(1,{\displaystyle \frac{1}{2}},{\displaystyle \frac{2}{3}},{\displaystyle \frac{7-\overline{q}}{14}},{\displaystyle \frac{7+\overline{q}}{14}},1\right),$$

and $\overline{q}=\sqrt{21}.$

It is important to observe that, due to the explicit nature of this RK method, one obtains ${\beta }_1=0$ in (43), which implies that the function is evaluated precisely at the beginning of the current time integration step. The resulting RK6 scheme employs seven stages and achieves sixth-order accuracy in the time direction. Specifically, the local truncation error for this method is of order $\mathcal{O}\left({\mathsf{\Theta }}^7\right)$, while the global error accumulated throughout the simulation behaves asymptotically as $\mathcal{O}\left({\mathsf{\Theta }}^6\right)$.

The explicit sixth-order time integrator allows a larger timestep while keeping the temporal error comparable to the explicit fourth-order spatial error. In other words, for a given spatial mesh, the RK6 method gives greater flexibility in choosing $\mathsf{\Theta }$ without degrading the overall accuracy—this is particularly useful when one wishes to reduce the number of time steps (and hence the number of expensive PDE solves per time unit). Higher-order time integrators reduce the accumulation of temporal truncation error over many time steps. For problems where the solution is evolved over many time steps (long maturity in option pricing), the lower per-step temporal error of RK6 yields substantially smaller global-in-time error compared with a fourth-order method at the same $\mathsf{\Theta }$.

In practice, increasing the RK order (and the number of stages) often enlarges the stable region in the complex plane compared to the most commonly used fourth-order explicit RK methods, which in turn can allow marginally larger stable timesteps for diffusion-dominated problems when an explicit scheme is employed. A higher-order method requires more arithmetic per time step (more stages), but as the error-balance argument shows, it often permits fewer time steps to achieve the same global error. Thus, the overall computational cost to reach a prescribed accuracy can be lower with RK6 than with RK4. In practice, the break-even point depends on the cost per stage (which includes the cost of evaluating the nonlinear terms and any linear algebra) and on how large a timestep each method can use while maintaining stability and accuracy.

Theorem 3.

Let the system of coupled homogeneous ODEs in (41) be such that the Lipschitz continuity condition is satisfied. Then, the RK method defined in (42)–(44) is conditionally stable with respect to the temporal step size.

Proof. 

To analyze the stability of the proposed time-stepping procedure, we substitute the RK scheme (42) into the ODE system (41), which yields the following discrete propagation relation:

$$\begin{array}{cc}{\mathbf{v}}_{\iota +1}=& \left(I+\mathsf{\Theta }B\left(\tau \right)+{\displaystyle \frac{(\mathsf{\Theta }B\left(\tau \right){)}^2}{2!}}+{\displaystyle \frac{(\mathsf{\Theta }B\left(\tau \right){)}^3}{3!}}+{\displaystyle \frac{(\mathsf{\Theta }B\left(\tau \right){)}^4}{4!}}\right.\\ & \left.+{\displaystyle \frac{(\mathsf{\Theta }B\left(\tau \right){)}^5}{5!}}+{\displaystyle \frac{(\mathsf{\Theta }B\left(\tau \right){)}^6}{6!}}-{\displaystyle \frac{(\mathsf{\Theta }B\left(\tau \right){)}^7}{2160}}\right){\mathbf{v}}_{\iota }.\end{array}$$

(45)

Accordingly, the computational stability of the method reduces to ensuring that the spectral radius of the iteration matrix remains bounded by unity. Specifically, the condition becomes:

$$\left|1+\mathsf{\Theta }{\varrho }_i+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_i{)}^2}{2}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_i{)}^3}{6}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_i{)}^4}{24}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_i{)}^5}{120}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_i{)}^6}{720}}-{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_i{)}^7}{2126}}\right|\le 1,$$

(46)

where ${\varrho }_i$ denotes the i-th eigenvalue of $B\left(\tau \right)$. Consequently, the overall stability constraint can be expressed in terms of the dominant eigenvalue ${\varrho }_{\max }$ as:

$$\begin{array}{c}\left|1+\mathsf{\Theta }{\varrho }_{\max }+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_{\max }{)}^2}{2}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_{\max }{)}^3}{6}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_{\max }{)}^4}{24}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_{\max }{)}^5}{120}}+{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_{\max }{)}^6}{720}}-{\displaystyle \frac{(\mathsf{\Theta }{\varrho }_{\max }{)}^7}{2126}}\right|\le 1.\end{array}$$

(47)

Therefore, the RK6 method retains numerical stability provided that the temporal step size $\mathsf{\Theta }$ is chosen to satisfy the inequality in (47). This completes the proof. □

The stability analysis is carried out on a linearized, homogeneous form of the ODE system (41). Although this approach is standard, the principal difficulty addressed in this paper lies in the presence of nonlinearity, a limitation that we explicitly acknowledge. A more comprehensive discussion of how nonlinearity may influence practical stability would indeed be valuable. In this regard, it is important to emphasize that CFL-type conditions are primarily associated with hyperbolic PDEs and are not directly applicable to the parabolic PDE considered here. Moreover, the condition stated in Theorem 3 should be interpreted as necessary but not sufficient. Investigating stability under the full nonlinear regime, however, is not essential, since the primary source of nonlinearity arises from the choice $0<a\ll 1$, a setting that in practice corresponds to small parameter values and therefore does not introduce significant nonlinear effects.

5. Numerical Results

The implicit characterization of the function $\mathsf{\Psi }\left(x\right)$ introduces computational difficulties, particularly when addressing nonlinear PDEs characterized by state-dependent volatility. To manage this challenge within our numerical implementation, we employ Newton’s iterative method in conjunction with the FindRoot[] routine available in Mathematica [28]. To mitigate numerical instabilities due to floating-point round-off errors, we further utilize the Chop[] function, which truncates values below the threshold ${10}^{-10}$, thereby ensuring cleaner numerical outputs.

The proposed method using RBF-HFD in space is called RK6, and the standard first-order FD method and the recent efficient method in [29] are named SFD and ZM, respectively. Note that to have fair comparisons, RK6 is used for all the compared solvers using a fixed temporal step size $\mathsf{\Theta }$.

It is well known that the standard approach to applying time-dependent boundary conditions in RK methods can degrade the formal accuracy of a space–time scheme, sometimes reducing it to first order locally and second order globally, regardless of the spatial discretization (see [30]).

In the present work, our main interest lies in accurately resolving the hot zone near the payoff discontinuity, which is far from the artificial computational boundaries. The numerical errors that govern our conclusions are dominated by behavior in this interior region, where nonlinearities and steep gradients occur. The computational boundaries are deliberately placed sufficiently far from the hot zone so that the influence of the boundary conditions on the interior solution remains negligible. It is also important to note that for parabolic-type problems such as the BS model, the influence of distant boundaries decays over time due to the smoothing nature of the operator.

We clarify that the boundaries are placed sufficiently far from the hot zone and that their values are chosen to avoid the conditions under which RK boundary errors become significant. This will demonstrate that the accuracy in the interior region remains unaffected by any potential boundary-order reduction. Thus, the methodology proposed in [31], which formulates corrected expressions for intermediate boundary conditions during RK time-stepping, may not be necessary for our procedure.

Here, we evaluate the feasibility and computational efficacy of the developed algorithm in resolving the time-dependent PDE described in Equation (32). The examination emphasizes the spatial discretization strategy using uniformly distributed nodes. For all experiments, $Y_{\max }=3K$, thus encompassing a sufficiently broad financial range relevant for practical modeling. All simulations are performed within the Wolfram Mathematica 14.0 framework, which facilitates both symbolic manipulations and high-precision numerical computations.

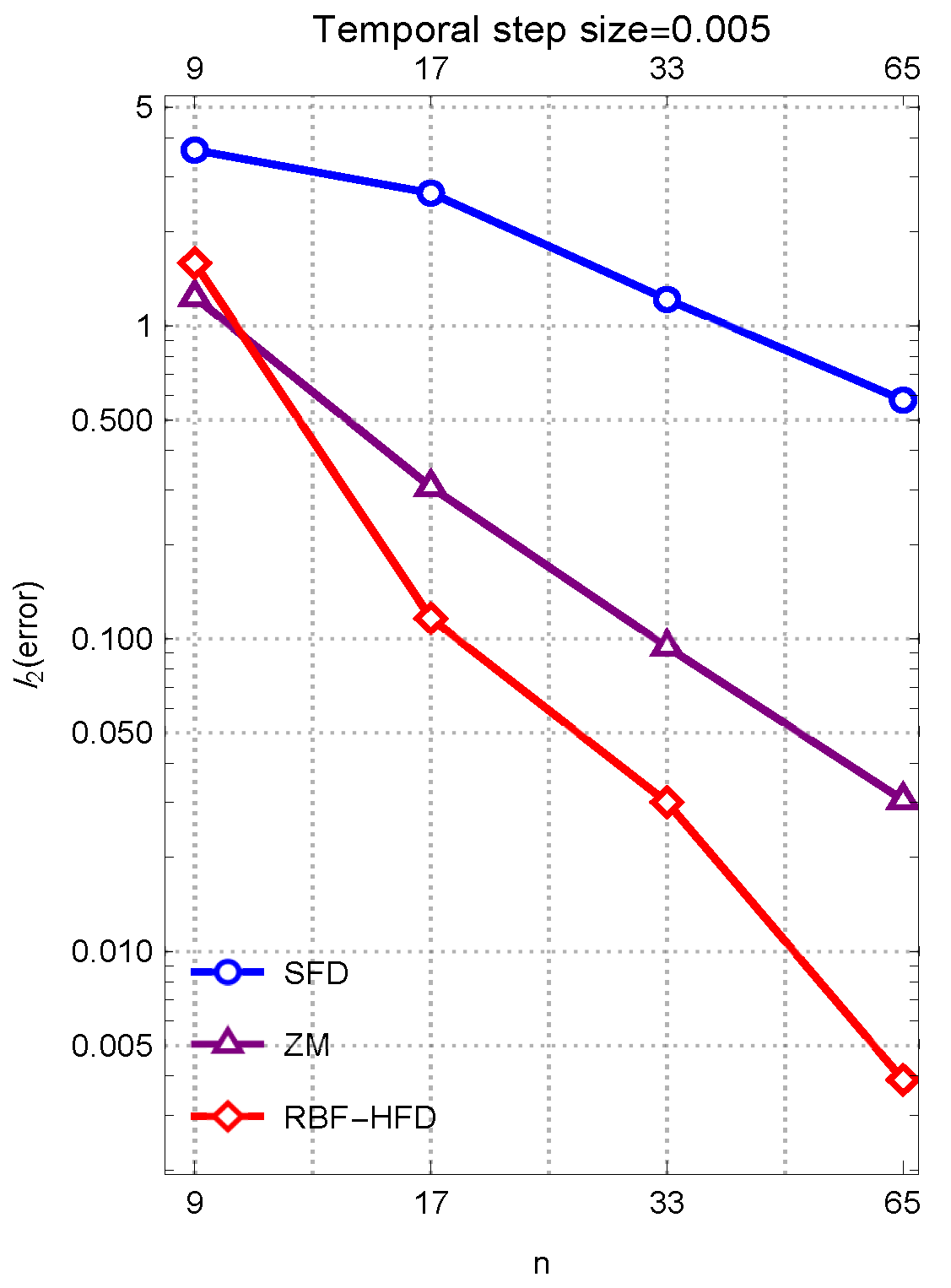
Example 1.

In this computational case study, the parameter set adopted is:

$$a=0.01,\sigma =0.2,K=100\$,q=0,r=0.1,T=1\mathrm{year}.$$

(48)

The choice of a small value for the market impact parameter a is motivated by its alignment with empirically observed, realistic market behavior.

To assess the accuracy of the numerical results, we refer to established benchmark values from [29], which provide approximate solutions at selected spatial locations:

$$U(K+10,T)\approx 22.2960,U(K,T)\approx 14.6457,U(K-10,T)\approx 8.4032.$$

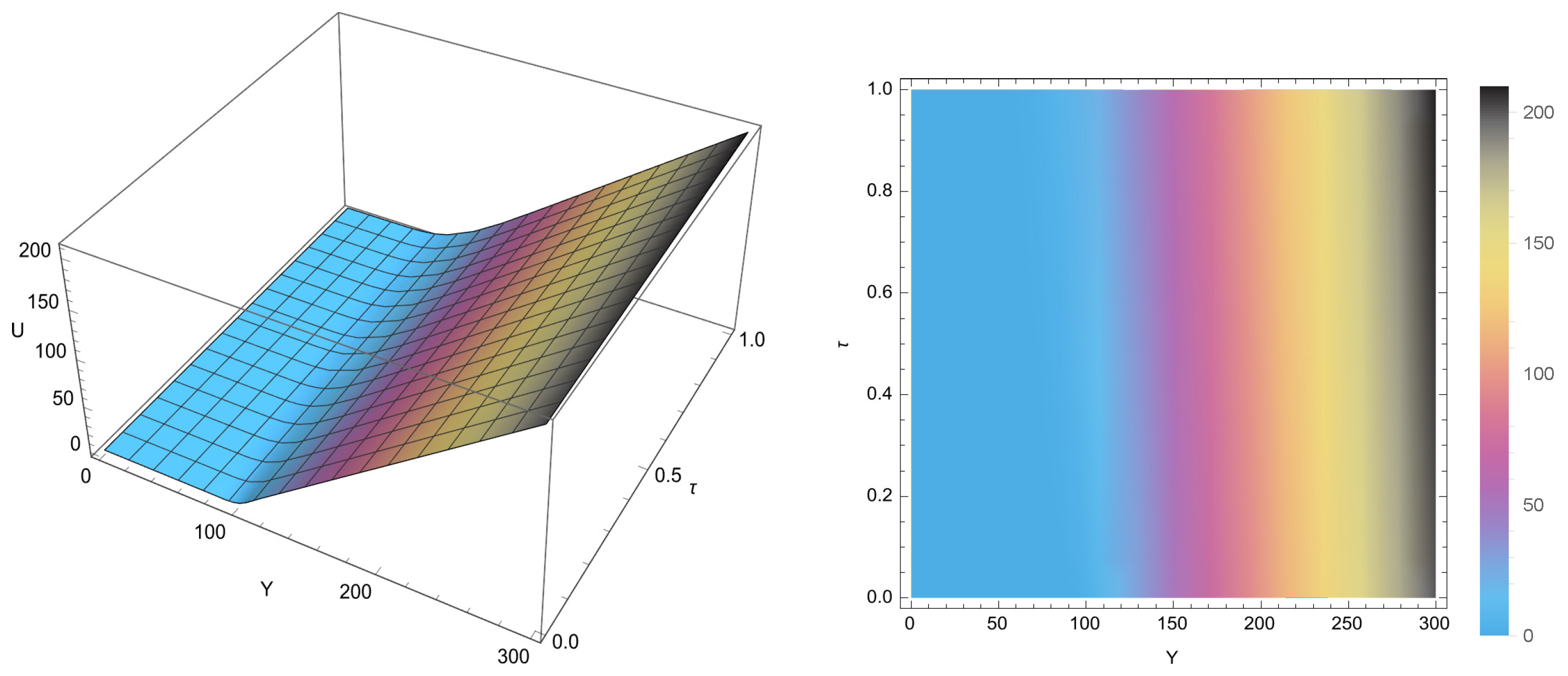
The presence of transaction cost effects in the current model setting leads to deviations from the classical solution, and the numerical observations attained via the proposed scheme are illustrated in Figure 1 and Figure 2. These figures demonstrate the algorithm’s strong performance in terms of both accuracy and calculational robustness, utilizing a spatial grid constructed uniformly. The comparison reveals that incorporating transaction costs systematically adjusts the option pricing outcomes, resulting in enhanced solution accuracy compared to those generated by traditional linearized models lacking such features.

Practical Financial Relevance of Example 1

The nonlinear BS model in (32) is not merely a theoretical extension of the classical PDE; it directly incorporates transaction cost effects, which are central to real-world option pricing and hedging. The market impact parameter a, introduced in Example 1, has a clear financial interpretation. It represents the degree to which frequent rebalancing in the presence of proportional transaction costs alters the effective volatility through the Gamma term $F_{YY}$. In practice, market makers and institutional hedgers face precisely such effects when managing large portfolios of options or when trading in less liquid markets.

From an applied perspective, the significance of the example can be highlighted as follows. First, incorporating transaction costs is crucial for pricing and hedging short-dated, near-the-money options, where the Gamma exposure is large and continuous rebalancing becomes prohibitively expensive. The nonlinear volatility adjustment in (32) systematically penalizes high-curvature regions of the option value, leading to more conservative prices that reflect the actual cost of replication. Second, in markets with non-negligible bid–ask spreads and liquidity constraints (for instance, single-name equities or certain commodities), models of this type are used to generate quotes that are robust to hedging costs. The small value chosen for $a=0.01$ corresponds to empirically reasonable estimates of trading frictions and ensures that the model remains consistent with observed market behavior. Third, the outputs of this model—option prices and Greeks—are directly useful to practitioners because they determine not only the fair value of contracts but also the adjusted hedging ratios. More accurate computation of $F_{YY}$ and $F_Y$, which our Hermite-based RBF-FD method provides, translates into reduced slippage and lower replication error when strategies are implemented in practice.

Therefore, the numerical study in Example 1 carries genuine financial meaning: it demonstrates how the proposed high-order Hermite finite difference method can produce option prices that are both computationally efficient and practically relevant in markets where transaction costs and hedging frictions cannot be ignored. This situates the present contribution within the broader class of nonlinear pricing models employed in real trading and risk management environments.

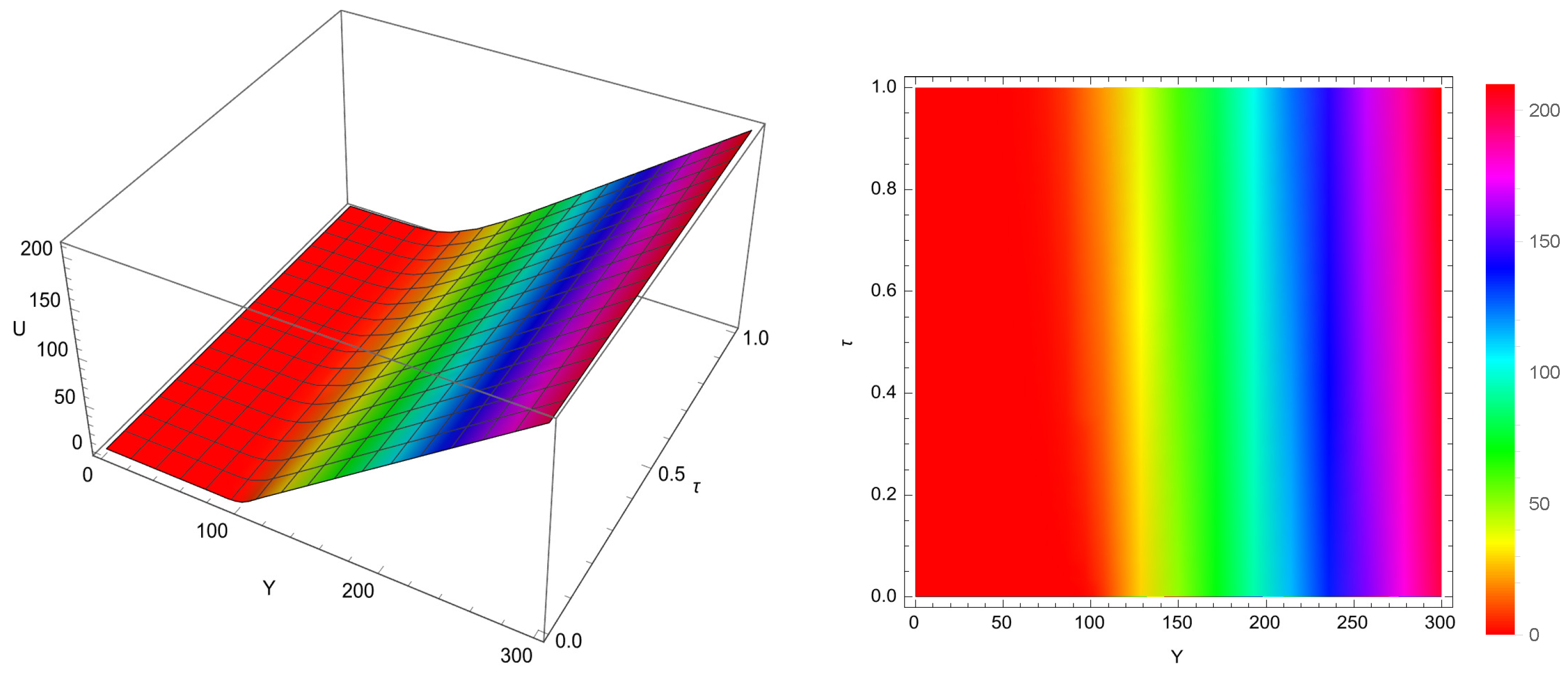
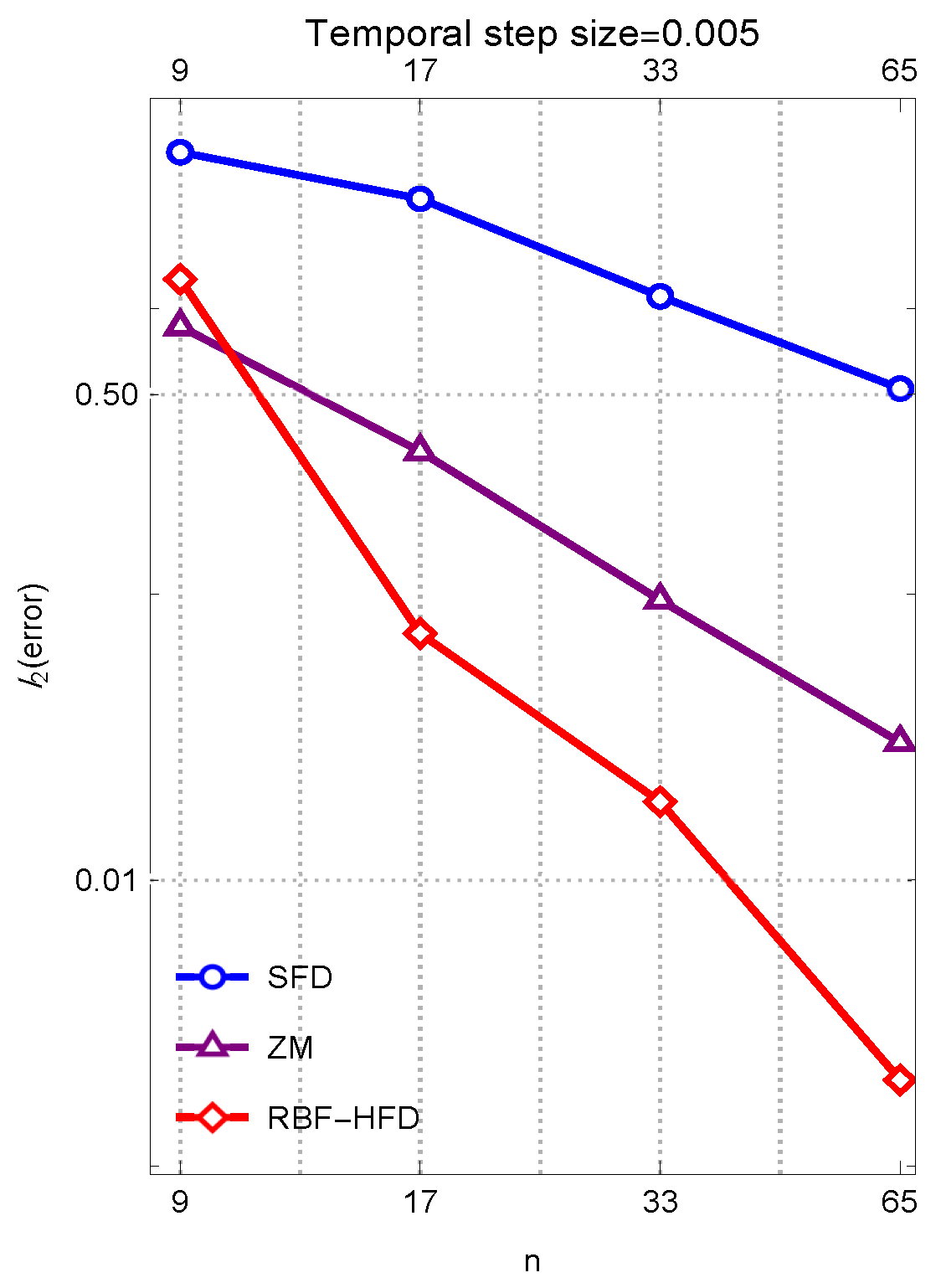
Example 2.

In this numerical experiment, we adopt the same set of parameters as specified in Example 1, with the exception that the degree of nonlinearity is intensified by selecting a larger value for the parameter a, specifically

$$a=0.02.$$

(49)

This adjustment reflects a scenario in which transaction cost effects become more pronounced, thereby allowing us to evaluate the robustness of the proposed numerical methodology under heightened nonlinear conditions.

To quantitatively evaluate the fidelity of the computed solutions, we draw upon reference data provided in [29], which offers reliable approximations of the solution at three strategically chosen asset price points:

$$U(K+10,T)\approx 23.0203,U(K,T)\approx 15.5181,U(K-10,T)\approx 9.2965.$$

Due to the enhanced influence of transaction costs introduced through the increased value of a, the solution exhibits noticeable deviations from the classical linear case. The numerical outcomes, obtained via the proposed high-order scheme, are depicted graphically in Figure 3 and Figure 4. These illustrations further substantiate the efficacy and adaptability of our method when applied to more complex financial models incorporating stronger nonlinearities.

Noting that although a fourth-order time integrator is, in principle, sufficient to match the fourth-order spatial discretization of Section 3, the sixth-order RK scheme was selected for the following reasons:

• It permits larger timesteps for the same spatial accuracy as RK4;
• It reduces the accumulation of temporal error in long-time evolutions;
• It enlarges the stability region and thus increases timestep flexibility;
• It can decrease total computational work to reach a prescribed error by reducing the required number of time steps and nonlinear evaluations.

The numerical experiments reveal that the proposed RBF-HFD scheme, when combined with the RK6, demonstrates superior performance in both accuracy and stability compared to SFD and recent ZM methods. This superiority is particularly evident in scenarios involving heightened nonlinearity, as seen in Example 2. The compact Hermite-based formulation of RBF-HFD captures derivative information efficiently while maintaining a minimal stencil size, thereby achieving fourth-order spatial convergence even with only three nodes. This compactness not only reduces the computational complexity but also enhances robustness in handling steep gradients caused by transaction costs. Furthermore, the high-order temporal integrator amplifies the accuracy, making the combined RK6-RBF-HFD framework especially well suited for solving nonlinear BS-type PDEs arising in illiquid markets. The spatial convergence of the proposed algorithms is seen according to their higher slopes.

The choice of the shape parameter $\beta$ plays a crucial role in the performance of RBF-based methods, since it directly influences both the accuracy and the conditioning of the resulting discretization matrix. Throughout this section, we choose $\beta$ as $\beta =3h$. To balance these competing effects, it is common in the literature to adopt scaling strategies that tie $\beta$ to the nodal spacing h. In our numerical experiments, we employed such an adaptive approach by setting $\beta$ proportional to $3h$, which allows the method to remain stable while preserving high-order accuracy. For instance, when $n=33$ uniformly distributed nodes are used in the computational domain, the corresponding spacing is $h=9.375$, leading to an effective parameter $\beta \approx 3h$. Similarly, for $n=17$, where $h=18.75$, the same scaling yields $\beta =3h$.

6. Concluding Discussion

We present a fourth-order accurate meshfree numerical method for solving nonlinear BS equations under transaction costs. By constructing compact RBF-HFD stencils, we successfully approximated first and second derivatives while preserving geometric flexibility and computational sparsity. The resulting method achieves high-order accuracy on uniform grids and is combined with a sixth-order explicit RK integrator for temporal advancement.

Through rigorous stability analysis and numerical experiments, we demonstrated that the proposed RBF-HFD scheme performs robustly even under strong nonlinearities introduced by Gamma-sensitive volatility functions. Our implementation, validated against benchmark solutions, confirms that including transaction costs yields more realistic and accurate option prices.

Future work will involve extending this framework to handle American options with free boundary conditions, exploring adaptive node refinement strategies in the spatial domain, and applying implicit–explicit (IMEX) schemes for handling stiff nonlinearities arising in stochastic volatility models.