Bayesian Optimization Meets Explainable AI: Enhanced Chronic Kidney Disease Risk Assessment
Abstract
1. Introduction
- An integrated Bayesian optimization framework combining XGBoost with Tree-structured Parzen Estimator (TPE) optimization for medical prediction;
- Intelligent computational pruning through medianpruner, reducing hyperparameter evaluations by 35-fold (from 3456 to 100 trials) with 4-fold time efficiency improvement;
- Macro-averaged evaluation methodologies addressing class imbalance and preventing algorithmic bias;
- Comprehensive SHAP integration resolving ensemble model “black-box” limitations while maintaining clinical interpretability;
- Extensive empirical validation demonstrating superior performance across 16 baseline algorithms with robust generalization capability;
- Comprehensive comparison of 4 hyperparameter optimization strategies demonstrating TPE-based approach superiority in both performance and computational efficiency.
2. Related Works
- Suboptimal hyperparameter optimization—current approaches predominantly rely on computationally inefficient traditional methods, failing to leverage advanced Bayesian optimization techniques;
- Insufficient interpretability integration—systematic integration of comprehensive interpretability analysis with optimized model performance remains largely unexplored;
- Limited robustness validation—existing models consistently lack thorough error analysis, uncertainty quantification, and parameter sensitivity assessment, crucial for clinical deployment.
3. Preliminary
3.1. Data Overview
3.2. Exploratory Data Analysis
3.3. Data Processing
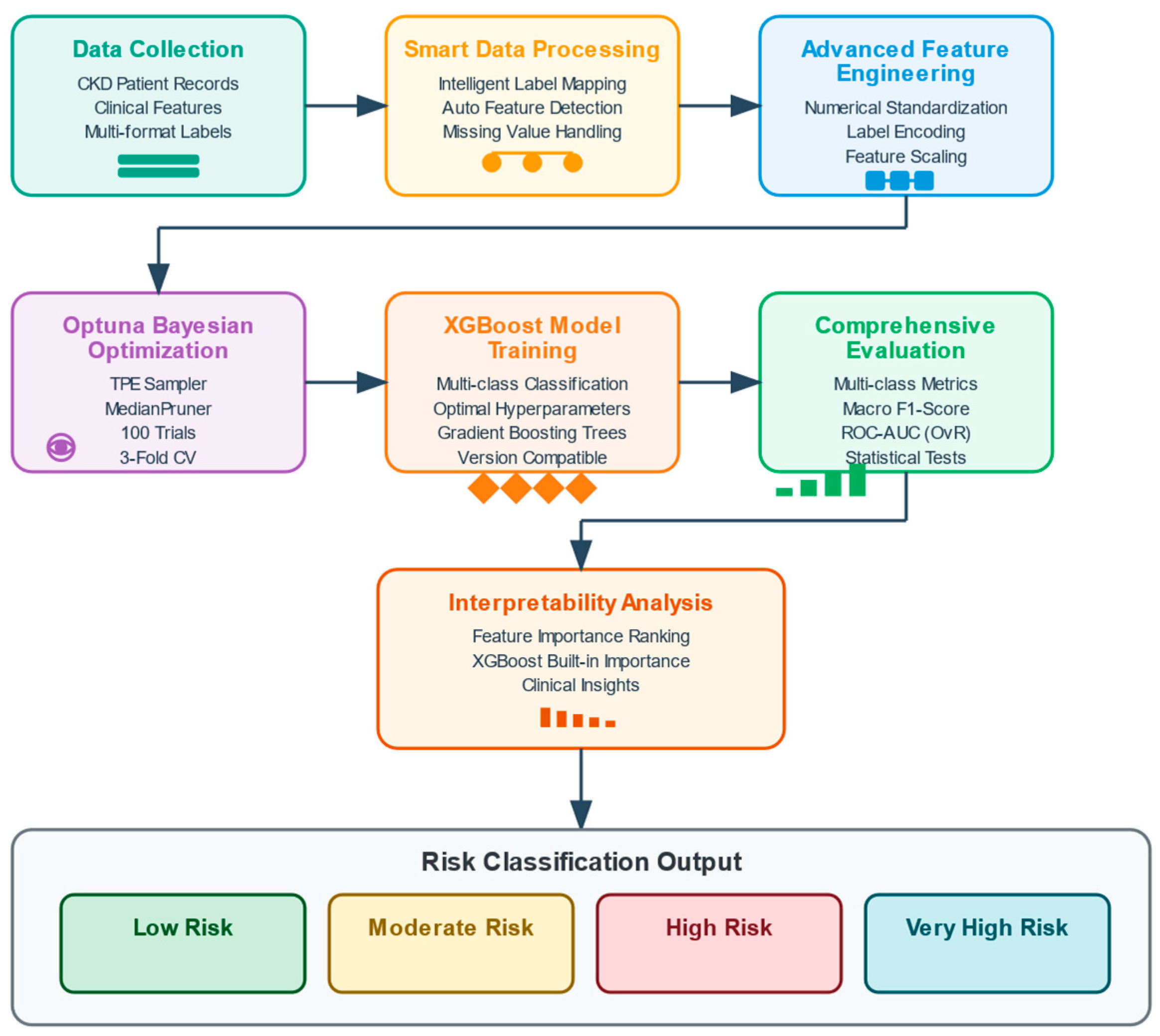
4. Methodology
4.1. XGBoost
4.2. Bayesian Optimization with Optuna
| Algorithm 1: Optuna XGBoost Hyperparameter Optimization | |
| Input: | |
| Initialization: | |
| 1: | def objective(trial): |
| 2: | params = { |
| 3: | n-estimators: trial.suggest_int(‘n_estimators’, 100, 1000), |
| 4: | max_depth: trial.suggest_int(‘max_depth’, 3, 10), |
| 5: | learning_rate: trial.suggest_float(‘learning_rate’, 0.01, 0.3, log = True), |
| 6: | subsample: trial.suggest_float(‘subsample’, 0.6, 1.0), |
| 7: | colsample_bytree:trial.suggest_float(‘colsample_bytree’,0.6,1.0), |
| 8: | reg_alpha: trial.suggest_float(‘reg_alpha’, 0.0, 10.0), |
| 9: | reg_lambda: trial.suggest_float(‘reg_lambda’, 1.0, 10.0)scoring = ‘f1macro’).mean() |
| 10: | } |
| 11: | model = XGBClassifier(**params) |
| 12: | cv_scores = cross_val_score(model, X, y, cv = 3, scoring = ‘f1_macro’) |
| 13: | Return cv_scores.mean() |
| 14: | study.optimize(objective, n_trials = T) |
| 15: | best_params = study.best_params |
| 16: | final_model = XGBClassifier(**best_params).fit(X_train, y_train) |
| 17: | predictions = final_model.predict(X_test) |
| Return: final_model, best_params, evaluate_metrics(y_test, predictions) | |
4.3. Model Validation Strategy
5. Experiment
5.1. Experimental Configuration and Setup
5.2. Performance Metrics
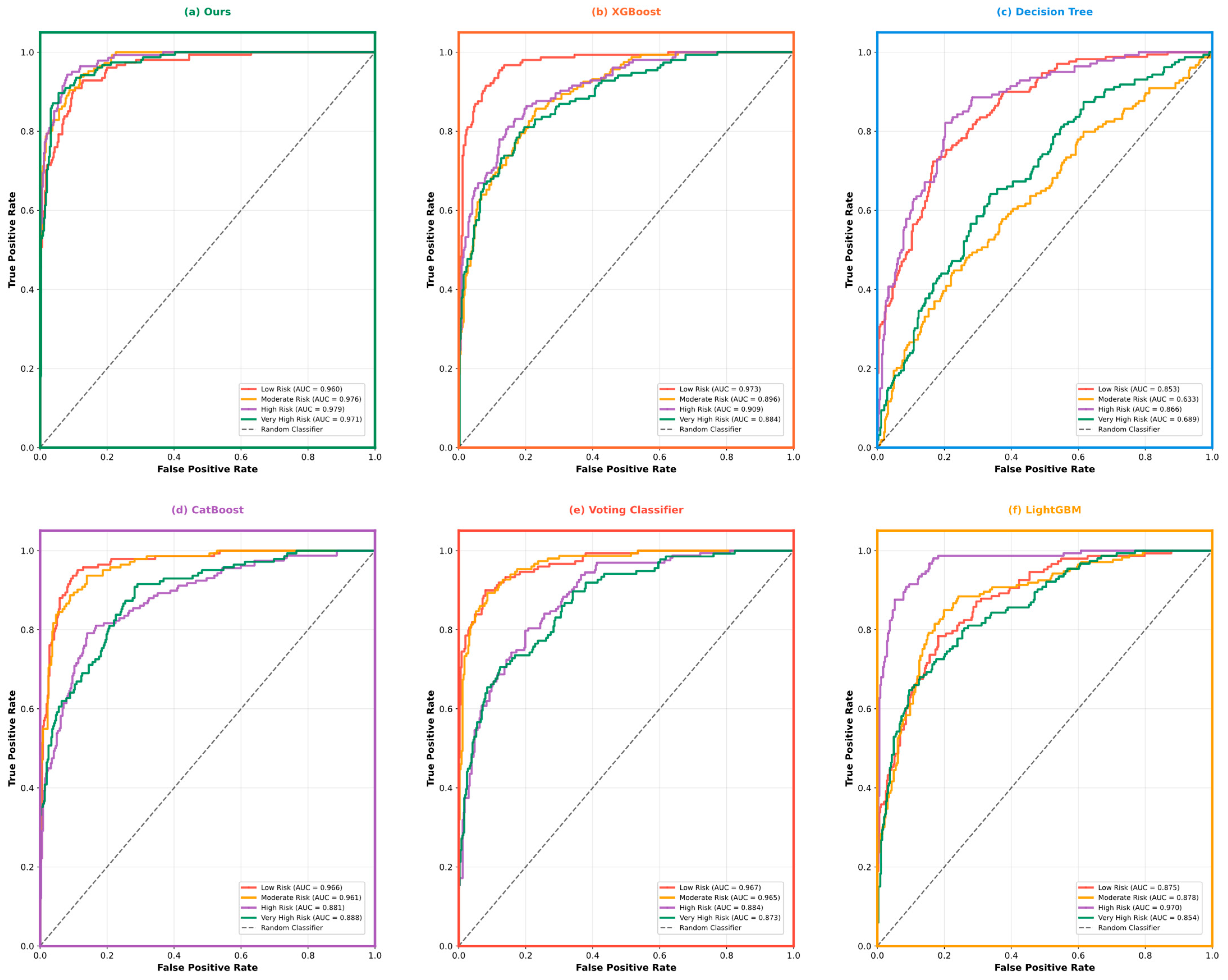
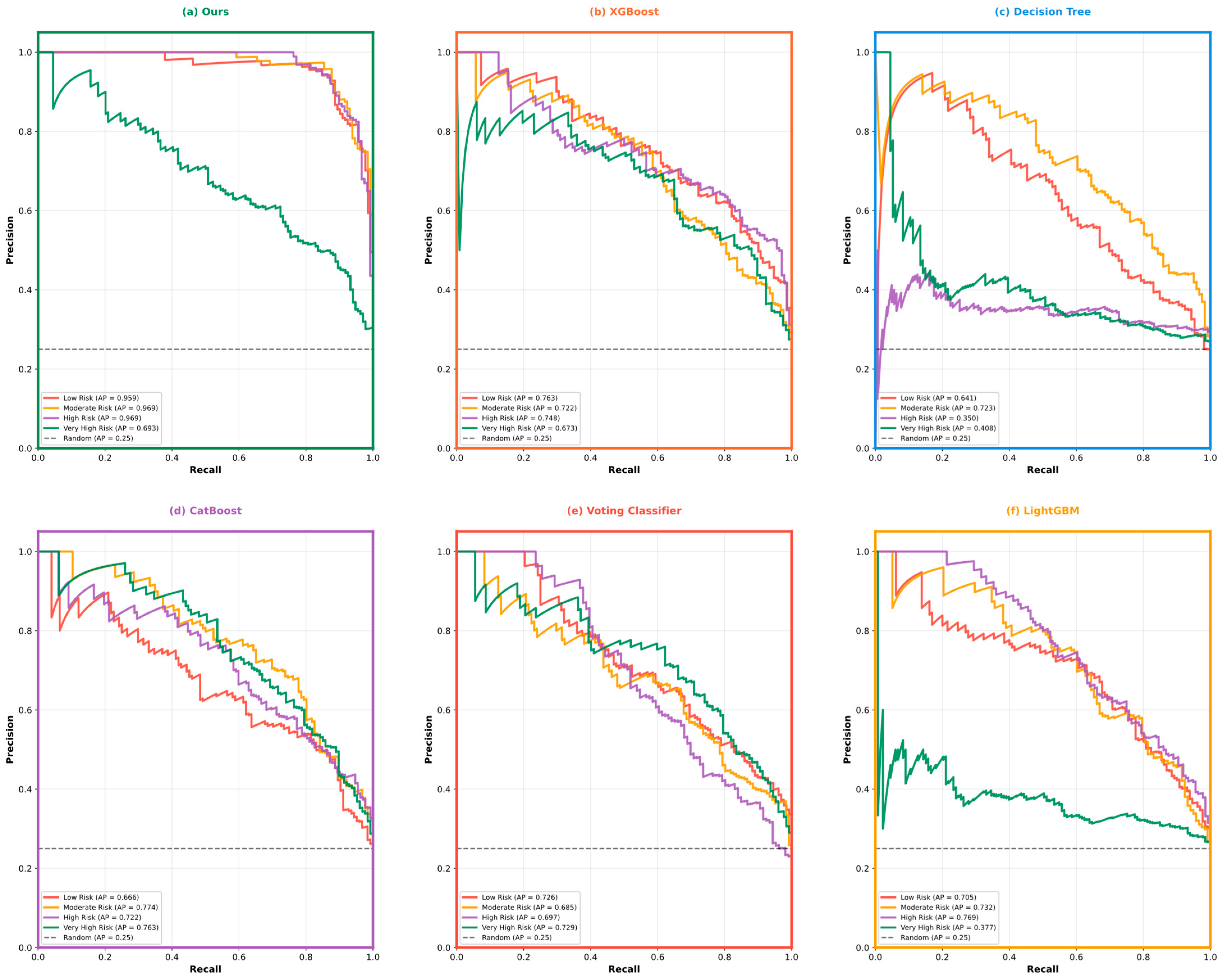
5.3. Model Performance Comparison and Analysis
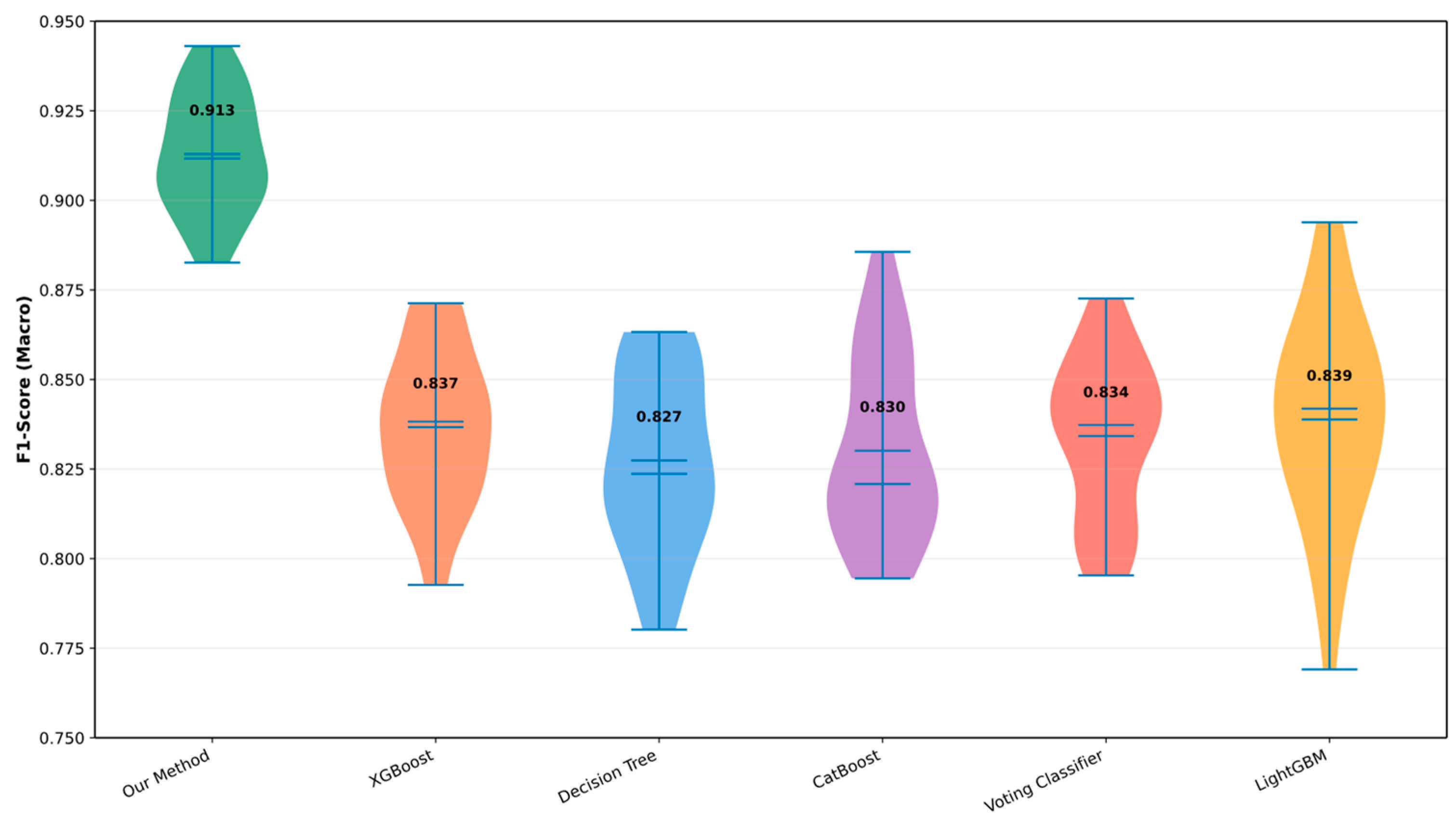
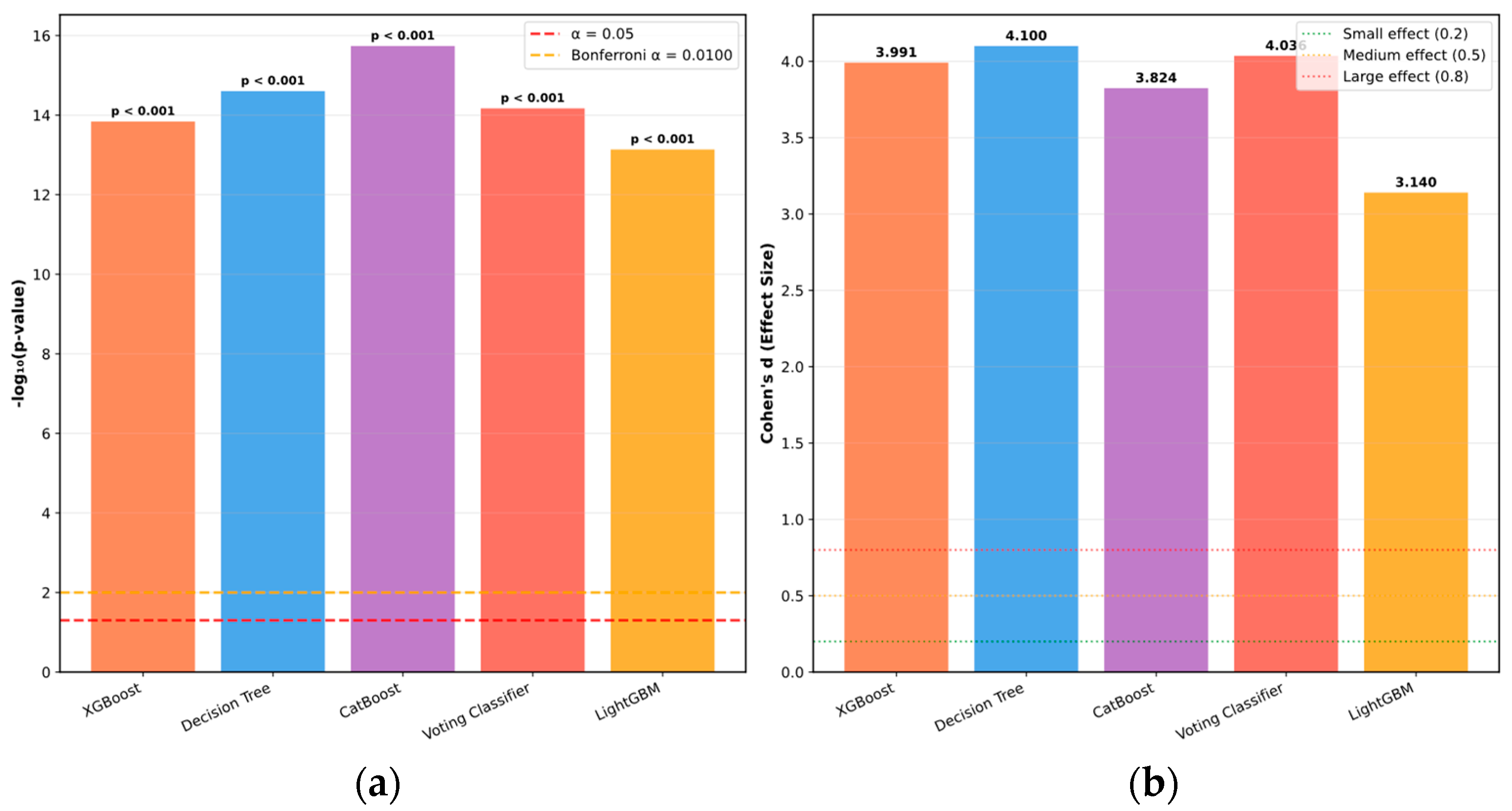
5.4. Statistical Validation and Reproducibility Analysis
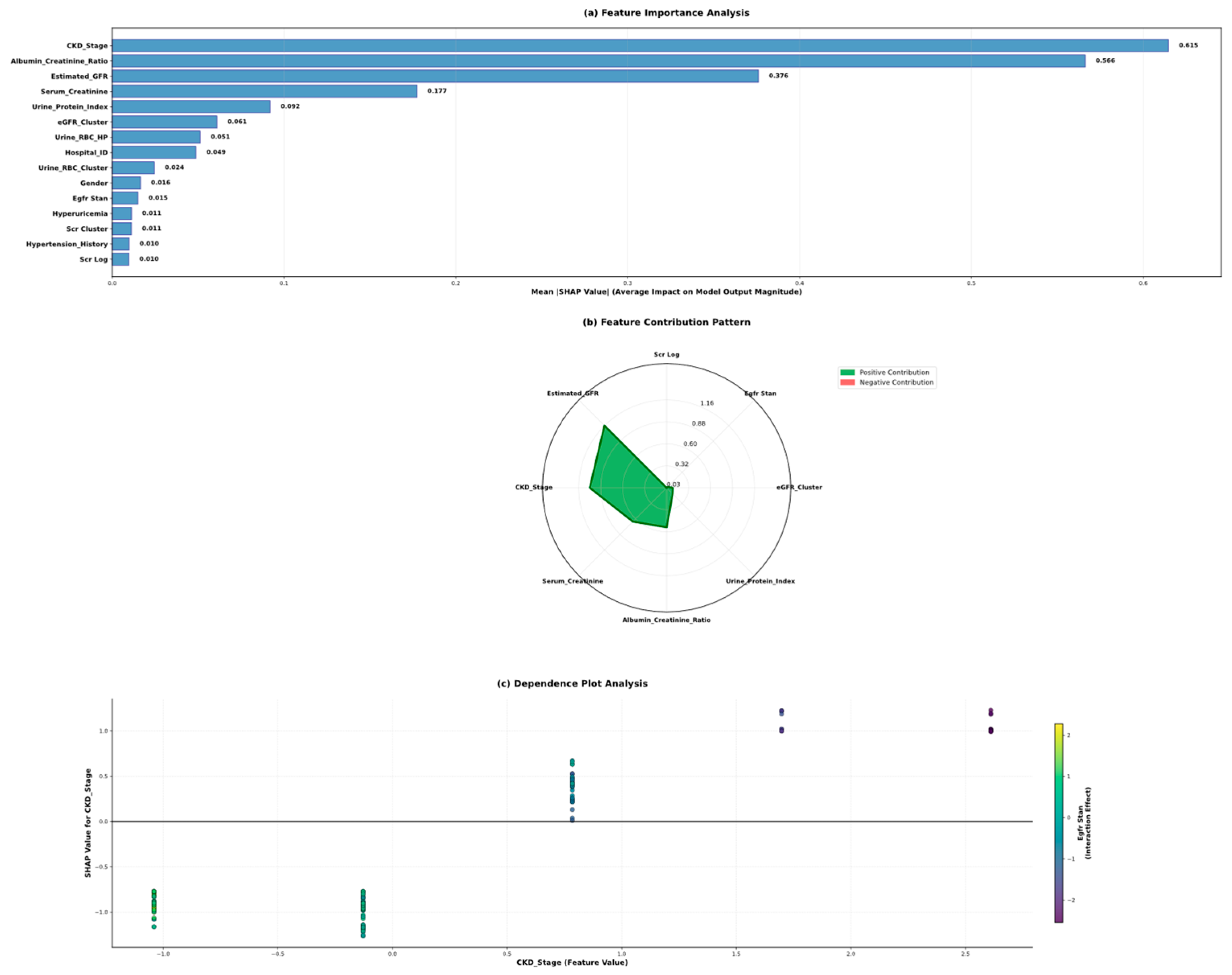
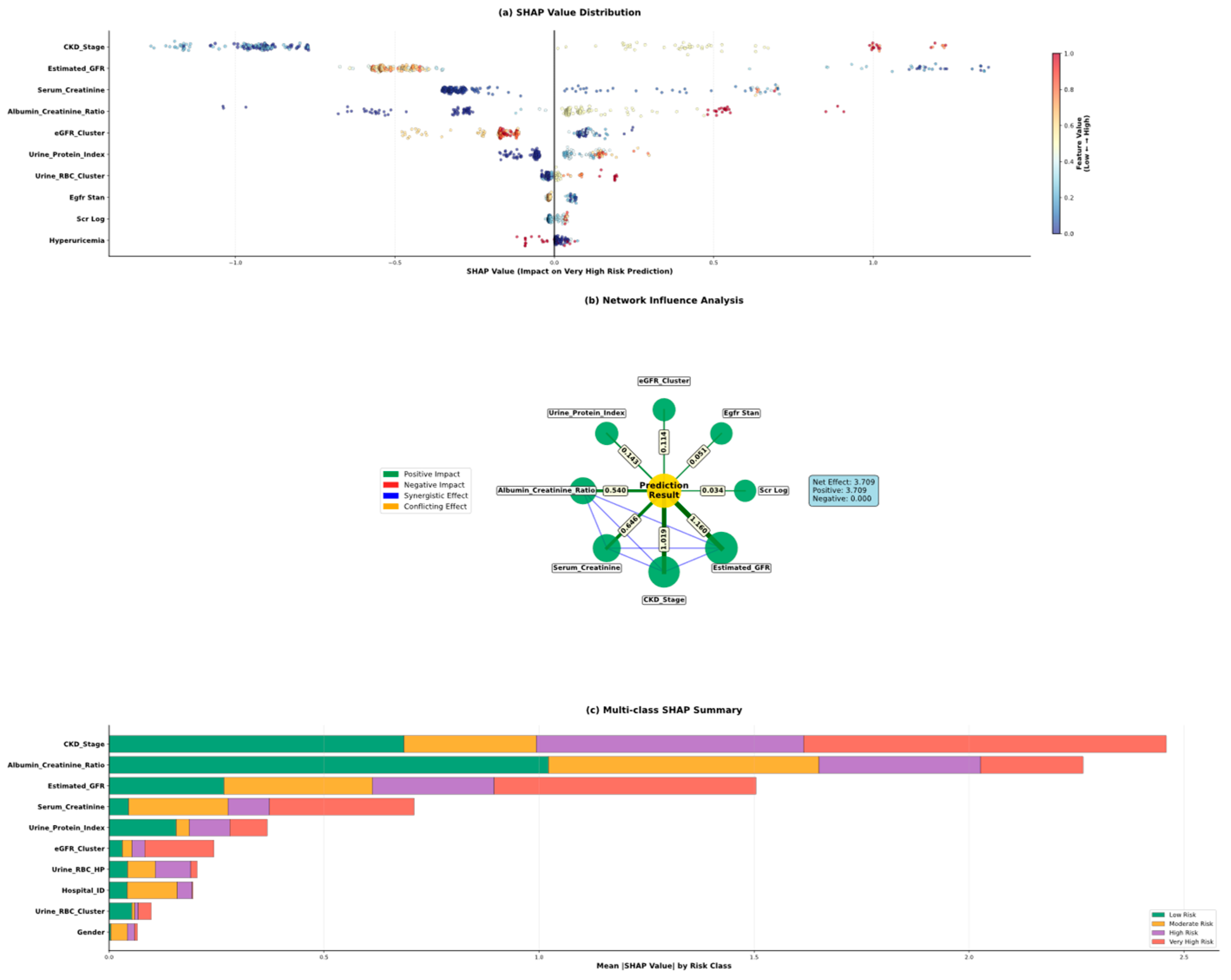
5.5. Model Interpretability Through Shap Analysis
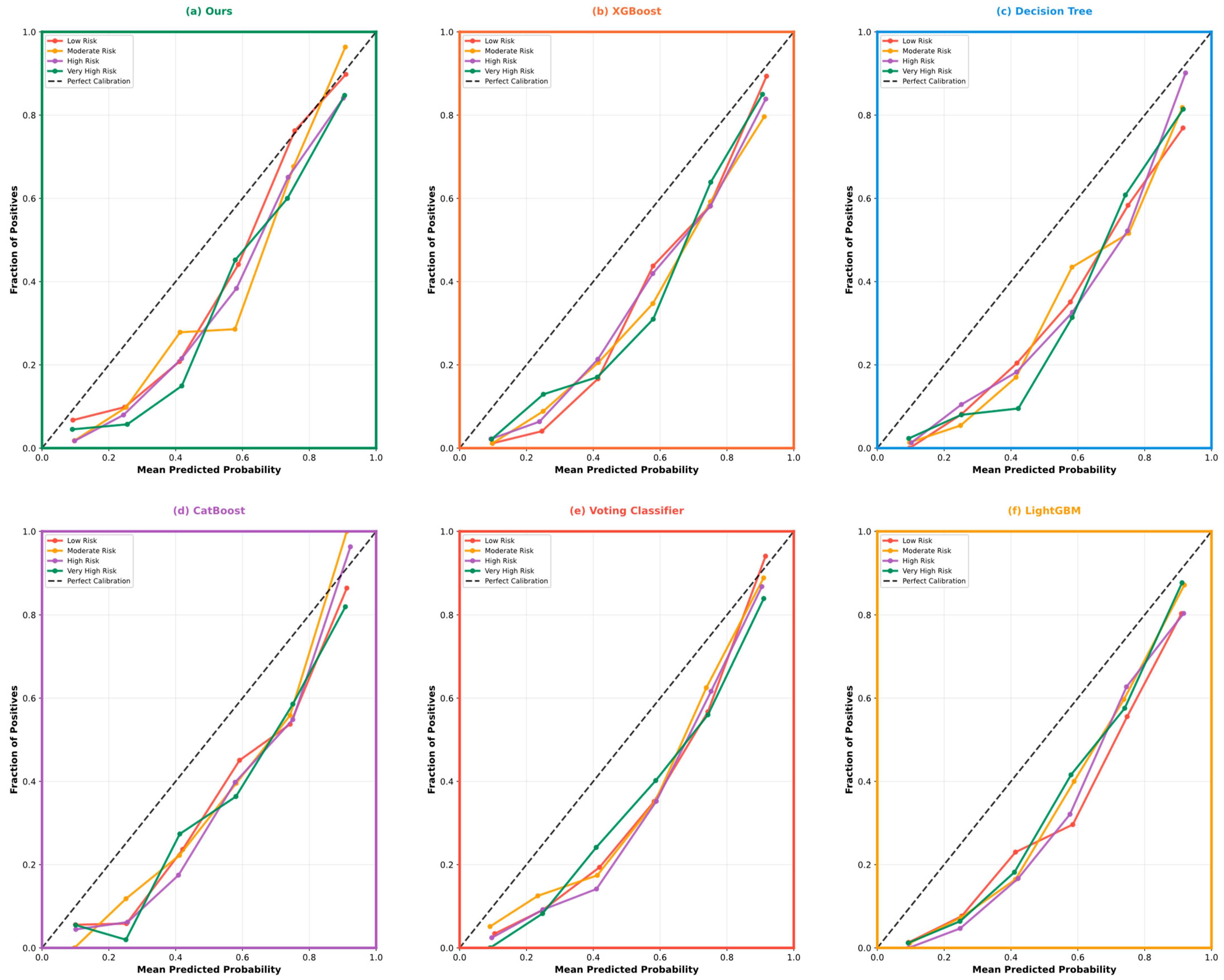
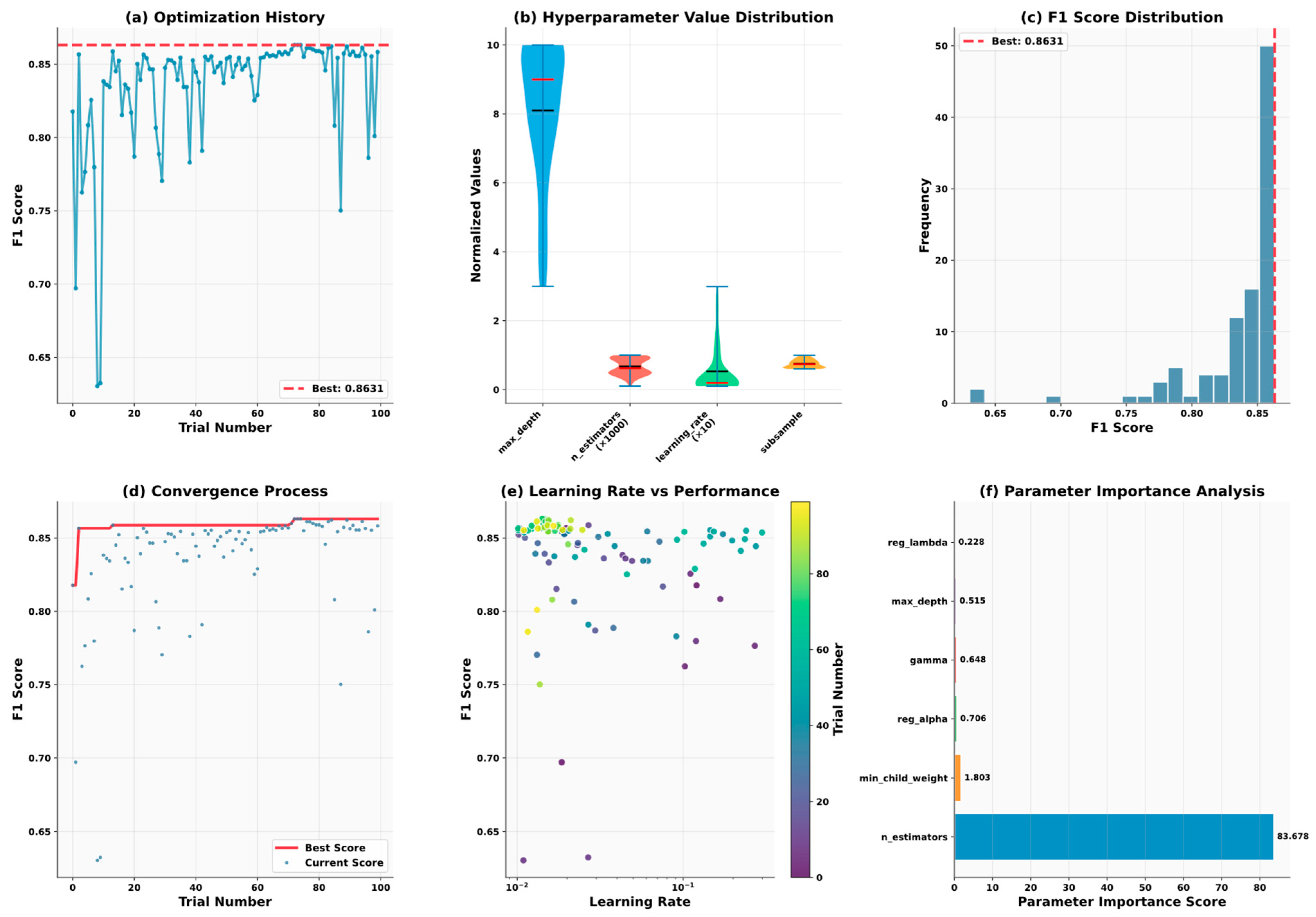
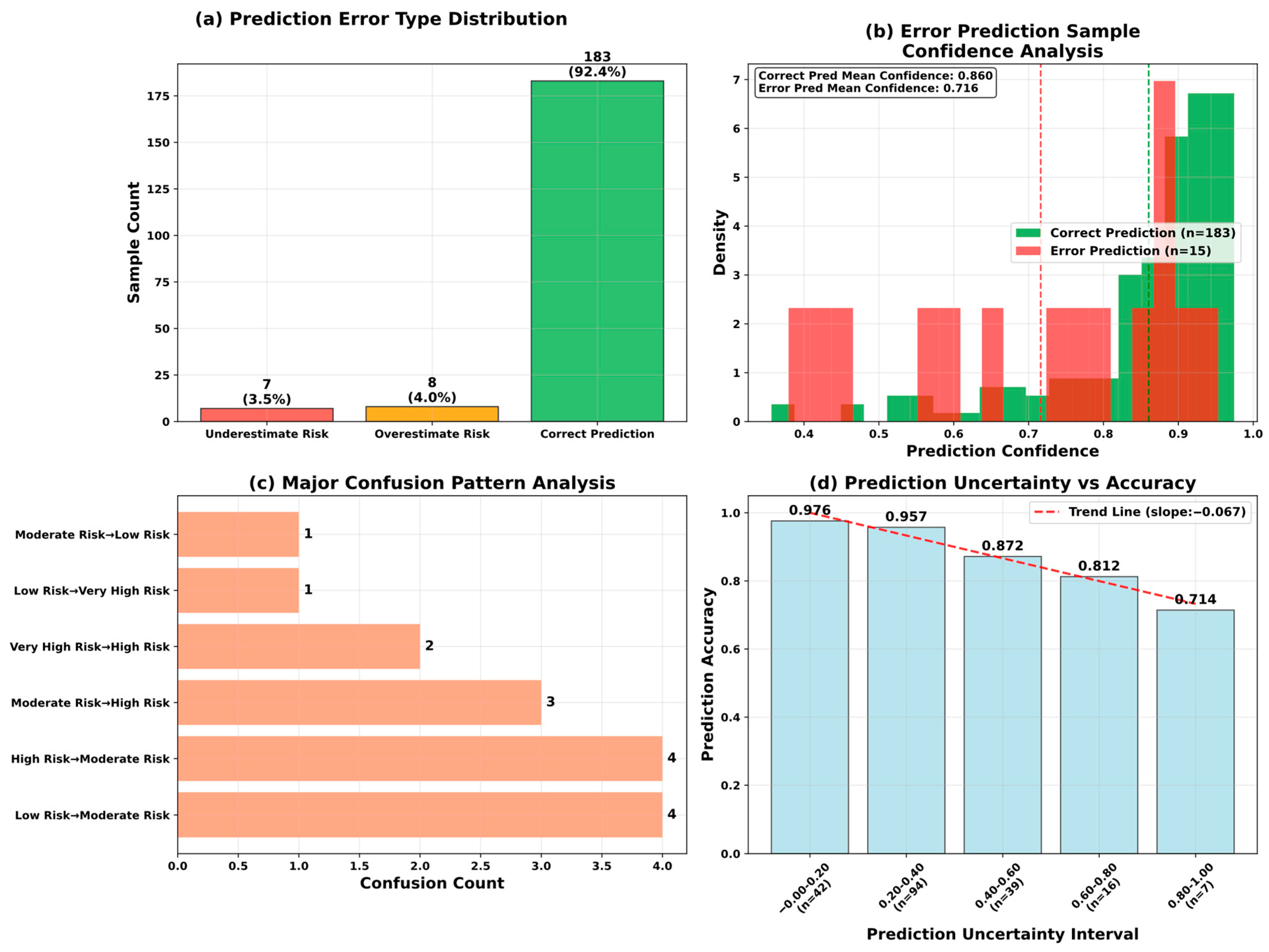
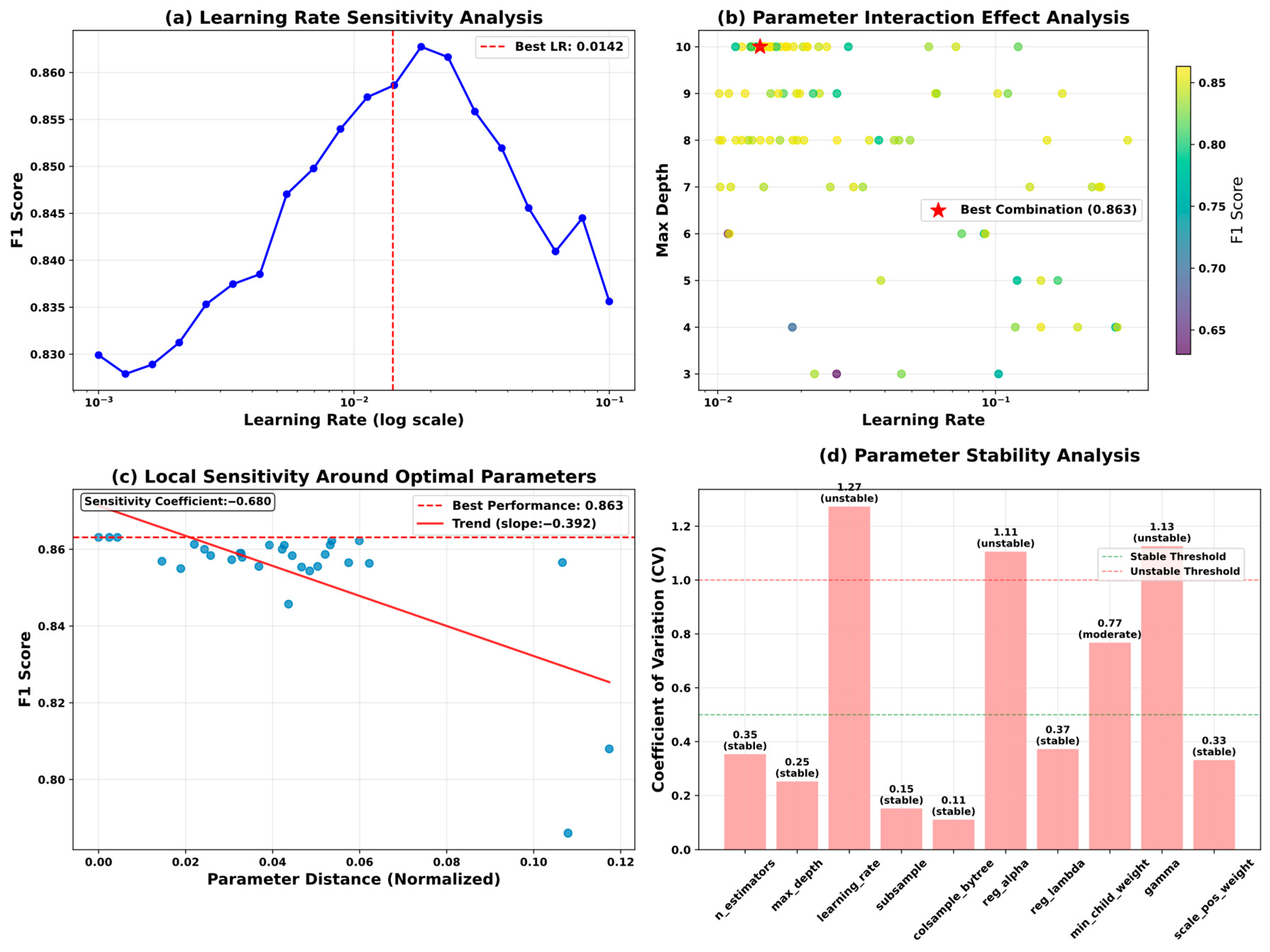
5.6. Model Optimization and Reliability Assessment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kovesdy, C.P. Epidemiology of Chronic Kidney Disease: An Update 2022. Kidney Int. Suppl. 2022, 12, 7–11. [Google Scholar] [CrossRef]
- Chesnaye, N.C.; Ortiz, A.; Zoccali, C.; Stel, V.S.; Jager, K.J. The Impact of Population Ageing on the Burden of Chronic Kidney Disease. Nat. Rev. Nephrol. 2024, 20, 569–585. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, F.; Wang, L.; Wang, W.; Liu, B.; Liu, J.; Chen, M.; He, Q.; Liao, Y.; Yu, X.; et al. Prevalence of Chronic Kidney Disease in China: A Cross-Sectional Survey. Lancet 2012, 379, 815–822. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Nadkarni, G.; Gottesman, O.; Ellis, S.B.; Bottinger, E.P.; Guttag, J.V. Incorporating Temporal EHR Data in Predictive Models for Risk Stratification of Renal Function Deterioration. J. Biomed. Inform. 2015, 53, 220–228. [Google Scholar] [CrossRef]
- Cueto-Manzano, A.M.; Cortés-Sanabria, L.; Martínez-Ramírez, H.R.; Rojas-Campos, E.; Gómez-Navarro, B.; Castillero-Manzano, M. Prevalence of Chronic Kidney Disease in an Adult Population. Arch. Med. Res. 2014, 45, 507–513. [Google Scholar] [CrossRef]
- Ghosh, B.P.; Imam, T.; Anjum, N.; Mia, M.T.; Siddiqua, C.U.; Sharif, K.S.; Khan, M.M.; Mamun, M.A.I.; Hossain, M.Z. Advancing Chronic Kidney Disease Prediction: Comparative Analysis of Machine Learning Algorithms and a Hybrid Model. J. Comput. Sci. Technol. Stud. 2024, 6, 15–21. [Google Scholar] [CrossRef]
- Hezam, A.A.M.; Shaghdar, H.B.M.; Chen, L. The Connection between Hypertension and Diabetes and Their Role in Heart and Kidney Disease Development. J. Res. Med. Sci. 2024, 29, 22. [Google Scholar] [CrossRef]
- Raju, M.A.H.; Imam, T.; Islam, J.; Rakin, A.A.; Nayyem, M.N.; Uddin, M.S. An Ontological Framework for Lung Carcinoma Prognostication via Sophisticated Stacking and Synthetic Minority Oversampling Techniques. In Proceedings of the 2024 IEEE Asia Pacific Conference on Wireless and Mobile (APWiMob), Bali, Indonesia, 28–30 November 2024; IEEE: Bali, Indonesia, 2024; pp. 125–130. [Google Scholar]
- Wang, Y.; Zhang, H.; Yue, Y.; Song, S.; Deng, C.; Feng, J.; Huang, G. Uni-AdaFocus: Spatial-Temporal Dynamic Computation for Video Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 1782–1799. [Google Scholar] [CrossRef]
- Ponnarengan, H.; Rajendran, S.; Khalkar, V.; Devarajan, G.; Kamaraj, L. Data-Driven Healthcare: The Role of Computational Methods in Medical Innovation. CMES 2025, 142, 1–48. [Google Scholar] [CrossRef]
- Nazir, A.; Hussain, A.; Singh, M.; Assad, A. Deep Learning in Medicine: Advancing Healthcare with Intelligent Solutions and the Future of Holography Imaging in Early Diagnosis. Multimed. Tools Appl. 2024, 84, 17677–17740. [Google Scholar] [CrossRef]
- Saravanakumar, S.M.; Revathi, T. Computer Aided Disease Detection and Prediction of Novel Corona Virus Disease Using Machine Learning. Multimed. Tools Appl. 2024, 83, 82177–82198. [Google Scholar] [CrossRef]
- Sadr, H.; Salari, A.; Ashoobi, M.T.; Nazari, M. Cardiovascular Disease Diagnosis: A Holistic Approach Using the Integration of Machine Learning and Deep Learning Models. Eur. J. Med. Res. 2024, 29, 455. [Google Scholar] [CrossRef]
- Dai, L.; Sheng, B.; Chen, T.; Wu, Q.; Liu, R.; Cai, C.; Wu, L.; Yang, D.; Hamzah, H.; Liu, Y.; et al. A Deep Learning System for Predicting Time to Progression of Diabetic Retinopathy. Nat. Med. 2024, 30, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhao, Z.; Yu, Z.; Liao, J.; Zhang, M. Machine Learning for Risk Prediction of Acute Kidney Injury in Patients with Diabetes Mellitus Combined with Heart Failure During Hospitalization. Sci. Rep. 2025, 15, 10728. [Google Scholar] [CrossRef] [PubMed]
- Rai, H.M. Cancer Detection and Segmentation Using Machine Learning and Deep Learning Techniques: A Review. Multimed. Tools Appl. 2023, 83, 27001–27035. [Google Scholar] [CrossRef]
- Ur Rehman, M.; Shafique, A.; Azhar, Q.-U.-A.; Jamal, S.S.; Gheraibia, Y.; Usman, A.B. Voice Disorder Detection Using Machine Learning Algorithms: An Application in Speech and Language Pathology. Eng. Appl. Artif. Intell. 2024, 133, 108047. [Google Scholar] [CrossRef]
- Senan, E.M.; Al-Adhaileh, M.H.; Alsaade, F.W.; Aldhyani, T.H.H.; Alqarni, A.A.; Alsharif, N.; Uddin, M.I.; Alahmadi, A.H.; Jadhav, M.E.; Alzahrani, M.Y. Diagnosis of Chronic Kidney Disease Using Effective Classification Algorithms and Recursive Feature Elimination Techniques. J. Healthc. Eng. 2021, 2021, 1004767. [Google Scholar] [CrossRef]
- Vasquez-Morales, G.R.; Martinez-Monterrubio, S.M.; Moreno-Ger, P.; Recio-Garcia, J.A. Explainable Prediction of Chronic Renal Disease in the Colombian Population Using Neural Networks and Case-Based Reasoning. IEEE Access 2019, 7, 152900–152910. [Google Scholar] [CrossRef]
- Ogunleye, A.; Wang, Q.-G. XGBoost Model for Chronic Kidney Disease Diagnosis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 17, 2131–2140. [Google Scholar] [CrossRef]
- Arif, M.S.; Mukheimer, A.; Asif, D. Enhancing the Early Detection of Chronic Kidney Disease: A Robust Machine Learning Model. Big Data Cogn. Comput. 2023, 7, 144. [Google Scholar] [CrossRef]
- Hassan, M.M.; Hassan, M.M.; Mollick, S.; Khan, M.A.R.; Yasmin, F.; Bairagi, A.K.; Raihan, M.; Arif, S.A.; Rahman, A. A Comparative Study, Prediction and Development of Chronic Kidney Disease Using Machine Learning on Patients Clinical Records. Hum.-Centric Intell. Syst. 2023, 3, 92–104. [Google Scholar] [CrossRef]
- Revathy, S.; Bharathi, B.; Jeyanthi, P.; Ramesh, M. Chronic Kidney Disease Prediction Using Machine Learning Models. IJEAT 2019, 9, 6364–6367. [Google Scholar] [CrossRef]
- Shams, M.Y.; Gamel, S.A.; Talaat, F.M. Enhancing Crop Recommendation Systems with Explainable Artificial Intelligence: A Study on Agricultural Decision-Making. Neural Comput. Appl. 2024, 36, 5695–5714. [Google Scholar] [CrossRef]
- Raihan, M.J.; Khan, M.A.-M.; Kee, S.-H.; Nahid, A.-A. Detection of the Chronic Kidney Disease Using XGBoost Classifier and Explaining the Influence of the Attributes on the Model Using SHAP. Sci. Rep. 2023, 13, 6263. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.-X.; Li, X.; Zhu, J.; Guan, S.-Y.; Zhang, S.-X.; Wang, W.-M. Interpretable Machine Learning for Predicting Chronic Kidney Disease Progression Risk. Digit. Health 2024, 10, 20552076231224225. [Google Scholar] [CrossRef]
- Tsai, M.-C.; Lojanapiwat, B.; Chang, C.-C.; Noppakun, K.; Khumrin, P.; Li, S.-H.; Lee, C.-Y.; Lee, H.-C.; Khwanngern, K. Risk Prediction Model for Chronic Kidney Disease in Thailand Using Artificial Intelligence and SHAP. Diagnostics 2023, 13, 3548. [Google Scholar] [CrossRef]
- Moreno-Sánchez, P.A. Data-Driven Early Diagnosis of Chronic Kidney Disease: Development and Evaluation of an Explainable AI Model. IEEE Access 2023, 11, 38359–38369. [Google Scholar] [CrossRef]
- Islam, M.A.; Akter, S.; Hossen, M.S.; Keya, S.A.; Tisha, S.A.; Hossain, S. Risk Factor Prediction of Chronic Kidney Disease Based on Machine Learning Algorithms. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020; IEEE: Thoothukudi, India, 2020; pp. 952–957. [Google Scholar]
- Ghosh, S.K.; Khandoker, A.H. Investigation on Explainable Machine Learning Models to Predict Chronic Kidney Diseases. Sci. Rep. 2024, 14, 3687. [Google Scholar] [CrossRef] [PubMed]
- Ebiaredoh-Mienye, S.A.; Swart, T.G.; Esenogho, E.; Mienye, I.D. A Machine Learning Method with Filter-Based Feature Selection for Improved Prediction of Chronic Kidney Disease. Bioengineering 2022, 9, 350. [Google Scholar] [CrossRef]
- Gudeti, B.; Mishra, S.; Malik, S.; Fernandez, T.F.; Tyagi, A.K.; Kumari, S. A Novel Approach to Predict Chronic Kidney Disease Using Machine Learning Algorithms. In Proceedings of the 2020 4th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 5–7 November 2020; IEEE: Coimbatore, India, 2020; pp. 1630–1635. [Google Scholar]
- Amirgaliyev, Y.; Shamiluulu, S.; Serek, A. Analysis of Chronic Kidney Disease Dataset by Applying Machine Learning Methods. In Proceedings of the 2018 IEEE 12th International Conference on Application of Information and Communication Technologies (AICT), Almaty, Kazakhstan, 17–19 October 2018; IEEE: Almaty, Kazakhstan, 2018; pp. 1–4. [Google Scholar]
- Chittora, P.; Chaurasia, S.; Chakrabarti, P.; Kumawat, G.; Chakrabarti, T.; Leonowicz, Z.; Jasinski, M.; Jasinski, L.; Gono, R.; Jasinska, E.; et al. Prediction of Chronic Kidney Disease—A Machine Learning Perspective. IEEE Access 2021, 9, 17312–17334. [Google Scholar] [CrossRef]
- Dutta, S.; Sikder, R.; Islam, M.R.; Al Mukaddim, A.; Hider, M.A.; Nasiruddin, M. Comparing Machine Learning Techniques for Detecting Chronic Kidney Disease in Early Stage. J. Comput. Sci. Technol. Stud. 2024, 6, 77–91. [Google Scholar] [CrossRef]
- Baswaraj, D.; Chatrapathy, K.; Prasad, M.L.; Pughazendi, N.; Kiran, A.; Partheeban, N.; Shaker Reddy, P.C. Chronic Kidney Disease Risk Prediction Using Machine Learning Techniques. J. Inf. Technol. Manag. 2024, 16, 118–134. [Google Scholar] [CrossRef]
- Nishat, M.M.; Faisal, F.; Dip, R.R.; Nasrullah, S.M.; Ahsan, R.; Shikder, F.; Asif, M.A.-A.-R.; Hoque, M.A. A Comprehensive Analysis on Detecting Chronic Kidney Disease by Employing Machine Learning Algorithms. EAI Endorsed Trans. Pervasive Health Technol. 2021, 7, e1. [Google Scholar] [CrossRef]
- Swain, D.; Mehta, U.; Bhatt, A.; Patel, H.; Patel, K.; Mehta, D.; Acharya, B.; Gerogiannis, V.C.; Kanavos, A.; Manika, S. A Robust Chronic Kidney Disease Classifier Using Machine Learning. Electronics 2023, 12, 212. [Google Scholar] [CrossRef]
- Rahman, M.M.; Al-Amin, M.; Hossain, J. Machine Learning Models for Chronic Kidney Disease Diagnosis and Prediction. Biomed. Signal Process. Control. 2024, 87, 105368. [Google Scholar] [CrossRef]
- Bai, Q.; Su, C.; Tang, W.; Li, Y. Machine Learning to Predict End Stage Kidney Disease in Chronic Kidney Disease. Sci. Rep. 2022, 12, 8377. [Google Scholar] [CrossRef]
- Debal, D.A.; Sitote, T.M. Chronic Kidney Disease Prediction Using Machine Learning Techniques. J. Big Data 2022, 9, 109. [Google Scholar] [CrossRef]
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Saha, S.; Hossen, R.; Ahmed, S.; Rony, M.A.T.; Akter, M.F. ML-CKDP: Machine Learning-Based Chronic Kidney Disease Prediction with Smart Web Application. J. Pathol. Inform. 2024, 15, 100371. [Google Scholar] [CrossRef] [PubMed]
- Kukkar, A.; Gupta, D.; Beram, S.M.; Soni, M.; Singh, N.K.; Sharma, A.; Neware, R.; Shabaz, M.; Rizwan, A. Optimizing Deep Learning Model Parameters Using Socially Implemented IoMT Systems for Diabetic Retinopathy Classification Problem. IEEE Trans. Comput. Soc. Syst. 2023, 10, 1654–1665. [Google Scholar] [CrossRef]
- Yousif, S.M.A.; Halawani, H.T.; Amoudi, G.; Birkea, F.M.O.; Almunajam, A.M.R.; Elhag, A.A. Early Detection of Chronic Kidney Disease Using Eurygasters Optimization Algorithm with Ensemble Deep Learning Approach. Alex. Eng. J. 2024, 100, 220–231. [Google Scholar] [CrossRef]
- Gokiladevi, M.; Santhoshkumar, S. Henry Gas Optimization Algorithm with Deep Learning Based Chronic Kidney Disease Detection and Classification Model. Int. J. Intell. Eng. Syst. 2024, 17, 645–655. [Google Scholar] [CrossRef]
- Khurshid, M.R.; Manzoor, S.; Sadiq, T.; Hussain, L.; Khan, M.S.; Dutta, A.K. Unveiling Diabetes Onset: Optimized XGBoost with Bayesian Optimization for Enhanced Prediction. PLoS ONE 2025, 20, e0310218. [Google Scholar] [CrossRef]
- Kurt, B.; Gürlek, B.; Keskin, S.; Özdemir, S.; Karadeniz, Ö.; Kırkbir, İ.B.; Kurt, T.; Ünsal, S.; Kart, C.; Baki, N.; et al. Prediction of Gestational Diabetes Using Deep Learning and Bayesian Optimization and Traditional Machine Learning Techniques. Med. Biol. Eng. Comput. 2023, 61, 1649–1660. [Google Scholar] [CrossRef]
- Rimal, Y.; Sharma, N. Hyperparameter Optimization: A Comparative Machine Learning Model Analysis for Enhanced Heart Disease Prediction Accuracy. Multimed. Tools Appl. 2023, 83, 55091–55107. [Google Scholar] [CrossRef]
- Al-Jamimi, H.A. Synergistic Feature Engineering and Ensemble Learning for Early Chronic Disease Prediction. IEEE Access 2024, 12, 62215–62233. [Google Scholar] [CrossRef]
- Arumugham, V.; Sankaralingam, B.P.; Jayachandran, U.M.; Krishna, K.V.S.S.R.; Sundarraj, S.; Mohammed, M. An Explainable Deep Learning Model for Prediction of Early-Stage Chronic Kidney Disease. Comput. Intell. 2023, 39, 1022–1038. [Google Scholar] [CrossRef]
- Jawad, K.M.T.; Verma, A.; Amsaad, F.; Ashraf, L. AI-Driven Predictive Analytics Approach for Early Prognosis of Chronic Kidney Disease Using Ensemble Learning and Explainable AI 2024. arXiv 2024, arXiv:2406.06728. [Google Scholar]
- Singamsetty, S.; Ghanta, S.; Biswas, S.; Pradhan, A. Enhancing Machine Learning-Based Forecasting of Chronic Renal Disease with Explainable AI. PeerJ Comput. Sci. 2024, 10, e2291. [Google Scholar] [CrossRef]
- Reiss, A.B.; Jacob, B.; Zubair, A.; Srivastava, A.; Johnson, M.; De Leon, J. Fibrosis in Chronic Kidney Disease: Pathophysiology and Therapeutic Targets. J. Clin. Med. 2024, 13, 1881. [Google Scholar] [CrossRef]
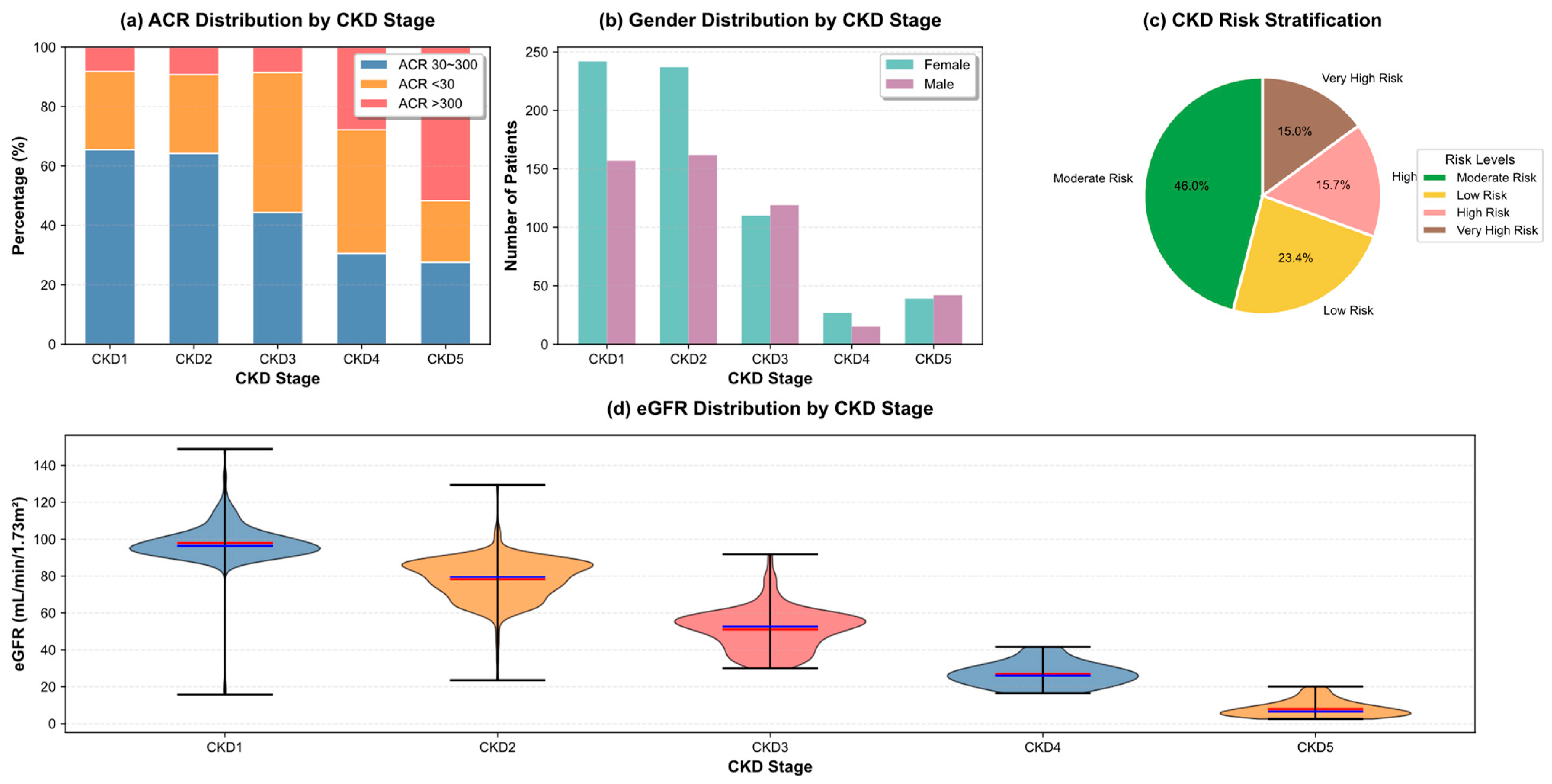
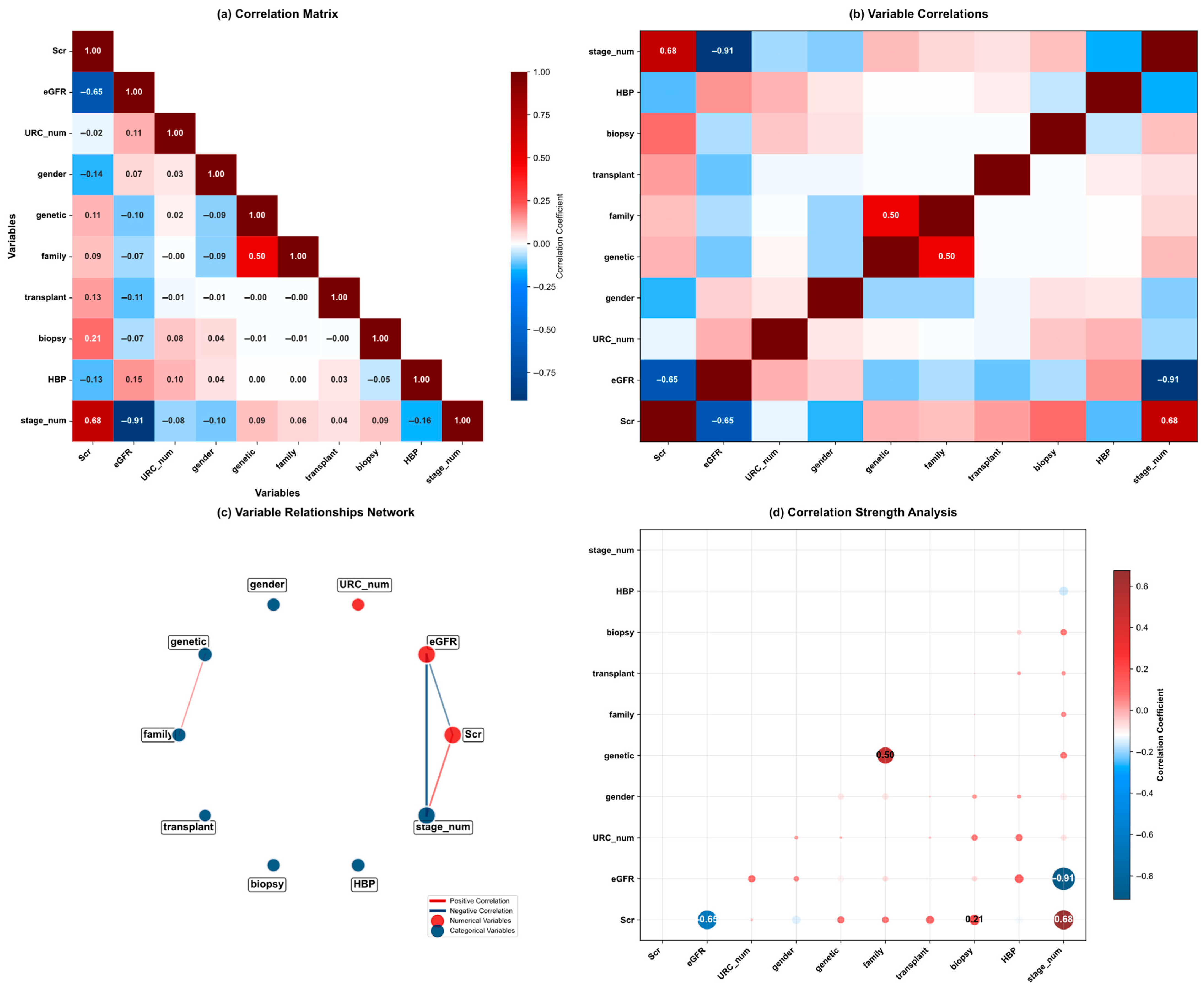
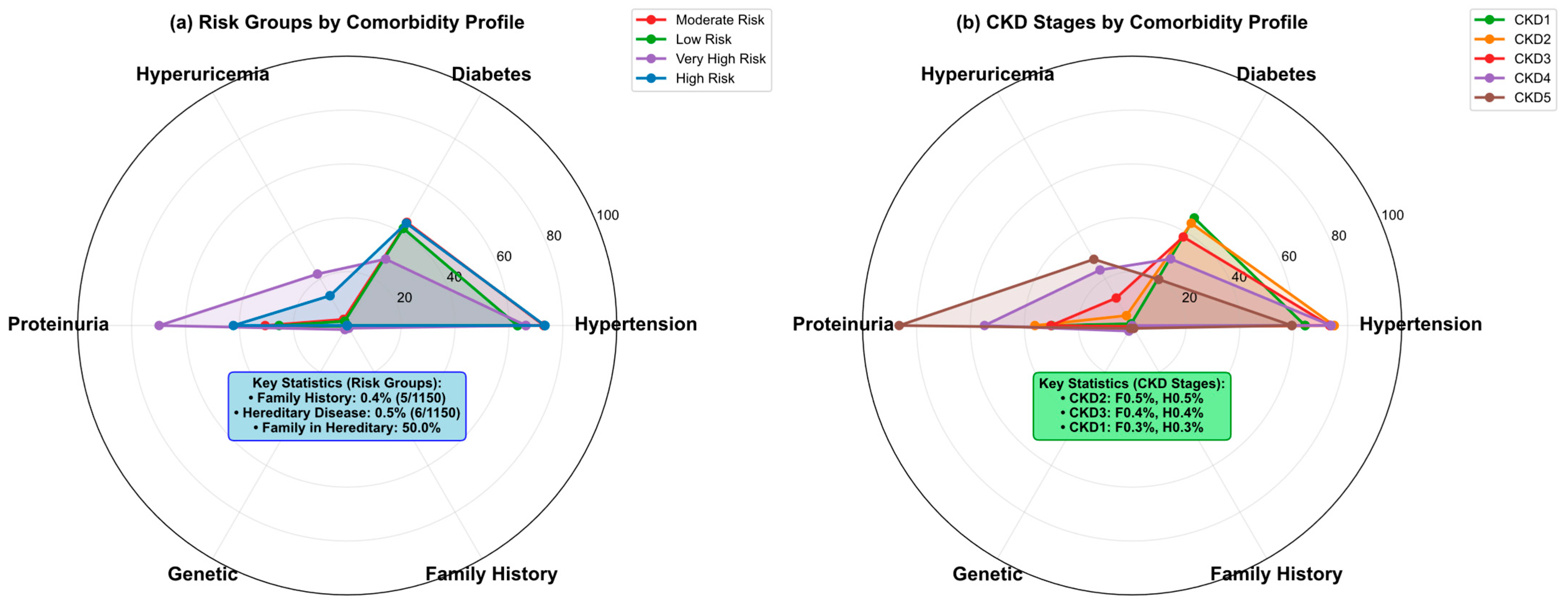

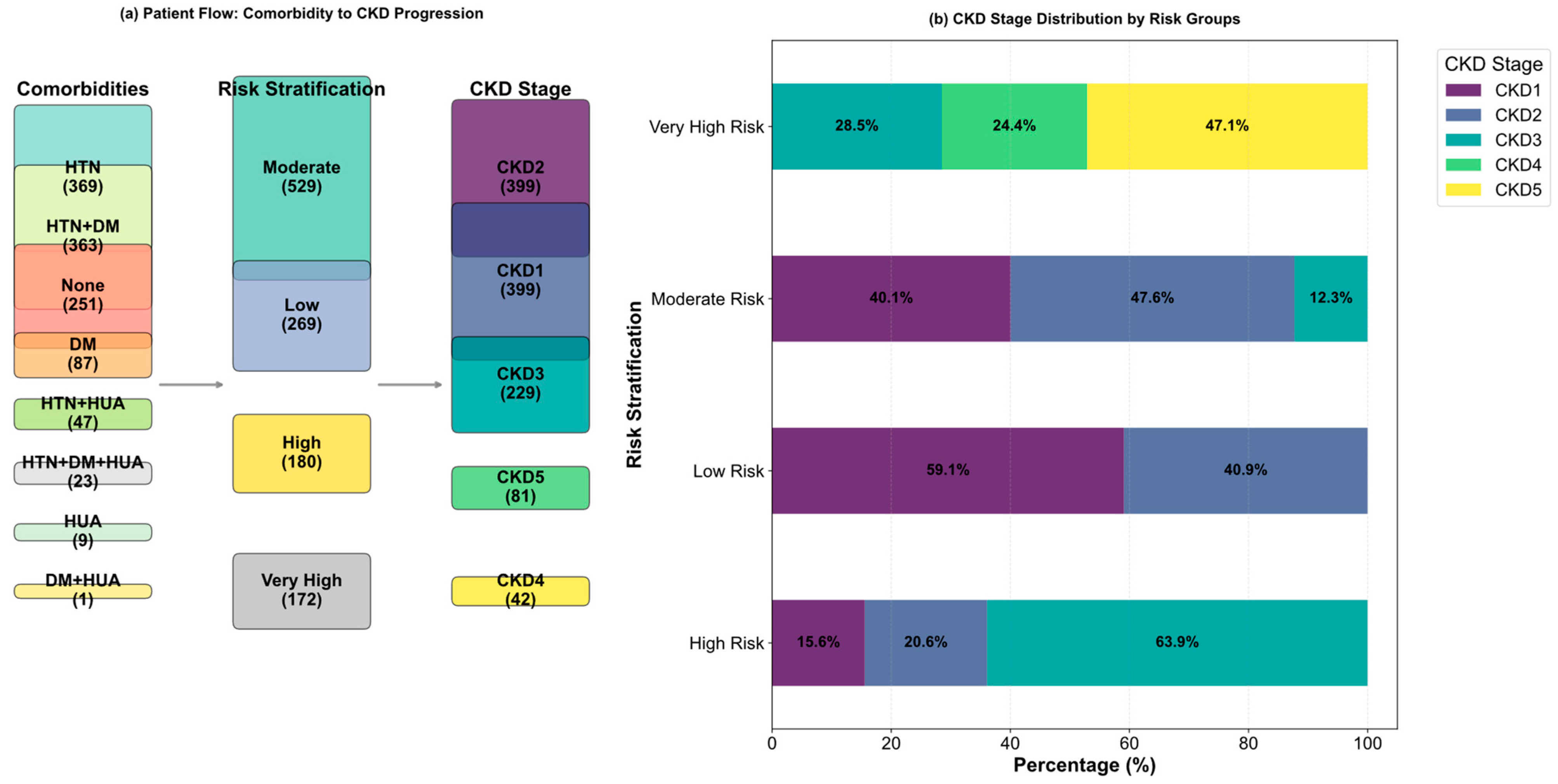
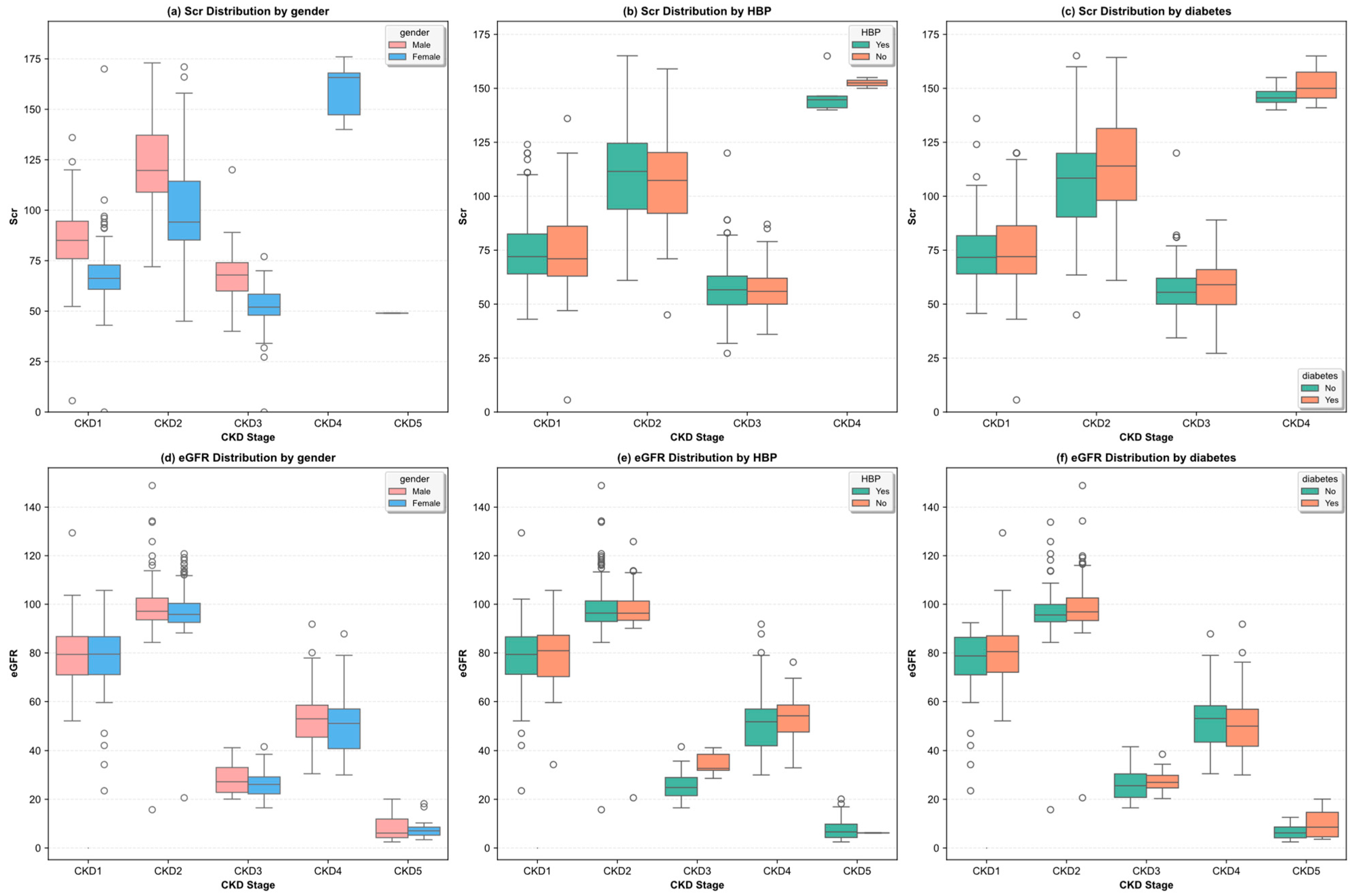
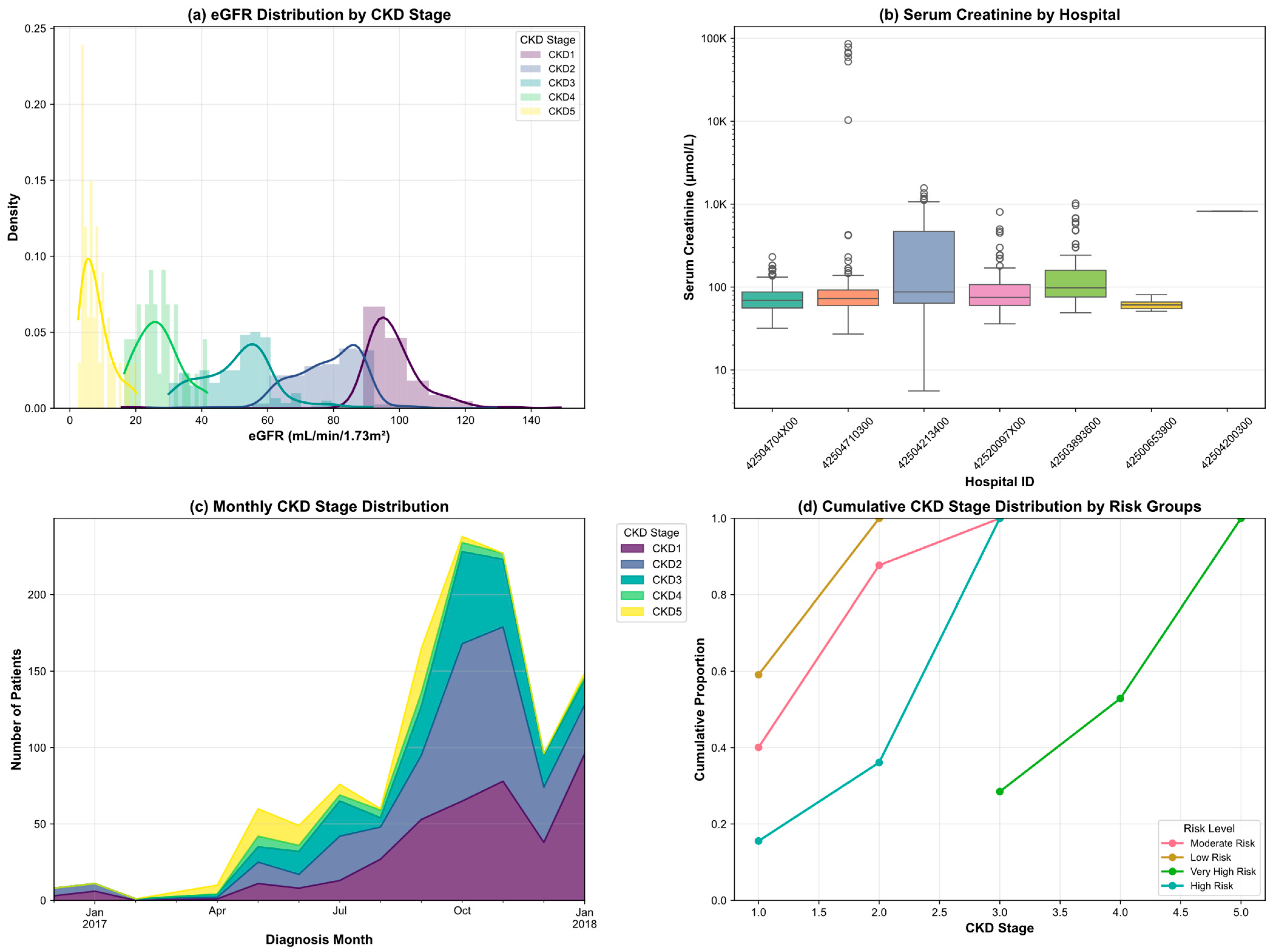


| Variable Name | Description | Values/Range |
|---|---|---|
| hos_id | Hospital ID | 7 hospitals |
| hos_name | Hospital Name | Hospital names |
| gender | Gender | Male/Female |
| genetic | Hereditary Kidney Disease | Yes/No |
| family | Family History of Chronic Nephritis | Yes/No |
| transplant | Kidney Transplant History | Yes/No |
| biopsy | Renal Biopsy History | Yes/No |
| HBP | Hypertension History | Yes/No |
| diabetes | Diabetes Mellitus History | Yes/No |
| hyperuricemia | Hyperuricemia | Yes/No |
| UAS | Urinary Anatomical Structure Abnormality | None/No/Yes |
| ACR | Albumin-to-Creatinine Ratio | <30/30–300/>300 mg/g |
| UP_positive | Urine Protein Test | Negative/Positive |
| UP_index | Urine Protein Index | ±(0.1–0.2 g/L) +(0.2–1.0) 2 + (1.0–2.0) 3 + (2.0–4.0) 5 + (>4.0) |
| URC_unit | Urine RBC Unit | HP—per high power field μL—per microliter |
| URC_num | Urine RBC Count | 0–93.9 Different units |
| Scr | Serum Creatinine | 0/27.2–85,800 μmol/L |
| eGFR | Estimated Glomerular Filtration Rate | 2.5–148 mL/min/1.73 m2 |
| date | Diagnosis Date | 13 December 2016 to 27 January 2018 |
| rate | CKD Risk Stratification | Low Risk/Moderate Risk High Risk/Very High Risk |
| stage | CKD Stage | CKD Stage 1–5 |
| Model | Dataset | Accuracy | Precision | Recall (Macro) | F1 (Macro) | ROC AUC |
|---|---|---|---|---|---|---|
| Ours | Train | 0.928 | 0.937 | 0.92 | 0.928 | 0.99 |
| Test | 0.924 | 0.927 | 0.912 | 0.919 | 0.977 | |
| Random Forest | Train | 0.867 | 0.88 | 0.826 | 0.849 | 0.975 |
| Test | 0.825 | 0.826 | 0.774 | 0.795 | 0.943 | |
| XGBoost | Train | 0.891 | 0.894 | 0.874 | 0.883 | 0.975 |
| Test | 0.855 | 0.847 | 0.836 | 0.841 | 0.941 | |
| Decision Tree | Train | 0.878 | 0.871 | 0.859 | 0.865 | 0.965 |
| Test | 0.848 | 0.833 | 0.831 | 0.832 | 0.903 | |
| SVM | Train | 0.871 | 0.888 | 0.838 | 0.859 | 0.962 |
| Test | 0.801 | 0.782 | 0.764 | 0.771 | 0.936 | |
| MLP | Train | 0.773 | 0.773 | 0.713 | 0.727 | 0.911 |
| Test | 0.734 | 0.713 | 0.685 | 0.687 | 0.908 | |
| Logistic Regression | Train | 0.835 | 0.83 | 0.799 | 0.812 | 0.944 |
| Test | 0.811 | 0.795 | 0.783 | 0.789 | 0.921 | |
| Ridge Classifier | Train | 0.719 | 0.725 | 0.637 | 0.617 | 0.883 |
| Test | 0.737 | 0.713 | 0.665 | 0.653 | 0.895 | |
| Lasso | Train | 0.836 | 0.829 | 0.803 | 0.814 | 0.944 |
| Test | 0.825 | 0.814 | 0.797 | 0.804 | 0.926 | |
| Elastic Net | Train | 0.838 | 0.833 | 0.803 | 0.815 | 0.944 |
| Test | 0.822 | 0.809 | 0.793 | 0.8 | 0.925 | |
| LightGBM | Train | 0.925 | 0.936 | 0.916 | 0.925 | 0.992 |
| Test | 0.845 | 0.834 | 0.835 | 0.834 | 0.938 | |
| CatBoost | Train | 0.891 | 0.897 | 0.878 | 0.887 | 0.975 |
| Test | 0.848 | 0.838 | 0.829 | 0.833 | 0.949 | |
| Gradient Boosting | Train | 0.893 | 0.902 | 0.876 | 0.888 | 0.972 |
| Test | 0.842 | 0.836 | 0.821 | 0.828 | 0.944 | |
| KNN | Train | 0.795 | 0.812 | 0.737 | 0.767 | 0.952 |
| Test | 0.697 | 0.679 | 0.624 | 0.645 | 0.867 | |
| Naive Bayes | Train | 0.315 | 0.482 | 0.428 | 0.335 | 0.833 |
| Test | 0.3 | 0.351 | 0.408 | 0.314 | 0.83 | |
| Voting Classifier | Train | 0.896 | 0.919 | 0.868 | 0.89 | 0.973 |
| Test | 0.848 | 0.854 | 0.828 | 0.839 | 0.947 | |
| Stacking Classifier | Train | 0.884 | 0.894 | 0.862 | 0.877 | 0.964 |
| Test | 0.828 | 0.815 | 0.799 | 0.806 | 0.933 |
| Hyperparameter | Ours | GridSearch | RandomSearch | Evolutionary |
|---|---|---|---|---|
| n_estimators | 487 | 500 | 450 | 520 |
| max_depth | 6 | 7 | 5 | 6 |
| learning_rate | 0.0142 | 0.015 | 0.018 | 0.012 |
| subsample | 0.847 | 0.8 | 0.85 | 0.82 |
| colsample_bytree | 0.923 | 0.9 | 0.95 | 0.88 |
| reg_alpha | 0.513 | 1.0 | 0.8 | 0.45 |
| reg_lambda | 2.847 | 3.0 | 2.5 | 3.2 |
| min_child_weight | 3.2 | 3 | 4 | 2.8 |
| gamma | 0.028 | 0.05 | 0.02 | 0.035 |
| scale_pos_weight | 1.247 | 1.0 | 1.3 | 1.15 |
| Method | F1 (Macro) | Accuray | Precision | Recall (Macro) | ROC AUC | Time (s) | Evaluations |
|---|---|---|---|---|---|---|---|
| Ours | 0.9186 | 0.9242 | 0.9272 | 0.9116 | 0.9764 | 183.15 | 100 |
| GridSearch | 0.9147 | 0.9242 | 0.9243 | 0.9066 | 0.966 | 711.31 | 3456 |
| RandomSearch | 0.9143 | 0.9192 | 0.9151 | 0.9152 | 0.979 | 22.05 | 100 |
| Evolutionary | 0.9015 | 0.9091 | 0.9 | 0.905 | 0.9777 | 108.76 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Li, L.; Hou, M.; Chen, J. Bayesian Optimization Meets Explainable AI: Enhanced Chronic Kidney Disease Risk Assessment. Mathematics 2025, 13, 2726. https://doi.org/10.3390/math13172726
Huang J, Li L, Hou M, Chen J. Bayesian Optimization Meets Explainable AI: Enhanced Chronic Kidney Disease Risk Assessment. Mathematics. 2025; 13(17):2726. https://doi.org/10.3390/math13172726
Chicago/Turabian StyleHuang, Jianbo, Long Li, Mengdi Hou, and Jia Chen. 2025. "Bayesian Optimization Meets Explainable AI: Enhanced Chronic Kidney Disease Risk Assessment" Mathematics 13, no. 17: 2726. https://doi.org/10.3390/math13172726
APA StyleHuang, J., Li, L., Hou, M., & Chen, J. (2025). Bayesian Optimization Meets Explainable AI: Enhanced Chronic Kidney Disease Risk Assessment. Mathematics, 13(17), 2726. https://doi.org/10.3390/math13172726






