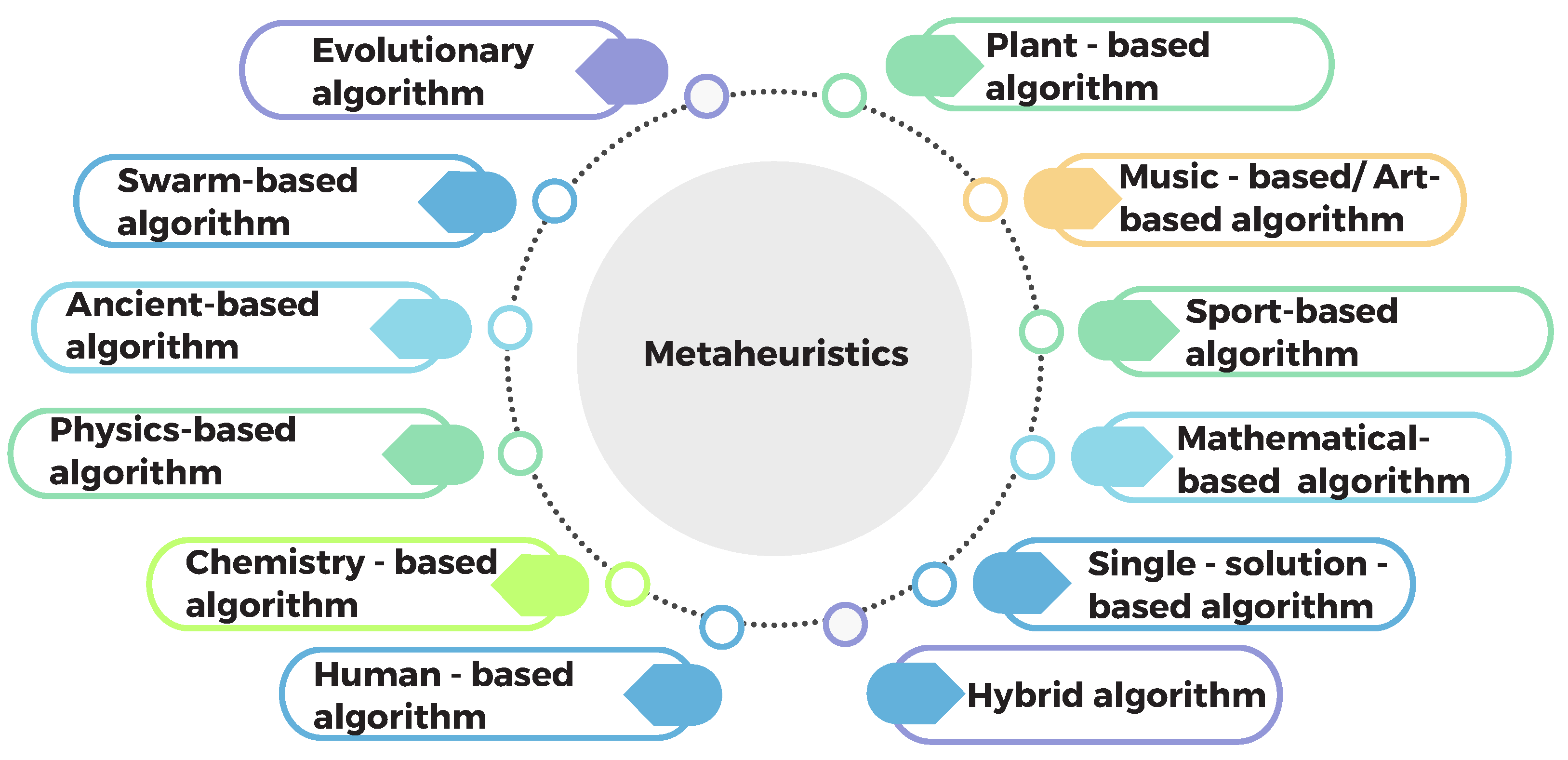
Figure 1.
Metaheuristic classification.
Figure 1.
Metaheuristic classification.
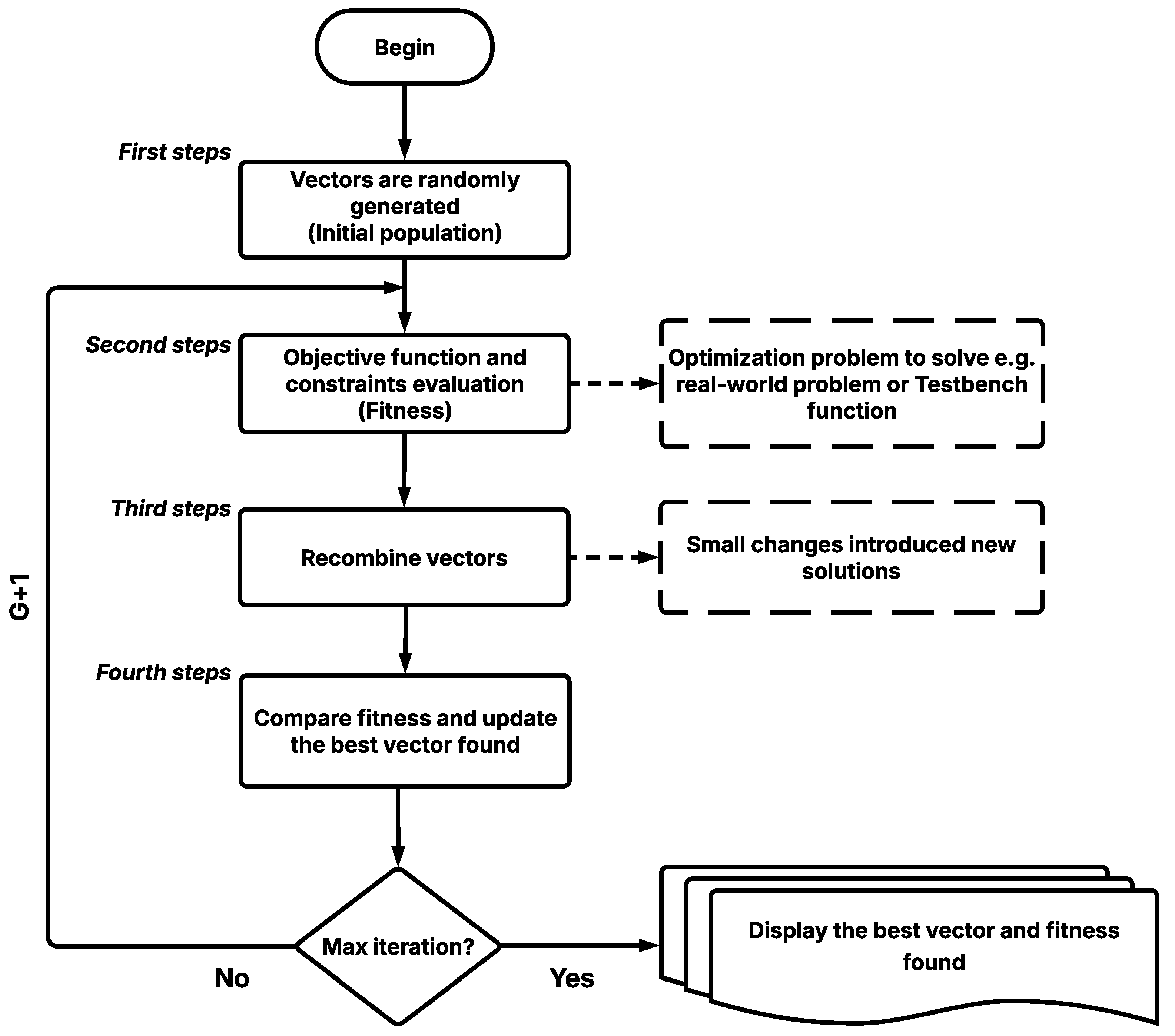
Figure 2.
A metaheuristic algorithm’s general framework.
Figure 2.
A metaheuristic algorithm’s general framework.
Figure 3.
The Tetragonula carbonaria bee. Photo by an unknown author, licensed under CC BY 2.0.
Figure 3.
The Tetragonula carbonaria bee. Photo by an unknown author, licensed under CC BY 2.0.
Figure 4.
Three-dimensional spiral architecture of Tetragonula carbonaria. Photo by an unknown author, licensed under CC BY.
Figure 4.
Three-dimensional spiral architecture of Tetragonula carbonaria. Photo by an unknown author, licensed under CC BY.
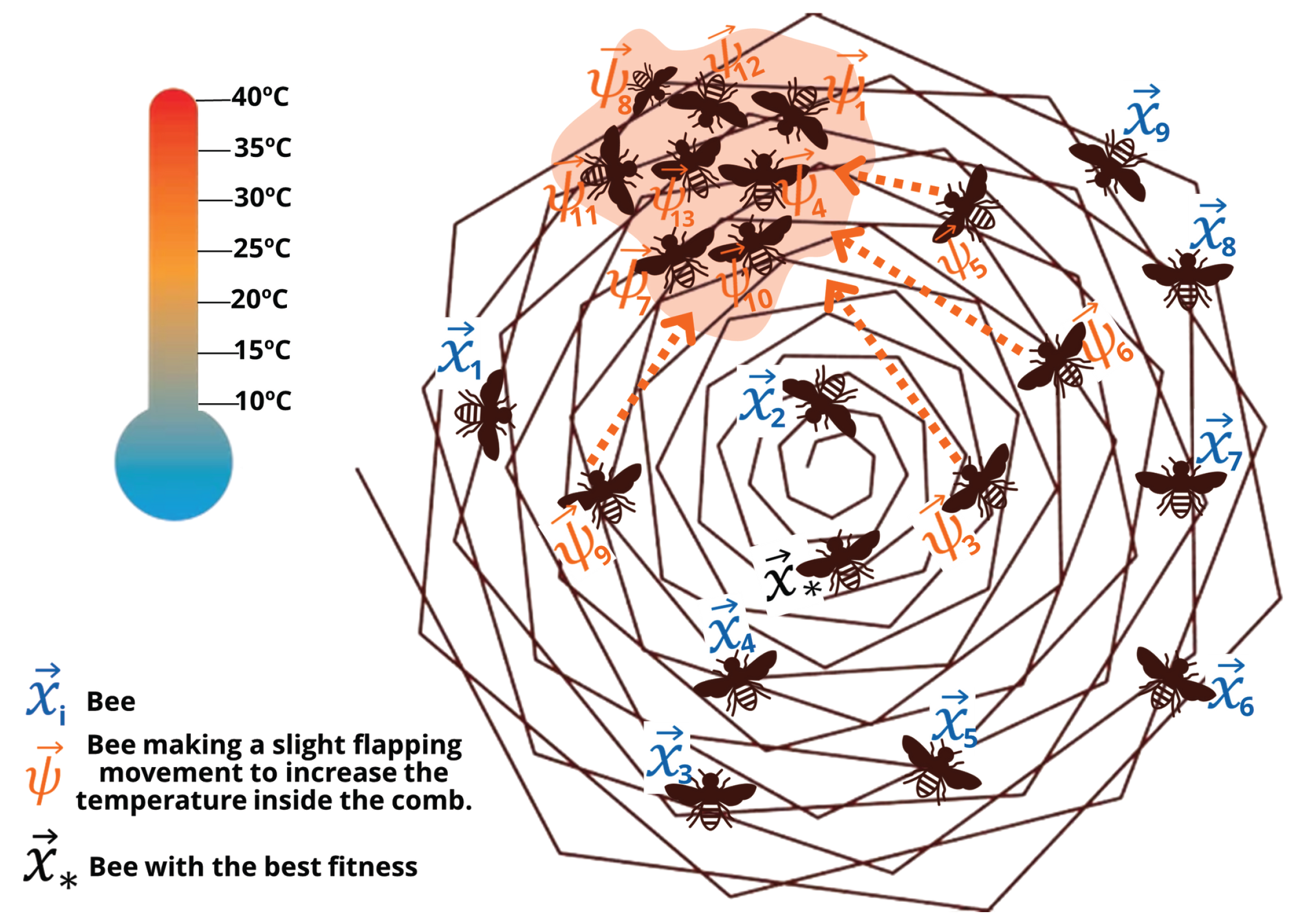
Figure 5.
Slight fluttering motion and cluster to warm the hive.
Figure 5.
Slight fluttering motion and cluster to warm the hive.
Figure 6.
Hive cooling by cooperative clustering. Licensed under CC BY-NC-ND.
Figure 6.
Hive cooling by cooperative clustering. Licensed under CC BY-NC-ND.
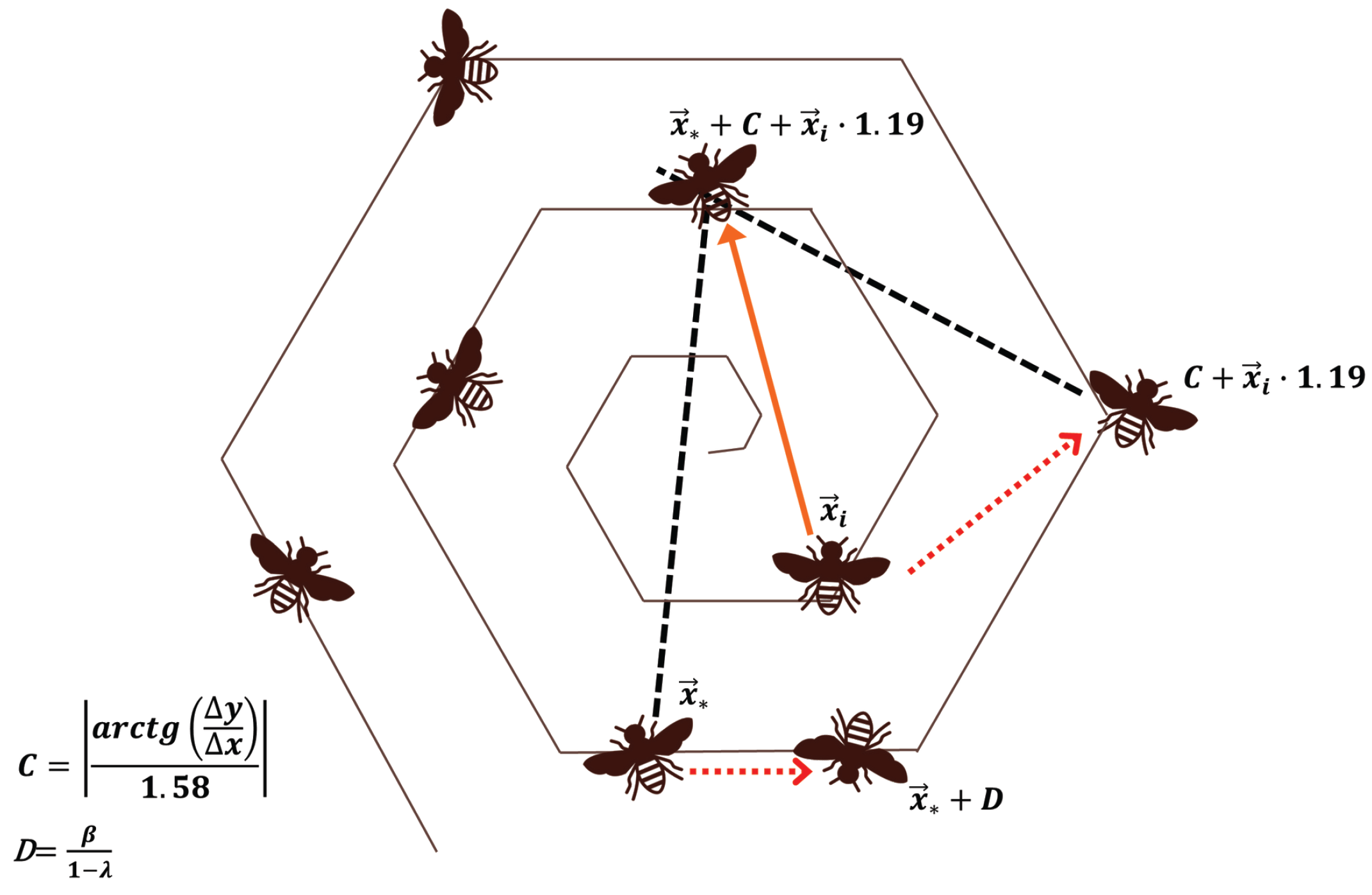
Figure 7.
Building the spiral hive.
Figure 7.
Building the spiral hive.
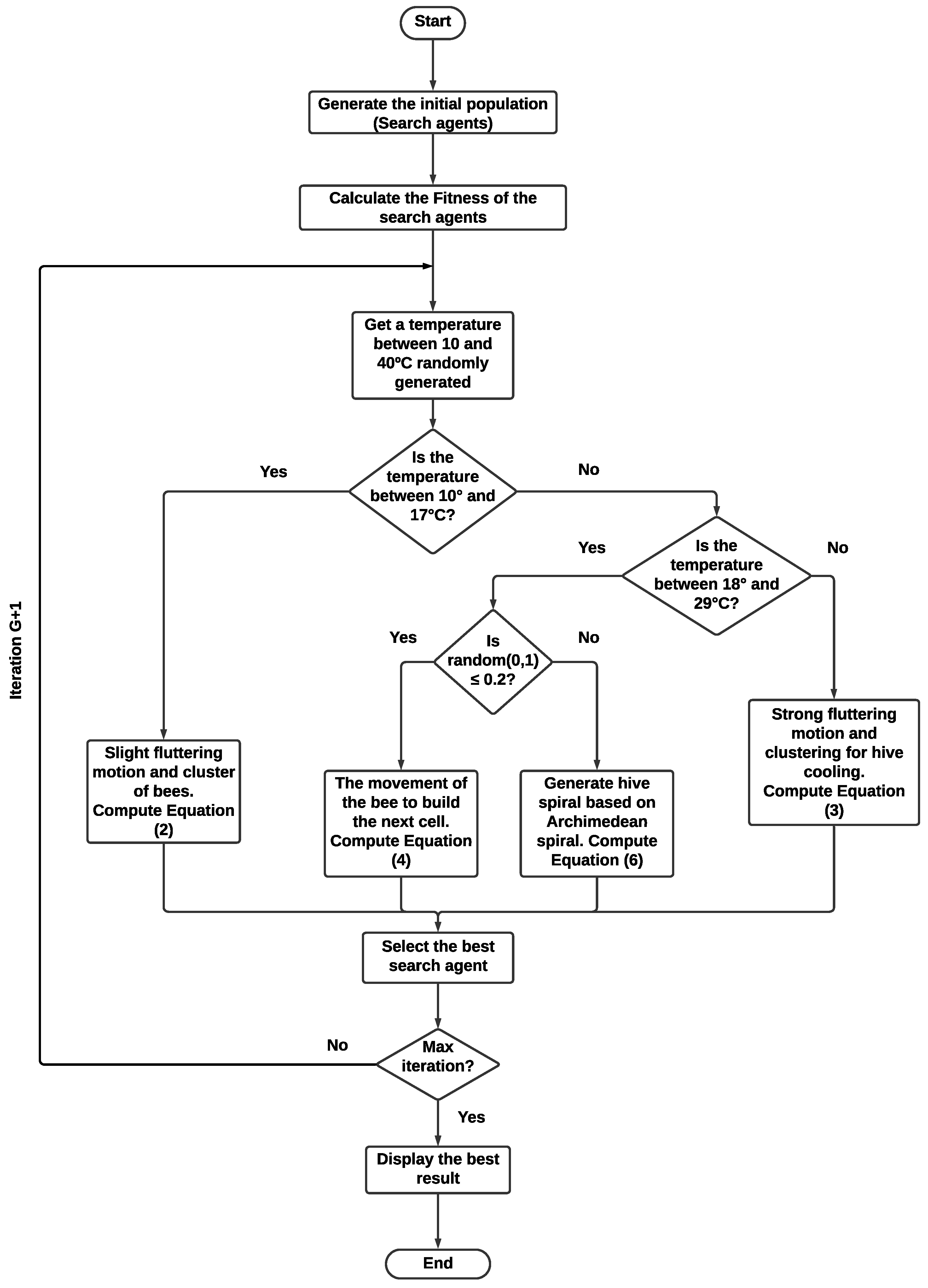
Figure 8.
TGCOA flowchart.
Figure 8.
TGCOA flowchart.
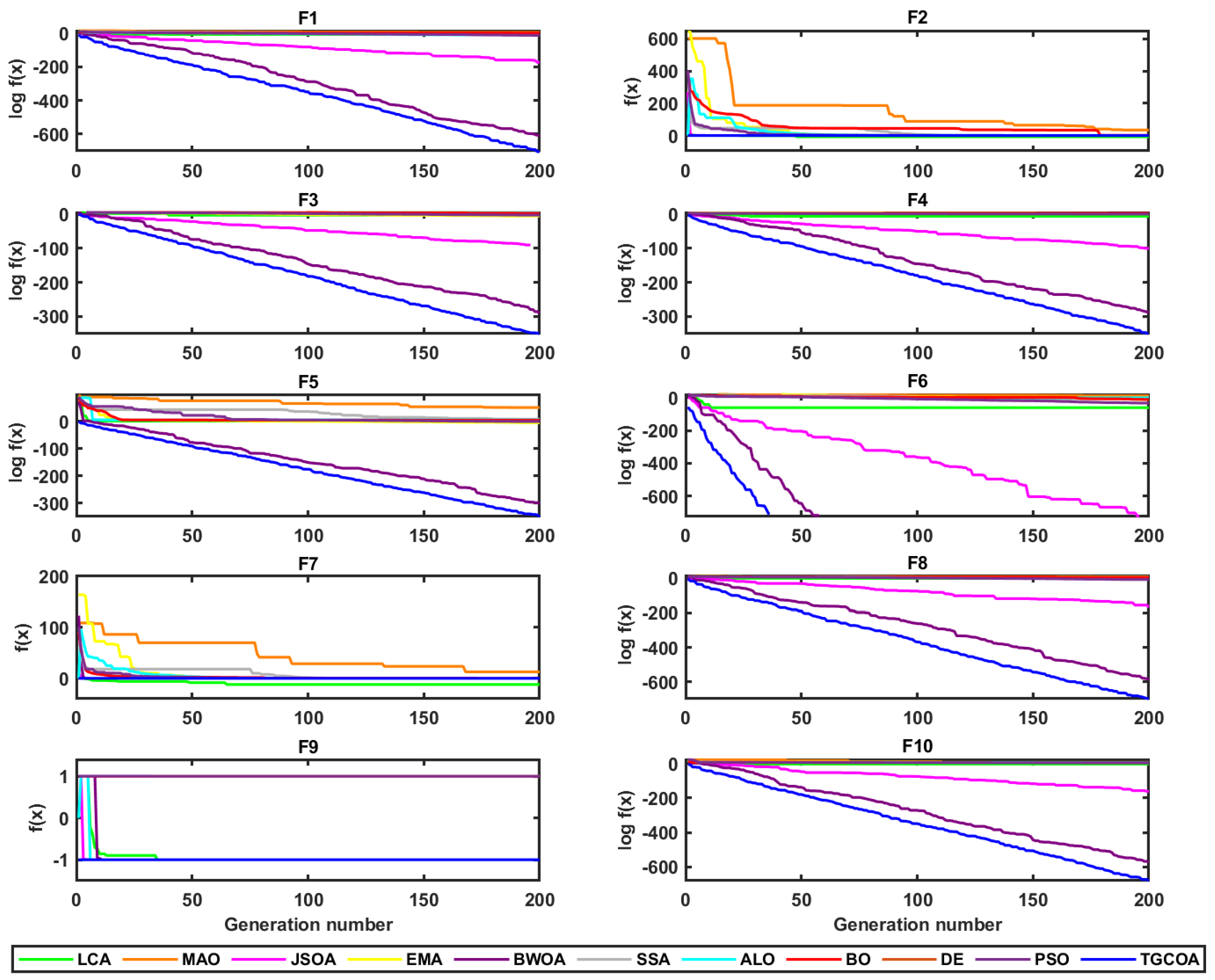
Figure 9.
Convergence curves of unimodal functions.
Figure 9.
Convergence curves of unimodal functions.
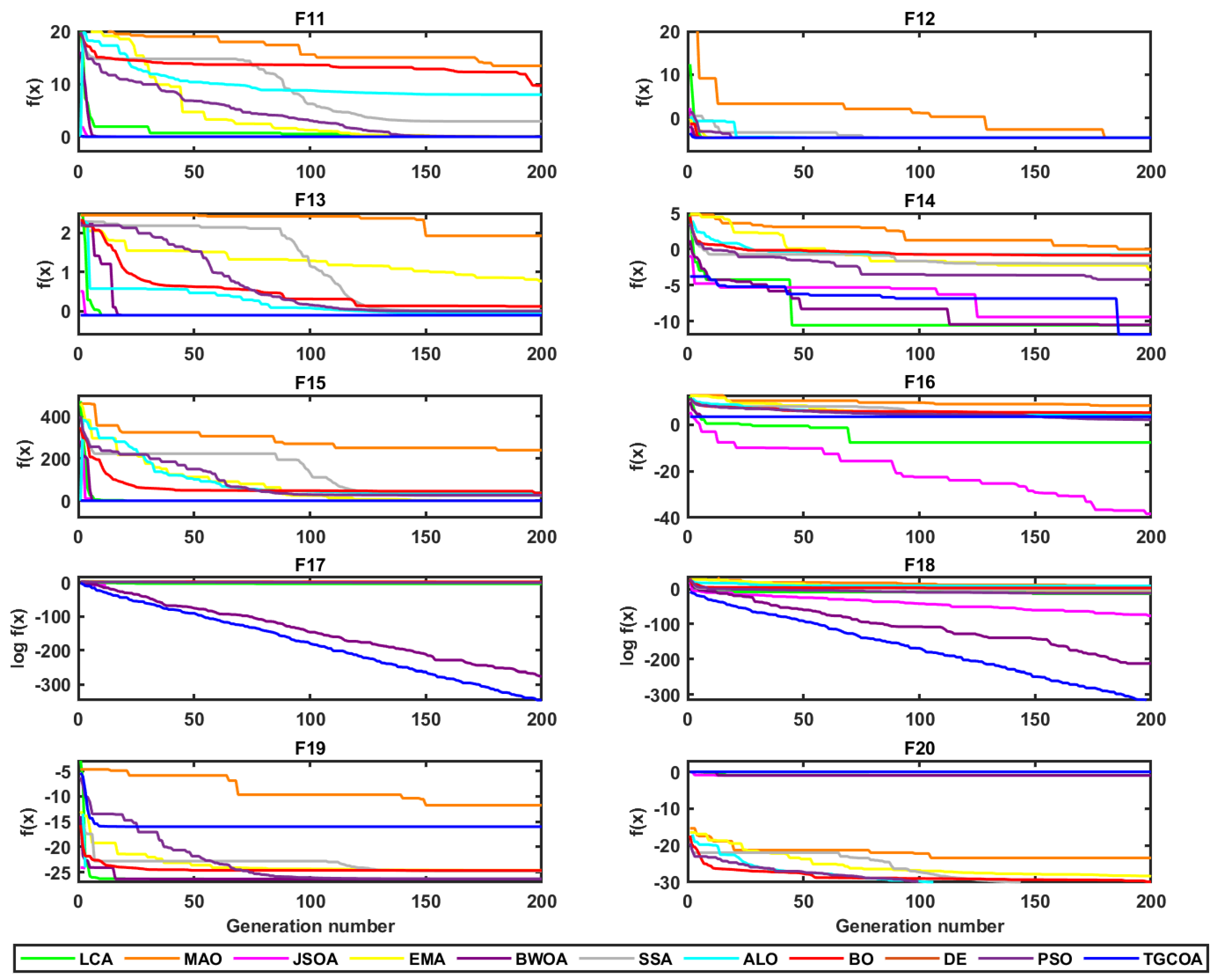
Figure 10.
Convergence curves of multimodal functions.
Figure 10.
Convergence curves of multimodal functions.
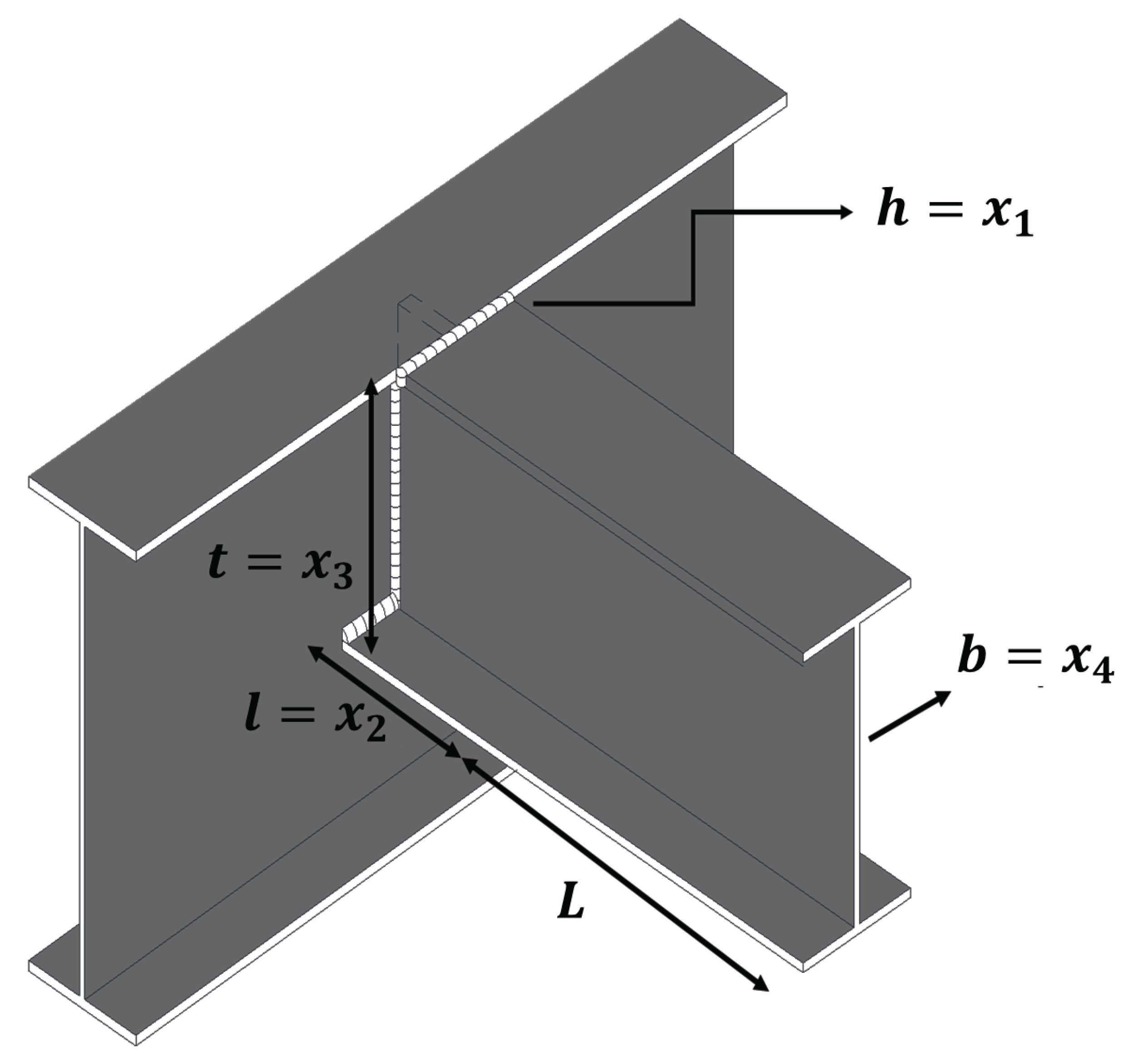
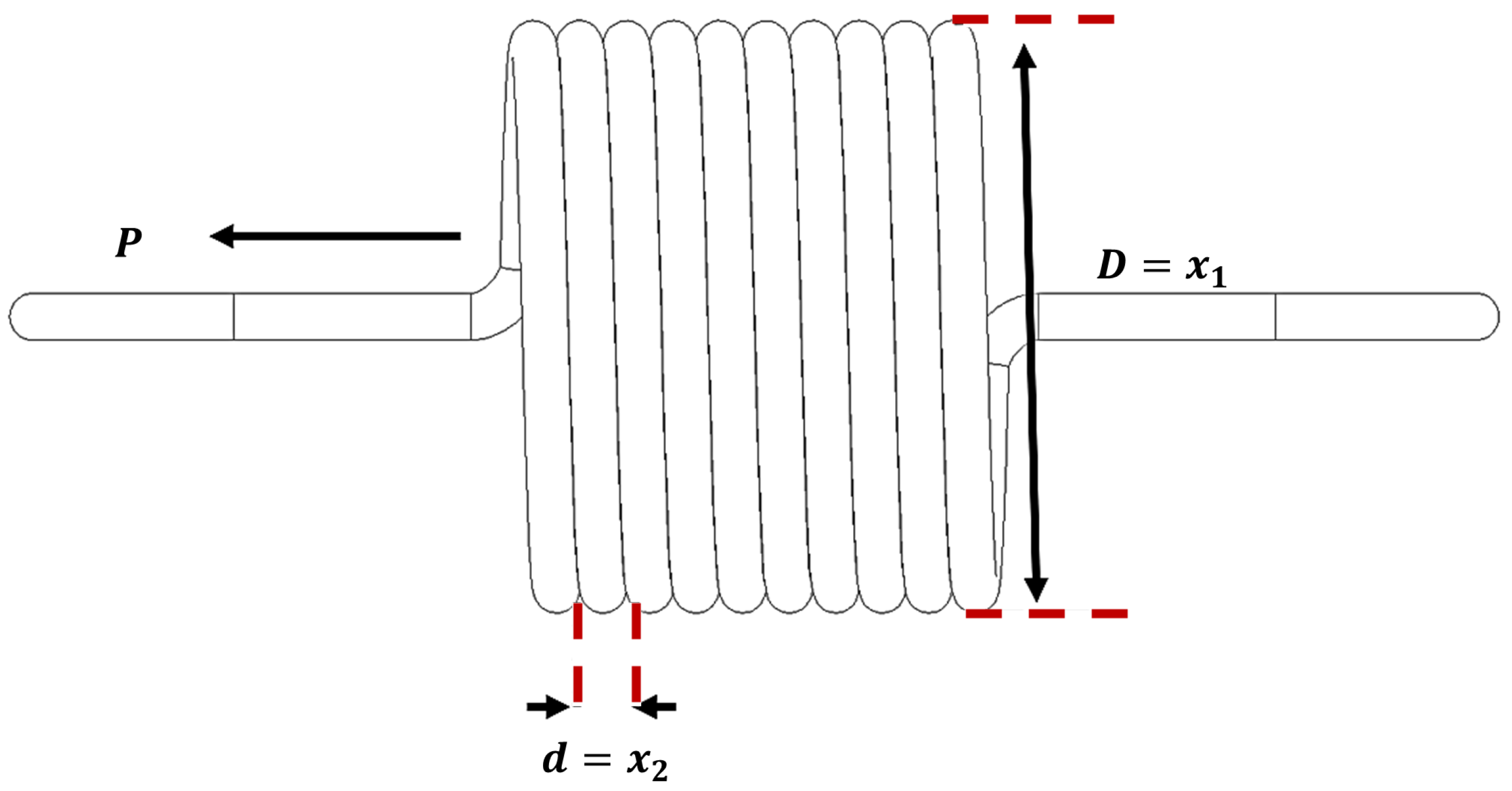
Figure 11.
Tension/compression spring design.
Figure 11.
Tension/compression spring design.
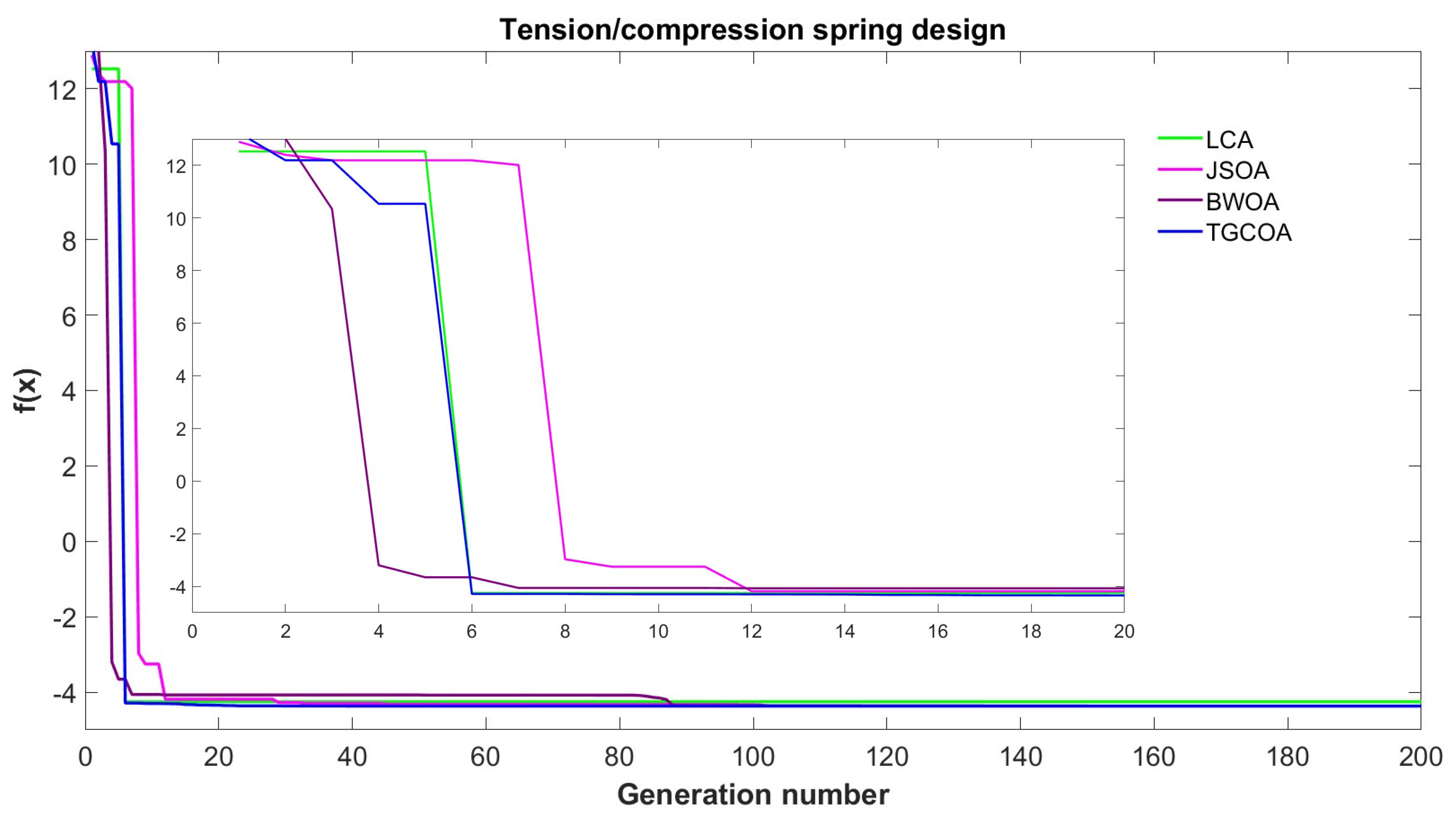
Figure 12.
Convergence graph of the tension/compression spring design.
Figure 12.
Convergence graph of the tension/compression spring design.
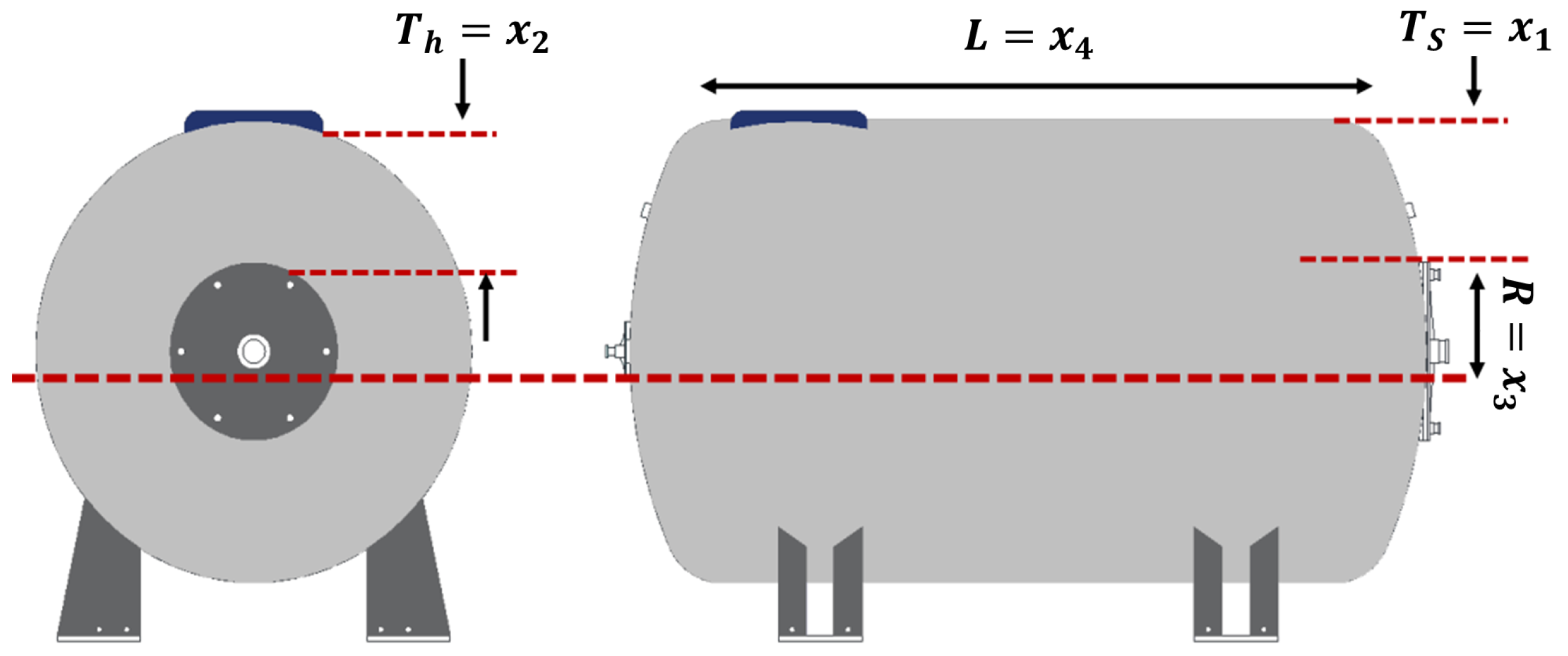
Figure 13.
An illustration of the design of a pressure vessel.
Figure 13.
An illustration of the design of a pressure vessel.
Figure 14.
Convergence graph of the pressure vessel design.
Figure 14.
Convergence graph of the pressure vessel design.
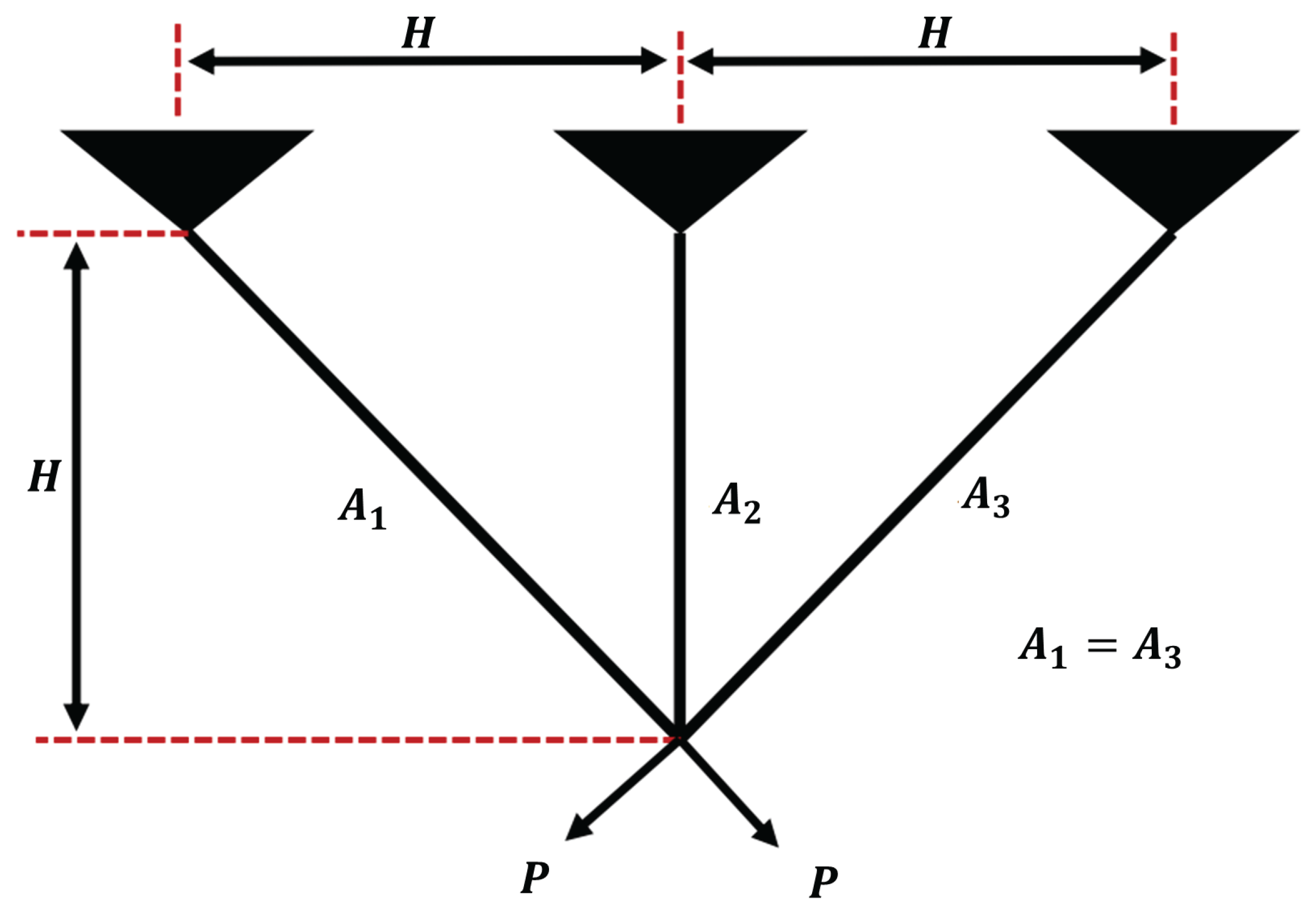
Figure 15.
A schematic model of three-bar truss.
Figure 15.
A schematic model of three-bar truss.
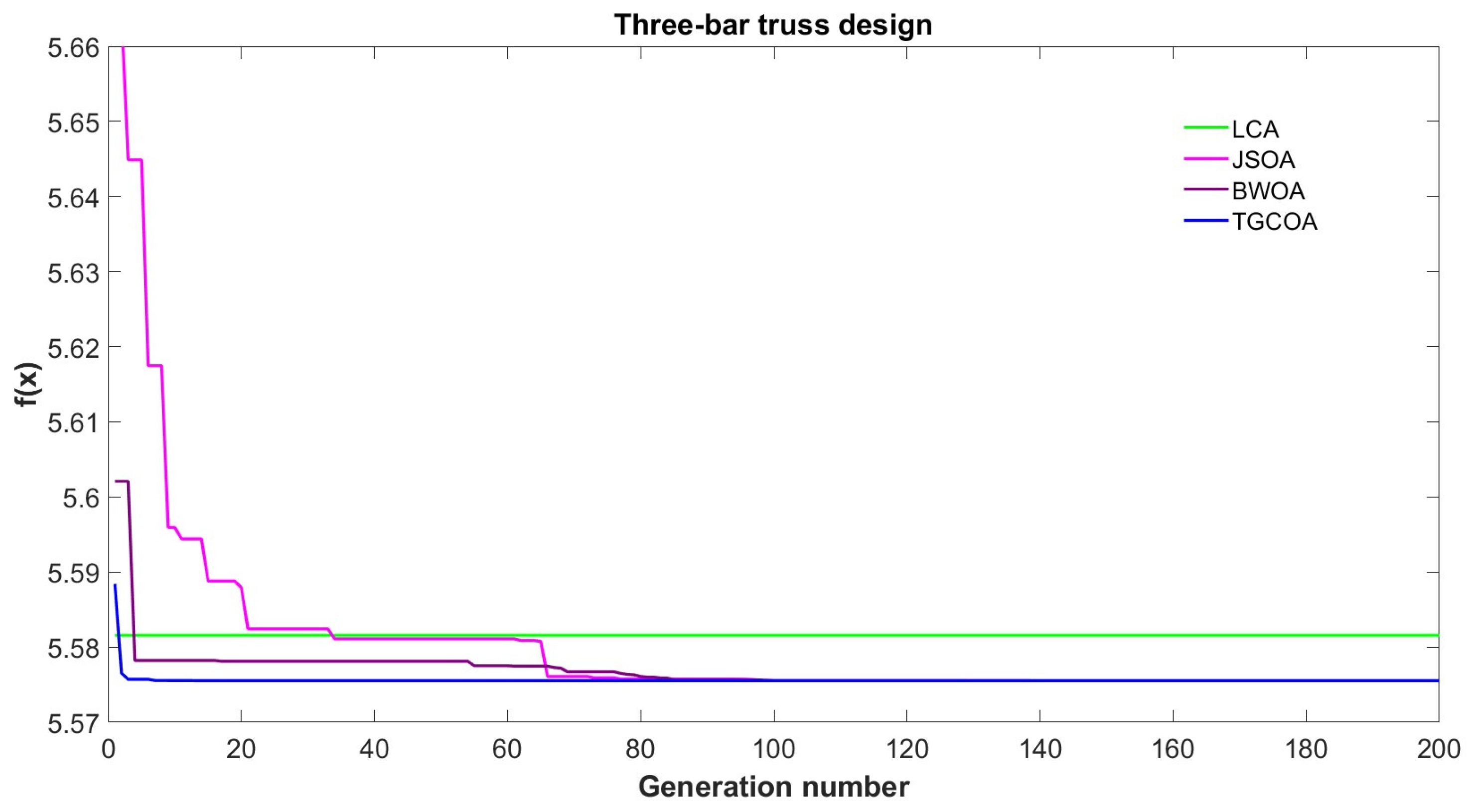
Figure 16.
Convergence graph of three-bar truss design problem.
Figure 16.
Convergence graph of three-bar truss design problem.
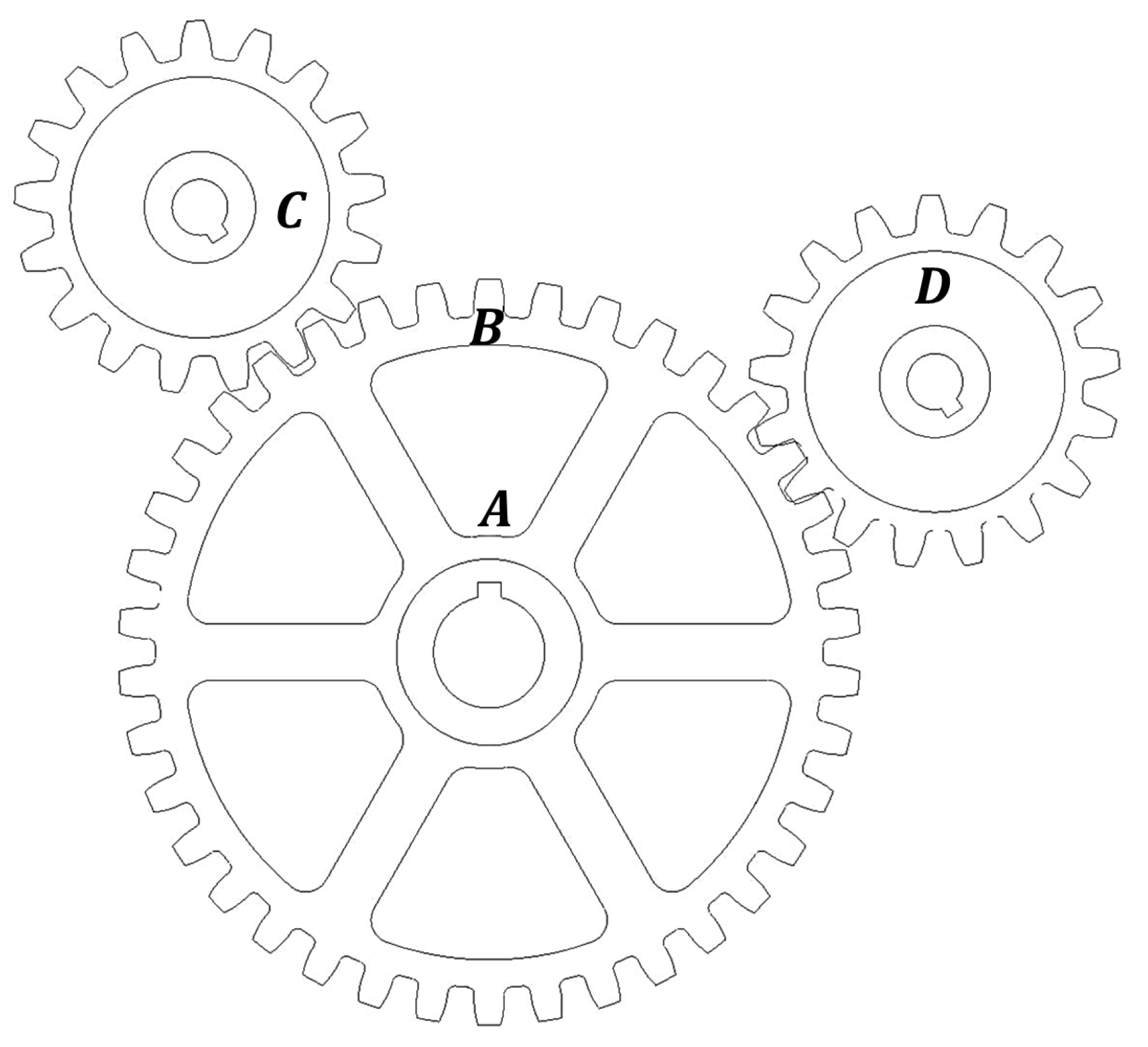
Figure 17.
Two-dimensional design of gear train.
Figure 17.
Two-dimensional design of gear train.
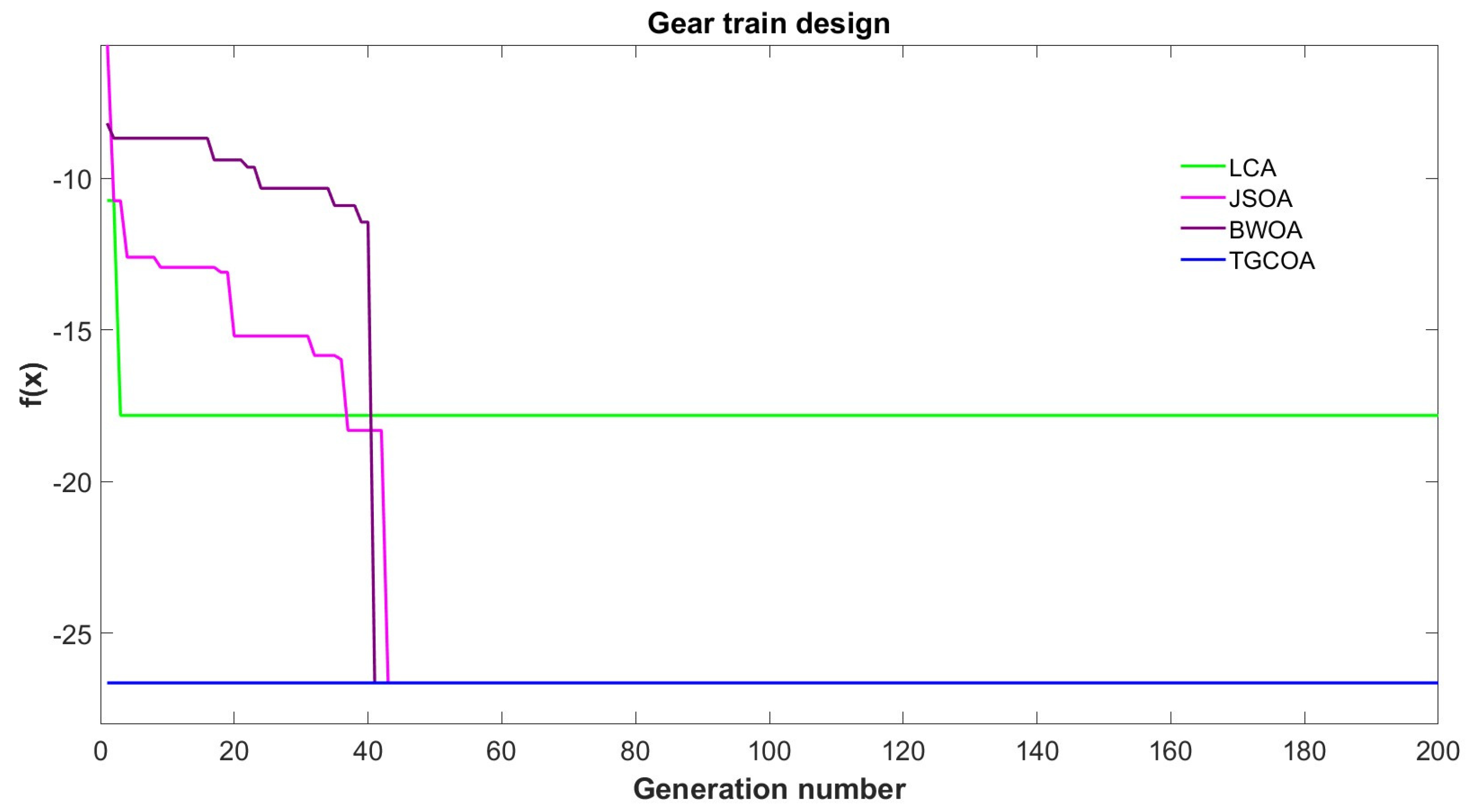
Figure 18.
Convergencegraph of design of gear train.
Figure 18.
Convergencegraph of design of gear train.
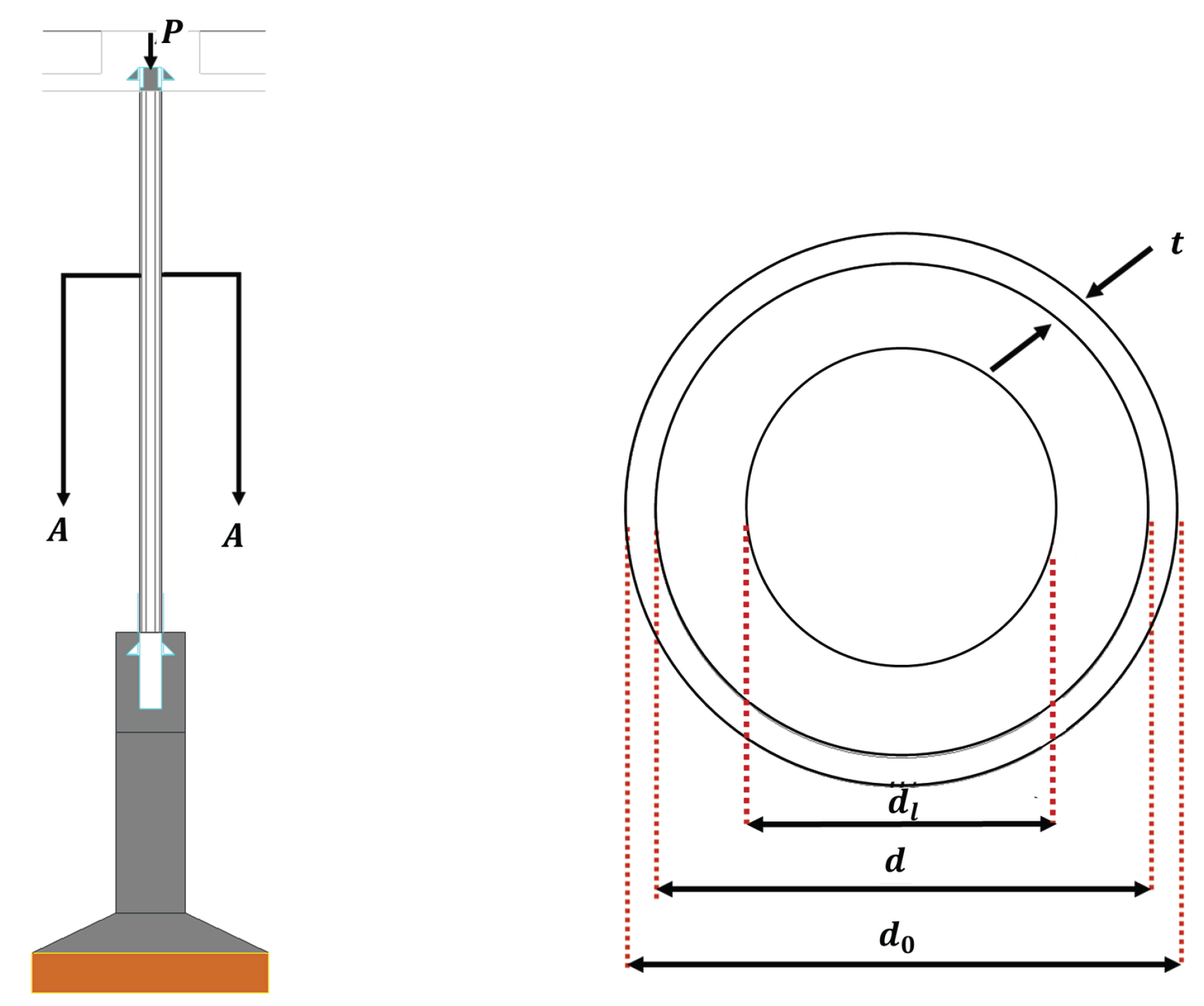
Figure 19.
Two-dimensional model of tubular column.
Figure 19.
Two-dimensional model of tubular column.
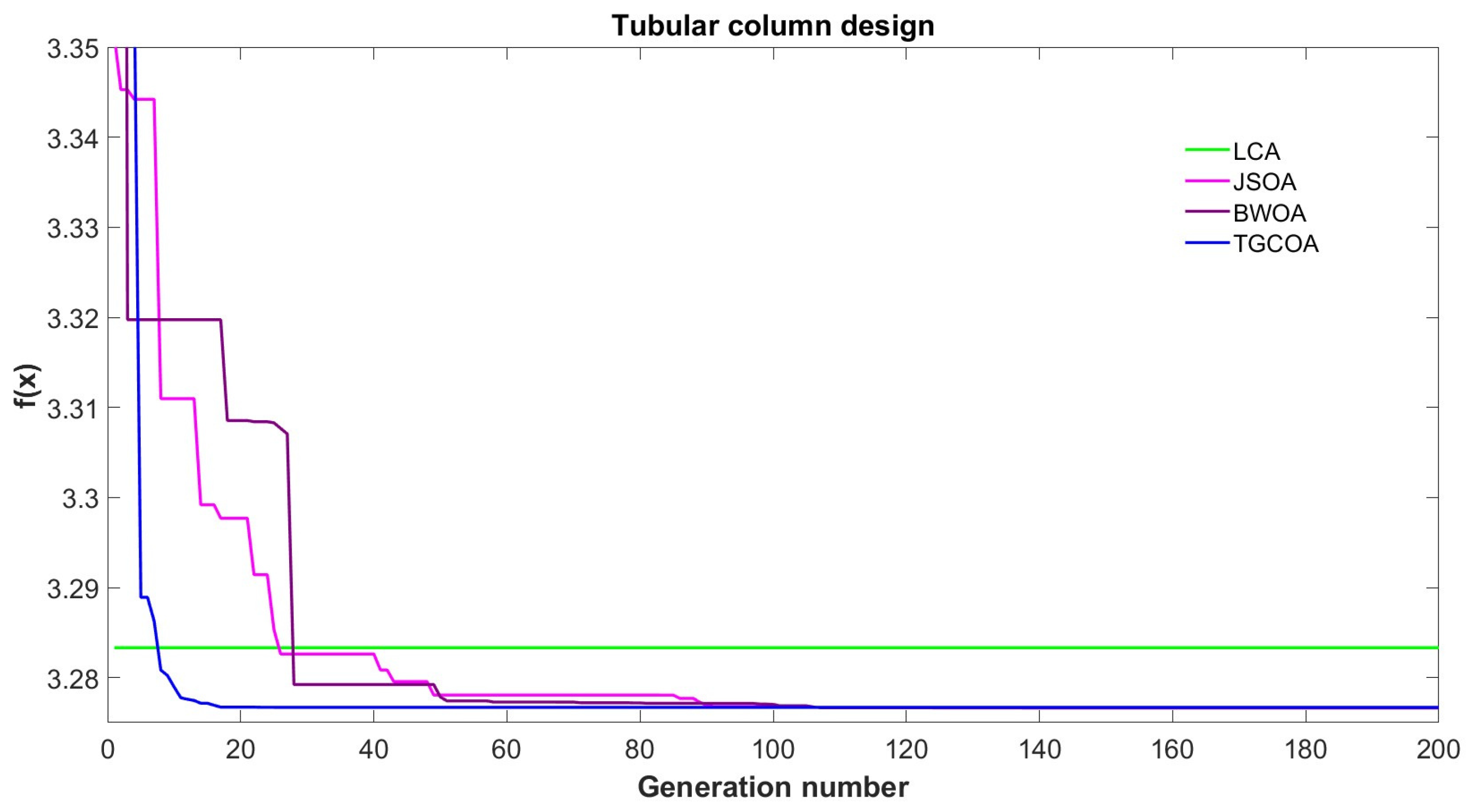
Figure 20.
A convergence graph for the design of tubular columns.
Figure 20.
A convergence graph for the design of tubular columns.
Figure 22.
Convergence graph of welded beam design.
Figure 22.
Convergence graph of welded beam design.
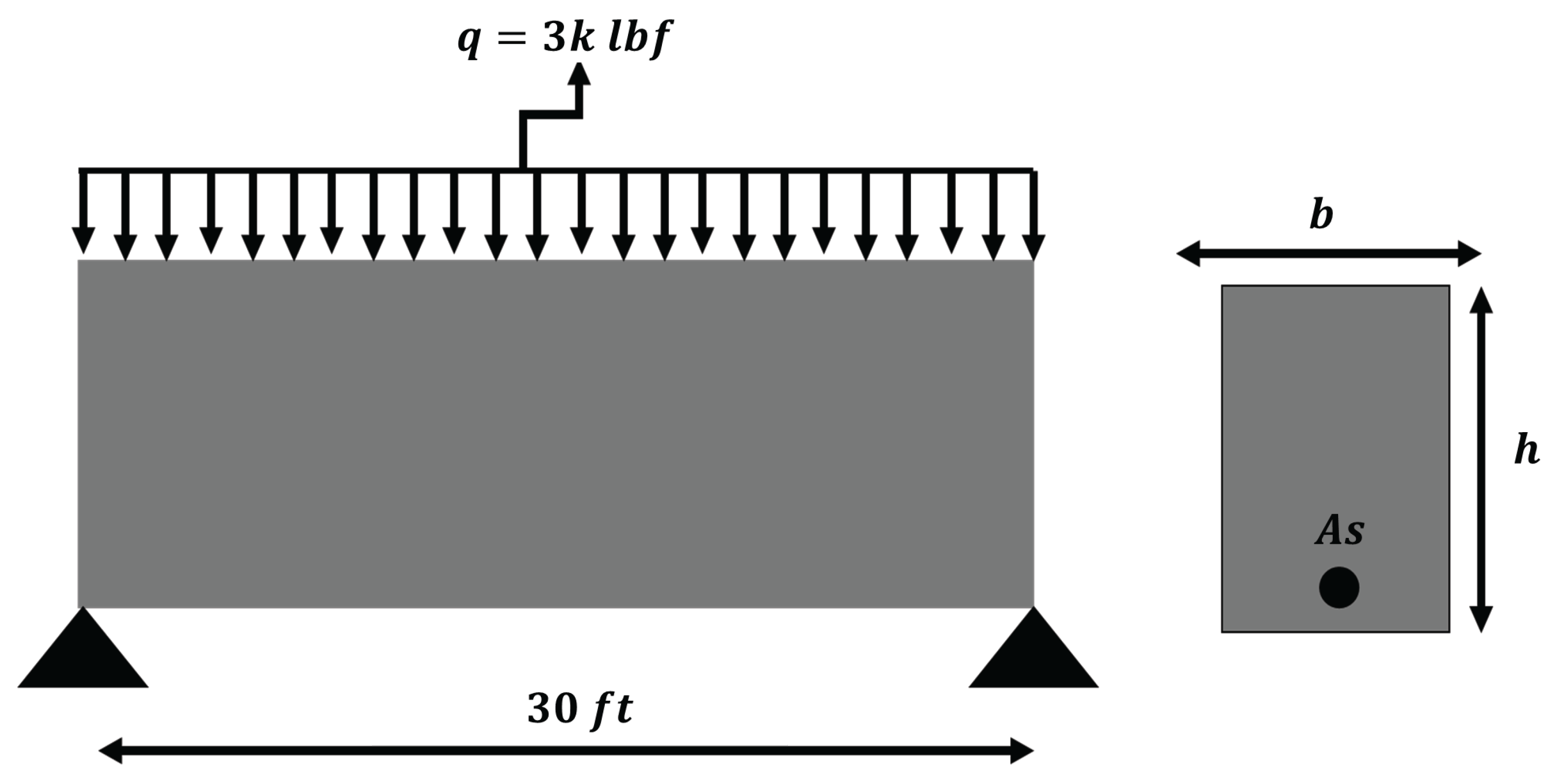
Figure 23.
Reinforced concrete beam design.
Figure 23.
Reinforced concrete beam design.
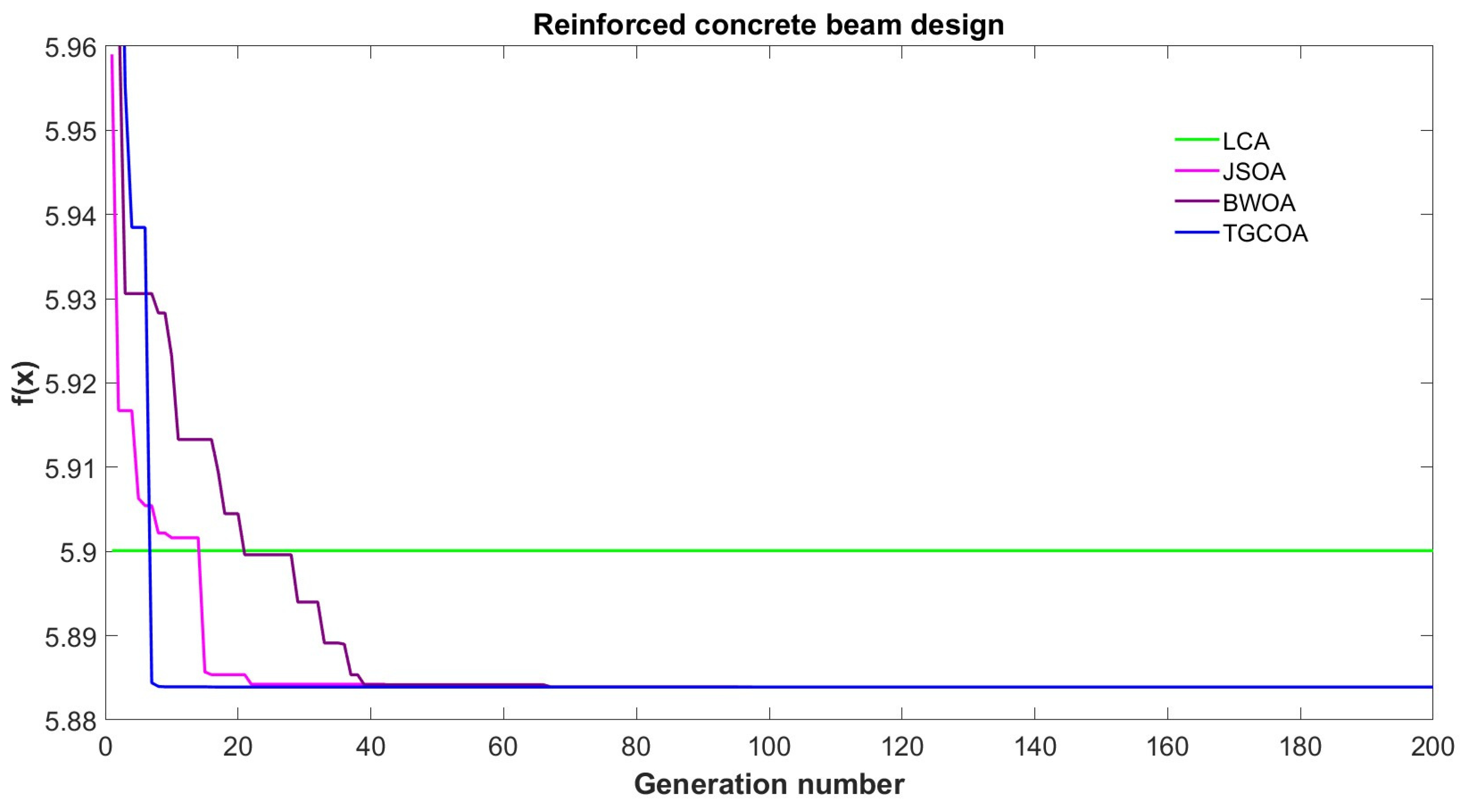
Figure 24.
Convergence graph for reinforced concrete beam design.
Figure 24.
Convergence graph for reinforced concrete beam design.
Table 1.
Time complexity analysis of TGCOA.
Table 1.
Time complexity analysis of TGCOA.
| Line in Algorithm 4 | Big-O | Description |
|---|
| 3 | | Initialization: Generate random solutions in D dimensions. |
| 5 | | Random temperature generation (constant-time operation). |
| 6–14 | | Temperature-based behavior: Update all agents’ positions in D dimensions (applies to Equations (2)–(4) or (6)). |
| 15 | | Fitness evaluation: Compute fitness for agents, where f is the cost of one evaluation. |
| 16–18 | | Update best solution: Single comparison and assignment. |
| 4–20 | | Main loop: Repeat lines 5–19 for iterations. Dominated by agent updates and fitness evaluations. |
| 21 | | Output the best solution (constant-time). |
Table 2.
Initial settings for algorithm control parameters.
Table 2.
Initial settings for algorithm control parameters.
| Algorithm | Parameters | Values |
|---|
| | Population size | 30 |
| All | Max. Iterations | 200 |
| | Executions | 30 |
| TGCOA | No additional parameters | |
| BWOA | No additional parameters | |
| EMA | Cr | [0, 1] |
| | r | [0, 0.2] |
| JSOA | No additional parameters | |
| LCA | f | 1 |
| BO | Scab | 1.5 |
| | r | [0, 1] |
| | Scsb | 1.6 |
| SSA | v | 0.0 |
| ALO | | 10 |
| | w | 2.0–0.6 |
| MAO | | 0.5 |
| | | 0.1 |
| | k | 3 |
| | | 0.5 |
| PSO | w | 0.8 |
| | and | 0.5 |
| DE | F | 0.5 |
| | | 0.9 |
Table 3.
Interpretation of the Average Convergence Rate (ACR) values.
Table 3.
Interpretation of the Average Convergence Rate (ACR) values.
| ACR Value | Interpretation |
|---|
| Optimal |
| Excellent |
| ACR | Good |
| ACR | Slow |
| No Improvement |
Table 4.
Comparison of optimization results obtained for 20 benchmark functions.
Table 4.
Comparison of optimization results obtained for 20 benchmark functions.
| F | Fmin | TGCOA | BWOA | EMA |
|---|
| Best | Ave | Std | Best | Ave | Std | Best | Ave | Std |
|---|
| F1 | 0 | | | | | | | | | |
| F2 | 0 | | | | | | | | | |
| F3 | 0 | | | | | | | | | |
| F4 | 0 | | | | | | | | | |
| F5 | 0 | | | | | | | | | |
| F6 | 0 | | | | | | | | | |
| F7 | 0 | | | | | | | | | |
| F8 | 0 | | | | | | | | | |
| F9 | −1 | | | | | | | | | |
| F10 | 0 | | | | | | | | | |
| F11 | 0 | | | | | | | | | |
| F12 | −4.59 | | | | | | | | | |
| F13 | 0.9 | | | | | | | | | |
| F14 | 0 | | | | | | | | | |
| F15 | 0 | | | | | | | | | |
| F16 | 0 | | | | | | | | | |
| F17 | 0 | | | | | | | | | |
| F18 | 0 | | | | | | | | | |
| F19 | 0 | | | | | | | | | |
| F20 | −1 | | | | | | | | | |
Table 5.
Comparison of optimization results obtained for 20 benchmark functions.
Table 5.
Comparison of optimization results obtained for 20 benchmark functions.
| F | Fmin | JSOA | LCA | BO |
|---|
| Best
| Ave
| Std | Best | Ave | Std | Best | Ave | Std |
|---|
| F1 | 0 | | | | | | | | | |
| F2 | 0 | | | | | | | | | |
| F3 | 0 | | | | | | | | | |
| F4 | 0 | | | | | | | | | |
| F5 | 0 | | | | | | | | | |
| F6 | 0 | | | | | | | | | |
| F7 | 0 | | | | | | | | | |
| F8 | 0 | | | | | | | | | |
| F9 | −1 | | | | | | | | | |
| F10 | 0 | | | | | | | | | |
| F11 | 0 | | | | | | | | | |
| F12 | −4.59 | | | | | | | | | |
| F13 | 0.9 | | | | | | | | | |
| F14 | 0 | | | | | | | | | |
| F15 | 0 | | | | | | | | | |
| F16 | 0 | | | | | | | | | |
| F17 | 0 | | | | | | | | | |
| F18 | 0 | | | | | | | | | |
| F19 | 0 | | | | | | | | | |
| F20 | −1 | | | | | | | | | |
Table 6.
Comparison of optimization results obtained for 20 benchmark functions.
Table 6.
Comparison of optimization results obtained for 20 benchmark functions.
| F | Fmin | SSA | ALO | MAO |
|---|
| Best | Ave | Std | Best | Ave | Std | Best | Ave | Std |
|---|
| F1 | 0 | | | | | | | | | |
| F2 | 0 | | | | | | | | | |
| F3 | 0 | | | | | | | | | |
| F4 | 0 | | | | | | | | | |
| F5 | 0 | | | | | | | | | |
| F6 | 0 | | | | | | | | | |
| F7 | 0 | | | | | | | | | |
| F8 | 0 | | | | | | | | | |
| F9 | −1 | | | | | | | | | |
| F10 | 0 | | | | | | | | | |
| F11 | 0 | | | | | | | | | |
| F12 | −4.59 | | | | | | | | | |
| F13 | 0.9 | | | | | | | | | |
| F14 | 0 | | | | | | | | | |
| F15 | 0 | | | | | | | | | |
| F16 | 0 | | | | | | | | | |
| F17 | 0 | | | | | | | | | |
| F18 | 0 | | | | | | | | | |
| F19 | 0 | | | | | | | | | |
| F20 | −1 | | | | | | | | | |
Table 7.
Comparison of optimization results obtained for 20 benchmark functions.
Table 7.
Comparison of optimization results obtained for 20 benchmark functions.
| F | Fmin | PSO | DE |
|---|
|
Best |
Ave |
Std |
Best |
Ave |
Std |
|---|
| F1 | 0 | | | | | | |
| F2 | 0 | | | | | | |
| F3 | 0 | | | | | | |
| F4 | 0 | | | | | | |
| F5 | 0 | | | | | | |
| F6 | 0 | | | | | | |
| F7 | 0 | | | | | | |
| F8 | 0 | | | | | | |
| F9 | −1 | | | | | | |
| F10 | 0 | | | | | | |
| F11 | 0 | | | | | | |
| F12 | −4.59 | | | | | | |
| F13 | 0.9 | | | | | | |
| F14 | 0 | | | | | | |
| F15 | 0 | | | | | | |
| F16 | 0 | | | | | | |
| F17 | 0 | | | | | | |
| F18 | 0 | | | | | | |
| F19 | 0 | | | | | | |
| F20 | −1 | | | | | | |
Table 8.
Statistical results of the Wilcoxon signed-rank test for the TGCOA versus other algorithms (20 functions, ).
Table 8.
Statistical results of the Wilcoxon signed-rank test for the TGCOA versus other algorithms (20 functions, ).
| TGCOA–BWOA | TGCOA–EMA | TGCOA–JSOA | TGCOA–LCA |
|---|
| p-value | | p-value | | p-value | | p-value |
| 2/7/11 | | 2/0/18 | | 3/6/11 | | 3/0/17 | |
| TGCOA–BO | TGCOA–SSA | TGCOA–ALO | TGCOA–MAO |
| p-value | | p-value | | p-value | | p-value |
| 2/0/18 | | 2/0/18 | | 2/0/18 | | 2/0/18 | |
| TGCOA–PSO | TGCOA–DE |
| p-value | | p-value |
| 2/0/18 | | 1/0/18 | |
Table 9.
All comparison algorithms of the Friedman test for function 20.
Table 9.
All comparison algorithms of the Friedman test for function 20.
| Algorithms | Mean Rank | Overall Rank |
|---|
| TGCOA | 2.45 | 1 |
| JSOA | 2.47 | 2 |
| BWOA | 2.71 | 3 |
| LCA | 4.68 | 4 |
| PSO | 4.95 | 5 |
| EMA | 6.26 | 6 |
| SSA | 6.66 | 7 |
| ALO | 7.24 | 8 |
| BO | 7.95 | 9 |
| MAO | 9.79 | 10 |
| DE | 10.84 | 11 |
Table 10.
Results of dimension 10 for the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
Table 10.
Results of dimension 10 for the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
| Function | TGCOA | BWOA | JSOA | LCA |
|---|
| Best | Ave | Std | Best | Ave | Std | Best | Ave | Std | Best | Ave | Std |
|---|
| C01 | | | | | | | | | | | | |
| C02 | | | | | | | | | | | | |
| C03 | | | | | | | | | | | | |
| C04 | | | | | | | | | | | | |
| C05 | | | | | | | | | | | | |
| C06 | | | | | | | | | | | | |
| C07 | | | | | | | | | | | | |
| C08 | | | | | | | | | | | | |
| C09 | | | | | | | | | | | | |
| C10 | | | | | | | | | | | | |
| C11 | | | | | | | | | | | | |
| C12 | | | | | | | | | | | | |
| C13 | | | | | | | | | | | | |
| C14 | | | | | | | | | | | | |
| C15 | | | | | | | | | | | | |
| C16 | | | | | | | | | | | | |
| C17 | | | | | | | | | | | | |
| C18 | | | | | | | | | | | | |
| C19 | | | | | | | | | | | | |
| C20 | | | | | | | | | | | | |
| C21 | | | | | | | | | | | | |
| C22 | | | | | | | | | | | | |
| C23 | | | | | | | | | | | | |
| C24 | | | | | | | | | | | | |
| C25 | | | | | | | | | | | | |
| C26 | | | | | | | | | | | | |
| C27 | | | | | | | | | | | | |
| C28 | | | | | | | | | | | | |
Table 11.
Results for dimension 30 of the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
Table 11.
Results for dimension 30 of the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
| Function | TGCOA | BWOA | JSOA | LCA |
|---|
| Best | Ave | Std | Best | Ave | Std | Best | Ave | Std | Best | Ave | Std |
|---|
| C01 | | | | | | | | | | | | |
| C02 | | | | | | | | | | | | |
| C03 | | | | | | | | | | | | |
| C04 | | | | | | | | | | | | |
| C05 | | | | | | | | | | | | |
| C06 | | | | | | | | | | | | |
| C07 | | | | | | | | | | | | |
| C08 | | | | | | | | | | | | |
| C09 | | | | | | | | | | | | |
| C10 | | | | | | | | | | | | |
| C11 | | | | | | | | | | | | |
| C12 | | | | | | | | | | | | |
| C13 | | | | | | | | | | | | |
| C14 | | | | | | | | | | | | |
| C15 | | | | | | | | | | | | |
| C16 | | | | | | | | | | | | |
| C17 | | | | | | | | | | | | |
| C18 | | | | | | | | | | | | |
| C19 | | | | | | | | | | | | |
| C20 | | | | | | | | | | | | |
| C21 | | | | | | | | | | | | |
| C22 | | | | | | | | | | | | |
| C23 | | | | | | | | | | | | |
| C24 | | | | | | | | | | | | |
| C25 | | | | | | | | | | | | |
| C26 | | | | | | | | | | | | |
| C27 | | | | | | | | | | | | |
| C28 | | | | | | | | | | | | |
Table 12.
Results for dimension 50 of the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
Table 12.
Results for dimension 50 of the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
| Function | TGCOA | BWOA | JSOA | LCA |
|---|
| Best | Ave | Std | Best | Ave | Std | Best | Ave | Std | Best | Ave | Std |
|---|
| C01 | | | | | | | | | | | | |
| C02 | | | | | | | | | | | | |
| C03 | | | | | | | | | | | | |
| C04 | | | | | | | | | | | | |
| C05 | | | | | | | | | | | | |
| C06 | | | | | | | | | | | | |
| C07 | | | | | | | | | | | | |
| C08 | | | | | | | | | | | | |
| C09 | | | | | | | | | | | | |
| C10 | | | | | | | | | | | | |
| C11 | | | | | | | | | | | | |
| C12 | | | | | | | | | | | | |
| C13 | | | | | | | | | | | | |
| C14 | | | | | | | | | | | | |
| C15 | | | | | | | | | | | | |
| C16 | | | | | | | | | | | | |
| C17 | | | | | | | | | | | | |
| C18 | | | | | | | | | | | | |
| C19 | | | | | | | | | | | | |
| C20 | | | | | | | | | | | | |
| C21 | | | | | | | | | | | | |
| C22 | | | | | | | | | | | | |
| C23 | | | | | | | | | | | | |
| C24 | | | | | | | | | | | | |
| C25 | | | | | | | | | | | | |
| C26 | | | | | | | | | | | | |
| C27 | | | | | | | | | | | | |
| C28 | | | | | | | | | | | | |
Table 13.
Results for dimension 100 of the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
Table 13.
Results for dimension 100 of the IEEE CEC 2017 comparative tests for “Constrained Real-Parameter Optimization”.
| Function | TGCOA | BWOA | JSOA | LCA |
|---|
| Best | Ave | Std | Best | Ave | Std | Best | Ave | Std | Best | Ave | Std |
|---|
| C01 | | | | | | | | | | | | |
| C02 | | | | | | | | | | | | |
| C03 | | | | | | | | | | | | |
| C04 | | | | | | | | | | | | |
| C05 | | | | | | | | | | | | |
| C06 | | | | | | | | | | | | |
| C07 | | | | | | | | | | | | |
| C08 | | | | | | | | | | | | |
| C09 | | | | | | | | | | | | |
| C10 | | | | | | | | | | | | |
| C11 | | | | | | | | | | | | |
| C12 | | | | | | | | | | | | |
| C13 | | | | | | | | | | | | |
| C14 | | | | | | | | | | | | |
| C15 | | | | | | | | | | | | |
| C16 | | | | | | | | | | | | |
| C17 | | | | | | | | | | | | |
| C18 | | | | | | | | | | | | |
| C19 | | | | | | | | | | | | |
| C20 | | | | | | | | | | | | |
| C21 | | | | | | | | | | | | |
| C22 | | | | | | | | | | | | |
| C23 | | | | | | | | | | | | |
| C24 | | | | | | | | | | | | |
| C25 | | | | | | | | | | | | |
| C26 | | | | | | | | | | | | |
| C27 | | | | | | | | | | | | |
| C28 | | | | | | | | | | | | |
Table 14.
Wilcoxon signed-rank test results for CEC 2017 functions, dimension 10, .
Table 14.
Wilcoxon signed-rank test results for CEC 2017 functions, dimension 10, .
| TGCOA–BWOA | TGCOA–JSOA | TGCOA–LCA |
|---|
| p-value | | p-value | | p-value |
| 23/2/3 | | 15/2/11 | | 3/0/25 | |
Table 15.
IEEE CEC 2017 benchmark functions for dimension 10, Friedman test.
Table 15.
IEEE CEC 2017 benchmark functions for dimension 10, Friedman test.
| Algorithms | Mean Rank | Overall Rank |
|---|
| BWOA | 1.46 | 1 |
| JSOA | 2.18 | 2 |
| TGCOA | 2.54 | 3 |
| LCA | 3.82 | 4 |
Table 16.
Wilcoxon signed-rank test results for CEC 2017 functions, dimension 30, .
Table 16.
Wilcoxon signed-rank test results for CEC 2017 functions, dimension 30, .
| TGCOA–BWOA | TGCOA–JSOA | TGCOA–LCA |
|---|
| p-value | | p-value | | p-value |
| 11/2/15 | | 12/2/14 | | 4/0/24 | |
Table 17.
IEEE CEC 2017 benchmark functions for dimension 30, Friedman test.
Table 17.
IEEE CEC 2017 benchmark functions for dimension 30, Friedman test.
| Algorithms | Mean Rank | Overall Rank |
|---|
| TGCOA | 2.04 | 1 |
| BWOA | 2.09 | 2 |
| JSOA | 2.23 | 3 |
| LCA | 3.64 | 4 |
Table 18.
Wilcoxon signed-rank test results for CEC 2017 functions, dimension 50, .
Table 18.
Wilcoxon signed-rank test results for CEC 2017 functions, dimension 50, .
| TGCOA–BWOA | TGCOA–JSOA | TGCOA–LCA |
|---|
| p-value | | p-value | | p-value |
| 11/1/16 | | 12/1/15 | | 5/0/23 | |
Table 19.
IEEE CEC 2017 benchmark functions for dimension 50, Friedman test.
Table 19.
IEEE CEC 2017 benchmark functions for dimension 50, Friedman test.
| Algorithms | Mean Rank | Overall Rank |
|---|
| TGCOA | 2.04 | 1 |
| BWOA | 2.09 | 2 |
| JSOA | 2.20 | 3 |
| LCA | 3.68 | 4 |
Table 20.
Wilcoxon signed-rank test statistical findings for IEEE CEC 2017 benchmark functions for dimension 100 at .
Table 20.
Wilcoxon signed-rank test statistical findings for IEEE CEC 2017 benchmark functions for dimension 100 at .
| TGCOA–BWOA | TGCOA–JSOA | TGCOA–LCA |
|---|
| p-value | | p-value | | p-value |
| 9/2/17 | | 10/2/16 | | 5/0/23 | |
Table 21.
IEEE CEC 2017 benchmark functions for dimension 100, Friedman test.
Table 21.
IEEE CEC 2017 benchmark functions for dimension 100, Friedman test.
| Algorithms | Mean Rank | Overall Rank |
|---|
| TGCOA | 1.93 | 1 |
| BWOA | 2.09 | 2 |
| JSOA | 2.41 | 3 |
| LCA | 3.57 | 4 |
Table 22.
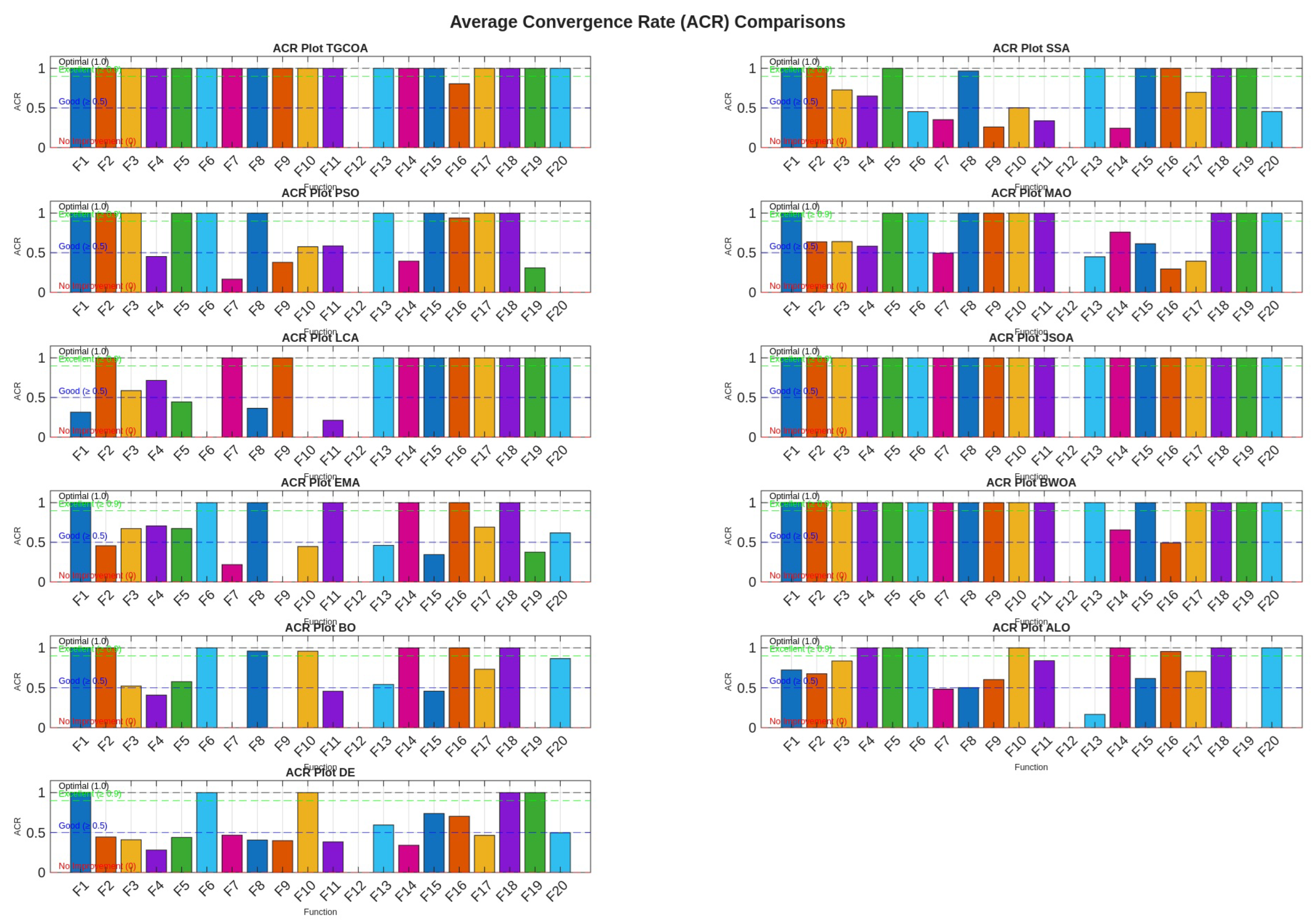
Average ACR values obtained by each algorithm.
Table 22.
Average ACR values obtained by each algorithm.
| Algorithm | Average ACR Value | Category |
|---|
| TGCOA | | Excellent |
| JSOA | 1 | Optimal |
| BWOA | | Excellent |
| LCA | | Good |
| PSO | | Good |
| EMA | | Good |
| SSA | | Good |
| ALO | | Good |
| BO | | Good |
| MAO | | Good |
| DE | | Good |
Table 23.
Best results of tension/compression spring design.
Table 23.
Best results of tension/compression spring design.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| | | | |
| | | | |
| 0 | | | |
| | | | |
| | | | |
| | | | |
Table 24.
Best results of pressure vessel design.
Table 24.
Best results of pressure vessel design.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Table 25.
Best results of three-bar truss design.
Table 25.
Best results of three-bar truss design.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| 0 | 0 | 0 | |
| | | | |
| | | | |
| | | | |
Table 26.
Best results of the gear train design.
Table 26.
Best results of the gear train design.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Table 27.
Best results of the tubular design problem.
Table 27.
Best results of the tubular design problem.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| 0 | | 0 | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Table 28.
Results obtained from welded beam design.
Table 28.
Results obtained from welded beam design.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| 0 | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Table 29.
Results obtained from reinforced concrete beam design.
Table 29.
Results obtained from reinforced concrete beam design.
| Variables | TGCOA | BWOA | JSOA | LCA |
|---|
| | | | |
| | | | |
| | | | |
| 0 | 0 | 0 | |
| | | | |
| | | | |