Stability Analysis and Finite Difference Approximations for a Damped Wave Equation with Distributed Delay

Abstract

This paper presents a fully implicit finite difference scheme for the numerical approximation of a wave equation featuring strong damping and a distributed delay term. The discretization employs second-order accurate approximations in both time and space. Although implicit, the scheme does not ensure unconditional stability due to the nonlocal nature of the delayed damping. To address this, we perform a stability analysis based on Rouché’s theorem from complex analysis and derive a sufficient condition for asymptotic stability of the discrete system. The resulting criterion highlights the interplay among the discretization parameters, the damping coefficient, and the delay kernel. Two quadrature techniques, the composite trapezoidal rule (CTR) and the Gaussian quadrature rule (GQR), are employed to approximate the convolution integral. Numerical experiments validate the theoretical predictions and illustrate both stable and unstable dynamics across different parameter regimes.

1. Introduction

Time delays are inherent in many natural and engineered systems, often arising from propagation effects, memory, or feedback mechanisms. These delays play a pivotal role in numerous applications, including wave propagation, structural dynamics, and signal processing, where their influence on system behavior is both significant and unavoidable. Similar delay-driven phenomena are also encountered in control theory and thermodynamics, particularly in the modeling of materials exhibiting memory-dependent heat conduction; see, for instance, refs. [1,2,3].

Given their wide-ranging impact, delayed partial differential equations (DPDEs) have attracted considerable research attention, especially in regard to their well-posedness, stability properties, and long-time behavior. Foundational work in this area has focused on the stabilization of wave and heat equations under various forms of delay; see [4,5,6,7,8,9,10,11,12], and references therein.

Parallel to theoretical investigations, the development of accurate and stable numerical methods for delayed differential equations (DDEs) has received sustained attention. For ODEs with delay, extensive work has been compiled in [13,14,15,16]. For PDEs, numerical techniques such as explicit and implicit finite difference methods, compact schemes, and weighted approaches have been actively explored [17,18,19,20,21,22,23].

Garcia et al. [18] proposed and analyzed an explicit finite difference method for a delayed diffusion equation of the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \frac{\partial u}{\partial t}}(t,x)=a^2{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}(t,x)+a^2{c}^2{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}(t-\tau ,x),\hfill & t>\tau ,0\le x\le l,\hfill \\ u(t,x)=\varphi (t,x),\hfill & 0\le t\le \tau ,0\le x\le l,\hfill \\ u(t,0)=u(t,l)=0,\hfill & t\ge 0,\hfill \end{array}\right.\end{array}$$

(1)

where $\tau >0$, $a\ne 0$, and $0<c<1$ are constants. Their work demonstrated convergence and asymptotic stability. This analysis was extended in [19] to an implicit scheme for the same model.

Further progress was made by Zhang et al. [23], who studied the asymptotic behavior of a compact $\theta$-method for generalized delay-diffusion equations. Similarly, Lekomtsev and Pimenov [21] developed a weighted scheme addressing variable thermal conductivity, with a focus on stability and convergence.

Li et al. [24] investigated the long-time behavior of non-Fickian delay reaction–diffusion equations incorporating both memory effects in the diffusion term and discrete delays in the reaction component. Their model takes the form of a Volterra integro-differential equation with exponentially decaying memory kernels. They established energy estimates, dissipativity, and asymptotic stability of the continuous problem, and showed that their implicit numerical scheme preserved the qualitative properties of the exact solution. In their formulation, the delay acts directly on the solution u, rather than on its time derivative. Their results highlight the challenges and importance of treating delay-diffusion systems with memory. This contrasts with the present work, where the delay is applied to the time derivative and is approximated via quadrature-based methods, leading to more intricate numerical stability considerations.

In [25], Xie and Zhang proposed a high-order compact multistep alternating direction implicit (ADI) scheme for solving two-dimensional nonlinear delayed reaction–diffusion equations (NDREs) with variable coefficients. Their model is provided by the following:

$${\displaystyle \frac{\partial u}{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\left(a\left(x\right){\displaystyle \frac{\partial u}{\partial x}}\right)-{\displaystyle \frac{\partial }{\partial y}}\left(b\left(y\right){\displaystyle \frac{\partial u}{\partial y}}\right)=f(u(x,y,t),u(x,y,t-s),x,y,t),$$

where $s>0$ is a constant delay. As in [24], the delay term here acts directly on the state u, and not on its time derivative. This structure simplifies the numerical treatment. Their ADI scheme achieves second-order accuracy in time and fourth-order in space, and is supported by rigorous convergence and stability analysis.

Qin et al. [26] introduced a linearized compact ADI scheme for semilinear parabolic problems with distributed delay. The governing equation is of the following form:

$${\displaystyle \frac{\partial u}{\partial t}}-a\Delta u=f\left(t,\mathbf{x},u(t,\mathbf{x}),{\int }_{t-\tau }^{t}g(t,s,u(s,\mathbf{x}))ds\right),$$

where the delay term again acts on the solution u rather than on its derivative. This structure permits a direct numerical approximation of the evolution term. In contrast, the model studied in this work features a delay applied to the time derivative of u, which introduces significant challenges both analytically and numerically, as it directly impacts the leading-order temporal behavior of the solution. Our work fills this gap by developing a discrete framework tailored to such delayed dynamics, along with a Rouché-based stability analysis suited for the resulting high-order characteristic polynomials.

In this paper, we investigate the stability criteria for a wave equation that incorporates both strong damping and a distributed delay term, modeled by the following system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle u_{tt}(x,t)=u_{xx}(x,t)+\mu u_{txx}(x,t)-{\int }_0^{t}h\left(s\right)u_t(x,t-s)ds,}\hfill & 0\le x\le L,t>0,\hfill \\ u(0,t)=u(L,t)=0,\hfill & t>0,\hfill \\ u(x,0)=u_0\left(x\right),u_t(x,0)=u_1\left(x\right),\hfill & 0\le x\le L,\hfill \end{array}\right.\end{array}$$

(2)

where $u_0$ and $u_1$ are prescribed initial data belonging to appropriate functional spaces. The parameter $\mu >0$ quantifies the strength of the strong damping, while the kernel $h:[0,\infty )\to \mathbb{R}$ is assumed to be non-increasing and characterizes the effect of the distributed delay. Specific assumptions on the regularity and decay properties of h will be introduced later to support the subsequent numerical analysis.

While DPDEs involving delays in the state variable u have been widely studied, and certain models have addressed delays in spatial derivatives such as $u_x$ or $u_{xx}$, the inclusion of a delay in the time derivative $u_t$ presents additional challenges. This type of delay directly affects the temporal dynamics of the system, introducing implicit memory effects that complicate both numerical discretization and stability analysis, particularly within finite difference frameworks. Most existing numerical studies have focused on models with discrete time delays, where the delayed term depends on a fixed past time. In contrast, distributed delay models, which depend on the entire past history of the solution, have received comparatively less attention in the numerical literature. These models are often more realistic in applications such as viscoelasticity, biological systems, and heat transfer with memory, where the influence of the past cannot be reduced to a single instant. However, from a numerical standpoint, the presence of convolution-type integral terms with time-dependent kernels introduces significant complexity and requires careful treatment. Specialized quadrature techniques and stability analyses are essential to address these challenges. To the best of our knowledge, the numerical approximation of wave equations with strong damping and distributed delay in the time derivative has not been extensively explored, and this work seeks to contribute to that direction.

In [17], the author presented both theoretical and numerical analyses of the symbiotic stability of System (2), where the distributed delay term was replaced with a discrete delay. A fully implicit finite difference scheme was employed [27], and Jury’s stability criterion [28] was used to derive a sufficient condition ensuring the stability of the discrete system.

In the present work, we adopt a similar discretization strategy to that presented in [17], applying an implicit finite difference method to System (2). However, in contrast to [17], which employed Jury’s stability criterion, our stability analysis is based on Rouché’s theorem (see Section 4.3.2). This theorem is used to localize the roots of the characteristic polynomial associated with the amplification matrix and ensure they lie strictly within the unit disk.

The use of Rouché’s theorem [29] is particularly motivated by the structure of the resulting polynomial, which is of high order and includes more than three nonzero terms. Such complexity renders standard techniques, like the Schur criterion or similar root-location tests for low-degree polynomials, ineffective or inapplicable.

An additional challenge arises in the numerical treatment of the distributed delay term, which involves a convolution integral. To address this, we consider two quadrature strategies. The first is the composite trapezoidal rule (CTR) [30], valued for its simplicity and reasonable accuracy when the integrand is smooth or slowly varying. The second is Gaussian quadrature (GQR) [30], which achieves higher-order accuracy by evaluating the integrand at optimally chosen points within each subinterval, making it particularly effective when the delay kernel or the time derivative exhibits sharp variation.

In light of these challenges and gaps, this work introduces a second-order fully implicit finite difference scheme for a damped wave equation with distributed delay acting on the time derivative, a setting that remains largely unexplored in the numerical literature. The convolution term is approximated using both the composite trapezoidal rule and Gaussian quadrature rule, and the stability of the resulting scheme is rigorously analyzed using Rouché’s theorem. This leads to a novel sufficient condition ensuring that all eigenvalues of the amplification matrix lie within the unit disk. Numerical experiments confirm the theoretical findings and show that asymptotic decay may still occur even when the sufficient condition is not strictly satisfied.

The remainder of the paper is structured as follows. In Section 2, we review the quadrature methods used to approximate the delay integral and introduce Rouché’s theorem, which forms the foundation for our root localization and stability analysis. Section 3 presents the construction of the fully discrete finite difference scheme for solving System (2), extending ideas from earlier works such as [18,19]. Section 4 contains the detailed stability analysis, in which Rouché’s theorem is applied to derive sufficient conditions for asymptotic stability. In Section 5, we present numerical experiments that illustrate the solution behavior and compare the effectiveness of CTR and GQR. Finally, Section 6 summarizes the main findings and outlines directions for future research.

2. Preliminaries

This section outlines key numerical tools used in the approximation of the model Problem (2). We begin by reviewing the quadrature rules employed to approximate the distributed delay integral term. We then present Rouché’s theorem, which serves as the foundation for our stability analysis.

2.1. Numerical Quadrature Rules

To approximate the integral term appearing in the delayed damping, we consider two standard quadrature techniques: the composite trapezoidal rule (CTR) and the Gaussian quadrature rule (GQR). These methods differ in terms of accuracy, implementation complexity, and effectiveness, depending on the regularity of the integrand. In this subsection, we briefly review the essential ideas behind each method.

Composite trapezoidal rule (CTR) [30]: The composite trapezoidal rule is a classical quadrature method used to approximate definite integrals by evaluating the integrand at a finite number of points within the integration interval. Specifically, let $[a,b]$ be the interval of integration, and let $a=x_0<x_1<\cdots <x_r=b$ be a uniform partition such that $x_{i+1}-x_i=\delta x$ for $i=0,\dots ,r-1$. The CTR approximation of the integral of a function $f\left(x\right)$ over $[a,b]$ is provided by the following:

$${\int }_a^{b}f\left(x\right)dx\approx \sum _{i=0}^r{\omega }_{i}f\left(x_i\right),$$

where the weights ${\omega }_i$ are defined as follows:

$${\omega }_i=\left\{\begin{array}{cc}{\displaystyle \frac{\delta x}{2}},\hfill & \mathrm{if}i=0\mathrm{or}i=r,\hfill \\ \delta x,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

This method is second-order accurate and particularly effective when the integrand is smooth or varies slowly. Its simplicity and compatibility with uniform discretizations make it a natural and efficient choice in finite difference schemes.

Gaussian quadrature rule (GQR) [30]: Gaussian quadrature is a numerical integration technique that achieves high accuracy by optimally choosing both the evaluation points (nodes) and corresponding weights within each integration interval. Unlike the trapezoidal rule, which uses equally spaced nodes, Gaussian quadrature selects nodes that maximize the degree of exactness for polynomials.

In this work, we use the two-point Gaussian quadrature rule, which exactly integrates polynomials of degree up to three. Let $[a,b]$ be the interval of integration. The two-point Gaussian quadrature approximation of ${\int }_a^{b}f\left(x\right)dx$ is provided by the following:

$${\int }_a^{b}f\left(x\right)dx\approx {\displaystyle \frac{b-a}{2}}\sum _{i=1}^2{w}_{i}f\left(x_i\right),$$

where the nodes and weights (defined on the reference interval $[-1,1]$) are

$$x_{1,2}={\displaystyle \frac{a+b}{2}}\pm {\displaystyle \frac{b-a}{2\sqrt{3}}},w_1=w_2=1.$$

This method provides greater accuracy than the composite trapezoidal rule for the same number of function evaluations, especially when the integrand varies rapidly within the integration interval. However, it requires evaluating the integrand at off-grid points, which may necessitate interpolation in time-dependent problems.

2.2. Rouché’s Theorem for Root Localization

Rouché’s theorem is a classical result from complex analysis used to determine whether two holomorphic functions have the same number of zeros inside a given closed contour. This tool is especially effective when the dominant term of a polynomial is isolated, and the remaining terms can be treated as perturbations.

 Theorem 1 

(Rouché’s theorem [29], p. 192). Suppose that f and g are holomorphic in an open set containing a circle $\mathcal{C}$ and its interior. If

$$|f(z)|>|g(z)|\mathrm{for}\mathrm{all}z\in \mathcal{C},$$

then f and $f+g$ have the same number of zeros inside the circle $\mathcal{C}$, counted with multiplicity.

For detailed background, we refer the reader to Stein and Shakarchi [29].

In this work, we apply Rouché’s theorem on the unit circle $C=\{z\in \mathbb{C}:|z|=1\}$ to analyze the root locations of characteristic polynomials arising from fully discretized schemes. We show that under suitable mesh-dependent conditions, all roots lie strictly inside the unit disk, ensuring asymptotic stability.

3. Finite Difference Scheme

Building on the foundational work in [18], we construct a finite difference scheme to approximate the solution of System (2). The spatial and temporal domains are discretized uniformly, and the resulting fully discrete scheme is subsequently reformulated into a two-level system (see [31]) to facilitate the stability analysis presented in the next section.

Spatial discretization: Let $L>0$, and define the spatial step size $\Delta x={\displaystyle \frac{L}{P}}$ for some integer P. The interval $[0,L]$ is divided into P uniform subintervals of length $\Delta x$, with grid points $x_i=i\Delta x$ for $i=0,1,\dots ,P$.

Time discretization: The time domain $(0,\infty )$ is truncated to $(0,T]$ for a sufficiently large $T>0$. This interval is partitioned into M uniform subintervals using a time step size $\Delta t={\displaystyle \frac{T}{M}}$, resulting in discrete time levels $t_n=n\Delta t$ for $n=0,1,\dots ,M$.

Finite difference approximations: We denote $u_i^n\approx u(x_i,t_n)=u(i\Delta x,n\Delta t)$ by the approximation of the continuous solution $u(x,t)$ at the grid points. All partial derivatives appearing in (2) are approximated using second-order central finite differences:

$$\begin{array}{cc}\hfill u_{tt}(x_i,t_n)& \approx {\displaystyle \frac{u_i^{n-1}-2u_i^n+u_i^{n+1}}{{(\Delta t)}^2}},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill u_{xx}(x_i,t_n)& \approx {\displaystyle \frac{u_{i-1}^n-2u_i^n+u_{i+1}^n}{{(\Delta x)}^2}},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill u_{txx}(x_i,t_n)& \approx {\displaystyle \frac{1}{2(\Delta t){(\Delta x)}^2}}\left[(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1})-(u_{i-1}^{n-1}-2u_i^{n-1}+u_{i+1}^{n-1})\right].\hfill \end{array}$$

(5)

Approximation of the delayed term: The distributed delay term in (2), evaluated at the grid point $(x_i,t_n)$, is provided by the following:

$${\int }_0^{t_n}h\left(s\right)u_t(x_i,t_n-s)ds={\int }_0^{t_n}h(t_n-s)u_t(x_i,s)ds.$$

To approximate this term, we apply numerical quadrature in time to the integral and approximate the time derivative $u_t(x_i,s)$ either using finite difference formulas (when s lies on the time grid) or via interpolation (when s falls between time levels).

In this work, we consider two quadrature strategies for evaluating the integral: the composite trapezoidal rule (CTR) and the Gaussian quadrature rule (GQR), as described below.

Composite trapezoidal rule (CTR): For each $n=0,1,\dots ,M$, the interval $[0,t_n]$ is partitioned uniformly into $r+1$ nodes with quadrature step size $\delta t$, such that

$$0=t_0<t_1<\cdots <t_r=t_n.$$

 Remark 1. 

To simplify implementation, we take $\delta t=\Delta t$, which leads to $r=n$ at each time step. In this case, the quadrature nodes $t_j=j\Delta t$ align exactly with the main time discretization grid.

The integral is approximated using the composite trapezoidal rule:

$$\begin{array}{cc}\hfill {\int }_0^{t_n}h(t_n-s)u_t(x_i,s)ds& \approx \sum _{j=0}^n{\omega }_{j}h(t_n-t_j)u_t(x_i,t_j),\hfill \end{array}$$

(6)

where the quadrature weights ${\omega }_j$ are provided by

$$\begin{array}{c}\hfill {\omega }_j=\left\{\begin{array}{cc}\Delta t/2,\hfill & \mathrm{if}j=0\mathrm{or}j=n,\hfill \\ \Delta t,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(7)

The time derivative $u_t(x_i,t_j)$ is approximated using a second-order central difference:

$$u_t(x_i,t_j)\approx {\displaystyle \frac{u_i^{j+1}-u_i^{j-1}}{2\Delta t}}.$$

Substituting this into the quadrature approximation yields the following:

$$\begin{array}{cc}\hfill {\int }_0^{t_n}h(t_n-s)u_t(x_i,s)ds\approx & \sum _{j=0}^n{\displaystyle \frac{{\omega }_j}{2\Delta t}}h(t_n-t_j)\left(u_i^{j+1}-u_i^{j-1}\right)\hfill \\ \hfill =& {\displaystyle \frac{h\left(t_n\right)}{4}}\left(u_i^1-u_i^{-1}\right)+{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}h(t_n-t_j)\left(u_i^{j+1}-u_i^{j-1}\right)\hfill \\ \hfill & +{\displaystyle \frac{h\left(0\right)}{4}}\left(u_i^{n+1}-u_i^{n-1}\right).\hfill \end{array}$$

We define ${\mathcal{R}}_i^n[h,u]$ to collect the summation terms in the CTR approximation from interior quadrature nodes, as well as the portion of the boundary contribution at $t_n$ that involves known values. Specifically,

$$\begin{array}{c}\hfill {\mathcal{R}}_i^n[h,u]:={\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}h(t_n-t_j)\left(u_i^{j+1}-u_i^{j-1}\right)-{\displaystyle \frac{h\left(0\right)}{4}}{u}_i^{n-1},\end{array}$$

(8)

so that the full approximation of the integral becomes

$$\begin{array}{c}\hfill {\int }_0^{t_n}h(t_n-s)u_t(x_i,s)ds\approx {\displaystyle \frac{h\left(t_n\right)}{4}}\left(u_i^1-u_i^{-1}\right)+{\mathcal{R}}_i^n[h,u]+{\displaystyle \frac{h\left(0\right)}{4}}{u}_i^{n+1}.\end{array}$$

(9)

Gaussian quadrature rule (GQR): Using the two-point Gaussian quadrature rule on the interval $[0,t_n]$, the distributed delay term at the grid point $(x_i,t_n)$ is approximated as follows:

$$\begin{array}{c}\hfill {\int }_0^{t_n}h(t_n-s)u_t(x_i,s)ds\approx {\mathcal{Q}}_i^n[h,u_t]:={\displaystyle \frac{t_n}{2}}\sum _{j=1}^2{w}_{j}h(t_n-{\xi }_j)u_t(x_i,{\xi }_j),\end{array}$$

(10)

where the quadrature weights and nodes are provided by the following:

$$w_1=w_2=1,{\xi }_1={\displaystyle \frac{t_n}{2}}\left(1-{\displaystyle \frac{1}{\sqrt{3}}}\right),{\xi }_2={\displaystyle \frac{t_n}{2}}\left(1+{\displaystyle \frac{1}{\sqrt{3}}}\right).$$

Since the quadrature nodes ${\xi }_j$ generally do not coincide with the discrete time levels, the time derivative $u_t(x_i,{\xi }_j)$ cannot be directly approximated using finite differences. Instead, it is estimated via interpolation from known grid values. A simple piecewise linear interpolation may be used, or higher-order interpolation can be adopted for improved accuracy (see Section 5).

We are now ready to introduce the fully discretized form of the PDE using the approximations developed above.

3.1. Fully Discretized Form of the PDE Using CTR

Applying the finite difference and CTR-based approximations described above to the PDE (2), evaluated at the grid point $(x_i,t_n)$ for $n>0$, yields the following discrete equation:

$$\begin{array}{cc}\hfill 2{(\Delta x)}^2{u}_i^{n-1}-4{(\Delta x)}^2{u}_i^n+2{(\Delta x)}^2{u}_i^{n+1}& =2{(\Delta t)}^2\left(u_{i-1}^n-2u_i^n+u_{i+1}^n\right)\hfill \\ \hfill & +\mu \Delta t\left(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1}\right)\hfill \\ \hfill & -\mu \Delta t\left(u_{i-1}^{n-1}-2u_i^{n-1}+u_{i+1}^{n-1}\right)\hfill \\ \hfill & +\beta h\left(t_n\right)\left(u_i^1-u_i^{-1}\right)\hfill \\ \hfill & +4\beta {\mathcal{R}}_i^n[h,u]\hfill \\ \hfill & +\beta h\left(0\right)u_i^{n+1},\hfill \end{array}$$

where we define $\beta :={(\Delta t)}^2{(\Delta x)}^2/2$. Rearranging the terms yields the update formula for $u_i^{n+1}$:

$$\begin{array}{cc}\hfill -\mu \Delta t{u}_{i-1}^{n+1}& +\left[2\left(\mu \Delta t+{(\Delta x)}^2\right)-\beta h\left(0\right)\right]u_i^{n+1}-\mu \Delta t{u}_{i+1}^{n+1}=-\mu \Delta t{u}_{i-1}^{n-1}\hfill \\ & +2(\mu \Delta t-{(\Delta x)}^2)u_i^{n-1}-\mu \Delta t{u}_{i+1}^{n-1}+2{(\Delta t)}^2(u_{i-1}^n+u_{i+1}^n)\hfill \\ \hfill & +4\left({(\Delta x)}^2-{(\Delta t)}^2\right)u_i^n+\beta h\left(t_n\right)\left(u_i^1-u_i^{-1}\right)+4\beta {\mathcal{R}}_i^n[h,u].\hfill \end{array}$$

(11)

Define

$$U^n:={[u_1^n,u_2^n,\dots ,u_{P-1}^n]}^T\in {\mathbb{R}}^{P-1},$$

and let

$$\begin{array}{c}\hfill V^n\left(h\right):=4\beta {[{\mathcal{R}}_1^n[h,u],{\mathcal{R}}_2^n[h,u],\dots ,{\mathcal{R}}_{P-1}^n[h,u]]}^T\in {\mathbb{R}}^{P-1},\end{array}$$

(12)

where ${\mathcal{R}}_i^n[h,u]$ is as defined in (8). Note that $V^0\left(h\right)=0$, with no delay at time $t=0$. Then, the recurrence (11) can be written in compact matrix form:

$$\begin{array}{c}\hfill A{U}^{n+1}=C{U}^n+B{U}^{n-1}+V^n\left(h\right)+{\alpha }_n(U^1-U^{-1}),n\ge 1,\end{array}$$

(13)

where ${\alpha }_n=\beta h\left(t_n\right)$, and A, B, and C are tridiagonal matrices provided by the following:

$$\begin{array}{cc}\hfill A& :=\mathrm{tridiag}(-\mu \Delta t,\left[2\left(\mu \Delta t+{(\Delta x)}^2\right)-\beta h\left(0\right)\right],-\mu \Delta t),\hfill \\ \hfill B& :=\mathrm{tridiag}(-\mu \Delta t,2(\mu \Delta t-{(\Delta x)}^2),-\mu \Delta t),\hfill \\ \hfill C& :=\mathrm{tridiag}(2{(\Delta t)}^2,4({(\Delta x)}^2-{(\Delta t)}^2),2{(\Delta t)}^2).\hfill \end{array}$$

(14)

Furthermore, we assume that the delay kernel $h\left(t\right)$ satisfies the following condition:

$$\begin{array}{c}\hfill \Delta t<\sqrt{{\displaystyle \frac{2}{h\left(0\right)}}}.\end{array}$$

(15)

Under the above assumption, the matrix A is symmetric positive definite, and hence invertible. This property will be justified later in the analysis.

 Remark 2. 

Assumption (15) is practically justified. Since the delay kernel $h\left(t\right)$ is typically known in advance and is non-increasing, the condition places a constraint on the time step $\Delta t$ based on the maximum contribution of the kernel at $t=0$. In practice, choosing sufficiently small time steps ensures that this condition is easily satisfied, making it both realistic and implementable in numerical settings (see Section 5 for details).

Finite difference approximations of the initial and boundary conditions: The initial and boundary conditions in (2) are discretized as follows:

$$\begin{array}{cc}\hfill u_0^n=u_P^n=0,& n=0,\dots ,M,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill u_i^0=u_0\left(x_i\right),& i=1,\dots ,P-1,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill u_i^1-u_i^{-1}=2\Delta t{u}_1\left(x_i\right),& i=1,\dots ,P-1.\hfill \end{array}$$

(18)

We define the initial vectors as

$$U^0:={[u_1^0,u_2^0,\dots ,u_{P-1}^0]}^T\in {\mathbb{R}}^{P-1}$$

and

$$\begin{array}{c}\hfill F^0:=U^1-U^{-1}=2\Delta t{[u_1\left(x_1\right),u_1\left(x_2\right),\dots ,u_1\left(x_{P-1}\right)]}^T\in {\mathbb{R}}^{P-1}.\end{array}$$

(19)

Substituting (19) into (13),the matrix recurrence becomes

$$\begin{array}{c}\hfill A{U}^{n+1}=C{U}^n+B{U}^{n-1}+V^n\left(h\right)+{\alpha }_n{F}^0,n\ge 0.\end{array}$$

(20)

 Remark 3. 

The vector $F^0$ depends solely on the initial velocity data $u_1\left(x\right)$ and remains fixed for all time steps.

At the initial time level $t_0=0$, the distributed delay term vanishes, as the system has no history prior to the initial time. However, the discretized scheme includes a term $\beta h\left(0\right)U^1$ on the left-hand side. To accommodate this, we define a modified matrix $A_0:=A+\beta h\left(0\right)I$, and the equation at $n=0$ becomes

$$A_0{U}^1=B{U}^{-1}+C{U}^0+{\alpha }_0{F}^0,$$

where ${\alpha }_0=\beta h\left(0\right)$, and $F^0$ is defined in (19). Substituting $U^{-1}=U^1-F^0$ yields the following form:

$$\begin{array}{c}\hfill (A_0-B)U^1=C{U}^0+({\alpha }_{0}I-B)F^0.\end{array}$$

(21)

The modified matrix System (21) contains only known quantities from the initial data and can therefore be solved explicitly for $U^1$. This provides a consistent and accurate starting point for advancing the scheme from $n=1$ onward.

 Remark 4. 

The matrix $A_0-B$ is diagonal, with entries $4{(\Delta x)}^2-\beta h\left(0\right)$. It is nonsingular provided that $\beta h\left(0\right)\ne 4{(\Delta x)}^2$, or equivalently, ${(\Delta t)}^{2}h\left(0\right)\ne 8$. This condition is automatically satisfied under the assumption given in (15), which is more restrictive and typically holds for standard discretization parameters. It ensures that equation (21) can be solved uniquely for $U^1$.

We conclude that the fully discretized form of the PDE using the CTR approximation is as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}(A_0-B)U^1=C{U}^0+({\alpha }_{0}I-B)F^0,\hfill \\ A{U}^{n+1}=C{U}^n+B{U}^{n-1}+V^n\left(h\right)+{\alpha }_n{F}^0,n\ge 1,\hfill \end{array}\right.\end{array}$$

(22)

where ${\alpha }_n=\beta h\left(t_n\right)$, and the delay vector $V^n\left(h\right)$ and the initial vector $F^0$ are provided in (12) and (19), respectively.

To express this recurrence in a uniform matrix form, we introduce a piecewise-defined vector $W^n\in {\mathbb{R}}^{P-1}$ for $n\ge -2$ as follows:

$$\begin{array}{c}\hfill W^n:=\left\{\begin{array}{cc}{U}^n,\hfill & n\ge 0,\hfill \\ V^n\left(h\right),\hfill & n=-1,\hfill \\ F^0,\hfill & n=-2,\hfill \end{array}\right.\end{array}$$

(23)

and define the block vector as

$${\mathcal{U}}^n:=\left[\begin{array}{c}{W}^n\\ W^{n-1}\\ ⋮\\ W^0\\ W^{-1}\\ W^{-2}\end{array}\right]\in {\mathbb{R}}^{(n+3)(P-1)},$$

which stacks $n+3$ vectors, each of size ${\mathbb{R}}^{P-1}$, into a single block column vector. In addition, we define the block diagonal matrix as follows:

$$\mathcal{A}:=\mathrm{diag}(A,I,I,\dots ,I)\in {\mathbb{R}}^{(n+3)(P-1)\times (n+3)(P-1)},$$

where the first block is the system matrix $A\in {\mathbb{R}}^{(P-1)\times (P-1)}$, and the remaining $n+2$ blocks are identity matrices of the same size. We then construct the block matrix:

$$\begin{array}{c}\hfill \mathrm{\Phi }:=\left[\begin{array}{ccccccc}C& B& 0& \cdots & 0& I& {\alpha }_{n}I\\ I& 0& 0& \cdots & 0& 0& 0\\ 0& I& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & I& 0& 0\\ 0& 0& 0& \cdots & 0& I& 0\end{array}\right]\in {\mathbb{R}}^{(n+3)(P-1)\times (n+3)(P-1)}.\end{array}$$

(24)

The second equation in (22) can now be equivalently written as follows:

$$\begin{array}{c}\hfill \mathcal{A}{\mathcal{U}}^{n+1}=\mathrm{\Phi }{\mathcal{U}}^n,n\ge 1.\end{array}$$

(25)

The block matrix $\mathcal{A}$, being block-diagonal with invertible blocks, is invertible. We define

$$\mathrm{\Psi }:={\mathcal{A}}^{-1}\mathrm{\Phi }$$

so that (25) becomes the recurrence

$$\begin{array}{c}\hfill {\mathcal{U}}^{n+1}=\mathrm{\Psi }{\mathcal{U}}^n,n\ge 1.\end{array}$$

(26)

3.2. Fully Discretized Form of the PDE Using GQR

Recalling the GQR-based delay approximation ${\mathcal{Q}}_i^n[h,u_t]$ from (10), the fully discretized equation becomes the following:

$$\begin{array}{cc}\hfill -\mu \Delta t{u}_{i-1}^{n+1}& +2\left(\mu \Delta t+{(\Delta x)}^2\right)u_i^{n+1}-\mu \Delta t{u}_{i+1}^{n+1}=-\mu \Delta t{u}_{i-1}^{n-1}\hfill \\ \hfill & +2(\mu \Delta t-{(\Delta x)}^2)u_i^{n-1}-\mu \Delta t{u}_{i+1}^{n-1}+2{(\Delta t)}^2(u_{i-1}^n+u_{i+1}^n)\hfill \\ \hfill & +4\left({(\Delta x)}^2-{(\Delta t)}^2\right)u_i^n+4\beta {\mathcal{Q}}_i^n[h,u_t].\hfill \end{array}$$

(27)

We define the delay vector as

$$\begin{array}{c}\hfill V_{*}^n\left(h\right):=4\beta {[{\mathcal{Q}}_1^n[h,u_t],{\mathcal{Q}}_2^n[h,u_t],\dots ,{\mathcal{Q}}_{P-1}^n[h,u_t]]}^T\in {\mathbb{R}}^{P-1}.\end{array}$$

(28)

Hence, the fully discretized system in matrix form using GQR becomes the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}(A_0-B)U^1=C{U}^0-B{F}^0,\hfill \\ A_0{U}^{n+1}=C{U}^n+B{U}^{n-1}+V_{*}^n\left(h\right),n\ge 1,\hfill \end{array}\right.\end{array}$$

(29)

where the matrices A, B, and C are the tridiagonal matrices defined in (14), and the modified matrix $A_0:=A+\beta h\left(0\right)I$.

We now reformulate the GQR-based scheme as a first-order recurrence system in an extended block space (i.e., computing the current block state from the previous one), following a similar approach to the CTR-based case. We begin by introducing a piecewise-defined vector $W_{*}^n\in {\mathbb{R}}^{P-1}$ for $n\ge -1$, defined as follows:

$$\begin{array}{c}\hfill W_{*}^n:=\left\{\begin{array}{cc}{U}^n,\hfill & n\ge 0,\hfill \\ V_{*}^n\left(h\right),\hfill & n=-1,\hfill \end{array}\right.\end{array}$$

(30)

where $V_{*}^n\left(h\right)\in {\mathbb{R}}^{P-1}$ is the delay vector defined in (28) using the Gaussian quadrature rule. Then, we define the block vector:

$${\mathcal{U}}_{*}^n:=\left[\begin{array}{c}{W}_{*}^n\\ W_{*}^{n-1}\\ ⋮\\ W_{*}^{-1}\end{array}\right]\in {\mathbb{R}}^{(n+2)(P-1)},$$

which stacks $n+2$ vectors, each of dimension ${\mathbb{R}}^{P-1}$, into a single column block vector. Additionally, we define the block diagonal matrix:

$${\mathcal{A}}_{*}:=\mathrm{diag}(A_0,I,I,\dots ,I)\in {\mathbb{R}}^{(n+2)(P-1)\times (n+2)(P-1)},$$

where $A_0\in {\mathbb{R}}^{(P-1)\times (P-1)}$ is the system matrix used in the GQR formulation, and the remaining diagonal blocks are identity matrices of the same size. Next, we construct the block matrix ${\mathrm{\Phi }}_{*}^n\in {\mathbb{R}}^{(n+2)(P-1)\times (n+2)(P-1)}$, which encodes the recurrence structure:

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_{*}:=\left[\begin{array}{ccccccc}C& B& 0& \cdots & 0& 0& I\\ I& 0& 0& \cdots & 0& 0& 0\\ 0& I& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & I& 0& 0\\ 0& 0& 0& \cdots & 0& I& 0\end{array}\right].\end{array}$$

(31)

The second equation in (29) can now be written in compact matrix form as follows:

$$\begin{array}{c}\hfill {\mathcal{A}}_{*}{\mathcal{U}}_{*}^{n+1}={\mathrm{\Phi }}_{*}{\mathcal{U}}_{*}^n,n\ge 1.\end{array}$$

(32)

Since ${\mathcal{A}}_{*}$ is block diagonal with invertible blocks (under condition (15)), it is itself invertible. We define

$${\mathrm{\Psi }}_{*}:={\mathcal{A}}_{*}^{-1}{\mathrm{\Phi }}_{*}$$

so that (32) becomes the following recurrence:

$$\begin{array}{c}\hfill {\mathcal{U}}_{*}^{n+1}={\mathrm{\Psi }}_{*}{\mathcal{U}}_{*}^n,n\ge 1.\end{array}$$

(33)

Our objective in the next section is to analyze the spectral properties of the update matrices $\mathrm{\Psi }$ and ${\mathrm{\Psi }}_{*}$ and establish that all their eigenvalues lie strictly inside the unit disk under suitable conditions.

4. Asymptotic Stability of the Fully Discrete Scheme

In this section, we establish conditions on the mesh parameters that ensure the asymptotic stability of fully discretized Systems (26) and (33), corresponding to the CTR- and GQR-based approximations of the delay integral term, respectively. In particular, we derive sufficient criteria under which all eigenvalues of the associated amplification matrices $\mathrm{\Psi }$ and ${\mathrm{\Psi }}_{*}$ lie strictly inside the unit disk. This guarantees that the discrete solution decays asymptotically in time, in accordance with Rouché’s theorem 1 and standard root localization techniques from complex analysis.

We begin by rewriting matrices $A_0$, A, B, and C in terms of the canonical tridiagonal matrix:

$$\mathcal{M}=\left[\begin{array}{ccccc}-2& 1& 0& \cdots & 0\\ 1& -2& 1& \cdots & 0\\ 0& 1& -2& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & 1\\ 0& 0& 0& 1& -2\end{array}\right],$$

which corresponds to the standard second-order finite difference approximation of the Laplacian with Dirichlet boundary conditions. Using this matrix, we express the system matrices as follows:

$$\begin{array}{cc}\hfill A_0& =2{(\Delta x)}^{2}I-\mu \Delta t\mathcal{M},\hfill \\ \hfill A& =\left[2{(\Delta x)}^2-\beta h\left(0\right)\right]I-\mu \Delta t\mathcal{M},\hfill \\ \hfill B& =-2{(\Delta x)}^{2}I-\mu \Delta t\mathcal{M},\hfill \\ \hfill C& =4{(\Delta x)}^{2}I+2{(\Delta t)}^2\mathcal{M}.\hfill \end{array}$$

(34)

The matrix $\mathcal{M}$ is symmetric and diagonalizable with real negative eigenvalues:

$$\begin{array}{c}\hfill {\lambda }_m=-4{\sin }^2\left({\displaystyle \frac{\pi m}{2P}}\right),m=1,\dots ,P-1,\end{array}$$

(35)

which decrease strictly as m increases. We denote its eigendecomposition by $\mathcal{M}=Q\Lambda Q^{-1}$, where Q is the matrix of eigenvectors and $\Lambda$ is a diagonal matrix of eigenvalues.

4.1. Spectral Decomposition and Modal Formulation: CTR Scheme

Using the spectral decomposition of $\mathcal{M}$, we diagonalize the CTR system (26). To this end, we define the block-diagonal matrix as

$$Q_{*}:=\mathrm{diag}(Q,Q,\dots ,Q)$$

and use it to diagonalize block matrices $\mathcal{A}$ and $\mathrm{\Phi }$. We write

$$\begin{array}{cc}\hfill \mathcal{A}& =Q_{*}\tilde{\mathcal{A}}{Q}_{*}^{-1},\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \mathrm{\Phi }& =Q_{*}\tilde{\mathrm{\Phi }}{Q}_{*}^{-1},\hfill \end{array}$$

(37)

where the diagonalized matrix $\tilde{\mathcal{A}}$ takes the following form:

$$\tilde{\mathcal{A}}=\mathrm{diag}\left([2{(\Delta x)}^2-\beta h\left(0\right)]I-\mu \Delta t\Lambda ,I,\dots ,I\right).$$

The corresponding block matrix $\tilde{\mathrm{\Phi }}$ is provided as follows:

$$\begin{array}{c}\hfill \tilde{\mathrm{\Phi }}=\left[\begin{array}{ccccccc}4{(\Delta x)}^{2}I+2{(\Delta t)}^2\Lambda & -2{(\Delta x)}^{2}I-\mu \Delta t\Lambda & 0& \cdots & 0& I& {\alpha }_{n}I\\ I& 0& 0& \cdots & 0& 0& 0\\ 0& I& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & I& 0& 0\\ 0& 0& 0& \cdots & 0& I& 0\end{array}\right].\end{array}$$

(38)

Substituting (36) and (37) into (25), we obtain

$$\begin{array}{c}\hfill Q_{*}\tilde{\mathcal{A}}\left(Q_{*}^{-1}{\mathcal{U}}^{n+1}\right)=Q_{*}\tilde{\mathrm{\Phi }}\left(Q_{*}^{-1}{\mathcal{U}}^n\right),n\ge 1.\end{array}$$

(39)

Let $Y^n:=Q^{-1}{W}^n={[{\phi }_1^n,{\phi }_2^n,\dots ,{\phi }_{P-1}^n]}^{\top }\in {\mathbb{R}}^{P-1}$, where $W^n$ is the vector defined in (23), and define the block vector as follows:

$${\mathcal{V}}^n:=\left[\begin{array}{c}{Y}^n\\ Y^{n-1}\\ ⋮\\ Y^0\\ Y^{-1}\\ Y^{-2}\end{array}\right]\in {\mathbb{R}}^{(n+3)(P-1)}.$$

Then, the diagonalized system becomes

$$\begin{array}{c}\hfill {\mathcal{V}}^{n+1}=\tilde{\mathrm{\Psi }}{\mathcal{V}}^n,n\ge 1,\end{array}$$

(40)

where $\tilde{\mathrm{\Psi }}:={\tilde{\mathcal{A}}}^{-1}\tilde{\mathrm{\Phi }}$. It follows that $\mathrm{\Psi }$ and $\tilde{\mathrm{\Psi }}$ are similar matrices and thus have identical eigenvalues. Equation (40) may be reformulated into an equivalent expression by reordering its components. For each mode $m=1,\dots ,P-1$, we define

$$H_m^n:={[{\phi }_m^n,{\phi }_m^{n-1},\dots ,{\phi }_m^0,{\phi }_m^{-1},{\phi }_m^{-2}]}^{\top }$$

and assemble these into a global block vector:

$${\mathcal{H}}^n:={[H_1^n,H_2^n,\dots ,H_{P-1}^n]}^{\top }\in {\mathbb{R}}^{(n+3)(P-1)}.$$

We now define, for each $m=1,\dots ,P-1$, the diagonal matrix

$$D_m:=\mathrm{diag}\left(2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m,1,\dots ,1\right)$$

and the corresponding recurrence matrix

$$G_m:=\left[\begin{array}{ccccccc}4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m& -(2{(\Delta x)}^2+\mu \Delta t{\lambda }_m)& 0& \cdots & 0& 1& {\alpha }_n\\ 1& 0& 0& \cdots & 0& 0& 0\\ 0& 1& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& 0\\ 0& 0& 0& \cdots & 0& 1& 0\end{array}\right].$$

Next, we define the block matrices

$$\mathcal{D}:=\mathrm{diag}(D_1,\dots ,D_{P-1}),\mathcal{G}:=\mathrm{diag}(G_1,\dots ,G_{P-1}),$$

and then introduce the modal amplification matrix

$$\widetilde{\tilde{\mathrm{\Psi }}}:={\mathcal{D}}^{-1}\mathcal{G}=\mathrm{diag}(D_1^{-1}{G}_1,\dots ,D_{P-1}^{-1}{G}_{P-1}).$$

This allows us to rewrite the recurrence (40) as

$$\begin{array}{c}\hfill {\mathcal{H}}^{n+1}=\widetilde{\tilde{\mathrm{\Psi }}}{\mathcal{H}}^n,n\ge 1.\end{array}$$

(41)

Since $\widetilde{\tilde{\mathrm{\Psi }}}$ and $\tilde{\mathrm{\Psi }}$ are similar block matrices, they have the same set of eigenvalues.

The matrices $D_m^{-1}{G}_m\in {\mathbb{R}}^{(n+3)\times (n+3)}$, for $m=1,\dots ,P-1$, are companion matrices corresponding to monic polynomials of degree $n+3$. Each matrix has the following form:

$$D_m^{-1}{G}_m=\left[\begin{array}{ccccccc}\gamma & \eta & 0& \cdots & 0& \zeta & {\alpha }_n\zeta \\ 1& 0& 0& \cdots & 0& 0& 0\\ 0& 1& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& 0\\ 0& 0& 0& \cdots & 0& 1& 0\end{array}\right],$$

where the coefficients are provided as follows:

$$\begin{array}{cc}\hfill \gamma & :=-{\displaystyle \frac{4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m}{2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill \eta & :={\displaystyle \frac{2{(\Delta x)}^2+\mu \Delta t{\lambda }_m}{2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill \zeta & :={\displaystyle \frac{1}{2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m}}.\hfill \end{array}$$

The corresponding monic polynomial ${\pi }_m\left(z\right)\in \mathbb{R}\left[z\right]$ is provided by the following:

$$\begin{array}{c}\hfill {\pi }_m\left(z\right)=z^{n+3}+\gamma z^{n+2}+\eta z^{n+1}+\zeta z+{\alpha }_n\zeta .\end{array}$$

(42)

The roots of ${\pi }_m\left(z\right)$ are precisely the eigenvalues of the matrix $D_m^{-1}{G}_m$. Therefore, verifying that all eigenvalues of the amplification matrix $\mathrm{\Psi }$ lie strictly inside the unit disk reduces to checking that all roots of ${\pi }_m\left(z\right)$, for $m=1,\dots ,P-1$, lie within the unit disk.

 Remark 5. 

While the polynomials ${\pi }_m\left(z\right)$ correspond directly to the eigenvalues of the modal matrices $D_m^{-1}{G}_m$, the global amplification matrix Ψ is similar to both $\tilde{\mathrm{\Psi }}$ and $\widetilde{\tilde{\mathrm{\Psi }}}$, and hence shares the same spectrum. We work with $\widetilde{\tilde{\mathrm{\Psi }}}$ here because its block-diagonal structure allows explicit identification of eigenvalues via the polynomials ${\pi }_m\left(z\right)$.

4.2. Spectral Decomposition and Modal Formulation: GQR Scheme

The GQR-based system has a similar structure but features a simplified delay term. We define the diagonalized matrices as follows:

$$\begin{array}{cc}\hfill {\mathcal{A}}_{*}& =Q_{*}{\tilde{\mathcal{A}}}_{*}{Q}_{*}^{-1},\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_{*}& =Q_{*}{\tilde{\mathrm{\Phi }}}_{*}{Q}_{*}^{-1},\hfill \end{array}$$

(44)

with

$${\tilde{\mathcal{A}}}_{*}=\mathrm{diag}\left(2{(\Delta x)}^{2}I-\mu \Delta t\Lambda ,I,\dots ,I\right).$$

The corresponding block matrix ${\tilde{\mathrm{\Phi }}}_{*}$ is the following:

$$\begin{array}{c}\hfill {\tilde{\mathrm{\Phi }}}_{*}=\left[\begin{array}{ccccccc}4{(\Delta x)}^{2}I+2{(\Delta t)}^2\Lambda & -2{(\Delta x)}^{2}I-\mu \Delta t\Lambda & 0& \cdots & 0& 0& I\\ I& 0& 0& \cdots & 0& 0& 0\\ 0& I& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & I& 0& 0\\ 0& 0& 0& \cdots & 0& I& 0\end{array}\right].\end{array}$$

(45)

Since ${\mathcal{A}}_{*}$ is invertible, we define the update operator as

$${\mathrm{\Psi }}_{*}:={\mathcal{A}}_{*}^{-1}{\mathrm{\Phi }}_{*}\Rightarrow {\tilde{\mathrm{\Psi }}}_{*}:={\tilde{\mathcal{A}}}_{*}^{-1}{\tilde{\mathrm{\Phi }}}_{*}.$$

Let $Y_{*}^n:=Q^{-1}{W}_{*}^n={[{\varphi }_1^n,{\varphi }_2^n,\dots ,{\varphi }_{P-1}^n]}^{\top }\in {\mathbb{R}}^{P-1}$, where $W_{*}^n$ is the vector defined in (30). We define the block vector:

$${\mathcal{V}}_{*}^n:=\left[\begin{array}{c}{Y}_{*}^n\\ Y_{*}^{n-1}\\ ⋮\\ Y_{*}^{-1}\end{array}\right]\in {\mathbb{R}}^{(n+2)(P-1)}.$$

Hence, the diagonalized GQR system becomes the following:

$$\begin{array}{c}\hfill {\mathcal{V}}_{*}^{n+1}={\tilde{\mathrm{\Psi }}}_{*}{\mathcal{V}}_{*}^n,n\ge 1.\end{array}$$

(46)

Since ${\mathrm{\Psi }}_{*}$ and ${\tilde{\mathrm{\Psi }}}_{*}$ are similar matrices, they share the same spectrum.

Equation (46) can be reformulated into an equivalent expression by reordering its components. For each mode $m=1,\dots ,P-1$, we define

$$K_m^n:={[{\varphi }_m^n,{\varphi }_m^{n-1},\dots ,{\varphi }_m^{-1}]}^{\top },$$

and construct the global block vector

$${\mathcal{K}}^n:={[K_1^n,K_2^n,\dots ,K_{P-1}^n]}^{\top }\in {\mathbb{R}}^{(n+2)(P-1)}.$$

For each mode m, we define the diagonal matrix

$$D_{{*}_m}:=\mathrm{diag}\left(2{(\Delta x)}^2-\mu \Delta t{\lambda }_m,1,\dots ,1\right)$$

and recurrence matrix

$$G_{{*}_m}:=\left[\begin{array}{ccccccc}4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m& -(2{(\Delta x)}^2+\mu \Delta t{\lambda }_m)& 0& \cdots & 0& 0& 1\\ 1& 0& 0& \cdots & 0& 0& 0\\ 0& 1& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& 0\\ 0& 0& 0& \cdots & 0& 1& 0\end{array}\right].$$

Next, we define the block-diagonal matrices as

$${\mathcal{D}}_{*}:=\mathrm{diag}(D_{{*}_1},\dots ,D_{{*}_{P-1}}),{\mathcal{G}}_{*}:=\mathrm{diag}(G_{{*}_1},\dots ,G_{{*}_{P-1}}),$$

and the modal amplification matrix as

$${\widetilde{\tilde{\mathrm{\Psi }}}}_{*}:={\mathcal{D}}_{*}^{-1}{\mathcal{G}}_{*}=\mathrm{diag}(D_{{*}_1}^{-1}{G}_{{*}_1},\dots ,D_{{*}_{P-1}}^{-1}{G}_{{*}_{P-1}}).$$

This allows us to rewrite the recurrence (46) as

$$\begin{array}{c}\hfill {\mathcal{K}}^{n+1}={\widetilde{\tilde{\mathrm{\Psi }}}}_{*}{\mathcal{K}}^n,n\ge 1.\end{array}$$

(47)

Since ${\widetilde{\tilde{\mathrm{\Psi }}}}_{*}$ and ${\tilde{\mathrm{\Psi }}}_{*}$ are similar matrices, they have the same set of eigenvalues.

The matrices $D_{{*}_m}^{-1}{G}_{{*}_m}\in {\mathbb{R}}^{(n+2)\times (n+2)}$ for $m=1,\dots ,P-1$ are companion matrices corresponding to monic polynomials of degree $n+2$. Each matrix has the following form:

$$D_{{*}_m}^{-1}{G}_{{*}_m}=\left[\begin{array}{ccccccc}{\gamma }_{*}& {\eta }_{*}& 0& \cdots & 0& 0& {\zeta }_{*}\\ 1& 0& 0& \cdots & 0& 0& 0\\ 0& 1& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& 0\\ 0& 0& 0& \cdots & 0& 1& 0\end{array}\right],$$

with coefficients provided as follows:

$$\begin{array}{cc}\hfill {\gamma }_{*}& :=-{\displaystyle \frac{4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m}{2{(\Delta x)}^2-\mu \Delta t{\lambda }_m}}\hfill \\ \hfill {\eta }_{*}& :={\displaystyle \frac{2{(\Delta x)}^2+\mu \Delta t{\lambda }_m}{2{(\Delta x)}^2-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill {\zeta }_{*}& :={\displaystyle \frac{1}{2{(\Delta x)}^2-\mu \Delta t{\lambda }_m}}.\hfill \end{array}$$

The corresponding monic polynomial ${\sigma }_m\left(z\right)\in \mathbb{R}\left[z\right]$ is provided by

$$\begin{array}{c}\hfill {\sigma }_m\left(z\right)=z^{n+2}+{\gamma }_{*}{z}^{n+1}+{\eta }_{*}{z}^n+{\zeta }_{*}.\end{array}$$

(48)

The roots of ${\sigma }_m\left(z\right)$ are precisely the eigenvalues of the companion matrix $D_{{*}_m}^{-1}{G}_{{*}_m}$. Since the amplification matrix ${\mathrm{\Psi }}_{*}$ is similar to the block-diagonal matrix ${\widetilde{\tilde{\mathrm{\Psi }}}}_{*}$, verifying that all eigenvalues of ${\mathrm{\Psi }}_{*}$ lie strictly within the unit disk reduces to checking that all roots of ${\sigma }_m\left(z\right)$ for $m=1,\dots ,P-1$ lie inside the unit disk.

Having derived the characteristic polynomials ${\pi }_m\left(z\right)$ and ${\sigma }_m\left(z\right)$ corresponding to the modal amplification matrices of the CTR and GQR systems, we now assess their root locations to establish asymptotic stability. The index m represents the spectral modes from the diagonalization of the spatial operator $\mathcal{M}$, and stability of the full system reduces to verifying that all roots of these polynomials lie strictly inside the unit disk.

In what follows, we apply Rouché’s theorem 1 to both ${\pi }_m\left(z\right)$ and ${\sigma }_m\left(z\right)$, and derive sufficient mesh-dependent conditions that ensure the asymptotic stability of the fully discrete scheme for all spectral modes m.

4.3. Stability Criteria via Rouché’s Theorem

The stability analysis carried out in this section is based on applying Rouché’s theorem 1 to assess the asymptotic stability of the modal amplification matrices derived in the previous sections. Specifically, we analyze the characteristic polynomials ${\pi }_m\left(z\right)$ and ${\sigma }_m\left(z\right)$, associated with the CTR and GQR schemes, respectively. Rather than checking each spectral mode $m=1,\dots ,P-1$ individually, we formulate sufficient conditions that guarantee all roots of the corresponding polynomials lie strictly inside the unit disk, uniformly across the spectrum.

4.3.1. Assumptions

Throughout our analysis, we assume the following conditions on the delay kernel, spatial discretization, and time step:

• Delay kernel regularity: The delay kernel $h\left(t\right):[0,\infty )\to \mathbb{R}$ is continuous, non-increasing, and satisfies $h\left(0\right)>0$. In particular, for all $n\ge 1$,

  $$\begin{array}{c}\hfill \mathrm{A}1:h\left(t_n\right)\le h\left(0\right).\end{array}$$

  (49)
• Spatial step constraint: The spatial step size $\Delta x$ satisfies

  $$\begin{array}{c}\hfill \mathrm{A}2:{(\Delta x)}^2\ge {\displaystyle \frac{\mu {\lambda }_{\max }}{2}}\Delta t.\end{array}$$

  (50)
• Time step constraint: The time step $\Delta t$ satisfies

  $$\begin{array}{c}\hfill \mathrm{A}3:{(\Delta t)}^2<\min \left\{{\displaystyle \frac{2}{h\left(0\right)}},{\displaystyle \frac{2{(\Delta x)}^2}{{\lambda }_{\max }}}\right\}.\end{array}$$

  (51)
  Here, ${\lambda }_{\min }=\min |{\lambda }_m|$ and ${\lambda }_{\max }=\max |{\lambda }_m|$ denote the minimum and maximum (in absolute value) eigenvalues of the spatial discretization matrix $\mathcal{M}$, respectively.

 Remark 6. 

We note that the condition stated in (15), which ensures the non-singularity of the matrix A, is implicitly included in Assumption A3. In particular, the upper bound on the square of the time step ${(\Delta t)}^2$ in (51) takes the minimum among the expressions on the right-hand side of (51), including ${\displaystyle \frac{2{(\Delta x)}^2}{{\lambda }_{\max }}}$. Therefore, Assumption A3 automatically guarantees the validity of (15).

The following proposition establishes key positivity properties of the coefficients appearing in the polynomials ${\pi }_m\left(z\right)$ and ${\sigma }_m\left(z\right)$. These properties are necessary to formulate uniform Rouché-based root location estimates.

 Proposition 1. 

Under Assumptions A1–A3, the following inequalities hold for all ${\lambda }_m$, $m=1,\dots ,P-1$:

$$\begin{array}{cc}\hfill & 4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m>0,\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill & 2{(\Delta x)}^2+\mu \Delta t{\lambda }_m>0,\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill & {(\Delta x)}^2-\beta h\left(0\right)>0.\hfill \end{array}$$

(54)

 Proof. 

Since the eigenvalues ${\lambda }_m$ of the matrix $\mathcal{M}$ are strictly negative for all $m=1,\dots ,P-1$, we can write $|{\lambda }_m|=-{\lambda }_m$. From Assumption A3, we have

$${(\Delta t)}^2<{\displaystyle \frac{2{(\Delta x)}^2}{|{\lambda }_m|}},\forall m=1,\cdots ,P-1.$$

Multiplying both sides by $2|{\lambda }_m|$ yields the following:

$$2{(\Delta t)}^2|{\lambda }_m{|<4(\Delta x)}^2\Rightarrow 4{(\Delta x)}^2-2{(\Delta t)}^2|{\lambda }_m|>0.$$

Substituting $|{\lambda }_m|=-{\lambda }_m$ provides inequality (52). Similarly, Assumption A2 implies

$${(\Delta x)}^2\ge {\displaystyle \frac{\mu |{\lambda }_m|}{2}}\Delta t\forall m=1,\cdots ,P-1.$$

Multiplying both sides by 2, we obtain the following:

$$2{(\Delta x)}^2\ge \mu \Delta t|{\lambda }_m{|\Rightarrow 2(\Delta x)}^2-\mu \Delta t|{\lambda }_m|\ge 0.$$

Again, using $|{\lambda }_m|=-{\lambda }_m$, we obtain inequality (53). For the last inequality, we again use Assumption A3, from which we obtain

$${(\Delta t)}^2<{\displaystyle \frac{2}{h\left(0\right)}}.$$

Multiplying both sides by ${\displaystyle \frac{{(\Delta x)}^{2}h\left(0\right)}{2}}$, we obtain the following:

$${\displaystyle \frac{{(\Delta x)}^2{(\Delta t)}^{2}h\left(0\right)}{2}}<{(\Delta x)}^2.$$

Recognizing the left-hand side as $\beta h\left(0\right)$, we conclude that

$$\beta h\left(0\right)<{(\Delta x)}^2\Rightarrow {(\Delta x)}^2-\beta h\left(0\right)>0,$$

which is inequality (54). □

4.3.2. Rouché-Based Stability Analysis for the CTR Scheme

We now turn to the analysis of the characteristic polynomial that arises in the modal decomposition of the amplification matrix associated with the composite trapezoidal rule (CTR) discretization. This polynomial governs the evolution of individual Fourier modes in the fully discrete system and forms the foundation of our root-location-based stability criterion. Specifically, for each spatial mode m, the corresponding companion matrix $D_m^{-1}{G}_m$ gives rise to a degree-$n+3$ polynomial of the following form:

$$\begin{array}{c}\hfill {\pi }_m\left(z\right)=z^{n+3}+\gamma z^{n+2}+\eta z^{n+1}+\zeta z+{\alpha }_n\zeta ,\end{array}$$

(55)

where the coefficients are functions of the discretization parameters, damping strength, and delay kernel:

$$\begin{array}{cc}\hfill \gamma & :=-{\displaystyle \frac{4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m}{2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill \eta & :={\displaystyle \frac{2{(\Delta x)}^2+\mu \Delta t{\lambda }_m}{2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill \zeta & :={\displaystyle \frac{1}{2{(\Delta x)}^2-\beta h\left(0\right)-\mu \Delta t{\lambda }_m}},\hfill \end{array}$$

${\lambda }_m<0$, and

$${\alpha }_n=\beta h\left(t_n\right)={\displaystyle \frac{{(\Delta t)}^2{(\Delta x)}^2}{2}}h\left(t_n\right).$$

Our goal is to show that, under the Assumptions A1–A3, the coefficients of ${\pi }_m\left(z\right)$ satisfy sign properties that make it amenable to Rouché’s theorem. This will allow us to derive a mesh-dependent condition ensuring that all roots of ${\pi }_m\left(z\right)$ lie strictly within the unit disk.

 Proposition 2. 

Under Assumptions A1–A3, the coefficients $\gamma ,\eta ,\zeta$, and ${\alpha }_n$ of the polynomial ${\pi }_m\left(z\right)$ defined in (55) satisfy the following:

• $\gamma <0$,
• $\eta >0$, $\zeta >0$,
• ${\alpha }_n>0$ for all $n\ge 1$.

 Proof. 

The positivity of ${\alpha }_n=\beta h\left(t_n\right)$ follows directly from the definition of $\beta ={\displaystyle \frac{{(\Delta t)}^2{(\Delta x)}^2}{2}}$ and Assumption A1, which ensures $h\left(t_n\right)\le h\left(0\right)$ and $h\left(0\right)>0$. To establish the signs of the remaining coefficients, we use the following denominator:

$$D:=2{(\Delta x)}^2-\beta h\left(0\right)+\mu \Delta t|{\lambda }_m|,$$

which is common to $\gamma ,\eta ,\zeta$. From Proposition 1, inequality (54) implies the following:

$${(\Delta x)}^2-\beta h\left(0\right)>0.$$

Hence,

$$D={(\Delta x)}^2+\left[{(\Delta x)}^2-\beta h\left(0\right)\right]+\mu \Delta t|{\lambda }_m|>0.$$

Thus, the denominator is positive. Next, from Proposition 1, inequalities (52) and (53) show that the numerators of $\gamma$ and $\eta$ are positive. Since $\gamma$ includes a minus sign, we conclude the following:

$$\gamma <0,\eta >0.$$

Finally, $\zeta =1/D>0$, since $D>0$, as shown above. This completes the proof. □

 Lemma 1. 

Let $\Delta x,\Delta t,\mu$ and $h\left(t\right)$ satisfy Assumptions A1–A3. Let $\mathcal{C}:=\{z\in \mathbb{C}:|z|=1\}$ be the unit circle, and define $f\left(z\right):=z^{n+3}$ and $g\left(z\right):={\pi }_m\left(z\right)-f\left(z\right)$, where ${\pi }_m\left(z\right)$ is the degree-$n+3$ polynomial defined in (55). Then, the sufficient condition for

$$|f(z)|>|g(z)|\mathit{for}\mathit{all}z\in \mathcal{C}$$

is

$$\begin{array}{cc}\hfill & {\mathit{SC}}_T:{\lambda }_{\mathit{min}}\Delta t\left(\Delta t+\mu \right)>3{(\Delta x)}^2+{\displaystyle \frac{1}{2}},\hfill \end{array}$$

(56)

where ${\lambda }_{\mathit{min}}={\min }_m|{\lambda }_m|$.

 Proof. 

On the unit circle $\mathcal{C}$, we have $|f\left(z\right)|=|z^{n+3}|=1$. Therefore, by Rouché’s theorem, it suffices to show that $|g(z)|<1$ for all $z\in \mathcal{C}$. Recall that

$$g\left(z\right)=\gamma z^{n+2}+\eta z^{n+1}+\zeta z+{\alpha }_n\zeta .$$

By the triangle inequality and Proposition 2, we estimate the following:

$$|g\left(z\right)|\le |\gamma |+|\eta |+|\zeta |+|{\alpha }_n\zeta |=-\gamma +\eta +\zeta (1+{\alpha }_n).$$

Substituting the expressions for the coefficients, we obtain

$$|g\left(z\right)|\le {\displaystyle \frac{4{(\Delta x)}^2-2{(\Delta t)}^2|{\lambda }_m{|+2(\Delta x)}^2-\mu \Delta t|{\lambda }_m|+1+\beta h\left(t_n\right)}{2{(\Delta x)}^2-\beta h\left(0\right)+\mu \Delta t|{\lambda }_m|}}.$$

Using Assumption A1, which ensures $h\left(t_n\right)\le h\left(0\right)$, we estimate the following:

$$|g\left(z\right)|\le {\displaystyle \frac{6{(\Delta x)}^2-|{\lambda }_m|\Delta t(2\Delta t+\mu )+1+\beta h\left(0\right)}{2{(\Delta x)}^2-\beta h\left(0\right)+\mu \Delta t|{\lambda }_m|}}.$$

To ensure $|g(z)|<1$, it suffices to require

$${\displaystyle \frac{6{(\Delta x)}^2-|{\lambda }_m|\Delta t(2\Delta t+\mu )+1+\beta h\left(0\right)}{2{(\Delta x)}^2-\beta h\left(0\right)+\mu \Delta t|{\lambda }_m|}}<1.$$

Rewriting the inequality obtains the following:

$$\begin{array}{cc}\hfill 6{(\Delta x)}^2-|{\lambda }_m|\Delta t(2\Delta t+\mu )+1+\beta h\left(0\right)& <2{(\Delta x)}^2-\beta h\left(0\right)+\mu \Delta t|{\lambda }_m|\hfill \\ \hfill \Rightarrow |{\lambda }_m|\Delta t(2\Delta t+2\mu )& >4{(\Delta x)}^2+1+2\beta h\left(0\right).\hfill \end{array}$$

Now, applying Assumption A3 (specifically the bound ${(\Delta t)}^2<{\displaystyle \frac{2}{h\left(0\right)}}$), we recall that

$$\beta ={\displaystyle \frac{{(\Delta t)}^2{(\Delta x)}^2}{2}}\Rightarrow 2\beta h\left(0\right)={(\Delta x)}^2{(\Delta t)}^{2}h\left(0\right)<2{(\Delta x)}^2.$$

Thus, the inequality becomes the following:

$$|{\lambda }_m{|\Delta t(2\Delta t+2\mu )>6(\Delta x)}^2+1.$$

Dividing both sides by two and using ${\lambda }_{\min }\le |{\lambda }_m|$, we obtain the global sufficient condition:

$${\lambda }_{\min }\Delta t(\Delta t+\mu )>3{(\Delta x)}^2+{\displaystyle \frac{1}{2}},$$

which is the statement of ${\mathrm{SC}}_T$, as claimed. □

The result of Lemma 1, together with Theorem 1, establishes the following:

 Lemma 2. 

All zeros of the polynomial ${\pi }_m\left(z\right)$ lie strictly inside the unit disk.

As a direct consequence, we obtain the following spectral result:

 Proposition 3. 

Under Assumptions A1–A3, if the parameters $\Delta t,\Delta x,\mu$ and $h\left(t\right)$ satisfy the sufficient condition ${\mathit{SC}}_T$ stated in (56), then all eigenvalues of the amplification matrix Ψ defined in (26) lie strictly inside the unit disk.

The following asymptotic stability theorem then follows immediately from Proposition 3 and Theorem 4.13 in [32], which characterizes stability in linear difference systems via the spectral radius of the transition matrix.

 Theorem 2 

(Stability of the Discrete CTR Scheme). Under Assumptions A1–A3, if the parameters $\Delta t,\Delta x,\mu$ and $h\left(t\right)$ satisfy the sufficient condition ${\mathit{SC}}_T$ in (56), then the finite difference scheme (26) is asymptotically stable.

4.3.3. Rouché-Based Stability Analysis for the GQR Scheme

We now analyze the characteristic polynomial arising from the GQR-based discretization of the delayed wave equation. As in the CTR case, the fully discrete system can be diagonalized and reduced to a recurrence involving a lower-degree companion matrix for each spectral mode. The corresponding polynomial, governing the behavior of each mode, is given by the following:

$$\begin{array}{c}\hfill {\sigma }_m\left(z\right)=z^{n+2}+{\gamma }_{*}{z}^{n+1}+{\eta }_{*}{z}^n+{\zeta }_{*},\end{array}$$

(57)

with coefficients

$$\begin{array}{cc}\hfill {\gamma }_{*}& :=-{\displaystyle \frac{4{(\Delta x)}^2+2{(\Delta t)}^2{\lambda }_m}{2{(\Delta x)}^2-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill {\eta }_{*}& :={\displaystyle \frac{2{(\Delta x)}^2+\mu \Delta t{\lambda }_m}{2{(\Delta x)}^2-\mu \Delta t{\lambda }_m}},\hfill \\ \hfill {\zeta }_{*}& :={\displaystyle \frac{1}{2{(\Delta x)}^2-\mu \Delta t{\lambda }_m}},\hfill \end{array}$$

where ${\lambda }_m<0$. Our goal is to apply Rouché’s theorem to this polynomial and derive a mesh-dependent condition under which all roots of ${\sigma }_m\left(z\right)$ lie strictly inside the unit disk. This will provide a sufficient condition for the asymptotic stability of the GQR-based scheme.

 Proposition 4. 

Under Assumptions A1–A3, coefficients ${\gamma }_{*},{\eta }_{*}$ and ${\zeta }_{*}$ of the polynomial ${\sigma }_m\left(z\right)$ defined in (57) satisfy the following:

• ${\gamma }_{*}<0$,
• ${\eta }_{*}>0$, ${\zeta }_{*}>0$.

 Proof. 

The denominator of all three coefficients is provided as follows:

$$D:=2{(\Delta x)}^2-\mu \Delta t{\lambda }_m=2{(\Delta x)}^2+\mu \Delta t|{\lambda }_m|>0,$$

where we used the fact that ${\lambda }_m<0$, so $-{\lambda }_m=|{\lambda }_m|$. The denominator is, therefore, strictly positive. On the other hand, from Proposition 1, the numerators of ${\gamma }_{*}$ and ${\eta }_{*}$ are

$$-4{(\Delta x)}^2-2{(\Delta t)}^2{\lambda }_m=-4{(\Delta x)}^2+2{(\Delta t)}^2|{\lambda }_m|<0,$$

$$2{(\Delta x)}^2+\mu \Delta t{\lambda }_m=2{(\Delta x)}^2-\mu \Delta t|{\lambda }_m|>0,$$

receptively, both of which satisfy the desired sign properties under Assumptions A2 and A3. Thus,

$${\gamma }_{*}<0,{\eta }_{*}>0,{\zeta }_{*}={\displaystyle \frac{1}{D}}>0.$$

□

 Lemma 3. 

Let $\Delta x,\Delta t,\mu$, and $h\left(t\right)$ satisfy Assumptions A1–A3. Let $\mathcal{C}:=\{z\in \mathbb{C}:|z|=1\}$ denote the unit circle, and define $\widehat{f}\left(z\right):=z^{n+2}$ and $\widehat{g}\left(z\right):={\sigma }_m\left(z\right)-\widehat{f}\left(z\right)$, where ${\sigma }_m\left(z\right)$ is the degree-$n+2$ polynomial defined in (57).

Then, a sufficient condition ensuring

$$|\widehat{f}\left(z\right)|>|\widehat{g}\left(z\right)|\mathit{for}\mathit{all}z\in \mathcal{C}$$

is provided by

$$\begin{array}{cc}\hfill & {\mathit{SC}}_G:{\lambda }_{\mathit{min}}\Delta t\left(\Delta t+\mu \right)>2{(\Delta x)}^2+\frac{1}{2},\hfill \end{array}$$

(58)

where ${\lambda }_{\mathit{min}}={\min }_m|{\lambda }_m|$.

 Proof. 

On the unit circle $\mathcal{C}$, we have $|\widehat{f}\left(z\right)|=|z^{n+2}|=1$. Therefore, by Rouché’s theorem, it suffices to show that $|\widehat{g}\left(z\right)|<1$ for all $z\in \mathcal{C}$. Recall that

$$\widehat{g}\left(z\right)={\gamma }_{*}{z}^{n+1}+{\eta }_{*}{z}^n+{\zeta }_{*}.$$

By the triangle inequality and Proposition 4, we estimate

$$|\widehat{g}\left(z\right)|\le |{\gamma }_{*}|+|{\eta }_{*}|+|{\zeta }_{*}|=-{\gamma }_{*}+{\eta }_{*}+{\zeta }_{*}.$$

Hence, we write the following:

$$|\widehat{g}\left(z\right)|\le {\displaystyle \frac{4{(\Delta x)}^2-2{(\Delta t)}^2|{\lambda }_m{|+2(\Delta x)}^2-\mu \Delta t|{\lambda }_m|+1}{2{(\Delta x)}^2+\mu \Delta t|{\lambda }_m|}}.$$

That is,

$$|\widehat{g}\left(z\right)|\le {\displaystyle \frac{6{(\Delta x)}^2-|{\lambda }_m|\Delta t(2\Delta t+\mu )+1}{2{(\Delta x)}^2+\mu \Delta t|{\lambda }_m|}}.$$

To ensure $|\widehat{g}\left(z\right)|<1$, it suffices to impose the following inequality:

$${\displaystyle \frac{6{(\Delta x)}^2-|{\lambda }_m|\Delta t(2\Delta t+\mu )+1}{2{(\Delta x)}^2+\mu \Delta t|{\lambda }_m|}}<1.$$

Rewriting this inequality provides the following:

$$\begin{array}{cc}\hfill 6{(\Delta x)}^2-|{\lambda }_m|\Delta t(2\Delta t+\mu )+1& <2{(\Delta x)}^2+\mu \Delta t|{\lambda }_m|\hfill \\ \hfill \Rightarrow |{\lambda }_m|\Delta t(2\Delta t+2\mu )& >4{(\Delta x)}^2+1.\hfill \end{array}$$

Dividing both sides by two and using ${\lambda }_{\min }\le |{\lambda }_m|$, we obtain the global sufficient condition:

$${\lambda }_{\min }\Delta t(\Delta t+\mu )>2{(\Delta x)}^2+\frac{1}{2},$$

which corresponds precisely to ${\mathrm{SC}}_G$, as stated. □

The result of Lemma 3, in conjunction with Theorem 1, leads to the following conclusion:

 Lemma 4. 

All zeros of the polynomial ${\sigma }_m\left(z\right)$ lie strictly inside the unit disk.

This immediately yields the spectral result for the GQR amplification matrix:

 Proposition 5. 

Under Assumptions A1–A3, if the parameters $\Delta t,\Delta x,\mu$ and $h\left(t\right)$ satisfy the sufficient condition ${\mathit{SC}}_G$ stated in (58), then all eigenvalues of the matrix ${\mathrm{\Psi }}_{*}$ defined in (33) lie strictly inside the unit disk.

As a consequence, and by invoking Theorem 4.13 from [32], which guarantees asymptotic stability for discrete linear systems whose amplification matrix has spectral radius strictly less than one, we establish the following result:

 Theorem 3 

(Stability of the GQR-Based Scheme). Under Assumptions A1–A3, if $\Delta t,\Delta x,\mu$ and $h\left(t\right)$ satisfy the sufficient condition ${\mathit{SC}}_G$, then the finite difference scheme (33) is asymptotically stable.

This concludes the stability analysis for both discretization strategies. In the next section, we turn to numerical simulations that validate the theoretical results and illustrate the influence of the delay kernel and discretization parameters on solution behavior.

5. Numerical Examples

In this section, we present numerical experiments with two primary objectives: (i) to validate the theoretical results established in Section 4 by verifying whether the assumptions and derived sufficient conditions for stability are satisfied for selected values of the discretization parameters; (ii) to illustrate the long-time behavior of the discrete solution in cases where stability is theoretically guaranteed, as well as in cases where stability is not guaranteed by the theory.

We explore how variations in the mesh parameters $\Delta x$, $\Delta t$, and the damping coefficient $\mu$ influence the asymptotic behavior of the discrete solution. Two quadrature strategies, the composite trapezoidal rule (CTR) and the Gaussian quadrature rule (GQR), are implemented and evaluated independently.

Throughout all tests, the initial conditions are taken as

$$\begin{array}{c}\hfill u_0\left(x\right)=2x(x-L),u_1\left(x\right)=0.\end{array}$$

(59)

The delay kernel $h\left(t\right)$ appearing in the convolution term is required to satisfy Assumption A1. In our numerical experiments, we adopt the exponentially decaying kernel

$$\begin{array}{c}\hfill h\left(t\right)=e^{-t},t\ge 0,\end{array}$$

(60)

which is smooth, non-increasing, and satisfies $h\left(0\right)>0$. This kernel models memory effects with exponential fading and is convenient due to its closed-form expression. Other admissible choices include polynomially decaying kernels such as $h\left(t\right)={(1+t)}^{-p}$ with $p>0$, which represent slower decay and long-memory behavior.

 Remark 7. 

Although the sufficient stability conditions ${\mathit{SC}1}_T$ and ${\mathit{SC}1}_G$ typically require a relatively large damping coefficient μ to be satisfied, our numerical experiments show that asymptotic decay of the energy norm may still occur for smaller values of μ, even when the conditions are not theoretically met. In particular, the case $\mu =5$ demonstrates stable behavior despite violating the sufficient condition, and similar decay can be observed for even smaller damping values under refined discretizations. This reinforces that the proposed conditions are sufficient but not necessary for stability.

5.1. Checking the Feasibility of Stability Conditions Under Parameter Variations

To validate the theoretical framework, we investigate whether the Assumptions A1–A3 and the sufficient stability conditions ${\mathrm{SC}}_T$ and ${\mathrm{SC}}_G$ are satisfied for selected combinations of the spatial step size $\Delta x$, time step $\Delta t$, and damping coefficient $\mu$.

Since Assumption A1 is automatically satisfied by our choice of the kernel $h\left(t\right)=e^{-t}$, we vary the values of $\mu$ and $\Delta t$ and then compute a corresponding spatial step size $\Delta x$, such that

$${(\Delta x)}^2>{\displaystyle \frac{\mu {\lambda }_{\max }}{2}}\Delta t,$$

to ensure Assumption A2 is satisfied. This reduces the feasibility check to verifying Assumption A3 and the first sufficient conditions ${\mathrm{SC}}_T$ and ${\mathrm{SC}}_G$, as presented in Lemmas 1 and 3, respectively.

Table 1. Verification of Assumption A3 and Stability Conditions ${\mathrm{SC}}_T$ and ${\mathrm{SC}}_G$.

$\mathit{\mu }$	$\mathbf{\Delta }\mathit{t}$	$\mathbf{\Delta }\mathit{x}$	A3	${\mathbf{SC}}_{\mathit{T}}$	${\mathbf{SC}}_{\mathit{G}}$
5	0.050	0.705	Yes	No	No
5	0.500	0.710	Yes	No	No
5	0.800	0.712	No	No	No
20	0.050	0.708	Yes	No	No
20	0.500	0.714	Yes	No	No
20	0.800	0.728	No	No	No
40	0.500	0.734	Yes	No	Yes
45	0.500	0.736	Yes	Yes	Yes
50	0.500	0.740	Yes	Yes	Yes

summarizes the results of this feasibility study. For various selected values of $\mu$ and $\Delta t$, the corresponding computed values of $\Delta x$ are listed, along with an indication of whether Assumption A3, ${\mathrm{SC}}_T$, and ${\mathrm{SC}}_G$ are satisfied.

As seen in Table 1, for small values of $\mu$, the sufficient conditions ${\mathrm{SC}}_T$ and ${\mathrm{SC}}_G$ are not satisfied. This is expected since both conditions require the left-hand side of the stability inequalities to be sufficiently large, which is enhanced by increasing either $\mu$ or $\Delta t$. On the other hand, Assumption A3 requires small values of $\Delta t$, making it challenging to satisfy all constraints simultaneously unless $\mu$ is large.

We also observe that ${\mathrm{SC}}_G$ is generally satisfied for slightly smaller values of $\mu$ than required for ${\mathrm{SC}}_T$. This is consistent with the structure of the conditions: ${\mathrm{SC}}_G$ involves a smaller right-hand-side term than ${\mathrm{SC}}_T$, making it less restrictive.

While it is theoretically possible to meet ${\mathrm{SC}}_T$ and ${\mathrm{SC}}_G$ with small $\mu$ by significantly decreasing $\Delta x$, doing so increases computational cost and may be impractical. Therefore, in this study, we prioritize configurations with moderately large $\mu$, which more easily satisfy the conditions and provide reliable validation of our theoretical stability results.

In both schemes, the transition from satisfying to violating the sufficient condition is primarily influenced by the damping coefficient $\mu$, highlighting its key role in the stabilization of distributed-delay wave systems.

It is also important to emphasize that ${\mathrm{SC}}_T$ and ${\mathrm{SC}}_G$ are only sufficient conditions. If satisfied, they guarantee asymptotic stability. However, their failure does not imply instability. In fact, our numerical simulations demonstrate that energy decay, and sometimes even exponential, may still occur in scenarios where the conditions are not met. This suggests that the stability region of the discrete schemes may extend beyond the theoretical bounds derived using Rouché’s theorem.

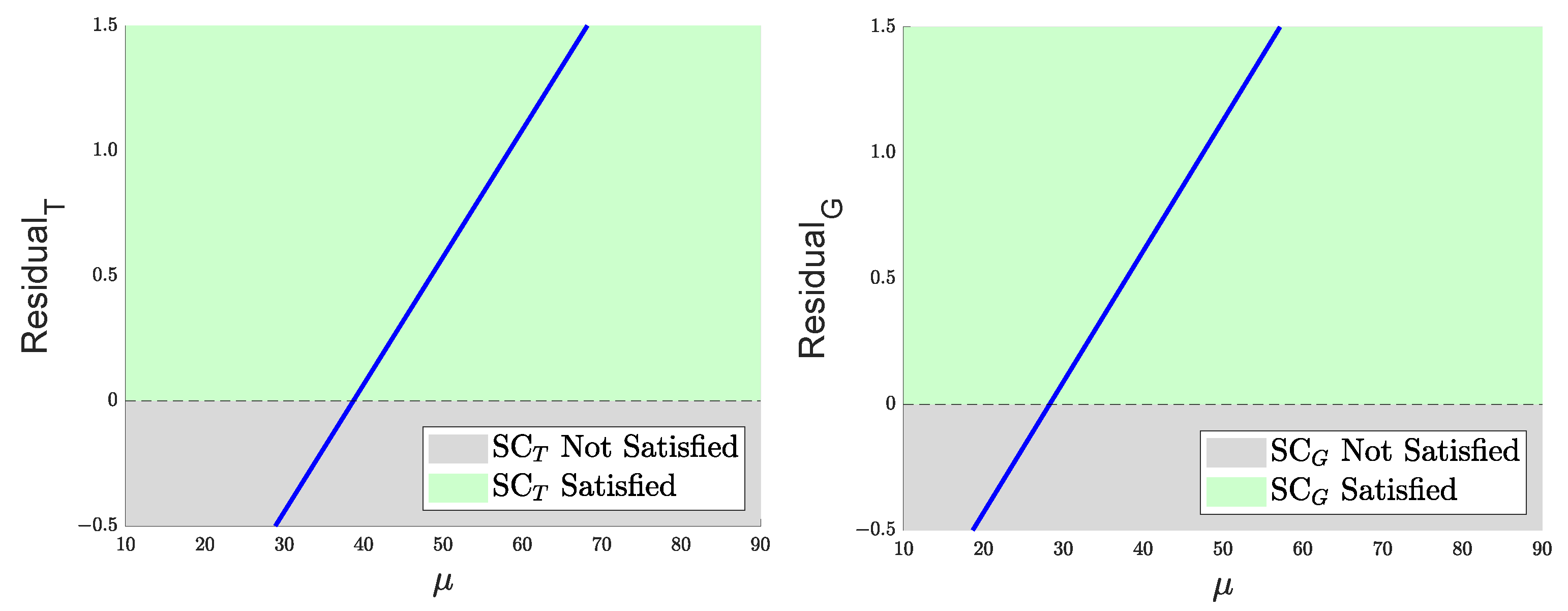
Figure 1 displays the residual functions corresponding to the two sufficient stability conditions:

$${\mathrm{Residual}}_T={\lambda }_{\min }\Delta t(\Delta t+\mu )-\left(3{(\Delta x)}^2+{\displaystyle \frac{1}{2}}\right),$$

$${\mathrm{Residual}}_G={\lambda }_{\min }\Delta t(\Delta t+\mu )-\left(2{(\Delta x)}^2+{\displaystyle \frac{1}{2}}\right).$$

The left panel shows the residual for the CTR-based scheme (${\mathrm{SC}}_T$), while the right panel corresponds to the GQR-based scheme (${\mathrm{SC}}_G$). In both cases, $\Delta t$ is fixed at 0.5530. As the damping coefficient $\mu$ increases, the residuals rise, and once they become positive, the corresponding stability condition is satisfied. The green regions in the plots indicate the parameter ranges where stability is theoretically guaranteed.

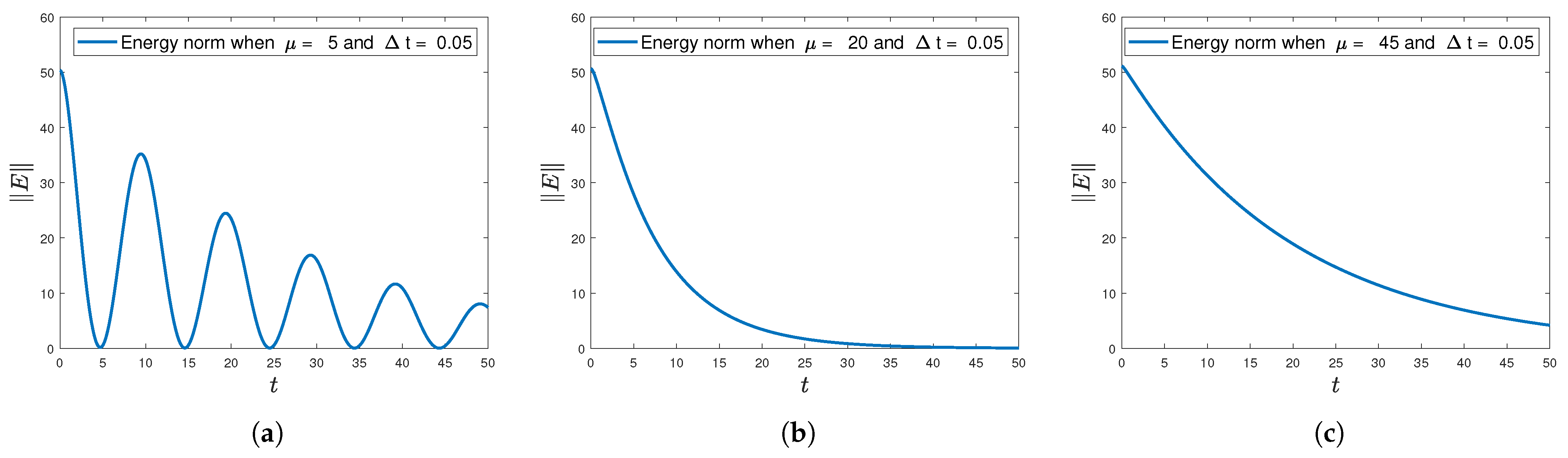
5.2. Energy Evolution Under the CTR-Based Scheme

We now simulate the delayed wave equation using the fully discrete finite difference scheme based on the composite trapezoidal rule (CTR), and investigate the evolution of the energy norm over time.

To measure the decay or growth of the solution, we compute the discrete energy associated with System (2), defined as follows:

$$\begin{array}{c}\hfill E\left(t\right)={\displaystyle \frac{1}{2}}\parallel u_t{\parallel }^2+{\displaystyle \frac{1}{2}}{\parallel \nabla u\parallel }^2,t\ge 0.\end{array}$$

(61)

Two representative test cases are selected to illustrate contrasting behaviors:

(i)

A configuration in which both sufficient stability conditions ${\mathrm{SC}}_T$ are satisfied. This is typically achieved by choosing a sufficiently large damping parameter $\mu$, for which our analysis guarantees asymptotic decay of the energy.

(ii)

A configuration in which the stability condition is not satisfied, allowing us to examine whether energy decay may still be observed in practice, despite the lack of theoretical guarantees.

This comparison highlights both the predictive value and the limitations of the Rouché-based sufficient stability conditions in guiding practical computations. While the condition ${\mathrm{SC}}_T$ offers valuable guarantees for asymptotic stability, it does not fully capture all scenarios where stability is observed in practice.

Figure 2 and Figure 3 illustrate the evolution of the energy norm $\parallel E\left(t\right)\parallel$, computed according to equation (61), for various choices of $\mu$ and $\Delta t$, covering both stable and unstable regimes. The results confirm that when both Assumption A3 and the condition ${\mathrm{SC}}_T$ are satisfied, the energy decays rapidly and smoothly. In contrast, when ${\mathrm{SC}}_T$ is not satisfied, even if A3 holds, stability may still be observed, albeit with slower decay or increased oscillatory behavior, especially for small values of $\mu$.

These simulations offer qualitative insight into how the choice of discretization parameters influences the long-time behavior of the discrete solution. The energy norm serves as an effective diagnostic tool to distinguish between configurations that exhibit stable decay and those that may be prone to growth or instability.

5.3. Energy Evolution Under GQR-Based Scheme

In this subsection, we apply the GQR-based finite difference scheme to simulate the delayed wave equation under various parameter configurations.

The distributed delay term is treated independently at each time level $t=t_n$, using the two-point Gaussian quadrature rule, as discussed in Section 3. Recall that the delay contribution vector $V_{*}^n$, defined in (28), is constructed using the nodal evaluations of the quadrature approximation:

$$V_{*}^n\left(h\right):=4\beta {[{\mathcal{Q}}_1^n[h,u_t],{\mathcal{Q}}_2^n[h,u_t],\dots ,{\mathcal{Q}}_{P-1}^n[h,u_t]]}^T\in {\mathbb{R}}^{P-1},$$

where each component is computed using

$${\mathcal{Q}}_i^n[h,u_t]={\displaystyle \frac{t_n}{2}}\sum _{j=1}^2{w}_{j}h(t_n-{\xi }_j)u_t(x_i,{\xi }_j).$$

Since the quadrature nodes ${\xi }_j\in [0,t_n]$ do not typically align with the discrete time levels, we interpolate the time derivative $u_t(x_i,{\xi }_j)$ using piecewise linear interpolation between grid values. Specifically, let ${\widehat{\xi }}_j$ be the Gaussian node ${\xi }_j$ and suppose it lies in the interval $[{\widehat{t}}_j,{\widehat{t}}_{j+1}]\subset [0,t_n]$. We approximate the derivative as follows:

$$u_t(x_i,{\widehat{\xi }}_j)\approx {\displaystyle \frac{u(x_i,{\widehat{t}}_{j+1})-u(x_i,{\widehat{t}}_j)}{\delta {\widehat{t}}_j}},$$

where $\delta {\widehat{t}}_j={\widehat{t}}_{j+1}-{\widehat{t}}_j$ is the length of the interval.

Once all components of the delay vector $V_{*}^n$ are computed, we solve the recurrence relation (33) to obtain the next solution state ${\mathcal{U}}_{*}^{n+1}$, and track the energy evolution using the discrete energy norm defined in (61).

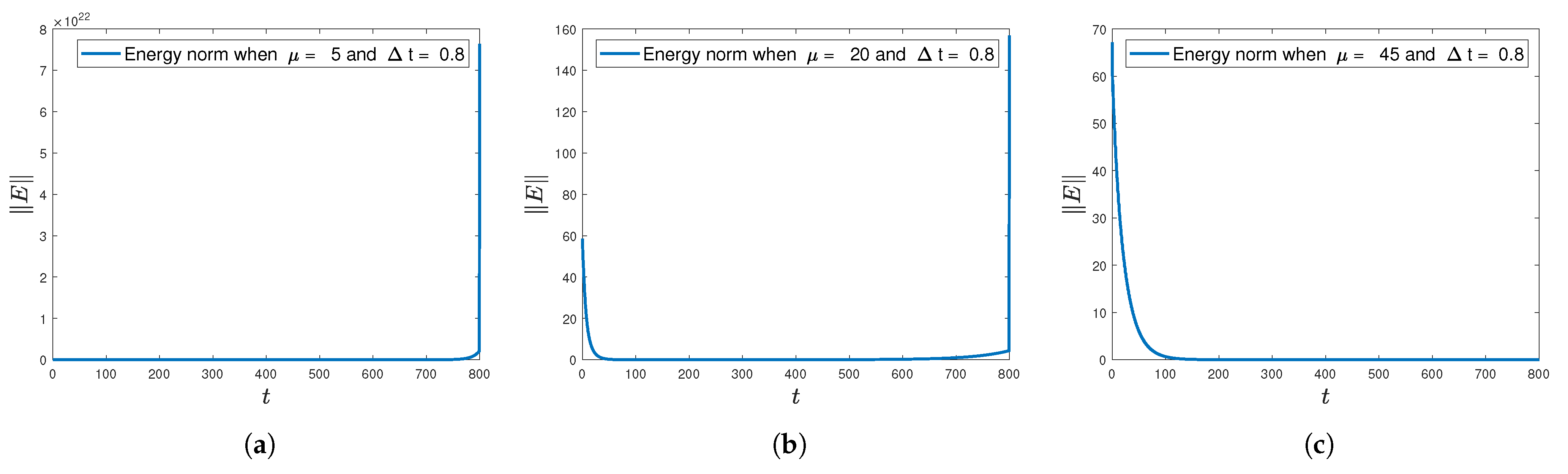
Plotting the energy norm obtained from the GQR-based scheme using the same parameter configurations tested for the CTR scheme (specifically, for $\mu =5,20,45$ and $\Delta t=0.05,0.8$) we observe a similar overall behavior. When both Assumption A3 and the sufficient stability condition ${\mathrm{SC}}_G$ are satisfied, the energy norm exhibits clear exponential decay, as expected. This is demonstrated in Figure 4 for $\Delta t=0.8$ and $\mu =45$, which lies in the stable regime.

When the stability condition is not satisfied (as is the case for smaller $\mu$), the energy norm grows rapidly, indicating numerical instability. Figure 4a,b reflect this behavior for $\mu =5$ and 20, respectively. This mirrors the CTR results, confirming that the sufficient stability conditions derived using Rouché’s theorem are predictive for both schemes.

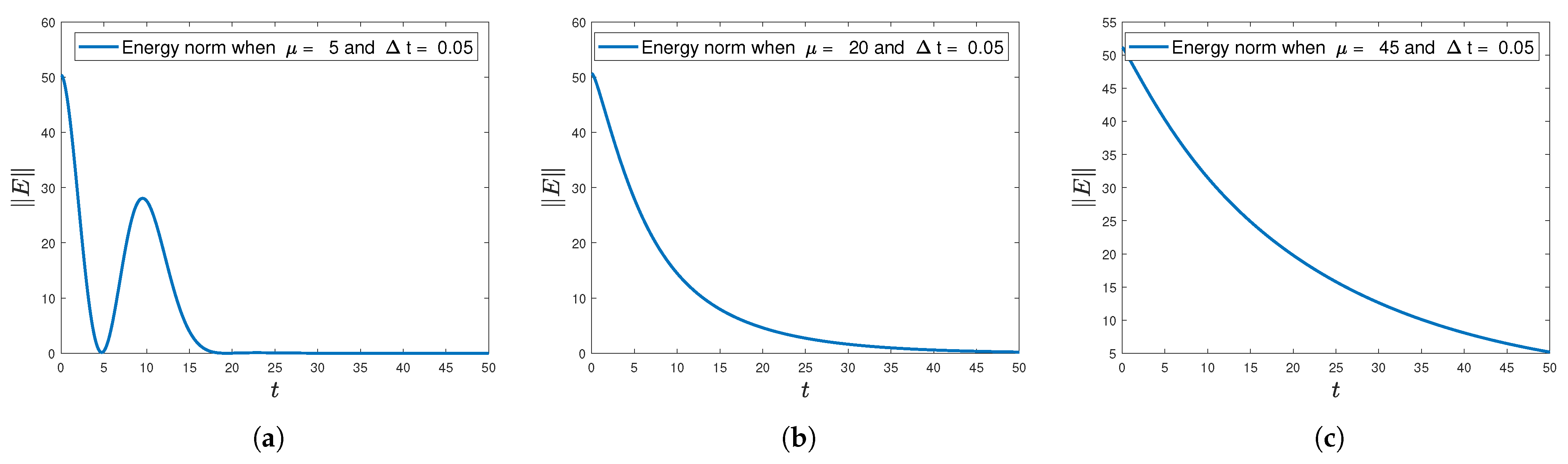
However, for small $\Delta t=0.05$, the GQR scheme demonstrates more favorable behavior even when ${\mathrm{SC}}_G$ is not satisfied. As seen in Figure 5, the energy norm decays in all cases, even for $\mu =5$. Interestingly, the level of oscillations observed for $\mu =5$ (see Figure 5a) is less pronounced than in the corresponding CTR plot, indicating that the GQR scheme provides better damping performance under small-$\mu$ regimes. This improvement is attributed to the higher-order accuracy of the Gaussian quadrature in resolving the convolution integral.

These results reinforce several key observations:

• When ${\mathrm{SC}}_G$ is satisfied, exponential decay is consistently observed.
• When ${\mathrm{SC}}_G$ is violated, instability or oscillatory behavior may arise—though not always—confirming that the condition is sufficient but not necessary.
• The GQR scheme performs comparably to CTR in the stable regime, and in some unstable regimes, it performs even better due to reduced oscillations and more accurate quadrature.

Overall, the GQR method exhibits enhanced robustness under coarse discretizations and low damping. This highlights the practical advantage of using Gaussian quadrature in memory-type delay PDEs, especially when high accuracy and stability are required over long-time simulations.

6. Conclusions and Future Work

In this work, we developed and analyzed two fully implicit finite difference schemes based on the composite trapezoidal rule (CTR) and the Gaussian quadrature rule (GQR) for a wave equation with strong damping and a distributed delay. By applying Rouché’s theorem, we established sufficient conditions for the asymptotic stability of the fully discrete system in terms of discretization parameters, damping strength, and the delay kernel.

We derived high-order characteristic polynomials and used a rigorous root localization technique to confirm that when the sufficient conditions are met, the eigenvalues of the update matrix lie strictly inside the unit disk. Numerical experiments supported the theoretical predictions and showed stable decay even in cases where the sufficient conditions were not fully satisfied.

While this work focuses primarily on the stability aspects, a convergence analysis, error quantification, and benchmarking against alternative numerical schemes remain important directions for future study. In particular, we plan to conduct a detailed convergence analysis and numerical error evaluation in a follow-up publication.

Overall, the techniques presented here provide a flexible and theoretically sound framework for simulating delay-damped wave systems, and may be extended to more general settings including higher spatial dimensions and variable-coefficient or nonlinear models.