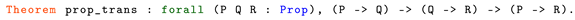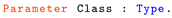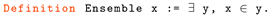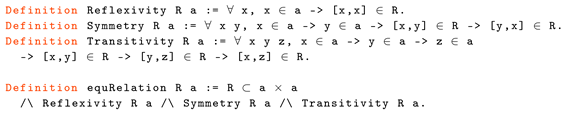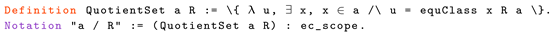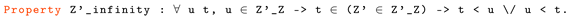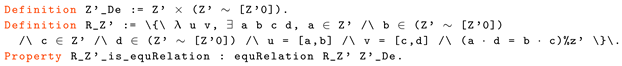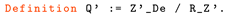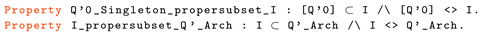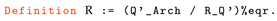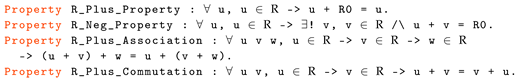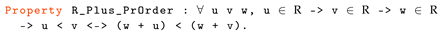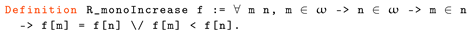A Machine Proof of the Filter-Method Construction for Real Numbers
Abstract
1. Introduction
2. Preliminary Knowledge
2.1. About Coq
2.2. About MK
2.3. About Filters
3. Construction of , and
3.1. Construction of
- (1)
- .
- (2)
- Order Preservation: .
- (3)
- Addition Preservation: .
- (4)
- Multiplication Preservation: .
3.2. Extension from to
 where represents an infinity integer.
where represents an infinity integer.3.3. Extension from to
4. Real Number Set
4.1. From to
4.2. What Are Real Numbers?
- (I)
- Properties of Addition
- (1)
- .
- (2)
- existence of negative element: .
- (3)
- associative law: .
- (4)
- commutative law: .
- (II)
- Properties of Multiplication
- (1)
- .
- (2)
- existence of inverse element: .
- (3)
- associative law: .
- (4)
- commutative law: .
- (I,II)
- Connection between Addition and Multiplication
- (1)
- distributive law: .
- (III)
- Properties of Order
- (1)
- .
- (2)
- reflexivity: .
- (3)
- transitivity: .
- (4)
- trichotomy: .
- (I,III)
- Connection between Addition and Order: .
- (II,III)
- Connection between Multiplication and Order: , where .
- Archimedean Property:
4.3. Formally Proving the Archimedean Property and Completeness
- (i)
- f becomes constant after some term, or
- (ii)
- there exists a strictly increasing subsequence of f.
5. Conclusions and Outlook
5.1. Non-Standard Extension of Number Systems
5.2. Notes on the Implementation
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Axiom of Choice |
| AUF | arithmetical ultrafilter |
| CH | Continuum Hypothesis |
| FEP | Filter Extension Principle |
| FMCR | the filter-method construction for reals |
| IDE | integrated development environment |
| MK | Morse–Kelley axiomatic set theory |
| NPAUF | non-principal arithmetical ultrafilter |
| ZFC | Zermelo–Fraenkel axiomatic set theory with AC |
Appendix A. Partial Definitions and Notations of MK
| Mathematical Meaning | Mathematical Symbol |
| Definition in Coq 1 | Notation in Coq |
| union of x and y | |
| Union x y := \{ z, z ∈ x \/ z ∈ y \} | x ∪ y |
| intersection of x and y | |
| Intersection x y := \{ z, z ∈ x /\ z ∈ y \} | x ∩ y |
| complement of x | |
| Complement x := \{ y, y ∉ x \} | ¬x |
| difference of x and y; complement of y relative to x | |
| Setminus x y := x ∩ (¬ y) | x ∼ y |
| void class; empty set | ∅; 0 |
| := \{ x, x <> x \} | |
| universe, the class including all sets | |
| := \{ x, x = x \} | |
| class of the intersection of the members of x | |
| Element_I x := \{ z, ∀ y, y ∈ x -> z ∈ y \} | ∩x |
| class of the union of the members of x | |
| Element_U x := \{ z, ∃ y, z ∈ y /\ y ∈ x \} | ∪x |
| x is a subclass of y; x is contained in y | ; |
| Included x y := ∀ z, z ∈ x -> z ∈ y | x ⊂ y |
| power class of x | |
| PowerClass x := \{ y, y ⊂ x \} | pow(x) |
| singleton class of x | |
| Singleton x := \{ z, x ∈ -> z = x \} | [x] |
| unordered pair of x and y | |
| Unordered x y := [x] ∪ [y] | [x|y] |
| ordered pair of x and y | |
| Ordered x y := [[x]|[x|y]] | [x,y] |
| the first coordinate of z | 1stcoord z |
| First z := z | – |
| the second coordinate of z | 2stcoord z |
| Second z := (z)∪(z) ∼ (z) | – |
| r is a relation iff its members are ordered pairs | – |
| Relation r := ∀ z, z ∈ r -> ∃ x y, z = [x,y] | – |
| composition of r and s | |
| Composition r s := \{\ x z, ∃ y, [x,y] ∈ s /\ [y,z] ∈ r \}\ 2 | r ∘ s |
| relation inverse to r | |
| Inverse r := \{\ x y, [y,x] ∈ r \}\ | |
| f is a function | – |
| Function f := Relation f /\ (∀ x y z, [x,y] ∈ f -> [x,z] ∈ f -> y = z) | – |
| domain of the class f | domain f |
| Domain f := \{ x, ∃ y, [x,y] ∈ f \} | dom(f) |
| range of the class f | range f |
| Range f := \{ y, ∃ x, [x,y] ∈ f \} | ran(f) |
| value of f at x or image of x under f | |
| Value f x := ∩(\{ y, [x,y] ∈ f \}) | f[x] |
| f is a 1-1 function (bijective function) | – |
| Function1_1 f := Function f /\ Function () | – |
| class consisting of functions whose domain is x and range is contained in y | |
| Exponent y x := \{ f, Function f /\ dom(f) = x /\ ran(f) ⊂ y \} | – |
| cartesian product of x and y | |
| Cartesian x y := \{\ u v, u ∈ x /\ v ∈ y \}\ | x × y |
| restriction of f to x | |
| Restriction f x := f ∩ (x ) | f|(x) |
| x is r-related to y or x r-precedes y | |
| Rrelation x r y := [x,y] ∈ r | – |
| r connects x (trichotomy) | – |
| Connect r x := ∀ u v, u ∈ x -> v ∈ x | – |
| -> (Rrelation u r v) \/ (Rrelation v r u) \/ (u = v) | |
| x is full (each member of a member of x is a member of x) | – |
| Full x := ∀ m, m ∈ x -> m ⊂ x | – |
| E is the ∈-relation | E |
| E := \{\ x y, x ∈ y \}\ | E |
| x is an ordinal | – |
| Ordinal x := Connect E x /\ Full x | – |
| class consisting of all ordinal numbers 3 | R |
| R := \{ x, Ordinal x \} | R |
| x is an ordinal number if and only if | – |
| Ordinal_Number x := x ∈ R | – |
| successor of x | ; |
| PlusOne x := x ∪ [x] | – |
| there exists a 1-1 function between x and y; | |
| x is equivalent (equipotent) to y; x and y are equipollent | |
| Equivalent x y := ∃ f, Function1_1 f /\ dom(f) = x /\ ran(f) = y | x ≈ y |
| x is a cardinal number | – |
| Cardinal_Number x := Ordinal_Number x /\ (∀ y, y ∈ R -> y ∈ x -> ∼ (x ≈ y)) | – |
| class consisting of all cardinal numbers | C |
| C := \{ x, Cardinal_Number x \} | C |
| cardinality function that maps a set to its cardinality | P |
| P := \{\ x y, x ≈ y /\ y ∈ C \}\ | P |
| set of non-negative integers (i.e., set of natural numbers) | |
| := \{ x, Integer x \} | |
| x is finite | – |
| Finite x := P[x] | – |
| 1 All definitions are defined with the command “Definition”. 2 The notation “ \{\ ⋯ \}\ ” is denoted for the classifiers whose members are ordered pairs: Notation "\{\ P \}\" := (\{ z, ∃ x y, z = [x,y] /\ P x y \})(at level 0), where the type of P is “Class -> Class -> Prop”. 3 R is an ordinal but not an ordinal number. | |
Appendix B. Partial Definitions and Notations About Filters
| Mathematical Meaning | Mathematical Symbol |
| Definition in Coq | Notation in Coq |
| B is a filter base over A | – |
| FilterBase B A := B <> /\ B ⊂ pow(A) /\ ∉ B | – |
| /\ (∀ a b, a ∈ B -> b ∈ B -> (a ∩ b) ∈ B) | |
| F is a filter over A | – |
| Filter F A := F ⊂ pow(A) /\ ∉ F /\ A ∈ F | – |
| /\ (∀ a b, a ∈ F -> b ∈ F -> (a ∩ b) ∈ F) | |
| /\ (∀ a b, a ⊂ b -> b ⊂ A -> a ∈ F -> b ∈ F) | |
| F is an ultrafilter over A | – |
| ultraFilter F A := Filter F A | – |
| /\ (∀ a, a ⊂ A -> a ∈ F \/ (A ∼ a) ∈ F) | |
| F is a maximal ultrafilter over A | – |
| maxFilter F A := Filter F A | – |
| /\ (∀ G, Filter G A -> F ⊂ G -> G = F) | |
| the principal ultrafilter corresponding to the element a of A | |
| F A a := \{ u, u ⊂ A /\ a ∈ u \} | denoted as “F A a” or “F a” when A is replaced by |
| F is a free ultrafilter (non-principal ultrafilter) over A | – |
| free_ultraFilter F A := ultraFilter F A | – |
| /\ (∀ a, a ⊂ A -> Finite a -> a ∉ F) | |
| Fréchet Filter over A | |
| Definition F A := \{ a, a ⊂ A /\ Finite (A ∼ a) \} | – |
| (ultrafilter space on A, the set consisting of all ultrafilters over A) | denoted as “” when A is replaced by |
| A := \{ u, ultraFilter u A \} | |
| (the image set of f at A) | |
| ImageSet f A := \{ u, ∃ m, u = f[m] /\ m ∈ A \} | f⌈A⌋ |
| (the preimage set of f at A) | |
| PreimageSet f A := \{ u, u ∈ dom(f) /\ f[u] ∈ A \} | ⌈A⌋ |
| (transformation of ultrafilter F under function f) | f〈F|B〉 ; denoted as “f〈F〉” when B is replaced by |
| Transform F f B := \{ u, u ⊂ B /\ ⌈u⌋ ∈ F \} | |
| , functions f and g are F-equivalent | |
| AlmostEqual f g A B F := Function f /\ Function g | – |
| /\ dom(f) = A /\ dom(g) = A /\ ran(f) ⊂ B /\ ran(g) ⊂ B | |
| /\ F ∈ ( A) /\ \{ u, u ∈ A /\ f[u] = g[u] \} ∈ F | |
| F is an arithmetical ultrafilter over A | |
| Arithmetical_ultraFilter F A := ∼ Finite A /\ F ∈ ( A) | – |
| /\ (∀ f g, Function f -> Function g | |
| -> dom(f) = A -> dom(g) = A -> ran(f) ⊂ A -> ran(g) ⊂ A | |
| -> f〈F∣A〉 = g〈F∣A〉 -> AlmostEqual f g A A F) |
References
- Wang, F. On a special kind of points in stone-cˇech compactification βω. J. China Univ. Sci. Technol. 1998, 28, 567–570. [Google Scholar]
- Wang, F. Mathematical Foundations, 2nd ed.; Higher Education Press: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Wang, F. A result on arithmetical ultrafilters. J. China Univ. Sci. Technol. 2000, 30, 517–522. [Google Scholar]
- Kelley, J.L. General Topology; Springer: New York, NY, USA, 1955. [Google Scholar]
- Jiang, N.; Li, Q.; Wang, L.; Zhang, X.; He, Y. Overview on mechanized theorem proving. J. Softw. 2020, 31, 82–112. (In Chinese) [Google Scholar] [CrossRef]
- Avigad, J. The machenization of mathematics. Not. Am. Math. Soc. 2018, 65, 681–690. [Google Scholar]
- Harrison, J.; Urban, J.; Wiedijk, F. History of interactive theorem proving. In Handbook of the History of Logic; North-Holland: Amsterdam, The Netherlands, 2014; Volume 9, pp. 135–214. [Google Scholar] [CrossRef]
- Wang, H. Toward mechanical mathematics. IBM J. Res. Dev. 1960, 4, 2–22. [Google Scholar] [CrossRef]
- Bertot, Y.; Castéran, P. Interactive Theorem Proving and Program Development–Coq’Art: The Calculus of Interactive Constructions; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- The Reference Manual of the Rocq Prover, v: 9.0.0. Available online: https://rocq-prover.org/doc/V9.0.0/refman (accessed on 15 June 2025).
- Nipow, T.; Paulson, L.C.; Wenzel, M. Isabelle/HOL: A Proof Assistant for Higher-Order Logic; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2002; Volume 2283. [Google Scholar] [CrossRef]
- The HOL Light Theorem Prover. Available online: https://hol-light.github.io/ (accessed on 15 June 2025).
- Bancerek, G.; Bylinski, C.; Grabowski, A.; Korniłowicz, A.; Matuszewski, R.; Naumowicz, A.; Pak, K.; Urban, J. Mizar: State-of-the-art and Beyond. In Proceedings of the 8th International Conference on Intelligent Computer Mathematics (CICM 2015), Washington, DC, USA, 13–17 July 2015; pp. 261–279. [Google Scholar] [CrossRef]
- Moura, L.; Ullrich, S. The Lean 4 theorem prover and programming language. In Proceedings of the 28th International Conference on Automated Deduction (CADE 2021), Virtual Event, 12–15 July 2021; pp. 625–635. [Google Scholar] [CrossRef]
- Avigad, J.; Harrison, J. Formally verified mathematics. Commun. ACM 2014, 57, 66–75. [Google Scholar] [CrossRef]
- Beeson, M. The mechanization of mathematics. In Alan Turing: Life and Legacy of a Great Thinker; Teuscher, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 77–134. [Google Scholar] [CrossRef]
- Avigad, J.; Donnelly, K.; Gray, D.; Raff, P. A formally verified proof of the prime number theorem. ACM Trans. Comput. Log. 2007, 9, 2-es. [Google Scholar] [CrossRef]
- Gonthier, G. Formal proof–the Four Color Theorem. Not. Am. Math. Soc. 2008, 55, 1382–1393. [Google Scholar]
- Hales, T. The Jordan curve theorem, formally and informally. Am. Math. Mon. 2007, 114, 882–894. [Google Scholar] [CrossRef]
- Paulson, L. A machine-assisted proof of Gödel’s incompleteness theorems for the theory of hreditarily finite sets. Rev. Symb. Log. 2014, 7, 484–498. [Google Scholar] [CrossRef]
- Ciolli, G.; Gentili, G. Maggesi, M. A certified proof of the Cartan Fixed Point Theorems. J. Autom. Reason. 2011, 47, 319–336. [Google Scholar] [CrossRef]
- Avigad, J.; Hölzl, J.; Serafin, L. A formally verified proof of the Central Limit Theorem. J. Autom. Reason. 2017, 59, 389–423. [Google Scholar] [CrossRef]
- Gonthier, G.; Asperti, A.; Avigad, J.; Bertot, Y.; Cohen, C.; Garillot, F.; Roux, S.L.; Mahboubi, A.; O’Connor, R.; Pasca, I.; et al. A machine-checked proof of the Odd Order Theorem. In Proceedings of the 4th International Conference on Interactive Theorem Proving (ITP 2013), Rennes, France, 22–26 July 2013; pp. 163–179. [Google Scholar] [CrossRef]
- Hales, T.; Adams, M.; Bauer, G.; Dang, T.D.; Harrison, J.; Hoang, L.T.; Kaliszyk, C.; Magron, V.; Mclaughlin, S.; Nguyen, Q.T.; et al. A formal proof of the Kepler Conjecture. arXiv 2015, arXiv:1501.02155. [Google Scholar] [CrossRef]
- Formalizing the Proof of PFR in Lean4 Using Blueprint: A Short Tour. Available online: https://terrytao.wordpress.com/2023/11/18/formalizing-the-proof-of-pfr-in-lean4-using-blueprint-a-short-tour/ (accessed on 15 June 2025).
- Wiedijk, F. Formal proof – getting started. Not. Am. Math. Soc. 2008, 55, 1408–1414. [Google Scholar]
- Weiss, I. Survey article: The real numbers—A survey of constructions. J. Math. 2015, 45, 737–762. [Google Scholar] [CrossRef]
- Dou, G.; Yu, W. Formalization of the Filter Extension Principle (FEP) in Coq. In Proceedings of the 6th Conference on Intelligent Networked Things (CINT 2024), Xi’an, China, 18 May 2024; pp. 95–106. [Google Scholar] [CrossRef]
- Dou, G.; Chen, S.; Yu, W.; Zhang, R. The Continuum Hypothesis Implies the Existence of Non-principal Arithmetical Ultrafilters—A Coq Formal Verification. In Proceedings of the 25th International Conference on Formal Engineering Methods (ICFEM 2024), Hiroshima, Japan, 2–6 December 2024; pp. 257–277. [Google Scholar] [CrossRef]
- Wang, F. Arithmetical Ultrafilters: End-Extenstions of N in βN; University of Science and Technology of China Press: Hefei, China, 2016. (In Chinese) [Google Scholar]
- Bell, J.L. Set Theory: Boolean-Valued Models and Independence Proofs (Oxford Logic Guides 47), 3rd ed.; Clarendon Press: Oxford, UK, 2005. [Google Scholar]
- Cohen, P.J. Set Theory and the Continuum Hypothesis; W.A.Benjamin, Inc.: New York, NY, USA, 1966. [Google Scholar]
- Robinson, A. Non-Standard Analysis, revised ed.; North Holland Publishing Company: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Hewitt, E. Rings of real-valued continuous functions. I. Trans. Am. Math. Soc. 1948, 64, 45–99. [Google Scholar] [CrossRef]
- Jin, R. Nonstandard analysis and its applications. Sci. Sin. Math. 2016, 46, 371–408. (In Chinese) [Google Scholar] [CrossRef]
- Sun, T.; Yu, W. A formal system of axiomatic set theory in Coq. IEEE Access 2020, 8, 21510–21523. [Google Scholar] [CrossRef]
- Yu, W.; Sun, T.; Fu, Y. A Machine Proof System for Axiomatic Set Theory; Science Press: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Riesz, F. Stetigkeitsbegriff und abstrakte Mengenlehre; Atti del IV Congresso Internazionale del Matematici; Castelnuovo, G., Ed.; Tipografia della R. Accademia dei Lincei: Rome, Italy, 1909; Volume 2, pp. 18–24. [Google Scholar]
- Comfort, W.W.; Negrepontis, S. The Theory of Ultrafilters; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Cartan, H.P. Théorie des filtres. Comptes Rendus Hebdomadaires des Séances de L’Académie des Sciences 1937, 205, 595–598. [Google Scholar]
- Cartan, H.P. Filtres et ultrafilters. Comptes Rendus Hebdomadaires des Séances de L’Académie des Sciences 1937, 205, 777–779. [Google Scholar]
- Bourbaki, N. Elements of Mathematics: General Topology: Chapters 1–4; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Thomsa, J.J. The Axiom of Choice; North-Holland Publishing Company: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Daguenet-Teissier, M. Ultrafilters à la Facon de Ramsey. Trans. Am. Math. Soc. 1979, 250, 91–120. [Google Scholar]
- Fu, Y.; Yu, W. Formalization of the equivalence among completeness theorems of real number in Coq. Mathematics 2021, 9, 38. [Google Scholar] [CrossRef]
- Zorich, V.A. Mathematical Analysis, 7th expanded version; MCCME Publ.: Moscow, Russia, 2015. [Google Scholar]
- de Bruijn, N.G. Checking mathematics with computer assistance. Not. Am. Math. Soc. 1991, 38, 8–15. [Google Scholar]
- Simpson, C. Computer theorem proving in mathematics. Lett. Math. Phys. 2004, 69, 287–315. [Google Scholar] [CrossRef]






| Tactic | Semantics |
|---|---|
| intro/intros | introduce a single premise/all premises to proof environment as hypotheses |
| pose proof H | introduce an existing hypothesis H or a previously established theorem |
| split | split the conjunction in the goal to generate two subgoals |
| destruct H | split disjunctions or conjunctions/instantiate existential quantifiers in hypothesis H, where H can be a proven theorem |
| assumption | search through all available hypotheses to find an exact match for the goal and solve it |
| apply H (in H1) | apply the hypothesis H to the proof goal (to the hypothesis H1), where H can be a proven theorem |
| unfold A (in H) | unfold definition A in the goal (in hypothesis H) |
| rewrite H (in H1) | perform equality substitution on the proof goal (or hypothesis H1) using equation H to replace corresponding variables |
| exists a | instantiate the existential quantifier in the goal with a |
| left/right | extract the left/right disjunct from the goal’s disjunction as a new subgoal |
| repeat T | repeat applying tactic T until it is no longer applicable |
| auto | automatically and repeatedly execute basic tactics including assumption, intros and apply |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, G.; Yu, W. A Machine Proof of the Filter-Method Construction for Real Numbers. Mathematics 2025, 13, 2707. https://doi.org/10.3390/math13172707
Dou G, Yu W. A Machine Proof of the Filter-Method Construction for Real Numbers. Mathematics. 2025; 13(17):2707. https://doi.org/10.3390/math13172707
Chicago/Turabian StyleDou, Guowei, and Wensheng Yu. 2025. "A Machine Proof of the Filter-Method Construction for Real Numbers" Mathematics 13, no. 17: 2707. https://doi.org/10.3390/math13172707
APA StyleDou, G., & Yu, W. (2025). A Machine Proof of the Filter-Method Construction for Real Numbers. Mathematics, 13(17), 2707. https://doi.org/10.3390/math13172707