Research on Endogenous Security Defense for Cloud-Edge Collaborative Industrial Control Systems Based on Luenberger Observer

Abstract

Industrial Control Systems (ICSs) are fundamental to critical infrastructure, yet they face increasing cybersecurity threats, particularly data integrity attacks like replay and data forgery attacks. Traditional IT-centric security measures are often inadequate for the Operational Technology (OT) environment due to stringent real-time and reliability requirements. This paper proposes an endogenous security defense mechanism based on the Luenberger observer and residual analysis. By embedding a mathematical model of the physical process into the control system, this approach enables real-time state estimation and anomaly detection. We model the ICS using a linear state-space representation and design a Luenberger observer to generate a residual signal, which is the difference between the actual sensor measurements and the observer’s predictions. Under normal conditions, this residual is minimal, but it deviates significantly during a replay attack. We formalize the system model, observer design, and attack detection algorithm. The effectiveness of the proposed method is validated through a simulation of an ICS under a replay attack. The results demonstrate that the residual-based approach can detect the attack promptly and effectively, providing a lightweight yet robust solution for enhancing ICS security.

1. Introduction

1.1. Research Background

Industrial Control Systems (ICSs) [1,2,3] serve as the “neural center” of modern critical infrastructure, underpinning the stable operation of sectors that are vital to societal functioning—from power grids regulating electricity distribution across cities, to oil refineries controlling chemical reactions, from smart factories automating production lines, to water treatment plants ensuring clean water supply. These systems bridge the physical and digital worlds: sensors collect real-time data on physical processes (e.g., temperature, pressure, flow rate), controllers analyze this data to issue operational commands (e.g., adjusting valves, modifying motor speed), and actuators execute these commands to maintain processes within safe thresholds. For decades, ICS operated in relatively isolated environments, relying on proprietary hardware and protocols to ensure stability. However, this isolation has eroded rapidly in recent years [4].

The accelerating convergence of Information Technology (IT) and Operational Technology (OT) has revolutionized ICS efficiency but also exposed them to unprecedented cybersecurity risks. Driven by the rise of the Industrial Internet of Things (IIoT), cloud-edge collaboration, and remote monitoring demands, ICSs are now integrated with enterprise networks, cloud platforms, and even public internet services. For example, a smart grid may use cloud platforms to optimize energy distribution based on real-time user data, while a manufacturing plant might adopt edge computing to enable real-time analytics on production lines [5]. This connectivity, while enabling innovations like predictive maintenance and dynamic resource allocation, has shattered the “air gap” that once protected OT environments, creating new attack surfaces for malicious actors [6].

Among the emerging threats, replay attacks and data forgery attacks stand out for their stealth and destructive potential. A replay attack [7] involves an attacker intercepting and storing legitimate sensor data (e.g., a 10 min window of normal pressure readings) and retransmitting it to the controller at a later time. This tricks the controller into relying on outdated information, masking deviations in the actual physical process—for instance, a replay of “normal” temperature data could hide a dangerous overheating in a chemical reactor. Data forgery attacks [8], meanwhile, involve directly manipulating sensor readings (e.g., falsifying a flow meter’s output to make it appear within safe limits) to mislead the controller into issuing incorrect commands, such as increasing fuel supply to an already overloaded generator. Both attack types exploit a critical vulnerability: ICS controllers often lack inherent mechanisms to verify whether incoming data reflects the current physical state of the system, rather than manipulated or stale information. The consequences can be catastrophic, ranging from production shutdowns and equipment damage to large-scale blackouts or environmental disasters [9].

Traditional cybersecurity measures, designed for IT environments, are ill-suited to address these threats. IT-focused solutions like firewalls, Intrusion Detection Systems (IDSs), and antivirus software prioritize confidentiality and general threat blocking but struggle to meet the unique demands of OT:

• Real-time performance [4]: ICSs require microsecond-level response times to maintain process stability. Complex security software, which introduces latency through deep packet inspection or signature matching, can disrupt control loops, leading to process oscillations or failures.
• Protocol specificity: OT relies on legacy protocols (e.g., Modbus, DNP3, PROFINET) that lack built-in security features. Firewalls designed for IT protocols (e.g., TCP/IP) often fail to filter malicious traffic over these specialized protocols.
• Resource constraints [10]: OT devices (e.g., programmable logic controllers, remote terminal units) typically have limited processing power and memory, making them unable to run heavyweight security tools.
• Adaptive threats [11]: Signature-based IDSs, which rely on known attack patterns, are ineffective against zero-day attacks or targeted campaigns (e.g., Advanced Persistent Threats (APTs)) tailored to specific ICS environments.

These limitations highlight the need for a paradigm shift: endogenous security defense [12]. Unlike exogenous measures (e.g., add-on firewalls), endogenous security embeds protection directly into the control system’s core, leveraging the inherent properties of the physical process it regulates. By modeling the mathematical relationships between system states (e.g., how pressure changes with flow rate) and using these models to validate sensor data, endogenous defense can detect anomalies that violate physical laws—even if the attack is novel. This approach is lightweight (integrated with existing control logic), real-time (aligned with control cycles), and robust (grounded in the immutable physics of the process), making it uniquely suited to OT environments [13].

The central novelty of our work lies in demonstrating that this intentionally simple, non-adaptive observer framework, when combined with sensitive statistical monitoring, offers a more robust defense against persistent data integrity attacks than more complex adaptive estimators, providing a practical and computationally efficient solution for resource-constrained OT devices.

1.2. Research Objectives

Against this backdrop, this study aims to develop an endogenous security defense mechanism tailored to ICSs, with a focus on countering replay attacks through Luenberger observers [14,15] and residual analysis. The specific objectives are as follows:

Design a lightweight, integrable defense scheme: The proposed mechanism must operate with minimal computational overhead, ensuring it can be deployed on resource-constrained OT devices (e.g., edge controllers in a cloud-edge collaborative ICS). This requires optimizing the observer’s mathematical complexity and ensuring it aligns with the control loop’s sampling frequency (typically 10–100 Hz in industrial settings).

Enable real-time detection of replay attacks: Replay attacks exploit temporal discrepancies between stored and current data. The solution must identify these discrepancies within milliseconds of the attack initiation, preventing the controller from acting on stale information. This involves refining residual analysis to distinguish attack-induced deviations from normal noise (e.g., sensor inaccuracies, minor process fluctuations).

Validate robustness across attack scenarios: The mechanism’s performance will be rigorously evaluated using metrics critical to ICS security:

• False Alarm Rate (FAR): Minimizing false alarms to avoid unnecessary process shutdowns (a single false alarm in a nuclear power plant could cost millions in downtime).
• Missed Detection Rate (MDR): Ensuring even low-intensity replay attacks (e.g., short windows of replayed data) are detected to prevent cumulative system drift.
• Detection Delay: Quantifying the time between attack initiation and alarm triggering, with a target of <5 control cycles for critical processes.

By achieving these objectives, the study seeks to provide a practical, model-driven solution that improves ICS resilience against data integrity attacks while preserving operational stability.

2. Related Work

2.1. Research on Industrial Control System Security Protection

Research on ICS security protection has evolved significantly in response to the increasing digitization and interconnectivity of industrial environments. Early efforts, as detailed in, primarily revolved around adapting traditional IT security mechanisms to the ICS domain. Firewalls, originally designed for IT networks, were customized to filter traffic specific to ICS protocols such as Modbus and DNP3. This allowed for the segmentation of OT subnets from enterprise networks to restrict unauthorized access. Intrusion Detection Systems (IDSs) were also developed, with a focus on identifying malicious patterns in industrial communication. Signature-based IDSs, for example, were trained to recognize known attack signatures within PROFINET or EtherCAT frames, leveraging the existing knowledge of common attack vectors in the IT realm [16].

During the same time, as the need for more comprehensive security became evident, researchers began to explore network traffic analysis based on process semantics [17]. This approach involved validating that sensor data transmission rates corresponded to the physical process dynamics. For instance, in a slow-heating reactor, a temperature sensor should not logically update at an extremely high frequency. Another direction was the use of physical process invariants for security monitoring. Ensuring that the flow rate in a pipeline adhered to the laws of fluid dynamics, where pressure and flow rate maintain a proportional relationship under steady-state conditions, was one such application.

However, these existing research efforts have several notable limitations. Industrial firewalls, despite their role in network segmentation, are ineffective against threats originating from compromised internal devices. A malicious insider with legitimate access can bypass firewall rules and manipulate sensors [18], as demonstrated in numerous real-world incidents. Signature-based IDSs [16], being reliant on pre-defined attack patterns, are ill-equipped to deal with zero-day attacks or novel attack vectors. In the case of replay attacks using previously unseen historical data, these IDS systems fail to raise alerts, leaving the ICS vulnerable. Additionally, the computational demands of complex security algorithms, such as deep packet inspection [19], pose a significant challenge in ICSs. Resource-constrained OT devices, like legacy Programmable Logic Controllers (PLCs), struggle to handle the associated latency, which can disrupt real-time control loops and lead to process instability [10].

The method proposed in this paper addresses these limitations by adopting an endogenous security framework. Instead of relying solely on external security measures like firewalls or signature-based IDS, our approach embeds security directly into the control loop. By integrating a Luenberger observer into the control system, we continuously compare real-time sensor measurements with values predicted by a mathematical model of the physical process. Deviations from the expected behavior, based on the underlying physics of the system, trigger alerts. This approach is not only more robust against zero-day and novel attacks but also operates with minimal latency, ensuring that the real-time requirements of ICS are maintained. It does not rely on pre-defined attack signatures, making it adaptable to a wide range of potential threats, and can be deployed on resource-constrained OT devices without sacrificing performance.

2.2. Detection of Data Integrity Attacks

Model-based detection methods leverage the physical laws governing industrial processes. For instance, the work by Pasqualetti et al. [13] established a foundational framework for attack detection in cyber-physical systems by characterizing the effect of attacks on system dynamics. While powerful, their approach often assumes a perfect system model, making it sensitive to the model mismatch and noise commonly found in real-world industrial settings [20]. Similarly, many approaches utilize Kalman filters for state estimation and anomaly detection due to their optimality under Gaussian noise [21]. However, a critical shortcoming is that Kalman filters are designed to adapt to new data, which can cause them to “learn” and incorporate the effects of a persistent attack, thereby reducing the residual and causing the attack to be missed over time—a limitation clearly demonstrated in our own simulation results.

Our work builds on these model-based principles but addresses their shortcomings by using a Luenberger observer with a fixed gain. This intentionally non-adaptive design prevents the detector from normalizing persistent attacks, ensuring a sustained residual signal. We further enhance robustness by combining thresholding with CUSUM analysis to reliably detect both abrupt and stealthy attacks.

Data-driven methods [4,22,23] have also gained substantial traction. These methods train algorithms like neural networks or autoencoders on historical data to learn the normal behavior of an ICS. Any deviation from these learned patterns is flagged as an anomaly. While effective for complex, non-linear systems where accurate models are unavailable, they have their own limitations. They require vast amounts of high-quality training data covering all operational states, which is often impractical to obtain. Furthermore, these models can be “black boxes,” suffering from low interpretability, and their computational demands can be too high for resource-constrained OT devices [24].

However, both model-based and data-driven methods have notable limitations. Model-based methods are highly sensitive to model mismatch [20]. Even small errors in the system model, such as incorrect friction coefficients in a fluid flow model, can lead to frequent false alarms. This is especially problematic in ICSs, where the processes often exhibit high levels of noise and time-varying dynamics. In such cases, distinguishing between normal process variations and attack-induced deviations becomes challenging.

Data-driven methods, on the other hand, require large volumes of high-quality historical data that comprehensively cover all possible normal operating conditions. In ICSs, obtaining such data can be a significant challenge. Historical data may lack rare but normal transient states, such as the startup and shutdown phases of industrial equipment, which are crucial for training a robust model. Additionally, data-driven models often suffer from low interpretability. It can be difficult to understand exactly why a particular data point is flagged as an anomaly, which can be a major drawback for ICS operators who need to quickly diagnose and respond to potential attacks. Moreover, these methods typically have high computational demands, which can be a bottleneck for resource-constrained ICS devices and may compromise the real-time performance requirements of the system [24].

The method proposed in this paper aims to address these limitations. We build on the model-based approach by using a Luenberger observer, which is optimized for robustness against model mismatch. We employ estimation techniques to ensure that the observer can handle noise and minor model errors without generating false alarms. Instead of relying solely on absolute deviations between measured and predicted values, we focus on residual statistics, such as mean shift and variance changes. This approach is particularly effective in detecting stealthy replay attacks, where the initial deviation may be small but gradually grows as the system state evolves. Compared to data-driven methods, our framework does not require large-scale training datasets. It operates with a fixed and relatively low computational complexity, making it highly suitable for real-time ICS environments where resource availability and immediate response times are critical.

2.3. Application of Observers and Residual Analysis in Security Defense

Observers and residual analysis have been increasingly adopted in ICS security, building on their long-standing use in fault detection [25,26]. The Luenberger observer [15,27], a foundational tool in control theory, estimates unmeasurable system states by combining a mathematical model with real-time measurements, generating residual signals as the discrepancy between actual and predicted outputs. In fault detection, residuals reflect anomalies like sensor malfunctions, and this principle has been extended to cybersecurity: attacks altering system behavior create detectable residual deviations.

Early applications focused on Kalman filters for detecting false data injection, leveraging their optimality under Gaussian noise. More recently, Luenberger observers have gained traction for their low computational overhead, which is critical for resource-constrained OT devices. Residuals under normal conditions follow a zero-mean stochastic process, while attacks (e.g., replay) induce statistically significant shifts, forming the basis for detection.

However, existing methods have limitations. They often target specific attacks (for example, only false data injection [21]) and do not generalize to replay attacks, which exploit temporal mismatches between stale data and current system states. Observer gains are rarely optimized for attack detectability, prioritizing state estimation accuracy instead, which delays the detection of stealthy attacks. Additionally, simple threshold-based residual monitoring struggles with noise, leading to high false alarms in industrial environments.

Furthermore, the security of discrete event systems, which are common in ICSs for modeling logical operations, faces challenges like intermittent observation loss that can be exploited by attackers. Recent work by Cong et al. [28] explores the critical observability of such systems, highlighting the fundamental importance of ensuring that system state can be reliably inferred, a principle that directly underpins the feasibility of our observer-based detection approach.

This study addresses these gaps by explicitly modeling replay attacks and optimizing the Luenberger observer for detectability via robust design (e.g., LMI optimization). Residual analysis combines static thresholds with CUSUM monitoring to track persistent shifts, critical for detecting slow-evolving replay attacks. This integration enhances sensitivity to temporal anomalies while mitigating noise-induced false alarms.

3. Model and Algorithm Design

3.1. Introduction to ICS Security Modeling

Industrial Control Systems (ICSs) are fundamental to the functioning of critical infrastructures such as energy distribution, chemical processing, and water treatment. These systems operate at the intersection of the physical and cyber domains, where the physical processes are regulated by embedded digital controllers connected via communication networks. Despite the long-standing stability of ICS environments, the increasing integration of open networks and Internet-facing services has exposed these systems to sophisticated cyber-attacks.

To ensure resilient operation under both stochastic disturbances and malicious interference, a rigorous model-based security approach is necessary. The core idea is to embed security functions—such as state estimation, anomaly detection, and fault isolation—directly into the control logic using mathematically grounded frameworks. This chapter focuses on constructing a detailed model of ICS dynamics and designing an observer-based detection algorithm that can uncover replay and data-injection attacks in real time.

3.2. Mathematical Modeling of Cyber-Physical ICS Systems

We consider a discrete-time Linear Time-Invariant (LTI) model that encapsulates the internal state evolution and the observation process of the ICS:

$$\begin{array}{cc}\hfill x_{k+1}& =A{x}_k+B{u}_k+E{d}_k+w_k\hfill \\ \hfill y_k& =C{x}_k+F{a}_k+v_k\hfill \end{array}$$

(1)

where:

• $x_k\in {\mathbb{R}}^n$ is the internal state vector at time step k, where ${\mathbb{R}}^n$ denotes the n-dimensional space of real numbers, representing system variables such as temperature, pressure, motor speed, etc.
• $u_k\in {\mathbb{R}}^m$ denotes the control input vector applied by the controller to the actuators.
• $y_k\in {\mathbb{R}}^p$ is the measurement output vector collected by sensors and used for control decisions.
• $d_k\in {\mathbb{R}}^q$ captures exogenous disturbances like ambient noise, load fluctuations, or supply variability.
• $a_k\in {\mathbb{R}}^p$ models potential adversarial actions including sensor spoofing or replay.
• $w_k\sim \mathcal{N}(0,Q)$ and $v_k\sim \mathcal{N}(0,R)$ are zero-mean, uncorrelated Gaussian process and measurement noise, respectively.

The matrices $A,B,C$ define the nominal dynamic behavior and measurement relationships. E represents the entry point of environmental disturbances into the plant’s internal state, and F models the effect of an attacker who can manipulate sensor outputs (e.g., injecting malicious measurements).

This modeling framework is expressive enough to support multi-loop control architectures, where different state components may be regulated by separate feedback channels, and it accommodates extensions to switching or hybrid dynamics through the inclusion of time-varying matrices or mode-dependent parameters.

For complex deployments, the system can be modeled as multiple interconnected subsystems:

$$\begin{array}{c}\hfill x_{k+1}^{\left(i\right)}=A^{\left(i\right)}{x}_k^{\left(i\right)}+\sum _{j\in {\mathcal{N}}_i}{A}^{\left(ij\right)}{x}_k^{\left(j\right)}+B^{\left(i\right)}{u}_k^{\left(i\right)}+w_k^{\left(i\right)}\end{array}$$

(2)

Here, ${\mathcal{N}}_i$ denotes the set of subsystems interacting with subsystem i, and $A^{\left(ij\right)}$ captures coupling dynamics. In matrix notation, this yields a block-sparse system structure, which has implications for observability and decentralized detection.

3.3. State Observability and Sensor Configuration

The ability to reconstruct $x_k$ from outputs ${\left\{y_i\right\}}_{i=0}^k$ is essential for anomaly detection. Observability is defined through the rank condition of the observability matrix:

$$\begin{array}{c}\hfill \mathcal{O}=\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^{n-1}\end{array}\right]\end{array}$$

(3)

If $\mathrm{rank}\left(\mathcal{O}\right)=n$, the system is observable. Otherwise, some internal modes are hidden from measurement and can be exploited by an attacker without being detected. In practice, observability is not guaranteed globally but can be enhanced via sensor placement strategies and input design.

For systems with limited sensors, reduced-order or sliding mode observers may be used. However, in this study we assume full observability and design a standard full-order Luenberger observer for its simplicity and well-understood convergence properties.

3.4. Design of Secure State Observers

To detect deviations from expected behavior, a Luenberger observer is employed:

$$\begin{array}{cc}\hfill {\widehat{x}}_{k+1}& =A{\widehat{x}}_k+B{u}_k+L(y_k-{\widehat{y}}_k)\hfill \\ \hfill {\widehat{y}}_k& =C{\widehat{x}}_k\hfill \end{array}$$

(4)

The observer corrects its internal prediction using the innovation term $y_k-{\widehat{y}}_k$. The gain L determines the rate and stability of error convergence.

The estimation error $e_k=x_k-{\widehat{x}}_k$ evolves as:

$$e_{k+1}=(A-LC)e_k+E{d}_k+w_k-L{v}_k+LF{a}_k$$

(5)

In the absence of disturbances and attacks, the error dynamics reduce to $e_{k+1}=(A-LC)e_k$, and stability is achieved when all eigenvalues of $(A-LC)$ lie strictly within the unit circle in the complex plane.

In practical conditions, bounded disturbances cause the error to fluctuate within a noise-correlated envelope. The key insight is that under normal operation, $r_k=C{e}_k+v_k$ remains zero-mean and bounded, whereas in the presence of attacks the $LF{a}_k$ term drives $e_k$ and hence $r_k$ into a statistically distinct regime.

Robust Observer Design Considerations

Robust observer design involves selecting L not only to stabilize the error dynamics but also to minimize the sensitivity to noise while maximizing attack detectability. Techniques from $H_{\infty }$ estimation, LMI optimization, and fault-tolerant observer theory can be used to formulate this tradeoff. For instance, one may minimize the worst-case gain from disturbance input $d_k$ to residual output $r_k$:

$$\begin{array}{c}\hfill \underset{L}{min}\underset{d_k}{sup}{\displaystyle \frac{\parallel r_k\parallel }{\parallel d_k\parallel }}\end{array}$$

(6)

Such robust formulations offer better real-world performance, especially in systems with poor SNR or adversarial environments.

3.5. Modeling Replay and Other Attack Types

We focus primarily on replay attacks, but the framework generalizes to several canonical ICS attack models:

• Replay Attack: $y_k^a=y_{k-T_r}$; historical data are re-sent to hide deviations.
• Bias Injection: $y_k^a=y_k+b$; attacker adds a persistent offset to mislead the controller.
• DoS Attack: $y_k^a$ is missing; the communication channel is jammed or blocked.
• False Data Injection: $y_k^a=y_k+f_k$; dynamic corruption injected via compromised sensor.

The proposed observer-based mechanism can detect all of these, provided that the corruption leads to an observable deviation in $r_k$.

3.6. Residual Generation and Detection Algorithm

The residual signal is defined as:

$$\begin{array}{c}\hfill r_k=y_k-C{\widehat{x}}_k=C{e}_k+v_k+F{a}_k\end{array}$$

(7)

Under attack-free conditions:

$$\begin{array}{c}\hfill \mathbb{E}\left[r_k\right]=0,\mathrm{Var}\left(r_k\right)=C{\Sigma }_e{C}^T+R\end{array}$$

(8)

where ${\Sigma }_e$ is the steady-state covariance of $e_k$. This provides residual-based detection tests for deviations in mean or variance from these nominal statistics.

The complete detection logic is summarized in Algorithm 1. The algorithm operates in a real-time loop for each time step k. It begins by predicting the next system state based on the current estimate and control input (Line 3). It then calculates the residual by comparing the actual sensor measurement $y_k$ with the predicted output ${\widehat{y}}_k$ (Line 5). This residual is used to correct the state estimate (Line 6). Finally, a two-level check is performed: the instantaneous residual $|r_k|$ is compared against a static threshold $\tau$, and the cumulative sum of residuals, $S_k$, is compared against a dynamic threshold H. An alarm is triggered if either threshold is breached (Lines 8–10), allowing the system to detect both large, abrupt attacks and small, persistent ones.

Algorithm 1 Observer with Real-Time Residual Monitoring

Require:  $A,B,C,L,\tau ,H,\omega$, initial estimate ${\widehat{x}}_0$ Ensure:  Residual signal $r_k$, anomaly alert     1: Initialize: ${\widehat{x}}_0$, $S_0\leftarrow 0$     2: for $k=0$ to N do     3:       Predict: ${\widehat{x}}_{k+1}\leftarrow A{\widehat{x}}_k+B{u}_k$     4:       Output estimate: ${\widehat{y}}_k\leftarrow C{\widehat{x}}_k$     5:       Residual: $r_k\leftarrow y_k-{\widehat{y}}_k$     6:       Correction: ${\widehat{x}}_{k+1}\leftarrow {\widehat{x}}_{k+1}+L{r}_k$     7:       CUSUM update: $S_k\leftarrow max(0,S_{k-1}+|r_k|-\omega )$     8:       if $|r_k|>\tau$ or $S_k>H$ then     9:             Raise alert: Anomaly detected   10:       else   11:             Continue monitoring   12:       end if   13: end for

4. Theoretical Analysis and Performance Evaluation

4.1. Overview and Motivation

Robust detection of cyber-attacks in Industrial Control Systems (ICSs) hinges on a rigorous understanding of the theoretical behavior of the system under both nominal and adversarial conditions. This chapter presents an in-depth analysis of the state estimation error dynamics, residual behavior, and attack detectability for the observer-based framework introduced previously. We systematically analyze the stability of the error dynamics, the statistical properties of the residual signal, and the response of the system under various attack scenarios. Furthermore, we evaluate the detection performance using statistical metrics such as false alarm rate, detection delay, and missed detection probability, and highlight how different system parameters influence detection sensitivity and robustness.

4.2. Estimation Error Dynamics and Stability Analysis

Consider the estimation error defined as $e_k=x_k-{\widehat{x}}_k$. The evolution of $e_k$ is governed by the recursive difference equation:

$$e_{k+1}=(A-LC)e_k+E{d}_k+w_k-L{v}_k+LF{a}_k$$

(9)

In the absence of attacks ($a_k=0$) and disturbances ($d_k=0$), the system reduces to:

$$e_{k+1}=(A-LC)e_k+w_k-L{v}_k$$

(10)

We assume that the gain L is chosen such that all eigenvalues of $(A-LC)$ lie strictly inside the unit circle. Then, the homogeneous part of the system is asymptotically stable. The particular solution of the inhomogeneous system remains bounded if the noise terms are bounded in variance.

Define the covariance of the estimation error as:

$${\Sigma }_k=\mathbb{E}\left[e_k{e}_k^T\right]$$

(11)

Then, under stationary noise conditions, ${\Sigma }_k$ converges to a steady-state solution $\Sigma$ that satisfies the discrete-time Lyapunov equation:

$$\Sigma =(A-LC)\Sigma {(A-LC)}^T+Q+LR{L}^T$$

(12)

This equation establishes the statistical envelope within which the error $e_k$ fluctuates in normal operation. As a consequence, the residual $r_k=C{e}_k+v_k$ also has zero-mean and bounded covariance.

4.3. Residual Analysis Under Normal Conditions

In normal operation, the residual signal reflects the deviation between actual and predicted output:

$$r_k=y_k-C{\widehat{x}}_k=C{e}_k+v_k$$

(13)

Assuming $e_k$ and $v_k$ are uncorrelated Gaussian random variables, the residual $r_k$ is also Gaussian with:

$$\begin{array}{cc}\hfill \mathbb{E}\left[r_k\right]& =0\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill \mathrm{Cov}\left(r_k\right)& =C\Sigma C^T+R\hfill \end{array}$$

(15)

This allows one to construct probabilistic bounds such as:

$$\mathbb{P}({\parallel r_k\parallel }_2>\tau )\le ϵ$$

(16)

where $\tau$ is chosen based on a desired false alarm probability $ϵ$, assuming Gaussianity.

4.4. Residual Behavior Under Replay Attacks

During a replay attack, the controller receives outdated measurements:

$$y_k^a=y_{k-T_r}=C{x}_{k-T_r}+v_{k-T_r}$$

(17)

The observer, however, uses the current estimate ${\widehat{x}}_k$, resulting in the residual:

$$r_k^a=y_k^a-C{\widehat{x}}_k=C(x_{k-T_r}-{\widehat{x}}_k)+v_{k-T_r}$$

(18)

Assuming the state evolves significantly over $T_r$ time steps, the quantity $x_{k-T_r}-{\widehat{x}}_k$ becomes large, leading to a detectable change in $r_k^a$. Furthermore, the residual now has nonzero mean:

$$\mathbb{E}\left[r_k^a\right]=C(\mathbb{E}\left[x_{k-T_r}\right]-\mathbb{E}\left[{\widehat{x}}_k\right])\ne 0$$

(19)

This shift from a zero-mean distribution is the statistical basis for detection.

4.5. Detection Algorithms and Performance Metrics

We consider two standard detection schemes:

Static Threshold Detection: Trigger an alarm when ${\left|\right|r_k\left|\right|}_2>\tau$. The threshold $\tau$ is chosen using the distribution of $r_k$ under nominal conditions (e.g., $\tau =3\sigma$ for Gaussian noise). The False Alarm Rate (FAR) is given by:

$$FAR=\mathbb{P}\left(\right||r_k\left|\right|>\tau |H_0)=2\Phi (-{\displaystyle \frac{\tau }{\sigma }})$$

(20)

CUSUM Detection: To detect small but persistent shifts in the mean of the residual signal, which may be missed by simple static thresholding, we employ the Cumulative Sum (CUSUM) algorithm. CUSUM is a sequential analysis technique that accumulates deviations from a target value over time. It is particularly effective for identifying gradually growing or stealthy attacks. The CUSUM statistic, $S_k$, is defined as:

$$S_k=max(0,S_{k-1}+|r_k|-\omega )$$

(21)

hlAn alarm is triggered if $S_k$ exceeds a predefined threshold H. The parameter $\omega$ (drift) is a slack parameter, typically chosen based on the expected noise level, which allows the algorithm to ignore minor fluctuations while remaining sensitive to true changes in the mean.

4.6. Detection Delay and Sensitivity Analysis

Define the detection delay D as the expected number of samples between the start of an attack and its detection. In CUSUM detection, the Average Detection Delay (ADD) under an attack with residual mean shift ${\mu }_a$ is:

$$\mathrm{ADD}\approx {\displaystyle \frac{H}{{\mu }_a-\omega }}$$

(22)

Hence, attacks that induce a small ${\mu }_a$ are harder to detect and require longer monitoring windows. The tradeoff between detection sensitivity and false alarms is governed by the gap between ${\mu }_a$ and $\omega$.

4.7. Robustness Considerations

In practice, model uncertainties, time delays, and noise mismatch can impair detection reliability. The following factors affect detection performance:

• Model mismatch: Incorrect matrices A, B, or C distort observer predictions.
• Parameter tuning: Thresholds $\tau$ and H and drift term $\omega$ must be calibrated based on historical data.
• Sensor placement: Redundant and strategically located sensors improve observability and residual quality.
• Correlated noise: Assumptions of Gaussian i.i.d. noise may not hold in practice.

Techniques such as adaptive thresholds, robust observers, and Kalman filtering with covariance adaptation can be used to mitigate these issues.

5. Simulation Verification

To empirically validate the proposed defense mechanism and rigorously assess its performance, a comprehensive simulation was conducted using MATLAB/Simulink. The experiment is designed to evaluate the Luenberger observer’s ability to identify common data integrity attacks within an Industrial Control System (ICS) environment, analyzing its detection delay, robustness, and limitations compared to an optimal state estimator.

5.1. Simulation Setup

The simulation environment was configured to closely mirror a realistic control process under attack.

• System and Observer Initialization: The simulation was run for 100 discrete time steps. The initial state of the system was set to $x_0={[0,0]}^T$, and the observer’s initial estimate was also initialized to ${\widehat{x}}_0={[0,0]}^T$ to simulate a scenario where the observer starts with perfect knowledge, isolating the effects of subsequent attacks. A constant control input $u_k=0.5$ was applied throughout the simulation to ensure persistent system excitation.
• Noise and Process Parameters: The system dynamics were subject to zero-mean Gaussian process noise $w_k$ and measurement noise $v_k$, with covariance matrices $Q=0.001·I$ and $R=0.01·I$, respectively. These values represent typical levels of process disturbances and sensor inaccuracies in industrial settings.
• Detection Threshold: Anomaly detection relies on a residual-based method. An attack is flagged if the absolute magnitude of the residual, $|r_k|$, exceeds a predefined threshold $\tau$. To balance detection sensitivity with a low false alarm rate, the threshold was determined based on the statistical properties of the residual during normal (attack-free) operation. The threshold was set to $\tau =3{\sigma }_r$, where ${\sigma }_r$ is the standard deviation of the residual under noise, effectively implementing a 3-sigma rule. This ensures that the probability of a false positive in any given time step is less than 0.3%.

5.2. System Simulation and Defense Model

The industrial process is modeled as a discrete-time Linear Time-Invariant (LTI) system, described by the state-space equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{k+1}=A{x}_k+B{u}_k+w_k\hfill \\ y_k=C{x}_k+v_k\hfill \end{array}\right.\end{array}$$

(23)

where $x_k\in {\mathbb{R}}^2$ is the system state, $u_k\in \mathbb{R}$ is the control input, and $y_k\in \mathbb{R}$ is the sensor measurement. The system parameters were defined as:

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}1.0& 0.1\\ 0& 1.0\end{array}\right],\hspace{0.33em}B=\left[\begin{array}{c}0\\ 0.1\end{array}\right],\hspace{0.33em}C=\left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(24)

The primary defense mechanism is a Luenberger observer, designed with a fixed gain of $L={[0.8,0.2]}^T$. The observer detects anomalies by analyzing the residual signal $r_k=y_k-{\widehat{y}}_k$, where ${\widehat{y}}_k=C{\widehat{x}}_k$ is the estimated output. The key characteristic of this observer is its static nature; its gain does not change in response to measurement data. For comparison, a standard Kalman filter was also simulated. As an optimal state estimator, the Kalman filter dynamically adjusts its gain at each time step to minimize the estimated state error covariance. This fundamental difference in design philosophy directly impacts their performance as attack detectors.

5.3. Attack Scenarios and Detection Analysis

To comprehensively evaluate the observer’s performance, three distinct data integrity attacks were simulated, each launched between time steps $k=40$ and $k=60$.

5.3.1. False Data Injection (FDI) Attack

In this scenario, the attacker injects a constant malicious offset, $f_k=2.0$, into the sensor measurements, making the compromised output $y_k^a=y_k+f_k$. This attack directly corrupts the data received by the controller and observer.

Results and Analysis: As shown in Figure 1 and summarized in

Table 1. Quantitative performance summary of the Luenberger observer.

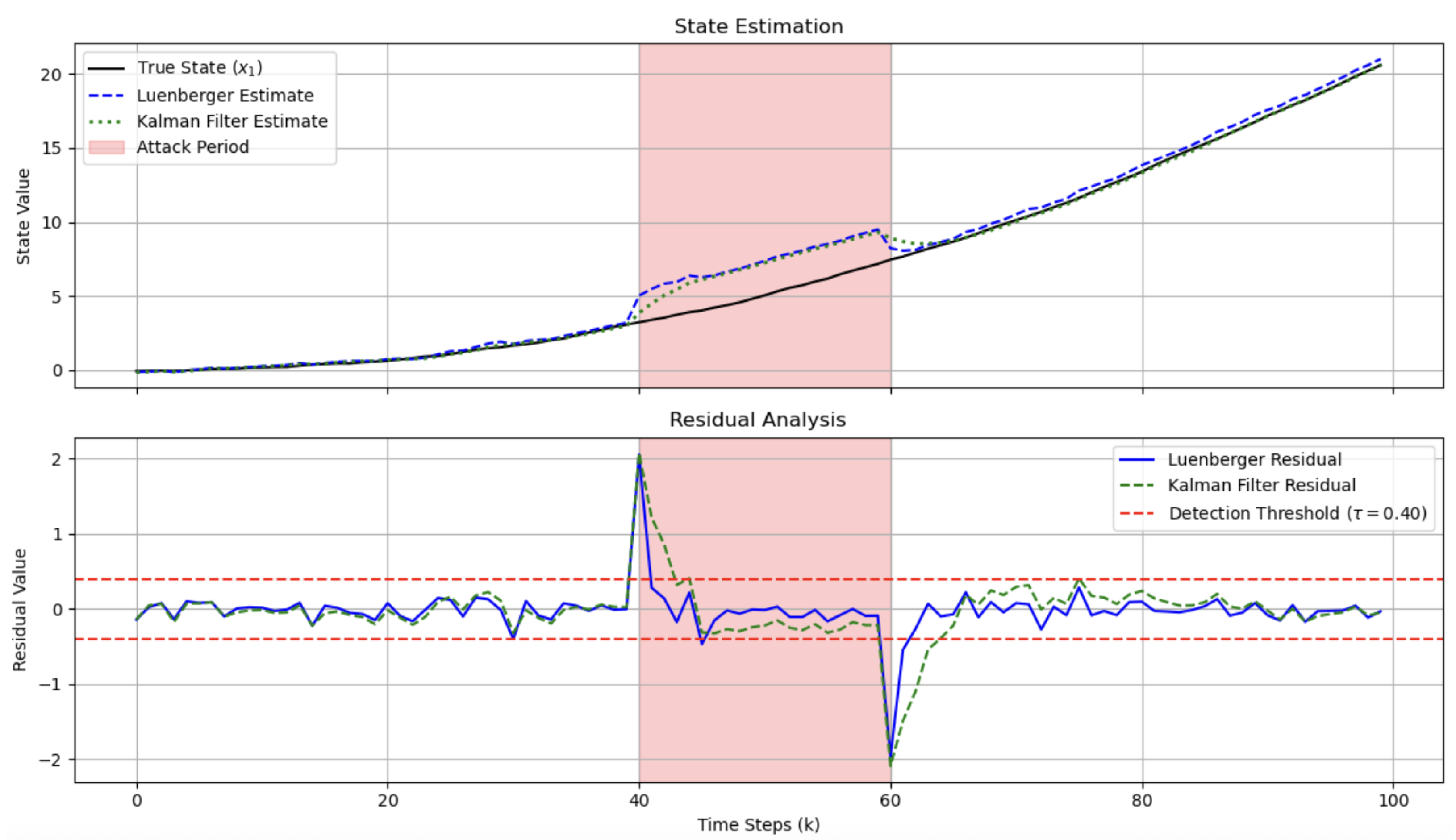
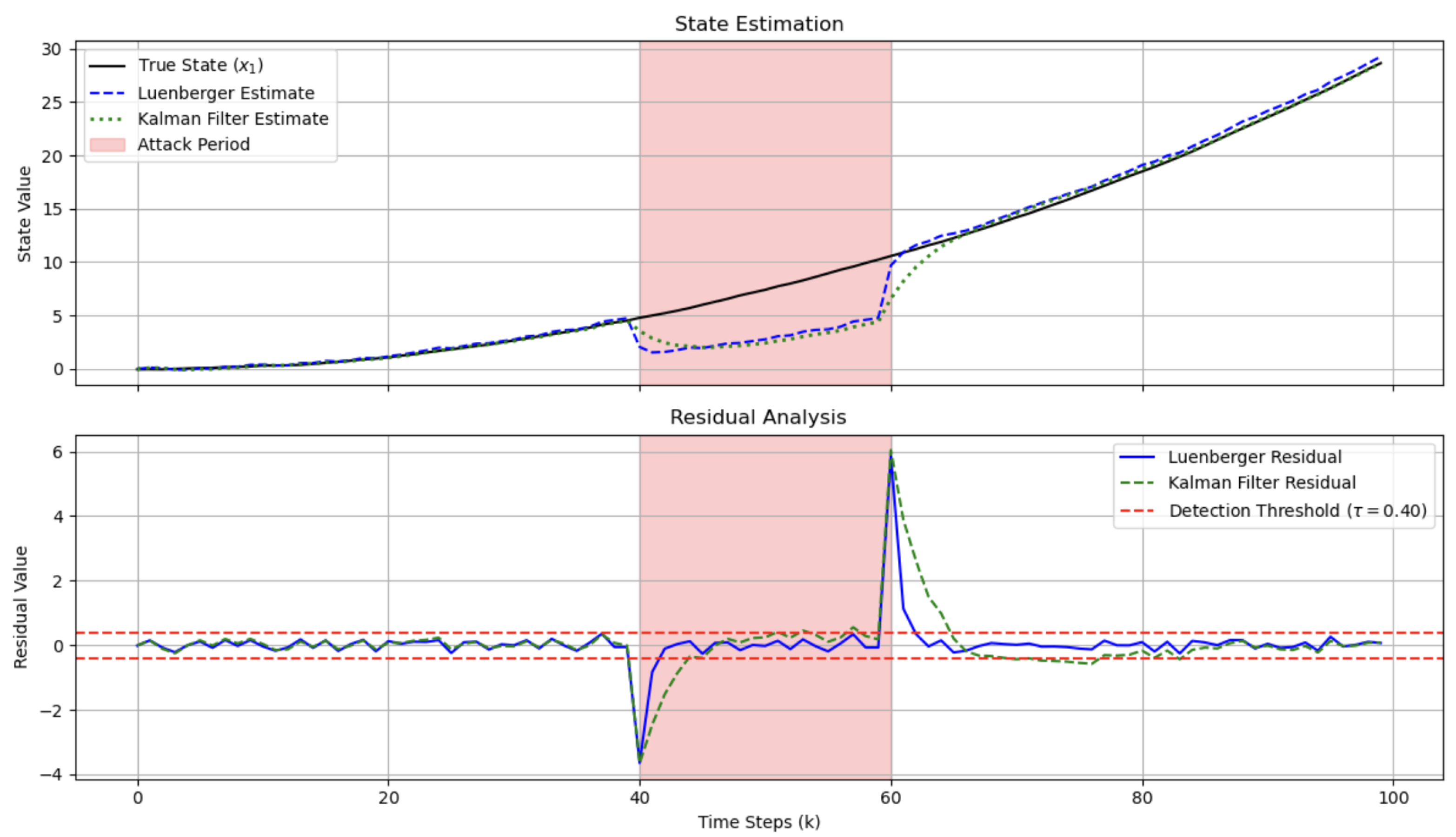
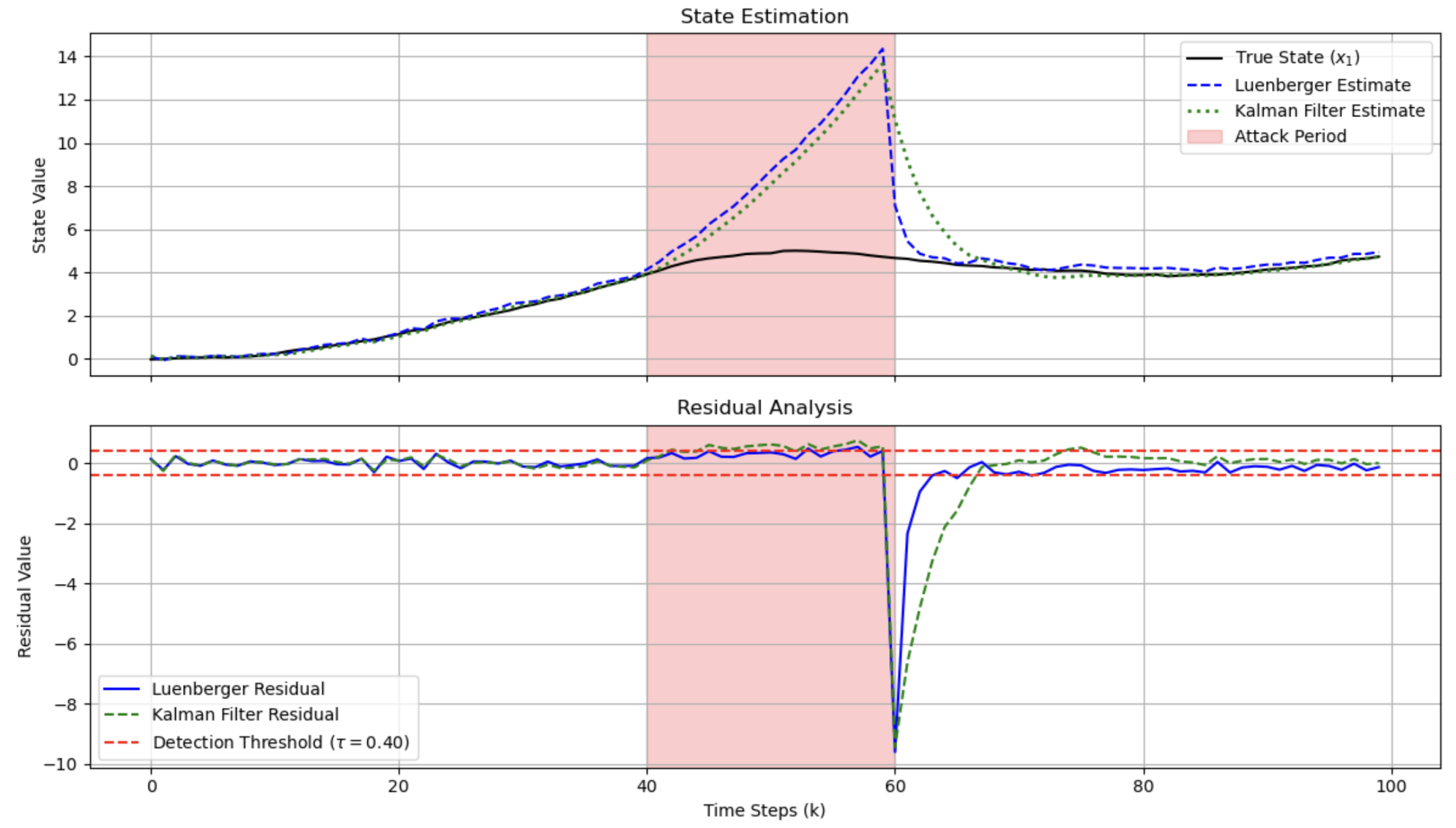
Attack Scenario	Detection Outcome	Detection Delay (Time Steps)
False Data Injection (FDI)	Success	1
Replay Attack	Success	1
Covert Attack	Fail	N/A 1

¹ N/A: Not Applicable. The detection delay is not applicable because the covert attack was not detected by the system.

, the Luenberger observer’s residual exhibits an immediate and sharp deviation from zero the moment the FDI attack begins at k = 40. The attack is successfully detected, crossing the detection threshold $\tau$ in the very first step of the attack (Detection Delay = 1). Because the observer gain L is fixed, it continuously expects measurements consistent with the original system model, treating the injected offset as a persistent anomaly. This results in a sustained alarm throughout the attack period. In contrast, while the Kalman filter’s residual initially spikes, it quickly diminishes. This occurs because the Kalman filter, designed for optimal estimation in the presence of noise, adapts its state estimate to what it perceives as new valid measurements. It effectively “learns” the attack’s offset, causing its residual to fall back within the normal bounds, thereby failing to provide a continuous alarm.

5.3.2. Replay Attack

The replay attack involves recording legitimate sensor data and re-transmitting it later. In the simulation, the current sensor output $y_k$ is replaced by a past measurement, $y_{k-T_r}$, where the delay $T_r$ was set to 20 steps. This attack is stealthy because the replayed values are individually valid, just temporally incorrect.

Results and Analysis: The simulation results in Figure 2, and quantified in Table 1, highlight the observer’s effectiveness against replay attacks. Although the replayed data point $y_{k-20}$ was valid when recorded, the system’s state has evolved due to the control input $u_k$ and internal dynamics. Consequently, the stale measurement does not align with the observer’s predicted output ${\widehat{y}}_k$, which is based on the estimated current state. This temporal inconsistency causes the residual $r_k$ to grow significantly, quickly crossing the detection threshold. The state estimate from the Luenberger observer visibly diverges from the true state, demonstrating that any attack breaking the temporal consistency of the system dynamics can be reliably detected.

5.3.3. Covert Attack

The covert attack is a sophisticated scenario where the attacker manipulates both the control input $u_k$ and the sensor output $y_k$ simultaneously. The goal is to alter the system’s physical state while ensuring the manipulated output $y_k^a$ appears consistent with the manipulated input $u_k^a$, thereby keeping the observer’s residual low.

Results and Analysis: Figure 3 illustrates the challenge posed by covert attacks, with the outcome noted in Table 1. By design, the attacker crafts the sensor signal to perfectly match the expected output of the compromised system dynamics. As a result, the residuals of both the Luenberger observer and the Kalman filter remain close to zero, and the attack goes completely undetected by the residual-based method. Both observers are successfully deceived into tracking a false state that does not correspond to the true physical state of the system, which diverges dangerously due to the hidden manipulation of the control input. This result underscores a fundamental limitation: an observer can only detect attacks that create a mismatch between the received measurements and the mathematical model it relies on.

5.4. Overall Performance and Discussion

The simulation study validates that the Luenberger observer is a lightweight and effective mechanism for detecting data integrity attacks like FDI and replay in industrial control systems. The superior performance against these attacks compared to the standard Kalman filter is a key finding. As discussed in Section 2.2, adaptive estimators like the Kalman filter can be deceived by persistent attacks because they treat the malicious data as a new normal, adjusting their state estimate accordingly. Our results in Figure 1 provide clear empirical evidence of this vulnerability. In contrast, the fixed-gain Luenberger observer continuously generates a large residual, demonstrating its robustness for security monitoring where the goal is to detect deviations from a fixed, trusted model, not adapt to them.

However, the experiment also highlights a critical limitation shared by many model-based detectors: its vulnerability to well-designed covert attacks (Figure 3). This finding is consistent with research on undetectable attack spaces [13], which shows that any observer-based method can be bypassed if the attacker has sufficient knowledge of the system model to manipulate both sensor and actuator signals simultaneously. This underscores that our proposed method is not a panacea but should be considered a foundational layer in a defense-in-depth strategy.

The choice of observer gain L and detection threshold tau also presents a fundamental trade-off. A higher gain leads to faster error convergence and quicker detection but increases sensitivity to measurement noise, potentially raising the false alarm rate. Conversely, a lower gain provides smoother estimation but may result in a longer detection delay. These parameters must be carefully calibrated for the specific process to balance detection sensitivity and operational stability.

6. Conclusions

This paper proposed and validated an endogenous security defense mechanism for industrial control systems based on a Luenberger observer and residual analysis. By leveraging a mathematical model of the system’s physical dynamics, the method provides a lightweight and real-time approach to detecting data integrity attacks. The theoretical analysis and simulation results confirmed that replay attacks induce a significant, detectable deviation in the observer’s residual signal, allowing for detection with minimal delay and high accuracy. This model-based approach does not rely on attack signatures and is computationally efficient, making it well-suited for deployment on resource-constrained devices within an ICS architecture.

Limitations and Future Work

While this foundational study demonstrates the viability of using a non-adaptive observer for security, we acknowledge several limitations that frame important directions for future research.

First, the proposed method is, by design, vulnerable to sophisticated covert attacks, as demonstrated in our simulations. This is a fundamental limitation of any single observer-based approach. Future work should focus on integrating this lightweight detector into a multi-layered defense strategy, potentially combined with methods like moving target defense or cryptographic verification to address such advanced threats.

Second, this study relied on several simplifying assumptions, namely that the system is linear and fully observable, and that observer gains and detection thresholds were manually tuned. These choices were made to establish a clear and tractable proof-of-concept. A critical next step is to extend this approach to nonlinear systems using techniques like extended or unscented observers. Furthermore, robust and optimal design methods, such as LMI optimization or H-infinity techniques, as suggested by the reviewer, should be investigated to systematically tune the observer gain for improved performance and disturbance rejection.

Finally, the validation was conducted entirely within a MATLAB simulation environment. While this provides a controlled and reproducible setting, the ultimate test requires real-world evaluation. Therefore, future work must include Hardware-in-the-Loop (HIL) testing and validation on a physical ICS testbed to assess the method’s performance and robustness under practical operational conditions.

Future work could extend this research by applying the method to more complex, nonlinear system models and validating it on a physical testbed. While this study demonstrated the mechanism’s effectiveness against common attacks, its primary limitation, as shown, is its inability to detect sophisticated covert attacks. Future research should investigate integrating this lightweight observer with complementary defense layers, such as moving target defense or cryptographic verification, to address this vulnerability. Furthermore, a critical next step is to conduct a comprehensive quantitative comparison with other state-of-the-art methods using large-scale datasets. This would involve evaluating performance using standard metrics such as detection rate, accuracy, precision, and recall to rigorously benchmark our approach against established techniques.