Optimal Consumption, Portfolio, and Retirement Under Implementation Delay

Abstract

We develop a continuous-time model of optimal consumption, portfolio allocation, and early retirement that, to our knowledge, is the first to incorporate an implementation delay —a fixed lag $\delta$ between the retirement decision and the actual cessation of labor and income. Using a dual-martingale approach, we obtain closed-form solutions and quantify how $\delta$ affects optimal behavior. For example, when $\delta$ increases from $0.5$ to 2 years (baseline parameters: $\beta =0.04$, $r=0.02$, $\mu =0.08$, $\sigma =0.2$, $\gamma =3$, $k_B=0.3$, and $\epsilon =1$), optimal pre-retirement consumption rises by approximately 7%, the risky asset share falls by about 5 percentage points, the expected retirement time increases by over 1 year, and the retirement wealth threshold $x_R$ grows by roughly 10%. These results provide policy-relevant insights for retirement systems where procedural lags can distort incentives and reduce welfare.

1. Introduction

The decision of when to retire is one of the most consequential financial choices individuals face over their lifetime. Early retirement, in particular, has far-reaching implications for personal well-being, financial preparedness, and the sustainability of public pension systems. As demographic trends continue to pressure retirement systems globally, understanding the economic mechanisms that govern early retirement behavior has become increasingly important—both for optimizing individual financial planning and for designing effective policy interventions.

A substantial body of literature in financial economics has analyzed the early retirement problem under a utility maximization framework. In these models, individuals choose the retirement timing endogenously along with their consumption and investment strategies in a complete financial market (see, e.g., Choi and Shim [1], Farhi and Panageas [2], Choi et al. [3], Dybvig and Liu [4], Lim and Kwak [5], Lim et al. [6] and references therein). These studies offer key insights into how financial incentives, preferences, and market parameters affect optimal lifecycle behavior.

However, one important institutional feature has been largely overlooked in this literature: the presence of an implementation delay between the decision to retire and the actual commencement of retirement. In practice, retirement does not take effect instantaneously. Rather, it is often subject to administrative, contractual, or logistical delays. For instance, pension schemes may require workers to submit notice months in advance, and benefits may not begin until the official retirement date. This delay alters the timing of utility and income realization, affecting both the incentive to retire and the dynamics of consumption and investment in the interim.

To the best of our knowledge, no prior work within the utility maximization tradition explicitly models such an implementation delay in the early retirement setting. Filling this gap is the primary goal of this paper. We develop a continuous-time optimal consumption and portfolio problem in which the agent endogenously selects a retirement time $\tau$, but actual retirement occurs at $\tau +\delta$, where $\delta >0$ is a fixed delay. During the interim $[\tau ,\tau +\delta ]$, the agent continues to receive labor income but derives reduced utility from consumption, modeled by a multiplicative utility weight $k_B\in (0,1)$, capturing the diminished enjoyment of consumption while still working.

We solve the problem using the dual-martingale approach of Karatzas and Wang [7], which reduces the original stochastic control problem to a dual optimal stopping problem. We prove a duality theorem and derive explicit closed-form solutions for the optimal consumption rule, portfolio strategy, and retirement threshold. Importantly, our analysis shows how the delay parameter $\delta$ fundamentally alters optimal behavior: a longer delay leads to higher pre-retirement consumption, lower risk-taking, delayed retirement, and a higher wealth threshold at which retirement is triggered. We also derive explicit expressions for the expected retirement time and the agent’s human capital, showing their systematic dependence on $\delta$.

The notion of implementation delay has previously been studied in the context of optimal stopping problems by Oksendal [8] and subsequently in applications such as real options (Alvarez and Keppo [9], Delaney [10], Jeon [11]) and American options with execution lags (Liang and Yang [12]). Our contribution is to introduce this concept into the context of household finance and early retirement, thereby extending its economic relevance to personal decision-making under institutional frictions.

In practice, pension systems in many countries experience procedural delays in the disbursement of retirement benefits, ranging from a few weeks to several months, due to administrative processing, eligibility verification, and institutional backlogs. Such institutional lags have the potential to affect individual retirement decisions. Motivated by this observation, we explicitly incorporate an implementation delay parameter into the theoretical framework.

To the best of our knowledge, this study is the first in the literature on retirement and portfolio choice to do so. This extension introduces substantial theoretical challenges, as the delay parameter $\delta$ alters both the timing of utility flows and the wealth dynamics, leading to a coupled optimal stopping and control problem in continuous time. From a computational perspective, solving the model requires handling a two-dimensional free boundary problem in the dual space, which significantly increases the complexity relative to standard retirement models without delay. While our quantitative illustrations are based on hypothetical parameter values for clarity and tractability, the framework can readily accommodate empirically estimated parameters from real-world pension systems. Incorporating such empirical calibration, as well as benchmarking against alternative retirement models, would be valuable directions for future work to further validate and contextualize our findings.

Our work builds on the foundational continuous-time consumption and portfolio choice framework of Merton [13] and its extensions to incorporate uncertain lifetimes [14], retirement timing [1], and labor–leisure trade-offs. More recent studies have integrated realistic institutional features into optimal retirement models, such as social security claiming options and family status [15], individual account guarantees [16], and labor supply decisions across business cycles [17]. By introducing an explicit implementation delay parameter, our model contributes to this growing literature on institutional and behavioral determinants of retirement, offering a novel channel through which policy and market frictions influence individual financial decisions.

In addition to the recent studies, we also revisit seminal works that form the foundation of retirement and portfolio choice theory, ensuring that the conceptual lineage of our model is clear. These include the lifecycle consumption framework, portfolio rebalancing under risk aversion, and the treatment of retirement as an optimal stopping problem. This expanded review clarifies how our framework connects to, and departs from, the most influential models in the literature.

Many countries are implementing delayed retirement policies in response to demographic aging and fiscal pressures. In this policy environment, understanding the trade-offs associated with early retirement under institutional delays is especially important. Our framework isolates the impact of such delays on individual decision-making, thereby offering a tool to assess how changes in pension processing speed or access rules could influence both micro-level behavior and macro-level retirement patterns.

The remainder of this paper is structured as follows. Section 2 presents the model setup and defines the agent’s optimization problem. Section 3 derives the closed-form solution using the duality approach. Section 4 investigates the role of the delay parameter $\delta$ through comparative statics and discusses policy implications. Section 5 concludes.

2. Model

We consider a continuous-time optimal consumption and portfolio choice problem in which the agent faces an infinite planning horizon and makes an endogenous retirement decision. A key feature of our model is the presence of a delay between the retirement decision and its actual implementation. That is, when the agent decides to retire at a stopping time $\tau$, the retirement takes effect only at time $\tau +\delta$, where $\delta >0$ represents a fixed operational delay arising from administrative, contractual, or transitional issues.

We consider a standard financial market with one risk-free asset and one risky asset. The risk-free asset yields a constant interest rate $r>0$. The risky asset price $S_t$ follows a geometric Brownian motion (GBM):

$$d{S}_t=\mu S_{t}dt+\sigma S_{t}d{B}_t,$$

(1)

where $\mu >r$ and $\sigma >0$. All stochastic processes are defined on a filtered probability space $(\Omega ,\mathbb{F},{\left({\mathcal{F}}_t\right)}_{t\ge 0}\mathbb{P})$ satisfying the usual conditions, and all controls are adapted to the available information flow. Here, ${\mathcal{F}}_t$ is the natural filtration generated by ${\left(B_s\right)}_{s\in [0,t]}$.

During the working period (i.e., for $t<\tau +\delta$), the agent receives a constant labor income $ϵ>0$. After retirement becomes effective, labor income ceases and consumption is funded solely from accumulated wealth.

Let ${\pi }_t$ denote the monetary amount the agent invests in the risky asset at time t and $c_t$ the consumption rate. The agent’s wealth process $X_t$ then evolves according to

$$d{X}_t=\left[r{X}_t+(\mu -r){\pi }_t-c_t+ϵ·{\mathbf{1}}_{\{t<\tau +\delta \}}\right]dt+\sigma {\pi }_{t}d{B}_t,$$

(2)

with initial wealth $X_0=x$. The indicator function ${\mathbf{1}}_{\{t<\tau +\delta \}}$ ensures that the labor income $ϵ$ is received only during the working period.

The agent derives utility from consumption over the entire horizon, but we distinguish between the pre- and post-retirement periods. As in Dybvig and Liu [4], to capture the disutility of simultaneously working and consuming, we assume that the utility from consumption before retirement is discounted by a multiplicative factor $k_B\in (0,1)$.

We assume that the agent’s preferences are represented by a constant relative risk aversion (CRRA) utility function:

$$u\left(c\right)={\displaystyle \frac{c^{1-\gamma }}{1-\gamma }},\gamma >0,\gamma \ne 1.$$

(3)

We are now ready to formally define the agent’s optimization problem. Given initial wealth $x>-{\displaystyle \frac{\epsilon }{r}}$, the agent aims to choose a retirement time $\tau$, a consumption process c, and a portfolio process $\pi$ to maximize expected discounted utility:

Problem 1. 

Let $x>-{\displaystyle \frac{\epsilon }{r}}$ be given. The agent’s value function is defined as

$$V\left(x\right)=\underset{(\tau ,c,\pi )\in \mathcal{A}\left(x\right)}{sup}\mathbb{E}\left[{\int }_0^{\tau +\delta }{e}^{-\beta t}u\left(k_B{c}_t\right)dt+{\int }_{\tau +\delta }^{\infty }{e}^{-\beta t}u\left(c_t\right)dt\right],$$

(4)

where $\beta >0$ is the subjective discount rate and $\mathcal{A}\left(x\right)$ denotes the set of all admissible strategies $(\tau ,c,\pi )$ such that τ is an $\mathbb{F}$-stopping time taking values in $[0,\infty )$; $c_t\ge 0$ and ${\pi }_t$ are $\mathbb{F}$-progressively measurable processes satisfying ${\int }_0^t(c_s+{\pi }_s^2)ds<\infty$ almost surely (a.s.) for all $t\ge 0$; and the wealth process $X_t$ respects the natural borrowing constraint $X_t\ge -{\displaystyle \frac{\epsilon }{r}}$ for all $t\ge 0$.

To ensure that the optimization problem is well-posed and the value function remains finite, we impose the following technical assumption on the model parameters:

$$K:=r+{\displaystyle \frac{\beta -r}{\gamma }}+{\displaystyle \frac{\gamma -1}{2{\gamma }^2}}{\theta }^2>0,\mathrm{where}\theta :={\displaystyle \frac{\mu -r}{\sigma }}.$$

(5)

This condition guarantees a proper trade-off between impatience, risk preferences, and investment opportunities and ensures that the agent does not accumulate infinite utility. The constant K is commonly referred to as the Merton constant (see Merton [13], Merton [18]).

Assumption 1. 

We assume constant labor income ε and a fixed disutility factor $k_B\in (0,1)$ before retirement. These simplifying assumptions allow us to isolate and analyze the impact of the implementation delay δ without additional confounding dynamics. In practice, labor income may evolve stochastically over time, and the disutility factor could vary with age, health, or labor conditions. Exploring time-varying or stochastic specifications for these elements is a natural extension for future research.

3. Optimization Problem

In this section, we briefly outline the solution approach to the agent’s utility maximization problem defined in Problem 1. Since the infinite-horizon retirement problem has been extensively studied in the utility maximization literature within the mathematical finance framework (see, e.g., Choi and Shim [1], Choi et al. [3], Jeon and Koo [19], Jeon et al. [20]), we omit detailed proofs.

In our model, since the stock price $S_t$ follows a GBM, the stochastic discount factor ${\xi }_t$ is given by

$${\xi }_t:=e^{-(r+{\displaystyle \frac{1}{2}}{\theta }^2)t-\theta B_t}.$$

(6)

Here, $\theta$ defined in (5) denotes the market price of risk.

As shown by Karatzas and Wang [7], under retirement delay, the wealth dynamics $X_t$ in (2) can be rewritten as the following static budget constraint:

$$\mathbb{E}\left[{\int }_0^{\tau +\delta }{\xi }_t(c_t-\epsilon )dt+{\int }_{\tau +\delta }^{\infty }{\xi }_t{c}_{t}dt\right]\le x.$$

(7)

Using the static budget constraint in (7), we can define the Lagrangian $\mathfrak{L}$ associated with Problem 1. For any given $y>0$ and $(\tau ,c,\pi )\in \mathcal{A}\left(x\right)$, the Lagrangian is given by

$$\begin{array}{cc}\hfill \mathfrak{L}:=& \mathbb{E}\left[{\int }_0^{\tau +\delta }{e}^{-\beta t}u\left(k_B{c}_t\right)dt+{\int }_{\tau +\delta }^{\infty }{e}^{-\beta t}u\left(c_t\right)dt\right]+y\left(x-\mathbb{E}\left[{\int }_0^{\tau +\delta }{\xi }_t(c_t-\epsilon )dt+{\int }_{\tau +\delta }^{\infty }{\xi }_t{c}_{t}dt\right]\right),\hfill \end{array}$$

(8)

where ${\mathbb{E}}_t:=\mathbb{E}[·\mid {\mathcal{F}}_t]$ denotes the conditional expectation given the filtration ${\mathcal{F}}_t$, $y>0$ is the Lagrangian multiplier of the static budget constraint (7), and ${\mathcal{Y}}_t^y:=y{e}^{\beta t}{\xi }_t$ is the dual process.

Consider the dual conjugate function $\tilde{u}(·)$ associated with the utility function $u(·)$, defined as

$$\tilde{u}\left(y\right)=\underset{c\ge 0}{sup}\left(u\left(c\right)-yc\right)={\displaystyle \frac{\gamma }{1-\gamma }}{y}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}.$$

Using this, we obtain the following inequality: for all $(\tau ,c,\pi )\in \mathcal{A}\left(x\right)$,

$$\begin{array}{cc}\hfill \mathfrak{L}\le \mathbb{E}& [{\int }_0^{\tau }{e}^{-\beta t}\left(\tilde{u}({\displaystyle \frac{{\mathcal{Y}}_t^y}{k_B}})+ϵ{\mathcal{Y}}_t^y\right)dt+{\mathbb{E}}_{\tau }\left[{\int }_{\tau }^{\tau +\delta }{e}^{-\beta t}\left(\tilde{u}({\displaystyle \frac{{\mathcal{Y}}_t^y}{k_B}})+ϵ{\mathcal{Y}}_t^y\right)dt+{\int }_{\tau +\delta }^{\infty }{e}^{-\beta t}\tilde{u}\left({\mathcal{Y}}_t^y\right)dt\right]]\hfill \\ & +yx,\hfill \end{array}$$

(9)

By the first-order condition, we derive a candidate for the optimal consumption process ${\widehat{c}}_t$ as follows:

$${\widehat{c}}_t:=\widehat{c}\left({\mathcal{Y}}_t^y\right)=\left\{\begin{array}{cc}{k}_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1}{\gamma }}},\hfill & \mathrm{for}0\le t<\tau +\delta ,\hfill \\ {\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1}{\gamma }}},\hfill & \mathrm{for}t\ge \tau +\delta .\hfill \end{array}\right.$$

(10)

That is, the inequality in (9) becomes an equality when $c_t$ is replaced by the candidate ${\widehat{c}}_t$.

Let us define the auxiliary function $J_R^{\delta }\left(y\right)$ as

$$J_R^{\delta }\left(y\right):=\mathbb{E}\left[{\int }_0^{\delta }{e}^{-\beta t}\left(k_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}{\displaystyle \frac{\gamma }{1-\gamma }}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+\epsilon {\mathcal{Y}}_t^y\right)dt+{\int }_{\delta }^{\infty }{e}^{-\beta t}{\displaystyle \frac{\gamma }{1-\gamma }}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}dt\right].$$

(11)

Theorem 1. 

The following weak duality holds:

$$\begin{array}{cc}\hfill V\left(x\right)\le & \underset{y>0}{inf}\left(\underset{\tau \in \mathcal{U}}{sup}\mathbb{E}\left[{\int }_0^{\tau }{e}^{-\beta t}\left(k_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}{\displaystyle \frac{\gamma }{1-\gamma }}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+ϵ{\mathcal{Y}}_t^y\right)dt+e^{-\beta \tau }{J}_R^{\delta }\left({\mathcal{Y}}_{\tau }^y\right)\right]+yx\right).\hfill \end{array}$$

(12)

Proof. 

Since ${\mathcal{Y}}_t^y=y{e}^{(\beta -r-{\displaystyle \frac{1}{2}}{\theta }^2)t-\theta B_t}$, direct computation yields

$$J_R^{\delta }\left(y\right)={\displaystyle \frac{1-e^{-K\delta }}{K}}·k_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}·{\displaystyle \frac{\gamma }{1-\gamma }}{y}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+{\displaystyle \frac{1-e^{-r\delta }}{r}}·\epsilon y+{\displaystyle \frac{e^{-K\delta }}{K}}·{\displaystyle \frac{\gamma }{1-\gamma }}{y}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}.$$

(13)

By the strong Markov property, we have

$$J_R^{\delta }\left({\mathcal{Y}}_{\tau }^y\right)={\mathbb{E}}_{\tau }\left[{\int }_{\tau }^{\tau +\delta }{e}^{-\beta t}\left(k_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}{\displaystyle \frac{\gamma }{1-\gamma }}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+ϵ{\mathcal{Y}}_t^y\right)dt+{\int }_{\tau +\delta }^{\infty }{e}^{-\beta t}{\displaystyle \frac{\gamma }{1-\gamma }}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}dt\right].$$

(14)

From (8), (9), and (14), we have just obtained desired results. □

We now can define the dual problem.

Problem 2. 

Let $y>0$ be given. Then the dual value function $J\left(y\right)$ is formulated as the following optimal stopping problem:

$$J\left(y\right):=\underset{\tau \in \mathcal{U}}{sup}\mathbb{E}\left[{\int }_0^{\tau }{e}^{-\beta t}\left(k_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}{\displaystyle \frac{\gamma }{1-\gamma }}{\left({\mathcal{Y}}_t^y\right)}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+ϵ{\mathcal{Y}}_t^y\right)dt+e^{-\beta \tau }{J}_R^{\delta }\left({\mathcal{Y}}_{\tau }^y\right)\right].$$

(15)

The retirement problem combines continuous portfolio consumption choice with a discrete retirement decision, making it a mixed control/stopping problem. Following Karatzas and Wang [7], we introduce the stochastic discount factor and transform the dynamic budget constraint into a static one, parameterized by the Lagrange multiplier y. This dual transformation converts the original problem into an optimal stopping problem in the dual variable ${\mathcal{Y}}_t^y$, where stopping corresponds to retirement. This reduction allows us to apply standard optimal stopping theory and obtain closed-form solutions.

According to the well-established theory of infinite-horizon optimal stopping, there exists a critical threshold $z_R>0$ such that the optimal stopping time solving Problem 2 is given by

$$\widehat{\tau }\left(y\right)=inf\{t\ge 0\mid {\mathcal{Y}}_t^y\le z_R\}.$$

(16)

Then, on the domain $y\in (z_R,\infty )$, the value function $J\left(y\right)$ satisfies the following ordinary differential equation (ODE):

$${\displaystyle \frac{{\theta }^2}{2}}{y}^2{J}^{″}\left(y\right)+(\beta -r)y{J}^{\prime }\left(y\right)-\beta J\left(y\right)+k_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}·{\displaystyle \frac{\gamma }{1-\gamma }}{y}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+\epsilon y=0.$$

Moreover, at the boundary $y=z_R$, the smooth-pasting condition (i.e., the $C^1$ matching condition) holds:

$$J\left(z_R\right)=J_R^{\delta }\left(z_R\right)\mathrm{and}{J}^{\prime }\left(z_R\right)={\left(J_R^{\delta }\right)}^{\prime }\left(z_R\right).$$

For $y>z_R$, we express the general solution of $J\left(y\right)$ as

$$J\left(y\right)=C{y}^{n_2}+{\displaystyle \frac{1}{K}}{k}_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}·{\displaystyle \frac{\gamma }{1-\gamma }}{y}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+{\displaystyle \frac{\epsilon }{r}}y,$$

(17)

where $n_2$ is the negative root of the quadratic equation

$${\displaystyle \frac{{\theta }^2}{2}}{n}^2+\left(\beta -r-{\displaystyle \frac{{\theta }^2}{2}}\right)n-\beta =0.$$

By applying the smooth-pasting conditions $J\left(z_R\right)=J_R^{\delta }\left(z_R\right)$ and $J^{\prime }\left(z_R\right)={\left(J_R^{\delta }\right)}^{\prime }\left(z_R\right)$, we obtain

$$z_R={\left(e^{(K-r)\delta }·{\displaystyle \frac{\epsilon K}{(1-k_B^{\frac{1-\gamma }{\gamma }})r}}·{\displaystyle \frac{(1-\gamma )(n_2-1)}{1-\gamma +n_2\gamma }}\right)}^{-\gamma },$$

(18)

and

$$C=-{\displaystyle \frac{\epsilon e^{-r\delta }}{r(1-\gamma +n_2\gamma )}}·{\displaystyle \frac{1}{z_R^{n_2-1}}}.$$

(19)

Therefore, we obtain the explicit form of $J\left(y\right)$ as

$$\begin{array}{c}\hfill J\left(y\right)=\left\{\begin{array}{cc}-{\displaystyle \frac{\epsilon e^{-r\delta }}{r(1-\gamma +n_2\gamma )}}·{\displaystyle \frac{1}{z_R^{n_2-1}}}{y}^{n_2}+{\displaystyle \frac{1}{K}}{k}_B^{{\displaystyle \frac{1-\gamma }{\gamma }}}·{\displaystyle \frac{\gamma }{1-\gamma }}{y}^{-{\displaystyle \frac{1-\gamma }{\gamma }}}+{\displaystyle \frac{\epsilon }{r}}y,\hfill & \mathrm{if}y>z_R,\hfill \\ J_R^{\delta }\left(y\right),\hfill & \mathrm{if}0<y\le z_R,\hfill \end{array}\right.\end{array}$$

(20)

where the critical level $z_R$ is given in (18).

As in Karatzas and Wang [7], we can show that the inequality in (12) actually holds with equality. That is,

$$V\left(x\right)=\underset{y>0}{inf}\left(J\left(y\right)+yx\right).$$

(21)

Moreover, there exists a unique $y^{*}$ such that $x=-J^{\prime }\left(y^{*}\right)$ and $V\left(x\right)=J\left(y^{*}\right)+y^{*}x.$

Then, the optimal strategies $({\tau }^{*},c^{*},{\pi }^{*})$ are given by

$${\tau }^{*}=\widehat{\tau }\left(y^{*}\right),c_t^{*}=\widehat{c}\left({\mathcal{Y}}_t^{*}\right),\mathrm{and}{\pi }_t^{*}={\displaystyle \frac{\theta }{\sigma }}{\mathcal{Y}}_t^{*}{J}^{″}\left({\mathcal{Y}}_t^{*}\right),$$

where ${\mathcal{Y}}_t^{*}:=y^{*}{e}^{\beta t}{\xi }_t$. Recall that $\widehat{c}(·)$ and $\widehat{\tau }(·)$ are defined in (10) and (16), respectively. The wealth process $X_t^{*}$ associated with the optimal strategy $({\tau }^{*},c^{*},{\pi }^{*})$ is given by

$$X_t^{*}=-J\left({\mathcal{Y}}_t^{*}\right).$$

(22)

We also define the retirement wealth boundary as $x_R:=-J^{\prime }\left(z_R\right)$. Then, the optimal retirement time ${\tau }^{*}$ is rewritten as ${\tau }^{*}=inf\{t\ge 0\mid X_t^{*}\ge x_R\}.$

For $x\in \left(-{\displaystyle \frac{\epsilon }{r}},x_R\right)$, following Dybvig and Liu [4] and Lim and Kwak [21], the expected retirement time $\mathbb{E}\left[{\tau }^{*}\right]$ and the human capital $HC\left(x\right)$ can be explicitly computed as

$$\mathbb{E}[{\tau }^{*}\mid X_0^{*}=x]=\left\{\begin{array}{cc}{\displaystyle \frac{log{y}^{*}-log{z}_R}{\frac{1}{2}{\theta }^2-\beta +r}},\hfill & \mathrm{if}{\displaystyle \frac{1}{2}}{\theta }^2-\beta +r>0,\hfill \\ \infty ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

and

$$HC\left(x\right):=\mathbb{E}\left[{\int }_0^{{\tau }^{*}}{\xi }_t\epsilon dt\right]={\displaystyle \frac{\epsilon }{r}}\left(1-{\left({\displaystyle \frac{y^{*}}{z_R}}\right)}^{n_2-1}\right).$$

The expected retirement time $\mathbb{E}\left[{\tau }^{*}\right]$ reflects the trade-off between delaying retirement and enjoying its utility later. A higher market return $\theta$ or a lower discount rate $\beta$ reduces the expected waiting time until retirement. However, if the agent’s subjective discounting outweighs the expected return (i.e., ${\displaystyle \frac{1}{2}}{\theta }^2-\beta +r\le 0$), the agent indefinitely postpones retirement, as future utility is too heavily discounted.

The human capital $HC\left(x\right)$ measures the present value of future wage income the agent expects to earn before retiring. As $y^{*}$ approaches the threshold $z_R$, the agent nears retirement, and the term ${\left({\displaystyle \frac{y^{*}}{z_R}}\right)}^{n_2-1}$ converges to one, making $HC\left(x\right)$ shrink toward zero. This captures the intuitive notion that human capital depreciates over time as the agent approaches the retirement boundary.

4. Implications

This section focuses on how the implementation delay parameter $\delta$ influences the agent’s optimal consumption, investment, and retirement behavior, building on the closed-form characterizations derived in the previous section. While the effects of other parameters have been extensively studied in the literature, we concentrate here on the role of $\delta$, which has received little attention. The following baseline parameters are used throughout the analysis:

$$\beta =0.04,r=0.02,\mu =0.08,\sigma =0.2,\gamma =3,k_B=0.3,\epsilon =1.$$

4.1. Consumption and Portfolio Strategies

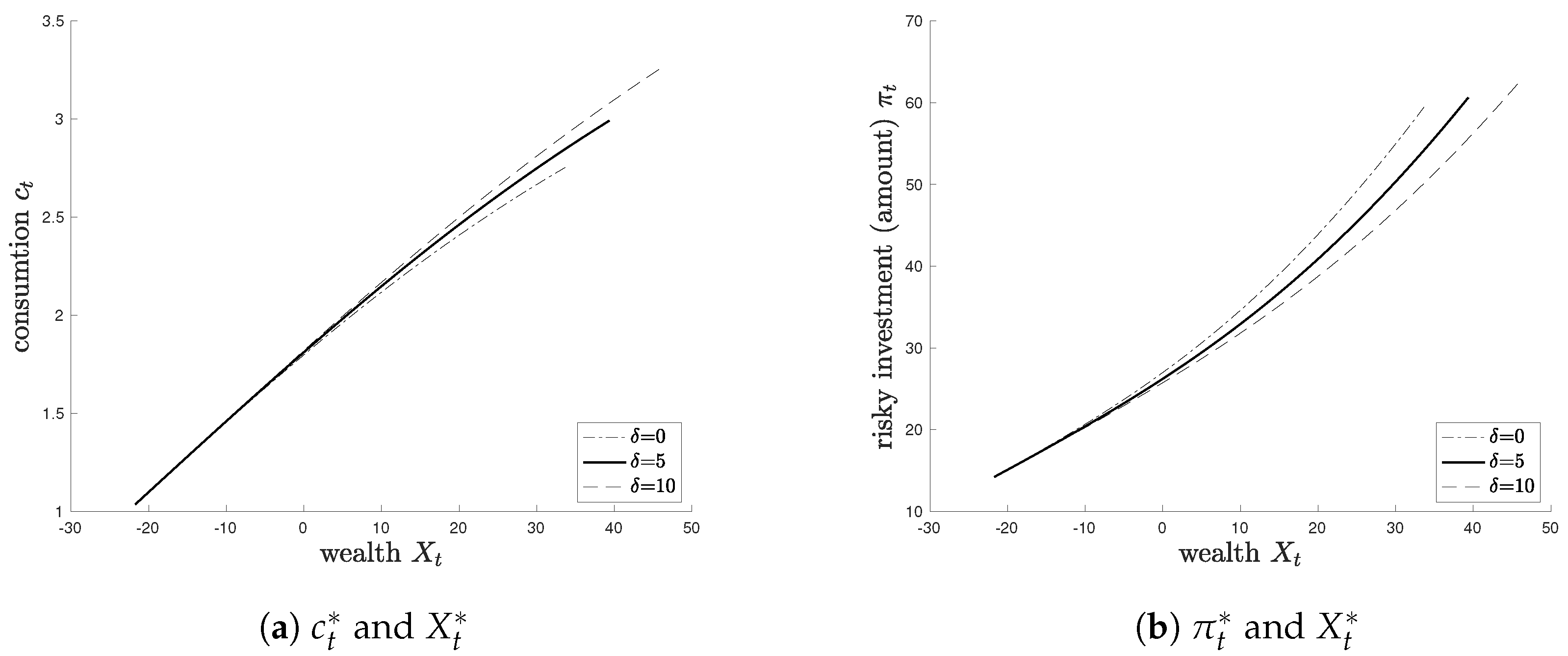
Figure 1 shows how increasing $\delta$ affects the optimal consumption and portfolio policies. As $\delta$ increases, the agent chooses to consume more aggressively before retirement while reducing their exposure to risky assets.

Economically, this behavior reflects a shift in utility timing. A longer delay implies that post-retirement utility is postponed further into the future and thus more heavily discounted. Since the agent receives utility from $u\left(k_B{c}_t\right)$ during the interval $[0,\tau +\delta ]$, where $k_B<1$, an increase in $\delta$ raises the value of consumption earlier in life relative to deferred utility. Therefore, the agent optimally increases current consumption to capture more near-term utility.

On the investment side, a longer delay diminishes the perceived marginal return on risky investments. Since the gains from risky assets materialize only after $\delta$ units of time, their present value is discounted by $e^{-\beta \delta }$, reducing their attractiveness. As a result, the agent reallocates towards safer assets, even if the expected return on risky assets remains unchanged. This has implications for portfolio management: individuals facing delayed access to retirement benefits may adopt more conservative investment positions in the pre-retirement phase.

4.2. Retirement Timing and Wealth Threshold

Figure 2 illustrates how $\delta$ affects two critical retirement indicators: the expected retirement time $\mathbb{E}\left[{\tau }^{*}\right]$ and the retirement wealth threshold $x_R=-J^{\prime }\left(z_R\right)$.

Panel (a) shows that $\mathbb{E}\left[{\tau }^{*}\right]$ increases with $\delta$. This reflects the agent’s desire to delay retirement when the benefit of leisure and post-retirement utility is postponed. The agent responds by remaining in the labor force longer, effectively working through the delay to maximize lifetime utility.

Panel (b) shows that the wealth threshold $x_R$ also increases with $\delta$. Since post-retirement consumption is delayed, the agent requires a larger buffer of wealth before retiring to ensure sufficient utility in the later phase. This effect mirrors a precautionary saving motive induced by delayed gratification: the longer the agent must wait to enjoy retirement, the more resources they need to accumulate to justify leaving the workforce.

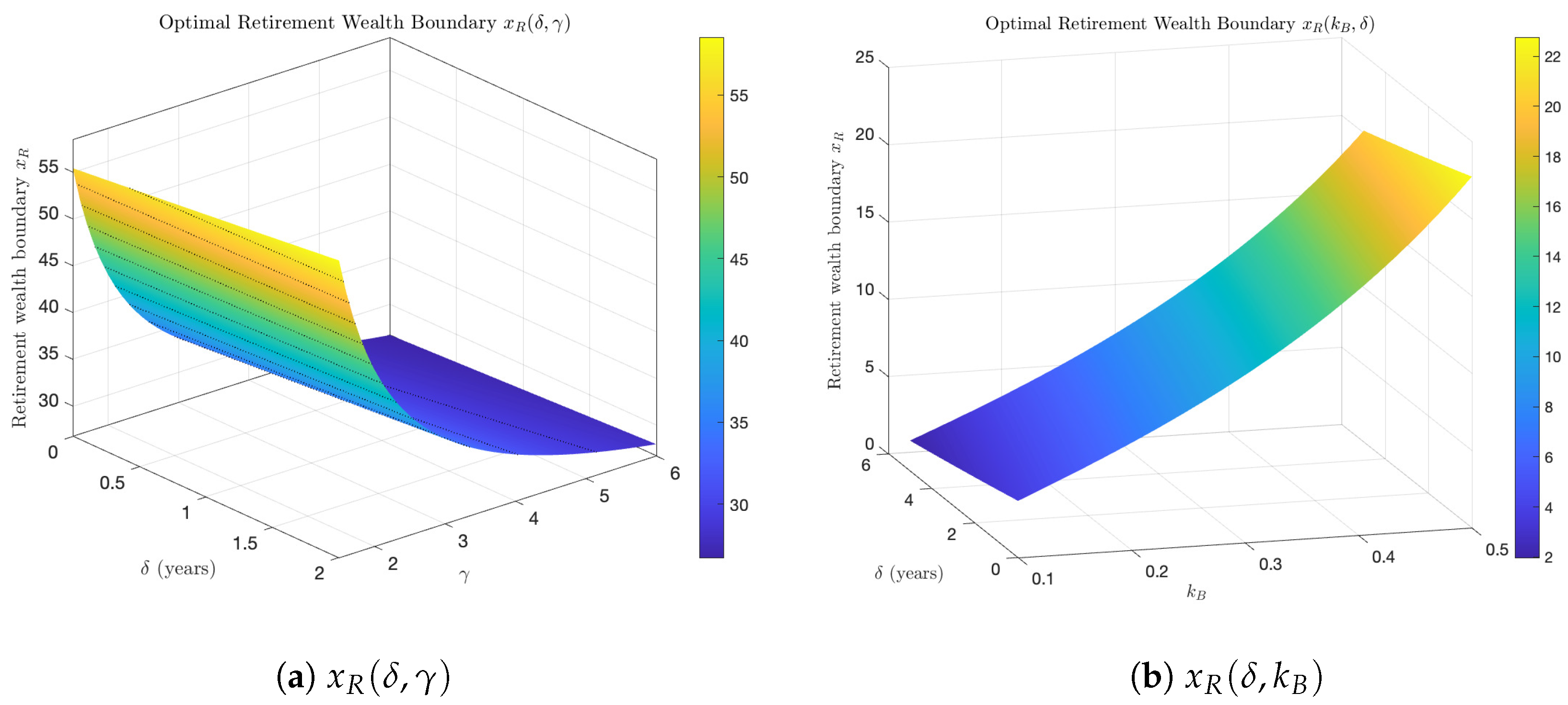
To further illustrate the interaction effects between the implementation delay $\delta$ and key preference parameters, Figure 3 presents the optimal retirement wealth boundary $x_R$ in three dimensions. Panel (a) depicts $x_R$ as a joint function of $\delta$ and the risk aversion coefficient $\gamma$. For any given $\delta$, higher $\gamma$ raises the retirement threshold, reflecting the more conservative investment behavior of highly risk-averse agents. Moreover, the slope with respect to $\gamma$ becomes steeper as $\delta$ increases, indicating that implementation delays amplify the impact of risk aversion on retirement timing.

Panel (b) shows $x_R$ as a function of $\delta$ and the pre-retirement disutility $k_B$. Larger $k_B$—representing greater aversion to continued work—lowers the attractiveness of delaying retirement, but in the presence of a long implementation delay, the effect reverses: agents require a higher wealth level before retiring to offset the lag in benefit realization. These patterns highlight the importance of considering parameter interactions, as the effect of $\delta$ cannot be fully understood without accounting for individual heterogeneity in preferences.

4.3. Human Capital Valuation

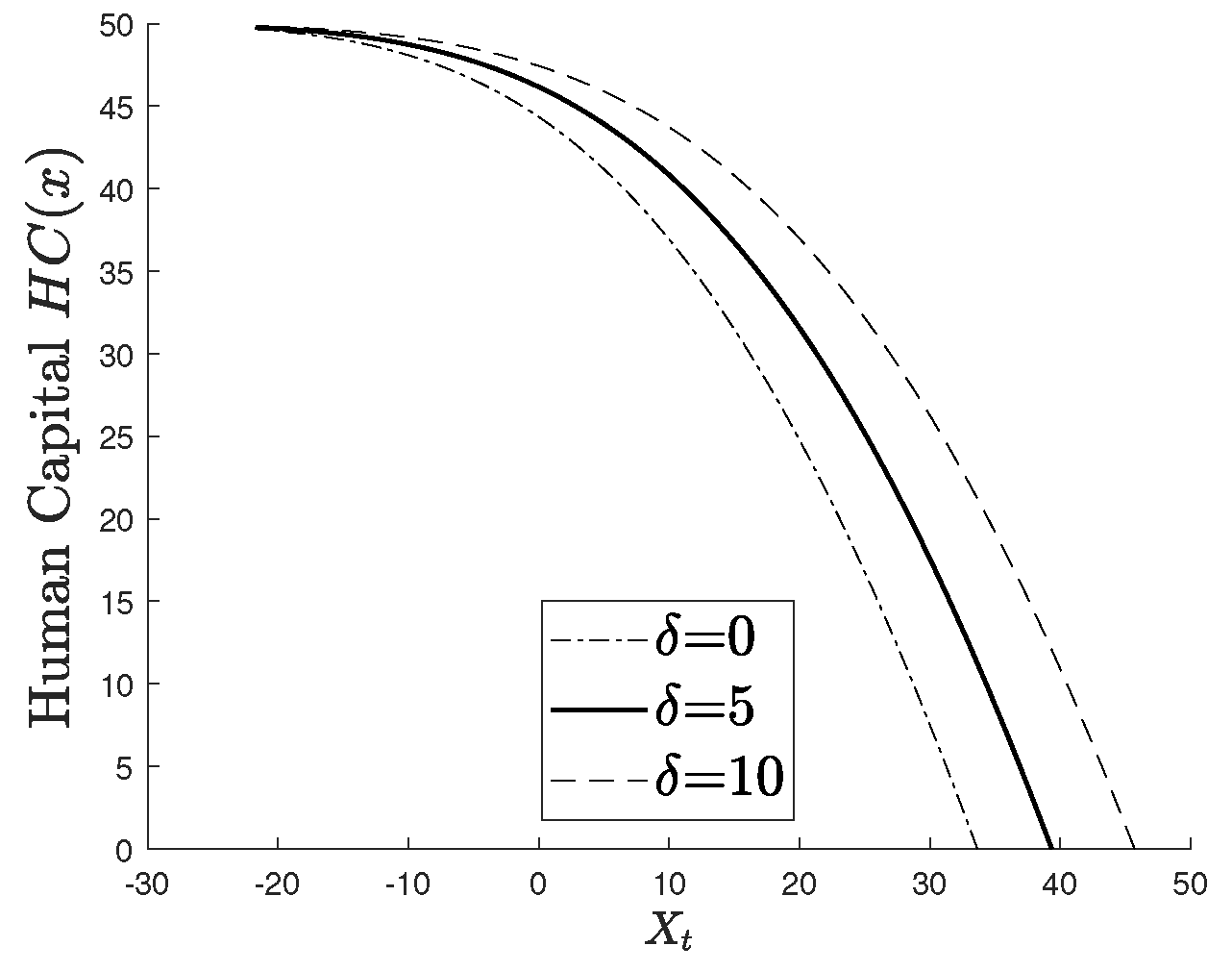
Figure 4 plots the human capital function $HC\left(x\right)$, which represents the present value of future labor income up to the optimal retirement time. As $\delta$ increases, $HC\left(x\right)$ declines for a given wealth level x.

This reflects two effects. First, the agent’s extended working horizon due to a larger $x_R$ implies a longer period of income generation, which tends to raise $HC\left(x\right)$. However, the increased delay in utility realization reduces the effective valuation of future income due to discounting. The second effect dominates, leading to a downward shift in $HC\left(x\right)$. This suggests that the perceived value of continued labor income diminishes when retirement benefits are pushed further into the future.

Economically, the human capital function $HC\left(x\right)$ measures the present value of future labor income, discounted both by market returns and the institutional delay $\delta$. An increase in $\delta$ effectively shortens the perceived working horizon, reducing $HC\left(x\right)$ even if the wage rate $\epsilon$ remains constant. This decline reflects the agent’s anticipation of a longer waiting period before benefit realization, which lowers the marginal value of continuing to work and thus raises the optimal retirement threshold.

4.4. Policy and Financial Implications

Our analysis provides several insights relevant to retirement planning and pension policy design:

• Incentives for Earlier Retirement: Policymakers aiming to encourage earlier retirement—e.g., to alleviate pressure on labor markets—should consider reducing institutional delays in pension benefit activation. Fast-tracking retirement benefit processing can lower $x_R$ and $\mathbb{E}\left[{\tau }^{*}\right]$.
• Default Investment Strategies: Financial advisors and retirement plan providers should incorporate delay parameters into glide path strategies. For individuals facing longer benefit delays, default portfolios may need to shift toward lower equity exposure pre-retirement.
• Target Wealth and Savings Benchmarks: Delay-induced increases in $x_R$ suggest that traditional retirement savings targets may be underestimated if implementation delays are ignored. Retirement calculators and financial planning tools should account for such lags explicitly.
• Welfare and Inequality Considerations: Low-income individuals are more vulnerable to the utility cost of delayed retirement benefits. Delay-sensitive retirement policies may disproportionately burden those with less flexibility to delay retirement or accumulate large buffers, exacerbating retirement inequality.

Overall, the delay parameter $\delta$ introduces a new dimension of intertemporal trade-offs in retirement behavior. Its inclusion in optimal control models allows for more realistic modeling and can generate valuable insights for both academic research and public policy. The numerical illustrations in this paper are based on theoretical parameter values (e.g., $\epsilon =1$, $\gamma =3$) to highlight the qualitative mechanisms of the model. However, the framework can be readily calibrated to real-world data—such as OECD statistics on pension processing lags for $\delta$, historical average wages for $\epsilon$, and long-term market return series for $(r,\mu ,\sigma )$—to evaluate country-specific policy implications. Such empirical calibration, while beyond the present scope, would allow for a quantitative assessment of the model’s predictions in actual pension systems without altering the theoretical contributions.

5. Concluding Remarks

In summary, our model demonstrates that the implementation delay $\delta$ plays a pivotal role in shaping optimal consumption, investment, and retirement decisions. A longer delay induces individuals to increase pre-retirement consumption, reduce exposure to risky assets, and postpone retirement until a higher wealth threshold is reached. These behavioral adjustments reflect the agent’s attempt to offset the diminished present value of delayed utility. The analysis further shows that an increase in $\delta$ lowers the agent’s human capital $HC\left(x\right)$—the present value of future labor income—by raising the optimal retirement threshold and shortening the effective working horizon, thereby influencing retirement timing through an additional channel.

Although our calibration uses hypothetical parameter values for tractability, the framework can readily accommodate empirically estimated parameters from real pension systems. For instance, linking the model to OECD or World Bank datasets on pension processing delays would provide applied validation and enhance its policy relevance. Such empirical integration would also allow benchmarking against alternative retirement models and enable case study-style applications.

The model has several limitations. We assume a fixed and known delay $\delta$, constant labor income $\epsilon$, and a fixed disutility factor $k_B$, which simplify the analysis but may not fully capture real-world complexities. In practice, delays may be stochastic due to administrative uncertainty, individual-specific processing times, or unforeseen events, and labor income or disutility may vary over the lifecycle. Furthermore, the calibration relies on illustrative values rather than empirical estimates. Future research could extend the framework to incorporate stochastic delays, time-varying or stochastic income and disutility, and empirical calibration to observed pension system parameters.

From a policy perspective, reducing delays in accessing retirement income—through faster benefit processing, digitalization of administrative procedures, or allowing partial early access—could encourage earlier retirement and lead to more balanced portfolio allocations. Such measures would be particularly beneficial for individuals with limited wealth or liquidity, for whom the cost of delayed utility realization is especially severe.

Finally, several promising extensions remain. Introducing a finite-life-horizon framework would allow mortality risk and bequest motives to interact with $\delta$. Incorporating behavioral factors—such as hyperbolic discounting or loss aversion—could capture deviations from the standard CRRA framework. Linking $\delta$ to macroeconomic or policy variables would provide a richer representation of institutional processes, further enhancing the model’s realism and applicability.