Bayesian Analysis of Bitcoin Volatility Using Minute-by-Minute Data and Flexible Stochastic Volatility Models

Abstract

This study analyzes the volatility of Bitcoin using stochastic volatility models fitted to one-minute transaction data for the BTC/USDT pair between 1 April 2023, and 31 March 2024. Bernstein polynomial terms were introduced to accommodate intraday and intraweek seasonality, and flexible return distributions were used to capture distributional characteristics. Seven return distributions—normal, Student-t, skew-t, Laplace, asymmetric Laplace (AL), variance gamma, and skew variance gamma—were considered. We further incorporated explanatory variables derived from the trading volume and price changes to assess the effects of order flow. Our results reveal structural market changes, including a clear regime shift around October 2023, when the asymmetric Laplace distribution became the dominant model. Regression coefficients suggest a weakening of the volume–volatility relationship after September and the presence of non-persistent leverage effects. These findings highlight the need for flexible, distribution-aware modeling in 24/7 digital asset markets, with implications for market monitoring, volatility forecasting, and crypto risk management.

1. Introduction

Risk assessment of financial instruments such as stocks strongly relies on the volatility of return rates, which exhibits similar characteristics and common patterns across different types of financial assets, time periods, or locations [1]. First, volatility fluctuates over time [2], with clustered periods of low and high volatility. This phenomenon is widely known as volatility clustering [3,4,5]. Second, the probability distribution of financial asset returns exhibits heavy tails—that is, it shows higher kurtosis than the normal distribution [6]. This property persists to some extent even after accounting for volatility clustering [7]. Third, volatility responds asymmetrically to the direction of return fluctuations [8]. More specifically, a negative fluctuation significantly increases volatility relative to a positive fluctuation of the same magnitude. This phenomenon is known as the leverage effect. Volatility clustering is captured by the Autoregressive Conditional Heteroskedasticity (ARCH) model [9], which expresses the variance of returns as a weighted sum of past squared error terms, and the Generalized ARCH (GARCH) model [10], which additionally incorporates the past variances. The ARCH/GARCH models have been extended to accommodate heavy tails [11] and to account for the leverage effect. The former extension employs the t-distribution, and the latter is known as the Exponential GARCH (EGARCH) model [12].

Whereas the GARCH model deterministically describes variance based on past error terms and past variances, the stochastic volatility (SV) model [13] characterizes return volatility as a latent stochastic process. Since the introduction of Markov Chain Monte Carlo (MCMC)-based Bayesian estimation methods [14,15], SV models have been widely adopted in financial econometrics [16]. As reported in several studies, SV models provide a better goodness of fit and higher forecasting power than ARCH/GARCH models [17,18,19]. Given this empirical evidence, the SV model was employed in the present study of volatility dynamics.

Electronic stock trading has recently generated large volumes of granular data, such as trade sizes. The availability of such data has shifted the focus of volatility analysis from interday to intraday frequencies. More specifically, volatility is now analyzed at intervals of one to five minutes [20]. The trading of financial instruments follows characteristic patterns throughout the day, a phenomenon known as intraday seasonality. Trading volume typically follows a U-shaped pattern, with heightened activity immediately after market opening and shortly before market closure [21]. Intraday volatility follows a similar U-shaped pattern [22,23]. However, some studies attribute intraday seasonality and day-of-the-week effects to other factors, such as the release of economic indicators [24,25]. These patterns may vary depending on the type of financial instrument, geographic region, and the analytical methodology applied. Although equities are the most commonly analyzed financial instruments, commodities [26,27] and foreign exchange [28] have also been studied.

Bitcoin [29] has garnered widespread attention for its anonymity and decentralized nature. At the time of writing, the market capitalization of Bitcoin is approximately USD 1.8 trillion. Although Bitcoin has been criticized for its use in illicit drug transactions [30] and for its highly speculative nature [31,32], interest in Bitcoin-based price prediction [33,34,35,36,37] and the development of automated trading systems based on such predictions [38,39] has not abated.

Bitcoin has been gradually recognized as an investment target and as a type of asset and currency. Seetharaman et al. [40] modeled the impact of BTC on fiat currencies such as the USD, whereas Al-Mansouri [41] noted that BTC had relatively low price correlation with the USD and could serve as a diversification asset for USD. Petti and Sergio [42] reported that BTC served as a safe haven for assets, similar to the gold market, during the global banking crisis on 9 March 2023. With increasing cryptocurrency trades and availability of high-frequency data, high-frequency price forecasting and risk estimation, such as minute-by-minute forecasts, are being actively studied [43,44,45]. As cryptocurrencies increasingly play an economic role, taxation and legal regulations for cryptocurrencies are being investigated [46,47,48].

In addition, research on Bitcoin volatility is progressing. Studies have found that fluctuations in Bitcoin price can be as much as 10-fold those of major currencies [49], with high intraday volatility t [50] reported that economic factors affect Bitcoin volatility [51]. Several studies have also used ARCH, GARCH, and their extensions such as E-GARCH to model Bitcoin volatility [52,53,54]. Despite the widespread adoption of cryptocurrencies and extensive research in the field, few studies have applied the SV model to cryptocurrencies [55,56,57]. In this study, we develop a model that simultaneously incorporates intraday seasonality, day-of-the-week seasonality, the leverage effect, asymmetry, and heavy tails. In addition, we adopt the Ancillarity–Sufficiency Interweaving Strategy to enhance the computational efficiency of MCMC [58].

2. Materials and Methods

2.1. Data

We analyzed the high-frequency transaction data of the BTC/USDT pair (Bitcoin quoted in Tether, hereafter referred to as “BTCUSD”) obtained from the Binance exchange, which recorded the highest spot volume in the cryptocurrency market over the study period. The sample comprises 364 consecutive calendar days, from 1 April 2023 to 29 March 2024. We selected this data period because Bitcoin underwent a halving event (hard fork) in April 2024, which is expected to considerably change the market structure of Bitcoin. Therefore, we extracted data for the one-year period, during which Bitcoin was not affected by this halving event.

For every matched order, Binance provides the trade price, trade size, a market–maker flag, and a millisecond time stamp. The flag equals 1 when the incoming order adds depth to the limit order book (“maker”) and 0 when the order is immediately executed against standing liquidity (“taker”).

Tick data are aggregated into non-overlapping one–minute intervals. We construct the following covariates at minute t:

• $x_{1t}$ = $log{V}_t$: logarithm of aggregate traded volume; and
• $x_{2t}$ = $\Delta Q_t=Q_t^{\mathrm{buy}}-Q_t^{\mathrm{sell}}$: signed volume imbalance;
• $x_{3t}$ = $\Delta P_t$: a one-minute change in the mid–price close;
• $x_{4t}$ = $log\left(V_t/Q_t^{\mathrm{sell}}\right)$: relative buyer intensity;
• $x_{5t}$ = $(Q_t^{\mathrm{buy}}-Q_t^{\mathrm{sell}})/V_t$: normalised order–flow imbalance;
• $x_{6t}$ = $D_t$ = 1$\{\Delta P_t<0\}$: A dummy set to 1 if the close price declines.

Using these variables, we can examine the co-movements of Bitcoin volatility with trade intensity and the order–flow imbalance and test the leverage effect, analogously to observing traditional financial markets.

2.2. Stochastic Volatility Model with Intraday and Intraweek Seasonalities

Consider the log-difference in price over a short interval. We divide the trading hours into T periods and normalize them such that the total length of the trading hours is unity; that is, the length of each period is ${\displaystyle \frac{1}{T}}$ and the time stamp of the t-th period is ${\displaystyle \frac{t}{T}}$$(t=1,\dots ,T)$. Because BTCUSD trading on Binance occurs 24 h a day, 365 days a year (365 days/year), we set T = 10,800; $(=7\times 24\times 60)$. Let $y_t$$(t=1,\dots ,T)$ denote the return during the t-th period (time ${\displaystyle \frac{t}{T}}$ in the trading hours). The SV model of $y_t$ with intraday seasonality is given as

$$\left\{\begin{array}{c}{y}_t=exp(x_t^{\prime }\beta +h_t){ϵ}_t,\hfill \\ h_{t+1}=\varphi h_t+{\eta }_t,\hfill \end{array}\right.\left[\begin{array}{c}{ϵ}_t\\ {\eta }_t\end{array}\right]\sim \mathrm{Normal}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}1& \rho \tau \\ \rho \tau & {\tau }^2\end{array}\right]\right),\left|\rho \right|<1,\tau >0,$$

(1)

and

$$h_1\sim \mathrm{Normal}\left(0,{\displaystyle \frac{{\tau }^2}{1-{\varphi }^2}}\right),\left|\varphi \right|<1.$$

As iswell known, the estimated correlation coefficient $\rho$ is negative in most financial markets. This negative correlation is often referred to as the leverage effect. The volatility in the t-th period (the natural logarithm of the conditional SD of $y_t$) is given as

$$log\sqrt{\mathrm{Var}\left[y_t\right|{\mathcal{F}}_{t-1}]}=x_t^{\prime }\beta +h_t,$$

where ${\mathcal{F}}_{t-1}$ is the filtration representing all available information at time ${\displaystyle \frac{t-1}{T}}$. Hence, the volatility in Equation (1) is decomposed into two parts: a linear combination of covariates $x_t^{\prime }\beta$, and the unobserved AR(1) process $h_t$. In this paper, $x_t^{\prime }\beta$ is regarded as the intraday seasonal component of volatility, but this term can be interpreted as a general function of the covariates $x_t$ in other settings. The term $h_t$, which captures volatility clustering, is unobservable and is therefore referred to as the latent log volatilityin this paper.

The exact functional forms of the intraday and intraweek seasonalities are unknown. To provide the required flexibility for intraday seasonality, we set $x_t^{\prime }\beta$ to the following Bernstein polynomial:

$$x_t^{\prime }\beta =\sum _{k=0}^n{\beta }_k{x}_{k,t}=\sum _{k=0}^n{\beta }_k{b}_{k,n}\left({\displaystyle \frac{t}{T}}\right),$$

(2)

where $b_{k,n}(·)$ is the Bernstein basis polynomial of degree n:

$$b_{k,n}\left(v\right)={}_{n}C_k{v}^k{(1-v)}^{n-k},k=0,\dots ,n,v\in [0,1].$$

Although the parameterized SV model in Equation (1) is widely used in the literature, we adopt the alternative parameterization of Nakakita and Nakatsuma [59], which facilitates MCMC implementation in non-Gaussian SV models. Specifically, we replace the covariance matrix in Equation (1) with

$$\left[\begin{array}{cc}\mathrm{Var}\left[{ϵ}_t\right]& \mathrm{Cov}[{\eta }_t,{ϵ}_t]\\ \mathrm{Cov}[{ϵ}_t,{\eta }_t]& \mathrm{Var}\left[{\eta }_t\right]\end{array}\right]=\left[\begin{array}{cc}1+{\gamma }^2{\tau }^2& \gamma {\tau }^2\\ \gamma {\tau }^2& {\tau }^2\end{array}\right].$$

(3)

The SV model is then alternatively formulated as

$$\left\{\begin{array}{c}{y}_t=exp(x_t^{\prime }\beta +h_t){ϵ}_t,\hfill \\ h_{t+1}=\varphi h_t+{\eta }_t,\hfill \end{array}\right.\left[\begin{array}{c}{ϵ}_t\\ {\eta }_t\end{array}\right]\sim \mathrm{Normal}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}1+{\gamma }^2{\tau }^2& \gamma {\tau }^2\\ \gamma {\tau }^2& {\tau }^2\end{array}\right]\right).$$

(4)

In Equation (4), the variance of ${ϵ}_t$ is no longer unity, so $\beta$ and $h_t$ in Equation (4) are interpreted slightly differently from those in Equation (1). However, Equation (4) preserves the basic characteristics of Equation (1). As the sign of $\gamma$ always coincides with the sign of the correlation coefficient.

$$\mathrm{Corr}[{ϵ}_t,{\eta }_t]={\displaystyle \frac{\gamma \tau }{\sqrt{1+{\gamma }^2{\tau }^2}}}$$

in Equation (3), the leverage effect exists if $\gamma <0$. To distinguish $\gamma$ in Equation (4) from the correlation parameter $\rho$ in Equation (1), we refer to $\gamma$ as the leverage parameter.

Equation (4) is equivalent to

$$\left\{\begin{array}{c}{y}_t=exp(x_t^{\prime }\beta +h_t)(z_t+\gamma {\eta }_t),\hfill \\ h_{t+1}=\varphi h_t+{\eta }_t,\hfill \end{array}\right.$$

(5)

where

$$z_t\sim \mathrm{Normal}(0,1),{\eta }_t\sim \mathrm{Normal}(0,{\tau }^2),z_t\perp {\eta }_t.$$

In the alternative formulation of Equation (5), we can interpret ${\eta }_t$ as a common shock that affects both the return $y_t$ and the log volatility $h_{t+1}$, whereas $z_t$ is an idiosyncratic shock that affects $y_t$ only.

Given observations $y_{1:T}=[y_1;\dots ;y_T]$ and the latent log volatility $h_{1:T+1}=[h_1;\dots ;h_{T+1}]$, the likelihood of Equation (5) is given by

$$p(y_{1:T},h_{1:T+1}|\theta )=\underset{p\left(y_{1:T}\right|h_{1:T+1},\theta )}{\underbrace{\prod _{t=1}^{T}p\left(y_t\right|h_t,h_{t+1},\theta )}}·\underset{p\left(h_{1:T+1}\right|\theta )}{\underbrace{p\left(h_1\right|\theta )\prod _{t=1}^{T}p\left(h_{t+1}\right|h_t,\theta )}},$$

(6)

where $\theta =(\beta ,\gamma ,{\tau }^2,\varphi )$. Since $h_t$ follows a stationary AR(1) process, the joint probability distribution of $h_{1:T+1}$ is multivariate normal with mean zero and covariance matrix ${\tau }^2{V}^{-1}$. Here, V is a tridiagonal matrix with diagonal elements of 1 at the first and last positions and $1+{\varphi }^2$ at all interior positions, super- and sub-diagonal elements of $-\varphi$, and zeros elsewhere. The matrix V is positive definite when $\left|\varphi \right|<1$.

Thus, the joint probability density function (p.d.f.) of $h_{1:T+1}$ is

$$p\left(h_{1:T+1}\right|\theta )={\left(2\pi {\tau }^2\right)}^{-{\displaystyle \frac{T+1}{2}}}{\left|V\right|}^{{\displaystyle \frac{1}{2}}}exp\left[-{\displaystyle \frac{1}{2{\tau }^2}}{h}_{1:T+1}^{\prime }V{h}_{1:T+1}\right],\left|V\right|=1-{\varphi }^2.$$

(7)

In our study, the prior distributions of $(\beta ,\gamma ,{\tau }^2,\varphi )$ are given by

$$\begin{array}{cc}\hfill & \beta \sim \mathrm{Normal}({\overline{\mu }}_{\beta },{\overline{\Omega }}_{\beta }^{-1}),\gamma \sim \mathrm{Normal}({\overline{\mu }}_{\gamma },{\overline{\omega }}_{\gamma }^{-1}),\hfill \\ \hfill & {\tau }^2\sim \mathrm{Inv}.\mathrm{Gamma}(a_{\tau },b_{\tau }),{\displaystyle \frac{\varphi +1}{2}}\sim \mathrm{Beta}(a_{\varphi },b_{\varphi }).\hfill \end{array}$$

(8)

The joint posterior density of $(h_{1:T+1},\theta )$ in Equation (5) is then given by

$$p(h_{1:T+1},\theta |y_{1:T})\propto \prod _{t=1}^{T}p\left(y_t\right|h_t,h_{t+1},\theta )·p\left(h_{1:T+1}\right|\theta )·p\left(\theta \right),$$

(9)

where $p\left(\theta \right)$ is the prior density of the parameters in Equation (8).

Since analytical evaluation of the joint posterior distribution in Equation (9) is impractical, we generated a random sample ${\left\{(h_{1:T+1}^{\left(r\right)},{\beta }^{\left(r\right)},{\gamma }^{\left(r\right)},{\tau }^{2\left(r\right)},{\varphi }^{\left(r\right)})\right\}}_{r=1}^R$ from the joint posterior distribution in Equation (9) using the MCMC method. We then numerically evaluated the posterior statistics required for Bayesian inference using Monte Carlo integration.

2.3. Conditional Posterior Distributions

2.3.1. Latent Log Volatility $h_{1:T+1}$

The conditional posterior density of latent log volatility $h_{1:T+1}$ is given by

$$p\left(h_{1:T+1}\right|\theta ,y_{1:T})\propto \prod _{t=1}^{T}p\left(y_t\right|h_t,h_{t+1},\theta )·p\left(h_{1:T+1}\right|\theta ).$$

(10)

Here, $h_{1:T+1}$ was sampled from Equation (10) using the Metropolis–Hastings (MH) algorithm. To derive a suitable proposal distribution for the algorithm, we first approximated $\mathcal{l}\left(h_{1:T+1}\right)=logp\left(y_{1:T}\right|h_{1:T+1},\theta )$ via a second-order Taylor expansion around $h_{1:T+1}^{*}$:

$$\begin{array}{cc}\hfill \mathcal{l}\left(h_{1:T+1}\right)& \approx \mathcal{l}\left(h_{1:T+1}^{*}\right)+g{\left(h_{1:T+1}^{*}\right)}^{\prime }(h_{1:T+1}-h_{1:T+1}^{*})\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{(h_{1:T+1}-h_{1:T+1}^{*})}^{\prime }Q\left(h_{1:T+1}^{*}\right)(h_{1:T+1}-h_{1:T+1}^{*}),\hfill \end{array}$$

(11)

where $g\left(h_{1:T+1}\right)$ is the gradient vector of $\mathcal{l}\left(h_{1:T+1}\right)$:

$$g\left(h_{1:T+1}\right)=\left[\begin{array}{c}⋮\\ g_t\left(h_{1:T+1}\right)\\ ⋮\end{array}\right]=\left[\begin{array}{c}⋮\\ {\nabla }_{t}logp\left(y_{1:T}\right|h_{1:T+1},\theta )\\ ⋮\end{array}\right],$$

and $Q\left(h_{1:T+1}\right)$ is the Hessian matrix of $logp\left(y_{1:T}\right|h_{1:T+1},\theta )$ times $-1$ and a $(T+1)\times (T+1)$ band matrix.

According to Nakakita and Nakatsuma [59],

$$\begin{array}{cc}\hfill g_t\left(h_{1:T+1}\right)& =\{-1+({ϵ}_t-\gamma {\eta }_t)({ϵ}_t-\gamma \varphi )\}\mathbf{1}(t\leqq T)+\gamma ({ϵ}_{t-1}-\gamma {\eta }_{t-1})\mathbf{1}(t\geqq 2),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill q_t\left(h_{1:T+1}\right)& =\{{({ϵ}_t-\gamma \varphi )}^2+{ϵ}_t({ϵ}_t-\gamma {\eta }_t)\}\mathbf{1}(t\leqq T)+{\gamma }^2\mathbf{1}(t\geqq 2),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill q_{t,t+1}\left(h_{1:T+1}\right)& =\gamma ({ϵ}_t-\gamma \varphi ).\hfill \end{array}$$

(14)

Then, $h_{1:T+1}$ is approximately sampled from

$$h_{1:T+1}\sim \mathrm{Normal}\left({\mu }_h\left(h_{1:T+1}^{*}\right),{\Sigma }_h\left(h_{1:T+1}^{*}\right)\right),$$

(15)

where

$$\begin{array}{cc}\hfill {\Sigma }_h\left(h_{1:T+1}^{*}\right)& ={\left(Q\left(h_{1:T+1}^{*}\right)+{\displaystyle \frac{1}{{\tau }^2}}V\right)}^{-1},\hfill \\ \hfill {\mu }_h\left(h_{1:T+1}^{*}\right)& ={\Sigma }_h\left(h_{1:T+1}^{*}\right)\left(g\left(h_{1:T+1}^{*}\right)+Q\left(h_{1:T+1}^{*}\right)h_{1:T+1}^{*}\right).\hfill \end{array}$$

In addition, because $h_{1:T+1}$ is high-dimensional, we improve the efficiency of MCMC sampling using a block sampler (see Omori and Watanabe [16], Nakakita and Nakatsuma [59]).

2.3.2. Regression Coefficients $\beta$

The sampling scheme for the regression coefficients $\beta$ closely follows that of the latent volatility $h_{1:T+1}$. Let $\mathcal{l}\left(\beta \right)$ be $logp\left(y_{1:T}\right|h_{1:T+1},\theta )$ given $y_{1:T}$ and the parameters except $\beta$. Analogously to Equation (11), we approximate $\mathcal{l}\left(\beta \right)$ as a second-order Taylor expansion around ${\beta }^{*}$:

$$\begin{array}{cc}\hfill \mathcal{l}\left(\beta \right)& \approx \mathcal{l}\left({\beta }^{*}\right)+g{\left({\beta }^{*}\right)}^{\prime }(\beta -{\beta }^{*})-{\displaystyle \frac{1}{2}}{(\beta -{\beta }^{*})}^{\prime }Q\left({\beta }^{*}\right)(\beta -{\beta }^{*}),\hfill \end{array}$$

(16)

where $g\left(\beta \right)$ is the gradient vector of $\mathcal{l}\left(\beta \right)$ and $Q\left(\beta \right)$ is the Hessian matrix of $\mathcal{l}\left(\beta \right)$ times $-1$. Therefore, $g\left(\beta \right)$ and $Q\left(\beta \right)$ are, respectively, obtained as follows:

$$\begin{array}{cc}\hfill g\left(\beta \right)& =\sum _{t=1}^T({ϵ}_t({ϵ}_t-\gamma {\eta }_t)-1)x_t,\hfill \\ \hfill Q\left(\beta \right)& =\sum _{t=1}^T{ϵ}_t(2{ϵ}_t-\gamma {\eta }_t)x_t{x}_t^{\prime }.\hfill \end{array}$$

Assuming the prior as $\beta \sim \mathrm{Normal}({\overline{\mu }}_{\beta },{\overline{\Omega }}_{\beta }^{-1})$, the conditional posterior density of $\beta$ can be approximated as follows:

$$\beta \sim \mathrm{Normal}\left({\mu }_{\beta }\left({\beta }^{*}\right),{\Sigma }_{\beta }\left({\beta }^{*}\right)\right),$$

(17)

where

$${\Sigma }_{\beta }\left({\beta }^{*}\right)={\left(Q\left({\beta }^{*}\right)+{\overline{\Omega }}_{\beta }\right)}^{-1},{\mu }_{\beta }\left({\beta }^{*}\right)={\Sigma }_{\beta }\left({\beta }^{*}\right)\left(g\left({\beta }^{*}\right)+Q\left({\beta }^{*}\right){\beta }^{*}+{\overline{\Omega }}_{\beta }{\overline{\mu }}_{\beta }\right).$$

2.3.3. Leverage Parameter $\gamma$

Given a standard conditionally conjugate prior distributions for $\gamma$, the conditional posterior distribution is given by

$$\gamma |h_{1:T+1},{\theta }_{-\gamma },y_{1:T}\sim \mathrm{Normal}\left({\displaystyle \frac{{\sum }_{t=1}^T{\eta }_t{ϵ}_t+{\overline{\omega }}_{\gamma }{\overline{\mu }}_{\gamma }}{{\sum }_{t=1}^T{\eta }_t^2+{\overline{\omega }}_{\gamma }}},{\displaystyle \frac{1}{{\sum }_{t=1}^T{\eta }_t^2+{\overline{\omega }}_{\gamma }}}\right).$$

(18)

2.3.4. Variance ${\tau }^2$

We also adopted the standard conditionally conjugate prior distribution for ${\tau }^2$. The conditional posterior distribution then becomes

$${\tau }^2|h_{1:T+1},{\theta }_{-{\tau }^2},y_{1:T}\sim \mathrm{Inv}.\mathrm{Gamma}\left({\displaystyle \frac{T+1}{2}}+a_{\tau },{\displaystyle \frac{1}{2}}{h}_{1:T+1}^{\prime }V{h}_{1:T+1}+b_{\tau }\right).$$

(19)

2.3.5. AR(1) Coefficient $\varphi$

Having generated the state variables $h_{1:T+1}$, the conditional posterior density of $\varphi$ is given by

$$\begin{array}{cc}\hfill p\left(\varphi \right|h_{1:T+1},{\theta }_{-\varphi },y_{1:T})& \propto \sqrt{1-{\varphi }^2}exp\left[-{\displaystyle \frac{(1-{\varphi }^2)h_1^2+{\sum }_{t=1}^T{(h_{t+1}-\varphi h_t)}^2}{2{\tau }^2}}\right]\hfill \\ \hfill & \times {(1+\varphi )}^{a_{\varphi }-1}{(1-\varphi )}^{b_{\varphi }-1}{\mathbf{1}}_{(-1,1)}\left(\varphi \right).\hfill \end{array}$$

(20)

Using Equation (20), we propose the truncated normal distribution.

$$\varphi \sim \mathrm{Normal}\left(\left.{\displaystyle \frac{{\sum }_{t=1}^T{h}_{t+1}{h}_t}{{\sum }_{t=2}^T{h}_t^2}},{\displaystyle \frac{{\tau }^2}{{\sum }_{t=2}^T{h}_t^2}}\right|-1<\varphi <1\right)$$

(21)

as the distribution of $\varphi$ in the MH algorithm.

3. Model Formulation with Skewness and Heavy Tails

3.1. Mean–Variance Mixture of the Normal Distribution

It is well known that the probability distributions of returns are typically heavy-tailed and often exhibit nonzero skewness. Although stochastic volatility and leverage can induce skewness and heavy tails in the distribution of $y_t$, they may not sufficiently capture the characteristics of real-world data. Accordingly, we introduce a skew heavy-tailed distribution (instead of a normal distribution) into the SV model.

We express $z_t$ in Equation (5) as a mean–variance mixture of the standard normal distribution:

$$z_t=\alpha {\delta }_t+\sqrt{{\delta }_t}{u}_t,u_t\sim \mathrm{Normal}(0,1),{\delta }_t\sim \mathrm{GIG}(\lambda ,\psi ,\xi ),$$

(22)

where $\mathrm{GIG}(\lambda ,\psi ,\xi )$ denotes the generalized inverse Gaussian distribution with the following probability density function:

$$p\left({\delta }_t\right)={\displaystyle \frac{{(\psi /\xi )}^{\lambda /2}}{2K_{\lambda }\left(\sqrt{\psi \xi }\right)}}{\delta }_t^{\lambda -1}exp\left[-{\displaystyle \frac{1}{2}}\left(\psi {\delta }_t+{\displaystyle \frac{\xi }{{\delta }_t}}\right)\right],$$

(23)

where

$$(\psi ,\xi )\in \left\{\begin{array}{cc}\left\{\right(\psi ,\xi ):\psi >0,\xi \ge 0\}\hfill & \mathrm{if}\lambda >0,\hfill \\ \left\{\right(\psi ,\xi ):\psi >0,\xi >0\}\hfill & \mathrm{if}\lambda =0,\hfill \\ \left\{\right(\psi ,\xi ):\psi \ge 0,\xi >0\}\hfill & \mathrm{if}\lambda <0,\hfill \end{array}\right.$$

and $K_{\lambda }(·)$ is the modified Bessel function of the second kind. The family of generalized inverse Gaussian distributions includes:

• the exponential distribution ($\lambda =1,\xi =0$);
• the gamma distribution ($\lambda >0,\xi =0$);
• the inverse gamma distribution ($\lambda <0,\psi =0$);
• the inverse Gaussian distribution ($\lambda =-{\displaystyle \frac{1}{2}}$).

Under assumption in Equation (22), the distribution of $z_t$ belongs to the family of generalized hyperbolic distributions proposed by Barndorff-Nielsen [60], which includes many well-known skew heavy-tailed distributions. Among these are:

• the asymmetric Laplace distribution;
• the skew variance gamma (VG) distribution;
• the skew t distribution ($\lambda =-{\displaystyle \frac{\nu }{2}},\psi =0,\xi =\nu$),

where $\nu >0$. Note that the SV model includes two additional parameters: $\alpha$, which controls the symmetry of the distribution of $y_t$ and $\nu$, which determines heaviness of the tails. Here, $\alpha$ and $\nu$ are referred to as the asymmetry parameter and tail parameter, respectively. Our study adopts these three skew heavy-tailed distributions as alternatives to the normal distribution. Extending the framework of Nakakita and Nakatsuma [59], which handles the normal, variance-gamma, and Student-t distributions, our model additionally incorporates Laplace distributions. The models used in this study are abbreviated as follows:

• SV-N: stochastic volatility model with leverage and normal error;
• SV-L: stochastic volatility model with leverage and Laplace error;
• SV-AL: stochastic volatility model with leverage and asymmetric Laplace error;
• SV-G: stochastic volatility model with leverage and VG error;
• SV-SG: stochastic volatility model with leverage and skew VG error;
• SV-T: stochastic volatility model with leverage and t error.
• SV-ST: stochastic volatility model with leverage and skew t error.

The SV-L, SV-G, and SV-T models are special cases of SV-AL, SV-SG, and SV-ST, respectively, with $\alpha =0$.

In this setup, the SV model with heavy-tailed error is expressed as

$$\left\{\begin{array}{c}{y}_t=exp(x_t^{\prime }\beta +h_t){ϵ}_t,\hfill \\ h_{t+1}=\varphi h_t+{\eta }_t,\hfill \end{array}\right.\left.\left[\begin{array}{c}{ϵ}_t\\ {\eta }_t\end{array}\right]\right|{\delta }_t\sim \mathrm{Normal}\left(\left[\begin{array}{c}\alpha {\delta }_t\\ 0\end{array}\right],\left[\begin{array}{cc}{\delta }_t+{\gamma }^2{\tau }^2& \gamma {\tau }^2\\ \gamma {\tau }^2& {\tau }^2\end{array}\right]\right).$$

(24)

Given $(h_t,h_{t+1})$, the conditional probability density of $y_t$ is given by

$$p\left(y_t\right|h_t,h_{t+1},\theta )={\int }_0^{\infty }p\left(y_t\right|h_t,h_{t+1},{\delta }_t,\theta )p\left({\delta }_t\right|\nu ){\delta }_t,$$

(25)

where $\theta =(\beta ,\gamma ,{\tau }^2,\varphi ,\alpha ,\nu )$,

$$\begin{array}{cc}\hfill & p\left(y_t\right|h_t,h_{t+1},{\delta }_t,\theta )\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2\pi {\delta }_t}}}exp\left[-x_t^{\prime }\beta -h_t-{\displaystyle \frac{{\left\{y_{t}exp\left(-x_t^{\prime }\beta -h_t\right)-\alpha {\delta }_t-\gamma (h_{t+1}-\varphi h_t)\right\}}^2}{2{\delta }_t}}\right],\hfill \end{array}$$

(26)

and

$$p\left({\delta }_t\right|\nu )=\left\{\begin{array}{cc}{\displaystyle exp\left(-{\delta }_t\right)}\hfill & \left(\mathrm{SV}\text{-}\mathrm{AL}\right),\hfill \\ {\displaystyle \frac{{(\nu /2)}^{\nu /2}}{\Gamma (\nu /2)}{\delta }_t^{\frac{\nu }{2}-1}exp\left(-\frac{\nu }{2}{\delta }_t\right)}\hfill & \left(\mathrm{SV}\text{-}\mathrm{SG}\right),\hfill \\ {\displaystyle \frac{{(\nu /2)}^{\nu /2}}{\Gamma (\nu /2)}{\delta }_t^{-\frac{\nu }{2}-1}exp\left(-\frac{\nu }{2{\delta }_t}\right)}\hfill & \left(\mathrm{SV}\text{-}\mathrm{ST}\right).\hfill \end{array}\right.$$

(27)

Rather than evaluate the multiple integral in Equation (25), which is impractical, we generate ${\delta }_{1:T}=({\delta }_1,\dots ,{\delta }_T)$ along with $h_{1:T+1}$ and $\theta$ from their joint posterior distribution. In this setup, the posterior simulation uses the following likelihood function:

$$\begin{array}{cc}\hfill p(y_{1:T},h_{1:T+1},{\delta }_{1:T}|\theta )& =p\left(y_{1:T}\right|h_{1:T+1},{\delta }_{1:T},\theta )p\left(h_{1:T+1}\right|\theta )\hfill \\ \hfill & =\prod _{t=1}^{T}p\left(y_t\right|h_t,h_{t+1},\theta )·p\left(h_{1:T+1}\right|\theta ).\hfill \end{array}$$

(28)

The prior distributions of $\alpha$ and $\nu$ are

$$\alpha \sim \mathrm{Normal}({\overline{\mu }}_{\alpha },{\overline{\omega }}_{\alpha }^{-1}),\nu \sim \mathrm{Gamma}(a_{\nu },b_{\nu }).$$

(29)

The prior distributions of the other parameters are the same as those in Equation (8).

3.2. Conditional Posterior Distributions

3.2.1. Latent Log Volatility $h_{1:T+1}$

The sampling scheme for $h_{1:T+1}$ is the same as described above but with different functional forms of $g\left(h_{1:T+1}\right)$ and $Q\left(h_{1:T+1}\right)$. Specifically,

$$\begin{array}{cc}\hfill g_t\left(h_{1:T+1}\right)& =\left\{-1+{\displaystyle \frac{1}{{\delta }_t}}\left({ϵ}_t-\alpha {\delta }_t-\gamma {\eta }_t\right)\left({ϵ}_t-\gamma \varphi \right)\right\}\mathbf{1}(t\leqq T)\hfill \\ \hfill & +{\displaystyle \frac{\gamma }{{\delta }_{t-1}}}\left({ϵ}_{t-1}-\alpha {\delta }_{t-1}-\gamma {\eta }_{t-1}\right)\mathbf{1}(t\geqq 2),(t=1,\dots ,T+1),\hfill \end{array}$$

(30)

where $\mathbf{1}(·)$ is the indicator function. Each diagonal element of $Q\left(h_{1:T+1}\right)$ is given by

$$\begin{array}{cc}\hfill q_{t,t}\left(h_{1:T+1}\right)& ={\displaystyle \frac{1}{{\delta }_t}}\left\{{ϵ}_t({ϵ}_t-\alpha {\delta }_t-\gamma {\eta }_t)+{\left({ϵ}_t-\gamma \varphi \right)}^2\right\}\mathbf{1}(t\leqq T)\hfill \\ \hfill & +{\displaystyle \frac{{\gamma }^2}{{\delta }_{t-1}}}\mathbf{1}(t\geqq 2),(t=1,\dots ,T+1),\hfill \end{array}$$

(31)

and each off-diagonal element of $Q\left(h_{1:T+1}\right)$ is given by

$$q_{t,t+1}\left(h_{1:T+1}\right)={\displaystyle \frac{\gamma }{{\delta }_t}}({ϵ}_t-\gamma \varphi ),(t=1,\dots ,T).$$

(32)

3.2.2. Regression Coefficients $\beta$

The sampling scheme for $\beta$ is the same as in Section 2.3.2, but with

$$\begin{array}{cc}\hfill g\left(\beta \right)& =\sum _{t=1}^T\left({\displaystyle \frac{{ϵ}_t}{{\delta }_t}}\left({ϵ}_t-\alpha {\delta }_t-\gamma {\eta }_t\right)-1\right)x_t,\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill Q\left(\beta \right)& =\sum _{t=1}^T{\displaystyle \frac{{ϵ}_t}{{\delta }_t}}\left(2{ϵ}_t-\alpha {\delta }_t-\gamma {\eta }_t\right)x_t{x}_t^{\prime }.\hfill \end{array}$$

(34)

3.2.3. Leverage Parameter $\gamma$

The conditional posterior distribution of $\gamma$ is given by

$$\gamma |h_{1:T+1},{\delta }_{1:T},{\theta }_{-\gamma },y_{1:T}\sim \mathrm{Normal}\left({\displaystyle \frac{{\sum }_{t=1}^T{\eta }_t({ϵ}_t/{\delta }_t-\alpha )+{\overline{\omega }}_{\gamma }{\overline{\mu }}_{\gamma }}{{\sum }_{t=1}^T{\eta }_t^2/{\delta }_t+{\overline{\omega }}_{\gamma }}},{\displaystyle \frac{1}{{\sum }_{t=1}^T{\eta }_t^2/{\delta }_t+{\overline{\omega }}_{\gamma }}}\right).$$

(35)

3.2.4. Random Scale ${\delta }_{1:T}$

The conditional posterior distribution of ${\delta }_t$ is obtained using Bayes’ theorem:

$${\delta }_t|h_{1:T+1},\theta ,y_{1:T}\sim \mathrm{GIG}({\lambda }_t,{\psi }_t,{\xi }_t),t=1,\dots ,T,$$

(36)

where

$$({\lambda }_t,{\psi }_t,{\xi }_t)=\left\{\begin{array}{cc}{\displaystyle \left(\frac{1}{2},{\alpha }^2+2,{({ϵ}_t-\gamma {\eta }_t)}^2\right),}\hfill & \left(\mathrm{SV}\text{-}\mathrm{AL}\right),\hfill \\ {\displaystyle \left(\frac{\nu -1}{2},{\alpha }^2+\nu ,{({ϵ}_t-\gamma {\eta }_t)}^2\right),}\hfill & \left(\mathrm{SV}\text{-}\mathrm{SG}\right),\hfill \\ {\displaystyle \left(-\frac{\nu +1}{2},{\alpha }^2,{({ϵ}_t-\gamma {\eta }_t)}^2+\nu \right),}\hfill & \left(\mathrm{SV}\text{-}\mathrm{ST}\right).\hfill \end{array}\right.$$

To improve MCMC performance, we applied the generalized Gibbs sampler of Liu and Sabatti [61] to ${\left\{{\delta }_t\right\}}_{t=1}^T$, using the conditional posterior distribution in Equation (36). It suffices to multiply each ${\left\{{\delta }_t\right\}}_{t=1}^T$ by a random number c generated from

$$c\sim \left\{\begin{array}{cc}{\displaystyle \mathrm{GIG}\left(\frac{T}{2},({\alpha }^2+2)\sum _{t=1}^T{\delta }_t,\sum _{t=1}^T\frac{{({ϵ}_t-\gamma {\eta }_t)}^2}{{\delta }_t}\right),}\hfill & \left(\mathrm{SV}\text{-}\mathrm{AL}\right),\hfill \\ {\displaystyle \mathrm{GIG}\left(\frac{(\nu -1)T}{2},({\alpha }^2+\nu )\sum _{t=1}^T{\delta }_t,\sum _{t=1}^T\frac{{({ϵ}_t-\gamma {\eta }_t)}^2}{{\delta }_t}\right),}\hfill & \left(\mathrm{SV}\text{-}\mathrm{SG}\right),\hfill \\ {\displaystyle \mathrm{GIG}\left(-\frac{(\nu +1)T}{2},{\alpha }^2\sum _{t=1}^T{\delta }_t,\sum _{t=1}^T\frac{{({ϵ}_t-\gamma {\eta }_t)}^2+\nu }{{\delta }_t}\right),}\hfill & \left(\mathrm{SV}\text{-}\mathrm{ST}\right).\hfill \end{array}\right.$$

(37)

3.2.5. Asymmetry Parameter $\alpha$

Again applying Bayes’ theorem, the conditional posterior distribution of $\alpha$ is obtained as

$$\begin{array}{cc}\hfill & \alpha |h_{1:T+1},{\delta }_{1:T},{\theta }_{-\alpha },y_{1:T}\hfill \\ \hfill & \sim \mathrm{Normal}\left({\displaystyle \frac{{\sum }_{t=1}^T({ϵ}_t-\gamma {\eta }_t)+{\overline{\omega }}_{\alpha }{\overline{\mu }}_{\alpha }}{{\sum }_{t=1}^T{\delta }_t+{\overline{\omega }}_{\alpha }}},{\displaystyle \frac{1}{{\sum }_{t=1}^T{\delta }_t+{\overline{\omega }}_{\alpha }}}\right).\hfill \end{array}$$

(38)

3.2.6. Tail Parameter $\nu$

Consider the second-order Taylor expansion of the log-conditional posterior density of $\nu$:

$$\begin{array}{c}\hfill f\left(\nu \right)=\sum _{t=1}^{T}logp\left({\delta }_t\right|\nu )+logp\left(\nu \right)+\mathrm{constant},\end{array}$$

(39)

with respect to $\nu$ in the neighborhood of ${\nu }^{*}>0$, i.e.,

$$\begin{array}{c}\hfill f\left(\nu \right)\approx f\left({\nu }^{*}\right)+g\left({\nu }^{*}\right)(\nu -{\nu }^{*})-{\displaystyle \frac{1}{2}}q\left({\nu }^{*}\right){(\nu -{\nu }^{*})}^2,\end{array}$$

(40)

where

$$g\left({\nu }^{*}\right)\equiv {\nabla }_{\nu }f\left({\nu }^{*}\right),q\left({\nu }^{*}\right)\equiv -{\nabla }_{\nu }^{2}f\left({\nu }^{*}\right).$$

By applying the completing-the-square technique to Equation (40), we obtain the proposal distribution as

$$\nu \sim \mathrm{Normal}\left({\mu }_{\nu }\left({\nu }^{*}\right),{\sigma }_{\nu }^2\left({\nu }^{*}\right)\right),$$

(41)

where

$${\sigma }_{\nu }^2\left({\nu }^{*}\right)={\displaystyle \frac{1}{q\left({\nu }^{*}\right)}},{\mu }_{\nu }\left({\nu }^{*}\right)={\nu }^{*}+{\displaystyle \frac{g\left({\nu }^{*}\right)}{q\left({\nu }^{*}\right)}}.$$

Defining the mode of $f\left(\nu \right)$ as ${\nu }^{*}$, $g\left({\nu }^{*}\right)=0$ always holds, because $f\left(\nu \right)$ is globally concave. Thus, ${\mu }_{\nu }\left({\nu }^{*}\right)$ is effectively equal to ${\nu }^{*}$.

4. Results and Discussion

4.1. Results

Before presenting the results of the hierarchical Bayesian analysis, we describe the prior distribution settings. The hyperparameters $({\overline{\mu }}_{\beta },{\overline{\Omega }}_{\beta }^{-1},{\overline{\mu }}_{\gamma },{\overline{\omega }}_{\gamma }^{-1},a_{\tau },b_{\tau },a_{\varphi },b_{\varphi })$ were set as follows:

$$\begin{array}{cc}\hfill {\overline{\mu }}_{\beta }& =\mathbf{0},{\overline{\Omega }}_{\beta }^{-1}=0.01I,{\overline{\mu }}_{\gamma }=0,{\overline{\omega }}_{\gamma }^{-1}=0.01,\hfill \\ \hfill a_{\tau }& =5,b_{\tau }=0.04,a_{\varphi }=1,b_{\varphi }=1,a_{\nu }=4,b_{\nu }=2.\hfill \end{array}$$

(42)

We generated 3000 Monte Carlo sample sequences using Gibbs sampling. After a burn-in period of 1000 samples to eliminate dependence on initial random draws, we used the remaining samples for estimation.

The posterior estimates of the parameters and regression coefficients from the best model selected under the WAIC in each period are listed in

Table 1. Posterior means and standard deviations of parameters.

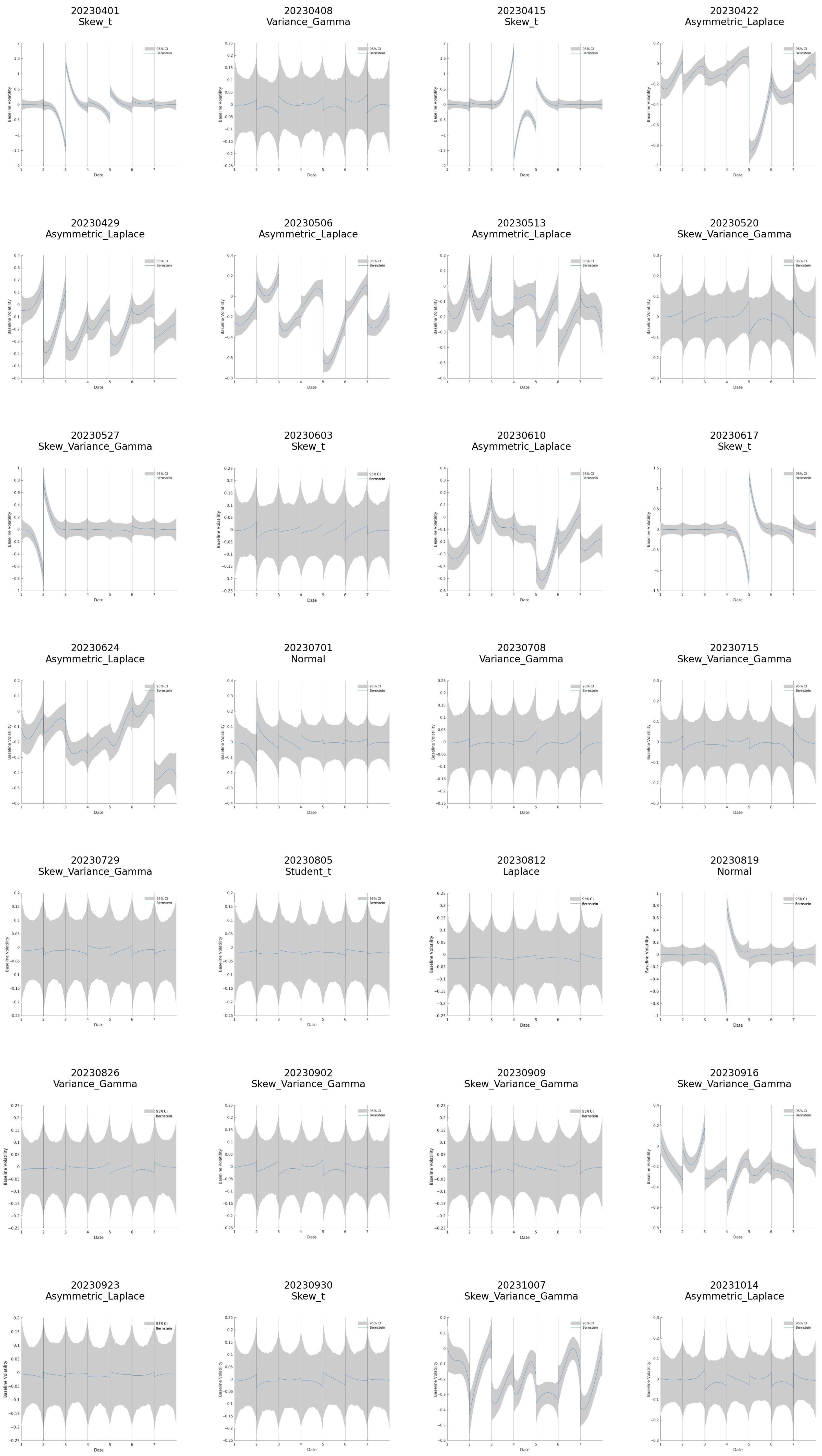
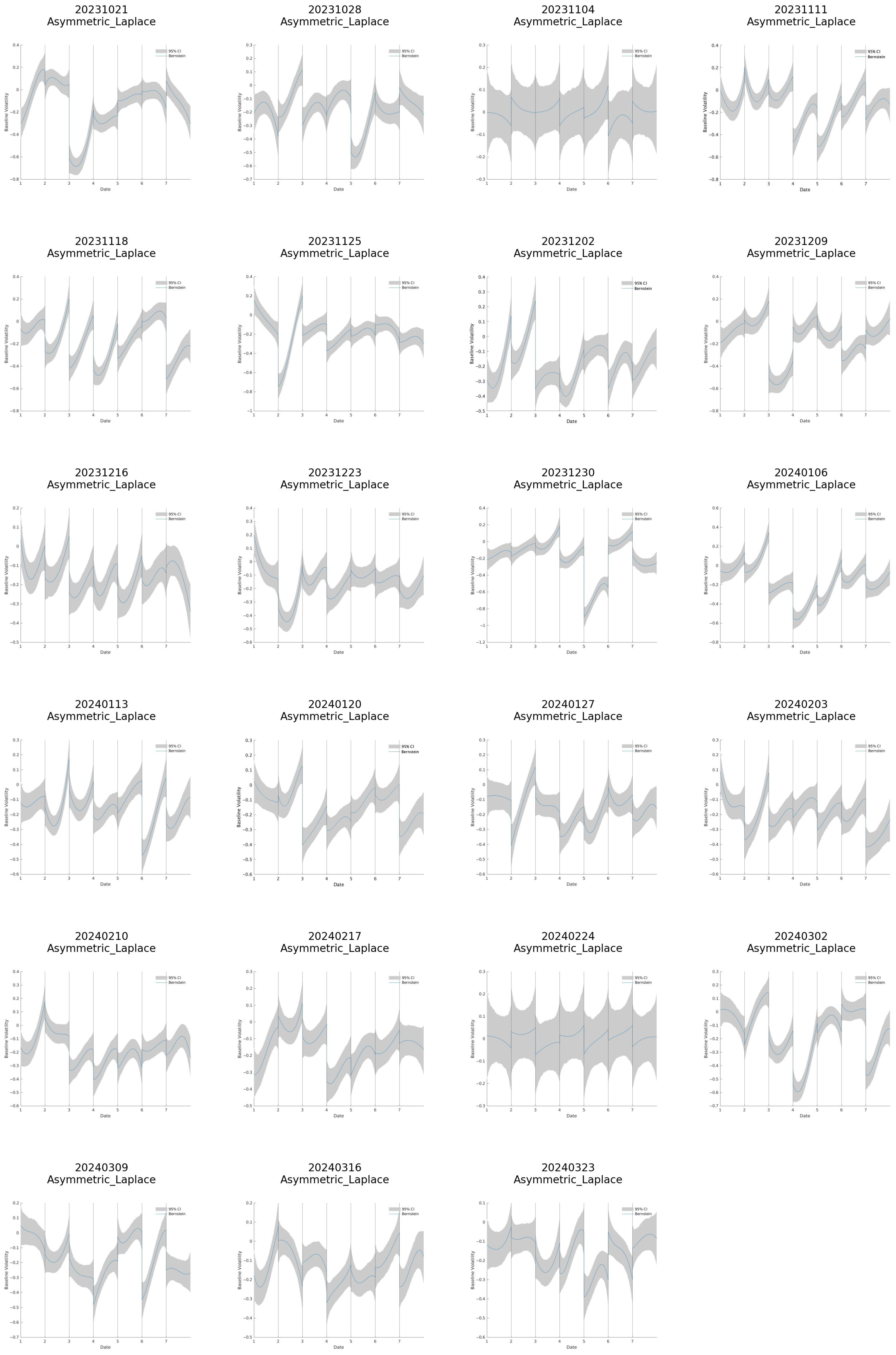
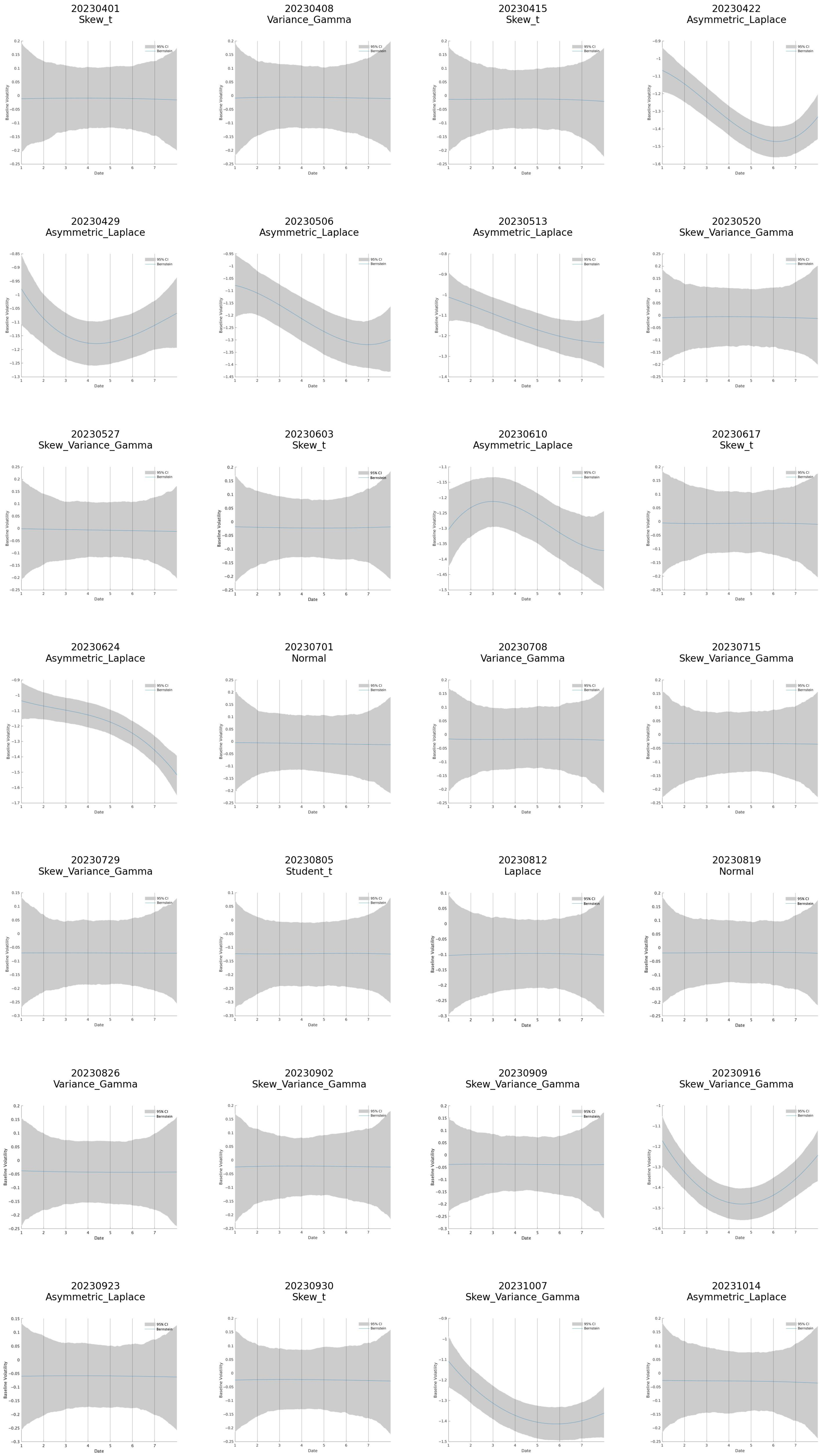
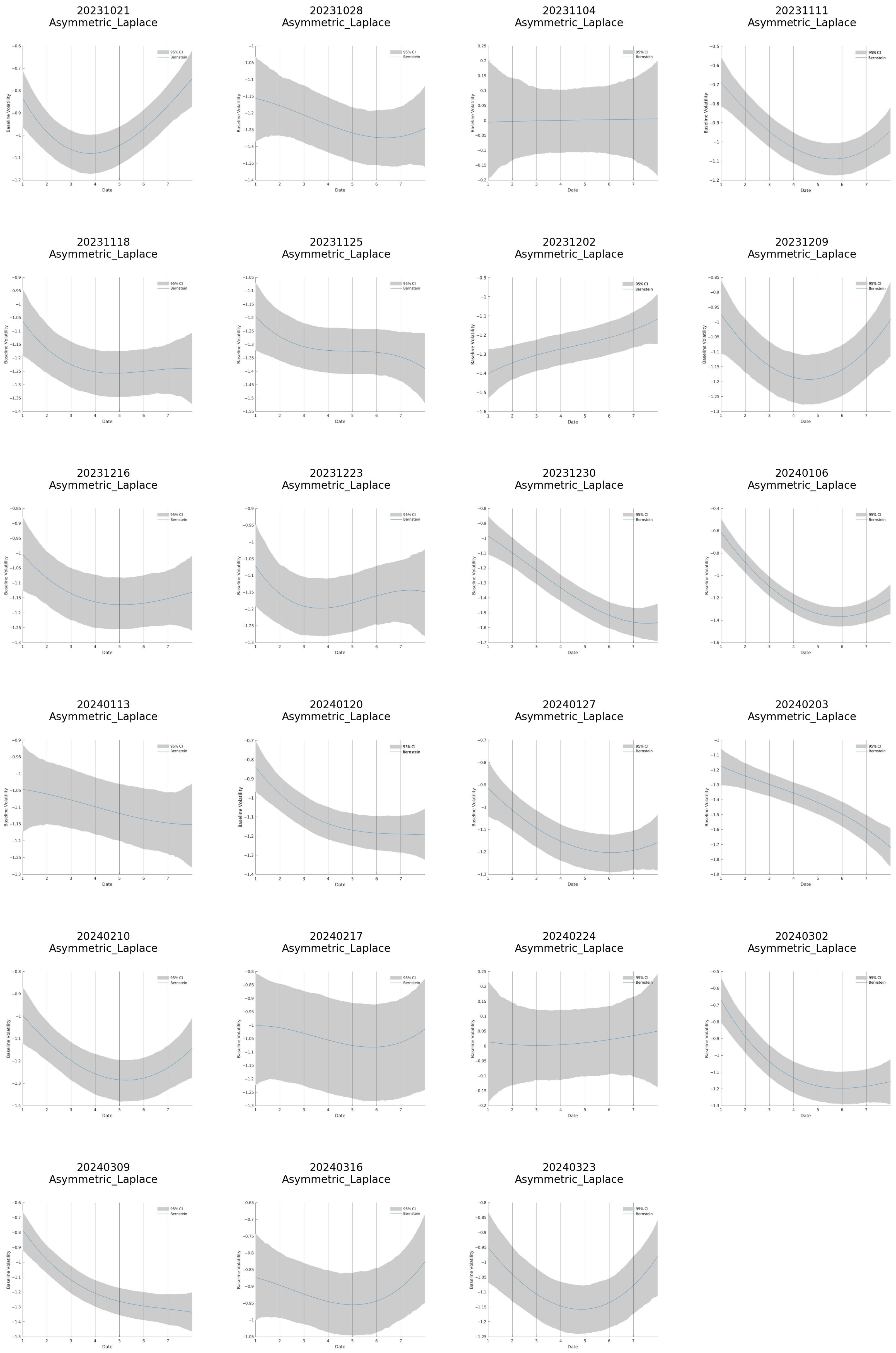
Date	Model	Gamma	Phi	Tau	Alpha	Nu	Rho
1 April 2023	Skew t	−0.1938 (0.0600)	0.9969 (0.0008)	0.2194 (0.0016)	0.0162 (0.0089)	8.3953 (0.3857)	–
8 April 2023	Variance Gamma	−0.0299 (0.0316)	0.9981 (0.0006)	0.2599 (0.0019)	–	2.2980 (0.1032)	–
15 April 2023	Skew t	−0.1287 (0.0608)	0.9970 (0.0008)	0.2079 (0.0015)	−0.0191 (0.0087)	8.9505 (0.4132)	–
22 April 2023	Asymmetric Laplace	10.1447 (0.6100)	0.3779 (0.0702)	0.0604 (0.0038)	−0.0350 (0.0158)	–	–
29 April 2023	Asymmetric Laplace	0.0056 (0.1212)	0.3392 (0.2271)	0.0578 (0.0055)	−0.0335 (0.0139)	–	–
6 May 2023	Asymmetric Laplace	13.4845 (0.9612)	−0.8653 (0.0257)	0.0402 (0.0025)	−0.0389 (0.0155)	–	–
13 May 2023	Asymmetric Laplace	0.0046 (0.0792)	0.0693 (0.1154)	0.0693 (0.0046)	−0.0542 (0.0138)	–	–
20 May 2023	Skew Variance Gamma	0.2112 (0.0522)	0.9982 (0.0006)	0.2192 (0.0015)	0.0122 (0.0125)	3.6051 (0.2405)	–
27 May 2023	Skew Variance Gamma	−0.0285 (0.0233)	0.9972 (0.0007)	0.2342 (0.0017)	−0.0182 (0.0107)	2.6176 (0.0000)	–
3 June 2023	Skew t	0.0241 (0.0379)	0.9944 (0.0011)	0.3642 (0.0025)	0.0554 (0.0112)	12.0888 (0.9164)	–
10 June 2023	Asymmetric Laplace	0.0002 (0.0929)	−0.0203 (0.1223)	0.0723 (0.0047)	−0.0046 (0.0143)	–	–
17 June 2023	Skew t	−0.0799 (0.0347)	0.9957 (0.0009)	0.3195 (0.0023)	−0.0033 (0.0091)	7.7869 (0.3313)	–
24 June 2023	Asymmetric Laplace	−0.0129 (0.1551)	−0.3315 (0.1055)	0.0578 (0.0073)	−0.0050 (0.0131)	–	–
1 July 2023	Normal	−0.3386 (0.0396)	0.9959 (0.0009)	0.2904 (0.0021)	–	–	−0.0979 (0.0114)
8 July 2023	Variance Gamma	−0.0167 (0.0232)	0.9947 (0.0010)	0.3435 (0.0024)	–	2.1427 (0.0821)	–
15 July 2023	Skew Variance Gamma	−0.0104 (0.0125)	0.9916 (0.0013)	0.4401 (0.0032)	0.0909 (0.0138)	2.0067 (0.0064)	–
29 July 2023	Skew Variance Gamma	−0.0160 (0.0102)	0.9806 (0.0021)	0.7038 (0.0052)	0.0551 (0.0134)	2.0163 (0.0159)	–
5 August 2023	Student t	−0.0140 (0.0121)	0.9579 (0.0032)	1.2001 (0.0084)	–	4.2870 (0.1585)	–
12 August 2023	Laplace	−0.0259 (0.0081)	0.9676 (0.0028)	0.9488 (0.0067)	–	–	–
19 August 2023	Normal	0.1913 (0.0408)	0.9952 (0.0010)	0.2961 (0.0022)	–	–	0.0566 (0.0121)
26 August 2023	Variance Gamma	−0.0260 (0.0130)	0.9874 (0.0017)	0.5679 (0.0040)	–	2.0341 (0.0301)	–
2 September 2023	Skew Variance Gamma	0.0237 (0.0135)	0.9936 (0.0011)	0.3992 (0.0028)	0.0512 (0.0132)	2.0193 (0.0188)	–
9 September 2023	Skew Variance Gamma	0.0032 (0.0121)	0.9886 (0.0016)	0.5789 (0.0042)	0.0590 (0.0141)	2.0213 (0.0203)	–
16 September 2023	Skew Variance Gamma	−0.0038 (0.0619)	0.3763 (0.1917)	0.0665 (0.0070)	0.0225 (0.0134)	2.0076 (0.0074)	–
23 September 2023	Asymmetric Laplace	−0.0081 (0.0095)	0.9828 (0.0019)	0.6777 (0.0047)	0.1033 (0.0138)	–	–
30 September 2023	Skew t	−0.1136 (0.0423)	0.9945 (0.0011)	0.3093 (0.0022)	0.0265 (0.0114)	12.8041 (1.0435)	–
7 October 2023	Skew Variance Gamma	−0.0020 (0.0692)	0.3427 (0.1129)	0.0683 (0.0061)	0.0118 (0.0137)	2.0093 (0.0091)	–
14 October 2023	Asymmetric Laplace	−0.0091 (0.0138)	0.9936 (0.0012)	0.3473 (0.0025)	0.0231 (0.0138)	–	–
21 October 2023	Asymmetric Laplace	−0.0117 (0.1809)	−0.0803 (0.1284)	0.0592 (0.0046)	0.0196 (0.0149)	–	–
28 October 2023	Asymmetric Laplace	0.0028 (0.1495)	0.3421 (0.0653)	0.0619 (0.0068)	−0.0030 (0.0144)	–	–
4 November 2023	Asymmetric Laplace	−7.2247 (0.1215)	0.9994 (0.0003)	0.0796 (0.0006)	0.0048 (0.0137)	–	–
11 November 2023	Asymmetric Laplace	−0.0255 (0.1627)	−0.1859 (0.1385)	0.0546 (0.0021)	0.0047 (0.0138)	–	–
18 November 2023	Asymmetric Laplace	−0.0124 (0.1423)	0.3553 (0.0859)	0.0599 (0.0032)	−0.0385 (0.0141)	–	–
25 November 2023	Asymmetric Laplace	−0.0111 (0.0852)	0.4516 (0.1054)	0.0700 (0.0085)	−0.0074 (0.0137)	–	–
2 December 2023	Asymmetric Laplace	−0.9621 (0.3984)	−0.1204 (0.1057)	0.0551 (0.0028)	0.0045 (0.0139)	–	–
9 December 2023	Asymmetric Laplace	0.0015 (0.1057)	−0.0161 (0.0924)	0.0579 (0.0031)	−0.0355 (0.0135)	–	–
16 December 2023	Asymmetric Laplace	10.9611 (1.7421)	0.3495 (0.0613)	0.0607 (0.0078)	−0.0380 (0.0175)	–	–
23 December 2023	Asymmetric Laplace	−0.0363 (0.2285)	−0.0318 (0.1030)	0.0679 (0.0061)	−0.0163 (0.0141)	–	–
30 December 2023	Asymmetric Laplace	−9.2337 (0.9112)	0.3621 (0.0693)	0.0650 (0.0045)	−0.0387 (0.0159)	–	–
6 January 2024	Asymmetric Laplace	−8.0833 (0.3543)	0.2194 (0.0552)	0.0725 (0.0029)	−0.0296 (0.0162)	–	–
13 January 2024	Asymmetric Laplace	11.4016 (0.7040)	−0.5694 (0.0544)	0.0572 (0.0030)	−0.0300 (0.0165)	–	–
20 January 2024	Asymmetric Laplace	0.0012 (0.1186)	−0.1640 (0.1146)	0.0540 (0.0025)	−0.0089 (0.0142)	–	–
27 January 2024	Asymmetric Laplace	0.0087 (0.1603)	0.4203 (0.1377)	0.0535 (0.0038)	−0.0260 (0.0133)	–	–
3 February 2024	Asymmetric Laplace	0.0133 (0.2243)	0.0530 (0.1113)	0.0517 (0.0032)	0.0079 (0.0132)	–	–
10 February 2024	Asymmetric Laplace	11.0248 (0.6504)	0.0184 (0.0877)	0.0588 (0.0025)	−0.0003 (0.0160)	–	–
17 February 2024	Asymmetric Laplace	−3.7797 (4.2423)	0.5738 (0.1756)	0.0607 (0.0060)	−0.0301 (0.0168)	–	–
24 February 2024	Asymmetric Laplace	−2.4906 (0.0536)	0.9860 (0.0018)	0.5889 (0.0042)	−0.1950 (0.0207)	–	–
2 March 2024	Asymmetric Laplace	−9.5323 (0.7461)	−0.1388 (0.0611)	0.0731 (0.0051)	0.0022 (0.0181)	–	–
9 March 2024	Asymmetric Laplace	−7.4220 (0.4976)	0.5811 (0.0681)	0.0751 (0.0035)	−0.0418 (0.0165)	–	–
16 March 2024	Asymmetric Laplace	16.4480 (1.4871)	−0.4310 (0.0532)	0.0510 (0.0032)	−0.0627 (0.0174)	–	–
23 March 2024	Asymmetric Laplace	14.3389 (1.0391)	−0.8258 (0.0263)	0.0452 (0.0031)	−0.0712 (0.0172)	–	–

Note: Bold values indicate the 95% credible interval for the posterior mean does not contain zero.

and

Table 2. Posterior means and standard deviations of regression coefficients.

Date	Model	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	${\mathit{\beta }}_3$	${\mathit{\beta }}_4$	${\mathit{\beta }}_5$	${\mathit{\beta }}_6$
1 April 2023	Skew t	0.0840 (0.0022)	0.0758 (0.0023)	1.0948 (0.0124)	−0.5181 (0.0060)	0.1602 (0.0045)	−0.0111 (0.1012)
8 April 2023	Variance Gamma	0.0577 (0.0148)	0.0992 (0.0137)	0.9380 (0.0649)	−0.4929 (0.0312)	0.4029 (0.0323)	−0.0087 (0.1024)
15 April 2023	Skew t	−0.0410 (0.0022)	−0.0442 (0.0023)	1.1504 (0.0095)	−0.6703 (0.0050)	−0.0035 (0.0045)	−0.0132 (0.0996)
22 April 2023	Asymmetric Laplace	−0.0187 (0.0111)	−0.0252 (0.0094)	−0.2656 (0.0338)	0.1902 (0.0216)	−0.2124 (0.0338)	−1.0674 (0.0656)
29 April 2023	Asymmetric Laplace	−0.0039 (0.0118)	−0.0142 (0.0115)	−0.3181 (0.0368)	0.1825 (0.0243)	−0.1628 (0.0391)	−0.9781 (0.0654)
6 May 2023	Asymmetric Laplace	0.0164 (0.0108)	−0.0336 (0.0108)	−0.3005 (0.0378)	0.1462 (0.0220)	−0.2303 (0.0331)	−1.0783 (0.0649)
13 May 2023	Asymmetric Laplace	0.0073 (0.0133)	0.0190 (0.0130)	−0.1614 (0.0301)	0.0788 (0.0238)	−0.0545 (0.0420)	−1.0112 (0.0609)
20 May 2023	Skew Variance Gamma	0.0674 (0.0156)	0.0729 (0.0135)	0.7886 (0.0358)	−0.6761 (0.0263)	0.4420 (0.0339)	−0.0098 (0.0959)
27 May 2023	Skew Variance Gamma	0.1547 (0.0025)	0.0811 (0.0026)	0.7707 (0.0070)	−0.6971 (0.0051)	0.3440 (0.0051)	−0.0012 (0.1042)
3 June 2023	Skew t	0.0544 (0.0133)	0.0580 (0.0115)	0.6193 (0.0303)	−0.5725 (0.0243)	0.4239 (0.0308)	−0.0185 (0.1000)
10 June 2023	Asymmetric Laplace	0.0507 (0.0133)	0.0060 (0.0112)	−0.2076 (0.0296)	0.0784 (0.0227)	−0.0236 (0.0394)	−1.3039 (0.0631)
17 June 2023	Skew t	0.1081 (0.0033)	0.1354 (0.0034)	0.9552 (0.0100)	−0.5906 (0.0067)	0.2454 (0.0067)	−0.0050 (0.1014)
24 June 2023	Asymmetric Laplace	0.0119 (0.0133)	−0.0233 (0.0125)	−0.1322 (0.0299)	0.0511 (0.0230)	−0.0518 (0.0355)	−1.0353 (0.0634)
1 July 2023	Normal	0.0169 (0.0032)	0.0477 (0.0031)	0.7033 (0.0074)	−0.5821 (0.0058)	0.3917 (0.0058)	−0.0049 (0.1007)
8 July 2023	Variance Gamma	0.0402 (0.0167)	0.0604 (0.0135)	0.6257 (0.0348)	−0.5980 (0.0274)	0.4611 (0.0336)	−0.0159 (0.0971)
15 July 2023	Skew Variance Gamma	0.0148 (0.0179)	0.0324 (0.0145)	0.6043 (0.0367)	−0.6550 (0.0305)	0.6031 (0.0406)	−0.0314 (0.0995)
29 July 2023	Skew Variance Gamma	0.0889 (0.0203)	0.0930 (0.0154)	0.4321 (0.0325)	−0.5805 (0.0302)	0.7434 (0.0367)	−0.0701 (0.1018)
5 August 2023	Student t	0.0775 (0.0188)	0.0948 (0.0160)	0.3104 (0.0334)	−0.4850 (0.0328)	0.6642 (0.0359)	−0.1227 (0.1002)
12 August 2023	Laplace	0.0119 (0.0189)	0.0328 (0.0163)	0.3446 (0.0420)	−0.4516 (0.0339)	0.4594 (0.0321)	−0.1036 (0.1007)
19 August 2023	Normal	0.0334 (0.0143)	0.0553 (0.0116)	0.6799 (0.0309)	−0.6789 (0.0236)	0.4539 (0.0295)	−0.0199 (0.0973)
26 August 2023	Variance Gamma	0.0468 (0.0149)	0.0689 (0.0143)	0.5080 (0.0366)	−0.5290 (0.0291)	0.3997 (0.0316)	−0.0385 (0.0990)
2 September 2023	Skew Variance Gamma	0.0832 (0.0178)	0.0951 (0.0146)	0.6376 (0.0371)	−0.7024 (0.0299)	0.6604 (0.0368)	−0.0247 (0.1002)
9 September 2023	Skew Variance Gamma	0.0475 (0.0173)	0.0814 (0.0158)	0.6576 (0.0381)	−0.6408 (0.0289)	0.6647 (0.0392)	−0.0390 (0.0989)
16 September 2023	Skew Variance Gamma	0.0249 (0.0149)	0.0257 (0.0127)	−0.0432 (0.0313)	−0.0302 (0.0264)	0.1923 (0.0395)	−1.1715 (0.0620)
23 September 2023	Asymmetric Laplace	0.0473 (0.0182)	0.0428 (0.0158)	0.5505 (0.0382)	−0.5527 (0.0305)	0.6116 (0.0376)	−0.0604 (0.0998)
30 September 2023	Skew t	0.0315 (0.0132)	0.0581 (0.0120)	0.6320 (0.0346)	−0.4853 (0.0239)	0.4217 (0.0310)	−0.0248 (0.0968)
7 October 2023	Skew Variance Gamma	0.0132 (0.0140)	0.0080 (0.0120)	−0.0743 (0.0285)	−0.0396 (0.0255)	0.1746 (0.0411)	−1.1079 (0.0635)
14 October 2023	Asymmetric Laplace	0.0660 (0.0147)	0.0687 (0.0131)	0.5755 (0.0409)	−0.4966 (0.0276)	0.4930 (0.0340)	−0.0263 (0.1024)
21 October 2023	Asymmetric Laplace	0.0057 (0.0116)	0.0107 (0.0094)	−0.2816 (0.0352)	0.1114 (0.0223)	0.1204 (0.0385)	−0.8340 (0.0650)
28 October 2023	Asymmetric Laplace	0.0083 (0.0131)	−0.0120 (0.0125)	−0.0933 (0.0315)	0.0037 (0.0241)	0.0280 (0.0403)	−1.1566 (0.0652)
4 November 2023	Asymmetric Laplace	0.0008 (0.0102)	−0.0082 (0.0108)	0.6459 (0.0447)	−0.3359 (0.0247)	0.1185 (0.0293)	−0.0057 (0.1015)
11 November 2023	Asymmetric Laplace	0.0015 (0.0095)	−0.0135 (0.0099)	−0.1442 (0.0379)	0.0940 (0.0230)	−0.0766 (0.0367)	−0.6882 (0.0648)
18 November 2023	Asymmetric Laplace	−0.0123 (0.0119)	−0.0126 (0.0114)	−0.0467 (0.0310)	−0.0011 (0.0229)	−0.0467 (0.0387)	−1.0642 (0.0644)
25 November 2023	Asymmetric Laplace	0.0147 (0.0128)	−0.0014 (0.0127)	0.0459 (0.0305)	−0.1187 (0.0247)	0.1200 (0.0407)	−1.1969 (0.0668)
2 December 2023	Asymmetric Laplace	−0.0136 (0.0111)	0.0099 (0.0123)	−0.2616 (0.0380)	0.0967 (0.0249)	0.1249 (0.0389)	−1.4022 (0.0656)
9 December 2023	Asymmetric Laplace	0.0063 (0.0134)	−0.0262 (0.0107)	−0.1026 (0.0354)	0.0353 (0.0243)	−0.1456 (0.0401)	−0.9739 (0.0629)
16 December 2023	Asymmetric Laplace	−0.0182 (0.0108)	−0.0308 (0.0112)	−0.0155 (0.0348)	0.0120 (0.0219)	−0.1448 (0.0366)	−1.0040 (0.0632)
23 December 2023	Asymmetric Laplace	0.0286 (0.0141)	−0.0112 (0.0123)	−0.0354 (0.0381)	0.0017 (0.0261)	−0.1042 (0.0407)	−1.0721 (0.0639)
30 December 2023	Asymmetric Laplace	0.0321 (0.0100)	0.0011 (0.0092)	−0.0706 (0.0353)	0.0424 (0.0219)	−0.1192 (0.0318)	−0.9861 (0.0669)
6 January 2024	Asymmetric Laplace	−0.0141 (0.0096)	−0.0443 (0.0088)	−0.2978 (0.0386)	0.1630 (0.0206)	−0.2362 (0.0331)	−0.6122 (0.0652)
13 January 2024	Asymmetric Laplace	0.0017 (0.0091)	−0.0269 (0.0100)	−0.1518 (0.0388)	0.0795 (0.0208)	−0.1773 (0.0336)	−1.0469 (0.0653)
20 January 2024	Asymmetric Laplace	0.0055 (0.0125)	−0.0071 (0.0116)	−0.0395 (0.0354)	0.0078 (0.0238)	−0.0322 (0.0387)	−0.8384 (0.0654)
27 January 2024	Asymmetric Laplace	−0.0143 (0.0136)	−0.0288 (0.0128)	−0.0770 (0.0289)	0.0279 (0.0235)	−0.0798 (0.0382)	−0.9145 (0.0620)
3 February 2024	Asymmetric Laplace	0.0266 (0.0121)	−0.0017 (0.0117)	−0.0016 (0.0286)	−0.0804 (0.0232)	0.1352 (0.0384)	−1.1753 (0.0629)
10 February 2024	Asymmetric Laplace	−0.0142 (0.0113)	−0.0262 (0.0108)	−0.1254 (0.0337)	0.0800 (0.0215)	−0.0711 (0.0334)	−0.9954 (0.0634)
17 February 2024	Asymmetric Laplace	−0.0001 (0.0141)	−0.0210 (0.0121)	−0.1348 (0.0414)	0.0726 (0.0239)	−0.1553 (0.0401)	−1.0019 (0.1193)
24 February 2024	Asymmetric Laplace	−0.1990 (0.0139)	−0.1035 (0.0099)	0.5571 (0.0468)	−0.2459 (0.0235)	0.2487 (0.0279)	0.0143 (0.1003)
2 March 2024	Asymmetric Laplace	0.0082 (0.0101)	−0.0329 (0.0088)	−0.5444 (0.0479)	0.2255 (0.0218)	−0.1394 (0.0310)	−0.6718 (0.0672)
9 March 2024	Asymmetric Laplace	0.0015 (0.0111)	−0.0090 (0.0109)	−0.5221 (0.0469)	0.2243 (0.0217)	−0.1744 (0.0385)	−0.7830 (0.0656)
16 March 2024	Asymmetric Laplace	−0.0041 (0.0107)	−0.0437 (0.0114)	−0.4849 (0.0495)	0.2051 (0.0213)	−0.3327 (0.0344)	−0.8736 (0.0657)
23 March 2024	Asymmetric Laplace	−0.0214 (0.0115)	−0.0377 (0.0105)	0.0045 (0.0395)	0.0239 (0.0213)	−0.2625 (0.0340)	−0.9507 (0.0636)

Note: Bold values indicate the 95% credible interval for the posterior mean does not contain zero.

, and the Watanabe–Akaike information criterion (WAIC) values for all model specifications across the full sample are reported in

Table 3. WAIC for each combination of model and week.

Date	Normal	Laplace	Asym Laplace	VG	SVG	Student t	Skew t
1 April 2023	$4.8335\times {10}^4$	–	$4.7926\times {10}^4$	$6.6130\times {10}^4$	$5.2677\times {10}^4$	$4.4790\times {10}^4$	$\mathbf{3.4003}\times {\mathbf{10}}^{\mathbf{4}}$
8 April 2023	$1.7347\times {10}^4$	$1.0364\times {10}^5$	$4.8057\times {10}^4$	$\mathbf{1.4026}\times {\mathbf{10}}^{\mathbf{4}}$	$1.4059\times {10}^4$	$3.4435\times {10}^4$	$2.9146\times {10}^4$
15 April 2023	$3.8749\times {10}^4$	$6.5312\times {10}^4$	$4.5472\times {10}^4$	$4.8601\times {10}^4$	$4.8240\times {10}^4$	$3.4800\times {10}^4$	$\mathbf{3.3590}\times {\mathbf{10}}^{\mathbf{4}}$
22 April 2023	$3.5913\times {10}^4$	$2.2093\times {10}^4$	$\mathbf{1.8436}\times {\mathbf{10}}^{\mathbf{4}}$	$2.0244\times {10}^4$	$2.1696\times {10}^4$	$2.4694\times {10}^4$	$3.2595\times {10}^4$
29 April 2023	$4.1681\times {10}^4$	$2.1607\times {10}^4$	$\mathbf{2.0031}\times {\mathbf{10}}^{\mathbf{4}}$	$5.2683\times {10}^4$	$2.0830\times {10}^4$	$3.5074\times {10}^4$	$4.6980\times {10}^4$
6 May 2023	$4.1416\times {10}^4$	$2.1692\times {10}^4$	$\mathbf{1.8084}\times {\mathbf{10}}^{\mathbf{4}}$	$2.1085\times {10}^4$	$2.1069\times {10}^4$	$3.0292\times {10}^4$	$3.9549\times {10}^4$
13 May 2023	$4.7185\times {10}^4$	$2.2594\times {10}^4$	$\mathbf{2.0730}\times {\mathbf{10}}^{\mathbf{4}}$	$7.3959\times {10}^4$	$4.5444\times {10}^4$	$3.9149\times {10}^4$	$3.5912\times {10}^4$
20 May 2023	$1.5410\times {10}^4$	$6.9283\times {10}^4$	–	$1.5519\times {10}^4$	$\mathbf{1.5383}\times {\mathbf{10}}^{\mathbf{4}}$	$2.7366\times {10}^4$	$4.7942\times {10}^4$
27 May 2023	$5.9721\times {10}^4$	$7.2556\times {10}^4$	$5.5491\times {10}^4$	$4.0508\times {10}^4$	$\mathbf{3.1690}\times {\mathbf{10}}^{\mathbf{4}}$	$4.8997\times {10}^4$	$5.0149\times {10}^4$
3 June 2023	$2.4778\times {10}^4$	$8.0099\times {10}^4$	$8.6562\times {10}^4$	$1.4845\times {10}^4$	–	$3.5044\times {10}^4$	$\mathbf{1.4463}\times {\mathbf{10}}^{\mathbf{4}}$
10 June 2023	–	$3.0358\times {10}^4$	$\mathbf{1.8819}\times {\mathbf{10}}^{\mathbf{4}}$	$6.4015\times {10}^4$	$6.1448\times {10}^4$	$4.6717\times {10}^4$	$5.3907\times {10}^4$
17 June 2023	$6.6187\times {10}^4$	$8.0475\times {10}^4$	$7.3281\times {10}^4$	$5.8493\times {10}^4$	$5.7791\times {10}^4$	$7.1499\times {10}^4$	$\mathbf{4.0286}\times {\mathbf{10}}^{\mathbf{4}}$
24 June 2023	$5.1444\times {10}^4$	$2.2434\times {10}^4$	$\mathbf{2.0705}\times {\mathbf{10}}^{\mathbf{4}}$	$2.1523\times {10}^4$	$3.3767\times {10}^4$	$5.2661\times {10}^4$	$5.1887\times {10}^4$
1 July 2023	$\mathbf{3.4705}\times {\mathbf{10}}^{\mathbf{4}}$	–	$4.9921\times {10}^4$	–	–	$5.3291\times {10}^4$	$3.5364\times {10}^4$
8 July 2023	$1.4745\times {10}^4$	–	$5.3872\times {10}^4$	$\mathbf{1.3849}\times {\mathbf{10}}^{\mathbf{4}}$	$1.3923\times {10}^4$	$3.7640\times {10}^4$	$3.7532\times {10}^4$
15 July 2023	$2.5789\times {10}^4$	–	–	$1.4552\times {10}^4$	$\mathbf{1.4104}\times {\mathbf{10}}^{\mathbf{4}}$	$3.3423\times {10}^4$	$3.2967\times {10}^4$
29 July 2023	$5.1356\times {10}^4$	$3.2219\times {10}^4$	–	$8.4280\times {10}^3$	$\mathbf{8.4193}\times {\mathbf{10}}^{\mathbf{3}}$	$4.7048\times {10}^4$	$3.4587\times {10}^4$
5 August 2023	$8.1564\times {10}^4$	–	$7.7016\times {10}^4$	–	–	$\mathbf{2.8638}\times {\mathbf{10}}^{\mathbf{3}}$	$3.1048\times {10}^3$
12 August 2023	–	$\mathbf{4.9114}\times {\mathbf{10}}^{\mathbf{3}}$	–	–	–	–	–
19 August 2023	$\mathbf{2.3824}\times {\mathbf{10}}^{\mathbf{4}}$	–	$3.6622\times {10}^4$	–	–	$3.8126\times {10}^4$	$2.6204\times {10}^4$
26 August 2023	$6.0664\times {10}^4$	–	$3.7915\times {10}^4$	$\mathbf{7.8581}\times {\mathbf{10}}^{\mathbf{3}}$	–	$6.0777\times {10}^4$	$7.4812\times {10}^4$
2 September 2023	$1.2754\times {10}^4$	–	$3.0083\times {10}^4$	$1.2430\times {10}^4$	$\mathbf{1.2230}\times {\mathbf{10}}^{\mathbf{4}}$	$1.2846\times {10}^4$	$3.8372\times {10}^4$
9 September 2023	–	–	$6.3060\times {10}^4$	$9.7106\times {10}^3$	$\mathbf{9.3958}\times {\mathbf{10}}^{\mathbf{3}}$	$5.7525\times {10}^4$	$4.7871\times {10}^4$
16 September 2023	$7.2035\times {10}^4$	$2.2505\times {10}^4$	$1.9988\times {10}^4$	–	$\mathbf{1.9980}\times {\mathbf{10}}^{\mathbf{4}}$	$3.9631\times {10}^4$	$3.4192\times {10}^4$
23 September 2023	–	–	$\mathbf{8.7325}\times {\mathbf{10}}^{\mathbf{3}}$	–	$8.7609\times {10}^3$	$6.2780\times {10}^4$	$5.4719\times {10}^4$
30 September 2023	$4.0755\times {10}^4$	$1.9667\times {10}^4$	$1.7321\times {10}^4$	$1.6039\times {10}^4$	$1.6077\times {10}^4$	$1.5909\times {10}^4$	$\mathbf{1.5886}\times {\mathbf{10}}^{\mathbf{4}}$
7 October 2023	$5.2594\times {10}^4$	–	$7.1685\times {10}^4$	–	$\mathbf{1.9675}\times {\mathbf{10}}^{\mathbf{4}}$	$4.7035\times {10}^4$	$7.1574\times {10}^4$
14 October 2023	$5.0498\times {10}^4$	$1.6568\times {10}^4$	$\mathbf{1.4037}\times {\mathbf{10}}^{\mathbf{4}}$	$1.4236\times {10}^4$	$1.4236\times {10}^4$	$4.8392\times {10}^4$	$4.6761\times {10}^4$
21 October 2023	$2.2423\times {10}^4$	$2.3389\times {10}^4$	$\mathbf{2.1668}\times {\mathbf{10}}^{\mathbf{4}}$	$2.2362\times {10}^4$	$2.2472\times {10}^4$	$5.5281\times {10}^4$	$2.2563\times {10}^4$
28 October 2023	$4.1999\times {10}^4$	$2.2977\times {10}^4$	$\mathbf{2.1061}\times {\mathbf{10}}^{\mathbf{4}}$	$4.5658\times {10}^4$	$5.1050\times {10}^4$	$4.0152\times {10}^4$	$5.6618\times {10}^4$
4 November 2023	$4.6895\times {10}^4$	$1.8393\times {10}^4$	$\mathbf{1.6852}\times {\mathbf{10}}^{\mathbf{4}}$	$5.4522\times {10}^4$	$2.2682\times {10}^4$	$4.4798\times {10}^4$	$4.8030\times {10}^4$
11 November 2023	$3.6703\times {10}^4$	$2.3608\times {10}^4$	$\mathbf{2.2070}\times {\mathbf{10}}^{\mathbf{4}}$	$6.2664\times {10}^4$	$7.4948\times {10}^4$	$4.6203\times {10}^4$	$5.7968\times {10}^4$
18 November 2023	$5.8413\times {10}^4$	$2.2250\times {10}^4$	$\mathbf{2.0591}\times {\mathbf{10}}^{\mathbf{4}}$	$6.9478\times {10}^4$	$2.1218\times {10}^4$	$4.2375\times {10}^4$	$7.1724\times {10}^4$
25 November 2023	$2.7234\times {10}^4$	$2.3325\times {10}^4$	$\mathbf{2.1237}\times {\mathbf{10}}^{\mathbf{4}}$	$2.1268\times {10}^4$	$2.1272\times {10}^4$	$3.0525\times {10}^4$	$3.9452\times {10}^4$
2 December 2023	$7.2295\times {10}^4$	$2.2459\times {10}^4$	$\mathbf{2.0634}\times {\mathbf{10}}^{\mathbf{4}}$	$7.3737\times {10}^4$	$7.3791\times {10}^4$	$7.5520\times {10}^4$	$6.6891\times {10}^4$
9 December 2023	–	–	$\mathbf{2.1748}\times {\mathbf{10}}^{\mathbf{4}}$	–	–	–	–
16 December 2023	$9.8148\times {10}^4$	$2.5268\times {10}^4$	$\mathbf{2.1415}\times {\mathbf{10}}^{\mathbf{4}}$	$5.4515\times {10}^4$	$6.3736\times {10}^4$	$3.2272\times {10}^4$	$6.2679\times {10}^4$
23 December 2023	–	$6.7372\times {10}^4$	$\mathbf{2.1954}\times {\mathbf{10}}^{\mathbf{4}}$	$5.5161\times {10}^4$	$5.8558\times {10}^4$	$8.6727\times {10}^4$	$6.1191\times {10}^4$
30 December 2023	$3.1163\times {10}^4$	$2.2095\times {10}^4$	$\mathbf{1.8497}\times {\mathbf{10}}^{\mathbf{4}}$	$2.4807\times {10}^4$	$2.0426\times {10}^4$	$3.8823\times {10}^4$	$2.6229\times {10}^4$
6 January 2024	$5.0012\times {10}^4$	$2.2278\times {10}^4$	$\mathbf{1.8314}\times {\mathbf{10}}^{\mathbf{4}}$	$2.1575\times {10}^4$	$2.1581\times {10}^4$	$4.8200\times {10}^4$	$4.1757\times {10}^4$
13 January 2024	$3.7391\times {10}^4$	$2.4290\times {10}^4$	$\mathbf{2.0336}\times {\mathbf{10}}^{\mathbf{4}}$	$2.3922\times {10}^4$	$6.2199\times {10}^4$	$4.3114\times {10}^4$	$3.9218\times {10}^4$
20 January 2024	$4.3409\times {10}^4$	$2.4231\times {10}^4$	$\mathbf{2.2625}\times {\mathbf{10}}^{\mathbf{4}}$	$4.4015\times {10}^4$	$6.2333\times {10}^4$	$4.9081\times {10}^4$	$4.7332\times {10}^4$
27 January 2024	$5.7341\times {10}^4$	$2.4011\times {10}^4$	$\mathbf{2.2642}\times {\mathbf{10}}^{\mathbf{4}}$	$5.2334\times {10}^4$	$6.4627\times {10}^4$	$3.7514\times {10}^4$	$3.4474\times {10}^4$
3 February 2024	$2.2105\times {10}^4$	$2.2643\times {10}^4$	$\mathbf{2.0782}\times {\mathbf{10}}^{\mathbf{4}}$	$5.3602\times {10}^4$	$6.1624\times {10}^4$	$5.6454\times {10}^4$	$2.6629\times {10}^4$
10 February 2024	$3.8108\times {10}^4$	$2.4184\times {10}^4$	$\mathbf{2.0280}\times {\mathbf{10}}^{\mathbf{4}}$	$2.3852\times {10}^4$	$2.3854\times {10}^4$	$6.4021\times {10}^4$	$3.2713\times {10}^4$
17 February 2024	$6.7202\times {10}^4$	$2.4028\times {10}^4$	$\mathbf{2.1814}\times {\mathbf{10}}^{\mathbf{4}}$	$6.9277\times {10}^4$	$5.8237\times {10}^4$	$4.8898\times {10}^4$	$4.2647\times {10}^4$
24 February 2024	$3.1021\times {10}^4$	$2.2543\times {10}^4$	$\mathbf{1.3618}\times {\mathbf{10}}^{\mathbf{4}}$	$2.0355\times {10}^4$	$2.0395\times {10}^4$	$3.2730\times {10}^4$	$2.7983\times {10}^4$
2 March 2024	$5.7066\times {10}^4$	$2.3967\times {10}^4$	$\mathbf{1.9458}\times {\mathbf{10}}^{\mathbf{4}}$	$6.1961\times {10}^4$	$5.4446\times {10}^4$	$5.0562\times {10}^4$	$5.1763\times {10}^4$
9 March 2024	$2.4982\times {10}^4$	$2.3484\times {10}^4$	$\mathbf{1.9897}\times {\mathbf{10}}^{\mathbf{4}}$	$4.9363\times {10}^4$	$5.6147\times {10}^4$	$5.3243\times {10}^4$	$5.8335\times {10}^4$
16 March 2024	$7.1878\times {10}^4$	$2.6540\times {10}^4$	$\mathbf{2.1261}\times {\mathbf{10}}^{\mathbf{4}}$	$5.0846\times {10}^4$	$2.5968\times {10}^4$	$4.7860\times {10}^4$	$3.9804\times {10}^4$
23 March 2024	$8.7115\times {10}^4$	$2.4762\times {10}^4$	$\mathbf{2.0825}\times {\mathbf{10}}^{\mathbf{4}}$	$2.4364\times {10}^4$	$6.9234\times {10}^4$	$5.2000\times {10}^4$	$6.0585\times {10}^4$

Note: Bold values indicate the best WAIC value for the week.

. The intraday and intraweek seasonalities are presented in Figure 1 and Figure 2.

4.2. Discussion

A detailed interpretation of these findings is provided. Table 1, Table 2 and Table 3 present, respectively, the posterior estimates obtained from the best-performing model for each individual week and the WAIC values for each specification across the entire sample. This section interprets the results and outlines their implications.

4.3. Evolution of the Best–Fitting Distribution

Up to the week of 7 October 2023, the WAIC selected different winning distributions, indicating an unstable market structure. However, from 14 October 2023 onward, the WAIC consistently selected the asymmetric Laplace (AL) distribution. A plausible explanation is that from mid-October 2023 onward, growing expectations of U.S. spot-BTC ETF approval generated a persistent buy-side imbalance, while the market-makers deepened liquidity. This combination of thinner extreme tails yet a lasting right-hand skew matched the shape captured most parsimoniously by the AL distribution. Various studies have supported the asymmetries in cryptocurrency distribution [62,63,64].

4.4. Model–Convergence Anomalies

Anomalies in model convergence were observed during the following periods:

• Week of 22 July 2023. During this week, none of the seven candidate distributions converged. This period coincided with a Federal Open Market Committee meeting and with the lowest recorded volatility in the Bitcoin market, which likely violated the regularity conditions of the MCMC samplers.
• Week of 9 December 2023. In this week, only the AL model successfully converged, further supporting the selection of the AL distribution as the best-fitting specification since 7 October 2023.

Two main factors may have caused the sampler failures observed during the weeks of 22 July and 9 December 2023. Distributional misfit: In the week of 22 July 2023, none of the seven candidate return distributions converged, whereas in the week of 9 December 2023, only AL succeeded. The July data combined extreme tails with pronounced skewness that could not be accommodated by any specification. In contrast, the December data showed a “thin-tail + skew” profile that fits only AL. Numerical propagation: Although the covariates show no abnormal summary statistics, misfitting models produced extreme parameter draws. These draws inflated the linear predictor inside the $exp(·)$ term of the observation equation, pushed the exponential beyond machine range, and forced the log-likelihood to Inf/NaN; these successively caused the samplers to abort. Therefore, nonconvergence stems from data-driven distributional misfit in those two weeks rather than from any structural flaw in the stochastic-volatility framework.

4.5. Regression Coefficients

4.5.1. ${\beta }_1$: Trading Volume

${\beta }_1$, which reflects the relationship between trading volume and volatility, was significantly positive in many weeks up to September, but its sign alternated and its significance diminished thereafter. This implies a positive volume–volatility relationship prior to October.

4.5.2. ${\beta }_2$: Order Imbalance

${\beta }_2$, which captures the difference between buy and sell volumes, was significant in many weeks, though its sign varied—indicating day-to-day fluctuations in the impact of order imbalance on volatility.

4.5.3. ${\beta }_3$: Price Changes

${\beta }_3$, which represents the effect of minute-by-minute price changes on volatility, was frequently significant with varying signs. This suggests that while price movements consistently influence volatility, the structure of the relationship varies week to week.

4.5.4. ${\beta }_4$: Buyer Proportion

${\beta }_4$, which captures the effect of buyer participation, was significantly negative in many September weeks, but became less consistent in sign and significance thereafter, reflecting market instability.

4.5.5. ${\beta }_5$: Normalized Imbalance

${\beta }_5$, which adjusts order imbalance for total trading volume, was often significantly positive up to September but shifted to significantly negative in many weeks after October. This suggests a structural shift in the Bitcoin market around that time.

4.5.6. ${\beta }_6$: Price Decline Dummy

${\beta }_6$, which measures the effect of price declines via a dummy variable, was predominantly negative throughout the sample period, indicating a leverage effect in the Bitcoin market.

4.6. Insights from the Parameters

4.6.1. Leverage Effect ($\gamma$)

The sign of the leverage effect corresponds to the sign of $\gamma$. Approximately half of the weekly estimates yielded statistically significant values $\gamma$ of either sign, with nearly equal numbers of positive and negative $\gamma$. This indicates that, unlike in equity and futures markets, Bitcoin lacks a systematic leverage effect. In the existing literature, Komarentsev [65] found no leverage effect for Bitcoin, whereas Wu et al. [66] detected a weak but statistically significant effect. These mixed results indicate that the presence of leverage may depend on the sample period and data frequency, necessitating a more nuanced investigation.

4.6.2. Persistence Parameter ($\varphi$)

Volatility persistence is the speed at which past shocks fade from the conditional variance: the closer the autoregressive parameter in the log-variance equation is to one, the more slowly volatility decays. When persistence is high, a single shock keeps volatility elevated for many consecutive one-minute intervals and causes prolonged turbulence. When persistence is low, volatility reverts quickly and any spike is brief. Thus, tracking the persistence parameter reveals whether a given volatility surge is likely to linger or fade rapidly.

In 20 out of 52 weeks, the AR(1) coefficient satisfied $\varphi \ge 0.9$, suggesting strong volatility persistence. However, several weeks exhibited significantly negative $\varphi$, indicating time-varying dynamics in those weeks. The persistence of the Bitcoin market has been extensively studied, with some studies Bouri et al. [67], Yaya et al. [68] suggesting its strong persistence and other studies Baur and Jha [69], Abakah et al. [70] suggesting its lack of persistence.

4.6.3. Asymmetry Parameter ($\alpha$)

The asymmetry parameter $\alpha$ governs the left–right asymmetry of the return distribution. Illustrative examples are given below:

• $\alpha >0$ (right-skewed, thicker right tail): price spikes driven by FOMO and short covering; bullish jumps dominate.
• $\alpha <0$ (left-skewed, thicker left tail): episodes of panic selling or large market sell orders trigger sharp downward moves.
• $\alpha \approx 0$ (symmetric): buying and selling pressures are balanced; upside and downside shocks occur with similar frequencies.

Among the 40 instances involving an asymmetric distribution, 23 exhibited a $5\%$-significant $\alpha$ (6 positive, 17 negative). The prevalence of negative skew mirrors that of the equity market, albeit with modest absolute magnitudes.

4.6.4. Tail–Thickness Parameter ($\nu$)

The tail-thickness parameter $\nu$ controls the kurtosis of the distribution. Typical scenarios include the following:

• Fat tail (small $\nu$): extreme returns occur frequently, reflecting thin order books, temporary liquidity droughts, or large one-off trades; volatility clustering is pronounced.
• Thin tail (large $\nu$): extreme moves are rare; ample liquidity and smooth price discovery prevail, leading to more stable volatility and lower-risk measures such as VaR and ES.

The estimated tail-thickness parameter $\nu$ ranged from 2 (heavy tails) to 13 (slight tails). In all heavy-tailed distributions, the tails were appreciably but not extremely thicker than Gaussian tails.

4.6.5. Intraday and Intraweek Seasonality

Figure 1 and Figure 2 reveal no consistent seasonal pattern across weeks. The continuous 24/7 nature of Bitcoin trading appears to suppress regularities like open–to–close effects, which are often prominent in traditional exchange-traded assets. Nevertheless, seasonal dummies help control for period–specific shocks that might otherwise confound the analysis. Previous studies have also suggested that Bitcoin does not exhibit significant intraday or intraweek seasonality Eross et al. [71], Kunimoto and Kakamu [72].

4.6.6. Policy Implications

The model’s ability to detect structural shifts and persistent volatility in real time is valuable for market surveillance and systemic risk monitoring. Regulators and exchanges could benefit from early warnings of volatility regime changes, particularly in 24/7 cryptomarkets where circuit breakers are not available. Furthermore, the weekly selection of optimal distributional forms can reveal any underlying stability or disorder in the market.

4.6.7. Applications to Financial Engineering

This modeling framework supports flexible volatility forecasting, essential for high-frequency risk management, algorithmic trading, and crypto-option pricing. Its accommodation of asymmetric and heavy-tailed distributions enhances short-term Value-at-Risk and expected shortfall estimates. The model also provides a basis for constructing volatility-linked derivatives and calibrating SV models for digital assets.

4.7. Limitations and Future Directions

The main limitation of our framework is estimation instability. The pronounced price swings of Bitcoin, combined with minute-by-minute data, can push the samplers beyond their stability region, as observed in the two non-convergent weeks (Section 4.4).

To more faithfully represent the market, we may require distributions beyond the seven return distributions examined in this study, particularly those with heavier or more flexible tails. Further research could also explore state-dependent distributions or regime-switching mechanisms to better accommodate the observed structural breaks.

5. Conclusions

Based on minute-by-minute transaction data over a one-year period, we conducted an empirical Bayesian analysis of Bitcoin volatility. By estimating a family of stochastic volatility models with flexible return distributions, including heavy-tailed and asymmetric specifications, we captured key structural features of the BTCUSD market. The framework also incorporates intraday and intraweek seasonalities through Bernstein polynomials and includes multiple order-flow-based covariates to explain volatility dynamics. A clear structural shift, suggesting a regime change in return behavior, was detected in October 2023. At that time, the asymmetric Laplace model began consistently outperforming the others. As revealed in the regression analyses, volume effects weakened after September, order-flow influences were inconsistent across weeks, and the leverage effect occasionally appeared but lacked persistence.

The findings of this study offer actionable guidance for market practitioners and regulators. For practitioners, a shift toward thinner tails generally implies lower adverse selection risk. Thus, bid-ask spreads and inventory control algorithms should be re-tuned to match the new risk–return balance. Continuous tracking of intraday and intraweek seasonality can uncover unusual concentrations of order flow, alerting traders when a single participant may be exerting outsized influence on prices. For regulators, any sustained change in the fitted return distribution can serve as an early warning signal that triggers a targeted review of the risk management framework of an exchange. In addition, distributional diagnostics should be embedded in stress tests conducted around major policy events to evaluate, in a statistically disciplined way, whether existing capital and margin buffers remain adequate.

However, this study has some limitations. The main limitation of our framework is the estimation instability. The pronounced price swings of Bitcoin combined with minute-by-minute data can push the samplers beyond their stability region, as observed in the two nonconvergent weeks (Section 4.4). To more faithfully represent the market, we may require distributions beyond the seven return distributions examined in this study, particularly those with heavier or more flexible tails. Further research could also explore state-dependent distributions or regime-switching mechanisms to better accommodate the observed structural breaks.