1. Introduction
The scheduling problem involves arranging job sequences under limited resources on the basis of due dates, processing times, and penalty weights to optimize the overall completion efficiency. However, early scheduling models seldom accounted for capacity constraints. When firms accept a large volume of orders, they may fail to deliver on time, thus damaging their reputation.
To address this problem, Bartal et al. [
1] proposed the order-acceptance scheduling (OAS) problem, in which job selection and sequencing decisions are integrated to increase overall efficiency and profit. Several studies have developed algorithms for solving the OAS problem, such as simulated-annealing-based permutation optimization (SABPO) [
2], a modified artificial bee colony algorithm [
3], a shuffled frog-leaping algorithm (SFLA) [
4], and a nonlinear 0–1 programming model [
5], all of which aim to maximize the total profit. Some studies have minimized the makespan by adopting memetic algorithms (MAs) [
6], parallel neighborhood search [
7], and adaptive MAs [
8] to boost objective function values in multimachine and dynamic environments.
Because of an increasing global focus on sustainability, some researchers have incorporated carbon-emission costs and energy policies into their OAS models. Chen et al. [
9] developed a single-machine model that considers carbon taxes and time-of-use electricity tariffs, revealing the trade-off between carbon emissions and power costs and offering practical insight for green OAS. OAS is widely implemented in manufacturing, flight scheduling, medical rostering, and vehicle dispatch.
Multiple studies have considered factors related to setup-time, especially sequence-dependent setup time [
10,
11,
12] to reflect real-world conditions in OAS. Jobs that appear later in the production sequence often require longer processing times because of resource fatigue. For instance, in machining lines, cumulative tool wear can increase setup durations by up to 15% over time, and human-operator fatigue in assembly tasks can similarly lengthen changeover intervals. Koulamas and Kyparisis [
13] have formulated the concept of a past-sequence-dependent (PSD) setup time to account for this phenomenon, with the setup times for future jobs multiplied by a constant portion of the cumulative processing time of preceding jobs to obtain more accurate estimates of setup times and overall job completion times. Despite extensive work on PFSS-OAWT and PSD setup times separately, no prior study has combined PSD effects with a surrogate-assisted GA in the order-acceptance flow-shop context. This paper is the first one to work on this problem.
The present study addressed this research gap by developing a simple genetic algorithm (SGA) enhanced by a random forest (RF) surrogate model, namely , to solve the PFSS problem with order acceptance under the conditions of limited capacity, due-date penalties, and PSD setup times.
Numerous studies have employed machine-learning (ML) techniques, such as Gaussian processes [
14], Kriging models [
15], and inexpensive surrogate functions [
16], to enhance traditional metaheuristic algorithms, especially evolutionary algorithms such as genetic algorithms (GA) and NSGA-II. These models have demonstrated improved convergence and reduced computational cost. However, most existing approaches do not address scheduling problems involving sequence-dependent setup times (PSD) in the context of order acceptance, nor do they fully exploit the potential of decision-tree-based models such as random forests. Furthermore, although surrogate models reduce computation complexity, achieving a suitable balance between speed and accuracy remains challenging.
Building upon the framework of Xiao et al. [
2], this study incorporates PSD setup times into the permutation flow-shop scheduling (PFSS) problem with order acceptance, and proposes a surrogate-assisted algorithm leveraging random forests to improve both accuracy and scheduling efficiency. Experimental results demonstrate that the proposed
algorithm significantly outperforms baseline models in terms of total profit and makespan, particularly under PSD conditions.
Table 1 highlights the distinctiveness of the proposed method by comparing it with existing surrogate-assisted approaches. Unlike previous studies, this work is the first to combine random-forest-based surrogate learning, PSD setup time considerations, and order acceptance decisions in PFSS optimization.
To contextualize our research, the following section reviews existing approaches to order-acceptance scheduling, with a focus on PFSS problems, PSD setup times, and the integration of machine learning.
2. Literature Review
This section surveys relevant studies on PFSS with order acceptance, as well as models incorporating PSD setup times. To better clarify this study, it also reviews how machine learning has been used to enhance optimization algorithms in scheduling problems.
2.1. PFSS Problem with Order Acceptance
Studies have combined the OAS problem with PFSS to improve operational performance. Esmaeilbeigi et al. [
24] improved the mixed-integer linear programming (MILP) models (PF1 and PF2) of Wang et al. [
25] by omitting the constraint
. They proved that such omission preserves the model’s validity and proposed two new models, namely NF1 and NF2, that have lower computational complexity and runtime. They improved the performance of these models through enhanced coefficient tuning. Experiments indicated that NF1 and NF2 outperformed PF1 and PF2, and could solve instances with up to five times more orders than the original models.
Lei and Tan [
4] developed an SFLA in which a tournament mechanism divides the population into memeplexes that conduct local search (LS) to maintain diversity and avoid local optima. In terms of maximum profit, the performance of this SFLA was compared with the SABPO [
2] and ABC algorithms [
3]. Across 28 instances, the SFLA found 24 best solutions, thus considerably outperforming the SABPO (8 solutions) and ABC (0 solutions) algorithms. Zaied et al. [
26] reviewed approaches for solving the PFSS problem, noting the strength of evolutionary multiobjective optimization algorithms, which can be useful for solving the PFSS problem with order acceptance.
Lee and Kim [
27] examined the distributed PFSS problem with order acceptance under heterogeneous manufacturing conditions, analyzing how resource allocation affects total profit, defined as revenue minus tardiness-related costs. Li et al. [
28] solved a PFSS problem with distributed blocking and order acceptance using a knowledge-driven version of the NSGA-II, demonstrating the promise of artificial intelligence in solving complex multi-objective scheduling problems effectively. Based on the research of Slotnick and Morton [
29], Wang et al. [
5] developed a nonlinear 0–1 programming model that integrates order selection and scheduling to maximize total profit. Compared to the original model by Slotnick and Morton, their approach achieved higher profits, especially in large instances. While the model can efficiently obtain optimal solutions for small-scale problems (i.e., with fewer orders and machines), its computational complexity increases significantly for large-scale problems. Although these studies have advanced the field, few have incorporated PSD setup times or machine learning (ML) to enhance decision making. This overlooked area represents a key research gap. The present study addresses this by extending the profit maximization model of Xiao et al. [
2], integrating both PSD setup times and ML to improve scheduling effectiveness.
Rahman et al. [
8] proposed an adaptive memetic algorithm that reschedules single-stage and multi-stage orders under uncertainties such as machine breakdowns. Their results indicated that the proposed algorithm achieved higher stability and better adaptability than conventional algorithms, including NEH, HGA_RMA,
, and
, particularly under resource fluctuations in the PFSS problem.
2.2. PSD Setup Time
PSD setup times depend on the cumulative processing time of all preceding operations. Traditional Sequence-Dependent Setup Time (SDST) models charge each job only for the setup required by its immediately preceding job. Thus, evaluating a sequence of
n jobs requires
time (where
b is the number of job families, typically a small constant) and yet the resulting flow-shop remains strongly NP-hard (even NP-complete for two machines) [
30]. In contrast, PSD (Past-Sequence-Dependent) setups let each job’s setup depend on the entire history—incurring an extra
overhead (e.g., for cumulative-time data structures), for a total of
per evaluation—and strictly generalize SDST, so the flow-shop problem remains strongly NP-hard as well [
31].
According to prior researches, PSD setup times have been effectively applied to single-machine scheduling. Kuo and Yang [
32] incorporated PSD setup time into ML, developing polynomial-time algorithms for optimizing multiple objectives (e.g., makespan, penalties, and processing time). Koulamas and Kyparisis [
13] integrated PSD setup time with an ML method to solve a two-objective problem with nonlinear setup behavior and obtained a solution in
time. Wang [
10] and Yin et al. [
11] proposed efficient shortest processing time (SPT)-based algorithms for reaching objectives such as the total weighted completion time and maximum lateness. Mani et al. [
12] developed a weight-section polynomial approach for improving sequencing efficiency and solution quality.
In production environments where setup times worsen due to cumulative wear or fatigue (deterioration), incorporating PSD setup models typically leads to a makespan increase of roughly 8–15% compared to traditional sequence-dependent setup time (SDST) schedules. Single-machine studies by Mosheiov [
33] reports average makespan increases of about 10%. Parallel-machine experiments by Kalaki Juybari et al. [
34] record increases up to 12%, and recent single-machine case studies with step-deterioration by Choi et al. [
35] confirm increases in the 8–15% range. These results underscore the practical impact of deterioration effects on shop-floor makespan.
Although PSD setup time has been frequency incorporated into single-machine problems, it has not yet been integrated into the PFSS problem with order acceptance. Therefore, this study combined PSD setup time with ML to solve the PFSS problem with order acceptance, aiming to achieve rapid, high quality scheduling.
2.3. ML-Enhanced Algorithms
ML methods, surrogate models, and evolutionary algorithms are increasingly used for multi-objective optimization and resource allocation. Shi et al. [
36] coupled a Gaussian radial-basis surrogate model with a genetic algorithm to optimize the design of micro-channel heat-exchanger inlets; they obtained reductions in flow maldistribution by 68.2% and pressure drop by 6.6%. Pan et al. [
37] proposed a classification-based surrogate-assisted evolutionary algorithm (EA) that uses an artificial neural network to predict dominance and filter solutions by uncertainty. This framework outperformed NSGA-III, MOEA/D-EGO, and other models.
Chugh et al. [
15] designed a kriging-assisted reference vector EA that balances convergence and diversity. This framework outperformed reference vector EA, ParEGO, SMS-EGO, and MOEA/D-EGO in terms of IGD. Chang et al. [
38] introduced an artificial-chromosome-embedded genetic algorithm for solving the PFSS problem. This algorithm exploited positional correlations in elite chromosomes to accelerate convergence and exhibited high performance on benchmark datasets.
Random forest (RF) models are widely used for predicting specific outcomes such as electricity demand and power load, particularly in nonlinear regression tasks. Li et al. [
39] combined RF with ensemble empirical mode decomposition to improve electricity demand forecasts. Moreover, Johannesen et al. [
40] employed RF, k-nearest neighbors (k-NN), and linear regression to forecast short-term and long-term urban power load based on weather and temporal variables. Their experiments showed that RF achieved the lowest mean absolute percentage error (0.86%) in 30-min forecasts. In our research, we used RF as a surrogate model to accelerate convergence and increase accuracy.
Table 1 summarizes recent advances in ML-enhanced methods for multiobjective optimization.
3. Method
Many scholars have incorporated sequence-dependent setup time into multimachine models for solving OAS problems, aiming to account for the time required to set up a job on each machine given previous setup time. However, jobs that appear later in the production sequence often have a higher processing difficulty and resource demands, resulting in having longer actual processing time.
3.1. Problem Definition
Order acceptance and scheduling decisions in multijob environments are typically constrained by due dates and tardiness penalties. Determining which orders to accept and how they should be sequenced under limited resources such that total profit can be maximized is a key challenge. This study incorporated PSD delay time into the completion time formula in the framework of Xiao et al. [
2]. The parameters in the developed framework are defined as follows:
Parameter definitions
i: job (order) index,
I: set of jobs,
j: machine index,
k: position of a job in the sequence,
: job index for position k
: revenue of job i
: due date of job i
: weight of the tardiness penalty for job i
: processing time of job i on machine j
: completion time of the k-th scheduled job on machine j
: completion time of job i on machine j
b: PSD constant,
In the objective function of the developed framework, the revenues of all accepted jobs are summed, and tardiness penalties are then subtracted from this sum. The tardiness penalties are calculated by comparing each job’s completion time on the last machine with its due date. Binary variables
determine acceptance. Sequence variables
and
determine the production order. Machine-level completion times
are computed recursively on the basis of prior stages, prior jobs, and PSD setup effects, which all capture the overall impact of prior processing. Stage-sequence constraints (SSCs) and order-sequence constraints maintain precedence across machines and global schedule consistency. Rejected jobs (
) are associated with processing and completion times of 0, which preserves stability and scalability of the developed model. Equation (10) calculates the completion time of each job by adding the previous machine’s completion time, the current processing time, and the weighted sum of the processing times of all prior jobs on the same machine to reflect PSD effects.
In Equation (11), indicates that the processing time of a rejected order () is zero. Rejected orders are defined in two ways: (1) the processing time at each stage is zero, and (2) stage-sequence constraints (SSC) do not apply. Specifically, for a null order (i.e., ), the condition implies the SSC is inactive. Equation (12) shows that can be calculated from , or alternatively, can be computed from .
The supplementary constraints for order acceptance in PFSS are as follows:
- (1)
For the order acceptance flow-shop scheduling problem, the completion time of a rejected order (at each stage) is set equal to the completion time of the preceding order.
- (2)
Inserting, deleting, or reordering “null” jobs () does not affect the completion times or total profit of accepted jobs.
- (3)
Changing to without altering does not affect schedule feasibility or completion times.
3.2. Numerical Example for PSD Completion Times
To illustrate how to calculate completion times of
4 jobs and
2 machines on a flow-shop scheduling problem, we provide a tiny example to show how to compute the PSD-adjusted completion times
when the PSD coefficient is
. First, the processing times
and due-dates
are given in
Table 2.
We set
and consider the job sequence
Using the PSD rule
with
and
, we compute:
Step-by-step calculation: Because Job 2 is the leading work, there is no PSD time to be added.
Job 2 on Machine 1 (
):
Job 2 on Machine 2 (
):
The rest of the jobs [4, 1, 3] should include the prior processing time with the PSD coefficient .
Job 4 on Machine 1 (
):
Job 4 on Machine 2 (
):
Job 1 on Machine 1 (
):
Job 1 on Machine 2 (
):
Job 3 on Machine 1 (
):
Job 3 on Machine 2 (
):
Table 3 summarizes for each job its completion times on Machine 1 and Machine 2, the due-date
, and the acceptance decision. A job is Accepted if its completion time on Machine 2 does not exceed its due-date (
); otherwise it is Rejected.
3.3. Framework of the Genetic Algorithm
A genetic algorithm forms the backbone of the developed framework. ML predictions of the objective function value are input to the algorithm to enhance profit maximization. The steps involved in this Algorithm 1 are as follows [
41]:
: create the initial population.
: compute the fitness for each generation.
t: current generation index.
G: max generations
: update the ML model trained in generation t.
: select parent solutions.
: generate offspring on the basis of the ML, predictions by using genetic operators.
N: size of .
| Algorithm 1 Main Framework of Genetic Evolution Framework with ML Model |
- 1:
Initialize ← population - 2:
Evaluate(population) - 3:
- 4:
Initialize - 5:
while
do - 6:
(population) - 7:
retrain the ML model(, ) - 8:
Generate through self-guided crossover - 9:
Apply self-guided mutation to - 10:
Evaluate() - 11:
Replace N worst solutions in the population with the best solutions in - 12:
- 13:
end while
|
Lines 1 and 2 of the aforementioned are related to the creation and assessment of the initial population. Line 3 focuses on the setting of the generation counter, and line 4 concerns initialization of the ML model. Finally, lines 6–11 are related to iterations of the following steps: selection of parent solutions, updating of the model, generation of offspring through crossover and mutation, evaluation of offspring fitness and updating of the population.
3.4. Chromosome Encoding
The single-chromosome, order-based encoding proposed by Tang et al. [
42] represents both acceptance and sequencing decisions. The initial sequence is sorted by due date and objective-value-guided heuristics. Then, it is dynamically partitioned into accepted and rejected jobs, and reordered to improve scheduling.
As displayed in
Figure 1 and
Figure 2, accepted jobs are placed first, and rejected jobs are arranged after the accepted jobs. Tang et al. [
42] showed that this two-parts layout preserves more diversity in both dimensions leading to better exploration of the combined decision space and, ultimately, higher-quality solutions. The job status may be re-evaluated during evolution. Besides, standard crossover operators could capture the good building blocks of the genes. This design enhances the flexibility and solution quality of the genetic algorithm.
3.5. Local Search Method
To further improve the performance of the adopted genetic algorithm, the LS method of Lin and Ying [
43] is embedded within each chromosome. The number of genes randomly selected for swapping is determined as follows:
where
is a user-defined parameter and
N is the total number of jobs.
Figure 3 depicts the LS process. Genes
are sampled (
-controlled) from an initial sequence
. The remaining jobs in the sequence form a new baseline sequence, and each sampled job is inserted into all possible positions. The arrangement that yields the optimal a objective value is accepted. These steps are performed for each sampled job to avoid local optima.
3.6. Prediction of Objective Values with an RF Model
Model selection through AutoWeka indicated that
RF was the best predictor for the dataset adapted from Xiao et al. [
2] used in this study. According to Breiman [
44] and Archer et al. [
45], RF offers high accuracy and robustness in optimization and regression tasks.
RF, which consists of an ensemble of decision trees, classification, and regression, is conducted through a voting mechanism and averaging mechanism, respectively. RF obtains excellent results in the modeling of nonlinear relationships. In the present study, the RF model is used in every iteration of the genetic algorithm (Algorithm 2). After crossover and mutation, RF predicts each offspring’s objective value and retains the offspring with higher predicted profit. To mitigate overfitting risks, we constrained tree depth, restricted the number of nodes, and avoided excessively fine parameter granularity during model tuning (
Table 4).
| Algorithm 2 Integration of RF into the genetic algorithm |
- 1:
Initialize ← population - 2:
Evaluate(population) - 3:
- 4:
Initialize - 5:
Initialize - 6:
while
do - 7:
Configure and construct the initial dataset - 8:
(population) - 9:
Re-train with - 10:
Generate through self-guided crossover - 11:
Apply self-guided mutation to - 12:
Evaluate objective values of all solutions in - 13:
Replace the N worst individuals in the population with the best solution from - 14:
- 15:
end while
|
The RF model predicts the performance of offspring generated through crossover and mutation. Offspring with higher predicted profit replace those with lower predicted profit, and this process accelerates the search process of the genetic algorithm. The performance of this
method was compared with that of SABPO [
2] and the genetic algorithm + LS method, with the number of iterations fixed as 100,000 for fairness in the comparison.
3.7. RF-Guided Selection of Crossover Offspring
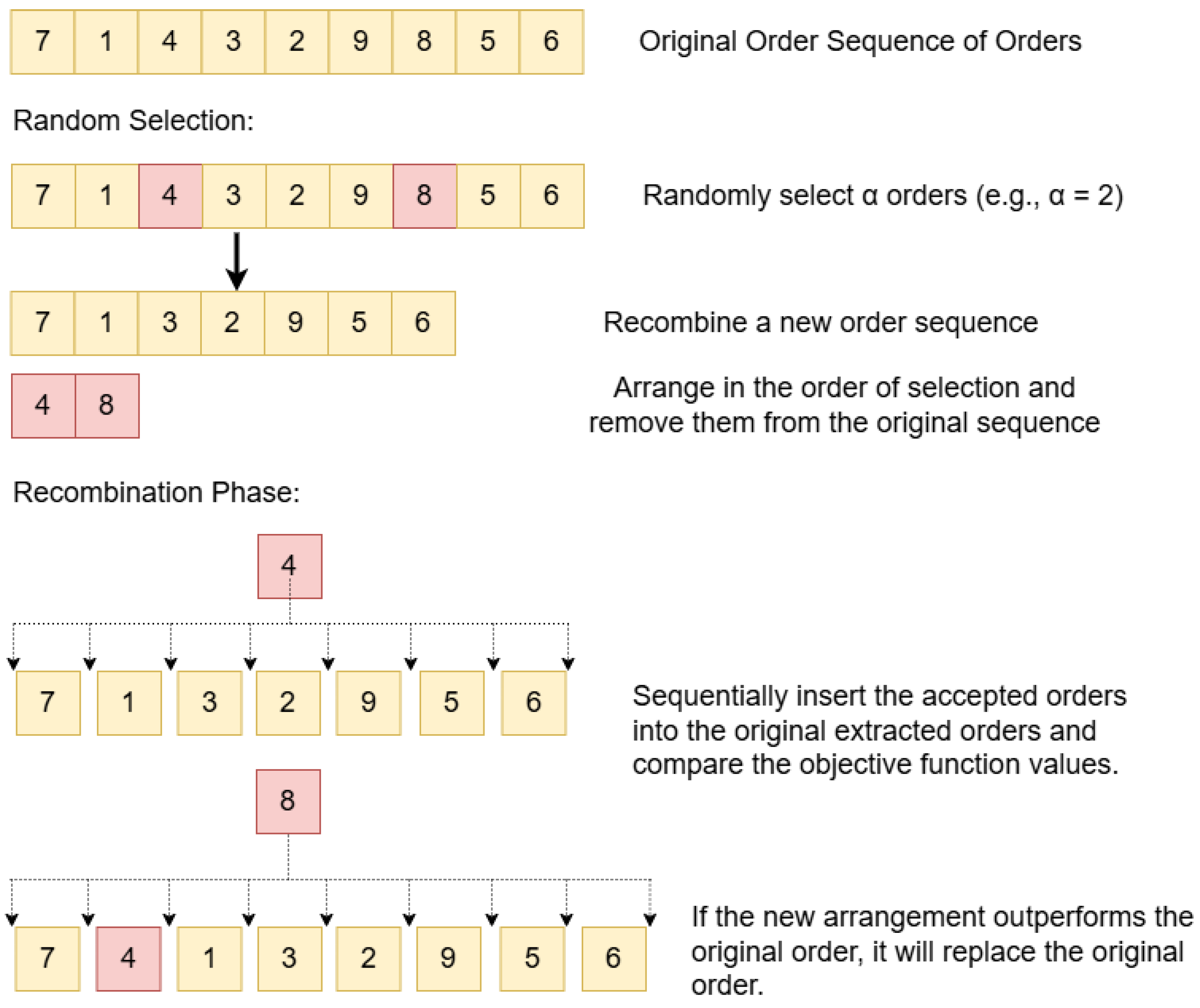
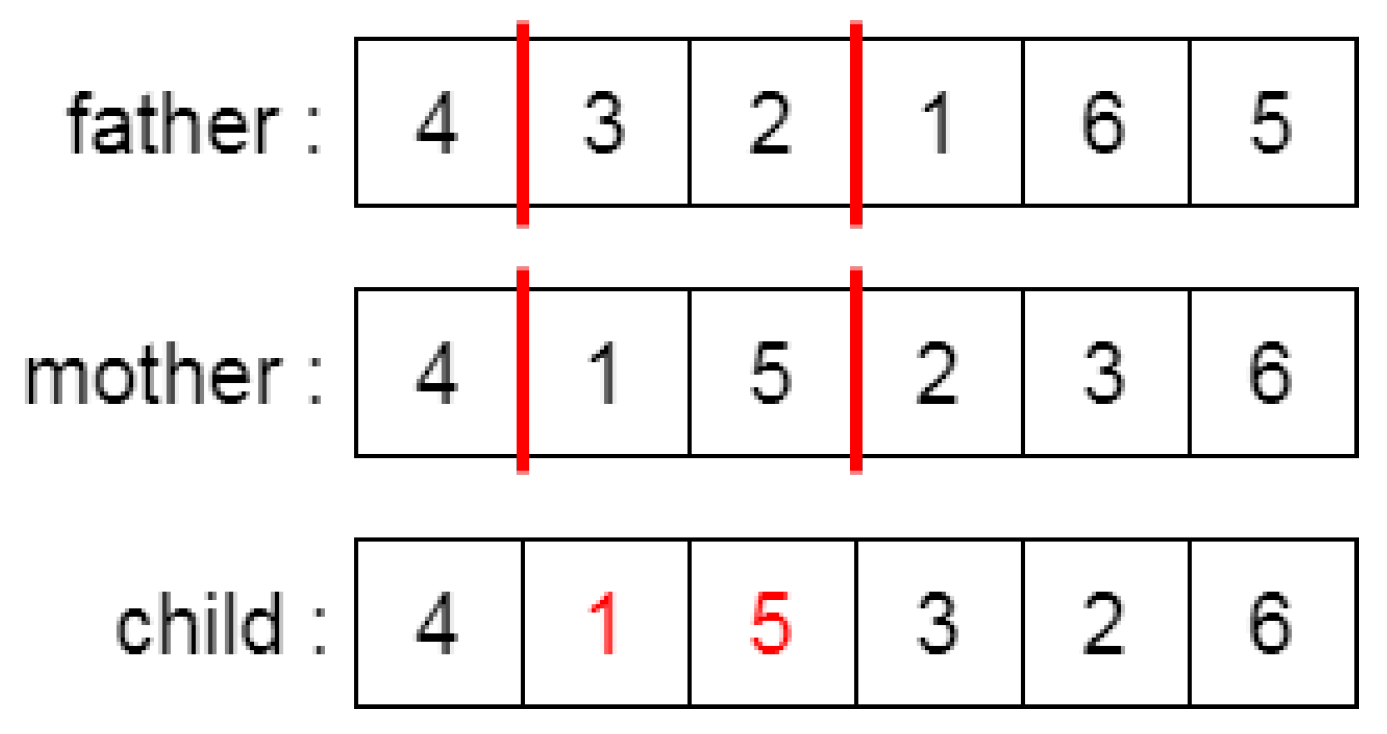
To maximize the objective function value, RF is applied during crossover. A two-point crossover process is conducted in which an elite chromosome is paired with a baseline chromosome to generate promising offspring. After crossover, RF predicts each candidate’s profit and retains the candidate with the highest profit.
The crossover begins by mating an initialized chromosome (father) with a better-performing chromosome (mother) to generate improved offspring. A two-point crossover is applied, as shown in
Figure 4. For example, two cut points [3,2] are randomly selected from the father [4,3,2,1,6,5]. The segment is replaced with values from the mother [4,1,5,2,3,6] while preserving the order. Remaining genes are filled in sequence from the mother without duplication, resulting in a new child chromosome [4,2,3,1,5,6], the best solution in this case, as illustrated in
Figure 4.
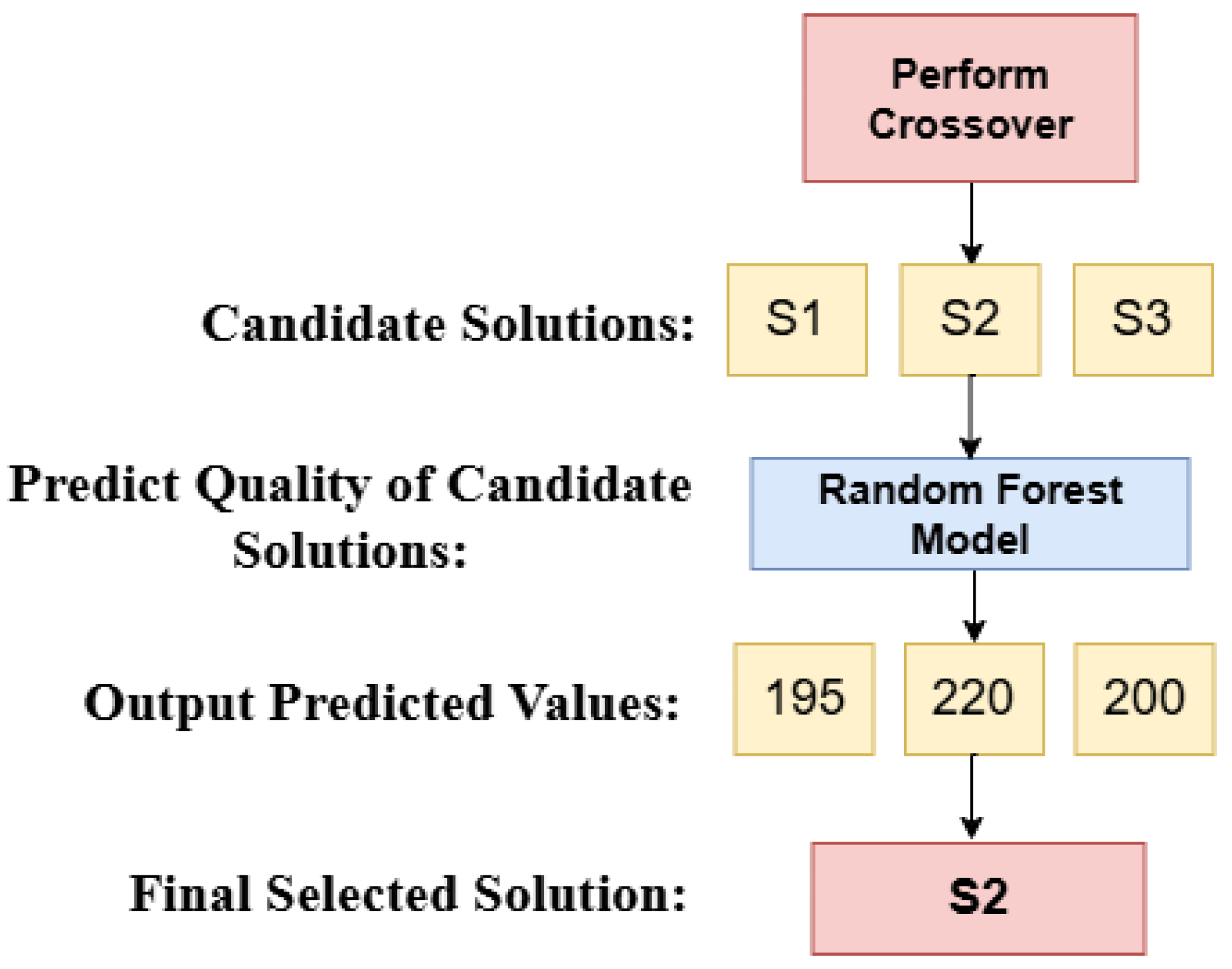
As shown in
Figure 5, the random forest algorithm is used to evaluate solutions generated by the two-point crossover. Suppose three candidate solutions S1, S2, and S3 are produced, with predicted values 195, 220, and 200, respectively. Since this is a maximization problem, S2 is selected. The process is repeated based on
N candidate solutions from
, using crossover probability to guide selection.
3.8. RF-Guided Selection of Mutations
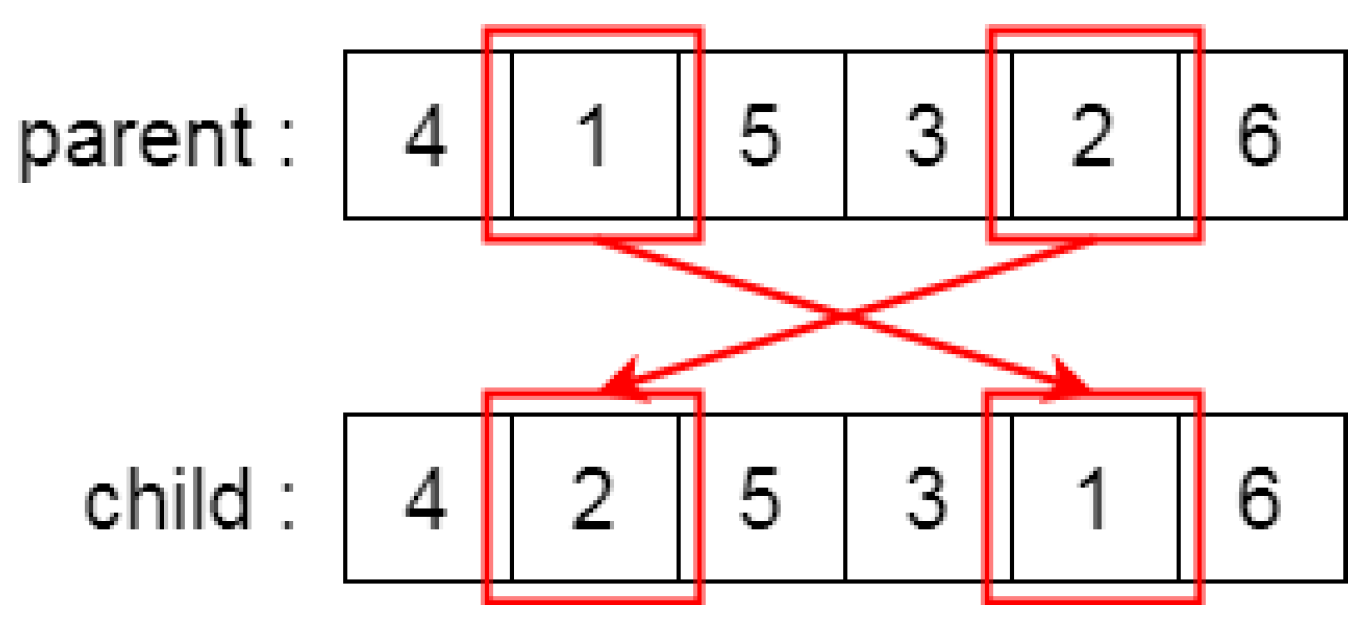
RF also guides mutation. Two genes are randomly exchanged through swap mutation, following which RF predicts the profits for both solutions, retaining the one with higher predicted profit.
After crossover, mutation is applied to further optimize the solution. This study uses the swap mutation method, which exchanges two gene positions. As shown in
Figure 6, the parent chromosome is [4,2,3,1,5,6]. A random value between 0 and 1 determines whether mutation occurs. If it meets the threshold, two random positions are selected for swapping. For example, swapping [2] and [5] results in a child chromosome [4,5,3,1,2,6], as illustrated in
Figure 6.
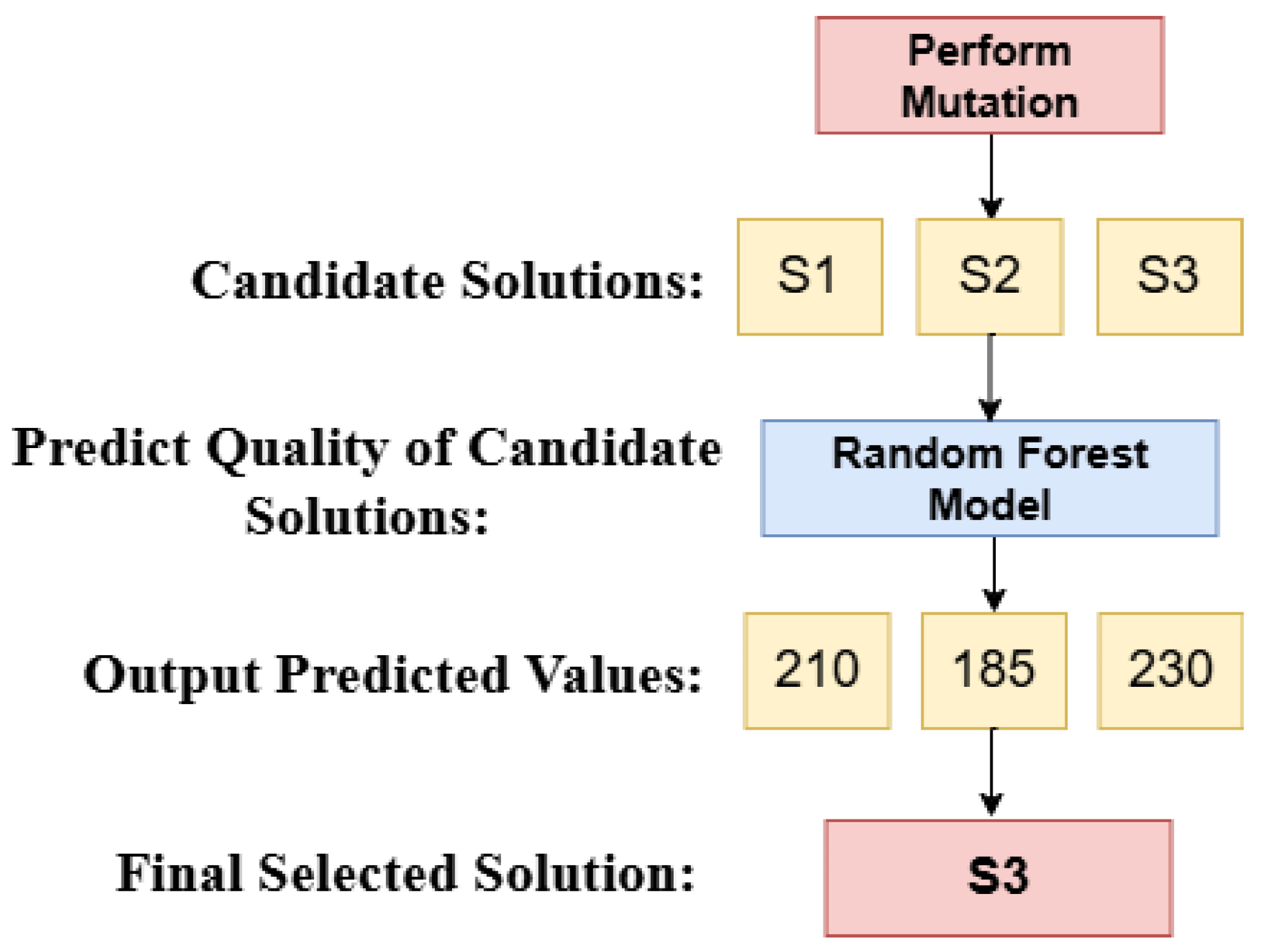
As shown in
Figure 7, the random forest algorithm is used to evaluate solutions generated by the swap mutation. Suppose the mutation process produces three candidate solutions, S1, S2, and S3, with predicted values 210, 185, and 230, respectively. Since this is a maximization problem, S3 is selected. This process is repeated for
N candidate solutions generated from
, guided by the mutation probability.
4. Experimental Results
This section presents the experimental evaluation of four scheduling algorithms under various PSD settings and benchmark instances. Results show that the proposed consistently achieves the highest profit, albeit with increased computation time.
4.1. Dataset and PSD Setup Times
The benchmark dataset proposed by Xiao et al. [
2] includes a comprehensive set of problem instances for the PFSS-OAWT problem, covering a wide range of problem sizes and machine configurations. The order quantities are set at six levels—10, 30, 50, 100, 200, and 500—representing small-sized (10), medium-sized (30, 50), large-sized (100, 200), and very large-sized (500) instances. For the small to large-sized problems (n = 10 to 200), three machine settings are considered: m = 3, 5, and 10, resulting in 15 unique combinations of job and machine counts. Each of these 15 combinations includes 10 randomly generated instances, leading to a total of 150 instances for this group.
Additionally, the dataset incorporates a group of very large-sized problems with 500 orders and 20 machines (m = 20). This group consists of 10 instances, further divided into two loading scenarios: five instances simulate a heavily loaded environment, in which the due dates are tight and delays or rejections are more likely, while the other five simulate a lightly loaded environment with more relaxed due dates. Across all instances, order revenues, weights, due dates, and processing times are generated randomly within specified ranges to ensure variability. In total, the dataset comprises 160 problem instances and provides a robust testing ground for evaluating the performance of scheduling and optimization algorithms under various levels of complexity and system load.
To increase realism, we extend the conventional
sequence-dependent setup time (SDST) by incorporating the notion of
past-sequence-dependent setup time (PSD). While SDST reflects machine switch-over costs, it often underestimates makespan because later jobs suffer from cumulative workload fatigue. PSD remedies this by adding an extra setup load equal to
b times the total processing time of all preceding jobs. Three PSD coefficients are tested,
, as listed in
Table 5, which represent under-loaded, nominal, and heavily constrained flow-shop scenarios, respectively.
4.2. Compared Algorithms
In this study, we proposed
, which embeds a random-forest surrogate to guide fitness evaluation. To assess the proposed model, we benchmark three algorithms: the standard genetic algorithm (SGA);
, which augments SGA with a local-search mechanism; and the surrogate-assisted-based population optimization (SABPO) heuristic originally developed by Xiao et al. [
2]. All four methods are applied to the same order-acceptance flow-shop setting so that solution quality and convergence behavior can be compared fairly.
We select the parameters of the compared by using design-of-experiments (DOE) in two stages. The first stage selects the key parameters (crossover rate and mutation rate) of genetic algorithms. The second stage conducts the DOE for selecting the parameters of and . After these DOE campaigns, each algorithm was tuned to its most effective settings. For , ANOVA revealed a significant NumIterations–MaxDepth interaction; the best configuration was NumIterations , MaxDepth , BagSizePercent , and BatchSize . In , only the local-search scope mattered, with striking the optimal balance between profit and runtime. For the plain SGA, profit was most sensitive to the mutation rate and the PSD coefficient b, yielding and , while the crossover rate was fixed at to minimise CPU time. All algorithms were run for a fixed generation count—200 for and the same order of magnitude for the others—without additional convergence thresholds to ensure a fair comparison.
To evaluate the performance of the four methods, we conducted ANOVA and post-hoc comparisons on both profit values and computation time.
Table 6 presents the ANOVA results for profit values, showing a significant effect of the method factor (
) under the 95% confidence intervals. The post-hoc comparison in
Table 7 further distinguishes the methods into three statistically different groups, with
, the method proposed in this study, achieving the highest mean profit and placed alone in Group A.
Similarly,
Table 8 reports the ANOVA results for computation time, which also reveals a significant method effect. The post-hoc grouping in
Table 9 shows that
requires the longest runtime (Group A), while SGA achieves the shortest (Group D). These results confirm a trade-off between solution quality and computational cost, with
offering the best profit performance at the expense of increased computation time.
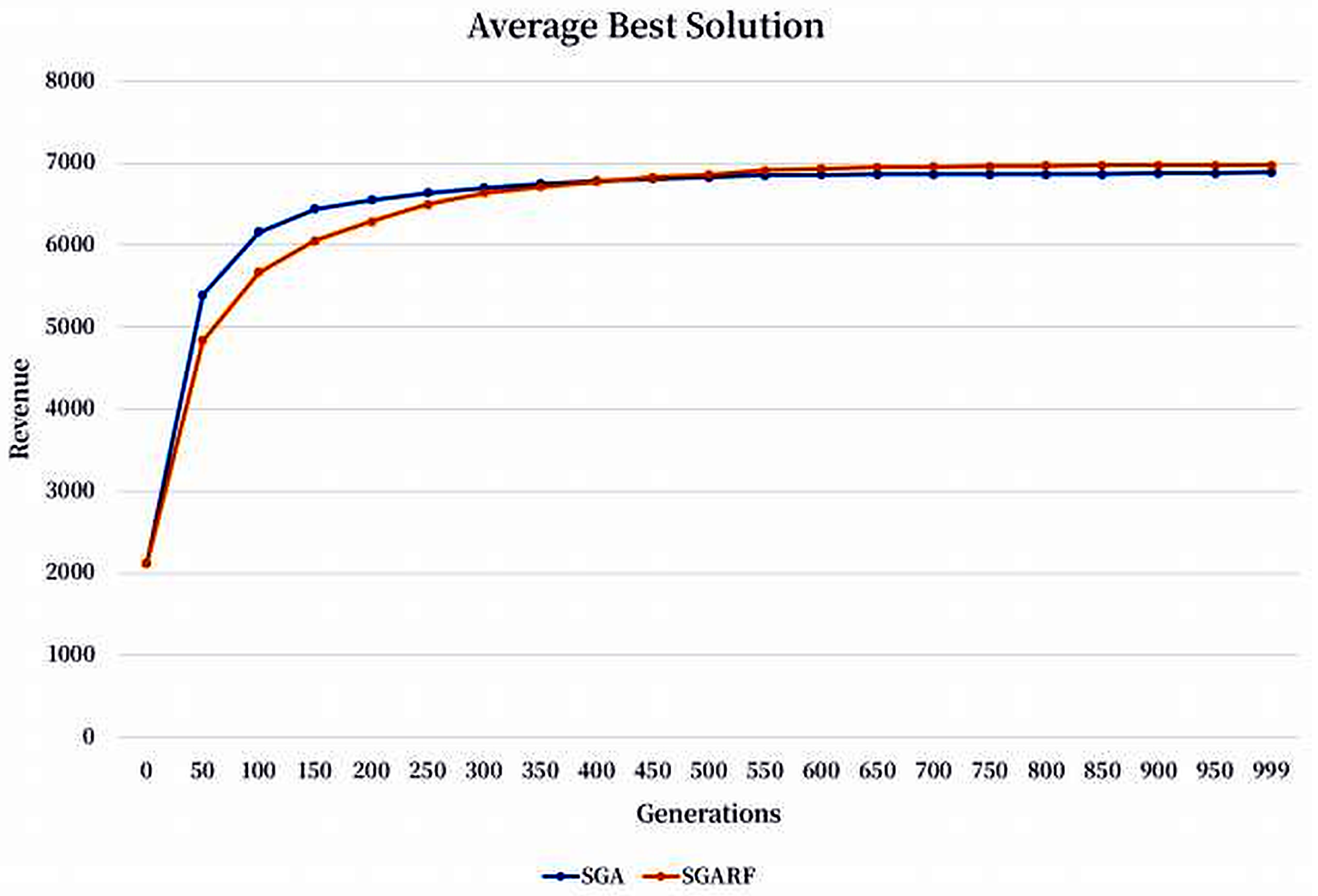
To evaluate the generation-by-generation performance of the proposed
against the baseline SGA, we ran each algorithm 10 times on the first replication of the instance of 50 orders, 10 machines, and instance replication as an example. We recorded the best objective value from each run and plotted the results over generations. Initially, due to insufficient training data for the random forest algorithms, the performance of
was inferior to that of SGA. However, as generations progressed and more data became available,
consistently outperformed SGA and achieved superior final results, as illustrated in
Figure 8.
4.3. Advanced Design
To reduce computational cost without compromising output quality, we implemented a modified design that reduces the number of RF executions during surrogate model training. The effectiveness of this approach was evaluated through a two-factor ANOVA and post-hoc tests.
According to
Table 10, the effect of the RF method (original vs. reduced generation) was not statistically significant (
), and no meaningful difference was found in
Table 11, where both methods were assigned to the same group. This confirms that reducing the training frequency does not negatively affect revenue outcomes.
However, in terms of computational time, the impact was substantial. As shown in
Table 12, the RF method factor yielded a highly significant difference (
), and the post-hoc analysis in
Table 13 revealed that the
had significantly lower mean computation time and was classified into a separate group. These results indicate that the modified approach significantly improves efficiency while maintaining revenue performance.
Finally, by deferring RF retraining until generation 900,
cuts total surrogate-training time by roughly 20.96% while incurring less than a 0.01% drop in final profit. This substantial reduction in training overhead suggests that, in a real-time scheduling setting. Besides, one could similarly postpone or trigger RF updates only at key milestones (or upon sufficient new data) according to
Figure 8 by balancing computational load and solution quality.
4.4. Discussion
The experimental results demonstrate that the
is an evolutionary search, guided by a random-forest surrogate, consistently yielding the highest profit across almost all benchmark categories. Its advantage becomes more pronounced as instance size and the PSD coefficient
b increase. Large instances with strong past-sequence effects produce a rugged, highly non-linear objective surface on which conventional GAs (with or without local search) and the stochastic-annealing-based SABPO are prone to wander. In contrast, the ensemble predictions generated by the random forest smooth local noise and provide a low-cost proxy for marginal profit, allowing the algorithm to discard weak offspring early and to intensify exploration around elite regions. The adaptive learning layer therefore converts a fixed evaluation budget into a denser sampling of promising neighborhoods, explaining why
dominates on medium- and large-scale cases (
Table 14 and
Table 15) while offering only marginal gains on the smallest two 10-job sets, where the search space is already tractable.
A second observation is that the surrogate retains its edge after PSD is activated—even though PSD compresses due-date slack, forces additional order rejections, and steepens the fitness landscape. The ensemble structure of the random forest mitigates over-fitting to any single ridge or basin and thus preserves robustness. Meanwhile, the local-search variant narrows the gap with in terms of CPU time but cannot match its profit because it lacks a learning mechanism; it merely exploits neighborhood moves around incumbent solutions. The plain SGA shares the same genetic backbone but spends many evaluations on low-quality chromosomes because all fitness values are computed exactly, with no predictive screening. SABPO fares worst in profit because its simulated-annealing acceptance criterion is less selective and its temperature schedule is not dynamically tuned to PSD-induced ruggedness.
The principal trade-off is computational cost: training and querying the random-forest model enlarges runtime by roughly one order of magnitude relative to the baseline GA. Nonetheless, even the longest mean CPU time (about 30 s for and 23 s for ) remains acceptable for off-line production planning and could be reduced through parallel tree construction or incremental learning. In practice, the choice of algorithm should reflect the planner’s priorities. If maximizing profit is paramount (e.g., for high-margin build-to-order environments) the surrogate-enhanced approach is justified. If real-time responsiveness outweighs marginal profit, we could design a Parallel RF construction: random forest trees can be built in parallel across multiple cores. Alternatively, the planners could directly adopt the tuned SGA or SABPO to provide faster, though less lucrative, alternatives, while offers a middle ground.
Finally, the sensitivity study on b suggests that higher PSD penalties amplify the value of learning-guided search; future work may investigate adaptive adjustment of b and online surrogate retraining to cope with dynamic shop-floor conditions.
5. Conclusions
This study developed a PFSS framework integrated with PSD setup time to solve the PFSS problem with order acceptance under the conditions of limited capacity and due-date penalties. In PFSS frameworks integrated with conventional sequence-dependent setup time, the time required for switching between consecutive jobs is considered to be fixed. However, in real production lines, jobs that appear later in the production sequence often have longer setup time because of resource fatigue. The PSD setup time captures this phenomenon through the addition of a constant proportion of the cumulative processing time for prior orders to each new order. Thus, the integration of PSD setup time into a PFSS framework results in more accurate predictions of completion times. Although the PSD setup time has been used in single and parallel-machine settings, this study is the first to integrate it into PFSS with order acceptance.
To evaluate the impact of PSD setup time on the developed framework, we tested an SGA, an LS-enhanced SGA (), an SGA coupled with an RF surrogate model (), and the SABPO algorithm. The first three algorithms were designed in the present study, and all algorithms were tested on the PFSS-OAWT benchmark dataset, with evaluations conducted in each case. The performance of these algorithms was assessed in terms of total profit and runtime. When PSD setup time was not incorporated into the aforementioned algorithms, the order of the algorithms in terms of total profit was as follows: > > SGA > SABPO. Moreover, their order in runtime was as follows: SGA < < SABPO < . Thus, although provided the highest profit, it also had the longest runtime.
We also found that the incorporation of PSD setup time did not change the aforementioned orders. remains as the most profitable algorithm, confirming its robustness under realistic setup assumptions. The use of PSD setup time reduced the available slack, thus forcing the rejection of some late orders, which reduced the absolute profit compared to that provided by the baseline algorithms. Nevertheless, the surrogate ML model (RF model) still guided the search toward higher-quality solutions, thereby mitigating loss.
Our PSD-aware PFSS-OAWT model captures sequence-dependent increases in setup time in semiconductor wafer fabrication, such as chamber cleans and calibrations that lengthen with each processed lot—allowing selective acceptance and optimized sequencing of high-value lots to minimize weighted tardiness. It similarly addresses the cumulative cleaning and calibration delays in automotive paint and assembly lines by rejecting low-margin jobs and arranging accepted jobs to balance throughput and on-time delivery. In both domains, leverages a two-zone encoding of accepted and rejected jobs to preserve flexibility and enhance solution quality under history-dependent setup growth.
Overall, our findings indicate that surrogate ML models, such as RF, can substantially improve the performance of classical heuristic and evolutionary solvers in scheduling problems. Future studies can combine more advanced learning models (e.g., XGBoost and deep neural networks) with other metaheuristic algorithms (e.g., ant colony optimization or particle swarm optimization). XGBoost’s gradient-boosting trees can better capture rare, high-profit order combinations by sequentially correcting residual errors, and deep neural networks can model temporal correlations in streaming job data. Moreover, there are some limitations in this paper. For example, this paper is confined to static, offline scheduling where all jobs are known in advance. We may extend the developed framework to settings involving dynamic orders and multi-objective balancing multiple metrics (e.g., energy consumption, resource utilization, and etc). In summary, despite the complexity introduced by PSD setup time, the proposed framework provides stable, high-quality scheduling results. It can be implemented in practical scenarios and may serve as a reference for future research.
Author Contributions
Conceptualization, Y.-Y.Z. and S.-H.C.; methodology, Y.-Y.Z. and S.-H.C.; software, C.-H.Y.; validation, Y.-Y.Z. and Y.-W.W.; formal analysis, Y.-Y.Z.; investigation, Y.-Y.Z.; resources, Y.-W.W.; data curation, Y.-Y.Z.; writing—original draft preparation, C.-H.L.; writing—review and editing, S.-H.C.; visualization, Y.-Y.Z. and S.-H.C.; supervision, S.-H.C.; project administration, S.-H.C.; funding acquisition, S.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science and Technology Council. (Grant number: NSTC 106-2221-E-230-009- and NSTC 113-2221-E-032-022-).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Acknowledgments
This study gratefully acknowledges the support received from the National Science and Technology Council [Grant numbers: NSTC 106-2221-E-230-009 and NSTC 113-2221-E-032-022].
Conflicts of Interest
Author Yu-Yan Zhang was employed by the ChungPeng Intelligence Services Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PFSS | Permutation Flow-Shop Scheduling |
| OAS | Order Acceptance Scheduling |
| PSD | Past-Sequence-Dependent |
| SGA | Simple Genetic Algorithm |
| SGA with Local Search |
| SGA with Random Forest |
| RF | Random Forest |
| ML | Machine Learning |
| SABPO | Simulated Annealing-Based Permutation Optimization |
| LS | Local Search |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| MAs | Memetic Algorithms |
| MILP | Mixed-Integer Linear Programming |
| SDST | Sequence-Dependent Setup Time |
| ELM | Extreme Learning Machine |
| RL | Reinforcement Learning |
| NEH | Nawaz–Enscore–Ham heuristic |
References
- Bartal, Y.; Leonardi, S.; Marchetti-Spaccamela, A.; Sgall, J.; Stougie, L. Multiprocessor scheduling with rejection. SIAM J. Discret. Math. 2000, 13, 64–78. [Google Scholar] [CrossRef]
- Xiao, Y.Y.; Zhang, R.Q.; Zhao, Q.H.; Kaku, I. Permutation flow shop scheduling with order acceptance and weighted tardiness. Appl. Math. Comput. 2012, 218, 7911–7926. [Google Scholar] [CrossRef]
- Wang, X.; Xie, X.; Cheng, T. A modified artificial bee colony algorithm for order acceptance in two-machine flow shops. Int. J. Prod. Econ. 2013, 141, 14–23. [Google Scholar] [CrossRef]
- Lei, D.; Tan, X. Shuffled frog-leaping algorithm for order acceptance and scheduling in flow shop. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 9445–9450. [Google Scholar]
- Wang, J.; Zhuang, X.; Wu, B. A New Model and Method for Order Selection Problems in Flow-Shop Production. In Optimization and Control for Systems in the Big-Data Era; Springer: Cham, Switzerland, 2017; pp. 245–251. [Google Scholar]
- Rahman, H.F.; Sarker, R.; Essam, D. A real-time order acceptance and scheduling approach for permutation flow shop problems. Eur. J. Oper. Res. 2015, 247, 488–503. [Google Scholar] [CrossRef]
- Lei, D.; Guo, X. A parallel neighborhood search for order acceptance and scheduling in flow shop environment. Int. J. Prod. Econ. 2015, 165, 12–18. [Google Scholar] [CrossRef]
- Rahman, H.F.; Sarker, R.; Essam, D. Multiple-order permutation flow shop scheduling under process interruptions. Int. J. Adv. Manuf. Technol. 2018, 97, 2781–2808. [Google Scholar] [CrossRef]
- Chen, S.H.; Liou, Y.C.; Chen, Y.H.; Wang, K.C. Order acceptance and scheduling problem with carbon emission reduction and electricity tariffs on a single machine. Sustainability 2019, 11, 5432. [Google Scholar] [CrossRef]
- Wang, J.B. Single-machine scheduling with past-sequence-dependent setup times and time-dependent learning effect. Comput. Ind. Eng. 2008, 55, 584–591. [Google Scholar] [CrossRef]
- Yin, Y.; Xu, D.; Wang, J. Some single-machine scheduling problems with past-sequence-dependent setup times and a general learning effect. Int. J. Adv. Manuf. Technol. 2010, 48, 1123–1132. [Google Scholar] [CrossRef]
- Mani, V.; Chang, P.C.; Chen, S.H. Single-machine scheduling with past-sequence-dependent setup times and learning effects: A parametric analysis. Int. J. Syst. Sci. 2011, 42, 2097–2102. [Google Scholar] [CrossRef]
- Koulamas, C.; Kyparisis, G.J. Single-machine scheduling problems with past-sequence-dependent setup times. Eur. J. Oper. Res. 2008, 187, 1045–1049. [Google Scholar] [CrossRef]
- Buche, D.; Schraudolph, N.N.; Koumoutsakos, P. Accelerating evolutionary algorithms with Gaussian process fitness function models. IEEE Trans. Syst. Man Cybern. Part C 2005, 35, 183–194. [Google Scholar] [CrossRef]
- Chugh, T.; Jin, Y.; Miettinen, K.; Hakanen, J.; Sindhya, K. A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization. IEEE Trans. Evol. Comput. 2018, 22, 129–142. [Google Scholar] [CrossRef]
- Díaz-Manríquez, A.; Toscano-Pulido, G.; Gómez-Flores, W. On the selection of surrogate models in evolutionary optimization algorithms. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 2155–2162. [Google Scholar]
- Peng, H.; Wang, W. Adaptive surrogate model based multi-objective transfer trajectory optimization between different libration points. Adv. Space Res. 2016, 58, 1331–1347. [Google Scholar] [CrossRef]
- Wang, H.; Jin, Y.; Jansen, J.O. Data-Driven Surrogate-Assisted Multiobjective Evolutionary Optimization of a Trauma System. IEEE Trans. Evol. Comput. 2016, 20, 939–952. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, W.; Wang, Y. Hybrid evolutionary algorithm with extreme machine learning fitness function evaluation for two-stage capacitated facility location problems. Expert Syst. Appl. 2017, 71, 57–68. [Google Scholar] [CrossRef]
- Bora, T.C.; Mariani, V.C.; dos Santos Coelho, L. Multi-objective optimization of the environmental-economic dispatch with reinforcement learning based on non-dominated sorting genetic algorithm. Appl. Therm. Eng. 2019, 146, 688–700. [Google Scholar] [CrossRef]
- Ko, Y.D. An efficient integration of the genetic algorithm and the reinforcement learning for optimal deployment of the wireless charging electric tram system. Comput. Ind. Eng. 2018, 128, 851–860. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; He, C.; Zhang, Y.; Li, F.; Song, X. A surrogate-assisted multi-objective evolutionary algorithm with multiple reference points. Expert Syst. Appl. 2025, 294, 128670. [Google Scholar] [CrossRef]
- Han, X.Y.; Wang, P.; Dong, H.; Wang, X. Data-driven multi-phase constrained optimization based on multi-surrogate collaboration mechanism and space reduction strategy. Appl. Soft Comput. 2025, 180, 113359. [Google Scholar] [CrossRef]
- Esmaeilbeigi, R.; Charkhgard, P.; Charkhgard, H. Order acceptance and scheduling problems in two-machine flow shops: New mixed integer programming formulations. Eur. J. Oper. Res. 2016, 251, 419–431. [Google Scholar] [CrossRef]
- Wang, X.; Xie, X.; Cheng, T. Order acceptance and scheduling in a two-machine flowshop. Int. J. Prod. Econ. 2013, 141, 366–376. [Google Scholar] [CrossRef]
- Zaied, A.N.H.; Ismail, M.M.; Mohamed, S.S. Permutation flow shop scheduling problem with makespan criterion: Literature review. J. Theor. Appl. Inf. Technol. 2021, 99, 830–848. [Google Scholar]
- Lee, S.J.; Kim, B.S. An Optimization Problem of Distributed Permutation Flowshop Scheduling with an Order Acceptance Strategy in Heterogeneous Factories. Mathematics 2025, 13, 877. [Google Scholar] [CrossRef]
- Li, T.; Li, J.Q.; Chen, X.L.; Li, J.K. Solving distributed assembly blocking flowshop with order acceptance by knowledge-driven multiobjective algorithm. Eng. Appl. Artif. Intell. 2024, 137, 109220. [Google Scholar] [CrossRef]
- Slotnick, S.A.; Morton, T.E. Order acceptance with weighted tardiness. Comput. Oper. Res. 2007, 34, 3029–3042. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of flowshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C.; Alcaraz, J. Solving the flowshop scheduling problem with sequence dependent setup times using advanced metaheuristics. Eur. J. Oper. Res. 2005, 165, 34–54. [Google Scholar] [CrossRef]
- Kuo, W.H.; Yang, D.L. Single machine scheduling with past-sequence-dependent setup times and learning effects. Inf. Process. Lett. 2007, 102, 22–26. [Google Scholar] [CrossRef]
- Mosheiov, G. A note on scheduling deteriorating jobs. Math. Comput. Simul. 2005, 41, 883–886. [Google Scholar] [CrossRef]
- Kalaki Juybari, J.; Kalaki Juybari, S.; Hasanzadeh, R. Parallel machines scheduling with exponential time-dependent deterioration, using meta-heuristic algorithms. SN Appl. Sci. 2021, 3, 333. [Google Scholar] [CrossRef]
- Choi, B.C.; Kim, E.S.; Lee, J.H. Scheduling step-deteriorating jobs on a single machine with multiple critical dates. J. Oper. Res. Soc. 2024, 75, 2612–2625. [Google Scholar] [CrossRef]
- Shi, H.N.; Ma, T.; Chu, W.X.; Wang, Q.W. Optimization of inlet part of a microchannel ceramic heat exchanger using surrogate model coupled with genetic algorithm. Energy Convers. Manag. 2017, 149, 988–996. [Google Scholar] [CrossRef]
- Pan, L.; He, C.; Tian, Y.; Wang, H.; Zhang, X.; Jin, Y. A Classification Based Surrogate-Assisted Evolutionary Algorithm for Expensive Many-Objective Optimization. IEEE Trans. Evol. Comput. 2018, 23, 74–88. [Google Scholar] [CrossRef]
- Chang, P.C.; Hsieh, J.C.; Chen, S.H.; Lin, J.L.; Huang, W.H. Artificial chromosomes embedded in genetic algorithm for a chip resistor scheduling problem in minimizing the makespan. Expert Syst. Appl. 2009, 36, 7135–7141. [Google Scholar] [CrossRef]
- Li, C.; Tao, Y.; Ao, W.; Yang, S.; Bai, Y. Improving forecasting accuracy of daily enterprise electricity consumption using a random forest based on ensemble empirical mode decomposition. Energy 2018, 165, 1220–1227. [Google Scholar] [CrossRef]
- Johannesen, N.J.; Kolhe, M.; Goodwin, M. Relative evaluation of regression tools for urban area electrical energy demand forecasting. J. Clean. Prod. 2019, 218, 555–564. [Google Scholar] [CrossRef]
- Chen, S.H.; Chen, M.C. Addressing the advantages of using ensemble probabilistic models in estimation of distribution algorithms for scheduling problems. Int. J. Prod. Econ. 2013, 141, 24–33. [Google Scholar] [CrossRef]
- Tang, L.; Liu, J.; Rong, A.; Yang, Z. A multiple traveling salesman problem model for hot rolling scheduling in Shanghai Baoshan Iron & Steel Complex. Eur. J. Oper. Res. 2000, 124, 267–282. [Google Scholar] [CrossRef]
- Lin, S.W.; Ying, K. Increasing the total net revenue for single machine order acceptance and scheduling problems using an artificial bee colony algorithm. J. Oper. Res. Soc. 2013, 64, 293–311. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
Figure 1.
Initial single-chromosome encoding. The gene background in yellow and red stand for accepted and rejected orders, respectively.
Figure 1.
Initial single-chromosome encoding. The gene background in yellow and red stand for accepted and rejected orders, respectively.
Figure 2.
Chromosome encoding after sorting and grouping of accepted and rejected jobs.
Figure 2.
Chromosome encoding after sorting and grouping of accepted and rejected jobs.
Figure 3.
Illustration of the local-search procedure.
Figure 3.
Illustration of the local-search procedure.
Figure 4.
Illustration of two-point crossover. The red lines refer to the cut-points.
Figure 4.
Illustration of two-point crossover. The red lines refer to the cut-points.
Figure 5.
RF-based selection of crossover offspring.
Figure 5.
RF-based selection of crossover offspring.
Figure 6.
Illustration of swap mutation by moving the gene positions.
Figure 6.
Illustration of swap mutation by moving the gene positions.
Figure 7.
RF-based selection of mutations.
Figure 7.
RF-based selection of mutations.
Figure 8.
Average best solution over generations for SGA and on a 50 orders and 10 machine instance.
Figure 8.
Average best solution over generations for SGA and on a 50 orders and 10 machine instance.
Table 1.
Advanced machine-learning-enhanced methods for optimization problem.
Table 1.
Advanced machine-learning-enhanced methods for optimization problem.
| Study | Problem and Method | Results |
|---|
| Peng and Wang [17] | A hybrid sampling-based adaptive surrogate model was proposed to minimize transfer time and fuel cost | 8.56× more Pareto-optimal solutions than baseline method; runtime reduced to 10.10% |
| Wang et al. [18] | Data-driven evolutionary algorithm (EA) for trauma resource allocation | Runtime reduced by ≈90%; method scalable to big data |
| Guo et al. [19] | ELM + evolutionary strategy for facility location | Mean deviation of 0.29; method outperformed tabu search and HFGA |
| Bora et al. [20] | NSGAII + reinforcement learning (RL) for solving the EELD problem | Method outperformed NPGA and; improved Pareto spread |
| Ko [21] | Genetic algorithm + RL for optimizing wireless charging buses | 0% gap from best-known solution; method found optimal deployment |
| Zhang et al. [22] | Surrogate-assisted MOEA with multi-reference-point strategy for discontinuous Pareto fronts | Achieved high-quality solutions on 20 benchmarks with lower computational cost |
| Han et al. [23] | Multi-surrogate collaborative optimization with space reduction strategy for black-box constrained problems | Outperformed three SOTA methods on 23 mathematical and 8 engineering benchmarks |
Table 2.
Processing times on 2 machines and due-dates for 4 jobs.
Table 2.
Processing times on 2 machines and due-dates for 4 jobs.
| Job i | | | Due-Date |
|---|
| 1 | 4 | 5 | 20 |
| 2 | 6 | 4 | 18 |
| 3 | 5 | 6 | 22 |
| 4 | 7 | 3 | 25 |
Table 3.
Completion times, due-dates, and acceptance decisions for the example sequence on 2 machines under PSD ().
Table 3.
Completion times, due-dates, and acceptance decisions for the example sequence on 2 machines under PSD ().
| Job i | | | Due-Date | Accepted |
|---|
| 2 | 6.0 | 10.0 | 18 | Yes |
| 4 | 13.6 | 17.0 | 25 | Yes |
| 1 | 18.3 | 23.6 | 20 | No |
| 3 | 23.7 | 30.2 | 22 | No |
Table 4.
Parameters of the random forest (RF) model.
Table 4.
Parameters of the random forest (RF) model.
| Parameter | Description |
|---|
| BagSizePercent | Size of each bootstrap sample as a percentage of the training set. |
| BatchSize | Number of instances processed per batch during prediction. |
| BreakTiesRandomly | Whether equal-importance ties should be broken through random feature selections. |
| CalcOutOfBag | Whether out-of-bag error should be computed. |
| ComputeAttributeImportance | Whether the importance score of EA should be output. |
| DoNotCheckCapabilities | Whether compatibility checks between data and model should be skipped. |
| MaxDepth | Maximum depth of each decision tree (prevents overfitting). |
| NumExecutionSlots | Number of parallel threads for model construction. |
| NumFeatures | Number of random features considered in each iteration. |
| NumIterations | Number of times to build trees. |
OutputOutOfBag
ComplexityStatistics | Whether complexity statistics should be produced for output samples. |
| Seed | Random seed for reproducibility. |
| StoreOutOfBagPredictions | Whether out-of-bag predictions should be stored for further analysis. |
Table 5.
Parameter settings for PSD experiments.
Table 5.
Parameter settings for PSD experiments.
| Parameter | Value (s) |
|---|
| b | 0.1, 0.2, 0.3 |
Table 6.
ANOVA table of profit values for four compared methods.
Table 6.
ANOVA table of profit values for four compared methods.
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|
| Orders | 149 | 4.12 × 1012 | 27,622,963,562 | 874,751.91 | 0 |
| Method | 3 | 2,242,973,707 | 747,657,902 | 23,676.5 | 0 |
| Orders* Method | 447 | 2,947,375,247 | 6,593,681 | 208.81 | 0 |
| Error | 17,400 | 549,458,153 | 31,578 | | |
| Total | 17,999 | 4.12 × 1012 | | | |
Table 7.
Post-hoc comparison for profit values.
Table 7.
Post-hoc comparison for profit values.
| Method | N | Mean | Grouping |
|---|
| 4500 | 16,957.2 | A |
| 4500 | 16,813.8 | B |
| SGA | 4500 | 16,807.9 | B |
| SABPO | 4500 | 16,056.2 | C |
Table 8.
ANOVA table of computation time for four compared methods.
Table 8.
ANOVA table of computation time for four compared methods.
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|
| Orders | 149 | 301,563 | 2024 | 11,639.35 | 0 |
| Method | 3 | 2,673,410 | 891,137 | 5,124,847.87 | 0 |
| Orders*Method | 447 | 386,580 | 865 | 4973.57 | 0 |
| Error | 17,400 | 3026 | 0 | | |
| Total | 17,999 | 3,364,579 | | | |
Table 9.
Post-hoc comparison table for method computation time.
Table 9.
Post-hoc comparison table for method computation time.
| Method | N | Mean | Grouping |
|---|
| 4500 | 29.7986 | A |
| SABPO | 4500 | 1.982 | B |
| 4500 | 1.5108 | C |
| SGA | 4500 | 1.4803 | D |
Table 10.
ANOVA table of revenue under reduced surrogate training frequency.
Table 10.
ANOVA table of revenue under reduced surrogate training frequency.
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|
| Orders | 149 | 2.13 × 1012 | 14,270,652,482 | 778,561.4 | 0 |
| Method | 1 | 4616 | 4616 | 0.25 | 0.616 |
| Orders*Method | 149 | 3,226,145 | 21,652 | 1.18 | 0.067 |
| Error | 8700 | 159,466,776 | 18,330 | | |
| Total | 8999 | 2.13 × 1012 | | | |
Table 11.
Post-hoc comparison table for revenue under reduced surrogate training frequency.
Table 11.
Post-hoc comparison table for revenue under reduced surrogate training frequency.
| Method | N | Mean | Grouping |
|---|
| RF | 4500 | 16,957.2 | A |
| 4500 | 16,955.7 | A |
Table 12.
ANOVA table of computation time under reduced surrogate training frequency.
Table 12.
ANOVA table of computation time under reduced surrogate training frequency.
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|
| Orders | 149 | 958,387 | 6432.1 | 12,812.84 | 0 |
| Method | 1 | 87,749 | 87,748.5 | 174,795.56 | 0 |
| Orders*Method | 149 | 26,013 | 174.6 | 347.78 | 0 |
| Error | 8700 | 4367 | 0.5 | | |
| Total | 8999 | 1,076,516 | | | |
Table 13.
Post-hoc comparison table for CPU time under reduced surrogate training frequency.
Table 13.
Post-hoc comparison table for CPU time under reduced surrogate training frequency.
| Method | N | Mean | Grouping |
|---|
| RF | 4500 | 29.8 | A |
| 4500 | 23.6 | B |
Table 14.
Descriptive statistics table of profit values.
Table 14.
Descriptive statistics table of profit values.
| | SABPO | SGA | | |
|---|
|
Orders
|
Min
|
Mean
|
Max
|
Min
|
Mean
|
Max
|
Min
|
Mean
|
Max
|
Min
|
Mean
|
Max
|
|---|
| p10x3_0 | 1733.2 | 1766.3 | 1769 | 1838.6 | 1862.7 | 1865.4 | 1838.6 | 1863.6 | 1865.4 | 1865.4 | 1865.4 | 1865.4 |
| p10x5_0 | 1034.9 | 1034.9 | 1034.9 | 1263.3 | 1273.7 | 1285.8 | 1263.3 | 1275.3 | 1285.8 | 1285.8 | 1285.8 | 1285.8 |
| p10x10_0 | 659.7 | 659.7 | 659.7 | 1031 | 1046.1 | 1046.6 | 1046.6 | 1046.6 | 1046.6 | 1046.6 | 1046.6 | 1046.6 |
| p30x3_0 | 4698.3 | 4954.6 | 5197.3 | 5336.7 | 5515.4 | 5598.7 | 5355.3 | 5528.1 | 5615.3 | 5549.3 | 5592.1 | 5619.1 |
| p30x5_0 | 3145.3 | 3656.8 | 3929.4 | 4658.6 | 4918.2 | 5045.1 | 4659.7 | 4858.7 | 5045.1 | 4857.1 | 5025.8 | 5045.1 |
| p30x10_0 | 1883.5 | 2416.6 | 2994.4 | 4406.8 | 4485.7 | 4552.1 | 4386 | 4471.9 | 4598.1 | 4492.2 | 4531.3 | 4600.4 |
| p50x3_0 | 8514.5 | 9161.3 | 9772.4 | 10,553 | 10,768 | 10,992 | 10,408 | 10,729 | 10,971 | 10,746 | 10,924 | 11,016 |
| p50x5_0 | 7507.8 | 8223.4 | 8537.7 | 10,221 | 10,572 | 10,849 | 10,293 | 10,566 | 10,813 | 10,581 | 10,767 | 10,936 |
| p50x10_0 | 4027.4 | 5009.3 | 5580.5 | 9089.2 | 9432.6 | 9687.3 | 9044.8 | 9450.2 | 9611.9 | 9390 | 9605.6 | 9813.7 |
| p100x3_0 | 17,563 | 18,939 | 19,257 | 20,275 | 21,082 | 21,656 | 20,551 | 21,092 | 21,486 | 21,148 | 21,529 | 21,886 |
| p100x5_0 | 13,541 | 14,547 | 14,973 | 17,429 | 18,063 | 18,633 | 17,516 | 18,012 | 18,668 | 18,443 | 18,769 | 19,111 |
| p100x10_0 | 9787 | 11,333 | 11,771 | 17,627 | 18,379 | 18,972 | 17,913 | 18,427 | 18,832 | 18,301 | 18,976 | 19,402 |
| p200x3_0 | 37,604 | 37,899 | 38,314 | 39,231 | 39,914 | 41,070 | 38,751 | 39,938 | 40,760 | 41,023 | 41,833 | 42,439 |
| p200x5_0 | 31,684 | 32,859 | 33,315 | 36,516 | 37,823 | 38,788 | 36,299 | 37,761 | 38,949 | 38,235 | 39,091 | 39,833 |
| p200x10_0 | 20,483 | 21,817 | 22,198 | 35,279 | 36,735 | 38,021 | 36,107 | 36,765 | 37,407 | 37,292 | 37,899 | 38,513 |
| Average | 10,924.4 | 11,618.5 | 11,953.6 | 14,317.0 | 14,791.4 | 15,204.1 | 14,362.2 | 14,785.6 | 15,130.3 | 14,950.4 | 15,249.4 | 15,494.1 |
Table 15.
Descriptive statistics table of computation time.
Table 15.
Descriptive statistics table of computation time.
| | | SABPO | | | SGA | | | | | | | |
|---|
|
Orders
|
Min
|
Mean
|
Max
|
Min
|
Mean
|
Max
|
Min
|
Mean
|
Max
|
Min
|
Mean
|
Max
|
|---|
| p10x3_0 | 0.14 | 0.15 | 0.17 | 0.17 | 0.30 | 0.52 | 0.20 | 0.30 | 0.55 | 24.55 | 30.91 | 36.39 |
| p10x5_0 | 0.19 | 0.19 | 0.20 | 0.17 | 0.22 | 0.28 | 0.23 | 0.28 | 0.31 | 21.91 | 22.73 | 23.52 |
| p10x10_0 | 0.28 | 0.30 | 0.33 | 0.36 | 0.38 | 0.42 | 0.31 | 0.34 | 0.38 | 22.86 | 23.65 | 24.50 |
| p30x3_0 | 0.27 | 0.28 | 0.31 | 0.55 | 0.58 | 0.61 | 0.50 | 0.54 | 0.58 | 14.98 | 15.23 | 15.44 |
| p30x5_0 | 0.70 | 0.73 | 0.75 | 0.59 | 0.64 | 0.69 | 0.52 | 0.59 | 0.64 | 15.06 | 15.28 | 15.52 |
| p30x10_0 | 1.13 | 1.20 | 1.31 | 0.75 | 0.79 | 0.81 | 0.70 | 0.76 | 0.81 | 15.13 | 15.36 | 15.55 |
| p50x3_0 | 0.59 | 0.65 | 0.70 | 0.78 | 1.26 | 1.90 | 0.75 | 0.91 | 1.60 | 30.48 | 35.72 | 41.05 |
| p50x5_0 | 0.63 | 0.66 | 0.77 | 0.94 | 0.99 | 1.03 | 0.83 | 0.91 | 0.95 | 26.97 | 27.73 | 28.34 |
| p50x10_0 | 1.17 | 1.21 | 1.27 | 1.19 | 1.24 | 1.34 | 1.08 | 1.18 | 1.28 | 25.63 | 26.58 | 27.30 |
| p100x3_0 | 0.78 | 0.82 | 0.95 | 1.64 | 1.74 | 1.81 | 1.56 | 1.65 | 1.70 | 31.78 | 32.70 | 33.38 |
| p100x5_0 | 1.25 | 1.43 | 1.58 | 1.84 | 1.92 | 2.03 | 1.55 | 1.66 | 1.77 | 32.70 | 33.24 | 33.94 |
| p100x10_0 | 4.23 | 4.41 | 4.53 | 2.33 | 2.43 | 2.63 | 1.83 | 2.04 | 2.25 | 33.22 | 33.83 | 34.45 |
| p200x3_0 | 2.92 | 3.03 | 3.13 | 2.75 | 2.90 | 3.06 | 3.27 | 3.43 | 3.58 | 47.31 | 49.59 | 50.88 |
| p200x5_0 | 4.89 | 5.06 | 5.14 | 3.11 | 3.31 | 3.44 | 3.66 | 3.85 | 4.16 | 49.45 | 50.46 | 51.45 |
| p200x10_0 | 10.06 | 10.27 | 10.42 | 4.08 | 4.36 | 4.67 | 4.24 | 4.60 | 4.88 | 50.36 | 51.50 | 52.42 |
| Average | 1.95 | 2.03 | 2.10 | 1.42 | 1.54 | 1.68 | 1.41 | 1.54 | 1.70 | 29.49 | 30.97 | 32.27 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).